- Department of Society and Infrastructure, GNS Science, Lower Hutt, New Zealand
This paper presents a generalization of the bias-variance tradeoff applied to the recent trend toward natural multi-hazard risk assessment. The bias-variance dilemma, a well-known machine learning theory, is presented in the context of natural hazard modeling. It is then argued that the bias-variance statistical concept can provide an analytical framework for the necessity to direct efforts toward systemic risk assessment using multi-hazard catastrophe modeling and inform future mitigation practices.
1 Introduction
Several examples of severe compounded impact from complex natural hazards interplay have occurred over the last decades. A few examples over such a limited timeline are the 2011 Tohoku earthquake and tsunami in Japan (Shibahara, 2011), the 2015 Gorkha (Kargel et al., 2016; Gautam, 2018) and 2016 Kaikoura earthquake (Dunant et al., 2021b; Jibson et al., 2018) with landslide and landslide dam events in Nepal and New Zealand respectively, the 2018 Sulawesi earthquake and subsequent tsunamis and liquefaction in Indonesia (Widiyanto et al., 2019) and the 2019 Cyclone Idai with catastrophic consequences due to strong winds and flooding (Chatiza, 2019; Devi, 2019). Already in 2005, a World bank report pointed out that approximately “3.8 million square kilometres and 790 million people are relatively highly exposed to at least two hazards. About 0.5 million square kilometres and 105 million people are relatively highly exposed to three or more hazards” (Dilley, 2005). In their paper, de Ruiter et al. (2020) mention that the “current state-of-the art risk assessment models” are not adequate anymore for dynamic and interacting hazards. Even though the Sendai Framework for Disaster Risk Reduction mentioned the need to assess the risks from “all hazards” (UNISDR, 2015) which echoes the previous Hyogo Framework for Action (UNISDR, 2005) as well as several acknowledgments by the scientific community (Kappes et al., 2012; Gill and Malamud, 2014; Alexander and Pescaroli, 2019), quantitative risk assessments of complex multi-hazard interplay are rare (Kappes et al., 2012). Natural hazard risk assessment are still frequently done through a “field of study” lens whereby experts would base the risk assessment on a specific hazard in their dedicated area of expertise (e.g., earthquake for seismologists). Quantitative risk assessment is usually a statistical endeavour and this paper will show how a statistical concept, the bias-variance dilemma, can inform the discussion on the future needs for natural hazard modeling. While the first part of this paper will be an introduction to multi-hazard risk models and the bias-variance dilemma, the Discussion will focus on generalizing the concept to the quantification of risk from natural hazard and its impact on disaster preparedness. Generalizing the bias-variance dilemma to the natural multi-hazard domain, might provide new insights, pragmatic perspectives and meaningful discussions on effort allocation toward quantitative hazard risk assessment.
2 Multi-Hazard Models
Many current risk studies still consider hazard in isolation, where the risk to exposed elements is sourced from one hazard in isolation also referred to as “single hazard” models (Gill and Malamud, 2014). As mentioned in the Introduction, disaster risk authorities and scientist pointed out the shortcoming of considering the hazards in silos (AghaKouchak et al., 2018; Arosio et al., 2018). In an effort to answer this call, and because of the difficulty inherent in considering interwoven hazards (Liu et al., 2015), current multi-hazard studies largely rely on semi-quantitative studies to assess the risk from multi-hazard (e.g., using indices, indexes) (Kappes et al., 2012). But a probabilistic quantification of the multi-hazard risk is often required to provide guidance on the allocation of resources to alleviate the risk. Recent studies are trying to find applicable ways to answer this complex challenge by considering natural hazards as part of an interconnected system (Mignan et al., 2014; Arosio et al., 2018; Dunant et al., 2021a; Dunant et al., 2021b). Few publications actually compare the results of single hazard models and multi-hazard models to generalise the argument for multi-hazard models. It can be understood as the hazard landscape can vary widely, a localized case study comparison would hardly be a valid argument. Following this limitation and in line with the argument of many risk scientists (Gill and Malamud, 2016; AghaKouchak et al., 2018), the following paragraphs are an attempt to frame, using an analytic approach, why single hazard model could distort the risk output and why multi-hazard modeling is necessary for more appropriate mitigation measures.
3 The Bias-Variance Dilemma
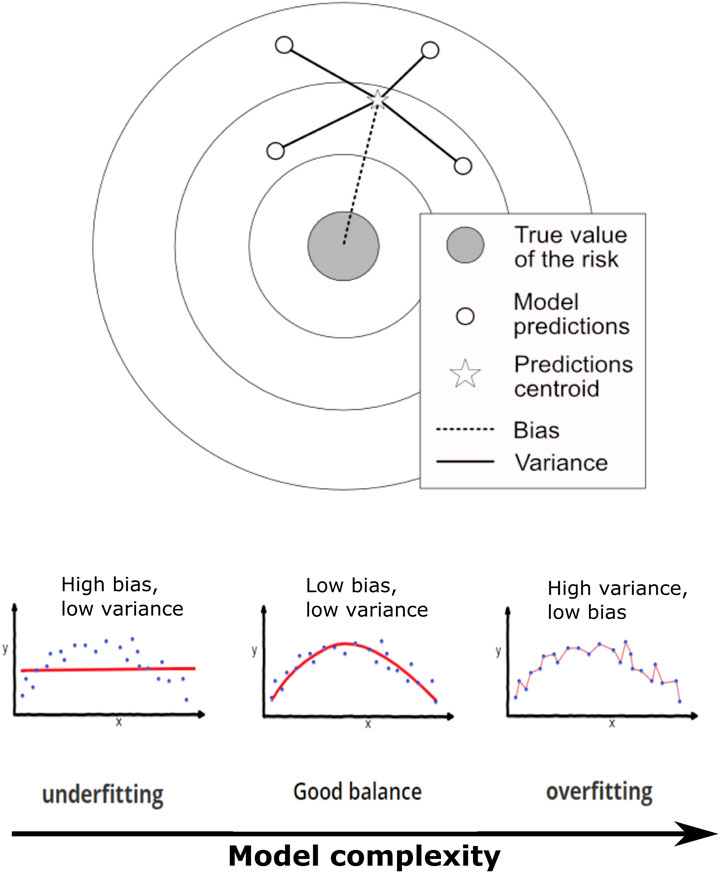
The concept originated from Geman et al. (1992), which shows that when an attempt is made to infer results from a stochastic prediction, a tradeoff is required between a model’s ability to maximize accuracy (minimize bias) and precision (minimize variance). The bias error would be the error between the exact value that is to be predicted and the value predicted by the model. In the case of a stochastic event set, the variance would be the spread between the different realizations of this predictive event set. To clarify what the bias and variance represent, a graphical representation is often used, where model predictions are attempting to reach an ideal case at the center of a target (Figure 1).
In Figure 1, the center of the target represents, for the purpose of the paper herein, the true value of the risk from “all hazards” (UNISDR, 2015) with a perfect model and an infinity of data point to calibrate it. The points on the target represent the attempts to aim at - or predict - the center of the target (via modeling in this case). The variance is represented as the distance between the centroid point of the predicted results whilst the bias is the distance between the centroid and the true value targeted. The center of the target would represent a bias and variance approaching 0. The concept of bias-variance is often used in machine learning and neural networks when trying to establish the best fit between a function and a reference dataset in order to minimize the error on the prediction. Bias-variance and a value representing the aleatory uncertainty of the system (a proxy to the “irreducible error”) are used to estimate (and hopefully minimize) the mean squared error following Equations 1, 2 (Geman et al., 1992; Hastie et al., 2009; Fortmann-Roe, 2012).
formally expressed as:
with Err(x) being the square prediction error at x by
Varying complexity of a stochastic model and data availability will translate in a tradeoff between minimizing bias and minimizing variance. In the context of artificial intelligence and machine learning this effect is referred to as underfitting when bias is too high or overfitting when variance is too high (Fortmann-Roe, 2012) (Figure 1). In simplistic terms, the four possible fringe combinations of the bias-variance states are low bias-low variance, low bias-high variance, high bias-high variance, and high bias-low variance. The ideal case - better predictability of the model - is low bias-low variance. Conversely, the worst case scenario is high bias-high variance. Intermediary states are high bias-low variance and low bias-high variance. As illustrated by Figure 1, correct prediction and modeling become a balancing act between too much complexity (overfitting-high variance) and not enough complexity (underfitting-high bias).
4 Discussion: Bias-Variance Perspective on Multi-Hazard Risk Assessments
4.1 Why Should We Bother With Multi-Hazard Risk Assessment?
The recent push to develop a more holistic approach to natural hazard assessment (multi-hazard) can be informed and, as the following paragraphs will try to demonstrate, supported by a generalization of the bias-variance concept. Despite the primary focus of this concept on machine learning related topics, the bias-variance tradeoff has been generalized outside its core contribution before, notably in scientific publication, to inform debates on topic such as education (Doroudi, 2020), cognition (Dwivedi et al., 2020), and pathology (Rashidi et al., 2019). To the author’s knowledge, it has not been used to inform the discussion on the evolution and direction of the research for natural hazard quantitative risk.
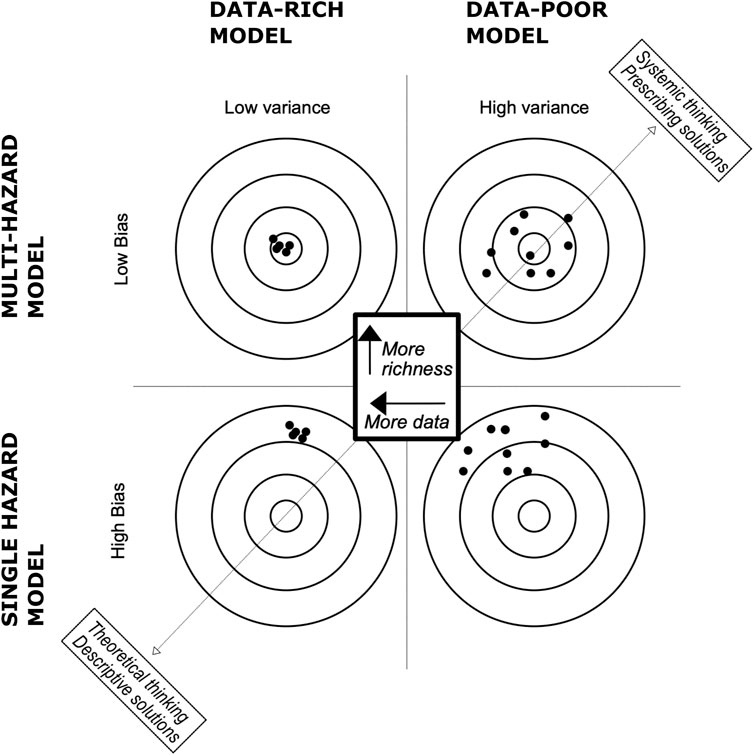
Several solutions have been proposed to decrease either bias or variance in order to improve model predictability. As a biased model is inclined towards some particular feature to predict the result (e.g., single hazard model in a multi-hazard environment are highly biased and high/low variance depending on the data availability), the remediation pass by the use of a broader scoping and an increase in complexity of the model (e.g., multi-hazard considered). On the other hand, high variance models are too broad in scope and require a more constrained model by, generally, the addition of more data (Figure 2) (Fortmann-Roe, 2012). Those options provide the basis for possible improvement of the risk modeling.
In the attempt to prepare for natural disasters, scientists attempt to simplify the problem at hand by providing explanation in terms of ever smaller entities. This process is also known as reductionism (Fang and Casadevall, 2011). In the context of earth sciences, this is represented by the division of the natural risk “system” into technical specialties (e.g., seismology, geomorphology, hydrology etc.). Those subsystems are easier to analyse and led to successful mitigation of natural disasters through engineering, policy, and planning. The direct consequence of reductionism to the topic presented herein is that current hazard related risk assessment treats the natural phenomena (hazards) mostly in isolation. In the context of the bias-variance perspective, “single-hazard” methods can be considered highly biased as isolation of phenomena leads to the omission of relational behaviours, causal processes, and their resulting emergent properties [e.g., risk amplification (Mignan et al., 2014; Mignan and Wang, 2020)]. From this perspective, using multi-hazard ensembles seems to be a valuable proposition for the future of risk assessment as the added complexity and richness (meaning gathering of data of different types as opposed to data gathering of the same type) (Figure 2) would lead to a reduction of the bias and predictive model closer to the “ground truth” [not dissimilar to “ensemble learning” approaches in machine learning (Opitz and Maclin, 1999)]. The use of biased single hazard models is therefore not considered an issue as long as they are part of a risk ensemble aimed at assessing the “true” risk. This notion reverts to the “micro-worlds” from Minsky and Papert (1972) [referred to as “highly developed (schematic) model of many phenomena”] where a set of biased model can be used to lower the ensemble bias at the expense of higher variance.
Low variance models, even though a solid option in a data rich environment, might prove to be difficult to access in the context of natural hazards. Natural hazard occurrences follow universally a power law linking probability of exceedance to intensity of phenomena (Malamud and Turcotte, 1999; Corral and González, 2019). Hence, it would indicate that the opportunities for data gathering decrease exponentially with the risk of damage or casualties (as higher intensity hazards are more likely to cause physical damage). If high intensity natural hazard data is harder to get, it would imply that the capacity to reduce the variance for hazard related risk models is bounded by the occurrence of severe events. This point can relate to the concept of the “costs of information search” (Stigler, 1961) in economics where an optimal behaviour is bounded by access to information/data. Data gathering should, obviously, remain of prime importance as the ultimate aim is still a low bias-low variance model. But, progress toward lower variance modeling will likely be slower than lower bias solutions when dealing with “long tail” natural processes.
The explanation from the previous paragraphs gives a hint that, in the near term, it would be easier to achieve progress through more accurate but less consistent (low bias-high variance) models driven by complexity and system thinking than consistent models with less accuracy (high bias-low variance) where progress is data-driven.
Lower bias methods can provide interesting progress in coming risk studies, but limitations will also appear. As the variance and complexity of the model increases, the risk of overfitting the data escalates too and the prediction of the model becomes less effective (Figure 2) (Fortmann-Roe, 2012). So, if multi-hazard modeling tends to approach more the true nature of the risk than current single hazard models, we have to be wary that too much complexity might impair the precision of our multi-hazard models in the future and a healthy medium between accuracy (bias) and precision (variance) would need to be found. This would call for effort in quantifying the relationship between model complexity and risk (Figure 2).
Not all landscape and environments are sensitive to multi-hazard in the same way. A bias-variance perspective can help to identify multi-hazard prone environment. From a bias-variance perspective, if the lower bias risk model gives the same results as the higher bias risk model, then we are probably not facing a multi-hazard problem (or the parameters influencing the risk have not been properly mapped out).
4.2 Unbiased Preparedness
The bias-network dilemma can also inform the action and preparedness to disasters. In a multi-hazard environment, single hazard model would not only strongly bias the risk assessment but, more dramatically, bias the action and response to such a model. As the risk assessment evolve toward complex risk assessments (lower bias hazard model), the solution space widens also as more scenarios need to be accounted for (lower bias “solution model”). Indeed, multi-hazard models can help generate “knowledge ensembles” (Spiro et al., 1991) as a direct consequence of a broader representation of the risk through complex model architecture. Lower bias models (multi-hazard models), because they are navigating outside bounded disciplines and theories, could potentially offer an easier access to “out-of-the-box” and innovative solutions. This point assumes that the “solution space” would be intrinsically correlated to the “problem space.” For example, let’s assume that a risk assessment focuses on earthquake hazard leading to the conclusion that retrofitting is the best option, while under the threat of earthquake and landslides, a combination of retrofitting and relocation would become the best option -as the “problem space” widens so does the “solution space.” We could then argue that a multi-hazard context (previously referred as problem space) give opportunities to develop synergistic solutions (win-win situations) against a wide spectrum of hazards.
It is also plausible that under a richer risk modeling framework-using a wider hazard spectrum-mitigation to unplanned disaster happens as a serendipitous consequence. To illustrate this point, let’s imagine an example based on the 2008 Wenchuan earthquake in China which caused cascading effects, one of the most significant being the “Tangjiashan landslide dam, which was triggered by the Ms = 8.0 Wenchuan earthquake in 2008 in China (which) threatened 1.2 million people downstream of the dam. All people in Beichuan Town 3.5 km downstream of the dam and 197,000 people in Mianyang City 85 km downstream of the dam were evacuated 10 days before the breaching of the dam.” (Peng and Zhang, 2013). If we consider a risk assessment of the Beichuan Town undergone before the Wenchuan event, it is clear that a biased approach only including earthquake would have missed a large part of the actual events and a multi-hazard approach (less biased) would have been closer to predict a range of disasters inline with what happened. A multi-hazard approach (e.g., earthquake, landslide, and flood) would have led toward a synergistic response to multipolar disasters which, inadvertently, could prepare better against unpredicted events (for the sake of arguments, let’s depict the example of a large pollutant release in the JiangJiang river upstream of the Beichuan township).
5 Conclusion
The paper present an analytical argument to the state and future of natural hazard modeling from a generalization of the bias-variance tradeoff concept. A look back at the work done on machine learning and previous papers on the generalization of the concept provide an additional case to existing positions for multi-hazard modeling as a standard to natural hazard risk assessment. The paper points out that achieving lower variance and data-driven related improvement might prove difficult because of the power law distribution of natural hazards. On the other hand, the implementation of lower bias multi-hazard models are relatively new to risk modeling and could still be a low-hanging fruit for rapid and significant improvement. An added, and concealed, advantage of a systemic, and multi-hazard models (low bias) to risk assessment is the possible emergence of new (synergistic) resilient solution outside existing frames of reference (high bias) and, also, positive serendipitous mitigations. A caveat still exists as excessively complex modeling will impair the predictability of multi-hazard risk models, hence the complexity of risk models should be studied further.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
GNS Science SSIF funding.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
AghaKouchak, A., Huning, L. S., Chiang, F., Sadegh, M., Vahedifard, F., Mazdiyasni, O., et al. (2018). How Do Natural Hazards cascade to Cause Disasters?. Nature 561, 458–460. doi:10.1038/d41586-018-06783-6
Alexander, D. R., and Pescaroli, G. (2019). What Are Cascading Disasters? UCL Open: Environment Preprint. London: UCL Press.
Arosio, M., Martina, M. L. V., and Figueiredo, R. (2018). Natural hazard Risk of Complex Systems - the Whole Is More Than the Sum of its Parts: I. A Holistic Modelling Approach Based on Graph Theory. Nat. Hazards Earth Syst. Sci. Discuss., 1–23. doi:10.5194/nhess-2018-277
Chatiza, K. (2019). Cyclone Idai in Zimbabwe: An Analysis of Policy Implications for post-disaster Institutional Development to Strengthen Disaster Risk Management. Oxfam. doi:10.21201/2019.5273
Corral, Á., and González, Á. (2019). Power Law Size Distributions in Geoscience Revisited. Earth Space Sci. 6, 673–697. doi:10.1029/2018EA000479
de Ruiter, M. C., Couasnon, A., van den Homberg, M. J., Daniell, J. E., Gill, J. C., and Ward, P. J. (2020). Why We Can No Longer Ignore Consecutive Disasters. Earth’s future 8, e2019EF001425. doi:10.1029/2019ef001425
Devi, S. (2019). Cyclone Idai: 1 Month Later, Devastation Persists. The Lancet 393, 1585. doi:10.1016/s0140-6736(19)30892-x
Dilley, M. (2005). Natural Disaster Hotspots: A Global Risk Analysis. World Bank Publications. doi:10.1596/0-8213-5930-4
Doroudi, S. (2020). The Bias-Variance Tradeoff: How Data Science Can Inform Educational Debates. AERA Open 6, 2332858420977208. doi:10.1177/2332858420977208
Dunant, A., Bebbington, M., Davies, T., and Horton, P. (2021b). Multihazards Scenario Generator: A Network-Based Simulation of Natural Disasters. Risk Analysis. doi:10.1111/risa.13723
Dunant, A., Bebbington, M., and Davies, T. (2021a). Probabilistic Cascading Multi-hazard Risk Assessment Methodology Using Graph Theory, a New Zealand Trial. Int. J. Disaster Risk Reduction 54, 102018. doi:10.1016/j.ijdrr.2020.102018
Dwivedi, R., Singh, C., Yu, B., and Wainwright, M. J. (2020). Revisiting Complexity and the Bias-Variance Tradeoff. Available at: http://arxiv.org/abs/2006.10189 [Accessed January 21, 2021].
Fang, F. C., and Casadevall, A. (2011). Reductionistic and Holistic Science. Infect. Immun. 79, 1401–1404. doi:10.1128/IAI.01343-10
Fortmann-Roe, S. (2012). Understanding the Bias-Variance Tradeoff. URL: http://scott.fortmann-roe.com/docs/BiasVariance.html(hämtad2019-03-27).
Gautam, D. (2018). “Past and Future of Earthquake Risk Reduction Policies and Intervention in Nepal,” in Impacts And Insights Of the Gorkha Earthquake (Elsevier), 173–182. doi:10.1016/b978-0-12-812808-4.00007-9
Geman, S., Bienenstock, E., and Doursat, R. (1992). Neural Networks and the Bias/variance Dilemma. Neural Comput. 4, 1–58. doi:10.1162/neco.1992.4.1.1
Gill, J. C., and Malamud, B. D. (2016). Hazard Interactions and Interaction Networks (Cascades) within Multi-hazard Methodologies. Earth Syst. Dynam. 7, 659–679. doi:10.5194/esd-7-659-2016
Gill, J. C., and Malamud, B. D. (2014). Reviewing and Visualizing the Interactions of Natural Hazards. Rev. Geophys. 52, 680–722. doi:10.1002/2013RG000445
Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Elements of Statistical Learnin. New York: Springer-Verlag.
Jibson, R. W., Allstadt, K. E., Rengers, F. K., and Godt, J. W. (2018). Overview of the Geologic Effects of the November 14, 2016, Mw 7.8 Kaikoura, New Zealand, Earthquake. Reston, VA: U.S. Geological SurveyAvailable at: http://pubs.er.usgs.gov/publication/sir20175146 doi:10.3133/sir20175146Accessed September 4, 2019)
Kappes, M. S., Keiler, M., von Elverfeldt, K., and Glade, T. (2012). Challenges of Analyzing Multi-hazard Risk: A Review. Nat. Hazards 64, 1925–1958. doi:10.1007/s11069-012-0294-2
Kargel, J. S., Leonard, G. J., Shugar, D. H., Haritashya, U. K., Bevington, A., Fielding, E., et al. (2016). Geomorphic and Geologic Controls of Geohazards Induced by Nepal’s 2015 Gorkha Earthquake. Science 351, aac8353. doi:10.1126/science.aac8353
Liu, Z., Nadim, F., Garcia-Aristizabal, A., Mignan, A., Fleming, K., and Luna, B. Q. (2015). A Three-Level Framework for Multi-Risk Assessment. Georisk: Assess. Manag. Risk Engineered Syst. Geohazards 9, 59–74. doi:10.1080/17499518.2015.1041989
Malamud, B. D., and Turcotte, D. L. (1999). Self-organized Criticality Applied to Natural Hazards. Nat. Hazards 20, 93–116. doi:10.1023/a:1008014000515
Mignan, A., and Wang, Z. (2020). Exploring the Space of Possibilities in Cascading Disasters with Catastrophe Dynamics. IJERPH 17, 7317. doi:10.3390/ijerph17197317
Mignan, A., Wiemer, S., and Giardini, D. (2014). The Quantification of Low-Probability-High-Consequences Events: Part I. A Generic Multi-Risk Approach. Nat. Hazards 73, 1999–2022. doi:10.1007/s11069-014-1178-4
Opitz, D., and Maclin, R. (1999). Popular Ensemble Methods: An Empirical Study. jair 11, 169–198. doi:10.1613/jair.614
Peng, M., and Zhang, L. M. (2013). Dynamic Decision Making for Dam-Break Emergency Management - Part 2: Application to Tangjiashan Landslide Dam Failure. Nat. Hazards Earth Syst. Sci. 13, 439–454. doi:10.5194/nhess-13-439-2013
Rashidi, H. H., Tran, N. K., Betts, E. V., Howell, L. P., and Green, R. (2019). Artificial Intelligence and Machine Learning in Pathology: The Present Landscape of Supervised Methods. Acad. Pathol. 6, 2374289519873088. doi:10.1177/2374289519873088
Shibahara, S. (2011). The 2011 Tohoku Earthquake and Devastating Tsunami. Tohoku J. Exp. Med. 223, 305–307. doi:10.1620/tjem.223.305
Spiro, R. J., Feltovich, P. J., Feltovich, P. L., Jacobson, M. J., and Coulson, R. L. (1991). Cognitive Flexibility, Constructivism, and Hypertext: Random Access Instruction for Advanced Knowledge Acquisition in Ill-Structured Domains. Educ. Technol. 31, 24–33.
Stigler, G. J. (1961). The Economics of Information. J. Polit. economy 69, 213–225. doi:10.1086/258464
UNISDR (2005). Hyogo Framework for Action 2005-2015: Building the Resilience of Nations and Communities to Disasters. Sendai, Japan: world conference on disaster reduction.
UNISDR (2015). Sendai Framework for Disaster Risk Reduction 2015 - 2030. Sendai, Japan: Third World Conference on Disaster Risk Reduction.
Keywords: bias/variance, multi-hazard, risk assessment, catastrophes and disasters, complex system
Citation: Dunant A (2021) Are We Missing the Target? A Bias-Variance Perspective on Multi-Hazard Risk Assessment. Front. Earth Sci. 9:685301. doi: 10.3389/feart.2021.685301
Received: 24 March 2021; Accepted: 11 May 2021;
Published: 31 May 2021.
Edited by:
Carmine Galasso, University College London, United KingdomReviewed by:
Gemma Cremen, University College London, United KingdomAnnalisa Cappello, National Institute of Geophysics and Volcanology, Italy
Copyright © 2021 Dunant. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexandre Dunant, YWxleGFuZHJlZHVuYW50ODJAZ21haWwuY29t
 Alexandre Dunant
Alexandre Dunant