
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 05 July 2021
Sec. Geohazards and Georisks
Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.670997
This article is part of the Research TopicFlood Susceptibility and Risk Maps as a Crucial Tool to Face the Hydrological Extremes in Developing Countries: Technical and Governance Aspects Linked by a Participatory ApproachView all 4 articles
Detecting and forecasting riverine floods is of paramount importance for adequate disaster risk management and humanitarian response. However, this is challenging in data-scarce and ungauged river basins in developing countries. Satellite remote sensing data offers a cost-effective, low-maintenance alternative to the limited in-situ data when training, parametrizing and operating flood models. Utilizing the signal difference between a measurement (M) and a dry calibration (C) location in Passive Microwave Remote Sensing (PMRS), the resulting rcm index simulates river discharge in the measurement pixel. Whilst this has been demonstrated for several river basins, it is as of yet unknown at what ratio of the spatial scales of the river width vs. the PMRS pixel resolution it remains effective in East-Africa. This study investigates whether PMRS imagery at 37 GHz can be effectively used for flood preparedness in two small-scale basins in Malawi, the Shire and North Rukuru river basins. Two indices were studied: The m index (rcm expressed as a magnitude relative to the average flow) and a new index that uses an additional wet calibration cell: rcmc. Furthermore, the results of both indices were benchmarked against discharge estimates from the Global Flood Awareness System (GloFAS). The results show that the indices have a similar seasonality as the observed discharge. For the Shire River, rcmc had a stronger correlation with discharge (ρ = 0.548) than m (ρ = 0.476), and the former predicts discharge more accurately (R2 = 0.369) than the latter (R2 = 0.245). In Karonga, the indices performed similarly. The indices do not perform well in detecting individual flood events when comparing the signal to a flood impact database. However, these results are sensitive to the threshold used and the impact database quality. The method presented simulated Shire River discharge and detected floods more accurately than GloFAS. It therefore shows potential for river monitoring in data-scarce areas, especially for rivers of a similar or larger spatial scale than the Shire River. Upstream pixels could not directly be used to forecast floods occurring downstream in these specific basins, as the time lag between discharge peaks did not provide sufficient warning time.
Natural hazards are considered disasters when they disrupt the functioning of a society and cause human, material, economic or environmental losses that the community or society cannot cope with using its own resources (IFRC, 2020). Floods are among the most frequent and globally widespread of disasters: Between 2000 and 2019, flooding accounted for 44% of all reported disasters, affecting 1.65 billion people globally (CRED and UNDRR, 2020). The intensity and number of floods occurring annually has also been rising in many locations in recent years, a trend likely to persist in the light of climate change (Chidanti-Malunga, 2011; Aich et al., 2013; IPCC, 2014). Simultaneously, floods have been increasingly causing economic, material, and human losses due to rapid population growth and economic development in developing countries, including in flood-prone areas (Hussain et al., 2005).
One region that is increasingly affected by weather-related disasters is Sub-Saharan Africa. Economies here are largely dependent on (often rain-fed) agriculture (Svendsen et al., 2009), leading to a substantial economic dependency on meteorological and hydrological conditions and a vulnerability to anomalies in these conditions (Chidanti-Malunga, 2011). Better monitoring and forecasting systems can improve respectively humanitarian response and anticipatory action (van den Homberg et al., 2020), whereby vulnerable people are supported in taking early action prior to the hazard happening (an approach called forecast-based financing). In this way, their vulnerability is reduced and resilience increased. Unfortunately, there are many data-sparse areas in Africa, and Malawi specifically (Ngongondo et al., 2011; Mwale et al., 2012), where hydrological and meteorological data, important components of these systems, are unavailable or not of satisfactory quality.
Alternative strategies for flood forecasting are being explored in countries facing these challenges, one of which being the application of satellite remote sensing for monitoring and forecasting (De Groeve, 2010; Palmer et al., 2015). The potential of optical remote sensing data is widely covered in literature, but optical data are less suitable for this purpose due to the cloudiness that often occurs in times of flood surges (Smith, 1997). Furthermore, satellites carrying optical sensors, such as SPOT or Landsat TM, have a relatively long return period (Weintrit et al., 2018), which is not ideal for preventative monitoring. Remote sensing from Global Navigation Satellite System-Reflectometry (GNSS-R), such as NASA’s CYGNSS mission, has recently gained attention as a viable alternative to optical sensors for flood monitoring due to its ability to operate under cloudy conditions (Chew et al., 2018; Chew and Small, 2020; Unnithan et al., 2020). However, CYGNSS currently does not provide (near-) daily spatial coverage over land due to the pseudo-random sampling technique of GNSS-R satellites, yielding this method less optimal for real-time applications until more satellites are launched (Chew and Small, 2020).
Passive sensors that operate on the microwave part of the electromagnetic spectrum (e.g., SSMI/I, SMMIS, AMSR-E) are also less limited by cloud cover, atmospheric haze or Sun illumination and have a near-daily revisit time (D'Addabbo et al., 2018). The relatively low radiation intensity in the microwave spectrum causes the spatial resolution of the data to be relatively low, meaning the data are most suitable for analyses over larger-scale water features (Smith, 1997) One of the ways in which floods can be assessed using passive microwave remote sensing (PMRS) is the CM-ratio (rcm), a method first developed by Brakenridge et al. (2007). This satellite-derived signal uses the brightness temperatures (Tb) obtained from Ka band passive microwave radiometry, comparing the values from a measurement cell M to those of a dry calibration cell C. In areas with a well delineated flood plain, increases of the ratio over time can be synchronous with discharge increases, as the in-pixel water area expands (Hirpa et al., 2013). In addition to this method, an additional “wet” calibration cell can be introduced to the equation. This surface water-covered cell provides an indication of the Tb of surface water in the area, which helps to convert the ratio into the fraction of surface water within the cell, a variable which is spatially interpretable. While van Dijk et al. (2016) introduced this method by estimating water extent from Short-Wave Infrared imagery from MODIS, assuming a value for the emissivity of water, Neisingh (2018) expanded on this by using PMRS data only, a method named the CMC-ratio (rcmc).
The applicability of rcm for flood detection and forecasting has been investigated in the Zambezi watershed (De Groeve, 2010), and the Brahmaputra and Ganges watersheds (Hirpa et al., 2013). Furthermore, the Global Disaster Alert and Coordination System (GDACS) has adapted an automated rcm system as presented by Kugler and De Groeve (2007) for development of a Global Flood Detection System (GFDS), which obtains and processes AMSR-E imagery for global flood monitoring in real-time. Whether or not the system performs well in simulating discharge, is dependent on local factors: GFDS stations in tropical climates with a river width of >1 km, a discharge of >500 m3 s−1, and a lower density of surrounding vegetation tend to perform better than smaller-scale rivers, rivers in more densely vegetated areas or in different climates (Revilla-Romero et al., 2014).
Whilst the GFDS does include stations in East-Africa, coverage in Malawi is sparse, and the applicability of the CM-method in smaller-scale watersheds in Malawi has not been studied as of yet in any published work. Although smaller rivers in this area may not have the optimal river width or discharge described by Revilla-Romero et al. (2014), the tropical climate and relatively open structure of the vegetation could still allow for Virtual Gauging Stations (VGSs) measurements with a high correlation with in-situ observed discharge. Furthermore, the potential of introducing a wet calibration cell in the microwave spectrum to estimate inundation extent has been proposed and analyzed in a thesis by Neisingh (2018), but was as of yet not further investigated.
This study therefore aims to investigate whether openly available PMRS data of 25 km-resolution can be used for monitoring and forecasting of floods in two relatively small-scale basins in Malawi. We will focus on two calibrated variants of the PMRS-derived index rcm. The first index is the m index, which represents the rcm as a magnitude relative to the average conditions, calibrated using historical signal data. The second is rcmc, which uses an additional wet calibration target and can be interpreted spatially. We will investigate what the potential is for PMRS-data to detect the occurrence and magnitude of riverine floods in downstream areas, comparing the indices with in-situ discharge data as well as a flood impact database. Secondly, we will investigate whether the smaller sizes of these specific basins allow for establishing a relationship between upstream and downstream m- and rcmc-signals, and we will discuss the potential use of PMRS for early warning purposes. We hypothesize that, although the footprint of typical PMRS sensors is relatively large, the wetting of smaller floodplains within this footprint may provide sufficient changes in both PMRS-indices for the detection and forecasting of floods. Furthermore, we hypothesize that the study area with the relatively wider river and larger basin will be more suitable for flood detection and forecasting using PMRS than the study area with the smaller-scale river. The results were benchmarked against a more widely used, global flood model, the Global Flood Awareness System (GloFAS), which is presently used by humanitarian organizations for early warning systems.
The Republic of Malawi is a landlocked country in the southeast of Africa, bordered by Lake Malawi. Malawi’s economy is mostly agro-based, with 35% of the country’s Gross Domestic Product (GDP) originating from the agricultural sector (DoDMA, 2015). However, only 2.3% of all cultivated land, and 66.0% of all arable land suitable for irrigation was irrigated in 2011 (FAO, 2011), yielding the country very dependent on the weather. It is estimated that floods and droughts together reduce the country’s GDP by 1.7% (Pauw et al., 2011).
Malawi has a subtropical climate with a wet and warm growing season that takes place from November to April (DoDMA, 2015; Malawi Meteorological Services, 2020). Flooding accounts for approximately 40% of all recorded disasters in the country (Mijoni and Izadkhah, 2009), affecting millions of lives and frequently causing displacement, economic damage and casualties. Despite the floods being a reoccurring phenomenon, the series of devastating floods in January 2015 was far more destructive than most recent disasters: it affected more than one million people in the country, with 230,000 people displaced, 172 reported missing, and 170 reported fatalities (Guha-Sapir, 2020). As recently as 2019, floods occurring in the wake of Cyclone Idai had a destructive impact on the country as well (Guha-Sapir, 2020). As extreme events like this are expected to happen more frequently in the near future (Mijoni and Izadkhah, 2009; DoDMA, 2015), flood risk will increase as well, unless more drastic disaster risk management measures are taken (Šakić Trogrlić et al., 2019).
Many of the current flood risk management practices in Malawi are the result of community-based systems, funded by international donors. An example of this is the CB-EWS, that monitors rainfall and water level gauges and disseminates messages downstream (Šakić Trogrlić et al., 2019). The official national Early Warning System (EWS) consists of the Operational Decision Support System (ODSS), a meteorological, hydrological and hydraulic flood forecasting and warning system that predicts riverine floods on the short-term, i.e., approximately three days (Ammentorp and Richaud, 2016). It is currently only operational in the Lower Shire Valley. This valley is considered one of the areas in Malawi that is most severely affected by floods (Mijoni and Izadkhah, 2009).
Several early warning systems in other countries include or are in the process of including triggers generated by the Global Flood Awareness System (GloFAS) (Boelee et al., 2017; Jjemba et al., 2018), a global flood model based on rainfall data and hydrological and hydraulic model output. GloFAS is freely available and provides medium-range forecasts. Its maximum lead time is 30 days, and the daily forecast data are provided with a maximum lead time of 15 days. The applicability of GloFAS for flood preparedness in Malawi has been investigated by 510, the data initiative of the Netherlands Red Cross, for the Lower Shire Valley. It was found that GloFAS cannot accurately predict absolute discharge values in the area, but that it could be used in forecasting systems if trigger levels would be set correctly (Teule, 2019).
Suitable administrative districts of interest for this study were selected based on their vulnerability, exposure to riverine floods and lack of coping capacity as reported on the Community Risk Dashboard by 510 (510 an initiative of the Netherlands Red Cross, 2020). From the resulting districts, Karonga and Chikwawa were deemed most relevant as they are labeled “areas of intervention” in the ECHO III and ECHO V projects of the Red Cross, emphasizing their importance for the work of the Malawi Red Cross Society and its partner National Societies.
Within each district, one downstream VGS was selected; A grid cell the size of a pixel from the PMRS-dataset (Figure 1). The VGSs had to be situated relatively downstream in the watershed, have a known record of riverine flooding, and have a visible flood plain as identified from optical satellite imagery. The latter was visually assessed, making use of the time slider function in Google Earth Pro 7.3.2. Series of upstream VGSs were subsequently selected in order to assess whether upstream and downstream satellite PMRS-signals are related. The headstream of both rivers was identified making use of a waterway shapefile line (OpenStreetMap contributors, 2020), supplemented with basin and flow accumulation maps (created with Arcmap 10.8 using the ASTER GDEM (NASA/METI/AIST/Japan Spacesystems and U.S./Japan ASTER Science Team, 2019). Subsequently, the river flow was traced upstream, where each PMRS-pixel upstream from the downstream VGS was marked as upstream VGS (Figure 1).
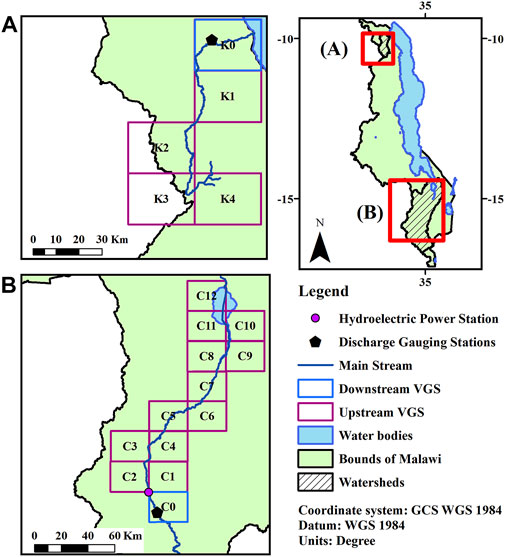
FIGURE 1. Upstream and downstream Virtual Gauging Stations (VGSs) along the North Rukuru (A) and Shire River (B) in Malawi. One grid cell is approximately 25 × 25 km. The labels on the cells are used for referencing throughout this thesis, with the letter corresponding to the district Chikwawa (C) or Karonga (K). Data sources: RCMRD (2015); Brodzik et al., (2016); National Statistics Office of Malawi, (2018); OpenStreetMap contributors (2020).
For the district of Karonga, the downstream VGS (9°56′15″S, 33°50′44″E, cell K0 on Figure 1A) is situated in the grid cell covering the capital of the district, Karonga Town. Riverine flooding of the North Rukuru River has occurred here every wet season between 2009 and 2016, with the floods in 2010 and 2016 reported especially severe (Manda and Wanda, 2017). The North Rukuru River is the main river in this low-lying region, meandering through the grid cell and eventually draining into Lake Malawi (Figure 1A). The river itself is up to 100 m wide during the wet season. Its floodplains (up to 125 m wide on each side) are home to many informal settlements, which are especially vulnerable to flood events, including frequent low-impact events (Manda and Wanda, 2017). The North Rukuru River shows a strong seasonal pattern in streamflow, with a wet season starting in November/December, reaching a peak that in most years does not exceed 100 m3 s−1, before gradually reclining from May onwards to a discharge of nearly 0 m3 s−1. Therefore, regarding width and size, the river does not meet the optimal conditions specified by Revilla-Romero et al. (2014).
For the district of Chikwawa, the focus is on the Shire River, the largest river in Malawi that originates in Lake Malawi and flows into the Zambezi River in Mozambique (Figure 1B). The downstream VGS is located along the Lower Shire River, covering the city of Chikwawa (16°04′07″S, 34°49′50″E, cell C0 on Figure 1B). The city is frequently hit by riverine floods, including the severe floods in 2015 and 2019 (Guha-Sapir, 2020). At Chikwawa, the Shire River showcases a unimodal seasonal pattern in streamflow, with a peak occurring in February or March. Discharge ranges from an average of approximately 400 m3 s−1 in the dry season to an average of 600 m3 s−1 in the wet season. During the latter season, the river is approximately 300 m wide in the VGS, its floodplains up to 800 m when measured from the center of the river. Thus, the “regular” river width is still narrower than the optimal conditions specified by Revilla-Romero et al. (2014), but its average discharge does meet the conditions in the wet season.
Tb data were obtained from NASA’s Making Earth System Data Records for Use in Research Environments (MEaSUREs) Calibrated Enhanced-Resolution Passive Microwave Daily EASE-Grid 2.0 Brightness Temperature ESDR, Version 1 (Brodzik et al., 2016), a freely available dataset including PMRS imagery from different platforms and sensors. The dataset itself spans from 1978 to 2017, but some platforms in the dataset are still operational. All acquired data were Level 3-processed to NASA standards prior to acquisition, meaning the raw data were processed to sensor units (Tb), calibrated, and mapped onto a resampled grid with a resolution of 25 km. Due to the gridding, the data may be temporally averaged or ignore overlapping satellite swaths altogether (Brodzik et al., 2016). A long-term timeseries of Tb was created by downloading MEaSUREs data from different platforms and sensors with the software WGet, and combining them in one dataset, spanning from 1978 to 2017 (see Supplementary Material).
Brakenridge et al. (2007) used the horizontally polarized Tb, from the descending node, measured in the 36.5 GHz channel of the Advanced Microwave Scanning Radiometer (AMSR-E), as this frequency suffered little interference from radio frequencies or the oxygen and water vapor spectral lines. This is in accordance with the optimal settings for rcmc as defined by Neisingh (2018), and those used by other research on the topic of rcm-signals (De Groeve et al., 2007; De Groeve, 2010; Hirpa et al., 2013). Horizontally polarized imagery from the descending node was therefore used here as well. As a frequency, 37 GHz was chosen over 36.5 GHz since data at this frequency in MEaSUREs covered a longer period.
Generally, electromagnetic radiation in the microwave region is unaffected by cloudy conditions. However, some cloud-induced noise could remain in the Tb-signal in cases of thunderstorms or heavy rain events. A filter method was applied to the data in order to eliminate this, and account for the fact that the satellites do not achieve full swath coverage near the equator. The filter method had to be able to be applied in real-time and could therefore not be looking to future neighboring values, as this would remove valuable flood response time in real-time. Therefore, the Tb data for each cell was filtered using the same approach as De Groeve (2010) and van Dijk et al. (2016): A filter was applied to the values that takes the average of the preceding four values and the current value. This window removes some data gaps, most notably in the period 1978–1987, when the satellite return period is two days rather than one, and eliminates some noise, while retaining the flood peaks in the data. However, this method does reduce and delay the effect of signal peaks occurring in real-time, as it averages them out with the lower values occurring previously.
Environmental factors such as physical surface temperature, differences in emissivity (e.g., through differences in vegetation cover), and atmospheric moisture have a considerable effect on raw Tb values measured by satellites (De Groeve, 2010; van Dijk et al., 2016). The CM-methodology is therefore based on the assumption that cells that are located within a reasonable distance from one another are similarly affected by these “noise factors” (van Dijk et al., 2016). The dry calibration cell Cd should be located within the temperature-correlation length of M, minimizing the influence of these variables from the ratio (Brakenridge et al., 2007; De Groeve, 2010; van Dijk et al., 2016). At the same time, however, Cd must be located outside of the river reach of M, yielding it a relatively stable calibration target.
M was represented by either the downstream VGS (downstream flood detection analysis) or the upstream VGSs (upstream-downstream relationship analysis) in each basin (Figure 1). Cd was chosen by applying a spatial buffer of 50 km (2 pixels of 25 km on each side) around M. Within this kernel, the cell with a yearly average Tb-signal closest to the 95th percentile of all cells was chosen as Cd, a method similar to that of van Dijk et al. (2016). This process was repeated for each year. While this would mean that Cd would likely not be at the same location each year, making the timeseries less homogenous, it would account for long-term changes in river reach and hydrometeorological conditions throughout time. The wet calibration target Cw, which is needed for the calculation of rcmc, was manually chosen as the nearest cell to M that was fully covered by a large water body. The Cw-cell for the Shire River was therefore located in Lake Chilwa, and that of the North Rukuru River in Lake Malawi, the closest large and permanent bodies of water for the two downstream VGSs (see Supplementary Material). It was assumed that surface temperatures, emissivity and atmospheric moisture in these locations were similar here as in the respective M-cells.
Satellite indices were calculated using Tb-timeseries from the located M, Cd, and Cw cells, after the filter method had been applied to it. The two signals that were compared in this study were m and rcmc, which are both related to the rcm, but standardized with respect to the average historical signal in this particular area (m) or recalculated into a surface water fraction (rcmc).
m is directly related to rcm and uses historical rcm-signals to express the observed rcm as the number of standard deviations from a base value. In order to calculate m, rcm was calculated first:
where
where rcm is the ratio as calculated in Eq. 1,
rcm represents a proxy for discharge, and not a quantitative hydrological variable, which means it is not easily interpretable in the context of flood mapping. The second index studied here, the rcmc, can be interpreted more easily, as it represents an estimate for the fraction of surface water within the M-cell. Whilst De Groeve (2010) and van Dijk et al. (2016) performed similar calculations with an assumed emissivity for water, Neisingh (2018) introduced the addition of a fully surface-water covered calibration cell to the equation. The index is calculated as
where
Average daily discharge at the gauging station at Chikwawa (1L12) between 1977 and 2009 was obtained from the Department of Water Resources of Malawi (2019). Data from the Mwakimeme station in Karonga (8A5) between 1968 and 1991 was obtained from the Global Runoff Data Centre (2020). For both stations, discharge entries older than 1979 (the first full year of the PMRS dataset) were not utilized.
A flood impact database was created by combining impact data from EM-DAT (Guha-Sapir, 2020), with flood hazard data from the Dartmouth Flood Observatory (Dartmouth Flood Observatory, 2020) and the GLIDE-database (GLIDE, 2020). All floods that were tagged to have taken place in the districts of Chikwawa and Karonga were selected. Floods tagged as flash floods or those with a duration of one day were dropped, as the distinction between natural, short-term signal fluctuations and flash floods cannot be made by just looking at the satellite signal, and because many flash floods tend to go unreported. Floods that only had a starting or ending month and no precise dates recorded were assumed to start on the first day of the month, or end on the last day of the month, respectively.
As many of the flood entries contained information on the affected districts and rivers only, and not the precise location where the flood took place, the resulting flood database was quality checked with an analysis of annual discharge extremes at our downstream points of interest. The maximum discharge observed within the timespan of these floods was extracted in order to check whether the reported flood occurred during annual peak discharge. If so, it was assumed that the flood took place in our downstream area of interest.
The relationship between the satellite signals and observed discharge was established in a regression analysis. The discharge data in Chikwawa showed a significant interannual baseflow trend (Kelly et al., 2019) due to variations in rainfall (Jury, 2014), whereas the satellite signals did not show this trend due to their standardized nature. As this would mean that the relationship with discharge would change throughout time, and as the aim of this research is to set up a forecasting system, yielding the recent values the most relevant, it was decided to apply the regression for both locations only on the five most recent years of discharge record, which were also relatively stable in baseflow. The seasonal oscillations were assumed to have an equal impact on both datasets in this relatively short period. Furthermore, only the months of December up to and including April were used in this step, as we are primarily interested in the wet season. Frequently occurring low discharge values in the dry season would potentially impact the relationship, and have also shown to not be well simulated by rcm (Brakenridge et al., 2007; Revilla-Romero et al., 2014).
The datasets from Chikwawa (cell C0) and Karonga (cell K2) were each divided into two random subsets, both comprising half of the five years of data. The relationships between the discharge data and m and rcmc were tested for normality of residuals, homoscedasticity, and linearity to assess whether a parametric or non-parametric correlation would be most appropriate. Normality was tested with a Shapiro-Wilk test at 5% significance level, and homoscedasticity was tested with a median-based Levene’s test. Both yielded a p-value of less than 0.05 for the discharge data and both rcmc and m, meaning the null hypotheses of normality and homoscedasticity were rejected. The assumption of linearity was assessed visually with a scatterplot (discharge vs. satellite signals), and rejected as well. A non-parametric test using Spearman’s correlation coefficient (ρ) was therefore deemed most appropriate. ρ is calculated as
where the data are ranked from 1 to n (the number of data points), and di = xi − yi, the difference in ranking i and n. The relationship was simulated with a second-degree polynomial regression, applied to the training data, as this was the lowest order at which monotonicity could be achieved in Chikwawa. In Karonga, monotonicity could not be achieved with any polynomial order. Spearman’s ρ was calculated using the testing data and the polynomial predictions. The significance of the coefficient was assessed by calculating a two-sided p-value to test the null hypothesis that the predictions and test-values are uncorrelated (α = 0.05).
A time-lagged cross correlation (TLCC) was conducted to identify which VGS, if any, could be used for forecasting downstream satellite signals, in the same manner as Hirpa et al. (2013) found upstream VGSs to be useful in forecasting downstream floods in larger-scale watersheds. If a VGS showed a strong correlation (ρ > 0.7) and also had a lag time of at least one day, this VGS would be suitable for forecasting.
As the TLCC assumed stationarity, the datasets were made stationary first. Whereas the Augmented Dickey-Fuller Test at a 95% confidence level rejected the null-hypothesis that the downstream (cells C0, K2) and upstream discharge data and satellite signals in the wet season (i.e. December to April) were non-stationary, this test does not account for seasonality but merely for the presence of a unit root. A visual examination of the datasets confirmed that the data indeed has a long-term trend (also see Seasonality of Discharge and Satellite Signals). This is especially true for the discharge at Chikwawa, which shows a clear and significant change in baseflow over the years. Interannual trends were removed from all datasets in linear segments. Locations where the changes in annual mean value shift from positive to negative or vice versa were used as break points. The data also showed strong seasonal oscillations, which is why the seasonal component was subsequently removed from the data by fitting a second-degree polynomial oscillating curve and subtracting this from the detrended values (see Supplementary Material for an illustration).
The TLCC was conducted by artificially shifting the stationary data with a lag time ranging from −20 to 20 days. At each lag time, a pairwise correlation was conducted and Spearman’s ρ was calculated to see how the correlation changed with different time steps, and at which lag time the correlation would be strongest.
To assess how well registered flood events are detected by our VGSs, a threshold of what a “relevant” flood is needs to be defined first. This was done by using the concept of the return period (treturn), the statistically estimated time it takes for a flood of a certain severity to repeat itself, where a flood with a treturn of five years has a probability each year of 0.2 (20%) to return. Whereas communities may be better prepared to cope with floods with a low treturn, floods with a higher treturn generally cause more damage. FbF-programmes are designed to be activated during floods with a treturn of at least five years, constituting a balance between the costs associated with activation and the benefits that the program bring to the affected communities. For this reason, this treturn was chosen for the flood threshold definition.
An extreme value analysis was conducted on the complete discharge dataset including the trend. For each hydrological year (May to April), the annual maximum was extracted. The corresponding PMRS signal values at these peaks were sorted, after which a rank was attributed to them. The probability (p) of each occurring value was calculated as
where n is the total number of peaks and r is the rank of the value. This number was then converted into a treturn in years by taking the inverse of p:
A polynomial curve was fitted to the existing data points to find the discharge value corresponding to five years, applying the lowest degree at which a smooth line through the points could be obtained (Figure 2). This was a 10th degree polynomial. The rcmc and m-thresholds were identified by using one of two alternative approaches, depending on the outcome of the discharge-signal regression relationship identified previously:
1. If the observed discharge to satellite signal correlation proved strong (ρ > 0.7) and significant, the m and rcmc values corresponding to treturn = 5 would be identified by solving the polynomial equation for the 5 years discharge threshold.
2. If the observed discharge to satellite signal correlation was not strong and/or not significant, the values corresponding to treturn = 5 would be calculated in a similar manner as the discharge threshold, applying the abovementioned flood frequency analysis on the original rcmc- and m-signals between 1978 and 2017.
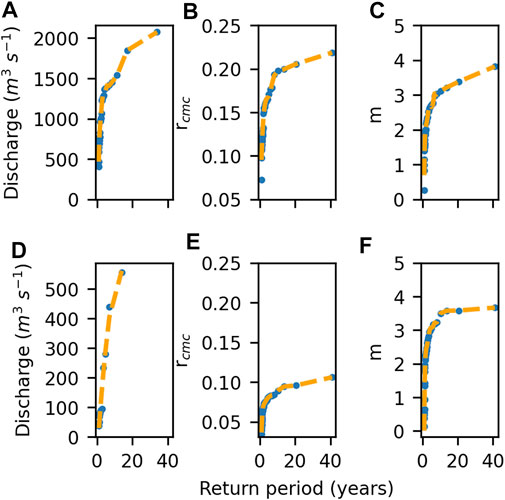
FIGURE 2. Peaks of the CMC-ratio (rcmc), m index (m) and discharge per hydrological year vs. their respective return periods in years for Chikwawa and Karonga. The red line is a 10th (K2-discharge: 2nd) degree polynomial curve through the data points. Data source: Brodzik et al., 2016.
The resulting discharge, m index and rcmc-thresholds with treturn = 5 were used in the detection performance assessment. To account for the uncertainties associated with using high-order polynomial equations, the resulting thresholds were visually compared with the graphs in Figure 2.
A confusion matrix was constructed for the different satellite indices (Table 1) to assess their performance in detecting floods, where each table entry represented one hydrological year (May to April). If a year included a registered flood event, and this event occurred within a maximum of 14 days from the exceedances of the determined satellite signal threshold, it was considered a “hit” (H), i.e. a correctly detected flood. This margin was chosen because observed flood peaks in discharge data may precede a maximum in floodplain inundation, and this time difference can be up to a couple of days (Brakenridge et al., 2007), and because the backwards-looking filter method may have delayed some signal increases by averaging with preceding (lower) values. More details and examples on how the “misses”, “false alarms” and “correct negatives” were determined can be found in the Supplementary Material. The confusion matrix was constructed using a per-year approach, because the large number of days in the year where no flood occurred (such as the dry season) would lead to a high number of “correct negatives”, distorting the results.
Different metrics can be calculated from the confusion matrix, which in turn can be used to evaluate the forecasting or detection skills of a model. Therefore, the Critical Success Index (CSI), False Alarm Ratio (FAR) and Probability of Detection (POD) were calculated using the equations
where nH is the number of hits, nM the number of misses and nFA the number of false alarms. The POD represents the fraction of the reported floods that was successfully forecasted, whereas the FAR represents the fraction of all alarms that were false according to the records, a measure of failure to exclude non-event cases. The CSI, also called the Threat Index, stands for the fraction of modeled floods that was also reported. As no single statistic can describe the skill of a model by itself, all three metrics were considered in evaluating the skill of the satellite signals in detecting discharge.
The PMRS-method’s performance was compared with hindcasting data from GloFAS in order to compare the detection skill of the presented method with an existing EWS. The global model had daily average discharge estimates available (2000–2018) in a global NetCDF-file with a grid of 0.1° × 0.1°, obtained through the Copernicus Climate Data Store and distributed by the Copernicus Climate Change Service by ECMWF (Harrigan et al., 2020). A 5 years treturn-threshold was generated from the discharge estimates (2000–2017) using the same method as was used for the satellite data. This threshold, the discharge estimates and the compiled flood database were used to generate a confusion matrix at both cell K0 and C0 and compare the performance of this global model with that of the PMRS-method when the data is treated similarly.
The timeseries of the Tb per cell (M, Cd and Cw) can be found in Figure 3. Points where a transition to a different satellite sensor/platform was made are clearly visible as amplitude shifts in the series, for example in 1996. This can be attributed to the fact that the MEaSUREs-dataset is resampled from different satellite overpasses and platforms, and each resampled cell corresponds to slightly different “real” ground footprints. The aforementioned phenomenon is especially apparent in cell K0, which is bordered by Lake Malawi (Figure 3B). This causes different signals depending on whether the original footprint covers a substantial part of the lake or not. The shifts in signal are mostly canceled out by converting Cd and M into a ratio-based index such as m or rcmc as visible in Figures 4A,B, since the ratios represent the relative difference between cells from the same platform in the same period. However, in Karonga especially, a shift remains visible in 1987 after conversion to a ratio, where the Nimbus-satellite was merged with the first satellite of the DMSP-series (Figures 5A,B). This might have to do with the orbit of the DMSP-satellites and the resulting fraction of water in the footprint of the data prior to resampling into the EASE Grid. The amplitude shift changes the satellite signals’ relationship with discharge throughout time.
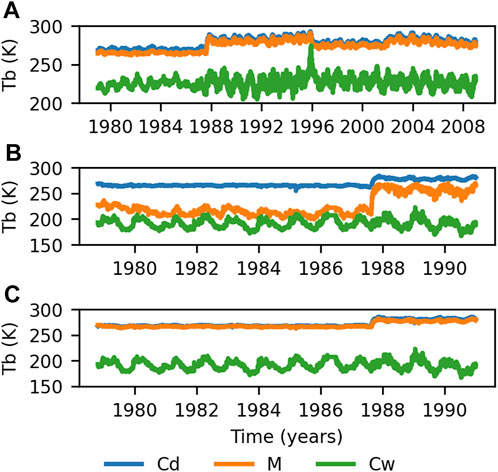
FIGURE 3. Brightness temperature (Tb) values in Kelvin (K) of the wet calibration (Cw, blue line), dry calibration (Cd, green line) and measurement (M, orange line) cells in the downstream virtual gauging station in (A) Chikwawa (cell C0), (B) Karonga (cell K0) and (C) the proxy Karonga cell (cell K2). Data source: Brodzik et al., 2016.
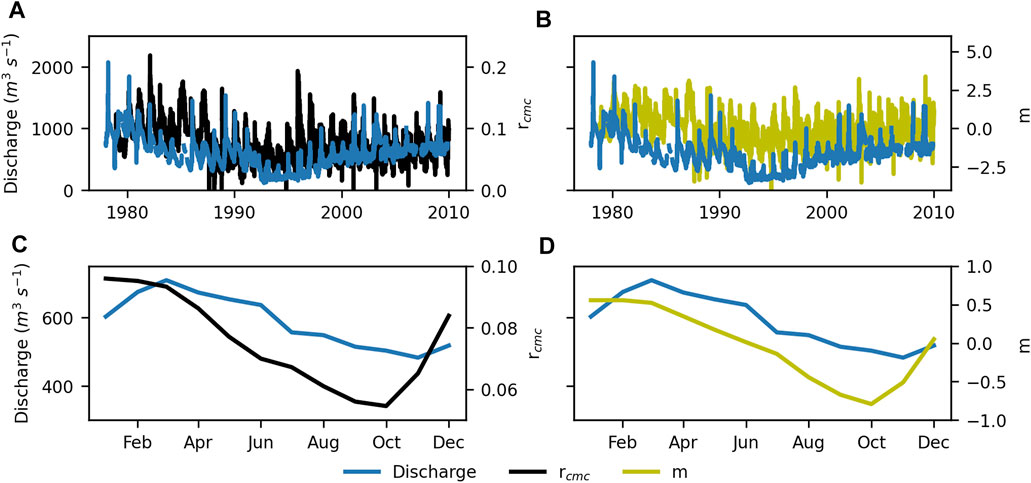
FIGURE 4. Observed discharge and downstream (cell C0) satellite signals rcmc(A), m(B) between 1979 and 2009, and mean monthly discharge and downstream satellite signals rcmc(C) and m(D). rcmc = CMC-ratio, m = m index. Data sources: Brodzik et al., 2016; National Hydrological Services of Malawi, 2019.
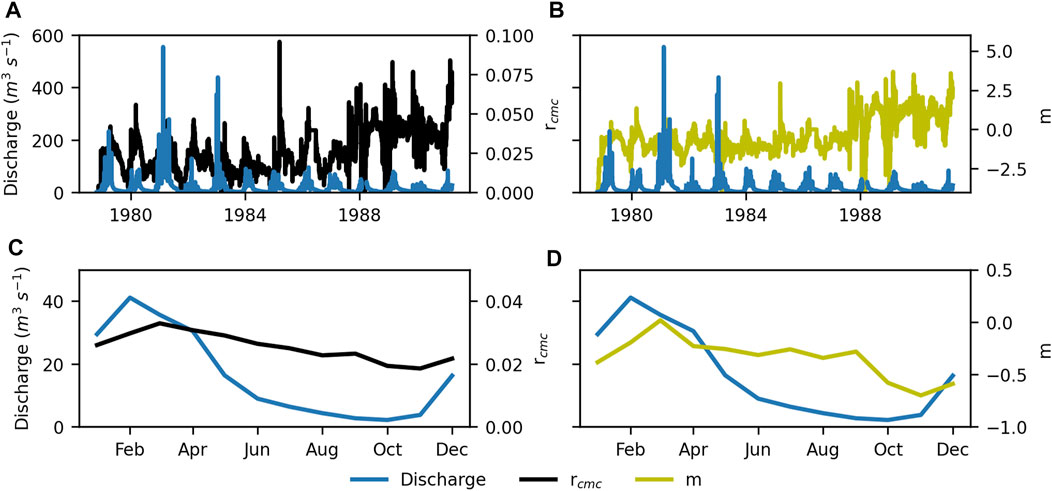
FIGURE 5. Observed discharge and downstream (cell K2) satellite signals rcmc(A), m(B) between 1979 and 1991, and mean monthly discharge and downstream satellite signals rcmc(C) and m(D). rcmc = CMC-ratio, m = m index. Data sources: Brodzik et al., 2016; Global Runoff Data Center, 2020.
Looking at the relative differences between the cells, Cd and M in Chikwawa (VGS C0) show a similar trend over time throughout the timeseries (Figure 3A), except during flood events, as one would expect. Cw shows a clear peak in 1996, that also impacted the rcmc-signal in this year. This can be attributed to severe receding of Lake Chilwa in 1995–1996 (Njaya et al., 2011), causing the Tb of Cw to rise and approximate the Tb-value of M.
In the downstream Karonga VGS (cell K0), Cd and M do not follow a similar trend throughout the timeseries, and the difference in Tb between Cd and M is much larger than was the case in the C0 VGS (Figure 3B). VGSs situated more upstream in the North Rukuru basin did show a Cd-M pattern more similar to the C0 VGS in Chikwawa. The reasons for this discrepancy will be discussed in Raw Tb Signals. As the first VGS with a realistic signal was cell K2 (Figure 3C), the rest of the research project therefore focused on K2 as a proxy for the downstream area of interest in Karonga, and did not take into account cell K0 anymore.
The satellite signals and discharge data follow a similar seasonal cycle in the Shire downstream VGS (cell C0) as well as the North Rukuru proxy downstream VGS (VGS K2) (Figure 4), supporting the assumption that seasonal differences have a similar influence on the discharge and satellite signals. The interannual trend present in the discharge series of Chikwawa is not visible in the satellite signals, due to the fact that the latter are standardized relative to the prevailing hydrometeorological conditions at that point in time (Figures 4A,B): in a wetter year, all cells will show a “wetter” signal’, meaning their relative difference and hence the ratios remain unaffected.
The seasonal oscillations of satellite signals and discharge data in cell K0 did not coincide. The resulting rcmc values were unusually high compared to the values found in cell C0 as a result of this, despite the narrower width of the North Rukuru River compared to the Shire River. K2, the proxy VGS situated more upstream, showed a better correspondence of seasonality (Figures 5A,B) compared to the discharge data, and more realistic rcmc-values (Figure 5D) (see Supplementary Material).
Figures 6, 7 show the correlation and regression analysis at both locations. For the Shire River in Chikwawa, both m and rcmc presented moderate correlations with discharge (Figure 6), with a ρ of 0.548 for rcmc and 0.476 for m. For the North Rukuru River in Karonga, which is by far the smallest stream of the two, no physically meaningful correlation was found (Figure 7), with a ρ of −0.067 for rcmc and −0.119 for m. All correlations yielded a p-value smaller than the α of 0.05 and were therefore considered significant, with the exception of the correlation between discharge and rcmc in Karonga (p-value = 0.190).
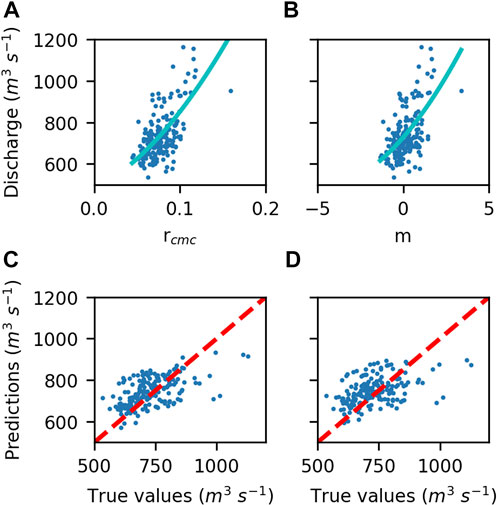
FIGURE 6. Chikwawa (cell C0) Spearman’s correlation of (A)rcmc, ρ = 0.548 and (B)m, ρ = 0.476. Regression results of (C)rcmc, R2 = 0.369 and (D)m, R2 = 0.245 for discharge and satellite signals. rcmc = CMC-ratio, m = m index. Data sources: Brodzik et al., 2016; National Hydrological Services of Malawi, 2019.
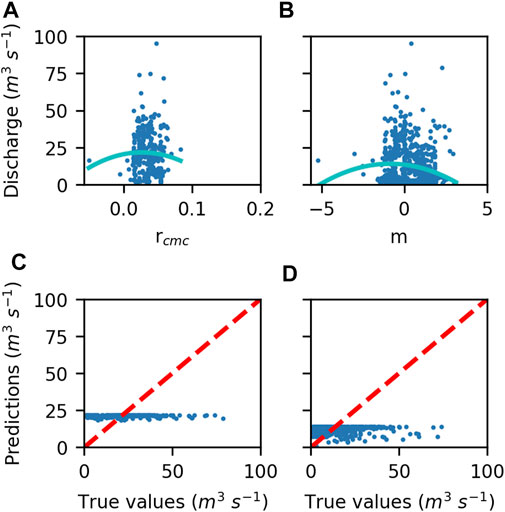
FIGURE 7. Karonga (cell K2) Spearman’s correlation of (A) rcmc, ρ = −0.067 and (B)m, ρ = −0.119. Regression results of (C)rcmc and (D)m, R2 = ∼0.000 for discharge and satellite signals. rcmc = CMC-ratio, m = m index. Data sources: Brodzik et al., 2016; Global Runoff Data Center, 2020.
Furthermore, the results of the regression based on the test data show that the model underpredicts higher discharge values in Karonga as well as Chikwawa (Figures 6, 7), which is the product of the insufficient fit of the regression line to the training data. The regression in VGS C0 yielded an R2 of 0.369 for rcmc and 0.245 for m. In cell K2, the regression indicated an R2 of ∼0.000 for rcmc and m.
In Chikwawa, a total of 15 floods were registered during the period 1989–2017, 12 of which occurred during the period of the available discharge data (until 2009), and three outside of this period. Of these resulting events, one flood took place during a data gap, and three took place in a period where the annual discharge peak did not occur (indicating that either no flood took place, or that it was not the most severe event of the year). The resulting eight reported floods in the database (i.e. 67% of the reported floods within the discharge dataset’s timespan) took place during annual discharge peaks at the downstream area of interest. In Karonga, the quality of the flood records could not be validated, as all registered floods occurred outside the timespan of the discharge dataset (1978–1991).
Due to the limited strength of the correlation between high discharge values and satellite signals, the satellite thresholds were defined with an extreme values analysis. The curves used to identify the satellite and discharge values with a 5 years treturn are found in Figure 2. The flood threshold was defined as a discharge of 1,358 m3 s−1, an rcmc of 0.168 and an m of 2.659 in Chikwawa. In Karonga, the flood threshold was defined as a discharge of 303 m3 s−1, with satellite thresholds 0.081 for rcmc and 3.076 for m.
For four of the 15 registered floods in Chikwawa, including the severe flooding in 2015, the treturn could not be calculated due to the absence of discharge data. A treturn of five years or higher was observed for four of the resulting 11 registered floods, based on their maximum discharge value. All exceedances of the discharge threshold occurred during registered flood events, meaning flash floods did not impact the average daily discharge to the extent that it increased the number of “Misses”.
In the K2-cell in Karonga, both rcmc and m exceeded the five-year threshold in seven flood seasons between 1989 and 2017 (Table 2A). Whereas most flood events from the database occurred at or near annual peaks in the satellite signals, only two of the 12 flood seasons with registered flood events were simulated by threshold exceedances of the satellite signals: the 2011 floods by rcmc, and the 2007 floods by m. The treturn of these floods could not be calculated due to absence of discharge data in this period. In the C0-cell in Chikwawa, m exceeded its five-year threshold in six flood seasons between 1989 and 2017, and rcmc in five flood seasons. m scored better than rcmc in the detection of registered flood events (Table 2B). m also performed comparatively better if just the floods with a treturn of five years or more were analyzed (Table 2C). The simulated GloFAS-values (2000–2017), extracted from the hindcast (Harrigan et al., 2020) at the coordinates of the C0 and K0-cell show very high discharge-values compared to the observed values. Because of this, the five-year treturn-thresholds of GloFAS were also relatively high: Approximately 3,432 m3 s−1 at cell C0, and 1,224 m3 s−1 at cell K0, based on discharge peaks from the wet seasons in these years. The corresponding confusion matrices can be found in Table 2.
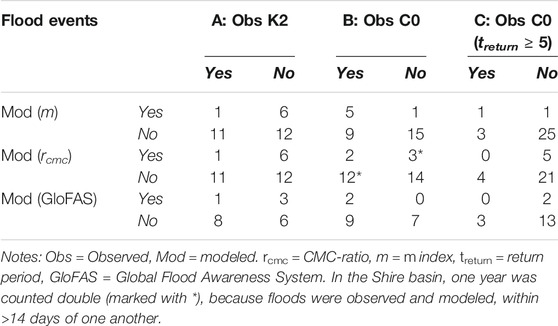
TABLE 2. Confusion matrix for the satellite signals and GloFAS model output at cells K2 and C0. 1 entry corresponds to 1 flood season between 1989 and 2017 (or 2000–2017 for GloFAS).
The majority of registered floods go undetected with the current threshold configuration (Table 2) Whereas the registered floods occur at or near annual peaks in m index and rcmc, these peaks often do not reach high enough to cross the five-year treturn threshold. In all cases where a peak did not occur directly within the period that was registered as a flood in the impact database, the satellite peak occurred 11–18 days after the discharge peak.
The low number of hits and high number of false alarms and misses led to relatively poor success metrics (low POD and CSI, and a high FAR) for both locations and satellite indices (Table 3). In Chikwawa, the best success metrics were found in the simulations done with m rather than rcmc or GloFAS. Hence, m has a lower chance than rcmc of under-reporting actual flood events (relatively high POD), a lower chance of misclassifying an event as a flood event (relatively low FAR), and a higher chance that a forecasted flood event was an actual flood event (relatively high CSI). The reason behind this is as of yet unclear, although it might have to do with the fact that the Cw-cell is situated too far from the M and Cd-cell, influencing the annual peak height and therefore the five-year threshold that was defined. Furthermore, the metrics proved better in the analysis done on all floods in the database, rather than just the floods that had been calculated to have a treturn of five years or more. In Karonga, however, the satellite signals performed similarly to one another, but more poorly than was the case for Chikwawa. Furthermore, GloFAS returned better success metrics than the PMRS method at this location (Table 3).

TABLE 3. Success metrics for flood detection by the satellite signals at Virtual Gauging Station (VGS) number K2 (A) and C0 (B). For VGS C0, success metrics were also calculated for just the floods with an observed peak discharge corresponding to a return period of 5 years or more (C).
The TLCC assessment showed that only a few upstream VGSs showed a moderate to strong positive correlation with the satellite signal observed at the downstream VGS (Figure 8). Furthermore, none reached their peak at a lag time of one or more days, as would be the case for VGSs that would be suitable for usage in an early warning setting (Figure 8). Instead, the lag times where the maximum ρ occurs (i.e., the optimal lag times) either tended toward negative or positive extremes that are not realistic for their location upstream or remained at zero days. This means that the upstream VGSs cannot be used for forecasting signals in the downstream VGS using the PMRS-method. The optimal lag times and their respective value for ρ are specified in the Supplementary Material.
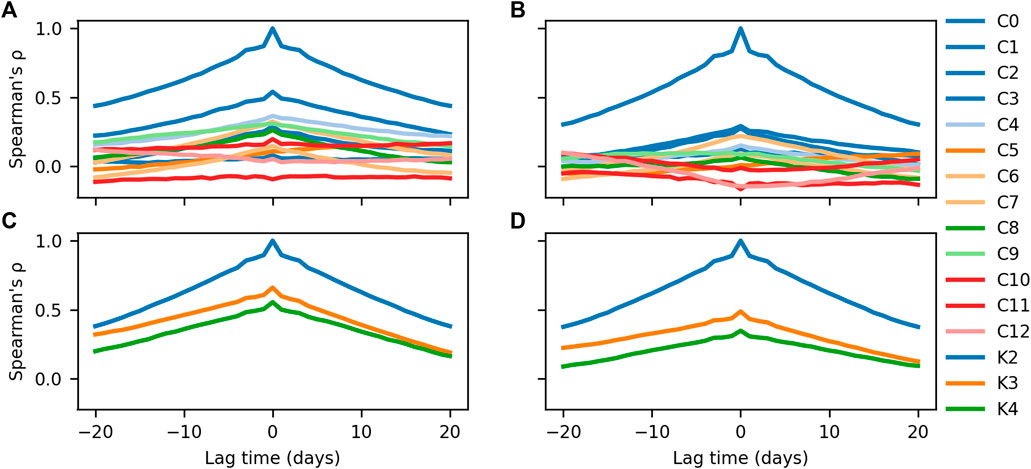
FIGURE 8. Non-parametric time-lagged cross correlation of upstream (cells K3-K4; cells C1-C12) and downstream (cell K2; cell C0) satellite-indices along the North Rukuru and Shire River. Correlations have been performed on stationary data, line labels correspond to VGSs depicted in Figure 1. Depicted are correlations for the m-signal along the North Rukuru River (A) and Shire River (B), and for the rcmc along the North Rukuru River (C) and Shire River (D).
The strongest correlations with cell C0 for the Shire River were found in VGS C1 (rcmc) and C2 (m). Along the North Rukuru, the correlations with cell K2 were strongest in VGS K3 for both indices, although only two upstream VGSs were available due to the use of K2 as a proxy as downstream VGS. Hence, while the VGSs situated close to the downstream VGS generally showed the highest correlations, correlation strength did not constantly decrease with distance.
The rcmc and m-index would ideally only show a spike if the Cd-signal and M-signal differ, indicating a flood event. The proximity of the Cd- and M-lines in Figure 3A indicate that this is roughly the case for cell C0 along the Shire River. Whereas the lines are not perfectly aligned, they follow a similar variability and a distinctly different oscillating pattern and amplitude when compared to the Cw-cell. In K0, the initial downstream VGS along the North Rukuru, the signal of M showed to be more similar in its oscillations to Cw (Lake Malawi) than to Cd (Figure 3B). This was also the case for K1, the first best upstream alternative to cell K0 (see Supplementary Material). The VGSs K0 and K1 are situated close to Lake Malawi, causing their Tb value to not follow the seasonal cycle of the river, but that of Lake Malawi (which also shows much larger fluctuations). As a result, the signal-to-noise ratio of the rcmc and m-signals is relatively high, and the detection skill of the ratios calculated from K0 and K1 is low. This was the reason that K2 was eventually selected as a proxy downstream VGS for Karonga.
The interannual trend in the discharge data of Chikwawa caused the relationship between discharge values and satellite signals to be different in dry and in wet years. This proved to be one of the main challenges encountered while performing a regression on the data in Chikwawa. When the last five years–which showcased relatively stable discharge values–were used in the regression, a positive relationship could be quantified between discharge and both rcmc and m (Figures 6A,B) in cell C0. The correlation coefficients for Chikwawa were significant, yet only moderate. The relatively low R2 shows that the model discharge predictions do not fit the test data very well and, according to Figures 6C,D, also underestimate high values, which are especially important for flood prediction.
In the regression analysis done on K2, the polynomial failed to identify the positive correlation that was expected between m/rcmc and discharge. The regression line did not cover the high discharge and satellite values in the training set (Figures 7A,B). The scatterplots provide more insight into this, showing it is not merely a statistical problem; the highest discharge-values in Karonga were not found where the highest satellite values occurred, whereas this was the case in Chikwawa. As a result of this, the regression on K2 has an R2 of nearly 0, and the model severely underestimates discharge values (Figures 7C,D). One possible explanation for the weak correlation at Karonga could be that the North Rukuru River and its flood plains are of a much smaller scale than the Shire River in both width and length (Figure 1), resulting in lower discharge values (Figures 4A, 5A). This means its contribution to signal changes in the relatively large PMRS-cell (25 × 25 km) is smaller than is the case for the Shire River.
Brakenridge et al. (2007) introduced the rcm with his research on a number of rivers, using a similar spatial resolution as was used in this study. He compared it to average daily discharge for three locations, and monthly values for three others (Table 4). Note that R2 in our study was calculated based on the relationship between predicted and observed discharge, rather than the relationship between observed discharge and the satellite signal. The scatterplots in Brakenridge et al. (2007) that included daily rather than monthly discharge data do indicate a slightly better fit between satellite data and discharge than could be observed in Figures 6A,B, 7A,B. An explorative survey through the historical satellite imagery available on Google Earth Pro 7.3.3 shows that the rivers where the experiment of Brakenridge et al. (2007) was done, range in width from 150 to 350 m (Wabash River), and 100–150 m (Red River). This is a similar size to the Shire River, although smaller floodplains are visible on the satellite imagery near Chikwawa compared to the study areas in the United States. As flooding increases the surface water fraction and therefore the value of the satellite indices changes considerably, this could explain why the PMRS-data from the United States is slightly more sensitive to high discharge values than the Malawian PMRS-data and shows stronger correlations.
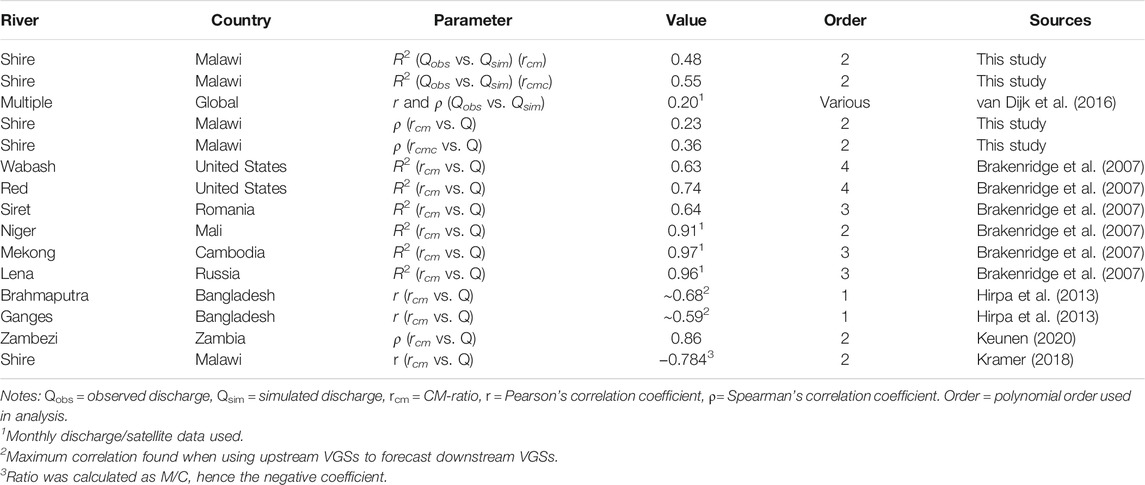
TABLE 4. Summary of relationships between passive microwave remote sensing indices and observed discharge found in existing literature.
In a study on PMRS flood detection in Namibia, De Groeve (2010) reports “excellent correlation” between discharge values and m. van Dijk et al. (2016) conducted a PMRS-experiment on a global scale, correlating simulated water extent to monthly discharge. Both the parametric and non-parametric correlation coefficient of the observed and simulated discharge were 0.2 on average (Table 4). The coefficient varied from region to region, with the stations in East-Africa showcasing particularly high coefficients in this study of larger than 0.9 (van Dijk et al., 2016). Analyses done on the Zambezi River and Shire River by respectively Keunen (2020) and Kramer (2018), the latter with fine-resolution, commercially available data, also yielded correlation coefficients higher than 0.7 (Table 4). In short, whereas the Chikwawa PMRS-data shows a moderate positive correlation and regression with the in-situ discharge data, they are relatively weak compared to the results from some other studies (Table 4).
PMRS-imagery is measured daily during a satellite overpass, while the discharge data are averaged values calculated from multiple sub-daily values. This may explain why the higher-end discharge values are not well captured in the regression relationship: Whereas a short-term discharge peak occurring on a given day will affect the average daily discharge dataset, the satellite overpass on that day might have occurred before or longer after the peak, meaning it will be less well represented in the satellite data. This could explain why in other studies, the R2 is much higher at locations where average monthly discharge data were used rather than daily values (Table 4). When discharge data are averaged over a longer period, short-term peaks affect the final value less than when they are averaged over a day, reducing the occurrence of extremely high discharge values. And, as Figures 6C,D, 7C,D show, high values are captured less well by the regression. Therefore, it can be expected that the R2 would be higher when the regression would be done on monthly hydrograph data.
As was the case in the regression analysis, the presented PMRS-method showed greater flood event detection skill and a lower rate of false alarms in the downstream cell of the Shire River than in the downstream cell of the North Rukuru River (Tables 2, 3), suggesting the PMRS-method may not be suitable for rivers with a width/discharge comparable to the latter. Furthermore, the analysis done with m in Chikwawa yielded more positive success metrics than the analysis done with rcmc, implying that m is best used for the detection of individual events at this specific location.
When comparing the results in Chikwawa when all floods are included to the results when just the floods with treturn ≥ 5 are considered, the success metrics are better for the latter subset of results. As the calculated thresholds were based on a treturn of five years, these relatively low scores for the treturn ≥ 5 analysis (Table 3C) can indicate two things: 1) The calculated 5-years threshold for discharge is not accurate. With a lower threshold, more floods would have been marked as having a treturn ≥ 5, leading to more observed flood entries into Table 2C and possibly a higher number of hits. And/or: 2) The threshold configuration for the PMRS-signals is not accurate. A lower threshold would include more events as a hit and less as a miss.
The analysis in Tables 2B, 3B included more observed flood events than in Tables 2C, 3C. The probability of achieving a “hit” or “miss” was therefore lower for the latter confusion matrix, causing comparisons between the two Shire confusion matrices to be biased. Whereas the use of success metrics (POD, CSI, FAR) should standardize some of this bias, research has shown that the CSI is still highly dependent on event frequency (Schaefer, 1990).
An adjustment of the threshold using more advanced calculations for treturn could improve the success metrics for both the North Rukuru and Shire River. For example, Jury (2014) defines floods in Chikwawa as events with a discharge of at least 1,200 m3 s−1. Whereas no treturn was mentioned with this threshold, it is substantially lower than the 1,358 m3 s−1 used in this study. De Groeve (2010) defined small regular floods to typically have an m value of 2, whereas large and unusual floods typically appear with an m of 4. This threshold is comparable to the thresholds for m found in this study, although the probabilities mentioned by the author of these floods occurring are much lower than the yearly 20% aimed for in this study. Yet, De Groeve (2010) studied a period of only seven years, which could explain these probability differences. We suggest more research is done on correctly setting the flood threshold. It is important to note that the calculated satellite thresholds are based on a sample size of roughly 30 years, meaning the sample size of floods with a treturn of five years is also relatively small. Looking at floods with a treturn of for example one or two years instead may provide better skill scores, although in an FbF-setting, activation every year would affect the cost-benefit ratio of the humanitarian program. For the same reason, the presented thresholding method can also not provide meaningful conclusions on floods with treturn values higher than 30.
A second factor that could improve the success metrics for Chikwawa, is adding more recent in-situ gauge data to the analysis. Some registered floods were omitted from the treturn ≥ 5 analysis due to lack of discharge records to calculate the treturn, one of which being the flood of 2015. This event is in fact detected by m and rcmc, but the event is not included in the confusion matrix. It is estimated by the government of Malawi that the flood event had a treturn of 500 years (Government of Malawi, 2015), meaning this is an example of a “hit” that went unreported in Table 2C.
Lastly, the success metrics could be improved if the dependency of the analysis on a complete flood impact database is reduced. Instead of comparing satellite threshold exceedances with a database, they could be directly compared with exceedances of certain observed discharge values as a proxy for floods, reducing the risk that false alarms are caused by a lack of impact data.
The fact that correlation strength did not constantly decrease with distance from the downstream VGS, suggests that more factors than the head stream influence m and rcmc signals, such as surface characteristics (flood plain width, geomorphology) or the presence of other rivers in the cells. When comparing the two satellite signals, the rcmc exhibited slightly stronger upstream-downstream correlations than m in the majority of VGS cells along both rivers.
The lines in Figure 8 with a maximum ρ at a lag time of 0 days, correspond to VGSs of which the delay of the detected signal is on average not longer than 24 h. The majority of the VGSs showed this pattern. This is in contrast with the findings of Hirpa et al. (2013), who used upstream VGSs to forecast discharge at a downstream point. The authors of this study did find positive lag times when using VGSs further upstream, but also studied larger-scale watersheds than was done in this study. Brakenridge et al. (2007) also found lag times at some of the downstream VGSs studied, but no lag time at others. The authors suggest that this has to do with the geography of the river floodplains; some floodplains are situated in flat terrain. Flooding there is induced by local precipitation or snowmelt, inducing a synchronous rise in discharge and satellite signal. However, floodplains with a steeper gradient situated in drier conditions have their inundation governed more by small-scale topography, hydraulic connectivity and local resistance to flow, which may lead to positive lag times (Brakenridge et al., 2007). The immediate response of the satellite signals in cells C0 and K2 compared to upstream signals, indicate that the North Rukuru River and the Shire River belong to the first group described, or that they are simply too small-scale for this forecasting method.
The TLCC was implemented using the data from the complete study period 1978–2017, and data points from only the wet season. When only a few recent years are studied, or data over the whole year are included, the ρ coefficients, lag times and therefore the suitability of the upstream VGSs may be different. Another factor that had a large influence on the analysis was the method used to detrend the data. Using more advanced methods may change the effect this step has on the forecasts and lag times. The focus in this paper was on the relationship between upstream VGSs with the downstream VGSs, due to the humanitarian importance of the latter areas (hazard exposure, vulnerability, etc.). From a hydrological perspective, however, it may also be useful to perform a test by correlating all VGSs along the river with one another, as floods may also take place at different points along the river.
The regression relationship between PMRS-indices and discharge found in this study is not strong enough to directly compare the discharge values with the values simulated by GloFAS. Furthermore, GloFAS represents a true weather-to-flow model, whereas the currently presented method is more hydrological in nature, which complicates a direct comparison between the two. An indication of the comparative detection skill of both methods can be made by comparing the statistical indices resulting from them. Teule (2019) did a regression analysis on the discharges as simulated by GloFAS in Chikwawa with observed discharge data. The global model showed to have a correlation with discharge in Chikwawa, quantified by the Pearson’s correlation coefficient (which can be interpreted similarly to Spearman’s ρ) of 0.25. The R2 was 0.06, indicating a lower skill than the statistics found for both rcmc and m index in this study. This suggests that in Chikwawa, the PMRS-method described in this study can more accurately estimate discharge values compared to GloFAS. This previous point was confirmed while doing the extreme value analysis. The 5-years treturn threshold found using the GloFAS data is more than double the threshold found for the observed discharge data. This is in line with the findings by Teule (2019), who also indicated that GloFAS tends to systematically overestimate discharge at this location.
Exceedances of trigger thresholds can also be compared directly, as GloFAS-data with a 0 day lead time is available for both (part of) the K0 and C0-cells. The success metrics at C0 show that, when the trigger thresholds for GloFAS are calculated the same way as the thresholds in the PMRS-model were calculated, m performs better than GloFAS in detecting flood events and it generates fewer false alarms (Table 3). In K2, GloFAS returned a low POD and CSI and a high FAR, but the success metrics suggested slightly better performance than the PMRS-method at this location. Caution should be taken when comparing the metrics, however, as the GloFAS study period (2000–2018) is shorter than the period used to construct the confusion matrices for m and rcmc.
GloFAS is used in (pilots of) several national EWSs and is also currently used by the Red Cross in Zambia. As it is a coupled ocean-atmosphere general circulation model, it can represent large-scale modes of variability such as the North Atlantic Oscillation (NAO) or the El Niño–Southern Oscillation (ENSO), among others (Emerton et al., 2018). In many countries in Sub-Saharan Africa, including Malawi, teleconnections are less prevalent to absent and the detection or forecasting skill of models such as GloFAS is likely to be lower, which explains the poor success metrics for this method in both locations. Unfortunately, no historical data on ODSS, the EWS currently in place in the Lower Shire River Basin, was available. The discharge detection-skill of our model can therefore not be compared to that of ODSS.
When used in a detection setting, the PMRS-method presented in this study performs better than GloFAS in both detecting absolute discharge and flood events in Chikwawa. However, the applicability of the PMRS-method is location-dependent: Whereas the detection skill for discharge is relatively high in Chikwawa (cell C0), this is not the case in Karonga (cell K2). For flood forecasting, the upstream VGSs in both locations did not provide a sufficiently strong correlation with the downstream satellite signal at a sufficient lag time to be qualified suitable for use in an early warning setting. The current EWS in the Lower Shire Basin, ODSS, makes use of high-frequency real-time rainfall and water level data and precipitation forecasts (Ammentorp and Richaud, 2016). As many data-scarce regions do not have access to this data, the realization of ODSS (or a comparable system) is not realistic there. In these areas, a coupled solution is possible including a global model such as GloFAS and the presented PMRS-method for calibration of discharge values, flood impact estimation and support for humanitarian operations. Revilla-Romero et al. (2015) showed that the use of raw PMRS-data as a proxy for streamflow in the calibration of the GloFAS system tends to improve the performance of this global model.
More research could be done in the potential spatial applicability of rcmc by linking rcmc-data to high-resolution Digital Elevation Models of the study area. Since rcmc can be interpreted spatially as a fraction of flood water in the cell (Neisingh, 2018), flood extents could be simulated on maps just after (or even during) flood events, before the sky has cleared up and therefore before optical satellite imagery of the affected region is available. This could facilitate humanitarian missions by being able to identify affected areas early on and reach the people who are in need of humanitarian aid the most.
This research was done by using historical PMRS-data from the MEaSUREs-dataset that spanned a period until 2017. Of course, should PMRS be included in an EWS, it is important to gain access to openly available recent data in real-time. At the time of writing, multiple satellites and sensors that operate at or near the 36.5–37.0 GHz frequency are currently operational and provide data in (near) real-time, for example RosHydromet’s Meteor-M N2 satellite series or the DMSP-F17 satellite, which was used in this study. More research could be done in which agencies provide open access to their PMRS-data, or where new partnerships could be made.
The way in which the calibration cells were chosen and the data were treated impacted the outcome of this study substantially. Firstly, the rcmc method is based upon the use of a wet calibration target (Cw) covering a complete grid cell. For the case study of Chikwawa, for example, the closest suitable target was located 125 km away, over Lake Chilwa. The drying of Lake Chilwa in 1996 is recognizable in Cw (Figure 3A) and the resulting rcmc for Chikwawa, but the discharge records do not show this pattern at all (Figures 4A,B), implying the Shire was likely unaffected by this change. Hence, this is an example of a situation where the large distance between M and Cw likely affected the accuracy of the analysis negatively. In the case of Karonga, Cw was located much closer to the VGSs. Here, however, the similarity of the signal originating from the M- and Cw-cells indicates that M should also not be in too close of a proximity to a large water body, as the signal of the water body may influence what is observed in the M-cell (Figure 3B). The choice to make use of Cw (and thus the rcmc-signal rather than the m-signal) in an analysis should therefore be taken cautiously, especially in the case of coastal regions and should depend on the geography of the study area in question. Secondly, the use of a dry calibration cell in the calculations of m index and rcmc is based upon the assumption that there is no water present in the dry calibration cell Cd, while there are small streams and puddles present even in the driest regions, it was therefore assumed that their influence would be negligible when observing the Tb of a large grid cell.
As mentioned in PMRS Data, a backwards-looking mean filter was applied to the raw Tb data prior to the calculation of the satellite indices. Applying a different filter method to the raw data, such as the Savitzky-Golay filter based on a centered window (Savitzky and Golay, 1964), could significantly alter the outcomes of this study, as a backwards-looking filter may delay the moment when flood-induced increases in satellite signals are visible in the ratio. However, whereas applying stronger filters to data can bend results more positively toward significance, the question remains when an advanced filtering method is justified, whether it can be used under operational conditions (such as triggering early action), that require forecasts based on only backward-looking data, and how it impacts the relevance of the satellite data in connection to the real hydrological relationships. More research should therefore be done on which filtering method is most optimal in the context of the use of PMRS for flood early warning.
This research is built upon the assumptions that generally, a widening of a river upstream will lead to a widening of the river and/or bank overflow downstream, and that an increase in discharge leads to a widening of the river. In reality, the propagation of a flood depends on many other factors, including antecedent soil moisture and river diversions caused by bank overflow. This could partially explain why the correlations of the upstream VGSs did not decrease in strength with distance from the downstream VGS in the TLCC. The impact of geomorphic factors on the signal response was also discussed by Brakenridge et al. (2007), who observed that the shape and slope of the river impact whether or not there is a lag between peak discharge records and peak signals.
Furthermore, presence of man-made barriers such as hydroelectric dams regulates the hydrological relationships between upstream and downstream points of interest. This factor has not been taken into account in this study, but it could be one of the reasons the TLCC did not produce a potential forecasting VGS, as the Kapichira Hydroelectric Power Station is situated just upstream from Chikwawa (Figure 1B).
Lastly, the relatively large size of the VGS cells means that one cannot be certain no other rivers or water bodies are present in the VGS. This became apparent when studying K0, where not only Lake Malawi is situated within the cell, but also some other, mainly non-perennial rivers. This factor may impact the signals in Chikwawa as well: Whereas no medium-to-large rivers other than one tributary of the Shire are visible within the bounds of the VGS, smaller streams and ponds can still influence the observed signal. Using finer-resolution PMRS-data could possibly exclude some of these disturbing factors, but calibration cells should be chosen carefully: the rcmc and m utilize relative signal differences, and fine resolution data tends to be spatially smooth. The correlation between the rcm and commercially available, high resolution (300 × 300 m) PMRS data in Malawi has been researched by 510 (Kramer, 2018), and a strong correlation was found in some pixels along the Shire River. Finer resolution grids are available in the MEaSUREs dataset, but were not used in this study due to the fact that they have been merely resampled from coarser-resolution data, and because longer timeseries were available of the coarser resolution grid. Hence, more research could be done on the exact impact of the spatial resolution of the PMRS-data on the detection skill.
Whereas it was assumed that the flood impact database was relatively complete, floods may have taken place and gone unreported, especially if they took place in a location with little to no settlement (low exposure) or where high protection led to a low impact (low vulnerability). Furthermore, floods may have taken place along the Shire or North Rukuru River, but not precisely at the location of our VGSs. This affects the relevance of the success metrics, as the trustworthiness of misses and false alarms depends on the assumption of a comprehensive database. Based on the conducted quality check of the database, it is assumed that floods that are described in the database did indeed take place at our downstream VGSs, and that the number of “hits” and “misses” and POD-metric derived from them can be trusted. The POD should therefore be leading in the interpretation of the success metrics in this study. In future research, the flood impact database could be expanded using methods such as text mining.
The aim of this research was to investigate whether openly available, relatively coarse-resolution PMRS-data could be used for flood-EWSs in the Shire River Basin in Chikwawa and the North Rukuru River Basin in Karonga. The specific novelty is that these represent two much smaller streams than so far used for flood detection with PMRS. Two satellite indices were used, including one relatively new one: the rcmc, which was proposed by Neisingh (2018), and m, which is rcm expressed as a relative magnitude.
We firstly hypothesized that the PMRS-method would be adequate for detecting and forecasting floods in both study areas. This hypothesis was only partially rejected; rcmc and m contain a similar seasonality to the discharge hydrographs at both locations, as long as the downstream VGS was located at a sufficient distance from a large water body. However, only the location in Chikwawa, which covers the relatively larger-scale river, provided a moderate positive correlation between observed discharge values and the satellite indices. Regarding the forecasting potential, no VGS was identified that had both a satellite signal that was strongly correlated to the downstream satellite signal, and a positive lag time of >0 days at the point of maximum correlation. This means that upstream VGSs cannot be integrated in a flood EWS to forecast downstream floods. Neither rcmc nor m detected the majority of registered individual flood events at the current threshold configuration. Considering the fact that the peaks of the satellite data that occur near the registered floods, however, we suggest more research is done in setting a correct trigger threshold or investigating events at different treturn values, as this could provide a substantial improvement from the success metrics presented in this research. When comparing the detection potential of m and rcmc, the latter performed better in estimating absolute discharge values. However, when looking at flood occurrence, the success metrics proved to be better for m. The previously summarized findings did confirm our second hypothesis, namely that the study area with the relatively wider river and larger basin (Shire) will be more suitable for flood detection and forecasting using PMRS than the smaller-scale study area (North Rukuru).
When benchmarking our findings against discharge values as simulated by the global model GloFAS, the presented PMRS-method would be preferred over GloFAS when it comes to both flood event detection and discharge estimation in Chikwawa. In Karonga, where the study area comprised a much smaller stream, neither method provided satisfactory results, although GloFAS performed slightly better. Relatively small streams such as the North Rukuru will therefore have to rely on different detection and forecasting tools than large-scale remote sensing data or global models. Yet, the relatively low data demand of the presented PMRS-method means that it has a potential to be used to support EWSs in data-scarce, ungauged regions, whereas this is more difficult to achieve for national EWSs such as ODSS due to their high data demand. Overall, a coupled EWS solution where a global forecasting model is calibrated with PMRS-estimated discharge, and supported by PMRS-estimated flood extent, seems optimal in these regions. Apart from further research on threshold setting and different spatial resolutions, research will be necessary on how to communicate the uncertainties associated with each of the systems, how to spatially interpret rcmc using a high-resolution digital elevation model, and how to practically implement such a coupled solution.
Publicly available datasets were analyzed in this study. This data can be found here: Satellite data: NSIDC (https://n5eil01u.ecs.nsidc.org/MEASURES/NSIDC-0630.001/) Discharge data: GRDC (https://portal.grdc.bafg.de) and Malawi’s Department of Water Resources. Flood impact data: EM-DAT (https://www.emdat.be/), Dartmouth Flood Observatory (https://www.dartmouth.edu/∼floods/) and GLIDE (https://glidenumber.net/glide/public).
This research was originally conducted as part of an MSc thesis by LM, under the supervision of AP and MH, who also contributed to the conception and design of this study. HW introduced some of the used techniques to the authors, including the CMC-ratio and data extraction scripts, and contributed to the final drafts. LM performed the statistical analysis and wrote the first draft of the manuscript. All authors contributed to manuscript revision, and read and approved the submitted version.
This project was carried out at 510, an initiative of the Netherlands Red Cross. The scope of the work is shaped to meet the goals and areas of intervention as stipulated in three Red Cross-led disaster preparedness projects that the European Civil Protection and Humanitarian Aid Operations funded in Malawi between 2017 and 2021. The publishing fees were partially funded by the Lund University APC Fund.
Author HW was employed by the company Rainbow Sensing.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Our sincere thanks to the Malawi Department of Water Resources (DWR) and the Global Runoff Data Center for providing the discharge datasets. We would also like to thank the Malawi Data Team (Gumbi and Simon Tembo) for their support, and Wouter Neisingh for his work on the CMC-ratio. Lastly, we would like to express our gratitude and respects to Piasi Kaunda of DWR, who, although he is no longer with us, has been instrumental for the FbF program over the course of his career.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.670997/full#supplementary-material
Aich, V., Liersch, S., Vetter, T., Huang, S., Tecklenburg, J., Hoffmann, P., et al. (2013). Comparing Impacts of Climate Change on Streamflow in Four Large African River Basins. Hydrol. Earth Syst. Sci. Discuss. 10, 13005–13052. doi:10.5194/hessd-10-13005-2013
Ammentorp, H. C., and Richaud, B. (2016). “Sub-components A3(II): Operational Decision Support System through Enhanced Hydro-Meteorological Services,” in ODSS System Design and Development. Editor S. R. B.M.P.P (Lilongwe: Ministry of Agriculture, Irrigation and Water Development).
Boelee, L., Zsoter, E., Lumbroso, D., Samuels, P., Bazo, J., and Cloke, H. (2017). “Analysis of the Uncertainty in Flood Predictions of GLoFAS for Piura in the Pacific Region of Peru,” in European Geosciences Union General Assembly 2017, Vienna, Austria, April 23–28, 2017.
Brakenridge, G. R., Nghiem, S. V., Anderson, E., and Mic, R. (2007). Orbital Microwave Measurement of River Discharge and Ice Status. Water Resour. Res. 43 (4), W04405. doi:10.1029/2006WR005238
Brodzik, M. J., Long, D. G., Hardman, M. A., Paget, A., and Armstrong, R. (2016). MEaSUREs Calibrated Enhanced-Resolution Passive Microwave Daily EASE-Grid 2.0 Brightness Temperature ESDR, Version 1. NSIDC. Available at: https://nsidc.org/sites/nsidc.org/files/technical-references/MEaSUREs_CETB_ATBD_v1.0.pdf.
Chew, C., Reager, J. T., and Small, E. (2018). CYGNSS Data Map Flood Inundation during the 2017 Atlantic hurricane Season. Sci. Rep. 8 (1), 9336. doi:10.1038/s41598-018-27673-x
Chew, C., and Small, E. (2020). Estimating Inundation Extent Using CYGNSS Data: A Conceptual Modeling Study. Remote Sensing Environ. 246, 111869. doi:10.1016/j.rse.2020.111869.Chidanti-
CREDUNDRR (2020). The Human Cost of Disasters - an Overview of the Last 20 Years 2000-2019. United Nations Office for Disaster Risk Reduction. Brussels, Belgium: Centre for Research on the Epidemiology of Disasters.
D'Addabbo, A., Capolongo, D., and Refice, A. (2018). Flood Monitoring through Remote Sensing. Switzerland, Springer International Publishing. SpringerLink.
Dartmouth Flood Observatory (2020). Global Active Archive of Large Flood Events. Available at: http://www.dartmouth.edu/∼floods/Archives/.
De Groeve, T. (2010). Flood Monitoring and Mapping Using Passive Microwave Remote Sensing in Namibia. Geomatics, Nat. Hazards Risk 1 (1), 19–35. doi:10.1080/19475701003648085
De Groeve, T., Kugler, Z., and Brakenridge, R. (2007). “Near Real Time Flood Alerting for the Global Disaster Alert and Coordination System,” in Proceedings of the 4th International Conference on Information Systems for Crisis Response and Management ISCRAM2007, Delft, Netherlands, May 13–16, 2007. 33–39.
DoDMA (2015). Malawi Hazards and Vulnerability Atlas. Nairobi, Kenya: Regional Centre for Mapping of Resources for Development.
Emerton, R., Zsoter, E., Arnal, L., Cloke, H. L., Muraro, D., Prudhomme, C., et al. (2018). Developing a Global Operational Seasonal Hydro-Meteorological Forecasting System: GloFAS-Seasonal v1.0. Geosci. Model. Dev. 11, 3327–3346. doi:10.5194/gmd-11-3327-2018
FAO (2011). Data From: Irrigation and Drainage Development. AQUASTAT database. Rome, Italy. Available at: http://www.fao.org/aquastat/en/
GLIDE (2020). GLIDE Search. Available at: https://glidenumber.net/glide/public/contact.jsp.
Global Runoff Data Centre (2020). MWAKIMEME (65312401) Daily Data. Koblenz, Germany: The Global Runoff Data Centre.
Government of Malawi (2015). Malawi 2015 Floods Post Disaster Needs Assessment Report. Lilongwe, Malawi: Government of Malawi.
Guha-Sapir, D. (2020). EM-DAT. Available at: https://public.emdat.be/.
Harrigan, S., Zsoter, E., Alfieri, L., Prudhomme, C., Salamon, P., Wetterhall, F., et al. (2020). River Discharge and Related Historical Data from the Global Flood Awareness System v2.1. Reading, United Kingdom: Copernicus Climate Change Service by ECMWF. Available at: https://cds.climate.copernicus.eu/cdsapp#!/dataset/cems-glofas-historical?tab=overview. doi:10.24381/cds.a4fdd6b9
Hirpa, F. A., Hopson, T. M., De Groeve, T., Brakenridge, G. R., Gebremichael, M., and Restrepo, P. J. (2013). Upstream Satellite Remote Sensing for River Discharge Forecasting: Application to Major Rivers in South Asia. Remote Sensing Environ. 131, 140–151. doi:10.1016/j.rse.2012.11.013
Hussain, M., Arsalan, M. H., Siddiqi, K., Naseem, B., and Rabab, U. (2005). Emerging Geo-Information Technologies (GIT) for Natural Disaster Management in Pakistan: an Overview. Proceedings of 2nd International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, June 9–11, 2005. RAST 2005, 487–493.
IFRC (2020). What Is a Disaster? Available at: https://www.ifrc.org/en/what-we-do/disaster-management/about-disasters/what-is-a-disaster/. (Accessed 2 21.2020)
initiative of the Netherlands Red Cross (2020). Community Risk Dashboard. Available at: https://profiles.510.global/#!/community_risk). (Accessed 3 2, 2020).
Jjemba, E. W., Mwebaze, B. K., Arrighi, J., de Perez, E. C., and Bailey, M. (2018). “Forecast-Based Financing and Climate Change Adaptation,” in Resilience. Editors Z. Zommers, and K. Alverson (Netherlands: Elsevier), 237–242. doi:10.1016/b978-0-12-811891-7.00019-0
Jury, M. R. (2014). Malawi's Shire River Fluctuations and Climate. J. Hydrometeorology 15 (5), 2039–2049. doi:10.1175/JHM-D-13-0195.1
Kelly, L., Bertram, D., Ngongondo, C., and Kalin, R. (2019). Characterization of Groundwater Discharge to Rivers in the Shire River Basin, Malawi. Water Sci. Eng. 5, 127–138.
Keunen, O. (2020). Flood Forecasting Using Passive Microwave Radiometry In the Zambezi River. Zambia: Water Management, Delft University of Technology.
Kramer, T. (2018). Relating VanderSat Microwave Brightness Temperature to Discharge of the Shire River in Southern Malawi. Internship Rep., 510.
Kugler, Z., and De Groeve, T. (2007). “The Global Flood Detection System,” in Scientific And Technical Research Series. (Luxembourg: Joint Research Centre – Institute for the Protection and Security of the Citizen).
Malawi Meteorological Services (2020). Climate Of Malawi [Online]. Available at: https://www.metmalawi.com/climate/climate.php.
Malunga, J. (2011). Adaptive Strategies to Climate Change in Southern Malawi. Phys. Chem. Earth, Parts A/B/C 36(14), 1043–1046. doi:10.1016/j.pce.2011.08.012
Manda, M., and Wanda, E. (2017). Understanding the Nature and Scale of Risks in Karonga, Malawi. Environ. Urbanization 29 (1), 15–32. doi:10.1177/0956247817692200
Mijoni, P. L., and Izadkhah, Y. O. (2009). Management of Floods in Malawi; Case Study of the Lower Shire River Valley. Disaster Prevention And Management. Int. J. 18 (5), 490–503. doi:10.1108/09653560911003688
Mwale, F. D., Adeloye, A. J., and Rustum, R. (2012). Infilling of Missing Rainfall and Streamflow Data in the Shire River basin, Malawi - A Self Organizing Map Approach. Phys. Chem. Earth, Parts A/B/C 50-52, 34–43. doi:10.1016/j.pce.2012.09.006
NASA/METI/AIST/Japan SpacesystemsU.S./Japan ASTER Science Team (2019). ASTER Global Digital Elevation Model V003. NASA EOSDIS Land Processes DAAC. doi:10.5067/ASTER/ASTGTM.003
National Statistics Office of Malawi (2018). Malawi Administrative Level 0-3 boundariesHumanitarian Data Exchange. Available at: https://data.humdata.org/dataset/malawi-administrative-level-0-3-boundaries.
Neisingh, W. (2018). Inundation Mapping in a Dynamic, Data-Scarce Environment Using Ka-Band Passive Microwave Radiometry. Ouémé Delta. Benin: MSc Watermanagement, TU Delft
Ngongondo, C., Xu, C.-Y., Gottschalk, L., and Alemaw, B. (2011). Evaluation of Spatial and Temporal Characteristics of Rainfall in Malawi: a Case of Data Scarce Region. Theor. Appl. Climatol 106 (1), 79–93. doi:10.1007/s00704-011-0413-0
Njaya, F., Snyder, K. A., Jamu, D., Wilson, J., Howard-Williams, C., Allison, E. H., et al. (2011). The Natural History and Fisheries Ecology of Lake Chilwa, Southern Malawi. J. Great Lakes Res. 37, 15–25. doi:10.1016/j.jglr.2010.09.008
OpenStreetMap contributors (2020). HOTOSM Malawi Waterways (OpenStreetMap Export). Cambridge, United Kingdom: Humanitarian Data ExchangeMarch 2020. Available at: https://data.humdata.org/dataset/hotosm_mwi_waterways.
Palmer, S. C. J., Kutser, T., and Hunter, P. D. (2015). Remote Sensing of Inland Waters: Challenges, Progress and Future Directions. Remote Sens. Environ. 157, 1–8. doi:10.1016/j.rse.2014.09.021
Pauw, K., Thurlow, J., Bachu, M., and Van Seventer, D. E. (2011). The Economic Costs of Extreme Weather Events: a Hydrometeorological CGE Analysis for Malawi. Envir. Dev. Econ. 16 (2), 177–198. doi:10.1017/S1355770X10000471
RCMRD (2015). Africa - Water Bodies. Available at: https://datacatalog.worldbank.org/dataset/resource/ba222d14-693c-4ba0-9bfd-671130934c1e.
Revilla-Romero, B., Beck, H. E., Burek, P., Salamon, P., de Roo, A., and Thielen, J. (2015). Filling the Gaps: Calibrating a Rainfall-Runoff Model Using Satellite-Derived Surface Water Extent. Remote Sensing Environ. 171, 118–131. doi:10.1016/j.rse.2015.10.022
Revilla-Romero, B., Thielen, J., Salamon, P., De Groeve, T., and Brakenridge, G. R. (2014). Evaluation of the Satellite-Based Global Flood Detection System for Measuring River Discharge: Influence of Local Factors. Hydrol. Earth Syst. Sci. 18 (11), 4467–4484. doi:10.5194/hess-18-4467-2014
Šakić Trogrlić, R., Wright, G. B., Duncan, M. J., van den Homberg, M. J. C., Adeloye, A. J., Mwale, F. D., et al. (2019). Characterising Local Knowledge across the Flood Risk Management Cycle: A Case Study of Southern Malawi. Sustainability 11 (6). doi:10.3390/su11061681
Savitzky, A., and Golay, M. J. E. (1964). Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 36 (8), 1627–1639. doi:10.1021/ac60214a047
Schaefer, J. T. (1990). The Critical Success Index as an Indicator of Warning Skill. Wea. Forecast. 5 (4), 570–575. doi:10.1175/1520-0434(1990)005<0570:tcsiaa>2.0.co;2
Smith, L. C. (1997). Satellite Remote Sensing of River Inundation Area, Stage, and Discharge: a Review. Hydrol. Process. 11 (10), 1427–1439. doi:10.1002/(sici)1099-1085(199708)11:10<1427::aid-hyp473>3.0.co;2-s
Svendsen, M., Ewing, M., and Msangi, S. (2009). Measuring Irrigation Performance in Africa. Washington: International Food Policy Research Institute. (IFPRI), IFPRI discussion papers
Teule, T. (2019). Assessing Two Methods to Potentially Improve the Flood Early Warning System in the Lower Shire Valley in Malawi. VU: MSc Hydrology.
Unnithan, S. L. K., Biswal, B., and Rüdiger, C. (2020). Flood Inundation Mapping by Combining GNSS-R Signals with Topographical Information. Remote Sensing 12 (3026), 3026. doi:10.3390/rs12183026
van den Homberg, M. J. C., Gevaert, C. M., and Georgiadou, Y. (2020). The Changing Face of Accountability in Humanitarianism: Using Artificial Intelligence for Anticipatory Action. PaG 8, 456–467. doi:10.17645/pag.v8i4.3158
van Dijk, A. I. J. M., Brakenridge, G. R., Kettner, A. J., Beck, H. E., De Groeve, T., and Schellekens, J. (2016). River Gauging at Global Scale Using Optical and Passive Microwave Remote Sensing. Water Resour. Res. 52 (8), 6404–6418. doi:10.1002/2015WR018545
Keywords: physical geography, riverine floods, flood modeling, malawi, remote sensing, early warning, disaster risk
Citation: Mokkenstorm LC, van den Homberg MJC, Winsemius H and Persson A (2021) River Flood Detection Using Passive Microwave Remote Sensing in a Data-Scarce Environment: A Case Study for Two River Basins in Malawi. Front. Earth Sci. 9:670997. doi: 10.3389/feart.2021.670997
Received: 22 February 2021; Accepted: 22 June 2021;
Published: 05 July 2021.
Edited by:
Rosanna Bonasia, Escuela Superior de Ingeniería y Arquitectura Unidad Zacatenco, Instituto Politécnico Nacional, MexicoReviewed by:
Guy Jean-Pierre Schumann, University of Bristol, United KingdomCopyright © 2021 Mokkenstorm, van den Homberg, Winsemius and Persson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lone C. Mokkenstorm, bGNtb2trZW5zdG9ybUBnbWFpbC5jb20=; Andreas Persson, YW5kcmVhcy5wZXJzc29uQG5hdGVrby5sdS5zZQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.