
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Complex Syst. , 08 October 2024
Sec. Complex Networks
Volume 2 - 2024 | https://doi.org/10.3389/fcpxs.2024.1479417
Understanding how neural networks process information is a fundamental challenge in neuroscience and artificial intelligence. A pivotal question in this context is how external stimuli, particularly noise, influence the dynamics and information flow within these networks. Traditionally, noise is perceived as a hindrance to information processing, introducing randomness and diminishing the fidelity of neural signals. However, distinguishing noise from structured input uncovers a paradoxical insight: under specific conditions, noise can actually enhance information processing. This intriguing possibility prompts a deeper investigation into the nuanced role of noise within neural networks. In specific motifs of three recurrently connected neurons with probabilistic response, the spontaneous information flux, defined as the mutual information between subsequent states, has been shown to increase by adding ongoing white noise of some optimal strength to each of the neurons. However, the precise conditions for and mechanisms of this phenomenon called ‘recurrence resonance’ (RR) remain largely unexplored. Using Boltzmann machines of different sizes and with various types of weight matrices, we show that RR can generally occur when a system has multiple dynamical attractors, but is trapped in one or a few of them. In probabilistic networks, the phenomenon is bound to a suitable observation time scale, as the system could autonomously access its entire attractor landscape even without the help of external noise, given enough time. Yet, even in large systems, where time scales for observing RR in the full network become too long, the resonance can still be detected in small subsets of neurons. Finally, we show that short noise pulses can be used to transfer recurrent neural networks, both probabilistic and deterministic, between their dynamical attractors. Our results are relevant to the fields of reservoir computing and neuroscience, where controlled noise may turn out a key factor for efficient information processing leading to more robust and adaptable systems.
Artificial neural networks are a cornerstone of many contemporary machine learning methods, especially in deep learning (LeCun et al., 2015). Over the past decades, these systems have found extensive applications in both industrial and scientific domains (Alzubaidi et al., 2021). Typically, neural networks in machine learning are organized in layered structures, where information flows unidirectionally from the input layer to the output layer. In contrast, Recurrent Neural Networks (RNNs) incorporate feedback loops within their neuronal connections, allowing information to continuously circulate within the system (Maheswaranathan et al., 2019). Consequently, RNNs function as autonomous dynamical systems with ongoing neural activity even in the absence of external input, and they are recognized as ‘universal approximators’ (Maximilian Schäfer and Zimmermann, 2006). These unique characteristics have spurred a significant increase in research on artificial RNNs, leading to both advancements and intriguing unresolved issues: Thanks to their recurrent connectivity, RNNs are particularly well-suited for processing time series data (Jaeger, 2001) and for storing sequential inputs over time (Schuecker et al., 2018; Büsing et al., 2010; Dambre et al., 2012; Wallace et al., 2013; Gonon and Ortega, 2021). For example, RNNs have been shown to learn robust representations by dynamically balancing compression and expansion (Farrell et al., 2022). Specifically, a dynamic state known as the ‘edge of chaos’, situated at the transition between periodic and chaotic behavior (Kadmon and Sompolinsky, 2015), has been extensively investigated and identified as crucial for computation (Wang et al., 2011; Boedecker et al., 2012; Langton, 1990; Natschläger et al., 2005; Legenstein and Maass, 2007; Bertschinger and Natschläger, 2004; Schrauwen et al., 2009; Toyoizumi and Abbott, 2011; Kaneko and Suzuki, 1994; Solé and Miramontes, 1995) and short-term memory (Haruna and Nakajima, 2019; Ichikawa and Kaneko, 2021). Moreover, several studies focus on controlling the dynamics of RNNs (Rajan et al., 2010; Jaeger, 2014; Haviv et al., 2019), particularly through the influence of external or internal noise (Molgedey et al., 1992; Ikemoto et al., 2018; Krauss et al., 2019a; Bönsel et al., 2022; Metzner and Krauss, 2022). RNNs are also proposed as versatile tools in neuroscience research (Barak, 2017). Notably, very sparse RNNs, similar to those found in the human brain (Song et al., 2005), exhibit remarkable properties such as superior information storage capacities (Brunel, 2016) (Narang et al., 2017; Gerum et al., 2020; Folli et al., 2018).
In our previous research, we systematically analyzed the relation between network structure and dynamical properties in recurrent three-neuron motifs (Krauss et al., 2019b). We also demonstrated how statistical parameters of the weight matrix can be used to control the dynamics in large RNNs (Krauss et al., 2019c; Metzner and Krauss, 2022). Another focus of our research are noise-induced resonance phenomena (Bönsel et al., 2022; Schilling et al., 2022; Krauss et al., 2016; Schilling et al., 2021; Schilling et al., 2023). In particular, we discovered that in specific recurrent motifs of three probabilistic neurons, connected with ternary
Since
The present work aims to understand, on a deeper level than before, the pre-conditions of the RR phenomenon, as well as its mechanism. As model systems, we will mainly use probabilistic SBMs, but we will also briefly consider deterministic networks with ‘
We consider a recurrent network of
Here, the first bracket contains a possible bias
In the deterministic model, neural output signals are continuous in the range
To initialize the deterministic network, the
In the probabilistic model, neural output signals are discrete with the two possible values
To initialize the probabilistic network, the
We also refer to our probabilistic model as a Symmetrical Boltzmann Machine (SBM), which is called ‘symmetric’ because the binary outputs are set to
Note that here we do not apply any input to the recurrent neural networks, and thus
After defining the weight matrix and randomly initializing a network, the time series of global system states
Numerical evaluation of information theoretic quantities requires data with discrete values. The binary output of the SBM is perfectly suited for this purpose, but in the case of the tanh-network we first needed to binarize the continuous outputs
The starting point for all our information theoretic quantities is the joint probability
The first information theoretical quantity of interest in the state entropy
where all terms with
The next relevant quantity is the mutual information
where all terms with
The final important quantity is the conditional entropy
Our first goal is to identify the preconditions of RR, in particular regarding the network weight matrices. For this purpose, we consider a Symmetric Boltzmann Machine (SBM, see Methods for details) (Equations 1–3) with
As a basis for the network’s weight matrix
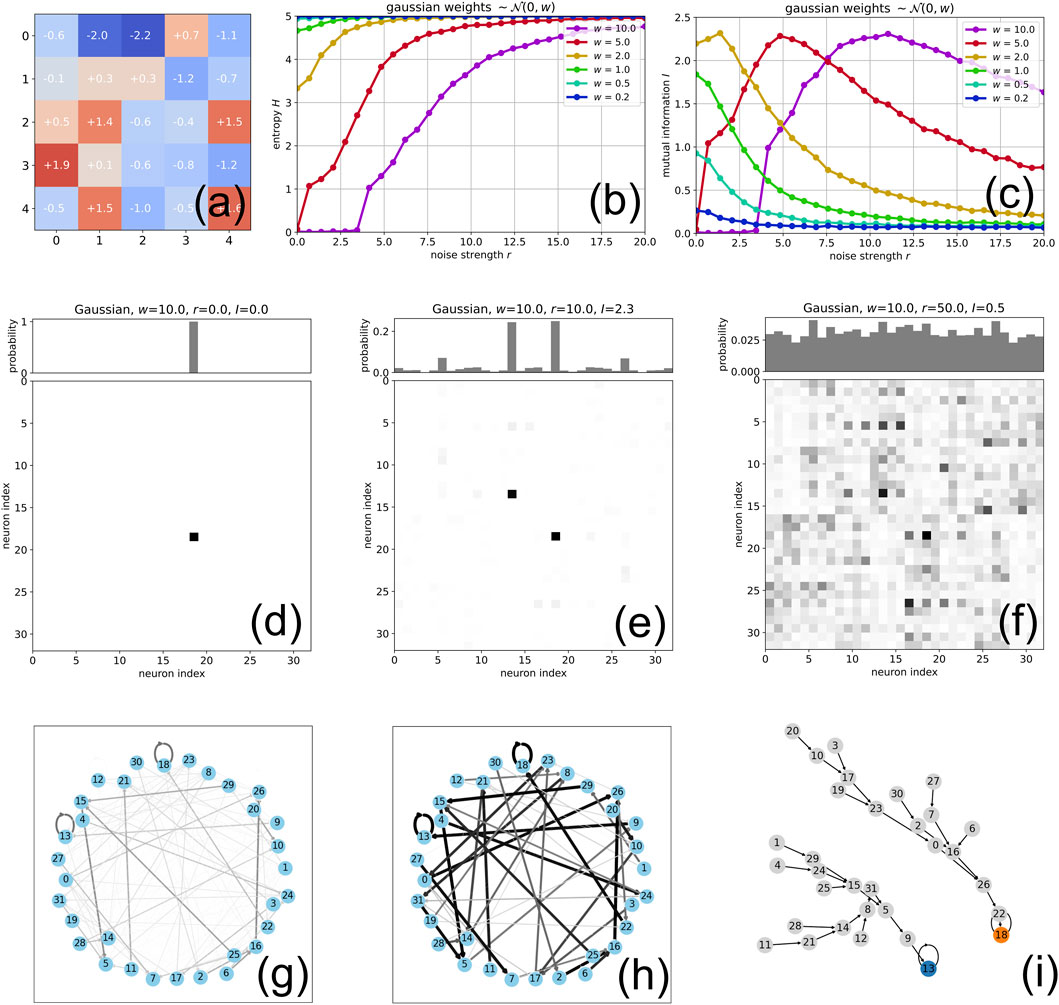
Figure 1. Effect of weight magnitude on Recurrence Resonance in Boltzmann Machines: (A) The elements of a
Before that, it is useful to imagine the dynamical structure of the SBM as a state transition graph, in which the 32 nodes represent the possible global states
and the weighted directional edges represent the possible transitions
Below, we will visualize the aggregated activity in the network by the joint probability
We first consider the system without applying external noise
Since the time scale of
As we tune the weight magnitude
However, since the entropy
This extreme situation of
We now go back to the case of relatively weak weight magnitudes
In contrast, a different behavior is found for stronger weight magnitudes
Generally, whenever the mutual information as a function of noise shows a clear maximum in a given network, the joint and marginal probability distributions are characteristically different at the points without noise (Figure 1D,
If RR is a process where noise helps neural networks to reach more attractors in a given time horizon, the phenomenon should be particularly pronounced in systems with multiple (as well as sufficiently stable) attractors. We therefore select the following three specific types of weight matrices, while keeping the network size of the SBM at
We first test a ‘autapses-only’ network, in which all non-diagonal elements of the weight matrix (corresponding to inter-neuron connections) are zero, whereas the diagonal elements (corresponding to neuron self-connections, or ‘autapses’) have the same positive value
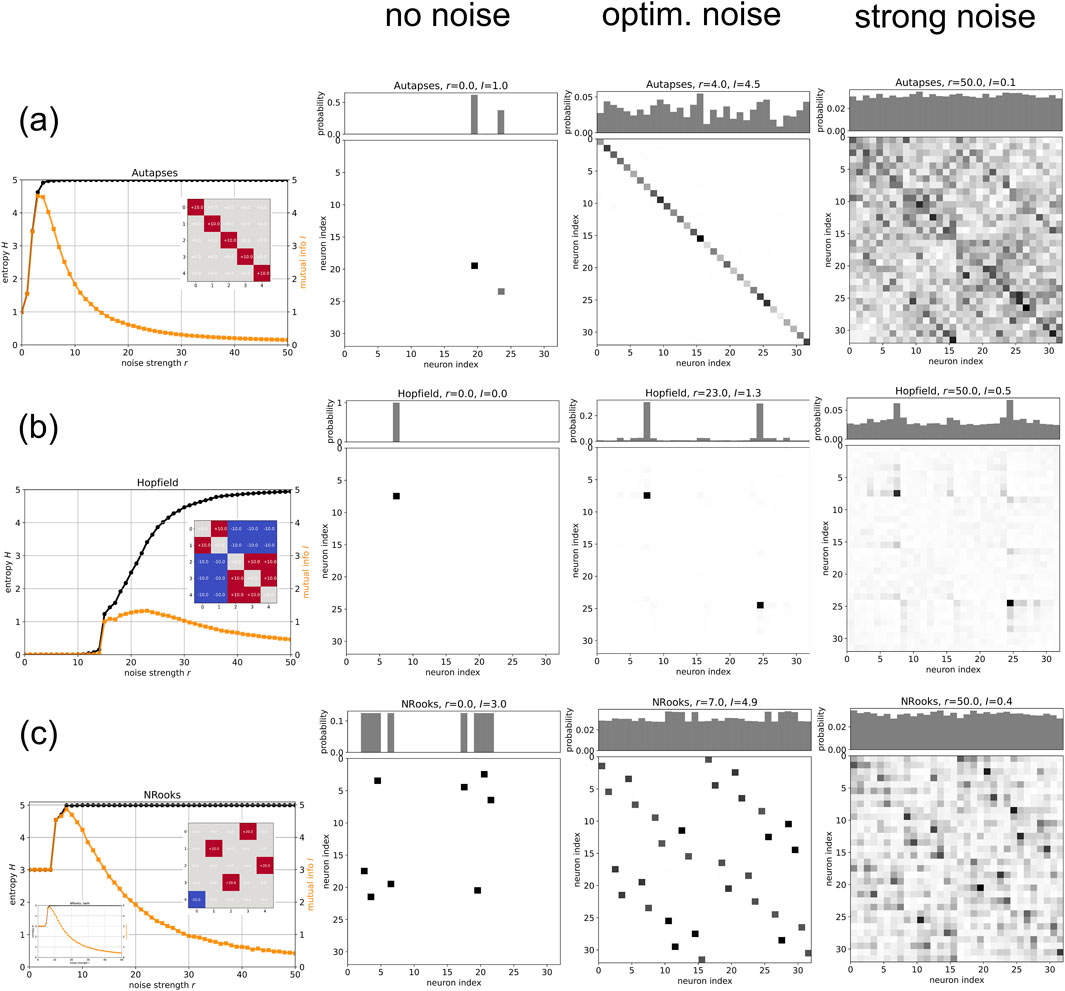
Figure 2. Recurrence Resonance in various multi-attractor RNNs: We consider three types (rows a,b,c) of Boltzmann Machines with five neurons. The first column in each row is a plot of the entropy
In our simulation, the autapse-only network without external noise is spending all of the
A remarkable feature of the autapse-only network’s RR-curve (Figure 2 (row (a)) is the part between zero and optimal noise. In this regime, the mutual information
Another type of recurrent neural network that is famous for its ability to have multiple (designable) fixed point attractors is the Hopfield network (Hopfield, 1982). Weight matrices of Hopfield networks are symmetric
We have designed the weight matrix to ‘store’ the two patterns
In a broad initial regime of noise strengths
Finally, we test the RR phenomenon in so-called ‘NRooks’ networks, which under ideal conditions (large magnitude
Our specific NRooks system turns out to have four different 8-cycles as attractors, and without noise it is trapped in one of them (Figure 2 (row (c), column ‘no noise’)). Since running for thousands of time steps within this attractor involves eight distinct states (creating entropy) in a perfectly predictable order (without divergence
In the above numerical experiments with multi-attractor SBMs, we have used relatively large weight magnitudes
In order to further demonstrate the saturation regime of the SBM, we have used the same weight matrix that was used in the NRooks example also in a network with deterministic tanh-Neurons (See Methods for details). The resulting RR-curve is indeed extremely similar to that of the probabilistic SBM (Figure 2 (row (c), lower inset of left plot)).
As already mentioned above, the observation time scale
For a demonstration, we now use a NRooks system of only three neurons (Figure 3A). Because of its extremely small state space
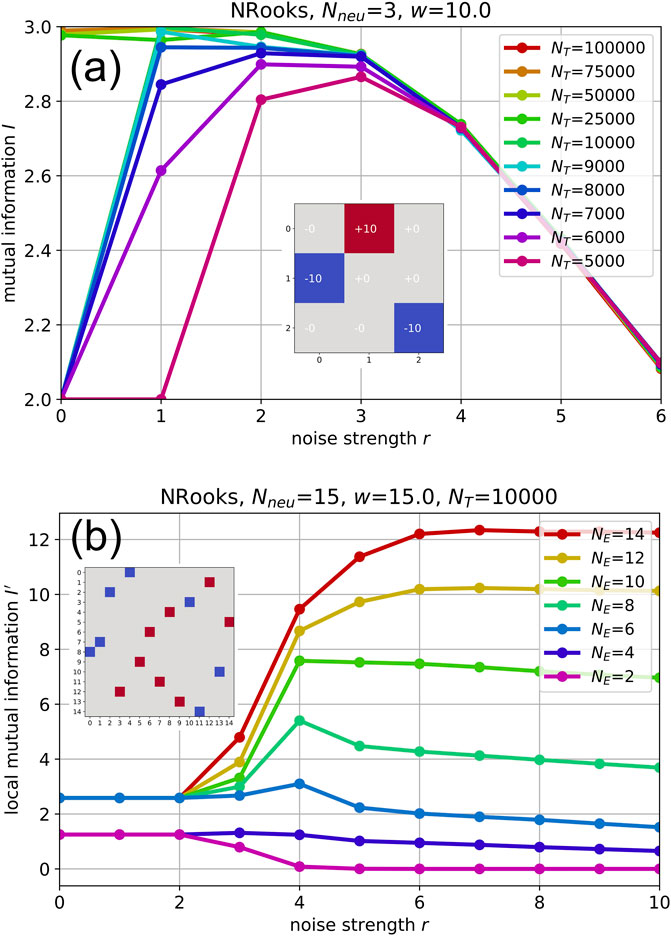
Figure 3. (A): Time-scale dependence of information quantities. Mutual information
We find that for too strong levels of noise (here
For a time scale of
For the moderate time scales
In actual applications of RNNs, such as reservoir computing, networks are typically so large
Although a detailed investigation of this question is beyond the scope of the present paper, we provide a first insight using a 15-neuron NRooks system, observed on the non-ergodic time scale of
For large sub-networks
In contrast, for very small sub-networks
However, for a certain intermediate range of sub-network sizes between
At the peak of the RR curve, the continuous white noise input of optimal strength
A natural extension (and putative application) of this concept are short noise pulses - applied only at times when a change of attractor state is required - instead of a continuous feed-in of noise. To test this concept, we have again used the 5-neuron NRooks system of Figure 2C, with its four different 8-cycles as attractors. The system is initially in one of its 8-cycle attractors (Figure 4A), and remains in this attractor for an arbitrarily long period that only depends on the weight magnitude
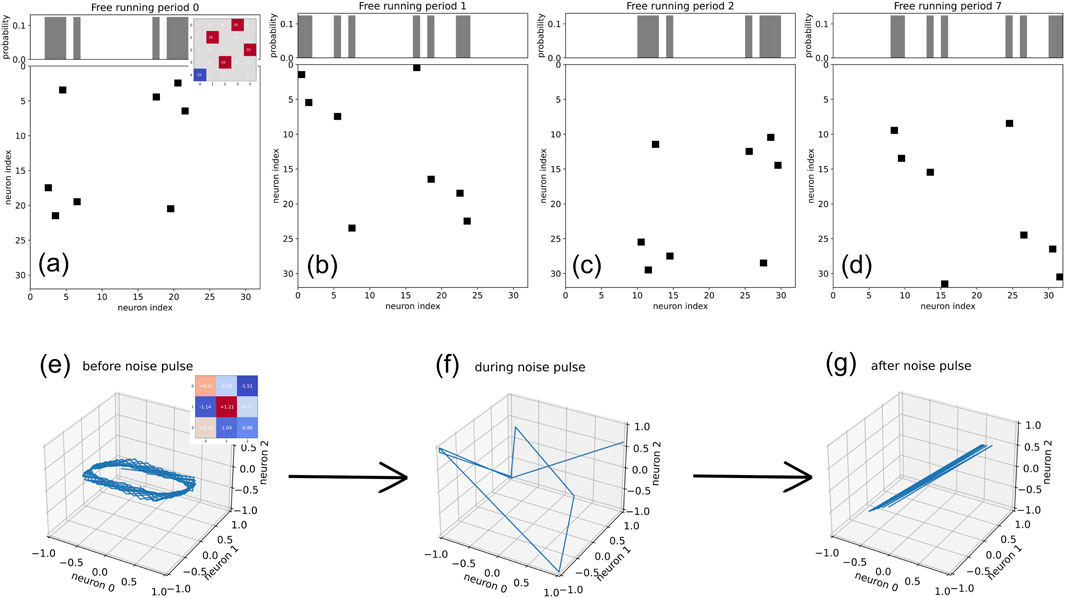
Figure 4. Applying noise pulses to RNNs. (A–D): 5-neuron NRooks system with a state space consisting of four 8-cycles. The system (weight matrix see inset) is originally trapped in one of these attractors (A). After applying a noise pulse with a duration of 10 steps and a strength of
In actual applications, the noise strength
So far, we have only briefly explored the effect of noise on networks of deterministic tanh-neurons (inset of Figure 2C). As a further glimpse into this alternative field of research, we apply a short (5 time steps) and weak
Before the noise pulse, the system is allowed to run freely for 100 time steps. The resulting system states at each time step are here continuous points within the three-dimensional cube
In this work, we have re-considered the phenomenon of Recurrence Resonance (RR), i.e., the peak-like dependence of an RNN’s internal information flux on the level
We have shown that a resonance-like peak of
We have demonstrated the RR phenomenon using Symmetric Boltzmann Machines (SBMs) with different types of weight matrices, including random Gaussian matrices, diagonal matrices (autapse-only networks), Hopfield networks trained on specific patterns, and in NRooks systems that are known to reach the upper limit of information flux. In each case, we demonstrated that the network without noise is trapped in a single or few attractors, based on the joint probability of subsequent system states. An optimal level of noise makes more (or even all) attractors available without too many unpredictable transitions. However, excessive levels of noise cause more or less random jumps between all possible pairs of states. In systems with a very high stability of attractors (induced by a large weight magnitude
We have also demonstrated that RR can only be observed in appropriate time scales
An interesting problem arises therefore in networks with many neurons and thus an exponentially large state space, such as reservoir computers, or brains. Such systems will necessarily spend all their lives within a negligible fraction of the fundamentally available state space, possibly consisting of only a tiny subset of attractors. One way to cope with this ‘practical non-ergodicity’ would be a repeated active switching between attractor subsets (perhaps using noise pulses), until a useful one is found, and then to stay there. Alternatively, the networks may be designed (or optimized) such that the useful attractors have a very large basin of attraction. A similar problem has been discussed in the context of protein folding with the ‘Levinthal paradox’, where naturally existing proteins fold into the desired conformation much faster than expected by a random thermal search in conformation space (Zwanzig et al., 1992; Karplus, 1997; Honig, 1999), probably due to funnel-type energy landscapes (Bryngelson et al., 1995; Martínez, 2014; Wolynes, 2015; Röder et al., 2019).
In our context of the RR phenomenon, practical non-ergodicity makes it impossible to compute the stationary information flux in a large network, because the system never reaches a stationary state (marked by constant probability distributions) within any practical time scale
Finally, we have explored the repeated application of short noise pulses, rather than feeding continuous noise into the neurons. We could demonstrate that each pulse offers the network a chance to switch to a new random attractor (such as an n-cycle), while the intermediate free running phases allow the system to deterministically and thus predictably follow the fixed order of states within each of the attractors.
If the random noise signals are delivered independently to each individual neuron, and if the levels of these external control signals are strong enough to override the recurrent internal signals from the other neurons, then the network could theoretically end up, after the noise application, in any of its
Based on this noise-induced random switching mechanism, an evolutionary optimization algorithm could be implemented in a recurrent neural network, in which various attractors are tried until one turns out useful for a given task. We speculate that this principle might be used in central pattern generators of biological brains (Hooper, 2000), for example, in order to find temporal activation patterns for certain motor tasks (Marder and Bucher, 2001).
In free running SBMs, a neuron’s probability of being ‘on’ in the next time step is computed by a logistic activation function
In this case, the system - after sufficiently long time - would come to thermal equilibrium, and the probability of finding it at any state
Note, however, that in our SBM model the system’s dynamics cannot be visualized as a simple probabilistic downhill relaxation within the energy landscape
In this work, we have mainly focused on probabilistic SBMs as model systems of recurrent neural networks. However, we have shown that for sufficiently large weight magnitudes
Neural networks, both artificial and biological, have a tendency to become trapped in low-entropy dynamical attractors, which correspond to repetitive, predictable patterns of activity (Khona and Fiete, 2022). These attractors are often associated with stable cognitive states or established perceptual interpretations (Beer and Barak, 2024). In particular, it has been shown that during spontaneous activity the brain does not randomly change between all theoretically possible states, but rather samples from the realm of possible sensory responses (Luczak et al., 2009; Schilling et al., 2024). This indicates that the brain’s spontaneous activity encompasses a spectrum of potential responses to stimuli, effectively preconfiguring the neural landscape for incoming sensory information. While stability and predictability are crucial for efficient functioning and reliable behavior, they can also limit the flexibility and adaptability of the system (Khona and Fiete, 2022; Beer and Barak, 2024). This is particularly problematic in contexts requiring learning, creativity, and the generation of novel ideas (Sandamirskaya, 2013).
The introduction of noise into neural networks has been suggested as a mechanism to overcome the limitations imposed by these low-entropy attractors (Hinton and Van Camp, 1993). Noise, in this context, refers to stochastic fluctuations that perturb the network’s activity, pushing it out of stable attractor states and into new regions of the state space (Bishop, 1995). This process can enhance the network’s ability to explore a wider range of potential states (Sietsma and Dow, 1991), thereby increasing its entropy and promoting the discovery of novel solutions or interpretations.
Biological neural systems, such as the human brain, provide compelling evidence for the utility of noise in cognitive processes. The brain is inherently noisy, with intrinsic fluctuations occurring at multiple levels, from ion channel gating to synaptic transmission and neural firing (Faisal et al., 2008). This noise is not merely a byproduct of biological imperfection; rather, it plays a functional role in various cognitive tasks (McDonnell and Ward, 2011). For example, noise-induced variability in neural firing can enhance sensory perception by enabling the brain to detect weak signals that would otherwise be drowned out by deterministic activity (Deco et al., 2009).
Another noise-based phenomenon of great importance in physical and biological systems is Stochastic Resonance (Gammaitoni et al., 1998; Moss et al., 1993). It is typically occurring in signal detection systems, where the incoming signal needs to exceed a minimal threshold in amplitude to be detected. Adding an appropriate level of noise to the input can then stochastically lift even weak signal above the threshold and thereby improve the detection performance, as it has indeed been observed in various sensory systems (Moss et al., 2004; Stein et al., 2005; Ward, 2013). The phenomenon of Recurrence Resonance discussed in this paper is different from Stochastic Resonance, as it improves the spontaneous, internal information flux in a neural network, rather than the signal transmission from the outside to the inside of the system. However, using mutual information or correlation-based measures, it is also possible to quantify the information flux from the input nodes of a RNN at time
Noise also facilitates learning and plasticity. During development, random fluctuations in neural activity contribute to the refinement of neural circuits, allowing for the fine-tuning of synaptic connections based on experience (Marzola et al., 2023; Zhang et al., 2021; Fang et al., 2020). In adulthood, noise can help the brain escape from local minima during learning processes, thereby preventing overfitting to specific patterns and promoting generalization (Zhang et al., 2021; Fang et al., 2020). This is particularly relevant in the context of reinforcement learning, where exploration of the state space is crucial for finding optimal strategies (Weng, 2020; Bai et al., 2023).
Moreover, noise-induced transitions between attractor states can support cognitive flexibility and creativity. For instance, the ability to switch between different interpretations of ambiguous stimuli (Panagiotaropoulos et al., 2013), or to generate novel ideas, relies on the brain’s capacity to break free from dominant attractor states and explore alternative possibilities (Wu and Koutstaal, 2020; Jaimes-Reátegui et al., 2022). This is consistent with the observation that certain cognitive disorders, characterized by rigidity and a lack of flexibility (e.g., autism, obsessive-compulsive disorder), are associated with reduced neural noise and hyper-stable attractor dynamics (Dwyer et al., 2024; Watanabe et al., 2019).
In conclusion, the investigations detailed in our study firmly establish Recurrence Resonance (RR) as a genuine emergent phenomenon within neural dynamics: the mutual information of the system is increased by the addition of noise that itself has zero mutual information. Hence, the application of optimal noise levels can transform neural systems from states of minimal information processing capabilities to significantly enhanced states where information flow is not only possible but also maximized. This effect, whereby noise beneficially modifies system dynamics, underscores the complex and non-intuitive nature of neural information processing, presenting noise not merely as a disruptor but as a critical facilitator of dynamic neural activity. This finding opens up new avenues for exploiting noise in the design and enhancement of neural network models, particularly in areas demanding robust and adaptive information processing.
The introduction of noise into neural networks can be seen as a fundamental mechanism by which the brain enhances its cognitive capabilities. By destabilizing low-entropy attractors and promoting the exploration of new states, noise enables learning, perception, and creativity. This perspective not only aligns with empirical findings from neuroscience but also offers a theoretical framework for understanding how complex cognitive functions can emerge from the interplay between deterministic and stochastic processes in neural systems.
Furthermore, the insights gained from our study provide a valuable foundation for advancing artificial intelligence (AI) technologies, particularly in the realms of reservoir computing and machine learning. Reservoir computing, which leverages the dynamic behavior of recurrent neural networks, can benefit from the strategic introduction of noise to enhance its computational power and adaptability. Similarly, machine learning models can incorporate noise to avoid overfitting, explore diverse solution spaces, and improve generalization. By integrating these principles, AI systems can emulate the brain’s ability to learn and adapt in complex, unpredictable environments, leading to more robust and innovative technological solutions. This convergence of neuroscience and AI not only deepens our understanding of cognitive processes but may also drive the development of next-generation intelligent systems capable of solving real-world problems with unprecedented efficiency and creativity.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
CM: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. AS: Funding acquisition, Validation, Writing–original draft. AM: Resources, Supervision, Validation, Writing–original draft. PK: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Writing–original draft, Writing–review and editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation): KR 5148/3-1 (project number 510395418), KR 5148/5-1 (project number 542747151), and GRK 2839 (project number 468527017) to PK, and grant SCHI 1482/3-1 (project number 451810794) to AS.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Aarts, E. H. L., and Van Laarhoven, P. J. M. (1989). Simulated annealing: an introduction. Stat. Neerl. 43 (1), 31–52. doi:10.1111/j.1467-9574.1989.tb01245.x
Alzubaidi, L., Zhang, J., Humaidi, A. J., Al-Dujaili, A., Duan, Ye, Al-Shamma, O., et al. (2021). Review of deep learning: concepts, cnn architectures, challenges, applications, future directions. J. big Data 8 (1), 53–74. doi:10.1186/s40537-021-00444-8
Bai, C., Liu, P., Liu, K., Wang, L., Zhao, Y., Han, L., et al. (2023). Exploration in deep reinforcement learning: from single-agent to multiagent domain. IEEE Trans. Neural Netw. Learn. Syst. 34, 4776–4790. doi:10.1109/tnnls.2021.3129160
Barak, O. (2017). Recurrent neural networks as versatile tools of neuroscience research. Curr. Opin. Neurobiol. 46, 1–6. doi:10.1016/j.conb.2017.06.003
Beer, C., and Barak, O. (2024). Revealing and reshaping attractor dynamics in large networks of cortical neurons. PLOS Comput. Biol. 20 (1), e1011784. doi:10.1371/journal.pcbi.1011784
Bertschinger, N., and Natschläger, T. (2004). Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput. 16 (7), 1413–1436. doi:10.1162/089976604323057443
Bertsimas, D., and Tsitsiklis, J. (1993). Simulated annealing. Stat. Sci. 8 (1), 10–15. doi:10.1214/ss/1177011077
Bishop, C. M. (1995). Training with noise is equivalent to tikhonov regularization. Neural Comput. 7 (1), 108–116. doi:10.1162/neco.1995.7.1.108
Boedecker, J., Obst, O., Lizier, J. T., Mayer, N. M., and Asada, M. (2012). Information processing in echo state networks at the edge of chaos. Theory Biosci. 131 (3), 205–213. doi:10.1007/s12064-011-0146-8
Bönsel, F., Krauss, P., Metzner, C., and Yamakou, M. E. (2022). Control of noise-induced coherent oscillations in three-neuron motifs. Cogn. Neurodynamics 16 (4), 941–960.
Brunel, N. (2016). Is cortical connectivity optimized for storing information? Nat. Neurosci. 19 (5), 749–755. doi:10.1038/nn.4286
Bryngelson, J. D., Onuchic, J. N., Socci, N. D., and Wolynes, P. G. (1995). Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins Struct. Funct. Bioinforma. 21 (3), 167–195. doi:10.1002/prot.340210302
Büsing, L., Schrauwen, B., and Legenstein, R. (2010). Connectivity, dynamics, and memory in reservoir computing with binary and analog neurons. Neural Comput. 22 (5), 1272–1311. doi:10.1162/neco.2009.01-09-947
Dambre, J., Verstraeten, D., Schrauwen, B., and Massar, S. (2012). Information processing capacity of dynamical systems. Sci. Rep. 2 (1), 514–517. doi:10.1038/srep00514
Deco, G., Rolls, E. T., and Romo, R. (2009). Stochastic dynamics as a principle of brain function. Prog. Neurobiol. 88 (1), 1–16. doi:10.1016/j.pneurobio.2009.01.006
Dwyer, P., Vukusic, S., Williams, Z. J., Saron, C. D., and Rivera, S. M. (2024). “neural noise” in auditory responses in young autistic and neurotypical children. J. autism Dev. Disord. 54 (2), 642–661. doi:10.1007/s10803-022-05797-4
Faisal, A. A., Selen, L. P. J., and Wolpert, D. M. (2008). Noise in the nervous system. Nat. Rev. Neurosci. 9 (4), 292–303. doi:10.1038/nrn2258
Fang, Y., Yu, Z., and Chen, F. (2020). Noise helps optimization escape from saddle points in the synaptic plasticity. Front. Neurosci. 14, 343. doi:10.3389/fnins.2020.00343
Farrell, M., Recanatesi, S., Moore, T., Lajoie, G., and Shea-Brown, E. (2022). Gradient-based learning drives robust representations in recurrent neural networks by balancing compression and expansion. Nat. Mach. Intell. 4 (6), 564–573. doi:10.1038/s42256-022-00498-0
Folli, V., Gosti, G., Leonetti, M., and Ruocco, G. (2018). Effect of dilution in asymmetric recurrent neural networks. Neural Netw. 104, 50–59. doi:10.1016/j.neunet.2018.04.003
Gammaitoni, L., Hänggi, P., Jung, P., and Marchesoni, F. (1998). Stochastic resonance. Rev. Mod. Phys. 70 (1), 223–287. doi:10.1103/revmodphys.70.223
Gerum, R. C., Erpenbeck, A., Krauss, P., and Schilling, A. (2020). Sparsity through evolutionary pruning prevents neuronal networks from overfitting. Neural Netw. 128, 305–312. doi:10.1016/j.neunet.2020.05.007
Gonon, L., and Ortega, J.-P. (2021). Fading memory echo state networks are universal. Neural Netw. 138, 10–13. doi:10.1016/j.neunet.2021.01.025
Haruna, T., and Nakajima, K. (2019). Optimal short-term memory before the edge of chaos in driven random recurrent networks. Phys. Rev. E 100 (6), 062312. doi:10.1103/physreve.100.062312
Haviv, D., Rivkind, A., and Barak, O. (2019). “Understanding and controlling memory in recurrent neural networks,” in International conference on machine learning (Long Beach, CA, United States: PMLR), 2663–2671.
Hinton, G. E., and Van Camp, D. (1993). “Keeping the neural networks simple by minimizing the description length of the weights,” in Proceedings of the sixth annual conference on Computational learning theory, 5–13.
Honig, B. (1999). Protein folding: from the levinthal paradox to structure prediction. J. Mol. Biol. 293 (2), 283–293. doi:10.1006/jmbi.1999.3006
Hooper, S. L. (2000). Central pattern generators. Curr. Biol. 10 (5), R176–R179. doi:10.1016/s0960-9822(00)00367-5
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. 79 (8), 2554–2558. doi:10.1073/pnas.79.8.2554
Ichikawa, K., and Kaneko, K. (2021). Short-term memory by transient oscillatory dynamics in recurrent neural networks. Phys. Rev. Res. 3 (3), 033193. doi:10.1103/physrevresearch.3.033193
Ikemoto, S., DallaLibera, F., and Hosoda, K. (2018). Noise-modulated neural networks as an application of stochastic resonance. Neurocomputing 277, 29–37. doi:10.1016/j.neucom.2016.12.111
Jaeger, H. (2001). The “echo state” approach to analysing and training recurrent neural networks-with an erratum note. Bonn, Germany: German National Research Center for Information Technology GMD Technical Report, 148.
Jaeger, H. (2014). Controlling recurrent neural networks by conceptors. arXiv Prepr. arXiv:1403.3369.
Jaimes-Reátegui, R., Huerta-Cuellar, G., García-López, J. H., and Pisarchik, A. N. (2022). Multistability and noise-induced transitions in the model of bidirectionally coupled neurons with electrical synaptic plasticity. Eur. Phys. J. Special Top. 231, 255–265. doi:10.1140/epjs/s11734-021-00349-w
Kadmon, J., and Sompolinsky, H. (2015). Transition to chaos in random neuronal networks. Phys. Rev. X 5 (4), 041030. doi:10.1103/physrevx.5.041030
Kaneko, K., and Suzuki, J. (1994). “Evolution to the edge of chaos in an imitation game,” in Artificial life III (Citeseer).
Karplus, M. (1997). The levinthal paradox: yesterday and today. Fold. Des. 2, S69–S75. doi:10.1016/s1359-0278(97)00067-9
Katz, L., and Sobel, M. (1972). “Coverage of generalized chess boards by randomly placed rooks,” in Proceedings of the sixth berkeley symposium on mathematical statistics and probability, probability theory (University of California Press), 6.3, 555–564. doi:10.1525/9780520375918-031Contributions to Probability Theory
Khona, M., and Fiete, I. R. (2022). Attractor and integrator networks in the brain. Nat. Rev. Neurosci. 23 (12), 744–766. doi:10.1038/s41583-022-00642-0
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. science 220 (4598), 671–680. doi:10.1126/science.220.4598.671
Krauss, P., Prebeck, K., Schilling, A., and Metzner, C. (2019a). Recurrence resonance in three-neuron motifs. Front. Comput. Neurosci. 13, 64. doi:10.3389/fncom.2019.00064
Krauss, P., Schuster, M., Dietrich, V., Schilling, A., Schulze, H., and Metzner, C. (2019c). Weight statistics controls dynamics in recurrent neural networks. PloS one 14 (4), e0214541. doi:10.1371/journal.pone.0214541
Krauss, P., Tziridis, K., Metzner, C., Schilling, A., Hoppe, U., and Schulze, H. (2016). Stochastic resonance controlled upregulation of internal noise after hearing loss as a putative cause of tinnitus-related neuronal hyperactivity. Front. Neurosci. 10, 597. doi:10.3389/fnins.2016.00597
Krauss, P., Zankl, A., Schilling, A., Schulze, H., and Metzner, C. (2019b). Analysis of structure and dynamics in three-neuron motifs. Front. Comput. Neurosci. 13 (5), 5. doi:10.3389/fncom.2019.00005
Langton, C. G. (1990). Computation at the edge of chaos: phase transitions and emergent computation. Phys. D. Nonlinear Phenom. 42 (1-3), 12–37. doi:10.1016/0167-2789(90)90064-v
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. nature 521 (7553), 436–444. doi:10.1038/nature14539
Legenstein, R., and Maass, W. (2007). Edge of chaos and prediction of computational performance for neural circuit models. Neural Netw. 20 (3), 323–334. doi:10.1016/j.neunet.2007.04.017
Luczak, A., Barthó, P., and Harris, K. D. (2009). Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron 62 (3), 413–425. doi:10.1016/j.neuron.2009.03.014
Maheswaranathan, N., Williams, A. H., Golub, M. D., Ganguli, S., and Sussillo, D. (2019). Universality and individuality in neural dynamics across large populations of recurrent networks. Adv. neural Inf. Process. Syst. 2019, 15629–15641.
Marder, E., and Bucher, D. (2001). Central pattern generators and the control of rhythmic movements. Curr. Biol. 11 (23), R986–R996. doi:10.1016/s0960-9822(01)00581-4
Martínez, L. (2014). Introducing the levinthal’s protein folding paradox and its solution. J. Chem. Educ. 91 (11), 1918–1923. doi:10.1021/ed300302h
Marzola, P., Melzer, T., Pavesi, E., Gil-Mohapel, J., and Brocardo, P. S. (2023). Exploring the role of neuroplasticity in development, aging, and neurodegeneration. Brain Sci. 13 (12), 1610. doi:10.3390/brainsci13121610
Maximilian Schäfer, A., and Zimmermann, H. G. (2006). “Recurrent neural networks are universal approximators,” in International conference on artificial neural networks (Springer), 632–640.
McDonnell, M. D., and Ward, L. M. (2011). The benefits of noise in neural systems: bridging theory and experiment. Nat. Rev. Neurosci. 12 (7), 415–425. doi:10.1038/nrn3061
Metzner, C., and Krauss, P. (2022). Dynamics and information import in recurrent neural networks. Front. Comput. Neurosci. 16, 876315. doi:10.3389/fncom.2022.876315
Metzner, C., Yamakou, M. E., Voelkl, D., Schilling, A., and Krauss, P. (2024). Quantifying and maximizing the information flux in recurrent neural networks. Neural Comput. 36 (3), 351–384. doi:10.1162/neco_a_01651
Molgedey, L., Schuchhardt, J., and Schuster, H. G. (1992). Suppressing chaos in neural networks by noise. Phys. Rev. Lett. 69 (26), 3717–3719. doi:10.1103/physrevlett.69.3717
Moss, F., Bulsara, A., and Shlesinger, M. F. (1993). Stochastic resonance in physics and biology. In Proceedings of the NATO Advanced Research Workshop. Karlsruhe, Germany. J. Stat. Phys., 70.
Moss, F., Ward, L. M., and Sannita, W. G. (2004). Stochastic resonance and sensory information processing: a tutorial and review of application. Clin. Neurophysiol. 115 (2), 267–281. doi:10.1016/j.clinph.2003.09.014
Narang, S., Elsen, E., Diamos, G., and Sengupta, S. (2017). Exploring sparsity in recurrent neural networks. arXiv Prepr. arXiv:1704.05119.
Natschläger, T., Bertschinger, N., and Legenstein, R. (2005). At the edge of chaos: real-time computations and self-organized criticality in recurrent neural networks. Adv. neural Inf. Process. Syst. 17, 145–152.
Panagiotaropoulos, T. I., Kapoor, V., Logothetis, N. K., and Deco, G. (2013). A common neurodynamical mechanism could mediate externally induced and intrinsically generated transitions in visual awareness. PLoS One 8 (1), e53833. doi:10.1371/journal.pone.0053833
Rajan, K., Abbott, L. F., and Sompolinsky, H. (2010). Stimulus-dependent suppression of chaos in recurrent neural networks. Phys. Rev. E 82 (1), 011903. doi:10.1103/physreve.82.011903
Röder, K., Joseph, J. A., Husic, B. E., and Wales, D. J. (2019). Energy landscapes for proteins: from single funnels to multifunctional systems. Adv. Theory Simulations 2 (4), 1800175. doi:10.1002/adts.201800175
Sandamirskaya, Y. (2013). Dynamic neural fields as a step toward cognitive neuromorphic architectures. Front. Neurosci. 7, 276. doi:10.3389/fnins.2013.00276
Schilling, A., Gerum, R., Boehm, C., Rasheed, J., Metzner, C., Maier, A., et al. (2024). Deep learning based decoding of single local field potential events. NeuroImage 120696. doi:10.1016/j.neuroimage.2024.120696
Schilling, A., Gerum, R., Metzner, C., Maier, A., and Krauss, P. (2022). Intrinsic noise improves speech recognition in a computational model of the auditory pathway. Front. Neurosci. 16, 908330. doi:10.3389/fnins.2022.908330
Schilling, A., Sedley, W., Gerum, R., Metzner, C., Tziridis, K., Maier, A., et al. (2023). Predictive coding and stochastic resonance as fundamental principles of auditory phantom perception. Brain 146 (12), 4809–4825. doi:10.1093/brain/awad255
Schilling, A., Tziridis, K., Schulze, H., and Krauss, P. (2021). The stochastic resonance model of auditory perception: a unified explanation of tinnitus development, zwicker tone illusion, and residual inhibition. Prog. Brain Res. 262, 139–157. doi:10.1016/bs.pbr.2021.01.025
Schrauwen, B., Buesing, L., and Legenstein, R. (2009). “On computational power and the order-chaos phase transition in reservoir computing,” in 22nd annual conference on neural information processing systems (NIPS 2008) (Vancouver, BC, Canada: NIPS Foundation), Vol. 21, 1425–1432.
Schuecker, J., Goedeke, S., and Helias, M. (2018). Optimal sequence memory in driven random networks. Phys. Rev. X 8 (4), 041029. doi:10.1103/physrevx.8.041029
Sietsma, J., and Dow, R. J. F. (1991). Creating artificial neural networks that generalize. Neural Netw. 4 (1), 67–79. doi:10.1016/0893-6080(91)90033-2
Solé, R. V., and Miramontes, O. (1995). Information at the edge of chaos in fluid neural networks. Phys. D. Nonlinear Phenom. 80 (1-2), 171–180. doi:10.1016/0167-2789(94)00158-m
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3 (3), e68. doi:10.1371/journal.pbio.0030068
Stein, R. B., Gossen, E. R., and Jones, K. E. (2005). Neuronal variability: noise or part of the signal? Nat. Rev. Neurosci. 6 (5), 389–397. doi:10.1038/nrn1668
Toyoizumi, T., and Abbott, L. F. (2011). Beyond the edge of chaos: amplification and temporal integration by recurrent networks in the chaotic regime. Phys. Rev. E 84 (5), 051908. doi:10.1103/physreve.84.051908
Van Laarhoven, P. J. M., Aarts, E. H. L., van Laarhoven, P. J. M., and Aarts, E. H. L. (1987). Simulated annealing. Springer.
Wallace, E., Maei, H. R., and Latham, P. E. (2013). Randomly connected networks have short temporal memory. Neural Comput. 25 (6), 1408–1439. doi:10.1162/neco_a_00449
Wang, X. R., Lizier, J. T., and Prokopenko, M. (2011). Fisher information at the edge of chaos in random boolean networks. Artif. life 17 (4), 315–329. doi:10.1162/artl_a_00041
Ward, L. M. (2013). The thalamus: gateway to the mind. WIREs Cognitive Sci. 4 (6), 609–622. doi:10.1002/wcs.1256
Watanabe, T., Lawson, R. P., Walldén, Y. S. E., and Rees, G. (2019). A neuroanatomical substrate linking perceptual stability to cognitive rigidity in autism. J. Neurosci. 39 (33), 6540–6554. doi:10.1523/jneurosci.2831-18.2019
Weng, L. (2020). Exploration strategies in deep reinforcement learning. Lilianweng. Github. io/lil-log.
Wolynes, P. G. (2015). Evolution, energy landscapes and the paradoxes of protein folding. Biochimie 119, 218–230. doi:10.1016/j.biochi.2014.12.007
Wu, Y., and Koutstaal, W. (2020). Charting the contributions of cognitive flexibility to creativity: self-guided transitions as a process-based index of creativity-related adaptivity. PloS one 15 (6), e0234473. doi:10.1371/journal.pone.0234473
Zhang, C., Zhang, D., and Stepanyants, A. (2021). Noise in neurons and synapses enables reliable associative memory storage in local cortical circuits. Eneuro 8 (1), ENEURO.0302–20.2020. doi:10.1523/eneuro.0302-20.2020
Keywords: recurrent neural networks (RNN), resonance, information processing, dynamics, noise
Citation: Metzner C, Schilling A, Maier A and Krauss P (2024) Recurrence resonance - noise-enhanced dynamics in recurrent neural networks. Front. Complex Syst. 2:1479417. doi: 10.3389/fcpxs.2024.1479417
Received: 12 August 2024; Accepted: 20 September 2024;
Published: 08 October 2024.
Edited by:
Byungjoon Min, Chungbuk National University, Republic of KoreaReviewed by:
Yukio Pegio Gunji, Waseda University, JapanCopyright © 2024 Metzner, Schilling, Maier and Krauss. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Patrick Krauss, cGF0cmljay5rcmF1c3NAZmF1LmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.