- 1National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
- 2Department of Science and Technology for Sustainable Development and One Health, Università Campus Bio-Medico di Roma, Rome, Italy
We develop a three-state agent-based language competition model that takes into account the fact that language learning and attrition are not instantaneous but occur over a finite time interval; i.e., we introduce memory in the system. We show that memory effects significantly impact the dynamics of language competition. Furthermore, we find that including heterogeneity in the linguistic skills of the agents affects the results substantially. We also explore the role of other factors, such as different levels of language learning difficulty, initial population fractions, and daily interaction rates.
1 Introduction
The past two decades have witnessed a significant growth of research interest in mathematical modeling of language dynamics. This has been mainly driven by the consideration that according to UNESCO, about 43% of the approximately 6,000 languages currently spoken in the world are at risk of extinction by as early as 2050 (Austin, 2008; Moseley, 2010). In fact, starting from the seminal work by Abrams and Strogatz (2003), the study and modeling of language competition have become one of the key research topics in complex systems theory.
While the Abrams–Strogatz model, based on Lotka–Volterra-type equations, is a two-state model that takes into account monolingual groups only, other models, including the first language competition models by Baggs and Freedman (Baggs et al., 1990; Baggs and Freedman, 1990; Baggs and Freedman, 1993), also incorporate bilingual communities. The various models introduced so far leverage a range of approaches derived not only from population–ecology models but also from statistical physics, game theory, and agent-based modeling (Castellano et al., 2009; Baronchelli, 2016; Marchetti et al., 2020b; Marchetti et al., 2020a; Patriarca et al., 2020; Marchetti et al., 2021; Minett and Wang, 2008; Vazquez et al., 2010; Ya-ping et al., 2015). The inclusion of bilingualism has led to models that demonstrate that under certain conditions, the survival of both competing languages, coexisting within a stable bilingual community, can be achieved (Castellano et al., 2009; Heinsalu et al., 2014; Marchetti et al., 2021).
A feature common to many language dynamics models, encompassing bilingualism or not, is the assumption that the key driving force for adopting one language versus another is its relative prestige or perceived status (Abrams and Strogatz, 2003). This makes sense as it seems plausible that perceived language status played a role, for instance, in the decline of Welsh and Scottish Gaelic in favor of English, or in the progressive disappearance of Quechua, still spoken in some areas of Peru, in favor of Spanish. However, there are other relevant factors that can lead to a language shift (Patriarca et al., 2020). For example, based on Indian census data, De Silva et al. pointed out that the competition between Hindi and English over two decades from 1991 to 2011 has resulted in the saturation of the bilingual community and a steady growth of Hindi monolinguals, in spite of English being a higher status language (De Silva et al., 2021). This is related to the Indian political background and educational infrastructures. Anyway, the main parameters of such language competition models are the transition rates, which reflect the influence of different factors, such as language prestige, the underlying socioeconomic and political situation, and language similarity.
It is to be noted that three-state language dynamics models, in which one of the states corresponds to bilinguals, are formally similar to three-state opinion dynamics models, where one of the states can represent undecided individuals (Castellano et al., 2009). Importantly, in opinion dynamics, in addition to other factors and mechanisms, the role of memory and how it influences even a simple choice, has been recognized and studied (Dall’Asta and Castellano, 2007). For example, some voter models incorporate memory effects in agent-based simulations or through fractional derivatives at the analytical level (Baron et al., 2022), mimicking an opinion change happening only after several interactions have taken place.
Memory effects are expected to play a relevant role whenever the constituent units themselves are complex and can exchange, record, and process information. Taking memory into account is even more relevant when considering the complex processes that underlie language learning and attrition. In fact, a closer analysis of the learning process reveals that even the acquisition of a single word is based on the memory association between the phoneme associated to the word and, e.g., the image corresponding to a real object (Odgen and Richards, 1923) and, thus, should be more properly treated at a cognitive modeling level (Marchetti et al., 2020b; Marchetti et al., 2020a; Marchetti et al., 2021; and references therein). Thus, the acquisition of a new language, as well as its retention, is a time-consuming process that depends on multiple interactions over a finite time interval. Cognitive processes and, in particular, memory-related effects, individual language learning aptitudes, and different degrees of difficulty of learning and retaining a language, from both a grammatical and a phonetic viewpoint, may play a crucial role in determining the outcome of language competition.
Most models of language dynamics describe language acquisition and shift as simple instantaneous transitions between different linguistic states driven by the current state of the system. Instead, in the present paper, we study the role of memory in language competition at a phenomenological level, focusing on the accompanying processes of language learning and attrition (Liivand, 2018). The impact of memory on language adoption is studied as a function of the frequency of interactions with other speakers, taking into account both the difficulty of learning and retaining a foreign language and the possibility of abandoning one’s mother tongue after becoming bilingual. The combination of these effects determines in our model the conditions that may lead to language extinction or survival or to the attainment of an equilibrium involving different linguistic communities.
Research on second language acquisition has shown that, in addition to different language usage frequencies among individuals, there exist additional relevant individual factors, including age, personal skills, aptitude, personality, learning style, motivation, and external (cultural and socioeconomical) environment (Ellis et al., 1994; Griffiths and Soruç, 2020), which shape the observed heterogeneous learning abilities of individuals. However, people also differ vastly in how fast they forget a language (Schmid and Köpke, 2019) for mother tongue attrition and (Mickan et al., 2020) for foreign language attrition. Without trying to model the detailed origin of individual differences but still willing to incorporate some degree of heterogeneity in individuals, we assigned diversified values to the parameters related to language learning and retaining. The inclusion of heterogeneity in the present study is motivated by the research in language acquisition, but the importance of heterogeneity and quenched disorder in complex processes, from economic stability to network synchronization (Bouchaud, 2009; Lafuerza and Toral, 2013; Zhang et al., 2021), is now well recognized.
This paper is organized as follows. Section 2 introduces a three-state agent-based language competition model that takes into account memory effects and the heterogeneity of speakers. We also provide the numerical algorithm to simulate the model. Section 3 presents the results for both homogeneous and heterogeneous populations with identical or diversified linguistic capabilities, respectively. We study the time evolutions and phase portraits of the systems and analyze how the language competition outcome depends on the interaction frequency, level of heterogeneity, initial fractions of the monolingual populations, and the asymmetry between language learning difficulties. Section 4 outlines the conclusions.
2 Model
2.1 Overall description
In order to investigate the impact of memory on language competition, we develop an agent-based model of a population of N speakers, of whom a fraction NX speak language X, a fraction NY speak language Y, and a fraction NZ are bilinguals speaking both languages X and Y; NX + NY + NZ = 1. In the following, the symbols X and Y also represent the language state of X- and Y-monolinguals, respectively, while Z represents the state of bilingual agents. It is assumed that initially, there are no bilinguals, i.e., NZ (t = 0) = 0.
During the time evolution of the system, agents communicate pair-wise. Each time step in the simulations corresponds to 1 day, and an agent is assumed to communicate every day on average with other Nint agents. Thus, there are daily Nint × N/2 interactions in the system.
For the choice of the language used in a communication, we apply the following rules.
• In the encounter between two monolinguals of different languages, since there is no common language to be used, it is assumed that either speaker will try to use their own language, which the other speaker will make an effort to understand so that eventually, either agent will learn something of the other agent’s language.
• The language employed in an interaction between a monolingual and a bilingual agent is that of the monolingual agent.
• In the case of an encounter between two bilinguals, both languages could be used in principle. The choice of the language employed takes into account the cost of language switching (Meuter and Allport, 1999; Jackson et al., 2001; Abutalebi and Green, 2007; Moritz-Gasser and Duffau, 2009; Iriberri and Uriarte, 2012); i.e., it depends on the native language and/or the number of previous communications in one or the other language (see Section 2.3 for details).
In the learning process, memory is taken into account, assuming that a monolingual agent can acquire the other language and become bilingual only through repeated interactions with monolingual speakers of the other language. In the model, we assume that in order to learn a new language and become bilingual, a monolingual agent has to use the new language at least K times within a time interval TK. If the monolingual agent has used the new language less than K times, as time interval TK elapses, the agent’s memory is reset. Importantly, the model will use, in general, two different parameters KX and KY for the two languages X and Y, respectively, reflecting the possible different difficulties of learning; i.e., KX (KY) expresses the difficulty of learning language X (Y) and, therefore, will be used to determine if a monolingual agent speaking language Y (X) meets the criterion to become bilingual or not.
Memory effects also influence language maintenance. In the model, we assume that a bilingual has to use both languages X and Y at least M times within a time interval TM in order to maintain them (for simplicity, we assume the same M and TM for both the first and second languages). If this condition is not fulfilled for one of the languages, that language will be forgotten.
The model variables are discussed in Section 2.2, and the dynamical rules of time evolution are listed in Section 2.3.
2.2 Microscopic variables
The state of agent i (i = 1, 2, … , N) at time step t is specified by the following set of individual variables:
• Language variables (all agents): The linguistic state of agent i is recorded by the variable
• Learning variables (monolinguals): For a monolingual agent i
• Maintenance variables (bilinguals): For a bilingual agent i
2.3 Numerical algorithm
The algorithm employed in the numerical simulations can be summarized as follows:
0. At time t = 0, the population contains only a fraction NX (0) of X-monolinguals and a fraction NY(0) of Y-monolinguals, i.e., NX (0) + NY(0) = 1 and NZ (0) = 0. Counters
1. A set of Nint × N/2 couples of agents are randomly selected from the population.
2. Agents i and j of each extracted couple interact, and their language use is tracked (Table 1; Table 2).
• If both agents i and j are monolinguals of the same language
• If agents i and j are monolinguals with different languages
• If agent i is bilingual and agent j is monolingual, it is assumed that they communicate in the language of the monolingual agent j. In this case, only the usage counter of the bilingual agent i is updated:
• If agents i and j are both bilinguals and have the same main language, this will be used in the communication, and therefore,
• If agents i and j are both bilinguals but their main languages are different, they will make a decision based on their memory information stored in the counters
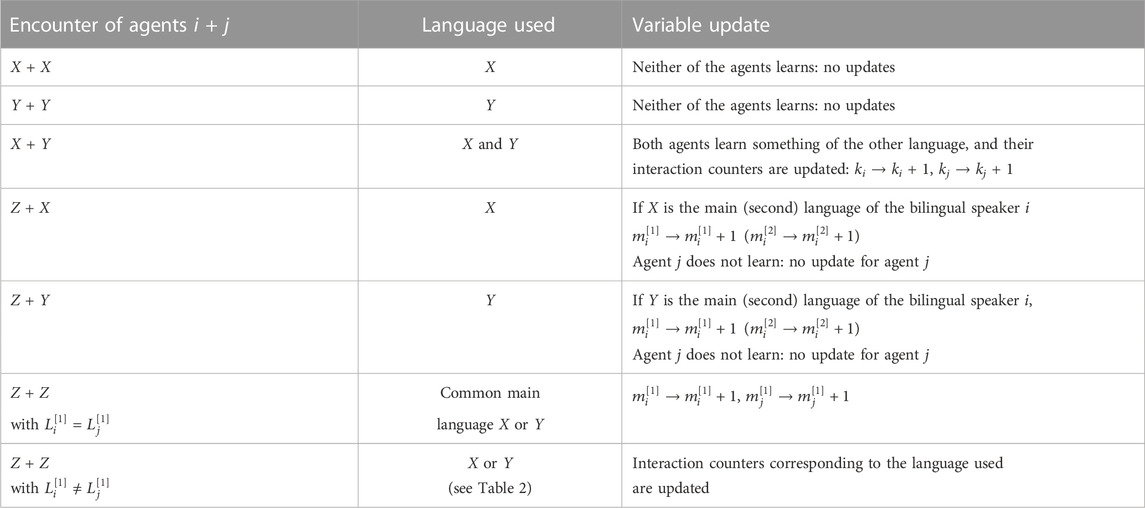
TABLE 1. Possible encounters between agents i and j, the language used, and corresponding updates of their variables (time counters are always updated; see text for details). Here, X, Y, and Z denote the linguistic state of the speaker.
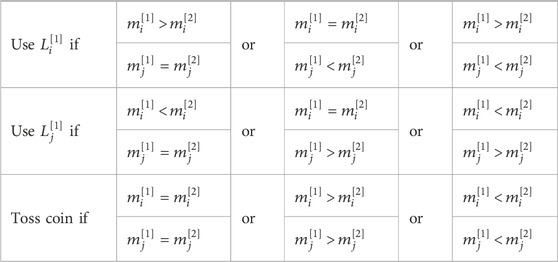
TABLE 2. Language selection and corresponding criteria in an encounter between two bilinguals with different main languages.
3. After the Nint × N/2 couples of agents extracted have interacted, the time variables are updated for each agent i: if agent i is monolingual, time counter
4. Language use counters, time counters, and possible transitions between the monolingual and bilingual state are checked for each agent i (see Table 3).
• If agent i is monolingual, the counters ki and
• If agent i is bilingual, the counter
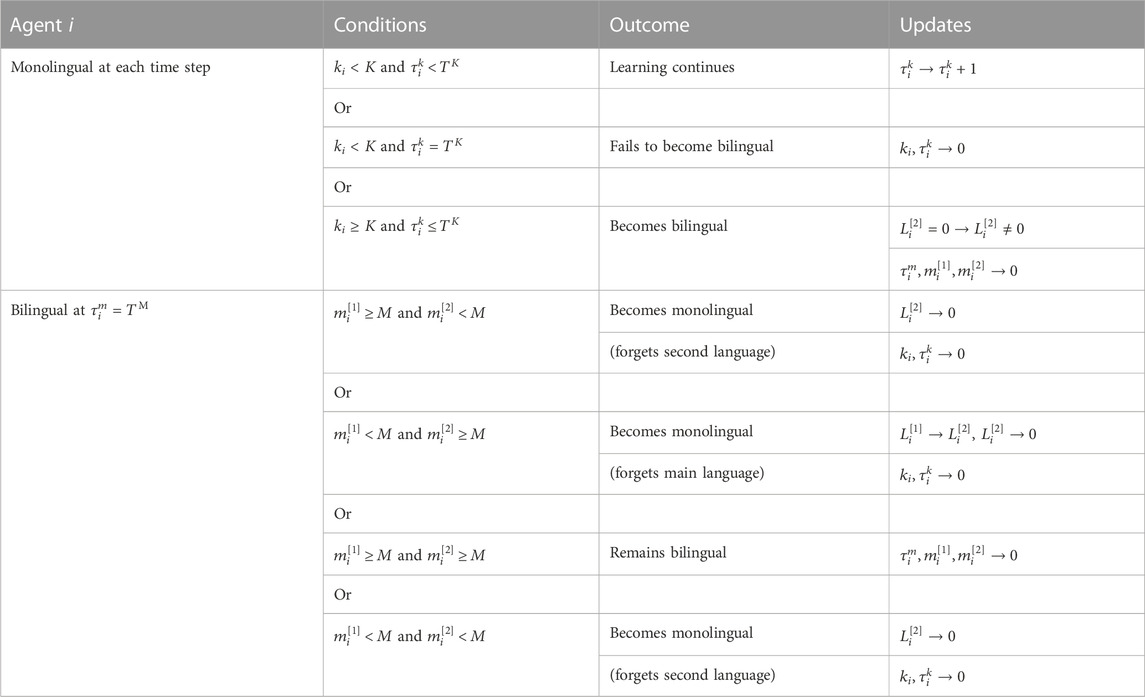
TABLE 3. Checks made on each agent i (i =1,… , N). If for individual i, the conditions are fulfilled, the change described in the column “outcome” takes place and variables are updated as described in column “Updates.”
5. The algorithm is reiterated from step 1 until the final simulation time t = tfin is reached or until all speakers become monolinguals of the same language.
It should be noted that instead of using an algorithm where the time and language use counters are reset, as explained previously, one could use an alternative more realistic algorithm based on a moving temporal window, i.e., checking at each time step the language use during the reference time intervals TK or TM. For computational convenience, we used the aforementioned algorithm, but we checked that within the parameter range used, the two methods provide equivalent results.
2.4 Including heterogeneity
As discussed in Introduction, in a language dynamics model that aims to scrutinize the impact of memory and learning processes, it is relevant to take into account that individual linguistic skills to learn or retain a language are different. This heterogeneity may depend on many factors. In our model, the effect of these factors is described in terms of a heterogeneous distribution of the parameters regulating the learning and maintenance of a language, i.e., the associated time intervals and language usage frequencies.
As far as the learning process is concerned, the global language usage thresholds KX and KY for learning language X and Y by monolingual speakers of language Y and X, respectively, are replaced by a heterogeneous set of parameters
In the following equation, we limit ourselves to considering a specific case with a simple correlation between the threshold values of language usage and attrition times of generic agent i.
In the aforementioned three equations, Si is the same random number extracted from a standard normal distribution, the values KX, KY, and TM represent the means, and σX, σY, and σM represent the relative standard deviations of the respective distributions. Thus, the standard deviations express the degree of heterogeneity of the agents. Equations 1, 2 describe the learning, and Eq. 3 describes the language maintenance features of individual i. The Gaussian distribution is the most natural one to describe the heterogeneity of the linguistic skills in a population. A value Si > 0 in Eq. 1 or 2 describes a speaker who needs for learning to practice language X or Y more times than on average; instead, Si < 0 corresponds to the opposite case. The negative sign in Eq. 3 reflects the fact that, in general, the individuals who learn more slowly are, at the same time, the ones who forget more quickly, and vice versa. For the sake of simplicity, we assume that σX = σY = σM ≡ σ.
It should be noted that since in Eqs 1–3 Si is extracted from a standard normal distribution,
3 Results and discussion
3.1 Simulation parameters
We simulate the model for a population comprising at least N = 103 agents, unless specified differently. We checked that this is a sufficient population size and the results remain unchanged when increasing the number of speakers even up to N = 104. The simulation time is Nt = 4 × 104 days
It should be noted that the choice of the minimum number of learning interactions needed to acquire a new language, determined by the thresholds KX, KY, and TK, as well as of the minimum number of practicing events required to retain a language, determined by M and TM, is arbitrary. However, studying the dependence of simulation results on the number of daily interactions Nint per agent is equivalent to varying the aforementioned thresholds while keeping Nint constant. This is because the competition outcome is mainly determined by the interplay between the daily interaction frequency and model thresholds.
3.2 Homogeneous population
We begin our study of the effects of memory on language competition dynamics by examining first the case of a homogeneous population.
As long as no bilinguals are present in the system (beginning of the time evolution), a speaker interacts daily, on average, NX(0)Nint times with X-monolinguals and NY(0)Nint times with Y-monolinguals. As discussed in Section 2.3, a monolingual → bilingual transformation, X → Z (or Y → Z), takes place only if an X (or Y)-monolingual has used the other language at least KY (or KX) times within the maximum allowed learning time TK. This implies the following conditions for the transition times tX and tY:
If both conditions are fulfilled, then which of the two possible transformations, Y → Z or X → Z, will take place, i.e., which monolingual community will form the bilingual population, depends on which of the two transition times, tX ≤ TK or tY ≤ TK, is smaller. For given values of Nint and TK, this depends on KX, KY, and the initial fractions NX (0) and NY(0). In the symmetrical case, when KX = KY ≡ K, the transition type is determined only by the values of NX (0) and NY(0); if NX (0) = NY(0), both monolingual populations turn into bilinguals; otherwise, it is the population of the minority language that becomes bilingual. In the asymmetrical case, when KX ≠ KY, for equal initial population fractions, NX (0) = NY(0), the transition type is determined by the values of KX and KY: for KX > KY, the bilingual community will be formed by X-monolinguals and for KY > KX by Y-monolinguals, i.e., by the monolinguals of the language that is more difficult to learn. If neither condition is fulfilled, no bilingual community will appear.
In order to illustrate the beginning of the system time evolution, let us consider the example of a population of 100 identical speakers (we use in this example only 100 individuals for the clarity of visualization) with initial population fractions NX (0) = 0.6 and NY(0) = 0.4. The daily interaction rate is Nint = 16, KX = KY = 5,110, and the transition times for the given parameters are tX = 532 and tY = 798, respectively. In this case, since tX < TK < tY, all the Y-monolinguals will become bilinguals around time t = tX. Accordingly, in Figure 1A, the lines depicting the usage counters ki of the Y-monolinguals stop, while the lines corresponding to the bilinguals’ language usage counters
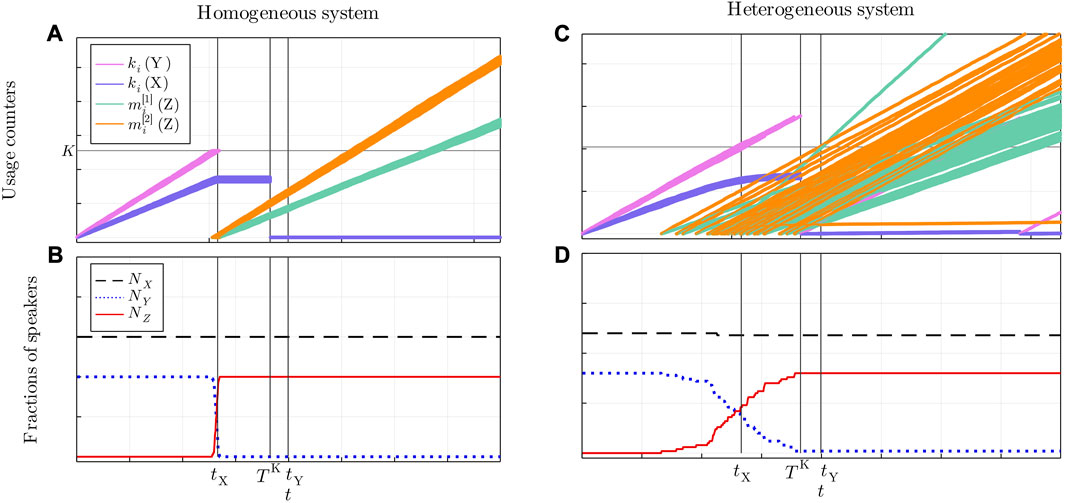
FIGURE 1. (Symmetrical case). Time evolutions in a homogeneous system [(A) and (B)] and in a heterogeneous system with σ = 0.2 [(C) and (D)]. (A), (C) Language usage counters ki,
Figure 1B shows the corresponding time evolution of the population fractions: at time tX, there is the transition Y → Z, i.e., all monolinguals of language Y learn language X and become bilinguals; instead, NX(t) = NX (0).
Now, if the parameters are such that one of the monolingual populations becomes bilingual, whether this state is stable or not, it depends on the parameters regulating the attrition process. It will be stable if bilinguals practice both languages at least M times during a time interval TM. Because in the current example in the communication between bilinguals, only their first language is used (all bilinguals have the same first language), then NZ(t) = NY(0) (as in our example depicted in Figure 1) or NZ(t) = NX (0); the second language is used by bilinguals only in the communication with monolinguals, whose population is equal to the initial one. Consequently, the conditions for the bilingual population to maintain languages X and Y are, respectively,
The bilingual community remains bilingual only if both conditions are satisfied. If one of the conditions is not fulfilled, the respective language is forgotten and the bilinguals become monolinguals of the language for which the condition is satisfied. If none of the conditions is fulfilled, the bilinguals become monolinguals of their original language. In the aforementioned example (Figures 1A, B), the bilinguals maintain both languages and the state reached is stable.
The behavior of the system under different initial conditions is illustrated by the phase portraits in Figure 2A for KX = KY (symmetrical language learning difficulty) and Figure 2B for KX ≠ KY (asymmetrical language learning difficulty). Possible initial conditions are represented by the points on the line NX (0) + NY(0) = 1, where NZ (0) = 0. In this example, we chose Nint = 10, allowing us to observe different regimes: some trajectories evolve toward a final state, where, in addition to bilingual speakers, there are also monolinguals of language X (or Y)—as shown by the dots on the NX-axis (NY-axis); for the rest of the initial conditions, the representative point remains in the initial state. This behavior can be understood by expressing conditions (4)–(5) in terms of the initial fractions NX (0) and NY(0).
which define implicitly the critical initial fractions
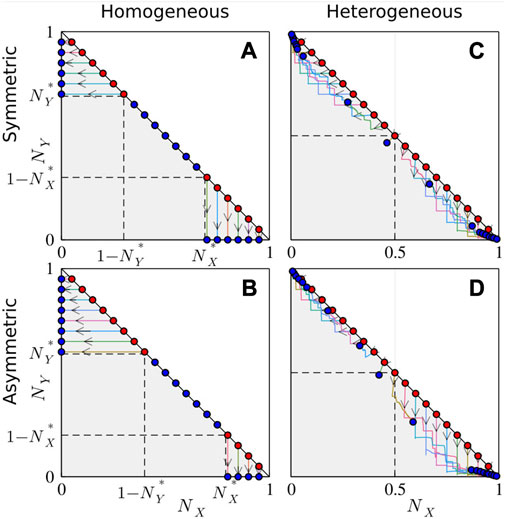
FIGURE 2. Phase portraits of homogeneous [σ = 0—(A) and (B)] and heterogeneous [σ = 0.2—(C) and (D)] systems with symmetrical [KX = KY = 5,110—(A) and (C)] and asymmetrical [KX = 5,840, KY = 4380—(B) and (D)] language learning difficulties. The gray triangle represents the area accessible to the system. The initial conditions are represented by the red dots, and the final positions are represented by the blue dots (overlapping the red ones on the diagonal). The results are obtained using N = 100 agents and Nint = 10. For the homogeneous system, the critical initial densities
Now, from the last remark, as well as from conditions (4)–(5) and (6)–(7), it is also clear that the number of daily interactions, Nint, is a very important quantity in determining the dynamics and outcome of the language competition. In Figure 3, the final population composition is plotted as a function of Nint, dashed lines, for the homogeneous system. This figure shows clearly how the final outcome of the language competition is determined by the interplay of the learning and attrition processes. Let us determine the conditions for the learning and maintenance of languages X and Y for the example with KX = KY = 5,110 and NX (0)/NY(0) = 60/40. From Eqs (4) and (5), one obtains the conditions on the interaction rate: Nint ≥ KX/NX (0)TK = 11.6 and Nint ≥ KY/NY(0)TK = 17.5, for X- and Y-monolinguals, respectively. Therefore, nothing happens until the value Nint = 11.6 is reached (it should be noted that in Figure 3, Nint assumes only integer values), and the two populations speaking languages X and Y remain isolated and do not generate any bilingual community. At Nint ≥ 11.6, Y-monolinguals learn language X and become bilingual. However, in order to remain as such, they have to maintain both languages. According to Eqs (6) and (7), the condition for a bilingual to maintain language X is Nint > M/NX (0)TM = 10, whereas for maintaining language Y, the interaction frequency has to satisfy the condition Nint > M/NY(0)TM = 15. Thus, in the interval 11.6 ≤ Nint ≤ 15, bilinguals who appeared in the system during the time evolution will turn into X-monolinguals so that there are only X-monolinguals in the final state of the system. Instead, for Nint > 15, the bilinguals can maintain both languages, and the final population consists of X-monolinguals and bilinguals. Thus, depending on the value of the interaction frequency, one can observe three regimes (see the dashed lines in Figure 3): 1) coexistence of the two monolingual populations (with NX(t) = NX (0) and NY(t) = NY(0)); 2) only the majority language surviving; and 3) coexistence of monolingual speakers of majority language and bilinguals whose first language is the minority language.
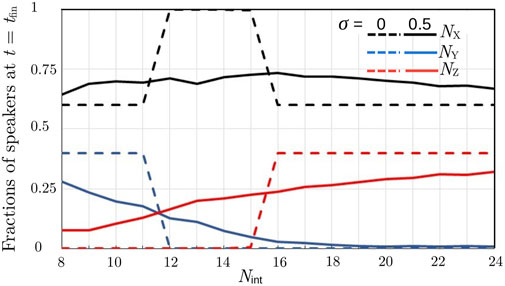
FIGURE 3. (Symmetrical case). Comparison of the final speakers’ compositions versus Nint for homogeneous (σ = 0) and heterogeneous (σ = 0.5) populations; NX (0)/NY(0) = 60/40.
Not taking the memory effects into account, i.e., assuming a time unit much larger than the time scales TK and TM, the homogeneous version of the proposed model, discussed in the this section, reduces to the Minett–Wang model that is local in time. The Minett–Wang model with neutral volatility has only two stable equilibrium points: one of the two competing languages surviving and the other one disappearing; which of the two languages survives depends on the model parameters. Instead, introducing the time-consuming language learning and retention processes, for a wide range of parameters, both languages can survive due to two opposing mechanisms: 1) not learning the other language (coexistence of the two isolated languages) or 2) frequent language contact between the minority language speakers, who eventually become bilinguals, and monolinguals of the majority language.
3.3 Heterogeneous population
In the example illustrating the time evolution in a homogeneous population—Figures 1A, B—all monolinguals of language Y become bilinguals around time tX. The population time evolution is characterized by a simple behavior and sharp transitions because agents are identical to each other in their features and they behave in the same way. The only source of randomness in the homogeneous system is related to the random choice of the interacting agents.
In the corresponding example of a heterogeneous population—Figures 1C, D—because in conditions (4)–(5), KX and KY are replaced by
As a consequence, the step-like curves describing the transitions NY → 0 and NZ → 0.4 are replaced by smoother sigmoids. Depending on the value of σ, it can also happen that not all monolinguals of language Y become bilingual at some time t ≤ TK, whereas some X-monolinguals may do so. Similar considerations are valid for the attrition. In fact, in Figure 1C, one can notice that there is a line
Such diversity in the behavior of individuals induces significant differences in the dynamics and final competition outcome between the homogeneous and heterogeneous systems. To understand how this happens, let us have a look at the time evolution of the speakers’ fractions NX, NY, and NZ on a longer time scale, depicted in Figure 4, for a heterogeneous population with σ = 0.5, initial ratio NX (0)/NY(0) = 60/40, KX = KY = 5,110, and three different values of Nint corresponding to low (Nint = 8), medium (Nint = 16), and high (Nint = 24) daily interaction rates.
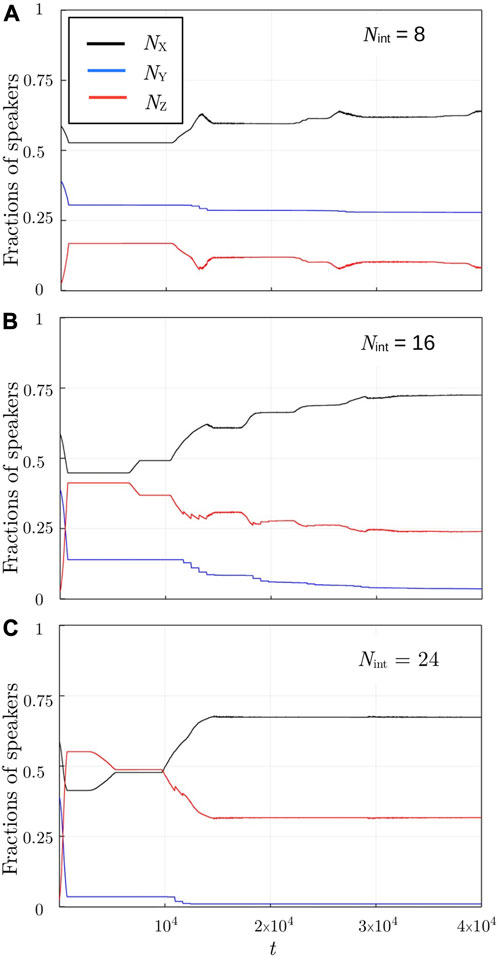
FIGURE 4. (Symmetrical case, heterogeneous population). Time evolution of speakers’ fractions evolving from NX (0)/NY(0) = 60/40 for different daily interaction rates: (A) Nint = 8, (B) Nint = 16, (C) Nint = 24.
In the example of the homogeneous system (Figures 1A, B), only the speakers of minority language Y contributed to the formation of the bilingual community. Instead, in the heterogeneous system, as shown already in Figure 1C, the speakers of majority language X also contribute (see the initial decrease in NX in all panels of Figure 4), but their contribution is smaller than that of Y-monolinguals. It should be noted that the larger the interaction rate, the larger the contribution of Y-monolinguals (compare the three panels in Figure 4). In the following, the formed bilingual community decreases in time due to the attrition process, leading to a corresponding growth of NX. The decrease in NZ and the corresponding increase in NX become larger for higher values of Nint.
The appearance of a maximum in the bilingual population size is also observed in the Minett–Wang model (Minett and Wang, 2008; Heinsalu et al., 2014), in which, however, finally only one of the languages survives, as mentioned previously.
Before proceeding with the discussion, we analyze the presence of the small zigzagged segments in the time evolution curves shown in Figure 4. They are related to attrition processes taking place at times close to each other due to diversity and initial conditions. We verified that they tend to disappear for t → ∞ and their amplitudes decrease with the system size, as N → ∞. We also checked that they do not significantly influence the final results.
Figures 4A, B show that in a heterogeneous system, it is possible for the two monolingual and bilingual populations to coexist in the final state. The same becomes evident from the phase portraits in Figures 2C, D and from the curves shown in Figure 3 for the heterogeneous system. Although in Figure 3, the dashed curves for the homogeneous system and the solid ones for the heterogeneous system might seem to be qualitatively similar, the fraction of Y-monolinguals decreases and the fraction of bilinguals increases with Nint, and the fraction of X-monolinguals passes through a maximum, and even the phase portraits for heterogeneous and homogeneous populations in Figure 2 might seem to be not so different, the systems are actually fundamentally different. That is, it appears that adding heterogeneity to the population can, for a wide range of parameters, lead to the coexistence of the three linguistic groups, which is not possible in a corresponding homogeneous system. Therefore, we conclude that diversity in linguistic abilities is one of the key factors leading to the possibility of the coexistence of all linguistic groups in a three-state system, and this is the most important difference between the homogeneous and heterogeneous systems.
The reason behind the smoothing of the curves shown in Figure 3 when adding heterogeneity in the population is similar to why the step-like transitions shown in Figures 1B are replaced by smoother curves shown in Figures 1D. That is, the replacement of KX, KY, and TM by
In order to evaluate how the degree of heterogeneity, expressed as the relative standard deviation σ, influences the results, we ran simulations for the same system with NX (0)/NY(0) = 60/40 and KX = KY = 5,110 studied previously, varying σ between 0 and 0.5. The results are depicted in Figure 5 for three different values of Nint. Furthermore, the figure shows that adding a certain level of heterogeneity to the system can result in a situation where, in the final state, all three linguistic groups are present in the system: see the lowest group of lines appearing as σ increases. For fixed parameter values and initial composition of the total population, the value of σ leading to such a final state increases slightly when Nint is increased. Furthermore, the diversity of individuals increases the competition advantage of the majority language, with respect to the homogeneous system, for all values of Nint (c.f. also Figure 3), and the effect of varying σ is the largest at intermediate values of Nint.
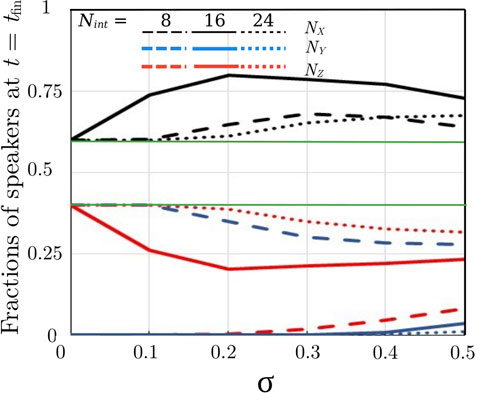
FIGURE 5. (Symmetrical case). Final population composition versus σ for three values of Nint; NX (0)/NY(0) = 60/40. The thin green horizontal lines are a guide to the eye corresponding to the case σ = 0.
From the discussion in Section 3.2, it became clear that the initial conditions play a relevant role in determining the final outcome of the language competition in the homogeneous system. This is also true in the case of heterogeneous populations, as observed from Figures 2C, D and from Figure 6. In the case of equal initial population sizes, NX (0) = NY(0) = 0.5, equal fractions of X- and Y-monolinguals become bilingual. If the interaction frequency is low, e.g., Nint = 8, at equilibrium, relatively large X- and Y-monolingual populations coexist with a small bilingual community. The size of the formed bilingual population increases as the interaction frequency Nint increases; Figure 6 shows the results for NX (0)/NY(0) = 50/50 for three different values of Nint. If the ratio NX (0)/NY(0) is increased, i.e., X becomes the majority language and Y becomes the minority language, the final population composition tends to be more and more dominated by majority language X, as shown in Figure 6. For NX (0)/NY(0) ≳ 80/20, minority language Y becomes extinct, unless the interaction frequency is very low (Nint = 8). In the low interaction limit, the two language populations remain practically isolated from one another and can, in this way, coexist.
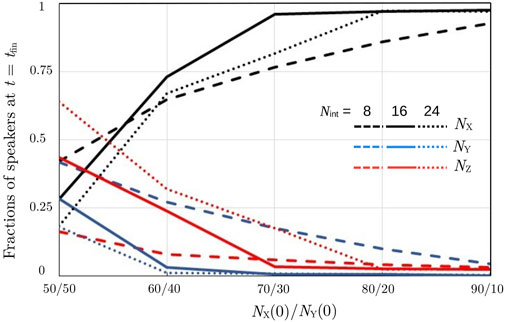
FIGURE 6. (Symmetrical case, heterogeneous population). Final speakers’ compositions as a function of NX (0)/NY(0) for different values of Nint.
3.4 Asymmetrical learning difficulty
So far, we mostly concentrated on the symmetrical case KX = KY ≡ K. Next, we examine in detail the asymmetrical case when KX ≠ KY, i.e., the two competing languages have different degrees of learning difficulty.
From conditions (8)–(9) for the homogeneous population, it is clear that the asymmetry between the parameters KX and KY induces asymmetry also in the critical fractions
Figure 7 presents the results for a heterogeneous system characterized by the parameter values summarized in Section 3.1 and with NX (0) = NY(0) = 0.5. In this figure, the value of KX is increased from KX = KY (corresponding to the symmetrical case) up to KX = 6KY in order to observe how the asymmetry in the language learning difficulty influences the language competition outcome. As observed already in Figure 6, for NX (0) = NY(0) and KX = KY, in the final state, NX = NY and the fraction of bilinguals increases with increasing values of Nint. Now, when KX > KY (see Figure 7), the final fractions of X-monolinguals and bilinguals are decreased with respect to the symmetrical case, while NY(tfin) is increased; the larger the Nint is, the larger the influence of asymmetry. However, increasing the asymmetry between the language learning difficulties beyond KX/KY ≈ 3 does not substantially influence the results. For KX/KY = 3, in order to become bilingual within the time interval TK, a speaker of language Y should practice language X, on average, 21 times per day. Comparing this with the number of average daily interactions (Nint ∈ [8, 24]), it is obvious that the task is very hard for any agent. Therefore, the monolinguals of language Y will remain monolinguals of their mother tongue and NY(tfin) ≈ NY(0) = 0.5 for all studied values of Nint. Instead, the monolinguals of language X will become bilingual, the final fraction of bilinguals being larger for larger Nint values. In fact, for Nint = 24, almost all monolinguals of language X will turn into bilinguals, leaving only a very small fraction of X-monolinguals in the system.
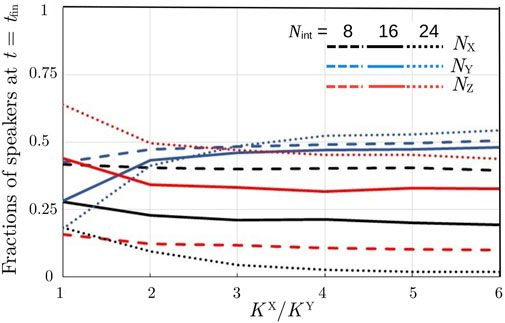
FIGURE 7. (Heterogeneous system). Final population composition versus KX/KY (KY = 5110) for three values of Nint; NX(0)/NY(0) = 50/50.
Figure 8 illustrates the case where the initial populations have different sizes and set NX (0)/NY(0) = 60/40. However, we now vary the value of KX so that the ratio KX/KY goes from 1/7 to 4 (i.e., we go from the case where minority language Y is seven times more difficult to learn for monolinguals of language X than majority language X for monolinguals of Y, to the symmetrical case corresponding to KX/KY = 1, up to the case where majority language X is three times more difficult to learn for monolinguals of Y than minority language Y for monolinguals of X). Figure 8 shows that for all studied values of Nint, an increase in KX/KY, i.e., the learning difficulty of language X, leads to a decrease in NX, as expected, and an increase in NY and NZ. It should be noted that while in the case NX (0)/NY(0) = 50/50, an increase of KX/KY leads to a decrease in bilinguals (see Figure 7), in the case NX (0)/NY(0) = 60/40, the fraction of bilinguals, instead, increases.
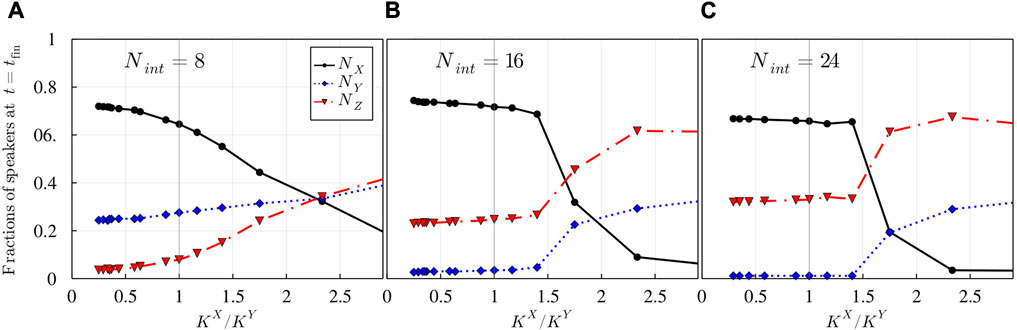
FIGURE 8. (Heterogeneous system). Final population composition versus KX/KY (KY = 5110) for different values of Nint; NX(0)/NY(0) = 60/40.
4 Conclusion
In this paper, we developed an agent-based three-state language competition model that incorporates elements mimicking language learning and retention and the underlying memory processes.
We showed that upon including memory in a Minett–Wang-type model with a population of speakers having homogeneous linguistic skills, the final outcome of the language competition can be 1) the extinction of one of the competing languages; 2) the coexistence of two isolated language communities; and 3) a state where the minority language survives due to the bilingual speakers. Which of the three possible scenarios is realized depends on the initial population composition, the parameters that determine learning/attrition (among which is the asymmetry between the language learning difficulties), and the interaction frequency between individuals.
The results of our study suggest that while language prestige is certainly crucial for language shift and in determining the outcome of language competition, memory effects may also play a critical role, and their relative importance versus prestige may depend on the specific features of the system under consideration.
Another relevant issue addressed in the present work concerns the impact of heterogeneity on language dynamics models. We showed that the outcome of language competition depends, in addition to other parameters, on the level of population diversity in terms of language learning and retention skills. In fact, adding heterogeneity to the model significantly changes the time evolution of population fractions and the final population composition. Diversity also allows us to observe, differently from the corresponding homogeneous system, a final equilibrium state where all three linguistic groups—the two monolingual and the bilingual groups—are present. Therefore, we conclude that, in addition to the learning and retention processes, the impact of heterogeneity on language dynamics deserves a broader investigation.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
SS: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, and writing—original draft and review and editing. JK-L: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, and writing—original draft and review and editing. MP: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, and writing—original draft and review and editing. EH: conceptualization, funding acquisition, visualization, investigation, methodology, project administration, supervision, and writing—original draft and review and editing.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. The authors acknowledge support from the Estonian Research Council through Grant PRG1059.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
SS, MP and EH declared that they were editorial board members of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abrams, D. M., and Strogatz, S. H. (2003). Modelling the dynamics of language death. Nature 424, 900. doi:10.1038/424900a
Abutalebi, J., and Green, D. (2007). Bilingual language production: the neurocognition of language representation and control. J. neurolinguistics 20, 242–275. doi:10.1016/j.jneuroling.2006.10.003
Austin, P. K. (2008). 1000 languages: The worldwide history of living and lost tongues. London: Thames and Hudson Ltd.
Baggs, I., and Freedman, H. (1990). A mathematical model for the dynamics of interactions between a unilingual and a bilingual population: persistence versus extinction. J. Math. Sociol. 16, 51–75. doi:10.1080/0022250x.1990.9990078
Baggs, I., Freedman, H., and Aiello, W. (1990). “Equilibrium characteristics in models of unilingual-bilingual population interactions,” in Ocean waves mechanics, computational fluid dynamics, and mathematical modelling: Proceedings of the 11th international annual conference of the Canadian applied mathematics society. Editor M. Rahman (Southampton: Computational Mechanics Publications Ltd), 879.
Baggs, I., and Freedman, H. (1993). Can the speakers of a dominated language survive as unilinguals — A mathematical-model of bilingualism. Math. Comput. Model. 18, 9–18. doi:10.1016/0895-7177(93)90122-f
Baron, J. W., Peralta, A. F., Galla, T., and Toral, R. (2022). Analytical and numerical treatment of continuous ageing in the voter model. Entropy 24, 1331. doi:10.3390/e24101331
Baronchelli, A. (2016). A gentle introduction to the minimal naming game. Comput. Constr. Gramm. Constr. Change 30, 171–192. doi:10.1075/bjl.30.08bar
Bouchaud, J.-P. (2009). The (unfortunate) complexity of the economy. Phys. World 22, 28–32. doi:10.1088/2058-7058/22/04/39
Castellano, C., Fortunato, S., and Loreto, V. (2009). Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646. doi:10.1103/RevModPhys.81.591
Dall’Asta, L., and Castellano, C. (2007). Effective surface-tension in the noise-reduced voter model. Europhys. Lett. (EPL) 77, 60005. doi:10.1209/0295-5075/77/60005
De Silva, K., Basheer, A., Antwi-Fordjour, K., Beauregard, M. A., Chand, V., and Parshad, R. (2021). The “higher” status language does not always win: the fall of English in India and the rise of Hindi. Adv. Complex Syst. 23, 2050021. doi:10.1142/s0219525920500216
Del Valle, S., Hyman, J. M., Hethcote, H. W., and Eubank, S. G. (2007). Mixing patterns between age groups in social networks. Soc. Netw. 29, 539–554. doi:10.1016/j.socnet.2007.04.005
Ellis, R., Ellis, P., and Ellis, R. (1994). The study of second language acquisition. Oxford, UK: Oxford University Press.
Griffiths, C., and Soruç, A. (2020). Individual differences in language learning: A complex systems theory perspective. Springer International Publishing.
Heinsalu, E., Patriarca, M., and Léonard, J. L. (2014). The role of bilinguals in language competition. Adv. Complex Syst. 17, 1450003. doi:10.1142/S0219525914500039
Iriberri, N., and Uriarte, J.-R. (2012). Minority language and the stability of bilingual equilibria. Ration. Soc. 24, 442–462. doi:10.1177/1043463112453556
Jackson, G. M., Swainson, R., Cunnington, R., and Jackson, S. R. (2001). Erp correlates of executive control during repeated language switching. Biling. Lang. Cognition 4, 169–178. doi:10.1017/S1366728901000268
Lafuerza, L., and Toral, R. (2013). On the effect of heterogeneity in stochastic interacting-particle systems. Sci. Rep. 3, 1189. doi:10.1038/srep01189
Liivand, J. K. (2018). Memory effects in language acquisition and attrition processes. Master’s thesis. Tartu: University of Tartu.
Marchetti, G., Patriarca, M., and Heinsalu, E. (2020a). A Bayesian approach to the naming game model. Front. Phys. 8, 10. doi:10.3389/fphy.2020.00010
Marchetti, G., Patriarca, M., and Heinsalu, E. (2020b). A bird’s-eye view of naming game dynamics: from trait competition to Bayesian inference. Chaos (Woodbury, N.Y.) 30, 063119. doi:10.1063/5.0009569
Marchetti, G., Patriarca, M., and Heinsalu, E. (2021). The role of bilinguals in the Bayesian naming game. Phys. D. Nonlinear Phenom. 428, 133062. doi:10.1016/j.physd.2021.133062
Meuter, R. F., and Allport, A. (1999). Bilingual language switching in naming: Asymmetrical costs of language selection. J. Mem. Lang. 40, 25–40. doi:10.1006/jmla.1998.2602
Mickan, A., McQueen, J. M., and Lemhöfer, K. (2020). Between-language competition as a driving force in foreign language attrition. Cognition 198, 104218. doi:10.1016/j.cognition.2020.104218
Minett, J. W., and Wang, W. S.-Y. (2008). Modelling endangered languages: the effects of bilingualism and social structure. Lingua 118, 19–45. doi:10.1016/j.lingua.2007.04.001
Moritz-Gasser, S., and Duffau, H. (2009). Cognitive processes and neural basis of language switching: Proposal of a new model. Neuroreport 20, 1577–1580. doi:10.1097/wnr.0b013e328333907e
Odgen, C. K., and Richards, I. A. (1923). The Meaning of Meaning. A study of the influence of thought and of the science of symbolism. New York: Harcourt, Brace and World, Inc.
Patriarca, M., Heinsalu, E., and Leonard, J. L. (2020). “Languages in space and time: models and methods from complex systems theory,” in Physics of society: Econophysics and sociophysics (Cambridge University Press). doi:10.1017/9781108480659
Schmid, M., and Köpke, B. (2019). The Oxford handbook of language attrition. Oxford Handbooks: OUP Oxford.
Vazquez, F., Castelló, X., and San Miguel, M. (2010). Agent based models of language competition: macroscopic descriptions and order–disorder transitions. J. Stat. Mech. Theory Exp. 2010, P04007. doi:10.1088/1742-5468/2010/04/p04007
Ya-ping, Q., Ya, L., Gui-hong, B., Kai-feng, Z., and Chao, W. (2015). “Complex agent network model for the competition among three languages,” in The 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23-25 May 2015 (IEEE), 5910–5917. doi:10.1109/CCDC.2015.7161868
Zhang, Y., Ocampo-Espindola, J. L., Kiss, I. Z., and Motter, A. E. (2021). Random heterogeneity outperforms design in network synchronization. Proc. Natl. Acad. Sci. U. S. A. 118, e2024299118. doi:10.1073/pnas.2024299118
Keywords: language dynamics, three-state language competition models, language learning, memory effects, heterogeneity
Citation: Scialla S, Liivand J-K, Patriarca M and Heinsalu E (2023) A three-state language competition model including language learning and attrition. Front. Complex Syst. 1:1266733. doi: 10.3389/fcpxs.2023.1266733
Received: 25 July 2023; Accepted: 07 August 2023;
Published: 24 August 2023.
Edited by:
Maxi San Miguel, Institute for Cross Disciplinary Physics and Complex Systems, IFISC (CSIC-UIB), SpainReviewed by:
Yoshifumi Kawasaki, The University of Tokyo, JapanElka Korutcheva, National University of Distance Education (UNED), Spain
Copyright © 2023 Scialla, Liivand, Patriarca and Heinsalu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marco Patriarca, bWFyY28ucGF0cmlhcmNhQGdtYWlsLmNvbQ==
†ORCID: Stefano Scialla, orcid.org/0000-0003-1582-8743; Marco Patriarca, orcid.org/0000-0001-6743-2914
 Stefano Scialla
Stefano Scialla Jens-Kristjan Liivand1
Jens-Kristjan Liivand1 Marco Patriarca
Marco Patriarca Els Heinsalu
Els Heinsalu