Defining quantum-ready primitives for hybrid HPC-QC supercomputing: a case study in Hamiltonian simulation

As computational demands in scientific applications continue to rise, hybrid high-performance computing (HPC) systems integrating classical and quantum computers (HPC-QC) are emerging as a promising approach to tackling complex computational challenges. One critical area of application is Hamiltonian simulation, a fundamental task in quantum physics and other large-scale scientific domains. This paper investigates strategies for quantum-classical integration to enhance Hamiltonian simulation within hybrid supercomputing environments. By analyzing computational primitives in HPC allocations dedicated to these tasks, we identify key components in Hamiltonian simulation workflows that stand to benefit from quantum acceleration. To this end, we systematically break down the Hamiltonian simulation process into discrete computational phases, highlighting specific primitives that could be effectively offloaded to quantum processors for improved efficiency. Our empirical findings provide insights into system integration, potential offloading techniques, and the challenges of achieving seamless quantum-classical interoperability. We assess the feasibility of quantum-ready primitives within HPC workflows and discuss key barriers such as synchronization, data transfer latency, and algorithmic adaptability. These results contribute to the ongoing development of optimized hybrid solutions, advancing the role of quantum-enhanced computing in scientific research.

1 Introduction

The convergence of high-performance computing (HPC) and quantum computing (QC) is emerging as a pivotal strategy for tackling problems that demand computational capabilities beyond the reach of classical systems alone. In domains such as quantum chemistry, material science, nuclear fusion, and high-energy physics, the simulations and calculations required can be computationally prohibitive, even for today's most advanced supercomputers (Bauer et al., 2023b; Di Meglio et al., 2024; Bauer et al., 2023a; Joseph et al., 2023). This is especially true for applications that involve simulating quantum phenomena, such as Hamiltonian dynamics, where capturing the intricacies of quantum interactions places extreme demands on resources (Ayral et al., 2023). For example, lattice QCD, a standard numerical technique where space-time is discretized, faces the “sign problem,” where integrals become highly oscillatory and challenging for numerical methods (Kronfeld et al., 2022; Davoudi et al., 2021). Different ideas have been pursued to overcome such sign problems (Alexandru et al., 2022; Nagata, 2022), but these problems are believed to be NP-hard (Troyer and Wiese, 2005). Lattice QCD relies on HPC and advanced software to provide precision calculations of the properties of particles that contain quarks and gluons. In HPC systems, the uniform space-time grid can be divided among the processors of a parallel computer. Some recent estimates on cost estimates for one of the most expensive physics simulations require 1.5 (1500) Exaflop hours at Cori (NSERC) and Summit (ORNL) for lattice volumes of 32³ × 64(128³ × 512) (Boyle et al., 2022).

While quantum computers inherently offer potential advantages in scientific computing applications–particularly for studying or simulating quantum phenomena due to their quantum nature–there remain significant challenges in achieving hardware readiness for widespread, reliable quantum deployment (Funcke et al., 2023; Li et al., 2023; Meth et al., 2023). Current quantum hardware faces limitations in terms of error rates, coherence times, and scalability, making it challenging to fully leverage its advantages independently.

For example, the resource estimation for state-of-the-art methods applicable to the the lattice QCD problem indicates a demand for resources beyond our current reach. For example, the gate count scales as dΛt^3/2(L/a)^3d/2ϵ^−1/2 for the SU(2) and SU(3) lattice gauge theories in the irrep basis, when approximating the time-evolution operator via Trotterization for a maximum error ϵ for an arbitrary state. Here, d denotes the dimensionality of space, Λ is the gauge-field truncation in the irrep basis, L is the spatial extent of a cubic lattice and a denotes the lattice spacing. For an accuracy goal of ϵ = 10⁻⁸ and a lattice with tens of sites along each spatial direction, the simulation requires hundreds of thousands of million qubits and $\mathcal{O}(10^{50})$ T-gates (Shaw et al., 2020; Kan and Nam, 2022). Recent studies estimating the resource requirements for the simulation of nuclear effective field theories (EFTs) report a T-gate count of 4 × 10¹² and 10,000 qubits for simulating a compact Pionless EFT (Watson et al., 2023).

Given these challenges, hybrid HPC-QC systems are increasingly explored as a practical solution to leverage the strengths of both classical and quantum computation. Hamiltonian simulation—a cornerstone of quantum physics for modeling energy and interactions in a quantum systems—is a particularly promising application for such hybridization. In traditional HPC environments, simulating Hamiltonian dynamics is computationally intensive due to the high dimensional operators involves. Hybrid systems have the potential to alleviate this burden by offloading specific computational primitives to quantum processors, thereby enhancing precision and efficiency (Shehata et al., 2024).

This study aims to break down the Hamiltonian simulation workflow into computational primitives and analyze the scaling trends when these primitives are executed using either purely quantum or purely classical resources. The objective is to provide further algorithm developers with actionable insights on how to integrate quantum and classical resources effectively for overall quantum simulation workflows. By systematically assessing the modularity and resource allocation for Hamiltonian simulation, we aim to inform strategies for hybrid HPC-QC architectures that optimize the synergy between these technologies.

In contrast to previous wok focusing primarily on algorithmic design or hardware capabilities, our study takes a pragmatic approach by mapping simulation workflows onto hybrid systems and identifying specific tasks most conducive to quantum execution. Although Hamiltonian simulation is our primary focus, its significance spans diverse applications, including spin-boson models, lattice gauge theories, and quantum chemistry, providing a foundation for benchmarking hybrid HPC-QC systems in broader contexts.

In this paper, we propose a systematic approach to integrating quantum resources within classical HPC environments. We begin by analyzing the typical computational primitives involved in Hamiltonian simulation and assess their potential for quantum offloading. Through case studies in Hamiltonian simulation, we identify tasks that are most amenable to quantum execution and highlight their scalability. This modular approach provides a roadmap for scaling hybrid HPC-QC systems as quantum technology advances, aiming to maximize the strengths of each platform in tandem.

2 Methods

Hamiltonian simulation is a cornerstone in quantum physics and chemistry, allowing researchers to model the energy and dynamic interactions within a quantum system. However, simulating these interactions at a scale sufficient for realistic applications can quickly outstrip classical computational capabilities.

Our goal is to understand how a hybrid HPC-QC approach, which distributes specific computational primitives across classical and quantum resources, offers a promising pathway to more scalable and accurate Hamiltonian simulation. To achieve this, we introduce a structured framework for identifying quantum-ready computational primitives based on a set of explicit selection criteria.

In this section, we dissect the Hamiltonian simulation workflow into three primary stages (Figure 1)—initialization, evolution, and measurement—and carry out a comparative analysis between quantum and classical resources. The tasks within each stage are evaluated using the following metrics:

• Computational complexity: We assess the time and space complexity of the task on classical systems and compare it with the estimated gate count, qubit requirements, and circuit depth for quantum execution.

• Potential speedup: Tasks are prioritized for quantum offloading if they demonstrate the potential for exponential or polynomial speedup on quantum hardware compared to classical methods.

• Resource scalability: The scalability of resources (e.g., qubits, memory, or compute nodes) required to execute the task as the problem size increases is evaluated to identify whether quantum systems can handle the task more efficiently at scale.

• Task modularity: We consider the task can be modularly integrated into a hybrid workflow without introducing excessive synchronization overhead between classical and quantum systems.

• Physical relevance: Tasks that are directly tied to simulating inherently quantum phenomena, such as unitary time evolution or entanglement measurements, are prioritized for quantum offloading.

Figure 1

Figure 1. Illustration depicting various components essential to the quantum simulation process.

Using these criteria, we identified specific computational primitives within each stage of the workflow that are well-suited for quantum execution. For example, in the evolution stage, tasks involving the time evolution of the system under a Hamiltonian operator, especially those with high-dimensional matrices, were selected due to their computational intensity and quantum advantage in simulating unitary dynamics. Conversely, tasks with minimal computational overhead or those involving extensive classical data manipulation, such as pre- and post-processing in the initialization and measurement stages, were excluded from quantum offloading.

To validate our framework, we apply it to a few relatively simple physics examples, quantifying the computational resources–such as qubits, gates, and circuit depth required for the quantum simulation, and memory and time complexity for the classical simulation–needed for each stage. We also discuss alternative primitives considered during the selection process and provide justification for their exclusion, ensuring transparency in our methodology.

By structuring our analysis around these metrics, we aim to provide a clear and rigorous foundation for identifying tasks most suitable for quantum offloading within hybrid HPC-QC workflows, thereby guiding the development of more effective and scalable simulation strategies.

2.1 Heisenberg model ground state preparation

The first step in Hamiltonian simulation is to initialize the system in a well-defined quantum state, which may represent the ground state or a specific excited state depending on the study's objectives (Gratsea et al., 2024). This stage typically involves encoding the initial quantum state. On classical hardware, this step requires generating large, structured datasets that represent quantum states in matrix form. Quantum computers, however, can naturally represent these states, potentially reducing data handling complexity (Wang and Jaiswal, 2023). For hybrid HPC-QC systems, state preparation could be offloaded to the quantum processor to leverage its ability to represent high-dimensional quantum states natively. Creating entangled states or superpositions in the initial state is computationally intensive classically, particularly for large systems. Quantum processors can establish entangled states more efficiently, potentially improving simulation fidelity by initializing more complex correlations between components in the quantum system.

To showcase the complexity of state preparation, we consider an initial quantum state that involves significant entanglement or complex correlations. One excellent choice is the preparation of a ground state for the Heisenberg model or preparation of an arbitrary quantum state with entanglement.

The Heisenberg model is a fundamental model in quantum mechanics used to describe interactions in a system of spins arranged on a lattice. It captures how neighboring spins interact and is widely used in studies of magnetism and condensed matter physics. The Hamiltonian for the one-dimensional Heisenberg model with nearest-neighbor interactions is given by:

$\begin{array}{ll}H=J{\displaystyle \sum _{i=1}^{N-1}}\left({\sigma }_x^{(i)}{\sigma }_x^{(i+1)}+{\sigma }_y^{(i)}{\sigma }_y^{(i+1)}+{\sigma }_z^{(i)}{\sigma }_z^{(i+1)}\right),& (1)\end{array}$

where J is the interaction strength between neighboring spins, N is the number of spins in the system, and σ_x, σ_y, and σ_z are the Pauli matrices acting on each spin. In the antiferromagnetic case, J>0, spins prefer to align in opposite directions, while in the ferromagnetic case, J < 0, spins prefer to align in the same direction. The Heisenberg model's rich ground state and excitation properties make it an ideal testbed for studying quantum entanglement, phase transitions, and quantum state preparation.

The Heisenberg model introduces significant complexity in state preparation because its ground state is entangled, especially in one or two dimensions. Preparing the ground state involves non-trivial entanglement across multiple qubits, making it an ideal choice for comparing quantum and classical state preparation methods.

In the quantum case, preparing the Heisenberg model ground state typically requires an adiabatic approach or variational quantum algorithms (VQAs) (Cerezo et al., 2021), like the variational quantum eigensolver (VQE) (Peruzzo et al., 2014). The VQE uses a parameterized circuit and classical optimization to iteratively find the ground state.

On the classical side, preparing the ground state can be done with exact diagonalization for small systems or tensor network methods [e.g., Density Matrix Renormalization Group, or DMRG (White, 1992, 1993)] for larger systems. Both of these methods become computationally intensive as the system size grows, allowing for a meaningful comparison of resource requirements.

Another approach to demonstrate complexity in state preparation is to prepare highly entangled states, such as W states or GHZ states, where all qubits are entangled in a non-trivial way. For W and Greenberger-Horne-Zeilinger (GHZ) states you need entangling gates (e.g., CNOT or controlled-phase gates) for quantum state preparation that scale in depth and complexity as the number of qubits grows. This type of state preparation grows polynomially in gate count. For classical simulation, the challenge lies in representing the entangled structure and handling the exponentially growing Hilbert space. In Table 1, we summarize our choice of states for state preparation.

Table 1

Table 1. Summary of example choices.

To analyze the scalability of gate count and circuit depth for different quantum state preparation methods, we compare the resource requirements for two representative quantum circuits: the Heisenberg ground state and the GHZ state. Figure 2 presents the total gate count and circuit depth for these circuits as functions of the number of qubits. The Heisenberg ground state, prepared using a VQE ansatz, requires a significantly higher gate count and circuit depth, especially as the number of qubits increases. This is due to the intricate entangling and parameterized gate structure of the variational ansatz, which is necessary to capture the entangled ground state properties. In contrast, the GHZ state circuit grows linearly in both gate count and depth, as each additional qubit only requires a single CNOT gate to entangle it with the chain. These results demonstrate the efficiency of entangled state circuits like GHZ in scaling, while also illustrating the computational cost of variational approaches for more complex states, such as those in many-body systems modeled by the Heisenberg Hamiltonian.

Figure 2

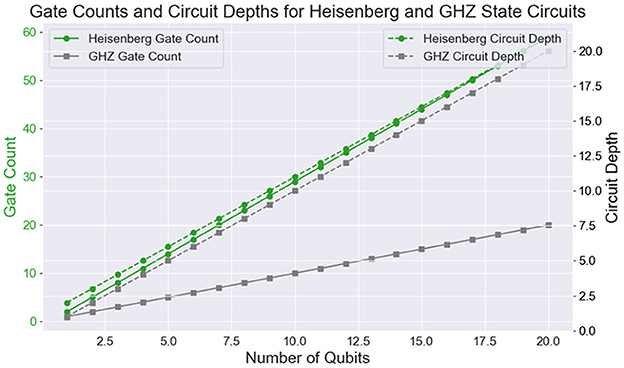
Figure 2. Gate count (left) and circuit depth (right) as a function of the number of qubits for the Heisenberg ground state circuit (green circles) and the GHZ state circuit (gray squares). The Heisenberg circuit exhibits a linear growth in gate count, increasing by 3 gates per additional qubit, reflecting the complexity of preparing an entangled ground state. In contrast, the GHZ circuit's gate count scales linearly with a constant rate of 1 gate per qubit, indicating its simpler structure. Similarly, the circuit depth for the Heisenberg circuit grows linearly by 1 per qubit, while the GHZ circuit depth increases at the same rate.

For the classical state preparation of the ground state of the Heisenberg model and the GHZ state, we can use metrics such as memory usage and time complexity as functions of the number of spins/qubits. For the Heisenberg model, we'll use exact diagonalization, which allows us to find the ground state vector but is memory-intensive and scales poorly with system size. For the GHZ state, we'll simulate the classical representation of the entangled state, which grows linearly in memory usage.

The Hamiltonian matrix for the Heisenberg model grows as 2ⁿ×2ⁿ, where n is the number of spins. The memory usages is calculated as (dim²)*8, where each element is assumed to be a double-precision float (8 bytes). We then compute the smallest eigenvalue, which corresponds to the ground state. The runtime is measured for this diagonalization step.

For the GHZ state, we simulate the memory needed to store a 2ⁿ-dimensional vector, as the state requires storing complex amplitudes for each basis state. This scales linearly with the number of amplitudes. The time to initialize a GHZ state classically is minimal, but we measure the allocation and initialization time as an indication of computational cost (Figure 3).

Figure 3

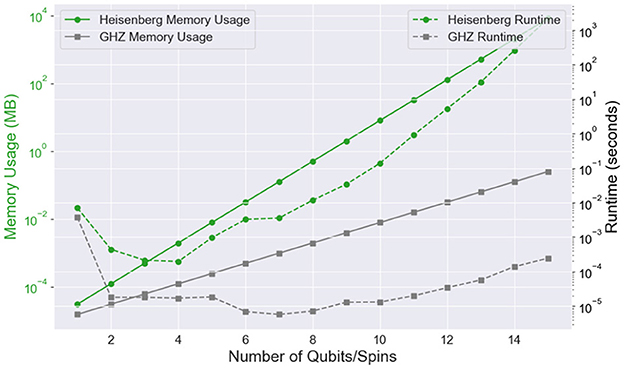
Figure 3. Memory usage and runtime for classical state preparation of the Heisenberg ground state (green circles) and GHZ state (gray squares) as functions of the number of qubits/spins. The left axis shows memory usage in megabytes (MB) as the system size increases. The right axis illustrates the runtime for each preparation method.

As we can see from Figure 3, the Heisenberg model's memory requirements grow exponentially with the number of spins due to the full matrix representation required for exact diagonalization. In contrast, the GHZ state, which requires storing only 2ⁿ amplitudes, has a lower memory complexity but still grows exponentially. Exact diagonalization for the Heisenberg ground state becomes computationally intensive as the number of spins increases, while the runtime for GHZ state preparation remains relatively small, reflecting its simpler structure.

In Table 2, we compare various classical and quantum state preparation methods based on their execution time scaling, resource requirements, and accuracy. This comparison highlights the computational trade-offs inherent in different approaches and provides insight into which methods may be best suited for hybrid HPC-QC workflows.

Table 2

Table 2. Comparison of classical and quantum state preparation methods in terms of execution time scaling, resource savings, and accuracy.

Classical methods such as direct encoding and approximate encoding techniques (e.g., tensor networks and neural quantum states [NQS] (Carleo and Troyer, 2017); see Lange et al., 2024 for a comprehensive review) typically scale polynomially or exponentially with system size (N). Direct encoding, while exact, suffers from an exponential growth in memory and computation time, scaling as $(\mathcal{O}(2^N))$, making it infeasible for large systems. In contrast, tensor networks reduce computational complexity to sub-cubic polynomial scaling, typically of the form $(\mathcal{O}(N^k))$ with (k < 3), by exploiting low-rank representations of quantum states. While this reduces resource consumption, it comes at the cost of accuracy. The Hartree-Fock (HF) method (Echenique and Alonso, 2007) is computationally efficient, scaling as $(\mathcal{O}(N^4))$, but it becomes inaccurate for strongly correlated systems. DMRG, which scales polynomially $((\mathcal{O}(N^3)))$ in one-dimensional systems, is an effective approach for low-entanglement states. NQS offer an alternative encoding scheme where a neural network parameterizes the quantum state, typically with complexity $(\mathcal{O}(N^{\alpha }))$, where (α~2), though accuracy depends on the expressivity of the network and the effectiveness of training.

Quantum computing methods such as Variational quantum state preparation methods, such as the VQE and the Quantum Approximate Optimization Algorithm (QAOA), introduce tunable parameters that affect both accuracy and computational complexity. VQA techniques scale polynomially in N. The scaling of VQE depends on the ansatz depth and the number of parameters used, typically expressed as $(\mathcal{O}(d·p))$, where (d) is the circuit depth and (p) is the number of variational parameters. QAOA performance is dictated by the number of optimization layers, scaling as $(\mathcal{O}(p))$, where (p) represents the number of QAOA layers required for convergence. Finally, adiabatic state preparation (Albash and Lidar, 2018; Babbush et al., 2014) follows a different paradigm, where execution time scales inversely with the spectral gap (Δ) of the Hamiltonian, resulting in a complexity of $(\mathcal{O}(1/{\Delta }^2))$. This dependence makes adiabatic methods particularly sensitive to problem-specific properties. For worst-case scenarios, it exhibits a complexity of $\mathcal{O}(exp(\sqrt{N}))$, though in favorable conditions, it can be more efficient.

2.2 Time evolution for the Ising model

Once the initial state is prepared, Hamiltonian simulation enters the evolution stage, where the system's time-dependent behavior under a Hamiltonian operator is simulated. This stage often comprises applying time-evolution operators that update the state according to Schrödinger's equation. However, as quantum systems grow in size, their state space expands exponentially, making exact simulation on classical computers infeasible beyond modestly sized systems. This exponential complexity has driven the development of specialized classical techniques, such as matrix exponentiation methods and tensor network approaches, and has spurred interest in quantum algorithms that leverage quantum hardware to simulate such systems more efficiently (Morrell et al., 2024).

In classical simulations, time evolution is commonly performed by directly exponentiating the Hamiltonian matrix, which provides an exact solution for small systems. For larger systems, classical approaches like the Chebyshev expansion (Gull et al., 2018) and Krylov subspace methods (Liesen and Strakos, 2012) approximate the action of the time-evolution operator on an initial state vector without needing to construct the entire matrix. These methods are highly efficient but require substantial computational resources as the number of spins increases.

Quantum computers, by contrast, can approximate these operators directly through quantum gates, which are well-suited for simulating unitary evolution (Buessen et al., 2023). Offloading this operation to QC can significantly reduce the computational burden on classical HPC, especially in high-dimensional systems.

For complex Hamiltonians, the evolution operator is often decomposed into simpler, sequential steps using techniques such as Trotterization (Suzuki, 1976). This decomposition approximates the Hamiltonian evolution by breaking it into multiple, smaller time steps, where each step corresponds to a simpler operator sequence. Quantum processors can handle this decomposition more naturally. Hybrid systems can also leverage quantum computing's strengths in optimizing these decompositions dynamically, with the classical system overseeing the simulation accuracy. The Trotterized approach divides the Hamiltonian into commuting parts and approximates U(t) by iteratively applying each part in sequence, allowing simulation of time evolution with native operations on a quantum processor (Ostmeyer, 2023). Although approximate, Trotterization is highly adaptable to the limitations of current quantum hardware, where gate depth and coherence times remain constraints.

In this experiment, we focus on the Ising model with a transverse magnetic field, a paradigmatic system used to study quantum phase transitions and magnetism. The Ising model describes a chain of spins with interactions between nearest neighbors and an external magnetic field. This model captures key aspects of more complex quantum systems and serves as an ideal testbed for simulating quantum dynamics due to its well-understood behavior and simplicity. The Hamiltonian for the 1D Ising model with an external magnetic field is given by:

$\begin{array}{ll}H=-J{\displaystyle \sum _i}{\sigma }_z^{(i)}{\sigma }_z^{(i+1)}-h{\displaystyle \sum _i}{\sigma }_x^{(i)}& (2)\end{array}$

where J represents the strength of the interaction between neighboring spins, encouraging alignment in the z-direction, and h represents the strength of the external magnetic field in the x-direction, which introduces a competing influence on the spins.

In this setup, each spin is represented by a qubit, with Pauli operators σ_z and σ_x applied to describe the interactions and external field effects, respectively. The Ising Hamiltonian's structure allows us to decompose the simulation into manageable computational steps, or primitives, that can be selectively run on classical or quantum hardware. This modular approach provides a basis for analyzing the resource demands of each stage in both quantum and classical environments. Accurately modeling the time evolution under this Hamiltonian requires calculating the unitary operator U(t) = e^−iHt, which evolves the quantum state over time t.

We conducted and experiment to analyze and compare the resource requirements for time evolution of the Ising model using both classical and quantum approaches. We simulate the time evolution on a classical computer by direct matrix exponentiation for small system sizes, tracking metrics such as memory usage and runtime to understand the classical computational burden as system size increases. These results provide a baseline for comparing with Trotterized quantum simulations, which have more favorable scaling on quantum devices due to their use of native gate operations. By examining both classical and quantum resources, this study provides insights into the practical trade-offs between accuracy and scalability in simulating quantum dynamics and underscores the potential of quantum algorithms for tasks that are computationally intensive on classical architectures.

Figure 4 illustrates the memory usage and runtime required for the classical simulation of time evolution in the Ising model, with the number of spins ranging from 2 to 14. As the system size increases, both memory usage (in MB) and runtime (in seconds) display significant growth, highlighting the resource-intensive nature of classical simulations for larger spin systems. The memory usage starts low, at around 0.04 MB for 2 spins, and increases exponentially, reaching approximately 6,760 MB (or 6.76 GB) for 14 spins. This trend reflects the exponential scaling of memory required to store the Hamiltonian matrix and perform matrix operations as the number of spins grows, which is a direct result of the 2ⁿ×2ⁿdimensionality of the Hamiltonian. Similarly, the runtime also grows exponentially, increasing from around 0.0005 s for 2 spins to 890 seconds (approximately 15 min) for 14 spins. The rapid increase in computational time is due to the matrix exponentiation and matrix-vector multiplications required for the time evolution of the quantum state, which become computationally prohibitive as the system size expands.

Figure 4

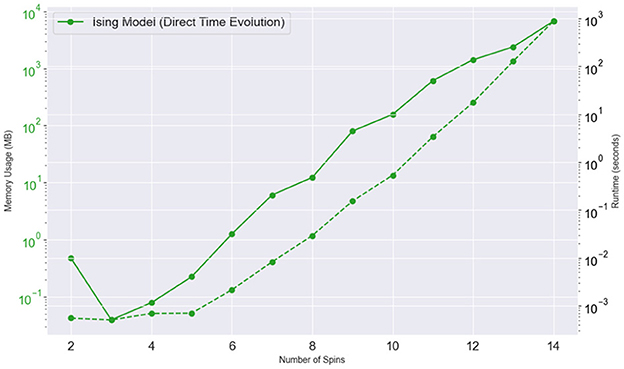
Figure 4. Memory usage (left) and runtime (right) for classical time evolution of the Ising model as functions of the number of qubits/spins. The left axis shows memory usage in megabytes (MB) as the system size increases. The right axis illustrates the runtime.

Both memory usage and runtime curves reveal the practical limitations of classical simulations for quantum systems, especially as the number of spins exceeds around 12–14. The exponential scaling observed here underscores why classical methods are infeasible for simulating large quantum systems and highlights the potential advantage of quantum computing, where resource requirements grow more slowly with system size for tasks like time evolution and measurement.

Figure 5 displays the gate count (in green) and circuit depth (in gray) required to perform first-order Trotterization for time evolution of the Ising model as a function of the number of spins. We used 10 Trotter steps consistently across all spin numbers, even though 10 steps provide more precision than necessary for smaller spin systems. This consistency in Trotter steps is intended to highlight the scaling behavior as the spin count increases, where higher precision becomes more crucial. The gate count increases significantly with the number of spins, reflecting the additional operations needed to simulate interactions between spins and apply the transverse magnetic field in the Ising model. As each Trotter step requires separate gates to simulate each term in the Hamiltonian, the total gate count scales quickly with the number of spins, indicating the intensive gate requirements for accurate time evolution as system size grows. Similarly, the circuit depth also increases with the number of spins, though at a slightly slower rate than the gate count. Circuit depth represents the longest sequence of dependent gates, meaning that as spin interactions increase, more gates must be applied sequentially to simulate the interactions accurately within each Trotter step. This increase in depth highlights the scaling challenge for quantum circuits, as greater circuit depth typically requires higher coherence times on quantum hardware.

Figure 5

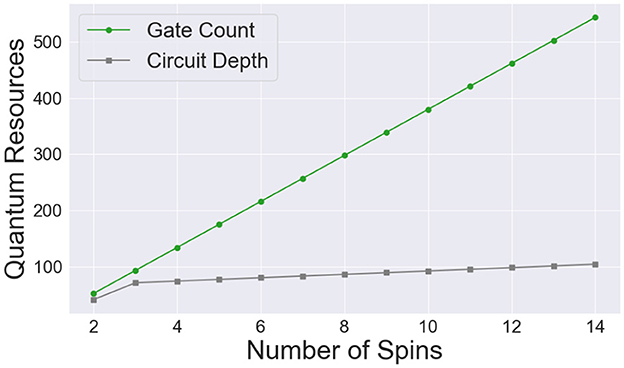
Figure 5. Gate count (green) and circuit depth (gray) needed to perform first order trotterization for the time evolution of the Ising model as a function of the number of qubits, ranging from 2 to 14. We used 10 Trotter steps for this experiment to showcase the scaling. The gate count increases approximately linearly with the number of qubits. The circuit depth also grows steadily, though at a slower rate.

The exponential growth in both gate count and circuit depth illustrates the practical considerations of simulating time evolution through Trotterization on quantum hardware. While the computational cost for small systems is manageable, the increasing complexity for larger systems underscores the need for efficient resource management and error mitigation on quantum devices. Consistently using 10 Trotter steps across all system sizes also illustrates how resource demands scale significantly as accuracy needs increase, especially in systems with more spins, reinforcing the importance of optimizing Trotter steps in practical applications.

2.3 Measurement in the Ising model

In this section, we delve into measurement, i.e., extracting and analyzing observable quantities. After the quantum system has evolved over a specified period, the next step is to measure observables to interpret key physical properties, such as energy levels, magnetization, or correlation functions. These measurements provide insight into the behavior and properties of the system and are essential for validating theoretical predictions or examining phenomena like phase transitions and entanglement.

Calculating the expectation values of various operators, such as spin or momentum, is a foundational measurement. Quantum processors offer a distinct advantage in this area by leveraging repeated sampling of the quantum state, a process that directly yields expectation values without requiring complex probabilistic approximations. On classical computers, however, this task is more resource-intensive, often relying on matrix-based methods that become computationally prohibitive as system size grows. As a result, offloading measurement calculations to quantum hardware can lead to faster and more accurate results, with significant reductions in computational resources.

When considering quantum measurements on a real quantum device, measurement involves preparing and measuring the system multiple times to obtain statistics, but each measurement is nearly instantaneous (on the order of microseconds to milliseconds and it does not require explicit storage of the state vector, as in classical simulations and thus doesn't suffer from exponential memory scaling. In a real-world scenario, comparing the number of measurements required to reach a certain precision in estimating an observable (e.g., an expectation value) would provide a fairer basis for resource comparison. For this reason, our experiment here consists in measuring an observable in a quantum device directly by repeating the experiment multiple times (each measurement or “shot" on a real quantum device is independent of system size). In contrast, classical algorithms often need to compute full probability distributions or use dense matrix methods, which scale exponentially with the number of qubits.

In Figure 6, we illustrate the resource demands for measuring the expectation value of the Ising model Hamiltonian using both quantum and classical methods. The quantum approach requires multiple measurements, or “shots,” to achieve a specified precision level. As shown by the green line, increasing the number of shots on a quantum device significantly improves precision, with the required shot count inversely proportional to the target accuracy. In contrast, the classical method (represented by the red dashed line) provides an exact result in a single computation but becomes computationally infeasible as system size increases. This comparison underscores the potential for quantum devices to achieve scalable precision through sampling, highlighting a trade-off between single exact computations classically and iterative measurements quantumly, which may offer resource efficiency in larger quantum systems.

Figure 6

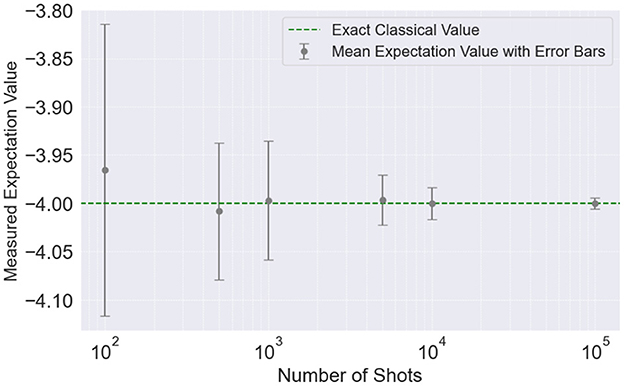
Figure 6. Mean measured expectation value (gray markers) as a function of the number of shots, with error bars representing the standard deviation across 100 repeated experiments, The exact classical simulation value (green dashed line) is shown for reference. As the number of shots increases, the mean measured expectation value approaches the classical value, and the variability (standard deviation) decreases, indicating improved precision with higher shot counts. The logarithmic scale highlights the convergence trends and the diminishing effect of statistical noise at larger shot counts.

2.4 Quantum offloading: feasible primitives and integration points

State preparation remains a major bottleneck in quantum simulation, requiring methods that balance accuracy, efficiency, and feasibility on near-term and future quantum hardware. From our comparison of state preparation methods (see Table 2), purely classical and purely quantum approaches each suffer from distinct scaling issues. Classical direct encoding scales exponentially with system size ($\mathcal{O}(2^N)$), making it infeasible for large quantum systems. Quantum variational methods scale polynomially but require extensive circuit optimization, which can be computationally prohibitive for complex systems. Adiabatic state preparation faces challenges in maintaining a sufficiently large spectral gap. Hybrid quantum-classical methods can bridge this gap by (1) using classical models (e.g., NQS or tensor networks) to generate an approximate quantum state before quantum refinement (Yang et al., 2019; Zhu et al., 2022; Chen and Heyl, 2024); (2) implementing quantum subroutines only for tasks that exhibit a clear quantum advantage, such as handling high-dimensional entanglement structure; and (3) employing classical heuristics.

One example of such quantum-classical approach is the integration of classical differential equation solving with adiabatic quantum state evolution. In Hejazi et al. (2024), the authors provide a resource-efficient approach (A-QITE) to quantum state preparation by reducing the need for quantum tomography and ancilla qubits. One of the key insights from A-QITE is that imaginary time evolution can be reinterpreted as an adiabatic process under a modified Hamiltonian $\tilde{H}(\tau )$, which can be precomputed classically and then used to evolve the quantum system without costly tomography. The classical strategy in this scheme involves soling the imaginary time evolution trajectory classically to determine an optimal adiabatic Hamiltonian or an efficient ansatz for the variational method. Then, the quantum evolution is implemented using a simplified adiabatic or variational approach, significantly reducing the depth of required quantum circuits.

Another promising avenue for improving state preparation in hybrid quantum-classical workflows is the integration of optimal control techniques (Ansel et al., 2024; Coello Pérez et al., 2022). These methods leverage classical optimization algorithms to engineer quantum control pulses, tailoring quantum state evolution to minimize errors and decoherence while reducing gate complexity. In Coello Pérez et al. (2022), the authors demonstrate that adiabatic state preparation is limited by long implementation times, which are often comparable to the decoherence times of near-term quantum devices. By introducing customized quantum gates optimized through classical control algorithms, the researchers achieved significant improvements in fidelity (up to 95%) while dramatically reducing circuit depth. This insight suggests that optimal control strategies could serve as a key ingredient in hybrid HPC-QC workflows, where classical algorithms compute optimal pulse sequences that guide quantum state evolution in the most efficient manner.

Another essential quantum-native operation is time evolution. Applying time-evolution operators over many iterations, as required for simulating dynamics in quantum systems, quickly becomes intractable for classical systems. In quantum computing, Trotterized methods approximate time evolution by decomposing the Hamiltonian into simpler components, each of which can be applied as a sequence of gates on a quantum device. This approach is advantageous in the NISQ context, as it reduces the depth of each circuit at the expense of exact precision. Hybrid workflows could exploit this Trotterized structure by running parallelized quantum circuits on separate quantum devices, while the classical system manages synchronization and error mitigation. Despite the approximation errors introduced by Trotterization, this hybrid strategy enhances computational speed and reduces memory requirements, making it particularly beneficial for early quantum processors. For example, in Carrera Vazquez et al. (2023), the authors introduce a hybrid quantum-classical approach to Hamiltonian simulation that leverages Multi-Product Formulas (MPFs) (Zhuk et al., 2024) to enhance the efficiency and accuracy of quantum computations. In this method, the expectation values are computed on a quantum processor and then classically combined using MPFs. This strategy avoids the need for additional qubits, controlled operations, and probabilistic outcomes, making it particularly suitable for current NISQ devices. the methodology is applied to the transverse field Ising model and theoretically analyzed for a classically intractable spin-boson model. These applications highlight the potential of hybrid approaches to tackle complex quantum systems that are challenging for classical simulations alone. Furthermore, by distributing the computation of expectation values across multiple quantum processors, the approach can parallelize tasks, reducing overall computation time and mitigating the impact of decoherence in NISQ devices. In a fault-tolerant quantum future, Hamiltonian exponentiation techniques could achieve exact time evolution on quantum hardware, simplifying integration by removing the need for frequent classical corrections and feedback loops in the workflow.

One of the most critical aspects of Hamiltonian simulation, particularly in the context of variational algorithms like the VQE, is the selection of an efficient ansatz. The ansatz is a parameterized quantum circuit that approximates the target quantum state, such as the ground state of a given Hamiltonian. The choice of ansatz directly impacts the algorithm's accuracy, convergence, or even failure to capture the necessary correlations within the quantum system. HPC systems, when integrated with quantum hardware, can play a pivotal role in addressing the challenges by enabling more efficient ansatz design and evaluation. The synergy between classical HPC resources and quantum devices provides opportunities for both pre- and post-processing that can enhance the overall workflow. For example, HPC systems can be used to perform classical simulations, such as mean-field approximations, tensor network simulations, or neural quantum states, to generate initial guesses for the quantum ansatz. By analyzing classical approximations of the target state, the quantum circuit can be pre-conditioned to focus on the correlations that are most challenging for classical methods, reducing the need for deep circuits. In addition, classical machine learning models, such as reinforcement learning or genetic algorithms, can optimize the ansatz structure by searching for configurations that balance expressivity and feasibility, tailoring it to the Hamiltonian and the hardware. Adaptive ansatz strategies, such as ADAPT-VQE (Grimsley et al., 2019), which iteratively build the circuit by adding gates that reduce the energy error, can benefit significantly from HPC support. Classical resources can pre-screen potential gate additions or evaluate their impact before implementation on the quantum device, optimizing the adaptive process. After the quantum simulation, HPC systems can validate the results by comparing them against high-precision classical benchmarks for smaller subsystems or by using extrapolation techniques to assess the accuracy of the ansatz. For example, in Jattana et al. (2022), the effectiveness of the VQE in computing the ground state energy of the anti-ferromagnetic Heisenberg model is evaluated. The study involves ground state preparation, utilizing a low-depth-circuit ansatz that leverages the efficiently preparable Néel initial state. The largest system simulated comprises 100 qubits, with extrapolation to the thermodynamic limit yielding results consistent with the analytical ground state energy obtained via the Bethe ansatz. The main bottlenecks identified include the selection of an appropriate ansatz, the choice of initial parameters, and the optimization method, as these factors significantly influence the convergence and accuracy of the VQE.

Expectation value calculations represent another ideal candidate for quantum offloading, as they involve measurements of observables like energy or magnetization from the quantum state. Classically, obtaining expectation values in large quantum systems requires computing dense probability distributions or matrix representations, both of which scale poorly with system size. Quantum devices, on the other hand, can measure expectation values directly through sampling, where repeated measurements of the quantum state yield statistically accurate results without needing to reconstruct the full state. This capability is advantageous even in the NISQ era, as it reduces the memory and processing demands on classical systems. However, the accuracy of quantum sampling is limited by the number of measurements (shots) and the fidelity of the quantum device, presenting a challenge for hybrid workflows – such as the VQE algorithm — that rely on high-precision data. The problem is highly exacerbated in complex Hamiltonians, where the number of operators to measure grows quickly, limiting the practical scalability of VQE on current quantum hardware. To address this, a hybrid approach could involve quantum measurements as an initial estimate, with a classical system refining the measurement using error-corrected feedback. For example, in Nykänen (et al.), the authors propose a classically boosted VQE approach that uses Bayesian inference to alleviate the measurement overhead, aiming to reduce the required number of quantum measurements while preserving accuracy. The strategy involves a hybrid scheme where classical computations assist the quantum measurements through Bayesian inference, a statistical approach that updates probability estimates based on prior information and new data. By integrating Bayesian inference, the algorithm reduces the need for repeated measurements, as the classical component makes use of prior measurement data to refine its estimates more efficiently. In Wang and Jaiswal (2023), the application of the VQE is explored in the preparation of ground states of the 1D generalized Heisenberg model, utilizing up to 12 qubits. The study demonstrates that VQE can effectively approximate ground states in the anisotropic XXZ model. Nonetheless, the study also highlights that achieving a target precision in expectation values is a significant challenge for larger quantum systems. Optimized sampling methods, which adaptively allocate measurement shots to terms with higher variance in the Hamiltonian decomposition, substantially reduce the number of measurements required to achieve the same precision compared to uniform sampling.

In the long term, fault-tolerant quantum systems will further alleviate these accuracy constraints, allowing precise measurements of complex observables with fewer classical resources involved in post-processing.

In designing hybrid workflows, it's critical to establish integration points that leverage the strengths of both quantum and classical systems. Parallel quantum execution is one such approach, allowing simultaneous quantum operations to reduce latency and manage decoherence on NISQ devices. In a hybrid workflow, multiple quantum devices could perform state preparation or expectation value calculations in parallel, with a classical system handling task scheduling, error correction, and result aggregation. This parallelism is particularly beneficial in Hamiltonian simulation, where operations can be distributed among quantum devices to maximize computational throughput. Furthermore, to support the development and benchmarking of quantum-HPC applications, frameworks that provide necessary abstractions for creating and executing primitives across heterogeneous quantum-HPC infrastructures are needed (Saurabh et al., 2024).

Another key integration technique is a real-time data pipeline, which enables efficient feedback loops between quantum and classical systems. This feedback is vital in applications like variational algorithms, where intermediate quantum outputs guide further optimization steps in the classical system. By continuously analyzing and refining quantum results, the classical system can improve overall workflow efficiency, a feature that becomes even more impactful with the increased reliability of fault-tolerant quantum devices.

Error mitigation and hybrid error correction are pivotal for the effective implementation of hybrid HPC-QC workflows, particularly in the NISQ era. Some key techniques for error mitigation and hybrid error correction can be integrated into HPC-QC workflows. For example, zero-noise extrapolation (ZNE) (Temme et al., 2017), a widely adopted error mitigation method. The core idea is to execute a quantum circuit at varying noise levels and extrapolate the results to the zero-noise limit. This approach involves artificially increasing the noise in the quantum system by stretching gate times or repeating gates, followed by applying polynomial fitting or Richardson extrapolation (Richardson and Gaunt, 1927) to predict results at the zero-noise limit. In hybrid HPC-QC systems, HPC resources can aid in the extrapolation step by performing high-precision statistical analysis and model fitting, significantly reducing the computational overhead on quantum devices. Additionally, ZNE can be used to mitigate errors associated with mid-circuit measurements (DeCross et al., 2023). Delays introduced by mid-circuit measurements often cause idle qubits to accumulate errors due to qubit cross-talk and state decay mechanisms such as T1 and T2 relaxation. By stretching these delays by multiple factors and applying dynamical decoupling pulses during idle periods, it is possible to suppress errors and extrapolate back to a zero-delay state. This technique not only reduces the impact of errors on dynamic circuits but also enhances the feasibility of applications that rely on mid-circuit measurements (Carrera Vazquez et al., 2024).

Probabilistic error cancellation (van den Berg et al., 2023) uses knowledge of noise models to construct virtual noise-free results. This technique requires accurately modeling the noise in the quantum hardware and combining multiple circuit runs with adjusted probabilities to cancel out the effects of noise. Though computationally expensive, HPC systems can efficiently perform the noise characterization and correction computations, leveraging their high processing power to enable this method on quantum devices with limited qubits (Gupta et al., 2023).

Dynamical decoupling (Ezzell et al., 2023) is a hardware-level technique that combats decoherence by applying sequences of carefully timed pulses to the quantum system. These pulses average out environmental noise effects over time. HPC systems can optimize pulse sequences using machine learning algorithms and validate and simulate the impact of different sequences on reducing decoherence (Rahman et al., 2024).

In hybrid workflows, classical post-processing plays a critical role in mitigating errors from quantum outputs. Shot noise reduction, which involves averaging multiple quantum measurements to improve precision, and Bayesian inference, which uses statistical models to refine measurement results and reduce the impact of quantum sampling noise, are common approaches. HPC systems can accelerate these processes by running parallelized statistical computations, enabling real-time feedback loops between quantum and classical systems.

Real-time error correction involves dynamically adjusting quantum operations based on feedback from classical computations. This can be achieved by monitoring noise profiles using classical systems to continuously track noise levels and adjust quantum gate parameters accordingly. Adaptive circuit compilation (Mato et al., 2022; Grimsley et al., 2019; Ge et al., 2024) can also modify quantum circuits on the fly to account for evolving noise conditions.

Hybrid error correction schemes integrate quantum error correction codes with classical error detection and mitigation techniques. For example, employing quantum error correction codes like surface codes for logical qubit protection while using HPC systems for syndrome decoding and recovery operations, or implementing hybrid decoding algorithms that split the computational load between quantum and classical systems, leveraging classical resources to handle parts of the decoding process that exceed quantum hardware capabilities.

To integrate these strategies into hybrid HPC-QC systems, noise modeling is essential. HPC resources can generate and maintain detailed noise models of quantum hardware, which are crucial for implementing error mitigation and correction techniques. Workflow integration ensures that error correction and mitigation are seamlessly incorporated into the quantum-classical workflow, involving real-time data exchange between quantum and classical systems facilitated by high-bandwidth communication channels. Scalability remains a key concern, as quantum systems scale and error mitigation techniques must evolve accordingly. HPC systems provide the necessary computational power to handle the increased complexity of error correction in larger quantum systems.

While current error mitigation and hybrid correction techniques address many challenges of the NISQ era, future quantum systems will require fault-tolerant architectures that reduce the reliance on error mitigation, though hybrid approaches will still play a role in optimizing performance. Advanced machine learning techniques powered by HPC systems can predict and counteract errors in real-time, further enhancing the efficiency of hybrid workflows. Integrated development frameworks that provide abstractions for error mitigation and correction in hybrid workflows will streamline the development and deployment of quantum applications.

Despite these advantages, quantum offloading comes with challenges that hybrid workflows can help mitigate. For example, noise and gate fidelity issues in NISQ devices limit the precision of offloaded primitives, such as time evolution and expectation value measurement. A hybrid workflow can employ classical error mitigation techniques, periodically recalibrating or correcting quantum operations based on classical simulations. Another challenge lies in the quantum hardware constraints on circuit depth and coherence time, which hybrid workflows can alleviate by dynamically adjusting which tasks are offloaded based on real-time device diagnostics. As quantum systems evolve toward fault tolerance, hybrid workflows could become more streamlined, with fewer dependencies on classical oversight. Ultimately, the road to fault tolerance will allow quantum devices to handle a greater share of computations independently, significantly enhancing the efficiency of Hamiltonian simulation and reducing reliance on classical resources.

The insights provided in this manuscript are invaluable for informing future hybrid workflow design. By identifying which primitives are best suited for quantum offloading and detailing integration techniques, the manuscript offers a foundation for implementing quantum-ready computational workflows in HPC settings. While NISQ-era devices present certain limitations, the strategic use of hybrid workflows enables computational efficiencies that traditional HPC cannot achieve alone. As quantum hardware improves, the integration points and offloading strategies discussed here will support the transition from NISQ devices to fault-tolerant quantum systems, establishing a sustainable path for quantum-classical hybridization in Hamiltonian simulation.

3 Conclusion

The integration of quantum computing with HPC systems holds transformative potential, particularly in areas like Hamiltonian simulation, where classical computational costs grow exponentially with system size. Quantum computing offers a natural framework for certain computational primitives in quantum simulation, promising to streamline complex tasks that classical systems handle inefficiently. However, designing effective hybrid workflows for Hamiltonian simulation requires careful consideration of which primitives are best suited for quantum offloading, how these operations can be integrated into existing HPC systems, and the unique challenges and limitations posed by current and future quantum hardware. The information in this manuscript provides a comprehensive roadmap for identifying and optimizing such primitives, helping to shape the development of efficient hybrid workflows.

This breakdown into primitives enables us to identify specific tasks best suited for quantum processors within Hamiltonian simulation workflows. By distributing initialization, evolution, and measurement tasks according to the strengths of each computing resource, hybrid HPC-QC systems can achieve significant computational savings while maintaining high accuracy and scalability. This modular approach also makes the workflow adaptable: as quantum hardware improves, additional primitives could be offloaded, enhancing the simulation's speed and depth.

Moreover, this approach lays the groundwork for scalable hybrid systems in more general scientific applications.

The modular workflow proposed for hybrid HPC-QC systems can be extended beyond Hamiltonian simulation to address computational challenges in a variety of scientific and industrial domains. By identifying computational primitives in specific workflows and evaluating their suitability for quantum acceleration, this approach provides a template for leveraging hybrid systems effectively. Below, we outline potential applications and adaptations of the workflow in other fields.

In quantum chemistry, many tasks involve solving the electronic structure problem, which requires diagonalizing large matrices or calculating molecular energies. Hybrid HPC-QC workflows can leverage quantum devices to prepare molecular ground states or approximate them through variational algorithms such as the VQE. Classical HPC resources can optimize initial parameters and refine variational circuits. Simulating chemical reactions involves modeling the time-dependent behavior of molecular systems under specific Hamiltonians, with quantum devices handling time-evolution operators while classical systems manage error mitigation and validate results. Observables such as bond lengths, dipole moments, and reaction rates can be extracted through quantum sampling, with classical post-processing improving precision.

In machine learning and data analytics, hybrid systems address challenges in big data and high-dimensional feature spaces. Quantum kernels accelerate kernel-based ML methods by encoding high-dimensional data into quantum feature spaces, enabling efficient computation of similarity measures. Hybrid quantum-classical generative models can be employed, where quantum circuits generate complex distributions while classical systems refine the models through training on large datasets (Delgado et al., 2024) Optimization problems commonly encountered in ML tasks, such as feature selection or clustering, benefit from quantum annealing or variational approaches.

Material discovery and property prediction in material science often involve simulating interactions at atomic or molecular scales. The workflow can be adapted to simulate novel materials using quantum processors to simulate material Hamiltonians while classical HPC resources evaluate structural and thermodynamic properties. Quantum-enhanced density functional theory (DFT) calculations improve accuracy and scalability in predicting electronic properties.

Optimization and operations research frequently involve problems in logistics, finance, and network design, where the solution space grows exponentially with problem size. Hybrid HPC-QC workflows can implement quantum annealing to solve combinatorial optimization problems, such as the traveling salesman problem or portfolio optimization. Large optimization tasks can be decomposed into subproblems solvable by quantum devices, with classical systems orchestrating the overall process and validating results.

In high-energy physics and cosmology, large-scale simulations are essential for understanding fundamental interactions and the evolution of the universe. Applications include lattice quantum chromodynamics (QCD) simulations, where quantum processors handle the highly oscillatory integrals in lattice QCD, while classical systems manage grid refinement and data aggregation. Cosmological simulations can model the large-scale structure of the universe by offloading computationally intensive tasks, such as N-body simulations, to quantum processors.

Generalizing the hybrid workflow to these domains requires careful consideration of integration points, identifying which computational primitives can be effectively offloaded to quantum hardware. Error mitigation ensures results from noisy quantum devices are corrected and validated through classical post-processing. Scalability is key, adapting the workflow to handle increasing problem sizes and complexities as quantum hardware capabilities improve. Customization of modular workflow components aligns with the unique requirements of each application. By leveraging the strengths of hybrid HPC-QC systems, researchers can address computational bottlenecks across a wide range of disciplines, driving advances in both fundamental science and applied research.

Finally, since quantum processors are prone to noise, post-processing is essential to mitigate error in measurement. This task is typically handled on the classical side, using machine learning or statistical correction techniques. A hybrid HPC-QC setup could integrate these error-mitigation methods into a feedback loop where classical hardware analyzes data from measurements and provides real-time adjustments to improve simulation fidelity.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AD: Writing – original draft, Writing – review & editing. PD: Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was partially supported by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the U. S. Department of Energy and the Quantum Horizons: QIS Research and Innovation for Nuclear Science program at ORNL under FWP ERKBP91.

Acknowledgments

This manuscript has been authored by UT-Battelle, LLC, under Contract No. DE-AC0500OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for the United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albash, T., and Lidar, D. A. (2018). Adiabatic quantum computation. Rev. Modern Phys. 90:1. doi: 10.1103/RevModPhys.90.015002

Crossref Full Text | Google Scholar

Alexandru, A., Ba, G., Bedaque, P. F., and Warrington, N. C. (2022). Complex paths around the sign problem. Rev. Mod. Phys. 94:015006. doi: 10.1103/RevModPhys.94.015006

Crossref Full Text | Google Scholar

Ansel, Q., Dionis, E., Arrouas, F., Peaudecerf, B., Guérin, S., Guéry-Odelin, D., et al. (2024). Introduction to theoretical and experimental aspects of quantum optimal control. J. Phys. B: Atomic, Mol. Opt. Phys. 57:133001. doi: 10.1088/1361-6455/ad46a5

Crossref Full Text | Google Scholar

Ayral, T., Besserve, P., Lacroix, D., and Ruiz Guzman, E. A. (2023). Quantum computing with and for many-body physics. Eur. Phys. J. A 59:227. doi: 10.1140/epja/s10050-023-01141-1

Crossref Full Text | Google Scholar

Babbush, R., Love, P. J., and Aspuru-Guzik, A. (2014). Adiabatic quantum simulation of quantum chemistry. Sci. Rep. 4:1. doi: 10.1038/srep06603

PubMed Abstract | Crossref Full Text | Google Scholar

Bauer, C. W., Davoudi, Z., Balantekin, A. B., Bhattacharya, T., Carena, M., De Jong, W. A., et al. (2023a). Quantum simulation for high-energy physics. PRX Quantum 4:027001. doi: 10.1103/PRXQuantum.4.027001

Crossref Full Text | Google Scholar

Bauer, C. W., Davoudi, Z., Klco, N., and Savage, M. J. (2023b). Quantum simulation of fundamental particles and forces. Nat. Rev. Phys. 5, 420–432. doi: 10.1038/s42254-023-00599-8

Crossref Full Text | Google Scholar

Boyle, P., Bollweg, D., Brower, R., Christ, N., DeTar, C., Edwards, R., et al. (2022). Lattice QCD and the computational frontier. arXiv [Preprint]. arXiv:2204.00039.

Google Scholar

Buessen, F. L., Segal, D., and Khait, I. (2023). Simulating time evolution on distributed quantum computers. Phys. Rev. Res. 5:L022003. doi: 10.1103/PhysRevResearch.5.L022003

Crossref Full Text | Google Scholar

Carleo, G., and Troyer, M. (2017). Solving the quantum many-body problem with artificial neural networks. Science 355:602–606. doi: 10.1126/science.aag2302

PubMed Abstract | Crossref Full Text | Google Scholar

Carrera Vazquez, A., Egger, D. J., Ochsner, D., and Woerner, S. (2023). Well-conditioned multi-product formulas for hardware-friendly hamiltonian simulation. Quantum 7:1067. doi: 10.22331/q-2023-07-25-1067

Crossref Full Text | Google Scholar

Carrera Vazquez, A., Tornow, C., Ristè, D., Woerner, S., Takita, M., and Egger, D. J. (2024). Combining quantum processors with real-time classical communication. Nature 636, 75–79. doi: 10.1038/s41586-024-08178-2

PubMed Abstract | Crossref Full Text | Google Scholar

Cerezo, M., Arrasmith, A., Babbush, R., Benjamin, S. C., Endo, S., Fujii, K., et al. (2021). Variational quantum algorithms. Nat. Rev. Phys. 3, 625–644. doi: 10.1038/s42254-021-00348-9

Crossref Full Text | Google Scholar

Chen, A., and Heyl, M. (2024). Empowering deep neural quantum states through efficient optimization. Nat. Phys. 20, 1476–1481. doi: 10.1038/s41567-024-02566-1

PubMed Abstract | Crossref Full Text | Google Scholar

Coello Pérez, E. A., Bonitati, J., Lee, D., Quaglioni, S., and Wendt, K. A. (2022). Quantum state preparation by adiabatic evolution with custom gates. Phys. Rev. A 105:32403. doi: 10.1103/PhysRevA.105.032403

Crossref Full Text | Google Scholar

Davoudi, Z., Detmold, W., Shanahan, P., Orginos, K., Parreño, A., Savage, M. J., et al. (2021). Nuclear matrix elements from lattice qcd for electroweak and beyond-standard-model processes. Phys. Rep. 900, 1–74. doi: 10.1016/j.physrep.2020.10.004

Crossref Full Text | Google Scholar

DeCross, M., Chertkov, E., Kohagen, M., and Foss-Feig, M. (2023). Qubit-reuse compilation with mid-circuit measurement and reset. Phys. Rev. 13:041057. doi: 10.1103/PhysRevX.13.041057

Crossref Full Text | Google Scholar

Delgado, A., Venegas-Vargas, D., Huynh, A., and Carroll, K. (2024). Towards designing scalable quantum-enhanced generative networks for neutrino physics experiments with liquid argon time projection chambers. arXiv [Preprint]. arXiv:2410.12650.

Google Scholar

Di Meglio, A., Jansen, K., Tavernelli, I., Alexandrou, C., Arunachalam, S., Bauer, C. W., et al. (2024). Quantum computing for high-energy physics: State of the art and challenges. PRX Quantum 5:037001. doi: 10.1103/PRXQuantum.5.037001

Crossref Full Text | Google Scholar

Echenique, P., and Alonso, J. L. (2007). A mathematical and computational review of hartree–fock scf methods in quantum chemistry. Mol. Phys. 105, 3057–3098. doi: 10.1080/00268970701757875

Crossref Full Text | Google Scholar

Ezzell, N., Pokharel, B., Tewala, L., Quiroz, G., and Lidar, D. A. (2023). Dynamical decoupling for superconducting qubits: a performance survey. Phys. Rev. Appl. 20:64027. doi: 10.1103/PhysRevApplied.20.064027

Crossref Full Text | Google Scholar

Funcke, L., Hartung, T., Jansen, K., and Kühn, S. (2023). Review on quantum computing for lattice field theory. arXiv [Preprint]. arXiv:2302.00467. doi: 10.22323/1.430.0228

Crossref Full Text | Google Scholar

Ge, Y., Wenjie, W., Yuheng, C., Kaisen, P., Xudong, L., Zixiang, Z., et al. (2024). Quantum circuit synthesis and compilation optimization: overview and prospects. arXiv [Preprint]. arXiv:2407.00736.

Google Scholar

Gratsea, K., Kottmann, J. S., Johnson, P. D., and Kunitsa, A. A. (2024). Comparing classical and quantum ground state preparation heuristics. arXiv [Preprint]. arXiv:2401.05306. doi: 10.48550/arXiv.2401.05306

Crossref Full Text | Google Scholar

Grimsley, H. R., Economou, S. E., Barnes, E., and Mayhall, N. J. (2019). An adaptive variational algorithm for exact molecular simulations on a quantum computer. Nat. Commun. 10:1. doi: 10.1038/s41467-019-10988-2

PubMed Abstract | Crossref Full Text | Google Scholar

Gull, E., Iskakov, S., Krivenko, I., Rusakov, A. A., and Zgid, D. (2018). Chebyshev polynomial representation of imaginary-time response functions. Phys. Rev. 98:075127. doi: 10.1103/PhysRevB.98.075127

Crossref Full Text | Google Scholar

Gupta, R. S., van den Berg, E., Takita, M., Riste, D., Temme, K., and Kandala, A. (2023). Probabilistic error cancellation for dynamic quantum circuits. Phys. Rev. A 109:062617. doi: 10.1103/PhysRevA.109.062617

Crossref Full Text | Google Scholar

Hejazi, K., Motta, M., and Chan, G. K.-L. (2024). Adiabatic quantum imaginary time evolution. Phys. Rev. Res. 6:033084. doi: 10.1103/PhysRevResearch.6.033084

Crossref Full Text | Google Scholar

Jattana, M. S., Jin, F., De Raedt, H., and Michielsen, K. (2022). Assessment of the variational quantum eigensolver: application to the heisenberg model. Front. Phys. 10:907160. doi: 10.3389/fphy.2022.907160

Crossref Full Text | Google Scholar

Joseph, I., Shi, Y., Porter, M., Castelli, A., Geyko, V., Graziani, F., et al. (2023). Quantum computing for fusion energy science applications. Phys. Plasmas 30:0123765. doi: 10.1063/5.0123765

Crossref Full Text | Google Scholar

Kan, A., and Nam, Y. (2022). Lattice quantum chromodynamics and electrodynamics on a universal quantum computer. arXiv [Preprint]. arXiv:2107.12769.

Google Scholar

Kronfeld, A. S., Bhattacharya, T., Blum, T., Christ, T., DeTar, C., Detmoid, W., et al. (2022). Lattice QCD and particle physics. arXiv [Preprint]. arXiv:2207.07641. doi: 10.48550/arXiv.2207.07641

Crossref Full Text | Google Scholar

Lange, H., de Walle, A. V., Abedinnia, A., and Bohrdt, A. (2024). From architectures to applications: a review of neural quantum states. Quantum Sci. Technol. 9:040501. doi: 10.1088/2058-9565/ad7168

Crossref Full Text | Google Scholar

Li, A. C., Macridin, A., Mrenna, S., and Spentzouris, P. (2023). Simulating scalar field theories on quantum computers with limited resources. Phys. Rev. A 107:032603. doi: 10.1103/PhysRevA.107.032603

Crossref Full Text | Google Scholar

Liesen, J., and Strakos, Z. (2012). Krylov Subspace Methods: Principles and Analysis. Oxford: Oxford University Press.

PubMed Abstract | Google Scholar

Mato, K., Ringbauer, M., Hillmich, S., and Wille, R. (2022). “Adaptive compilation of multi-level quantum operations,” in 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) (Broomfield, CO: IEEE), 484–491.

Google Scholar

Meth, M., Haase, J. F., Zhang, J., Edmunds, C., Postler, L., Steiner, A., et al. (2023). Simulating 2d lattice gauge theories on a qudit quantum computer. arXiv [Preprint]. arXiv:2310.12110. doi: 10.48550/arXiv.2310.12110

Crossref Full Text | Google Scholar

Morrell, Z., Vuffray, M., Misra, S., and Coffrin, C. (2024). Quantumannealing: a julia package for simulating dynamics of transverse field ising models. arXiv [Preprint]. arXiv:2404.14501. doi: 10.1109/QCE60285.2024.00096

Crossref Full Text | Google Scholar

Nagata, K. (2022). Finite-density lattice QCD and sign problem: Current status and open problems. Prog. Part. Nucl. Phys. 127:103991. doi: 10.1016/j.ppnp.2022.103991

Crossref Full Text | Google Scholar

Nykänen, A., Rossi, M. A. C., Borrelli, E., Maniscalco, S., and García-érez, G. (2023). Mitigating the measurement overhead of ADAPT-VQE with optimised informationally complete generalised measurements. arXiv [Preprint]. arXiv:2212.09719. doi: 10.48550/arXiv.2212.09719

Crossref Full Text | Google Scholar

Ostmeyer, J. (2023). Optimised trotter decompositions for classical and quantum computing. J. Phys. A: Mathem. Theoret. 56:285303. doi: 10.1088/1751-8121/acde7a

Crossref Full Text | Google Scholar

Peruzzo, A., McClean, J., Shadbolt, P., Yung, M.-H., Zhou, X.-Q., Love, P. J., et al. (2014). A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5:5213. doi: 10.1038/ncomms5213

PubMed Abstract | Crossref Full Text | Google Scholar

Rahman, A., Egger, D. J., and Arenz, C. (2024). Learning how to dynamically decouple. arXiv [Preprint]. arXiv:2405.08689. doi: 10.1103/PhysRevApplied.22.054074

Crossref Full Text | Google Scholar

Richardson, L. F., and Gaunt, J. A. (1927). The deferred approach to the limit. Philos. Trans. Royal Soc. London. 226, 299–361.

Google Scholar

Saurabh, N., Mantha, P., Kiwit, F. J., Jha, S., and Luckow, A. (2024). “Quantum mini-apps: a framework for developing and benchmarking quantum-HPC applications,” in Proceedings of the 2024 Workshop on High Performance and Quantum Computing Integration, HPQCI '24 (New York, NY: Association for Computing Machinery), 11–18.

Google Scholar

Shaw, A. F., Lougovski, P., Stryker, J. R., and Wiebe, N. (2020). Quantum algorithms for simulating the lattice schwinger model. Quantum 4:306. doi: 10.22331/q-2020-08-10-306

Crossref Full Text | Google Scholar

Shehata, A., Naughton, T., and Suh, I.-S. (2024). A framework for integrating quantum simulation and high performance computing. arXiv [Preprint]. arXiv:2408.08098. doi: 10.1109/QCE60285.2024.10296

Crossref Full Text | Google Scholar

Suzuki, M. (1976). Generalized trotter's formula and systematic approximants of exponential operators and inner derivations with applications to many-body problems. Commun. Mathem. Phys. 51, 183–190. doi: 10.1007/BF01609348

Crossref Full Text | Google Scholar

Temme, K., Bravyi, S., and Gambetta, J. M. (2017). Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119:180509. doi: 10.1103/PhysRevLett.119.180509

PubMed Abstract | Crossref Full Text | Google Scholar

Troyer, M., and Wiese, U.-J. (2005). Computational complexity and fundamental limitations to fermionic quantum monte carlo simulations. Phys. Rev. Lett. 94:170201. doi: 10.1103/PhysRevLett.94.170201

PubMed Abstract | Crossref Full Text | Google Scholar

van den Berg, E., Minev, Z. K., Kandala, A., and Temme, K. (2023). Probabilistic error cancellation with sparse pauli–lindblad models on noisy quantum processors. Nat. Phys. 19, 1116–1121. doi: 10.1038/s41567-023-02042-2

Crossref Full Text | Google Scholar

Wang, J., and Jaiswal, R. (2023). Scalable quantum ground state preparation of the heisenberg model: A variational quantum eigensolver approach. arXiv [Preprint]. arXiv:2308.12020. doi: 10.48550/arXiv.2308.12020

Crossref Full Text | Google Scholar

Watson, J. D., Bringewatt, J., Shaw, A. F., Childs, A. M., Gorshkov, A. V., and Davoudi, Z. (2023). Quantum algorithms for simulating nuclear effective field theories. arXiv [Preprint]. arXiv:2312.05344. doi: 10.48550/arXiv.2312.05344

Crossref Full Text | Google Scholar

White, S. R. (1992). Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866. doi: 10.1103/PhysRevLett.69.2863

PubMed Abstract | Crossref Full Text | Google Scholar

White, S. R. (1993). Density-matrix algorithms for quantum renormalization groups. Phys. Rev. 48, 10345–10356. doi: 10.1103/PhysRevB.48.10345

PubMed Abstract | Crossref Full Text | Google Scholar

Yang, Y., Cao, H., and Zhang, Z. (2019). Neural network representations of quantum many-body states. Sci. China Physics, Mech. Astron. 63:1. doi: 10.1007/s11433-018-9407-5

Crossref Full Text | Google Scholar

Zhu, Y., Wu, Y.-D., Bai, G., Wang, D.-S., Wang, Y., and Chiribella, G. (2022). Flexible learning of quantum states with generative query neural networks. Nat. Commun. 13:1. doi: 10.1038/s41467-022-33928-z

PubMed Abstract | Crossref Full Text | Google Scholar

Zhuk, S., Robertson, N. F., and Bravyi, S. (2024). Trotter error bounds and dynamic multi-product formulas for hamiltonian simulation. Phys. Rev. Res. 6:033309. doi: 10.1103/PhysRevResearch.6.033309

Crossref Full Text | Google Scholar