- 1Department of Psychology, Loyola University Chicago, Chicago, IL, United States
- 2Department of Psychology, University of California, Los Angeles, Los Angeles, CA, United States
Introduction: A remarkable phenomenon in perception is that the visual system spontaneously organizes sets of discrete elements into abstract shape representations. We studied perceptual performance with dot displays to discover what spatial relationships support shape perception.
Methods: In Experiment 1, we tested conditions that lead dot arrays to be perceived as smooth contours vs. having vertices. We found that the perception of a smooth contour vs. a vertex was influenced by spatial relations between dots beyond the three points that define the angle of the point in question. However, there appeared to be a hard boundary around 90° such that any angle 90° or less was perceived as a vertex regardless of the spatial relations of ancillary dots. We hypothesized that dot arrays whose triplets were perceived as smooth curves would be more readily perceived as a unitary object because they can be encoded more economically. In Experiment 2, we generated dot arrays with and without such “vertex triplets” and compared participants’ phenomenological reports of a unified shape with smooth curves vs. shapes with angular corners. Observers gave higher shape ratings for dot arrays from curvilinear shapes. In Experiment 3, we tested shape encoding using a mental rotation task. Participants judged whether two dot arrays were the same or different at five angular differences. Subjects responded reliably faster for displays without vertex triplets, suggesting economical encoding of smooth displays. We followed this up in Experiment 4 using a visual search task. Shapes with and without vertex triplets were embedded in arrays with 25 distractor dots. Participants were asked to detect which display in a 2IFC paradigm contained a shape against a distractor with random dots. Performance was better when the dots were sampled from a smooth shape than when they were sampled from a shape with vertex triplets.
Results and discussion: These results suggest that the visual system processes dot arrangements as coherent shapes automatically using precise smoothness constraints. This ability may be a consequence of processes that extract curvature in defining object shape and is consistent with recent theory and evidence suggesting that 2D contour representations are composed of constant curvature primitives.
Introduction
Among the most useful functions of the visual system is the perception and representation of shape. A striking and revealing example is the spontaneous perception of a unified shape from disconnected dot elements. Consider, for example, the array of dots presented in Figure 1A. Although the dots are disconnected and the shape unfamiliar, a well-defined, coherent shape is spontaneously perceived. Organization into a configural whole does not depend on similarity in the elements’ size, color, or element shapes, as shown in Figures 1B–D. Unlike displays used in research on path integration (e.g., Field et al., 1993; c.f., Kellman and Fuchser, 2023), the dot elements have no explicit orientation. The visual system could, in principle, interpolate any number of possible contours between dots in this array (c.f., Kanizsa, 1979).

Figure 1. Different dot displays giving rise to the same perceived shape. Perceivers organize the elements in each of the four displays into a similar unified shape representation despite variations in element size, color, and shape. (A) A shape defined by uniform elements. (B) The same shape defined by elements with nonuniform size. (C) The same shape defined by elements with nonuniform color. (D) The same shape defined by elements with nonuniform shape.
A familiar example of observers spontaneously perceiving shape from separated points in space is the perception of constellations in the night sky (Metzger, 2009). These organizations turn out to be surprisingly consistent across cultures (Kemp et al., 2022), suggesting that the extraction of shapes from stars depends on basic processes of human perception (Kelly et al., 2024). There also seems to be a high degree of consistency in the shapes observers extract from disconnected dots sampled from novel contours.
Although these observations are commonplace, they are remarkable manifestations of processes of abstraction in visual perception. Baker and Kellman (2018) found that brief exposures of dot arrays to human observers produced perceptual representations that readily supported matching of shape across transformations of position, scale, and orientation. They also found that, even when tasked exclusively with trying to detect changes in the positions of dots, observers had no ability to distinguish changes in dot positions (across two exposures) when dots were moved along a never-shown virtual contour from which the first array of dots was sampled (see Figure 2). These findings provided evidence that perception of these displays produced abstract shape representations, not tied to the particular stimulus elements presented. Such representations are extracted from relations of stimulus elements, but those specific elements are only transiently encoded. Metzger (2009) likewise observed that viewers exposed to a pattern of dots will often substitute the shape defined by the dots in visual memory, and these observations are consistent with many other demonstrations about perception of shape by Gestalt psychologists (see Koffka, 1935 for a review).
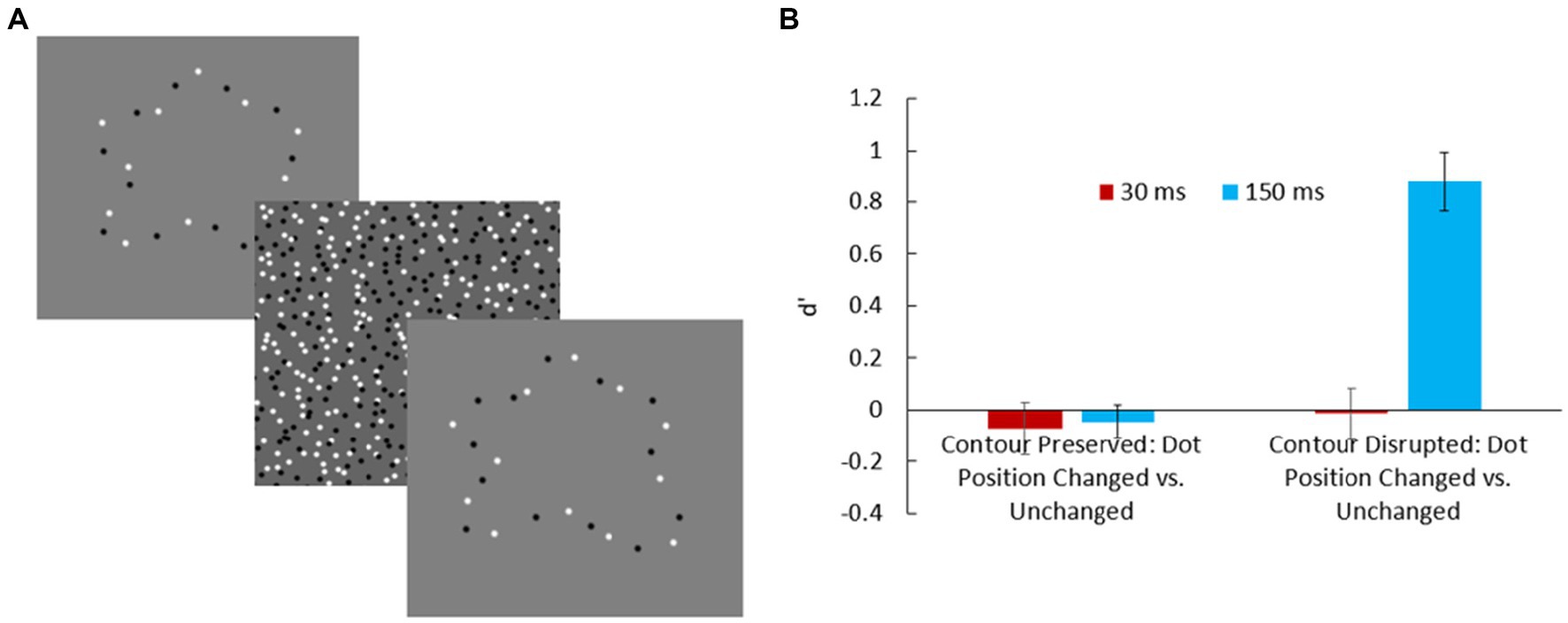
Figure 2. (A) Trial from Baker and Kellman (2018) in which dots were shifted along a shape’s virtual contour. (B) Sensitivity to dot position change. The observer’s task was to indicate whether any dots moved between the first and second exposures. When dot positions changed, they could either preserve or disrupt the virtual shape. For 30 ms exposures, there was no sensitivity to dot position changes, indicating that observers did not reliably encode specific dot positions, and, as earlier experiments indicated, 30 ms exposures are too short to allow formation of abstract shape representations. At 150 ms, when dots were shifted along the virtual contour, participants showed no sensitivity to the change; however, dot position changes that disrupted the virtual shape were more detectable, presumably due to their effect on the overall shape representation extracted.
Shape perception from dots comprises an especially valuable example of the abstract, relational character of visual perception (Baker and Kellman, 2018; c.f., Kellman and Massey, 2013). Because the notion of abstraction has been used in diverse ways in cognition and perception (e.g., Barsalou, 2003), it is reasonable to ask what we mean in describing a perceptual representation as abstract or a perceptual process as performing abstraction. Baker et al. (2021) suggested that three criteria characterize abstraction in perceptual encoding. Perceptual representations are abstract when they are: (1) relational, such that the relevant information encoded, as in the case of shape, is defined over, but not by, constituent elements; (2) economical, in that they involve summary descriptions from which much information relating to specific stimulus elements has been discarded; and (3) additive, in that abstract perceptual representations may add information that was not strictly in the stimulus information given. Perception of shape from dots exhibits all of these properties. From the relations of dots, a shape representation is obtained that transfers across changes in elements, scale, orientation, etc.; the stimulus elements themselves are not durably encoded, and in fact, many different sets of elements may give rise to the same abstract representation; and the shape representation itself has continuity of contour and a unity that is not given in the stimulus. Recognizing that abstraction—as indicated by these properties—is pervasive in perception may be valuable in clarifying a number of issues in both classical views of perception and recent proposals (e.g., Barsalou, 1999) about the relation between perception and cognition (Kellman and Massey, 2013).
Arguably, perceiving shape from contours that are not made from dots, i.e., that are continuous in the projection to the eyes, also involves all of these same characteristics. If an early level of cortical processing encodes the input into activations of cortical units having orientation sensitivity in local receptive fields, we encounter the same issues of how numerous local activations become organized into tokens of continuous contours and well-defined shape. When the stimulus itself has continuity, it may be harder to realize that an abstract re-description of the input occurs in those cases as well. Shape from dots provides a unique window into these processes, both intuitively and experimentally, as it is easier to point to aspects of perceptual representations that do not exist in the stimulus.
As remarkable as it is that the visual system encodes shape representations from unconnected dots, not all dot arrays give rise to a shape percept. Why do some spatial relations among dots result in a configural whol while others do not? Experiments testing dot perception with a highly constrained number of dots have found that certain relations between dots result in emergent features, relations among groups of dots that are more salient than the sum of the dot’s individual properties. Pomerantz and Portillo (2011) studied how different spatial relations among two to four dots influence the perception of emergent features in a dot array. They found that observers are highly sensitive to orientation and proximity relations between pairs of dots (see also Hawkins et al., 2016). These relations were shown to influence performance in an odd-one-out task even as differences between the target and distractor approached the minimum threshold for detection (Costa and Wagemans, 2021). Higher-order relations among dots resulted in emergent features less consistently. Dots that are collinear tended to be perceived configurally, but other relations of three dots, such as symmetry, resulted in an emergent feature only for certain displays.
These results provide important insight into how even the simplest displays are perceived configurally, but they cannot fully explain how shape emerges from arrays of dots. As Pomerantz and Portillo (2011) point out, the systematic tracking of emergent features becomes difficult or impossible as the number of elements in a display increases. Studies on the percept of shape from randomly placed dots have found that certain configurations are much more frequently perceived to have a unitary shape description than others, depending on proximity and good continuation between the dot elements (van den Berg, 2006). Considerable research has been done on how the visual system organizes an array of dots into multiple distinct shapes, or into a single shape among random dot distractors. Proximity appears to play a major role in these computations (Van Oeffelen and Vos, 1983; Kubovy and Wagemans, 1995; Papari and Petkov, 2005), although similarity (Zucker et al., 1983) and good continuation are also important cues (Smits et al., 1985; Lezama et al., 2016).
Notions of proximity and similarity are perhaps intuitive with respect to dot configurations, but good continuation requires some elaboration. Good continuation in Gestalt psychology has always been somewhat vague: Wertheimer (1923) said that “one knows” what it is, and Kanizsa said that it resists simple definition (Kanizsa, 1979). Other work has provided more rigorous, but highly varied, definitions of good continuation.
A common view is that good continuation depends on the degree to which dots are collinear with each other (Smits et al., 1985; Wouterlood and Boselie, 1992; van den Berg, 2006), which has been shown to aid contour detection using simple segments (Uttal, 1973; Prinzmetal and Banks, 1977). Another definition that has been proposed quantifies good continuation by measuring the degree of symmetry between the middle and first dot and the middle and third dot in a triplet. Sequences of dots with more symmetrical triplets are considered less accidental and are therefore more likely to be organized together (Lezama et al., 2016). Still another view is that the visual system evaluates good continuation in quartets. According such theories, the goodness of dots’ continuation is quantified by the degree to which the turn angle between consecutive dots in a quartet remains constant (Feldman, 1997; Kelly et al., 2024). This definition is similar to one proposed by Pizlo et al. (1997) which theorizes that a dot sequence has good continuation if it is smooth, which they define as consisting of successive pairs of dots whose orientations are similar to each other. For example, a four-dot sequence, ABCD, is considered smooth if the difference in orientation between AB and BC is small and the difference in orientation between BC and CD is small.
A theme shared among many of these theories is that good continuation is primarily a summation of many local computations (Feldman, 1997; Pizlo et al., 1997; Lezama et al., 2016; Kelly et al., 2024). This is consistent with path integration work done using oriented Gabors (Field et al., 1993; Hess and Field, 1999). However, others have argued that good continuation is a more global consideration and is strengthened by monotonicity and curvature regularity along the extent of the dot sequence (Smits and Vos, 1986; Yuen et al., 1990; van den Berg, 2006).
Our goal is not to test these competing formulations of good continuation but to better specify how the manipulation of spatial relations between dots influences. Understanding this could provide crucial insight into how the visual system forms abstract shape representations. This effort is specifically relevant to understanding how contours are formed. Dot arrays, with no continuous contour physically given, may provide unique insight into underlying visual processes in shape representation (Baker and Kellman, 2018).
One way the visual system could form a contour representation from unconnected dots is by interpolating straight edges between adjacent boundary points (e.g., O'Callaghan, 1974). Under this view, dot displays with longer sequences of collinear dots would be simplest because a new line segment would be required for any change in orientation between sequential dot pairs. It would also be consistent, within a certain size range, with modest activation of large, orientation-sensitive units in visual cortex by pairs or sets of dots. The straight line interpolation process is computationally simple and would effectively minimize the total length of the contour connecting the dots.
On the other hand, we have the phenomenological experience of perceiving smooth curves in displays like the dots in Figure 1. Moreover, connecting straight edges at each point would result in a very jagged percept of the dot array, albeit one that is invariant to rigid 2D transformations. Under this view, any dot between two other dots, A and B, would either need to be collinear with A and B or would be perceived as a corner in the contour representation of the display. Attneave (1954), in classic work, proposed that corners are the positions on the contour with the greatest informational content and are consequently more salient in our perception (Troncoso et al., 2005; De Winter and Wagemans, 2008). Previously, we shifted all dots in an array along a virtual contour, which would result in a contour representation with a completely different set of corners if observers were indeed encoding the shape with straight line interpolation. Given the perceptual importance of corners, such a change should be easily detected, but we found that humans had no sensitivity at all to the positional shift. This suggests that the visual system does not form shape representations of dot arrays by simply interpolating straight lines between adjacent points. Curved edges may instead be interpolated across spans of dots such that shifts to any other position on the interpolated curve are largely undetectable.
There is other empirical evidence that the visual system does not always represent dots as corners in a contour. Koffka (1931) placed points along a circle to estimate the number of dots at which the virtual contour was perceived as smooth. He estimated that this transition occurred at around eight evenly spaced dots (which produces inclusive angles of 135° for each dot triplet). Bouma (1976) gave a more conservative estimate that 10 dots were needed for the virtual contour to be perceived as smooth. Smits and Vos (1987) used more systematic tests to estimate this transition point and found that when the inclusive angle between triplets of dots was sufficiently large (greater than about 140°), the dots were perceived as curvilinear (Figure 3A). In a later study, van Assen and Vos (1999) developed a more objective measure of perceived curvilinearity by measuring participants’ bias to say whether a target dot was below or above a virtual contour defined by four other dots. They found that when the inclusive angle between the central dots was 135° to 150°, participants’ bias was consistent with perceiving a curved contour. Feldman (1996) systematically varied the inclusive angle for three dot displays and found that the 50% threshold for curvilinear responses vs. angular responses was at around 120°. He found that when a fourth dot was added to the configuration to create two similar angles from dot triplets, the threshold went down (Feldman, 1997; Figure 3B).
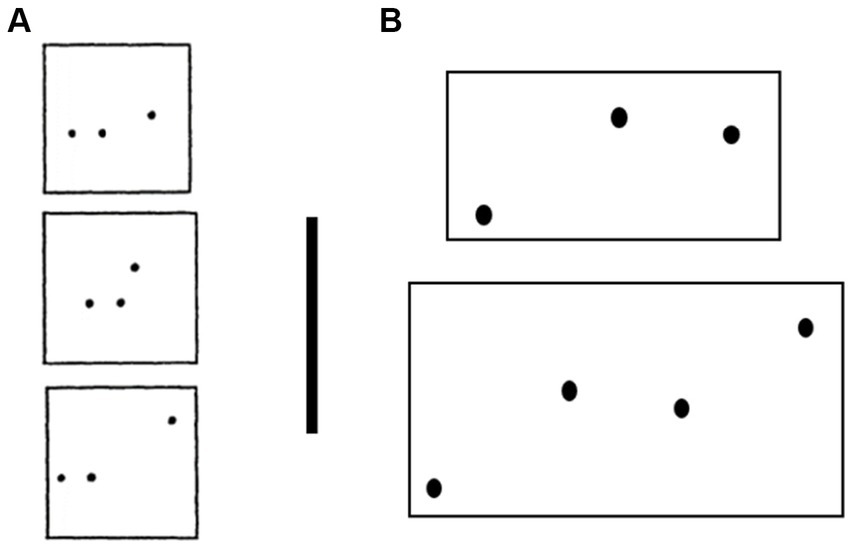
Figure 3. (A) Dot triplets used by Smits and Vos (1987). (B) Comparison of a dot triplet and quadruplet from Feldman (1997). Feldman found that the addition of a fourth dot with similar turn angle increased the probability of a curvilinear response. Reprinted with permission from Perception and Vision Research, respectively.
If forming a shape representation by encoding each dot position as a corner is both parsimonious and computationally simple, why would the visual system ever extract contour representations with smooth curves from dot arrays? One possibility is that the visual system is sensitive to curvature-specific contour segments and can encode curvilinear contours from a dot array as easily as straight lines (Smits and Vos, 1986; Yuen et al., 1990). Past research on connected contours has shown that perceptual tasks requiring a shape representation are accomplished better and more quickly with smooth contours than with angular contours (Bertamini et al., 2019). Other work has shown that visual system has special facility for encoding contours of constant curvature (Baker et al., 2021). A perceptual corner has a first-order (tangent) discontinuity at its vertex, meaning there will always be a segment boundary at that point. On the other hand, if the contour is perceptually smooth at that point, the entire segment could be represented as a single curvature segment. As a consequence, representing dot patterns’ shape with curvilinear segments may be computationally simpler because the shape description consists of fewer parts. Moreover, the presence of a corner or first-order discontinuity, in this case an L-junction, not only forms a boundary within a single contour or object representation, but under some circumstances in visual perception plays a key role in determining that intersecting contours belong to different objects (Clowes, 1971; Shipley and Kellman, 1990; Heitger et al., 1998; Kalar et al., 2010).
These considerations suggest that the abstract shape representation that is ultimately encoded by an array of dots might be stored more efficiently as a set of relatively few curved segments than a larger set of straight segments. If this is the case, we expected that it would be easier to encode arrangements of dots that appear to have few or no sharp corners as a shape than arrangements of dots with many perceived corners. A different framing of the question is that both smooth contours and first-order contour discontinuities exist in the world and are important to encode. Discrete dots provide sparse information about what structure might best represent their relations. Under what conditions does the visual system encode smooth continuation through an element vs. representing that element as a contour junction?
We studied information that might be used by the visual system to represent smooth curves vs. corners and tested its effects on shape encoding, using both subjective and objective measures. In Experiment 1, we experimentally estimated the angle at which dots in an array are perceived to be on corners vs. smooth curves in a virtual contour, both in conditions with only three points and in conditions where other configural aspects of the display facilitate or inhibit the perception of a corner. In Experiment 2, we used these estimates to create larger dot arrays and asked participants to judge how much each dot array looked like a coherent shape. In Experiment 3, we showed pairs of dot arrays sampled from smooth or corner shapes at different orientations and measured the time it took for participants to judge whether the shape formed by the dots was the same or different. In Experiment 4, we hid dot arrays sampled from both kinds of shapes among randomly placed distractor dots and measured participants’ ability to detect the shape in both conditions.
Experiment 1
The general goals of our study were to understand the conditions under which arrangements of dots are perceived as smooth curves vs. corners and to test the consequences of curve vs. corner encoding on shape perception and representation. As a starting point, we first needed to determine the angles at which a dot is perceived to be on a corner (i.e., a first order discontinuity) vs. when the dot is perceived to be on a smoothly changing edge (i.e., a differentiable point on the contour). Previous work suggests that the threshold between corners and smooth edges is between 120° and 150° (Koffka, 1931; Bouma, 1976; Smits and Vos, 1987; Van Assen and Vos, 1999).
In Experiment 1, we sought to replicate these findings. Because the displays we intended to use in subsequent experiments involved many more dots than the three that define a single vertex, we also wished to test whether the perception of curves vs. corners depended only on the local geometry among dot triplets or if dots more remote from the potential vertex also influenced perception of corners.
Methods
Participants
Thirty (23 female, seven male, Mage = 20.5) participants from the University of California, Los Angeles participated in this study for course credit. All participants had normal or corrected-to-normal vision.
Display and apparatus
Subjects were seated 70 cm from a 20-inch View Sonic Graphic Series G225f monitor. The monitor was set to a resolution of 1024 × 768 pixels with a refresh rate of 100 hz. Except when noted otherwise, all aspects of the displays and apparatus in subsequent experiments were the same as in Experiment 1.
Stimuli
We had three stimulus categories: convex, concave-convex-concave, and convex-convex-convex, referring to the direction of curvature of the second dot in a sequence of triplets. Convex vs. concave was defined by reference to the upward direction of visual field, so that dot triplets were considered convex if their central dot was above its flankers and concave if it was below its flankers. The “convex” condition had the simplest displays, with a central dot flanked by two lower dots on either side. (This base of three dots was always convex upward.) The distance between the central dot and its two flankers was kept constant, but the position of the flankers could change to manipulate the angle defined by the dot triplet with the central dot as a vertex. These angles were not predetermined but increased or decreased depending on participants’ responses.
In the “concave-convex-concave” condition, the central triplet was flanked by one additional dot on each side. The contour defined by the central dot and its two flankers on each side bent upward such that the central dot appeared to be the joining point between two concave edges (see Figure 4 for examples). The two concave edges could rotate around the central dot to increase or decrease the angle between the central dot and its two closest flankers. The convex-convex-convex condition was like the concave-convex-concave condition except that the contour defined by the central dot and its two flankers on either side appeared to be bending downward so that the two edges meeting at the join point were both convex (as viewed from above). This created an array of dots where the direction of curvature (as defined by the turning angle between dot) for the central point matched the direction of curvature for the two points on either side of it. The opposite was true for the concave-convex-concave condition, where the direction of curvature alternated twice. For both five-dot conditions, the arms on either side of the central dot were symmetrical and the angle centered on the second and fourth dot (from left to right—see Figure 4) was fixed at 135°. In the first presentation of the stimulus in any of these conditions, the angle between the central dot (the red dot in Figure 4) and the dots directly to its left and right was 90° (Figure 4, botttom). Subsequent angles were determined by participants’ responses.
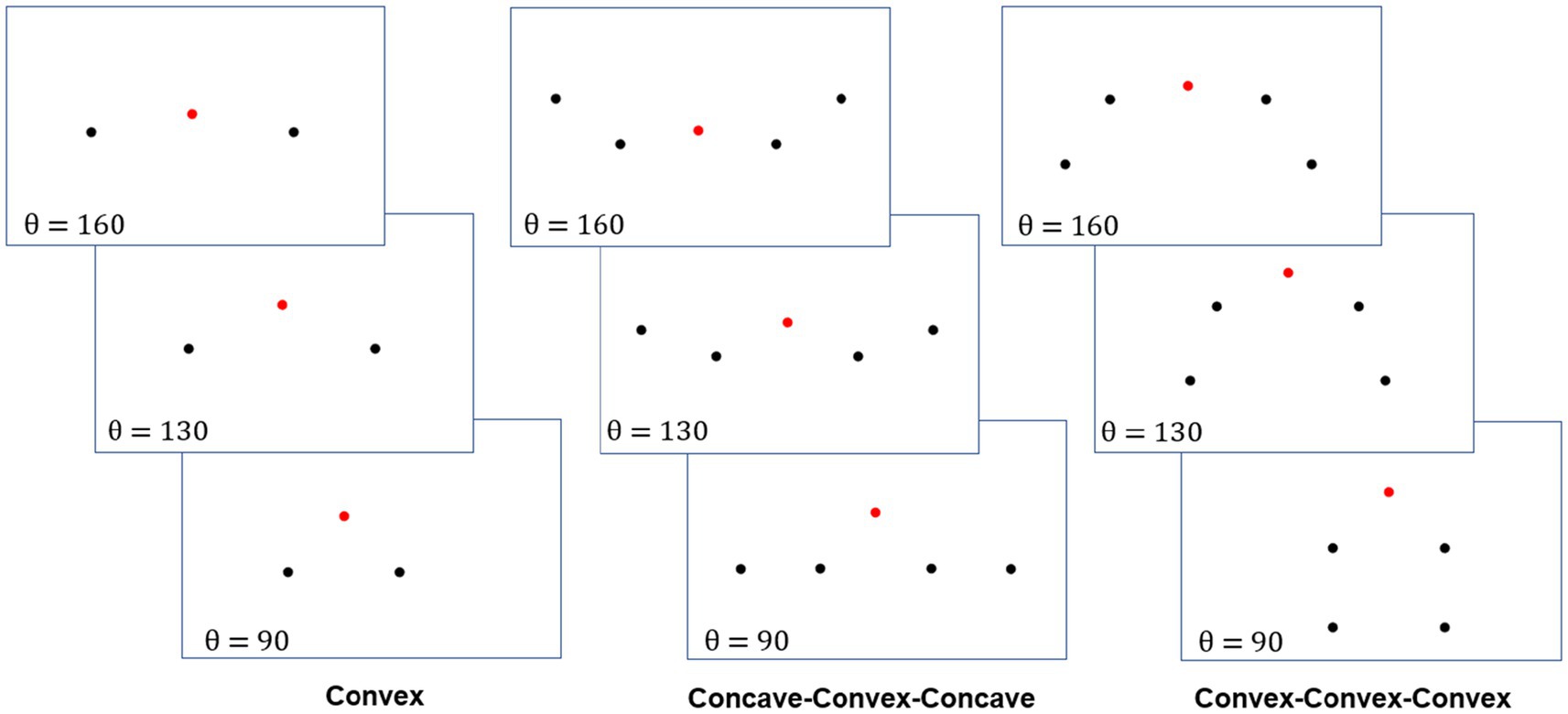
Figure 4. Sample displays from Experiment 1. Left: Convex condition. Middle: Concave-Convex-Concave condition. Right: Convex-Convex-Convex condition. The values of θ shown in the bottom left of each display correspond to the angle between the central dot and its nearest flanker on either side. The central dot is highlighted in red only for presentation purposes: it was black in the displays shown to be participants.
Dots were evenly spaced 1.8° of visual angle apart from each other. Each dot in the arrangement subtended 7.2 arcmin and the maximum total height or width of a dot arrangement was 9.6° of visual angle. Dots were rendered black (luma = 0) of the on a gray background (luma = 100).
Design
The experiment consisted of three conditions corresponding to the three stimulus categories (convex, concave-convex-concave, and convex-convex-convex). Trials were interleaved among the three conditions, with the aim of determining the threshold for seeing a corner in each. We used interleaved staircase procedures to determine participants’ 50% probability of responding “corner” for each of the three conditions, manipulating the angle between the central dot and its two flankers. Participants completed at least 24 trials per condition. If their responses converged to a 50% threshold after 24 trials, they ceased to see trials for that condition. If their responses had not converged, they continued seeing trials until we found at least three crossover points (Leek, 2001).
Procedure
In each trial, participants were shown a fixation cross followed by a single arrangement of dots in the center of their screen. The dot arrangement could be from any of the three stimulus categories. Participants were instructed that they would be shown a group of dots on the screen in each trial, with a central dot and 1 or 2 dots on either side of it. Participants’ instructions were to look at the display and imagine that the dots are connected in some way. They were then told that “Your task is to decide whether the middle dot appears to be a corner or not.” They were told to respond “curve” if the middle dot appeared to be on a smooth, curved edge, and “corner” if it appeared to be a pointy feature. Based on pilot work, we found that the correct task could be communicated effectively through this combination of instructing subjects to imagine that the dots are connected in some way and also stressing that they should indicate how the middle dot appeared. Together, these instructions overcame confusion that some participants had in pilot work about instructions to respond based on a perceived virtual contour. Participants were told that there was no expectation that half the trials should be smooth and half should be corners. If they saw the middle dot as the vertex of a corner in all trials, they should say so, and likewise if they saw the middle dot as lying on a smooth curve in all trials.
We used an adaptive staircase procedure, starting with a central angle of 90° for each of the three conditions. After participants responded, we adjusted the angle between the central dot and its flankers based on their response. For the first eight trials in each stimulus category, we adjusted the angle by a larger amount, increasing the angle between the three central dots by 11° if participants reported seeing a corner or decreasing it by 11° if participants reported seeing a smooth curve. In the next eight trials for each stimulus category, the angle increased or decreased by 4.5° depending on participants’ responses. After participants had completed 16 trials in a condition, the angle increased or decreased by 1.2° based on participants’ responses for all remaining trials. This approach was used to adjust quickly early to get near to participants’ 50% threshold, and then to make smaller changes to get a more precise estimation of participants’ true threshold. Staircases for each of the three conditions were interleaved to minimize any carryover effects that might occur from sequences of trials with changing angles in a single condition.
A condition ended when participants switched from reporting a curved percept to reporting a corner percept (or vice versa) three times or when they had completed 24 trials of the condition, whichever came later.
Dependent measures and data analysis
We measured the threshold at which participants reported seeing a corner vs. a smooth curve equally often in each of the three conditions. Our expectation was that the threshold for the convex condition (consisting of only three dots) would be between 135° and 150°, consistent with previous findings (Koffka, 1931; Bouma, 1976; Smits and Vos, 1987; Van Assen and Vos, 1999). We predicted that if dots beyond the central three dots influence the perception of a corner vs. a smooth curve, then the concave-convex-concave condition would have a larger threshold than the convex condition because participants would be more likely to perceive a first order discontinuity at the middle point. By the same token, we predicted that the convex-convex-convex condition would have a lower angular threshold because the series of vertices would be consistent with a monotonically curved contour.
Results
The results of Experiment 1 are shown in Figure 5. A one way repeated measures ANOVA confirmed a significant main effect for dot arrangement condition, F(2,58) = 32.99, p < 0.001, η2partial = 0.53. The 50% threshold for three points (the convex condition) closely matches earlier findings. In our experiment, participants’ mean threshold was 140°, consistent with the 120° to 150° range reported in previous studies. The concave-convex-concave condition, which we hypothesized would induce more corner percepts, had a mean threshold of 148°. This threshold was not significantly different from the threshold estimated in the convex condition, t(29) = 0.93, p = 0.36, Cohen’s D = 0.17. The convex-convex-convex condition, which we hypothesized would induce fewer corner percepts, had a mean threshold of 82°. This difference did significantly differ from both the convex condition, t(29) = 6.18, p < 0.001, Cohen’s D = 1.13 and the concave-convex-concave condition, t(29) = 7.54, p < 0.001 Cohen’s D = 1.38.
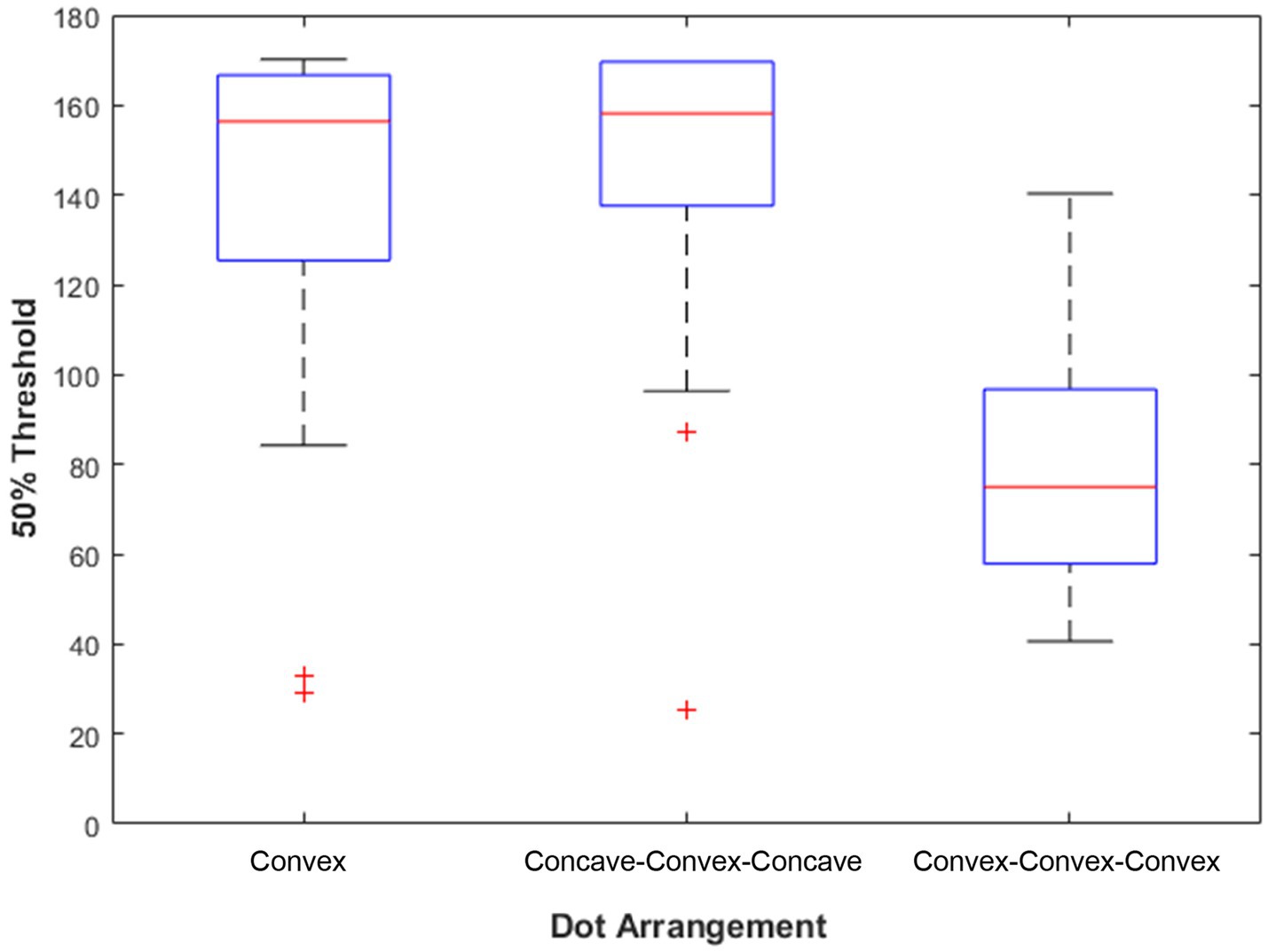
Figure 5. Experiment 1 results. The box shows the interquartile range of thresholds for individual participants. The red line shows the sample median for the 50% threshold—the median angle at which participants were as likely to report perceiving the central dot to be on a corner as to report perceiving it on a smooth curve. The “whiskers” extend to the most extreme datapoint within 1.5 times the length of the interquartile range from the top or bottom edge of the box (covering 99.3% of the data if they are normally distributed; McGill et al., 1978; Krzywinski and Altman, 2014). Outliers are data points beyond the whisker and are plotted as red +‘s.
Analysis of the skew and kurtosis of our data suggested that they were not normally distributed, so we applied the Box-Cox transformation (Box and Cox, 1964) and reanalyzed these effects. Analyses of the transformed data found the same general effects as were observed in the untransformed data. A repeated measures ANOVA confirmed significant differences among the three conditions, F(2,58) = 39.35, p < 0.001, η2partial = 0.58 and significant differences were found between the convex and convex-convex-convex conditions [t(29) = 7.18, p < 0.001, Cohens’ D = 1.31] but not between the convex and concave-convex-concave conditions [t(29) = 1.29, p = 0.21, Cohen’s D = 0.24].
Discussion
The first aim of Experiment 1 was to understand the geometric conditions under which a dot in a sequence of dots would be perceived as a corner. Our data suggest that the threshold for equal probability of perceiving a dot as a corner vs. lying on a smooth contour is around 140°, with angles smaller than that increasingly tending to be seen as corners. The second aim of Experiment 1 was to understand whether the perception of corners vs. smooth curves was a local computation only (i.e., it depended only on the angle between a central dot and the dots on either side of it in a triplet) or if dots outside of the triplet also played a role. Given that the displays we planned to use in subsequent experiments would include arrays of 25 dots, it was important to know whether the corner percept was a purely local computation among the dots defining the angle or if other dots could shift viewers’ judgments by changing the way the dot array was perceived.
We found no statistically reliable difference in participants’ thresholds for concave-convex-concave displays that were designed to facilitate the perception of a corner. In these displays, there are at least two ways that participants could interpolate virtual contours between the five presented dots. The first way involves two curvature segments that join at the central dot in the display (Figure 6A). This representation of the virtual contour will almost always result in a perceived corner because the tangent of the contour where the first curvature segment ends is very different from the tangent of the contour where the second curvature segment begins, resulting in a first-order discontinuity. The second way a contour could be interpolated is by organizing the central three dots into a curvature segment and the two flanking dots on either side into other segments (Figure 6B). This representation predicts no difference in threshold between the concave-convex-concave condition and the convex condition (Figure 6C) because the same three dots are encoded as their own chunk. Our results suggest either that participants favored the second organization of dots to the first, grouping the central three dots as one unit and the flanking pairs of dots as separate units or that the perception of a corner depends only on the angle between the vertex and the dot on either side of it.
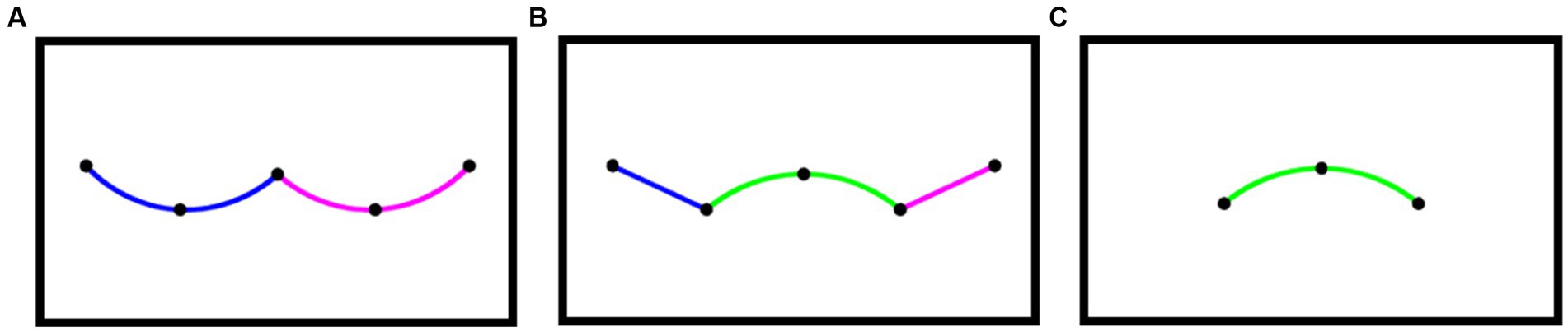
Figure 6. Two ways of interpolating contours between dots in the concave condition. (A) Two curved segments join at the middle (left). (B) Three segments join at the second and fourth dot (middle). (C) A curved interpolation between the three central points in (A,B) (right). The physical contours chosen to represent the interpolation between dots are chosen arbitrarily in this figure. The edge perceived between dots may be neither a straight edge nor a constant curvature segment. We used these forms of interpolating lines only to help visualize possible organizational structures of the display.
One reason that the second grouping is preferred could have to do with symmetry. The central three dots in the display were always symmetrical over a vertical axis, while the first three and last three dots were symmetrical over diagonal lines in some displays (see Figure 4, bottom middle). Previous research has found that symmetry is much more likely to be an emergent feature when elements are symmetrical about a cardinal axis than when they are symmetrical about a noncardinal axis (Pomerantz and Portillo, 2011), which may have result in better grouping of the central three dots with each other.
By contrast, the convex-convex-convex arrangement of dots did have a significant influence on observers’ tendency to perceive a corner. Observers were significantly more likely to see the central dot as placed on a smooth curve when additional dots were added that were consistent with a virtual contour with constant curvature polarity. This suggests that there is an asymmetry in the way that additional dots influence our perception of corners. While adding dots to strengthen the percept of a smooth, monotonic curve does weaken the perception of corners, the opposite approach of placing dots so that the contour cannot be monotonic does not appear to have a strengthening effect on the perception of corners.
Gestalt cues shown to produce emergent features like proximity are unlikely to explain differences in the perception of corners in the convex-convex-convex vs. concave-convex-concave conditions. Both displays had identically spaced adjacent dots, but the first and fifth dots in the convex-convex-convex condition were closer to each other than in the concave-convex-concave condition. This difference in proximity may have resulted in a greater overall percept of configural structure in the convex-convex-convex condition, but it is unlikely to have influenced the perception of curvature at the central point. In fact, dots whose extreme points were moved closer together by reducing the angle at the central point were perceived as curvilinear less often than dots whose extreme point remained more distant.
The Gestalt cue likely to be playing the greatest role in observers’ perception of a corner vs. a smooth edge is good continuation. As previously discussed, however, there are many different definitions of good continuation in the perception literature, and those that are readily applicable to dots make different predictions about how the five-element dot arrays should be perceived. The data from the convex-convex-convex condition suggest that the perception of good continuation is not solely determined by the local spatial relations in a sequence of dot triplets (e.g., Lezama et al., 2016), but depends on larger clusters of local dot relations (Feldman, 1997; Kelly et al., 2024), or on the global monotonicity of the dot sequence (Smits and Vos, 1986; Yuen et al., 1990).
Experiment 2
In Experiment 1, we studied the tendency of a series of dots to be represented as a connected contour and estimated the threshold, in terms of angular relations, at which a dot in the series is perceived to contain a first order discontinuity. What do these data reflect about perception and representation of contours from sets of separated dots? Experiments 2, 3, and 4 investigated the perceptual reality and impact of perception of seeing a vertex or smooth continuation in sequences of dots. In Experiment 2 we used the thresholds estimated in Experiment 1 to measure the strength of a shape percept in three different kinds of dot displays. We created arrays of dots by sampling from (a) novel shapes with smooth curves; (b) novel shapes with sharp corners, and (c) random dot arrangements. We then asked subjects to rate the degree to which the dots appeared to form a coherent shape. Our prediction was that dots sampled from smooth contours would be judged more shape-like than dots sampled from shapes with corners, which would in turn be judged more shape-like than random dot arrangements.
Methods
Participants
Twenty-five undergraduates (3 male, 22 female, Mage = 20.6) from the University of California, Los Angeles participated in the study for course credit. All participants had normal or corrected-to-normal vision.
Stimuli
Experiment 2 included three different kinds of dot arrays: Smooth, Corner, and Random. “Smooth” dot arrays were created by placing nine control points at evenly spaced angular positions around a circle and then moving each control point toward or away from the circle’s center by a random distance, then fitting cubic splines through the nine control points in polar space (see Figure 7A). The control points’ signed displacements were sampled from a normal distribution centered at 0% with a standard deviation of 18%. The mean absolute distance of the control points’ displacement was 14.34% (SD = 11%). We made use of our findings from Experiment 1 to create shapes that we expected to generally be perceived as Smooth or Corner shapes. In Experiment 1, we found that when the angle between dots exceeded 140°, the point tended be perceived as smooth, regardless of the spatial relations between dots beyond the triplet determining the angle. In the range between 82° and 140°, the point could be made to appear smoother by adding additional dot triplets whose turn angle had the same polarity as the point in question. The displays used in Experiment 2 were significantly more complex than those used to estimate these thresholds in Experiment 1. They consisted of many more dots and were not symmetrical on either side of any possible vertex. Still, we expected that displays with dot triplets whose angle mostly exceeded 140° would generally be perceived as smooth and displays that included dots triplets whose angle was less than 90° would generally be perceived as angular.

Figure 7. Shape stimuli used in Experiment 2. (A) A Smooth shape contour. (B) A Corner shape contour. (C) Dots sampled from the Smooth shape. (D) Dots sampled from the Corner shape. (E) Random dot arrays.
We did not directly manipulate the angle between dots in the Smooth condition, but the cubic spline fitting shape generation algorithm produced shapes that were always differentiable at all positions. With nine control points and the possible distances they could be displaced, the angles among dots sampled at these positions tended to be obtuse with an angle that exceeded 140° (Mangle = 154°, SD = 16°). The average minimum angle in Smooth displays was 123° (SD = 13°).
From each smooth shape generated as described above, we then sampled 25 points along the contour to get the dot array. The points were sampled nonuniformly by taking 25 evenly sampled points and moving them in a random direction along the contour. Though not directly relevant to this experiment, we included jittering along the contour to prevent participants from using local spatial relationships between a small set of dots rather than the overall shape of a dot array in subsequent experiments using objective performance methods (see Experiment 3 for more explanation). The amount of jitter was randomly sampled from the normal distribution. Dots were shifted along the shape’s virtual contour by a random signed distance from a normal distribution, with a mean distance of zero and a standard deviation equal to 4% of the contour’s total length. We constrained the display to enforce a minimum distance of 7.2 arcmin between any two points to prevent them from overlapping or appearing to touch each other (Figures 7C,D).
“Corner” dot array stimuli were created by generating a smooth dot array, reducing the angle between some of the dots, fitting straight lines between the set of dots, and then resampling from the straight line contour. To distinguish two closely related concepts here, we refer to a generating figure that consists of all straight line connections between dots as a “cornered figure,” and we refer to the resultant derived dot stimuli as “corner stimuli” used in the “Corner condition”. We began with a dot array generated by evenly sampling 25 dots from the same kind of shape from which the Smooth dots were sampled. We then altered between 8 and 13 dot triplets in the display (determined for each display by randomly sampling from a uniform distribution of integer values). For a given dot triplet, ABC, we imposed a corner percept by interpolating a line between points A and C, then moving point B perpendicularly away from the interpolated line while simultaneously moving A and C along the line until the vertex at B was between 78° and 90°. This range was chosen so that the Corner shapes would be reliably perceived to have first-order discontinuities based on our Experiment 1 findings while also including some natural variability in the angle between dot triplets. Because the angle reduction process resulted in shapes with much less regular spacing than in the Smooth condition, we interpolated straight lines between the 25 repositioned points to get a new shape contour with corners (Figure 7B). From each such shape, we used the same nonuniform sampling procedure as for smooth dot displays to sample 25 new dots and generate a dot figure (Figure 7D). The resulting dot display had between one and two dot triplets whose angle was less than 90° and several more whose angle was between 90° and 100°.
“Random” dot array stimuli also began with the smooth dot array. Rather than moving dots to reduce the angle between them, dots were moved in random directions. Each of the 25 points was moved a distance equal to the total length of the contour divided by 25 in a random direction, with the constraint that dots could not be closer together than 7.2 arcmin (Figure 7E). We used this method instead of truly random placement to prevent subjects from judging shape based on whether there was an open center within the dot array, a feature that was naturally present in both the “Smooth” and “Corner” displays. The method we used to generate “Random” dot arrays matched the open center of the other two conditions without appearing to define a shape.
Dot arrays for each of the three conditions were matched in size, subtending on average 12.0° of visual field along the longer of their horizontal and vertical dimension, and at most 20.7° of visual field.
Design
Experiment 2 had three conditions, with 70 trials in each. In the Smooth condition, we showed dot arrays from smooth shapes. In the Corner condition, we showed dot arrays from shapes with corners. In the Random condition, we showed random dot arrays. Trials with all three conditions were randomly interleaved.
Procedure
On each trial, participants were shown one of the three stimulus types and asked to evaluate the degree to which the dot array seemed to form a shape. The dot array remained on the screen until a response was given. Participants were instructed to rate the display on a 6-point scale, ranging from “The dots look totally random” to “The dots look totally like a shape.” Integer responses between 1 and 3 reflect that the dots looked more random than like a shape to viewers, either slightly so (3), moderately so (2) or strongly so (1). Integer responses between 4 and 6 reflect that the dots appeared more like a shape than a random set of dots and followed the same progression. We instructed participants to use all 6 response options to reflect qualitative differences in the degree to which different dot arrays appeared to be shapes. Before beginning the main experiment, participants completed five practice trials to familiarize themselves with the response buttons and to view all three stimulus types before giving recorded shape judgments.
Results
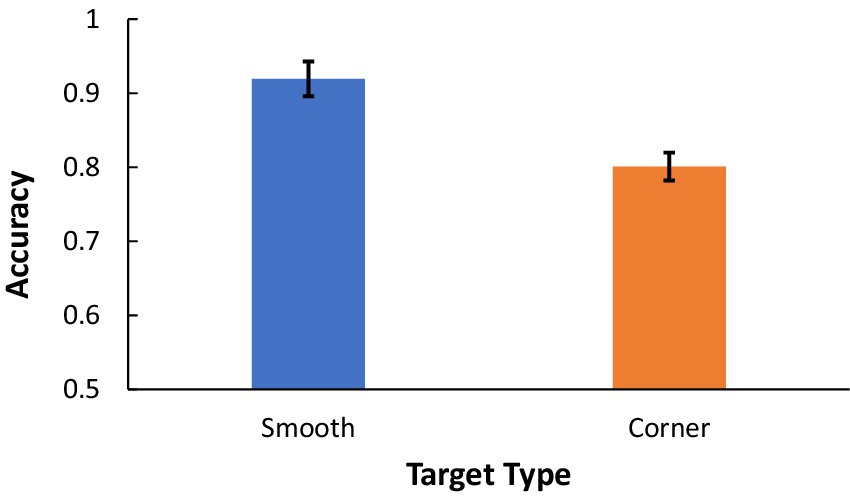
Figure 8 shows the primary results of this experiment. Figure 8A shows the mean subjective rating for each of the three stimulus types. There is a clear ordering in which dots sampled from Smooth contours were perceived as most shape-like, followed by dots sampled from cornered contours, followed by randomly sampled dots. This pattern was shown by every participant who completed the experiment. A one-way ANOVA confirmed a significant difference between the groups, F(2,48) = 681.86, p < 0.001, η2partial = 0.97 and Bonferroni-corrected paired sample t-tests confirmed that dots sampled from smooth contours were rated more shape-like than dots sampled from cornered contours, t(24) = 14.93, p < 0.001, Cohen’s d = 2.89 and that dots sampled from cornered contours were rated more shape-like than randomly sampled dots, t(24) = 20.64, Cohen’s d = 4.13 p < 0.001.
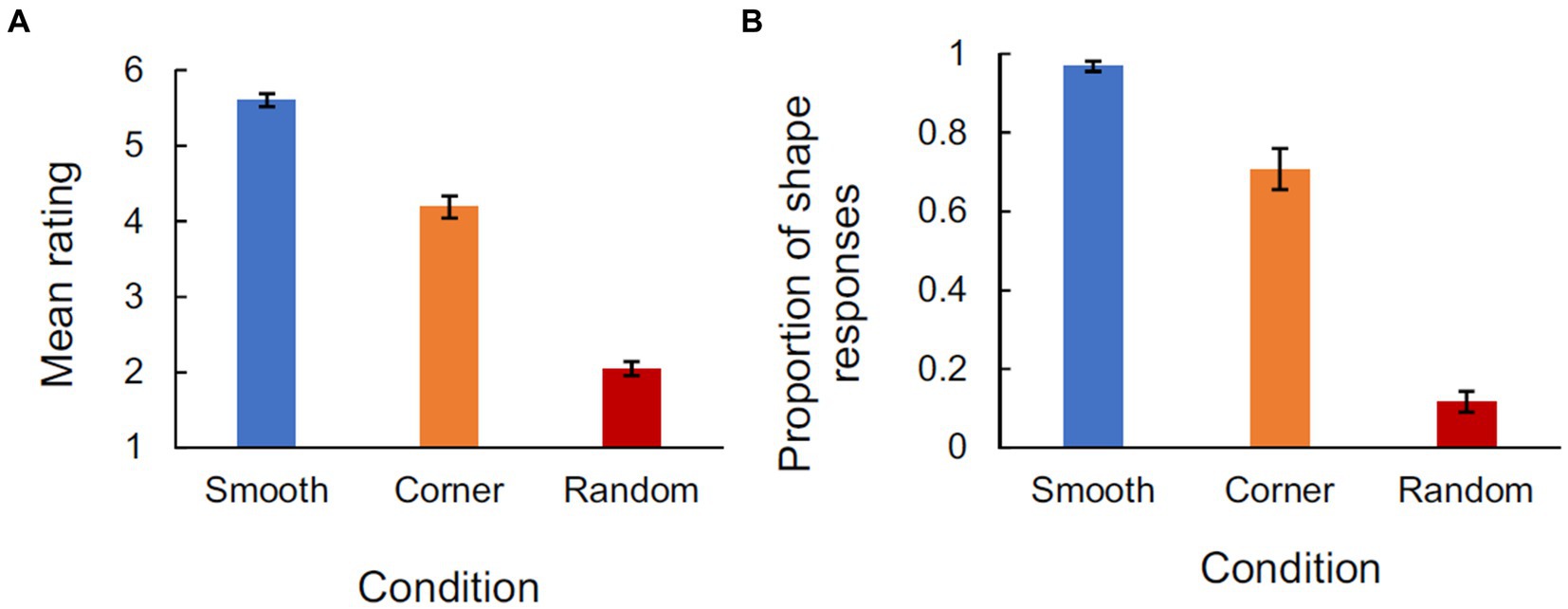
Figure 8. Experiment 2 results. (A) Participants rating of shape for each of the three conditions. (B) The percentage of ratings that were more shape-like (i.e., rating > 3) for each condition.
We also analyzed the average number of trials in which subjects perceived a shape at all. For this measure, we included any display that received a subjective rating greater than 3. The results are shown in Figure 8B. Paired samples t-tests confirmed that subjects’ perceived significantly more of the dots sampled from smooth contours as a shape than they did dots sampled from cornered contours, t(24) = 6.04, p < 0.001, Cohen’s d = 1.21 and that dots sampled from cornered contours were perceived as shapes significantly more often than randomly sampled dots, t(24) = 13.81, p < 0.001, Cohen’s d = 2.76.
Discussion
Experiment 2 furnished evidence that dots sampled from smooth contours are more phenomenologically shape-like than dots sampled from contours with sharp corners. Every participant gave higher shape ratings for the smooth contour condition and reported perceiving more of the smooth contours as shapes than the cornered contours. Participants never saw the underlying contour from which the dot arrays were sampled. Geometrically, all the dots sampled from shapes with corners could be represented with curvilinear contours, but participants made qualitatively different responses for Corner dot arrays.
One reason that participants may have given lower shape ratings for the Corner stimuli is that they were interpolating a curvilinear contour through the dots in the Corner displays, but the process was more difficult for dot arrays with sharper angles. Though the data cannot rule out this possibility, we consider it unlikely because the results of Experiment 1 suggest that we perceive corners at certain points in the Corner displays. Our phenomenological experience of Corner displays like the one in Figure 7D also suggest that the array is perceived with corners.
A more likely possibility is that Corner displays were harder to encode as shapes than Smooth displays because there was more variety in the presented angles. Corner displays were likely perceived as having a mix of smooth curves and corners, whereas the Smooth displays were likely only perceived with smooth curves. As a result, there would be greater perceived homogeneity among dot triplets in the Smooth displays than in the corner displays. The irregularity between smoothly bending and/or straight edges and edges that abruptly change direction could make it more difficult to resolve Corner displays into shapes.
Experiment 1 tested in simple dot arrays the relations that lead to perception of corners. Experiment 2 used the results of Experiment 1 and showed that in more complex arrays, the quantitative estimate of what angular relation produces corner perception in simple arrays also predicts perception of smooth shapes in more complex ones. Both of these experiments, however, used only subjective measures of smoothness or perception of a shape. Subjective methods have a useful role in perception research. It is important to know what subjects believe they are seeing, and subjective reports shed light on this phenomenological question. Such reports may also, however, be affected by biases or demand characteristics. If the results of Experiments 1 and 2 reflect perception and representation of smooth virtual contours and corners under various conditions, it should be possible to find some objective performance task in which these percepts or representations obtained from perception make participants better or worse in a situation where there is an objectively correct answer (c.f., Kellman et al., 2005). We assessed differences in the degree to which dots sampled from smooth and cornered contours were perceived as shapes using objective measures in Experiments 3 and 4.
Experiment 3
One of the key functions that encoding an abstract shape representation serves is allowing comparison of shapes across different orientations (Baker and Kellman, 2018). In Experiment 3, we compared subjects’ ability to encode a shape representation for dots sampled from smooth and cornered contours by testing them on a shape matching mental rotation task. Inspired by Shepard and Metzler (1971), we simultaneously presented two differently oriented dot arrays and asked subjects to judge whether they defined the same shape. We expected that if dots sampled from smooth contours are more naturally perceived as shapes, subjects should have an advantage in the mental rotation task on trials where the shape is perceived as smooth.
Methods
Participants
Participants included 25 undergraduates (4 male, 21 female, Mage = 19.8) from the University of California, Los Angeles who enrolled in the study for course credit. All participants had normal or corrected-to-normal vision.
Stimuli
Smooth and Corner dot arrays were generated as in Experiment 2. In Experiment 3, each array was a member of a pair with either the same shape or a different shape. When the shape was the same, we used the same virtual contour, but sampled a different set of dots so that local spatial relations between dots could not be used as a cue. When the shapes were different, we generated the second member of the pair by moving one of the control points for the original shape a random distance between 1.93° and 4.11° of visual angle toward or away from the center of the shape. We then randomly selected an adjacent control point to the one we just moved and moved it toward or away from the center such that the total contour length for the new shape was the same as the total contour length for the original shape (see Figure 9 for an example pair). For Corner shapes, we then applied the same set of changes described in Experiment 2 to the new shape. Dot arrays also differed in orientation. In each trial, the second dot array could be rotated 0°, 45°, 90°, 135°, or 180° relative to the first.
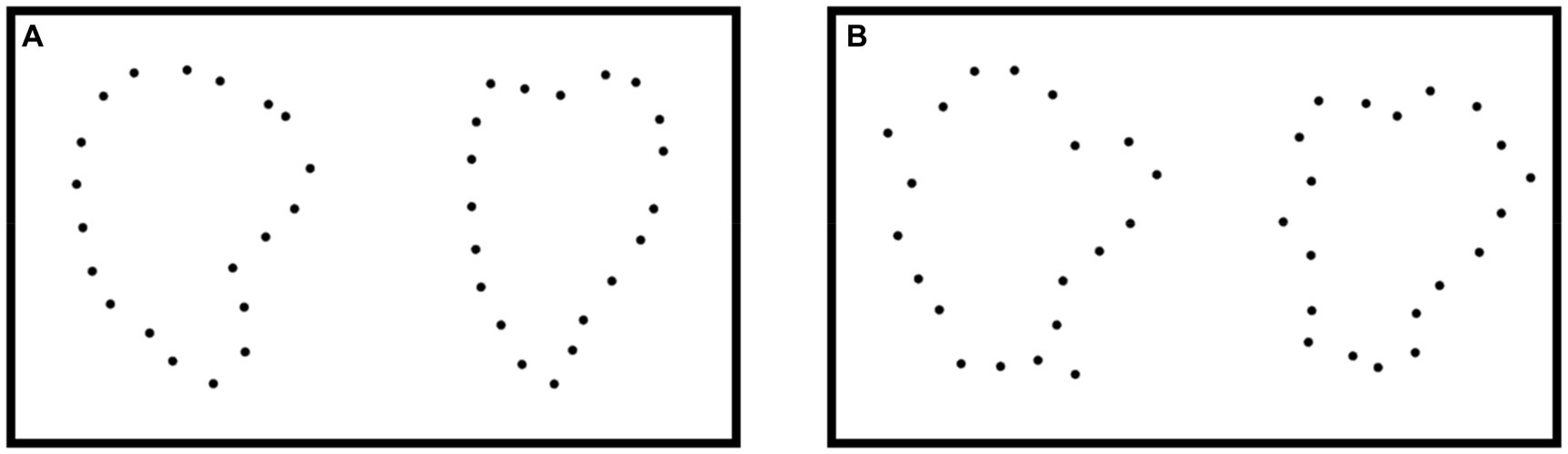
Figure 9. Pairs of smooth and angular shapes used in Experiment 3. (A) A pair of different shapes from the “Smooth” condition. (B) A pair of different shapes from the “Corner” condition.
Design
The experiment consisted of 200 trials, half of which showed shape pairs sampled from smooth virtual contours, and half of which showed shape pairs sampled from cornered contours. For each of these two conditions, there were 20 trials at each of the five magnitudes of rotation, 10 of which included the same shape, and 10 of which included different shapes.
Procedure
On each trial, two arrays of dots were shown on the screen simultaneously, one centered in the left half of the monitor screen, and one centered in the right half. Subjects were instructed to look at both dot arrays and determine whether the shape defined by each array of dots was the same or different, irrespective of a difference in orientation and the local positions of dots. The two dot arrays remained on the screen until subjects responded. Participants were told that response time was being measured, but that they should emphasize responding correctly over responding quickly. Before beginning the main experiment, subjects completed 12 practice trials to familiarize themselves with the task. Performance in the practice trials was not analyzed. A sample trial for each condition is shown in Figure 10.
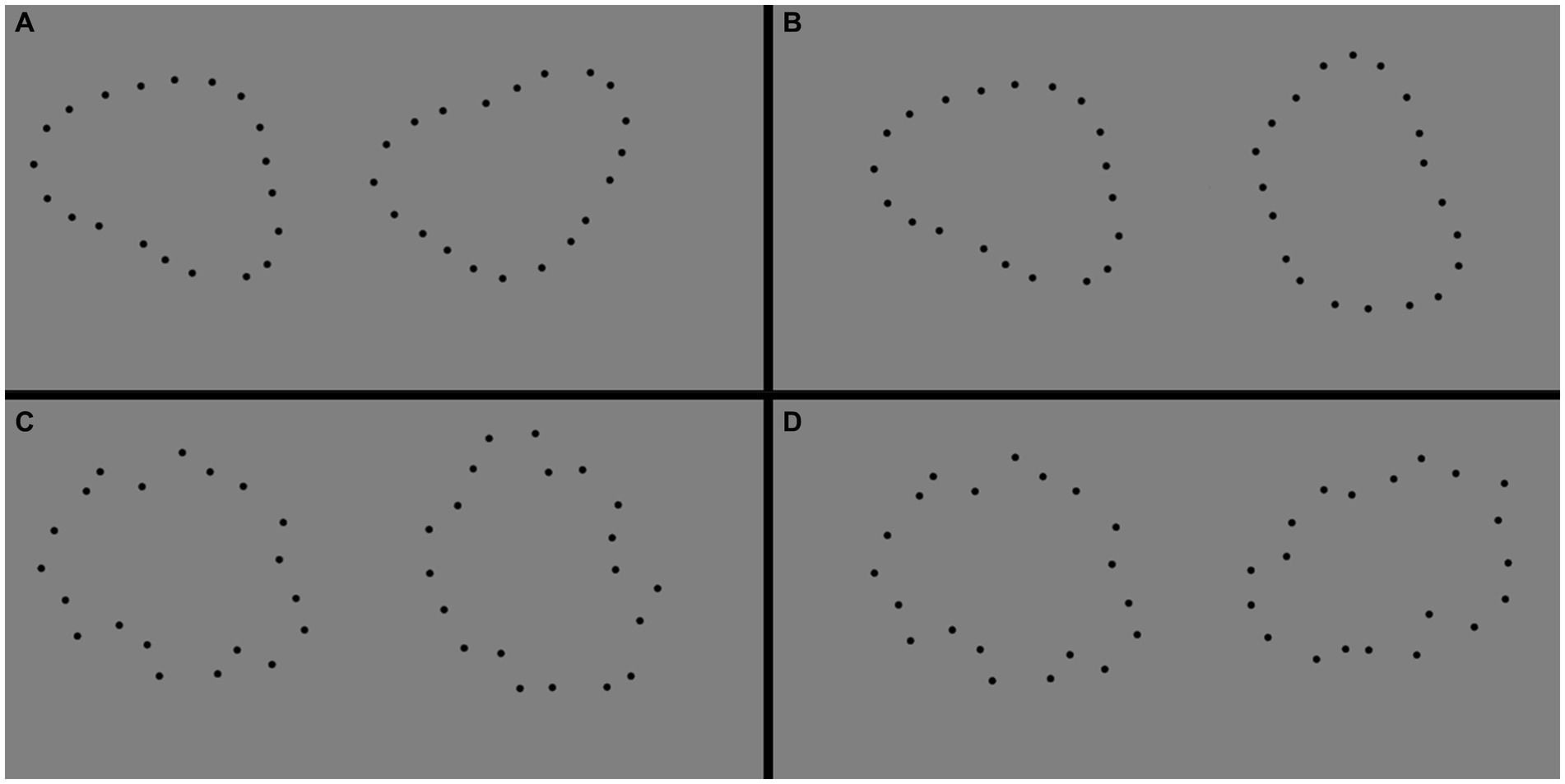
Figure 10. Sample trials from Experiment 3. (A) “Smooth” trials with the same shape. (B) “Smooth” trials with different shape. (C) “Corner” contours with the same shape. (D) “Corner” contours with different shape with different shape. All shapes are rotated 135°.
Results
Following Shepard and Metzler (1971), we analyzed the reaction time only for trials in which the two shapes were the same and subjects responded correctly. Mean response times for each magnitude of rotation are shown in Figure 11A. A 2 (dot array type) × 5 (magnitude of rotation) repeated measures ANOVA confirmed a significant main effect for the type of shape from which the dots were sampled, F(1,25) = 5.33, p = 0.03, η2partial = 0.18 and a significant main effect for magnitude of rotation, F(4,100) = 4.51, p = 0.002, η2partial = 0.15. A linear regression test found a significant overall effect of magnitude of rotation on reaction time, F(1,25) = 14.59, p < 0.001, η2partial = 0.37. The slope was numerically greater for response time as a function of magnitude of rotation for cornered stimuli (RT = 154 * Degrotated + 2056 msec) than for smooth stimuli (RT = 38 * Degrotated + 1,262 msec), although the interaction between condition and magnitude of rotation was not significant, F(4,100) = 0.98, p = 0.42, η2partial = 0.04.
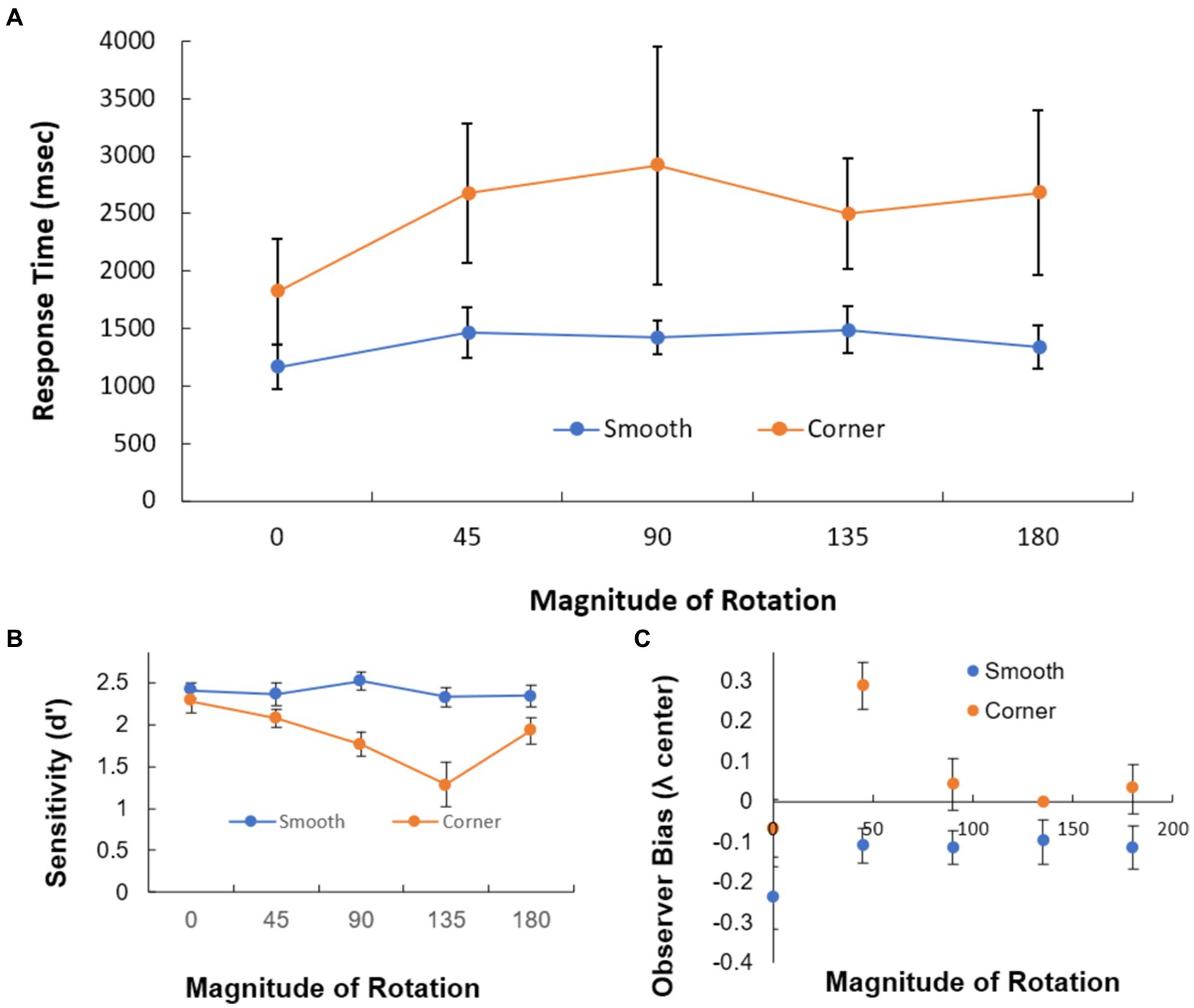
Figure 11. Response time, sensitivity, and bias for “Smooth” and “Corner” trials in the mental rotation task of Experiment 3. (A) Response time on correct trials as a function of orientation difference between the two displays. (B) Sensitivity to shape change. Hits were defined as correct detection of a shape change and false alarms were defined as reports of a shape change when none occurred. (C) Response bias in all conditions. λcenter reflects the distance between the criterion and the midpoint between the signal and noise distributions. Negative values indicate bias to say there was a shape change. Positive values indicate a bias to say there was not a shape change.
Superiority in performance for dots sampled from smooth contours was also reflected in sensitivity measures, calculated as the proportion of trials in which participants correctly reported that the shape had changed (“hits”) vs. the proportion of trials in which participants incorrectly reported that the shape had changed (“false alarms”; Figure 11B). In trials with no misses or no false alarms, we used the correction recommended by Wickens (2001) of adding half an observation of a miss or false alarm when none was present. A 2 (dot array type) × 5 (magnitude of rotation) repeated measures ANOVA confirmed that sensitivity was significantly higher in displays in which the dots were sampled from smooth contours than displays with dots sampled from contours with sharp corners F(1,24) = 29.36, p < 0.001, η2partial = 0.55. The effect of magnitude of rotation on sensitivity was also significant, F(4,96) = 4.90, p = 0.001, η2partial = 0.17, as was the interaction between dot array type and angle, F(4,96) = 4.51, p = 0.002, η2partial = 0.16.
We also compared participants’ bias to report a shape change in each of the 10 conditions. We computed bias as λcenter, or the distance between the criterion and the midpoint between the signal and noise distribution. Values of λcenter less than 0 indicate a bias to respond “yes” to a shape change and values of λcenter greater than 0 indicate a bias to respond “no.” The estimates of bias for each condition are plotted in Figure 11C. A repeated measures ANOVA on the estimates of bias found a significant main effect for dot array type on participants’ bias, F(1,24) = 19.36, p < 0.001, η2partial = 0.45. Participants were more biased to report a shape change in the smooth condition and more biased to report no shape change in the corner condition. There was also a significant main effect for magnitude of rotation on participants’ bias [F(4,96) = 5.89, p < 0.001, η2partial = 0.20]. There was no significant interaction between dot array type and magnitude of rotation on observer bias, F(4,96) = 2.23, p = 0.07, η2partial = 0.09.
Discussion
Experiment 2 found that participants rated dots sampled from contours with cornered contours as less shape-like than dots sampled from smooth curves. In Experiment 3, we tested whether these subjective differences would be reflected in an objective measure of perceptual performance. Because they were rotated and had positions along the contour resampled, the target pairs of dot arrays we showed in Experiment 3 differed from each other both in absolute orientation and in terms of the specific positions of the elements with respect to each other. Accurate responding for the task therefore required forming a representation of a shape’s contour from the set of dots that was object-centric and invariant to orientation changes (Baker and Kellman, 2018). Differences in response time and/or sensitivity for the two kinds of dot arrays therefore presumably correspond to the ease with which participants encoded the array as a shape.
We found that dots sampled from shapes with smooth contours could be compared across orientation changes more quickly than dots sampled from shapes with perceived corners, which suggests that these dot arrays are more easily encoded and perceived as orientation-invariant shapes than arrays sampled from shapes with corners. Participants were less accurate when mentally rotating dots sampled from smooth contours than dots sampled from cornered contours. Lower response times therefore cannot be explained by a speed-accuracy tradeoff.
One puzzling aspect of our data is that we found only a small effect of magnitude of orientation difference for the two shapes in each display on response time for either trial type. Slopes in both conditions were flat and explained a smaller proportion of the variance than the Smooth vs. Corner manipulation. The work of Shepard and Metzler (1971), after which we modeled our experiment, showed a strong linear relationship between response time and magnitude of rotation for shapes rotated in the picture plane. Response time has also been shown to vary with degree of change from a canonical orientation in naming tasks for familiar objects (Jolicoeur, 1985). One possibility for why angular difference had such a small effect in our study is that subjects responded after a somewhat fixed period of time, even if more or less time was needed to make an accurate decision. This could explain why we see a reduction in sensitivity as a function of magnitude of rotation in the sharp corner condition even though response time does not increase. Importantly, though, even if subjects are using a more fixed period of time, this amount of time is different for the smooth and corner conditions. Participants consistently required more time to decide if dot displays sampled from shapes with sharp corners were the same or different, even if response times did not increase monotonically with orientation differences in either condition.
Another intriguing possibility is that dot configurations represent a special class of stimuli whose time for recognition does not scale with magnitude of rotation. Past work on mental rotation has shown that certain kinds of stimuli with salient landmark features have much flatter recognition slopes than stimuli without salient landmarks (Hochberg and Gellman, 1977). Flat slopes have also been found for familiar objects when participants were informed ahead of time what object they would be shown (Cooper and Shepard, 1973). Why mental rotation of dot patterns would have flat slopes is mysterious in view of these findings, as they are neither familiar nor do they have salient local features. In fact, any salient local feature obtained from a local group of dots in one of the arrays would not be present in the other matching array, since dot positions along the contour are independently sampled in matched pairs. One possibility is that the simplicity of dot arrays gives rise to flat mental rotation slopes. According to Hochberg and Gellman (1977), mental rotation of shapes will scale with angular distance if representations must be built up from successive glances. Possibly, the relatively few bits of information in an array of 25 dots can be extracted with only one glance. This is partially supported by previous findings that the spatial positions of an array of 25 dots are registered within the first 30 ms of exposure (Baker and Kellman, 2018).
Experiment 4
As we have discussed, the visual system has a remarkable capacity to form contour representations from unconnected dots. In Experiment 4, we further tested these capabilities by showing dot displays embedded among a field of random noise dots. The experimental paradigm was similar to one devised by Uttal (1973) for dots along a curved or straight line segment. Uttal found that for these simple segments, participants had significantly more trouble detecting the target when it deviated more from a straight line, but there seemed to be little difference for angular vs. curvilinear deviations. In the present study, we tested participants’ ability to detect whole forms defined by dots.
To do this, we used a two-interval forced choice (2IFC) paradigm in which one stimulus contained a shape embedded in noise and the other stimulus contained noise alone. Participants’ task was to choose the interval that contained a coherent shape. In order to group together and detect the shape of a set of dots in noise, subjects would have to first use some spatial relationships between the dots in the array to identify which dots belonged to a shape outline and which were random. Typically, important cues such as proximity could be potentially misleading for this kind of display. Manipulating the kind of shape contour that the target dots were sampled from, we tested participants’ ability to decide which of the two intervals contained a shape and which consisted only of noise dots. We predicted that unlike simple segments, dot arrays sampled from whole shapes with smooth contours would be more easily detected than dots sampled from whole shapes with sharp corners.
Methods
Participants
Twenty-six undergraduates (6 male, 20 female, Mage = 21.6) from the University of California, Los Angeles participated in this study for course credit. All participants had normal or corrected-to-normal vision. One subject’s data was excluded prior to analyzing his results because he did not appear to understand the instructions by the time he had finished the practice portion of the experiment.
Stimuli
Dot arrays from smooth and cornered shape contours were generated as in Experiment 1. In Experiment 4, however, the dots sampled from contours were hidden among 25 distractor dots. Distractor dots were created by uniformly sampling from the rectangular area that contained the target dots. Each trial also included a dot display with no shape. Rather than placing all 50 dots in the other display completely randomly, we created random displays of 25 dots as in Experiment 1, with the only difference being that we moved each dot twice the average distance between dots. This was to create displays with no shape that still had some emptiness in the middle of the array to prevent participants from using that as a low-level cue. We then added 25 dots by uniformly sampling from the encompassing rectangle as in the target displays. Figure 12 shows a target display with dots from a smooth contour, a target display with dots from a corner contour, and a non-target display.
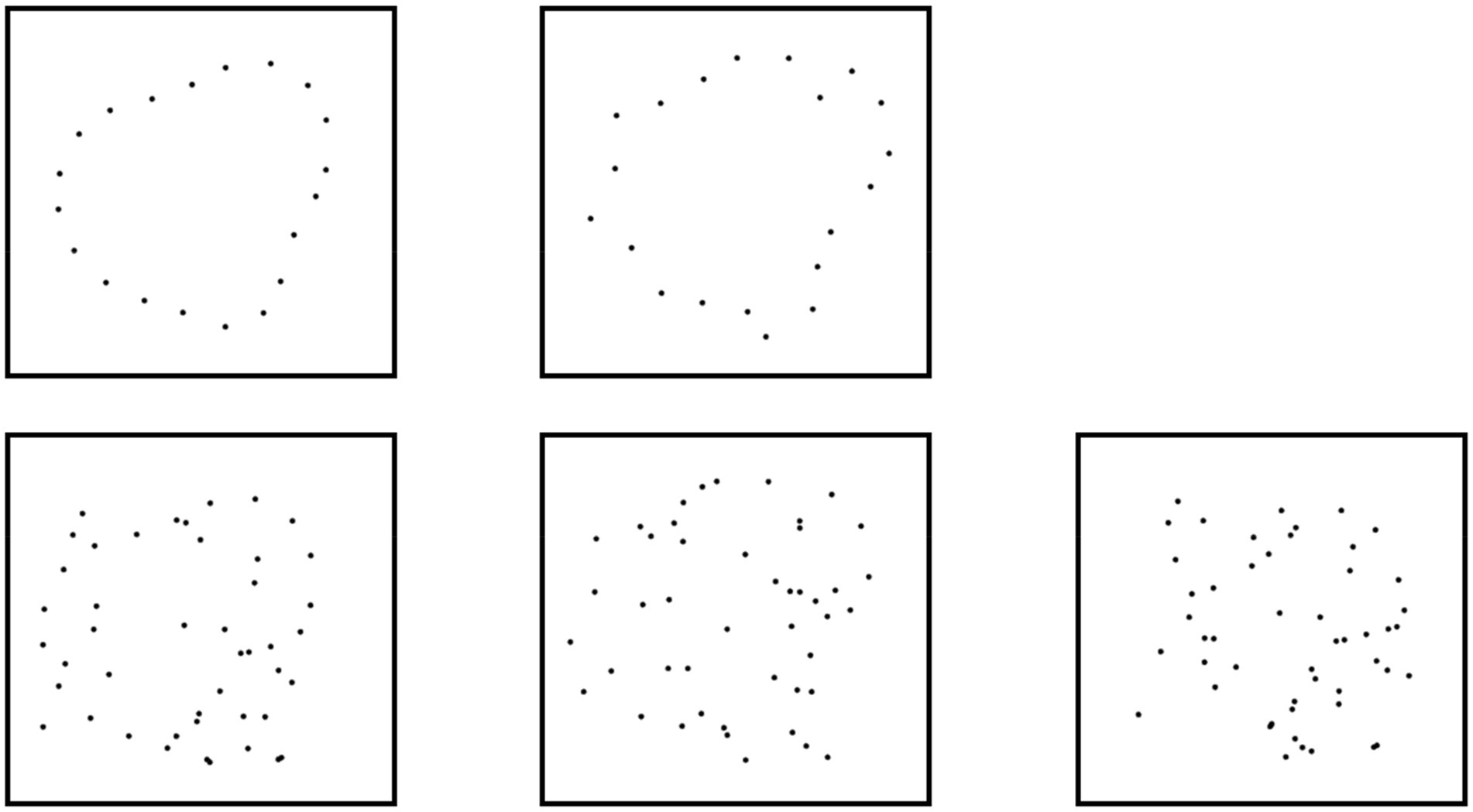
Figure 12. Target and distractor displays for Experiment 3. The leftmost column shows a smooth target without (top) and with (bottom) distractor dots added. The middle column shows a cornered target without (top) and with (bottom) distractor dots added. The rightmost column shows a non-target display. In each trial, one of the two kinds of target display (with distractor dots) and the distractor display were presented in a randomized order.
Design
The experiment had two conditions, a Smooth condition, in which the target dots were sampled from a smooth contour, and a Corner condition, in which the target dots were sampled from a corner contour. For both conditions, the target display was shown first in half of the trials second in the other half. There were 120 total trials for each condition. Participants completed 12 practice trials before beginning the main experiment.
Procedure
We used a 2IFC task in which one display consisted of dots sampled from a smooth or cornered contour among noise dots and the other display consisted only of noise dots. Before beginning the experiment, subjects were told they would be looking for shapes hidden in dots. We showed participants 20 (10 Smooth, 10 Corner) examples of the kind of targets they would be asked to detect in the main experiment. The example targets were shown without distractors.
In each trial, we first presented a fixation cross at the center of the screen for 600 ms, then showed the first of the two dot displays for 800 ms. The dot display was then masked by a pattern of black and white dots for 500 ms, after which the second dot display was shown, also for 800 ms. This display was masked for 500 ms, and then subjects were asked to report whether a shape was hidden in the first or second of the two dot displays. Subjects were not cued to look for any specific shape in the displays and were told to pick whichever one they thought had dot arrangements that contained any shape. During practice, subjects were given feedback telling them if they were correct or incorrect and showing the hidden shape highlighted in white dots. No feedback was given during the main experiment. A sample trial from the Smooth and Corner condition are shown in Figure 13.
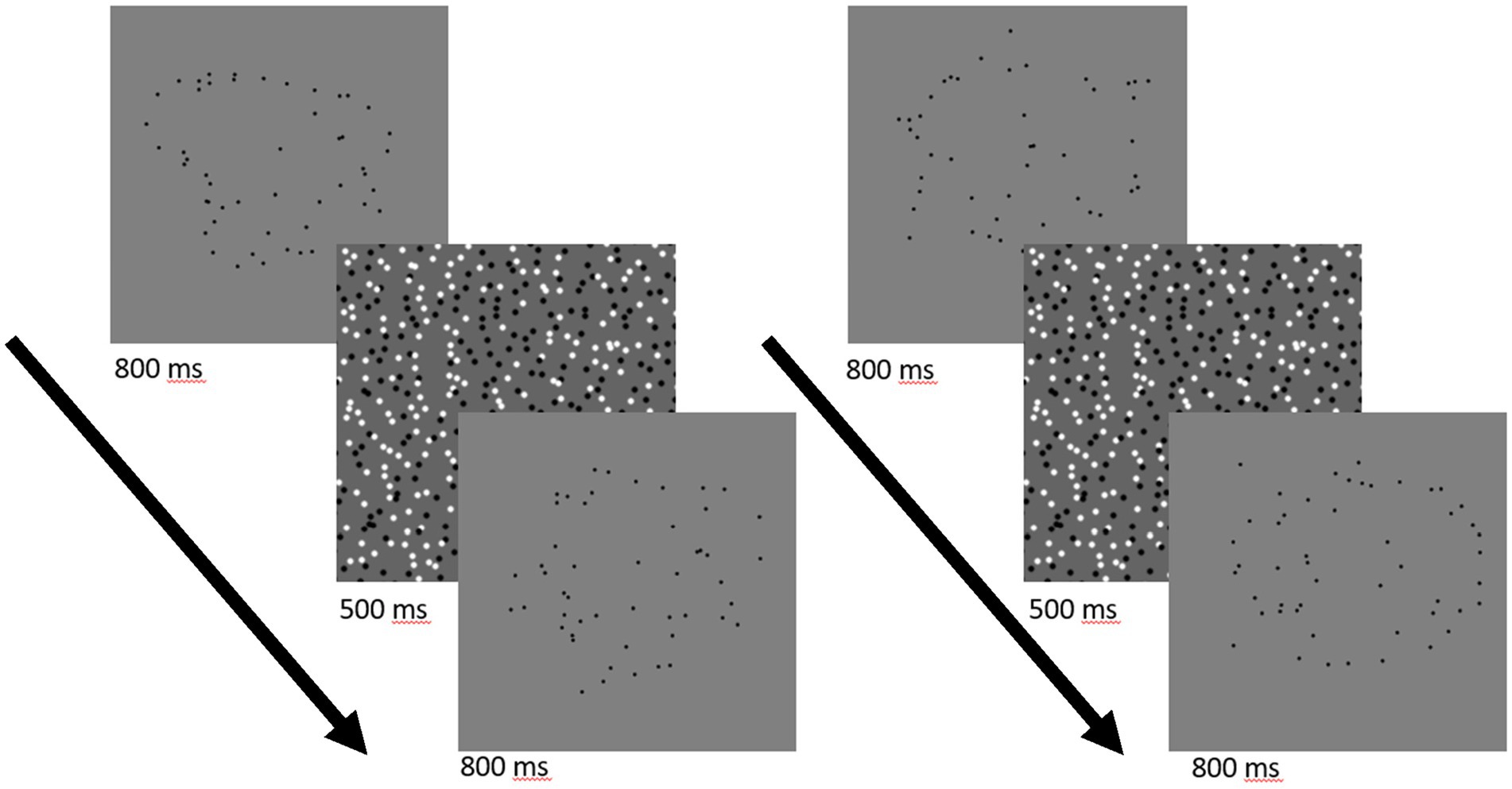
Figure 13. Sample trials from Experiment 4. The target shape is sampled from a smooth contour and is shown first (left). The target shape is sampled from an cornered contour and is shown second (right).
Results
The primary results for Experiment 4 are shown in Figure 14. Performance was significantly better than chance both when the dots were sampled from a smooth contour [t(24) 17.59, p < 0.001] and when they were sampled from an cornered contour [t(24) = 15.69, p < 0.001]. Participants were significantly better at detecting the target shape when the dots were sampled from a smooth contour than when they were sampled from a corner contour [t(24) = 10.3, p < 0.001, Cohen’s d = 2.05].
Discussion
The results of Experiment 4 show that dot displays embedded in noise were more detectable as shapes when they had been sampled form smooth contours than from cornered ones. In turn, these designations (“smooth” vs. “cornered”) were derived from perceptual responses in Experiment 1 (and in prior work by other investigators) to simple dot arrays, consisting of as few as three elements. The superior detection of shapes in noise for the Smooth condition here indicates that these more elementary responses to local dot configurations influence perceptual performance in an objective performance task, and they provide evidence that smooth shapes are more readily encoded from sampled dots. What is required to extract a shape in this task? Surely, relations among elements are crucial, but the task is made more challenging by the fact that the dot elements comprising a shape were physically identical to the distractor dots. The local spatial relationships between small groups of target dots are also not different from relationships between groups of distractor dots or groups that are a mix of targets and distractors. We might compare shape or contour detection to the path detection task developed by Field et al. (1993), which is similar in concept. A crucial difference, however, is that in conventional path detection, individual oriented elements are used, either Gabor patches (Field et al., 1993) or line segments (Pettet, 1999; Baker et al., 2021). In these cases, local orientation relationships described as contour relatability (Kellman and Shipley, 1991) or an association field (Field et al., 1993) are the primary drivers of path detection. Local orientation relationships between the dots determine whether the path is detected depending on the relatability of the local elements. The perceptual salience of paths likely depends on a contour-linking process that produces an intermediate representation in the process of contour interpolation (Kellman et al., 2016; Kellman and Fuchser, 2023).
The situation is different in our Experiment 4. Individual circular dots have no orientation from which relatability can be defined. Unlike the targets used by Uttal (1973), the local spatial relationships between target dots are not consistent. Neither the spacing nor the turning angle is the same between nearby dot triplets in our displays. Detection of the target in our task must depend on more global relations among dots. The visual system might be considering multiple possible dot organizations and determining whether they configure into a global shape. Or, somewhat more local relations among small sets of dots may allow discovery of an extended virtual contour that is perceivable as smooth all along its extent.
Participants’ good performance for target dots sampled from both smooth and corner contours suggests that the visual system has a quite robust capability to detect a variety of shapes from distractors. However, there is also a clear performance advantage for detection of shapes with smooth contours over detection of cornered shapes. If detection of perceptually smooth sequences of dots underlies shape detection, dots sampled from smooth shapes exhibit this property along their entire contour, whereas sets of dots perceived as cornered may interrupt perceptual continuity. We develop this idea more fully in the General discussion below.
The perceptual continuity for dots sampled from smooth shapes may also lead to simpler representations than sets of dots sampled from shapes with sharp corners. If first-order discontinuities serve to mark separate parts, or simply indicate important features to be represented, cornered shapes may have more complex representations than smooth ones. Detection of potential connected shapes may be facilitated more by perceptually smooth relations among dots than dot sequences that are more representationally complex in terms of containing corners connecting shorter smooth segments. A similar effect and explanation have been given for search for constant curvature vs. non-constant curvature targets formed by oriented elements (Baker et al., 2021).
General discussion
Perception of contours and shapes from arrangements of separated dots or other tokens is commonplace yet remarkable. Our overall goal in this research was to understand how spatial relations among dots create perceived contours and shapes, and to connect this understanding to general processes of shape perception and representation. Perception of shape from dots offers a special window into abstract shape representations in general. Because no continuous contour is physically present in a display consisting of separated dots, evidence from perceptual tasks that implicates connection, continuity, smoothness, or shape in perceptual representations reveals contributions of processes not directly attributable to the physical stimulus.
In the experiments reported here, we first tested perception of smooth connections vs. corners in small arrays of dots—triplets, or triplets with two additional flanking dots. The results of Experiment 1 indicated that for triplets alone and those with flanking dots that created concave arms, angles relating the triplet dots below 150°–160° more often produced “corner” responses, and “smooth” responses were very rare for angles less than 100°. With flanking dots that continued the convexity of a triplet, smoothness responses were preserved through a greater angular range, with parity between “smooth” and “corner” responses occurring at about 78°.
Based on these findings of smoothness vs. corner perception determined with small arrays and local angular relations, we tested in further experiments the impact of local relations that were smooth (with triplet angles averaging 154°) vs. cornered (78°–90°) in more complex arrays. In Experiment 2 we compared participants’ perception of 25-dot arrays sampled from angular contours with dot arrays sampled from smooth contours. Participants’ subjective ratings revealed that dots sampled from smooth shapes were more often and more strongly perceived as coherent shapes than dots sampled from angular shapes. In Experiment 3, we used an objective performance paradigm to assess the effects of local dot relations in processing forms; participants judged as same or different two dot arrays that differed in orientation. We hypothesized that this task would be done, as in classic experiments, by participants mentally rotating one an array to match the orientation of the other, with the expectation that comparison of two dot arrays in this manner would be easier for dot arrangements that were more easily encoded as shapes. We found that participants judged that two dot arrays were the same more quickly and more accurately when they were sampled from smooth contours. In Experiment 4, we embedded a target arrangement of dots defining a virtual contour among an equal number of distractor dots. We found that subjects were more able to detect smooth virtual contours than angular virtual contours, likely because the shape representation the dots give rise to is simpler and therefore easier to search (see Baker et al., 2021 for a similar paradigm).
The results of both Experiments 3 and 4 extend previous research into the perception of dot arrays with a very small number of dots (Pomerantz and Portillo, 2011; Hawkins et al., 2016; Costa and Wagemans, 2021). In those experiments, the configural superiority effect (CSE) paradigm was used to show that an odd-one-out task could be facilitated by the addition of identical elements provided those elements resulted in different emergent features like orientation or proximity in the target display than the distractors. Though the stimuli we used consisted of many more elements than the CSE displays, curvilinear displays were perceived as more configural than displays that contained perceived corners. Experiments 3 and 4 also introduce two additional experimental paradigms, mental rotation and object detection, that can be used as objective indices of the strength of configural structure of dot arrays. The CSE task works extremely well for arrays with a small number of elements to test the effect of local relations between dots. The rotation and detection tasks we used would not work for such sparse displays but showed robust effects for differences in the perception of shape defined by a larger set of elements.
Other research into the organization of dot elements based on Gestalt cues may also explain the perceptual advantage for dot arrays perceived to be curvilinear. For example, notions of similarity might explain why smooth displays, whose vertices were uniformly perceived as curved are more easily perceived as shapes than corner displays, whose vertices would be inhomogeneous, consisting of both perceived curves and perceived corners. Note, however, that these descriptions of inhomogeneity, while related to certain stimulus properties, refer most directly to outcomes of perception (i.e., properties in perceptual representations). The dots in and of themselves are neither corners nor smooth curves. Certain theories of good continuation also predict that smoothness among adjacent pairs or triplets of dots in a sequence facilitates contour perception. According to these theories (e.g., Feldman, 1997; Pizlo et al., 1997; Lezama et al., 2016; Kelly et al., 2024), continuation would be better in displays with fewer extreme deviations from smooth continuation that comes with the addition of perceived corners, which could result in arrays that are more easily resolved into shapes. Definitions of good continuation that explicitly favor collinearity of dots (e.g., Uttal, 1973; van den Berg, 2006) would make the opposite prediction that continuation would be better in corner displays, which have more collinear dots.
Greater facility in encoding shapes with fewer corners and more curvilinear segments would also not be predicted by many other theories of shape and object perception. Much work in middle and high-level vision emphasizes the importance of junctions and non-accidental properties. Geons in Biederman’s (1987) work depend crucially on corners and junctions, for example. Under such a theory, we would expect the visual system to be particularly suited to the detection of corners. Indeed, neurophysiological work points to the importance of corners in early visual areas (Heitger et al., 1998) and angular cusps in V4 (Pasupathy and Connor, 2001). Information theoretical work on contour complexity also predicts that objects with straight edges will be perceptually simpler (Attneave, 1954; Norman et al., 2001; Feldman and Singh, 2005). Structural information theory makes the same prediction, positing straight line connections between dots are more economical than curvilinear arcs because arcs are a continuation of both length and angle, thus requiring two bits of information for every one bit of information required for straight line connections (Smits and Vos, 1987, personal communication with Leeuwenberg).
Why, then, are shapes with smooth contours easier to encode than shapes with sharp corners? As Bertamini et al. (2019) point out, there are several reasons to expect angular contours would be more easily processed. Angular contours are comparatively simple to compute, requiring only linear interpolation between salient key points of high curvature (Bertamini et al., 2013). There may also be evolutionary advantages to registering the shapes of angular contours quickly to assess danger (Bar and Neta, 2006). On the other hand, the evolutionary environment in which our visual system evolved likely had many fewer straight edges and sharp angles than the one in which we currently live. Even today, research on scene statistics has found that many of the contours people process in their daily lives are made up of smooth curves (Chow et al., 2002). An analysis of scene statistics can only take us so far, however. The visual system may have evolved to process smooth contours because there were more objects made from smooth contours in our visual environment, but we must still determine what specific visual mechanisms confer this advantage in perceptual processing.
One possibility is that the primitives from which the visual system builds abstract shape representations more easily describe a shape with smooth contours. Elsewhere, we have hypothesized that shape representations are built up from relatively few smoothly joined segments of constant curvature (Garrigan and Kellman, 2011; Kellman et al., 2013; Baker et al., 2021; Baker and Kellman, 2021). Under this theory, corners (first-order or tangent discontinuities) have two important consequences. One is that the presence of a corner would always require spans on either side to be two segment primitives, whereas smoothly changing curvature could be captured by a single segment, provided that the variation in curvature was sufficiently small. The other consequence is that corners need to be separately encoded in such a representation and may be taken as part boundaries at a certain basic level of representation.
Even when part of a smooth contour requires multiple constant curvature primitives, the smoothly joined segments tend to be perceived as belonging to a single part if they are smooth and monotonic. For example, consider Figures 15A,B. Both displays are made up of two different curvature segments, but the fragment made from two smoothly joined curves looks like a single token, while the fragment made from two straight segments does not.
Figure 15. Contours made up of more than one curvature segment. (A) A contour made up of two smoothly joined constant curvature segments. (B) A contour made up of two straight segments joined at a vertex. (C) A contour made up of two smoothly joined constant curvature segments and one straight segment joined at a vertex. Individual parts are marked by letters A, B, or C. (D,E) Displays show examples redrawn from Wertheimer (1923), corresponding to his Figures 8 and 11, respectively. (F) Illustration of the role of perceived corners in dot displays in determining segmentation. Redrawn from Wertheimer (1923), Figure 3.
This observation is closely related to analyses by Wertheimer (1923) in his classic work “Laws of Organization in Perceptual Forms,” and it underlies his description of what has come to be called “good continuation.” He showed contour displays similar to the ones in Figure 15D and asked observers to divide them into two parts, finding that they almost always organized the two smoothly joined curvature pieces together, separating this connected segment from the straight segment. In terms of derivatives, we may consider any continuous (unbroken) contour to have zero order continuity. Wertheimer’s examples show that, despite zero-order continuity, a 1st-order or tangent discontinuity (undefined first derivative) produces some degree of perceptual segmentation. Figure 15E shows another of his examples; here, we can consider 4 segments, A, B, C, and D, and the perceptual impression is that A and C are a unified segment, as are B and D, but observers do not naturally partition such a display into BC and AD, or AB and CD. Although Wertheimer did not invoke presence or absence of discontinuities in the first derivative as the relevant information, he gave a number of examples (in his Figures 1–19), all of which indicate that a contour junction (tangent discontinuity) breaks contiguous line drawings into discernible parts, whereas the smooth continuation (absence of a tangent discontinuity) produces perception of a single contour or contour segment. It is interesting that despite offering two formal names for this principle (the “Factor of Direction” and the “Factor of Good Curve”), it is a phrase he used in passing—“good continuation” that has stuck as the name of this principle.
Figures 15A,C also illustrate that higher-order discontinuities, such as the 2nd-order discontinuity where two curves different smoothly join (matched slope at the join point), do not produce obvious perceptual segmentation. Evidence from visual search in noise shows that search for a contour segment with a 0-order or first-order discontinuity from other segments is easy, but a segment having 0-order and first-order continuity, but a second-order discontinuity, is effortful, slow, and error-prone (Kellman et al., 2003). If shapes made up of sharp corners are perceived to have significantly more parts than shapes made up of smoothly connected contours, it follows that they will be more representationally complex and therefore more difficult to encode.
Consistent with the above reasons that sharp corners may impose an additional encoding burden is that corners are important features for other perceptual processing goals, such as identifying points at which one object might be occluding another (Ratoosh, 1949; Dinnerstein and Wertheimer, 1957; Shipley and Kellman, 1990; Kellman and Shipley, 1991; Rubin, 2001). Also, as we mentioned earlier, corners are important in theories of object representation and recognition (e.g., Biederman, 1987). Although some of these accounts suggest that encoding of corners might be beneficial for comparing objects, it may increase the complexity relative to smooth objects.
Conclusion
The results from these experiments suggest that the visual system perceives shapes from arrays of dots more easily when the perceived contour between the points is smooth rather than angular. Although consistent with previous literature concerning good continuation between dots, these findings refute other formulations of good continuation that explicitly favor linear continuations. They also point to a more general phenomenon in shape perception that extraction of curvature is a fundamental process in the formation of an abstract shape representation and allows for efficient encoding of contours with changing orientation. Virtual contours that can be described by a relatively constrained set of curvature primitives appear to give rise to shapes more often, more quickly, and more precisely than virtual contours that are perceived and represented as segments connected by corners.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: DOI: 10.17605/OSF.IO/7DGJC.
Ethics statement
The studies involving humans were approved by IRB University of California, Los Angeles. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
NB: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. PK: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. We gratefully acknowledge support from the National Institutes of Health award number R01 CA236791 to PK.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Attneave, F. (1954). Some informational aspects of visual perception. Psychol. Rev. 61, 183–193. doi: 10.1037/h0054663
Baker, N., Garrigan, P., and Kellman, P. J. (2021). Constant curvature segments as building blocks of 2D shape representation. J. Exp. Psychol. Gen. 150, 1556–1580. doi: 10.1037/xge0001007
Baker, N., and Kellman, P. J. (2018). Abstract shape representation in human visual perception. J. Exp. Psychol. Gen. 147, 1295–1308. doi: 10.1037/xge0000409
Baker, N., and Kellman, P. J. (2021). Constant curvature modeling of abstract shape representation. PLoS One 16:e0254719. doi: 10.1371/journal.pone.0254719
Bar, M., and Neta, M. (2006). Humans prefer curved visual objects. Psychol. Sci. 17, 645–648. doi: 10.1111/j.1467-9280.2006.01759.x
Barsalou, L. W. (2003). Situated simulation in the human conceptual system. Language and cognitive processes. 18, 513–562.
Bertamini, M., Helmy, M., and Bates, D. (2013). The visual system prioritizes locations near corners of surfaces (not just locations near a corner). Atten. Percept. Psychophys. 75, 1748–1760. doi: 10.3758/s13414-013-0514-1
Bertamini, M., Palumbo, L., and Redies, C. (2019). An advantage for smooth compared with angular contours in the speed of processing shape. J. Exp. Psychol. Hum. Percept. Perform. 45, 1304–1318. doi: 10.1037/xhp0000669
Biederman, I. (1987). Recognition-by-components: a theory of human image understanding. Psychol. Rev. 94, 115–147. doi: 10.1037/0033-295X.94.2.115
Bouma, H. (1976). Perceptual functions. In J. A. Michon, E. G. Eijkman, and L. F. KlerkDe. Dutch handbook of psychonomy (pp. 229–287). Deventer, Netherlands: Van Loghem Slaterus (in Dutch).
Box, G. E., and Cox, D. R. (1964). An analysis of transformations. Journal of the Royal Statistical Society Series B: Statistical Methodology. 26, 211–243.
Chow, C. C., Jin, D. Z., and Treves, A. (2002). Is the world full of circles? J. Vis. 2:4. doi: 10.1167/2.8.4
Cooper, L. A., and Shepard, R. N. (1973). “Chronometric studies of the rotation of mental images” in Visual information processing. ed. Chase W. G. (New York: Academic Press), 75–176.
Costa, T. L., and Wagemans, J. (2021). Gestalts at threshold could reveal gestalts as predictions. Sci. Rep. 11:18308. doi: 10.1038/s41598-021-97878-0
De Winter, J., and Wagemans, J. (2008). Perceptual saliency of points along the contour of everyday objects: a large-scale study. Percept. Psychophys. 70, 50–64. doi: 10.3758/PP.70.1.50
Dinnerstein, D., and Wertheimer, M. (1957). Some determinants of phenomenal overlapping. Am. J. Psychol. 70, 21–37. doi: 10.2307/1419226
Feldman, J. (1996). Regularity vs genericity in the perception of collinearity. Perception 25, 335–342. doi: 10.1068/p250335
Feldman, J. (1997). Curvilinearity, covariance, and regularity in perceptual groups. Vision Res. 37, 2835–2848. doi: 10.1016/S0042-6989(97)00096-5
Feldman, J., and Singh, M. (2005). Information along contours and object boundaries. Psychol. Rev. 112, 243–252. doi: 10.1037/0033-295X.112.1.243
Field, D. J., Hayes, A., and Hess, R. F. (1993). Contour integration by the human visual system: evidence for a local “association field”. Vision Res. 33, 173–193. doi: 10.1016/0042-6989(93)90156-Q
Garrigan, P., and Kellman, P. J. (2011). The role of constant curvature in 2-D contour shape representations. Perception 40, 1290–1308. doi: 10.1068/p6970
Hawkins, R. X., Houpt, J. W., Eidels, A., and Townsend, J. T. (2016). Can two dots form a gestalt? Measuring emergent features with the capacity coefficient. Vision Res. 126, 19–33. doi: 10.1016/j.visres.2015.04.019
Heitger, F., Von Der Heydt, R., Peterhans, E., Rosenthaler, L., and Kübler, O. (1998). Simulation of neural contour mechanisms: representing anomalous contours. Image Vis. Comput. 16, 407–421. doi: 10.1016/S0262-8856(97)00083-8
Hess, R., and Field, D. (1999). Integration of contours: new insights. Trends Cogn. Sci. 3, 480–486. doi: 10.1016/S1364-6613(99)01410-2
Hochberg, J., and Gellman, L. (1977). The effect of landmark features on mental rotation times. Mem. Cognit. 5, 23–26. doi: 10.3758/BF03209187
Jolicoeur, P. (1985). The time to name disoriented natural objects. Mem. Cognit. 13, 289–303. doi: 10.3758/BF03202498
Kalar, D. J., Garrigan, P., Wickens, T. D., Hilger, J. D., and Kellman, P. J. (2010). A unified model of illusory and occluded contour interpolation. Vision Res. 50, 284–299. doi: 10.1016/j.visres.2009.10.011
Kellman, P., Erlikhman, G., and Carrigan, S. (2016). Is there a common mechanism for path integration and illusory contour formation? J. Vis. 16:311. doi: 10.1167/16.12.311
Kellman, P. J., and Fuchser, V. (2023). Visual completion and intermediate. Sensory Individuals: Unimodal and Multimodal Perspectives, 55.
Kellman, P. J., and Massey, C. M. (2013). “Perceptual learning, cognition, and expertise,” in The psychology of learning and motivatio. (Ed.) S. J. Dickinson and Z. Pizlo, Vol. 58, (Amsterdam: Elsevier Inc.), 117–165.
Kellman, P. J., Garrigan, P. B., Kalar, D., and Shipley, T. F. (2003). Good continuation and relatability: related but distinct principles. J. Vis. 3:120. doi: 10.1167/3.9.120
Kellman, P. J., Garrigan, P., Shipley, T. F., Yin, C., and Machado, L. (2005). 3-d interpolation in object perception: evidence from an objective performance paradigm. J. Exp. Psychol. Hum. Percept. Perform. 31, 558–583. doi: 10.1037/0096-1523.31.3.558
Kellman, P. J., and Shipley, T. F. (1991). A theory of visual interpolation in object perception. Cogn. Psychol. 23, 141–221. doi: 10.1016/0010-0285(91)90009-D
Kelly, B. A., Kemp, C., Little, D. R., Hamacher, D., and Cropper, S. J. (2024). Visual perception principles in constellation creation. Top. Cogn. Sci. 16, 25–37. doi: 10.1111/tops.12720
Kemp, C., Hamacher, D. W., Little, D. R., and Cropper, S. J. (2022). Perceptual grouping explains similarities in constellations across cultures. Psychol. Sci. 33, 354–363. doi: 10.1177/09567976211044157
Koffka, K. (1931). “Psychology of visual perception” in Handbook of normal and pathological physiology. ed. A. Bethe (Berlin: Dessoir), 1215–1271.
Krzywinski, M., and Altman, N. (2014). Visualizing samples with box plots. Nat. Methods 11, 119–120. doi: 10.1038/nmeth.2813
Kubovy, M., and Wagemans, J. (1995). Grouping by proximity and multistability in dot lattices: a quantitative gestalt theory. Psychol. Sci. 6, 225–234. doi: 10.1111/j.1467-9280.1995.tb00597.x
Leek, M. R. (2001). Adaptive procedures in psychophysical research. Percept. Psychophys. 63, 1279–1292. doi: 10.3758/BF03194543
Lezama, J., Randall, G., Morel, J. M., and von Gioi, R. G. (2016). Good continuation in dot patterns: a quantitative approach based on local symmetry and non-accidentalness. Vision Res. 126, 183–191. doi: 10.1016/j.visres.2015.09.004
McGill, R., Tukey, J. W., and Larsen, W. A. (1978). Variations of box plots. Am. Stat. 32, 12–16. doi: 10.1080/00031305.1978.10479236
Norman, J. F., Phillips, F., and Ross, H. E. (2001). Information concentration along the boundary contours of naturally shaped solid objects. Perception 30, 1285–1294. doi: 10.1068/p3272
O'Callaghan, J. F. (1974). Computing the perceptual boundaries of dot patterns. Comput Graph Image Process 3, 141–162. doi: 10.1016/S0146-664X(74)80004-3
Papari, G., and Petkov, N. (2005). “Algorithm that mimics human perceptual grouping of dot patterns” in International symposium on brain, vision, and artificial intelligence. (Eds.) Gregorio, M. D., Frucci, D. M., and Musio, C. (Berlin, Heidelberg: Springer), 497–506.
Pasupathy, A., and Connor, C. E. (2001). Shape representation in area V4: position-specific tuning for boundary conformation. J. Neurophysiol. 86, 2505–2519. doi: 10.1152/jn.2001.86.5.2505
Pettet, M. W. (1999). Shape and contour detection. Vision Res. 39, 551–557. doi: 10.1016/S0042-6989(98)00130-8
Pizlo, Z., Salach-Golyska, M., and Rosenfeld, A. (1997). Curve detection in a noisy image. Vision Res. 37, 1217–1241. doi: 10.1016/S0042-6989(96)00220-9
Pomerantz, J. R., and Portillo, M. C. (2011). Grouping and emergent features in vision: toward a theory of basic gestalts. J. Exp. Psychol. Hum. Percept. Perform. 37, 1331–1349. doi: 10.1037/a0024330
Prinzmetal, W., and Banks, W. P. (1977). Good continuation affects visual detection. Percept. Psychophys. 21, 389–395. doi: 10.3758/BF03199491
Ratoosh, P. (1949). On interposition as a cue for the perception of distance. Proc. Natl. Acad. Sci. U. S. A. 35, 257–259. doi: 10.1073/pnas.35.5.257
Rubin, N. (2001). The role of junctions in surface completion and contour matching. Perception 30, 339–366. doi: 10.1068/p3173
Shepard, R. N., and Metzler, J. (1971). Mental rotation of three-dimensional objects. Science 171, 701–703. doi: 10.1126/science.171.3972.701
Shipley, T. F., and Kellman, P. J. (1990). The role of discontinuities in the perception of subjective figures. Percept. Psychophys. 48, 259–270. doi: 10.3758/BF03211526
Smits, J. T. S., and Vos, P. G. (1986). A model for the perception of curves in dot figures: the role of local salience of “virtual lines”. Biol. Cybern. 54, 407–416. doi: 10.1007/BF00355546
Smits, J. T., and Vos, P. G. (1987). The perception of continuous curves in dot stimuli. Perception 16, 121–131. doi: 10.1068/p160121
Smits, J. T., Vos, P. G., and Van Oeffelen, M. P. (1985). The perception of a dotted line in noise: a model of good continuation and some experimental results. Spat. Vis. 1, 163–177. doi: 10.1163/156856885X00170
Troncoso, X. G., Macknik, S. L., and Martinez-Conde, S. (2005). Novel visual illusions related to Vasarely's ‘nested squares’ show that corner salience varies with corner angle. Perception 34, 409–420. doi: 10.1068/p5383
Uttal, W. R. (1973). The effect of deviations from linearity on the detection of dotted line patterns. Vision Res. 13, 2155–2163. doi: 10.1016/0042-6989(73)90193-4
Van Assen, M. A., and Vos, P. G. (1999). Evidence for curvilinear interpolation from dot alignment judgements. Vision Res. 39, 4378–4392. doi: 10.1016/S0042-6989(99)00150-9
van den Berg, M. (2006). Grouping by proximity and grouping by good continuation in the perceptual organization of random dot patterns. Wickens: New York, NY: Unpublished doctoral dissertation, University of Virginia, Charlottesville.
Van Oeffelen, M. P., and Vos, P. G. (1983). An algorithm for pattern description on the level of relative proximity. Pattern Recogn. 16, 341–348. doi: 10.1016/0031-3203(83)90040-7
Wertheimer, M. (1923). “Laws of organization in perceptual forms” in A source book of Gestalt Psychology. (Ed.) W. D. Ellis, London: Kegan Paul, Trench, Trubner & Co.
Wouterlood, D., and Boselie, F. (1992). A good-continuation model of some occlusion phenomena. Psychol. Res. 54, 267–277. doi: 10.1007/BF01358264
Yuen, H. K., Princen, J., Illingworth, J., and Kittler, J. (1990). Comparative study of Hough transform methods for circle finding. Image Vis. Comput. 8, 71–77. doi: 10.1016/0262-8856(90)90059-E
Keywords: perceptual organization, shape, Gestalt, contour perception, abstraction, curvature, visual perception
Citation: Baker N and Kellman PJ (2024) Shape from dots: a window into abstraction processes in visual perception. Front. Comput. Sci. 6:1367534. doi: 10.3389/fcomp.2024.1367534
Edited by:
Dirk Bernhardt-Walther, University of Toronto, CanadaCopyright © 2024 Baker and Kellman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicholas Baker, bmJha2VyMUBsdWMuZWR1
 Nicholas Baker
Nicholas Baker Philip J. Kellman
Philip J. Kellman