Experimenting with D-Wave quantum annealers on prime factorization problems

This paper builds on top of a paper we have published very recently, in which we have proposed a novel approach to prime factorization (PF) by quantum annealing, where 8, 219, 999 = 32, 749 × 251 was the highest prime product we were able to factorize—which, to the best of our knowledge is the largest number which was ever factorized by means of a quantum device. The series of annealing experiments which led us to these results, however, did not follow a straight-line path; rather, they involved a convoluted trial-and-error process, full of failed or partially-failed attempts and backtracks, which only in the end drove us to find the successful annealing strategies. In this paper, we delve into the reasoning behind our experimental decisions and provide an account of some of the attempts we have taken before conceiving the final strategies that allowed us to achieve the results. This involves also a bunch of ideas, techniques, and strategies we investigated which, although turned out to be inferior wrt. those we adopted in the end, may instead provide insights to a more-specialized audience of D-Wave users and practitioners. In particular, we show the following insights: (i) different initialization techniques affect performances, among which flux biases are effective when targeting locally-structured embeddings; (ii) chain strengths have a lower impact in locally-structured embeddings compared to problem relying on global embeddings; (iii) there is a trade-off between broken chain and excited CFAs, suggesting an incremental annealing offset remedy approach based on the modules instead of single qubits. Thus, by sharing the details of our experiences, we aim to provide insights into the evolving landscape of quantum annealing, and help people access and effectively use D-Wave quantum annealers.

1 Introduction

Quantum computing has emerged as a novel paradigm in computer science, offering the potential capabilities to solve complex problems that have long remained intractable for classical computers. Among the various approaches within quantum computing, quantum annealers (QA) stand out as a promising tool for tackling challenging computational tasks. To this extent, prime factorization (PF)—i.e., the problem of breaking down a number into its prime factors—is a good candidate to be effectively solved by quantum computing, in particular by quantum annealing. This problem is of utmost significance in modern cryptography, where the security of systems often relies on the presumed computational intractability of PF (Rivest et al., 1978). Several approaches have been presented to address PF by quantum computing (e.g., Vandersypen et al., 2001; Lucero et al., 2012; Martín-López et al., 2012; Monz et al., 2016; Amico et al., 2019; Selvarajan et al., 2021), by quantum annealing (e.g., Dridi and Alghassi, 2017; Jiang et al., 2018; Mengoni et al., 2020), or by hybrid quantum-classical technologies (e.g., Wang et al., 2020; Karamlou et al., 2021). See Willsch et al. (2023) and Ding et al. (2024) for a summary.

This paper builds on top of a paper we have published very recently (Ding et al., 2024), in which we have proposed a novel approach to PF by quantum annealing, with two main results. First, we have presented a very compact modular encoding of a binary multiplier circuit into the Pegasus QA architecture, which allowed us to encode up to a 21 × 12-bit multiplier (or alternatively a 22 × 8-bit one) into the Pegasus 5760-qubit topology of D-Wave Advantage annealers. Due to the modularity of the encoding, this number will scale up automatically with the growth of the qubit number in future chips. Second, we have investigated the problem of actually solving encoded PF problems by running an extensive experimental evaluation on a D-Wave Advantage 4.1 quantum annealer. In these experiments we have introduced different approaches to initialize the multiplier qubits, and adopted several performance-enhancement annealing strategies. Overall, within the limits of our QPU resources, 8, 219, 999 = 32, 749 × 251 was the highest prime product we were able to factorize—which, to the best of our knowledge, is the largest number which was ever factorized by means of a “pure” quantum device (i.e., without adopting hybrid quantum-classical techniques).

In this paper we delve into the reasoning behind our experimental decisions and provide a more comprehensive account of the steps and attempts we have taken before conceiving the final strategies which allowed us to achieve the results in Ding et al. (2024). We illustrate a bunch of ideas, techniques, and strategies we investigated which, although turned out to be inferior wrt. those we adopted in the end —and as such were not of interest for the more general public targeted in Ding et al. (2024)— may instead provide insights to a more-specialized audience of D-Wave QA users and practitioners. In particular, we show the following insights: (i) different initialization techniques affect performance, among which flux biases are effective when targeting locally-structured embeddings; (ii) chain strengths have a lower impact in locally-structured embeddings compared to problems relying on global embeddings; (iii) there is a trade-off between a broken chain and excited CFAs, suggesting an incremental annealing offset remedy approach based on the modules instead of single qubits. Thus, by sharing the details of our experiences, including both successes and setbacks, we aim to provide insights into the evolving landscape of quantum annealing and help people access and effectively use D-Wave quantum annealers.

2 Methods

We first summarize a few concepts from Ding et al. (2024). The prime factorization problem (PF) of a biprime number N can be addressed by SAT solvers by encoding a n×m multiplier into a Boolean formula, fixing the values of the output bits s.t. to encode N. In Ding et al. (2024), we presented a modular embedding of a binary multiplier circuit into the Pegasus QA architecture, based on locally-structured embedding of SAT problems (Bian et al., 2020). The multiplier circuit, represented in terms of a conjunction of Controlled Full-adder (CFA) Boolean functions linked by means of equivalences between variables, is embedded into the Pegasus topology, with each CFA embedded into a 8-qubit tile and with the variable equivalences implemented through chains. Each CFA F(x) is encoded in terms of a penalty function:

$\begin{array}{c}{P}_F(\stackrel{\underset{\_}{z}}{\overbrace{\underset{\_}{x},\underset{\_}{a}}}|\underset{\_}{\theta })\stackrel{\text{def}}{=}{\theta }_0\\ +{\displaystyle {\sum }_{z_i\in V}{\theta }_i}{z}_i+{\displaystyle {\sum }_{(z_i,z_j)\in E,i<j}{\theta }_{ij}}{z}_i{z}_j;z_i\in \{-1,1\};& (1)\end{array}$

$\begin{array}{ll}s.t.\forall \underset{\_}{x}mi{n}_{\left\{\underset{\_}{a}\right\}}{P}_F\left(\underset{\_}{x},\underset{\_}{a}|\underset{\_}{\theta }\right)\{\begin{array}{ll}=0\hfill & \text{ if }F(\underset{\_}{x})=\top \hfill \\ \ge g_{min}\hfill & \text{ if }F(\underset{\_}{x})=\perp \hfill \end{array}& (2)\end{array}$

where the Boolean variables x and a are mapped into a subset z ⊆ V of the qubits in the topology graph (V, E), s.t. the qubit values {1, −1} are interpreted as the truth values {⊤, ⊥} respectively; θ₀, θ_i, θ_ij and g_min are called respectively offset, biases, couplings and the gap; the offset has no bounds, whereas the range for biases and couplings is [−4, +4] and [−2, +1] respectively. (The ancilla variables a are needed to address the over-constrainedness of the encoding problem.) The θ values in P_F(x, a|θ) have been synthesized by means of OPTIMATHSAT (Sebastiani and Trentin, 2020) s.t. to maximize g_min.¹ The penalty function of the whole multiplier is thus produced as the sum of the penalty functions of the CFAs, plus a term (2 − 2zz′) for every chain 〈z, z′〉. Then it is fed to the annealer, forcing the values of the output qubits so that to represent the biprime number N, and forcing to −1 the value of the carry-in qubit of the rightmost CFA of each row, and the value of the in2 qubit of the CFAs in the first row in the multiplier. Therefore, if the annealer finds a ground state s.t. such penalty function is zero, then the values of the qubit represent a solution of the PF problem.² (We refer the reader to Ding et al. (2024) for a much more detailed explanation).

2.1 Alternative approaches to initialize qubits

Solving prime factorization of a specific number N requires some of the qubits to be initialized to some fixed value in {−1, 1}. For instance, given an 8-bit multiplier and N = 42, whose binary representation is 00101010, then the qubits of the CFAs corresponding to the output number should be initialized respectively to {−1, −1, 1, −1, 1, −1, 1, −1}; also, e.g., the carry-in qubit of the CFA for the least significant bit in a number must be set to −1. D-Wave API offers a native function, fix_variables(), that replaces the truth values of the qubits into the penalty function. Unfortunately, this causes a subsequent rescaling of all weights if one bias or coupling does not fit into the proper range, reducing thus the gap g_min accordingly.

The initialization of qubits can be implemented either at the encoding level [i.e., by imposing qubit values directly into the penalty function P_F(x|θ)], or at the hardware level (i.e., by imposing the qubit values through the tuning of the quantum annealer hardware). In Ding et al. (2024) we adopted the latter implementation by tuning flux biases, and showed the benefits they brought to the success probability of reaching the ground state. In this paper, we mainly focus on the former type of implementation, proposing a few alternatives to fix_variables():

• Ad-hoc encoding for the CFAs: we substitute the values of the input variables into the corresponding CFAs and then re-encode these initialized CFAs, with reduced graphs, into new CFA penalty functions. For instance, suppose we want to set the value of c_in to false. Then we feed to the OMT solver the extended formula F′(x) = F(x)∧¬c_in to generate a new specialized penalty function. To prevent the g_min from being scaled down due to the input values, during the re-encoding process we take into account all combinations of possible inputs that occur in the CFAs.³ This results into the generation of an offline library of specialized CFAs, with increased minimal gaps, g_min∈[3, 18]. Notice that, using these modified encodings, we obtained some solutions where F(x) = ⊤ and 0 < P_F(x, a|θ) < g_min (see text footnote 2), which never occurred in the experiments reported in Ding et al. (2024). Both the gap increment and the extra solutions can increase the probability to find solutions.

• Extra chaining: we notice that in the penalty functions of CFA we have obtained, the biases of the qubits are all within [−1, 1], whereas the range for the D-Wave Advantage 4.1 is [−4, 4]. Based on these facts, we have explored a simple alternative way to initialize qubits, without the risk of rescaling down the g_min value. Specially, in order to assign qubit z to 1 [resp. −1], we can add the penalty function for z = 1 (2 − 2z) [resp. for z = −1 (2+2z)] to the penalty function of the multiplier, s.t. the bias of z safely remains in [−3, 3]. Equivalently, we can find an unused neighbor qubit z′ (if any), add an equivalence chain between z and z′, and then initialize z′ to 1 (resp −1) by fix_variables().

2.2 The impact of chain strength in QA for modular encodings

The effect of chain strength has been previously studied in the context of global embedding, where the input problem is first encoded into a QUBO problem, which is then embedded into the hardware by means of embedding algorithms. The main issue of that approach is that the QUBO model does not know in advance how many chains are there in a specific topology and where they will be placed. Thus, the addition of chains a-posteriori—whose length and placement are out of the control of the user—and the consequent re-scaling of biases and coupling may affect the performances of the algorithm.

Our locally-structured embedding approach in Ding et al. (2024) differs from the above approach because the Ising model that is generated is already hardware-compliant, so that there is no risk of weights rescaling, and we do not need a fine-grained analysis of chain strength. Given the modularity of our encoding and the presence of chains to allow communication between neighboring modules, however, it is still important to investigate the side effects of chain strength in modular encoding. To this extent, we choose a set of chain strengths, c∈{1, 1.5, 2}, as representatives for investigating their effects on the performance of our locally structured embedding approach on QA systems.

2.3 Incrementally remedying excited CFAs

We assume that if all CFAs in a multiplier reach the ground state with high probability, then the success probability of the whole multiplier will be positively affected. Based on this assumption, we have proposed an incremental remedy strategy, to remedy the most excited CFAs during the solving process.

The remedy approach is based on anneal offsets (DWave, 2021). In the standard annealing process of D-Wave systems, the annealing schedules are set identically for all qubits. However, the system also allows for adjusting the annealing schedule for each qubit. This is implemented by offsetting the global, time-dependent bias signal c(s) that controls the annealing process. More specially, for a qubit q_i, its anneal offsets ±δc_i≠0 correspond to advancing and delaying the standard annealing schedule, respectively.

In a fashion similar to Andriyash et al. (2016), Lanting et al. (2017), Yarkoni et al. (2019), and Adame and McMahon (2020) we adopted the idea of incrementally fixing annealing offset weights to increase the probability of reaching a ground state. Differently from these papers, however, where the annealing offset is set to qubits, we set modules of our encoding (i.e., CFAs) as the target of annealing offset tuning, and we choose the number of excitations of these modules as a measure to guide the remedy strategy process.

In each step of our incremental remedy approach, we first find the most-excited CFA —i.e., the CFA whose number of excitation occurrences out of the 1,000 samples is maximum— and then continue to advance the annealing process of all its qubits by annealing offset δc_i = 0.01, on top of the previous remedying history, until the CFA is no longer the most excited. The procedure terminates either if the system reaches one ground state or if it reaches a certain number of steps set as a threshold. This threshold is chosen according to the limitation on the access of QuPU, e.g., the perimeter of the multiplier embedded.

3 Results

3.1 Results of different initialization approaches of qubits

In the experiments, we compare the proposed initialization approaches on D-Wave Advantage system 4.1 for factoring small integers of up to 5 × 5 bits, with the annealing time (T_a = 10μs) and 1,000 samples set for each problem instance. Table 1 by comparing the performances of the initialization techniques , we notice that the ad-hoc re-encoding outperforms the native API and the extra-chain approaches, but it still does not perform as well as the flux-bias tuning, which we finally adopted in Ding et al. (2024). In Ding et al. (2024) we also proposed a variant of the CFA function, namely CFA1, minimizing the number of unsatisfying assignments with g_min equal to 2. For the sake of completeness, we also tested this encoding in combination with initialization techniques other than flux biases. These results confirm that the combination of the flux-bias initialization and the improved CFA1, which we adopted in Ding et al. (2024), produces the highest success probability for D-Wave Advantage 4.1 in finding solutions. For this reason, we continue to use this combination, the flux-bias initialization + CFA1, in the following experiments of this paper.

Table 1

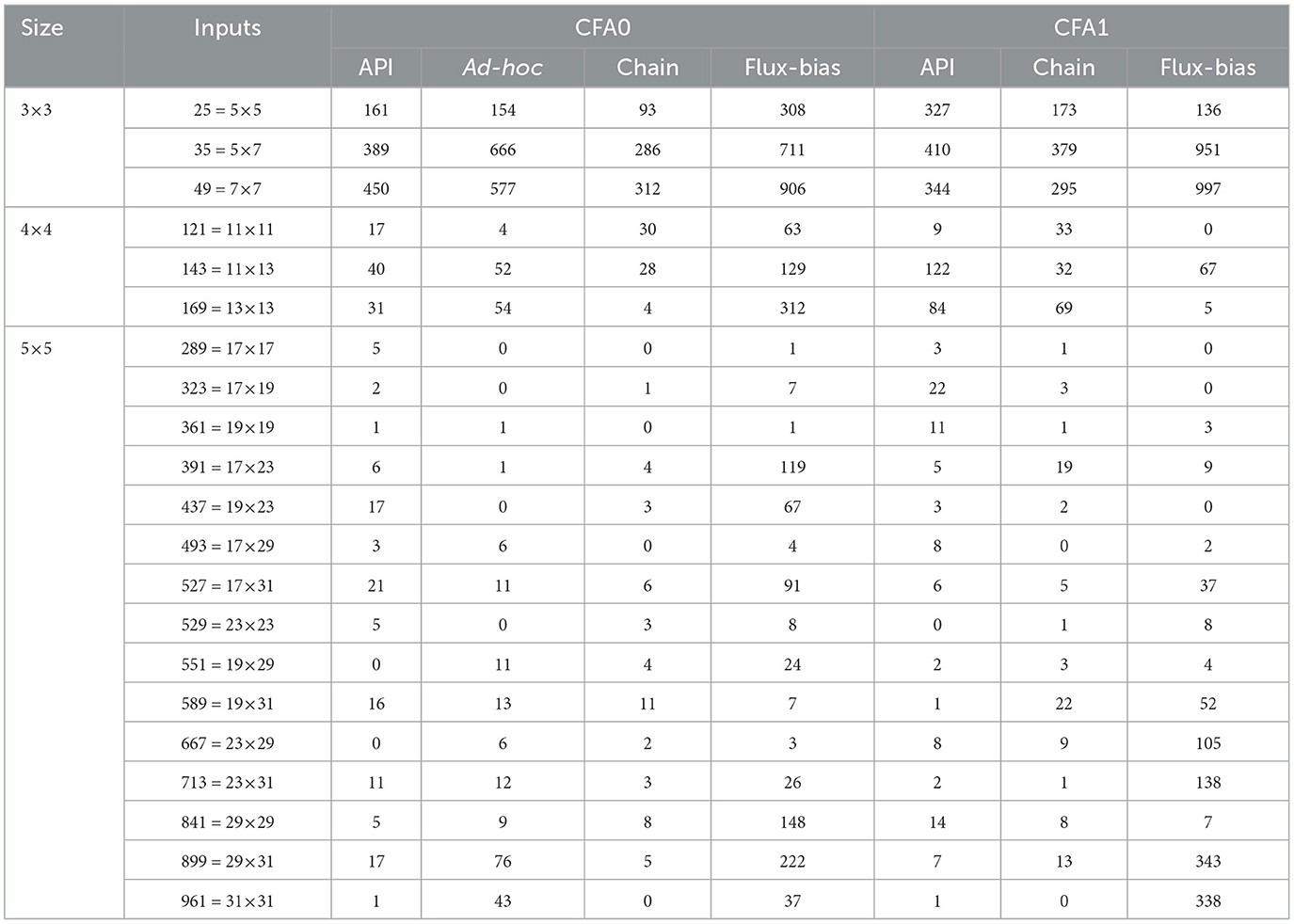
Table 1. Different initialization approaches for solving small-size PF, with the annealing time T_a = 10 μs and 1,000 samples for each problem instance.

3.2 Results of different chain strengths

Using the initialization approach based on CFA1 + flux biases and the same configuration of the annealing system (T_a = 10μs, 1, 000 samples for each problem instance) of previous experiments, we test different chain strengths (c∈{1, 1.5, 2}) for QA factoring integers from 3 × 3 up to 11 × 8 bits, using the 10 highest co-prime number for each multiplier size.

In Figure 1, left we summarize the results of all samples provided the QA. Sorting them by the size of the input problem (x-axis), we plot respectively the number of samples successfully reaching the ground state (first plot), the number of samples having no broken chain (second plot), and the number of samples having no excited CFA (third plot). In general, we report the score of the median sample among all problems (dashed line) as a summary of the annealer behavior for each sample size. In addition, for each sample size, we provide information on the problem that reaches the ground state the least frequently (represented by the minimum dotted line in Figure 1, left), as well as the one that reaches the ground state the most frequently (represented by the maximum solid line in Figure 1, left).

Figure 1

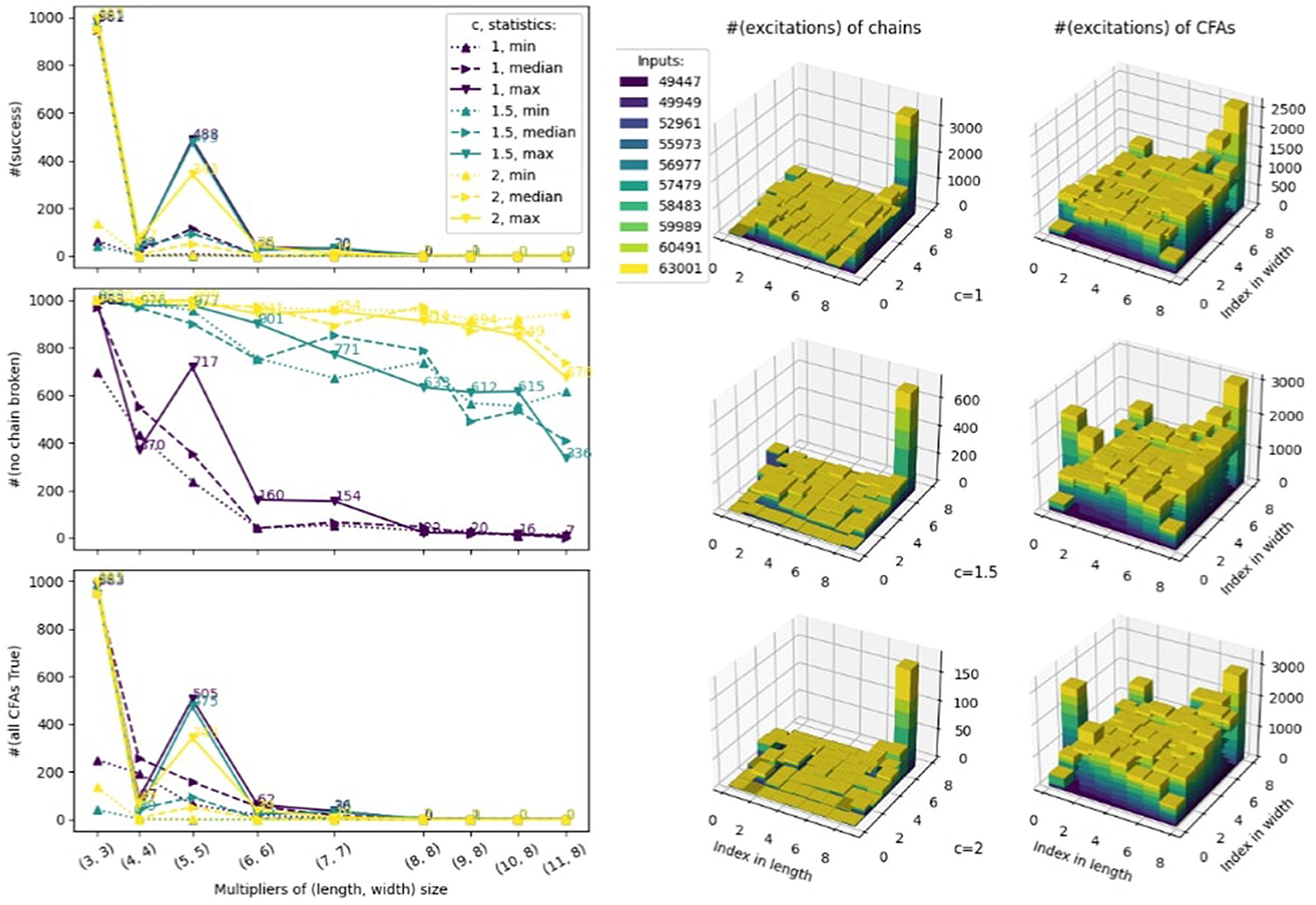
Figure 1. (Left) Comparison of different chain strengths c, c ∈ {1, 1.5, 2}, for QA to factor integers of 3 + 3 bits up to 11 + 8 bits, with the annealing time T_a = 10 μs and 1,000 samples set for each problem instance. (Right) Excitations distribution of chains (first column) and CFAs (second column) for factoring 10 integers of 8 + 8 bits tested in the previous experiments, with chain strength equal to c ∈ {1, 1.5, 2} (respectively top, middle, and bottom row).

We see that stronger chains (c ∈ {1.5, 2}) do not always bring us a higher success probability in general for the chosen problem sizes, and that weaker chains (c = 1) can produce higher success probabilities than stronger chains occasionally for middle-size problems. Notice that this result, in terms of the success probability, is consistent with what is mentioned by Lanting et al. (2017), suggesting that locally-structured embedding does not behave differently from global embedding regarding chain strengths. We also observe that as the problem size increases, weaker chains tend to be broken more easily than stronger chains. The rapidly declining dotted yellow lines confirm this phenomenon, approaching 0 for problems of bigger size. Based on these two observations, we speculate that the strongest chain, which was chosen in Ding et al. (2024), is the best candidate for factoring integers of up to 17 × 8 bits, the maximal problem size they could encode into the target QA system with a locally-structured embedding.

3.3 Results of incrementally fixing excited CFAs

From the experiment of the previous subsection, we can see that there seems to be a trade-off between broken chains and the excitations of CFAs: the weaker the chains are, the more likely they are broken, and the fewer the samples where the CFAs are excited. Moreover, the excitations of CFAs are not uniformly distributed. To this extent, we studied the distribution of broken chains and CFAs in 10 8 × 8 factoring problems, shown in Figure 1, right. The results on excitations of chains and CFAs are reported as 3D bar plots in Figure (3rd and 4th row, respectively). Each problem instance is mapped with its color. The x and the y axis correspond to the column and row of the multiplier respectively; the z axis represents the sum of excitations of each chain or CFA for the tested 10 problem instances. These results support testing an incremental remedy strategy based on modules.

With the strongest chain strength and the same configuration of the annealing system as the other experiments in the paper, we test the approach of incrementally fixing excited CFAs for QA factoring the highest integers of 8 × 8 bits up to 10 × 8 bits from the experiments shown in Figure 1. The results are shown in Table 2. To get an extensive analysis of the novel remedy strategy, we tested three different configurations, with the only difference being the number of samples obtained for each iteration (respectively 1,000, 2,000, and 3,000). We also show in Figure 2 the behavior of the remedy strategy on one of the problem instances.

Table 2

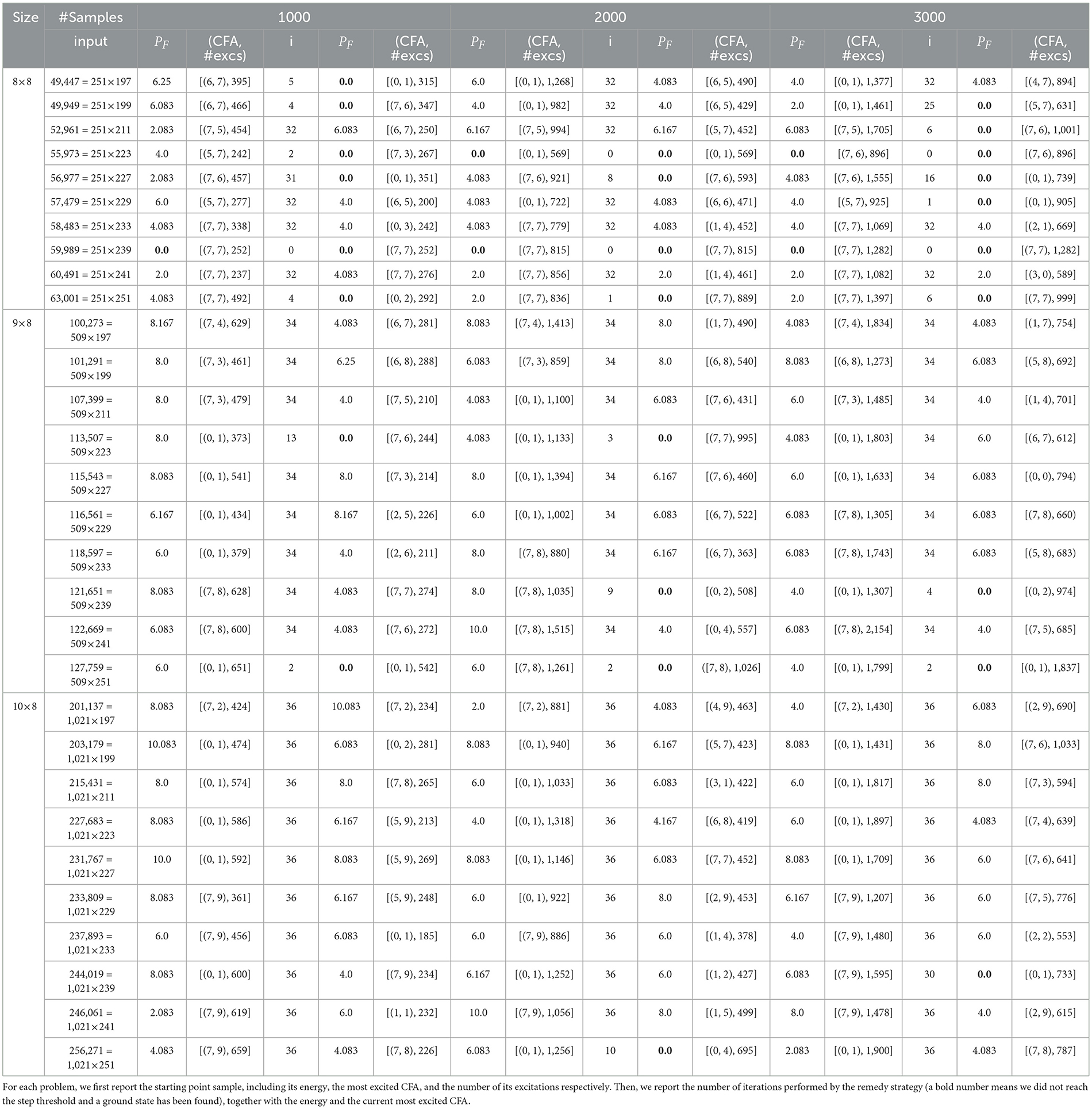
Table 2. Results of incrementally remedying excited CFAs for factoring integers of 8 × 8 bits up to 10 × 8 bits, with the same annealing time T_a = 10 μs with the number of samples ranging from 1,000 to 3,000 set for each problem instance.

Figure 2

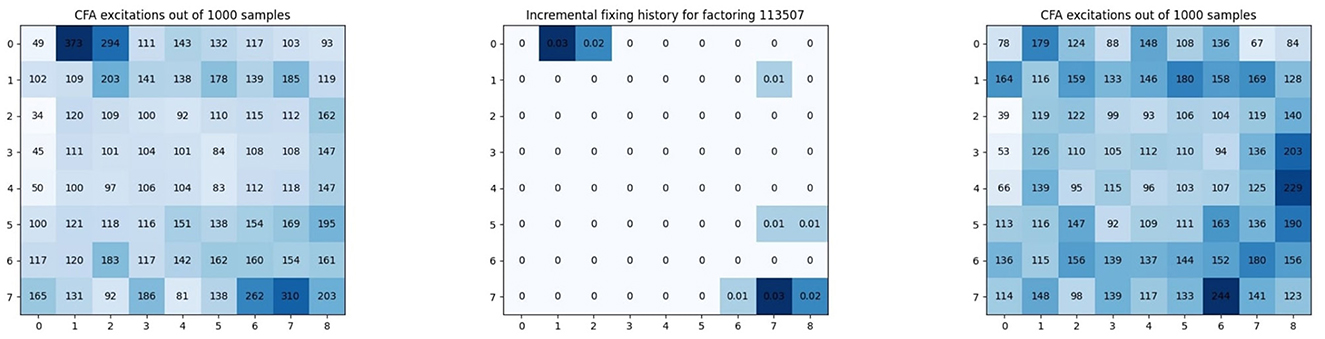
Figure 2. Fixing results for factoring 16-bit 113,507 in Table 2. Each coordinate corresponds to the CFA in the multiplier circuit. The numbers in the figures in the leftmost and rightmost columns represent the number of excitations out of 1,000 samples, whereas the number in the figure in the middle denotes the anneal offset used in the whole fixing process, for advancing the annealing schedule of the specific CFA. Notice the less homogeneous distribution of excitations of CFAs in the leftmost figure compared to the rightmost figure. (Left) Before the fixing. (Middle) The fixing history. (Right) After the fixing.

From the results, we can see that the remedy strategy helps in solving some of the problem instances. In particular, this approach works under the assumption the user has a limited amount of QPU time (i.e., the annealing time is confined to values ≲20μ)s, showing its effectiveness when users are bound to tight constraints in accessing the D-Wave devices. This approach works more effectively with smaller instances, reaching the ground state more frequently and with fewer iteration steps. Moreover, increasing the sample size does not impact performances, showing sporadically improvements in reaching the ground state when the number of samples increases. Nevertheless, setting the annealing offset scores based on the modules' properties instead of targeting qubits independently seems promising, and further investigations could define different conditions to prioritize the annealing of some CFAs.

4 Discussion

This paper has built upon the recent work presented in our previous publication (Ding et al., 2024), which introduced a novel approach to the problem of PF through quantum annealing. In contrast to our previous paper, which showcased exclusively the effective techniques that highly benefited our task, here we discussed several intermediate and less successful approaches. This comprehensive exploration provides insights into the intricacies that influenced our final results in Ding et al. (2024). The code to replicate these experiments is reported in the following publicly available repository: https://gitlab.com/jingwen.ding/multiplier-encoder-2nd.

Our experiments revealed several insights:

• Effectiveness of flux biases tuning: We showed that the techniques to initialize qubits implemented at the encoding level were not as effective as flux-biases tuning. Nevertheless, they can be considered as viable alternative to the usage of fix_variables() in other contexts.

• Chains coupling strength: Even though using the highest value for chains coupling strength might not be optimal for small-sized problems, it proved crucial for solving more complex problems. This highlights the delicate balance between problem size and annealing parameters, e.g., chain strength.

• Trade-off between broken chains and CFA excitations: We observed a trade-off between the presence of broken chains and the excitations of CFAs when the QA generates its samples. This further highlights the importance of monitoring chain strength in other contexts.

• Non-uniform distribution of CFA excitations: The excitations of CFAs were found to be non-uniformly distributed for different samples on the same problem instance. Understanding this distribution can be valuable for tailoring annealing strategies to specific problem instances.

• Remedy strategy for middle-size problems: The remedy strategy we proposed in Section 2.4, based on the above observations, showed minor benefits in solving middle-sized problems. Nevertheless, it could be useful in other contexts.

By delving into the details of our experimental journey, listing both our successes and setbacks, we aim to provide valuable insights to a more specialized audience of D-Wave Quantum Annealer users and practitioners. Our work contributes to the evolving world of quantum annealing and equips researchers and professionals with additional knowledge to effectively use D-Wave quantum annealers in their applications.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://gitlab.com/jingwen.ding/multiplier-encoder-2nd.

Author contributions

RS: Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing – original draft, Writing – review & editing. JD: Data curation, Investigation, Software, Writing – original draft, Writing – review & editing. GS: Data curation, Validation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the European Union. Grant Agreement No. 101120763—TANGO and supported by Q@TN, the joint lab between University of Trento, FBK—Fondazione Bruno Kessler, INFN—National Institute for Nuclear Physics, and CNR—National Research Council. We acknowledge the support from CINECA in terms of QUPU-time availability via the project WCRI-QCSC. We acknowledge the previous support from D-Wave Systems Inc, in terms of both financial support and QUPU-time availability, via the former project QuASI. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication. This research was supported in part by TAILOR, a project funded by the EU Horizon 2020 research and innovation program under GA No. 952215. The work was partially supported by the project: AI@TN funded by the Autonomous Province of Trento. We acknowledge the support of the MUR PNRR project FAIR—Future AI Research (PE00000013), under the NRRP MUR program funded by the NextGenerationEU.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Health and Digital Executive Agency (HaDEA). Neither the European Union nor the granting authority can be held responsible for them.

Abbreviations

CFA, Controlled Full-Adder; OMT, Optimization Modulo Theories; PF, Prime Factorization; QA, Quantum Annealer; SAT, Propositional Satisfiability.

Footnotes

1. ^The bigger is g_min, the easier is for the annealer to discriminate solutions from non-solutions (Bian et al., 2020).

2. ^From Equations (1) and (2) we notice that, due to non-minimum values of a, in principle we can have solution scenarios where F(x) = ⊤ and 0 < P_F(x, a|θ) < g_min, which we can recognize as solutions, or even s.t. P_F(x, a|θ)≥g_min, for recognizing which we need testing F(x) = ⊤ explicitly, which can be performed very easily.

3. ^This is made necessary by one further technique, namely qubit sharing, which we have introduced in Ding et al. (2024) and which is not explained here.

References

Adame, J. I., and McMahon, P. L. (2020). Inhomogeneous driving in quantum annealers can result in orders-of-magnitude improvements in performance. Quant. Sci. Technol. 5:e035011. doi: 10.1088/2058-9565/ab935a

Crossref Full Text | Google Scholar

Amico, M., Saleem, Z. H., and Kumph, M. (2019). Experimental study of Shor's factoring algorithm using the IBM Q experience. Phys. Rev. A 100:e012305. doi: 10.1103/PhysRevA.100.012305

Crossref Full Text | Google Scholar

Andriyash, E., Bian, Z., Chudak, F., Drew-Brook, M., King, A. D., Macready, W. G., et al. (2016). Boosting Integer Factoring Performance via Quantum Annealing Offsets. D-Wave Technical Report Series, 14.

Google Scholar

Bian, Z., Chudak, F., Macready, W., Roy, A., Sebastiani, R., and Varotti, S. (2020). Solving SAT (and MaxSAT) with a quantum annealer: foundations, encodings, and preliminary results. Inform. Comput. 275:104609. doi: 10.1016/j.ic.2020.104609

Crossref Full Text | Google Scholar

Ding, J., Spallitta, G., and Sebastiani, R. (2024). Effective prime factorization via quantum annealing by modular locally-structured embedding. Sci. Rep. 14:3518. doi: 10.1038/s41598-024-53708-7

PubMed Abstract | Crossref Full Text | Google Scholar

Dridi, R., and Alghassi, H. (2017). Prime factorization using quantum annealing and computational algebraic geometry. Sci. Rep. 7:43048. doi: 10.1038/srep43048

PubMed Abstract | Crossref Full Text | Google Scholar

DWave (2021). Anneal Offsets. Available online at: https://docs.dwavesys.com/docs/latest/c_qpu_annealing.html (accessed October 25, 2023).

Google Scholar

Jiang, S., Britt, K. A., McCaskey, A. J., Humble, T. S., and Kais, S. (2018). Quantum annealing for prime factorization. Sci. Rep. 8:17667. doi: 10.1038/s41598-018-36058-z

PubMed Abstract | Crossref Full Text | Google Scholar

Karamlou, A., Simon, W., and Katabarwa, A. E. A. (2021). Analyzing the performance of variational quantum factoring on a superconducting quantum processor. Quant. Inf . 7:478. doi: 10.1038/s41534-021-00478-z

Crossref Full Text | Google Scholar

Lanting, T., King, A. D., Evert, B., and Hoskinson, E. (2017). Experimental demonstration of perturbative anticrossing mitigation using nonuniform driver hamiltonians. Phys. Rev. A 96:e042322. doi: 10.1103/PhysRevA.96.042322

Crossref Full Text | Google Scholar

Lucero, E., Barends, R., Chen, Y., Kelly, J., Mariantoni, M., Megrant, A., et al. (2012). Computing prime factors with a josephson phase qubit quantum processor. Nat. Phys. 8, 719–723. doi: 10.1038/nphys2385

Crossref Full Text | Google Scholar

Martín-López, E., Laing, A., Lawson, T., Alvarez, R., Zhou, X. Q., and O'Brien, J. L. (2012). Experimental realization of Shor's quantum factoring algorithm using qubit recycling. Nat. Photon. 6, 773–776. doi: 10.1038/nphoton.2012.259

PubMed Abstract | Crossref Full Text | Google Scholar

Mengoni, R., Ottaviani, D., and Iorio, P. (2020). Breaking RSA Security With a Low Noise D-Wave 2000Q Quantum Annealer: Computational Times, Limitations and Prospects.

Google Scholar

Monz, T., Nigg, D., Martinez, E. A., Brandl, M. F., Schindler, P., Rines, R., et al. (2016). Realization of a scalable Shor algorithm. Science 351, 1068–1070. doi: 10.1126/science.aad9480

PubMed Abstract | Crossref Full Text | Google Scholar

Rivest, R. L., Shamir, A., and Adleman, L. (1978). A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 120–126.

Google Scholar

Sebastiani, R., and Trentin, P. (2020). OptiMathSAT: a tool for optimization modulo theories. J. Automat. Reason. 64, 423–460. doi: 10.1007/s10817-018-09508-6

Crossref Full Text | Google Scholar

Selvarajan, R., Dixit, V., and Cui, X. E. A. (2021). Prime factorization using quantum variational imaginary time evolution. Sci. Rep. 11:20835. doi: 10.1038/s41598-021-00339-x

PubMed Abstract | Crossref Full Text | Google Scholar

Vandersypen, L. M. K., Steffen, M., Breyta, G., Yannoni, C. S., Sherwood, M. H., and Chuang, I. L. (2001). Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887. doi: 10.1038/414883a

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, B., Hu, F., and Yao, H. (2020). Prime factorization algorithm based on parameter optimization of ising model. Sci. Rep. 10:2020. doi: 10.1038/s41598-020-62802-5

PubMed Abstract | Crossref Full Text | Google Scholar

Willsch, D., Willsch, M., Jin, F., De Raedt, H., and Michielsen, K. (2023). Large-scale simulation of Shor's quantum factoring algorithm. Mathematics 11:4222. doi: 10.3390/math11194222

Crossref Full Text | Google Scholar

Yarkoni, S., Wang, H., Plaat, A., and Bäck, T. (2019). "Boosting quantum annealing performance using evolution strategies for annealing offsets tuning," in Quantum Technology and Optimization Problems: First International Workshop, QTOP 2019, Munich, Germany, March 18, 2019, Proceedings 1 (Berlin: Springer), 157–168.

Google Scholar