
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Comput. Sci. , 14 February 2024
Sec. Computer Vision
Volume 6 - 2024 | https://doi.org/10.3389/fcomp.2024.1274181
This article is part of the Research Topic Geometries of Learning View all 13 articles
 Aaron Mahler1*
Aaron Mahler1* Tyrus Berry2*
Tyrus Berry2* Tom Stephens1
Tom Stephens1 Harbir Antil2
Harbir Antil2 Michael Merritt1
Michael Merritt1 Jeanie Schreiber2
Jeanie Schreiber2 Ioannis Kevrekidis3
Ioannis Kevrekidis3This study provides a computable, direct, and mathematically rigorous approximation to the differential geometry of class manifolds for high-dimensional data, along with non-linear projections from input space onto these class manifolds. The tools are applied to the setting of neural network image classifiers, where we generate novel, on-manifold data samples and implement a projected gradient descent algorithm for on-manifold adversarial training. The susceptibility of neural networks (NNs) to adversarial attack highlights the brittle nature of NN decision boundaries in input space. Introducing adversarial examples during training has been shown to reduce the susceptibility of NNs to adversarial attack; however, it has also been shown to reduce the accuracy of the classifier if the examples are not valid examples for that class. Realistic “on-manifold” examples have been previously generated from class manifolds in the latent space of an autoencoder. Our study explores these phenomena in a geometric and computational setting that is much closer to the raw, high-dimensional input space than what can be provided by VAE or other black box dimensionality reductions. We employ conformally invariant diffusion maps (CIDM) to approximate class manifolds in diffusion coordinates and develop the Nyström projection to project novel points onto class manifolds in this setting. On top of the manifold approximation, we leverage the spectral exterior calculus (SEC) to determine geometric quantities such as tangent vectors of the manifold. We use these tools to obtain adversarial examples that reside on a class manifold, yet fool a classifier. These misclassifications then become explainable in terms of human-understandable manipulations within the data, by expressing the on-manifold adversary in the semantic basis on the manifold.
Despite their superior performance at image recognition, neural network (NN) classifiers are susceptible to adversarial attack, and their performance can degrade significantly with small perturbations to the input (Szegedy et al., 2014; Tabacof and Valle, 2016; Moosavi-Dezfooli et al., 2017). The brittle performance of NNs when given novel inputs can be attributed to their intricate high-dimensional decision boundaries, which fail to generalize robustly outside of the training data. This problem is epitomized by the observation that NNs are excellent interpolators but poor extrapolaters.
Crafting attacks to deceive NNs with minimal changes to the input has been shown to be remarkably easy when the attacker has full access to the NN architecture and weights. The fast gradient sign method is one of the earliest attack methods that crafts adversarial examples by taking the sign of the gradient of the loss function to perturb the input in the direction that maximizes the loss in pixel space (Goodfellow et al., 2015). Other methods take a number of smaller steps in directions to find the smallest perturbation required to misclassify an input (Moosavi-Dezfooli et al., 2016; Carlini and Wagner, 2017; Samy Bengio, 2018; Madry et al., 2019). Most of these methods use the gradient of the NN loss function for a given input as a way to determine directions of maximal confusion, i.e., directions leading to the closest decision boundary in the high-dimensional pixel space. There also exists single-pixel attacks that use differential evolution with no gradient information and are able to reliably fool NNs (Su et al., 2019).
Various methods have been proposed to make NNs more robust to adversarial attack. Adversarial training is a common choice because it involves using attack inputs as additional training data, thereby allowing the NN decision boundary to more correctly classify that data. Commonly, the gradient of the NN will be used to augment the data set for this purpose (Goodfellow et al., 2015; Madry et al., 2019). On the other hand, gradient masking is a method that attempts to create a network that does not have useful information in the gradient, so that it cannot be exploited for creating attacks (Papernot et al., 2017). These types of networks have been found to still be vulnerable though to similar attacks that work on NNs with useful gradients (Papernot et al., 2017; Athalye et al., 2018). Defensive distillation is a gradient-free method that uses two networks, where the second network is trained using the distilled (softened) outputs of the first network (Papernot et al., 2017). Training on distilled outputs is done to create less irregular decision boundaries, which in turn results in being less prone to misclassifying small perturbations. Ensemble methods use the output of multiple models, which results in less effective attacks since it is unlikely the models are sensitive to the exact same attacks (Tramèr et al., 2020). Input preprocessing can also be applied to try to mitigate or remove adversarial perturbations. This can be done in a model agnostic way such as filtering or compressing the data (Yin et al., 2020), detecting adverasial inputs with feature squeezing (Xu et al., 2018), or using an autoencoder to denoise the input (Cho et al., 2020).
One popular method of adversarial training uses small steps along the network gradient that are only allowed to step so far away from the original input, called projected gradient descent (PGD) (Madry et al., 2019). The data set is augmented with examples that are maximally confusing to the NN during training, but the augmented data points are only allowed to be ϵ far away from true data points. This results in a marked improvement to the NN when it is attacked with perturbations of the same strength. However, PGD trained networks show a decrease in accuracy on clean inputs and the accuracy goes down as the size of the ϵ-ball allowed for augmentations increases (Engstrom et al., 2019). The degradation of accuracy and the rise of robustness could be due to several factors, such as overfitting the model to adversarial examples or from adversarial examples that are not actually representative of the class of the input that was perturbed. The trade-off between robustness and accuracy has been noted to occur with many flavors of adversarial training, and it has even been conjectured that robustness and accuracy may be opposed to each other for certain NNs (Su et al., 2018; Tsipras et al., 2019).
On the other hand, it has also been shown that in some cases, a more careful choice of adversarial examples can create robust NNs that are also on-par with standard networks at generalizing to unseen validation data (Stutz et al., 2019). This was explained by the fact that adversarial training such as PGD creates samples that are not truly on the manifold of that data's class label. The NN is then tasked with learning a decision boundary for the training data as well as randomly noisy data, resulting in the compromise between accuracy and robustness for those types of adversarial training. In Stutz et al. (2019), they found perturbations in a latent space learned from the training data. Perturbing in an ϵ ball in the latent space was surmised to be on a class manifold and therefore a new augmentation that was representative of that class. Adversarial training in a way that is agnostic to the underlying geometry of the data itself therefore seems to be a root cause for the trade-off between robustness and accuracy.
The above mitigations to adversarial attacks all proceed from the perspective that the neural network has simply not been fed enough variation in the collected training data to learn decision boundaries that adhere to the full underlying data manifolds. From this perspective, injecting adversarial examples into the original training data “pushes out” incursions by the decision boundary into the true manifold. An alternative perspective is that the adversarial examples do not result from so-called bugs in the decision boundaries but are instead features of the data (Ilyas et al., 2019). From the features perspective, adversarial training is a data cleaning process; the original data has pixel correlations across classes that our eyes cannot detect, and computed adversarial perturbations act to wash those away. While we do not embark on our applications from this perspective, the mathematical tools developed here are ideally suited for extending their hypotheses and results.
Our application of on-manifold adversarial training connects the learning problem to the manifold hypothesis and manifold modeling techniques. For natural images, the manifold hypothesis suggests that the pixels that encode an image of an object, together with the pixel-level manipulations that transform the scene through its natural, within-class variations (rotations, articulations, etc), organize along class manifolds in input space. In other words, out of all possible images drawn from an input space, while the vast majority look like random noise, the collection of images that encode a recognizable object (a tree, a cat, or an ocean shoreline) are incredibly rare, and the manifold hypothesis claims that those images should be distributed throughout input space along some coherent geometric structure. On-manifold adversarial training aims for an NN to better capture the underlying structure in the data. In this study, we use novel manifold modeling techniques that do not rely on autoencoders or black box neural networks.
To construct and leverage a data-driven representation of an embedded manifold, we use a collection of tools that have grown out of the diffusion maps-based methods in the manifold learning community. Diffusion maps methods are based on learning a manifold by estimating a certain operator called the Laplace–Beltrami operator, which encodes all the geometric properties of the manifold. The advantage of this approach is that is does not require constructing a simplicial complex (or triangularization) from data, which can be quite challenging. However, diffusion maps-based manifold learning requires several additional tools to access needed geometric quantities for on-manifold adversarial learning. In particular, we need the ability to find the tangent directions to the manifold, walk along a tangent direction, and then project down onto the manifold. To find the tangent directions to the manifold, we use a recent development known as the Spectral Exterior Calculus (SEC) that builds these estimators directly from the diffusion maps constructions. The SEC uses global information to find the principal tangent directions, and is thus less susceptible to noise and large ambient dimensions than local (nearest neighbor)-based methods. Finally, to project a point from data space onto the manifold, we discover a surprising and powerful new tool which we call the Nyström projection. Using these methods, we demonstrate creating on-manifold adversarial examples that are explainable in terms of their semantic labels.
Manifold learning emerged as an explanation for how kernel methods were able to perform regressions and identify low-dimensional coordinates from much higher dimensional data sets than would be possible according to normal statistics. Assuming that the data were lying on a submanifold of the data space, it appeared that the kernel methods (kernel regression, kernel PCA, etc.) were able to leverage this intrinsically low-dimensional structure.
The first advance in understanding this effect rigorously was Laplacian eigenmaps (Belkin and Niyogi, 2003). They employed a Gaussian kernel to build a complete weighted graph on the data set with weights . This was a very common choice of radial basis kernel at the time and a natural first choice for analysis. Laplacian Eigenmaps then constructs the weighted graph Laplacian , where diagonal matrix is called the degree matrix. In the limit, as the number of data points goes to infinity, the Laplacian matrices become larger and larger, and if the bandwidth, ϵ, is taken to zero at an appropriate rate, this sequence of matrices are shown to converge to the Laplace–Beltrami operator on the manifold that the data were sampled from. This was the first rigorous connection between the somewhat ad hoc kernel methods and the intrinsic geometry of the data.
Unfortunately, the assumptions required to prove the key theorem of Laplacian eigenmaps were overly restrictive in practical settings. In addition to only applying to a single kernel function (when in practice, many different kernel functions were known empirically to have similar behavior), Laplacian eigenmaps also required the data to be sampled uniformly from the underlying manifold. This is a somewhat technical requirement, an embedded manifold (such as the one the data are assumed to lie on), that inherits a natural measure from the ambient data space which is called the volume form. We can think of this volume form as a distribution, and when the data are sampled from this natural distribution, it is called uniformly sampled. However, there is no reason for the data to have been be uniformly collected in this sense. For example, if your data lie on a unit circle, there is no reason that the data could not be more densely collected on one side of the circle and more sparsely collected on the other side, but Laplacian eigenmaps did not allow for this in their theorem. These restrictions meant that the applicability of kernel methods to resolving the intrinsic geometry of a real data set was still seen as rather tenuous.
Diffusion maps (Coifman and Lafon, 2006a) resolved these concerns and solidified the connection between a large class of kernel methods and the intrinsic geometry of the data. The idea of diffusion maps turns out to be fairly simple, although the technical details of the theorems are somewhat challenging. The key idea is that the degree matrix, , is actually a classical kernel density estimator, meaning that if the data are not sampled uniformly, then Dii will be proportional to the true sampling density (up to higher order terms in ϵ which can be carefully accounted for). Diffusion maps begins by generalizing the kernel density estimation results to data sampled on manifolds, and then uses the estimated density to de-bias the kernel. De-biasing the kernel turns out to be a simple normalization procedure called the diffusion maps normalization, which constructs the normalized kernel,
and then recomputes the new degree matrix and finally the diffusion maps graph Laplacian . The diffusion maps theorems showed that for any radial basis kernel that had exponential decay in distance, and for data collected from any smooth distribution on the manifold, their new graph Laplacian, , converged to the Laplace–Beltrami operator on the manifold. Moreover, the diffusion maps theorems also showed (although this was only realized in later works, e.g., Berry and Sauer, 2016) that even when their normalization was not used, the classical graph Laplacian converged to a Laplace–Beltrami operator with respect to a conformal change of metric. This ultimately showed that all kernel methods with radial basis kernels that had fast decay were finding the intrinsic geometry of the data (possibly up to a change of measure). Later works would generalize the diffusion maps theorems to include all kernels that had sufficiently fast decay in the distance between points (so not just radial basis functions) (Berry and Sauer, 2016).
At this point, we should address why both Laplacian eigenmaps and diffusion maps have the word “Maps” in them. This goes back to the motivation that was driving the development of these new theories. In particular, both methods were motivated by Kernel PCA, which interpreted the eigenvectors of the kernel matrix as providing the coordinates of a mapping into a new space, often called a ‘feature space'. Ironically, this mapping interpretation arose from the theory of Reproducing Kernel Hilbert Spaces, where the kernel induces a map into a function space (not a Euclidean space). However, since the kernel matrix, K, has as many rows and columns as there were data points, the eigenvectors of the kernel matrix have as many entries as there are data points, so inevitably these were visualized and interpreted as new coordinates. Diffusion maps and Laplacian eigenmaps were trying to show that this “mapping” preserved intrinsic aspects of the geometry while also reducing dimension, and while the first part is partially correct, the dimensionality reduction aspect of the diffusion maps turns out to not be guaranteed. However, this was merely a case of applying the wrong interpretation to the results. In fact what diffusion maps had proven was much better than any fact about a mapping. By recovering the Laplace–Beltrami operator on the manifold, and its eigenfunctions, diffusion maps unlocked the door and allowed access to every single aspect of the geometry of the data. Moreover, the eigenfunctions provide a generalized Fourier basis for analysis of functions and operators on the data set, and have been used in regression, interpolation, forecasting, filtering, and control applications.
To leverage the opening that diffusion maps has created to learning manifold geometry from data, we will need several recent advances that improve and apply the original theory. First, it turns out that for real data sets in high dimensions, the fixed bandwidth kernels discussed so far have difficulty adjusting to large variations in sampling density. To compensate for this, a variable bandwidth kernel is needed (Berry and Harlim, 2016), which can automatically adjust to have a small bandwidth and high resolution in areas of data space that are densely sampled, while keeping a large bandwidth and a lower resolution representation of sparsely sampled regions of data space. The ultimate evolution of the variable bandwidth kernels is the Conformally Invariant Diffusion Map (CIDM) (Berry and Sauer, 2016, 2019), which we introduce in Section 1.1.1.
The next tool we will need is a rigorous method for extending/interpolating all of the discrete representations of functions, mappings, and operators to be able to operate on any new input data. Here, we use a regularized version of a standard method called the Nyström extension, introduced in Section 1.1.2. Although this basic method of interpolation is well-established, we will apply it in ways that have never been considered before to achieve powerful new methods and results.
Finally, we mentioned above that the Laplace–Beltrami operator unlocks the door to access all the hidden geometry of the data. This is due to a technical result which says that if you know the Laplace–Beltrami operator, you can recover the Riemannian metric on the manifold, and the Riemannian metric completely determines all aspects of the geometry (from dimension and volume to curvature to geodesics and everything in between). However, until recently, this was a purely abstract possibility, and there was no actual method for constructing these geometric quantities starting from the Laplace–Beltrami operator. This was achieved in 2020 with the creation of the Spectral Exterior Calculus (SEC), which re-builds all of differential geometry starting just from the Laplace–Beltrami operator. While we will not require every aspect of the SEC here, the basic philosophy of its construction will be fundamental to the way that we will construct vector fields and in a particular tangent vectors on the manifold, so a brief introduction will be given in Appendix A.1.
As mentioned above, the original version of diffusion maps uses a fixed bandwidth kernel of the form J(x, y) = h(||x−y||2/ϵ2). Here, h is called the shape function and is assumed to decay quickly to zero as the input (distance) goes to infinity. A typical choice for h is the exponential function h(z) = exp(−z), so moderate differences in distances leads to large differences in the values of h. This becomes particularly problematic in terms of the distance to the nearest neighbors. If the distances from a data point to its nearest neighbors are large (relative to the bandwidth ϵ), then the values of the kernel become very close to zero. This means that even though our weighted graph is technically still connected, the weights are so close to zero that it becomes numerically disconnected, which causes the diffusion map to interpret such data points as disconnected from the rest of the data set. On the other hand, we want the kernel function to decay quickly beyond the nearest neighbors to localize the analysis and make the resulting kernel matrix approximately sparse.
When the density of points varies widely, it becomes very difficult to find a single bandwidth parameter ϵ which achieves these two goals across the data set. One tends to have to choose the bandwidth large enough to connect with the sparsest region of data, and this large bandwidth value results in a loss of resolution in the denser sampled regions. This trade-off is examined rigorously in Berry and Harlim (2016), which introduces variable bandwidth kernels and generalizes the diffusion maps expansions for such kernels. The best practical implementation of a variable bandwidth approach was introduced in Berry and Sauer (2019), which is a variable bandwidth version of the Conformally Invariant Diffusion Map (CIDM) that was introduced in Berry and Sauer (2016).
The CIDM starts by re-scaling the distance using the distances to the nearest neighbors, namely
Where kNN returns the k-th nearest neighbor of the input point from the training data set. Note that the distance to the k-th nearest neighbor is a consistent estimator of the density to the power of −1/d where d is the dimension of the manifold. Thus, when the local density is high, the distance to the kNN will be small, and conversely when the local density is sparse, the distance to the kNN will be large. Thus, δ(x, y) has re-scaled the distances into a unit-less quantity which will be on the same order of magnitude for the k-th nearest neighbors of all the data points.
Inside the kernel, we will use the square of this quantity,
which is also more convenient for derivatives. Next, we use the dissimilarity δ in a kernel,
Where ϵ is a global bandwidth parameter and h:[0, ∞) → [0, ∞) is a called a shape function (examples include h(z) = e−z as mentioned above or even simply the indicator function h(z) = 1[0, 1](z)). We can then build the kernel matrix Kij = k(xi, xj) on the training data set, and the diagonal degree matrix and the normalized graph Laplacian L≡I−D−1K.
We should note that in Berry and Sauer (2019), it was shown that, uniquely for the CIDM, the unnormalized Laplacian Lun≡D−K has the same limit as the normalized Laplacian in the limit of large data; however, the normalized Laplacian, L, has some numerical advantages. Numerically, it is advantageous to maintain the symmetry of the problem by finding the eigenvectors of the similar matrix, . Finally, we are interested in the smoothest functions on the manifold, which are the minimizers of the energy defined by L; however, it is easier to find the largest eigenvalues of (Recall that maximal eigenvalues can be found with power iteration methods which are fast than the inverse power iterations required for finding smallest eigenvalues). Once we have computed the eigenvectors , then it is easy to see that are eigenvectors of D−1K with the same eigenvalues, and are also eigenvectors of L with eigenvalues ξ = 1−λ. Thus, when λ are the largest eigenvalues of Ksym, the corresponding ξ will be the smallest eigenvalues of L.
We will refer to L as the CIDM Laplacian, and we will use the eigenvectors and eigenvalues of L to represent the geometry of the data manifold. The eigenvectors of the CIDM Laplacian, are vectors of the same length as the data set, so the entries of these eigenvectors are often interpreted as the values of a function on the data set, namely . Of course, we have not really defined a function ϕ since we have only specified its values on the data set. However, in the next section, we will show how to define a function ϕ on the whole data space that takes the specified values on data set. This method is called the Nyström extension because it extends the function from the training data set to the entire data space.
In Berry and Sauer (2016), the CIDM Laplacian, L, was shown to converge (in the limit of infinite data and bandwidth going to zero) to the Laplace–Beltrami operator of the hidden manifold with respect to a conformal change of metric that has volume form given by the sampling density. The Laplace–Beltrami operator encodes all the information about the geometry of the manifold (see Appendix A for details), which is why methods such as diffusion maps and the CIDM are called manifold learning methods. Moreover, it was shown in Berry and Harlim (2016) and Berry and Sauer (2016, 2019) that the CIDM construction using the k-nearest neighbors density estimator, as described above, does not require the so-called “Diffusion Maps normalization”. The CIDM gives the unique choice of conformal geometry for which a standard unnormalized graph Laplacian is a consistent estimator of a Laplace–Beltrami operator (Berry and Sauer, 2019). Empirically, we have found that this variable bandwidth kernel construction is much more robust to wide variations in sampling density.
We should note that in the Nyström extension section below, we will make use of the following normalized kernel,
since this corresponds to D−1K as discussed above [namely if K = k(xi, xj), then ]. Finally, to reduce sensitivity, we often use the average of the distances to the k-nearest neighbors in the re-scaling, so the dissimilarity would then be,
Where iNN refers to the i-th nearest neighbor so the summations are averaging the distances to the k-nearest neighbors.
In this section, we introduce the Nyström extension, which is the standard approach for extending diffusion maps eigenfunctions (and thus the “diffusion map”) to new data points. Once the eigenfunctions can be extended, arbitrary functions can also be extended by representing them in the basis of eigenfunctions; this approach can be used to extend any sufficiently smooth function to new data points in input space. Since, in practice, we can only represent a function with finitely many eigenfunctions, the truncation onto this finite set gives us a regularized, or smoothed, regression. The Nyström extensions of the diffusion maps eigenfunctions are sometimes called geometric harmonics (Coifman and Lafon, 2006b) and these out-of-sample extensions are related to the method of Kriging in Gaussian Processes, a connection which is explored in Dietrich et al. (2021).
Given an eigenvector of a kernel matrix Kij = k(xi, xj), we can extend the eigenvector to the entire input space by,
which is called the Nyström extension. Note that here k is an abstract kernel which may incorporate CIDM normalizations inside the shape function as well as normalization such as the diffusion maps normalization and/or Markov normalization outside of the shape function. For example, for CIDM, the Nyström extension of an eigenfunctions is,
Where the CIDM kernel takes the place of the abstract kernel k in Equation (2). Notice that evaluating involves computing the dissimilarity δ between arbitrary point x and a training data point xj, which in turn requires finding the k nearest neighbors of the point x from the training data set. Thus, evaluating the abstract kernel k may actually depend on the entire training data set; however, in this section, we will consider the training data set as fixed and treat its influence on k as hidden parameters that define the kernel k. We should note that although everything in this section can be applied to any kernel, a simple radial basis function kernel with no normalizations and a fixed bandwidth has fairly poor performance for the off-manifold extensions we will discuss later in this section.
A key property of the Nyström extension is that on the training data points, we have
So if we interpret as the value of a function on the data point xi, then the Nyström extension agrees with these function values on the original data set and extends the function to the entire input space.
Moreover, given an arbitrary vector of function values on the data set, we can extend this function to the entire data set by representing in the basis of eigenvectors and then applying the Nyström extension to these eigenvectors. Let be the collection of eigenvectors of the kernel matrix K. Note that will refer to the i-th entry of the ℓ-th eigenvector. Notice that,
so if we replace the vector with the Nyström extension, we have the Nyström extension of f given by
Notice that this can be viewed as a kernel extension of f by rewriting the above as
In other words, the Nyström extension of a function is given by , which is a linear combination of the kernel basis functions k(·, xi), with coefficients . This formula can be truncated for ℓ = 1, ..., L, with L < N to get a smoothed, low-pass filtered version of the function. When all of the eigenvectors are used, we have
So again the Nyström extension agrees with the original vector of function values on the original data points. When fewer than N eigenfunctions are used, the Nyström extension is a smoothing of the original function, so it does not interpolate the values on the training data, which can be useful for de-noising. Finally, if we substitute in the definition of the vector inner product, we have the following expression for the Nyström extension:
Where L is the number of eigenfunctions used and is typically much less than N to smooth and denoise the function.
Here, we introduce some tools for analyzing data on manifolds in the input data space. The first tool is a novel method of projecting arbitrary data points non-linearly down onto the manifold. This method is based on using the Nyström extension to build a projection, so we call this new method the Nyström projection in Section 2.1. The next tool is the Spectral Exterior Calculus (SEC), which was developed in Berry and Giannakis (2020) and is able to identify vector fields that respect the global structure of the data. Here, we overview the interpretation of the SEC on vector fields in Section 2.2 and describe how we use these vector fields to approximate the tangent space to the manifold in a way that is more robust than local linear methods. Together, by using linear projection of vectors (such as perturbation directions) onto the tangent space and the non-linear Nyström projection of perturbations of data points down onto the manifold itself, we introduce an on-manifold technique for projected gradient descent in Section 2.3.
In Section 1.1.2, we reviewed the Nyström extension as an established method of out-of-sample extension for functions on the data space. In this section, we introduce a novel application of this extension, which we will call the Nyström projection. The Nyström projection will be defined below as the Nyström extension of the original data coordinate functions. This special case is deserving of extra scrutiny because it is the only function which maps a new data point through the diffusion maps embedding and back into the original data space, meaning that the Nyström projection can be iterated with surprising and useful results.
The next (and crucial) question is: How does the Nyström extension perform out-of-sample? In the case of manifold learning, this question has two cases, first, when the out-of-sample data lie on the manifold, and, second, when they are off the manifold (and potentially far from the manifold). For data points on the manifold, the behavior of Nyström is well-understood as a band-limited interpolation of the function f, which minimizes a certain cost function. The on-manifold out-of-sample interpretation is easy because we started by assuming that there was a given function on the manifold and that we had sampled values of that function on our in-sample training data. Thus, there is a natural “true” function in the background to compare our Nyström interpolation to.
The case of extension to off-manifold points is much more interesting and less is known about this case. Clearly, for any fixed “true” function defined on the manifold, there will be infinitely many smooth extensions to the entire space, so the Nyström extension is selecting one of these extensions, and in the limit of infinitely many data points and eigenfunctions, this extension is minimizing a certain functional. While this is an open area of research, empirically, we observe that for a normalized CIDM kernel, the Nyström extends the function to an off-manifold data point by essentially taking the function value of the nearest point on the manifold. Since almost every point in the ambient data space has a unique nearest point on the manifold, this is well-defined up to a set of measure zero, and, in practice, there is a smoothing effect in a neighborhood of this measure zero set; however, we will ignore these effects for simplicity.
To demonstrate empirically how the Nyström extension performs far from the training data set, in Figure 1 we show an example of a data set lying near the unit circle in the plane. Given a simple smooth function, shown in the first panel of Figure 1, we can use various methods to learn this function and attempt to extend it to the entire input data space (the plane in this case). Notice that when well-tuned, performance near the training data set, shown by the “localized” panels of Figure 1, is comparable for a simple two-layer neural network as well as the Nyström extension with both the standard diffusion maps kernel and the CIDM kernel. However, Figure 1 shows that these methods have very different behavior far from the data set, with the neural network behaving somewhat unpredictably, and the standard diffusion map kernel having difficulty extrapolating when far from the training data, whereas the CIDM makes a smooth choice of extension which is well-defined even very far from the training data.
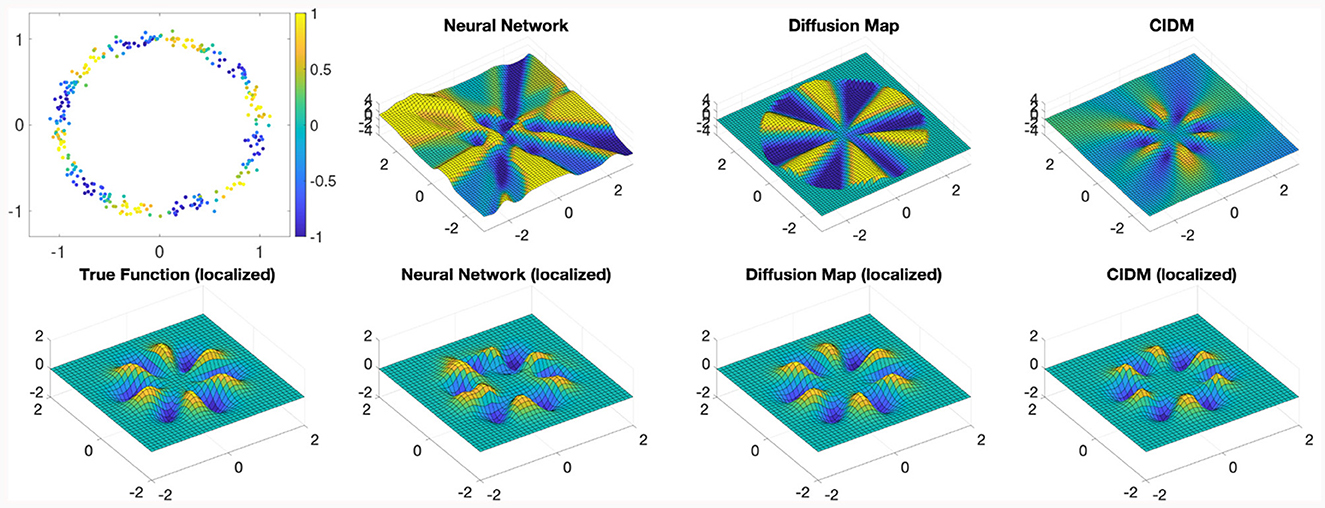
Figure 1. Nyström extension comparison. Consider data points near a unit circle (top left) and a function to learn given by the color (also shown bottom left) localized near the unit circle. We consider three methods of learning the function, a simple 2-layer neural net, the standard diffusion map Nyström extension, and the CIDM Nyström extension. Each extension is shown on a large region (top row) as well as localized near the unit circle (bottom row). The CIDM provides the smoothest extension to the entire input space.
This interpretation of the Nyström extension as taking the value of the nearest point on the manifold is critical since it lead us to a novel and powerful method of achieving a non-linear projection onto the manifold. The idea is actually quite simple, think of the original data set as a function on the manifold and build the Nyström extension of this function. In fact, this is how we often think of a data set mathematically in the manifold learning literature. Thus, we will apply the Nyström extension of the original data coordinates into a function on the entire data space, and we call the resulting function the Nyström projection.
While it is perfectly valid to consider the data manifold as a subset of the ambient data space, in differential geometry, it is useful to think of an abstract manifold that is simply an abstract set of points, and then think of the data set as the image of this abstract manifold under an embedding into Euclidean space, so . Now, the points in data space, , are the images of an abstract point , such that . In this interpretation, each of the coordinates of the data are actually scalar valued component functions of the embedding function, so , where are the component functions of the embedding. Of course, since we know the value of these coordinate functions on the training data set, we can apply the Nyström extension to each of the ιs functions, and extend the entire ι embedding map to the entire data space. In this way, we obtain the Nyström projection , which is given by
Where is the s-th coordinate of the i-th data point. We can also write the Nyström projection more compactly in terms of the Nyström extension of the eigenfunctions, as
Where is a vector-valued generalized Fourier coefficient given by . Thus, we can think of as encoding the embedding function that takes the abstract manifold to the realized data coordinates.
In fact, does much more than the original embedding function, since it extends the embedding function to the entire data space. This is because when input data points are off-manifold, the Nyström extension of a function is well-approximated by selecting the values of the function for the nearest point on the manifold. Since we are applying the Nyström extension to the embedding function itself, this means that for an off-manifold point, the Nyström projection will actually return the coordinates of the nearest point on the manifold. In other words, Nyström projection acts as the identity for points on the manifold and projects off-manifold points down to the nearest point on manifold. This novel yet simple tool gives us a powerful new ability in manifold learning and has opened up several promising new research directions. Moreover, the choice of L in the Nyström projection gives us control over the resolution of the manifold we wish to project on. Thus, for a noisy data, we can intentionally choose a smaller L value to project down through the noise to a manifold that cuts through the noisy data. This is demonstrated in Figure 2 (rightmost panels), where we set L = 20 and recovered a smooth circle that cuts through the noisy input data set (red points).
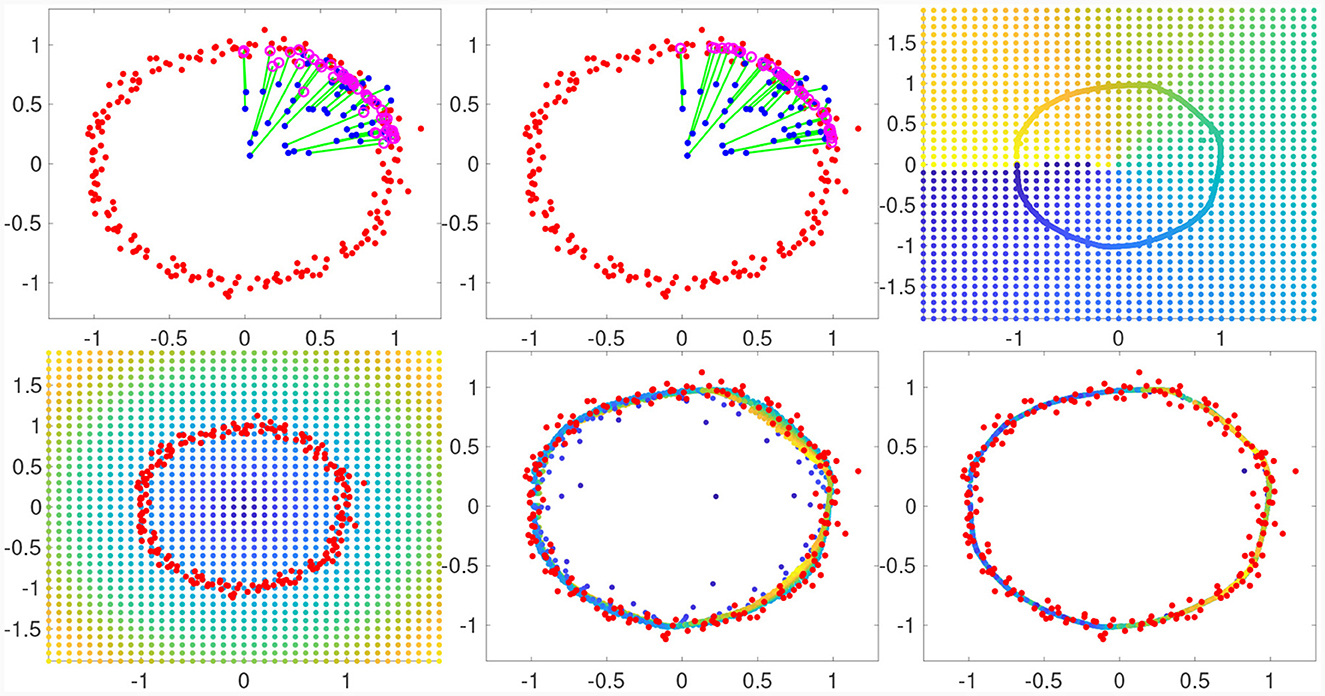
Figure 2. Nyström projection onto the Unit Circle. We use the Nyström projection to project points on the plane onto the unit circle using a noisy training data set (red) to learn the manifold. Top: After learning from the red training data set, blue data points far from the manifold are projected onto the magenta points using a single iteration of the Nyström projection (left) and two iterations (middle); the green line connects each initial point to its Nyström projection. Top Right: Applying two iterations to a grid in the plane projects onto a circle, the original grid points are colored by the angle computed after they are projected to show where they land. Bottom Row: A grid colored by radius (left) is projected once (middle) and twice (right) using the Nyström projection learned from the same data set (red) as the top row.
It is useful to formulate the Nyström projection as a composition of a non-linear map (related to the Diffusion Map) and a linear map. Often, we consider the map which takes an input point in data space and returns the coordinates of the first L eigenfunctions, Φ:ℝn → ℝL given by . This is the so-called diffusion map (with t = 0). While we have argued above that this is not necessarily the best embedding of the data, it is useful to express the projection we have just constructed. Note that the is an n×L matrix containing the first L generalized Fourier coefficients of each of the n coordinates of our data set. Thus, defines a linear map from ℝL (the image of Φ) back to the data space, ℝn (where is simply given by left multiplication by the matrix ). The Nyström projection onto the manifold is the composition of these two maps, namely , so that we have a map,
such that and .
The fact that the Nyström projection maps back into the original data space has the significant consequence that it actually forms a dynamical system which can be iterated. Moreover, we have seen that its behavior can be extremely useful in that it tends to project data points “down onto onto the manifold”. This feature, that applying (and iterating when necessary) the Nyström projection pushes new data points down toward the manifold inside of the ambient data space, is what allows us to search for on-manifold adversaries.
Before continuing, we consider a future application of the Nyström projection as an input layer to a neural network. If we are performing optimization with respect to a loss function L:ℝn → ℝ and we want to restrict our optimization to the manifold, we can simply compose with the projection to find,
which has gradient,
Here, we assume that the gradient of L is already computable, and we are merely evaluating gradL on which is still a point in data space and just happens to have been projected down onto the manifold. Moreover, we already have the matrix , so the only additional component that is needed is the gradient of Φ, which simply requires computing the gradient of each of the Nyström eigenfunctions.
Our goal is to find vector fields that span the tangent spaces of the manifold at each point. While this is not always possible with just d vector fields (where d is the intrinsic dimension of the manifold), the Whitney embedding theorem guarantees that it is always possible with 2d vector fields. The L2 inner product,
induced on vector fields by the Riemannian metric provides a natural notion of orthogonality that can help to identify non-redundant vector fields. Here, we use the notation v·w≡g(v, w) to denote the function which at each point is the Riemannian dot product of the two vectors at fields at that point.
In addition to being orthogonal, we also need these vector fields to cut through noise and follow the coarse (principal) geometric structure of the manifold. For this purpose, we introduce the Dirichlet energy on vector fields, induced by the weak form of the Hodge 1-Laplacian, δ1 = dδ+δd, where d, δ are the exterior derivative and codifferential, respectively. These operators are defined on differential forms, which are dual to tensor fields, and, in particular, the dual of a vector field is a 1-form. The musical isomorphisms switch back and forth between forms and fields, with sharp, ♯, turning forms into fields, and flat, ♭, going back. As an example, the codifferential on 1-forms is related to the divergence operator by,
Similarly, the exterior derivative, which acts on forms, induces an operator on smooth fields which generalizes the curl operator,
This operator coincides with the curl when manifold is three-dimensional, so we use the same name, but in general, on an n-dimensional manifold, the output of the generalized curl operator will be a n−2 tensor field. Using the generalized divergence and curl operators, we can now define the Dirichlet energy on smooth vector fields as
Where we note that the dot product in the first term is the extension of the Riemannian metric to n−2 forms. By minimizing this energy, we will ensure that we have the smoothest possible vector fields, as seen by a global (integrated) measure of smoothness. As discussed in Appendix A, the Dirichlet energy on vector fields is motivated by a dual energy on differential 1-forms. Note that while measuring smoothness on functions only requires a single term, the integral of the gradient of the function, measuring smoothness of vector fields requires two different types of derivatives. This is because neither the divergence nor the curl can completely measure the different types of oscillations a vector field can have, but when combined they provide a robust measure of smoothness.
The Dirichlet energy and Riemannian metric together will define a natural function for identifying good sets of vector fields, which in turn will reduce to a generalized eigenvalue problem. In Appendix A, we overview the SEC construction of the Dirichlet energy and how to find its minimizers relative to the Riemannian inner product. For now, we demonstrate the advantage of this approach to finding vector fields that respect the global structure of the data set. In Figure 3, we show a data set that while near a simple manifold exhibits variations in density and noise levels characteristic of real data. This example clearly demonstrates how the SEC principal vectors respect the principal global structure of the manifold, rather than getting lost in local details the way local linearization is. This is possible because the Dirichlet energy captures a measure of smoothness that is balanced over the entire global structure of the data set.
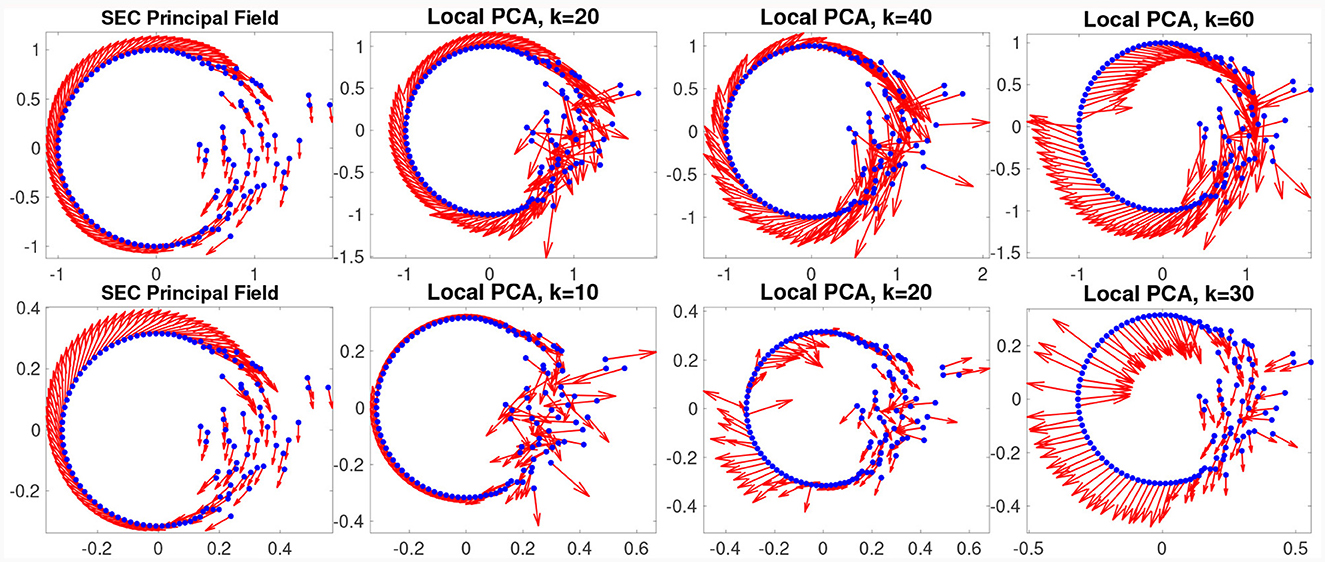
Figure 3. SEC vector fields (left) respect global structure. Here, we consider a data set (blue points) localized near the unit circle but with varying density and varying amounts of noise. In the top left plot, we show the principal vector field identified by the SEC (the global minimizer of the Dirichlet energy). We compare this to a local PCA approach using k = 20, 40, and 60 nearest neighbors of each point (middle left to right). Note how the SEC vector field smoothly respects the dominant mode of variation in the data set; while the local PCA approach can find the tangent direction in the clean sections, it loses track in the noisy section of the data. The problem is further exacerbated in higher dimensions, and in the bottom row, we repeat the same experiment using an isometric embedding of the circle into four dimensions. Again, we show the SEC principal vector (bottom left) and local PCA with k = 10, 20, and 30 nearest neighbors from middle left to right.
Finally, we should note an important caveat and related direction for future research. The vector fields identified here are only globally orthonormal, meaning in an integrated sense. This means that they are not required to be orthonormal in each coordinate chart, since positive alignment in some regions can be canceled by negative alignment in others. In future study, one could consider a local orthonormality condition. This is related to the search for minimal embeddings.
As discussed in Section 1, projected gradient descent (PGD) relies on computing the network loss gradient with respect to the input rather than the weights of the model. Once these input gradients have been computed via backpropagation with respect to a target class, the input is perturbed in the direction of the gradient to create an adversarial example. If the resulting perturbed image is farther than ϵ away from the starting image for a given distance metric (typically ℓ2 or ℓ∞), then the perturbed image is projected onto the ϵ-ball surface around the starting image. This is done with the intent of keeping the adversarial example from becoming unrecognizable as the original class. We use the SEC and Nyström projection to create an on-manifold PGD that is representative of the original class but not constrained to an ϵ-ball. First, we take the gradient of the network for an input with respect to the input's class. Then, we find the input point's position on the manifold with the Nyström projection, see Section 2.1. Using the SEC, we then compute the vector fields that are tangent to the manifold and obtain the tangent bundle at the position of the starting point's position on the manifold, see Figure 3 for a comparison of vector fields from SEC to local PCA. Next, we project the gradient onto the orthonormalized subspace spanned by a subset of tangent vectors at the input point depending on the dimensionality of the underlying data. For instance, if the underlying manifold had an estimated dimension of 2 then you would choose the 2 tangent vectors from the smoothest vector fields computed by the SEC. We orthonormalize the subspace by using the non-zero eigenvectors of the singular value decomposition (SVD) to obtain an unbiased basis. Then, we step along the direction of the gradient in the tangent space by an amount determined by a hyperparameter so that the input is sufficiently perturbed. As the final step, we use the Nyström projection to return this perturbed sample back to the manifold, see Figure 2 for an example. The Nyström projection ensures that the resulting example is on that particular class's manifold and provides the information for determining the example's semantic labels (intrinsic coordinates) and tangent vectors. We can obtain the on-manifold example's semantic labels using the same methodology used to obtain the mapping from CIDM coordinates to pixel, see Figure 1 for an example of obtaining semantic labels on a learned manifold. The perturbation and projection steps are repeated until a misclassification is found, see Figure 4 for an pictoral overview and Algorithm 1 for a pseudo-code description. We use the same tangent basis from the starting image at all steps because we found that updating the tangent basis at each step did not appreciably change the result after performing Nyström projection. If the on-manifold PGD is successful, then it produces an adversarial example that fools the classifier and is also on the input class's manifold.
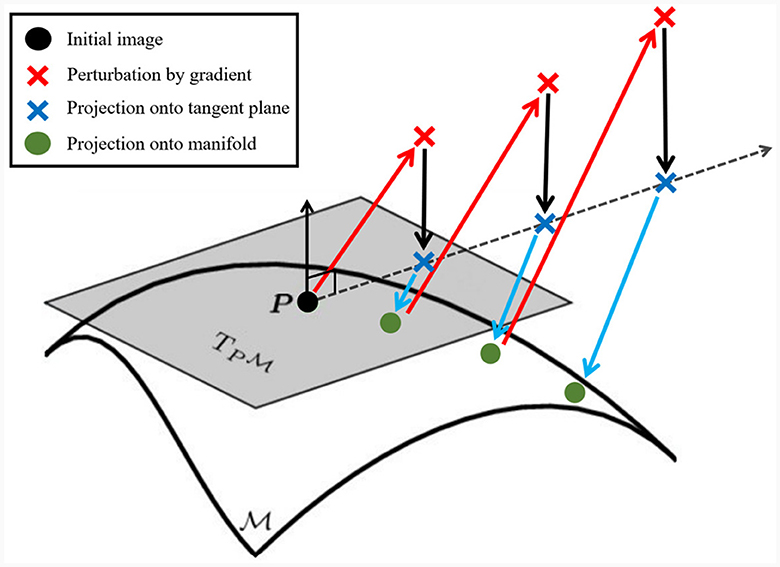
Figure 4. On-manifold PGD steps for a 2D tangent space. Starting with an initial image (black dot), we follow the network gradient (red arrow). The perturbed sample (red X) is then projected (black arrow) onto the tangent plane, (gray surface), from the geometry found around the initial image. The upwards black arrow pointing out of the tangent plane at the black dot is normal to the tangent plane for visual clarity. The on-plane perturbation (blue X) is then Nyström projected (blue arrow) onto the manifold (curved surface ). The on-manifold point (green dot) is then classified to determine if the network has classified it correctly. If the on-manifold point is classified correctly, then it is fed back into the network and the process is repeated, although it reuses the same manifold and from the starting point.
The main result we present shows on-manifold adversarial examples that are explainable in human understandable terms by using the adversaries' semantic labels on the manifold. We present experimental results for finding on-manifold adversaries using a VGG11 classifier (Simonyan and Zisserman, 2014) and a synthetic data set. Our classifier is trained and validated to classify RGB images of various vehicles (see Figure 5 for examples), which were generated using synthetic data collected in Microsoft's AirSim platform, allowing for insertion of various vehicle classes in a range of locations. Each vehicle class is sampled over two sets of intrinsic parameters, represented by the azimuth angle and down look angle (DLA) from which the image is captured. The azimuth angles are sampled one degree apart from 1 to 360 and the down look angle is sampled one degree apart from 1 to 45 degrees. The dense sampling in intrinsinc parameters will enable CIDM and SEC computations, while also allowing for NN models trained on the data to be fairly robust.

Figure 5. Examples of RGB vehicle datatset, consisting of seven vehicle types (pickup truck, SUV, sedan, dump truck, box truck, jeep, and fork lift), varying in 360 degrees azimuth and 45 degrees down look angle. The data contains six types of scene backgrounds including urban and rural environments. The full resolution data is 256 by 256 pixels, although it has been downsampled to 128 by 128. Top row: vehicle images with flat backgrounds generated using image segmentation maps. Bottom row: vehicle images with randomly sampled location backgrounds (images are again inserted into backgrounds using segmentation maps).
We trained a VGG11 classifier on a subset of the down look angles (10°−30°) and all azimuth angles. See Figure 6 for the loss and decision boundaries of the classifier for a single class over all view angles available, including those the classifier was not trained on. We use an image from the training set that was in a region close to a decision boundary at 30° down look and 100° azimuth. We then apply our on-manifold PGD to that point using a manifold modeled on the points surrounding that point from 0° to 40° DLA and 80° to 120° azimuth, see Figure 7. The output of the on-manifold PGD for this example results in a misclassification that correlates with the decision boundary for this class near that sample in view angle as seen in Figure 6. Note that the results of projecting onto the manifold provide not only the on-manifold point in pixel space but also in intrinsic parameter coordinates. This means that the misclassification can be explained in terms of human-understandable features. In this case, the on-manifold adversarial example seen at step 5 in Figure 7 is shown to be at 39.36 DLA and 101.22 azimuth, which can be confirmed to be a region of misclassification by looking at the explicit sampling of that region in the decision boundary map of Figure 6.
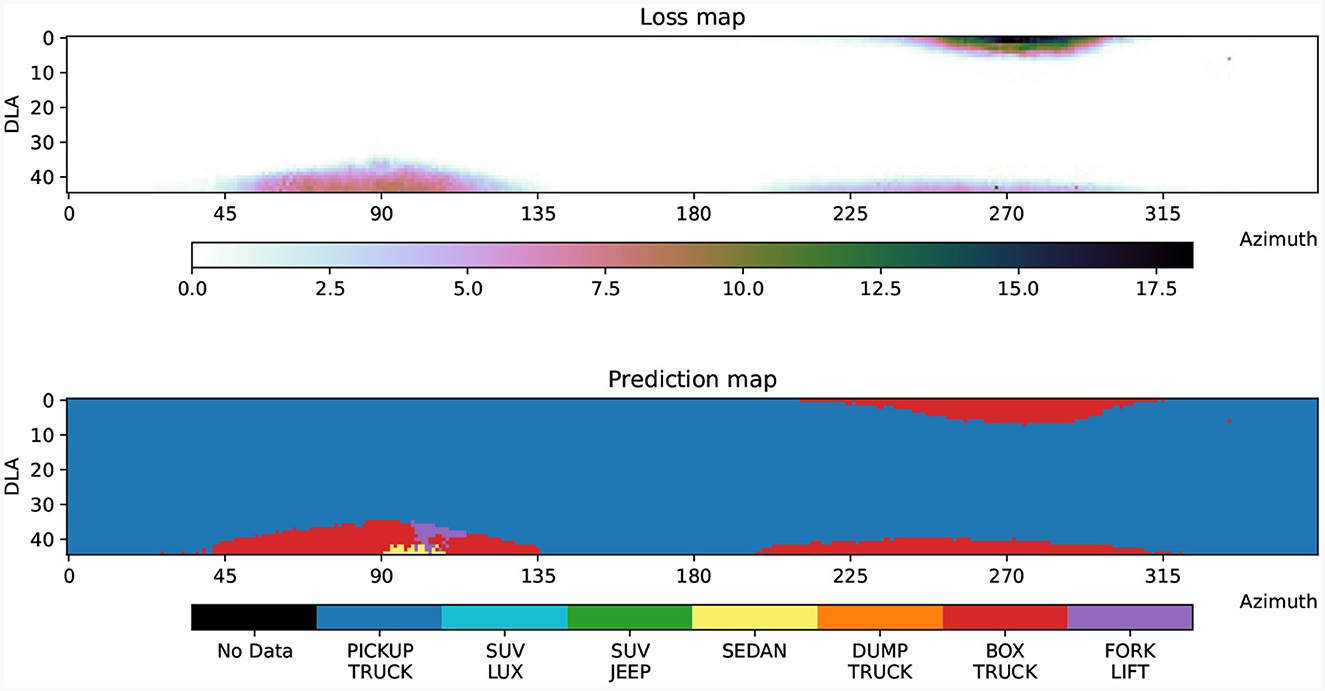
Figure 6. Network loss and prediction map (pickup truck class). Loss map and decision boundary map for the Pickup Truck class on a VGG11 network. The classifier was trained with the seven vehicle types shown in Figure 5 using down look angles from 10° to 30° and azimuths from 0° to 359°.

Figure 7. Generation of an on-manifold adversarial image. The first column is the Nystöm projection of the input from the previous step with the step number on the vertical axis and the predicted intrinsic parameters on the horizontal axis. The second column is the first column after adding the network gradient times 106.38. The third column adds the image from the first column and 107 times the gradient after it is projected onto the manifold subspace spanned by the tangent subspace. The fourth column is the result of Nystöm projecting the third column so that it is on the manifold. Each image includes the network prediction of that image at the top, and the outline color corresponds to the steps in Figure 4.
When perturbing the on-manifold images with the gradient, X′ = X+α∇X, we use a fixed step size, α = 106.38 for convenience. We tested a range of step sizes ranging on a log scale to find the smallest step that sufficiently perturbed the input into misclassifying with the on-manifold PGD algorithm. The size of the parameter α is due to the fact that the network gradient is mostly contained in a space not spanned by the tangent vectors. After projecting the gradient onto the tangent plane, the magnitude of the projected gradient is several orders of magnitude smaller than the raw gradient, which is visibly discernible in the second and third columns of Figures 7, 10. To obtain a sufficient perturbation for the classifier to misclass, this required a large value for α. Due to the fact that the ℓ2 norm of the gradient was typically on the order of 10−3 for these examples, the gradient could also be normalized so that smaller values of α could be used.
We choose the first two tangent vectors from the SEC because the output of the SEC code returns the vector fields ordered by smoothness, which typically results in the first vector fields being best aligned with the manifold. We visually confirmed this in CIDM coordinate space as seen in Figure 8.
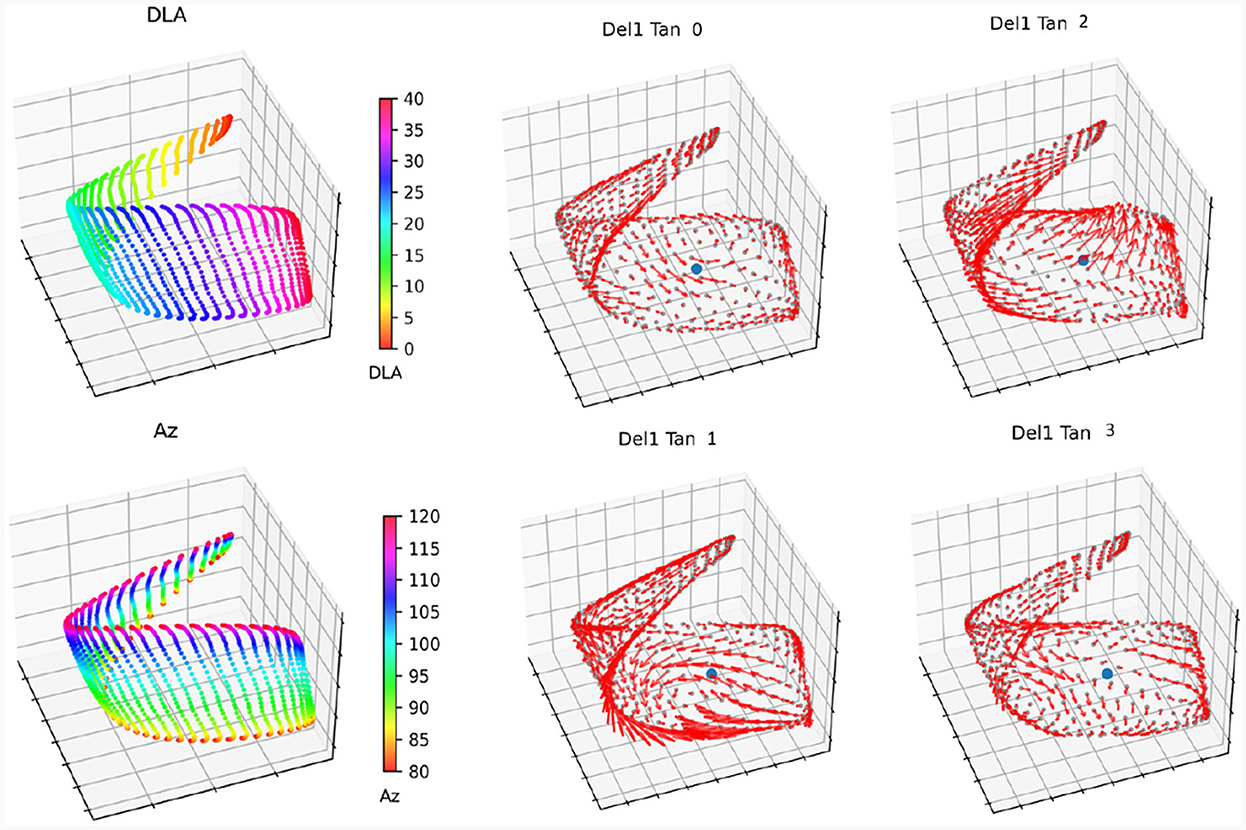
Figure 8. Pickup truck manifold approximation. The top two images show the manifold of the Pickup Truck plotted using the first three coordinates from CIDM. The top left image is colored by the azimuth angle, and the top right is colored by the down look angle. The bottom four plots show the tangent vector fields of the SEC as red arrows, and the initial point around which the geometry approximation was built as a blue dot.
We present another on-manifold PGD result using an adversarially trained network. The model is a CNN with two convolutional layers and a final fully connected layer. Both of the 2D convolutional layers have a kernel size of 3, stride of 1, padding 1, and are followed by a 2D max pooling with a kernel size of 2 and then ReLu activations. The first layer has 12 filters and the second layer has 24 filters. For our data set with images sizes of 128 × 128, this leads to an input of size 32 × 32 × 24 into the last fully connected layer. The output of the final layer is set to the number of classes in the data set and we apply the softmax activation function. The training paradigm for this experiment consists of using images with randomly generated backgrounds, as shown in Figure 5, with the result that the trained network will be background-agnostic. We train on images from all azimuth angles and DLA from 20 to 30 degrees. After six epochs of standard training, we switch to adversarial training, where adversarial images are generated by following the network gradient. We continue until we reach 100 total epochs of training. Figure 9 then plots the loss and prediction maps over azimuth and DLA for the luxury SUV class.
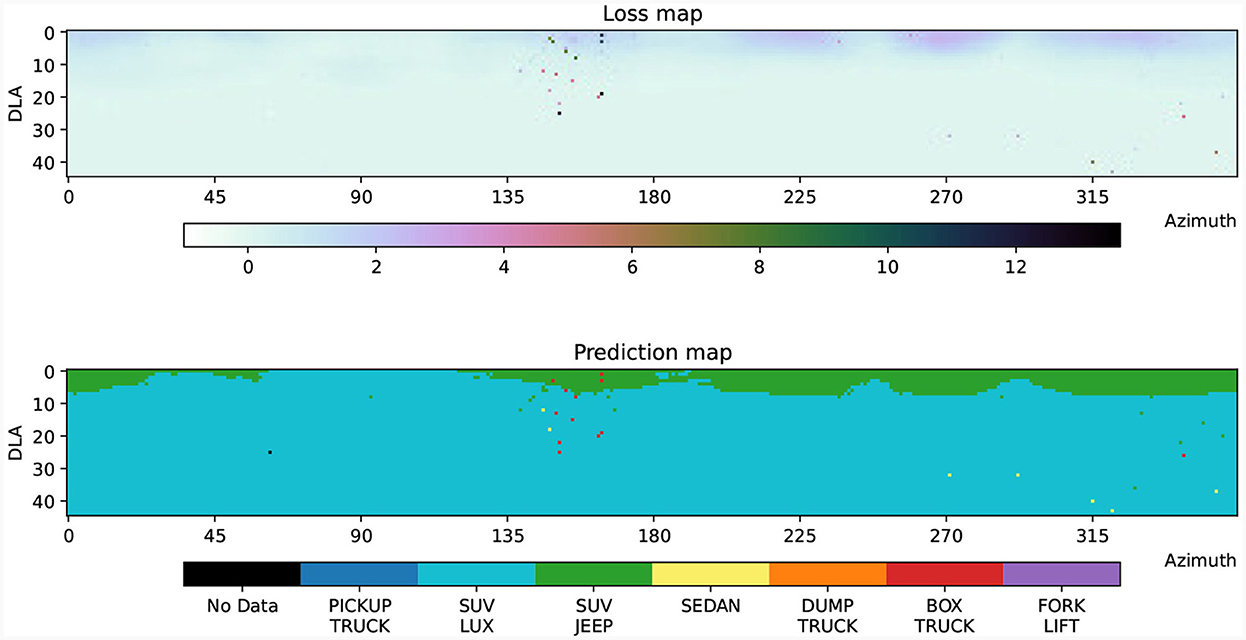
Figure 9. Network loss and prediction map (luxury SUV class). Loss map and decision boundary map for the Luxury SUV class on a CNN. The classifier was trained with seven vehicle types as shown in Figure 5 using down look angles from 20° to 30° and azimuths from 0° to 359°. Adversarial training begun after epoch 6 and continued until epoch 100, where the network gradients were used to generate adversaries. Network evaluation takes place with scene background images, while the network was trained with a randomized set of backgrounds to avoid an over-dependence of the network on the image background.
We note in Figure 9 that the majority of the misclassifications occur outside of the training regime, with a few rare misclassifications in the training regime, given as scattered predictions of the box truck and sedan classes. We seek to generate on-manifold adversarial examples in the range 20°−30° for DLA and 135°−165° for azimuth, which is the range we use in geometry calculations. Notice, in this experiment, we are only providing our geometry tools with data from the intrinsic parameter range that the network was trained on. The goal of this experiment is to use our geometry tools to find and correctly explain an adversarial example that caused the network to mislcassify, without giving the geometry tools preferential treatment in the form of additional data that the network was not trained on. Figure 10 illustrates our on-manifold PGD iteration, as described in Section 2.3, with the starting point at DLA 20° and azimuth 150°.

Figure 10. Generation of an on-manifold adversarial image. The first column is the Nystöm projection of the input from the previous step with the step number on the vertical axis and the predicted intrinsic parameters on the horizontal axis. The second column is the first column after adding the network gradient times 105.23. The third column shows the gradient after it is projected onto the manifold subspace spanned by the tangent subspace. The fourth column is the result of Nystöm projecting the third column so that it is on the manifold. Each image includes the network prediction of that image at the top and the outline color corresponds to the steps in Figure 4.
Figure 10 depicts the iteration of on-manifold PGD to an on-manifold adversarial example, which is classified as a box truck (as one would expect from Figure 9). In this experiment, we note that adversarial examples causing a misclassification often contain a reflection on the side of the vehicle. We have verified that this matches with a rare feature in the training data, where images containing a reflection commonly cause the luxury SUV to be misclassified as the white box truck. These reflections are a result of AirSim's environment and they represent an unexpected challenge that network mislcassified but was identified by our on-manifold PGD approach. Evidently, not only is this approach able to generate adversarial example which can be explained in terms of their semantic labels but it also provides explainable insights into which features of an image cause a network to misclassify.
In conclusion, we have presented a formal introduction of CIDM, a type of variable bandwidth kernel diffusion map that is adept at dealing with heterogenous data density. We have also introduced a novel application of the Nyström method for extending the CIDM eigenfunctions to new data points. We use the Nyström projection to map off-manifold points onto the manifold inside PGD to implement an on-manifold PGD. Additionally, we showed how to use SEC to find vector fields of the manifold for points on the manifold, which we use as a local linear space around the data to project to for intermediate points in our on-manifold PGD implementation. We were able to successfully obtain on-manifold examples that the trained NN misclassifies, showing the promise of on-manifold examples that can be found in input space without reducing down to a latent space. Our reported results provided the geometry approximation tool with data that was outside the data used to train the NN classifier, meaning that the output of the on-manifold PGD algorithm would not be a valid input for adversarial regularization. However, the experiment did provide novel tools for modeling the data manifold in a manner that allowed the on-manifold PGD algorithm to walk in the direction of the NN gradient while remaining on the manifold. This provided novel examples that were on-manifold but not simply part of the hold out data. In addition, the Nyström projection onto the manifold provided the intrinsic parameters of the adversarial examples so that the misclassification was human interpretable. The ability to report the intrinsic parameter of arbitrary points on the manifold opens the door to being able to explain NN decision boundaries in human understandable terms without explicitly sampling all possible inputs. In non-synthetic data, a single class will typically not have continuously varying intrinsic parameters, so additional work needs to done to transition these tools to real-world data sets.
The datasets presented in this article are not readily available because the way the dataset was generated was described for reproducibility, but it is not available due to commercial restrictions. Requests to access the datasets should be directed to aaron.mahler@teledyne.com.
AM: Conceptualization, Investigation, Methodology, Software, Supervision, Visualization, Writing – original draft. TB: Conceptualization, Funding acquisition, Investigation, Methodology, Visualization, Writing – original draft. TS: Conceptualization, Funding acquisition, Investigation, Methodology, Software, Writing – review & editing. HA: Investigation, Project administration, Writing – review & editing. MM: Investigation, Software, Visualization, Writing – original draft. JS: Investigation, Software, Writing – review & editing. IK: Conceptualization, Methodology, Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This material was based upon study supported by the Defense Advanced Research Projects Agency (DARPA) under Agreement No. HR00112290079, and it has been approved for public release; distribution is unlimited.
The authors would also like to thank Juan M. Bello-Rivas for many helpful and insightful discussions related to these topics.
AM, TS, and MM were employed by Teledyne Scientific & Imaging, LLC.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2024.1274181/full#supplementary-material
Athalye, A., Carlini, N., and Wagner, D. (2018). “Obfuscated gradients give a false sense of security: circumventing defenses to adversarial examples,” in Proceedings of the 35th International Conference on Machine Learning (Cambridge, MA: PMLR), 274–283.
Belkin, M., and Niyogi, P. (2003). Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 15, 1373–1396. doi: 10.1162/089976603321780317
Berry, T., and Giannakis, D. (2020). Spectral exterior calculus. Commun. Pure Appl. Math. 73, 689–770. doi: 10.1002/cpa.21885
Berry, T., and Harlim, J. (2016). Variable bandwidth diffusion kernels. Appl. Comput. Harmon. Anal. 40, 68–96. doi: 10.1016/j.acha.2015.01.001
Berry, T., and Sauer, T. (2016). Local kernels and the geometric structure of data. Appl. Comput. Harmon. Anal. 40, 439–469. doi: 10.1016/j.acha.2015.03.002
Berry, T., and Sauer, T. (2019). Consistent manifold representation for topological data analysis. Foundations of Data Science 1, 1. doi: 10.3934/fods.2019001
Carlini, N., and Wagner, D. (2017). Towards evaluating the robustness of neural networks. arXiv [preprint]. doi: 10.1109/SP.2017.49
Cho, S., Jun, T. J., Oh, B., and Kim, D. (2020). “DAPAS: denoising autoencoder to prevent adversarial attack in semantic segmentation,” in 2020 International Joint Conference on Neural Networks (IJCNN), pages 1-8. Conference Name: 2020 International Joint Conference on Neural Networks (IJCNN) (Glasgow: IEEE).
Coifman, R. R., and Lafon, S. (2006a). Diffusion maps. Appl. Comput. Harmon. Anal. 21, 5–30. doi: 10.1016/j.acha.2006.04.006
Coifman, R. R., and Lafon, S. (2006b). Geometric harmonics: a novel tool for multiscale out-of-sample extension of empirical functions. Appl. Comput. Harmon. Anal. 21, 31–52. doi: 10.1016/j.acha.2005.07.005
Dietrich, F., Bello-Rivas, J. M., and Kevrekidis, I. G. (2021). On the correspondence between gaussian processes and geometric harmonics. arXiv [preprint]. doi: 10.48550/arXiv.2110.02296
Engstrom, L., Ilyas, A., Salman, H., Santurkar, S., and Tsipras, D. (2019). Robustness. Python Library. Available online at: https://github.com/MadryLab/robustness
Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Explaining and harnessing adversarial examples. arXiv [preprint]. doi: 10.48550/arXiv.1412.6572
Ilyas, A., Santurkar, S., Tsipras, D., Engstrom, L., Tran, B., and Madry, A. (2019). Adversarial examples are not bugs, they are features. arXiv [preprint]. doi: 10.48550/arXiv.1905.02175
Kurakin, A., Bengio, A., and Goodfellow, A. K. (2018). “Adversarial examples in the physical world,” in Artificial Intelligence Safety and Security (Boca Raton, FL: Chapman and Hall/CRC), 14.
Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. (2019). Towards deep learning models resistant to adversarial attacks. arXiv. [preprint]. doi: 10.48550/arXiv.1706.06083
Moosavi-Dezfooli, S.-M., Fawzi, A., Fawzi, O., and Frossard, P. (2017). “Universal adversarial perturbations,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Honolulu, HI: IEEE), 1765–1773. Available online at: https://ieeexplore.ieee.org/document/8099500
Moosavi-Dezfooli, S.-M., Fawzi, A., and Frossard, P. (2016). “DeepFool: a simple and accurate method to fool deep neural networks,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Las Vegas, NV: IEEE), 2574–2582.
Papernot, N., McDaniel, P., Goodfellow, I., Jha, S., Celik, Z. B., and Swami, A. (2017). “Practical black-box attacks against machine learning,” in Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, ASIA CCS '17 (New York, NY: Association for Computing Machinery), 506–519.
Simonyan, K., and Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv [preprint]. doi: 10.48550/arXiv.1409.1556
Stutz, D., Hein, M., and Schiele, B. (2019). Disentangling adversarial robustness and generalization. arXiv [preprint]. doi: 10.1109/CVPR.2019.00714
Su, D., Zhang, H., Chen, H., Yi, J., Chen, P.-Y., and Gao, Y. (2018). Is robustness the cost of accuracy?-A comprehensive study on the robustness of 18 deep image classification models. arXiv [preprint]. 631–648. doi: 10.1007/978-3-030-01258-8_39
Su, J., Vargas, D. V., and Kouichi, S. (2019). One pixel attack for fooling deep neural networks. IEEE Transact. Evol. Comp. 23, 828–841. doi: 10.1109/TEVC.2019.2890858
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., et al. (2014). Intriguing properties of neural networks. Technical Report. arXiv. doi: 10.48550/arXiv.1312.6199
Tabacof, P., and Valle, E. (2016). “Exploring the space of adversarial images,” in 2016 International Joint Conference on Neural Networks (IJCNN) (Vancouver, BC: IEEE), 426–433.
Tramèr, F., Kurakin, A., Papernot, N., Goodfellow, I., Boneh, D., and McDaniel, P. (2020). Ensemble adversarial training: attacks and defenses. arXiv [preprint]. doi: 10.48550/arXiv.1705.07204
Tsipras, D., Santurkar, S., Engstrom, L., Turner, A., and Madry, A. (2019). Robustness may be at odds with accuracy. arXiv [preprint]. doi: 10.48550/arXiv.1805.12152
Xu, W., Evans, D., and Qi, Y. (2018). “Feature squeezing: detecting adversarial examples in deep neural networks,” in Proceedings 2018 Network and Distributed System Security Symposium (San Diego, CA: Internet Society).
Keywords: diffusion maps, kernel methods, manifold learning, Nyström approximation, adversarial attack, image classification, projected gradient descent
Citation: Mahler A, Berry T, Stephens T, Antil H, Merritt M, Schreiber J and Kevrekidis I (2024) On-manifold projected gradient descent. Front. Comput. Sci. 6:1274181. doi: 10.3389/fcomp.2024.1274181
Received: 07 August 2023; Accepted: 22 January 2024;
Published: 14 February 2024.
Edited by:
Pavan Turaga, Arizona State University, United StatesReviewed by:
Chao Tong, Beihang University, ChinaCopyright © 2024 Mahler, Berry, Stephens, Antil, Merritt, Schreiber and Kevrekidis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aaron Mahler, YWFyb24ubWFobGVyQHRlbGVkeW5lLmNvbQ==; Tyrus Berry, dGJlcnJ5QGdtdS5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.