- LGPM, CentraleSupélec, Université Paris-Saclay, Centre Européen de Biotechnologie et de Bioéconomie (CEBB), Pomacle, France
In this study, we present a fast algorithm for the numerical solution of the heat equation. The heat equation models the heat diffusion over time and through a given region. We engage a finite difference method to solve this equation numerically. The performance of its parallel implementation is considered using Message Passing Interface (MPI), Compute Unified Device Architecture (CUDA), and time schemes, such as Forward Euler (FE) and Runge-Kutta (RK) methods. The originality of this study is research on parallel implementations of the fourth-order Runge-Kutta method (RK4) for sparse matrices on Graphics Processing Unit (GPU) architecture. The supreme proprietary framework for GPU computing is CUDA, provided by NVIDIA. We will show three metrics through this parallelization to compare the computing performance: time-to-solution, speed-up, and performance. The spectral method is investigated by utilizing the FFTW software library, based on the computation of the fast Fourier transforms (FFT) in parallel and distributed memory architectures. Our CUDA-based FFT, named CUFFT, is performed in platforms, which is a highly optimized FFTW implementation. We will give numerical tests to reveal that this method is up-and-coming for solving the heat equation. The final result demonstrates that CUDA has a significant advantage and performance since the computational cost is tiny compared with the MPI implementation. This vital performance gain is also achieved through careful attention of managing memory communication and access.
1 Introduction
Initially, partial differential equations are widely used to express many phenomena in nature. These equations are known for their complexity, so the finite difference method is needed to solve them. This approach consists of iterating from a given initial condition to converging to a solution. The heat diffusion is one of these equations, in which there are many recent studies on numerical schemes (Belhocine and Wan Omar, 2018; Sene, 2019; Rasheed et al., 2021) applied to discretize it. For instance, authors propose in a new approach in the study mentioned in the reference (Singer, 1938; Kravčenko et al., 2019) for parallelizing space-time BEM (boundary element method) for the heat equation. It consists of distributing each block corresponding to a submesh obtained from an input mesh over processors. It is important to note that this method is based on a decomposition technique, providing good accuracy compared with other classical ones (Bluman and Cole, 1969; Cannon, 1984). The authors have developed other methods of continuous-in-time financial and computational fluid models (Chakkour and Frénod, 2016; Chakkour, 2017, 2019, 2022, 2023).
The Runge-Kutta (RK) method is a finite difference technique for solving partial differential equations. It is usually used to reach efficiency requirements with low dissipation errors and limitations of oscillatory solutions. There are a great variety of different schemes based on RK (Anastassi and Simos, 2005; Tselios and Simos, 2005). In the present work, we propose a fourth-order RK4 method (Ben Amma et al., 2019; Xu et al., 2020; Habibi et al., 2022) that considered sufficient to guarantee dissipation. Using it indicates that it is efficient for the numerical solution of the heat equation with a periodic solution. In this case, our suggested method is suitable for a small time step, not only when oscillations occur.
The massively parallel computer system has emerged as an important research topic in recent years. It is involved in various computational methods, particularly the finite difference approach to solve some partial differential equations. The present study aims to apply the parallel computer system to the finite difference method to accelerate solutions from the heat equation using the fast Fourier transform algorithm, which plays a more prominent role in this method.
The originality of our study is the adaptation of numerical schemes and the FFTW parallel library to solve this equation. A conceptual framework is running in parallel with distributed memory architectures. Particularly, numerical solution on regular grids is efficiently performed in the best way of parallelization. The data are decomposed onto different processes with minimizing the required message passing. Using the FFTW library, which is written with MPI, allows for independent benefits. One of them is to avoid having to code routines when Fourier operators are utilized. The symmetry property satisfied by operators and implemented by this library is taken into account for a full advantage of a wasted memory. On the other hand, CUFFT is introduced as an efficient parallel algorithm for computing FFT on massively parallel processors, such as GPUs. It is used in our implementation and is considered a faster algorithm (Wang et al., 2016; Pirgov et al., 2021) than other modern FFT libraries. This implementation aims to satisfy the computationally demanding application.
The remainder of the study is organized as follows. In Section (2), the approach of using the adaptive library FFTW for the discrete Fourier transform is presented. This library is highly optimized and always has degrees of freedom concerning the chosen DFT algorithm strategy. Section (3) describes how to solve the heat equation with discretization. Section (4) focuses on developing parallel algorithms using the Finite Difference Method and FFTW. Several tests are presented to analyze the impact of computing architectures GPU and MPI on the performance of parallel implementations. Finally, Section (5) provides a conclusion with some perspectives in future studies.
2 FFTW software library
The FFTW (Frigo and Johnson, 2005) is a software library based on Message Passing Interface standard (MPI) for calculating Fast Fourier Transforms (FFT) on parallel memory architectures. Certainly, FFT is one of the principal algorithms in scientific computing. The so-called Cooley and Tukey FFT algorithm (Cooley and Tukey, 1965) was published in 1965 and is known for its recursive method based on the divide and conquer approach. It provides a wide number of applications in various scientific fields, such as engineering and mathematics. A number of algorithms are derived from this existing and simple version to produce a suitable version dependent on the need. A new version described in the study mentioned in the reference (Cicone and Zhou, 2021) consists of efficiently implementing the iterative filtering algorithm based on FFT. The objective of this class of algorithm FFT is to compute the Discrete Fourier Transform (DFT) of length N assumed to be a power of two, with a lower cost in time. In fact, it requires just O[Nlog2(N)] operations. This significant gain shows that this library performs well in calculating the FFT of complex or real data.
The FFTW is able to compute globally a discrete approximate solution to many spectral methods (Burns et al., 2020) which were challenging to parallelize in a distributed memory environment. The spectral methods are considered one of the most frequently used methods due to its versatility and high efficiency. These methods are often recommended than finite difference methods since they converge faster with rising degrees of freedom (Feng and Zhao, 2020). This library is exploited in a wide variety of other fields, such as computer science and engineering. It is the heart of many signal processing and exploring the best algorithmic tool. Examples of their modern applications and usage include image reconstruction in life sciences (Dan et al., 2021; Prigent et al., 2023), visualization of large biological specimens in bioinformatics (Muhlich et al., 2022), weather simulations (Khouzami et al., 2022; Grady et al., 2023), option price prediction in financial mathematics (Alfeus and Schlögl, 2019; Phelan et al., 2019; Salavi et al., 2022), and machine learning (Dao et al., 2019; Aradhya et al., 2022). There are also other applications of FFTW in audio engineering (Faerman et al., 2021, 2020). The paper (Vijendra Babu et al., 2023) aims to suggest a digital code-modulated MIMO system; this code is based on the maximum a posteriori machine learning algorithm. The research (Gangadhar et al., 2023) completes this study and is devoted to Engineering computational models and procedures to address real-world issues with language comprehension. FFTW is utilized to create a wide range of audio effects and correct vocal recordings (Arts and van den Broek, 2022). The capacity to manipulate complex signals is a powerful tool in audio engineering. To validate the FFTW library, we will test the discrete Fourier transform (DFT) over the trigonometric polynomial function sampled at a finite number of points. Consider we have a Cosinus function f, which is defined on the interval en[0, 2π]. For our purposes, these points will be equally spaced, xi and yj means the 2D grid coordinates based on the coordinates contained in vectors x and y, where N is the number of sample points, i.e., Δx = Δy. The approximation to function f at these sample points is written as a finite dimensional vector given as follows:
where,
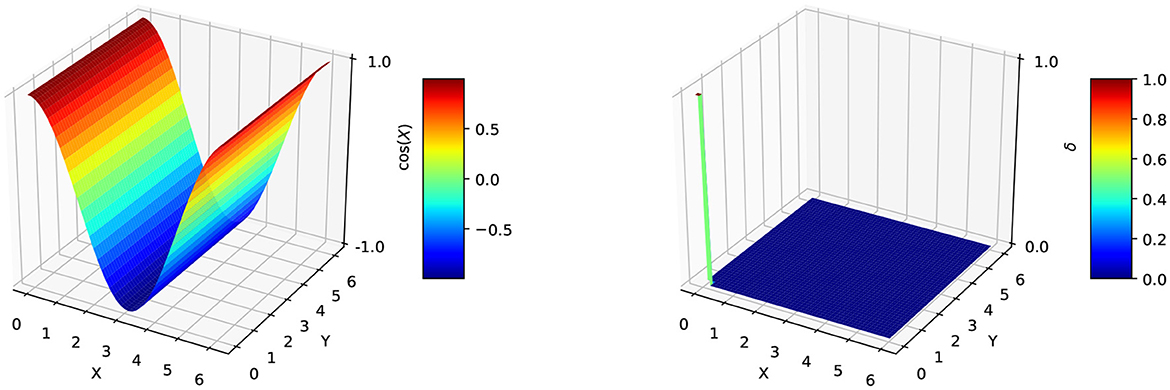
When the input function is considered real, two situations are presented to implement data in FFTW. The first one is Real-to-Real Transform, and the second one is Real-to-Complex Transform. Figure 1 illustrates the case of Real-to-Real Transform applied to Cosinus data function defined in relation (2). The obtained function is consequently the Dirac distribution, achieving this verification.
3 Heat equation
This section is dedicated to determining approximate numerical solutions of the heat equation using Fourier spectral methods. In order to simplify the model, the imposed boundary conditions are considered periodic. The heat equation is initially introduced to describe heat conduction, which appears in other branches of theoretical physics. For instance, it allows the report of diffusion phenomena and the probabilistic representation of Wiener process.
Let be Ω the square with side length 2π, the bidimensional heat equation is given as follows:
where the parameter α is the thermal diffusivity, and u(x, t) accounts for the temperature distribution. First, discretizing x such that nodes xi, j are uniformly distributed in en[0, 2π], where indexes i and j mean theirs labels according, respectively, to each direction, i = 0, 1, 2, …, nx, j = 0, 1, 2, …, ny. Furthermore, since the partial differential equation defined in the study mentioned in the reference (3) could not be solved exactly, a new technique is investigated to get approximate solutions. The purpose is to transform this initial linear equation into a set of independent ordinary differential equations that can be solved easily. The Fast Fourier transform is used to solve the linearized equation, applying the Fourier Transform operator to both sides of Equation (3) to obtain:
Here, kx and ky are the coefficients of the kth Fourier mode following x and y-directions, respectively. We implement time schemes such as forward Euler and Runge-Kutta methods to compute solutions in the spectral space. After obtaining solutions in this space, the inverse Fast Fourier Transform yields them in the real space. We will let ûn denote the approximate solution at time step n, and h denote the time step, i.e., . The discretization with the forward Euler scheme in time is explored in relation (4) to get:
Formally,
The suite function defined in the study mentioned in the reference (6) converges exponentially to the unique solution . Since we have the exact solution, we will compare the numerical solution produced by the code with this analytical solution. Next, the inverse Fast Fourier Transform (IFFT) denoted by is applied to obtain a solution in a real space.
A new time scheme, the explicit four-stage fourth-order Runge-Kutta method, is applied to ensure the quadratic conservation laws. For that, defining the function f as follows:
Then, the approximation of in the initial problem (4), when is known, can be expressed by the following relation:
where the coefficients f1, f2, f3, and f4 are classically computed in four intermediate points as follows:
Denoting C⋆ a potentially large constant independent of the time step h. The Forward Euler (FE) scheme is convergent over compact spectral space and is said to be convergent since the global error tends toward zero when h requires to be much smaller. The definition of this convergence means:
Similarly, the Runge-Kutta method (RK4) with time step h is said to be convergent with order four on compact spectral space, if it holds
Now, we briefly deal with how to solve the initial problem, which is the heat equation in spectral space. Let us start with basic ODE (4) with fixing the initial condition, . Figure 2 is shared into four diagrams that illustrate these two exact and approximate solutions, with plotting the order of this scheme in wide and thin logarithmic scales. These two numerical solutions are computed using the fourth-order RK4 method, in which the exact one is computed using relation (6), as shown in Figure 2A. The aim is to verify the sharpness of our error. To explore in detail the behavior of this numerical error, as shown in the top right diagram Figure 2B, it oscillates well over thin logarithmic scale [10−7, 1]. Concerning the order, the Runge-Kutta RK4 of the fourth-order is faster with respect to the explicit Euler scheme. Indeed, as long as a time step is finer, the two graphs are adjacent (see Figures 2B–D).
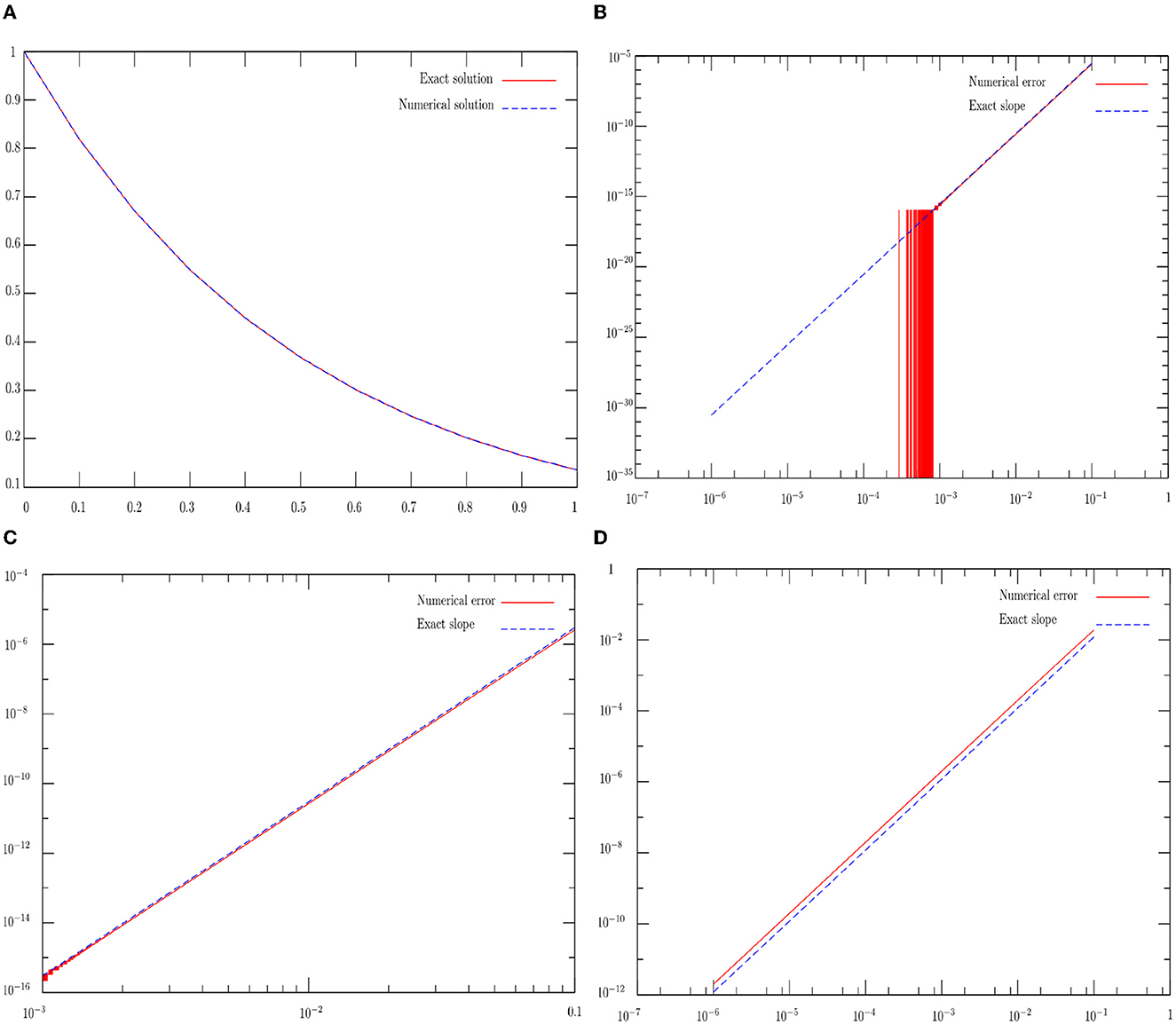
Figure 2. A numerical solution to the ODE defined in Equation (4) demonstrates the accuracy of the Runge-Kutta (RK4) for an one time step is presented in the top left diagram. The top right diagram illustrates the error's order of RK4 in thin logarithmic scale [10−7, 1]. The bottom left diagram shows the same previous error in wide scale interval [10−3, 10−1]. The bottom right diagram illustrates the error's order of the Forward Euler (FE) time scheme. (A) Numerical solution with RK4. (B) Error's order of RK4 in [10−7, 1]. (C) Error's order of RK4 in [10−3, 10−1]. (D) Error's order of FE in [10−7, 1].
4 GPU programming and CUDA
This section is devoted to presenting the background knowledge of GPU architecture and CUDA programming model to make the best way to use them. The latest development activity in Graphics Processing Units (GPUs; Brodtkorb et al., 2013) permits an extension of high-performance computing in many purpose fields. This technology is involved highly in parallelization, multithreading, and many-core processing with very high memory bandwidth and enormous computational horsepower. The GPU utilized in the current study was the GeForce GTX-480, the second generation of the CUDA enabled NVIDIA GPUs. This high-end graphics card is built on the 40 nm process and structured on the GF100 graphics processor; in its GF100-375-A3 variant, the card supports DirectX 12. Figure 3 shows NVIDIA GeForce GTX 480 that is connected to the rest of the system using a PCI-Express 2.0 × 16 interface. This card measures 267 mm in length, and its price at launch was 499 US Dollars. The oldest driver is used because all necessary bugs are fixed and supported on the CUDA version. GTX-480 architecture is based on the Scalable Processor Array (SPA) framework. The SPA architecture in GTX-480 consists of 10 Thread Processing Clusters (TPCs).
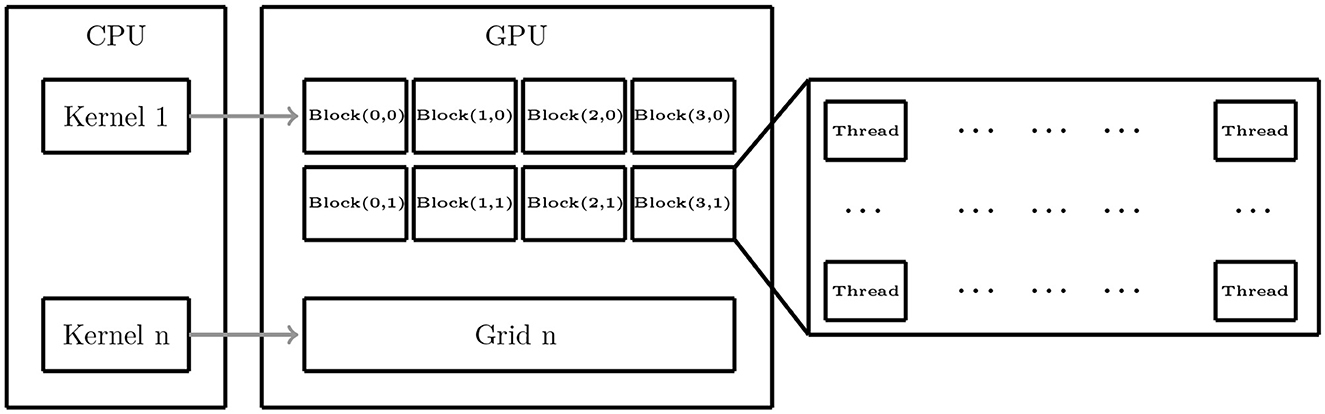
A multi-core contains multiple streaming multiprocessors (SMs) in the GPU hardware architecture. Each SM incorporates a fixed number of streaming processors (SPs). CUDA (Compute Unified Device Architecture; Buck, 2007; Nickolls et al., 2008) is a C-language a compiler that relies on the PathScale C compiler. For this reason, it is viewed as a minimal extension of the C and C++ programming languages. CUDA is supported on NVIDIA GPUs with unified graphics and computing architecture. The aim of using NVIDIA is to have access to a software platform called Compute Unified Device Architecture to authorize most translations of C code onto the GPU. Our motivation for using this architecture comes from choosing an excellent programming environment and harnessing the power of the available parallel processors with relative facility. It allows us to achieve speed-ups of a hundred times on the developed application. The CUDA programming model conveys parallelism absolutely, and each kernel executes on a fixed number of threads. A kernel is an entirely conventional C program for one thread from the hierarchy of thread groups. This function is also defined as the unit of parallelism issued by the host computer to the GPU. It is usually started by the CPU and executed by the GPU. When invoking a kernel, a kernel is executed in parallel across a set of parallel threads. Since a kernel can create dynamically a new grid with the exact number of thread blocks, CUDA is more flexible than most realizations of the SPMD (single-program multiple-data) model. The user arranges these threads into a grid defined as a set of thread blocks. Then, the parallel execution and thread management are automatic with a simple scheduler. Figure 4 illustrates a clear flowchart in CUDA architecture (Nvidia, 2008).
To clarify the manipulation of lot numbers of threads in CUDA, this C-language compiler provides the conception of grids and blocks of threads. The bidimensional computational domain Ω, introduced previously, is divided into sets of blocks called grids containing hundred of threads, as shown in the right side of Figure 4. The installed driver proposes the possibility to determine the location of the block in the grid, even the location of the thread in the block. This determination is realized through the system variables, which makes this identification operate threads in the best way. The command syncthreads() are used to execute the synchronization between a collection of threads of the same block. However, synchronizing a group of threads between them from various blocks is impossible. Indeed, these threads in a single block communicate through the shared memory. The user does not affect the result while the processing of a single thread or threads group begins. In this situation, the hardware is subjected to managing this result. If a kernel has been run on the GPU platform, the CPU gives all the necessary allocation memory to the GPU. This allocation is accompanied by transmitting the associated data to this memory. Consequently, the CPU makes the kernel work on the GPU. Then, the results come back to the CPU.
Due to the significant advantages of GPUs, we would like to explore the performance of the parallelized heat equation on CUDA architecture. Several software packages are needed to execute the developed framework model on the GPU. These packages are consistent with different hardware types. This implementation focuses on packages, such as CUDA parallel computing platform, OpenCL, and Petsc library, as described hereafter. The model is run on NVIDIA GPUs. The framework is inherently parallel and can profit from the GPU technology.
Due to the different features of various architectures, many existing FFT algorithms and their implementation are required. For the CPU implementation with CUDA, we will be able to use a library called CUFFT (Nvidia, 2007), which is actually based on the FFTW library. CUFFT handles FFTs of varying sizes on both real and complex data. We do not develop our own custom GPU FFT implementation in this framework since a simple interface for computing FFT is provided for utilizing GPU devices. NVIDIA has developed the CUFFT to achieve performance improvements on the CUDA platform. One applicable property of this library is that it can be used to expertly compute several FFTs at one feature. This use is also motivated by supporting more elaborated input and output data layouts. The way this library is involved in the computation is to issue a configuration mechanism named a plan that uses some specific building blocks to advance the Fourier Transform after applying the FFT function from the CUFFT library to various variables. Then, the specific implementation of the heat equation on CUDA architecture will be carried out to obtain the iterated vector in the spectral space. Some operations are requested, such as element-wise multiplication will be done with high computing capacity. GPUs offer the possibility of parallelizing these operations. On the other hand, Sparse matrices power the implementation of these operations. Next, Equations (9)–(10) are written in the form of a sparse linear algebraic system used to implement these operations since the matrix contains some zero elements.
For solving the heat Equation (3) through algebraic equations, several possible approaches (Cerovskỳ et al., 2014; Sivanandan et al., 2015) may be used to obtain the discrete-space model. These approaches are summarized by employing numerical schemes based on mathematical discretization, mainly the forward time-centered space, explicit scheme, or Crank-Nicolson scheme. Many studies (Widder, 1976; Eldén, 1995; Hutzenthaler, 2020) are aimed at using the central scheme to approximate the derivative at each mesh point. Denoting to guarantee numerical scheme stabilization. The approximation of second derivatives is described in these contributions over the equidistributed grid as follows:
The numerical scheme presented by the relation (13) provides all the information to generate the code in parallel. In the beginning, a quantity u has to be computed. Then, the computation at a time iteration n+1 depends on the results at time iteration n. Then, at each time iteration, an applier matrix is called and instantiated to manage the output of this scheme, as we will explain hereafter.
The main contribution of this part consists of illustrating the impact of the CUFFT (based on FFTW library) on the efficiency of parallelization. To better achieve this contribution, Algorithm 1 is proposed and implemented to parallelize the heat equation in two-dimensional space that illustrates the classical program from the literature. On the other hand, the targeted algorithm to compute the temperature vector û in a given time t has been introduced by the formula (9). Its general form is presented as Algorithm 2; the matrix (the infinitesimal generator) is associated with the function f defined by the study mentioned in the reference (8) applied to the grid with the initial condition û0 and the step h. Then, these both algorithms are compared later to benchmark their performance on the CUDA platform.
Notably, during two fast Fourier operations, the iterations in the loop in time will be run greatly to assure convergence. The execution in time costs a lot compared with the direct and inverse operators. In addition this, at each time, many matrix-vector multiplications are involved in this calculation. For this reason, A High-Performance Sparse Fast Fourier Transform Algorithm CUSFFT is not requested in the implementation. The authors in the study mentioned in the reference (Hassanieh et al., 2012) propose a new sub-linear algorithm for sparse Fourier transform. This algorithm is explored in the study mentioned in the reference (Wang et al., 2016) and performed on massively parallel processors. We just use the CUFFT library on massively parallel architectures GPUs as described before. For both algorithms, the parallelized implementation technique using CUDA begins with several initializations, such as the mesh grid, the initial temperature, and the necessary memory to transfer the data to the allocated memory. This technique is based on Divide and Conquer (Horowitz and Zorat, 1983; Atallah et al., 1989) to improve the division of blocks of data under analysis. Precisions for Algorithm 1; the bidimensional cartesian topology is subdivided into four regions: east uOld[ET], weast uOld[WT], north uOld[NT], and south uOld[ST] presenting, respectively, ui+1, j, ui−1, j, ui, j+1, and ui, j−1, as can shown in Figure 5. Each region is a square block of equal size that interchanges information in each direction. The temperature is defined on discrete positions within each block.
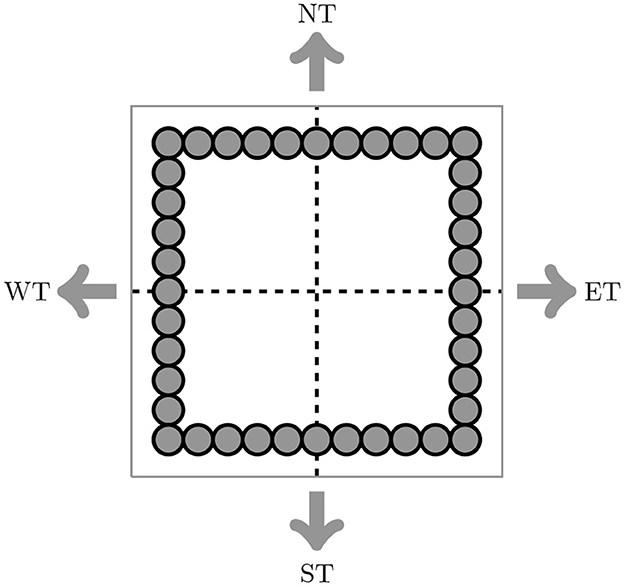
Figure 5. Communication mode shows the domain partition into four blocks in each direction (north, south, east, and west).
Recalling that the three types of GPU memory are mainly global memory, shared memory, and registers. Shared memory is located on the GPU chip and is much faster and smaller than global memory. Notably, the shared memory is more complicated to build but easy to use, while the distributed one is easier to build but difficult to use. Since the CUDA shared memory is an extremely powerful feature of the CUDA kernel, the parallel programming model using the CUFFT library is run on this memory hardware architecture (Algorithm 2). The heat equation has been parallelized on high-performance and distributed architectures MPI (Algorithm 1) to comprise these two types of memories. We will better achieve the comparison later between these Algorithms on these two different memories with the same collection of threads.
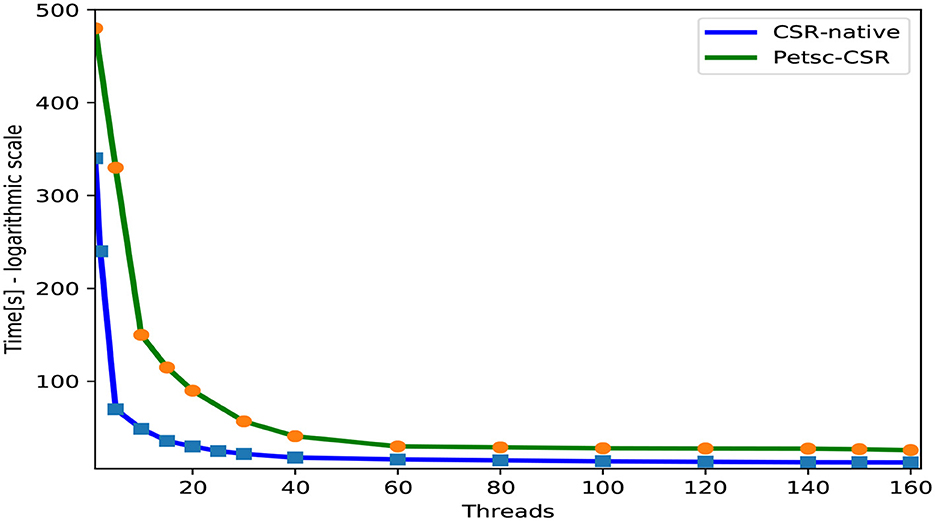
On the other hand, the parallel implementation provided on Algorithm 2 is based on available functions in Petsc library of computing routines over processors and adapted to multi-processor systems. There are functionalities from this library perform the linear algebraic operation acting on sparse matrices. The information concerning the matrice storage format in the memory is examined as the CSR (Compressed Sparse Rows) format supported naturally by this library on Intel processors. The native CSR mode has its constraints through High-performance parallel computers. The native one is based on sequential CPU implementation using the LAPACK package (Anderson et al., 1999). Although, CSR format defined in Petsc is advanced itself with a simple parallel algorithm for computing the matrix-vector multiplication. In this case, the product of a square m2-matrix and a vector with m components is realized with a given number of threads, where every thread computes each component of the result. This strategy investigated in Petsc is efficient because the operations are executed without considering zeros. These suitable data structures and associated fragment routines existed in Petsc using the massive parallelism grant to accelerate the operation and decrease the runtime. This storage format admits an efficient parallel algorithm compared with the native one. Additionally, since this multiplication is generally limited by memory for sparse matrices, the Petsc CSR mode remains the performing one from the memory compared with the native one. Three array lists describe this storage. The non-null values are stored in an element's array in row order, named Val. Each component of these values array has an entry in the column index Col to express its location in the matrix . Array Ptr contains the offset of each matrix row in arrays Val and Col. Moreover, it is desirable to use another analogous storage format to CSR for sparse matrices, named CSC (Compressed Sparse Columns). The non-zeros of each column in CSC format are stored in contiguous memory locations. There are many studies (Elafrou et al., 2019; Hong et al., 2019; Aliaga et al., 2022) that present other new storage formats for sparse matrices, such as compressed sparse blocks (CSB). Notably, the CSR format is straightforward to be implemented on the GPU, and storing data matrix in the format of these arrays improves the efficiency of data transfer and the expected matrix-vector multiplication. In addition, the operations acting on matrix stored in this format are part of the Petsc library. For the implementation of the matrix-vector multiplication, a routine MatMult is used. In parallel, each process possesses a successive row block of the matrix and a part of the input vector corresponding to these rows. After this implementation, the operation of the vector addition is requested in this algorithm. Next, the routine VecSum is used to compute the sum of two compatible vectors. Implementing the parallel product of the non-zero structure matrix by vector allows for accelerating the fourth-order Runge-Kutta method (RK4). This approach is used to the good advantage of the thread-level parallelism, thread-level parallelism, and vectorization for vector addition.
In what follows, we will demonstrate the efficacy of the CSR storage format in the implementation of the Runge-Kutta method (RK4). We evaluate our approach with the native format and the adaptive CSR storage mode in PETSc for various numbers of cores. Figure 6 shows the elapsed time of the algorithm in several CSR storage schemes for each testing matrix . These tests are carried out with the most advantageous affinity setting. The proposed implementation of these formats makes use of the Intel compiler. For each test, the numerical code is compiled by using the Intel Fortran compiler (ifort), accompanied by the -O3 optimization flag, to perform automatic vectorization and maintain the ability to optimize the code. The results show that the runtime decreases along with the rise in the number of threads.
FFT is used widely in many scientific fields, such as mathematical applications and engineering. We have shown in Section 2 that the Fast Fourier Transform (FFT) implemented in the FFTW library is an algorithm to calculate the discrete Fourier transform (DFT) from a data array. The aim here is to express various performances between GPU and CPU by some numerical test cases using this algorithm since it is involved in the heat equation resolution. When computing the FFT, the GPU has a considerable advantage in terms of computation time compared with the MPI. Table 1 shows that the GPU takes approximately six percent of the time as the CPU for the larger vector size. Notably, the time cost for the GPU and CPU computation is approximately the same for small-size problems.
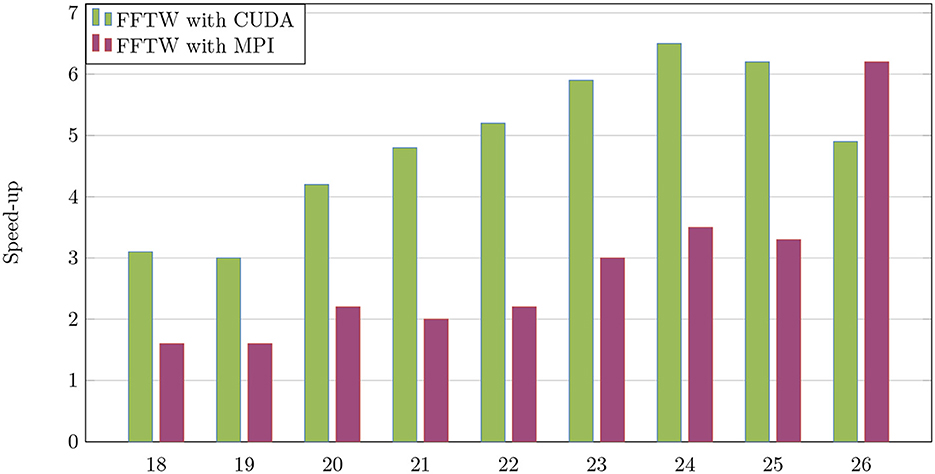
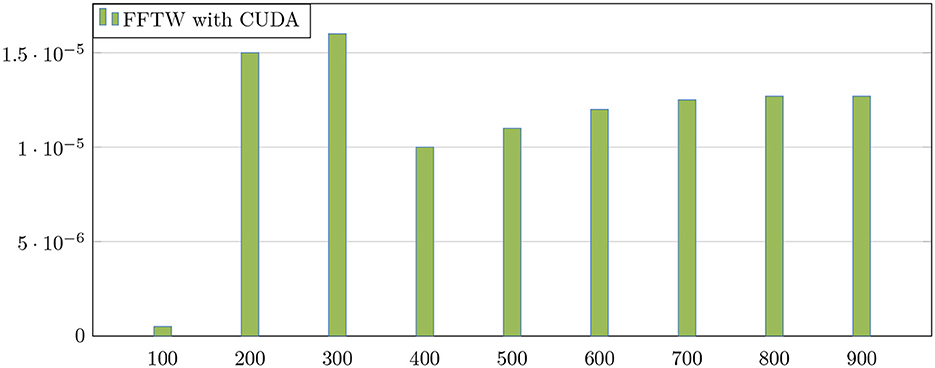
In what follows, we will evaluate the performance of sparse FFT on GPUs. This performance is considered the fastest implementation compared with the same run on the MPI platform. The sparsity parameter is fixed as follows: k = 500. We report the performance from the FFTW algorithm for various signal sizes n ranging from 218 to 226. We plot the speed-up and error precision on the parallel FFTW on GPU. Figure 7 shows the comparison of the speed-up of the FFTW algorithm between both platform CUDA and MPI. It shows that the acceleration grows with the signal size until reaching the maximum value 6.5 for n = 224. In Figure 8, we have fixed the parameter n = 226, and the average 1 error is plotted for different sparsity values k. Recalling that the first common discrete signal quantity is 1-norm, which is defined from any given signal A as follows:
The aim is to show how this error is accumulated per large coefficient. Figure 8 proves that this error is tiny and minimal, preserving consequently the accuracy of the algorithm. Increasing the sparsity parameter k ensures that the achieved precision is stable.
Let us consider the heat equation given by Equation (3) with an initial condition generated randomly in the spectral space. In order to explain what we can see in pictures of Figure 9 is shared into six diagrams that can be interpreted as follows. An intrinsic routine RAND is used in order to return to a real pseudo-random number. The inverse Fast Fourier Transform of this initial condition gives a new function in the physical space (see the top left diagram). Solving the heat equation in physical space demonstrates that a solution takes the form of Cosinus function with a higher step time, as shown in the top right diagram. It shows that the heat equation using backward Euler's method is convergent at the final iteration. Notably, even after 10 successive iterations, which remain sufficiently small, the solution changes slowly. This solution, compared with the initial one, is presented in the top middle diagram. An adaptive method is applied to the solution in order to identify the energy spectrum. This identification is carried out by the propagation of heat flow modeled through the domain Ω (see the bottom diagrams). They illustrate good physical results for transferring the heat energy from zones of higher temperatures to zones of lower ones.
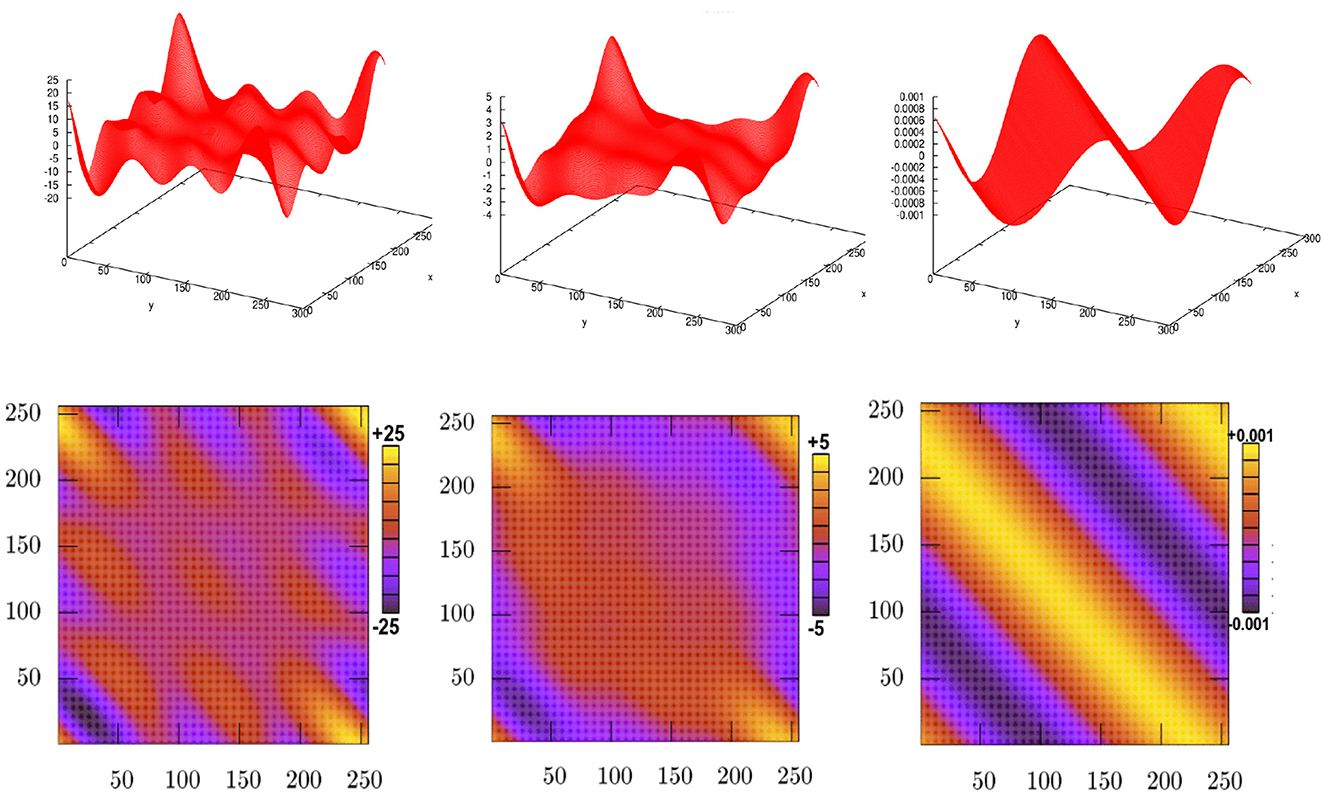
Figure 9. Numerical solution to the heat equation with an initial random function in different times, presented at the top diagrams. Each solution given in the (top) diagram is associated with its energy spectrum at each (bottom) diagram.
To illustrate the validation of our analytical model in parallel, we ran it on four processors. In fact, the job is shared with them, in which each task is affected by each one. Each processor has a partial part of the solution. The total solution is obtained by transferring the three parts acquired on each processor to the remaining one. Different solutions to the heat equation are obtained using the separation technique of variables. The basic idea is to verify that this solution corresponds to one form of a combination of trigonometric functions. Additionally, notably, the heat equation is simulated in a periodic setting, in which an initial condition is given. Then, it explains that the approximated solution behaves as a Cosinus function at equally spaced points.
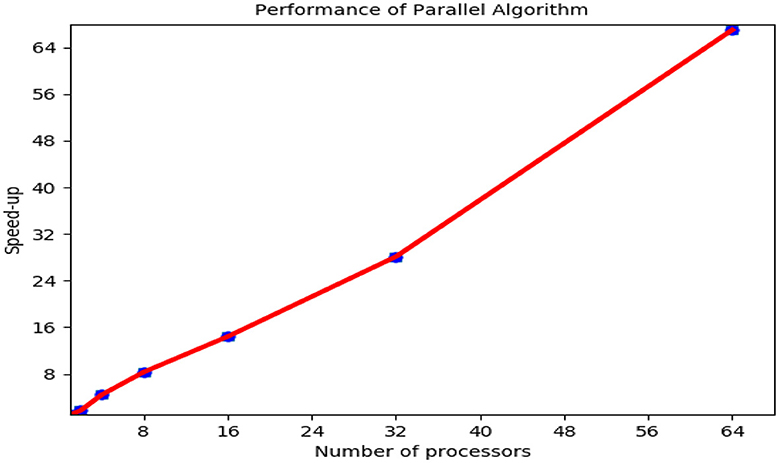
Our implementation relies on the distributed programming method performed by the Message Passing Interface (MPI) 1.2.6 version of the ifort compiler. By choice, an N-processor system has to generate a program speed-up. First, a comparative analysis of the serial performance has been carried out. Figure 10 shows the measured parallel performance of the heat equation. We run a parallel code on a cluster sized at hundreds–thousands of nodes. This cluster is based on 64-node architecture computer system. The code executed in time was tested on various numbers of processors. The speed-up acquired (e.g., 67 for 64 processors) was very motivating. In other words, the speed-up is still notable even for the rest of the processors. Increasing the time step will achieve a good parallel speed-up. As shown, the solution was obtained satisfactorily on the multicore computer for the communication of the computing platform.
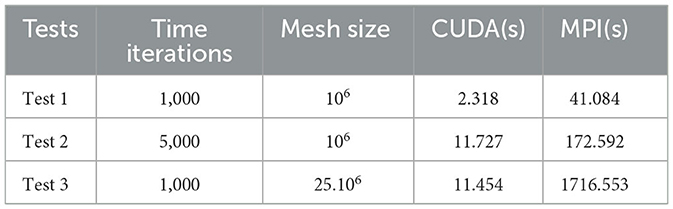
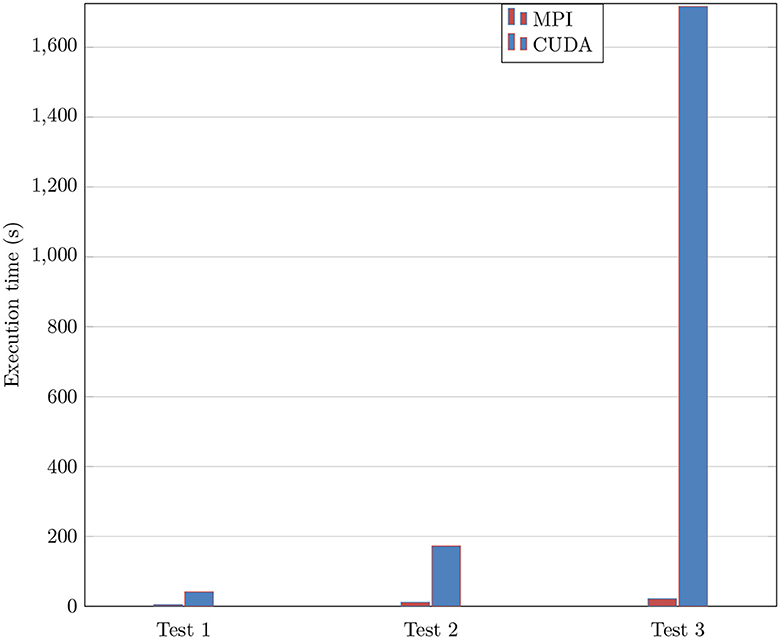
The number of applications exploiting the CUDA platform has expanded significantly. This choice is motivated by the ability to deliver more excellent performance in parallel processing. A new programming approach with CUDA is investigated to make our application more effective. The aim is to achieve superior performance than the MPI standard in our purpose application. In this approach, the data distribution is based on GPU nodes is considered the main computing mechanism. Table 2 shows the execution time performed to obtain the solution of the heat equation following three main tests. These tests are run over two platforms having the same cores to evaluate the robustness. The first test is a mesh of one million elements with 1,000 in time iterations. In this test, the code is executed in 2.318(s) with the CUDA technology with 820 cores. In the second test, the domain size is always the same as the previous one with modifying the number of iterations, which will be 5, 000. The execution time is amplified by five as the number of iterations. In the last test, the time iterations remain the same with respect to the first one, and the number of domain sizes will be changed. These tests demonstrate that the mesh size has more influence on the result than the time iterations. Figure 11 shows the progression of time execution according to these tests, as shown in Table 2. The implementation results on a GPU platform are very significant and best compared with the MPI one. Furthermore, the execution of the heat equation on the CUDA platform with graphics processing is a hundred times faster than the MPI one for refined mesh. Then, GPU architecture provides high efficiency at a very low valuation.
5 Impact and conclusion
The new 2D numerical code allows the parallelization of the heat equation under the MPI parallelizable library, which has been successfully realized. The validation of the parallelized numerical results was an essential asset in achieving the objectives of this article. Through these results, we have demonstrated that the execution time of the CUDA implementation is almost faster compared with the other MPI and OpenMP implementations. In future studies, we would like to move directly from the heat equation to Navier-Stokes ones by parallelizing the advective term. The efficient implementation of the FFTW library will be applied to solve the Navier-Stokes equations numerically in a cubic domain.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
TC: Writing - original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was carried out in the Centre Européen de Biotechnologie et de Bioéconomie (CEBB), supported by the Région Grand Est, Département de la Marne, Greater Reims, and the European Union. In particular, the authors would like to thank the Département de la Marne, Greater Reims, Région Grand Est, and the European Union along with the European Regional Development Fund (ERDF Champagne Ardenne 2014-2020) for their financial support of the Chair of Biotechnology of CentraleSupélec.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alfeus, M., and Schlögl, E. (2019). On spread option pricing using two-dimensional Fourier transform. Int. J. Theor. Appl. Fin. 22:1950023. doi: 10.1142/S0219024919500237
Aliaga, J. I., Anzt, H., Grützmacher, T., Quintana-Ortí, E. S., and Tomás, A. E. (2022). Compression and load balancing for efficient sparse matrix-vector product on multicore processors and graphics processing units. Concurr. Comput. 34:e6515. doi: 10.1002/cpe.6515
Anastassi, Z., and Simos, T. (2005). An optimized Runge-Kutta method for the solution of orbital problems. J. Comput. Appl. Math. 175:1–9. doi: 10.1016/j.cam.2004.06.004
Anderson, E., Bai, Z., Bischof, C., Blackford, L. S., Demmel, J., Dongarra, J., et al. (1999). LAPACK Users' Guide. SIAM. doi: 10.1137/1.9780898719604
Aradhya, S., Thejaswini, S., and Nagaveni, V. (2022). “Multicore embedded worst-case task design issues and analysis using machine learning logic,” in IOT with Smart Systems: Proceedings of ICTIS 2021, Vol. 2, (Springer), 531–540. doi: 10.1007/978-981-16-3945-6_52
Arts, L. P. A., and van den Broek, E. L. (2022). The fast continuous wavelet transformation (fCWT) for real-time, high-quality, noise-resistant time-frequency analysis. Nat. Comput. Sci. 2, 47–58. doi: 10.1038/s43588-021-00183-z
Atallah, M. J., Cole, R., and Goodrich, M. T. (1989). Cascading divide-and-conquer: a technique for designing parallel algorithms. SIAM J. Comput. 18, 499–532. doi: 10.1137/0218035
Belhocine, A., and Wan Omar, W. Z. (2018). Similarity solution and Runge–Kutta method to a thermal boundary layer model at the entrance region of a circular tube: the Lévêque approximation. Rev. Cient. 31, 6–18. doi: 10.14483/23448350.12506
Ben Amma, B., Melliani, S., and Chadli, L. (2019). “A fourth order Runge-Kutta gill method for the numerical solution of intuitionistic fuzzy differential equations,” in Recent Advances in Intuitionistic Fuzzy Logic Systems, eds M. Said and C. Oscar (Springer), 55–68. doi: 10.1007/978-3-030-02155-9_5
Bluman, G. W., and Cole, J. D. (1969). The general similarity solution of the heat equation. J. Math. Mech. 18, 1025–1042. doi: 10.1512/iumj.1969.18.18074
Brodtkorb, A. R., Hagen, T. R., and Sætra, M. L. (2013). Graphics processing unit (GPU) programming strategies and trends in GPU computing. J. Parallel Distrib. Comput. 73, 4–13. doi: 10.1016/j.jpdc.2012.04.003
Buck, I. (2007). “GPU computing: programming a massively parallel processor,” in International Symposium on Code Generation and Optimization (CGO'07), 17. doi: 10.1109/CGO.2007.13
Burns, K. J., Vasil, G. M., Oishi, J. S., Lecoanet, D., and Brown, B. P. (2020). Dedalus: a flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2:023068. doi: 10.1103/PhysRevResearch.2.023068
Cannon, J. R. (1984). The One-Dimensional Heat Equation. Cambridge University Press. doi: 10.1017/CBO9781139086967. Available online at: https://books.google.fr/books?hl=fr&lr=&id=XWSnBZxbz2oC&oi=fnd&pg=PR19&ots=6edC5xJawK&sig=5gdjTITX22AumpTfF_er7iKt7pI&redir_esc=y#v=onepage&q&f=false
Cerovskỳ, A., Dulce, A., and Ferreira, A. (2014). Application of the Finite Difference Method and the Finite Element Method to Solve a Thermal Problem. Department of Mechanical Engineering, Integrated Masters in Mechanical Engineering, University Porto, Porto, Portugal.
Chakkour, T. (2017). Some notes about the continuous-in-time financial model. Abstr. Appl. Anal. 2017:6985820. doi: 10.1155/2017/6985820
Chakkour, T. (2019). Inverse problem stability of a continuous-in-time financial model. Acta Math. Sci. 39, 1423–1439. doi: 10.1007/s10473-019-0519-5
Chakkour, T. (2022). “Numerical simulation of pipes with an abrupt contraction using openfoam,” in Fluid Mechanics at Interfaces 2: Case Studies and Instabilities, eds R. Prud'homme and S. Vincent (Wiley Online Library), 45–75. doi: 10.1002/9781119903000.ch3
Chakkour, T. (2023). Some inverse problem remarks of a continuous-in-time financial model in l 1 ([t i, θ max]). Math. Model. Comput. 10, 864–874. doi: 10.23939/mmc2023.03.864
Chakkour, T., and Frénod, E. (2016). Inverse problem and concentration method of a continuous-in-time financial model. Int. J. Financ. Eng. 3:1650016. doi: 10.1142/S242478631650016X
Cicone, A., and Zhou, H. (2021). Numerical analysis for iterative filtering with new efficient implementations based on FFT. Numer. Math. 147, 1–28. doi: 10.1007/s00211-020-01165-5
Cooley, J. W., and Tukey, J. W. (1965). An algorithm for the machine calculation of complex Fourier series. Math. Comput. 19, 297–301. doi: 10.1090/S0025-5718-1965-0178586-1
Dan, D., Wang, Z., Zhou, X., Lei, M., Zhao, T., Qian, J., et al. (2021). Rapid image reconstruction of structured illumination microscopy directly in the spatial domain. IEEE Photon. J. 13, 1–11. doi: 10.1109/JPHOT.2021.3053110
Dao, T., Gu, A., Eichhorn, M., Rudra, A., and Ré, C. (2019). “Learning fast algorithms for linear transforms using butterfly factorizations,” in International Conference on Machine Learning, 1517–1527. Available online at: https://proceedings.mlr.press/v97/dao19a.html
Elafrou, A., Goumas, G., and Koziris, N. (2019). “Conflict-free symmetric sparse matrix-vector multiplication on multicore architectures,” in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 1–15. doi: 10.1145/3295500.3356148
Eldén, L. (1995). Numerical solution of the sideways heat equation by difference approximation in time. Inverse Probl. 11:913. doi: 10.1088/0266-5611/11/4/017
Faerman, V., Avramchuk, V., Voevodin, K., and Shvetsov, M. (2021). “Real-time correlation processing of vibroacoustic signals on single board raspberry pi computers with hifiberry cards,” in International Conference on High-Performance Computing Systems and Technologies in Scientific Research, Automation of Control and Production (Springer), 55–71. doi: 10.1007/978-3-030-94141-3_6
Faerman, V. A., Shvetsov, M. P., and Tsavnin, A. V. (2020). Computations of cross-correlation functions on a single board Raspberry Pi computer. J. Phys. 1615:12004. doi: 10.1088/1742-6596/1615/1/012004
Feng, H., and Zhao, S. (2020). FFT-based high order central difference schemes for three-dimensional Poisson's equation with various types of boundary conditions. J. Comput. Phys. 410:109391. doi: 10.1016/j.jcp.2020.109391
Frigo, M., and Johnson, S. G. (2005). The design and implementation of FFTW3. Proc. IEEE 93, 216–231. doi: 10.1109/JPROC.2004.840301
Gangadhar, C., Moutteyan, M., Vallabhuni, R. R., Vijayan, V. P., Sharma, N., and Theivadas, R. (2023). Analysis of optimization algorithms for stability and convergence for natural language processing using deep learning algorithms. Meas. Sens. 27:100784. doi: 10.1016/j.measen.2023.100784
Grady, T. J., Khan, R., Louboutin, M., Yin, Z., Witte, P. A., Chandra, R., et al. (2023). Model-parallel Fourier neural operators as learned surrogates for large-scale parametric PDEs. Comput. Geosci. 2023:105402. doi: 10.1016/j.cageo.2023.105402
Habibi, M., Safarpour, M., and Safarpour, H. (2022). Vibrational characteristics of a FG-GPLRC viscoelastic thick annular plate using fourth-order Runge-Kutta and GDQ methods. Mech. Based Des. Struct. Mach. 50, 2471–2492. doi: 10.1080/15397734.2020.1779086
Hassanieh, H., Indyk, P., Katabi, D., and Price, E. (2012). “Simple and practical algorithm for sparse Fourier transform,” in Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms, 1183–1194. doi: 10.1137/1.9781611973099.93
Hong, C., Sukumaran-Rajam, A., Nisa, I., Singh, K., and Sadayappan, P. (2019). “Adaptive sparse tiling for sparse matrix multiplication,” in Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming, 300–314. doi: 10.1145/3293883.3295712
Horowitz and Zorat (1983). Divide-and-conquer for parallel processing. IEEE Trans. Comput. 100, 582–585. doi: 10.1109/TC.1983.1676280
Hutzenthaler, M., Jentzen, A., Kruse, T., and Nguyen, T. A. (2020). A proof that rectified deep neural networks overcome the curse of dimensionality in the numerical approximation of semi-linear heat equations. SN Part. Diff. Equ. Appl. 1, 1–34. doi: 10.1007/s42985-019-0006-9
Khouzami, N., Michel, F., Incardona, P., Castrillon, J., and Sbalzarini, I. F. (2022). Model-based autotuning of discretization methods in numerical simulations of partial differential equations. J. Comput. Sci. 57:101489. doi: 10.1016/j.jocs.2021.101489
Kravčenko, M., Merta, M., and Zapletal, J. (2019). Distributed fast boundary element methods for Helmholtz problems. Appl. Math. Comput. 362:124503. doi: 10.1016/j.amc.2019.06.017
Muhlich, J. L., Chen, Y.-A., Yapp, C., Russell, D., Santagata, S., and Sorger, P. K. (2022). Stitching and registering highly multiplexed whole-slide images of tissues and tumors using ASHLAR. Bioinformatics 38, 4613–4621. doi: 10.1093/bioinformatics/btac544
Nickolls, J., Buck, I., Garland, M., and Skadron, K. (2008). Scalable parallel programming with CUDA: is CUDA the parallel programming model that application developers have been waiting for? Queue 6, 40–53. doi: 10.1145/1365490.1365500
Nvidia, C. (2007). CUFFT Library. Available online at: https://docs.nvidia.com/cuda/cufft/index
Phelan, C. E., Marazzina, D., Fusai, G., and Germano, G. (2019). Hilbert transform, spectral filters and option pricing. Ann. Oper. Res. 282, 273–298. doi: 10.1007/s10479-018-2881-4
Pirgov, P., Mullin, L., and Khan, R. (2021). “Out-of-GPU FFT: a case study in GPU prefetching,” in 2021 International Conference on Computational Science and Computational Intelligence (CSCI), 1771–1776. doi: 10.1109/CSCI54926.2021.00336
Prigent, S., Nguyen, H.-N., Leconte, L., Valades-Cruz, C. A., Hajj, B., Salamero, J., et al. (2023). SPITFIR (e): a supermaneuverable algorithm for fast denoising and deconvolution of 3D fluorescence microscopy images and videos. Sci. Rep. 13:1489. doi: 10.1038/s41598-022-26178-y
Rasheed, M., Ali, A. H., Alabdali, O., Shihab, S., Rashid, A., Rashid, T., et al. (2021). The effectiveness of the finite differences method on physical and medical images based on a heat diffusion equation. J. Phys. 1999:012080. doi: 10.1088/1742-6596/1999/1/012080
Salavi, R., Math, M., and Kulkarni, U. (2022). A comprehensive survey of fully homomorphic encryption from its theory to applications. Cyber Secur. Digit. Forens. 73–90. doi: 10.1002/9781119795667.ch4
Sene, N. (2019). Solutions of fractional diffusion equations and Cattaneo-Hristov diffusion model. Int. J. Anal. Appl. 17, 191–207. doi: 10.28924/2291-8639
Singer, J. (1938). A theorem in finite projective geometry and some applications to number theory. Trans. Am. Math. Soc. 43, 377–385. doi: 10.1090/S0002-9947-1938-1501951-4
Sivanandan, V., Kumar, V., and Meher, S. (2015). “Designing a parallel algorithm for Heat conduction using MPI, OpenMP and CUDA,” in 2015 National Conference on Parallel Computing Technologies (PARCOMPTECH), 1–7. doi: 10.1109/PARCOMPTECH.2015.7084516
Tselios, K., and Simos, T. E. (2005). Runge-Kutta methods with minimal dispersion and dissipation for problems arising from computational acoustics. J. Comput. Appl. Math. 175, 173–181. doi: 10.1016/j.cam.2004.06.012
Vijendra Babu, D., Basha, S.A., Kavitha, D., Sahaya Anselin Nisha, A., Vallabhuni, R. R., and Radha, N. (2023). Digital code modulation-based MIMO system for underwater localization and navigation using MAP algorithm. Soft Comput. doi: 10.1007/s00500-023-08244-3
Wang, C., Chandrasekaran, S., and Chapman, B. (2016). “cusFFT: a high-performance sparse fast Fourier transform algorithm on GPUs,” in 2016 IEEE International Parallel and Distributed Processing Symposium (IPDPS), 963–972. doi: 10.1109/IPDPS.2016.95
Widder, D. V. (1976). The Heat Equation, Vol. 67. Academic Press. Available online at: https://books.google.fr/books?hl=fr&lr=&id=5BPILpGGGXsC&oi=fnd&pg=PP1&ots=TKsJ9J2GsM&sig=oowW-N8QmeEQXvSZfZqK2ZDAF_g&redir_esc=y#v=onepage&q&f=false
Keywords: heat conduction equation, parallelization, numerical schemes, Runge-Kutta, MPI, Navier-Stokes Cuda
Citation: Chakkour T (2024) Parallel computation to bidimensional heat equation using MPI/CUDA and FFTW package. Front. Comput. Sci. 5:1305800. doi: 10.3389/fcomp.2023.1305800
Received: 02 October 2023; Accepted: 01 December 2023;
Published: 11 January 2024.
Edited by:
Xing Cai, Simula Research Laboratory, NorwayReviewed by:
Rajeev Ratna Vallabhuni, Bayview Asset Management, LLC, United StatesAlfredo Daniel Sánchez, The Institute of Photonic Sciences (ICFO), Spain
Copyright © 2024 Chakkour. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tarik Chakkour, dGFyaWsuY2hha2tvdXJAY2VudHJhbGVzdXBlbGVjLmZy
 Tarik Chakkour
Tarik Chakkour