Quantum annealing research at CMU: algorithms, hardware, applications

1 Introduction

Quantum annealing has emerged as a promising approach because a variety of Combinatorial Optimization (CO) problems that arise in practical situations (Smelyanskiy et al., 2012; Tanahashi et al., 2019; Hauke et al., 2020) can be formulated as a Quadratic Unconstrained Binary Optimization (QUBO) problem, which maps naturally to an Ising model, and solved on specially constructed quantum and semi-classical hardware (Wang et al., 2013; Lucas, 2014; McMahon et al., 2016; Glover et al., 2018; Harris et al., 2018; King et al., 2018; Chou et al., 2019; Wang and Roychowdhury, 2019; Mohseni et al., 2022). A lucid introduction to quantum annealing can be found in McGeoch (2014).

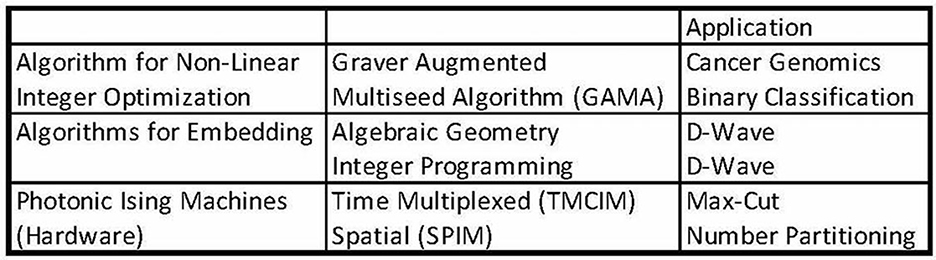
At Carnegie Mellon University's Quantum Technologies Group (QTG), we have been working on several initiatives¹ related to computational aspects of quantum annealing (Figure 1).

1. While unconstrained optimization problems expressed as QUBO can be directly passed to an annealer solver, it is also of practical interest to develop scalable decomposition methods that solve general non-linear constrained optimization problems. We describe a novel quantum-classical algorithm, Graver Augmented Multiseed Algorithm (GAMA) (Alghassi et al., 2019b,c) for solving such optimization problems, building on previous work on the use of algebraic geometry for Integer Optimization with a linear objective function (Tayur et al., 1995). GAMA is motivated by test sets, and (a) uses partial Graver bases (Graver, 1975) instead of the complete Graver basis and (b) many feasible solutions as starting points (rather than just one) for augmentation. Both the partial Graver basis and a number of feasible solutions are obtained from the constraint equation expressed as QUBOs (that is solved by an annealer). A particular advantage of this algorithm is that it separates the constraints from the objective function, allowing us to tackle situations where the computation of objective function value may need an oracle call (such as a simulation).

2. Many devices such as D-Wave have limited coupling connectivity between qubits. For a dense problem graph, it is therefore necessary to develop a mapping - minor embedding—to the sparse hardware graph. We have developed two methods, based on algebraic geometry and Integer Programming (Dridi et al., 2018a; Bernal et al., 2020).

3. Building fully connected Ising hardware is another exciting area of current research. We have re-constructed (with some refinements) two Photonic Ising Machines (PIM), building on the time-multiplexed coherent Ising machine (TMCIM) (Böhm et al., 2019) and the spatial multiplexed Ising machine (SPIM) (Pierangeli et al., 2020). We have studied the performance of the annealers on Max-Cut and Number Partitioning Problem with D-Wave (McGeoch, 2014) and Gurobi (LLC Gurobi Optimization, 2023).

Figure 1

Figure 1. Some computational quantum annealing initiatives at Quantum Technology Group (QTG).

The rest of the review is organized as follows. In Section 2, we describe GAMA. In Section 3, we illustrate the application of the GAMA on identifying altered pathways in cancer genomics as a proof-of-principle and recovering known results. An algebraic geometry-based embedding algorithm and its Integer Programming reformulation are outlined in Section 4 and compared to the default heuristic that is used by D-Wave. The performance of two Photonic Ising Machines is discussed in Section 5. We conclude in Section 6.

2 Graver augmented multiseed algorithm (GAMA)

We begin with three definitions, taken verbatim from Alghassi et al. (2019c).

Definition 1. A set S ∈ ℤⁿ is a Test Set or an optimality certificate if for every non-optimal, feasible solution, x₀, there exists t ∈ S and λ ∈ Z₊ such that f(x₀+ λ t) < f(x₀). The vector, t is called the augmenting direction.

The following partial order is defined on ℝⁿ.

Definition 2. Given x, y ∈ ℝⁿ, we define x is conformal to y, written as x ⊑ y, if x_iy_i ≥ 0 (x and y lie in the same orthant), and |x_i| ≤ |y_i|, ∀ i ∈ {1..n}. A sum $u=\sum _i{v}_i$ is called conformal if v_i ⊑ u, ∀i.

For a matrix A ∈ ℤ^m×n, define the lattice

$\begin{array}{ll}{L}^{*}(A)=\left\{x|Ax=0,x\in {\mathbb{Z}}^n,A\in {\mathbb{Z}}^{m\times n}\right\}\backslash \left\{0\right\}.& (1)\end{array}$

Definition 3. The Graver basis, $\mathcal{G}(A)\subset {\mathbb{Z}}^n$, of an integer matrix A is defined as the finite set of ⊑ minimal elements in L^*(A).

The Graver basis (Graver, 1975) of an integer matrix, A ∈ ℤ^m×n is known to be a test set for integer linear programs. Graver basis is also a test set for certain non-linear objective functions including Separable convex minimization (Murota et al., 2004), Convex integer maximization (De Loera et al., 2009), Norm p minimization (Hemmecke et al., 2011), Quadratic (Murota et al., 2004; Lee et al., 2010) and Polynomial minimization (Lee et al., 2010). It has also been shown that for these problem classes, the number of augmentation steps needed is polynomial (De Loera et al., 2009; Hemmecke et al., 2011). Graver basis can be computed (only for small size problems) using classical methods such as the algorithms developed by Pottier (1996) and Sturmfels and Thomas (1997).

At QTG, we are exploring (a) the effectiveness of computing partial Graver basis using annealers by solving a QUBO (for kernel elements) and (b) instead of relying on just one feasible solution as the seed for augmentation, using multiple feasible solutions (that are also obtained via annealing, by solving a second QUBO), as parallel starting points. The GAMA heuristic (Alghassi et al., 2019b,c) thus aims to find good solutions to constrained non-linear optimization problems of the form in Equation 2, using multiple seeds as starting points for augmentation, with partial Graver basis elements as the augmenting directions:

$\begin{array}{ll}{(IP)}_{A,b,l,u,f}=\{\begin{array}{ll}minf(x)\hfill & \hfill \\ Ax=b\hfill & l\le x\le nx,l,u\in {\mathbb{Z}}^n\hfill \\ A\in {\mathbb{Z}}^{m\times n}\hfill & b\in {\mathbb{Z}}^n\hfill \end{array}& (2)\end{array}$

where f : ℝⁿ−>ℝ is a real valued function.

2.1 QUBO for kernel calculation

In order to find a sample of the kernel elements for the constraint matrix A, we solve the Quadratic Unconstrained Integer Optimization (QUIO), given by

$\begin{array}{c}\begin{array}{c}min{x}^T{Q}_{I}x,Q_I=A^{T}A,x\in {\mathbb{Z}}^n\\ x^T=\left[x_1,x_2...x_n\right],x_i\in \mathbb{Z}.\end{array}(3)\end{array}$

Since the inputs to the annealer are binary variables, we create a binary encoding of the integer variable. Writing

$\begin{array}{l}x=L+EX,(4)\end{array}$

with L as the lower bound vector and E as the encoding matrix, the QUIO is equivalent to the QUBO

$\begin{array}{l}\begin{array}{c}min{X}^T{Q}_{B}X,Q_B=E^T{Q}_{I}E+diag(2L^T{Q}_{I}E),\\ X\in {\left\{0,1\right\}}^{nk},Q_I=A^{T}A.\end{array}(5)\end{array}$

The above QUBO is solved by an annealer to obtain kernel elements. A partial Graver basis can be obtained from the kernel elements in a classical post-processing step by ⊑-minimal filtering (Alghassi et al., 2019b).

2.2 QUBO for feasible solutions

Similar to the kernel sampling, the Ax = b constraint can be expressed in the QUIO form as

$\begin{array}{l}\begin{array}{c}min{x}^T{Q}_{I}x-2b^{T}Ax\\ Q_I=A^{T}A,x\in {\mathbb{Z}}^n.\end{array}(6)\end{array}$

After binary encoding, we get the QUBO given by

$\begin{array}{l}\begin{array}{c}min{X}^T{Q}_{B}X,Q_B=E^T{Q}_{I}E+2diag\left[(L^T{Q}_I-b^{T}A)E\right]\\ X\in {\left\{0,1\right\}}^{nk},Q_I=A^{T}A.\end{array}(7)\end{array}$

The above QUBO can be solved by an annealer to obtain a sample of feasible solutions.

3 An application of GAMA: cancer genomics

As a proof-of-principle testing of GAMA, we describe an application (Alghassi et al., 2019a) to identify cancer pathways de novo (Vogelstein and Kinzler, 2004; Haber and Settleman, 2007; Ciriello et al., 2012; Vandin et al., 2012a,b; Zhao et al., 2012) from mutation co-occurrence and mutual exclusivity (Leiserson et al., 2013; Weinberg and Weinberg, 2013).

Data from The Cancer Genome Atlas (TCGA) are now available for a variety of cancers, providing information about which genes are mutated for which patient for any given cancer. With this, we can create a matrix. The rows of the matrix are patients, the columns are the genes, and the elements of the matrix (row i, column j) are zero or one (a binary matrix), where “one” in (row i, column j) means that gene j is mutated for patient i.

However, not all mutations matter. The mutations that do not matter are called passengers. Those mutations that matter are called drivers. We want to isolate drivers from passengers (Most mutations are passengers). Furthermore, the same cancer can manifest itself due to different driver mutations, because different mutated driver genes can impact different cellular signaling and regulatory pathways. This mutational heterogeneity complicates efforts to identify drivers solely by their frequency of occurrence.

A pathway is a collection of genes. To find k pathways means finding k different collections of genes. Each collection of genes can be of a different size. To make the discovery of these pathways computationally manageable, we also make two commonly accepted simplifications:

Simplification 1: A pathway has at most one mutated driver gene. This is because driver genes are quite rare. Thus, two different pathways will not likely share a common driver gene. This is called (mutual) exclusivity.

Simplification 2: A pathway should apply to many patients. This is called coverage. The important thing to note is that even though two patients share a pathway, they can have a different mutated gene from that shared pathway as an explanatory reason for their cancer.

Another complexity that we need to handle is that real data are noisy because of measurement errors and passenger mutations. This means that we cannot impose exclusivity as a hard constraint. Instead, we allow for some overlap or “approximate exclusivity” and this is a parameter in our formulation. Similar considerations force a modification of Simplification 2 as well, in the sense that we now can only reasonably hope that most patients have at least one mutation in a pathway. Recall that mutual exclusivity problems even without the modification above are NP-hard (Karp, 1972).

3.1 Multiple-pathway QUBO formulation for GAMA

Alghassi et al. (2019a) developed a novel formulation tailored for GAMA to discover the cancer pathways. Consider a hypergraph H_g = (V_g, E_p) with incidence matrix B, where each gene (g_i) is represented by a vertex v_i ∈ V_g, i = 1, 2, ..., n and the mutation list of each patient P_i is represented by a hyperedge e_i ∈ E_p, i = 1, 2, ..., m.

The incidence matrix is mapped to its primal graph (G). This is a graph with the same vertices as that of the hypergraph and with edges between all pairs of vertices contained within the same hyperedge. The primal graph can be expressed in terms of the (positive) Laplacian matrix:

$\begin{array}{l}{L}^{+}(G)=B{B}^T=D(G)+A(G).(8)\end{array}$

The weighted adjacency matrix A = [a(i, j)]^n×n is symmetric and has zero as the diagonal elements. The number of patients that have gene pairs (g_i, g_j) mutated is given by a(i, j). The number of patients with gene g_i mutated is given by the element, d_i in the degree matrix, D = diag{d₁, d₂, ..., d_n}, where d_i is the degree of the vertex v_i in the primal graph.

A k-pathway QUBO formulation simultaneously finds k pathways in a single optimization run. The solution vector is represented by the binary vector $x_i={\left[x_{i1},x_{i2},...,x_{in}\right]}^T,i=1,2,...,k$ where, each element x_ij indicates if a vertex v_j belongs to the i^th pathway. Let $\mathbf{\text{X}}={\left[x_1,x_2,...,x_k\right]}^T$. The QUBO formulation is given by the following (where L = (D−A) is the negative Laplacian matrix).

$\begin{array}{r}\begin{array}{r}min{\text{X}}^T({\text{Q}}_{main}+\alpha {\text{Q}}_{orth})\text{X}\\ {\text{Q}}_{main}=-I_k\otimes L\\ {\text{Q}}_{orth}=(J_k-I_k)\otimes I_n\end{array}(9)\end{array}$

Note that I_k and I_n are k × k and n × n identity matrices. J_k is the k × k matrix with all entries equal to 1.

Rewriting the system of equations(9) as

$\begin{array}{r}\begin{array}{r}min{\text{X}}^T\text{Q}\text{X}\\ ({\text{1}}_k^T\otimes I_n)\text{X}\le {\text{1}}_n\\ \text{Q}=-I_k\otimes L\end{array}(10)\end{array}$

brings it in the form suitable for GAMA (Alghassi et al., 2019b).

This is a non-linear (quadratic) non-convex integer problem and of a Quadratic Semi Assignment Problem (QSAP) form. We can alternatively extract Graver basis and generate feasible solutions systematically, in this case, Alghassi et al. (2019b) instead of solving QUBOs on a quantum annealer.

3.2 Numerical results

GAMA algorithm is used to solve the k-pathway problem using the mutation data of 33 genes for Acute Myeloid Leukemia (AML) for 200 patients (Network, 2013). By construction, the number of binary variables required is lower than available methods (?). For k = 3, the pathways discovered by GAMA are consistent with those reported by the TCGA authors. For k = 6, three additional pathways are discovered by GAMA albeit with lower coverage.

4 Embedding algorithms

If an annealer hardware is not fully connected (e.g. the D-Wave system), it is necessary to map the logical graph, Y associated with the optimization problem into the processor graph, X (Choi, 2011, Boothby et al., 2016). We describe embedding algorithms² based on algebraic geometry (Dridi et al., 2018a).

Definition 4. Let X be a hardware graph. A minor-embedding of the the graph, Y is a map, ϕ : Vertices(Y)− > connectedSubtrees(X) such that, ∀(y₁, y₂) ∈ Edges(Y), there exists at least one edge connecting the subtrees, ϕ(y₁) and ϕ(y₂).

Given an embedding of a logical graph, Y into a physical graph, X, the Y minor is a subgraph of X given by

$\begin{array}{l}\varphi (Y)={\cup }_{y\in Vertices(Y)}\varphi (y)(11)\end{array}$

This is the input graph to the quantum processor. The information regarding the mapping of each logical qubit is stored in a hash map,

$\begin{array}{l}id\times \varphi :Vertices(Y)\times Vertices(Y)->Vertices(Y)\times Subtrees(X)(12)\end{array}$

which can be used to unembed the desired solution returned by the processor.

4.1 Algebraic geometry method

The set of embeddings can be viewed as an algebraic variety, which is the set of zeros of a system of polynomial equations (Cox et al., 2007). Given an embedding the mapping, π : Vertices(X)− > Vertices(Y) ∪ {0}, where the pre-image (fiber) π⁻¹(y) = ϕ(y), ∀y ∈ Vertices(Y) has the form:

$\begin{array}{r}\begin{array}{r}\pi (x_i)={\displaystyle \sum _j}{\alpha }_{ij}{y}_j\\ \text{with}{\displaystyle \sum _j}{\alpha }_{ij}={\beta }_i,{\alpha }_{ij}({\alpha }_{ij}-1)=0\\ {\alpha }_{i{j}_1}{\alpha }_{i{j}_2}=0,\text{ for }{j}_1\ne j_2\end{array}(13)\end{array}$

where β_i ∈ {0, 1} is equal to 1, if the physical qubit x_i is used, and 0 otherwise. The conditions on the embedding ϕ in Definition 4 along with a limit on the number of usable physical qubits can be translated into a system of polynomial constraints on α_ij and β_i. This system defines an algebraic ideal $\mathcal{I}$, and the embeddings can be obtained using the Groebner basis of $\mathcal{I}$.

4.2 Integer programming (IP) method

An IP formulation of the embedding algorithm (Bernal et al., 2020) is developed by expressing the polynomial conditions in Dridi et al. (2018a) as linear constraints involving integer variables. This formulation includes constraints for Minimum and Maximum size. Embeddings are obtained by optimizing the Embedding size within the feasible region. A decomposition approach, iterating between a qubit assignment master problem and a fiber condition checking subproblem is also developed. Bernal et al. (2020) tested these methods using random graphs that vary in structure, size, and density. The results are compared with the D-Wave default heuristic, minorminer (Cai et al., 2014). The IP-based approaches are found to be slower whenever the heuristic can find an embedding. However, it is possible to obtain infeasibility proofs and bounds on solution quality with the IP methods, but not from the heuristics. The decomposition approach outperforms the monolithic IP approach.

5 Hardware

Two fully connected Coherent Ising Machines (CIM) - the Temporal Multiplexed Coherent Ising Machine (TMCIM) (based on Böhm et al., 2019, 2021) and the Spatial Photonic Ising Machine (SPIM) (an enhancement of that of Pierangeli et al., 2019)—were built by collaborators at IIT-Madras (Prabhakar et al., 2023).

5.1 Temporal Multiplexed Ising Machine

The TMCIM was tested on the Max-Cut problem (Karp, 1972) and the results on various instances are compared with Gurobi run on an Intel Core i3 processor and also with a D-Wave machine. The graph instances for the problem are generated using rudy (Rendl et al., 2010). See Prabhakar et al. (2023) for details.

First, at a fixed graph size (100 nodes), and varying density, TMCIM performed better than Gurobi up to a graph density of 40%. However, above 50%, the performance of TMCIM degraded. Next, the results with a fixed graph density of 40% and varying size of the graph from 100 to 1, 000 were obtained. For larger graphs, the performance of TMCIM was found to be considerably lower than Gurobi.

Second, the results are compared with the D-Wave Advantage 1.1 (DWA) annealer with the graph size varying from 20 to 100 nodes and the graph density fixed at 10%. For all the graph sizes, TMCIM is able to always give a Max-Cut value which is at least 96% of the value obtained using Gurobi (see Figure 6 in Prabhakar et al., 2023). A solution accuracy of 99% can be attained up to 30 nodes. For DWA, the solution accuracy degrades beyond 20 nodes. This can be attributed to the limited connectivity of its Pegasus graph.

5.2 Spatial Photonic Ising Machine

The SPIM was tested on a Number Partitioning Problem (NPP) with instance sizes varying from 16 to 16, 384 variables. The performance of the SPIM was compared with that of Gurobi and DWA. See Tables 3, 4 in Prabhakar et al. (2023). For DWA, the number of variables that can be embedded is limited to 11 × 11 fully connected graph and is not competitive. For problem sizes up to 1024 variables, Gurobi performs better than SPIM. However, Gurobi is unable to find solutions as the problem size gets larger while SPIM can handle up to 16,384 variables.

6 Conclusion

We have developed GAMA (Graver Augmented Multi-seed Algorithm), a novel hybrid quantum-classical algorithm for non-linear constrained integer optimization. As an application, we have explored a new formulation for the discovery of de-novo cancer pathways. This tailored formulation is found to require fewer binary variables when compared with existing methods, and the pathways detected have been found to be consistent with previously published results.

For minor embedding that is usually required in Ising hardware that does not have an all-to-all connectivity, we have developed algebraic geometry and IP-based algorithms. The IP algorithm is found to perform well for highly structured source graphs when compared with the currently employed heuristic, minorminer and the Groebner basis method. While slower overall when compared with the heuristic, the algorithm can detect instance infeasibility and obtain bounds on solution quality.

We have built two photonic Ising machines, TMCIM and SPIM. We have studied their performance on Max-Cut and NPP problems, respectively, by comparing them with D-Wave and Gurobi. For the Max-Cut, TMCIM gave better results than Gurobi at smaller graph sizes (< 100 nodes) and lower densities (< 40%), while its accuracy is lower for larger problems. However, the performance is better than D-Wave, which can be attributed to better connectivity. SPIM can solve NPP problems up to 16384 spins, which is larger than the problem sizes solved by D-Wave and Gurobi. Gurobi's performance is better at smaller sizes, but cannot exceed more than 1024 spins.

We conclude by noting some current work in quantum annealing. We are testing GAMA³ against state-of-the-art classical approaches for an application in disaster preparation, in collaboration with researchers at Koc University, as part of an initiative of the Turkish Ministry of Transportation and Infrastructure, focused on probable earthquakes in Istanbul. As noted earlier, the performance of the annealers depends crucially on connectivity in the hardware. We are in the process of building another fully connected annealer, based on Floquet Theory, collaborating with researchers at Cornell University and Raytheon BBN Technologies, that is implemented using superconducting circuits (Onodera et al., 2020), adding to a growing set of devices with all-to-all connectivity being developed on other technologies (such as trapped ions or cold Rydberg atoms, such as QuEra processor). Nevertheless, we expect the size of complete connectivity in any hardware in the foreseeable future to be limited. It is therefore necessary to develop additional decomposition techniques for efficiently partitioning (and then recombining) large-scale optimization problems, an area of active algorithmic research at QTG.

Author contributions

ST: Conceptualization, Supervision, Writing—review & editing. AT: Writing—original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. ST and AT were supported by a DARPA Grant (through BBN Raytheon Technologies) on an AFRL Contract entitled GLIMPSE. BBN Raytheon Technologies was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

Dr. Hedayat Alghassi (IBM) and Dr. Raouf Dridi (QCI) were part of QTG and co-developed content described in Sections 2–4. Dr. David Bernal (Purdue) and researchers at NASA QuAIL collaborated on research in Section 4.2. Faculty (Dr. A. Prabhakar and Dr. N. Chandrachoodan) and students (P. Shah, U. Gautham, V. Natarajan, and V. Ramesh) at IIT-Madras collaborated on the photonic devices discussed in Section 5.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^QTG is also engaged in theoretical research on understanding speed up in adiabatic quantum computing (Dridi et al., 2018b, 2019a), and other connections between algebraic geometry and Ising models (Dridi et al., 2019b), topics not covered here.

2. ^Note that X can be any graph in general, not just the hardware graph, which is the focus here.

3. ^A parallel article in this issue explores GAMA for Binary Classification of X-ray images via Support Vector Machine (SVM) to detect pneumonia (Guddanti et al., 2023).

References

Alghassi, H., Dridi, R., Robertson, A. G., and Tayur, S. (2019a). Quantum and Quantum-inspired methods for de novo discovery of altered cancer pathways. bioRxiv. doi: 10.1101/845719

Crossref Full Text | Google Scholar

Alghassi, H., Dridi, R., and Tayur, S. (2019b). GAMA: a novel algorithm for non-convex integer programs. arXiv [Preprint]. doi: 10.48550/arXiv.1907.10930

Crossref Full Text | Google Scholar

Alghassi, H., Dridi, R., and Tayur, S. (2019c). Graver bases via quantum annealing with application to non-linear integer programs. arXiv [Preprint]. doi: 10.48550/arXiv.1902.04215

Crossref Full Text | Google Scholar

Bernal, D. E., Booth, K. E., Dridi, R., Alghassi, H., Tayur, S., and Venturelli, D. (2020). “Integer programming techniques for minor-embedding in quantum annealers,” in Integration of Constraint Programming, Artificial Intelligence, and Operations Research: 17th International Conference, CPAIOR 2020. Vienna, Austria: Springer, 112–129.

Google Scholar

Böhm, F., Vaerenbergh, T. V., Verschaffelt, G., and Van der Sande, G. (2021). Order-of-magnitude differences in computational performance of analog Ising machines induced by the choice of nonlinearity. Communications Physics 4:149. doi: 10.1038/s42005-021-00655-8

Crossref Full Text | Google Scholar

Böhm, F., Verschaffelt, G., and Van der Sande, G. (2019). A poor man coherent Ising machine based on opto-electronic feedback systems for solving optimization problems. Nat. Commun. 10, 3538. doi: 10.1038/s41467-019-11484-3

PubMed Abstract | Crossref Full Text | Google Scholar

Boothby, T., King, A. D., and Roy, A. (2016). Fast clique minor generation in Chimera qubit connectivity graphs. Quant. Inform. Proc. 15, 495–508. doi: 10.1007/s11128-015-1150-6

Crossref Full Text | Google Scholar

Cai, J., Macready, W. G., and Roy, A. (2014). A practical heuristic for finding graph minors. arXiv [Preprint]. doi: 10.48550/arXiv.1406.2741

Crossref Full Text | Google Scholar

Choi, V. (2011). Minor-embedding in adiabatic quantum computation: II minor-universal graph design. Quant. Inform. Proc. 10, 343–353. doi: 10.1007/s11128-010-0200-3

Crossref Full Text | Google Scholar

Chou, J. B., Bramhavar, S., Ghosh, S., and Herzog, W. (2019). Analog coupled oscillator based weighted Ising machine. Sci. Rep. 9, 5. doi: 10.1038/s41598-019-49699-5

PubMed Abstract | Crossref Full Text | Google Scholar

Ciriello, G., Cerami, E., Sander, C., and Schultz, N. (2012). Mutual exclusivity analysis identifies oncogenic network modules. Genome Res. 22, 398–406. doi: 10.1101/gr.125567.111

PubMed Abstract | Crossref Full Text | Google Scholar

Cox, D. A., Little, J., and O'Shea, D. (2007). Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra. Berlin, Heidelberg: Springer-Verlag.

Google Scholar

De Loera, J., Hemmecke, R., Onn, S., Rothblum, U., and Weismantel, R. (2009). Convex integer maximization via Graver bases. J. Pure Appl. Algeb. 213, 1569–1577. doi: 10.1016/j.jpaa.2008.11.033

Crossref Full Text | Google Scholar

Dridi, R., Alghassi, H., and Tayur, S. (2018b). Homological description of the quantum adiabatic evolution with a view toward quantum computations. arXiv [Preprint]. arXiv:1811.00675.

Google Scholar

Dridi, R., Alghassi, H., and Tayur, S. (2019a). Enhancing the efficiency of adiabatic quantum computations. arXiv [Preprint]. doi: 10.48550/arXiv.1903.01486

Crossref Full Text | Google Scholar

Dridi, R., Alghassi, H., and Tayur, S. (2019b). Minimizing polynomial functions on quantum computers. arXiv [Preprint]. doi: 10.48550/arXiv.1903.08270

Crossref Full Text | Google Scholar

Dridi, R., Alghassi, H., and Tayur, S. (2018a). A novel algebraic geometry compiling framework for adiabatic quantum computations. arXiv [Preprint]. doi: 10.48550/arXiv.1810.01440

Crossref Full Text | Google Scholar

Glover, F. W., Kochenberger, G. A., and Du, Y. (2018). Quantum Bridge Analytics I: a tutorial on formulating and using QUBO models. 4OR 17, 335–371. doi: 10.1007/s10288-019-00424-y

Crossref Full Text | Google Scholar

Graver, J. E. (1975). On the foundations of linear and integer linear programming I. Math. Program. 9, 207–226. doi: 10.1007/BF01681344

Crossref Full Text | Google Scholar

Guddanti, S. S., Padhye, A., Prabhakar, A., and Tayur, S. (2023). Pneumonia Detection by Binary Classification: Classical, Quantum and Hybrid Approaches for Support Vector Machine (SVM). doi: 10.3389/fcomp.2023.1286657

Crossref Full Text | Google Scholar

Haber, D. A., and Settleman, J. (2007). Cancer: drivers and passengers. Nature 446, 145–146. doi: 10.1038/446145a

Crossref Full Text | Google Scholar

Harris, R., Sato, Y., Berkley, A. J., Reis, M., Altomare, F., Amin, M. H., et al. (2018). Phase transitions in a programmable quantum spin glass simulator. Science 361, 162–165. doi: 10.1126/science.aat2025

PubMed Abstract | Crossref Full Text | Google Scholar

Hauke, P., Katzgraber, H. G., Lechner, W., Nishimori, H., and Oliver, W. D. (2020). Perspectives of quantum annealing: methods and implementations. Rep. Prog. Phys. 83, 054401. doi: 10.1088/1361-6633/ab85b8

PubMed Abstract | Crossref Full Text | Google Scholar

Hemmecke, R., Onn, S., and Weismantel, R. (2011). A polynomial oracle-time algorithm for convex integer minimization. Math.Program. 126, 97–117. doi: 10.1007/s10107-009-0276-7

Crossref Full Text | Google Scholar

Karp, R. M. (1972). Reducibility among Combinatorial Problems. Boston, MA: Springer US, 85-103.

Google Scholar

King, A. D., Carrasquilla, J., Raymond, J., Ozfidan, I., Andriyash, E., Berkley, A., et al. (2018). Observation of topological phenomena in a programmable lattice of 1,800 qubits. Nature 560, 456–460. doi: 10.1038/s41586-018-0410-x

PubMed Abstract | Crossref Full Text | Google Scholar

Lee, J., Onn, S., Romanchuk, L., and Weismantel, R. (2010). The quadratic Graver cone, quadratic integer minimization, and extensions. Math. Program. 136, 301–323. doi: 10.1007/s10107-012-0605-0

Crossref Full Text | Google Scholar

Leiserson, M. D. M., Blokh, D., Sharan, R., and Raphael, B. J. (2013). Simultaneous identification of multiple driver pathways in cancer. PLoS Comput. Biol. 9, 5. doi: 10.1371/journal.pcbi.1003054

PubMed Abstract | Crossref Full Text | Google Scholar

LLC Gurobi Optimization (2023). Gurobi Optimizer Reference Manual. Available online at: https://www.gurobi.com

Google Scholar

Lucas, A. (2014). Ising formulations of many NP problems. Front. Phys. 2, 5. doi: 10.3389/fphy.2014.00005

Crossref Full Text | Google Scholar

McGeoch, C. C. (2014). Adiabatic Quantum Compuutation and Quantum Annealing. Kenfield, CA: Morgan & Claypool.

Google Scholar

McMahon, P. L., Marandi, A., Haribara, Y., Hamerly, R., Langrock, C., Tamate, S., et al. (2016). A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614–617. doi: 10.1126/science.aah5178

PubMed Abstract | Crossref Full Text | Google Scholar

Mohseni, N., McMahon, P. L., and Byrnes, T. (2022). Ising machines as hardware solvers of combinatorial optimization problems. Nat. Rev. Phys. 4, 363–379. doi: 10.1038/s42254-022-00440-8

Crossref Full Text | Google Scholar

Murota, K., Saito, H., and Weismantel, R. (2004). Optimality criterion for a class of nonlinear integer programs. Oper. Res. Lett. 32, 468–472. doi: 10.1016/j.orl.2003.11.007

Crossref Full Text | Google Scholar

Network, C. G. A. R. (2013). Genomic and epigenomic landscapes of adult de novo acute myeloid leukemia. N. Engl. J. Med. 368, 2059–2074. doi: 10.1056/NEJMoa1301689

PubMed Abstract | Crossref Full Text | Google Scholar

Onodera, T., Ng, E., and McMahon, P. L. (2020). A quantum annealer with fully programmable all-to-all coupling via Floquet engineering. NPJ Quant. Inform. 6, 48. doi: 10.1038/s41534-020-0279-z

Crossref Full Text | Google Scholar

Pierangeli, D., Marcucci, G., Brunner, D., and Conti, C. (2020). Noise-enhanced spatial-photonic Ising machine. Nanophotonics 9, 4109–4116. doi: 10.1515/nanoph-2020-0119

Crossref Full Text | Google Scholar

Pierangeli, D., Marcucci, G., and Conti, C. (2019). Large-scale photonic Ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902. doi: 10.1103/PhysRevLett.122.213902

PubMed Abstract | Crossref Full Text | Google Scholar

Pottier, L. (1996). “The Euclidean Algorithm in Dimension n,” in Proceedings of the 1996 International Symposium on Symbolic and Algebraic Computation, ISSAC '96. New York, NY, USA: Association for Computing Machinery, 40–42.

Google Scholar

Prabhakar, A., Shah, P., Gautham, U., Natarajan, V., V, R., N, C., et al. (2023). Optimization with photonic wave-based annealers. Philos. Trans. Math. Phys. Eng. 381, 18. doi: 10.1098/rsta.2021.0409

PubMed Abstract | Crossref Full Text | Google Scholar

Rendl, F., Rinaldi, G., and Wiegele, A. (2010). Solving Max-cut to optimality by intersecting semidefinite and polyhedral relaxations. Math. Program. 121, 307–335. doi: 10.1007/s10107-008-0235-8

Crossref Full Text | Google Scholar

Smelyanskiy, V. N., Rieffel, E. G., Knysh, S. I., Williams, C. P., Johnson, M. W., Thom, M. C., et al. (2012). A near-term quantum computing approach for hard computational problems in space exploration. arXiv [Preprint]. doi: 10.48550/arXiv.1204.2821

Crossref Full Text | Google Scholar

Sturmfels, B., and Thomas, R. R. (1997). Variation of cost functions in integer programming. Math. Program. 77, 357–387. doi: 10.1007/BF02614622

Crossref Full Text | Google Scholar

Tanahashi, K., Takayanagi, S., Motohashi, T., and Tanaka, S. (2019). Application of ising machines and a software development for ising machines. J. Phys. Soc. Japan 88, 061010. doi: 10.7566/JPSJ.88.061010

Crossref Full Text | Google Scholar

Tayur, S. R., Thomas, R. R., and Natraj, N. R. (1995). An algebraic geometry algorithm for scheduling in presence of setups and correlated demands. Math. Program. 69, 369–401. doi: 10.1007/BF01585566

Crossref Full Text | Google Scholar

Vandin, F., Upfal, E., and Raphael, B. J. (2012b). De novo discovery of mutated driver pathways in cancer. Genome Res. 22, 375–385. doi: 10.1101/gr.120477.111

PubMed Abstract | Crossref Full Text | Google Scholar

Vandin, F., Clay, P., Upfal, E., and Raphael, B. J. (2012a). “Discovery of mutated subnetworks associated with clinical data in cancer,” in Pacific Symposium on Biocomputing (Stanford University), 55–66.

PubMed Abstract | Google Scholar

Vogelstein, B., and Kinzler, K. W. (2004). Cancer genes and the pathways they control. Nat. Med. 10, 789–799. doi: 10.1038/nm1087

Crossref Full Text | Google Scholar

Wang, T., and Roychowdhury, J. (2019). Oim: Oscillator-based Ising machines for solving combinatorial optimisation problems. In Unconventional Computation and Natural Computation: 18th International Conference, UCNC 2019. Berlin, Heidelberg: Springer-Verlag, 232–256.

Google Scholar

Wang, Z., Marandi, A., Wen, K., Byer, R. L., and Yamamoto, Y. (2013). Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A. 88, 063853. doi: 10.1103/PhysRevA.88.063853

Crossref Full Text | Google Scholar

Weinberg, R. A., and Weinberg, R. A. (2013). The Biology of Cancer. New York: Garland Science.

Google Scholar

Zhao, J., Zhang, S., Wu, L.-Y., and Zhang, X.-S. (2012). Efficient methods for identifying mutated driver pathways in cancer. Bioinformatics (Oxford, England) 28, 2940–2947. doi: 10.1093/bioinformatics/bts564

PubMed Abstract | Crossref Full Text | Google Scholar