- 1T. H. Chan School of Public Health, Harvard University, Boston, MA, United States
- 2Los Alamos National Laboratory, CCS-3 Information Sciences, Los Alamos, NM, United States
- 3Institute of Information and Communication Technologies, Bulgarian Academy of Sciences, Sofia, Bulgaria
We are interested in benchmarking both quantum annealing and classical algorithms for minimizing quadratic unconstrained binary optimization (QUBO) problems. Such problems are NP-hard in general, implying that the exact minima of randomly generated instances are hard to find and thus typically unknown. While brute forcing smaller instances is possible, such instances are typically not interesting due to being too easy for both quantum and classical algorithms. In this contribution, we propose a novel method, called posiform planting, for generating random QUBO instances of arbitrary size with known optimal solutions, and use those instances to benchmark the sampling quality of four D-Wave quantum annealers utilizing different interconnection structures (Chimera, Pegasus, and Zephyr hardware graphs) and the simulated annealing algorithm. Posiform planting differs from many existing methods in two key ways. It ensures the uniqueness of the planted optimal solution, thus avoiding groundstate degeneracy, and it enables the generation of QUBOs that are tailored to a given hardware connectivity structure, provided that the connectivity is not too sparse. Posiform planted QUBOs are a type of 2-SAT boolean satisfiability combinatorial optimization problems. Our experiments demonstrate the capability of the D-Wave quantum annealers to sample the optimal planted solution of combinatorial optimization problems with up to 5, 627 qubits.
1 Introduction
Many important NP-hard optimization problems can be easily expressed in a QUBO (quadratic unconstrained binary optimization) or an Ising form (Lucas, 2014), given by the quadratic function
in n∈ℕ binary variables. In Equation (1), the linear weights ai∈ℝ and the quadratic couplers aij∈ℝ define the problem under investigation and are chosen by the user. The assignments of the variables xi for i∈{1, …, n} are unknown, and we seek a configuration of (x1, …, xn) minimizing Equation (1). If xi∈{0, 1}, then Equation (1) is called a QUBO problem, and if xi∈{−1, +1}, then it is called an Ising model.
Since many NP hard problems can be formulated as QUBO models, it is of interest to efficiently compute the optimal solution(s) of general QUBO problems. To this end, researchers have developed a variety of classical approaches (Kirkpatrick et al., 1983; Boros et al., 2006, 2007) to compute solutions of high quality that minimize Equation (1). Quantum annealing offers an experimental route to sample combinatorial problems. Quantum annealing is a type of analog quantum computation that uses quantum fluctuations to attempt to arrive at an optimal (or a very good) minimum of Equation (1) (Kadowaki and Nishimori, 1998; Das and Chakrabarti, 2008; Morita and Nishimori, 2008; Hauke et al., 2020). The quantum annealing algorithm has been physically instantiated in a number of ways, including superconducting flux qubit hardware that is manufactured by D-Wave Systems, Inc. The D-Wave quantum annealers have been evaluated for sampling a large number of different types of problems, typically focusing on combinatorial optimization problems or Hamiltonian dynamics (Boixo et al., 2013, 2014, 2016; Lanting et al., 2014; Venturelli et al., 2015; Harris et al., 2018; King et al., 2021, 2022, 2023; Tasseff et al., 2022). D-Wave quantum annealing devices offer on the scale of hundreds to thousands of qubits, but are still subject to connectivity constraints, control errors, and noise from the environment (Pearson et al., 2019; Lanting et al., 2020; Nelson et al., 2021; Zaborniak and de Sousa, 2021; Grant and Humble, 2022; Pelofske et al., 2023). To map a QUBO Q of Equation (1) directly on the hardware chip of a quantum annealer, its connectivity structure should be consistent with the connectivity structure of the quantum device. Specifically, each variable xi is mapped to a distinct qubit qi. For each non-zero coefficient aij, there should be a coupler (direct link) between qubits qi and qj. If a direct embedding is not possible, then a minor embedding of the graph representing the sparsity structure of the QUBO Q onto the graph defined by the hardware structure can be used (Choi, 2008, 2011; Könz et al., 2021; Marshall et al., 2022). However, the number of qubits required in that case may grow quadratically with the size of Q.
To better assess the capabilities of both classical and quantum approaches for sampling (approximate) solutions of combinatorial optimization problems, methods are needed that generate benchmark problems with (ideally) known solutions. Two strategies exist to achieve this goal. First, one can generate problems of the type of Equation (1) with randomly sampled linear and quadratic weights, and then brute force them. However, brute forcing is only feasible for problems with a relatively small number of variables (roughly 30 variables for full brute force computations). Second, methods have been developed that allow one to generate QUBO problems with planted solutions, that is, problems generated to have a solution that is specified a priori. A detailed overview of such methods is given in Section 1.1. Importantly, existing methods often have two shortcomings. Many approaches only ensure that the generated problem has a minimum at the planted solution, but do not guarantee its uniqueness. Moreover, for many methods, the sparsity structure of the generated QUBO cannot be chosen, which means the QUBO cannot directly be solved on certain hardware devices. Naturally, since the minimization of Equation (1) is NP-hard, all methods exploit some form of shortcut or mathematical device to generate large problems with non-trivial structures and known solutions.
In this contribution, we introduce a new method to generate QUBO problems of the type of Equation (1) with a single planted solution. The method is called posiform planting, in reference to the mechanism we exploit that generates a QUBO in posiform representation. The posiforms are converted to QUBOs only at a later stage when the solution has been planted. Two features of our algorithm are noteworthy. First, it guarantees the uniqueness of the planted solution. Moreover, the connectivity structure of the QUBO can, in principle, be chosen freely. Naturally, the generated QUBOs need to have at least a certain number of quadratic terms to guarantee the uniqueness of the planted solution and thus cannot be too sparse, although this also depends on the solution being planted. In contrast to some existing solution-planting methods, such as the tile planting or deceptive cluster loops methods of the Chook toolbox (Perera et al., 2021), posiform planting generates QUBO problems which include linear terms.
The adaptation to an arbitrary connectivity structure is of importance when generating problems that are tailored to, for instance, the qubit connectivity structure of the D-Wave quantum annealers. In particular, the physical qubits across currently existing D-Wave generations use connections determined by Chimera, Pegasus, or Zephyr graphs (Dattani et al., 2019; Boothby et al., 2020). Being able to tailor the generated problems to any arbitrary architecture allows one to generate much larger benchmark problems compared to the case where the problems cannot be directly embedded, thus necessitating the computation of a minor embedding onto the D-Wave QPU chip structure.
One of the properties of the transverse field driver in quantum annealing and other approximate quantum optimization algorithms is that degenerate ground states are not in general sampled uniformly (Matsuda et al., 2009; Mandrà et al., 2017; Zhang et al., 2017; Könz, 2019; Könz et al., 2019; Kumar et al., 2020; Pelofske et al., 2021; Nelson et al., 2022). Posiform planting guarantees the uniqueness of the planted optimal solution. Thus, any use cases in which biased sampling of degenerate solutions needs to be avoided could benefit from posiform planting. Some use cases in which biased sampling of degenerate solutions should be avoided include the estimation the ground-state entropy of a degenerate physical systems, estimating the count of the total number of solutions in combinatorics or the estimation of ground state probabilities in industrial applications where the problem has several solutions by design (Mandrà et al., 2017).
This article is structured as follows. After a literature review in Section 1.1, we introduce the idea of posiform planting in Section 2. We evaluate the QUBO problems generated by posiform planting on D-Wave devices using both native connectivity (using the Chimera, Pegasus, and Zephyr hardware graphs), and arbitrarily connected minor embedded problem instances (Section 3). The hardware native QUBOs are also sampled using the classical heuristics simulated annealing and steepest gradient descent. The article concludes with a discussion in Section 4. Data and extra figures generated from this research are publicly available as a Zenodo dataset (Hahn et al., 2023).
1.1 Literature review
A variety of contributions in the literature focus on the generation of QUBO or Ising models of the type of Equation (1) that can serve as benchmark problems. These methods can be grouped according to the underlying mechanism they use to generate problems and the properties they guarantee. Originally, this property of known planted solutions was introduced from satisfiability problems (Barthel et al., 2002; Krzakala and Zdeborová, 2009).
One popular way to generate problems is with the help of frustrated loops, meaning Ising models of the form , where each Qj only contains a subset of the variables. For instance, Hen et al. (2015) and King A. D. et al. (2015) generated frustrated Ising models with tunable hardness, though the authors explicitly pointed out that they cannot guarantee uniqueness. Similar methods are the so-called tile-planting (Perera et al., 2020) and patch-planting for Ising models (Wang et al., 2017). In Pei et al. (2020), the authors generate weighted MAX-2-SAT instances with the help of frustrated loops that have known solutions. Notably, the hardness of their problems can be tuned through a parameter called the frustration index.
One major drawback of many published planted solution methods is the fact that they do not guarantee the uniqueness of the planted solution, meaning that the input configuration is only guaranteed to be one of a possibly unknown number of minima. A notable exception is Kowalsky et al. (2022), who ensure the uniqueness of solution with an approach based on equation planting. However, the resulting QUBOs have a very special form as each linear equation is required to contain exactly three binary variables.
Another route is called equation planting, that is, the generation of QUBO problems from a set of (linear) equations. In Hen (2019), the author considers a set of linear equations modulo 2 to pin down the bitstring to be planted, and then recasts it as an Ising model. Their method is based on the experimental observation that although linear equations are easy to solve, they disguise the solution well for machines when being recast as an optimization problem. According to the author, equation planting guarantees the uniqueness of the planted solution. However, tailoring the instances to a given connectivity structure is not mentioned.
A popular tool for generating binary optimization problems with planted solutions is the Chook toolbox of Perera et al. (2021). Chook implements several approaches, such as “tile planting,” “Wishart planting,” “equation planting,” and “k-local planting.” However, none of those approaches guarantees uniqueness, and some of them (such as Wishart planting) are not designed to tailor to arbitrary connectivity structures. Notably, the method “deceptive cluster loops” is tailored to the D-Wave Chimera topology.
The software package dwig contains Python implementations of several existing planted solution methods, specifically, RAN-pr (Zdeborova and Krzakala, 2016), RAN-k (King J. et al., 2015), FL-k (King A. D. et al., 2015), FCL-k (King et al., 2017), weak–strong cluster network (Denchev et al., 2016), frustrated cluster loops (Albash and Lidar, 2018), and corrupted biased ferromagnet (Pang et al., 2021).
There are several studies which have examined the sampling of MAX 2-SAT combinatorial optimization problems using quantum annealing, some with an emphasis on generating MAX 2-SAT, which are challenging for quantum annealing to sample (Crosson et al., 2014; Santra et al., 2014; Hsu et al., 2018; Mehta et al., 2021, 2022; Mirkarimi et al., 2023).
The above methods have been used in a number of studies on sampling characteristics of quantum annealers (King J. et al., 2015; Zhang et al., 2017; Barash et al., 2019; Marshall et al., 2019).
2 Methods
This section introduces a novel method to generate QUBO models of the type of Equation (1) for a customized connectivity structure and with a guarantee of uniqueness for the planted solution. The method is based on the generation of a posiform representation of Equation (1), which is introduced in Section 2.1. The construction of the posiform and the guarantee of uniqueness are based on the fact that testing if a posiform attains the value zero is equivalent to a 2-SAT problem, which can be solved in polynomial time (Section 2.2). The complete algorithm is summarized in Section 2.3. A note on how the generation can naturally be adapted to a given connectivity structure is discussed in Section 2.4.
2.1 Conversion from QUBO to posiform
A posiform is a quadratic function with positive coefficients on an extended set of variables , meaning that a posiform can contain either a variable xi∈{0, 1} or its complement , where i∈{1, …, n}. A posiform can be expressed as
where each and stand for one of the variables xi or its complement , i∈{1, …, n} and the coefficients bz and are non-negative.
Any QUBO of the form of Equation (1) can be written as a posiform. To this end, consider first the linear terms. If ai>0 for some i∈{1, …, n} in Equation (1), it remains unchanged in the posiform. If ai < 0, we rewrite . The single summand ai is constant and can be omitted as it does not impact the location of the minimum of Equation (1). The term complies with the posiform requirement as −ai>0 given ai < 0.
Similarly, any quadratic term aijxixj with aij>0 in Equation (1) remains unchanged in the posiform. If aijxixj with aij < 0 in Equation (1), we rewrite it as either or . Both options are valid choices and none is preferable over the other. As can be seen, apart from the constant term aij, which can be omitted, the remaining summands have positive coefficients −aij>0 given aij < 0.
As a simple example, consider the following QUBO in three variables, Q(x1, x2, x3) = 2x1−x2+x1x2−2x2x3. In posiform representation, it can be written as , where we omitted the offset −3 that results from the conversion.
2.2 Connection to 2-SAT problems
The idea of posiform planting is to generate posiforms that attain a value zero at a unique known (planted) combination of values of the variables. Assume a posiform of the type of Equation (2) is given. Clearly the minimum of Equation (2) is bounded below by zero as all coefficients and variables are non-negative. Moreover, we can test if there is a configuration x = (x1, …, xn) that achieves P(x1, …, xn) = 0 in linear time.
This can be seen as follows. If P(x1, …, xn) = 0, then all summands in Equation (2) must be zero. Therefore, we aim to find x = (x1, …, xn) such that z = 0 for all linear terms, and zz′ = 0 for all quadratic terms in Equation (2), where . For the quadratic terms, zz′ = 0 is equivalent to . We thus rewrite all linear and quadratic terms in Equation (2) without their coefficients into a 2-SAT problem, which can be solved in linear time (Krom, 1967; Even et al., 1976; Aspvall et al., 1979). Any solution to the constructed 2-SAT problem will satisfy P(x1, …, xn) = 0 and vice versa. Importantly, if the 2-SAT problem has a unique solution, so does the corresponding posiform.
2.3 QUBO generation with given connectivity and planted unique solution
We are given a bitstring , denoting the solution to be planted. The first step is to generate a 2-SAT problem having x* as its unique solution. We aim to construct a 2-SAT problem having x* as its unique solution with the help of an exclusion argument, meaning that we add clauses to the 2-SAT problem that exclude any bitstring other than x*. This is achieved as follows.
We select two random indices i, j∈{1, …, n} with i≠j and consider the two bits and in the solution to be planted. We then randomly select one of the three possible binary tuples satisfying . Depending on the choice of , we add a clause to the current 2-SAT problem that excludes the possibility of in an optimal solution, precisely, the clause
After each added clause, we attempt to solve the generated 2-SAT problem at its current stage. By construction, the choice of the clauses added to the 2-SAT problem will never exclude the planted bitstring x* from the solution set of the generated 2-SAT problem.
We continue in this fashion until we arrive at a 2-SAT problem which has x* as its unique solution. Our procedure only requires polynomial effort. Indeed, it is known that the phase transition in 2-SAT problems occurs for n variables at O(n) clauses (Gent and Walsh, 1994; Coja-Oghlan and Panagiotou, 2016), thus we expect to only add a linear number of clauses until x* remains as the unique solution of the 2-SAT problem. Moreover, solving a 2-SAT problem can be done in linear time (Krom, 1967; Even et al., 1976; Aspvall et al., 1979). Note that, to save computational effort, it is not necessary to solve the 2-SAT problem being generated each time a new clause is added. Instead, it suffices to solve it after adding a certain batch size B∈ℕ of new clauses. In the experiments of Section 3, we use the MiniSat solver of Eén and Sörensson (2023).
Once a 2-SAT problem is constructed with x* as its unique solution, we construct a posiform from it. Thus, in the second step, we convert each clause into the quadratic term , where . The negation is necessary here as each clause (z∨z′), that is, True (value 1) in the 2-SAT problem needs to be zero in the posiform (see Section 2.2) as it is a function to be minimized. Importantly, the coefficient of the posiform is actually freely choosable (as long as it is positive). Substituting any complement as 1−xi and multiplying out the expression yields a QUBO with (typically) both positive and negative QUBO coefficients.
As an example, suppose we aim to plant the solution x* = (1, 0, 1) in n = 3 variables. For the random indices (i, j) = (2, 3), we choose , thus satisfying . According to Equation (6), we add the clause to the 2-SAT problem being generated. By continuing in this fashion for other randomly chosen variable pairs in x*, we might obtain the 2-SAT instance
which can easily be checked to have the unique solution x*. Rewriting Equation (4) into a posiform results in . Note that the coefficients of P (set here to 1) can be freely chosen as long as they are positive. Multiplying out the posiform leads to the QUBO Q(x1, x2, x3) = x2+x3−2x1x3, which can easily be verified to have a unique minimum at x*.
2.4 Adaptation to connectivity structures
Apart from the guarantee of uniqueness, the algorithm of Section 2.3 allows one to adapt the generated QUBOs to a given connectivity structure. This is possible since there are no restrictions on the choice of tuples with i, j∈{1, …, n} that are being used to narrow down the solution space to x* in the 2-SAT problem.
To be precise, instead of sampling i, j∈{1, …, n}, it is valid to sample for some edge set . When converting the generated 2-SAT problem to a posiform, the clauses become the quadratic terms, and when multiplying out the posiform into a QUBO, no further couplers are being introduced. Therefore, the edges in will translate 1-to-1 to the quadratic couplers in the posiform and in the QUBO. For instance, can be chosen as the fixed connectivity graph of one of the D-Wave annealer generations. Naturally, if is too sparse, it might not be guaranteed any more that enough clauses can be sampled to narrow down x* as the unique solution; however, this problem was not encountered for any of the D-Wave hardware graphs.
3 Results
In this section, we investigate the performance of the posiform planting methodology introduced in Section 2. The section starts with an overview of the D-Wave devices and their parameters in Section 3.1. In Section 3.2, we use posiform planting to generate and solve QUBO instances on four D-Wave machines that fit their hardware natively, thus allowing for very large instance sizes. The hardness of the generated instances is assessed by computing the ground state probability (GSP) and the time-to-solution (TTS) metrics. In Section 3.3, we investigate instances with arbitrary qubit connectivity, thus requiring a minor embedding of the problem QUBO onto the D-Wave hardware.
3.1 Parameter settings
Table 1 shows the four generations of the D-Wave quantum annealer used in the experiments of this section. Apart from the Chip ID and the name of the D-Wave topology, Table 1 displays the number of available qubits and couplers and the annealing times supported by the device.
The posiform planting method requires solving a 2-SAT problem repeatedly during the planting process to verify the uniqueness of the planted solution (see Section 2.3). For efficiency reasons, we add an initial batch of B clauses to the 2-SAT problem before starting to check for uniqueness. In Section 3.2, we employ the choice B = 2, 000 for the Chimera hardware graph of DW_2000Q_6, B = 30, 000 for the Pegasus hardware graph of Advantage_system4.1 and Advantage_system6.1, and B = 1, 000 for the Zephyr hardware graph of Advantage2_prototype1.1. In Section 3.3, we employ B = 1 to generate the 52 variable all-to-all graphs. These choices of B are arbitrary, they do not influence the uniqueness of the solution but the runtime of the generation process, and they were selected to correspond to the number of variables in the hardware graph. Similarly, the posiform coefficients can be chosen arbitrarily in posiform planting. We select the posiform coefficients from the set {1, 2} for both the hardware native QUBOs and the minor embedded QUBOs, which depending on the hardware graph can result in highly variable QUBO coefficients after converting the posiform to a QUBO. However, the QUBO models can still be mapped onto the D-Wave hardware due to the auto coefficient scaling and the maximum energy scale that is programmable onto the chip. Choosing the posiform coefficients as integers also ensures that the QUBO coefficients will be integers. Visualizations of the hardware native QUBO coefficients can be found in Appendix 1.
The hardware native QUBOs in Section 3.2 are sampled using annealing times of 0.5 μs for the Advantage_system6.1 and Advantage_system4.1, and in the range {1, 2, …, 10} and {20, 30, …, 1, 990, 2, 000} μs for all four D-Wave quantum annealers. Each hardware native QUBO is sampled using two D-Wave device calls, each having 400 anneal-readout cycles, resulting in a total of 800 measurements made per annealing time and per hardware native QUBO.
3.2 Results for hardware native QUBOs
We generate 100 unique QUBO problems tailored to the four D-Wave quantum annealers outlined in Table 1. Those are being solved as a function of the anneal time, using the D-Wave settings described in Section 3.1. Since the unique solution and thus the ground state of each QUBO is known, computing the ground state success probability (GSP) is straightforward.
Figure 1 shows the GSP for the hardware native QUBOs measured on the four D-Wave devices. Each subplot shows the results of the 100 randomly generated QUBOs on each device, with one line per QUBO visualizing probability of reaching the ground state (among the 800 anneals) as a function of the annealing time.
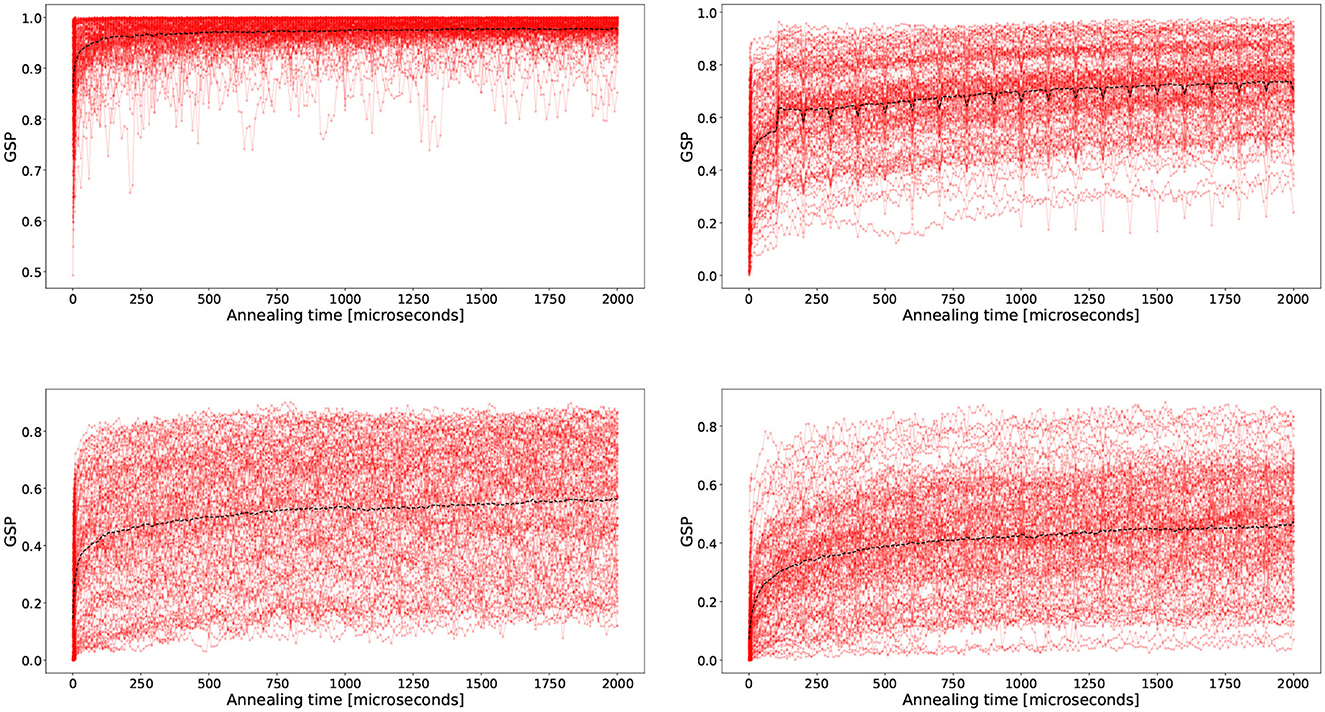
Figure 1. Ground state success probability (GSP) for hardware native QUBOs computed on the devices Advantage2_prototype1.1 (top left), DW_2000Q_6 (top right), Advantage_system4.1 (bottom left), and Advantage_system6.1 (bottom right). Each subplot corresponds to one D-Wave annealer and contains 100 separate lines which are showing GSP results for the 100 unique random hardware native posiform planted QUBOs. Each line shows the probability of reaching the ground state (among the 800 anneals) as a function of the annealing time. The dashed black line denotes the mean GSP computed at each evaluated annealing time.
Several observations are noteworthy. Since the GSP is mostly non-zero, the D-Wave quantum annealers are able to sample the optimal solution during some anneal. This even holds true for QUBO instances with up to 5, 627 variables in the case of Advantage_system4.1. Although it is difficult to see in the plots, at small annealing times, in particular, 500 ns and 1 μs, the two Pegasus chip devices fail to sample the optimal solution across all 100 problem instances.
We observe an increasing trend in the measured GSP as a function of the annealing time, but with diminishing returns as annealing time increases. The results show a difference in behavior between the four D-Wave devices. In particular, the 563 qubit system Advantage2_prototype1.1 samples the optimal solution at a much higher rate than the other devices. This finding can be attributed to the fact that the number of variables on this device is less than on the other devices, while also being the newest generation of the D-Wave annealer with reported lower error rates than the previous generations.
We observe that the results for DW_2000Q_6 in Figure 1 show periodic variations of the measured GSP. This is because the annealing time measurements in increments of 100 μs were made several weeks apart from the measurements made for all other annealing times in increments of 10 μs, and previous studies (Pelofske et al., 2023) have shown that there are long-term variations (in solution quality) of the computations carried out on current D-Wave quantum annealing devices. Therefore, the variations that have a periodicity of 100 μs are due to variance of the noise profile of the device, rather than variations that are a function of the annealing time.
Next, we examine the time-to-solution (TTS) metric for the 100 QUBO instances that were generated for each of the four D-Wave annealers. TTS is an estimate of the time it takes to reach an optimum solution with a 99% confidence. It is defined as
where QPU-access-time (in seconds) is the real compute time used on the D-Wave backend (including the hardware programming time, anneal-readout cycle, and anneal times), A is the number of anneals and p∈(0, 1) is the success probability observed among the A anneals, that is, the proportion of anneals that found the ground state. The QPU-access-time also includes all communication time with the device on top of the annealing time used in the computation. When p = 1, we set TTS0.99 = QPU-access-time/A. When p = 0, TTS0.99 is undefined, and therefore is not computed.
Figure 2 plots the TTS (computed with Equation 5) to reach the optimal planted solution for the set of 100 randomly generated hardware native QUBOs for each of the four D-Wave annealers. We observe that for Advantage2_prototype1.1, the lowest TTS is achieved for short annealing times, whereas for the other three generations of the D-Wave annealer, both low and high annealing times incur higher TTS values, with the lowest TTS being achieved in-between.

Figure 2. TTS as a function of the annealing time on the 100 hardware QUBO problems for each of the four D-Wave quantum annealers, in particular, Advantage2_prototype1.1 (top left), DW_2000Q_6 (top right), Advantage_system4.1 (bottom left), and Advantage_system6.1 (bottom right). One line per QUBO instance. Log scale on both axes.
In addition to solving the 100 native hardware QUBOs sampled on each of the four D-Wave devices, we also investigate how successfully classical heuristics can solve them. Figure 3 shows histograms for the achieved GSP when sampling the same set of hardware native QUBO problems using the classical heuristics Simulated Annealing (SA), implemented in the function neal in the D-Wave SDK (D-Wave Systems, 2023b), and greedy Steepest Descent (analogous to steepest gradient descent), implemented in the function greedy in the D-Wave SDK (D-Wave Systems, 2023a). Figure 3 demonstrates that the SA algorithm, in particular, is able to find the optimal solution of the QUBOs generated with posiform planting with very high success probability.
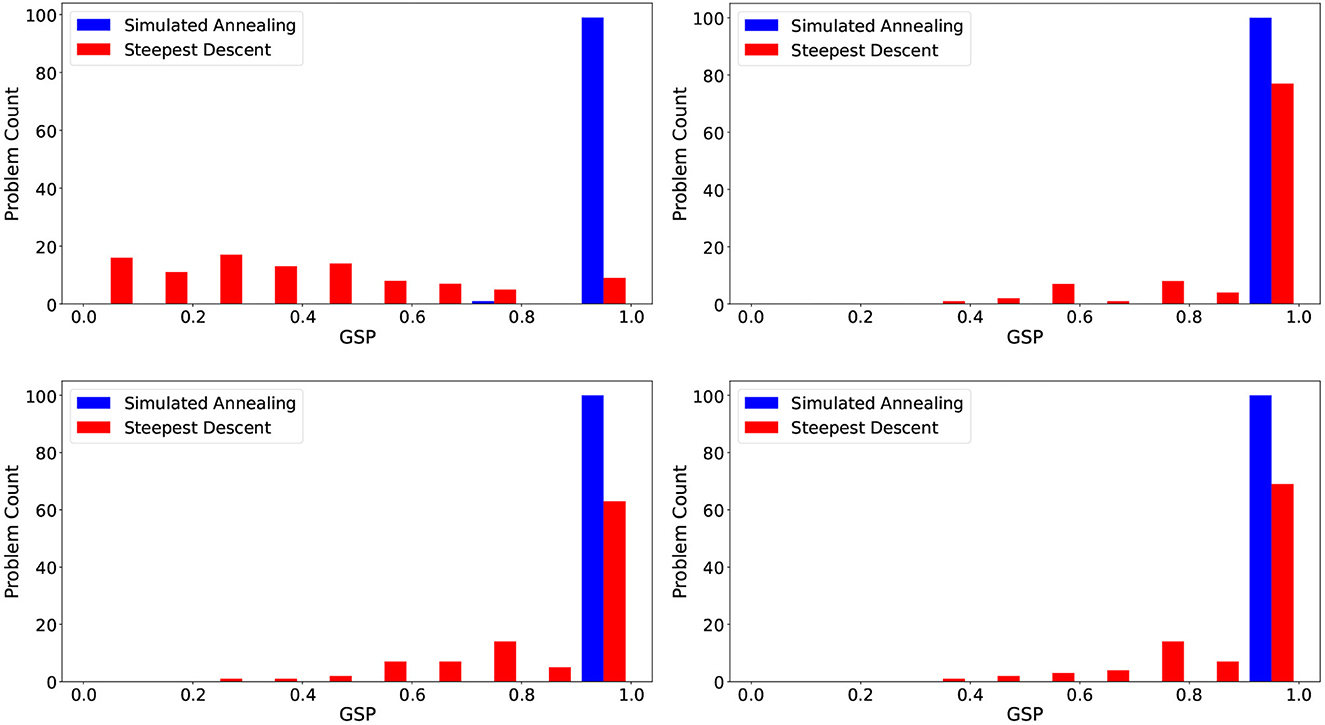
Figure 3. Histograms of the GSP for the same hardware native posiform planted QUBOs used in Figure 1 sampled using classical heuristics. Simulated annealing and steepest descent heuristics applied to the QUBOs generated for the hardware graphs of DW_2000Q_6 (top left), Advantage2_prototype1.1 (top right), Advantage_system4.1 (bottom left), and Advantage_system6.1 (bottom right). The side-by-side histogram bars correspond to each bin, so the sampling rates for simulated annealing are extremely high (usually at a proportion of 1).
3.3 Results for minor embedded QUBOs
Posiform planting as introduced in Section 2.3 generates new clauses to be added to the 2-SAT instance without any constraints on the indices. Although clauses are arbitrary, the generated QUBOs are usually not fully connected. Using generated QUBOs with all-to-all connectivity require a minor embedding onto the D-Wave quantum hardware before being solved, since the D-Wave hardware graphs are (relatively) sparse. Despite the challenges associated with minor-embedded QUBO instances, which require chained qubits and pose issues such as selecting appropriate chain strengths, utilizing such QUBOs enables a direct comparison of D-Wave devices on the same set of input problems. A diagram showing these complete minor embeddings on the four hardware graphs is shown in Figure A4 in the Appendix.
We generate five QUBOs with varying density with the aim to allow for a range of GSP rates among those planted QUBOs. Each QUBO instance has 52 logical variables, which is the largest problem size with an all-to-all connectivity that can be minor embedded on the Advantage2_prototype1.1 device. Since Advantage2_prototype1.1 has the smallest such embedding, the same QUBO instances are guaranteed to be executed on all four D-Wave quantum annealers, thereby allowing for a fair comparison. Note that these 52 variable QUBOs are not fully connected, but they are arbitrarily connected in that the generator can select arbitrary edges to include.
Figure 4 shows ground state success probability (GSP) measurements as a function of the chain strength, computed for the five fixed QUBO instances on the four D-Wave annealers of Table 1. Each subplot additionally showcases the behavior for different annealing times. The figure highlights several observations. First, the DW_2000Q_6 device seems to achieve a considerably lower GSP than the other devices, followed by Advantage_system4.1 and Advantage_system6.1, while Advantage2_prototype1.1 achieves highest GSP across the instances. Second, the anneal times do influence the solution quality throughout all instances, with longer annealing times usually resulting in an increased solution quality. Third, although the 5 QUBO instances were generated with the same parameters, there seems to be a considerable range in difficulty, with the instances in the left columns being harder to solve than the ones in the rightmost columns.
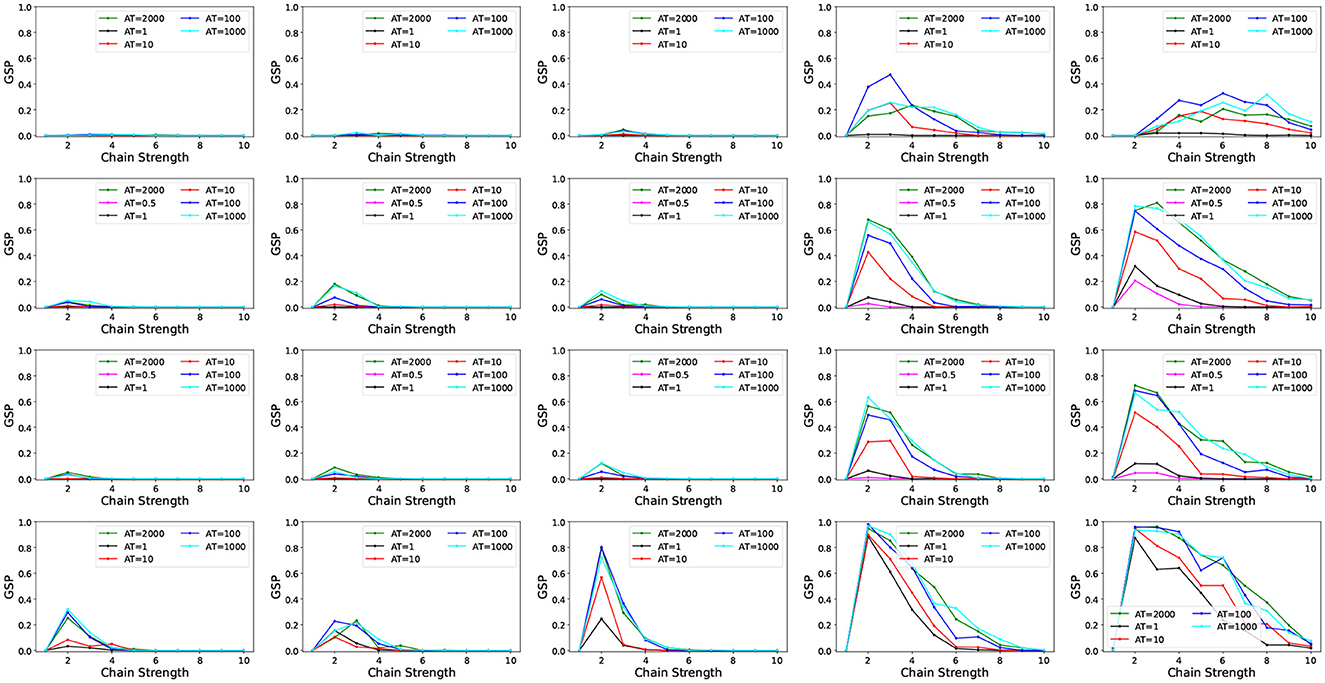
Figure 4. GSP measurements as a function of the chain strength for the five minor-embedded QUBO instances. The five columns correspond to the five QUBO instances being solved, and the four rows correspond to the four D-Wave quantum annealers (DW_2000Q_6, Advantage_system4.1, Advantage_system6.1, and Advantage2_prototype1.1 from top to bottom). The annealing times are varied (see legends).
4 Discussion
This study proposes a new method, called posiform planting, to generate QUBOs with a unique planted solution. Apart from guaranteeing the uniqueness, posiform planting can be adapted to any arbitrary connectivity structure, meaning that it allows one to generate tailored QUBO instances whose quadratic couplers fit, for instance, the hardware connectivity of modern quantum annealers. Therefore, posiform planting allows one to efficiently generate QUBO instances with thousands of variables and a unique planted solution. Posiform planting also generates QUBOs that have linear terms, a property that not all of existing planted solution methods have.
Interestingly, our construction shows that, for the generation of a QUBO with a planted solution, the coefficients in a posiform representation do not matter and can be freely chosen (as long as they are positive as required by definition of a posiform). Since the choice of the posiform coefficients does not impact the planted solution or its uniqueness, posiform planted allows for an efficient generation of a set of QUBO instances having the same planted solution. Posiform planting also allows for an arbitrary bitstring to be chosen as the planted solution.
Posiform planting can be used to verify whether good classical heuristic algorithms, such as simulated annealing, are able to find the single optimal solution for extremely large QUBOs. This not only applies to classical algorithms but also other emerging computing technologies such as spiking neuromorphic computing (Alom et al., 2017; Mniszewski, 2019) or the hybrid quantum-classical gate model algorithm QAOA (Farhi et al., 2014; Hadfield et al., 2019). We experimentally demonstrated that four D-Wave quantum annealers, with a total of three different classes of hardware graphs, can sample the unique planted solution for hardware native QUBO problems that use the entire hardware chip. Since we scaled our instances to the maximal size that can be embedded on D-Wave, the current hardware limitations (of maximally 5,627 qubits on D-Wave Advantage) somewhat limit us from scaling our instances to sizes where D-Wave starts to struggle.
Posiform planting generates QUBOs of a special form to guarantee the uniqueness of the planted solution. To be precise, all QUBOs generated by posiform planting have the property that when converted to a posiform representation, they are solvable (meaning they attain a value of zero). However, not all QUBOs have this property. Nevertheless, posiform planting is complete in the sense that it can generate any QUBO whose posiform representation is solvable.
The study leaves scope for further avenues of research. Most importantly, it remains to investigate if posiform planting allows one to tune the difficulty of the QUBO problems, for instance, via the choice of the posiform coefficients (which can be tuned without constraints other than being positive). Another topic for future research is to be able to vary the ground state degeneracy of posiform planted QUBOs, if there are specific use cases where obtaining a QUBO with a specific number of ground states would be advantageous.
Finally, posiform planting can enhance an existing planted solution method, denoted as M, to guarantee the uniqueness of the planted solution. For instance, given the desired solution x* to be planted, we first use M to produce a QUBO Q1 with the planted solution x*, which may be non-unique. Subsequently, leveraging posiform planting, we generate a QUBO Q2 that ensures x* is a unique optimal solution. By forming the linear combination Qnew = α1Q1+α2Q2 with α1, α2>0, we obtain a problem with a unique solution x*, while potentially preserving any desired properties of M.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://doi.org/10.5281/zenodo.8336707.
Author contributions
GH: Conceptualization, Investigation, Methodology, Software, Writing—original draft, Writing—review & editing, Supervision, Validation, Formal analysis. EP: Data curation, Investigation, Methodology, Software, Visualization, Writing—original draft, Writing—review & editing, Validation, Resources. HD: Methodology, Project administration, Supervision, Writing—review & editing, Investigation.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by the U.S. Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory was operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (with Contract No. 89233218CNA000001). Research presented in this article was supported by the NNSA's Advanced Simulation and Computing Beyond Moore's Law Program at Los Alamos National Laboratory, and was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project 20210114ER. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which was supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001. This research used resources provided by the Darwin testbed at Los Alamos National Laboratory (LANL), which was funded by the Computational Systems and Software Environments subprogram of LANL's Advanced Simulation and Computing program (NNSA/DOE). This study has been assigned LANL technical report number LA-UR-23-27170. The study of HD was supported by grant number KP-06-DB/1 of the Bulgarian National Science Fund. Funding for GH was provided through Cure Alzheimer's Fund, the National Institutes of Health [1R01 AI 154470-01; 2U01 HG 008685; R21 HD 095228 008976; U01 HL 089856; U01 HL 089897; P01 HL 120839; P01 HL 132825; 2U01 HG 008685; R21 HD 095228, and P01HL132825], the National Science Foundation [NSF PHY 2033046 and NSF GRFP 1745302], and a NIH Center grant [P30-ES002109].
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2023.1275948/full#supplementary-material
References
Albash, T., and Lidar, D. A. (2018). Demonstration of a scaling advantage for a quantum annealer over simulated annealing. Phys. Rev. X 8:031016. doi: 10.1103/PhysRevX.8.031016
Alom, M., Van Essen, B., Moody, A., Widemann, D., and Taha, T. M. (2017). “Quadratic unconstrained binary optimization (QUBO) on neuromorphic computing system,” in 2017 International Joint Conference on Neural Networks (IJCNN) (IEEE), 3922–3929. doi: 10.1109/IJCNN.2017.7966350
Aspvall, B., Plass, M., and Tarjan, R. (1979). A linear-time algorithm for testing the truth of certain quantified Boolean formulas. Inform. Process. Lett. 8, 121–123. doi: 10.1016/0020-0190(79)90002-4
Barash, L., Marshall, J., Weigel, M., and Hen, I. (2019). Estimating the density of states of frustrated spin systems. N. J. Phys. 21:073065. doi: 10.1088/1367-2630/ab2e39
Barthel, W., Hartmann, A. K., Leone, M., Ricci-Tersenghi, F., Weigt, M., and Zecchina, R. (2002). Hiding solutions in random satisfiability problems: a statistical mechanics approach. Phys. Rev. Lett. 88:188701. doi: 10.1103/PhysRevLett.88.188701
Boixo, S., Albash, T., Spedalieri, F. M., Chancellor, N., and Lidar, D. A. (2013). Experimental signature of programmable quantum annealing. Nat. Commun. 4:2067. doi: 10.1038/ncomms3067
Boixo, S., Rønnow, T. F., Isakov, S. V., Wang, Z., Wecker, D., Lidar, D. A., et al. (2014). Evidence for quantum annealing with more than one hundred qubits. Nat. Phys. 10, 218–224. doi: 10.1038/nphys2900
Boixo, S., Smelyanskiy, V. N., Shabani, A., Isakov, S. V., Dykman, M., Denchev, V. S., et al. (2016). Computational multiqubit tunnelling in programmable quantum annealers. Nat. Commun. 7:10327. doi: 10.1038/ncomms10327
Boothby, K., Bunyk, P., Raymond, J., and Roy, A. (2020). Next-generation topology of d-wave quantum processors. arXiv [Preprint]. arXiv: 2003.00133.
Boros, E., Hammer, P., and Tavares, G. (2006). Preprocessing of unconstrained quadratic binary optimization. Rutcor Res. Rep. 10, 1–58.
Boros, E., Hammer, P., and Tavares, G. (2007). Local search heuristics for Quadratic Unconstrained Binary Optimization (QUBO). J. Heurist. 13, 99–132. doi: 10.1007/s10732-007-9009-3
Choi, V. (2008). Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quant. Inform. Process. 7, 193–209. doi: 10.1007/s11128-008-0082-9
Choi, V. (2011). Minor-embedding in adiabatic quantum computation: II. Minor-universal graph design. Quant. Inform. Process. 10, 343–353. doi: 10.1007/s11128-010-0200-3
Coja-Oghlan, A., and Panagiotou, K. (2016). The asymptotic k-SAT threshold. Adv. Math. 288, 985–1068. doi: 10.1016/j.aim.2015.11.007
Crosson, E., Farhi, E., Lin, C. Y.-Y., Lin, H.-H., and Shor, P. (2014). Different strategies for optimization using the quantum adiabatic algorithm. arXiv [Preprint]. arXiv: 1401.7320.
Das, A., and Chakrabarti, B. K. (2008). Colloquium: Quantum annealing and analog quantum computation. Rev. Modern Phys. 80:1061. doi: 10.1103/RevModPhys.80.1061
Dattani, N., Szalay, S., and Chancellor, N. (2019). Pegasus: the second connectivity graph for large-scale quantum annealing hardware. arXiv [Preprint]. arXiv: 1901.07636.
Denchev, V. S., Boixo, S., Isakov, S. V., Ding, N., Babbush, R., Smelyanskiy, V., et al. (2016). What is the computational value of finite-range tunneling? Phys. Rev. X 6:031015. doi: 10.1103/PhysRevX.6.031015
D-Wave Systems (2023a). Dwave-Greedy: An Implementation of a Steepest Descent Solver for Binary Quadratic Models. Available online at: https://github.com/dwavesystems/dwave-greedy
D-Wave Systems (2023b). Dwave-Neal: An Implementation of a Simulated Annealing Sampler. Available online at: https://github.com/dwavesystems/dwave-neal
Eén, N., and Sörensson, N. (2023). MiniSat Solver. Available online at: http://minisat.se
Even, S., Itai, A., and Shamir, A. (1976). On the complexity of time table and multi-commodity flow problems. SIAM J. Comput. 5, 691–703. doi: 10.1137/0205048
Farhi, E., Goldstone, J., and Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv [Preprint]. arXiv: 1411.4028.
Gent, I. P., and Walsh, T. (1994). “The SAT phase transition,” in ECAI'94: Proceedings of the 11th European Conference on Artificial Intelligence (PITMAN), 105–109.
Grant, E., and Humble, T. S. (2022). Benchmarking embedded chain breaking in quantum annealing. Quant. Sci. Technol. 7:025029. doi: 10.1088/2058-9565/ac26d2
Hadfield, S., Wang, Z., O'Gorman, B., Rieffel, E., Venturelli, D., and Biswas, R. (2019). From the quantum approximate optimization algorithm to a quantum alternating operator Ansatz. Algorithms 12:34. doi: 10.3390/a12020034
Hahn, G., Pelofske, E., and Djidjev, H. (2023). Dataset for Posiform Planting: Generating QUBO Instances for Benchmarking [Data set]. Zenodo. doi: 10.5281/zenodo.8336707
Harris, R., Sato, Y., Berkley, A., Reis, M., Altomare, F., Amin, M., et al. (2018). Phase transitions in a programmable quantum spin glass simulator. Science 361, 162–165. doi: 10.1126/science.aat2025
Hauke, P., Katzgraber, H. G., Lechner, W., Nishimori, H., and Oliver, W. D. (2020). Perspectives of quantum annealing: methods and implementations. Rep. Prog. Phys. 83:054401. doi: 10.1088/1361-6633/ab85b8
Hen, I. (2019). Equation planting: a tool for benchmarking Ising machines. Phys. Rev. Appl. 12:011003. doi: 10.1103/PhysRevApplied.12.011003
Hen, I., Job, J., Albash, T., Rønnow, T., Troyer, M., and Lidar, D. (2015). Probing for quantum speedup in spin-glass problems with planted solutions. Phys. Rev. A 92:042325. doi: 10.1103/PhysRevA.92.042325
Hsu, T.-J., Jin, F., Seidel, C., Neukart, F., Raedt, H. D., and Michielsen, K. (2018). Quantum annealing with anneal path control: application to 2-sat problems with known energy landscapes. Commun. Comput. Phys. 26, 928–946. doi: 10.4208/cicp.OA-2018-0257
Kadowaki, T., and Nishimori, H. (1998). Quantum annealing in the transverse Ising model. Phys. Rev. E 58, 5355–5363. doi: 10.1103/PhysRevE.58.5355
King, A. D., Lanting, T., and Harris, R. (2015). Performance of a quantum Annealer on range-limited constraint satisfaction problems. arXiv [Preprint]. arXiv: 1502.02098.
King, A. D., Raymond, J., Lanting, T., Harris, R., Zucca, A., Altomare, F., et al. (2023). Quantum critical dynamics in a 5,000-qubit programmable spin glass. Nature 617, 61–66. doi: 10.1038/s41586-023-05867-2
King, A. D., Raymond, J., Lanting, T., Isakov, S. V., Mohseni, M., Poulin-Lamarre, G., et al. (2021). Scaling advantage over path-integral Monte Carlo in quantum simulation of geometrically frustrated magnets. Nat. Commun. 12, 1–6. doi: 10.1038/s41467-021-20901-5
King, A. D., Suzuki, S., Raymond, J., Zucca, A., Lanting, T., Altomare, F., et al. (2022). Coherent quantum annealing in a programmable 2,000 qubit Ising chain. Nat. Phys. 18, 1324–1328. doi: 10.1038/s41567-022-01741-6
King, J., Yarkoni, S., Nevisi, M. M., Hilton, J. P., and McGeoch, C. C. (2015). Benchmarking a quantum annealing processor with the time-to-target metric. arXiv [Preprint]. arXiv:1508.05087.
King, J., Yarkoni, S., Raymond, J., Ozfidan, I., King, A. D., Nevisi, M. M., et al. (2017). Quantum annealing amid local ruggedness and global frustration. J. Phys. Soc. Jpn. 88:061007. doi: 10.7566/JPSJ.88.061007
Kirkpatrick, S., Gelatt, C. D. Jr, and Vecchi, M. P. (1983). Optimization by simulated annealing. Science 220, 671–680. doi: 10.1126/science.220.4598.671
Könz, M. (2019). Embedding penalties for quantum hardware architectures and performance of simulated quantum annealing (Ph.D. thesis). ETH Zurich, Zurich, Switzerland.
Könz, M. S., Lechner, W., Katzgraber, H. G., and Troyer, M. (2021). Embedding overhead scaling of optimization problems in quantum annealing. PRX Quant. 2:040322. doi: 10.1103/PRXQuantum.2.040322
Könz, M. S., Mazzola, G., Ochoa, A. J., Katzgraber, H. G., and Troyer, M. (2019). Uncertain fate of fair sampling in quantum annealing. Phys. Rev. A 100:030303. doi: 10.1103/PhysRevA.100.030303
Kowalsky, M., Albash, T., Hen, I., and Lidar, D. (2022). 3-regular three-XORSAT planted solutions benchmark of classical and quantum heuristic optimizers. Quant. Sci. Technol. 7:025008. doi: 10.1088/2058-9565/ac4d1b
Krom, M. (1967). The decision problem for a class of first-order formulas in which all disjunctions are binary. Zeitschr. Math. Log. Grund. Math. 13, 15–20. doi: 10.1002/malq.19670130104
Krzakala, F., and Zdeborová, L. (2009). Hiding quiet solutions in random constraint satisfaction problems. Phys. Rev. Lett. 102:238701. doi: 10.1103/PhysRevLett.102.238701
Kumar, V., Tomlin, C., Nehrkorn, C., O'Malley, D., and Dulny, J. (2020). Achieving fair sampling in quantum annealing. arXiv [Preprint]. arXiv: 2007.08487.
Lanting, T., Amin, M. H., Baron, C., Babcock, M., Boschee, J., Boixo, S., et al. (2020). Probing environmental spin polarization with superconducting flux qubits. arXiv [Preprint]. arXiv: 2003.14244.
Lanting, T., Przybysz, A., Smirnov, A., Spedalieri, F., Amin, M., Berkley, A., et al. (2014). Entanglement in a quantum annealing processor. Phys. Rev. X 4:21041. doi: 10.1103/PhysRevX.4.021041
Lucas, A. (2014). Ising formulations of many NP problems. Front. Phys. 2:5. doi: 10.3389/fphy.2014.00005
Mandrà, S., Zhu, Z., and Katzgraber, H. G. (2017). Exponentially biased ground-state sampling of quantum annealing machines with transverse-field driving Hamiltonians. Phys. Rev. Lett. 118:070502. doi: 10.1103/PhysRevLett.118.070502
Marshall, J., Mossi, G., and Rieffel, E. G. (2022). Perils of embedding for quantum sampling. Phys. Rev. A 105:022615. doi: 10.1103/PhysRevA.105.022615
Marshall, J., Venturelli, D., Hen, I., and Rieffel, E. G. (2019). Power of pausing: advancing understanding of thermalization in experimental quantum Annealers. Phys. Rev. Appl. 11:044083. doi: 10.1103/PhysRevApplied.11.044083
Matsuda, Y., Nishimori, H., and Katzgraber, H. G. (2009). Quantum annealing for problems with ground-state degeneracy. J. Phys. 143:012003. doi: 10.1088/1742-6596/143/1/012003
Mehta, V., Jin, F., Raedt, H. D., and Michielsen, K. (2021). Quantum annealing with trigger hamiltonians: application to 2-satisfiability and nonstoquastic problems. Phys. Rev. A 104:032421. doi: 10.1103/PhysRevA.104.032421
Mehta, V., Jin, F., Raedt, H. D., and Michielsen, K. (2022). Quantum annealing for hard 2-satisfiability problems: distribution and scaling of minimum energy gap and success probability. Phys. Rev. A 105:062406. doi: 10.1103/PhysRevA.105.062406
Mirkarimi, P., Callison, A., Light, L., Chancellor, N., and Kendon, V. (2023). Comparing the hardness of max 2-sat problem instances for quantum and classical algorithms. Phys. Rev. Res. 5:023151. doi: 10.1103/PhysRevResearch.5.023151
Mniszewski, S. (2019). “Graph partitioning as quadratic unconstrained binary optimization (QUBO) on spiking neuromorphic hardware,” in Proceedings of the International Conference on Neuromorphic Systems, ICONS '19 (New York, NY: Association for Computing Machinery), 1–5. doi: 10.1145/3354265.3354269
Morita, S., and Nishimori, H. (2008). Mathematical foundation of quantum annealing. J. Math. Phys. 49:125210. doi: 10.1063/1.2995837
Nelson, J., Vuffray, M., Lokhov, A. Y., Albash, T., and Coffrin, C. (2022). High-quality thermal Gibbs sampling with quantum annealing hardware. Phys. Rev. Appl. 17:044046. doi: 10.1103/PhysRevApplied.17.044046
Nelson, J., Vuffray, M., Lokhov, A. Y., and Coffrin, C. (2021). Single-qubit fidelity assessment of quantum annealing hardware. doi: 10.1109/TQE.2021.3092710
Pang, Y., Coffrin, C., Lokhov, A. Y., and Vuffray, M. (2021). The potential of quantum annealing for rapid solution structure identification. Constraints 26, 1–25. doi: 10.1007/s10601-020-09315-0
Pearson, A., Mishra, A., Hen, I., and Lidar, D. A. (2019). Analog errors in quantum annealing: doom and hope. NPJ Quant. Inform. 5:107. doi: 10.1038/s41534-019-0210-7
Pei, Y., Manukian, H., and Di Ventra, M. (2020). Generating weighted MAX-2-SAT instances with frustrated loops: an RBM case study. J. Mach. Learn. Res. 21, 1532–4435.
Pelofske, E., Golden, J., Bärtschi, A., O'Malley, D., and Eidenbenz, S. (2021). “Sampling on NISQ devices: ‘Who's the fairest one of all?',” in 2021 IEEE International Conference on Quantum Computing and Engineering (QCE), 207–217. doi: 10.1109/QCE52317.2021.00038
Pelofske, E., Hahn, G., and Djidjev, H. (2023). Noise dynamics of quantum annealers: estimating the effective noise using idle qubits. Quant. Sci. Technol. 8:035005. doi: 10.1088/2058-9565/accbe6
Perera, D., Akpabio, I., Hamze, F., Mandrà, S., Rose, N., Aramon, M., et al. (2021). Chook-A comprehensive suite for generating binary optimization problems with planted solutions. arXiv[Preprint]. arXiv:2005.14344.
Perera, D., Hamze, F., Raymond, J., Weigel, M., and Katzgraber, H. (2020). Computational hardness of spin-glass problems with tile-planted solutions. Phys. Rev. E 101:023316. doi: 10.1103/PhysRevE.101.023316
Santra, S., Quiroz, G., Steeg, G. V., and Lidar, D. A. (2014). Max 2-SAT with up to 108 qubits. N. J. Phys. 16:045006. doi: 10.1088/1367-2630/16/4/045006
Tasseff, B., Albash, T., Morrell, Z., Vuffray, M., Lokhov, A. Y., Misra, S., et al. (2022). On the emerging potential of quantum annealing hardware for combinatorial optimization. arXiv [Preprint]. arXiv: 2210.04291.
Venturelli, D., Mandrà, S., Knysh, S., O'Gorman, B., Biswas, R., and Smelyanskiy, V. (2015). Quantum optimization of fully connected spin glasses. Phys. Rev. X 5:31040. doi: 10.1103/PhysRevX.5.031040
Wang, W., Mandrà, S., and Katzgraber, H. (2017). Patch-planting spin-glass solution for benchmarking. Phys. Rev. E 96:023312. doi: 10.1103/PhysRevE.96.023312
Zaborniak, T., and de Sousa, R. (2021). Benchmarking Hamiltonian noise in the d-wave quantum annealer. IEEE Trans. Quant. Eng. 2, 1–6. doi: 10.1109/TQE.2021.3050449
Zdeborova, L., and Krzakala, F. (2016). Statistical physics of inference: thresholds and algorithms. Adv. Phys. 65, 453–552. doi: 10.1080/00018732.2016.1211393
Keywords: quantum annealing (QA), QUBO problem, MAX-2-SAT, planted solution, time-to-solution, combinatorial optimization problem, boolean satisfiability (SAT), quadratic unconstrained binary optimization
Citation: Hahn G, Pelofske E and Djidjev HN (2023) Posiform planting: generating QUBO instances for benchmarking. Front. Comput. Sci. 5:1275948. doi: 10.3389/fcomp.2023.1275948
Received: 10 August 2023; Accepted: 16 October 2023;
Published: 21 November 2023.
Edited by:
Nicholas Chancellor, Durham University, United KingdomReviewed by:
Itay Hen, University of Southern California, United StatesJie-Hong Jiang, National Taiwan University, Taiwan
Copyright © 2023 Hahn, Pelofske and Djidjev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Georg Hahn, Z2hhaG5AaHNwaC5oYXJ2YXJkLmVkdQ==
 Georg Hahn1*
Georg Hahn1* Elijah Pelofske
Elijah Pelofske Hristo N. Djidjev
Hristo N. Djidjev