
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Comput. Sci., 31 October 2022
Sec. Software
Volume 4 - 2022 | https://doi.org/10.3389/fcomp.2022.931312
The problem of producing portable high-performance computing (HPC) software that is cheap to develop and maintain is called the P3 (performance, portability, productivity) problem. Good solutions to the P3 problem have been achieved when the performance profiles of the target machines have been similar. The variety of HPC architectures is, however, large and can be expected to grow larger. Software for HPC therefore needs to be highly adaptable, and there is a pressing need to provide developers with tools to produce software that can target machines with vastly different profiles. Multi-dimensional array manipulation constitutes a core component of numerous numerical methods, such as finite difference solvers of Partial Differential Equations (PDEs). The efficiency of these computations is tightly connected to traversing and distributing array data in a hardware-friendly way. The Mathematics of Arrays (MoA) allows for formally reasoning about array computations and enables systematic transformations of array-based programs, e.g., to use data layouts that fit to a specific architecture. This paper presents a programming methodology aimed for tackling the P3 problem in domains that are well-explored using Magnolia, a language designed to embody generic programming. The Magnolia programmer can restrict the semantic properties of abstract generic types and operations by defining so-called axioms. Axioms can be used to produce tests for concrete implementations of specifications, for formal verification, or to perform semantics-preserving program transformations. We leverage Magnolia's semantic specification facilities to extend the Magnolia compiler with a term rewriting system. We implement MoA's transformation rules in Magnolia, and demonstrate through a case study on a finite difference solver of PDEs how our rewriting system allows exploring the space of possible optimizations.
The quest for higher performance fuels innovation on hardware architectures; we have seen a wide variety of high-performance computing (HPC) architectures in the past and can expect new ones to keep appearing. Long-lived and successful HPC software must thus be highly adaptable, adjustable to different memory hierarchies and changing intra- and inter-process communication hardware.
The problem of producing HPC software that is easy, or at least not unreasonably difficult, to develop and maintain across multiple architectures is called the P3 (performance, portability, productivity) problem. Good solutions to the P3 problem have been achieved when the performance profiles of the target machines have been similar (Wolfe, 2021). As more new hardware architectures emerge, there is a pressing need to provide developers with tools to produce such software for targets with vastly different profiles. This includes architectures that fit within Wolfe's P3 machine performance model (CPUs, GPUs, or other accelerators, possibly distributed; Wolfe, 2021) but also those that do not (e.g., Groq's Tensor Streaming Processor; Abts et al., 2020).
Multidimensional array manipulation is at the core of numerous numerical methods. The topic of optimizing the performance of array computations is therefore extremely relevant to the P3 problem. We have previously explored the Mathematics of Arrays (MoA) formalism (Mullin, 1988) as a tool to optimize array computations for different hardware architectures, first through their Denotational Normal Form (DNF; Chetioui et al., 2019) and then through their Operational Forms (OFs; Chetioui et al., 2021). A thorough mathematical understanding of a given domain is key to enabling domain-specific semantic-preserving rewrites—and therefore optimizations.
The portability and productivity pillars of P3 are both strongly related to the notion of code reuse. Portability as meant here is the ability to run the same code with high performance on different machines. Productivity means that applications can be developed and maintained with a reasonable and predicable effort. Research unequivocally shows that productivity increases through reuse (Basili et al., 1996; Frakes and Succi, 2001; Nazareth and Rothenberger, 2004). Generic programming has proven to be an effective method of constructing libraries of reusable software components. The Magnolia programming language (Bagge, 2009) is designed as an embodiment of generic programming (Chetioui et al., 2022). It allows the flexible intermixing of specifications and implementations. Specifications can additionally be restricted by semantic requirements (called axioms) in the form of assertions. These axioms can be used for testing (Bagge et al., 2011), but also for optimization when used as directed rewrite rules, in the case of equational or conditional equational axioms (Bagge and Haveraaen, 2009).
In their 2012 paper on Halide, Ragan-Kelley et al. (2012) introduce the term schedule to refer to decisions about storage and about the order of computations in a program. The insight is that the essence of an algorithm is distinct from its schedule—allowing the advent of a programming model where both kinds of computations are not anymore intertwined but instead expressed independently from each other.
Stepanov-style generic programming abstracts algorithms and data structures by specifying minimum syntactic and semantic requirements on instantiations. Said differently, the types and operations underlying a generic implementation are only characterized by the part of their observable behavior that is relevant to the generic algorithm.
When observed through the lens of generic programming, a schedule is an abstraction for the kind of hardware architecture underlying the computations. We consider only the information about the hardware that is relevant for executing our algorithm efficiently: how computations should be ordered, and how data should be stored. Similar hardware architectures are then valid instantiations for the same schedule.
Scheduling, in the case of array computations, relates particularly to the access patterns of the arrays. As a motivating example, consider an array program running on a single CPU with memory, the classical model of a computer. We may have three standard traversal patterns for computations over our arrays:
1. a row-major traversal;
2. a column-major traversal;
3. a tiled traversal.
While the original algorithm can be expressed without making any assumption about the underlying hardware, the choice of a particular hardware will dictate which traversal pattern is most efficient. In other cases, the choice of a particular schedule may be desirable. For example, on hardware consisting of several distributed CPUs connected through some communication network, we may want the schedule to handle inter-CPU communication using MPI. If each one of these CPUs is connected to several GPUs, we may also want the schedule to load data on and off the GPUs as needed. Such choices will affect the desired data layout, and consequently the data access patterns so as to match the distribution of the data. These changes will have to be reflected in the presentation of the algorithm.
The execution time for an algorithm adapted to its schedule may be dramatically shorter than for an algorithm exhibiting less well-suited data access patterns. While an algorithm and its schedule can be expressed independently, choices in the latter may affect what is an appropriate expression of the former, and vice versa. Our approach uses rewriting technology to adapt a unique algorithm to adequately exploit the data traversal pattern of a schedule, and underlying hardware characteristics.
Throughout the rest of the paper, we view schedules as hardware abstractions. This view is fully compatible with Ragan-Kelley et al. (2012)'s definition of schedules, but conveys our intent more accurately.
This paper presents a programming methodology aimed for tackling the P3 problem in well-explored domains. We define well-explored domains as those for which significant domain-specific knowledge and a mathematical formalization exist.
Our approach keeps the essence of the algorithm separate from its schedule, which makes it convenient to explore different mappings of the algorithm's computations to hardware. To achieve this, we extend our Magnolia compiler with code generation and term rewriting facilities based on axioms. We use these new facilities to implement, in Magnolia, a library of generic and hardware-specific optimization rules based on MoA and its formal guarantees.
To assess our approach and how it alleviates the P3 problem, we apply it to a Partial Differential Equation (PDE) solver based on Finite Difference Methods (FDM). With this case study, we demonstrate that in the case of a finite difference solver, our methodology allows for easily producing different versions of the solver program with different performance characteristics on both CPU and GPU. To be clear about our assessment, we note that we did not compare our performance to hand-crafted fine-tuned implementations, or quantitatively measure the effort of producing different solver versions against implementing those by hand. The productivity benefits of approaches emphasizing code reuse, such as ours, become more apparent as the number of programs to implement in a given domain grows. The API we use is suitable for any explicit finite difference solver, and our contribution thus extends beyond the particular problem configuration chosen in the case study (Burrows et al., 2018).
The paper is structured as follows. Section 2 provides necessary background on Magnolia. Section 3 describes our methodology in detail, and illustrates it with a PDE solver based on FDM. Section 4 reflects on our work and ties it together with relevant related work. All the code is available as an example in the repository for magnoliac (Chetioui, 2020; see the examples/pde folder at https://github.com/magnolia-lang/magnolia-lang/tree/base-program).
The phrase generic programming has over decades of programming language development come to have a variety of interpretations, depending on the main type of genericity considered. Gibbons gives a taxonomy of interpretations (Gibbons, 2006). Stepanov-style generic programming (Dehnert and Stepanov, 1998) corresponds to what Gibbons calls genericity by property, where one describes data structures and algorithms in terms of syntactic and semantic requirements. This is the essence of Stepanov's and Musser's concepts (Musser and Stepanov, 1988). They are the direct inspiration behind C++0x concepts (Gregor et al., 2006); the C++20 concepts are a scaled back realization of those that only allow syntactic requirements on instantiations (In this latter case, we talk of genericity by structure.).
Magnolia is a programming language designed as an embodiment of Stepanov-style generic programming (Bagge, 2009). Magnolia code is structured into modules that mix abstract specifications of operations and their concrete implementations flexibly, following the work of Goguen and Burstall (1984) on the theory of institutions. The language does not offer any primitive types aside from predicates: every data structure is implemented in a configurable host programming language. As of today, Magnolia can target C++ and Python (Chetioui, 2020). Our prior work coins the term genericity by host language to refer to this axis of parameterization, in the style of Gibbons' taxonomy (Chetioui et al., 2022). Composite operations can be implemented in Magnolia, while the base types and operations, including loop structures, are implemented in the host language. The programmer can freely decide where to set the boundary between the operations implemented in Magnolia, and those implemented in the base library written in the host language—depending on what is more convenient. An appropriate choice of underlying data structures results in code that is as performant as if implemented directly in the host language (Chetioui et al., 2022). Because the axiom formalism is semantically compatible with the program code, Magnolia avoids the semantic gap common in approaches to formal software verification (Sannella and Tarlecki, 1996).
A Magnolia signature declares types and operations. A signature can be augmented with axioms that restrict the properties of its types and operations: the resulting module is a concept. An implementation allows the same declarations as a signature, but also (generic) implementations for the declared operations. The last kind of module in Magnolia is a program, a specific kind of implementation in which all the specified operations and types are matched with implementations. Crucially, types and operations in a program are no longer generic but instead fully concrete. An implementation can be a model of a concept; a concept can also be a model of another concept. Such modeling relations can be specified directly in Magnolia using the satisfaction language construct.
Magnolia operations can be functions, procedures, and predicates. The arguments to functions and predicates are immutable, while arguments to procedures are given explicit modes: obs (read-only), upd (read/write), and out (write-only, and the procedure promises to initialize the argument). Procedures do not return a value. Calls to procedures are prefixed with the call keyword.
Listing 1 gives a general overview of the different kinds of Magnolia modules. We first specify the signature of a magma (a set T with a closed binary operation bop). By asserting the associativity property on a magma, we get a semigroup. The ConcretePartialSemigroup implementation describes an external C++ API providing a guarded multiplication operator over integer matrices, where the guard is intended to ensure that the argument matrices have compatible dimensions (i.e., that the number of columns of the matrix on the left is equal to the number of rows of the matrix on the right). ExampleProgram builds multiplyThreeMatrices off of the primitive building blocks provided by ConcretePartialSemigroup. The ExampleProgramHasMulPartialSemigroup satisfaction relation indicates that ExampleProgram satisfies the semigroup axioms, with the set of integer matrices and guarded multiplication on it. The guard specified on the multiplication operation in the left-hand side module expression of the satisfaction relation is implicitly added to the corresponding operation in the right-hand size module expression—i.e., the right-hand side specification implicitly becomes the specification of a partial semigroup. The resulting satisfaction relation thus asserts that ExampleProgram has a partial semigroup structure. A block of renamings ([ T => IntMatrix, bop => _*_ ]) is applied to Semigroup. Magnolia's renamings allow changing the names of types and operations in places where a module is “opened.” This is a powerful feature which allows normalizing the names exposed by modules when we open them in a given scope, independently of how their types and operations were initially named.
signature Magma = {
type T;
function bop(a: T, b: T): T;
}
concept Semigroup = {
use Magma;
axiom associativity(a: T, b: T, c: T) {
assert bop(bop(a, b), c) ==
bop(a, bop(b, c));
}
}
implementation ConcretePartialSemigroup =
external C++ lib.int_matrices {
type Nat;
type IntMatrix;
predicate lhsNcolsIsRhsNrows(
m1: IntMatrix, m2: IntMatrix);
function _*_(m1: IntMatrix,
m2: IntMatrix): IntMatrix
guard lhsNcolsIsRhsNrows(m1, m2);
}
program ExampleProgram = {
use ConcretePartialSemigroup;
function multiplyThreeMatrices(
A: IntMatrix, B: IntMatrix,
C: IntMatrix): IntMatrix = A * B * C;
}
// The guard on _*_ in ExampleProgram is
// lifted to the specification on
// Semigroup in the left-hand
// side---this satisfaction relation thus
// states that ExampleProgram has a
// partial semigroup structure.
satisfaction
ExampleProgramHasMulPartialSemigroup =
ExampleProgram
models Semigroup[ T => IntMatrix,
bop => _*_ ];
Listing 1. Multiplying three matrices in Magnolia.
Concept axioms have previously found use as test oracles (Bagge et al., 2011) and as generic optimization rules (Bagge and Haveraaen, 2009; Tang and Järvi, 2015). We implement two module transformations called rewrite and implement in magnoliac, the Magnolia compiler under active development (Chetioui, 2020).
The rewrite transformation extracts all assertions of equations from a given concept, and uses them as directed rewrite rules within a target module expression. The maximum allowed number of applications of these directed rewrite rules is provided as an argument to the transformation. The rewrite rules can only be applied from left to right in the current implementation, and there is thus no need to specify how to orient them.
The implement transformation highlights a third possible use case for Magnolia axioms, i.e., code generation. The transformation extracts all the assertions of equations from a given concept where the left-hand side is a call to a declared function (or predicate) with pairwise distinct universally quantified arguments, and generates an implementation for the function where the body is the right-hand side of the assertion. Intuitively, an assertion with the properties we outlined describes the behavior of the function on the left-hand side at every point. Therefore, such assertions are not only a way to specify the intended behavior of a function, but also a way to derive an actual implementation for it in case one was not already provided.
The intuition behind implement is that it transforms a specification into an implementation. The implement transformation produces changes visible at the module level, while rewrite replaces expressions within already implemented operations. Figure 1 describes the grammar for the rewrite and implement transformations.
Consider the multiplyThreeMatrices function in Listing 1. The function is intended to multiply three matrices together—and its body A * B * C desugars to the expression _*_(_*_(A, B), C). Due to the associativity property, the order in which the multiplications are executed does not matter when it comes to the correctness of the result. However, it matters a lot when it comes to performance: suppose A is of dimensions 100 × 2, B of dimensions 2 × 20, and C of dimensions 20 × 90. Executing A * B requires 100 × 2 × 20 scalar multiplications, and executing (A * B) * C thus requires 100 × 2 × 20 + 100 × 20 × 90 = 184,000 scalar multiplications. On the other side, executing B * C requires 2 × 20 × 90 scalar multiplications, and executing A * (B * C) requires executing 2 × 20 × 90 + 100 × 2 × 90 = 21, 600 scalar multiplications, nearly ten times fewer.
Suppose that a developer wants to use the multiplyThreeMatrices function in their program. They care about efficiency, and know that the input matrices A, B, and C have the same dimensions as specified above. They can use the assertion provided in the associativity property of the Semigroup concept defined in Listing 1 as a rewrite rule in multiplyThreeMatrices to optimize the expression from (A * B) * C to A * (B * C). Listing 2 shows how.
program DevProgram =
rewrite ExampleProgram with
Semigroup[ bop => _*_,
T => IntMatrix ] 1;
Listing 2. Demonstration of the Magnolia rewrite transformation.
The Magnolia rewrite module transformation takes three arguments: the module on which to perform the rewrite (ExampleProgram in the example), the module from which to extract rewriting rules (Semigroup with some renamings applied in the example), and a maximum allowed number of rule applications (1 in the example).
Here, multiplyThreeMatrices is a toy example, and defined directly in the program being transpiled—it would therefore be very easy to reimplement it manually. However, this is not always the case: the function one wants to transform could be very complicated, and hidden deep inside an external dependency. Without the ability to perform rewritings on functions that have been previously defined, the developer would have to write their own version of this function.
We describe here our proposed methodology for writing performant and portable code productively using the Magnolia programming language. Each step of this methodology is first described from a high-level perspective, and then concretely demonstrated for our PDE solver example. Figure 2 gives a graphical overview of the concrete steps we take to optimize the PDE solver example in the following.
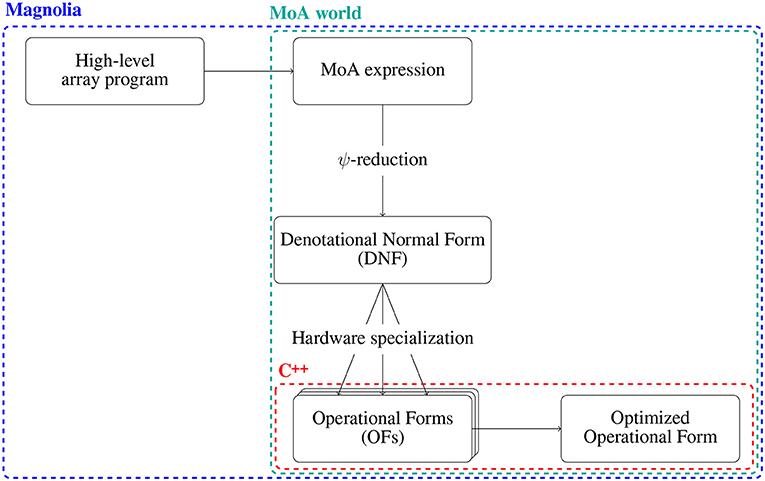
Figure 2. A graphical overview of the methodology presented in the paper. A high-level array program is passed as input, and translated to a corresponding MoA expression. This MoA expression is then normalized using a process known as ψ-reduction to produce the DNF. ψ-reduction gives hardware-independent rewriting rules on MoA expressions. By adding in knowledge about the specific hardware architecture underlying the computation, the DNF can be transformed into one of its OFs. This enables also hardware-specific optimization rules, which we can apply to the OF so as to produce an optimized OF. The program is initially written in Magnolia, and all the manipulation steps in the MoA world are done in Magnolia. The hardware specialization is implemented in the host language underlying the implementation (here C++), and the code contributing to the production of an optimized OF is thereby split between Magnolia and C++.
The first step of our methodology is to build a thorough understanding of the targeted problem. We do that by identifying and formalizing the domain underlying the problem. Formalizing the domain gives us a mathematical understanding of the properties expected of the types and operations involved in the problem. These in turn allow specifying semantics-preserving optimization rules on them, whose correctness can be proven.
PDE solvers using FDM are based on multi-dimensional array computations. Burrows et al. (2018) identified an array API for FDM solvers. Chetioui et al. (2019) followed up with a formalization of the identified array API using MoA. We will first give an overview of PDE solvers as described by Burrows et al. (2018), and an introduction to the corresponding MoA theory. With this background in place, we will reimplement the PDE solver based on FDM from the work of Chetioui et al. (2019), and implement hardware-agnostic and hardware-dependent rewriting rules. We show how they can be applied to our Magnolia program, and measure the resulting performance improvements.
PDE solvers have many application areas. One example is numerical simulations of wind flow—e.g., for optimizing windmill positioning in large-scale wind farms.
Computing solutions to PDEs numerically requires discretizing continuous equations to a discrete domain. This approach to PDE solvers is often illustrated in the literature with Burgers' equation (Burgers, 1948). Equation (1) presents the equation in its coordinate-free form.
where is velocity, t time, and ν the viscosity coefficient.
Assuming a 3D space, we can use a Cartesian coordinate system to rewrite Equation (1) as the following system of equations
where .
To discretize the domain, we describe a Nx × Ny × Nz grid of velocity values bounded by Lx (respectively Ly and Lz) on axis x (respectively y and z) such that the u component of the velocity at index (i, j, k) and timestep n is given by
with , , and .
Similarly, the partial derivative of u in the x direction at index (i, j, k) and timestep n is
In the FDM, we compute a partial derivative as a weighted sum of neighboring grid points—where the weights are given by a list of factors called a stencil. The stencil is chosen by a numerical expert. This paper, following the work of Burrows et al. (2018) uses the numerical stencils and (1, −2, 1) for the first and second order partial derivatives, respectively.
Given these stencils, the partial derivative of u in the x direction at index (i, j, k) and timestep n is approximated by
which is accurate to O((Δx)2, Δt). Computing the partial derivative along the y (respectively z) axis follows a similar pattern, where j (respectively k) varies instead of i.
The standard 3D explicit finite difference approximation of Equation (2) is then given by
The discretization of Equations (3) and (4) follows the same pattern.
The API of Burrows et al. (2018) is sufficient to compute numerical solutions to PDEs using FDM. It consists of elementwise arithmetic operations at the array level (+, -, *), a rotation operation on arrays (called “shift”), and arithmetic operations at the scalar level—corresponding to the behavior of the elementwise operations at each index of the array.
MoA (Mullin, 1988; Mullin and Jenkins, 1996) is an algebra for describing operations on arrays. MoA distinguishes between two abstraction levels: the Denotational Normal Form (DNF), which describes an array by its shape together with a function describing its value at every index, and the Operational Form (OF) which describes it on the level of the memory layout. Programs written at the DNF level do not presume knowledge of a hardware architecture. Reasoning at the DNF level is thus completely hardware agnostic. By repeatedly applying a set of terminating rewrite rules, any MoA expression can be reduced to its DNF (Mullin and Thibault, 1994; Chetioui et al., 2019)—where the resulting array is described at each index by indexing into the input arrays and scalar-level operations.
Given information about the hardware architecture and the memory layout of the arrays, the ψ-correspondence theorem (Mullin and Jenkins, 1996) allows transforming a DNF expression into a corresponding hardware-dependent OF—in which the access patterns on the array are described in terms of start, stride, and length.
We give an informal overview of some operations at the DNF and OF levels below. We refer the interested reader to previous work for formal definitions (Mullin, 1988; Chetioui et al., 2021).
The dimension of an array A is denoted dim(A). It corresponds to the number of axes of the array. For dim(A) = n, the shape of A is an n-element vector ρ(A) = 〈s0, …, sn−1〉 where si is the length of axis i. The total number of elements (or size) of A is given by the product of the shape, .
In the definitions below A stands for an arbitrary array with dimension n and shape as defined above. Further, we use the following array in examples:
Thus, ρ(M) = 〈3, 2〉.
The relevant MoA operations on the DNF level are:
• the indexing function ψ, which takes an index i into an array and returns the subarray at the indexed position. When i's length equals the dimension of the array, i is a total index. Otherwise, it is partial. 〈〉 ψ A = A holds. For our example, we have
• the reshape function that takes an array A and a shape s such that Πs = Πρ(A), and creates a new array with shape s containing the elements of A. Thus, ρ[reshape(s, A)] = s holds. For example,
• a rotation function rotate that takes an array A, an axis j and an offset o, and shift A by o along its jth axis. The shape is unchanged, i.e., ρ(rotate(A, j, o)) = ρ(A) holds. We give a few examples of how rotation behaves on axis 0 and 1 of M:
Mullin and Thibault (1994) described a rewriting system for MoA expressions at the DNF level, referred to as ψ-reduction. They conjectured that ψ-reduction is canonical (i.e., it is terminating and confluent)—and thus takes any MoA expression to its unique DNF. In their work on embedding Burrows et al.'s (2018) array API for FDM solvers in MoA, Chetioui et al. (2019) outline a rewriting system sufficient to transform a program based on this API to its DNF and show that this rewriting system is indeed canonical. This draws appeal to MoA as a framework for the optimization of PDE solvers based on FDM. ψ-reduction essentially consists of rules that move indexing operations inwards—until eventually, the expression does not contain any collective operation, but consists only of indexing and scalar operations. As a consequence, it is guaranteed that the resulting array expression can be computed without the need to materialize any intermediate array. Because the rewriting system is canonical, another consequence is that the form in which we choose to express our computation is irrelevant: all equivalent expressions in the language of MoA reduce to the same DNF expression.
At the OF level, we assume knowledge of the target architecture, and an intended memory layout of the array. The central MoA operations on the OF level are:
• the family of lifting operations liftj that take two natural numbers d, q such that d · q = sj, and reshape A into the shape 〈s0, …, sj−1, d, q, sj+1, …, sn−1〉;
• the flattening function rav that transforms a multidimensional array into its linear representation in memory. Thus, ρ(rav(A)) = 〈Πρ(A)〉 holds;
• the mapping function γ, which takes a shape s with Πs = Πρ(A) and a total index into A and returns the corresponding index into rav(A). In this paper, we assume a row-major ordering.
The OF operations presented here are crucial to the theory of MoA. We thus include them for the sake of completion. These operations however do not appear explicitly in the development of our methodology.
We implemented a PDE solver using the MoA array API. The implementation consists of four components:
1. a specification of the necessary MoA types and operations, with axioms asserting that they respect the relevant properties;
2. a foreign API exposing the core types and operations of the MoA specification;
3. an external implementation of the foreign API in a host language (C++);
4. an implementation of the PDE solver built upon the external MoA building blocks.
The ψ-calculus conflates arrays, indices, shapes, and scalars into a single array type. While convenient in the formalism, we distinguish these types in our Magnolia implementation for ease of reasoning, and to leverage the language's type system to avoid programming errors. For that reason also, the version of ψ we implement in our code takes in only total indices, and returns “unwrapped” scalars—as opposed to arrays with an empty shape.
Listing 3 shows the API from Burrows et al. (2018) in the language of MoA.
signature ArrayAPI = {
type Array;
type E;
type Axis;
type Index;
type Offset;
/* Scalar-Scalar operations */
function _+_(lhs: E, rhs: E): E;
function _-_(lhs: E, rhs: E): E;
function _*_(lhs: E, rhs: E): E;
function _/_(lhs: E, rhs: E): E;
/* Scalar-Array operations */
function _+_(lhs: E, rhs: Array): Array;
// prototypes as above for _-_, _*_, _/_
/* Array-Array operations */
function _+_(lhs: Array, rhs: Array):
Array;
// prototypes as above for _-_, _*_, _/_
/* Rotation */
function rotate(array: Array,
axis: Axis,
offset: Offset): Array;
/* Indexing */
function psi(ix: Index,
array: Array): E;
}
Listing 3. An array API for FDM solvers in Magnolia.
The declaration of the types and operations form an algebraic signature. We augment that signature with semantic properties in the form of axioms to obtain a concept. Listing 4 relates each array-level arithmetic operation in the API to its corresponding scalar-level operation (Burrows et al., 2018; Chetioui et al., 2019). The axioms for all binary operations follow the same pattern, we hence only show axiom bodies for the + operation for the sake of brevity.
concept ArrayAPI_ArithmeticAxioms = {
require ArrayAPI;
/* Scalar-Array Axioms */
axiom scalarBinaryPlusAxiom(lhs: E,
rhs: Array, ix: Index) {
assert psi(ix, lhs + rhs) ==
lhs + psi(ix, rhs);
}
// axiom scalarBinarySubAxiom(lhs: E,
// rhs: Array, ix: Index)
// axiom scalarMulAxiom(lhs: E,
// rhs: Array, ix: Index)
// axiom scalarDivAxiom(lhs: E,
// rhs: Array, ix: Index)
/* Array-Array Axioms */
axiom arrayBinaryPlusAxiom(lhs: Array,
rhs: Array, ix: Index) {
assert psi(ix, lhs + rhs) ==
psi(ix, lhs) + psi(ix, rhs);
}
// axiom arrayBinarySubAxiom(lhs: Array,
// rhs: Array, ix: Index)
// axiom arrayMulAxiom(lhs: Array,
// rhs: Array, ix: Index)
// axiom arrayDivAxiom(lhs: Array,
// rhs: Array, ix: Index)
}
Listing 4. Axioms for the arithmetic operations of our array API.
The specifications in Listing 3 are (straightforwardly) implemented as external C++ functions and types, not shown here. Lastly, Listing 5 shows our implementation of one full step of the PDE.
/* Solver */
procedure step(upd u0: Array,
upd u1: Array, upd u2: Array) {
var v0 = u0;
var v1 = u1;
var v2 = u2;
v0 = substep(v0, u0, u0, u1, u2);
v1 = substep(v1, u1, u0, u1, u2);
v2 = substep(v2, u2, u0, u1, u2);
u0 = substep(u0, v0, u0, u1, u2);
u1 = substep(u1, v1, u0, u1, u2);
u2 = substep(u2, v2, u0, u1, u2);
}
function substep(u: Array, v: Array,
u0: Array, u1: Array,
u2: Array): Array =
u + dt()/(two(): Float) * (nu() * (
(one(): Float)/dx()/dx() *
(rotate(v, zero(),
-one(): Offset) +
rotate(v, zero(),
one(): Offset) +
rotate(v, one(): Axis,
-one(): Offset) +
rotate(v, one(): Axis,
one(): Offset) +
rotate(v, two(): Axis,
-one(): Offset) +
rotate(v, two(): Axis,
one(): Offset)) -
three() * (
two(): Float)/dx()/dx() * u0) -
(one(): Float)/(two(): Float)/dx() *
((rotate(v, zero(),
one(): Offset) -
rotate(v, zero(),
-one(): Offset)) * u0 +
(rotate(v, one(): Axis,
one(): Offset) -
rotate(v, one(): Axis,
-one(): Offset)) * u1 +
(rotate(v, two(): Axis,
one(): Offset) -
rotate(v, two(): Axis,
-one(): Offset)) * u2));
/* Float ops */
require function -_(f: Float): Float;
// magnoliac does not offer support for
// literals as of yet, and we must thus
// define constant functions in the host
// language for each number of a given
// type we want to use.
require function one(): Float;
require function two(): Float;
require function three(): Float;
/* Axis utils */
require function zero(): Axis;
require function one(): Axis;
require function two(): Axis;
/* Offset utils */
require function one(): Offset;
require function -_(o: Offset): Offset;
/* Problem-specific parameters */
require function nu(): Float;
require function dt(): Float;
require function dx(): Float;
Listing 5. Implementation of one full step of the PDE solver in Magnolia.
Armed with a thorough understanding of the problem, we can now derive semantics-preserving optimization rules—hardware-specific or otherwise.
Before we can apply rewriting rules defined using MoA to our program, we need to change its level of abstraction, i.e., go from an implementation that describes the resulting array using whole-array operations to one that describes its value at every index. This transformation corresponds to the step from the high-level array program to a corresponding MoA expression in Figure 2.
We define a Magnolia program called BasePDEProgram that contains the functions in Listing 5, giving a concrete implementation to the basic underlying operations and data structures in a host language. Listing 6 shows how we achieve the transformation from the high-level array program to a corresponding MoA expression in Magnolia. We break down the components of the listing in the following.
program PDEProgramMoA = {
use (rewrite
(implement ToIxwiseGenerator
in BasePDEProgram)
with ToIxwise 1);
use ExtBasicSchedule;
};
Listing 6. Lowering step from a high-level array program to a MoA expression.
The ToIxwiseGenerator concept is shown in Listing 7. The toIxwiseGenerator axiom consists of a single assertion, which describes the behavior of the substepIx function when all of its arguments are universally quantified distinct variables. The right-hand side of the equation is thus a valid implementation for substepIx. Because this function is not implemented in the original program, we can use the implement transformation with ToIxwiseGenerator to generate an implementation of substepIx in the implementation given in Listing 5. So as to enable further optimizations, implement unfolds function calls in the right-hand side of the equation. The resulting index-level code is shown in Listing 18 (in Appendix A).
concept ToIxwiseGenerator = {
type Array;
type Float;
type Index;
function substepIx(u: Array, v: Array,
u0: Array, u1: Array, u2: Array,
ix: Index): Float;
function substep(u: Array, v: Array,
u0: Array, u1: Array,
u2: Array): Array;
function psi(ix: Index,
array: Array): Float;
axiom toIxwiseGenerator(
u: Array, v: Array, u0: Array,
u1: Array, u2: Array, ix: Index) {
assert
substepIx(u, v, u0, u1, u2, ix) ==
psi(ix, substep(u, v, u0, u1, u2));
}
}
Listing 7. A generator for an index-level implementation of substep.
To make use of substepIx within the program, we need to replace calls to substep with calls to a scheduling function schedule that uses substepIx to describe the value of the result array at every index. This is achieved through the outermost program transformation in Listing 10, that uses the ToIxwise concept of Listing 8. Throughout the rest of the paper, we use the term schedule as in Halide (Ragan-Kelley et al., 2012).
concept ToIxwise = {
type Array;
function substep(u: Array, v: Array,
u0: Array, u1: Array,
u2: Array): Array;
function schedule(u: Array, v: Array,
u0: Array, u1: Array,
u2: Array): Array;
axiom toIxwiseRule(u: Array, v: Array,
u0: Array, u1: Array,
u2: Array) {
assert substep(u, v, u0, u1, u2) ==
schedule(u, v, u0, u1, u2);
}
}
Listing 8. A concept with a rewrite rule from substep to a new scheduling function.
Magnolia does not expose native looping constructs. For that reason, the implementation of schedule is done in the host language, and imported through ExtBasicSchedule. From that point onwards, we can use MoA's transformation rules on the part of our program implemented in Magnolia.
Of the modules presented in Listings 6–8, PDEProgramMoA is the only one that is completely problem-specific. The ToIxwise and ToIxwiseGenerator concepts's types and operations are given names that relate to our domain of application. Due to the renaming feature however, specific names within a module are largely irrelevant: two signatures that expose the same set of types and operations (and overloads) up to renaming (of types and operations) can be made to match.
For example, the ToIxwise concept states that there exists two functions with the same prototype (they take in five arguments of the same type that is also the return type), such that calling one of them is equivalent to calling the other. Listing 9 shows a more generic presentation of the ToIxwise concept.
concept FunctionEquality5 = {
type T;
function f(t1: T, t2: T, t3: T,
t4: T, t5: T): T;
function g(t1: T, t2: T, t3: T,
t4: T, t5: T): T;
axiom functionEqualityRule(t1: T,
t2: T, t3: T, t4: T, t5: T) {
assert f(t1, t2, t3, t4, t5) ==
g(t1, t2, t3, t4, t5);
}
}
// ToIxwise can be defined from
// FunctionEquality5, and vice-versa.
concept ToIxwise =
FunctionEquality5[ f => substep
, g => schedule
, T => Array
, functionEquality5Rule
=> toIxwiseRule
];
Listing 9. A domain-generic formulation of the ToIxwise concept.
The FunctionEquality5 concept can be further generalized by taking in arguments of five different types, and returning an element of a sixth different type—all of which would be mapped to Array for defining ToIxwise. The concept could also be stated more concisely for any number of arguments using variadics. Magnolia does not support variadics today, but the feature is a desired future language extension (Chetioui et al., 2022).
The next step outlined in Figure 2 is to reduce the MoA expression we just constructed to its DNF. Rewriting rules at the DNF level do not require hardware knowledge, and therefore constitute hardware-agnostic transformation rules. Listing 10 shows how we achieve this transformation in Magnolia. The DNFRules concept is spelled out in Listing 17, which can be found in Appendix A. The choice of applying the rewrite rules defined in DNFRules twenty times is carefully made by the developer, as this is the number of applications required to full reduce the MoA expression produced previously to its DNF. In this case, the rewriting system has been shown to be confluent and terminating, and specifying a higher number would yield the same result with negligible overhead (namely, one additional application of the rewrite rules). The rewrite rules are applied by magnoliac until the number of maximum applications has been reached, or until no progress is made.
program PDEProgramDNF =
rewrite PDEProgramMoA with DNFRules 20;
Listing 10. Transforming the MoA expression to its DNF.
The DNF reduction rules discussed here mirror the specification presented in Listing 4 for the arithmetic operations of the API, and are completely reusable for any program based on this API. These axioms describe for each operation the content of the resulting array at each index, turning the array from a large opaque block to a function from its index space to its content. Applying the DNF rules pushes computations down from the array-level to the index-level, i.e., the resulting computations are devoid of whole-array operations and contain only indexing and scalar arithmetic operations. This can be thought of as loop fusion, or also as some kind of function composition.
The external schedule implemented in Listing 6 describes how the indexwise computation is executed on the underlying hardware. The psi function is also given an external implementation that thus describes how the arrays are actually laid out in memory. This hardware “specialization” gives us an initial executable OF—as outlined in Figure 2. For the sake of completeness, our (non-specific) C++ implementation of schedule is shown in Listing 19, and another CUDA implementation is shown in Listing 20 (both available in Appendix A).
The reduction of our MoA expression to its DNF (and resulting “default” OF) already leads to significant performance improvements. Table 1 shows runtime results for our PDE solver implementation in Magnolia, before and after full DNF reduction using the DNF rewriting rules. The baseline implementation shown here is a direct lowering of the program written in Magnolia to C++, and we do not perform any transformation beyond what is offered by g++'s optimization level O3 (for the CPUs) and what is offered by nvcc by default (for the GPU). Every array is allocated on the heap, and every intermediate array in the computation is materialized—resulting in a baseline that is inefficient. DNF reduction speeds up the code by a factor between roughly 5.78× and 14.11× depending on the targeted device, and significantly reduces memory usage. At the DNF level, the expression is written in terms of scalar and indexing operations, eliminating the costly need to compute temporary arrays, and increasing computational density.
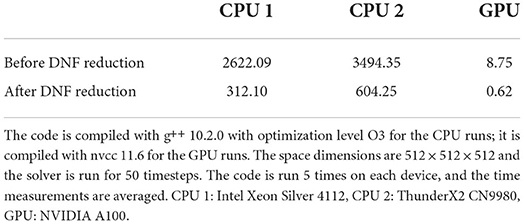
Table 1. Execution time (in seconds) of the 3-dimensional PDE solver Magnolia implementation compiled to C++, with and without reduction to DNF.
This experiment shows that such a rewriting system gives the ability to write programs using whole-array operations without losing out on the benefits of writing index-level code. The ability to write algorithms in different ways without inducing a loss of performance is key to the productive development of performant code.
Which hardware-specific transformation rules are relevant to implement is by nature dependent on the underlying hardware architecture we are interested in. For example, Chetioui et al. (2021)'s previous work on formalizing PDE computations in MoA gave rise to rules for introducing padding into array expressions. Their work also discusses rewrites rules that use the dimension lifting operation, which is a reshape operation with the explicit purpose of matching the shape of arrays with characteristics of the underlying hardware—more commonly called array partitioning. For example, lifting by d1 across the first axis allows one to scatter the resulting subarrays across d1 processes; or, lifting by 4 across the last axis of an array of 32-bit floats allows one to vectorize computations on an architecture with 128-bit vector registers. The hardware architecture combined with the data dependencies of the algorithm determine the shape and layout of the arrays.
We discuss an example of a hardware-dependent rewriting system for padding below.
Our example assumes a toroidal space—i.e., the first element is a neighbor of the last element for each dimension. Figure 3 shows the dependency patterns for one third of a half-step of the PDE across the last axis of the array. The element at index i at time t + 1 depends on the elements at index i, (i − 1) mod N, and (i + 1) mod N at time t. The modulo operation serves to index the right dependencies for the first (respectively last) element of the array, where decrementing (respectively incrementing) the index would create an out-of-bounds index. Modulo operations are still expensive, even on modern hardware (Lemire et al., 2019). Additionally, if N is large, the computations at the boundary need to access elements that are far apart in memory—therefore benefitting less from data locality than the computations in the middle of the array.
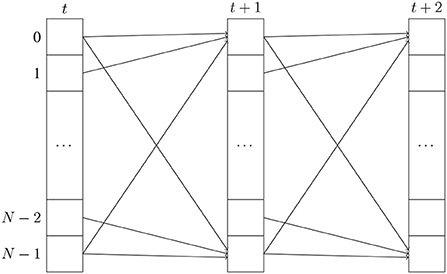
Figure 3. The dependency pattern for one third of a half-step of the PDE across the last axis of the array. Each column represents an array of length N indexed from 0 to N − 1 for a given timestep. The element at index i of the array at time t + 1 depends on the elements at indices i, (i − 1) mod N and (i + 1) mod N of the array at time t.
How boundaries are handled in our computation is not relevant for our previous rewrite rules. Circular boundary handling computations in PDE codes can be optimized in different ways. For example, the expensive modulo operations (i − 1) mod N and (i + 1) mod N, assuming a valid index i between 0 and N − 1, can be, respectively, replaced by i = = 0 ? N − 1 : i − 1 and i = = N − 1 ? 0 : i + 1—or even with i ± 1 & (N − 1), if N is a power of two. With padding, we can do even better and completely eliminate the modulo computations (Chetioui et al., 2021). Padding also increases data locality for such dependency patterns. The cost of padding is at the duplication of data in memory.
Figure 4 shows the dependency patterns for one third of a half-step of the PDE across the last axis of the array when the array is padded. In that case, the computation at the boundaries of the array can be rewritten to depend on three adjacent elements in the array. The modulo computation can also be eliminated. We pay for these improvements by using more space, and by refilling the padding before every timestep.
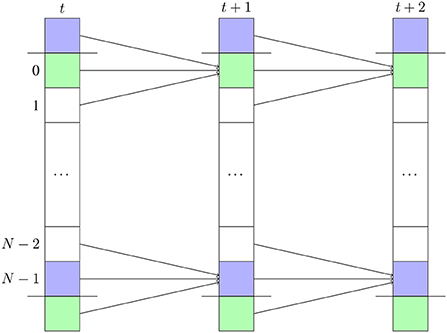
Figure 4. The dependency pattern for one third of a half-step of the PDE across the last axis of the array when the array is padded once on each side on the last axis. Each column represents an array of length N indexed from 0 to N − 1 for a given timestep. The elements colored in the same color have the same value. The element at index i of the array at time t + 1 depends on the elements at indices i, i − 1, and i + 1 of the array at time t.
Listing 11 shows one way of introducing padding in the PDEProgramDNF program introduced in Listing 10. We truncate some of the modules in the following listings so as not to clutter the presentation, and add corresponding listings containing the full modules to Appendix A for the sake of completeness.
program PDEProgramPadded = {
use (rewrite PDEProgramDNF
with OFPad 1);
// imports a new schedule, a new
// function for index rotation, and a
// procedure for refilling padding
use ExtExtendPadding;
}
concept OFPad = {
...
procedure refillPadding(upd a: Array);
function schedulePadded(
u: Array, v: Array, u0: Array,
u1: Array, u2: Array): Array;
function schedule(u: Array, v: Array,
u0: Array, u1: Array,
u2: Array): Array;
axiom padRule(u: Array, v: Array,
u0: Array, u1: Array, u2: Array) {
assert schedule(u, v, u0, u1, u2) ==
{ var result = schedulePadded(
u, v, u0, u1, u2);
call refillPadding(result);
value result;
};
}
function rotateIx(ix: Index, axis: Axis,
offset: Offset): Index;
function rotateIxPadded(ix: Index,
axis: Axis, offset: Offset): Index;
axiom rotateIxPadRule(ix: Index,
axis: Axis, offset: Offset) {
assert rotateIx(ix, axis, offset) ==
rotateIxPadded(ix, axis,
offset);
}
}
Listing 11. Introducing padding into PDEProgramDNF. The full specification of OFPad can be found in Listing 21.
The transformations given by OFPad act on the OF of the program. The transformation rules replace calls to rotateIx with calls to rotateIxPadded within the implementation of substepIx, and calls to schedule with calls to schedulePadded succeeded by an operation refilling the padding within the implementation of step. The resulting step procedure is shown in Listing 23. Likewise, the schedule is now replaced by one that is mindful of padding—whose C++ implementation is shown in Listing 22. The result is a program with a different—a priori more optimized—OF. The rewrites correspond to the last transformation step in the methodology presented in Figure 2.
Our implementation in Listing 11 assumes that the input arrays are padded arbitrarily across each axis in the host language, in a way that is compatible with the new rotateIxPadded function. Details such as the amount of padding across each axis are therefore not visible in Magnolia. This is however purely a design choice, insofar as we have chosen to make the Index type completely opaque. This has the benefit of making the program naturally shape polymorphic to a degree—though the program is not as interesting for input arrays with initial number of dimensions different than three.
We can control padding across each axis more explicitly by specializing our code further. This can also be achieved using transformation rules, as is shown in Listing 12.
program PDEProgram3DPadded = {
use (rewrite
(rewrite
(rewrite
(rewrite
(implement
OFSpecializeSubstepGenerator
in PDEProgramDNF)
with OFSpecializePsi 10)
with OFReduceMakeIxRotate 20)
with OFPad[schedulePadded =>
schedule3DPadded] 1)
with OFEliminateModuloPadding 10);
// pulling in ScalarIndex utils
use ExtScalarIndex;
// pulling in AxisLength utils
use ExtAxisLength;
// pulling in psi
use ExtSpecializeBase;
// pulling in schedule3DPadded
use Ext3DSchedule;
}
Listing 12. Adding padding to and specializing PDEProgramDNF to 3 dimensions.
The content of OFSpecializeSubstepGenerator is shown in Listing 13. The concept contains an axiom following the generator pattern to specialize the shape polymorphic substepIx to three dimensions. As previously, the call to substepIx on the right-hand side of the equation is unfolded to enable additional optimizations.
concept OFSpecializeSubstepGenerator = {
type Index;
type Array;
type Float;
type ScalarIndex;
function mkIx(i: ScalarIndex,
j: ScalarIndex,
k: ScalarIndex): Index;
function substepIx(u: Array, v: Array,
u0: Array, u1: Array, u2: Array,
ix: Index): Float;
function substepIx3D(u: Array, v: Array,
u0: Array, u1: Array, u2: Array,
i: ScalarIndex, j: ScalarIndex,
k: ScalarIndex): Float;
axiom specializeSubstepRule(u: Array,
v: Array, u0: Array, u1: Array,
u2: Array, i: ScalarIndex,
j: ScalarIndex, k: ScalarIndex) {
assert substepIx3D(u, v, u0, u1, u2,
i, j, k) ==
substepIx(u, v, u0, u1, u2,
mkIx(i, j, k));
}
};
Listing 13. A generator for a 3D implementation of substepIx.
Recall the original implementation of substepIx given in Listing 18. Every indexing operation of some array a in the resulting implementation of substepIx3D is now either of the form psi(mkIx(i, j, k), a), or of the form psi(rotateIx(mkIx(i, j, k), x, o), a) for some axis x and some offset o.
The OFSpecializePsi (shown in Listing 14) then introduces a specialized psi function for 3D arrays. It does that by introducing three projection functions ix0, ix1, and ix2 on Indexes. General indexing operations of the form psi(mkIx(i, j, k), a) are first specialized to expressions of the form psi(ix0(mkIx(i, j, k)), ix1(mkIx(i, j, k)), ix2(mkIx(i, j, k)), a) by an application of specializePsiRule—which can then be reduced to psi(i, j, k, a)via three applications of reduceMakeIxRule.
concept OFSpecializePsi = {
...
type ScalarIndex;
function ix0(ix: Index): ScalarIndex;
...
function mkIx(i: ScalarIndex,
j: ScalarIndex,
k: ScalarIndex): Index;
function psi(i: ScalarIndex,
j: ScalarIndex,
k: ScalarIndex,
array: Array): E;
axiom specializePsiRule(ix: Index,
array: Array) {
assert psi(ix, array) ==
psi(ix0(ix), ix1(ix), ix2(ix),
array);
}
axiom reduceMakeIxRule(i: ScalarIndex,
j: ScalarIndex, k: ScalarIndex) {
var ix = mkIx(i, j, k);
assert ix0(ix) == i;
assert ix1(ix) == j;
assert ix2(ix) == k;
}
}[ E => Float ];
Listing 14. Specializing calls to the indexing function ψ. The full specification of the concept can be found in Listing 24.
We also want to call our specialized version of psi instead of the general one in expressions now of the form psi(ix0(rx), ix1(rx), ix2(rx), a) where rx = rotateIx(mkIx(i, j, k), x, o). For that purpose, we apply the rewriting rules defined in OFReduceMakeIxRotate—shown in Listing 15. These rewriting rules essentially unfold rotateIx. All the indexing operations in substepIx3D now use the specialized form of psi, and the scalar indices are either constants or of the form (i + o) % s, with i a scalar index, o an offset, and s the length of the relevant axis of the array.
concept OFReduceMakeIxRotate = {
...
function rotateIx(ix: Index, axis: Axis,
offset: Offset): Index;
type AxisLength;
function shape0(): AxisLength;
...
function _+_(six: ScalarIndex,
o: Offset): ScalarIndex;
function _%_(six: ScalarIndex,
sc: AxisLength): ScalarIndex;
axiom reduceMakeIxRotateRule(
i: ScalarIndex, j: ScalarIndex,
k: ScalarIndex, o: Offset) {
var ix = mkIx(i, j, k);
assert ix0(rotateIx(ix, zero(), o)) ==
(i + o) % shape0();
assert
ix0(rotateIx(ix, one(), o)) == i;
assert
ix0(rotateIx(ix, two(), o)) == i;
...
assert ix1(rotateIx(ix, one(), o)) ==
(j + o) % shape1();
...
assert ix2(rotateIx(ix, two(), o)) ==
(k + o) % shape2();
}
}
Listing 15. A rewriting system to specialize the index rotation operation. The full specification of the concept can be found in Listing 25.
At this point, we can reintroduce padding using the rules previously defined in Listing 11, and renaming schedulePadded to schedule3DPadded. As we are in the case when an implementation for schedulePadded is not in scope before the rules defined in OFPad are applied, we can replace the rewrite by a simple renaming—as shown in Listing 12.
The function schedule3DPadded is imported through Ext3DSchedule, and calls substepIx3D to compute the result of the computation at every index. We decide to implement this function externally such that the array is always circularly padded at least once on each side of each axis—a decision made based on the width of the stencil. With that knowledge, we can completely eliminate the modulo operations in substepIx3D. The OFEliminateModuloPadding concept (shown in Listing 16) defines the relevant rewriting rules.
// We suppose here that the amount of
// padding is sufficient across each axis
// for every indexing operation.
concept OFEliminateModuloPadding = {
...
function psi(i: ScalarIndex,
j: ScalarIndex, k: ScalarIndex,
a: Array): Float;
axiom eliminateModuloPaddingRule(
i: ScalarIndex, j: ScalarIndex,
k: ScalarIndex, a: Array,
o: Offset) {
assert
psi((i + o) % shape0(), j, k, a) ==
psi(i + o, j, k, a);
assert
psi(i, (j + o) % shape1(), k, a) ==
psi(i, j + o, k, a);
assert
psi(i, j, (k + o) % shape2(), a) ==
psi(i, j, k + o, a);
}
}
Listing 16. Elimination of the modulo operations in the program. The full specification of the concept can be found in Listing 26.
Table 2 gives an overview of the performance variations for four different implementations, all produced by the application of rewriting rules on our original solver implementation presented in Listing 5. We briefly describe the resulting implementations below.
DNF reduction This implementation is the same as PDEProgramDNF as described in Listing 10.
DNF reduction + Padding This implementation adds padding to PDEProgramDNF, i.e. it is the same as PDEProgramPadded as described in Listing 11.
DNF reduction + Index specialization This implementation is a version of PDEProgramDNF in which each element of type Index is transformed into three elements of type ScalarIndex, e.g. a call of the form psi(ix, a) is transformed into a call of the form psi(i, j, k, a), and rotation along a specific axis is implemented as a modular addition over that axis.
DNF reduction + Index specialization + Padding This implementation is a version of PDEProgramPadded in which elements of type Index are also decomposed into three elements of type ScalarIndex. It is assumed that each axis is padded sufficiently such that rotation can be implemented as a non-modular addition.
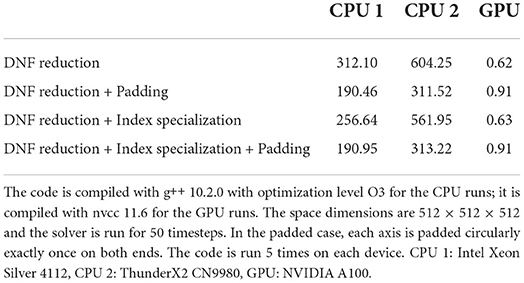
Table 2. Execution time (in seconds) of the three-dimensional PDE solver Magnolia implementation compiled to C++ with specialized indexing and with or without padding.
On both CPUs, the performance variation follows the same pattern. The fastest runs are achieved by the padded versions of the baseline implementation with DNF reduction applied, and its counterpart with also specialized indexing. In the unpadded case, the version of the code that incorporates specialized indexing runs faster—1.22× faster on CPU 1, and 1.08× faster on CPU 2. As outlined above, we expect padded implementations to perform better due to increased data locality at the boundaries of the computations. On the GPU considered, the variations are different: the unpadded programs (with or without specialized indexing) perform best. We confirm with a profiler that this is due to additional calls to the expensive cudaMemcpy in the implementation of replenishPadding—which add a significant cost to the computation. Padding does not seem to have an effect on the execution time of each substep, at least for this particular problem size on the GPU considered.
Crucially, the performance improvements and variations we observe here did not require any reimplementation of the core algorithm. Building our core algorithm generically allows us to introduce specialized underlying types and operations, once more information is known about our input data or the underlying hardware architecture. The Magnolia term rewriting engine then allows us to introduce new operations and to replace calls to existing concrete implementations with calls to other functions with possibly different argument lists.
This is another twist of generic programming: rewrite and implement allow to replace operations (or combinations of operations) in a generic module with others that have potentially different argument lists — so long as we can describe the behavior of the former at all points in terms of calls to the new operation(s).
We presented a methodology aimed for tackling the P3 problem on existing and emerging architectures and applied it to the domain of array computations. Instead of developing one program to target n hardware architectures, we implement a single program, along with hardware-specific rewriting rules. By relating the high-level problem to a mathematical basis, we ensure that the set of optimization rules we implement is correct, and reusable for problems that can be embedded within the same formalism. For example, the exact set of optimization rules we defined may be reused with other explicit finite difference solvers—and likely for stencil computations in general—as these are problems for which Burrows et al.'s API is suitable (Burrows et al., 2018).
Magnolia gives developers the tools to write high-level, domain-specific compilers with custom optimization rules, and a custom target language. The ability to choose flexibly to which opaque building blocks a Magnolia program reduces allows the application of optimization rules at various abstraction levels, until the boundary between Magnolia and the external primitives implemented in the host language is reached. Our approach is centered around the idea of expressing generic algorithms independently from any particular schedule, i.e., independently from any hardware abstraction.
As we mentioned in Section 1.1, the term schedule as used throughout the paper originates in the work of Ragan-Kelley et al. on Halide (Ragan-Kelley et al., 2012). SPIRAL (Puschel et al., 2005) and Sequoia (Fatahalian et al., 2006) predate Halide, but make a similar distinction between an algorithm and its mapping to the underlying hardware architecture. Halide exposes a set of scheduling primitives from which developers can build their own schedules. TVM (Chen et al., 2018) follows this idea and extends Halide's set of scheduling primitives. The set of schedules that can be expressed in such systems is necessarily limited by the set of available scheduling primitives. Extending this set requires modifications to the language and its compiler, and is thus costly. Recent work by Liu et al. (2022) shows that carefully choosing high-level rewriting rules on schedules allows optimizing tensor programs beyond what is currently possible in these languages. Exo allows for expressing schedules for different hardware targets through composable rewrites and user-defined hardware abstractions (Ikarashi et al., 2022). Ikarashi et al. (2022) note that adding support for new hardware using a library approach (as in Exo) appears to require one order of magnitude less development time than in systems like Halide or TVM. In our system, schedules are fully specified by the developer—similarly to the work of Ikarashi et al. (2022). Compared to the approach taken by Halide or TVM, the developer has full control over how their computations are executed, but incur a higher implementation cost when no scheduling algorithm exists for their particular flavor of target hardware architecture. Adding “default” scheduling primitives to Magnolia as a convenience could improve the developer experience, and is therefore a consideration for future work.
MLIR (Lattner et al., 2021) makes heavy use of rewrite rules through the MLIR PatternRewrite infrastructure (Vasilache et al., 2022). Their design is influenced by LIFT (Steuwer et al., 2015, 2017), another programming language exploiting rewrite rules for high-performance array computations. In LIFT, the application of rewrite rules is automated by a stochastic search method. Hagedorn et al. (2018) extend LIFT specifically for optimizing stencil programs. Such rewrite approaches are so far limited in that they do not always deliver high enough performance for real-world use (Hagedorn et al., 2020). This is in contrast to autoscheduling in Halide, which outperforms human experts on average (Adams et al., 2019). Automatic scheduling techniques are key to improving solutions to the P3 problem, and are thus an important topic to further explore also for rewrite rules-based optimizers. A potentially promising approach for semi-automatic optimization using rewrite rules is sketch-guided equality saturation (Koehler et al., 2021).
Approaches to optimization based on rewrite rules, such as the one presented here, can benefit from rewriting strategies, e.g., for localizing rewrites to only a particular chunk of the input program or for traversing the AST in a specific order. Kirchner (2015) gives a recent survey of strategic rewriting. Example of tools implementing such strategies include Maude (Martí-Oliet et al., 2005, 2009; Clavel et al., 2007) and Stratego (Visser, 2005). Hagedorn et al. (2020) introduce a functional approach to high-performance code generation based on rewriting strategies: computations are expressed in the RISE programming language, and rewrite rules and strategies in the ELEVATE strategy language. Fu et al. (2021) later added a type system to ELEVATE to ensure statically that rewrites are composed correctly. As shown throughout the paper, our rewriting system today only provides the ability to apply sets of rewrite rules a certain number of times, in sequence. Given a rule e1 = e2, the sequence e1; e1 can be rewritten to e2; e1, but not directly to e1; e2. Such a transformation can be expressed today by applying the rule e1 = e2 twice, and then applying the opposite rule e2 = e1 once, but this is both embarassingly verbose and inefficient. Adding rewriting strategies to Magnolia will unlock those rewrites that are not easily accessible today, and thus further improve the system's code reuse capabilities. The implementation of Magnolia strategies is of particular interest, and fits into our larger project of exploring module transformations through the lens of Syntactic Theory Functors (Haveraaen and Roggenbach, 2020).
For future work, we also envision the implementation of an extension to the Magnolia rewriting system that supports conditional rewrite rules. Conditional equations can already be expressed in Magnolia, but the rewriting system is not yet able to exploit them.
Whether axioms constitute valid rewriting rules is verifiable by extending Magnolia with formal verification tools—insofar as the relevant properties that a program must satisfy can be derived from the stated axioms about its external building blocks. The properties asserted about externally implemented code can however only be assumed to hold, and constitute the trusted computing base of the whole program. Work on connecting verification tools with Magnolia's specification facilities is already underway, with encouraging results (Hamre, 2022).
Publicly available datasets were analyzed in this study. This programs discussed in this paper can be found at: https://github.com/magnolia-lang/magnolia-lang.
BC extended the Magnolia compiler, implemented the PDE solver, the underlying array library, and the rewriting rules, ran experiments, and wrote the development of the paper. ML worked on an initial Magnolia MoA specification, ran some experiments, and contributed background to the manuscript. JJ and MH contributed to formulating the research question and general approach, and helped refine the manuscript throughout revisions. LM is an expert on MoA and helped revise the manuscript. All authors approved the submitted revision.
The research presented in this paper has benefited from the Experiment Infrastructure for Exploration of Exascale Computing (eX3), which is financially supported by the Research Council of Norway under contract 270053. We thank our reviewers JD and NR for their insights and for truly helping us raise the quality of our paper throughout the reviewing process.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abts, D., Ross, J., Sparling, J., Wong-VanHaren, M., Baker, M., Hawkins, T., et al. (2020). “Think fast: A tensor streaming processor (TSP) for accelerating deep learning workloads,” in 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA), 145–158. doi: 10.1109/ISCA45697.2020.00023
Adams, A., Ma, K., Anderson, L., Baghdadi, R., Li, T.-M., Gharbi, M., et al. (2019). Learning to optimize Halide with tree search and random programs. ACM Trans. Graph. 38, 1–12. doi: 10.1145/3306346.3322967
Bagge, A. H. (2009). Constructs & concepts: language design for flexibility and reliability (Ph.D. thesis). Research School in Information and Communication Technology; Department of Informatics; University of Bergen, Bergen, Norway.
Bagge, A. H., David, V., and Haveraaen, M. (2011). Testing with axioms in C++2011. J. Object Technol. 10, 1–32. doi: 10.5381/jot.2011.10.1.a10
Bagge, A. H., and Haveraaen, M. (2009). “Axiom-based transformations: optimisation and testing,” in Proceedings of the Eighth Workshop on Language Descriptions, Tools and Applications (LDTA 2008), Vol. 238, eds J. J. Vinju and A. Johnstone (Budapest: Elsevier), 17–33. Available online at: https://people.cs.kuleuven.be/~dirk.craeynest/ada-belgium/events/08/080405-etaps-ldta.html
Basili, V. R., Briand, L. C., and Melo, W. L. (1996). How reuse influences productivity in object-oriented systems. Commun. ACM 39, 104–116. doi: 10.1145/236156.236184
Burgers, J. M. (1948). “A mathematical model illustrating the theory of turbulence,” in Advances in Applied Mechanics, Vol. 1 (Elsevier), 171–199. Available online at: https://www.sciencedirect.com/science/article/abs/pii/S0065215608701005?via%3Dihub
Burrows, E., Friis, H. A., and Haveraaen, M. (2018). “An array API for finite difference methods,” in Proceedings of the 5th ACM SIGPLAN International Workshop on Libraries, Languages, and Compilers for Array Programming, ARRAY 2018 (New York, NY: ACM), 59–66. doi: 10.1145/3219753.3219761
Chen, T., Moreau, T., Jiang, Z., Zheng, L., Yan, E., Cowan, M., et al. (2018). “TVM: an automated end-to-end optimizing compiler for deep learning,” in Proceedings of the 13th USENIX Conference on Operating Systems Design and Implementation, OSDI'18 (Carlsbad, CA: USENIX Association), 579–594. Available online at: https://www.usenix.org/system/files/osdi18-chen.pdf
Chetioui, B., Abusdal, O., Haveraaen, M., Järvi, J., and Mullin, L. (2021). “Padding in the mathematics of arrays,” in Proceedings of the 7th ACM SIGPLAN International Workshop on Libraries, Languages and Compilers for Array Programming, ARRAY 2021 (New York, NY: Association for Computing Machinery), 15–26. doi: 10.1145/3460944.3464311
Chetioui, B., Järvi, J., and Haveraaen, M. (2022). Revisiting language support for generic programming: when genericity is a core design goal, in The Art, Science, and Engineering of Programming, 7. doi: 10.22152/programming-journal.org/2023/7/4
Chetioui, B., Mullin, L., Abusdal, O., Haveraaen, M., Järvi, J., and Macià, S. (2019). “Finite difference methods fengshui: alignment through a mathematics of arrays,” in Proceedings of the 6th ACM SIGPLAN International Workshop on Libraries, Languages and Compilers for Array Programming, ARRAY 2019 (New York, NY: Association for Computing Machinery), 2–13. doi: 10.1145/3315454.3329954
Clavel, M., Durán, F., Eker, S., Lincoln, P., Martí-Oliet, N., Meseguer, J., et al. (2007). All about Maude–a High-Performance Logical Framework: How to Specify, Program and Verify Systems in Rewriting Logic. Berlin; Heidelberg: Springer-Verlag.
Dehnert, J. C., and Stepanov, A. A. (1998). “Fundamentals of generic programming,” in Selected Papers from the International Seminar on Generic Programming (Berlin; Heidelberg: Springer-Verlag), 1–11. doi: 10.1007/3-540-39953-4_1
Fatahalian, K., Horn, D. R., Knight, T. J., Leem, L., Houston, M., Park, J. Y., et al. (2006). “Sequoia: programming the memory hierarchy,” in Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, SC '06 (New York, NY: Association for Computing Machinery), 83. doi: 10.1109/SC.2006.55
Frakes, W. B., and Succi, G. (2001). An industrial study of reuse, quality, and productivity. J. Syst. Softw. 57, 99–106. doi: 10.1016/S0164-1212(00)00121-7
Fu, R., Qin, X., Dardha, O., and Steuwer, M. (2021). Row-polymorphic types for strategic rewriting. arXiv [Preprint]. arXiv:2103.13390. doi: 10.48550/arXiv.2103.13390
Gibbons, J. (2006). “Datatype-generic programming,” in Proceedings of the 2006 International Conference on Datatype-Generic Programming, SSDGP'06 (Berlin; Heidelberg: Springer-Verlag), 1–71. doi: 10.1007/978-3-540-76786-2_1
Goguen, J. A., and Burstall, R. M. (1984). “Introducing institutions,” in Logics of Programs, eds E. Clarke and D. Kozen (Berlin; Heidelberg: Springer Berlin Heidelberg), 221–256. doi: 10.1007/3-540-12896-4_366
Gregor, D., Järvi, J., Siek, J., Stroustrup, B., Dos Reis, G., and Lumsdaine, A. (2006). “Concepts: linguistic support for generic programming in C++,” in OOPSLA '06: Proceedings of the 21st Annual ACM SIGPLAN Conference on Object-Oriented Programming Systems, Languages, and Applications (New York, NY: ACM Press), 291–310. doi: 10.1145/1167473.1167499
Hagedorn, B., Lenfers, J., Kundefinedhler, T., Qin, X., Gorlatch, S., and Steuwer, M. (2020). Achieving high-performance the functional way: a functional pearl on expressing high-performance optimizations as rewrite strategies. Proc. ACM Program. Lang. 4, 1–29. doi: 10.1145/3408974
Hagedorn, B., Stoltzfus, L., Steuwer, M., Gorlatch, S., and Dubach, C. (2018). “High performance stencil code generation with Lift,” in Proceedings of the 2018 International Symposium on Code Generation and Optimization, CGO 2018 (New York, NY: ACM), 100–112. doi: 10.1145/3179541.3168824
Hamre, H.-C. (2022). Automated verifications for magnolia satisfactions (Master's thesis). The University of Bergen, Bergen, Norway.
Haveraaen, M., and Roggenbach, M. (2020). Specifying with syntactic theory functors. J. Logic. Algeb. Methods Prog. 113:100543. doi: 10.1016/j.jlamp.2020.100543
Ikarashi, Y., Bernstein, G. L., Reinking, A., Genc, H., and Ragan-Kelley, J. (2022). “Exocompilation for productive programming of hardware accelerators,” in Proceedings of the 43rd ACM SIGPLAN International Conference on Programming Language Design and Implementation, PLDI 2022 (New York, NY: Association for Computing Machinery), 703–718. doi: 10.1145/3519939.3523446
Kirchner, H. (2015). Rewriting Strategies and Strategic Rewrite Programs. Cham: Springer International Publishing. 380–403. doi: 10.1007/978-3-319-23165-5_18
Koehler, T., Trinder, P., and Steuwer, M. (2021). Sketch-guided equality saturation: scaling equality saturation to complex optimizations in languages with bindings. arXiv [Preprint]. arXiv:2111.13040. doi: 10.48550/arXiv.2111.13040
Lattner, C., Amini, M., Bondhugula, U., Cohen, A., Davis, A., Pienaar, J., et al. (2021). “MLIR: scaling compiler infrastructure for domain specific computation,” in 2021 IEEE/ACM International Symposium on Code Generation and Optimization (CGO), 2–14. Available online at: https://conf.researchr.org/home/cgo-2021
Lemire, D., Kaser, O., and Kurz, N. (2019). Faster remainder by direct computation: Applications to compilers and software libraries. Softw. Pract. Exp. 49, 953–970. doi: 10.1002/spe.2689
Liu, A., Bernstein, G. L., Chlipala, A., and Ragan-Kelley, J. (2022). Verified tensor-program optimization via high-level scheduling rewrites. Proc. ACM Prog. Lang. 6, 1–28. doi: 10.1145/3498717
Martí-Oliet, N., Meseguer, J., and Verdejo, A. (2005). Towards a strategy language for Maude. Electron. Notes Theor. Comput. Sci. 117, 417–441. doi: 10.1016/j.entcs.2004.06.020
Martí-Oliet, N., Meseguer, J., and Verdejo, A. (2009). A rewriting semantics for Maude strategies. Electron. Notes Theor. Comput. Sci. 238, 227–247. doi: 10.1016/j.entcs.2009.05.022
Mullin, L. (1988). A mathematics of arrays (Ph.D. thesis). Syracuse University, Syracuse, NY, United States.
Mullin, L., and Thibault, S. (1994). Reduction Semantics for Array Expressions: The PSI Compiler. Technical Report CSC 94-05, Department of CS; University of Missouri-Rolla.
Mullin, L. M. R., and Jenkins, M. A. (1996). Effective data parallel computation using the PSI calculus. Concurr. Pract. Exp. 8, 499–515. doi: 10.1002/(SICI)1096-9128(199609)8:7<499::AID-CPE230>3.0.CO;2-1
Musser, D. R., and Stepanov, A. A. (1988). “Generic programming,” in Symbolic and Algebraic Computation, International Symposium ISSAC'88, Vol. 358 of Lecture Notes in Computer Science, ed P. M. Gianni (Rome: Springer), 13–25.
Nazareth, D. L., and Rothenberger, M. A. (2004). Assessing the cost-effectiveness of software reuse: a model for planned reuse. J. Syst. Softw. 73, 245–255. doi: 10.1016/S0164-1212(03)00248-6
Puschel, M., Moura, J., Johnson, J., Padua, D., Veloso, M., Singer, B., et al. (2005). SPIRAL: code generation for DSP transforms. Proc. IEEE 93, 232–275. doi: 10.1109/JPROC.2004.840306
Ragan-Kelley, J., Adams, A., Paris, S., Levoy, M., Amarasinghe, S., and Durand, F. (2012). Decoupling algorithms from schedules for easy optimization of image processing pipelines. ACM Trans. Graph. 31, 1–12. doi: 10.1145/2185520.2185528
Sannella, D., and Tarlecki, A. (1996). “Mind the gap! Abstract versus concrete models of specifications,” in Mathematical Foundations of Computer Science 1996, 21st International Symposium, MFCS'96, Vol. 1113 of Lecture Notes in Computer Science, eds W. Penczek and A. Szalas (Cracow: Springer), 114–134. doi: 10.1007/3-540-61550-4_143
Steuwer, M., Fensch, C., Lindley, S., and Dubach, C. (2015). “Generating performance portable code using rewrite rules: from high-level functional expressions to high-performance OpenCL code,” in Proceedings of the 20th ACM SIGPLAN International Conference on Functional Programming, ICFP 2015 (New York, NY: Association for Computing Machinery), 205–217. doi: 10.1145/2784731.2784754
Steuwer, M., Remmelg, T., and Dubach, C. (2017). “Lift: A functional data-parallel IR for high-performance GPU code generation,” in Proceedings of the 2017 International Symposium on Code Generation and Optimization, CGO '17 (Austin, TX: IEEE Press), 74–85. Available online at: https://cgo.org/cgo2017/
Tang, X., and Järvi, J. (2015). Axioms as generic rewrite rules in C++with concepts. Sci. Comput. Prog. 97, 320–330. doi: 10.1016/j.scico.2014.05.006
Vasilache, N., Zinenko, O., Bik, A. J. C., Ravishankar, M., Raoux, T., Belyaev, A., et al. (2022). Composable and modular code generation in MLIR: A structured and retargetable approach to tensor compiler construction. arXiv [Preprint]. arXiv:2202.03293. doi: 10.48550/arXiv.2202.03293
Visser, E. (2005). A survey of strategies in rule-based program transformation systems. J. Symb. Comput. 40, 831–873. doi: 10.1016/j.jsc.2004.12.011
Wolfe, M. (2021). Performant, portable, and productive parallel programming with standard languages. Comput. Sci. Eng. 23, 39–45. doi: 10.1109/MCSE.2021.3097167
concept GenericBinopRules = {
type E;
type Array;
type Index;
function binop(lhs: E, rhs: E): E;
function binop(lhs: E,
rhs: Array): Array;
function binop(lhs: Array,
rhs: Array): Array;
function psi(ix: Index,
array: Array): E;
// Rule 1
axiom binopArrayRule(ix: Index,
lhs: Array, rhs: Array) {
assert psi(ix, binop(lhs, rhs)) ==
binop(psi(ix, lhs),
psi(ix, rhs));
}
// Rule 2
axiom binopScalarRule(ix: Index,
lhs: E, rhs: Array) {
assert psi(ix, binop(lhs, rhs)) ==
binop(lhs, psi(ix, rhs));
}
}
concept DNFRules = {
use GenericBinopRules[
binop => _+_,
binopScalarRule => addScalarRule,
binopArrayRule => addArrayRule
];
use GenericBinopRules[
binop => _-_,
binopScalarRule => subScalarRule,
binopArrayRule => subArrayRule
];
use GenericBinopRules[
binop => _*_,
binopScalarRule => mulScalarRule,
binopArrayRule => mulArrayRule
];
use GenericBinopRules[
binop => _/_,
binopScalarRule => divScalarRule,
binopArrayRule => divArrayRule
];
type Axis;
type Offset;
function rotate(array: Array,
axis: Axis, offset: Offset): Array;
function rotateIx(ix: Index,
axis: Axis, offset: Offset): Index;
// Rule 3
axiom rotateRule(ix: Index,
array: Array, axis: Axis,
offset: Offset) {
assert psi(ix, rotate(array, axis,
offset)) ==
psi(rotateIx(ix, axis, offset),
array);
}
}[ E => Float ];
Listing 17. The DNF rewriting rules in Magnolia.
function substepIx(u: Array, v: Array,
u0: Array, u1: Array, u2: Array,
ix: Index) : Array =
psi(ix,
u + dt()/(two(): Float) * (nu() * (
(one(): Float)/dx()/dx() *
(rotate(v, zero(),
-one(): Offset) +
rotate(v, zero(),
one(): Offset) +
rotate(v, one(): Axis,
-one(): Offset) +
rotate(v, one(): Axis,
one(): Offset) +
rotate(v, two(): Axis,
-one(): Offset) +
rotate(v, two(): Axis,
one(): Offset)) -
three() * (
two(): Float)/dx()/dx() * u0) -
(one(): Float)/(two(): Float)/dx() *
((rotate(v, zero(),
one(): Offset) -
rotate(v, zero(),
-one(): Offset)) * u0 +
(rotate(v, one(): Axis,
one(): Offset) -
rotate(v, one(): Axis,
-one(): Offset)) * u1 +
(rotate(v, two(): Axis,
one(): Offset) -
rotate(v, two(): Axis,
-one(): Offset)) * u2)));
Listing 18. Generated index-level implementation of substep in Magnolia.
Array schedule(const Array &u,
const Array &v, const Array &u0,
const Array &u1, const Array &u2) {
Array result;
for (size_t i = 0;
i < TOTAL_ARRAY_SIZE;
++i) {
result[i] = substepIx(u, v, u0, u1,
u2, i);
}
return result;
}
Listing 19. A naive and non-specific C++ implementation of a scheduling function. TOTAL_ARRAY_SIZE corresponds to the number of elements within one array. Every array has the same number of elements.
size_t threadsPerBlock = 1024;
size_t nbBlocks =
(TOTAL_PADDED_SIZE / threadsPerBlock) +
(TOTAL_PADDED_SIZE % threadsPerBlock > 0
? 1 : 0);
// This kernel assumes that it is launched
// on at least TOTAL_ARRAY_SIZE threads
template <class _substepIx>
__global__ void substepIxGlobal(
Array *res, const Array *u,
const Array *v, const Array *u0,
const Array *u1, const Array *u2) {
size_t ix = blockIdx.x * blockDim.x + threadIdx.x;
// Create the function object substepIx
_substepIx substepIx;
if (ix < TOTAL_PADDED_SIZE) {
res->content[ix] =
substepIx(*u,*v,*u0,*u1,*u2,ix);
}
}
__host__ Array schedule(const Array &u,
const Array &v, const Array &u0,
const Array &u1, const Array &u2) {
Array result;
Array *result_dev = NULL,
*u_dev = NULL,
*v_dev = NULL,
*u0_dev = NULL,
*u1_dev = NULL,
*u2_dev = NULL;
// Creating arrays on device
// ...
// Copying pointer to device data from
// the input arrays
// ...
// Calling the kernel to compute the
// result at every index
substepIxGlobal < _substepIx><<<nbBlocks,
threadsPerBlock>>>(
result_dev, u_dev, v_dev, u0_dev,
u1_dev, u2_dev);
// Clean up device arrays
// ...
return result;
}
Listing 20. Our CUDA implementation of a scheduling function. TOTAL_ARRAY_SIZE corresponds to the number of elements within one array. Every array has the same number of elements. Some code related to memory allocation and copying is omitted from this listing, for the sake of conciseness.
program PDEProgramPadded = {
use
(rewrite PDEProgramDNF with OFPad 1);
// imports a new schedule, a new
// function for index rotation, and a
// procedure for refilling padding
use ExtExtendPadding;
}
concept OFPad = {
type Array;
type Float;
procedure refillPadding(upd a: Array);
function schedulePadded(u: Array,
v: Array, u0: Array, u1: Array,
u2: Array): Array;
function schedule(u: Array, v: Array,
u0: Array, u1: Array,
u2: Array): Array;
axiom padRule(u: Array, v: Array,
u0: Array, u1: Array, u2: Array) {
assert schedule(u, v, u0, u1, u2) ==
{ var result = schedulePadded(u, v,
u0, u1, u2);
call refillPadding(result);
value result;
};
}
type Index;
type Axis;
type Offset;
function rotateIx(ix: Index, axis: Axis,
offset: Offset): Index;
function rotateIxPadded(ix: Index,
axis: Axis, offset: Offset): Index;
axiom rotateIxPadRule(ix: Index,
axis: Axis, offset: Offset) {
assert rotateIx(ix, axis, offset) ==
rotateIxPadded(ix, axis,
offset);
}
}
Listing 21. Introducing padding into PDEProgramDNF.
Array schedulePadded(const Array &u,
const Array &v, const Array &u0,
const Array &u1, const Array &u2) {
Array result;
size_t paddedS1 = S1 + 2 * PAD1;
size_t paddedS2 = S2 + 2 * PAD2;
for (size_t i = PAD0; i < S0 + PAD0;
++i) {
for (size_t j = PAD1; j < S1 + PAD1;
++j) {
for (size_t k = PAD2; k < S2 + PAD2;
++k) {
size_t ix =
i * paddedS1 * paddedS2 +
j * paddedS2 + k;
result[ix] =
substepIx(u, v, u0, u1, u2, ix);
}
}
}
return result;
}
Listing 22. A C++ implementation of a scheduling function for padded arrays. All the arrays have the same (three dimensional) shape and each axis is padded by the same amount on each ends. S0, S1, and S2 respectively represent the length of the first, second, and third axis of the arrays. PAD0, PAD1, and PAD2 respectively represent the amount of padding for one end of the first, second, and third axis of the arrays.
procedure step(upd u0: Array, upd u1:
Array, upd u2: Array) = {
var v0: Array = u0;
var v1: Array = u1;
var v2: Array = u2;
v0 = {
var result: Array = schedulePadded(
v0, u0, u0, u1, u2);
refillPadding(result);
value result;
};
v1 = {
var result: Array = schedulePadded(
v1, u1, u0, u1, u2);
refillPadding(result);
value result;
};
v2 = {
var result: Array = schedulePadded(
v2, u2, u0, u1, u2);
refillPadding(result);
value result;
};
u0 = {
var result: Array = schedulePadded(
u0, v0, u0, u1, u2);
refillPadding(result);
value result;
};
u1 = {
var result: Array = schedulePadded(
u1, v1, u0, u1, u2);
refillPadding(result);
value result;
};
u2 = {
var result: Array = schedulePadded(
u2, v2, u0, u1, u2);
refillPadding(result);
value result;
};
};
Listing 23. The implementation of step produced by an application of rewrite with OFPad.
concept OFSpecializePsi = {
type Index;
type Array;
type E;
type ScalarIndex;
/* 3D index projection functions */
function ix0(ix: Index): ScalarIndex;
function ix1(ix: Index): ScalarIndex;
function ix2(ix: Index): ScalarIndex;
/* 3D index constructor */
function mkIx(i: ScalarIndex,
j: ScalarIndex,
k: ScalarIndex): Index;
function psi(ix: Index,
array: Array): E;
function psi(i: ScalarIndex,
j: ScalarIndex, k: ScalarIndex,
array: Array): E;
axiom specializePsiRule(ix: Index,
array: Array) {
assert psi(ix, array) ==
psi(ix0(ix), ix1(ix), ix2(ix),
array);
}
axiom reduceMakeIxRule(i: ScalarIndex,
j: ScalarIndex, k: ScalarIndex) {
var ix = mkIx(i, j, k);
assert ix0(ix) == i;
assert ix1(ix) == j;
assert ix2(ix) == k;
}
}[ E => Float ];
Listing 24. Specializing calls to the indexing function ψ.
concept OFReduceMakeIxRotate = {
use signature(OFSpecializePsi);
type Axis;
type Offset;
function zero(): Axis;
function one(): Axis;
function two(): Axis;
function rotateIx(ix: Index, axis: Axis,
offset: Offset): Index;
type AxisLength;
function shape0(): AxisLength;
function shape1(): AxisLength;
function shape2(): AxisLength;
function _+_(six: ScalarIndex,
o: Offset): ScalarIndex;
function _%_(six: ScalarIndex,
sc: AxisLength): ScalarIndex;
axiom reduceMakeIxRotateRule(
i: ScalarIndex, j: ScalarIndex,
k: ScalarIndex, array: Array,
o: Offset) {
var ix = mkIx(i, j, k);
var s0 = shape0();
var s1 = shape1();
var s2 = shape2();
assert ix0(rotateIx(ix, zero(), o)) ==
(i + o) % s0;
assert
ix0(rotateIx(ix, one(), o)) == i;
assert
ix0(rotateIx(ix, two(), o)) == i;
assert
ix1(rotateIx(ix, zero(), o)) == j;
assert ix1(rotateIx(ix, one(), o)) ==
(j + o) % s1;
assert
ix1(rotateIx(ix, two(), o)) == j;
assert
ix2(rotateIx(ix, zero(), o)) == k;
assert
ix2(rotateIx(ix, one(), o)) == k;
assert ix2(rotateIx(ix, two(), o)) ==
(k + o) % s2;
}
}
Listing 25. A rewriting system to specialize the index rotation operation.
// We suppose here that the amount of
padding is sufficient across
// each axis for every indexing operation.
concept OFEliminateModuloPadding = {
use signature(OFReduceMakeIxRotate);
type Array;
type Float;
function psi(i: ScalarIndex,
j: ScalarIndex, k: ScalarIndex,
a: Array): Float;
axiom eliminateModuloPaddingRule(
i: ScalarIndex, j: ScalarIndex,
k: ScalarIndex, a: Array,
o: Offset) {
var s0 = shape0();
var s1 = shape1();
var s2 = shape2();
assert psi((i + o) % s0, j, k, a) ==
psi(i + o, j, k, a);
assert psi(i, (j + o) % s1, k, a) ==
psi(i, j + o, k, a);
assert psi(i, j, (k + o) % s2, a) ==
psi(i, j, k + o, a);
}
}
Listing 26. Elimination of the modulo operations in the program.
Keywords: partial differential equations, generic programming, Magnolia language, mathematics of arrays, term rewriting, high-performance computing
Citation: Chetioui B, Larnøy MK, Järvi J, Haveraaen M and Mullin L (2022) P3 problem and Magnolia language: Specializing array computations for emerging architectures. Front. Comput. Sci. 4:931312. doi: 10.3389/fcomp.2022.931312
Received: 28 April 2022; Accepted: 16 August 2022;
Published: 31 October 2022.
Edited by:
Jeronimo Castrillon, Technical University Dresden, GermanyReviewed by:
James Harold Davenport, University of Bath, United KingdomCopyright © 2022 Chetioui, Larnøy, Järvi, Haveraaen and Mullin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Benjamin Chetioui, YmVuamFtaW4uY2hldGlvdWlAdWliLm5v
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.