Embodiment enables non-predictive ways of coping with self-caused sensory stimuli

Living systems process sensory data to facilitate adaptive behavior. A given sensor can be stimulated as the result of internally driven activity, or by purely external (environmental) sources. It is clear that these inputs are processed differently—have you ever tried tickling yourself? Self-caused stimuli have been shown to be attenuated compared to externally caused stimuli. A classical explanation of this effect is that when the brain sends a signal that would result in motor activity, it uses a copy of that signal to predict the sensory consequences of the resulting motor activity. The predicted sensory input is then subtracted from the actual sensory input, resulting in attenuation of the stimuli. To critically evaluate the utility of this predictive approach for coping with self-caused stimuli, and investigate when non-predictive solutions may be viable, we implement a computational model of a simple embodied system with self-caused sensorimotor dynamics, and use a genetic algorithm to explore the solutions possible in this model. We find that in this simple system the solutions that emerge modify their behavior to shape or avoid self-caused sensory inputs, rather than predicting these self-caused inputs and filtering them out. In some cases, solutions take advantage of the presence of these self-caused inputs. The existence of these non-predictive solutions demonstrates that embodiment provides possibilities for coping with self-caused sensory interference without the need for an internal, predictive model.

1. Introduction

The remarkable adaptive behavior displayed by living organisms would not be possible without the capacity to respond to sensory stimuli appropriately. The same sensors can be stimulated due to external (environmental) causes, as well as by internally driven activity. Intuitively, it seems like responding appropriately must require distinguishing the two. We can hear sounds in the world around us, but we can also hear our own voice when talking, and our own footsteps when walking. We can see our environment, but we can also see our own bodies. Not only do we perceive both the world and the results of our own actions, but the exact same sensory stimulus can be caused by an external event, or by our own activity. For example the sight of a hand being waved before your eyes could be your own hand or a friend snapping you out of a daydream. However, we typically have no trouble telling the difference. Indeed, the phenomenology of a self-caused stimulus can be very different from that of an externally caused one. A great example of this is the sensation of touch, which can reduce you to helpless laughter when externally applied—but trying to tickle yourself just isn't the same! (Blakemore et al., 2000). Understanding exactly how these inputs are processed differently can facilitate building artificial systems as capable and flexible as living ones.

One concrete way this has been studied is in research on the sensory attenuation of self-caused stimuli, where researchers have investigated how these stimuli are perceived as diminished in comparison to externally caused stimuli (Hughes and Waszak, 2011). This is clearly demonstrated in the force-matching paradigm. Here an external force is applied to a subject's finger, after which they must use their other hand to recreate that force as precisely as possible. This takes place under two conditions. In the direct condition, the subject applies force to their finger in a manner as close as possible to pressing on their own finger (given the constraints of the experimental apparatus). In the indirect condition, they apply the force via a mechanism located elsewhere, such as a lever to one side. Healthy subjects consistently apply too much force when pressing directly on their finger, indicating that the perceived force is attenuated compared to the other conditions (Pareés et al., 2014). The classical explanation of this effect is that when the brain issues a motor command, it uses a copy of that command to predict the sensory consequences of the resulting motor activity. The predicted sensory input is then subtracted from the actual sensory input, resulting in the attenuation of the stimulus (Klaffehn et al., 2019). This is a representationalist explanation in that it explicitly posits that the brain contains an internal model used to simulate the motor system (Wolpert et al., 1995).

While there is indeed evidence to support the presence of neural correlates of motor activity subsequently influencing sensory perception in different species, specifically via corollary discharge circuits (Crapse and Sommer, 2008), the aim of this paper is to interrogate the necessity and utility of internal representations in general and internal predictive models in particular for maintaining adaptive behavior in the presence of self-caused sensory interference. We examine the predict-and-subtract explanation of the sensory attenuation phenomena by using a genetic algorithm (GA) to explore the viable solutions in a dynamical model of a simple embodied system with non-trivial self-caused sensorimotor dynamics, where the task the controller must solve relies on engaging with an environmental stimulus, while its own motor activity also directly stimulates its environmental sensors. Here we focus on the classical, predict-and-subtract approach, which would in theory perfectly solve the interference problem that we have designed, though our GA instead finds alternative, non-predictive solutions which leverage the system's embodiment.

In general, expected stimuli produce a reduced neural response (de Lange et al., 2018). This has been explained in terms of an internal predictive model (e.g., Blakemore et al., 1998, 2000; Wolpert and Flanagan, 2001; Bays et al., 2005; Kilteni and Ehrsson, 2017, 2022; Kilteni et al., 2020; Lalouni et al., 2021). This type of explanation has been described as “cancellation theory,” where expected sensations are suppressed (Press et al., 2020). In the interest of completeness, we should mention that there are other predictive accounts of perception, such as Bayesian predictive processing, where attention also plays a major role (Friston, 2009; Clark, 2013; de Lange et al., 2018). The roles of prediction in Bayesian and cancellation theories have been considered contradictory, and “opposing process theory” is one attempt to reconcile them (Press et al., 2020). These alternative approaches are somewhat orthogonal to this project, as they address different potential roles for prediction, whereas we aim to engage with the classical account by investigating the role of embodiment in coping with self-caused sensory interference in a context where prediction and subtraction of that interference is a perfect solution. Likewise, while externally-caused stimuli can also be attenuated, for instance when expected (de Lange et al., 2018), or during movement (Kilteni and Ehrsson, 2022), this paper focuses specifically on coping with self-caused stimuli by modeling a task which requires responsiveness to environmental sensor stimulation despite the presence of self-caused sensory interference.

The problem of ego-noise in robotics hints at why subtracting out self-produced stimuli seems like a natural thing for the brain to do. Ego-noise refers to self caused noise, including that of motors. This noise can interfere with the data collecting sensors of a robot, and the straightforward engineering solution is to cancel out the noise. The explicitly representational and predictive explanation of the sensory attenuation effect meshes well with this engineering perspective, and has informed a predictive approach to dealing with ego-noise (Schillaci et al., 2016). We cite Schillaci et al. here as an illustration that this exact approach has indeed been used in recent work in robotics, and thus our results should have relevance to the field. Of course this is not the only approach to dealing with the general problem of making the self-other distinction in robotics—see for instance Chatila et al. (2018) and Kahl et al. (2022).

In our model, the embodiment is a simple, simulated, two-wheeled system with a pair of light sensors. It is coupled to a controller—a continuous-time, recurrent neural network (CTRNN)—which determines its motor activity. The sensory input to this robot is a linear combination of environmental factors (a function of its position relative to a light) and a self-caused component—a function of the robot's motor activity.

This model is designed to allow both representationalist and non-representationalist solutions to emerge. For the representationalist predict-and-subtract solution to be viable in this model, two criteria need to be met. Firstly, the controller must be able to model the interference. As the controller is a CTRNN, which is a universal approximator of smooth dynamics (Beer, 2006), it can indeed model the interfering dynamics, which are produced by simple, smooth functions. Secondly, the interference must be able to be removed from the input, given a prediction of the interference. Since the interference is summed with the actual sensor data, it can be removed by subtracting a prediction of the interference from the sensory inputs. This explicitly representational solution would fit with the classical explanation of sensory attenuation. Non-representationalist solutions that take advantage of the system's embodiment are also possible in this model, since the interfering dynamics are a function of the system's motor activity, and are coupled to the controller in a tight sensorimotor loop, embracing the situated, embodied and dynamical (SED) approach. In the classical account, the environmental stimulation of the sensor can be treated as independent of the system's activity, and the self-caused stimulation of the sensor is similarly compartmentalized—the decision to take a particular action is made independently of its incidental sensory consequences, and compensation for these consequences is left to downstream predictive and subtractive processes. In contrast with this approach, modeling how embodied systems are coupled to their environment, in particular how both the system's environmentally and self-caused sensory inputs are influenced by the system's own motor activity, enables additional ways of coping with self-caused stimuli, as will be seen in our results.

Following the evolutionary robotics methodology we explore the space of possible solutions using a genetic algorithm (GA) (Harvey et al., 2005). We then analyze the behavioral strategies of controllers tuned to successfully accomplish a task (phototaxis), in the presence of several different forms of motor-driven sensory interference. This permits us examine a range of ways embodied systems may cope with different self-caused sensory stimuli, and reveals that a number of alternatives to the classical predict-and-subtract approach are viable in our model.

Clearly the simulated robot and neural network controller that we are investigating are very different from humans and their brains. This limits the ability to make direct predictions about humans based on the results found in our model—we don't expect to find people using exactly the same strategies used by the two-wheeled robot. Nevertheless, this type of model can highlight how the solutions found by evolution are not always the same as the solutions that might be identified by a human engineer. As argued by Thompson et al. (1999), humans need to understand what they engineer, to divide and subdivide the problem and solution into smaller units until those units are simple enough to address directly. For example, dividing the problem of coping with self-caused stimuli from the general problems of perception and action, and further dividing it into the prediction and subtraction of self-caused stimuli. Natural or artificial evolution, on the other hand, is under no such constraint. The solutions it finds are the result of iterative improvement with no need for understanding, simplification or compartmentalization. Accordingly, it can find solutions that are “messy” and difficult, perhaps in some cases even impossible, for us to understand. Our evolutionary robotics model, like others before it (Beer, 2003; Phattanasri et al., 2007; Beer and Williams, 2015), allows us to see that there are alternatives to how an engineer might approach solving this particular problem. Furthermore, it allows us to generate concrete examples of alternative strategies for solving the problem at hand, and due to the simplicity of the model these examples are easier to analyze and come to understand than the incredibly complex behavior found in living systems.

In Section 2 we explain the model we developed and the GA we use to optimize its parameters. Then in Section 3 we present the results of our investigation, describing each form of interference used, and explaining the behavior of the most successful system evolved to perform phototaxis in the presence of each form of interference. Finally in Section 4 we summarize the different behaviors evolved to cope with these forms of interference, and discuss how these findings can inform our understanding of the role embodiment plays in coping with self-caused sensory stimuli. We draw attention to how the problem of disentangling self-caused and environmental stimulation of the sensors is made easier for embodied systems by the influence embodied systems have over both self-caused and environmental stimulation of their sensors, and we argue that, for embodied systems, this problem need not require the use of an internal model.

2. Model and methods

In this section we first describe our model of an embodied system with self-caused, motor-driven sensory interference, which must perform a task where clear perception of the environment is beneficial. We then describe the genetic algorithm (GA) that we use to investigate how embodied systems can cope with self-caused sensory input.

2.1. Model

We model a simple light-sensing robot, controlled by a neural network, where the robot's light sensors can also be directly stimulated by the robot's own motor activity. The two-wheeled robot moves about an infinite, flat plane. It has a pair of directional light sensors, and the environment contains a single light source. Over the course of a single simulation, this light source's position remains fixed. The robot is controlled by a continuous-time, recurrent neural network (CTRNN). Motor-driven interference is ipsilateral and non-saturating, and is determined by one of three different functions, which are detailed in the Experiments section. Figure 1 provides a visual overview of the model architecture. As the model is fully deterministic, the course of each simulation is fully determined by the robot's initial distance from and orientation toward the light. In each simulation, the robot begins at the origin (0, 0), facing toward positive y, and initial conditions are varied by positioning the light at a different (x, y) coordinate.

FIGURE 1

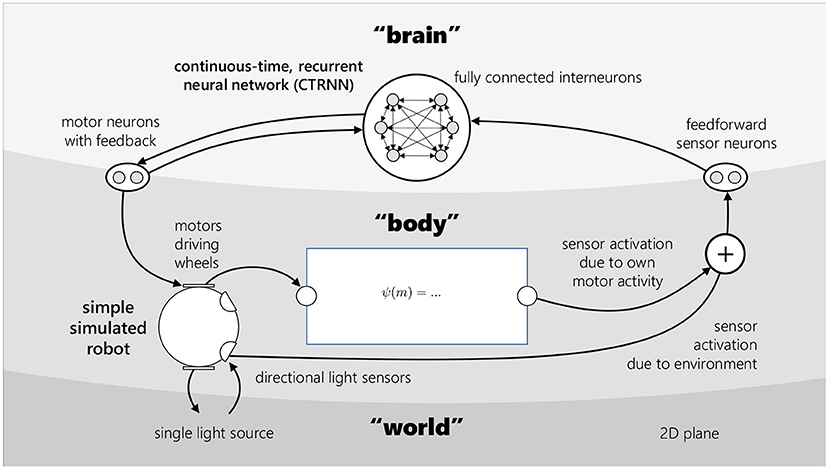
Figure 1. An embodied model with motor-driven sensory interference. This model is used throughout the paper. It consists of three parts—the “brain,” the “body” and the “world.” The brain is a continuous-time, recurrent neural network (CTRNN), with 6 fully connected interneurons, 2 sensor neurons which project to all interneurons, and 2 motor neurons which project to and receive projections from all interneurons. The motor neurons determine the activation of the body's 2 motors. The body's position and orientation relative to the single light source in the environment determine the activation of its 2 light sensors. The value received at a given point in time by the right sensor neuron is a linear combination of the right light sensor activation, and a function ψ of the right motor's activation, representing self-caused sensory stimulation—and likewise for the left sensor, sensor neuron, and motor.

2.1.1. Embodiment

The robot is circular, with two idealized wheels situated on its perimeter π radians apart, at −π/2 and π/2 relative to its facing. The wheels can be independently driven forwards or backwards. Its two light sensors are located on its perimeter at −π/3 and π/3 relative to its facing. The environment it inhabits is defined entirely by the spatial coordinates of the single light source. The robot's movement in its environment is described by the following set of equations:

$\begin{array}{ll}\hfill ẋ=(m_L+m_R)cos(\alpha )& (1)\end{array}$

$\begin{array}{ll}ẏ=(m_L+m_R)sin(\alpha )& (2)\end{array}$

$\begin{array}{ll}\dot{\alpha }=(m_R-m_L)r& (3)\end{array}$

Where x and y are the robot's spatial coordinates, and α is the robot's facing in radians. m_L and m_R are the robot's left and right motor activation, respectively, and are always in the range [−1, 1]. The values of m_L and m_R are specified by the controller, which is described later. r = 0.25 is the robot's radius. We simulate this system using Euler integration with Δ_t = 0.01.

Physically this describes positive motor activation turning its respective wheel forwards, and conversely for negative motor activation. If the sum of the two motors' activation is positive, the robot as a whole moves forwards with respect to its facing, while if it is negative, the robot moves backwards. The amount that the robot turns is also determined by the relationship between the two wheels.

The robot's two light sensors are located at the coordinates (x + cos(α + θ)r, y + sin(α + θ)r), where θ is the sensor's angular offset. For the left sensor, θ = π/3 and for the right sensor, θ = −π/3. The environmental stimulation of the sensors is given by:

$\begin{array}{ll}s=\frac{{(b·ĉ)}^{+}}{1+D^2}ϵ& (4)\end{array}$

Where b = [cos(α + θ), sin(α + θ)] is the unit vector pointing in the direction the sensor is facing, and c is the vector from the sensor to the light, with ĉ denoting that the vector is normalized to have a unit length. That is ĉ = c/|c|, where |c| is the magnitude of c. The symbol · denotes the dot product of the two vectors, and the superscript ⁺ indicates that any negative values are replaced with 0. D is the Euclidean distance from the sensor to the light, and ϵ = 5 is a fixed environmental intensity factor. s_L denotes the activation of the left sensor, with θ = π/3, while s_R denotes the activation of the right sensor, θ = −π/3.

The numerator is maximized at 1 when the sensor is directly facing the light, and minimized at 0 when the sensor is facing π/2 radians (90°) or more away from the light. The denominator is minimized at 1 when the distance from the sensor to the light is 0. This means that the activation of a sensor grows both as the sensor faces more toward the light, and as the sensor approaches the light (so long as it is facing less than π/2 radians away from the light).

2.1.2. Controller

The controller is a continuous-time recurrent neural network (CTRNN) defined by the state equation below, following Beer (1996):

$\begin{array}{ll}{\tau }_i\stackrel{·}{y_i}=-y_i+{\displaystyle \sum _{j=1}^N}{\omega }_{ji}\sigma (y_j+{\beta }_j)+I_i& (5)\end{array}$

Here N = 10 denotes the number of neurons in the network. y_i indicates the activation of the ith neuron. The parameter τ_i is the time constant of that neuron, where 0 < τ_i < 3, while the parameter β_i is its bias, where −5 < β_i < 5. I_i is any external input to the neuron. σ(x) = 1/(1 + e^−x) is the standard logistic activation function for neural networks, and is a sigmoid function in the range [0, 1]. ω_ji is a weight determining the influence of the jth neuron on the ith neuron, where −5 < ω_ji < 5.

Two neurons are designated as input neurons, and all their incoming interneuron weights ω_ji are set to 0, including the recurrent weight ω_ii. With the robot described above, neurons 1 and 2 are designated as input neurons, and I₁ = w_Is_L, while I₂ = w_Is_R, where w_I = 5 is a fixed input scaling weight. These are the only neurons which receive an external input, so I_3..N = 0 always.

Two neurons are designated as output neurons (neurons 9 and 10), and their activation values y are treated as the output of the network. In our case, y_N−1 and y_N provide the values m_L and m_R, respectively. Output is scaled to be in the range [−1, 1] by the function:

$\begin{array}{ll}o(y)=\frac{2}{1+exp(\frac{-y}{\sqrt{{\omega }_{\text{max}}}})}-1& (6)\end{array}$

Where ω_max = 5 denotes the maximum weight value ω permitted for a node in this CTRNN. The two output neurons do not receive stimulus from the input neurons. That is if j ∈ {1, 2} and i ∈ {9, 10} then ω_ji = 0. The remaining six neurons are interneurons, each of which receives inputs from all other neurons in the network. This neural network architecture is illustrated in Figure 1.

2.1.3. Motor-driven interference

Perception necessarily involves both the system and its environment. Nevertheless, we can consider the degree to which the activity of the system or environment contributes to a given stimulus. Let us take three very different points in this space. (1) If our robot passively sat still, while a light in the environment turned on and off, the change in the light sensors' activations would primarily be due to external causes—the robot's own activity would not play a role. (2) On the other hand, in the model described above, all changes in the light sensors' activations are the result of a change in the relationship between the light's position and the robot's position and facing. Because the light is static, the change is induced by the robot's activity, but determined by the robot's spatial relationship with its environment. (3) At the other end of the scale from (1), consider the case where the robot inhabits a lightless environment in which its sensors are directly and exclusively stimulated by its own motor activity. In this case, neither external causes, nor the relationship between the system and the environment play a role—the change in the sensors' activation is due solely to the robot's own activity.

For living systems in the real world, none of these three points are typically possible—for (1) perception is rarely (if ever) purely passive, for (2) movement will likely involve self-produced sensations even if the environment is passive, and for (3) self-produced sensations will depend on environmental conditions. Nevertheless, our own experiences may lie closer to one of these points than to another. Consider the visual experience of (1) sitting watching a movie (a passive experience, yet one whose visual sensations will still depend on activities like movement or blinking), (2) turning to look around the otherwise still room briefly (where the visual stimulation is largely determined by the spatial relationship between the eyes and the room, but still influenced by changes in the environment like the ongoing movie, and self-produced sensations like the peripheral vision of bodily movement), then (3) scratching your nose (where a change in visual stimulation is caused by your own hand entering the visual field, but depends also on static and dynamic environmental factors like the general lighting of the room and the flickering light of the movie screen).

In the model described so far, there is no possibility for directly self-caused stimuli like (3). This is precisely the kind of self-caused sensory input we are concerned with here, so we extend the model with an interference function ψ(m). The various interference functions we study are described in Section (3). The interference function is used in a new sensory input equation:

$\begin{array}{ll}{s}^{\prime }=\lambda \psi (m)+(1-\lambda )s& (7)\end{array}$

Where s is the original light sensor activation, m is the ipsilateral motor's output, and λ is a scaling term controlling how much of the sensory input is due to the environment, and how much is due to the system's motor activity. Substituting for the original input neuron equations, this gives:

$\begin{array}{ll}{I}_1={\omega }_I{s}_L^{\prime }={\omega }_I(\lambda \psi (m_L)+(1-\lambda )s_L)& (8)\end{array}$

$\begin{array}{ll}{I}_2={\omega }_I{s}_R^{\prime }={\omega }_I(\lambda \psi (m_R)+(1-\lambda )s_R)& (9)\end{array}$

This combination of motor-driven interference with sensor activity is additive and non-saturating. That is, the interference ψ(m) can never be so high that change in the environmental stimulation s of the sensor does not result in a change in s′. This means that if ψ(m) can be predicted by the network, then this value can simply be subtracted from the input neuron's output to other nodes. This mapping also uses the ipsilateral motor to generate interference for each sensor. This was chosen for two reasons. Firstly, it is physically intuitive. Secondly, because the motor neurons have recurrent connections to the interneurons, this means that the neural activity determining m_L and m_R [and thus ψ(m_L) and ψ(m_R)] contributes to the interneurons' synaptic inputs, making prediction easier.

To summarize, we start with a model of a two-wheeled robot with two light sensors, controlled by a CTRNN. In this model, changes in a light sensor's activation are purely the result of the robot's position and orientation changing relative to the light. We extend this model by adding a function which, given a motor activation value, produces an interfering output. Instead of the input neurons of the controller directly receiving the current activation of the light sensor, the light sensor's activation is first combined with this interference. The parameter λ controls the weighting given to the sensor activation vs. the interference in this combined term. For example, with λ = 0.05, instead of the light sensor's true reading s, the controller receives 0.95 s + 0.05ψ(m). The interference functions ψ(m) are described in the Section 3.

2.2. Methods

Parameters for the CTRNN controller were evolved using a tournament based genetic algorithm (GA) based on the microbial GA (Harvey, 2011). The GA operates on a population, which consists of a number of solutions specifying the parameters for the CTRNN. In a tournament, two randomly chosen solutions from the population are evaluated independently. Their fitness is compared, and then in the reproduction step the lower scoring solution is removed from the population and replaced by a mutated copy of the higher scoring solution. Our microbial GA differs from the classic presentation in that it ensures that each member of the population participates in exactly one tournament before the reproduction step is performed for the entire population. This allows generations of the population to easily be counted.

The following parameters were evolved for each node i in the CTRNN: the time factor τ_i, the bias β_i, and a weight vector specifying the incoming interneural weights for node i, where ω_ji refers to the weight applied to the connection from j to i.

Each evolvable parameter of the network is encoded in the genome as a single 32 bit floating point number in the range [0, 1]. The weights and biases are translated from gene g to phenotype ω or β via the linear scaling function (ω_min + ω_max)g + ω_min, where ω_min and ω_max are the minimum and maximum neural weights, respectively –5 and 5, while for τ we use the exponential mapping e^3g/10.

The reproduction procedure used, based on the result of a tournament, is to remove the loser from the population, and add in its place a copy of the winning genome. Each gene in this copy is then mutated by the function

$\begin{array}{ll}m(g)=((g+X\mu )+1)mod1& (10)\end{array}$

Where $X~{N}(0,1)$ is a random variable drawn from a normal distribution with a mean of 0 and a standard deviation of 1, μ = 0.2 is the mutation factor, and the result is scaled by adding 1 and taking the modulo with 1 to ensure the result is in the range [0, 1].

In all cases the system was evolved to perform phototaxis using the following fitness function:

$\begin{array}{ll}\frac{{\displaystyle {\sum }_{t=0}^T}d{(x_t,y_t)}^{2}t}{{\displaystyle {\sum }_{t=0}^T}t}& (11)\end{array}$

Where t is the time at the current integration step, T is the trial duration, and d(x, y) is the euclidean distance from the point (x, y) to the light. The squared distance is used rather then the actual distance here solely for computational efficiency. Multiplying the distance by the current time means that minimizing distance later in the trial is more important to the fitness score than doing so earlier is. The final distance is the most important, while the original distance from the light at t = 0 is completely disregarded. However, improvement at any time is always relevant: t = 99 is almost as important as t = 100.

In each trial, the robot begins at the origin. Each generation, four light coordinates are stochastically generated. The first coordinate is chosen uniformly at random to lie on a circle of radius 3 centered on the origin. The other three coordinates lie on the same circle and form a square with the first. Each solution in the population has its fitness score calculated for each of the four light coordinates. These scores are combined before comparison in the tournament. This means that a given solution's score may go up or down from generation to generation, as it may perform better or worse on that generation's set of light coordinates. This helps prevent the GA becoming stuck in a local optima.

A population of 50 individuals was used. The trial duration was chosen to allow enough time for robust phototaxis to be selected for, either 10 or 20 time units depending on the interference function. The GA was allowed to run for a sufficient number of generations for fitness gains to plateau and for the population of solutions to converge.

3. Experiments

To investigate how embodied systems cope with motor-driven interference, we began by using the GA to find parameters that would allow a CTRNN controller to perform phototaxis in the basic model with λ = 0 (i.e., with no motor-driven sensor interference). The population of controllers that were the product of this GA run are taken as the ancestral population for the subsequently evolved populations in Experiments 2–4. That is, parameters for these populations were evolved starting from this ancestral population, rather than starting from a new, random population. We chose to use an ancestral population, rather than evolving subsequent populations from scratch, in order to allow for direct comparison between the behavior of the systems optimized with and without the presence of motor-driven interference. The results of Experiment 1 are presented in Section 3.1.

In addition to Experiment 1 with the basic version of the model where λ = 0 (and therefore s′ = s), we consider three further versions of the model in Experiments 2–4, each corresponding to a different interference function ψ(m). We use λ = 0.5 with each of these three functions. In turn we consider: (i) a threshold-like sigmoidal function, whose interference can be completely avoided by appropriately modified behavior; (ii) a form of unavoidable interference, taking the square of the motor activity; and (iii) a time-dependent interference function, a sine wave whose frequency depends on the motor activity, which eliminates a degree of control that was present with the squared interference. The three interference functions used for these experiments can be seen in Figure 2, and are introduced and explained in more depth in Sections 3.2–3.4, where the corresponding results are also presented.

FIGURE 2

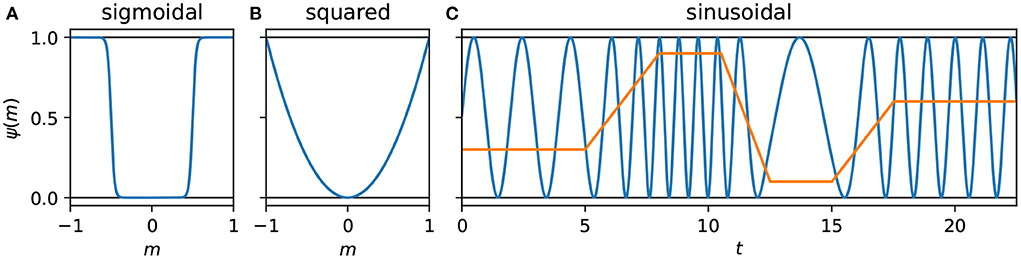
Figure 2. Plots of the interference functions used in Experiments 2–4. (A,B) Plot pure functions of m corresponding to Equations (12) and (13) (Experiments 2 and 3, respectively). (C) Plots a function of time that depends on the cumulative history of m, Equation (14) (Experiment 4). The blue line is the interference, while the orange line is the motor activity.

3.1. Experiment 1: Phototaxis without interference

A highly fit population of controllers was evolved to perform phototaxis in the basic model, with no motor-driven interference. Evolution of this population began from a population of solutions with uniformly random interneuron weight and time constant values, and with center-crossing biases (Mathayomchan and Beer, 2002). A trial duration of 10 time units was used. After evolution, genomes for this population are highly convergent, indicating that the population has become dominated by a single solution. Examining the fittest member of this population, we found that the controller reliably brought the robot close to the light across a collection of light coordinates representative of those used during evolution (Figure 3). The robot's behavior results in it remaining close to the light even over time periods orders of magnitude longer than the trial duration used during evolution. This indicates that the solution produces a long term, stable relationship with the environmental stimulus.

FIGURE 3

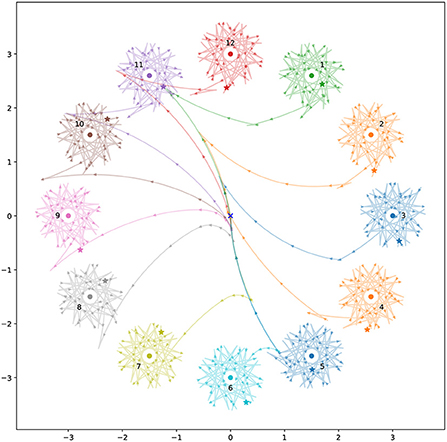
Figure 3. Spatial trajectories for the best individual from the ancestral population for 12 different light coordinates. The robot always begins at the origin, facing toward positive y (upwards). Stars mark the final position reached during the trial duration used during evolution. The colored circles show the light position for the correspondingly colored trajectory. The triangles along the trajectories point in the direction the robot is facing. They are plotted at uniform time intervals, so more spaced out triangles indicate faster movement.

The ancestral solution's behavior is well preserved in the descendent populations evolved to handle the various interference functions studied. Understanding how this solution works is helpful for understanding how the descendent solutions handle motor-driven sensory interference.

The ancestral solution's behavior can be divided into 2 phases:

(A) The approach phase, where the robot makes its way close to the light. This phase has to account for the light starting at an unknown point relative to the robot.

(B) The orbit phase, where the robot's long-term periodic activity maintains a close position to the light.

Note that this two phase description does not imply switching between two different sets of internal rules. These phases are driven by the ongoing relationship between the robot and its environment, and are better thought of in dynamical systems terms as a transient and a periodic attractor.

The orbit phase (Phase B) is simpler to explain, so we will begin with it. Here we can approximate the robot's behavior with a simple program:

1. Approach the light while driving backwards, such that you will pass the light with the light on your right hand side.

2. When the light abruptly enters your field of vision, it causes a spike in your right sensor: quickly respond by switching to driving forwards instead, turning gently to the left.

3. After driving forward has brought the light behind you and out of the sensor's field, go to 1.

We observed this behavior across all the light coordinates we examined. Figure 4 and the corresponding caption explains how this behavior applies to the trajectory for a specific light coordinate, showing how the simple program described above matches its behavior. The left sensor is completely uninvolved in this process. In fact for some initial light positions, namely when the robot begins with the light on its right, the left sensor is also completely uninvolved in the approach phase. That is, if the left sensor is completely deactivated throughout certain trials, the trajectory is completely identical to if it were active.

FIGURE 4

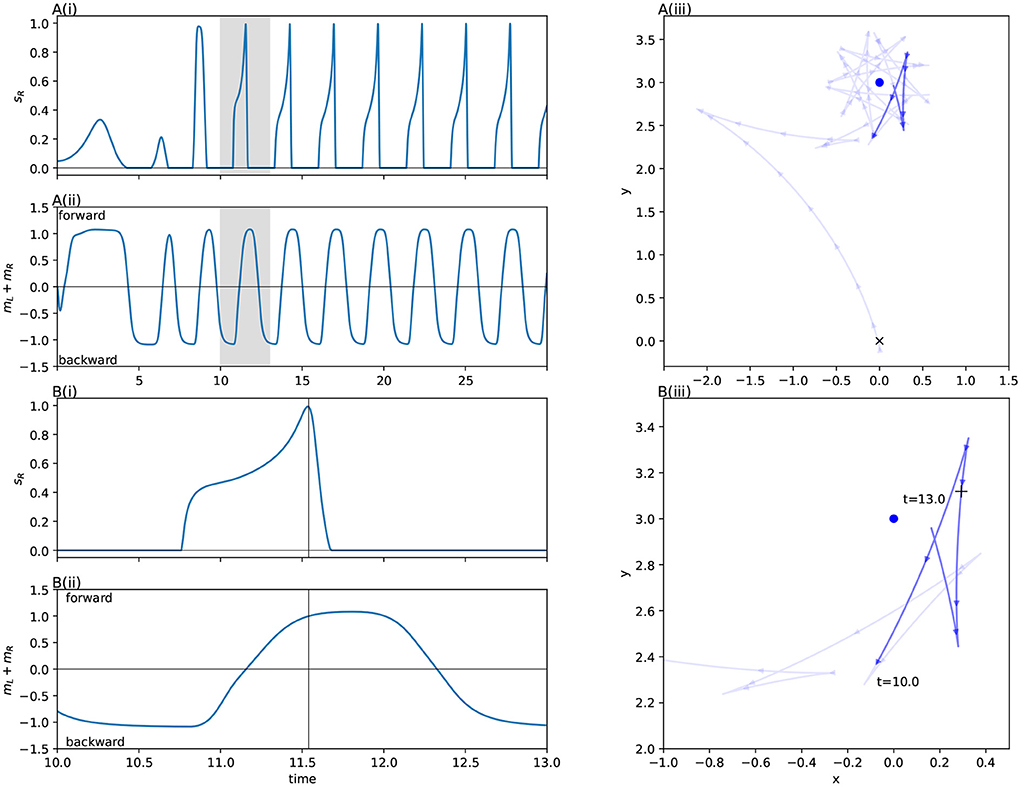
Figure 4. Detail of the orbit phase (Phase B) for the ancestral solution. The plots marked (A) Show the ancestral solution when the light is at coordinates (0, 3)—position 12 in Figure 3. The highlighted sections of these figures mark the time period 10–13, which is shown in more detail in (B). The vertical line in B(i,ii) marks the peak of right sensor activation, which corresponds to the + in B(iii). The activity shown in (B) corresponds to the Phase B program (see main text). Before t = 11, the robot drives backwards, passing the light on its right side. As the right sensor is stimulated, the robot changes direction, driving forwards. After the right sensor stimulation peaks and dies down, the robot changes direction again, reversing toward the light. (A) Show how the process repeats.

The approach phase (Phase A) often consists of simply driving forwards, and then continuing to drive forwards until the right sensor is not stimulated. Thereafter the procedure for Phase B is followed, with the approach differing from the orbit primarily in that the amount of time spent on each step of the ‘program' while approaching the light varies more than it does when the robot is stably orbiting the light. This is what we see in trajectory shown in Figure 4, and in all conditions when the left sensor is not stimulated. However in conditions when the left sensor is stimulated during the approach phase, the left sensor is involved in guiding the robot into a state where Phase B takes over. This can be seen in Figure 5.

FIGURE 5

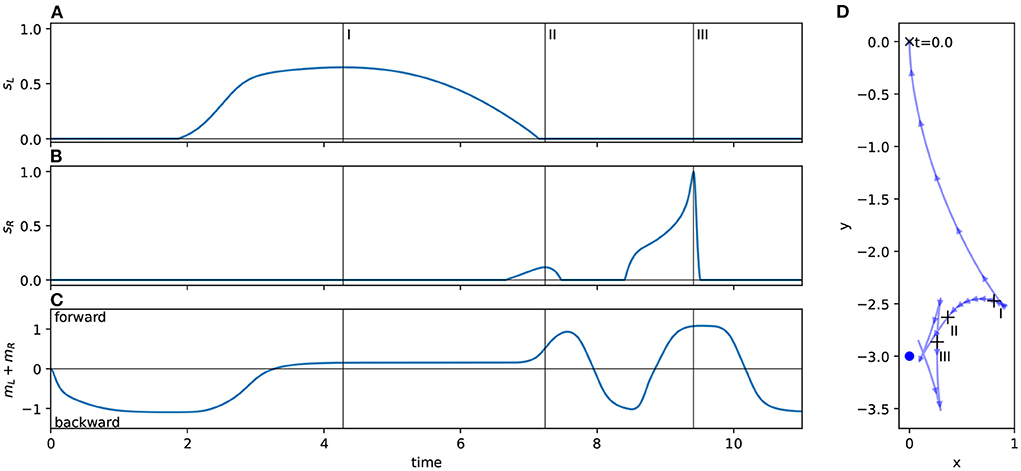
Figure 5. An example approach phase (Phase A) for the ancestral solution which is guided by the left sensor. (A–C) Show the sensorimotor activity of the ancestral solution when the light is at coordinates (0, –3), position 6 in Figure 3. (D) Plots the spatial trajectory of the robot. The vertical lines in plots (A–C) show the peaks in sensor activity. These correspond to the + markers in (D). Initially the robot drives backwards. The left sensor stimulation between t = 2 and t = 8 is associated with the robot to driving forwards while turning strongly to the left. Once this turn has oriented the robot such that the right sensor is being stimulated and the left sensor is no longer being stimulated, the robot drives forward until the right sensor is no longer stimulated. From here, this is just the same Phase B behavior presented in Figure 4.

This solution is an instance of a more general robust strategy for performing phototaxis in this model, which can be summarized even more simply as:

• If you don't see the light, drive backwards (it must be behind you).

• If you do see the light, drive forwards until you can't see it any longer.

The reason this does not result in just driving backwards and forwards along the same arc is that the robot turns a different amount when driving forwards vs. when driving backwards. The turn amount is determined by m_R−m_L, while the direction of travel is determined by whether m_R + m_L is negative or positive. When adjusting motor activity to change directions, it's trivial to also change the amount of turn. Of course this general strategy is not a complete description of the robot's behavior, the effect of sensor stimulation can be time dependent and differ for the left and right sensors. Particularly during Phase A, the approach to the light, the exact trajectories taken by the robot depend on continually regulating the 2 independent motors' speed and direction of activity to perform both gradual turns and sharp changes in direction via 3 point turns with sufficient precision to reliably enter Phase B and maintain it. However, we see this general strategy well preserved in populations descendent from this ancestral population as well as evolved independently in non-descendent populations.

To summarize, the ancestral solution takes advantage of the particular nature of its sensors, driving backwards so that the sensors are stimulated sharply. It adjusts its motor activity in response to this sharp stimulation in such a way that the stimulation is extinguished. This environmentally mediated negative feedback loop plays a critical role in enabling the system to remain stably in close proximity to the light source. Capturing this type of natural feedback loop is a strength of modeling work following the SED approach. In the subsequent sections, we will see the role this pattern of behavior plays in coping with additional self-caused interference, and how this behavior is modified when this population of solutions is taken as the ancestral population for subsequent optimisation via the GA with the addition of motor-driven interference.

3.2. Experiment 2: Avoidable interference

Having evolved a system to perform phototaxis in the absence of directly self-caused sensory stimuli, we take this population of solutions as the ancestral population for subsequent evolution in the presence of motor-driven interference functions to begin investigating how embodied systems can cope with this type of interference. In this section we describe the first form of self-caused sensory interference modeled, and how the ancestral solution is modified to accommodate it.

The simplest possible interference would be adding a constant value to all the sensor inputs. However this would not depend on the system's motor activity. Therefore the first ψ(m) that we model is a threshold-like interference function, where interference is maximized when motor activation is above a threshold value, and ≈ 0 elsewhere. To achieve this effect with a smooth function, we use a relatively steep sigmoidal function, with the equation:

$\begin{array}{ll}\psi (m)=\frac{1}{1+exp(-k(\left|m\right|-p))}& (12)\end{array}$

Where exp(x) = e^x and |m| is the absolute value of m, and where k = 50 is the term controlling the steepness of the sigmoid's transition from 0 to 1, while p = 0.5 determines the midpoint of the transition. So when m < −0.5 or m > 0.5: ψ(m) ≈ 1 and when −0.5 < m < 0.5: ψ(m) ≈ 0. This function is unique among the three in that were the system to constrain its motor activity to the appropriate range, it would avoid the interference altogether. We will refer to the interference generated by this function as avoidable or sigmoidal interference.

With motor activity capped at 50%, motor-driven interference can be avoided, and phototaxis can still be performed, just more slowly. Moving more slowly comes at a cost to fitness though, since the fitness function (Equation 11) rewards reaching the light quickly. Therefore, a predict-and-subtract solution to the interference which preserves the speed of the high-performance ancestral solution should outperform a solution which simply avoids the interference. However, we instead found that the fittest solution from the 5 populations evolved to perform phototaxis with the sigmoidal interference function modifies the motor activity of the ancestral solution significantly.

Figure 6 illustrates how the characteristic motor activity of the solution evolved with sigmoidal interference differs from that of the ancestral solution. Keeping in mind that the ancestral solution often involved minimal environmental stimulation of the left sensor, we observe that the left motor in this evolved solution never produces interference. This comes at the cost of greatly decreased absolute motor activity relative to the ancestral solution. The ancestral solution's left motor activity ranges widely, from –0.96 to 0.10 with a median of –0.82, close to the maximum possible absolute value of 1. See Figure 4A(ii) for ancestral motor activity as a time series. In contrast, the left motor activity of this solution ranges only between –0.42 and –0.32 with a median value of –0.38. Time series of this motor activity can be seen in Figures 8A(iv),B(iv). This drastic decrease in motor activity lowers the speeds attainable by the robot, but prevents motor-driven interference with the left sensor. While the activity of the left motor is kept below the threshold for producing interference at all times, keeping the left sensor free of interference, the right motor does produce interference. The distribution of right motor activity is bimodal, with peaks just below the interference threshold of 0.5, and close to its maximum value of 0.84. This bimodal distribution is the result of this solution producing two distinctly different orbit types.

FIGURE 6

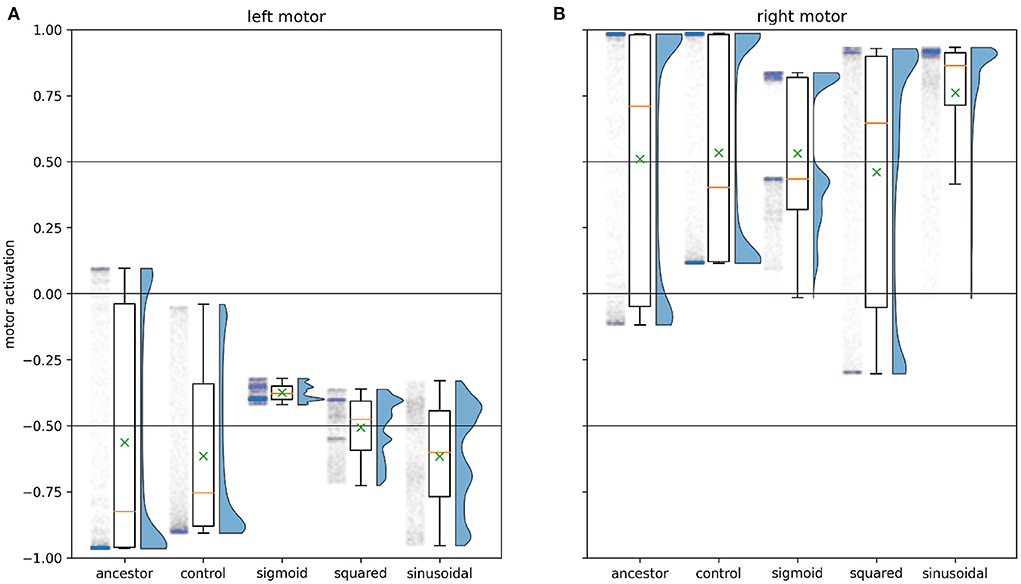
Figure 6. Motor activity for the 12 light positions shown in Figure 3 for time 20 to time 50 (integration steps 2,000–5,000), for the evolved solution to each experiment. This is one way of visualizing aspects of the ancestral behavior that have (and have not) been modified by further evolution in the presence of an interference function. The boxes extend from the first to the third quartile of the motor activity, and contain a yellow line showing the median, and a green × showing the mean. The whiskers extend to 1.5 times the inter-quartile range. The half-violin plot to the right of each box plot estimates the distribution of the motor activity, while to the left is a scatter plot of each simulated moment of motor activity with randomized horizontal placement. The column labeled control plots exactly the same information for the fittest solution evolved with λ = 0.5 and the null interference function ψ(m) = 0, showing the scope of change seen simply due to the presence of λ and to genetic drift. (A) plots the motor activity for the left motor of each system, while (B) plots this information for the right motor. Of particular relevance to the solutions cataloged in this paper are the depressed (absolute) left motor activation with sigmoidal interference and the corresponding bimodal distribution of right motor activity; the reduced range of left motor activity with squared interference, and the fact that the right motor activation with squared interference continues to cover a wide range; and the reduction in low (absolute) values of motor activity with the sinusoidal interference function.

The orbiting behaviors of this system are of interest because they demonstrate ways in which a long term, stable relationship with an environmental source of sensor stimulation can be maintained in a model with motor-driven sensor interference. As with the ancestral population, a trial duration of 10 time units was used for this population. Due to the decreased overall motor activation relative to the ancestor, and the consequently decreased speed, the robot does not get as close to the light in that time as the ancestor did. This means that what has been selected for by the genetic algorithm here is modification of the approach phase to maintain accuracy in the presence of this novel interference. However, due to a sufficiently accurate approach and the evolved regulation of the motor-driven interference, stable orbits are still achieved across all light positions in the very long term. Unlike the ancestor, we see two distinctly different orbit behaviors. Across all interference functions we refer to those orbits reminiscent of the ancestral solution, involving forward and backward motion around the light, as Type 1 orbits, and to orbits which loosely circle the light while driving forwards as Type 2 orbits. These are easily distinguished visually (see Figure 7). As with the ancestor, approaches can broadly be divided into those guided by the left sensor, and those that are not. In the majority of cases for this solution, the approach phase preceding Type 1 orbits is guided exclusively by the right sensor, while Type 2 orbits tend to follow a left sensor guided approach phase.

FIGURE 7

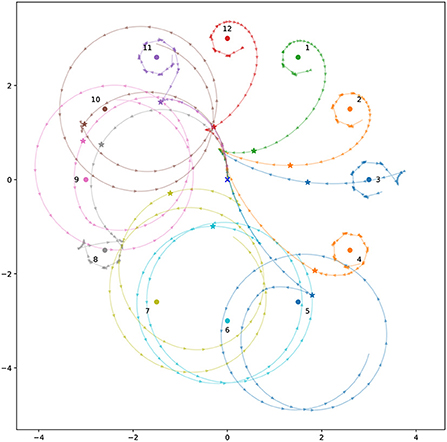
Figure 7. Two distinct types of orbits are visible in the spatial trajectories for the best individual from populations evolved with sigmoidal interference (Equation 12). Type 1 orbits, reminiscent of the ancestral solution, are seen for Lights 11, 12, 1, 2, 3, and 4. Type 2 orbits, which feature a forward moving, counter-clockwise orbit of the light are seen for Lights 5, 6, 7, 9, and 10. For Light 8, an approach typical of a Type 2 orbit instead puts the robot in position for a Type 1 orbit.

Type 1 orbits come much closer to the light. They display similar sensorimotor behavior to the ancestor's orbit behavior (Phase B), maintaining a stable relationship to the light by repeatedly driving backwards and forwards, albeit with greatly reduced motor activity compared to the ancestor. Figure 8A shows a typical example of sensorimotor activity for Type 1 orbits. Right motor-sensor interference is almost entirely avoided. A very low amount (not visible in the figure) coincides with the robot driving forwards slowly. This interference is necessary because the left motor's activity is negative, and is maintained very closely to the threshold for interference, so the right motor's positive activity cannot be raised sufficiently highly to drive forwards without producing at least a small amount of interference. We summarize this orbit strategy as performing the known good ancestral strategy while constraining motor activity to avoid sensor interference.

FIGURE 8

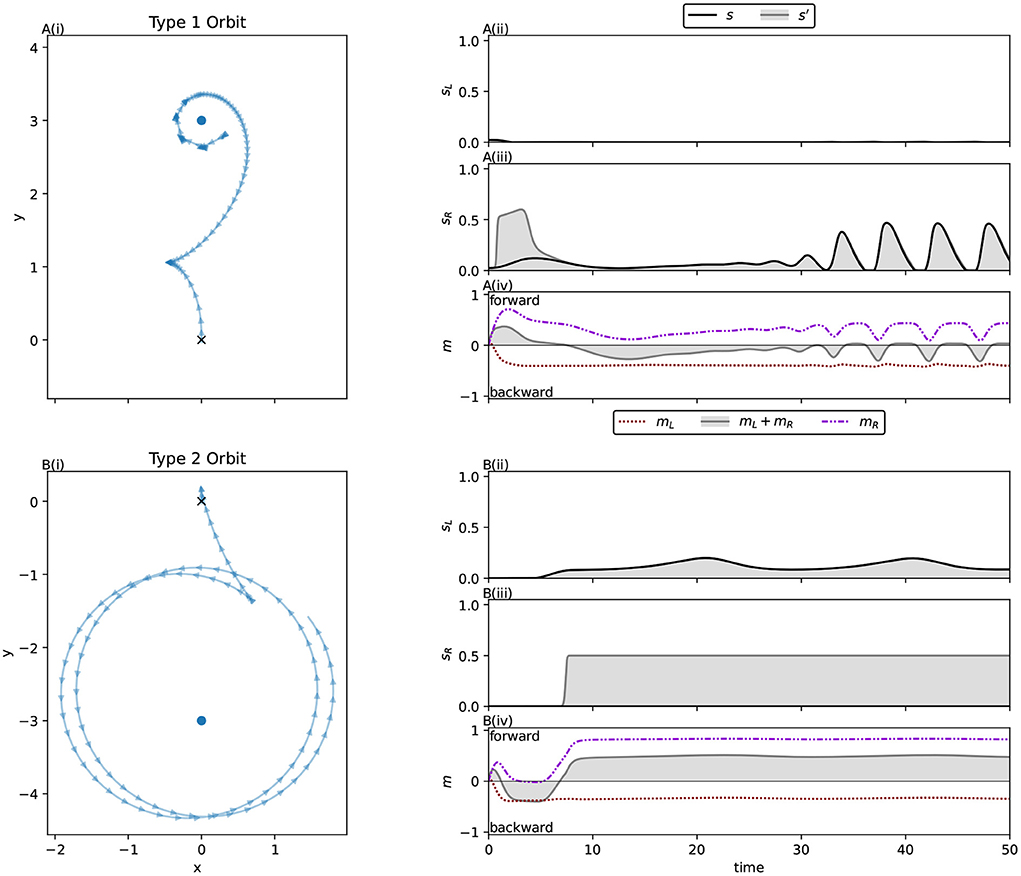
Figure 8. Two distinct orbit types produce the bimodal right motor activity distribution seen for the solution evolved with sigmoidal interference in Figure 6B. (A) The type 1 orbit, which alternates between driving forwards and backwards to stay close to the light. (B) The type 2 orbit, where the robot exclusively drives forwards during the orbit phase. (i) The spatial trajectory of the robots, (ii,iii) the robots left and right sensor activities respectively, and (iv) the robots' left and right motor activations. The black line in (ii,iii) shows the environmental stimulation of the sensor, while the grey line and corresponding shaded region shows the total activation of the sensor when both the environmental and motor-driven stimulation are combined. Note the minimization of interference during the Type 1 orbit, in contrast with high level of right sensor interference during the Type 2 orbit.

Type 2 orbits loosely circle the light, and are very different from the ancestral orbit behavior. Figure 8B shows an example of typical sensorimotor activity for this type of orbit. These orbits do not involve environmental stimulation of the right sensor, instead the left sensor is stimulated throughout the orbit phase. Unlike Type 1 orbits, where the relationship to the light is maintained by repeatedly driving forwards and backwards, the robot exclusively drives forwards. It does so very quickly, producing high right motor-sensor interference. We characterize this orbit strategy as keeping “one eye on the prize,” where the left sensor, facing the light, is kept free of interference. Meanwhile the right sensor, facing away, is continually stimulated by the right motor's activity. This orbit strategy is uniquely enabled by the ipsilateral nature of the motor-driven sensory interference.

In the presence of this threshold based interference, the best solution found by our GA when modifying the ancestral population to accommodate this interference constrains the ancestral solution's motor activity to avoid interference while performing the same function of phototaxis, using (in some situations) the same basic strategy. This approach contrasts with the predict-and-subtract approach of modifying the controller to subtract the anticipated interference from the sensor neurons' outputs, allowing the behavior of the ancestral solution to be performed without modification. This suggests that in our model such solutions are far closer in evolutionary space to the ancestral solution than a predict-and-subtract solution would be. The relevance of this to the evolutionary history of biological control systems is unclear, however it may suggest that adjusting neural activity to accommodate a novel form of motor-driven sensory interference would involve regulation of the behavior producing that interference in addition to or instead of the neural subtraction of internally predicted interference. This demonstrates that behavior modification does indeed work as a solution to motor-driven sensory interference, and that the precise way in which behavior is modified can depend heavily on the particularities of the sensorimotor contingency in question. Specifically we have seen how two ways of compensating for motor-driven sensory interference emerged in our model. Firstly, motor activity may be constrained to ranges that minimize or avoid interference with the sensors. Secondly, interference can be avoided for only one sensor, which is kept trained on relevant environmental stimuli. This permits unconstrained use of motor activity which interferes with the other sensor. While this robot is clearly much simpler than a human, this demonstration of how pre-existing behavior can be modified to avoid the effects of novel, self-produced sensory interference may suggest a role for such solutions in other contexts, such as less complex organisms (including perhaps our deep evolutionary past) and simple robots.

3.3. Experiment 3: Unavoidable interference

Sigmoidal interference certainly does not exhaust the possibilities for modeling interference, nor does it capture the fact that many self-caused stimuli cannot be avoided when taking action. Therefore, we also model non-avoidable interference, where the interference increases with the absolute magnitude of the motor activation. To minimize discontinuities in the system, and to ensure the interference can be approximated by the CTRNN controller, we use a smooth function—the square of the motor activity:

$\begin{array}{ll}\psi (m)=m^2& (13)\end{array}$

We will refer to the interference generated by Equation (13) as unavoidable or squared interference. Like the avoidable, sigmoidal interference function modeled previously, the magnitude of the interference correlates with the magnitude of the motor activity. However, unlike with the avoidable interference function, now all changes in motor activity produce a corresponding change in the sensory interference.

Examining the fittest solution produced by the GA's modification of the ancestral solution, we again find the ancestral solution well preserved. A trial duration of 20 time units was used during evolution to compensate for any decreased speed compared to the ancestor. The general strategy of approaching the light while driving backwards is maintained, however motor activity has changed to accommodate the addition of the squared interference function. The left motor's activity is now constrained to a much smaller range (see Figure 6A), which lowers interference dramatically compared to the interference that would be produced by the ancestral solution's motor activity (see Figure 9A). The right motor generates significant interference, but we find that rather than destructively interfering with the sensor in such a way that the environmental stimulus is masked, this motor-driven sensor stimulation is actually constructive in that it synchronizes with and amplifies the environmental stimulus's effect on the sensor. Figure 6B makes it clear that the right motor's activity has not been lowered or even constrained to a tighter range the way the left motor's has—though we still see a slight reduction in interference compared to what the ancestral solution would produce (see Figure 9B). How the system performs so accurately in the presence of this interference becomes clear when we consider the relationship between the right motor activity and the right sensor. As with the ancestor, the robot approaches the light while driving backwards, in such a way that the light enters the right sensor's field from it's blind spot at very close proximity to the sensor. Figure 10A shows an example of this approach. When the light enters the right sensor's field, its activation immediately spikes. In response, the right motor's activity also spikes, causing the robot to drive forwards, and also causing a spike of interference in the same sensor. This is a version of the ancestral Phase B orbit behavior, executed with reduced baseline motor activity, and high right motor activity coordinated with right sensor stimulation. By keeping motor activity at a low baseline and interacting with the environment in such a way that environmental stimuli are sharp and intense, this solution facilitates distinguishing environmental stimuli from low levels of self-caused background noise. By then coordinating motor activity with elevated environmental stimulation of the ipsilateral sensor, motor-driven interference can be raised to high levels without interfering with the system's function, “hiding” in the shadow of the environmental stimulus. Not only does this activity not interfere with perception of the environment, the stimulation caused by right motor's activity actually reinforces and amplifies the environmental stimulus's effect on the sensor above the maximum level it would be able to achieve on its own.

FIGURE 9

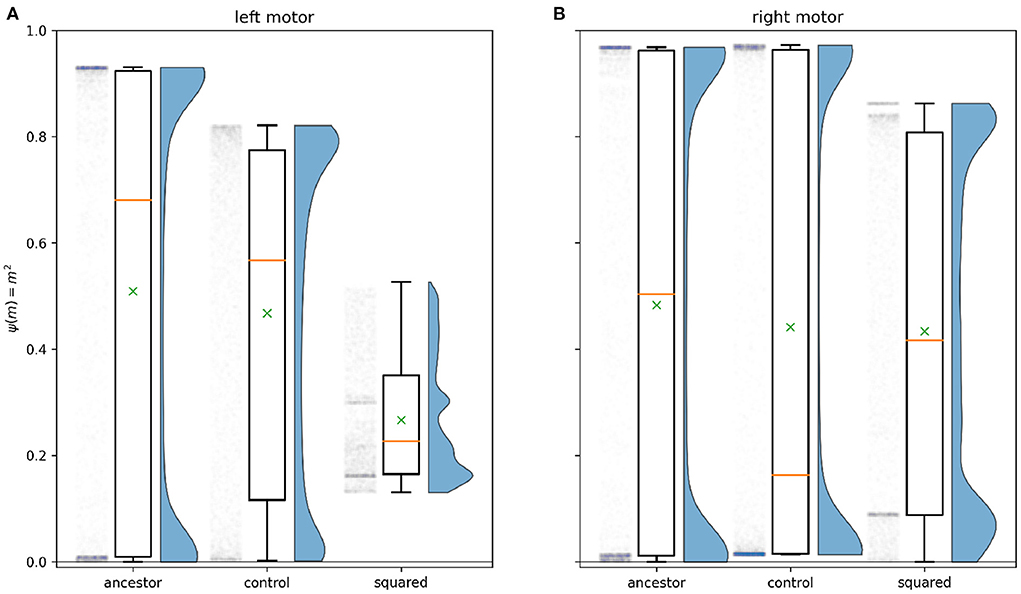
Figure 9. Motor-driven interference is reduced in Experiment 2 relative to the ancestral population. The figure shows ψ(m) = m² for the 12 light coordinates shown in Figure 3, for 20 < t < 50. (A) Note primarily the lowered mean, median and maximum interference with the left motor. Despite the right motor's activity being spread across a wider range than either ancestor or control (see Figure 6), this spread is to low motor activity values, decreasing maximum right motor-sensor interference. (B) However, the right motor activity has definitely not been suppressed the way the left has, and the systems successful performance in the presence of this interference ultimately depends on the coordination of right motor-sensor interference with environmental stimulation of the right sensor (see main text).

FIGURE 10

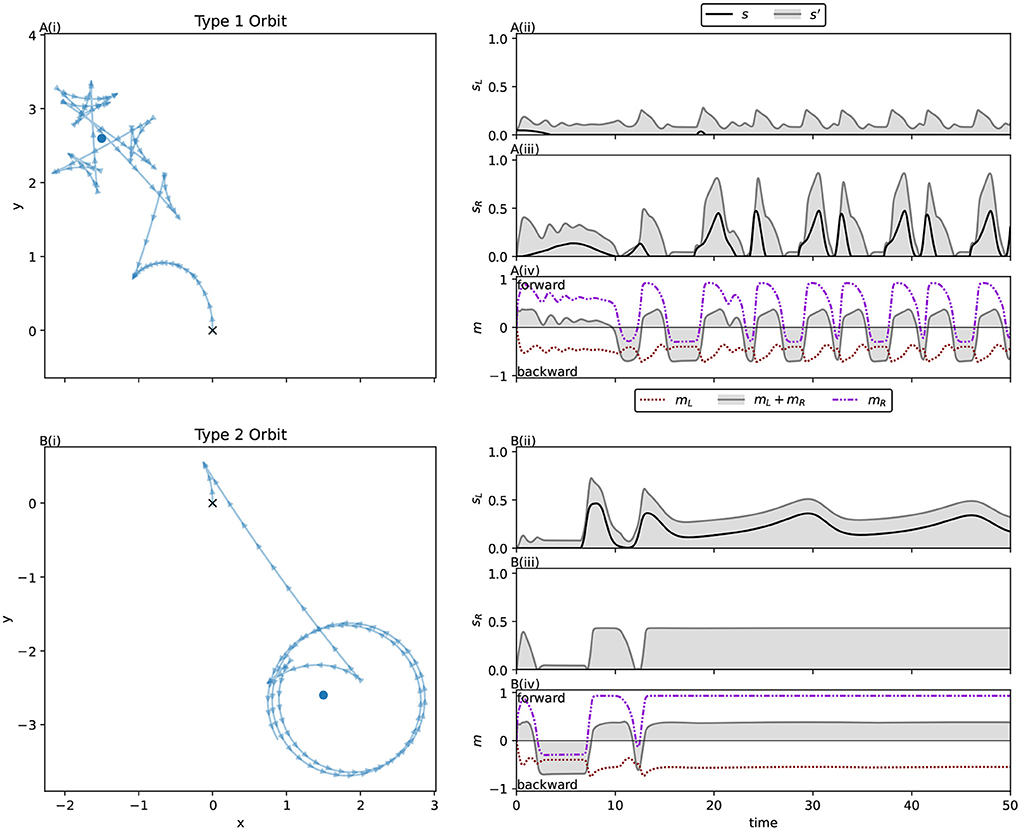
Figure 10. Spatial trajectories and sensorimotor activity showing a Type 1 and Type 2 orbit for the solution evolved with squared interference. Subfigures are labeled as in Figure 8. (A) Shows a Type 1 orbit reminiscent of the ancestral solution, where motor activity is coordinated with sharp spikes of environmental stimulation of the right sensor. A(iii) Shows how elevated right motor interference coincides with environmental right sensor stimulation, amplifying it. The spiking activity is characteristic of negative feedback in this solution, where action resulting from sensor stimulation leads to the stimulus diminishing. (B) Shows a Type 2 orbit, where the robot orbits while driving forwards. B(iv) Shows how the motor activity plateaus during the orbit, with high right motor interference seen in B(iii). This is associated with positive feedback in this solution, where sensor stimulation leads to activity prolonging that stimulation.

Since right sensor stimulation leads to right motor activity, which in turn leads to more right sensor stimulation, we should address the possibility of a self-sustaining positive feedback loop. This possibility is limited by two forms of negative feedback. The system's relationship to the light source is structured in such a way that elevated right motor activity in response to the environmental stimulus moves the right sensor away from the light, eliminating that stimulus. This is environmentally mediated negative feedback. It is complimented by internal negative feedback. Figure 11A shows how a spike in right sensor stimulation causes an initial strong response in motor activity. However, despite continued stimulation at an elevated level, sufficient to saturate the output of the sensor neuron, motor activity quickly falls from the initial peak. Thus, both internal and environmentally mediated negative feedback play a role in preventing this orbit behavior from being disrupted by motor-driven positive feedback.

FIGURE 11

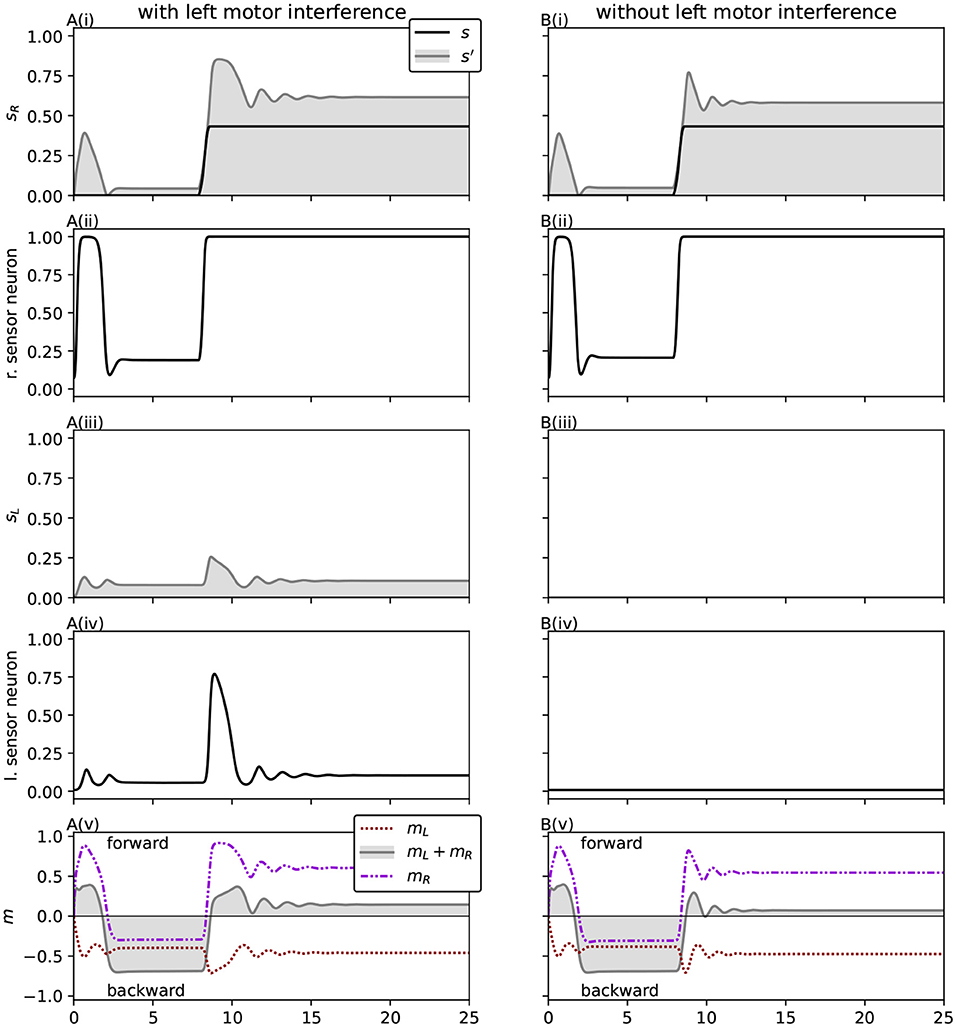
Figure 11. The magnitude and duration of the initial motor response to sensor stimuli are strengthened by the presence of left motor interference. Sensorimotor activity and sensory neuron output time series are shown for the solution evolved with squared interference (Equation 13), when the right sensor is presented with an artificial environmental stimulus, which spikes and plateaus around t = 8. (A) Shows the response under the condition of evolutionary adaptation for the robot, with motor interference present. (B) Shows the response when the left motor-sensor interference is removed. The duration and intensity of the motor response to the stimulus is diminished without the interference, indicating that the interference plays a functional role in the evolved behavior. Additionally, it can be seen that the response to sudden right sensor stimulation is accompanied by internal negative feedback—even when the stimulation persists, motor activity quickly falls from the initial peak.

As we also saw with sigmoidal interference, this solution realizes a second orbit pattern of Type 2. Positive rather than negative feedback plays a dominant role in this orbit, which comes into effect when the robot is close to the light, but the light is on its left (see Figure 10B). The system's response to left sensor stimulation does not feature the internal negative feedback that right sensor stimulation does, and it produces a response in both right and left motor activity. This in turn produces interference in both sensors. The ultimate effect is that the robot drives forwards in a counter-clockwise orbit around the light. This keeps the left sensor continually stimulated by the light, while the right sensor is continually stimulated by the right motor's activity. In this case we have an environmentally mediated, positive feedback loop, where left sensor stimulation causes the robot to turn toward that stimulus, and the resulting motor-sensor interference produces the same effect.

The way this system has been parametrized by the GA relies on the presence of motor-driven stimulation to perform phototaxis. Recall that the ancestor evolved to have zero left sensor activation in many situations, with a left sensor guided approach phase (Phase A) for a number of initial light positions. This trait remains in a way, where the left sensor is often completely free of environmental stimulation, and the left motor activity is constrained to produce lower levels of interference. Nevertheless, this interference plays an important role. Figure 12 illustrates how removing the motor-driven sensor stimulation from just the left sensor causes the approach phase to fail in the majority of cases, succeeding only when its trajectory inadvertently brings it close to the light. This is not unexpected, given that the system was optimized for the presence of motor-driven interference. However, it means that accurate control of the system's motor activity has been optimized in such a way that it now depends on perceiving the direct sensory effects of its own activity. Like the right motor, the left motor responds to sensor stimuli, though in a smaller range and with elevated negative rather than positive activation. This plays an interesting role in the system's response to right sensor stimulation (as in the Type 1 orbit shown in Figure 10A). Note how the coordinated peaks of right environmental and motor-driven sensor stimulation coincide with elevated left motor activity and corresponding motor-driven left sensor stimulation. Figure 11 shows how the presence of left motor-sensor interference amplifies and extends the initial motor activity response to right sensor stimulation. This demonstrates not only a specific way in which the system has been optimized for the presence of interference, but also how self-caused stimuli can play a directly functional role in behavior.

FIGURE 12

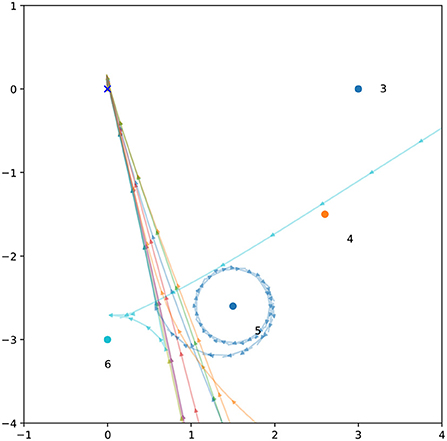
Figure 12. When motor-driven interference is removed, the behavior evolved with squared interference fails. Spatial trajectories for 12 light coordinates (Figure 3) are plotted with all motor-sensor interference removed. The approach phase now only succeeds in two out of 12 cases, where the blind approach brings the robot close to the light. The orbit phase only succeeds in one of these two cases.

To summarize, we see the ancestral strategy is well preserved in this evolved solution. This solution can be characterized as minimizing interference to an extent, as we also saw in the case of sigmoidal interference. We also see a condition where motor-driven sensor interference does not need to be minimized, namely when it can be made to coincide temporally with environmental stimulation of the same sensor. Here the onset of the environmental stimulus prompts the interfering motor activity, and a combination of internal and environmentally mediated negative feedback extinguishes both interfering activity and stimulus. In this case the motor-driven stimulation does not interfere with perception of the environmental stimulus, instead reinforcing and amplifying it. This obviates the need to distinguish or subtract the self-caused stimulus from the environmental. Separately, we also see that a stable, periodic orbit phase can be facilitated by positive feedback. Finally, we found that while left motor-sensor interference is confined to a narrow range, the system has been optimized to rely on its presence and even incorporate it functionally.

3.4. Experiment 4: Time dependent interference

With both of the preceding interference functions, if the motor activity is held constant, then the interference will also take on a constant value. Since the interference is additive and non-saturating, subtracting a constant term can remove the interference and leave only the environmental signal—no prediction required. In general a CTRNN with a sufficiently high bias β for the input neurons can do this, though in our case the maximum value we permit the GA to assign to β is too low to fully compensate for maximal interference. Nevertheless, solutions to the previous two interference functions have shown both the utility of avoiding or minimizing motor-sensor interference, as well as the role that holding motor activity and its corresponding interference constant can have in constructing long-term stable relationships with environmental sources of sensor stimulation. With the following function it is not possible for the interference to plateau at a constant value. It describes a sine wave with a maximum of 1 and a minimum of 0, whose frequency is determined by the motor activation:

$\begin{array}{ll}\hfill \psi =\frac{sin(c)+1}{2}& (14)\end{array}$

$\begin{array}{ll}\stackrel{·}{c}=(b+\left|m\right|)r& (15)\end{array}$

Here c gives the phase of the sinusoidal, capturing the previous values of m. b = 0.1 determines the base frequency of the sinusoidal in the absence of any motor activity, while r = 8 is the frequency range term determining the maximum frequency the sinusoidal can reach. The effect of adding 1 and dividing by 2 is simply to shift the wave from the range [−1, 1] to the range [0, 1]. This equation essentially advances through a standard sine wave at a rate determined by the motor activity. As with the previous interference functions, the interference for a given sensor is calculated from the ipsilateral motor, such that when computing the interference for the left sensor we have m = m_L, and for the right sensor m = m_R.

Unlike the previous interference functions, this is not purely a function of the motor activity, such that if you know m at time t, you know ψ at time t. Instead it is a function of time, depending on the prior history of the system, specifically on all the previous motor activity up to the current time. More importantly for our purposes, if the input is held constant, the output continues to vary over time. We will refer to the interference generated by Equation (14) as time dependent or sinusoidal interference. A trial duration of 20 time units was used during evolution for this interference function.

Using this time dependent interference function we find that while avoiding interference, minimizing it, or holding it constant are all important ways of coping with self-caused stimuli, they are not the only ways. Timescale differences between the frequency of the motor-driven interference and the frequency of environmental stimulation of the sensor can be exploited to distinguish the two, and behavior can shape both interference and environmental stimuli to amplify these differences.

In this system the environmental signal is able to be detected despite the presence of interference, due to differences in timescale between the motor-driven interference and the frequency of environmental stimulation of the sensors. First let's demonstrate that the system actually can respond to environmental stimuli. Figure 13 illustrates how a spike in environmental stimulation of the left sensor has an excitatory effect on both motors, causing the system to switch from driving backwards to driving forwards. Observing the behavior of the output functions of this system's two sensor neurons, we found elevated neural biases β compared to the ancestral solution: remembering that −5 ≤ β ≤ 5, we observe 4.67 and 3.73 for the left and right motor, respectively, compared to –0.75 and 0.99 in the ancestral solution. These sensor neuron biases are calibrated such that (A) with no environmental stimulation, the neuron's output function is maximized only with the peaks of the sinusoidal interference, and (B) when combined with sufficient environmental stimulation, the troughs of the sinusoidal interference are high enough that the output function is maximized continually. This can be seen in the neural response to environmental stimulation shown in Figure 13B. This makes the environmental signal detectable despite the continuously varying interference. This solution is made possible by the large difference in timescale between the frequency of the sinusoidal interference and the frequency with which the sensor receives the environmental stimulation. In this system, the frequency of the interference can be an order of magnitude higher than the frequency of environmental stimulation, as can be seen in Figure 14. This difference in timescale means that the minimum value of the sinusoidal interference is bound to coincide multiple times with each period where there is no environmental sensor stimulation. This means that a drop in neuron firing always coincides with the absence of environmental sensor stimulation, so over time the system can reliably respond to environmental stimuli.

FIGURE 13

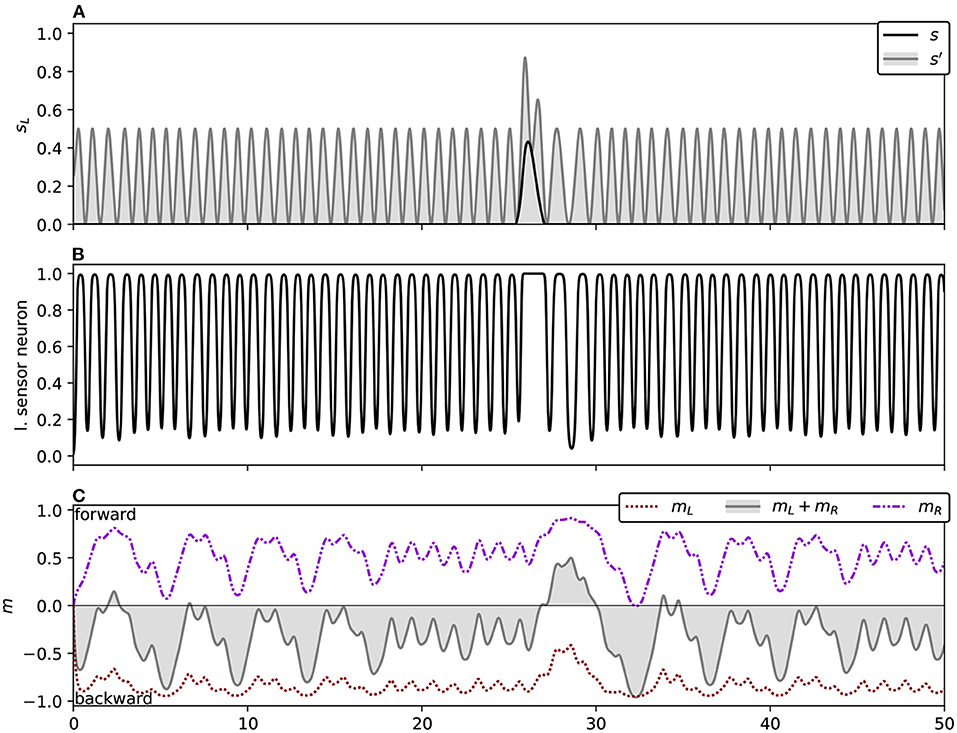
Figure 13. Sensorimotor activity and sensory neuron output time series are shown for the solution evolved with sinusoidal interference (Equation 14), (A) The left sensor is presented with a spike in environmental stimulation at around t = 28. (B) The neural response to the environmental stimulus is clearly visible—prolonged saturation of the left sensor neuron's output function (see Equation 5). (C) The spike of environmental sensor stimulation causes the robot to drive forward instead of backwards for a time, demonstrating that the system can respond to environmental stimuli.

FIGURE 14

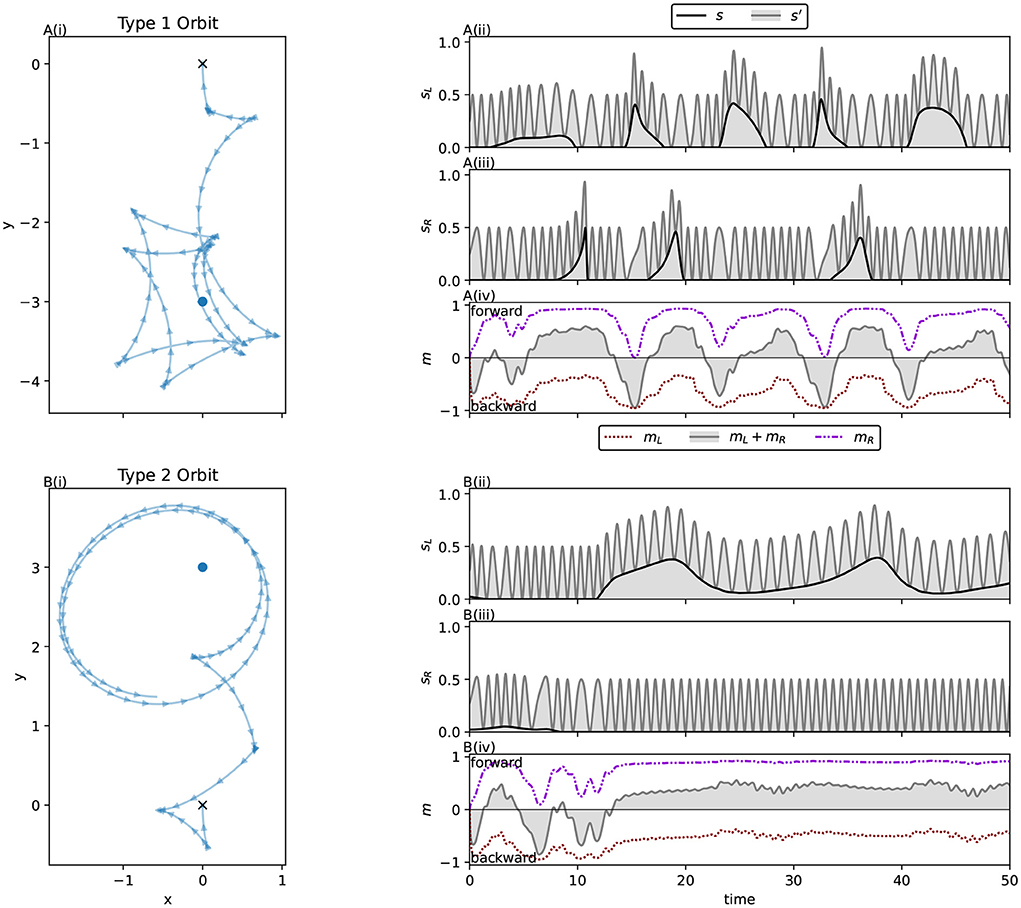
Figure 14. Spatial trajectories and sensorimotor activity for the solution evolved with squared interference. Subfigures are labeled as in Figure 8. The sensor plots show how the relatively slowly changing environmental sensor stimulation raises the minima of the high frequency interference, allowing the environmental stimulus to be responded to despite the interference. The difference in timescale that makes this possible is clearly visible here. Responsiveness to the environment is most clearly visible in A(iv), where more positive motor activity is associated with environmental stimulation of the left or right sensor. The continual oscillations in motor activity (most clearly visible in the gray net motor activity line) are driven by the high frequency interference. These oscillations produce the elliptical Type 2 orbit seen in B(i).

While the evolution of our model was constrained in such a way that it could not implement it, there is another solution for filtering out interference of a sufficiently high timescale relative to the frequency of environmental sensor stimulation that peak interference is guaranteed to coincide with all instances of environmental stimulation. The maximum bias of nodes in our model was constrained to the maximum weight of a single incoming connection (5), which is lower than the product of the environmental intensity factor with the input scaling factor applied to inputs to the sensor neurons (5 × 5 = 25). However, a sufficiently high bias (around 12) can indeed induce the sensor neurons' output function to only be maximized when environmental stimulation is high.

These two ways of adjusting the neural biases demonstrate how a large difference in timescale between environmental signal and interference means that over time it is possible to extract the environmental signal from the summation of the two. However, such differences in timescale are not guaranteed, and it is here that the embodied nature of this system comes into play. The robot's motor activity actually amplifies any pre-existing difference in timescale, as typical motor activity is constrained to higher absolute ranges than the ancestral solution—see Figure 6.

Due to the way this time dependent interference periodically saturates the input neurons, the system is not sensitive to environmental stimuli spikes that are of sufficiently low duration to perfectly coincide with motor interference peaks as the corresponding input neuron's output function would already be saturated. Note that spikes of this duration do reliably induce a motor response in the other systems we've examined in this paper. This represents a problem for the ancestral solution's strategy of taking advantage of sharp spikes in the right sensor. Significantly—and despite the system's elevated right motor activity—this system's Type 1 orbit is much slower than the ancestor's, with the periods of environmental stimulation of the sensor lasting for longer. This avoids the problem of the environmental stimulus being too short duration, and further amplifies the differences in time scale. So when it comes to distinguishing environmental and self-caused stimuli, the motor activity of the system not only shapes the self-caused stimuli to facilitate this, it shapes the environmental stimuli too.

As with the unavoidable squared interference, the behavior of this system depends on the presence of its motor-driven interference. For example, with the left motor-sensor interference removed, environmental stimulation of the left sensor inhibits rather than excites the activation of both motors. Significantly, in the absence of environmental stimulation, the motor activity and corresponding interference of this system features a long transient before settling into lower magnitude oscillations, and this transient is restarted by environmental sensor stimulation. This effect can be seen in Figure 13. These prolonged effects of momentary environmental stimulation are not seen in the systems examined in Experiments 1–3. They mean that the frequency of the motor-driven interference varies significantly both during the approach to the light and during Type 1 orbits. Altogether these qualities demonstrate that the evolved behavior of this system depends on its motor-driven interference, emphasizing that even interference as seemingly unruly as this can be incorporated into successful behavior.

To summarize, this system has the ability to respond to environmental stimuli despite continually varying sinusoidal interference. Rather than subtracting out the motor-driven interference, the behavior of the system is deeply entangled with it, displaying oscillatory motor activity driven by the interference and prolonged transient motor activity following activation of the motors in response to stimuli. Additionally, whether an environmental stimulus is excitatory or inhibitory depends, respectively on the presence or absence of motor-driven sensor stimulation. This demonstrates that rather than suppressing self-caused stimuli, proper functioning for some systems relies on the presence of self-caused stimuli. In this system we see responsiveness to the environment facilitated by a fixed solution that is implemented at the evolutionary timescale, rather than prediction and subtraction of self-caused stimuli on the timescale of actions. Because of the difference in timescale between the frequency of the sinusoidal interference and the frequency of environmental stimulation, a CTRNN neuron can be parametrized such that the maximization of its output function only coincides with environmental sensor stimulation, or such that the minimization of its output function only coincides with the absence of such stimulation. Most significantly for the role of embodiment in coping with self-caused sensory stimuli, we see that this difference in time scale between motor-driven and environmental sensor stimulation is amplified by the system's behavior, which both elevates the frequency of motor-driven sensory stimulation and lowers the frequency of environmental sensor stimulation.

4. Discussion

One explanation of the sensory attenuation effect is that self-caused sensory stimuli are predicted internally using a copy of the relevant neural outputs, and then subtracted out of the sensory inputs (Wolpert et al., 1995; Miall and Wolpert, 1996; Roussel et al., 2013; Klaffehn et al., 2019). This may well be the case, but even in a model where this predict-and-subtract mechanism would be a perfect solution, our GA instead found other viable alternatives. We have shown that a neural network controller can be successfully adapted to handle several different forms of motor-driven sensory interference, and significantly, the adaptations we have cataloged here do not rely on predicting this interference. We now summarize these adaptations.

Avoidance: When self-caused sensory interference is only triggered by certain motor outputs, and if the task at hand can be accomplished while avoiding those outputs, it may be easiest for a control system to simply modify its behavior to avoid motor-sensor interference. We saw this emerge when our model was evolved with sigmoidal interference. It is not clear whether we should expect this avoidance approach to scale well to a more numerous and complex arrangement of sensors and motors, though it seems that the problem of prediction would also become more complex in such circumstances. In the special case where there are multiple independent sensors and motors, where each motor interferes with only one sensor, an alternative solution is possible. If the task can be accomplished using only one sensor, then only one source of interference needs to be regulated. Doing so permits the other motors to operate freely over a wider range of activity. We describe this strategy as “keeping one eye on the prize”. This is arguably just avoiding the interference, with extra steps. We again saw this strategy used in the case of sigmoidal interference.

Where interference is unavoidable but the magnitude of the interference does depend on motor activity, motor activity can be constrained to ranges that limit the quantity of interference, reducing its magnitude relative to environmental stimuli. This is used in the case of the unavoidable squared interference.

Minimization and avoidance could be seen as special cases of causing the interference to plateau at a constant value. If interference is additive and non-saturating, as it is in our model, it can be eliminated by simply subtracting a constant term from the input. In general this is trivial for a CTRNN. However even without subtracting the interference out directly, constant interference just shifts an environmental stimulus's contribution to the sensor to a higher range, which does not actually change the information available when the interference is non-saturating.

Coordination: The timing of motor-driven interference with a sensor may be regulated to coincide with environmental stimulation of that same sensor. One way to look at this is that the detection of a sufficiently ‘loud' environmental stimulus renders any coincident interference irrelevant. With a one dimensional sensor like those used in this model, the interference is actually constructive, that is the coincidence of motor-driven and environmental stimuli amplifies the effect of the environmental stimulus on the sensor. If the response to such a stimulus tends to diminish that stimulus (negative feedback), as we see when stimulation of the sensor causes the robot to turn away from the light, then this strategy of coordination can play a powerful role in establishing a stable relationship with environmental stimuli. This can be effectively combined with a strategy of avoiding or minimizing interference, which we saw with the squared interference function. The constructive interference we saw here may not be possible with more complex collections of sensors, where environmental and self-caused stimulation do not interact as straightforwardly as in our model. This is not to say that non-predictive, embodied solutions would not be found in such situations. On the contrary, discovering solutions afforded by richer embodiments may be a fruitful avenue for future work.

Time scale differences: The previous solutions don't work for interference which is continually varying in such a manner that the interference's minima and maxima are not under direct control of the motors. However, if such interference is of a high enough frequency relative to the frequency of environmental sensor stimulation, then this difference in time scale can be leveraged to separate interference from environmental stimuli. Slowly varying stimuli can be perceived through quickly varying interference, which we saw with the sinusoidal interference function. The evolved behavior we saw with this interference function elevated the frequency of motor-driven stimulation further, amplifying this differential.

Shaping environmental stimuli: Time scale differences are a case of natural differences between the characteristics of the interference and the environmental stimuli. So far we've described how the system can shape the interference to minimize its negative effects or make it easier to distinguish from the environmental stimuli. However, the ancestral solution demonstrates that the shape that environmental sensor stimulation takes depends on the system's activity—sharp spikes in sensor stimulation are produced by passing close to the light while driving backwards. With the sinusoidal interference function, we found that sharp spikes could be lost in the high frequency interference, and that in addition to the system's behavior raising the frequency of the motor-driven interference, its behavior also lowered the frequency of environmental stimulation. Embodied systems can reliably respond differently to environmentally and self-caused stimuli because the characteristics of both forms of stimuli are at least partially determined by the system's own activity.

Removing motor-driven interference from a system optimized to perform a task in the presence of that interference does not necessarily improve performance, and may instead degrade it significantly. Instead the successful phototactic behavior of the systems we've studied often incorporates interference functionally. Coordination of interference with environmental sensor stimulation is one case of this, where the coordination amplifies the stimulus, but we also saw how the response to environmental stimulation of one sensor can be mediated by motor-driven stimulation of the contralateral sensor. This suggests that it is a mistake to view the problem of coping with self-caused sensory stimuli as primarily about subtracting out the interference—even viewing it in terms of perceiving the environment clearly despite the interference may be going too far. It's natural to think of the phototaxis task this way, but the evolutionary algorithm we used selected purely for phototactic ability, and as we've seen this can involve incorporating motor-driven interference into behavior. Despite our attempt to set up a model and problem where sensory attenuation is a perfect solution, the solutions cataloged here for coping with self-caused sensory interference do not align with the sensory attenuation phenomena that has been studied experimentally (e.g., Pareés et al., 2014), raising the broad question of what conditions would lead to sensory attenuation emerging.

This all reinforces that prediction and subtraction cannot tell the whole story when it comes to coping with self-caused sensory stimuli. In some ways this is obvious, as self-caused sensory stimuli are involved in a range of activities in which they do not play an interfering role. For example, the sensation of self-touch when kneading an aching muscle, or occlusion of the visual field when engaging in visually guided reaching and grasping. In these activities, self-caused sensory stimuli are actually desirable. Nevertheless, our model shows that even in situations where clear perception of the environment is prima facie desirable, self-caused sensory stimuli may not play an entirely interfering role. Furthermore, we see that even when responsiveness to the environment is needed, prediction and subtraction are not the only game in town.

How do these results actually relate to the predictive account of coping with self-caused stimuli? A criticism of our results may be that the problems being solved in our model are insufficiently “representation-hungry” to require prediction. Representation-hungry problems are those that seem to require the use of internal representations to be solved, defined by Clark and Toribio (1994) to be a problem where one or both of the following conditions hold. Condition one is that the problem involves reasoning about absent, non-existent, or counterfactual states of affairs. Condition two is that the problem demands selective sensitivity to parameters whose sensory manifestations are “complex and unruly” - that is, the system must be able to treat differently inputs whose sensory manifestations are highly similar, and conversely be able to treat similarly inputs whose sensory manifestations are very different. We actually agree that our model does not solve a representation-hungry problem, and in fact see this is a primary contribution of our results. In general, coping with self-caused sensory stimuli need not be a representation-hungry problem.

How we process self-caused stimuli is often taken to involve an internal predictive model (e.g., Roussel et al., 2013; Klaffehn et al., 2019). Prediction itself is a task which meets Clark and Toribo's first condition, since prediction inherently involves states of affairs that do not yet exist. However, the fundamental problem the predictive model is being used to solve meets only the second criteria, that is treating differently self-caused and externally-caused inputs whose sensory manifestations may be identical. Otherwise identical inputs can be distinguished by predicting, based on an internal model, whether an input is self-caused or externally-caused. If prediction is necessary then the problem of coping with self-caused stimuli would seem to meet the criteria for representation-hunger.

The way self-caused stimuli have been studied experimentally highlights what we see as a key limitation of the representational paradigm. Experiments such as force matching (intentionally and justifiably) aim to isolate specific psychological phenomena and neural mechanisms. We would like to suggest that doing so may naturally lead to overemphasizing the role of these studied mechanisms when extrapolating explanations back from the experiment to real world behavior. Specifically, a limitation of the force matching experiment is the highly constrained motor outputs of the subject—the subject is responding to one specific stimulus (force applied to a finger) with a very limited range of motor outputs, either pressing on that finger or moving a mechanism with their other hand (Pareés et al., 2014). In contrast, coping with analogous perceptual problems in the “real world” might tend to take advantage of their less constrained sensorimotor coupling with the environment—but this wouldn't show up in force matching experiments. This is not a criticism of the experiments, but we do suggest that evolutionary robotics models like this one can help highlight that behaviors depending on a more dynamical, ongoing, and open ended context may play important roles in problem-solving, which may not manifest clearly in the deliberately restricted range of sensorimotor interactions possible in tightly controlled experiments. Under laboratory conditions, a strict interpretation of Clark and Toribio's second criteria may hold—where self-caused and externally-caused stimuli are identical to the extent that only knowledge over and above their sensory manifestations can distinguish them. However, the everyday problem of coping with self-caused sensory stimuli occurs outside the lab, where these stimuli are part of our ongoing sensorimotor activity. In this case our model has shown that there are diverse ways to perform successfully and even to disentangle self-caused and externally-caused stimuli. A key part of this is that both types of stimuli are shaped by our own activity, and thus encountered on our own terms. In these circumstances, the strict definition is unlikely to hold, as we can shape both self and externally caused stimuli to differentiate them.

While the problem of distinguishing truly identical sensory inputs may well be representation-hungry, our model's embodiment allows it to shape its inputs such that they are distinguishable by non-predictive means. Thus, we grant that our model does not capture a strictly representation-hungry problem, a conclusion directly supported by our results. This is a not a limitation of this study, it's a feature. Our model shows that representational cognition is not necessary in general to cope with self-caused stimuli, because of the capabilities afforded by embodiment. In effect, this shrinks the set of human capabilities which are taken to require representational cognition.

The idea of representation-hunger highlights a long running critique of embodied cognition, where solving tasks in representation-free, embodied ways aren't considered central examples of what we really mean by cognition. A distinction is drawn between tasks solvable via online and potentially representation-free sensorimotor processing, and offline cognition operating on internal, representational models (Zahnoun, 2019). It is worth noting that similarly minimal, CTRNN controlled models have successfully solved problems with requirements like memory without the use of internal representations. Beer and Williams (2015) demonstrate how a robot can both remember a cue and categorize a subsequent probe relative to that cue by offloading memory to the environment and structuring its relationship with its environment to facilitate direct perception on the relative difference between cue and probe. It was only when the robot's ability to move while being presented with the cue was removed that information about the cue was retained internally in the neural activation. Studies like this push back at the idea that internal representation is necessary to solve problems requiring responses to abstract or absent stimuli, by showing that other possibilities are facilitated by the way embodiment structures the ongoing relationship between controller and environment.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JG and ME conceived of the idea for this project together. JG wrote the code, ran the experiments, analyzed the data, produced the figures, and wrote the manuscript. ME provided feedback on the experiments and on multiple drafts of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by a University of Auckland Doctoral Scholarship. OAP fees were funded by the School of Computer Science, University of Auckland.

Acknowledgments

The authors wish to acknowledge the use of New Zealand eScience Infrastructure (NeSI) high performance computing facilities, consulting support and/or training services as part of this research. New Zealand's national facilities are provided by NeSI and funded jointly by NeSI's collaborator institutions and through the Ministry of Business, Innovation & Employment's Research Infrastructure programme. URL https://www.nesi.org.nz. Figures were produced with Matplotlib (Hunter, 2007). The idea for the rain-cloud presentation of the data used in Figure 6 is due to Allen et al. (2019). An extended abstract summarizing parts of this work was presented at the ALIFE 2022 conference (Garner and Egbert, 2022).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, M., Poggiali, D., Whitaker, K., Marshall, T. R., and Kievit, R. A. (2019). Raincloud plots: a multi-platform tool for robust data visualization. Wellcome Open Res. 4, 63. doi: 10.12688/wellcomeopenres.15191.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bays, P. M., Wolpert, D. M., and Flanagan, J. R. (2005). Perception of the consequences of self-action is temporally tuned and event driven. Curr. Biol. 15, 1125–1128. doi: 10.1016/j.cub.2005.05.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Beer, R. D. (1996). “Toward the evolution of dynamical neural networks for minimally cognitive behavior,” in From Animals to Animats 4: Proceedings of the Fourth International Conference on Simulation of Adaptive Behavior, eds P. Maes, M. Mataric, J. Meyer, J. Pollack, and S. Wilson (MIT Press), 421–429.

Google Scholar

Beer, R. D. (2003). The dynamics of active categorical perception in an evolved model agent. Adapt Behav. 11, 209–243. doi: 10.1177/1059712303114001

CrossRef Full Text | Google Scholar

Beer, R. D. (2006). Parameter space structure of continuous-time recurrent neural networks. Neural Comput. 18, 3009–3051. doi: 10.1162/neco.2006.18.12.3009

PubMed Abstract | CrossRef Full Text | Google Scholar

Beer, R. D., and Williams, P. L. (2015). Information processing and dynamics in minimally cognitive agents. Cogn. Sci. 39, 1–38. doi: 10.1111/cogs.12142

PubMed Abstract | CrossRef Full Text | Google Scholar

Blakemore, S.-J., Wolpert, D., and Frith, C. (2000). Why can't you tickle yourself? Neuroreport 11, R11-R16. doi: 10.1097/00001756-200008030-00002

PubMed Abstract | CrossRef Full Text

Blakemore, S.-J., Wolpert, D. M., and Frith, C. D. (1998). Central cancellation of self-produced tickle sensation. Nat. Neurosci. 1, 635–640. doi: 10.1038/2870

PubMed Abstract | CrossRef Full Text | Google Scholar

Chatila, R., Renaudo, E., Andries, M., Chavez-Garcia, R.-O., Luce-Vayrac, P., Gottstein, R., et al. (2018). Toward self-aware robots. Front. Rob. AI 5, 88. doi: 10.3389/frobt.2018.00088

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, A. (2013). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 36, 181–204. doi: 10.1017/S0140525X12000477

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, A., and Toribio, J. (1994). Doing without representing? Synthese 101, 401–431. doi: 10.1007/BF01063896

CrossRef Full Text | Google Scholar

Crapse, T. B., and Sommer, M. A. (2008). Corollary discharge across the animal kingdom. Nat. Rev. Neurosci. 9, 587–600. doi: 10.1038/nrn2457

PubMed Abstract | CrossRef Full Text | Google Scholar

de Lange, F. P., Heilbron, M., and Kok, P. (2018). How do expectations shape perception? Trends Cogn. Sci. 22, 764–779. doi: 10.1016/j.tics.2018.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Friston, K. (2009). The free-energy principle: a rough guide to the brain? Trends Cogn. Sci. 13, 293–301. doi: 10.1016/j.tics.2009.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Garner, J., and Egbert, M. (2022). “Is prediction required? using evolutionary robotics to investigate how systems cope with self-caused sensory stimuli,” in ALIFE 2022: The 2022 Conference on Artificial Life (MIT Press).

Google Scholar

Harvey, I. (2011). “The microbial genetic algorithm,” in Advances in Artificial Life. Darwin Meets von Neumann. ECAL 2009. Lecture Notes in Computer Science, Vol. 5778, eds G. Kampis, I. Karsai, and E. Szathmáry (Berlin; Heidelberg: Springer). doi: 10.1007/978-3-642-21314-4_16

CrossRef Full Text | Google Scholar

Harvey, I., Paolo, E. D., Wood, R., Quinn, M., and Tuci, E. (2005). Evolutionary robotics: a new scientific tool for studying cognition. Artif. Life 11, 79–98. doi: 10.1162/1064546053278991

PubMed Abstract | CrossRef Full Text | Google Scholar

Hughes, G., and Waszak, F. (2011). ERP correlates of action effect prediction and visual sensory attenuation in voluntary action. Neuroimage 56, 1632–1640. doi: 10.1016/j.neuroimage.2011.02.057

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunter, J. D. (2007). Matplotlib: a 2d graphics environment. Comput. Sci. Eng. 9, 90–95. doi: 10.1109/MCSE.2007.55

CrossRef Full Text | Google Scholar

Kahl, S., Wiese, S., Russwinkel, N., and Kopp, S. (2022). Towards autonomous artificial agents with an active self: modeling sense of control in situated action. Cogn. Syst. Res. 72, 50–62. doi: 10.1016/j.cogsys.2021.11.005

CrossRef Full Text | Google Scholar

Kilteni, K., and Ehrsson, H. H. (2017). Body ownership determines the attenuation of self-generated tactile sensations. Proc. Natl. Acad. Sci. U.S.A. 114, 8426–8431. doi: 10.1073/pnas.1703347114

PubMed Abstract | CrossRef Full Text | Google Scholar

Kilteni, K., and Ehrsson, H. H. (2022). Predictive attenuation of touch and tactile gating are distinct perceptual phenomena. iScience 25, 104077. doi: 10.1016/j.isci.2022.104077

PubMed Abstract | CrossRef Full Text | Google Scholar

Kilteni, K., Engeler, P., and Ehrsson, H. H. (2020). Efference copy is necessary for the attenuation of self-generated touch. iScience 23, 100843. doi: 10.1016/j.isci.2020.100843

PubMed Abstract | CrossRef Full Text | Google Scholar

Klaffehn, A. L., Baess, P., Kunde, W., and Pfister, R. (2019). Sensory attenuation prevails when controlling for temporal predictability of self- and externally generated tones. Neuropsychologia 132, 107145. doi: 10.1016/j.neuropsychologia.2019.107145

PubMed Abstract | CrossRef Full Text | Google Scholar

Lalouni, M., Fust, J., Vadenmark-Lundqvist, V., Ehrsson, H. H., Kilteni, K., and Birgitta Jensen, K. (2021). Predicting pain: differential pain thresholds during self-induced, externally induced, and imagined self-induced pressure pain. Pain 162, 1539–1544. doi: 10.1097/j.pain.0000000000002151

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathayomchan, B., and Beer, R. D. (2002). Center-crossing recurrent neural networks for the evolution of rhythmic behavior. Neural Comput. 14, 2043–2051. doi: 10.1162/089976602320263999

PubMed Abstract | CrossRef Full Text | Google Scholar

Miall, R. C., and Wolpert, D. M. (1996). Forward models for physiological motor control. Neural Netw. 9, 1265–1279. doi: 10.1016/S0893-6080(96)00035-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Pareés, I., Brown, H., Nuruki, A., Adams, R. A., Davare, M., Bhatia, K. P., et al. (2014). Loss of sensory attenuation in patients with functional (psychogenic) movement disorders. Brain 137, 2916–2921. doi: 10.1093/brain/awu237

PubMed Abstract | CrossRef Full Text | Google Scholar

Phattanasri, P., Chiel, H. J., and Beer, R. D. (2007). The dynamics of associative learning in evolved model circuits. Adapt Behav. 15, 377–396. doi: 10.1177/1059712307084688

PubMed Abstract | CrossRef Full Text | Google Scholar

Press C. Kok P. Yon D. (2020). The perceptual prediction paradox. Trends Cogn. Sci. 24, 13–24. doi: 10.1016/j.tics.2019.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Roussel, C., Hughes, G., and Waszak, F. (2013). A preactivation account of sensory attenuation. Neuropsychologia 51, 922–929. doi: 10.1016/j.neuropsychologia.2013.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Schillaci, G., Ritter, C.-N., Hafner, V. V., and Lara, B. (2016). Body “Representations for robot ego-noise modelling and prediction. towards the development of a sense of agency in artificial agents,” in Proceedings of the Artificial Life Conference 2016 (Cancun: MIT Press), 390–397.

Google Scholar

Thompson, A., Layzell, P., and Zebulum, R. (1999). Explorations in design space: unconventional electronics design through artificial evolution. IEEE Trans. Evolut. Comput. 3, 167–196. doi: 10.1109/4235.788489

CrossRef Full Text | Google Scholar

Wolpert, D. M., and Flanagan, J. R. (2001). Motor prediction. Curr. Biol. 11, R729-R732. doi: 10.1016/S0960-9822(01)00432-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolpert, D. M., Ghahramani, Z., and Jordan, M. I. (1995). An internal model for sensorimotor integration. Science 269, 1880–1882. doi: 10.1126/science.7569931

PubMed Abstract | CrossRef Full Text | Google Scholar

Zahnoun, F. (2019). On representation hungry cognition (and why we should stop feeding it). Synthese 198, 267–284. doi: 10.1007/s11229-019-02277-8

CrossRef Full Text | Google Scholar