Unifying Physical Interaction, Linguistic Communication, and Language Acquisition of Cognitive Agents by Minimalist Grammars

Cognitive agents that act independently and solve problems in their environment on behalf of a user are referred to as autonomous. In order to increase the degree of autonomy, advanced cognitive architectures also contain higher-level psychological modules with which needs and motives of the agent are also taken into account and with which the behavior of the agent can be controlled. Regardless of the level of autonomy, successful behavior is based on interacting with the environment and being able to communicate with other agents or users. The agent can use these skills to learn a truthful knowledge model of the environment and thus predict the consequences of its own actions. For this purpose, the symbolic information received during the interaction and communication must be converted into representational data structures so that they can be stored in the knowledge model, processed logically and retrieved from there. Here, we firstly outline a grammar-based transformation mechanism that unifies the description of physical interaction and linguistic communication and on which the language acquisition is based. Specifically, we use minimalist grammar (MG) for this aim, which is a recent computational implementation of generative linguistics. In order to develop proper cognitive information and communication technologies, we are using utterance meaning transducers (UMT) that are based on semantic parsers and a mental lexicon, comprising syntactic and semantic features of the language under consideration. This lexicon must be acquired by a cognitive agent during interaction with its users. To this aim we outline a reinforcement learning algorithm for the acquisition of syntax and semantics of English utterances. English declarative sentences are presented to the agent by a teacher in form of utterance meaning pairs (UMP) where the meanings are encoded as formulas of predicate logic. Since MG codifies universal linguistic competence through inference rules, thereby separating innate linguistic knowledge from the contingently acquired lexicon, our approach unifies generative grammar and reinforcement learning, hence potentially resolving the still pending Chomsky-Skinner controversy.

1. Introduction

Traditionally, the technical replication of cognitive systems is based on cognitive architectures with which the most important principles of human cognition are captured. The best known traditional architectures are SOAR and ACT (Funke, 2006). Such architectures serve to integrate psychological findings in a formal model that is as economical as possible and capable of being simulated. It assumes that all cognitive processes can be traced back to a few basic principles. According to Eliasmith (2013), this means that cognitive architectures have suitable representational data structures, that they support the composition-, adaptation- and classification principle and that they are autonomously capable to gain knowledge by logical reasoning and learning. Further criteria are productivity, robustness, scalability and compactness. In psychological research, these architectures are available as computer programs, which are used to empirically test psychological theories. In contrast, the utility of cognitive architectures in artificial intelligence (AI) research lies primarily in the construction of intelligent machines and the ability to explain their behavior.

Explainability of intelligent machines is closely tied to the idea of a physical symbol system (PSS) (Newell and Simon, 1976). A PSS takes physical symbols from its sensory equipment, composing them into symbolic structures (expressions) and transforms them to new expressions (Vera and Simon, 1993). For our approach it is crucial that the symbols or the symbol structures, respectively, can be assigned a meaning and that the transformation of these symbol structures leads to logically processable knowledge on which problem solving is based. In order to build meaningful symbols, the agent must be embedded in a perception-action-cycle (PAC) and it must be taken into account that the truthfulness or veridicality of the translation of sensory information into symbolic structures is not necessarily guaranteed due to deceptions or dysfunctions (Bischof, 2009). To overcome these difficulties, more sophisticated agents are able to build a dynamic model of their environment that can be simulated. In this case, the agent has to distinguish between redundancy expectations (model-based prior knowledge) and sensory data (observations), so that information from two sources has to be processed. To achieve veridicality, both pieces of information must be combined in a suitable manner (e.g., through a Bayesian model). The structure required for this kind of information processing is depicted by the inner cognitive loop in Figure 1 and is denoted as interaction¹. This picture illustrates that autonomous behavior can arise if the interaction process is based on truthful information processing that is controlled by higher-level psychological modules. This includes necessities, motives and acquired authorizations that support well-being. In addition to the associated autonomous interaction scenarios, human-machine communication is another area of application for cognitive agents. In this case, the tool or service character of cognitive agents plays a prominent role. This property allows the user to solve certain tasks or problems through the agent. For this purpose, linguistic descriptions must be articulated, understood and exchanged. This results in the requirement for a speech-enabled agent and an additional outer cognitive loop (see Figure 1) which is denoted as communication².

FIGURE 1

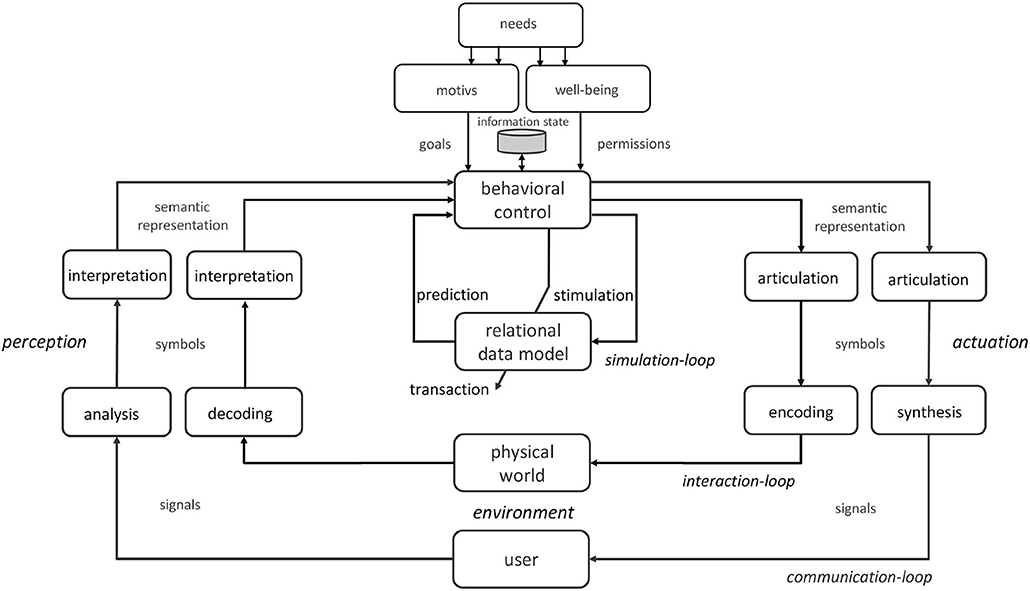
Figure 1. Double cognitive loop using an embedded relational data model. The inner cognitive loop corresponds to the interaction between the agent and the environment (nonverbal information exchange). The outer cognitive loop is used for the communication between a speech-enabled agent and any other cognitive agent or natural language user (verbal information exchange). The flow of information between the behavioral control and the relational data model is embedded in a simulation loop and enables the simulation of actions as well as the prediction of effects. Since the simulation loop is not linked to the environment through perception and action, this loop is not referred to as a PAC. The exchange of information between two systems with different cognitive abilities (e.g., between humans and cognitive agents) is denoted as Inter-Cognitive Communication (Baranyi et al., 2015).

In our application scenario, the communications between cognitive agents and human users are related to a common physical environment that is modeled through a network of objects that are in static or dynamic relationships with one another. Such objects can be described and distinguished by a set of attributes and its admissible values. Objects, attributes and relationships between objects are the information of interest to which both nonverbal interaction and verbal communication refer. However, in order to ensure veridical behavior, the representational data structures of the environment model must be compared with those that have resulted from communication and interaction. Only by using an appropriate comparison mechanism the agent can understand what is actually going on in reality and what the respective observations mean. It largely depends on this ability whether the right actions are selected to achieve the agent's goals. In case of interaction, the comparison must be made between the representational data of the sensor information and the content of the agents knowledge base. In communication, on the other hand, it is necessary that the representational data structures of the user's utterances (semantics) are referenced to the shared environmental context (Hausser, 2014). The agent can receive this information using the interaction loop. Note that this comparison may result in an adaptation of the knowledge base.

Research in computational linguistics has demonstrated that quite different grammar formalisms, such as tree-adjoining grammar (Joshi et al., 1975), multiple context-free grammar (Seki et al., 1991), range concatenation grammar (Boullier, 2005), and minimalist grammar (Stabler, 1997; Stabler and Keenan, 2003) converge toward universal description models (Joshi et al., 1990; Michaelis, 2001; Stabler, 2011a; Kuhlmann et al., 2015). Minimalist grammar has been developed by Stabler (1997) to mathematically codify Chomsky's Minimalist Program (Chomsky, 1995) in the generative grammar framework. A minimalist grammar consists of a mental lexicon storing linguistic signs as arrays of syntactic, phonetic and semantic features, on the one hand, and of two structure-building functions, called “merge” and “move,” on the other hand. Furthermore, syntax and compositional semantics can be combined via the lambda calculus (Niyogi, 2001; Kobele, 2009), while MG parsing can be straightforwardly implemented through bottom-up (Harkema, 2001), top-down (Harkema, 2001; Mainguy, 2010; Stabler, 2011b), and in the meantime also by left-corner automata (Stanojević and Stabler, 2018).

One important property of MG is their effective learnability in the sense of Gold's formal learning theory (Gold, 1967). Specifically, MG can be acquired by positive examples (Bonato and Retoré, 2001; Kobele et al., 2002; Stabler et al., 2003) from linguistic dependence graphs (Nivre, 2003; Klein and Manning, 2004; Boston et al., 2010), which is consistent with psycholinguistic findings on early-child language acquisition (Gee, 1994; Pinker, 1995; Ellis, 2006; Tomasello, 2006; Diessel, 2013). However, learning through positive examples only, could easily lead to overgeneralization. According to Pinker (1995) this could substantially be avoided through reinforcement learning (Skinner, 2015; Sutton and Barto, 2018). Although there is only little psycholinguistic evidence for reinforcement learning in human language acquisition (Moerk, 1983; Sundberg et al., 1996), we outline a machine learning algorithm for the acquisition of an MG mental lexicon (beim Graben et al., 2020) of the syntax and semantics for English declarative sentences through reinforcement learning in this article. Our approach chosen here is inspired by similar work on linguistic reinforcement learning (Zettlemoyer and Collins, 2005; Kwiatkowski et al., 2012; Artzi and Zettlemoyer, 2013). Instead of looking at pure syntactic dependencies as Bonato and Retoré (2001), Kobele et al. (2002), and Stabler et al. (2003), our approach directly uses their underlying semantic dependencies for the simultaneous segmentation of syntax and semantics, in some analogy to van Zaanen (2001).

With this work we are pursuing two main goals. The first goal is to represent the received or released information about the properties of objects or the relationships between objects in the form of relational expressions and to store it in a knowledge model so that these expressions can be used for knowledge processing for the purpose of behavior control or problem solving. In order to assign a meaning and a context to the symbolic structures (symbol grounding problem), the comparability between the expressions of the knowledge model and the expressions of the two cognitive loops (interaction and communication) must be guaranteed. We fulfill this requirement by uniformly describing the information transformation in both loops using the formalism of minimalist grammar and thus with linguistic means. To solve the symbol grounding problem, the relationship between the symbol structures and the actual facts is established through a model of the agent's environment. Such a model can be acquired on the principle of reinforcement learning. Since the information transformation is also based on a model—here in the form of the mental lexicon—the second aim of this work is to acquire the mental lexicon of an MG based on this learning principle.

The paper is organized as follows: First, we address the problem statement and the experimental environment. Subsequently, we summarize the necessary mathematical basics and the notations used. Then we come to the first focus of this work and describe the unified information transformation for interaction and communication using minimalist grammar and lambda calculus. We start with the simple case of interaction and explain the transformation mechanism using formal linguistic means and the assumption that the agent has already aquired a minimalist lexicon. Subsequently, the more demanding case of communication is discussed, where the transformation mechanism has to convert natural language utterances into predicate logical expressions. In both cases we discuss language production (articulation) and language understanding (interpretation). The integration of the acquired representational data structures into the agent's knowledge base concludes the first main focus. The following section covers the second main focus and deals with the acquisition of minimalist lexicons through the method of reinforcement learning. The paper concludes with a summary and a discussion of the achieved results.

2. Problem Statement and Experimental Setup

We consider the well-known mouse-maze problem (Shannon, 1953; Wolff et al., 2015, 2018), where an artificial mouse lives in a simple N × M maze world that is given by a certain configuration of walls. For the mouse to survive, one ore more target objects are located at some places in the maze. In our setup we are using the target object types cheese/carrot (C) and water (W) to satisfy the primary needs hunger and thirst. These object types are defined symbolically by the set ${O}=\left\{C,W,NOB\right\}$ where NOB refers to no object at all. The agent is able to move around the maze and to perceive information about its environment via physical interaction. This is organized by the inner perception-action-cycle (interaction-loop) of Figure 1 that allows the agent to navigate to these target objects. To this end, the agent needs to measure its current position (x, y) by two sensors, where x ∈ X = {1, ..., N} and y ∈ Y = {1, ..., M} apply. It also has to determine the presence or absence of target objects by an object classifier, which we consider as a single complex sensor. Then the current situation can be described on the basis of the measurement result for the current position and the result of object classification. Subsequently, the measurement information needs to be encoded as a string of symbols and has to be translated into a representational data structure saved in a knowledge base. This kind of knowledge (“situations”) should be stored as the result of an exploration phase if no logical contradictions occure. A further kind of knowledge is the set of movements in the maze. These “movements” are based on permissible actions $a\in {A}$, which initially correspond to the four geographic directions, north (N), south (S), west (W), and east (E), that are defined symbolically by the set ${A}=\left\{N,S,W,E,NOP\right\}$ (NOP denoting no operation here). Each action starts at a position z = (x, y) and ends at a position z′ = (x′, y′). For this purpose, the actuators associated to the x- or y- direction, respectively, can be incremented or decremented by one step. Hence, to establish the parameterization of the four geographic directions we define the sets ΔX = ΔY = {−1, 0, 1}. Thus, the south action is parameterized, for example, by the ordered pair (0, −1). Note that with the knowledge about “movements” the agents behavior can be described in the sense of “causality.” From a technical point of view, the relationship between a cause [z = ((x, y), a)] and an effect [z′ = (x′, y′)] can be expressed, for example, by the transition equation of a finite state automaton. To implement “movement” instructions the reverse flow of the sensory information must be realized. That is, in order to be able to control the agent's actuators, actions must be described as representative data structures and converted into a string of symbols. It follows, that physical interaction requires both, the agent's capability to interpret a linearly ordered time series of symbolized measurement results as a (partially ordered) semantic representations and to transform semantic representations into a linear sequence of actuator instructions during articulation.

The ability to communicate with natural language users is another demand that a cognitive agent should meet. To this end, the agent should first of all be speech-enabled. Communication is organized by the outer perception-action-cycle (communication-loop) shown in Figure 1 which is mainly characterized by the articulation and interpretation of speech signals. Therefore, we essentially need the very same capabilities for the transformation of linearly ordered symbolic messages (the “scores” of communication) into partially ordered semantic representations. For this reason, we devise a bidirectional utterance meaning transducer to encode and decode the meaning of symbolic messages. The encoded meaning corresponds to the representational data structure of utterances and can be saved in the agent's knowledge base.

In order to avoid logical conflicts between the results of the interaction- and communication loop, it is also necessary that the representational data structures generated by these loops must be comparable. Hence, in our approach non-verbal physical interaction and verbal communication are uniformly modeled using linguistic description means. This approach can be also supported by two salient arguments borrowed from Hausser (2014) that have already been presented by Römer et al. (2019): (1) “Without a carefully built physical grounding any symbolic representation will be mismatched to the sensors and actuators. These groundings provide the constraints on symbols necessary for them to be truly useful.” (2) “The analysis of nonverbal cognition is needed in order to be able to plausibly explain the phylogenetic and ontogenetic development of language from earlier stages of evolution without language.” Further, according to the “Physical Symbol Systems Hypothesis” (PSSH) all cognitive processes can be described as the transformation of symbol structures (Newell and Simon, 1976). This transformation process obeys the composition principle (“infinite use of finite means”) and aims to recast incoming sensor information into logically processable knowledge, which is saved in a knowledge model. Notably, we assume that the transformation from signal to symbol space can be solved by a transduction stage, proposed by Wolff et al. (2013). According to the PSSH, this low-level transduction stage is the crucial processing step for recognition, designation and arrangement of the observed sensor events through symbol sequences in terms of a formal or natural language.

The use of linguistic description means includes the use of a suitable grammar formalism that is based on a mental lexicon as part of the agent's knowledge base and on transformation rules for how to arrange symbols into linear sequences. It is the second aim of the present study, to suggest minimalist grammar and logical lambda calculus as a unifying framework to this end. While the user can be assumed to already have the linguistic resources, the agent must acquire them through learning. Thus, a further aim of our work is the description of an algorithm with which a mental lexicon can be learned and dynamically updated through reinforcement learning. Starting point of our algorithm are utterance meaning pairs (Kwiatkowski et al., 2012; Wirsching and Lorenz, 2013; beim Graben et al., 2019b).

$\begin{array}{ll}u=\langle e,\sigma \rangle ,& (1)\end{array}$

where e ∈ E is the spoken or written utterance while σ ∈ Σ is a logical term, expressed by means of predicate logic and the (untyped) lambda calculus (Church, 1936) denoting the semantics of the utterance. We assume that UMPs are continuously delivered by a “teacher” to the agent during language acquisition.

As an example, consider the simple UMP

$\begin{array}{ll}u=\langle \text{the mouse eats cheese},\text{eat}(\text{chesse})(\text{mouse})\rangle .& (2)\end{array}$

In the sequel we use typewriter font to emphasize that utterances are regarded plainly as symbolic tokens without any intended meaning in the first place. This applies even to the “semantic” representation in terms of first order predicate logic where we use the Schönfinkel-Curry (Schönfinkel, 1924; Lohnstein, 2011) notation here. Therefore, the expression above eat(cheese)(mouse) indicates that eat is a binary predicate, fetching first its direct object cheese to form a unary predicate, eat(cheese), that then takes its subject mouse in the second step to build the proposition of the utterance (2).

3. Preliminaries

In this section we summarize some fundamental concepts needed for system modeling and information transformation: state space representation and formal languages. We also briefly refer to the set-theoretical connection between simple predicate logic expressions (without quantifiers) and semantic representations based on relational schemes. Subsequently, we explain the concept of minimalist grammar and its suitability for a transformation mechanism that can be used to mediate between linearly ordered symbolic perception/action sequences and semi- or disordered semantic representations. The expressiveness and flexibility of natural language is mainly due to the compositional principle, according to which new semantic terms can be formed from a few elementary terms. In order to anchor this principle in the transformation mechanism, we need the approach of the lambda calculus and the representation of n-ary functions using the Schönfinkel-Curry notation.

3.1. Basic Concepts

State Space Representation. To describe the system behavior in terms of cause and effect, we distinguish states $z\in {Z}$, actions $a\in {A}$ and outputs³ $o\in {O}$. A behavioral relation is then given by

$\begin{array}{ll}{R}_V\subseteq {Z}\times {A}\times {Z}\times {O},& (3)\end{array}$

which determines the system dynamics. To decide, whether a tuple (z, a, z′, o) belongs to this relation or not, the characteristic function $f_{R_V}:{Z}\times {A}\times {Z}\times {O}\to \left\{0,1\right\}$ can be applied. Further, this relation corresponds to a network of causal relations. Due to causality, a recursive calculation rule divided into a system equation and an output equation is given, which allows forecasting the system's behavior

$\begin{array}{ll}\begin{array}{cccc}{z}^{\prime }=G(z,a)& \text{with}& G:{Z}& \times {A}\to {Z},\\ o=H(z,a)& \text{with}& H:{Z}& \times {A}\to {O}.\end{array}& (4)\end{array}$

Because in our setting the system response $o\in {O}$ depends exclusively on the current state $z\in {Z}$, we get a simplification of the output equation o = H(z) that corresponds to the idea of the Moore automaton.

Formal Language. In order to specify any technical communication between source and sink, we have to arrange an alphabet Σ_A = {a, b, …} and to establish a language ${L}\subseteq {{\Sigma }_A}^{*}$ (the symbol * is called Kleene star). Words or sentences are then described by an ordered sequence $\mathbf{\text{s}}=(s_1,s_2,\dots ,s_k)\in {L}$, where s ∈ Σ_A. To decide whether a word s belongs to the language ${L}$ we can devise a grammar $G=({N},{T},{P},\mathtt{\text{S}})$. It is specified by the sets ${N}$ of nonterminals, ${T}$ of terminals and ${P}$ of production rules as well as a start symbol S. The grammatical rules determine the arrangement of the symbols within a symbol sequence. Based on these rules permissible sentences of a language can be produced or derived. In contrast to sentence production, sentence analysis reveals the underlying grammatical structure. This analysis method is known as parsing and will be exploited below.

3.2. Predicate Logic Expressions

A linguistic expression that articulates the characteristics of an object or a relation between objects is called a predicate (Jungclaussen, 2001). It does not always have to be about definite objects. In the case of indefinite objects, so-called individual variables are used. Usually the letters P or Q are used as symbols for predicate names. As arguments for predicates we use either individual constants, individual variables or function values. For the sake of simplicity, we limit ourselves to individual constants and individual variables here. An n-ary predicate is then denoted by the expression Q(a₁, a₂, …, a_n), where a are values of the corresponding set A (e.g., admissible values from the domain of an attribute A). According to set theory the predicate Q(a₁, a₂, …, a_n) can be interpreted as relation R_Q ⊆ A₁ × A₂ × … × A_n and can be understood as a binary classifier. In this case the classification task refers to finding in the set of ordered tuples of individuals or objects the class [Q] of those individuals for which the predicate is true. This class is called the denotation of Q. The following notation is used for this:

$\begin{array}{ll}\left[Q\right]=\left\{(a_1,\dots ,a_n)\in A_1\times \dots \times A_n\mid Q(a_1,\dots ,a_n)\text{is true}\right\}& (5)\end{array}$

The mathematical description of a predicate can also be done using the corresponding characteristic function: f_[Q] :A₁ × A₂ × … × A_n → {0, 1}. This is particularly required for the formalism of composing semantic representations.

3.3. Semantic Representations

In semantics we distinguish between objects that are described by attributes and relations between such objects (Chen, 1975). To represent semantics we will focus on feature-value pairs (FVP), which have a flat structure and correspond to tuples of database relations. The notation used here was taken from Lausen (2005). We start from a universe ${U}=\left\{A_1,A_2,\dots ,A_m\right\}$ which comprises a finite set of attributes. Further, we have a set of domains ${D}=\left\{D_1,D_2,\dots ,D_m\right\}$ and a mapping $dom:{U}\to {D}$. The values of the different attributes are elements of the associated domains. Based on these definitions we can specify types of objects or relations between objects by a set of attributes ${X}=\left\{A_1,A_2\dots ,A_n\right\}\subset {U}$. Objects are defined as mappings, which are called tuples:

$\begin{array}{ll}\tau :\left\{A_1,A_2,\dots ,A_n\right\}\to {\displaystyle \bigcup _{i=1}^n}dom(A_i),n\le m.& (6)\end{array}$

A set of such tuples corresponds to a set of distinguishable objects. Note that in database notation the elements of tuples are not ordered. This corresponds to the idea that the order of attributes is not relevant for describing the type of any object (Lausen, 2005). An object or relation type is defined by a relation scheme:

$\begin{array}{ll}R({X})=(A_1:dom(A_1),A_2:dom(A_2),\dots ,A_n:dom(A_n)).& (7)\end{array}$

In database representations a scheme is associated to the head of a relational data table. The entries of a table correspond to a set of tuples. This set of tuples corresponds to a relation, which is given by:

$\begin{array}{ll}{R}_{{X}}\subseteq Tup(X):=\left\{\tau |\tau :X\to dom({X})\right\},& (8)\end{array}$

where $Tup({X})$ is the set of all possible tuples of a relation scheme $R({X})$. The set of all relations over this scheme is denoted as $Rel({X})$.

3.4. Minimalist Grammars

Minimalist grammars (MG) were introduced to describe natural languages (Stabler, 1997). For nonverbal interaction it is crucial that MG provide a translation mechanism between linearly ordered perceptions/actions and semi- or disordered semantic representations. Based on such a grammar, knowledge can be formally represented and stored consistently in a relational data model. Following Kracht (2003), we regard a linguistic sign as an ordered triple

$\begin{array}{ll}q=\langle \mathtt{\text{e}},\mathtt{\text{t}},\sigma \rangle & (9)\end{array}$

with exponent e ∈ E, semantics σ ∈ Σ and a syntactic type t ∈ T that we encode by means of MG in its chain representation (Stabler and Keenan, 2003). The type controls the generation of the syntactic and semantic structure of an utterance. An MG consists of a data base, the mental lexicon, containing signs as arrays of syntactic, phonetic and semantic features, and of two structure-generating functions, called “merge” and “move.” For our purposes, it is sufficient to point out some syntactic features: Selectors (e.g., “ = S”) are required to search for syntactic types of the same category (e.g., “S”). Licensors (e.g., “+k”) and licensees (e.g., “-k”) are required to control the symbol order at the surface. The symbol “::” indicates simple, lexical categories while “:” denotes complex, derived categories (“·” is just a placeholder for one of these signs). A sequence of signs “q” is called a minimalist expression. For further details we refer to beim Graben et al. (2019b). We just repeat the two kinds of structure-building rules here. The MG function “merge” is defined through inference schemes

$\begin{array}{ll}\begin{array}{cc}\frac{\langle e_1,\mathtt{\text{::=}}f\text{t},{\sigma }_1\rangle \langle e_2,·f,{\sigma }_2\rangle \text{q}}{\langle e_1{e}_2,\mathtt{\text{:}}\text{t},{\sigma }_1{\sigma }_2\rangle \text{q}}& \text{merge-1},\\ \frac{\langle e_1,\mathtt{\text{:=}}f\text{t},{\sigma }_1\rangle {\text{q}}_1\langle e_2,·f,{\sigma }_2\rangle {\text{q}}_2}{\langle e_2{e}_1,\mathtt{\text{:}}\text{t},{\sigma }_1{\sigma }_2\rangle {\text{q}}_1{\text{q}}_2}& \text{merge-2},\\ \frac{\langle e_1,·\mathtt{\text{=}}f{\text{t}}_1,{\sigma }_1\rangle {\text{q}}_1\langle e_2,·f{\text{t}}_2,{\sigma }_2\rangle {\text{q}}_2}{\langle e_1,\mathtt{\text{:}}{\text{t}}_1,{\sigma }_1\rangle {\text{q}}_1\langle e_2,\mathtt{\text{:}}{\text{t}}_2,{\sigma }_2\rangle {\text{q}}_2}& \text{merge-3}.\end{array}& (10)\end{array}$

Correspondingly, “move” is given through,

$\begin{array}{ll}\begin{array}{cc}\frac{\langle e_1,\mathtt{\text{:+}}f\text{t},{\sigma }_1\rangle {\text{q}}_1\langle e_2,\mathtt{\text{:-}}f,{\sigma }_2\rangle {\text{q}}_2}{\langle e_2{e}_1,\mathtt{\text{:}}\text{t},{\sigma }_1{\sigma }_2\rangle {\text{q}}_1{\text{q}}_2}& \text{move-1},\\ \frac{\langle e_1,\mathtt{\text{:+}}f{\text{t}}_1,{\sigma }_1\rangle {\text{q}}_1\langle e_2,\mathtt{\text{:-}}f{\text{t}}_2,{\sigma }_2\rangle {\text{q}}_2}{\langle e_1,\mathtt{\text{:}}{\text{t}}_1,{\sigma }_1\rangle {\text{q}}_1\langle e_2,\mathtt{\text{:}}{\text{t}}_2,{\sigma }_2\rangle {\text{q}}_2}& \text{move-2}.\end{array}& (11)\end{array}$

3.5. Schönfinkel-Curry Notation and Lambda Calculus

Schönfinkel-Curry Notation. Let us consider a binary function

$\begin{array}{ll}f:A\times B\to Z,& (12)\end{array}$

where its domain is defined by the cartesian product over two sets A and B and its value range is given by the set Z. Such a binary function can be decomposed into two unary functions, which are calculated in two steps

$\begin{array}{ll}F:A\to (B\to Z).& (13)\end{array}$

First, with the assignment of the first argument a ∈ A, a mapping F(a):B → Z is selected. Secondly, the function value F(a)(b) = f(a, b) = z is calculated when the second argument b ∈ B is assigned. This principle can be generalized to n-ary functions

$\begin{array}{ll}f:A_1\times A_2\times ,\dots ,\times A_n\to A_{n+1}.& (14)\end{array}$

Whereby a one-to-one relationship between n-ary functions and unary functions of n-th order is established

$\begin{array}{ll}F:A_1\to (A_2\to (A_3\dots (A_n\to A_{n+1})\dots )).& (15)\end{array}$

In computational linguistics this representation is used in terms of the description of relations by their characteristic function. In this case an n-tuple (a₁, a₂, …, a_n) ∈ A₁ × A₂ ×, …, × A_n is mapped to the elements of the binary set {0, 1}. However, the representation in computational linguistics is in a slightly modified form, because the arguments appear in the reverse order F(a_n)(a_n−1) … (a₁).

Lambda calculus is a mathematical formalism developed by Church in the 1930s “to model the mathematical notion of substitution of values for bound variables” according to Wegner (2003). Although the original application was in the area of computability (cf. Church, 1936) the substitution of parts of a term with other terms is often the central notion when lambda calculus is used. This is also true in our case and we have to clarify the concepts first; namely variable, bound and free, term, and substitution.

To be applicable to any universe of discourse a prerequisite of lambda calculus is “an enumerably infinite set of symbols” (Church, 1936) which can be used as variables. However, for usage in a specific domain, a finite set is sufficient. Since we aim at terms from first order predicate logic, treating them with the operations from lambda calculus, all their predicates P and individuals I need to be in the set of variables. Additionally, we will use the symbols I_V: = {x, y, …} as variables for individuals and T_V: = {P, Q, …} as variables for (parts of) logical terms. The set V: = P ∪ I ∪ I_V ∪ T_V is thus used as the set of variables. Note, that the distinction made by I_V and T_V is not on the level of lambda calculus calculus but rather a meta-theoretical clue for the reader.

The following definitions hold for lambda calculus in general and hence we simply use “normal” typeface letters for variables. The term algebra of lambda calculus is inductively defined as follows. i) Every variable v ∈ V is a term and v is a free variable in the term v; specifically, also every well-formed formula of predicate logic is a term. ii) Given a term T and a variable v ∈ V which is free in T, the expression λv.T is also a term and the variable v is now bound in λv.T. Every other variable in T different from v is free resp. bound in λv.T if it is free resp. bound in T. iii) Given two terms T and U, the expression T(U) is also a term and every variable which is free resp. bound in T or U is free resp. bound in T(U). Such a term is often referred to as operator-operand combination (Wegner, 2003) or functional application (Lohnstein, 2011). For disambiguation we also allow parentheses around terms. The introduced syntax differs from the original one where additionally braces and brackets are used to mark the different types of terms (cf. Church, 1936). Sometimes, T(U) is also written as (TU) and the dot between λ and the variable is left out (cf. Wegner, 2003).

For a given variable v ∈ V and two terms T and U the operation of substitution is T[v ← U] [originally written as $S_U^{v}T$ in Church (1936) and sometimes without the right bar, i. e. as in Wegner (2003)] and stands for the result of substituting U for all instances of v in T.

Church defined three conversions based on substitution.

• Renaming bound variables by replacing any part λv.T of a term by λw.T[v ← w] when the variable w does not occur in the term T.

• Lambda application by replacing any part λv.T(U) of a term by T[v ← U], when the bound variables in T are distinct both from v and the free variables in U.

• Lambda abstraction by replacing any part T[v ← U] of a term by λv.T(U), when the bound variables in T are distinct both from v and the free variables in U.

The first conversion simply states that names of bound variables have no particular meaning on their own. The second and third conversions are of special interest to our aims. Lambda application allows the composition of logical terms out of predicates, individuals and other logical terms while lambda abstraction allows the creation of templates of logical terms.

Applied to our example (2), we have the sign

$\begin{array}{l}q=\langle \mathtt{\text{the mouse eats cheese}},:\mathtt{\text{c}},\\ \mathtt{\text{ eat}}(\mathtt{\text{cheese}})(\mathtt{\text{mouse}})\rangle & (16)\end{array}$

where the now appearing MG type :c indicates that the sign is complex (not lexical) and a complementizer phrase of type c. Its compositional semantics (Lohnstein, 2011) can be described by the terms λP.λx.P(x) and λx.λP.P(x), the predicate eat and the individuals cheese and mouse. Consider the term λP.λx.P(x)(eat)(cheese). This is converted by two successive lambda applications via λx.eat(x)(cheese) into the logical term eat(cheese). It is also possible to rearrange parts of the term in a different way. Consider now the term λx.λP.P(x), the logical term eat(cheese) and the individual mouse. Then the term λx.λP.P(x)(mouse)(eat(cheese)) is converted by two successive lambda applications into the logical term eat(cheese)(mouse). Thus, logical terms can be composed through lambda application.

Moreover, given the logical term eat(cheese)(mouse) two successive lambda abstractions yield the term λx.λy.eat(x)(y), leaving out the operand parts. In that way, templates of logical terms are created where different individuals can be inserted for term evaluation. Both processes are crucial for our utterance-meaning transducer and machine language acquisition algorithms below.

4. Physical Interaction

In order to explain the translation process for the interaction, we first rely on a regular grammar, which only comprises two rules: S → eS and S → e with $\mathtt{\text{e}}\in {T}$ and $S\in {N}$. To better understand the formalism we use the following indexed derivation scheme: S₀ → e₀S₁, S₁ → e₁S₂, S₂ → e₂S₃, …, S_n → e_nS_n+1, S_n+1 → e_n+1. The inner words e₁, e₂, …, e_n correspond to the values of attributes that are specified in a relational scheme $R({X})$. The embracing words e₀ and e_n+1 correspond to the symbols <start> and <end>, respectively, which indicate the beginning and the end of a sentence. The database semantics is made up of sets, the elements of which are assignments of values to attributes τ:A → e ∈ dom(A). To apply the translation formalism based on minimalist grammars we substitute semantic terms σ with σ(e). Then we define the semantic concatenation as a set operation: σ₁σ₂: = σ(e₁) ∪ σ(e₂): = {σ(e₁)} ∪ {σ(e₂)}.

Minimalist lexicon. The MG formalism works with linguistic signs that are saved in a minimalist lexicon. In case of interaction three types of linguistic signs that are saved in a minimalist lexicon (see Table 1) are required.

TABLE 1

Table 1. Minimalist lexicon for physical interaction.

The semantics of these sign types are represented by λ-terms using the set-theoretical union operator in the Schönfinkel-Curry-notation ∪(σ(e₂))(σ(e₁)): = ∪(σ(e₁), σ(e₂)) = σ(e₁)∪σ(e₂). According to the following formalism in each iteration step exactly one mapping is added to the semantic expression generated so far. In λ-calculus the composition is achieved through consecutive λ-applications, where the position for the argument a is alternately opened and closed. In this way, mappings are added one after the other to a disordered set, which results to the entries of a relational scheme.

4.1. Interpretation

During the interpretation process, a sequence of symbols is converted into a set of mappings that describe a situation. Such situations are encoded in the form: s = (e₀, e₁, e₂, e₃, e₄) which corresponds in the mouse-maze scenario to messages s = (<start>, x, y, o, <end>). That is, the exponents contain the (x, y)-coordinates and the name of an object type $o\in {O}$. Permissible sentences are elements of the observation language ${{L}}_{obs}$. The configuration of these sentences is subject to a fixed agreement. For this purpose we assign a role to every exponent index and use a bijective mapping $\beta :{R}\to {X}$, which maps each role $r\in {R}$ to the attributes $A\in {X}$ of the relational schemes $R({X})$. The semantics of an exponent e_i with 0 < i < n + 1 is then defined by σ(e_i): = β(r_i) ↦ ω_i ∈ dom(β(r_i)) and σ(e₀) = σ(e_n+1) = ∅. Based on this role-dependent semantics we obtain with the MG formalism a linguistic structure in which the syntactic and semantic structure are built up in parallel. At its core, a key-lock principle is applied, in which a selector (e. g. “ = S”) always requests a syntactic type of the same category (e. g. “S”) and licensors and licensees are used to control the order of the symbols on the surface. Note that this principle is not restricted to natural languages. Now we come to the description of the formalism using the λ-calculus. First, the symbol sequence $\mathbf{\text{s}}\in {{L}}_{obs}$ is converted into a sequence of linguistic signs (taken from the minimalist lexicon), which the formalism processes step by step. During processing, the formalism alternates between the rules merge-3 and move-1. After processing the start type, the iterative processing of the mapping types takes place until the end type is reached. To calculate the semantics of s, the argument position for the new set element to be integrated is opened and closed again by consecutive λ-applications after the current feature-value pair has been added. Finally, the formalism replies with a tuple τ_obs ∈ Tup(Situation).

$\begin{array}{l}Start:\frac{\langle {\mathtt{\text{e}}}_1,::={\mathtt{\text{S}}}_0+\mathtt{\text{k}}{\mathtt{\text{S}}}_1-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_1))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0,::{\mathtt{\text{S}}}_0-\mathtt{\text{k}},\sigma ({\mathtt{\text{e}}}_0)\rangle }{\langle {\mathtt{\text{e}}}_1,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_1-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_1))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0,:-\mathtt{\text{k}},\sigma ({\mathtt{\text{e}}}_0)\rangle }\text{merge-3}\\ \frac{\langle {\mathtt{\text{e}}}_1,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_1-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_1))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0,:-\mathtt{\text{k}},\sigma ({\mathtt{\text{e}}}_0)\rangle }{\langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1,:{\mathtt{\text{S}}}_1-\mathtt{\text{k}},\cup (\sigma ({\mathtt{\text{e}}}_1))(\sigma ({\mathtt{\text{e}}}_0))\rangle }\text{move-1}.\\ It\mathtt{\text{e}}rations:\frac{\langle {\mathtt{\text{e}}}_2,::={\mathtt{\text{S}}}_1+\mathtt{\text{k}}{\mathtt{\text{S}}}_2-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_2))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1,:{\mathtt{\text{S}}}_1-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{1}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }{\langle {\mathtt{\text{e}}}_2,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_2-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_2))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1,:-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{1}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }\text{merge-3}\\ \frac{\langle {\mathtt{\text{e}}}_2,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_2-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_2))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1,:-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{1}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }{\langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2,:{\mathtt{\text{S}}}_2-\mathtt{\text{k}},\cup (\sigma ({\mathtt{\text{e}}}_2))({\displaystyle \underset{i=0}{\overset{1}{\cup }}\sigma }({\mathtt{\text{e}}}_i))\rangle }\text{move-1}.\\ \frac{\langle {\mathtt{\text{e}}}_3,::={\mathtt{\text{S}}}_2+\mathtt{\text{k}}{\mathtt{\text{S}}}_3-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_3))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2,:{\mathtt{\text{S}}}_2-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{2}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }{\langle {\mathtt{\text{e}}}_3,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_3-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_3))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2,:-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{2}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }\text{merge-3}\\ \frac{\langle {\mathtt{\text{e}}}_3,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_3-\mathtt{\text{k}},\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_3))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2,:-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{2}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }{\langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2{\mathtt{\text{e}}}_3,:{\mathtt{\text{S}}}_3-\mathtt{\text{k}},\cup (\sigma ({\mathtt{\text{e}}}_3))({\displaystyle \underset{i=0}{\overset{2}{\cup }}\sigma }({\mathtt{\text{e}}}_i))\rangle }\text{move-1}.\\ End:\frac{\langle {\mathtt{\text{e}}}_4,::={\mathtt{\text{S}}}_3+\mathtt{\text{k}}{\mathtt{\text{S}}}_4,\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_4))(\mathtt{\text{a}})})\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2{\mathtt{\text{e}}}_3,:{\mathtt{\text{S}}}_3-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{3}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }{\langle {\mathtt{\text{e}}}_4,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_4,\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_4))(\mathtt{\text{a}})})\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2{\mathtt{\text{e}}}_3,:-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{3}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }\text{merge-3}\\ \frac{\langle {\mathtt{\text{e}}}_4,:+\mathtt{\text{k}}{\mathtt{\text{S}}}_4,\lambda \mathtt{\text{a}}.{\displaystyle \cup (\sigma ({\mathtt{\text{e}}}_4))(\mathtt{\text{a}})}\rangle \langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2{\mathtt{\text{e}}}_3,:-\mathtt{\text{k}},{\displaystyle \underset{i=0}{\overset{3}{\cup }}\sigma }({\mathtt{\text{e}}}_i)\rangle }{\langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2{\mathtt{\text{e}}}_3{\mathtt{\text{e}}}_4,:{\mathtt{\text{S}}}_4,\cup (\sigma ({\mathtt{\text{e}}}_4))({\displaystyle \underset{i=0}{\overset{3}{\cup }}\sigma }({\mathtt{\text{e}}}_i))\rangle }\text{move-1}.\end{array}$

The last compositional step generates the linguistic sign $\langle {\mathtt{\text{e}}}_0{\mathtt{\text{e}}}_1{\mathtt{\text{e}}}_2{\mathtt{\text{e}}}_3{\mathtt{\text{e}}}_4,{\mathtt{\text{:S}}}_4,{\displaystyle \bigcup _{i=0}^4}\sigma (e_i)\rangle$. The associated semantics corresponds to the structure of tuples, as defined for relational schemes according to Equation (6). If this formalism is applied to the relational scheme R(Situation) (for relation scheme definitions see section 5.4) it results to the semantic representation of the observed situation

$\begin{array}{l}{\tau }_{obs}={\displaystyle \underset{i=0}{\overset{n+1}{\cup }}\sigma }(e_i)=\{X\to x\in \mathtt{\text{ dom}}(X),Y\to y\in \mathtt{\text{ dom}}(Y),\\ O\to o\in \mathtt{\text{ dom}}(O)\}.& (17)\end{array}$

The observation tuple τ_obs contains the set of disordered feature-value-mappings, which corresponds to the translation result of the interpretation. Based on this tuple the next action is selected and a further perception-action-cycle is initiated.

4.2. Articulation

After the action decision by the behavior control (see Figure 1), the MG formalism must be applied to a semantic representation for the action in question. To this end, the formalism is fed with an action tuple τ_act ∈ Tup(Action). Each action tuple is initially given in the form.

$\begin{array}{ll}{\tau }_{act}=\left\{\Delta X\to \Delta x\in dom(\Delta X),\Delta Y\to \Delta y\in dom(\Delta Y)\right\}.& (18)\end{array}$

In order to generate an actuator instruction a = (e₀, e₁, e₂, e₃) or a = (<start>, Δx, Δy, <end>), respectively, the feature value pairs of the relational scheme R(Action) must be mapped to the associated linguistic signs. These signs are stored in the linguistic lexicon of the articulation (analogous to the interpretation). In this case too, the formalism alternately switches between the rules merge-3 and move-1. The difference to the interpretation is that the formalism is now fed with a set of linguistic signs and responds with a sequence of symbols. In our mouse-maze scenario this set comprises the following elements: 〈e₀, ::S₀-k, ∅〉, 〈e₃, :: = S₂+kS₃, ∅〉 as well as 〈e₁, :: = S₀+kS₁-k, σ(e₁)〉 and 〈e₂, :: = S₁+kS₂-k, σ(e₂)〉. Applying the production rules of a regular grammar, the derivation would result to the following rule sequence: S₀ → e₀S₁, S₁ → e₁S₂, S₂ → e₂S₃ and S₃ → e₃. This results in S₀ → e₀e₁e₂e₃, in which the root of the derivation tree S₀ comprises the whole action sequence.

The MG-formalism preserves this order through the selectors of the associated exponents: After the formalism is starting with the sign 〈e₀, ::S₀-k, ∅〉 the exponent e₁ is required by the selector “ = S₀” of the sign 〈e₁, :: = S₀+kS₁-k, σ(e₁)〉. Next, the exponent e₂ is required by the selector “ = S₁” of the sign 〈e₂, :: = S₁+kS₂-k, σ(e₂)〉. Finally, the exponent e₃ is required by the selector “ = S₂” of the remaining sign in the articulation set 〈e₃, :: = S₂+kS₃, ∅〉. The complete concatenated string a = (e₀, e₁, e₂, e₃) = (<start>, Δx, Δy, <end>) is inferred then by the last move-1 rule and corresponds to the action sequence that is subsequently transmitted to the agent's actuators.

5. Linguistic Communication

As in the case of physical interaction, we also describe linguistic communication through a minimalist grammar. However, while interaction suffices with a minimalist implementation of regular grammars, exploiting only merge-3 and move-1 operations for the processing of linear time series of observation and actuation, natural language processing requires the full complexity of the MG formalism.

5.1. Utterance-Meaning Transducer (UMT)

In this section we propose a bidirectional Utterance-Meaning-Transducer (UMT) for both speech understanding and speech production by means of MG. For further illustrating the rules (10–11) and their applicability, let us stick with the example UMP (2) given in Sect. 2. Its syntactic analysis in terms of generative grammar (Haegeman, 1994) yields the (simplified) phrase structure tree in Figure 2A⁴.

FIGURE 2

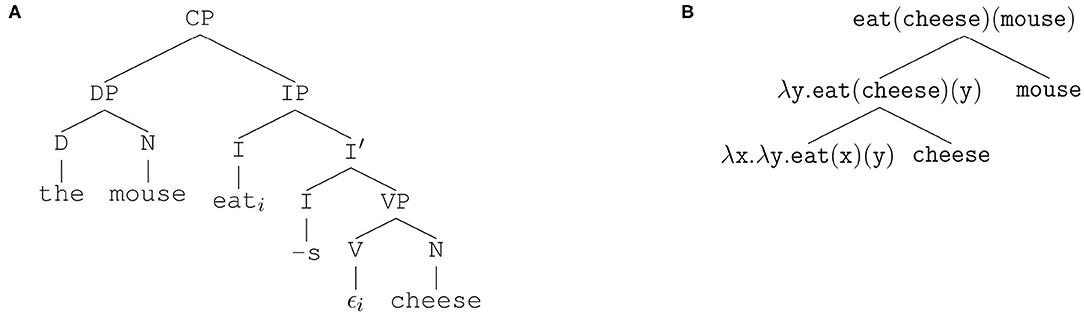
Figure 2. Generative grammar analysis of example UMP (Equation 2). (A) Syntactic phrase structure tree. (B) Semantic tree from lambda calculus.

The syntactic categories in Figure 2A are the maximal projections CP (complementizer phrase), IP (inflection phrase), VP (verbal phrase), and DP (determiner phrase). Furthermore, there are the intermediary node I′ and the heads I (inflection), D (determiner), V (verb), and N (noun), corresponding to t, d, v, and n in MG, respectively. Note that inflection is lexically realized only by the present tense suffix -s. Moreover, the verb eat has been moved out of its base-generated position leaving the empty string ϵ there. Movement is indicated by co-indexing with i.

Correspondingly, we present a simple semantic analysis in Figure 2B using the notation from Sect. 3.5 together with the lambda calculus of the binary predicate in its Schönfinkel-Curry notation (Schönfinkel, 1924; Lohnstein, 2011).

Guided by the linguistic analyses in Figure 2, an expert could construe a minimalist lexicon as given in Table 2 by hand (Stabler and Keenan, 2003).

TABLE 2

Table 2. UMT minimalist lexicon for example grammar (Figure 2).

We adopt a shallow semantic model, where the universe of discourse only contains two individuals, the mouse and a piece of cheese⁵. Then, the lexicon (Table 2) is interpreted as follows. Since all entries are contained in the MG lexicon, they are of category “::.” There are two nouns (n), mouse and cheese with their respective semantics as individual constants, mouse and cheese. In contrast to mouse, the latter possesses a licensee -k for case marking. The same holds for the determiner the selecting a noun (=n) as its complement to form a determiner phrase d which also requires case assignment (-k) afterwards. The verb (v) eat selects a noun as a complement and has to be moved for inflection -f. Its compositional compositional semantics is given by the binary predicate eat(x)(y) whose argument variables are bound by two lambda expressions λx.λy. Moreover, we have an inflection suffix -s for present tense in third person singular, taking a predicate (pred) as complement, then triggering firstly inflection movement +f and secondly case assignment +k, whose type is tense (t). Finally, there are two entries that are phonetically not realized. The first one selects a verbal phrase =v and assigns case +k afterwards; then, it selects a determiner phrase =d as subject and has its own type predicate pred; additionally, we prescribe an intertwiner of two abstract lambda expressions Q, P as its semantics. The last entry provides a simple type conversion from tense t to complementizer c in order to arrive at a well-formed sentence with start symbol c.

Using the lexicon (Table 2), the sign (16) is obtained by the minimalist derivation (19).

$\begin{array}{ll}\frac{\langle \text{the},\text{::=n d -k},ϵ\rangle \langle \text{mouse},\text{::n},mouse\rangle }{\langle \text{the mouse},\text{:d -k},mouse\rangle }\text{merge-1}& (\mathrm{19-1})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eat},\text{::=n v -f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{cheese},\text{::n -k},cheese\rangle }{\langle \text{eat},\text{:v -f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{cheese},\text{:-k},cheese\rangle }\text{merge-3}& (\mathrm{19-2})\end{array}$

$\begin{array}{ll}\frac{\langle ϵ,\text{::=v +k =d pred},\lambda P.\lambda Q.Q(P)\rangle \langle \text{eat},\text{:v -f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{cheese},\text{:-k},cheese\rangle }{\langle ϵ,\text{:+k =d pred},\lambda P.\lambda Q.Q(P)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{cheese},\text{:-k},cheese\rangle }\text{merge-3}& (\mathrm{19-3})\end{array}$

$\begin{array}{ll}\frac{\langle ϵ,\text{:+k =d pred},\lambda P.\lambda Q.Q(P)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{cheese},\text{:-k},cheese\rangle }{\langle \text{cheese},\text{:=d pred},(\lambda P.\lambda Q.Q(P))(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle }\text{move-1}& (\mathrm{19-4})\end{array}$

$\begin{array}{ll}\frac{\langle \text{cheese},\text{:=d pred},(\lambda P.\lambda Q.Q(P))(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle }{\langle \text{cheese},\text{:=d pred},\lambda Q.Q(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle }\lambda \text{-app.}& (\mathrm{19-5})\end{array}$

$\begin{array}{ll}\frac{\langle \text{cheese},\text{:=d pred},\lambda Q.Q(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{the mouse},\text{:d -k},mouse\rangle }{\langle \text{cheese},\text{:pred},\lambda Q.Q(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }\text{merge-3}& (\mathrm{19-6})\end{array}$

$\begin{array}{ll}\frac{\langle \text{-s},\text{::=pred +f +k t},ϵ\rangle \langle \text{cheese},\text{:pred},\lambda Q.Q(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }{\langle \text{-s cheese},\text{:+f +k t},\lambda Q.Q(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }\text{merge-1}& (\mathrm{19-7})\end{array}$

$\begin{array}{ll}\frac{\langle \text{-s cheese},\text{:+f +k t},\lambda Q.Q(cheese)\rangle \langle \text{eat},\text{:-f},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }{\langle \text{eat-s cheese},\text{:+k t},(\lambda Q.Q(cheese))(\lambda x.\lambda y.eat(x)(y))\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }\text{move-1}& (\mathrm{19-8})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats cheese},\text{:+k t},(\lambda Q.Q(cheese))(\lambda x.\lambda y.eat(x)(y))\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }{\langle \text{eats cheese},\text{:+k t},(\lambda x.\lambda y.eat(x)(y))(cheese)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }\lambda \text{-app.}& (\mathrm{19-9})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats cheese},\text{:+k t},(\lambda x.\lambda y.eat(x)(y))(cheese)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }{\langle \text{eats cheese},\text{:+k t},\lambda y.eat(cheese)(y)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }\lambda \text{-app.}& (\mathrm{19-10})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats cheese},\text{:+k t},\lambda y.eat(cheese)(y)\rangle \langle \text{the mouse},\text{:-k},mouse\rangle }{\langle \text{the mouse eats cheese},\text{:t},(\lambda y.eat(cheese)(y))(mouse)\rangle }\text{move-1}& (\mathrm{19-11})\end{array}$

$\begin{array}{ll}\frac{\langle \text{the mouse eats cheese},\text{:t},(\lambda y.eat(cheese)(y))(mouse)\rangle }{\langle \text{the mouse eats cheese},\text{:t},eat(cheese)(mouse)\rangle }\lambda \text{-app.}& (\mathrm{19-12})\end{array}$

$\begin{array}{ll}\frac{\langle ϵ,\text{::=t c},ϵ\rangle \langle \text{the mouse eats cheese},\text{:t},eat(cheese)(mouse)\rangle }{\langle \text{the mouse eats cheese},\text{:c},eat(cheese)(mouse)\rangle }\text{merge-1}.& (\mathrm{19-13})\end{array}$

In the first step, (19-1), the determiner the takes the noun mouse as its complement to form a determiner phrase d that requires licensing through case marking afterwards. In step 2, the finite verb eat selects the noun cheese as direct object, thus forming a verbal phrase v. As there remain unchecked features, only merge-3 applies yielding a minimalist expression, i. e. a sequence of signs. In step 3, the phonetically empty predicate pred merges with the formerly built verbal phrase. Since pred assigns accusative case, the direct object is moved in (19-4) toward the first position through case marking by simultaneously concatenating the respective lambda terms. Thus, lambda application entails the expression in step 5. Then, in step 6, the predicate selects its subject, the formerly construed determiner phrase. In the seventh step, (19-7), the present-tense suffix unifies with the predicate, entailing an inflection phrase pred, whose verb is moved into the first position in step 8, thereby yielding the inflected verb eat-s. In steps 9 and 10 two lambda applications result into the correct semantics, already displayed in Figure 2B. Step 11 assigns nominative case to the subject through movement into specifier position. A further lambda application in step 12 yields the intended interpretation of predicate logics. Finally, in step 13, the syntactic type t is converted into c to obtain the proper start symbol of the grammar.

Derivations such as (19) are essential for MG. However, their computation is neither incremental nor predictive. Therefore, they are not suitable for natural language processing in their present form of data-driven bottom-up processing. A number of different parsing architectures have been suggested in the literature to remedy this problem (Harkema, 2001; Mainguy, 2010; Stabler, 2011b; Stanojević and Stabler, 2018). From a psycholinguistic point of view, predictive parsing appears most plausible, because a cognitive agent should be able to make informed guesses about a speaker's intents as early as possible, without waiting for the end of an utterance (Hale, 2011). This makes either an hypothesis-driven top-down parser, or a mixed-strategy left-corner parser desirable also for language engineering applications. In this section, we briefly describe a bidirectional utterance-meaning transducer (UMT) for MG that is based upon Stabler (2011b)'s top-down recognizer as outlined earlier by beim Graben et al. (2019a). Its generalization toward the recent left-corner parser (Stanojević and Stabler, 2018) is straightforward.

The central object for MG language processing is the derivation tree obtained from a bottom-up derivation as in (19). Figure 3 depicts this derivation tree, where we present a comma-separated sequence of exponents for the sake of simplicity. Additionally, every node is addressed by an index tuple that is computed according to Stabler (2011b)'s algorithm.

FIGURE 3

Figure 3. Simplified derivation tree of Equation (19). Exponents of different signs are separated by commas. Nodes are also addressed by index tuples.

Pursuing the tree paths in Figure 3 from the bottom to the top, provides exactly the derivation (19). However, reading it from the top toward the bottom allows for an interpretation in terms of multiple context-free grammars (Seki et al., 1991; Michaelis, 2001) (MCFG) where categories are n-ary predicates over string exponents. Like in context-free grammars, every branching in the derivation tree (Figure 3) leads to one phrase structure rule in the MCFG. Thus, the MCFG enumerated in (20) codifies the MG (Table 2).

$\begin{array}{ll}\langle \text{:c}\rangle (e_0{e}_1)\leftarrow \langle \text{::=t c}\rangle (e_0)\langle \text{:t}\rangle (e_1)& (\mathrm{20-1})\end{array}$

$\begin{array}{ll}\langle \text{:t}\rangle (e_1{e}_0)\leftarrow \langle \text{:+k t, -k}\rangle (e_0,e_1)& (\mathrm{20-2})\end{array}$

$\begin{array}{ll}\langle \text{:+k t, -k}\rangle (e_1{e}_0,e_2)\leftarrow \langle \text{:+f +k t, -f, -k}\rangle (e_0,e_1,e_2)& (\mathrm{20-3})\end{array}$

$\begin{array}{l}\langle \text{:+f +k t, -f, -k}\rangle (e_0{e}_1,e_2,e_3)\leftarrow \langle \text{::=pred +f +k t}\rangle (e_0)\\ \langle \text{:pred, -f, -k}\rangle (e_1,e_2,e_3)& (\mathrm{20-4})\end{array}$

$\begin{array}{ll}\langle \text{:pred, -f, -k}\rangle (e_0,e_1,e_2)\leftarrow \langle \text{:=d pred, -f}\rangle (e_0,e_1)\langle \text{:d -k}\rangle (e_2)& (\mathrm{20-5})\end{array}$

$\begin{array}{ll}\langle \text{:=d pred, -f}\rangle (e_2{e}_0,e_1)\leftarrow \langle \text{:+k =d pred, -f, -k}\rangle (e_0,e_1,e_2)& (\mathrm{20-6})\end{array}$

$\begin{array}{l}\langle \text{:+k =d pred, -f, -k}\rangle (e_0,e_1,e_2)\leftarrow \langle \text{::=v +k =d pred}\rangle (e_0)\\ \langle \text{:v -f, -k}\rangle (e_1,e_2)& (\mathrm{20-7})\end{array}$

$\begin{array}{ll}\langle \text{:v -f, -k}\rangle (e_0,e_1)\leftarrow \langle \text{::=n v -f}\rangle (e_0)\langle \text{::n -k}\rangle (e_1)& (\mathrm{20-8})\end{array}$

$\begin{array}{ll}\langle \text{:d -k}\rangle (e_0{e}_1)\leftarrow \langle \text{::=n d -k}\rangle (e_0)\langle \text{::n}\rangle (e_1)& (\mathrm{20-9})\end{array}$

$\begin{array}{ll}\langle \text{::n}\rangle (\text{mouse})& (\mathrm{20-10})\end{array}$

$\begin{array}{ll}\langle \text{::n -k}\rangle (\text{cheese})& (\mathrm{20-11})\end{array}$

$\begin{array}{ll}\langle \text{::=n d -k}\rangle (\text{the})& (\mathrm{20-12})\end{array}$

$\begin{array}{ll}\langle \text{::=n v -f}\rangle (\text{eat})& (\mathrm{20-13})\end{array}$

$\begin{array}{ll}\langle \text{::=pred +f +k t}\rangle (\text{-s})& (\mathrm{20-14})\end{array}$

$\begin{array}{ll}\langle \text{::=v +k =d pred}\rangle (ϵ)& (\mathrm{20-15})\end{array}$

$\begin{array}{ll}\langle \text{::=t c}\rangle (ϵ)& (\mathrm{20-16})\end{array}$

In (20), the angular brackets enclose the MCFG categories that are obviously formed by tuples of MG categories and syntactic types. These categories have the same number of string arguments e_k as prescribed in the type tuples. Because MCFG serve only for syntactic parsing in our UMT, we deliberately omit the semantic terms here; they are reintroduced below. The MCFG rules (20a–20i) are directly obtained from the derivation tree (Figure 3) by reverting the merge and move operations of (19) through their “unmerge” and “unmove” counterparts (Harkema, 2001). The MCFG axioms, i. e. the lexical rules (20j – 20p), are reformulations of the entries in the MG lexicon (Table 2).

The UMT's language production module finds a semantic representation of an intended utterance in form of a Schönfinkel-Curry (Schönfinkel, 1924; Lohnstein, 2011) formula of predicate logic, such as eat(cheese)(mouse), for instance. According to Figure 2B this is a hierarchical data structure that can control the MG derivation (19). Thus, the cognitive agent accesses its mental lexicon, either through Table 2 or its MCFG twin (20) in order to retrieve the linguistic signs for the denotations eat, cheese, and mouse. Then, the semantic tree (Figure 2B) governs the correct derivation (19) up to lexicon entries that are phonetically empty. These must occasionally be queried from the data base whenever required. At the end of the derivation the computed exponent the mouse eats cheese is uttered.

The language understanding module of our UMT, by contrast, comprises three memory tapes: the input sequence, a syntactic priority queue, and also a semantic priority queue. Input tape and syntactic priority queue together constitute Stabler (2011b)'s priority queue top-down parser. Yet, in order to compute the meaning of an utterance in the semantic priority queue, we slightly depart from the original proposal by omitting the simplifying trim function. Table 3 presents the temporal evolution of the top-down recognizer's configurations while processing the utterance the mouse eats cheese.

TABLE 3

Table 3. MG top-down parse of the mouse eats cheese.

The parser is initialized with the input string to be processed and the MCFG start symbol 〈:c〉(ϵ)—corresponding to the MG start symbol c—at the top of the priority queue. For each rule of the MCFG (20), the algorithm replaces its string variables by an index tuple that addresses the corresponding nodes in the derivation tree (Figure 3) (Stabler, 2011b). These indices allow for an ordering relation where shorter indices are smaller than longer ones, while indices of equal length are ordered lexicographically. As a consequence, the MCFG axioms in (20) become ordered according to their temporal appearance in the utterance. Using the notation of the derivation tree (Figure 3), we get

$\begin{array}{l}\text{the}(100)<\text{mouse}(101)<\text{eat}(110)<\text{-s}(1110)\\ <\text{cheese}(11110).\end{array}$

Hence, index sorting ensures incremental parsing.

Besides the occasional sorting of the syntactic priority queue, the automaton behaves as a conventional context-free top-down parser. When the first item in the queue is an MCFG category appearing at the left hand side of an MCFG rule, this item is expanded into the right hand side of that rule. When the first item in the queue is a predicted MCFG axiom whose exponent also appears on top of the input tape, this item is scanned from the input and thereby removed from queue and input simultaneously. Finally, if queue and input both contain only the empty word, the utterance has been successfully recognized and the parser terminates in the accepting state.

Interestingly, the index formalism leads to a straightforward implementation of the UMT's semantic parser as well. The derivation tree (Figure 3) reveals that the index length correlates with the tree depth. In our example, the items 〈::n -k〉(11110) and 〈:: = v +k = d pred〉(11111) in the priority queue have the longest indices. These correspond precisely to the lambda terms cheese and λP.λQ.Q(P), respectively, that are unified by lambda application in derivation step (19-5). Moreover, also the semantic analysis in Figure 2B illustrates that the deepest nodes are semantically unified first.

Every time, when the syntactic parser scans a correctly predicted item from the input tape, this item is removed from both input tape and syntactic priority queue. Simultaneously, the semantic content of its sign is pushed on top of the semantic priority queue, yet preserving its index. When some or all semantic items are stored in the queue, they are sorted in reversed index order to get highest semantic priority on top of the queue. Table 4 illustrates the semantic parsing for the given example.

TABLE 4

Table 4. Semantic processing of the mouse eats cheese.

In analogy to the syntactic recognizer, the semantic parser operates in similar modes. Both processors share their common scan operation. In contrast to the syntactic parser which sorts indices in ascending order, the semantic module sorts them in descending order for operating on the deepest nodes in the derivation tree first. Most of the time, it attempts lambda application (apply) which is always preferred for ϵ-items on the queue. When apply has been sufficiently performed upon a term, the last index number is removed from its index (sometimes it might also be necessary to exchange two items for lambda application). Finally, the semantic parser terminates in the understanding state.

5.2. Interpretation

After preparing the UMT, we come back to our particular mouse-maze example. As previously explained, the agent could find its target objects by physically exploring its state space through interaction. Yet, another possibility is linguistic communication where an operator may inform the agent about the correct position of a target. For this case, we present another MG in Table 5. It contains the linguistic signs that can be used to compose the meaning of a message.

TABLE 5

Table 5. Minimalist lexicon–communication.

Our “communication” lexicon comprises two verbs, contains and lies, of the basic type v, which we want to consider here as the start symbol of the MG. The verb contains is transitive and therefore corresponds to a binary predicate, as indicated above by the lambda term in the Schönfinkel representation (Lohnstein, 2011). Syntactically, this binary predicate is expressed by two selectors =n, whereas in linguistics we have to take into account, that a transitive verb first selects a direct object and subsequently its subject (both nouns of the type n “noun”). The verb lies is intransitive, but can be modified by a prepositional phrase through a selector (=p). There are two nouns in the lexicon: field and cheese, their semantics are the corresponding individual names. The field coordinates (x, y) in the labyrinth are expressed by the exponent (x,y), whose syntactic function is an adjunct of the basic type p (prepositional phrase). This must be moved once in the course of the structure development, for which the licensee -f is intended. The adjunction itself is triggered by a phonetically empty entry of the basic type m (modifier). This has two selectors: =n selects the noun phrase to be modified, while =p selects the adjoint prepositional phrase. Then -g licenses a movement. The semantics of the adjunction here expressed in a simplified manner as the predication λP.λp.P(p). That is, there is an object p which has the property P. Another phonetically empty expression selects a modified noun phrase (=m), then licenses two movements (+f +g) and generates itself a noun phrase of the base type n. Semantically, an argument movement is canceled again by the exchange operator λP.λQ.QP. Finally, there is a preposition in of the basic type p, which also selects a noun phrase for adjunction (=n). Instead of formalizing their locative semantics in concrete terms, we simplify them with an empty lambda expression ϵ. In order to reduce the effort for the exploration phase, we can send the following message “field (x,y) contains cheese” to the mouse. This utterance can be processed by our UMT above, for which we present the minimalist bottom-up derivation as follows.

$\begin{array}{l}\frac{\langle \text{contains},\text{::=n =n v},\lambda q.\lambda p.contain(q)(p)\rangle \langle \text{cheese},\text{::n},cheese\rangle }{\langle \text{contains cheese},\text{:=n v},(\lambda q.\lambda p.contain(q)(p))(cheese)\rangle }\text{merge-1}\\ \frac{\langle ϵ,\text{::=n =p m -g},\lambda P.\lambda p.P(p)\rangle \langle \text{field},\text{::n},field\rangle }{\langle \text{field},\text{:=p m -g},(\lambda P.\lambda p.P(p))(field)\rangle }\text{merge-1}\\ \frac{\langle \text{field},\text{::=p m -g},\lambda p.field(p)\rangle \langle \text{(x,y)},\text{:p -f},(x,y)\rangle }{\langle \text{field},\text{:m -g},\lambda p.field(p)\rangle \langle \text{(x,y)},\text{:-f},(x,y)\rangle }\text{merge-3}\\ \frac{\langle ϵ,\text{::=m +f +g n},\lambda P.\lambda Q.QP\rangle \langle \text{field},\text{:m -g},\lambda p.field(p)\rangle \langle \text{(x,y)},\text{:-f},(x,y)\rangle }{\langle ϵ,\text{:+f +g n},\lambda P.\lambda Q.QP\rangle \langle \text{field},\text{:-g},\lambda p.field(p)\rangle \langle \text{(x,y)},\text{:-f},(x,y)\rangle }\text{merge-3}\\ \frac{\langle ϵ,\text{:+f +g n},\lambda P.\lambda Q.QP\rangle \langle \text{field},\text{:-g},\lambda p.field(p)\rangle \langle \text{(x,y)},\text{:-f},(x,y)\rangle }{\langle \text{(x,y)},\text{:+g n},(\lambda P.\lambda Q.QP)((x,y))\rangle \langle \text{field},\text{:-g},\lambda p.field(p)\rangle }\text{move-1}\\ \frac{\langle \text{(x,y)},\text{:+g n},\lambda Q.Q((x,y))\rangle \langle \text{field},\text{:-g},\lambda p.field(p)\rangle }{\langle \text{field (x,y)},\text{:n},(\lambda Q.Q((x,y)))(\lambda p.Feld(p))\rangle }\text{move-1}\\ \frac{\langle \text{contains cheese},\text{:=n v},\lambda p.contain(cheese)(p)\rangle \langle \text{field (x,y)},\text{:n},field((x,y))\rangle }{\langle \text{field (x,y) contains cheese},\text{:v},(\lambda p.contain(cheese)(p))(field((x,y)))\rangle }\text{merge-2}\end{array}$

Thereby, the utterance “field (x,y) contains cheese” is recognized in the exponent, so that its semantics can be interpreted in terms of model theory as a predicate logic formula after a last lambda application (λp.contain(cheese)(p))(field((x, y))) = contain(cheese)(field((x, y))). The denotation of this predicate assignment results to

$\begin{array}{l}[\text{contain}(\text{cheese})(\text{field}((x,y)))]=(\text{[cheese]},\\ \text{ [field}((x,y))])\in [\text{contain]},& (21)\end{array}$

This corresponds to a representational data structure which can be inserted in an associated relational scheme.

5.3. Articulation

For speech production, we start from the fact “field (x,y) contains cheese” and show the possibility of stylistic creativity. First, we note that the denotation of contain is coextensive with that of lie, i. e. [contain] = [lie] applies. Based on this capability an agent is able to express what it has understood in its own words. In this way, the adjustment of common ideas or concepts required for successful communication can take place. If the agent wants to articulate such an utterance, it must first translate the facts into a predicate logic formula and has to consider, that the order of arguments of the subject and the direct object must be swapped: lie(field((x, y)))(cheese). A query in the minimalist lexicon then leads to the following derivation, whereby we reuse the previously derived expression 〈field (x, y), :n, field((x, y))〉 in the sense of dynamic programming.

$\begin{array}{l}\frac{\langle \text{in},\text{::=n p},ϵ\rangle \langle \text{field (x,y)},\text{:n},field((x,y))\rangle }{\langle \text{in field (x,y)},\text{:p},field((x,y))\rangle }\text{merge-1}\\ \frac{\langle \text{lies},\text{::=p =n v},\lambda q.\lambda p.lie(q)(p)\rangle \langle \text{in field (x,y)},\text{:p},field((x,y))\rangle }{\langle \text{lies in field (x,y)},\text{:=n v},(\lambda q.\lambda p.lie(q)(p))(field((x,y)))\rangle }\text{merge-1}\\ \frac{\langle \text{lies in field (x,y)},\text{:=n v},\lambda p.lie(field((x,y)))(p)\rangle \langle \text{cheese},\text{::n},cheese\rangle }{\langle \text{cheese lies in field (x,y)},\text{:v},(\lambda p.lie(field((x,y)))(p))(cheese)\rangle }\text{ merge-2}\end{array}$

The present derivation finally comprises after a final lambda application the intended semantics (λp.lie(field((x, y)))(p))(cheese) = lie(field((x, y))) (cheese) and leads also to the synonymous utterance “cheese lies in field (x,y).”

5.4. Knowledge Integration

In the previous sections we described how the information of symbolic sequences can be transformed into logically processable knowledge and vice versa by interaction or communication, respectively. In order to process knowledge, it has to be saved and retrieved again. These operations are essential characteristics of a universal algorithmic system with which calculation rules can be implemented. Based on such a knowledge processing system a cognitive agent is able to pursue goals, understand situations, select cost optimal actions and to predict its consequences. Further, the agent should be able to learn behavioral relations and to adapt to changing environmental conditions. These requirements can be satisfied more efficiently if the required knowledge is structured and available as a (dynamic) model of the external world. To this end, we apply the state space model, with which we can describe the relations $R_{Situation}\subseteq States\times {O}$ and $R_{Movement}\subseteq States\times {A}\times States$, where the set States corresponds to the set ${Z}$ of the state space model. Based on these relations predictions about the next state and the associated observations can be made. Prediction errors can either be used to recognize changes in the environmental conditions or in the realization of the selected actions, which can initiate an adaptation or diagnosis process. The states $z\in {Z}$ correspond to the maze fields and have a finer inner structure based on ordered pairs z = (x, y) ∈ X × Y, which are associated with the two-dimensional coordinates of the maze. They can be measured by sensors. The same applies to the elements $a\in {A}$, where the finer structure is given by a = (Δx, Δy) ∈ ΔX × ΔY. The elements $o\in {O}$ correspond to the target object types, which can be identified by an object classifier.

In order to build a dynamic model, the agent must have the ability to analyze experimentally. In the course of this experimentation process (exploration), knowledge about “situations” and “movements” is stored in relational schemes as long as no contradictions occur. Such an exploration process results—mathematically speaking—in a relation $R_{{X}}\in Rel({X})$, whereby the identified relation $R_{{X}}$ can be expressed by its characteristic function (e.g., $f_{R_{Situation}}:X\times Y\times {O}\to \left\{0,1\right\}$), which assigns exactly one truth value to each tuple $\tau \in Tup({X})$. After completion of the exploration phase, the evaluation of the characteristic functions can be used to answer questions like “What is the case?” or “What does this observation mean?” in a truth-functional sense and therefore leads to a veridical model. Such a model enables the agent to gain knowledge through simulation or inference, which in turn can then be transfered to reality. To this end, the agent has to compare the representational data structure of the perception (e. g. ${\tau }_{obs}=\left\{X\to x\in dom(X),Y\to y\in dom(Y),\to o\in dom({O})\right\}$) with some of the learned representational data structures of the associated relational scheme:

$\begin{array}{l}{f}_{R_X}(\tau )=\{\begin{array}{ll}True,\hfill & \text{if}\tau \in R_X,\hfill \\ False,\hfill & \text{if} \tau \notin {\text{R}}_X.\hfill \end{array}\end{array}$

If matches are found, the agent understands the incoming information. In semiotics, this process is called denotation and can be realized by a logical compound system (see Figure 4). If no matches are found, an adaptation or coping process is triggered (Wolff et al., 2015).

FIGURE 4

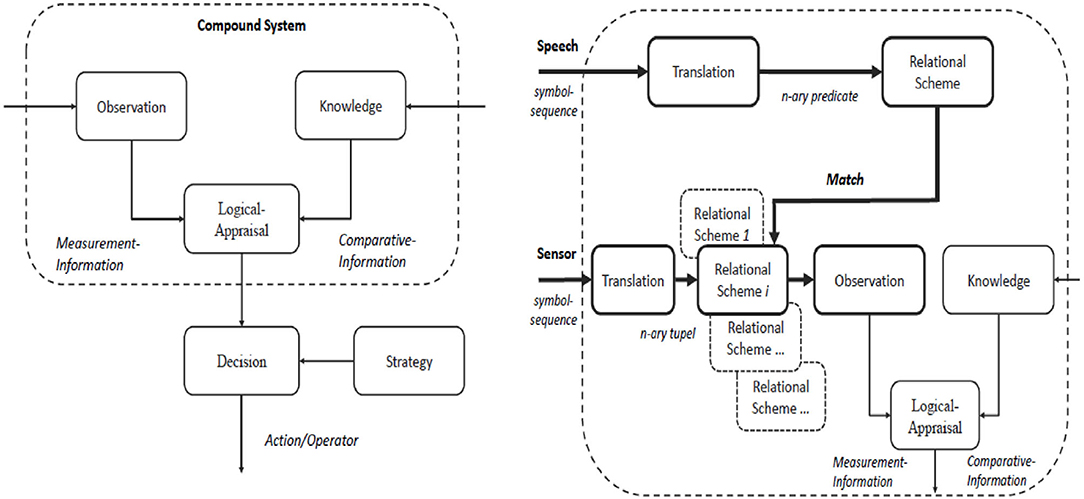
Figure 4. Left: A logical compound system compares measurement information and model knowledge, subsequently a strategy based action is selected. Right: Merging of sensory information (interaction) and language information (communication) based on a double cognitive loop.

In order to apply the dynamic model to the mouse-maze-application properly, we have to specify all attributes and relation schemes of states, situations, actions and movements as well as the corresponding relations that are required: $States=\left\{X,Y\right\}\subset {U}$, R(States) = (X:dom(X), Y:dom(Y)), R_States ⊆ Tup(States), $Situation=\left\{States,{O}\right\}\subset {U}$, $R(Situation)=(X:dom(X),Y:dom(Y),{O}:dom({O}))$ and R_Situation ⊆ Tup(Situation). $Action=\left\{\Delta X,\Delta Y\right\}\subset {U}$, R(Action) = (ΔX:dom(ΔX), ΔY:dom(ΔY)) and R_Action ⊆ Tup(Action). $Movement=\left\{States,Action\right\}\subset {U}$, R(Movement) = (States:dom(States), Action:dom(Action), States′:dom(States))and R_Movement ⊆ Tup(Movement).

With these definitions suitable representational data structures are provided that are needed for the transformation and integration processes. However, despite the uniform description of the two cognitive loops using linguistic means, there is an essential difference between interaction and communication. Verbal communication operates primarily with object types and refers to predicate symbols as well. In contrast, the perceptive part of interaction is based on sensors and classifiers only, so that no relations between any object types can be directly encoded (Hausser, 2014). Hence, such relations have to be learned by the agent (Wolff et al., 2018). Yet, in a shared environment these different kinds of information can be used to solve the context problem. For this end, we consider the following example, in which the linguistic message “field(x,y) contains cheese” is translated into the binary predicate contain(field(x, y), cheese). In order to obtain the truth value of this statement, it must be checked whether an instance of the object type “cheese” is located at the specified position z = (x, y). That means the agent has to move to this position and take measurements. Then, the corresponding symbol sequence must be transformed into the tuple ${\tau }_{obs}=\left\{X\to x\in dom(X),Y\to y\in dom(Y),{O}\to o\in dom({O})\right\}\in R_{Situation}$, which can now be compared with the entries of the relation $R_{contain}\subseteq \times X\times Y\times {O}$. Please note that this relation is associated to the translated predicate and that an interpretation of the sensor values appropriate to the context is only possible if the proper scheme has been selected (Figure 4). Since both relations are designated by different names, it must be ensured that their denotation is identical, i. e. [contain] = [Situation] must apply.

6. Language Acquisition

So far we discussed how a cognitive agent, being either human or an intelligent machine, could produce and understand utterances that are described in terms of minimalist grammar. An MG is given by a mental lexicon as in example (Table 2), encoding a large amount of linguistic expert knowledge. Therefore, it seems unlikely that speech-controlled user interfaces could be build and sold by engineering companies for little expenses.

Yet, it has been shown that MG are effectively learnable in the sense of Gold's formal learning theory (Gold, 1967). The studies of Bonato and Retoré (2001); Kobele et al. (2002), and Stabler et al. (2003) demonstrated how MG can be acquired by positive examples from linguistic dependence graphs (Nivre, 2003; Boston et al., 2010). The required dependency structures can be extracted from linguistic corpora by means of big data machine learning techniques, such as the expectation maximization (EM) algorithm (Klein and Manning, 2004).

In our terminology, such statistical learning methods only reveal correlations at the exponent level of linguistic signs. By contrast, in the present study we propose an alternative training algorithm that simultaneously analyzes similarities between exponents and semantic terms. Moreover, we exploit both positive and negative examples to obtain a better performance through reinforcement learning (Skinner, 2015; Sutton and Barto, 2018).

The language learner is a cognitive agent 𝔏 in a state X_t, to be identified with 𝔏's mental lexicon at training time t. At time t = 0, X₀ is initialized as a tabula rasa with the empty lexicon

$\begin{array}{ll}{X}_0\leftarrow \varnothing & (22)\end{array}$

and exposed to UMPs produced by a teacher 𝔗. Note that we assume 𝔗 presenting already complete UMPs and not singular utterances to 𝔏. Thus, we circumvent the symbol grounding problem of firstly assigning meanings σ to uttered exponents e (Harnad, 1990), which will be addressed in future research. Moreover, we assume that 𝔏 is instructed to reproduce 𝔗's utterances based on its own semantic understanding. This provides a feedback loop and therefore applicability of reinforcement learning (Skinner, 2015; Sutton and Barto, 2018). For our introductory example, we adopt the simple semantic model from Sect. 5. In each iteration, the teacher utters an UMP that should be learned by the learner.

6.1. First Iteration

Let the teacher 𝔗 make the first utterance (2)

$u_1=\langle \text{the mouse eats cheese},eat(cheese)(mouse)\rangle .$

As long as 𝔏 is not able to detect patterns or common similarities in 𝔗's UMPs, it simply adds new entries directly to its mental lexicon, assuming that all utterances are complex “:” and possessing base type c, i. e. the MG start symbol. Hence, 𝔏's state X_t evolves according to the update rule

$\begin{array}{ll}{X}_t\leftarrow X_{t-1}\cup \left\{\langle e_t,\text{:c},{\sigma }_t\rangle \right\},& (23)\end{array}$

when u_t = 〈e_t, σ_t〉 is the UMP presented at time t by 𝔗.

In this way, the mental lexicon X₁ shown in Table 6 has been acquired at time t = 1.

TABLE 6

Table 6. Learned minimalist lexicon X₁ at time t = 1.

6.2. Second Iteration

Next, let the teacher be uttering another proposition

$\begin{array}{ll}{u}_2=\langle \text{the rat eats cheese},eat(cheese)(rat)\rangle .& (24)\end{array}$

Looking at u₁, u₂ together, the agent's pattern matching module (cf. van Zaanen, 2001) is able to find similarities between exponents and semantics, underlined in Equation (25).

$\begin{array}{ll}{u}_{\text{1}}=\langle \underset{\_}{\text{the}}\text{ mouse }\underset{\_}{\text{eats cheese}}\text{, }\underset{\_}{\text{eat}(\text{cheese})}(\text{mouse})\rangle & (\mathrm{25-1})\end{array}$

$\begin{array}{ll}{u}_{\text{2}}\text{=}\langle \underset{\_}{\text{the}}\text{ rat }\underset{\_}{\text{eats cheese}}\text{, }\underset{\_}{\text{eat(cheese)}}\text{(rat)}\rangle .& (\mathrm{25-2})\end{array}$

Thus, 𝔏 creates two distinct items for the mouse and the rat, respectively, and carries out lambda abstraction to obtain the updated lexicon X₂ in Table 7.

TABLE 7

Table 7. Learned minimalist lexicon X₂ at time t = 2.

Note that the induced variable symbol y and syntactic types d, c are completely arbitrary and do not have any particular meaning to the agent.

As indicated by underlines in Table 7, the exponents the mouse and the rat, could be further segmented through pattern matching, that is not reflected by their semantic counterparts, though. Therefore, a revised lexicon X₂₁, displayed in Table 8 can be devised.

TABLE 8

Table 8. Revised minimalist lexicon X₂₁.

For closing the reinforcement cycle, 𝔏 is supposed to produce utterances upon its own understanding. Thus, we assume that 𝔏 wants to express the proposition eat(cheese)(rat). According to our discussion in Sect. 5, the corresponding signs are retrieved from the lexicon X₂₁ and processed through a valid derivation leading to the correct utterance the rat eats cheese, that is subsequently endorsed by 𝔗.

6.3. Third Iteration

In the third training session, the teacher's utterance might be

$\begin{array}{ll}{u}_3=\langle \text{the mouse eats carrot},eat(carrot)(mouse)\rangle .& (26)\end{array}$

Now we have to compare u₃ with the lexicon entry for eats cheese in (27).

$\begin{array}{ll}\langle \text{the mouse }\underset{\_}{\text{eats}}\text{ carrot, }\underset{\_}{\text{eat}}(\text{carrot})(\text{mouse})\rangle & (\mathrm{27-1})\end{array}$

$\begin{array}{ll}\langle \underset{\_}{\text{eats}}\text{ cheese},\text{ :c},\text{ λy }.\underset{\_}{\text{eat}}(\text{cheese})(\text{y})\rangle .& (\mathrm{27-2})\end{array}$

Another lambda abstraction entails the lexicon X₃ in Table 9.

TABLE 9

Table 9. Learned minimalist lexicon X₃ at time t = 3.

Here, the learner assumes that eats is a simple, lexical category without having further evidence as in Sect. 5.

Since 𝔏 is instructed to produce well-formed utterances, it could now generate a novel semantic representation, such as eat(carrot)(rat). This leads through data base query from the mental lexicon X₃ to the correct derivation (28) that is rewarded by 𝔗.

$\begin{array}{ll}\frac{\langle \text{the},\text{::=n d},ϵ\rangle \langle \text{rat},\text{::n},rat\rangle }{\langle \text{the rat},\text{:d},rat\rangle }\text{ merge-1}& (\mathrm{28-1})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats},\text{::=n =d c},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{carrot},\text{::n},carrot\rangle }{\langle \text{eats carrot},\text{:=d c},(\lambda x.\lambda y.eat(x)(y))(carrot)\rangle }\text{ merge-1}& (\mathrm{28-2})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats carrot},\text{:=d c},(\lambda x.\lambda y.eat(x)(y))(carrot)\rangle }{\langle \text{eats carrot},\text{:=d c},\lambda y.eat(carrot)(y)\rangle }\lambda \text{-appl.}& (\mathrm{28-3})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats carrot},\text{:=d c},\lambda y.eat(carrot)(y)\rangle \langle \text{the rat},\text{:d},rat\rangle }{\langle \text{the rat eats carrot},\text{:c},(\lambda y.eat(carrot)(y))(rat)\rangle }\text{ merge-2}& (\mathrm{28-4})\end{array}$

$\begin{array}{ll}\frac{\langle \text{the rat eats carrot},\text{:c},(\lambda y.eat(carrot)(y))(rat)\rangle }{\langle \text{the rat eats carrot},\text{:c},eat(carrot)(rat)\rangle }\lambda \text{-appl.}& (\mathrm{28-5})\end{array}$

6.4. Fourth Iteration

In the fourth iteration, we suppose that 𝔗 utters

$\begin{array}{ll}{u}_4=\langle \text{the rats eat cheese},eat(cheese)(rats)\rangle & (29)\end{array}$

that is unified with the previous lexicon X₃ through our pattern matching algorithm to yield X₄ in Table 10 in the first place.

TABLE 10

Table 10. Learned minimalist lexicon X₄ at time t = 4.

Underlined are again common strings in exponents or semantics that could entail further revisions of the MG lexicon.

Next, let us assume that 𝔏 would express the meaning eat(carrot)(rats). It could then attempt the following derivation (30).

$\begin{array}{ll}\frac{\langle \text{the},\text{::=n d},ϵ\rangle \langle \text{rats},\text{::n},rats\rangle }{\langle \text{the rats},\text{:d},rats\rangle }\text{ merge-1}& (\mathrm{30-1})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats},\text{::=n =d c},\lambda x.\lambda y.eat(x)(y)\rangle \langle \text{carrot},\text{::n},carrot\rangle }{\langle \text{eats carrot},\text{:=d c},(\lambda x.\lambda y.eat(x)(y))(carrot)\rangle }\text{ merge-1}& (\mathrm{30-2})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats carrot},\text{:=d c},(\lambda x.\lambda y.eat(x)(y))(carrot)\rangle }{\langle \text{eats carrot},\text{:=d c},\lambda y.eat(carrot)(y)\rangle }\lambda \text{-appl.}& (\mathrm{30-3})\end{array}$

$\begin{array}{ll}\frac{\langle \text{eats carrot},\text{:=d c},\lambda y.eat(carrot)(y)\rangle \langle \text{the rats},\text{:d},rats\rangle }{\langle \text{the rats eats carrot},\text{:c},(\lambda y.eat(carrot)(y))(rats)\rangle }\text{ merge-2}& (\mathrm{30-4})\end{array}$

$\begin{array}{ll}\frac{\langle \text{the rats eats carrot},\text{:c},(\lambda y.eat(carrot)(y))(rats)\rangle }{\langle \text{the rats eats carrot},\text{:c},eat(carrot)(rats)\rangle }\lambda \text{-appl.}& (\mathrm{30-5})\end{array}$

However, uttering the rats eats carrot will probably be rejected by the teacher 𝔗 because of the grammatical number agreement error, thus causing punishment by 𝔗. As a consequence, 𝔏 has to find a suitable revision of its lexicon X₄ that is guided by the underlined matches in Table 10.

To this aim, the agent first modifies X₄ as given in Table 11.

TABLE 11

Table 11. Revised minimalist lexicon X₄₁.

In Table 11 the entries for mouse and rat have been updated by a number licensee -a (for Anzahl). Moreover, the entry for the now selects a number type =num instead of a noun. Even more crucially, two novel entries of number type num have been added: a phonetically empty item 〈ϵ, :: = n +a num, ϵ〉 selecting a noun =n and licensing number movement +a, and an item for the plural suffix 〈-s, :: = n +a num, ϵ〉 with the same feature sequence.

Upon the latter revision, the agent may successfully derive rat, rats, and mouse, but also mouses, which will be rejected by the teacher. In order to avoid punishment, the learner had to wait for the well-formed item mice once to be uttered by 𝔗. Yet, the current evidence prevents the agent from correctly segmenting eats, because our shallow semantic model does not sufficiently constrain any further pattern matching. This could possibly be remedied in case of sophisticated numeral and temporal semantic models. At the end of the day, we would expect something alike the hand-crafted lexicon (Table 2) above. For now, however, we leave this important problem for future research.

7. Discussion

With the present study we have continued our work on language aquisition and on the unified description of physical interaction and linguistic communication of cognitive agents (Römer et al., 2019; beim Graben et al., 2020). The requirements for a unified description are primarily given by cognitive architectures. That includes the availability of suitable representational data structures, the satisfiability of the composition-, adaptation- and classification principles as well as the capability for logical reasoning and learning. Such an architecture will be particularly useful if it can explain the behavior of cognitive agents as well as the phylogenetic and ontogenetic development of language from earlier stages of evolution without language. Hence, the agent should be based on a physical symbol system (PSS) (Newell and Simon, 1976), that takes physical symbols from its sensory equipment, composing them into symbolic structures (expressions) and transforms them to new expressions that can generate goal directed actions. For this purpose we devised a grammar-based transformation mechanism that unifies physical interaction and linguistic communication using minimalist grammars (MG) and lambda calculus. To explain how the mechanism works, we have selected some example scenarios of the well known mouse-maze problem (Shannon, 1953). With this mechanism, the incoming sensory information from both cognitive loops can be brought together and transformed into meaningful information that can be saved now in a knowledge base and processed logically. The truth-functional approach that is required for the acquisition of a veridical model of a shared environment is dependent on this mechanism. Further, based on the uniform linguistic processing of interaction and communication the communication participants are able to exchange and synchronize their ideas about a common environment. The use of the information arising from both cognitive loops is also useful here, since linguistic ambiguities can be resolved in this way.

Additionally, we have outlined an algorithm for effectively learning the syntax and semantics of English declarative sentences. Such sentences are presented to a cognitive agent by a teacher in form of utterance meaning pairs (UMP) where the meanings are encoded as formulas of first order predicate logic. This representation allows for the application of compositional semantics via lambda calculus (Church, 1936). For the description of syntactic categories we use Stabler's minimalist grammar (Stabler, 1997; Stabler and Keenan, 2003), (MG) a powerful computational implementation of Chomsky's recent Minimalist Program for generative linguistics (Chomsky, 1995). Despite the controversy between Chomsky and Skinner (Chomsky, 1995), we exploit reinforcement learning (Skinner, 2015; Sutton and Barto, 2018) as training paradigm. Since MG codifies universal linguistic competence through the five inference rules (10–11), thereby separating innate linguistic knowledge from the contingently acquired lexicon, our approach could potentially unify generative grammar and reinforcement learning, hence resolving the abovementioned dispute.

Minimalist grammar can be learned from linguistic dependency structures (Kobele et al., 2002; Stabler et al., 2003; Klein and Manning, 2004; Boston et al., 2010) by positive examples, which is supported by psycholinguistic findings on early human language acquisition (Pinker, 1995; Ellis, 2006; Tomasello, 2006). However, as Pinker (1995) has emphasized, learning through positive examples alone, could lead to undesired overgeneralization. Therefore, reinforcement learning that might play a role in children language acquisition as well (Moerk, 1983; Sundberg et al., 1996), could effectively avoid such problems. The required dependency structures are directly provided by the semantics in the training UMPs. Thus, our approach is explicitly semantically driven, in contrast to the algorithm of Klein and Manning (2004) that regards dependencies as latent variables for EM training.

As a proof-of-concept we suggested an algorithm for simple English declarative sentences. We also have evidence that it works for German and French as well and hopefully for other languages also. Our approach will open up an entirely new avenue for the further development of speech-controlled cognitive user interfaces (Young, 2010; Baranyi et al., 2015).

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was partly funded by the Federal Ministry of Education and Research in Germany under the grant no. 03IHS022A.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work was partly based on former joint publications of the authors with Werner Meyer, Günther Wirsching, and Ingo Schmitt (Wolff et al., 2018; beim Graben et al., 2019b, 2020; Römer et al., 2019). The content of this manuscript has been presented in part at the 10th IEEE International Conference on Cognitive Infocommunications (CogInfoCom 2019, Naples, Italy) (beim Graben et al., 2019b; Römer et al., 2019). According to the IEEE author guidelines a preprint of beim Graben et al. (2020) has been uploaded to arXiv.org.

Footnotes

1. ^Based on the terms used in control theory, we represent the cyclical flow of information in a circular form and denote the cyclical flow as a loop.

2. ^Note, that the opposite point of view is also of interest, in which the agent learns user behavior by analyzing dialogs.

3. ^To avoid confusion in terms of the set ${O}$, we would like to point out that the outputs of the state space model in this work correspond to the specified object types of the mouse-maze-application.

4. ^For the sake of simplicity we refrain from presenting full-fledged X-bar hierarchies (Haegeman, 1994).

5. ^Moreover, we abstract our analysis from temporal and numeral semantics and also from the intricacies of the semantics of noun phrases in the present exposition.

References

Artzi, Y., and Zettlemoyer, L. (2013). Weakly supervised learning of semantic parsers for mapping instructions to actions. Trans. Assoc. Comput. Linguist. 1, 49–62. doi: 10.1162/tacl_a_00209

CrossRef Full Text | Google Scholar

Baranyi, P., Csapo, A., and Sallai, G. (2015). Cognitive Infocommunications (CogInfoCom). Springer. ISBN 9783319196077.

beim Graben, P., Meyer, W., Römer, R., and Wolff, M. (2019a). “Bidirektionale Utterance-Meaning-Transducer für Zahlworte durch kompositionale minimalistische Grammatiken,” in Tagungsband der 30. Konferenz Elektronische Sprachsignalverarbeitung (ESSV), Volume 91 of Studientexte zur Sprachkommunikation, eds P. Birkholz and S. Stone (Dresden: TU-Dresden Press), 76–82.

beim Graben, P., Römer, R., Meyer, W., Huber, M., and Wolff, M. (2019b). “Reinforcement learning of minimalist numeral grammar,” in Proceedings of the 10th IEEE International Conference on Cognitive Infocommunications (CogInfoCom) (Naples: IEEE), 67–72.

beim Graben, P, Römer, R., Meyer, W., Huber, M., and Wolff, M. (2020). Reinforcement learning of minimalist grammars. arXiv[Preprint].arXiv:2005.00359.

Bischof, N. (2009). Psychologie, ein Grundkurs for Anspruchsvolle, 2nd Edn. Stuttgart: Verlag Kohlhammer.

Bonato, R., and Retoré, C. (2001). “Learning rigid Lambek grammars and minimalist grammars from structured sentences,” in Proceedings of the Third Workshop on Learning Language in Logic (Strasbourg), 23–34.

Boston, M. F., Hale, J. T., and Kuhlmann, M. (2010). “Dependency structures derived from minimalist grammars,” in The Mathematics of Language, Vol. 6149 of Lecture Notes in Computer Science, eds C. Ebert, G. Jäger and J. Michaelis (Berlin: Springer), 1–12.

Boullier, P. (2005). “Range concatenation grammars,” in New Developments in Parsing Technology, volume 23 of Text, Speech and Language Technology, eds H. Bunt, J. Carroll, and G. Satta (Berlin: Springer), 269–289.

Chen, P. P. S. (1975). “The entity-relationship model: toward a unified view of data,” in Proceedings of the 1st International Conference on Very Large Data Bases (VLDB75), ed D. S. Kerr (New York, NY: ACM Press), 173.

Chomsky, N. (1995). The Minimalist Program. Number 28 in Current Studies in Linguistics, 3rd printing 1997. Cambridge, MA: MIT Press.

Church, A. (1936). An unsolvable problem of elementary number theory. Am. J. Math. 58, 345. doi: 10.2307/2371045

CrossRef Full Text | Google Scholar

Diessel, H. (2013). “Construction grammar and first language acquisition,” in The Oxford Handbook of Construction Grammar, eds T. Hoffmann and G. Trousdale (Oxford: Oxford University Press), 347–364.

Eliasmith, C. (2013). How to Build a Brain: A Neural Architecture for Biological Cognition. Oxford: Oxford University Press.

Ellis, N. C. (2006). Language acquisition as rational contingency learning. Appl. Linguist. 27, 1–24. doi: 10.1093/applin/ami038

CrossRef Full Text | Google Scholar

Funke, J., (ed.). (2006). Denken und Problemlsen, Enzyklopdie der Psychologie, 8th Edn. Hogrefe: Verlag for Psychologie.

Gee, J. P. (1994). First language acquisition as a guide for theories of learning and pedagogy. Linguist. Educ. 6, 331–354. doi: 10.1016/0898-5898(94)90002-7

CrossRef Full Text | Google Scholar

Gold, E. M. (1967). Language identification in the limit. Inform. Control 10, 447–474. doi: 10.1016/S0019-9958(67)91165-5

CrossRef Full Text | Google Scholar

Haegeman, L. (1994). Introduction to Goverment &Binding Theory, volume 1 of Blackwell Textbooks in Linguistics, 2nd Edn, 1st Edn 1991. Oxford: Blackwell Publishers.

Hale, J. T. (2011). What a rational parser would do. Cogn. Sci. 35, 399–443. doi: 10.1111/j.1551-6709.2010.01145.x

CrossRef Full Text | Google Scholar

Harkema, H. (2001). Parsing Minimalist Languages (Ph.D. thesis), University of California, Los Angeles, CA.

Harnad, S. (1990). The symbol grounding problem. Physica D 42, 335–346. doi: 10.1016/0167-2789(90)90087-6

CrossRef Full Text | Google Scholar

Hausser, R. (2014). Foundations of Computational Linguistics. Berlin; Heidelberg; New York, NY: Springer Verlag.

Joshi, A. K., Levy, L. S., and Takahashi, M. (1975). Tree adjunct grammars. J. Comput. Syst. Sci. 10, 136–163. doi: 10.1016/S0022-0000(75)80019-5

CrossRef Full Text | Google Scholar

Joshi, A. K., Vijay-Shanker, K., and Weir, D. (1990). The convergence of mildly context-sensitive grammar formalisms. Technical Report MS-CIS-90-01, University of Pennsylvania.

Jungclaussen, H. (2001). Kausale Informatik. Wiesbaden: Deutscher Universittsverlag.

Klein, D., and Manning, C. D. (2004). “Corpus-based induction of syntactic structure: models of dependency and constituency,” in Proceedings of the 42nd Annual Meeting of the Association for Computational Linguistics, eds D. Scott, W. Daelemans, and M. A. Walker (Stroudsburg, PA: Association for Computational Linguistics), 478–485.

Kobele, G. M. (2009). “Syntax and semantics in minimalist grammars,” in Proceedings of ESSLLI 2009 (Bordeaux).

Kobele, G. M., Collier, T. C., Taylor, C. E., and Stabler, E. P. (2002). “Learning mirror theory,” in Proceedings of the Sixth International Workshop on Tree Adjoining Grammar and Related Frameworks (TAG+2002), ed R. Frank (Stroudsburg, PA: Association for Computational Linguistics), 66–73.

Kracht, M. (2003). The Mathematics of Language. Berlin; New York, NY: Mouton de Gruyter.

Kuhlmann, M., Koller, A., and Satta, G. (2015). Lexicalization and generative power in CCG. Comput. Linguist. 41, 215–247. doi: 10.1162/COLI_a_00219

CrossRef Full Text | Google Scholar

Kwiatkowski, T., Goldwater, S., Zettlemoyer, L., and Steedman, M. (2012). “A probabilistic model of syntactic and semantic acquisition from child-directed utterances and their meanings,” in Proceedings of the 13th Conference of the European Chapter of the Association for Computational Linguistics, EACL '12 (Stroudsburg, PA: Association for Computational Linguistics), 234–244.

PubMed Abstract | Google Scholar

Lausen, G. (2005). Datenbanken, Grundlagen und XML-Technologien. München: Elsevier GmbH, Spektrum Akademischer Verlag. 1. Auflage.

Lohnstein, H. (2011). Formale Semantik und natrliche Sprache, 2nd Edn. Berlin: De Gruyter.

Mainguy, T. (2010). A probabilistic top-down parser for minimalist grammars. ArXiv, abs/1010.1826v11.

PubMed Abstract | Google Scholar

Michaelis, J. (2001). “Derivational minimalism is mildly context-sensitive,” in Logical Aspects of Computational Linguistics, Volume 2014 of Lecture Notes in Artificial Intelligence (Berlin: Springer), 179–198.

Moerk, E. L. (1983). A behavioral analysis of controversial topics in first language acquisition: reinforcements, corrections, modeling, input frequencies, and the three-term contingency pattern. J. Psycholinguist. Res. 12, 129–155. doi: 10.1007/BF01067408

CrossRef Full Text | Google Scholar

Newell, A., and Simon, H. A. (1976). Computer science as empirical inquiry: Symbols and search. Commun. ACM 19, 113–126. doi: 10.1145/360018.360022

CrossRef Full Text | Google Scholar

Nivre, J. (2003). “An efficient algorithm for projective dependency parsing,” in Proceedings of the Eighth International Workshop on Parsing Technologies (IWPT2003) (Nancy), 149–160.

Niyogi, S. (2001). “A minimalist implementation of verb subcategorization,” in Proceedings of the Seventh International Workshop on Parsing Technologies (IWPT2001) (Beijing).

Pinker, S. (1995). “Language acquisition,” in Language: An Invitation to Cognitive Science, Chapter 6, eds L. R. Gleitman, D. N. Osherson, M. Liberman, L. R. Gleitman, D. N. Osherson, and M. Liberman (Cambridge, MA: MIT Press), 135–182.

Römer, R., beim Graben, P., Huber, M., Wolff, M., Wirsching, G., and Schmitt, I. (2019). “Behavioral control of cognitive agents using database semantics and minimalist grammars,” in 2019 10th IEEE International Conference on Cognitive Infocommunications (CogInfoCom) (Naples).

Schönfinkel, M. (1924). Über die Bausteine der mathematischen Logik. Mathematische Annalen 92, 305–316. doi: 10.1007/BF01448013

CrossRef Full Text | Google Scholar

Seki, H., Matsumura, T., Fujii, M., and Kasami, T. (1991). On multiple context-free grammars. Theor. Comput. Sci. 88, 191–229. doi: 10.1016/0304-3975(91)90374-B

CrossRef Full Text | Google Scholar

Shannon, C. E. (1953). Computers and automata. Proc. Institute Radio Eng. 41, 1234–1241. doi: 10.1109/JRPROC.1953.274273

PubMed Abstract | CrossRef Full Text | Google Scholar

Skinner, B. F. (2015). Verbal Behavior, 1st Edn 1957. Mansfield Centre, CT: Martino Publishing.

Stabler, E. (1997). “Derivational minimalism,” in Logical Aspects of Computational Linguistics (LACL96), volume 1328 of Lecture Notes in Computer Science, ed C. Retoré (New York, NY: Springer), 68–95.

PubMed Abstract | Google Scholar

Stabler, E. P. (2011a). “Computational perspectives on minimalism,” in Oxford Handbook of Linguistic Minimalism, ed C. Boeckx (Oxford: Oxford University Press), 617–641.

Stabler, E. P. (2011b). “Top-down recognizers for MCFGs and MGs,” in Proceedings of the 2nd Workshop on Cognitive Modeling and Computational Linguistics (Portland, OR: Association for Computational Linguistics), 39–48.

Stabler, E. P., Collier, T. C., Kobele, G. M., Lee, Y., Lin, Y., Riggle, J., et al. (2003). “The learning and emergence of mildly context sensitive languages,” in Advances in Artificial Life, volume 2801 of Lecture Notes in Computer Science, eds W. Banzhaf, T. Christaller, P. Dittrich, J. T. Kim, and J. Ziegler (Berlin: Springer), 525–534.

Stabler, E. P., and Keenan, E. L. (2003). Structural similarity within and among languages. Theor. Comput. Sci. 293, 345–363. doi: 10.1016/S0304-3975(01)00351-6

CrossRef Full Text | Google Scholar

Stanojević, M., and Stabler, E. (2018). “A sound and complete left-corner parsing for minimalist grammars,” in Proceedings of the Eight Workshop on Cognitive Aspects of Computational Language Learning and Processing, eds M. Idiart, A. Lenci, T. Poibeau, and A. Villavicencio (Stroudsburg, PA: Association for Computational Linguistics), 65–74.

Sundberg, M. L., Michael, J., Partington, J. W., and Sundberg, C. A. (1996). The role of automatic reinforcement in early language acquisition. Anal. Verbal Behav. 13, 21–37. doi: 10.1007/BF03392904

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutton, R. S., and Barto, A. G. (2018). Reinforcement Learning: An Introduction. Cambridge, MA; London: The MIT Press.

Tomasello, M. (2006). First steps toward a usage-based theory of language acquisition. Cogn. Linguist. 11:61. doi: 10.1515/cogl.2001.012

CrossRef Full Text | Google Scholar

van Zaanen, M. (2001). “Bootstrapping syntax and recursion using alignment-based learning,” in Proceedings of the Seventeenth International Conference on Machine Learning (San Francisco, CA), 1063–1070.

Vera, A., and Simon, H. (1993). Situated action: a symbolic interpretation. Cogn. Sci. 17, 7–48. doi: 10.1207/s15516709cog1701_2

CrossRef Full Text | Google Scholar

Wegner, P. (2003). Lambda Calculus. Hoboken, NJ: John Wiley and Sons Ltd., GBR.

Wirsching, G., and Lorenz, R. (2013). “Towards meaning-oriented language modeling,” in Proceedings of the 4th IEEE International Conference on Cognitive Infocommunications (CogInfoCom) (Budapest), 369–374.

Wolff, M., Huber, M., Wirsching, G., Römer, R., Graben, P., and Schmitt, I. (2018). “Towards a quantum mechanical model of the inner stage of cognitive agents,” in 2018 9th IEEE International Conference on Cognitive Infocommunications (CogInfoCom) (Budapest: IEEE).

Wolff, M., Römer, R., and Wirsching, G. (2015). “Towards coping and imagination for cognitive agents,” in 2015 6th IEEE International Conference on Cognitive Infocommunications (CogInfoCom) (Gyor: IEEE), 307–312.

Wolff, M., Tschpe, C., Römer, R., and Wirsching, G. (2013). “Subsymbol-symbol-transduktoren,” in Proceedings of “Elektronische Sprachsignalverarbeitung (ESSV),” volume 65 of Studientexte zur Sprachkommunikation, eds P. Wagner (Dresden: TUDpress), 197–204.

Young, S. (2010). “Still talking to machines (cognitively speaking),” in Conference of the International Speech Communication Association, INTERSPEECH 2010, eds T. Kobayashi, K. Hirose, and S. Nakamura (Makuhari: ISCA), 1–10.

Zettlemoyer, L. S., and Collins, M. (2005). “Learning to map sentences to logical form: structured classification with probabilistic categorial grammars,” in Proceedings of the Twenty-First Conference on Uncertainty in Artificial Intelligence, UAI'05 (Arlington, VA: AUAI Press), 658–666.