Automated Deep Lineage Tree Analysis Using a Bayesian Single Cell Tracking Approach

Single-cell methods are beginning to reveal the intrinsic heterogeneity in cell populations, arising from the interplay of deterministic and stochastic processes. However, it remains challenging to quantify single-cell behaviour from time-lapse microscopy data, owing to the difficulty of extracting reliable cell trajectories and lineage information over long time-scales and across several generations. Therefore, we developed a hybrid deep learning and Bayesian cell tracking approach to reconstruct lineage trees from live-cell microscopy data. We implemented a residual U-Net model coupled with a classification CNN to allow accurate instance segmentation of the cell nuclei. To track the cells over time and through cell divisions, we developed a Bayesian cell tracking methodology that uses input features from the images to enable the retrieval of multi-generational lineage information from a corpus of thousands of hours of live-cell imaging data. Using our approach, we extracted 20,000 + fully annotated single-cell trajectories from over 3,500 h of video footage, organised into multi-generational lineage trees spanning up to eight generations and fourth cousin distances. Benchmarking tests, including lineage tree reconstruction assessments, demonstrate that our approach yields high-fidelity results with our data, with minimal requirement for manual curation. To demonstrate the robustness of our minimally supervised cell tracking methodology, we retrieve cell cycle durations and their extended inter- and intra-generational family relationships in 5,000 + fully annotated cell lineages. We observe vanishing cycle duration correlations across ancestral relatives, yet reveal correlated cyclings between cells sharing the same generation in extended lineages. These findings expand the depth and breadth of investigated cell lineage relationships in approximately two orders of magnitude more data than in previous studies of cell cycle heritability, which were reliant on semi-manual lineage data analysis.

1 Introduction

Individual cells grown in identical conditions within populations of either clonal or closely related origin often exhibit highly heterogeneous proliferative behaviour (Skylaki et al., 2016). Deciphering why and how cell heterogeneity is established, maintained and propagated over generations remains a key challenge (Figure 1A). This is increasingly important in studying dynamic developmental processes involving the emergence of diverse cell types committed to different cell fates (Bendall et al., 2014), as well as in pathological scenarios, including cancer (Dagogo-jack and Shaw, 2017).

FIGURE 1

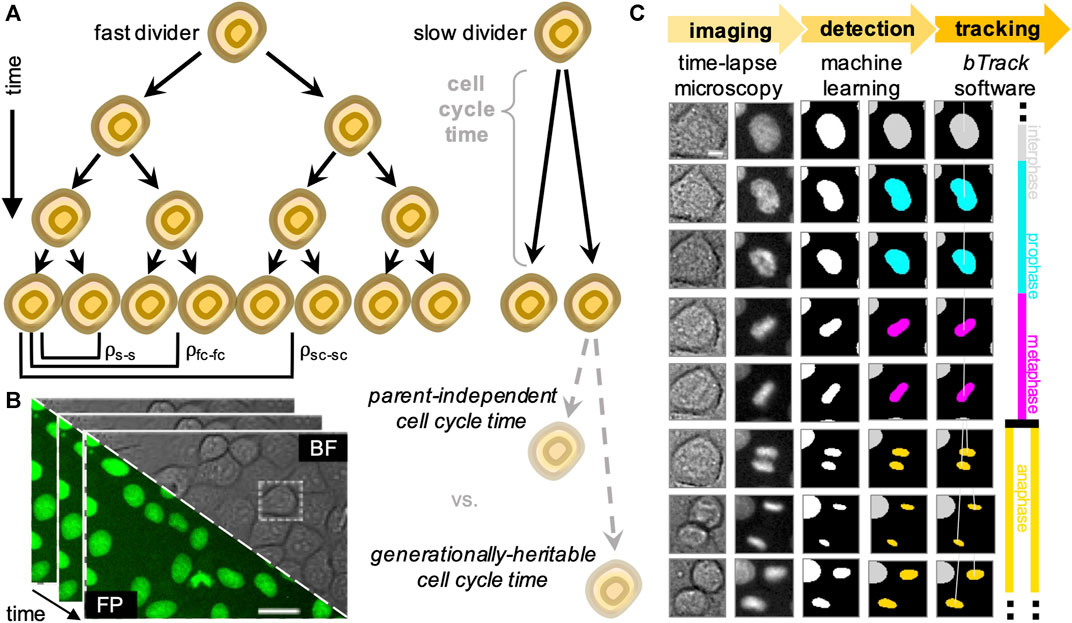
FIGURE 1. Overview of the experimental (data acquisition) and computational (data analysis) design to track single cells and generate lineage trees. (A) We analyse heritability of cell cycle duration across multiple cell generations using automatically reconstructed multi-generational lineage trees. (B) Sequential fields of view obtained by live-cell imaging experiments, showing both brightfield (BF) and fluorescence (FP). Scale bar = 20 μ m. (C) Fully automated, deep learning-based movie analysis consists of a cell detection step using information from bright-field (col. 1) and fluorescence (col. 2) time-lapse microscopy channels. Cells are localised using the segmentation network (col. 3) and labelled according to their mitotic state by a trained classifier (col. 4). Our software then performs multi-object tracking to reconstruct individual cell trajectories (col. 5) and assembles the parent-children relationships (col. 6) into lineage tree representations. Scale bar = 5 μ m.

The contribution of stochasticity and determinism to the origins of cell cycle duration heterogeneity in cultured populations has been examined previously (Sandler et al., 2015; Chakrabarti et al., 2018; Kuchen et al., 2020). However, these analyses have been performed by manually annotating movies, which is laborious and limits the depth and statistical power to study more distant relationships amid noisy data. Despite major efforts in the area of automated cell detection and tracking (Bao et al., 2006; Jaqaman et al., 2008; Downey et al., 2011; Amat et al., 2014; Magnusson et al., 2015; Schiegg et al., 2015; Faure et al., 2016; Hilsenbeck et al., 2016; Skylaki et al., 2016; Stegmaier et al., 2016; Akram et al., 2017; Tinevez et al., 2017; Ulman et al., 2017; Allan et al., 2018; Hernandez et al., 2018; McQuin et al., 2018; Schmidt et al., 2018; Wen et al., 2018; Wolff et al., 2018; Berg et al., 2019; Han et al., 2019; Moen et al., 2019; Tsai et al., 2019; Fazeli et al., 2020; Lugagne et al., 2020; Stringer et al., 2020; Bannon et al., 2021; Fazeli et al., 2021; Mandal and Uhlmann, 2021; Sugawara et al., 2021; Tinevez, 2021), high-fidelity extraction of multi-generational lineages remains a major bottleneck and rate-limiting step in microscopy image analysis. The requirement for additional human oversight to manually curate, or correct, the tracker outputs represents a laborious, time-consuming and often error-prone task. This results in trade-offs being made between the minimum experimental replicates sufficient for reliable low-throughput analysis and maximum volumes of imaging data that researchers are capable to semi-manually process. Further, no single tracking algorithm is likely to be universally performant across all experimental datasets, necessitating an ecosystem of algorithms for scientists to choose from.

To increase the throughput of single-cell studies focusing on cell relationships within their lineages, we developed a hybrid deep learning and cell tracking approach to automatically reconstruct lineage trees from a corpus of live-cell data with single-cell resolution (Figure 1B). Our workflow consists of a cell detection step, where individual cells are segmented from live-cell images with a wide range of cell densities and fluorescence intensities. The segmented nuclei are subsequently classified according to their cell cycle stage based on their chromatin morphology, followed by a Bayesian tracking algorithm for unsupervised single-cell tracking of cell populations imaged using time-lapse microscopy (Figure 1C).

Benchmarking results confirm that our open-source Python pipeline connects single-cell observations into biologically relevant trajectories and correctly identifies cell divisions and relationships within cell families with high fidelity. Enabled by our fully automated approach, we extracted 20,074 single cells organised into 5,325 multi-generational cell lineages with annotated ancestor-descendant relationships in graphical lineage tree representations. This repository of fully annotated cell tracks corresponds to two orders of magnitude more single-cell data than in previous studies of cell cycle heritability (Sandler et al., 2015; Chakrabarti et al., 2018; Kuchen et al., 2020). To demonstrate the utility of our pipeline, we analyse cell cycle durations of our heterogeneous cell population on single-cell level and determine their cross-generational correlations in extended cell lineages.

2 Methods and Materials

2.1 Image Acquisition

2.1.1 Automated Widefield Microscopy

A custom-built automated epifluorescence microscope was built inside a standard CO₂ incubator (Heraeus BL20) which maintained the environment at 37°C and 5% CO₂. The microscope utilised an 20× air objective (Olympus Plan Fluorite, 0.5 NA, 2.1 mm WD), high performance encoded motorized XY and focus motor stages (Prior H117E2IX, FB203E and ProScan III controller) and a 9.1 MP CCD camera (Point Grey GS3-U3-91S6M). Brightfield illumination was provided by a fibre-coupled green LED (Thorlabs, 530 nm). GFP and mCherry/RFP fluorescence excitation was provided by a LED light engine (Bluebox Optics niji). Cameras and light sources were synchronised using TTL pulses from an external D/A converter (Data Translation DT9834). Sample humidity was maintained using a custom-built chamber humidifier. The microscope was controlled by MicroManager (Edelstein et al., 2014) and the custom-written software OctopusLite, available at: https://github.com/quantumjot/OctopusLite.

2.1.2 Cell Culture Conditions

We used Madin-Darby Canine Kidney (MDCK) epithelial cells as a model system. Wild-type MDCK cells were grown, plated and imaged as described previously (Norman et al., 2012; Bove et al., 2017). To enable visualisation and tracking of the cells, we used a previously establish MDCK line stably expressing H2B-GFP (Bove et al., 2017). Cells were seeded at initial density of ≈3 × 10⁴ cells/cm² in 24-well glass-bottom plates (ibidi). The imaging was started 2–3 h after seeding. Imaging medium used during the assay was phenol red free DMEM (Thermo Fisher Scientific, 31053), supplemented with fetal calf serum (Thermo Fisher Scientific, 10270106) and antibiotics.

2.1.3 Time-Lapse Movie Acquisition

We acquired a dataset of 44 long duration (∼ 80 h) time-lapse movies of MDCK wild-type cells in culture across nine biological replicates. A typical experiment captured multiple locations for over 80 h with a constant frame acquisition frequency of 4 min for each position. Multi-location imaging was performed inside the incubator-scope for durations of ≈1,200 images (80 h). In total, the dataset comprised 52,896 individual 1,600 × 1,200 × 2 (530 × 400 μm) channel images (brightfield and the nuclear marker H2B-GFP), containing ∼250,000 unique cells. This dataset of >3,500 h spans densities from isolated cells to highly confluent monolayers.

2.2 Software Implementation

2.2.1 Image Processing

All image processing was performed in Python, using scikit-image, scikit-learn, Tensorflow 2.4, on a rack server running Ubuntu 18.04LTS with 256 Gb RAM and NVIDIA GTX1080Ti GPUs. The btrack package was implemented in Python 3.7 and C/C++ using CVXOPT, GLPK, Numpy and Scipy libraries. We tested the software on OS X, Ubuntu and Windows 10 and found the btrack algorithm to be performant even on basic commodity hardware such as laptops. We have provided extensive documentation online, visualisation tools, and user-friendly tutorials with tracking examples, example data and installation instructions.

2.2.2 Data Visualisation Tools

In addition, we developed a track visualization layer and interactive lineage tree plugin for the open-source multi-dimensional image viewer, napari-arboretum (Sofroniew et al., 2021) available at: https://github.com/quantumjot/Arboretum. To visualize single cell tracking data using the napari-integrated Tracks layer, follow the fundamentals tutorial available at: https://napari.org/tutorials/applications/cell_tracking.

2.3 Cell Tracking Pipeline

In this subsection, we provide a detailed description of our step-wise pipeline to process the raw microscopy image data to extract reconstructed lineage tree information in a fully automated manner. However, it should be noted that the steps in our workflow function independently, allowing users to integrate different software tools into our modular pipeline based on their preference. This is including, but not limited to, the popular segmentation algorithms such as CellPose (Stringer et al., 2020) or StarDist (Schmidt et al., 2018).

2.3.1 Cell Instance Segmentation

To localise cells in the raw fluorescence images, we constructed a U-Net (Ronneberger et al., 2015) to first segment cell nuclei in the time-lapse microscopy images (Figure 2) using a semantic segmentation approach. We used residual blocks (He et al., 2015) in each of the five convolutional up and down layers (3 × 3 kernels), and uses max-pooling and nearest neighbor upscaling to down and upsample respectively. The final layer of the network is a 1 × 1 convolution with two kernels in the case of a binary segmentation, with a per-pixel softmax activation. The final segmentation map is decided by arg max function on the stack of class-corresponding maps, outputting the class with highest probability at each position in the FoV. We trained the network with 150 hand-segmented training images with ranging levels of cell confluency, from which regions of 768 × 768 pixels were randomly cropped using on-the-fly augmentations such as cropping, rotation, flipping, noise addition, uneven illumination simulation, scale and affine deformations. At train time, we used a weighted per-pixel cross entropy loss function (Ronneberger et al., 2015) to force the network to prioritise regions separating proximal nuclei. To achieve accurate learning of the border pixels, we constructed pixel-wise weight maps using a difference of Gaussian (DoG) filter on a Euclidean distance map to upweight the importance of pixels at either foreground-background interface or pixels separating two or more proximal cells. We trained the network using the Adam optimizer (Kingma and Ba, 2015) with batch normalisation, a batch size of 16 for 500 epochs after an extensive search for the most optimal hyperparameters. In the following step, each segmentation mask has all of its non-zero values labelled as individual cell instances while zero values are considered the background. This turns the semantic map into instance segmentation mask, in which each cell can be counted and localized by the centre of mass of each segmented region (Figure 2).

FIGURE 2

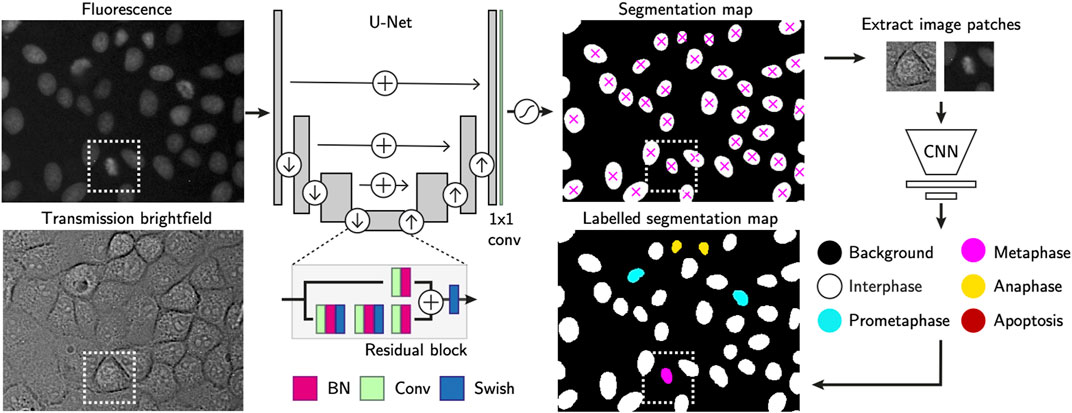
FIGURE 2. Single-cell annotation workflow. Cell instances are segmented from fluorescence images of their H2B-GFP labelled nuclei. The U-Net consists of residual blocks and residual skip connections. A final 1 × 1 convolution layer, followed by softmax activation generates the output. Detected cells are localised using the centre of mass and used to crop nucleus-centred image patches from both transmission and fluorescence images. These serve as inputs to a CNN-based cell state classifier to label instantaneous phase of each segmented object. Labels indicate whether the cell is in interphase, mitosis or apoptosis. Scale bars = 20 µm.

2.3.2 Cell State Classification

In the following, optional step, the segmentation masks have each single cell region cropped as image patches of 64 × 64 pixels. Those are extracted from the corresponding cell positions in both transmission and fluorescence channel images. Our proprietary cell state classifier (Figure 2) is used to label the phase of the current state each cell is in [s ∈ (Interphase, Prometaphase, Metaphase, Anaphase, Apoptosis)].

The instantaneous cell state is labelled by a convolutional neural network based classifier. Its feature extractor consists of five connvolutional layers with 3 × 3 kernels, each of which doubles the 3D input image in depth. Max-pooling operations downsample the activations after each convolution layer. A fully connected layer outputs a flattened array of 256 features-long representation, after which dropout is applied to perform implicit data augmentation. The final linear classifier outputs the softmax probability for each of the five classes, with the highest score considered to be the predicted label.

We performed the cell state classifier training with ∼15,000 manually annotated examples of the extent of the cell nucleus, capturing the diversity of cell nuclear morphology during the cell cycle or at cell cessation. We used categorical cross entropy to calculate loss. The detailed protocol together with user-friendly tutorial to train-your-own-model for cell cycle classification is available at: https://github.com/lowe-lab-ucl/cnn-annotator.

2.3.3 Tracklet Linking Using a Bayesian Belief Matrix

The first step of the tracking algorithm is to assemble tracklets by linking cell detections over time that do not contain cell division events (Figure 3A).

FIGURE 3

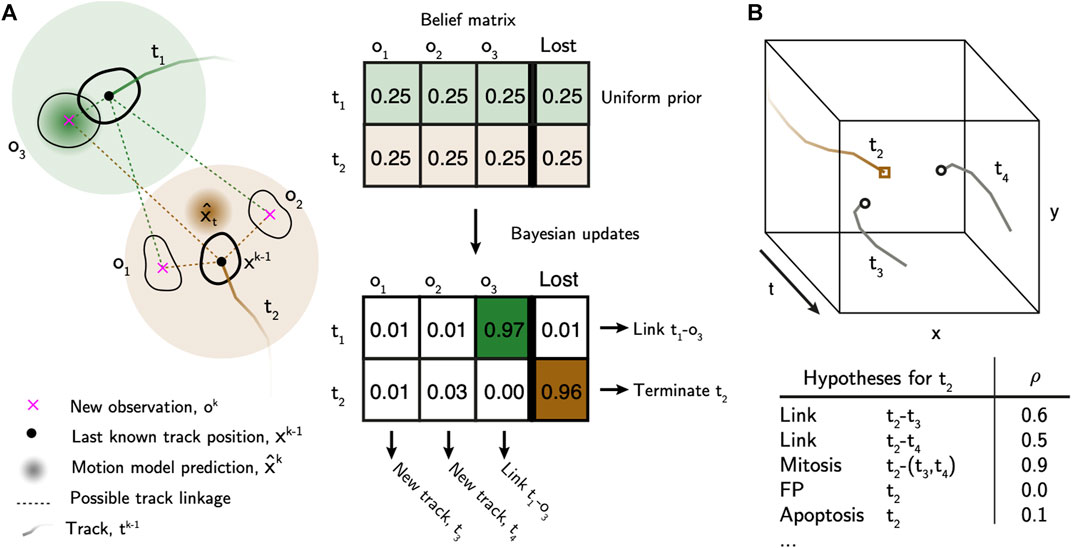
FIGURE 3. Bayesian tracking approach overview. (A) Bayesian belief matrix with uniform prior is constructed for tracklet association. Using the localised and labelled cell observations, btrack uses Kalman filters to predict the future state of the cell (x̂) from previous observations. Each object appearing in the new frame has uniform prior probability of track association or loss. The belief matrix is an N x (M+1) matrix where N equals number of active tracks and M is the number of detected objects per field of view. Bayesian updates are performed using the predicted track positions and state information to calculate the probability that tracks are considered lost, or to be linked to an object. Objects which are not assigned, initialise new tracks. T1 represents a simple association, where the prediction matches the observation O1. In T2 the cell divides, meaning that there is no simple association. New tracks T3 and T4 are initialised. (B) Global track optimisation. An n-dimensional local search creates all possible hypotheses, each with an associated likelihood, for each track based on user defined parameters. Several hypotheses are generated for Track T2, as in (A): possible linkage to T3 or T4, T2 undergoes mitosis generating T3 and T4, T2 is a false positive track or that T2 undergoes apoptosis. The log-likelihood of each hypothesis (ρ) is calculated using the image and motion features. These hypotheses are evaluated in a global optimisation step to generate the final tracking results.

Let ${\mathcal{T}}^{k-1}$ be the set of tracklets in frame k − 1 and ${\mathcal{O}}^k$ be the set of cells observed in the current frame k, where track $t_j\in {\mathcal{T}}^{k-1}$ and object $o_i\in {\mathcal{O}}^k$. The algorithm attempts to calculate the posterior probability of assigning $t_j^{k-1}\to o_i^k$ and also of being lost. To do so, we create a Bayesian belief matrix (Narayana and Haverkamp, 2007) of all possible associations, B^n×(m+1), where n is the number of active tracklets ($|{\mathcal{T}}^{k-1}|$), and m is the number of cell observations ($|{\mathcal{O}}^k|$). We initialize B with a uniform prior probability of association b_ji = P(t_j → o_i) = 1/(m + 1), where m + 1 denotes the fact that the association can be to another object, or lost.

Next, we perform Bayesian updates on B using evidence from motion models and the cell state classifier. Each tracklet initialises its own Kalman filter (Kalman, 1960) that is used to provide estimates of the future state of the cell. The state labels from the cell classifier are then used to associate observations to tracklets, based on visual features observed by the cell classifier which distinguishes typical nuclear morphology changes and chromatin condensation levels. For a given object o_i and a given tracklet t_j, we first update the belief matrix given the evidence E:

$b_{ji}≔\frac{P(E|t_j\to o_i)\times b_{ji}}{P(E)}(1)$

We use estimates from the Kalman filters, and a transition matrix of cell state transitions using the CNN features, to determine P(E|t_j → o_i). For the motion estimates, we use a constant velocity model in this case, although other models are possible. The output of the Kalman filter is an estimate of the future position and error in position, modelled as a multivariate normal distribution with a diagonal covariance matrix. As such, we can define a computationally simple approximation of the probability that the estimated new position of t_j lies within a units (e.g. pixels) of the new observation o_i:

$\begin{array}{c}\hfill f(x,\mu ,\sigma ,a)=\frac{1}{2}\left[\text{erf}\left(\frac{x-\mu +a}{\sigma \sqrt{2}}\right)-\text{erf}\left(\frac{x-\mu -a}{\sigma \sqrt{2}}\right)\right]\\ \hfill P(E_{\text{motion}}|t_j\to o_i)\approx \prod _{d\in \{x,y,z\}}f(x_d,{\mu }_d,{\sigma }_d,a)\end{array}(2)$

where μ_d and σ_d represent the estimate of the position and standard deviation of the motion model prediction in each spatial dimension. The advantage of this approach is that, not only do we include the difference between the new object position and the motion model prediction, but also include the motion model uncertainty into the Bayesian update. Further, we can use appearance information to inform the update. Let S be the set of states that each object is labelled with by the cell state classifier. We use a transition matrix of cell state transitions to determine the probability of linking two observations based on their respective states:

$P(E_{\text{appearance}}|t_j\to o_i)=P(S_j={\text{s}}_j,S_i={\text{s}}_i),s\in S(3)$

where s_i and s_j are the states (as labelled by the cell state classifier) for the new observation and the last observation of the tracklet respectively. Importantly, this transition matrix enables the tracker to penalise transitions such as Metaphase → Anaphase, preventing track linking for these cases, and allowing later steps of the algorithm to more accurately identify cell divisions. Combining these motion and appearance features, we arrive upon our estimate of P(E|t_j → o_i):

$P(E|t_j\to o_i)=P(E_{\text{motion}}|t_j\to o_i)\cdot P(E_{\text{appearance}}|t_j\to o_i)(4)$

and:

$P(E)=P(E|t_j\to o_i)\cdot b_{ji}+P(E|\neg t\to o)\cdot (1-b_{ji})(5)$

where, P(E|¬t → o) represents the probability of not assigning an object to a tracklet (i.e. the false positive detection rate), and is a hyper-parameter of the model. We then update beliefs for all other objects (≠ i), and the lost column, with track t_j, normalizing such that ${\sum }_{i=1}^{m+1}{b}_{ji}=1$. As such, we treat the lost column of the belief matrix as with the real objects, and do not need to perform explicit updates.

The tracking algorithm can be used with two different methods to update the belief matrix, B:

• EXACT—where the updates use the full sets of objects, ${\mathcal{O}}^k$, which is the method of choice for all the downstream analysis in this paper, or

• APPROXIMATE—where the updates use a subset of the objects within a user defined distance from the current track. This is computationally more efficient for very large numbers of objects and tracks, at the expense of evaluating all possible linkages and penalising, for example, a mixture of fast moving objects in a field of slow moving ones.

Finally, given the belief matrix, we associate observations by choosing the hypothesis with the maximum posterior probability for each tracklet. Objects without an association initialise a new set of tracklets. Tracklets without an object association are flagged as lost and are maintained as active until reaching a threshold number of missing observations. Tracklets associated with an object are linked, and the motion and state models are updated with the new evidence. This combination of motion and cell state information in the belief matrix approach improves, for example, the subsequent detection of cell divisions, by ensuring that daughter cells are not incorrectly linked to parent cells.

2.3.4 Global Track Optimization

After linking observations into tracklets, they are next assembled into tracks and lineage trees using multiple hypothesis testing (Al-Kofahi et al., 2006; Bise et al., 2011) to identify a globally optimal solution. We built an efficient hypothesis engine, which proposes possible origin and termination fates for each track based on their appearance and motion features (Figure 3B, Supplementary Materials). The following hypotheses are generated: 1) false positive track, 2) initializing at the beginning of the movie or near the edge of the FoV, 3) termination at the end of the movie or near the edge of the FoV, 4) a merge between two tracklets, 5) a division event, or 6) an apoptotic event. In addition, we added “lazy” initialization and termination hypotheses, allowing cells to initialize or terminate anywhere in the movie. These lazy hypotheses are strongly penalized, but their inclusion significantly improves the output by relaxing the constraints on the optimization problem. The log likelihood of each hypothesis (ρ) is calculated based on the observable features and heuristics. We construct a sparse binary matrix A^(h×2n) ∈ {0, 1} that assigns the h hypotheses to n tracks. The matrix has 2n columns to account for the fact that each hypothesis may describe the initialization and termination of the same or multiple different tracklets. For example, in the case of track joining between tracklets t_i and t_j, a 1 is placed in columns i and n + j. In the case of a mitotic branch, a 1 is placed in column i for the parent tracklet t_i, and columns n + j and n + k for the two child tracklets t_j and t_k. As such, the matrix A can be used to account for all tracklets in the set. We then solve for the optimal set of hypotheses (x*) that maximises the likelihood function:

$x*=\arg {\max }_x{\rho }^{\top }x,\text{s.t.}{\mathbf{A}}^{\top }x=1(6)$

where the optimization space of x is also a binary variable (x ∈ {0, 1}). As a result, the optimal set of hypotheses (x*) accounts for all tracklets in the set. Once the optimal solution has been identified, tracklet merging into the final tracks can be performed. A graph-based search is then used to assemble the tracks into lineage trees, and propagate lineage information such as generational depth, parent and root IDs, from which the tree root (founder cell identity) and leaf cells (those with no known progeny) can be identified.

3 Results

To assess the heterogeneity and the heritability of cell-cycle duration in a population of cells, we sought to automatically reconstruct family trees from individual cells in long-term time-lapse movies. Our time-lapse microscopy dataset (see Section 2.1) spans densities from single cells to highly confluent monolayers, providing a unique dataset to thoroughly test the computational framework.

To provide an initial baseline for our pipeline’s performance on our non-trivial imaging dataset, the assessment of our movie analysis workflow was contrasted to 1) a Python-based, general-purpose particle tracking package, TrackPy (Allan et al., 2018), and 2) a cell tracking-specific ImageJ/FiJi plugin, TrackMate (Tinevez et al., 2017). Both of these tracking engines represent recently-developed popular cell and/or particle tracking frameworks which function as backbones to the current state-of-the-art cell tracking software, such as Usiigaci (Tsai et al., 2019) and MaMuT (Wolff et al., 2018) or Mastodon (Tinevez, 2021), respectively. Detailed description of the tracking softwares calibration can be found in the Supplementary Materials section.

3.1 Bayesian Cell Tracking Approach

To automate data analysis, we developed a fast, open source and easy-to-use cell tracking library to enable calculation of intermitotic durations and the capture of multi-generational lineage relationships. Our pipeline consists of three steps: 1) cell segmentation, 2) cell state labelling, where progression of cells towards division is classified, and 3) cell tracking with lineage tree reconstruction.

3.1.1 Cell Detection Performance

To assess the quality of the cell detection step, we selected three representative fields of view capturing fluorescently labelled nuclei of cells at low, medium and high confluency. We manually annotated the nuclear areas by circling around the cell nuclei to create an instance segmentation mask where pixels of value 0 = background, 1 = foreground, i.e. individual cells. We then computed the nuclear centroid of each cell instance and measured the fidelity of cell detection and localisation by calculating multi-object tracking precision (MOTP, Supplementary Equation S1). Out of 869 cells in total, 847 cells had their centroid localized within acceptable error of ≈1 nuclear radius length (<20 pixels ≈ 7 µm) compared to the ground truth annotations. We report that our pipeline reached sub-pixel precision and outperforms both particle detection approaches with > 5-fold enhancement of the TrackPy- and >2.5-fold higher localisation precision than TrackMate-embedded cell detection method (Figure 4A).

FIGURE 4

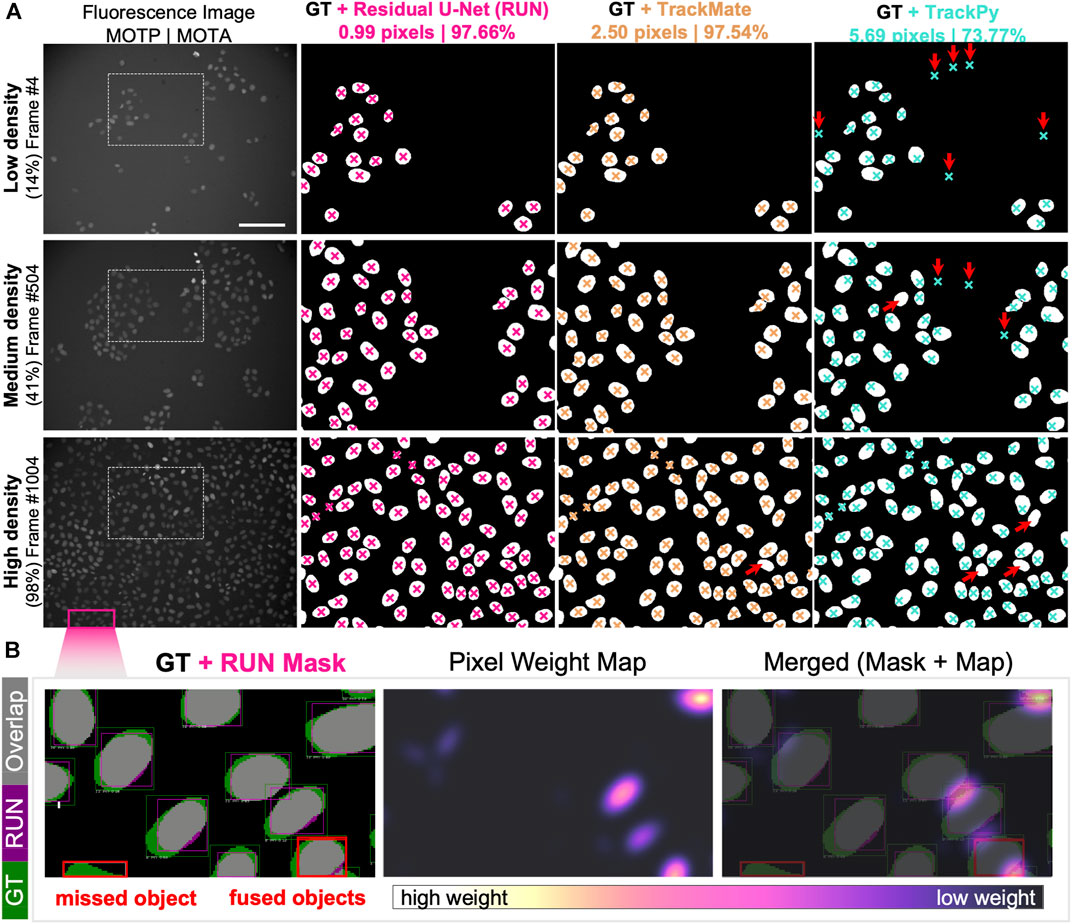
FIGURE 4. Single-cell Segmentation Performance. (A) Comparison of Residual U-Net (pink), TrackMate (beige) and TrackPy (cyan) algorithms in detecting and localising cells in three representative fields of view with low, medium and high cell density. Overlaid are the cropped regions of ground truth segmentation masks with cell centroid markers depicted for zoomed-in region of the original fluorescence channel image (leftmost column). Cell localisation scores for multi-object tracking precision (MOTP) and accuracy (MOTA) are listed above. Red arrows indicate the presence of false-negative (upward right) and false-positive (downward facing arrow) cell detection errors. (B) Detailed overview of segmentation performance on portion of high cell density field of view. (Left) Per-object bounding boxes indicate visual matches between ground truth (GT, green) and Residual U-Net segmentation mask (RUN, magenta) for intersection-over-union score calculation (overlapping areas IoU, grey). Two typical segmentation error types are highlighted (red boxes), where an object is mis-detected (left) and two separate objects are detected as one instance (right). (Centre) Pixel weight map designed to prioritise regions between proximal nuclei. Pixel upweighting is indirectly proportional to amount of free space between cell nuclear instances, as demonstrated in the merged image overlap (Right).

Our cell localisation approach performs a pixel-wise image classification, which offers the opportunity to segment the whole area belonging to the cell nucleus from which centroid coordinates are calculated. To calculate the accuracy of the nuclear area segmentation, we computed the per-object metrics from the residual U-Net and compared them to the manually labelled ground truth (Figure 4B). We report that out of 616 ground truth nuclei in a nearly confluent FoV (Figure 4A), 574 nuclei had at least 50% Intersection over Union (IoU, Supplementary Equation S2), yielding a Jaccard Index (J, Supplementary Equation S3) of 0.933, meaning that 93% of all objects in the FoV were correctly detected. Across the total of 869 cells detected in all assessed FoVs, we achieved an IoU equal to 0.802 and a J of 0.975, while retaining a pixel identity (PI, Supplementary Equation S4) at 0.874 (Supplementary Materials).

To assess the cell state classification performance, we calculated a harmonic mean between the precision and recall (F1-score, Supplementary Equation S5) for each class to be distinguished by our model classifier (Figure 5A). To do this, we plotted a confusion matrix of >2,600 single cell image patches and compared the classifier predictions with human annotations (Figure 5B). Our optional cell state labelling step yields an overall accuracy of >97% with all state labels classified with >96% F1-scores (Figure 5A).

FIGURE 5

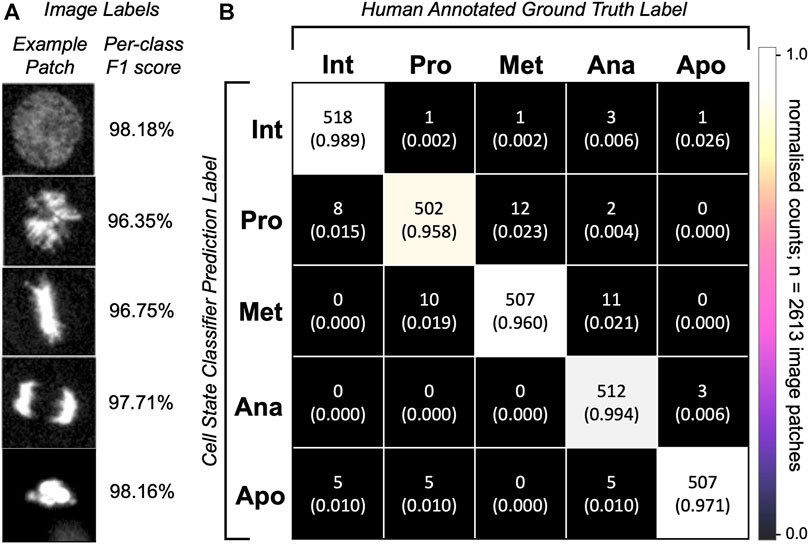
FIGURE 5. Single-cell classification performance. (A) Representative predictions from the trained network for the given images patches. Depicted is an image patch (fluorescence channel only) centred at the cell nucleus representative of the class label with a per-class F1-score calculated on 2,613 single-cell images in the testing dataset. (B) Confusion matrix for cell state labelling of the testing patch dataset (>500 images per class) of cell image crops. Per-class image patch counts and their normalised counts are depicted. Comparison of human annotations vs. the classifier-generated annotations are shown.

3.1.2 Trajectory Following Accuracy

Next, we calculated the multi-object tracking accuracy (MOTA, Supplementary Equation S6) which scores the tracker’s ability to retain cell’s identity and trajectory over longer periods of time. The MOTA score intrinsically penalises the tracking pipeline for static (falsely positive and falsely negative detections) as well as dynamic (identity switches) errors, which often strongly rely on the detection algorithm performance.

We used short movie sequences of up to 20 successive frames from a FoV at three different cell density levels. Observing 2,161 individual cell objects over time, our tracking pipeline performed with 97.66% accuracy of between-frames associations. Identical dataset assessed by TrackMate resulted in a comparable score of 97.54%, while tracking by TrackPy yielded 73.77% accuracy. These results confirm that tracklet linking and object associations between subsequent frames are performed with comparably high fidelity across both tracking tools designed specifically for cell tracking.

However, because the MOTA score is not designed to detect track splitting events, we sought alternative metrics to assess the fidelity of cell division history recording. Although multiple approaches exist to cross-compare tracking performances (Ulman et al., 2017), few of those look specifically at the assessment of branching events of parent tracks and correct assignment of generational depth to the resulting children tracks. Below, we describe the adopted as well as newly defined metrics for measuring the fidelity of track splitting events. Although we continued with using TrackMate for additional comparisons on our validation dataset (Supplementary Materials), it should be noted that further analysis by TrackPy was excluded as this tracking algorithm currently lacks the capacity to follow cases of track branching, typical for dividing cells.

3.1.3 Lineage Tree Reconstruction Fidelity

Reconstructing lineages represents a complex challenge and a common source of tracking errors in multigenerational cell observations. From our track validation dataset, we automatically reconstructed 154 lineage trees which contained at least one mitotic event. These trees were initiated in three instances: 1) through their initial presence in the FoV at the beginning of a movie, 2) as a consequence of migration into the FoV, or 3) upon breakage of an existing branch from its tree.

We manually reconstructed the ground truth lineage trees of 24 randomly selected founder cells, the subsequent progeny of which spanned the entire movie duration and accounted for 1,032 cells including tree founders (Supplementary Materials). This sample accounted for more than 1/3 of initially seeded cells and served as validation dataset for comparison of the ground truth observations to their respective automatically reconstructed lineages. We subjected these trees to multiple lineage fidelity metrics for benchmarking to robustly assess the cell tracking performance with and without manual curation.

For ease of lineage tree visualisation, we provide a convenient visualisation for track survival over time (Supplementary Movie S1), revealing trajectories that can be tracked all the way to the movie start via their ancestors, as an easy way to visually demonstrate the tracking fidelity and identify errors.

3.1.4 Cell Division Correctness

To measure the correctness of parent-child relationships, we calculated the mitotic branching correctness score (MBC, Supplementary Equation S7; Figure 6A and Supplementary Materials) for the detection of mitosis. Here, cell divisions are correctly identified when computer-identified mitoses can be mapped to human-annotated ground truth lineage trees (Bise et al., 2011). Additionally, we introduced a penalty for excessive branching assignment where cells were only scored as “hits” when they were assigned the correct generational depth relative to their founder cell. Similarly, we defined a leaf retrieval score (LRS, Supplementary Equation S8; Figure 6A and Supplementary Materials), which computes the number of all terminal cells in the respective lineage tree appearing in the last frame of the movie. To account for the fidelity of generational depth, in the penalty-applied MBC and LRS calculations, the progeny were considered as correct only when the generational depth relative to the tree root matched the ground truth (Supplementary Materials).

FIGURE 6

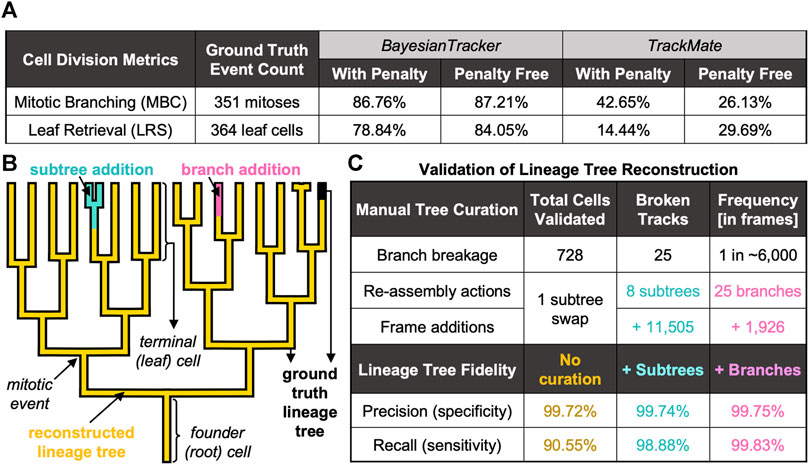
FIGURE 6. Summary of Benchmarking Metrics to Evaluate the Tracking Performance. (A) Summary of cell division-specific metrics for tracker benchmarking on identical number of ground truth events. (B) Visual overview of automated tree reconstruction with additional manual tree re-assembly. Highlighted are the regions of ground truth trees (black thick background) which were correctly recapitulated by btrack (overlaid golden lineage). Upon branch breakage, two types of assembly actions were applied: subtree attachment (cyan), where the branch underwent further splitting, or branch attachment (pink), where the track did not further branch. (C) Summary of additional benchmarking metrics to score the performance of btrack approach with respect to single-cell trajectory following and lineage tree reconstruction in naïve btrack outputs and expert annotator re-assembled trees.

Keeping record of cell division history over the entire duration of the live-cell imaging is necessary to elucidate whether cells with shorter cell cycles have the capacity to dominate the population and competitively outgrow the slowly dividing cells over time. Our software correctly records the cell division history as reflected by both MBC and LRS scores, >86% with and >87% without penalty for MBC and >78% with and >84% without penalisation for LRS (Figure 6A). We report that both the MBC and LRS scores were considerably higher for our btrack algorithm with between ∼ 2-fold and 5.5-fold better performance than our benchmarking standard using both penalised and penalty-free variants (Figure 6A), respectively.

These results highlight the utility of the extra labelling information for cell tracking, as well as our tracker’s sophistication upon building complex predictions based on position and state of each cell. This is in contrast to approaches which employ hard distance thresholding to account for splitting events, or which minimise link distances by connecting cells with their closest neighbour in the subsequent frames. Such algorithms are by default unable to discriminate between false cell divisions, where two independent cells migrate into close proximity below set threshold, and true mitotic events which are accompanied by characteristic morphological changes in nucleic acid organisation in the parent dividing cells as well as progeny cells. Accounting for the “metaphase” and “anaphase” labels in our approach leads to minimising of the occurrence of parent-to-child track fusions (Supplementary Materials). Our scoring system therefore manifests the importance of our optional cell state classification step, which generates additional information for correct division hypotheses creation utilised by the global optimisation engine on the tracking data.

3.1.5 Manual Tree Re-Assembly

To compute further metrics for assessing btrack performance in multi-generational lineage reconstruction, we performed manual tree re-assemblies of our automated btrack output data, where necessary (Figure 6B, Supplementary Materials). This allowed us to perform detailed error analysis by aligning re-assembled trees to the ground truth observations and evaluate the overall extent of the need for human lineage curations, discussed next.

Branch breakages occur due to incorrect cell segmentation (e.g. due to low fluorescence signal), or through tracking errors. However, these breakage errors were very rare (one breakage per ∼6,000 correctly linked frame observations, Figure 6C). When the lost cell is re-detected, it becomes the founder of a newly initialised track. This track now becomes the root of a new tree, which can continue to further grow and divide as a “subtree” of the true tree or exist without further splitting as “branch” (Figure 6B).

3.1.6 Tracking Effectiveness

Finally, we computed metrics reflecting how well the human-annotated cell trajectories are followed by the reconstructed lineage trees (recall; Supplementary Equation S9) and vice versa (precision; Supplementary Equation S10) (Bise et al., 2011).

Without any manual curation, our btrack algorithm faithfully follows >90% of the human-annotated cell trajectories (recall) with over >99% of observations in agreement with the ground truth trees (precision) (Figure 6C). Taking further advantage of our large dataset, we randomly sampled an additional 302 unseen, automatically reconstructed trees from multiple movies. For each tree, we visually scored them as sufficient if they had >90% recall of the ground truth tree as determined by an expert annotator, which added up to 201 out of 370 reconstructed trees overall.

To quantify the remainder of the trees containing one or more errors, we returned to our fully annotated validation dataset to manually re-assemble the broken trees. We needed to perform only eight “subtree” re-assembly actions to the original trees (Supplementary Materials), which added 11,505 frame observations, and a single subtree swap (where part of the tree was falsely associated with another tree). Although the accuracy scores were further enhanced to >99% recall by additional human annotation via tree re-assembly (Figure 6B), we report that our workflow achieves competitive performance on long-term live-cell imaging data even in fully unsupervised manner (Figure 6C). This is essential to investigate the existence of inheritable cell cycle characteristics and their regulation using large datasets.

3.2 Single Cell Cycling Duration Analysis

Having validated the lineage tree reconstructions, we pooled the tracking data from the entire dataset of 44 time-lapse movies. First, we removed those cells which were partially resolved i.e. founding parents (root cells) or progeny (leaf cells) in the reconstructed lineages. This yielded 22,519 cells, organised into lineage trees spanning up to eight generations. Next, we calculated the per-cell inter-mitotic time as the time between the first appearance of separated chromosomes during mitosis (labelled as anaphase by the CNN; due to the temporal sampling this may be before cytokinesis occurs) to the frame preceding the next anaphase (Figure 7A).

FIGURE 7

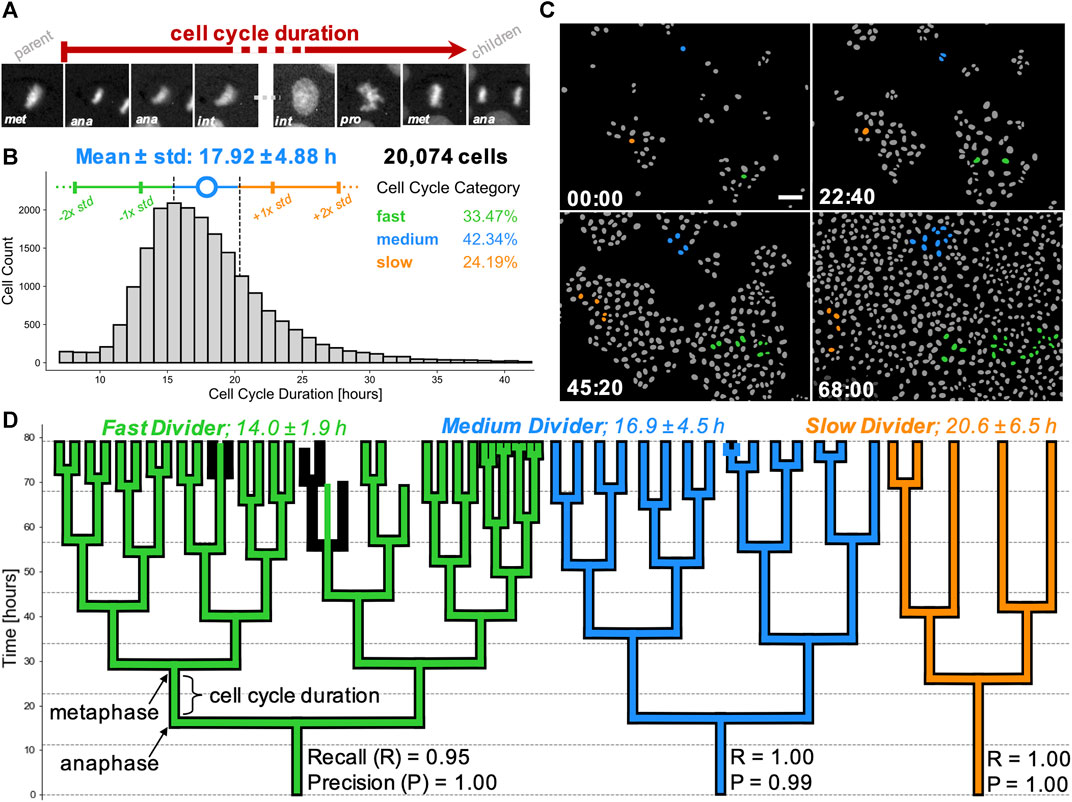
FIGURE 7. Cell cycling heterogeneity and colony expansion capacity within single cell clones. (A) Cell cycle duration, defined here as the time elapsed between two subsequent anaphases, from the mitosis of reference cell’s parent (first image patch) to division into two children cells (last image patch). Scale bar = 5 µm. (B) Calculated cell cycle duration distribution over the pooled MDCK live-cell imaging dataset from 5,325 unique lineage trees. Error bars (colored vertical bars) show one and two standard deviations around the mean (blue circle) of tracked cells for generational depths spanning 1 to 6 (generations #0 and #7 were excluded as those corresponded to the tree root of leaf cells). Cell categorisation into fast (green), medium (blue) and slow (orange) dividers is depicted as below, within or above 1/2 standard deviation away from the mean (dashed black vertical lines), respectively. Percentages of single cells belonging to each category are stated. (C) Sequence of four colourised binary masks with segmented individual cells (grey) on background (black), highlighting cell proliferation from the start (top left) to the end (bottom right) of a representative movie. Time in hh:mm is indicated in the bottom left corner. Founder cells and progeny corresponding to slow (orange), medium (blue) and fast (green) dividers are highlighted. Scale bar = 50 µm. (D) 2D representations of typical lineage trees captured from data, showing slow (orange), medium (blue) and fast (green) dividing cells. Computer-generated tracks (colour) are overlaid on human-reconstructed ground truth trajectories (black). Individual recall and precision scores are shown for each lineage tree, with vertical branch lengths corresponding to intermitotic time (cell cycle duration) elapsed between the first post-division frame (anaphase) to the last frame prior to the next cell division (metaphase). Trees illustrate an error-free tracking (orange tree) and two types of tracking errors, i.e. falsely identified mitosis (blue tree) and missed mitotic event (green tree).

Detailed inspection of the nuclear areas and CNN labels lead us to exclude certain cells from our distribution. We found that the tracks with inter-mitotic time below 7 h had high incidence of start with a non-anaphase label, did not end with pro-(meta)phase label, or a combination of both. This observation suggested that these short tracks represent fragments of cell trajectories where branch breakages occurred, rather than being representative of ultra-fast cycling cells. Visual observation of the nuclear growth (increase of cell nucleus segmentation mask area over time) indicated that tracks with cycling time over 42 h often captured track instances where a parent cell (undergoing mitosis) was falsely linked to one of the arising children cells, most likely due to imperfection in the segmentation step.

3.2.1 Heterogeneity in Cell Cycling Durations

To avoid possible incorporation of prematurely terminated tracks, concatenated parent-to-child tracks or other tracking errors, we filtered our pooled dataset to only consider cells with cycling lengths between and including 7 and 42 h for further analysis (Figure 7B). Our final dataset consisted of 20,074 cells with known lineage over up to eight generations, representing at least two orders of magnitude greater numbers than in previous studies (Puliafito et al., 2012). Importantly, the whole process to filter the relevant cells, calculate their division times and pool the single-cell information across 44 movies took less than a minute to produce, illustrating the utility of our tracking pipeline for large data analyses.

The pooled dataset shows a positively skewed normal distribution of cell cycle durations (Figure 7B). This distribution confirms the presence of division time heterogeneity at very large population numbers, while standing in good agreement with previously published work (Puliafito et al., 2012; Bove et al., 2017). We also confirmed that cell cycle length was not correlated with the time at which a cell was born for the first 60 h of time-lapse imaging (Supplementary Materials).

We used the population distribution to categorise individual cells as fast, medium and slow dividers based on whether their cycling duration was below (<15.5 h), within or above (>20.3 h) half a standard deviation away from the sample mean (Figure 7B). This definition yields a subpopulation of fast dividing cells (n = 6,719 cells; 33.5% of the population), medium dividers (n = 8,500 cells; 42.3%) and slow dividers (n = 4,855 cells; 24.2%).

We extended this categorisation to describe individual cell families and contrasted three lineages extracted from our representative movie, with the trees observed from the movie start frame. Mapping the number of progeny originating from these three founder cells (Figure 7C, Supplementary Movie S2), we confirmed our large-scale observation of broad cycling heterogeneity spectrum. Based on the average cell cycle length of all fully-resolved cells within the tree, we classified the cell families as slow, medium and fast cyclers. Visual inspection of their lineage tree representations reveals that variability in intermitotic durations amongst single cells directly influences the cell capacity to divide and raises the potential for fast cycling cells to eventually dominate the population by overgrowing the slower-cycling clones (Figures 7C,D), as suggested previously (Mura et al., 2019).

Indeed, taking trees corresponding to three different root cells, we find that at the end of the movie, the slow dividing family results in five leaf cells, the medium dividing family in 15 cells and the fast dividing family in 31 leaf cells, over the same period of 80 h. These correspond to mean intermitotic durations of 20.6 ± 6.5 h (n = 3 cells), 16.9 ± 4.5 h (n = 14 cells), and 14.0 ± 1.9 h (n = 29 cells) for each tree, respectively (Figure 7D). Our findings suggest a high degree of intrinsic cell cycling heterogeneity present in the wild-type MDCK cell population. This cycle-time heterogeneity appears to be maintained within cell lineages.

3.2.2 Cell Cycle Duration Correlations in Deep Lineages

To study whether the observed cell cycle duration could represent an inheritable characteristic, we extracted 20 different types of cell pair relatedness from up to 8-generation deep lineages (Figure 8A). It was previously observed (Sandler et al., 2015) that cell cycle durations within lineages show poor correlation when observing the directly ancestral, inter-generational cell pairs (mother-daughter and grandmother-granddaughter), but remain highly correlated when examining intra-generational relationships (sister and cousin cells) (Sandler et al., 2015; Chakrabarti et al., 2018; Kuchen et al., 2020). However, due to lack of deep datasets, the analysis has traditionally focused on immediate cell relatives, including mother, grandmother, sister and first cousin relationships (Sandler et al., 2015; Chakrabarti et al., 2018) and less frequently on more remote family members, such as great-grandmothers or second cousins (Kuchen et al., 2020).

FIGURE 8

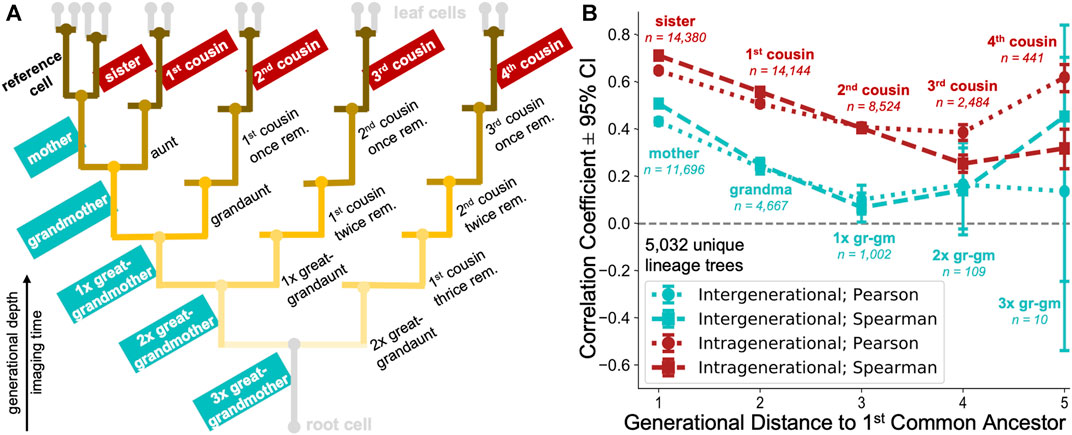
FIGURE 8. Large-scale multigenerational analysis of single-cell cycling durations. (A) Illustrative lineage tree showing 20 types of family relationships of a reference cell (bold) to its lineage relatives determined using our automated approach. The tree captures extended kinships on ancestral (inter-generational; generationally unequal) to fourth cousin span (intra-generational; generationally equal). Strength of the branch colour shading illustrates the generational distance to nearest common ancestor between family member and reference cell. (B) Cycling length correlations in cell lineages. intra-generational (red) correlations appear to be consistently higher than the inter-generational (cyan) correlations in directly ancestral branches. Pearson (dotted) and Spearman (dashed) rank correlation coefficients with 95% confidence interval (CI) are shown for selected relationship pairs as in the lineage tree schematic, categorised according to the generational distance to first common ancestor.

Enabled by our automated approach, we calculated the correlation between cell cycle duration in lineages captured for >8 generational depths, extending previous studies (Sandler et al., 2015; Chakrabarti et al., 2018; Kuchen et al., 2020) using the enhanced depth, breadth and number (5,032 trees) of automatically reconstructed lineages in our tree pool. If the cell cycle duration is not controlled in a heritable fashion, we would expect poor cycling correlations across inter-generational (generationally unequal) as well as intra-generational (generationally equal) family relationships (Figure 8A).

Our analysis revealed moderate correlations in immediate inter-generational relationships (Pearson and Spearman rank coefficients of 0.43 and 0.51, respectively between 11,696 reference and mother cell pairs), which rapidly decreased over 2–3 rounds of division (Figure 8B). Such diminishing ancestral correlations would be strongly indicative of cell cycle duration inheritance being a stochastic event, as previously speculated (Sandler et al., 2015). Alternatively, this behaviour could also indicate that the accumulation of noise across inter-generational lineage relationships represents a very rapid process.

Our analysis confirmed a previously observed trend of highly synchronised cell cycling durations in sister cell pairs (Pearson and Spearman rank coefficients of 0.65 and 0.71, respectively between 14,380 sister cells examined). In addition, our analysis revealed that intra-generational correlations remained above 0.5 in 1st and 2nd cousins. Over five generations, intragenerational correlations became progressively less marked but remained consistently larger than inter-generational correlations.

Our results derived from high-replicate lineage data are in good agreement with previously published studies, using manually annotated data (Sandler et al., 2015; Chakrabarti et al., 2018; Kuchen et al., 2020). Overall, the data provide additional evidence that cycling length is correlated across longer-range relationships (4 and 5 generations to nearest common ancestor) than previously examined. These long-term correlations may suggest heritability in cell cycle durations, as proposed by others (Mura et al., 2019). However, it is possible that, as culture conditions evolve with time (nutrients become depleted and cells more confluent), the highly correlated behaviour between same generation family members represents a consequence of environmental synchronisation. Further experiments are needed to discriminate between these hypotheses.

4 Discussion

We developed an easy-to-use, open-source Python package to enable rapid and accurate reconstruction of multi-generational lineage trees from large datasets without time-consuming manual curation. We show that the addition of cell state information into a probabilistic single cell tracking framework improves multi-generational lineage tree reconstruction over other approaches. Our software enables users to characterise population-level relationships with single-cell resolution from time-lapse microscopy data in an unsupervised manner. As a demonstration of our fully automated approach, we extend the cell cycling analysis to family relationships which could not be previously examined in (semi-) manual annotation-dependent studies (Sandler et al., 2015; Chakrabarti et al., 2018; Kuchen et al., 2020) due to lack of experimental data. We envisage our tracking software could further be applied to analysis of (cancer) stem cell identification in tissues, detection of differentiation and/or reprogramming success in populations, studying of cell cycle control mechanisms in cell lineages and dynamic high-throughput screens of various pharmaceutical compounds with live-cell imaging.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

GC and AL conceived and designed the research. KU and GV performed experiments. KU developed and performed computational analysis. AL wrote the image processing and cell tracking code. KU, GV, GC, and AL evaluated the results and wrote the paper.

Funding

KU was supported by a BBSRC LIDo studentship. GV was supported by BBSRC grant BB/S009329/1 to AL and GC.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank members of the AL and GC labs for helpful discussions. We thank the reviewers for their time and insightful comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2021.734559/full#supplementary-material

Supplementary Video S1 | https://youtu.be/ZxywQ7LaihI

Supplementary Video S2 | https://youtu.be/gScvX89JeYQ

References

Akram, S. U., Kannala, J., Eklund, L., and Heikkilä, J. (2017). Cell Tracking via Proposal Generation and Selection, CoRR abs/1705, 03386.

Google Scholar

Al-Kofahi, O., Radke, R. J., Goderie, S. K., Shen, Q., Temple, S., and Roysam, B. (2006). Automated Cell Lineage Construction: A Rapid Method to Analyze Clonal Development Established with Murine Neural Progenitor Cells. Cell Cycle 5, 327–335. doi:10.4161/cc.5.3.2426

PubMed Abstract | CrossRef Full Text | Google Scholar

Allan, D. B., Caswell, T., Keim, N. C., and van der Wel, C. M. (2018). Trackpy: Trackpy v0.4.1. doi:10.5281/ZENODO.1226458

CrossRef Full Text | Google Scholar

Amat, F., Lemon, W., Mossing, D. P., McDole, K., Wan, Y., Branson, K., et al. (2014). Fast, Accurate Reconstruction of Cell Lineages from Large-Scale Fluorescence Microscopy Data. Nat. Methods 11, 951–958. doi:10.1038/nmeth.3036

PubMed Abstract | CrossRef Full Text | Google Scholar

Bannon, D., Moen, E., Schwartz, M., Borba, E., Kudo, T., Greenwald, N., et al. (2021). DeepCell Kiosk: Scaling Deep Learning-Enabled Cellular Image Analysis with Kubernetes. Nat. Methods 18, 43–45. doi:10.1038/s41592-020-01023-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bao, Z., Murray, J. I., Boyle, T., Ooi, S. L., Sandel, M. J., and Waterston, R. H. (2006). Automated Cell Lineage Tracing in Caenorhabditis elegans. Proc. Natl. Acad. Sci. 103, 2707–2712. doi:10.1073/pnas.0511111103

PubMed Abstract | CrossRef Full Text | Google Scholar

Bendall, S. C., Davis, K. L., Amir, E.-a. D., Tadmor, M. D., Simonds, E. F., Chen, T. J., et al. (2014). Single-cell Trajectory Detection Uncovers Progression and Regulatory Coordination in Human B Cell Development. Cell 157, 714–725. doi:10.1016/j.cell.2014.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, S., Kutra, D., Kroeger, T., Straehle, C. N., Kausler, B. X., Haubold, C., et al. (2019). Ilastik: Interactive Machine Learning for (Bio)image Analysis. Nat. Methods 16, 1226–1232. doi:10.1038/s41592-019-0582-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Bise, R., Yin, Z., and Kanade, T. (2011). “Reliable Cell Tracking by Global Data Association,” in 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March-2 April 2011, 1004–1010. doi:10.1109/ISBI.2011.5872571

CrossRef Full Text | Google Scholar

Bove, A., Gradeci, D., Fujita, Y., Banerjee, S., Charras, G., and Lowe, A. R. (2017). Local Cellular Neighborhood Controls Proliferation in Cell Competition. MBoC 28, 3215–3228. doi:10.1091/mbc.E17-06-0368

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakrabarti, S., Paek, A. L., Reyes, J., Lasick, K. A., Lahav, G., and Michor, F. (2018). Hidden Heterogeneity and Circadian-Controlled Cell Fate Inferred from Single Cell Lineages. Nat. Commun. 9, 1–13. doi:10.1038/s41467-018-07788-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Dagogo-jack, I., and Shaw, A. T. (2017). Tumour Heterogeneity and Resistance to Cancer Therapies. Nat. Rev. Clin. Oncol. 15, 81–94. doi:10.1038/nrclinonc.2017.166

PubMed Abstract | CrossRef Full Text | Google Scholar

Downey, M. J., Jeziorska, D. M., Ott, S., Tamai, T. K., Koentges, G., Vance, K. W., et al. (2011). Extracting Fluorescent Reporter Time Courses of Cell Lineages from High-Throughput Microscopy at Low Temporal Resolution. PLoS ONE 6, e27886. doi:10.1371/journal.pone.0027886

PubMed Abstract | CrossRef Full Text | Google Scholar

Edelstein, A. D., Tsuchida, M. A., Amodaj, N., Pinkard, H., Vale, R. D., and Stuurman, N. (2014). Advanced Methods of Microscope Control Using μManager Software. J. Biol. Methods 1, 10. doi:10.14440/jbm.2014.36

CrossRef Full Text | Google Scholar

Faure, E., Savy, T., Rizzi, B., Melani, C., Stašová, O., Fabrèges, D., et al. (2016). A Workflow to Process 3D+time Microscopy Images of Developing Organisms and Reconstruct Their Cell Lineage. Nat. Commun. 7. doi:10.1038/ncomms9674

CrossRef Full Text | Google Scholar

Fazeli, E., Roy, N. H., Follain, G., Laine, R. F., Chamier, L. V., Hänninen, P. E., et al. (2021). Automated Cell Tracking Using StarDist and TrackMate [ Version 1 ; Peer Review : 2 Approved , 1 Approved with Reservations, 1–13.

Google Scholar

Fazeli, E., Roy, N. H., Follain, G., Laine, R. F., von Chamier, L., Hänninen, P. E., et al. (2020). Automated Cell Tracking Using Stardist and Trackmate. Cold Spring Harbour Laboratories. doi:10.1101/2020.09.22.306233

CrossRef Full Text | Google Scholar

Han, H., Wu, G., Li, Y., and Zi, Z. (2019). eDetect: A Fast Error Detection and Correction Tool for Live Cell Imaging Data Analysis. iScience 13, 1–8. doi:10.1016/j.isci.2019.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep Residual Learning for Image Recognition, 03385. CoRR abs/1512.

Google Scholar

Hernandez, D. E., Chen, S. W., Hunter, E. E., Steager, E. B., and Kumar, V. (2018). “Cell Tracking with Deep Learning and the Viterbi Algorithm,” in 2018 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Nagoya, Japan, 4-8 July 2018, 1–6. doi:10.1109/MARSS.2018.8481231

CrossRef Full Text | Google Scholar

Hilsenbeck, O., Schwarzfischer, M., Skylaki, S., Schauberger, B., Hoppe, P. S., Loeffler, D., et al. (2016). Software Tools for Single-Cell Tracking and Quantification of Cellular and Molecular Properties. Nat. Biotechnol. 34, 703–706. doi:10.1038/nbt.3626

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaqaman, K., Loerke, D., Mettlen, M., Kuwata, H., Grinstein, S., Schmid, S. L., et al. (2008). Robust Single-Particle Tracking in Live-Cell Time-Lapse Sequences. Nat. Methods 5, 695–702. doi:10.1038/nmeth.1237

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalman, R. E. (1960). A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 82 (1), 35–45. doi:10.1115/1.3662552

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. L. (2015). “Adam: A Method for Stochastic Optimization. 3rd International Conference on Learning Representations,” in ICLR 2015 - Conference Track Proceedings, San Diego, 2015, 1–15.

Google Scholar

Kuchen, E. E., Becker, N. B., Claudino, N., and Höfer, T. (2020). Hidden Long-Range Memories of Growth and Cycle Speed Correlate Cell Cycles in Lineage Trees. eLife 9, e51002. doi:10.7554/eLife.51002

PubMed Abstract | CrossRef Full Text | Google Scholar

Lugagne, J.-B., Lin, H., and Dunlop, M. J. (2020). DeLTA: Automated Cell Segmentation, Tracking, and Lineage Reconstruction Using Deep Learning. Plos Comput. Biol. 16 (4), e1007673. doi:10.1371/journal.pcbi.1007673

PubMed Abstract | CrossRef Full Text | Google Scholar

Magnusson, K. E. G., Jaldén, J., Gilbert, P. M., and Blau, H. M. (2015). Global Linking of Cell Tracks Using the Viterbi Algorithm. IEEE Trans. Med. Imaging 34, 911–929. doi:10.1109/TMI.2014.2370951

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandal, S., and Uhlmann, V. (2021). Splinedist: Automated Cell Segmentation with Spline Curves. Cold Spring Harbour Laboratories. doi:10.1101/2020.10.27.357640

CrossRef Full Text | Google Scholar

McQuin, C., Goodman, A., Chernyshev, V., Kamentsky, L., Cimini, B. A., Karhohs, K. W., et al. (2018). Cellprofiler 3.0: Next-Generation Image Processing for Biology. Plos Biol. 16, e2005970–17. doi:10.1371/journal.pbio.2005970

PubMed Abstract | CrossRef Full Text | Google Scholar

Moen, E., Borba, E., Miller, G., Schwartz, M., Bannon, D., Koe, N., et al. (2019). Accurate Cell Tracking and Lineage Construction in Live-Cell Imaging Experiments with Deep Learning. Cold Spring Harbour Laboratories. doi:10.1101/803205

CrossRef Full Text | Google Scholar

Mura, M., Feillet, C., Bertolusso, R., Delaunay, F., and Kimmel, M. (2019). Mathematical Modelling Reveals Unexpected Inheritance and Variability Patterns of Cell Cycle Parameters in Mammalian Cells. Plos Comput. Biol. 15, e1007054–26. doi:10.1371/journal.pcbi.1007054

PubMed Abstract | CrossRef Full Text | Google Scholar

Narayana, M., and Haverkamp, D. (2007). “A Bayesian Algorithm for Tracking Multiple Moving Objects in Outdoor Surveillance Video,” in 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17-22 June 2007. doi:10.1109/cvpr.2007.383446

CrossRef Full Text | Google Scholar

Norman, M., Wisniewska, K. A., Lawrenson, K., Garcia-Miranda, P., Tada, M., Kajita, M., et al. (2012). Loss of Scribble Causes Cell Competition in Mammalian Cells. J. Cel Sci. 125, 59–66. doi:10.1242/jcs.085803

CrossRef Full Text | Google Scholar

Puliafito, A., Hufnagel, L., Neveu, P., Streichan, S., Sigal, A., Fygenson, D. K., et al. (2012). Collective and Single Cell Behavior in Epithelial Contact Inhibition. Proc. Natl. Acad. Sci. 109, 739–744. doi:10.1073/pnas.1007809109

CrossRef Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net: Convolutional Networks for Biomedical Image Segmentation. Lecture Notes Computer Sci. (including subseries Lecture Notes Artif. Intelligence Lecture Notes Bioinformatics) 9351, 234–241. doi:10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

Sandler, O., Mizrahi, S. P., Weiss, N., Agam, O., Simon, I., and Balaban, N. Q. (2015). Lineage Correlations of Single Cell Division Time as a Probe of Cell-Cycle Dynamics. Nature 519, 468–471. doi:10.1038/nature14318

PubMed Abstract | CrossRef Full Text | Google Scholar

Schiegg, M., Hanslovsky, P., Haubold, C., Koethe, U., Hufnagel, L., and Hamprecht, F. A. (2015). Graphical Model for Joint Segmentation and Tracking of Multiple Dividing Cells. Bioinformatics 31, 948–956. doi:10.1093/bioinformatics/btu764

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, U., Weigert, M., Broaddus, C., and Myers, G. (2018). Cell Detection with star-convex Polygons. Lecture Notes Computer Sci. (including subseries Lecture Notes Artif. Intelligence Lecture Notes Bioinformatics) 11071 LNCS 11071, 265–273. doi:10.1007/978-3-030-00934-2_30

CrossRef Full Text | Google Scholar

Skylaki, S., Hilsenbeck, O., and Schroeder, T. (2016). Challenges in Long-Term Imaging and Quantification of Single-Cell Dynamics. Nat. Biotechnol. 34, 1137–1144. doi:10.1038/nbt.3713

PubMed Abstract | CrossRef Full Text | Google Scholar

Sofroniew, N., Lambert, T., Evans, K., Nunez-Iglesias, J., Winston, P., Bokota, G., et al. (2021). Napari/Napari: 0.4.7rc1. doi:10.5281/zenodo.4633896

CrossRef Full Text | Google Scholar

Stegmaier, J., Amat, F., Lemon, W. C., McDole, K., Wan, Y., Teodoro, G., et al. (2016). Real-Time Three-Dimensional Cell Segmentation in Large-Scale Microscopy Data of Developing Embryos. Developmental Cel 36, 225–240. doi:10.1016/j.devcel.2015.12.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Stringer, C., Wang, T., Michaelos, M., and Pachitariu, M. (2020). Cellpose: a Generalist Algorithm for Cellular Segmentation. Nat. Methods 18 (1), 100–106. doi:10.1101/2020.02.02.93123810.1038/s41592-020-01018-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugawara, K., Cevrim, C., and Averof, M. (2021). Tracking Cell Lineages in 3D by Incremental Deep Learning. Cold Spring Harbour Laboratories. doi:10.1101/2021.02.26.432552

CrossRef Full Text | Google Scholar

Tinevez, J.-Y., Perry, N., Schindelin, J., Hoopes, G. M., Reynolds, G. D., Laplantine, E., et al. (2017). TrackMate: An Open and Extensible Platform for Single-Particle Tracking. Methods 115, 80–90. doi:10.1016/j.ymeth.2016.09.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Tinevez, J. Y. (2021). Mastodon. Available at https://github.com/mastodon-sc/mastodon.

Google Scholar

Tsai, H.-F., Gajda, J., Sloan, T. F. W., Rares, A., and Shen, A. Q. (2019). Usiigaci: Instance-Aware Cell Tracking in Stain-free Phase Contrast Microscopy Enabled by Machine Learning. SoftwareX 9, 230–237. doi:10.1016/j.softx.2019.02.007

CrossRef Full Text | Google Scholar

Ulman, V., Maška, M., Magnusson, K. E. G., Ronneberger, O., Haubold, C., Harder, N., et al. (2017). An Objective Comparison of Cell-Tracking Algorithms. Nat. Methods 14, 1141–1152. doi:10.1038/nmeth.4473

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, C., Miura, T., Fujie, Y., Teramoto, T., Ishihara, T., and Kimura, K. D. (2018). Deep-learning-based Flexible Pipeline for Segmenting and Tracking Cells in 3D Image Time Series for Whole Brain Imaging. Cold Spring Harbour Laboratories, 385567. doi:10.1101/385567

CrossRef Full Text | Google Scholar

Wolff, C., Tinevez, J.-Y., Pietzsch, T., Stamataki, E., Harich, B., Guignard, L., et al. (2018). Multi-view Light-Sheet Imaging and Tracking with the MaMuT Software Reveals the Cell Lineage of a Direct Developing Arthropod Limb. eLife 7, 1–31. doi:10.7554/eLife.34410

CrossRef Full Text | Google Scholar