Visual Continuity of Protein Secondary Structure Rendering: Application to SARS-CoV-2 Mpro in Virtual Reality

Ribbon diagrams are important for protein visualization, used to convey the secondary structure in a clear and concise manner. However, most algorithms used to generate these diagrams do not maintain visual continuity when viewing a molecular trajectory, with certain sections of ribbons flipping between clockwise and counterclockwise twists. Here we outline a new method which prevents this artifact by morphing between consecutive cross sections instead of rotating. This yields diagrams which are well suited for viewing dynamic simulations, such as those used for interactive molecular dynamics. We illustrate the utility of this algorithm by using it to visualize iMD-VR (interactive molecular dynamics in virtual reality) simulations of the secondary structure of the SARS-CoV-2 main protease (Mpro), which is being investigated as a potential target for COVID drug therapies.

1 Introduction

The ribbon diagrams used to visualize protein secondary structure can trace their origins to hand-drawn illustrations. This culminated in the production of diagrams for all 75 protein structures currently determined, by Richardson (1981, 2000). These diagrams were first and foremost tasked with conveying the three dimensional structure of proteins upon the two-dimensional page. Starting from a trace of the experimentally determined positions of the alpha carbons, subjective decisions were made to smooth the final curves such that they clearly conveyed the structures in question (Richardson (1985)). These diagrams also guided the form that future diagrams would take, with the secondary structure motifs of helices and beta sheets appearing as wide flat ribbons, in contrast to the cylindrical tubes of the intervening backbone.

One of the first computer algorithms for reproducing these diagrams was described by Carson and Bugg (1986), and utilized in several early programs (Carson and Bugg (1988), Carson (1991), Carson (1997)). Richardson had described aligning ribbons with the axes of the helices and hydrogen bonds of the beta sheets (Richardson (1985)), which is reflected in Carson and Bugg’s choice to align the normals of the ribbons with that of the peptide plane. Examples of ribbon diagrams as seen in modern molecular visualization programs are shown in Figure 1.

FIGURE 1

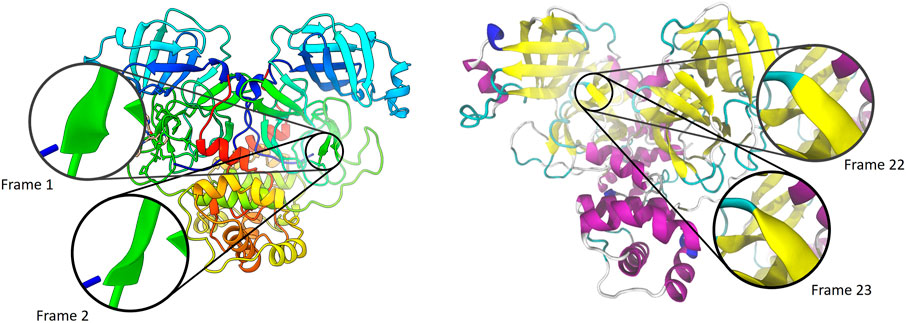
FIGURE 1. Comparison of ribbon visualizations in ChimeraX 1.1 (left,Goddard et al. (2018)) and VMD 1.9.3 (right,Humphrey et al. (1996)) of the SARS-CoV-2 main protease (PDB ID 6W63). The trajectory from which these were taken was run within the Narupa framework (Jamieson-Binnie et al. (2020)), based upon input files used by Deeks et al. (2020). Each frame is separated by a timestep of 10 femtoseconds.

The mathematical construct used to represent these smooth paths is commonly a spline, which consists of piecewise polynomial curves which are connected to give a continuous curve. The path of the spline is driven by a set of control points, which the spline may or may not pass through. Often ribbon diagrams use splines that fall into the latter category, as the ribbon adopting a pleasing smooth path outweighs the need for it to pass through the exact positions of the α carbons that dictate its shape.

A spline defines a one dimensional curve that passes through three dimensional space, consisting of individual segments which share end points. To generate an actual ribbon, a cross section (commonly either a rectangle or ellipse) is extruded along the curve. The alignment of the ribbon at the end points is determined either by the shape of the curve, or features of the underlying molecular topology. Therefore, there also has to be a choice in how to smoothly twist the ribbon such that it is correctly oriented at each end point. Most algorithms choose to turn either clockwise or counterclockwise, depending on which would involve the smallest twist. This is achieved by inverting the second normal if the two face in opposite directions.

When considering a single static diagram, this is a suitable approach. However, a problem arises when continuity is required between consecutive ribbon diagrams representing subsequent snapshots of a single trajectory. Most algorithms for generating the positions along the splines are well-conditioned—a small shift in the position of the control points leads to a small shift in the spline’s path. However, defining the orientation of the ribbon as that of minimizing the rotation along the curve is not well conditioned. The maximal twist that can occur over a single segment is 90°, at which point the end normal is inverted and a flip occurs where the segment goes from twisting in a clockwise direction to a counterclockwise direction, or vice-versa. Figure 1 highlights this issue for the SARS-CoV-2 main protease, showing flipping between two adjacent trajectories. Supplementary Videos S1–S3 are provided in the supplementary materials to highlight this issue in other molecular visualization packages.

We posit that this issue has not received much prior attention because ribbon diagrams are used predominately for static structures or short image sequences of trajectories in which the timestep between each image is large. The large timesteps between frames means that though the flipping occurs, it is not noticeable in comparison to the changes in atomic positions between the frames. However, interactive molecular dynamics (iMD) uses simulations which are displayed to the user in real time. This means that in iMD the simulation timestep between different rendered frames is smaller than that used for animated images. Therefore, in this domain the visual artifact of ribbon flipping becomes apparent, and may obscure small fluctuations in atomic positions which may be important.

These discontinuities are particularly apparent for iMD simulations carried out in virtual reality (iMD-VR), such as used by O’Connor et al. (2019). For example, in recent work, we have shown how iMD-VR can be applied to interactive studies of the SARS-CoV-2 main protease, by Deeks et al. (2020). The immersive quality of virtual reality means that the user may be more readily distracted by the visual noise of sudden changes in their peripheral vision.

2 Methods

Here we will outline a method for generating a ribbon representation of a protein which avoids discontinuities due to ribbon flipping. We have implemented this within our VR-enabled molecular viewer Narupa iMD (Jamieson-Binnie et al. (2020)), in which readers can see iMD-VR simulations rendered using the methods described in this paper.

2.1 Spline

We choose a cubic hermite spline (Eq. 1), which guarantees that the ribbon passes through each alpha carbon. A spline segment passes from one alpha carbon to the next, and is defined purely in terms of the positions of the two alpha carbons ${\overrightarrow{\mathbf{p}}}_0$ and ${\overrightarrow{\mathbf{p}}}_1$, and two tangents ${\overrightarrow{\mathbf{m}}}_0$ and ${\overrightarrow{\mathbf{m}}}_1$. It is parameterized in terms of a variable t in the range $\left[\mathrm{0,1}\right]$.

$\overrightarrow{\mathbf{p}}\left(t\right)=\left(2t^3-3t^2+1\right){\overrightarrow{\mathbf{p}}}_0+\left(t^3-2t^2+t\right){\overrightarrow{\mathbf{m}}}_0+\left(-2t^3+3t^2\right){\overrightarrow{\mathbf{p}}}_1+\left(t^3-t^2\right){\overrightarrow{\mathbf{m}}}_1(1)$

This function explicitly contains the position and tangent at each end point, and hence two adjacent spline segments will have $C^0$ and $C^1$ continuity (continuity of both positions and tangents).

Whilst the positions are defined by the alpha carbons, there is not a unique choice for the tangents. There are several methods for choosing tangents for this class of splines, such as cardinal splines, Catmull-Rom splines (Catmull and Rom (1974)) and Kochanek–Bartels splines (Kochanek and Bartels (1984)), all of which define the tangents in terms of the control point positions ${\overrightarrow{\mathbf{p}}}_i$ and zero or more parameters. By default we use the cardinal spline approach for simplicity, with the shape of the curve dictated by a single parameter.

2.2 Coordinate Frames

To define the ribbon, we require an orthonormal coordinate frame to be defined at each point along the curve, consisting of an origin, a tangent, a normal and a binormal. Given the position and tangent we have determined for the spline, we must also define at least one of either the normal or binormal, with the third axis being determined as a cross product. Often, ribbon representations use a normal which is based upon one or more bond directions within the peptide plane. However, this limits the ribbon representation to the visualizing of polypeptides, where in general it can be applied to other polymers such as nucleic acids and polysaccharides.

The normal at each control point is instead found by first taking the second derivative of the curve (Eq. 1) with respect to t. This vector points in a direction determined by the curvature of the spline. By taking the perpendicular component of this vector relative to the tangent at each end point, we obtain a start and end normal for each segment. To ensure continuity in normals between adjacent segments, the normal at each control point is taken as the average of two: the end normal of the preceding segment, and the start normal of the subsequent segment. This normal vector is defined purely by the geometry of the curve, rather than the geometry of the peptide planes. For the two common cases of helices and beta sheets in protein secondary structure, these normals align well with those commonly chosen based upon bond directions.

These initial spline calculations are performed on the CPU, and yield a set of curve points (consisting of a position, tangent, normal, scale and color) and a set of pairs of consecutive points. Each pair corresponds to a single segment, which will be drawn as a cubic hermite spline on the GPU. For this, a single high resolution mesh of a cylinder is uploaded to the GPU and rendered using GPU instancing. Within the vertex shader of the GPU, the end points of each segment are used to deform the unit cylinder to yield the correct position and orientation of a single ribbon segment.

Given the coordinate frames at either end of the segment, some method is required to generate intermediate coordinate frames along the spline. These coordinate frames must be positioned along the curve, with their tangents aligned with the tangent of the curve at that point.

There are several techniques for generating a set of frames along a curve. The two common methods are Frenet-Serret frames (Willmore (2000)), which are defined purely in terms of the curvature of the parameterized function, and rotationally minimized or Bishop frames (Bishop (1975)), which minimize the rotation of the normal along the curve. However, both have drawbacks, with Frenet-Serret frames exhibiting sharp twists around inflection points, and Bishop frames requiring iterative methods to propagate the frame along the curve. These two methods for assigning coordinate frames, along with the method we will propose, are illustrated in Figure 2.

FIGURE 2

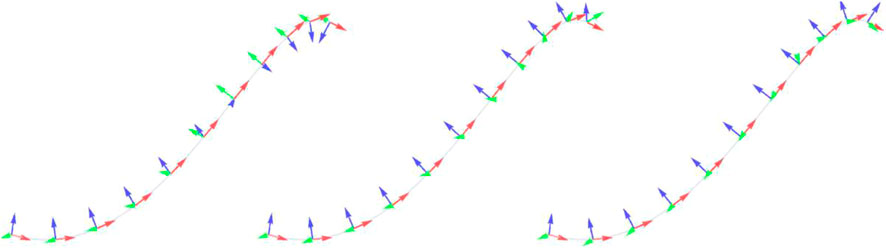
FIGURE 2. Comparison of three different methods of assigning a coordinate frame to each point along a cubic curve (From left to right) The Frenet-Serret frame, defined in terms of the geometry of the curve (Willmore (2000)); The rotationally minimized frame, generated using the double reflection method of Wang et al. (2008); and our method, using an average of the start and end binormals. Axes shown are the tangent (red), normal (blue) and binormal (green).

For our implementation within iMD-VR, we require a set of reference frames that are easy to compute, and—whilst not necessarily minimizing the rotation of the normal—they should aim to reduce it. Therefore, we propose the following algorithm to calculate the set of frames:

• Compute the start and end binormals ${\overrightarrow{\mathbf{b}}}_0$ and ${\overrightarrow{\mathbf{b}}}_1$ using ${\overrightarrow{\mathbf{b}}}_i={\overrightarrow{\mathbf{t}}}_i\times {\overrightarrow{\mathbf{n}}}_i$ where ${\overrightarrow{\mathbf{t}}}_i$ is the normalized tangent and ${\overrightarrow{\mathbf{n}}}_i$ is the normalized normal at each end point.

• Take the average of these two to give a reference binormal ${\overrightarrow{\mathbf{b}}}_{\mathrm{ref}}$

• For an arbitrary point $\overrightarrow{\mathbf{p}}\left(t\right)$ along the curve, the tangent $\overrightarrow{\mathbf{t}}\left(t\right)$ is given by the (normalized) derivative of Eq. 1.

• The binormal $\overrightarrow{\mathbf{b}}\left(t\right)$ at this point is given by the (normalized) perpendicular component of the reference binormal ${\overrightarrow{\mathbf{b}}}_{\mathrm{ref}}$ to the tangent $\overrightarrow{\mathbf{t}}\left(t\right)$.

• The normal $\overrightarrow{\mathbf{n}}\left(t\right)$ is given by $\overrightarrow{\mathbf{n}}\left(t\right)=\overrightarrow{\mathbf{b}}\left(t\right)\times \overrightarrow{\mathbf{t}}\left(t\right)$

This method yields a set of coordinate frames for a given curve.

Given these coordinate frames, we transform the cylinder such that its cross sections lie on the planes spanned by the normal and binormals at a given point along the curve. By using this approach, we’ve transformed the problem from considering a fixed ribbon being extruded along a set of coordinate frames that are twisting to a cross section that is rotating along a set of coordinate frames that are aligned. This reduces the problem down to a two dimensional problem, in which we wish to transform an ellipse aligned with one normalized vector on the 2D plane to another.

2.3 Morphing Cross Sections

At any point along our spline, we have a 2D plane in which to define our cross section which is spanned by the normal and binormal of the coordinate frame. Projecting the start and end normals of our curve points onto these 2D planes yields two unit directions, ${\overrightarrow{\eta }}_0\left(t\right)$ and ${\overrightarrow{\eta }}_1\left(t\right)$. Here, ${\overrightarrow{\eta }}_i\left(t\right)$ is the projection of the binormal ${\overrightarrow{\mathbf{b}}}_i$ onto the 2D coordinate system spanned by the axes $\overrightarrow{\mathbf{n}}\left(t\right)$ and $\overrightarrow{\mathbf{b}}\left(t\right)$. These two vectors define the direction of the major axis of the ellipse at either end of the segment. As an ellipse can be flipped in the direction of either of its axes, we invert ${\overrightarrow{\mathit{\eta }}}_1\left(t\right)$ if the dot product ${\overrightarrow{\mathit{\eta }}}_0\left(t\right)\cdot {\overrightarrow{\mathit{\eta }}}_1\left(t\right)<0$. This ensures that the maximal rotation that occurs along a single segment is 90°. From here, the simplest method that could be used is to continuously rotate the vector $\overrightarrow{\mathit{\eta }}\left(t\right)$ from ${\overrightarrow{\mathit{\eta }}}_0\left(t\right)$ to ${\overrightarrow{\mathit{\eta }}}_1\left(t\right)$. This method is shown in the first row of Figure 3, which highlights the discontinuity that occurs when the difference between the start and end vector is close to 90°.

FIGURE 3

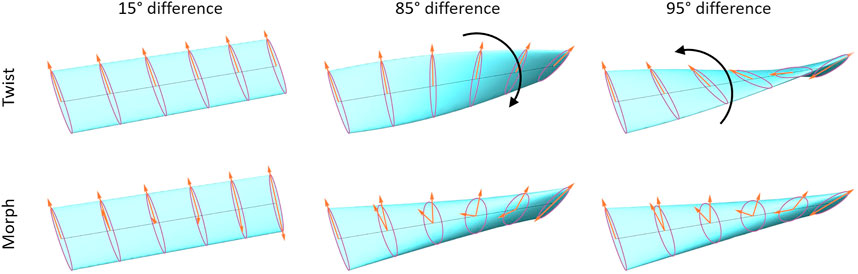
FIGURE 3. Comparison of rotating elliptical cross sections at angles of (Left to Right) 15°, 85, and 95°. The top row rotates the normal vector from the initial alignment to the final alignment, exhibiting a flip between 85 and 95°. The bottom row shows our method, with a circular cross section occurring at angles approaching 90° to avoid a discontinuity. Animated versions of this diagram can be found in Supplementary Videos S5, S6 in the supplementary materials.

We propose a solution to this problem by using an alternative to a simple rotation of the ellipse from the initial cross section to the final cross section. As previously mentioned, negating either vector has no effect on the ellipse at the start or end of each segment. Therefore, we consider two separate vectors—one which goes from ${\overrightarrow{\mathit{\eta }}}_0\left(t\right)$ to ${\overrightarrow{\mathit{\eta }}}_1\left(t\right)$, and one which goes from ${\overrightarrow{\mathit{\eta }}}_0\left(t\right)$ to $-{\overrightarrow{\mathit{\eta }}}_1\left(t\right)$. Therefore, one vector rotates clockwise toward the final vector, and one rotates counterclockwise.

For this method, instead of rotating the vectors, we use a simple linear interpolation to yield two different vectors (Eq. 2). Though a spherical interpolation would be more correct when considering a single vector rotating from the start point to the end point, linear interpolation yields a compression in the ribbon’s cross sectional area which we consider to be aesthetically pleasing.

${\overrightarrow{\eta }}^{+}\left(t\right)=\left(1-t\right){\overrightarrow{\eta }}_0\left(t\right)+t{\overrightarrow{\eta }}_1\left(t\right){\overrightarrow{\eta }}^{-}\left(t\right)=\left(1-t\right){\overrightarrow{\eta }}_0\left(t\right)-t{\overrightarrow{\eta }}_1\left(t\right)(2)$

The first of these represents the linear interpolation from the start vector to the end vector. The second however is a linear interpolation toward the reflected end vector. Therefore, if one of these vectors is rotating clockwise, the other must go counterclockwise and vice-versa. Therefore, by using both of these vectors to generate the cross section of the ellipse, the ellipse will end up as some kind of superposition of both a clockwise and counterclockwise twist. We also note that exchanging ${\eta }^{+}\left(t\right)$ and ${\eta }^{-}\left(t\right)$ has no effect on the generated cross section, and hence flipping either ${\overrightarrow{\eta }}_0\left(t\right)$ or ${\overrightarrow{\eta }}_1\left(t\right)$ has no effect.

These two vectors are used to generate two other vectors called and ${\overrightarrow{\mathbf{d}}}^{-}\left(t\right)$ (Eq. 3), which will be used to deform the circular cross section of the cylinder.

${\overrightarrow{\mathbf{d}}}^{+}\left(t\right)=\frac{{\overrightarrow{\eta }}^{+}\left(t\right)+{\overrightarrow{\eta }}^{-}\left(t\right)}{2}=\left(1-t\right){\overrightarrow{\eta }}_0\left(t\right){\overrightarrow{\mathbf{d}}}^{-}\left(t\right)=\frac{{\overrightarrow{\eta }}^{+}\left(t\right)-{\overrightarrow{\eta }}^{-}\left(t\right)}{2}=t{\overrightarrow{\eta }}_1\left(t\right)(3)$

For a given cross section, we have a set of points $\left\{\overrightarrow{\mathbf{v}}\right\}$ from the cylindrical mesh which lie on the unit circle. We wish to transform these points so they form an ellipse dictated by the vectors ${\overrightarrow{\mathbf{d}}}^{+}\left(t\right)$ and ${\overrightarrow{\mathbf{d}}}^{-}\left(t\right)$. This is achieved by taking the dot product of each point with both ${\overrightarrow{\mathbf{d}}}^{+}\left(t\right)$ and ${\overrightarrow{\mathbf{d}}}^{-}\left(t\right)$ and using that to translate the point in that direction. Combined with a radial scaling r, this yields a cross section as defined in Eq. 4.

$\overrightarrow{\mathbf{v}}\mapsto r\overrightarrow{\mathbf{v}}+\left(\overrightarrow{\mathbf{v}}\cdot \frac{{\overrightarrow{\mathbf{d}}}^{+}\left(t\right)}{\left|{\overrightarrow{\mathbf{d}}}^{+}\left(t\right)\right|}\right){\overrightarrow{\mathbf{d}}}^{+}\left(t\right)+\left(\overrightarrow{\mathbf{v}}\cdot \frac{{\overrightarrow{\mathbf{d}}}^{-}\left(t\right)}{\left|{\overrightarrow{\mathbf{d}}}^{-}\left(t\right)\right|}\right){\overrightarrow{\mathbf{d}}}^{-}\left(t\right)(4)$

These cross sections are similar to rotating the ellipse when the angle between ${\overrightarrow{\mathbf{\eta }}}_0\left(t\right)$ and ${\overrightarrow{\mathbf{\eta }}}_1\left(t\right)$ is small. However, as this angle approaches 90°, the cross sections begin to go through an intermediate circular cross section (see Figure 3). Therefore, when the angle between the vectors is 90°, the ellipse can’t be said to be rotating either clockwise or anticlockwise, and instead morphs continuously between the two. This could be seen as stating that at these angles, it is ill defined at intermediate points which way the ribbon is aligned, and this uncertainty is represented by deforming the ellipse toward a circle which has no defined orientation.

3 Discussion

Figure 4 shows our approach applied to a SARS-CoV-2 protein. Our method yields visually pleasing results that pass through all the alpha carbons, which allows side chains to connect directly to the ribbon backbone if visualized. The method is not dependent on the type of spline or normals used. We therefore expect this method to be readily applicable to existing approaches, such as those using b-splines or those aligning normals with bond directions.

FIGURE 4

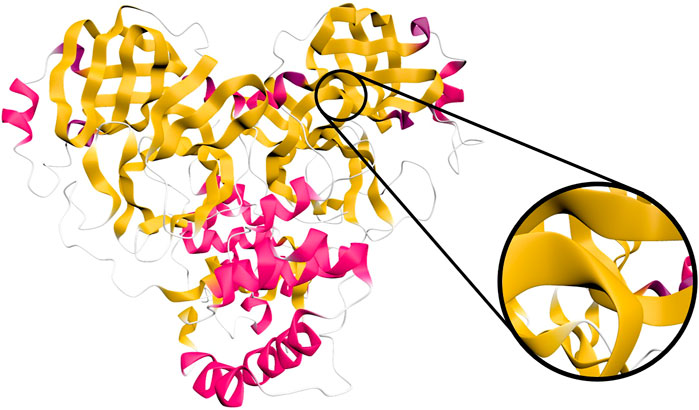
FIGURE 4. Ribbon diagram of the SARS-CoV-2 main protease (PDB ID 6W63), as rendered in Narupa iMD using the cartoon representation. Shown inset is a close-up of a beta strand which exhibits a turn close to 90°, highlighting its similarity to a twist when viewed from a distance. An animation of this is provided in Supplementary Video S4 of the supplementary materials.

Another source of visual discontinuity in these systems is the discrete assignment of each amino acid residue to a single secondary structure motif. There exist several algorithms for performing this assignment, including DSSP (Kabsch and Sander (1983)) and STRIDE (Frishman and Argos (1995)). These methods act upon a single set of coordinates, giving the secondary structure at a specific point in time. However, between frames there may be discrete changes in assignment for certain residues. There has been previous work by Schulz et al. (2018) on visualizing uncertainty in secondary structure due to dynamics, with uncertainty being visualized as a sinusoidal distortion of the ribbon.

In Narupa iMD, rather than compute the secondary structure assignment for each frame, we instead only calculate it once a second. Based upon settings provided by the user, this provides a width and color for each part of the ribbon. We then linearly interpolate between the existing colors and widths from the previous assignment and those which have just been assigned. This gives a smooth fading between different motifs as the protein backbone moves. This approach also gives the user a sense of which secondary structure elements are unstable, as those near the threshold required to define a specific secondary structure can oscillate between two or more over time.

The use of ribbons as a visualization technique, and hence this issue with visual continuity, is not limited to proteins. The Twister visualization is a ribbon-like algorithm used for polysaccharide chains, which has been implemented in VMD (Kuttel et al. (2006); Cross et al. (2009)). The orientation of the ribbon is related to the orientation of the individual rings involved in the polysaccharide. Both the polypeptide and polysaccharide case are linked by the freedom of rotation that exists between adjacent monomers, which makes the existence of visual artifacts due to flipping inevitable. We expect this method to be applicable to these systems as well.

The secondary structure visualization approach outlined herein has been implemented within our software Narupa iMD, and is available open source to enable readers of this paper to inspect the results generated using this approach. Narupa iMD can be accessed at https://narupa.readthedocs.io/. This can be used in conjunction with a cloud mounted simulation server https://app.narupa.xyz/, where simulations of the SARS-CoV-2 main protease in both apo (PDB ID 6MO3) and inhibitor complex (PDB ID 6W63) forms are available. Other simulations are available, including a 40-alanine polypeptide which shows our algorithm’s application to a flexible system. See Deeks et al. (2020) for more information on running these simulations and viewing them in virtual reality.

Once the simulation is running, the rendering can be altered using a python script. Information on how to set up ribbon rendering is provided in the supplementary information.

4 Conclusion

Ribbon rendering is ubiquitous for visualizing the secondary structure of proteins, but existing algorithms have been aimed at visualizing discrete snapshots of a system. We propose a method for generating ribbons with elliptic cross sections which do not exhibit discontinuities where they flip from a clockwise twist to a counterclockwise and vice-versa. Combined with linear interpolation to fade between different secondary structure assignments, this yields a smooth continuous representation with no sudden changes. This continuity helps reduce visual clutter and immerse the user in the environment when utilizing virtual reality to interact with the system.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

AJ-B created the method, implemented it within the open-source Narupa iMD platform, and contributed to the writing and editing of this manuscript. DG provided funding, advised AJ-B, and contributed to writing and editing of this manuscript. All authors contributed to the article and approved the submitted version.

Funding

ADJB is supported by the EPSRC TMCS CDT (EP/L015722/1). DRG recognizes funding from the Leverhulme Trust (Philip Leverhulme Prize), Royal Society (URF/R/180033) and BBSRC (BB/R00661X/1).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Dasha Shchepanovska, Jonathan Barnoud, Jennifer Winstone and Ella Gale for feedback and advice on this manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2021.642172/full#supplementary-material

References

Bishop, R. L. (1975). There Is More Than One Way to Frame a Curve. The Am. Math. Monthly 82, 246. doi:10.2307/2319846

CrossRef Full Text | Google Scholar

Carson, M. (1997). [25] Ribbons. Methods Enzymol. 277, 493–505. doi:10.1016/S0076-6879(97)77027-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Carson, M., and Bugg, C. E. (1986). Algorithm for Ribbon Models of Proteins. J. Mol. Graphics 4, 121–122. doi:10.1016/0263-7855(86)80010-8

CrossRef Full Text | Google Scholar

Carson, M., and Bugg, C. E. (1988). BSRIBBON- Program for Producing 3D Ribbon Models of Macromolecules Suitable for Interactive Graphics Display. J. Appl. Cryst. 21, 578. doi:10.1107/S0021889888005825

CrossRef Full Text | Google Scholar

Carson, M. (1991). RIBBONS 2.0. J. Appl. Cryst. 24, 958–961. doi:10.1107/S0021889891007240

CrossRef Full Text | Google Scholar

Catmull, E., and Rom, R. (1974). “A Class of Local Interpolating Splines,” in Computer Aided Geometric Design (Amsterdam, Netherlands: Elsevier), 317–326. doi:10.1016/B978-0-12-079050-0.50020-5

CrossRef Full Text | Google Scholar

Cross, S., Kuttel, M. M., Stone, J. E., and Gain, J. E. (2009). Visualisation of Cyclic and Multi-Branched Molecules with VMD. J. Mol. Graphics Model. 28, 131–139. doi:10.1016/j.jmgm.2009.04.010

CrossRef Full Text | Google Scholar

Deeks, H. M., Walters, R. K., Barnoud, J., Glowacki, D. R., and Mulholland, A. J. (2020). Interactive Molecular Dynamics in Virtual Reality Is an Effective Tool for Flexible Substrate and Inhibitor Docking to the SARS-CoV-2 Main Protease. J. Chem. Inf. Model. 60, 5803–5814. doi:10.1021/acs.jcim.0c01030

PubMed Abstract | CrossRef Full Text | Google Scholar

Frishman, D., and Argos, P. (1995). Knowledge-based Protein Secondary Structure Assignment. Proteins 23, 566–579. doi:10.1002/prot.340230412

PubMed Abstract | CrossRef Full Text | Google Scholar

Goddard, T. D., Huang, C. C., Meng, E. C., Pettersen, E. F., Couch, G. S., Morris, J. H., et al. (2018). UCSF ChimeraX: Meeting Modern Challenges in Visualization and Analysis. Protein Sci. 27, 14–25. doi:10.1002/pro.3235

PubMed Abstract | CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: Visual Molecular Dynamics. J. Mol. Graphics 14, 33–38. doi:10.1016/0263-7855(96)00018-5

CrossRef Full Text | Google Scholar

Jamieson-Binnie, A. D., O'Connor, M. B., Barnoud, J., Wonnacott, M. D., Bennie, S. J., and Glowacki, D. R. (2020). “Narupa iMD: A VR-Enabled Multiplayer Framework for Streaming Interactive Molecular Simulations,” in ACM SIGGRAPH 2020 Immersive Pavilion (New York, NY, USA: ACM), 1–2. doi:10.1145/3388536.3407891

CrossRef Full Text | Google Scholar

Kabsch, W., and Sander, C. (1983). Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers 22, 2577–2637. doi:10.1002/bip.360221211

PubMed Abstract | CrossRef Full Text | Google Scholar

Kochanek, D. H. U., and Bartels, R. H. (1984). Interpolating Splines with Local Tension, Continuity, and Bias Control. SIGGRAPH Comput. Graph. 18, 33–41. doi:10.1145/964965.808575

CrossRef Full Text | Google Scholar

Kuttel, M., Gain, J., Burger, A., and Eborn, I. (2006). Techniques for Visualization of Carbohydrate Molecules. J. Mol. Graphics Model. 25, 380–388. doi:10.1016/j.jmgm.2006.02.007

CrossRef Full Text | Google Scholar

O’Connor, M. B., Bennie, S. J., Deeks, H. M., Jamieson-Binnie, A., Jones, A. J., Shannon, R. J., et al. (2019). Interactive Molecular Dynamics in Virtual Reality from Quantum Chemistry to Drug Binding: An Open-Source Multi-Person Framework. J. Chem. Phys. 150, 220901. doi:10.1063/1.5092590

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, J. S. (2000). Early Ribbon Drawings of Proteins. Nat. Struct. Biol. 7, 624–625. doi:10.1038/77912

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, J. S. (1985). Schematic Drawings of Protein Structures. Methods Enzymol. 115, 359–380. doi:10.1016/0076-6879(85)15026-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, J. S. (1981). The Anatomy and Taxonomy of Protein Structure. Adv. Protein Chem. 34, 167–339. doi:10.1016/S0065-3233(08)60520-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulz, C., Schatz, K., Krone, M., Braun, M., Ertl, T., and Weiskopf, D. (2018). “Uncertainty Visualization for Secondary Structures of Proteins,” in 2018 IEEE Pacific Visualization Symposium (PacificVis) (Piscataway, New Jersey: IEEE), 96–105. doi:10.1109/PacificVis.2018.00020

CrossRef Full Text | Google Scholar

Wang, W., Jüttler, B., Zheng, D., and Liu, Y. (2008). Computation of Rotation Minimizing Frames. ACM Trans. Graph. 27, 1–18. doi:10.1145/1330511.1330513

CrossRef Full Text | Google Scholar

Willmore, T. (2000). Curves. Handbook of Differential Geometry 1, 997–1023. doi:10.1016/S1874-5741(00)80014-X

CrossRef Full Text | Google Scholar