- 1Department of Psychology, University of Washington, Seattle, WA, United States
- 2Human Centered Design and Engineering, University of Washington, Seattle, WA, United States
There is a growing body of evidence that numerical uncertainty expressions can be used by non-experts to improve decision quality. Moreover, there is some evidence that similar advantages extend to graphic expressions of uncertainty. However, visualizing uncertainty introduces challenges as well. Here, we discuss key misunderstandings that may arise from uncertainty visualizations, in particular the evidence that users sometimes fail to realize that the graphic depicts uncertainty. Instead they have a tendency to interpret the image as representing some deterministic quantity. We refer to this as the deterministic construal error. Although there is now growing evidence for the deterministic construal error, few studies are designed to detect it directly because they inform participants upfront that the visualization expresses uncertainty. In a natural setting such cues would be absent, perhaps making the deterministic assumption more likely. Here we discuss the psychological roots of this key but underappreciated misunderstanding as well as possible solutions. This is a critical question because it is now clear that members of the public understand that predictions involve uncertainty and have greater trust when uncertainty is included. Moreover, they can understand and use uncertainty predictions to tailor decisions to their own risk tolerance, as long as they are carefully expressed, taking into account the cognitive processes involved.
Introduction
Many of the important decisions that we face involve outcomes that are uncertain, such as how to protect oneself from the possibility of severe weather or infectious disease. In many cases the uncertainty is quantifiable and could potentially inform decisions. Here, by “uncertainty” we mean likelihood estimates of future events, such as those produced by modeling techniques employed in weather forecasting (e.g., Gneiting and Raftery, 2005), although the true likelihood is not known, as it is with the flip of a coin. Whether and how to provide uncertainty information (e.g., 40% chance of freezing temperatures) to members of the public continues to be debated among experts. Although uncertainty estimates more truthfully represent experts’ understanding of most situations, the fear is that uncertainty expressions will be misunderstood by non-experts, making things worse rather than better. Visualizations are sometimes considered a solution (e.g., Kinkeldey et al., 2014; Tak et al., 2014; Taylor et al., 2015; Cheong et al., 2016; Mulder et al., 2019; Padilla et al., 2019; Padilla et al., 2020). As we all know “A picture is worth a thousand words”—or is it? The question we address here is whether uncertainty visualizations are more or less comprehensible to non-expert end-users than are other forms of uncertainty communication, in particular when it comes to misunderstandings. Perhaps the most serious misunderstanding and the focus here, is failing to realize that the graphic depicts uncertainty, i.e., mistaking it as representing some deterministic quantity.
Although at present little uncertainty information reaches members of the public, communication of uncertainty has been studied by social and behavioral scientists as well as by cartographers and visualization researchers for decades (van der Bles et al., 2019). Initially it was thought that verbal phrases such as “likely” or “unlikely” would better communicate uncertainty to non-experts than numerical expressions (e.g., 40% chance), which might be difficult to understand especially for those with less education. However, numerous studies demonstrated early on that verbal phrases are not precise (see Reagan et al., 1989 for a review). People can have very different interpretations when translating them back into numbers. For instance, the word “likely” has been assigned a probability of anywhere between 0.5 and 0.99 (Wallsten et al., 1986). The word “possible” has a bi-model distribution. One meaning at about 0.05 and another at 0.55 (Mosteller and Youltz, 1990). Thus, although verbal expressions probably communicate the fact of uncertainty and are currently in use in many domains, they do not adequately communicate the degree of uncertainty. This led some to wonder if perhaps numerical expressions might be better (Windschitl and Wells, 1996; Nadav-Greenberg and Joslyn, 2009).
Indeed, it is clear that most people understand probabilities on a practical, if not on a theoretical level. In one early experiment (Patt, 2001), Zimbabwean farmers made crop choices and spun a wheel with proportions representing varying probabilities of a wet and a dry year. These rural farmers, with little to no formal math education, were able to make increasingly better decisions from an economic standpoint. There is evidence of similar intuitions among Americans who do not expect weather forecasts to verify exactly, even when single value deterministic forecasts are provided (Morss et al., 2008; Joslyn and Savelli, 2010). This suggests that people are aware of the inherent uncertainty in such predictions.
Moreover, there is a growing body of evidence that numerical expressions of uncertainty can be used by non-experts to improve decision quality. Evidence from our own lab has shown in numerous experimental studies that numeric expressions of uncertainty better convey likelihood than do verbal expressions (Nadav-Greenberg and Joslyn, 2009), as well as inspire greater trust and lead to better decisions from an economic standpoint than do single value forecasts (Joslyn and LeClerc, 2012). In addition, numeric uncertainty expressions appear to counteract the negative effects for forecast error (Joslyn and LeClerc, 2012) and false alarms (LeClerc and Joslyn, 2015). Somewhat surprisingly, and contradicting what people might think, the advantages conferred by numeric uncertainty estimates, including better decisions and greater trust, hold regardless of education level (Grounds et al., 2017; Grounds and Joslyn, 2018). In other words, the same advantages for numeric uncertainty expressions are observed among those with a high school education or less as among those who are college educated.
What about visualizations? Do the same advantages extend to graphic expressions of uncertainty? It is obvious that many experts think so, as there are hundreds of them currently in use (Greis, 2017). In addition, there is an abundance of advice about how uncertainty should be represented visually (Gershon, 1998; Tufte 2006; Kinkeldey et al., 2014; Hullman et al., 2015). Tak et al. (2015) have suggested that these strategies can be classified under three broad categories. One is using graphical techniques such as blur, fading, sketchiness, dotted or broken lines, transparency, size, texture, and color saturation. The second is to overlay uncertainty information (sometimes in the formats listed in the first category) and the third is to use animations (see also Evans, 1997). However, for many of these suggestions, while they make intuitive sense, the evidence that they actually convey the meaning intended or how they compare with non-visualized forms of uncertainty expression is limited.
That is not to say that there is no research on uncertainty visualization. Indeed, there is a growing body of research addressing a variety of questions about uncertainty visualization (see Hullman et al., 2019 for a recent review). It is important, however, to understand what questions are addressed and how they are tested when evaluating this research (Hullman, 2016; van der Bles et al., 2019). Much of the early work was based on preference judgments (Kinkeldey et al., 2015; Hullman et al., 2019) in which participants were shown a group of visualizations and asked to indicate the formats they preferred. For instance, there is evidence that people prefer color-coded probability (limited spectral) to black and white trajectory forecasts for hurricanes (Radford et al., 2013). Although preference judgments are informative, they do not reveal whether users understand the format they prefer or how that format affects their decisions. Moreover, it has long been known that preference judgments are often governed by familiarity (Zajonc, 1968; Bornstein, 1989; Parrott et al., 2005; Taylor et al., 2015) known as the “mere exposure” effect. Thus, newer formats may be rejected simply because they are less familiar, when in fact they would be more useful in the long run. Even when participants are asked specifically whether they think they would understand a graphic, the judgment does not always line up with objectively measured understanding. For example, in a study comparing perceived comprehension of graphics illustrating forecast uncertainty (“Which figure did you find the easiest to understand?”) to objective measures (e.g., “How many models project a decrease in summer temperature?”), the two measures were largely uncorrelated (Lorenz et al., 2015). In other words, true understanding was unrelated to participants’ assessment of their understanding, although perceived comprehension was closely related to preference.
Many recent studies (reviewed below) have begun to ask participants questions that more directly test their understanding, comparing visualizations to one another. When evaluating these studies, however, it is important to consider the control groups that are included (Savelli and Joslyn, 2013; Hullman, 2016; Hullman et al., 2019). For instance, unless a non-visualized control is included, it is not possible to determine whether visualizations do a better or worse job in communicating uncertainty than do non-visualized expressions (e.g., numerical information presented in text format). It is also informative to include a control group that receives forecasts that do not include uncertainty information. That is because people already have many valid intuitions about uncertainty in some domains, such as weather (Morss et al., 2008; Joslyn and Savelli, 2010). We found, for instance, that given single value deterministic forecasts, not only do participants expect uncertainty, they correctly expect it to increase with lead time (Joslyn and Savelli, 2010). Therefore, unless a “no uncertainty” control is included, it is not possible to determine whether people learn anything new from the uncertainty expression (or whether they would have anticipated the same level of uncertainty with a deterministic expression). Finally, it is important to consider what questions participants are asked in order to determine whether the questions are capable of revealing misunderstandings. Some questions can be “leading” in the sense that they reveal information about what kind of answer is required, precluding misunderstandings that would occur in natural, extra-experimental settings.
In Sections two through five below, we provide a brief overview of how visualizations have been evaluated (for a more thorough review see Hullman et al., 2019). Interpretation Biases Arising From Uncertainty Visualizations and Deterministic Construal Error summarize some of the main interpretation biases that have been detected, focusing on misinterpreting uncertainty as some other quantity, known as the deterministic construal error (DCE). Psychological Explanation provides a psychological explanation for this effect while Ask the Right Question outlines methodologies for revealing DCEs. Solutions provides some suggestions for reducing the error and Discussion summarizes our contribution.
Comparison Between Visualizations
Much of the research on user understanding compares different uncertainty visualizations to one another. For instance, there is evidence that uncertainty animations, showing a set of possible outcomes over rapidly alternating frames, better help users to extract trend information than do static visualizations such as error bars (Kale et al., 2019). Animations may also facilitate comparison between variables when uncertainty is involved (Hullman et al., 2015).
There is also research comparing features of color-coding in which participants ranked and rated map overlays differing in saturation, brightness, transparency, and hue, intended to indicate the chance that a thunderstorm would occur (Bisantz et al., 2009). Participants responses were highly correlated with the values intended by researchers for all of these features except hue, suggesting that hue variations may indicate different likelihoods than what was intended.
In addition, there is evidence for substantial variability in how people rank order hue intended to convey risk. Although the notion of risk is slightly different than that of “uncertainty,” it is related. Within the communication literature at least, risk generally means some combination of the likelihood and the severity of the event (Kaplan and Garrick, 1991; Eiser et al., 2012). Indeed, many risk scales employ color-coding based on variation in hue. However, with the exception of red, often found to convey the greatest risk (Borade et al., 2008; Hellier et al., 2010), there is little consensus on the rank order of other colors (Chapanis, 1994; Wogalter et al., 1995; Rashid and Wogalter, 1997). For instance, in a study of the long retired American Homeland Security Advisory System that used hue to indicate terrorist threat, more than half of the participants (57.8%) ranked the colors from most to least threatening in an order that conflicted with what was intended (Mayhorn et al., 2004). This suggests that hue may convey different levels of risk to different individuals as well as different levels of risk than what was intended. Again, these are risk displays (rather than uncertainty per se) which intentionally confound the constructs of severity and likelihood. However, the prevalence of such visualizations may influence people’s interpretation of color-coded uncertainty, an issue that we address in Deterministic Construal Error below.
The approach of comparing visualizations to one another has also uncovered inferences about information not explicitly depicted in the visualization. In a study that compared several visualizations of an uncertainty interval, a range of values within which the observation is expected, participants judgements of “probability of exceedance” revealed that most inferred a roughly normal distribution within the interval with all visualizations tested (Tak et al., 2015). However, the estimates of participants with low numeracy suggested a flatter distribution.
Our own early work, investigating uncertainty visualizations among professional forecasters, had a similar design (Nadav-Greenberg et al., 2008). We found that some visualizations such as boxplots, were better for reading precise values, while others, such as color-coded (spectral) charts, were better for judging relative uncertainty or appreciating the big picture. Thus, the value of a particular visualization format may depend on the task for which it is used.
This kind of research is useful, particularly in situations in which visualizations are the only option such a cartography (See Kinkeldey et al., 2014 for a more complete review), in that it reveals the relative characteristics of various forms of uncertainty visualization. However, it does not reveal whether visualizations communicate uncertainty more or less well than do non-visualized formats such as numerical expressions. This is important when non-visualization is an option, because sometimes visualizations come with costs in terms of potential misunderstandings (see Interpretation Biases Arising From Uncertainty Visualizations and Deterministic Construal Error, below). Therefore, a control condition with the same information in numeric text format (omitting the visualization) is useful to determine whether there are benefits to visualizations over other formats.
Comparison Between Visualizations and Numerical Formats
There is some research that makes this important comparison as well. For instance, one study using a shipping decision task (Mulder et al., 2019), tested three different visualizations representing the uncertainty in ice thickness, spaghetti plots (multiple lines each representing one possible outcome), fan plots (quartiles and extremes plotted around a median), and box plots. These were compared to a numerical representation of the same information (“30% chance of ice >1 m thick”). In this case, there were no consistent differences in decisions or best guess estimates (single value ice thickness estimate) between any of the expressions tested. In other words, all three visualizations and the non-visualized numeric control yielded similar decisions and estimates. However, spaghetti plots gave rise to the impression of greater uncertainty, suggesting a bias with that format.
Another example is an experiment comparing visualizations of the likelihood of wildfire in a particular geographic area to a text format (e.g., 80–100% burn likelihood zone). Although there were few differences in participants’ decisions about whether or not to evacuate when allowed the time to consider, spectral-color hue visualizations (warmer colors indicating higher likelihood) allowed participants to make better decisions under time pressure (Cheong et al., 2016).
It is important to realize however that even when comparisons between visualizations and numerical expressions are included, it is often unclear whether participants understood the situation any better or made better decisions than they would have if uncertainty were omitted altogether. This is also an important comparison to make because people often have numerous, fairly accurate, pre-experimental intuitions about uncertainty in some domains (Joslyn and Savelli, 2010; Savelli and Joslyn, 2012). The only way to know whether uncertainty visualizations provide additional information is to compare them to a control condition with a deterministic prediction.
Comparison Between Visualizations and Deterministic Formats
Indeed, there are also many experiments comparing uncertainty visualizations to a deterministic control. For instance, there is evidence that some uncertainty visualizations (dot plots, probability density functions, confidence intervals) allow people to better aggregate across varying estimates of the same value (Greis et al., 2018). Participants using uncertainty visualizations weighted discrepant sensors by their reliability whereas those using point estimates tended to take a simple average. Somewhat surprisingly, more complex visualizations, dot plots and probability density functions, resulted in better weighting than did confidence intervals.
Other studies comparing uncertainty visualizations to deterministic formats have revealed that color-coded uncertainty visualizations improve likelihood understanding compared to the conventional tornado warning polygon. In one study, participants using either spectral or monochromatic color-coded visualizations better understood the distribution of tornado likelihood across the area, than did participants using the conventional warning polygon (Ash et al., 2014). Another study comparing spectral and monochromatic formats to the conventional polygon, demonstrated that perceived likelihood was more accurate with both color-coded formats than with the conventional polygon (Miran et al., 2019). Thus, it is clear that there are several advantages for uncertainty visualizations when compared to a deterministic control.
However, the benefit of similar visualizations to decisions may have some limitations. In one example (Miran et al., 2019) protective decisions based on color-coded probabilistic tornado warnings were compared to those based on a deterministic warning polygon. The main advantages for the color-coded probabilistic warnings were in areas with greater than a 60% chance of a tornado. In that range, probabilistic visualizations increased concern, fear, and protective action as compared to the deterministic polygon. However, at lower probabilities (0–40%), mean ratings for concern, fear, and protective action were similar in the two formats.
Similarly, another study also using tornado warning graphics (Klockow-McClain et al., 2020), showed increased protective decisions for uncertainty visualizations above 50% chance of a tornado, but little difference from the deterministic control below 50%. This is clearly important information that was only discovered because the deterministic control condition was included in the experimental design. Based on these results, the advantage to user decisions for uncertainty visualizations may be confined to higher probabilities when compared to other warning information (such as the conventional polygon).
In addition, sometimes such comparisons reveal important misunderstandings. A study comparing a visualization of a single hurricane path (deterministic control) to variations of the cone of uncertainty and an ensemble of paths (Ruginski et al., 2016), demonstrated that people mistakenly infer that the hurricane damage is predicted to increase over time when viewing the uncertainty visualizations but not when the single deterministic path was shown. It is important to note that these visualizations were not intended to convey information about relative damage, an issue that we will return to in Deterministic Construal Error below. Thus, it is clear that critical information about both advantages and disadvantages can be revealed by comparing uncertainty visualizations to representations of the same information without uncertainty.
Comparison Between Visualizations, Numerical, and Deterministic Formats
Finally, there are also studies that include both controls, a non-visualized uncertainty expression and a single value or “deterministic” control. One example incorporated a decision task based on bus arrival times (Fernandes et al., 2018). Five graphs, using different visualization techniques to show the likelihood of arrival plotted over time (e.g., probability density function) were compared to a graph showing a single arrival time and a text format indicating the probability of exceeding a particular time (“Arriving in 9 min. Very good chance [∼85%] of arriving 7 min from now or later”). Participants with uncertainty information made better decisions about when to be at the bus stop than did those with the single value control. Cumulative distribution function plots and frequency based “dotplots,” in which more dots plotted over a particular time indicates greater likelihood, allowed for better performance overall. However, the probabilistic text format, which, as the authors noted, included somewhat less information, was comparable at some probability levels.
We have tested visualizations of a similar uncertainty expression, a predictive interval for daytime high and nighttime low temperature (Savelli and Joslyn, 2013). The visualization was a simplified box plot, essentially a bracket (see Figure 1A), to inform users of the temperatures between which the observed temperature was expected with 80% probability. There were a number of important advantages for predictive intervals compared to a control condition in which only the deterministic temperature was provided. By asking participants to indicate the highest and lowest values that would not surprise them, we discovered that predictive intervals, based on realistic values, led to a narrower range of expectations than the deterministic forecast alone. In other words, participants expected greater uncertainty when uncertainty information was not provided. Predictive intervals also helped participants to make better decisions (issue a freeze warning) by indicating whether the decision-relevant value was within or outside of the 80% predictive interval. This was rather surprising given the complex ideas upon which the predictive interval was based. Indeed, other research suggested that most participants were not able to provide an accurate explanation of the interval in response to open-ended questions (Joslyn et al., 2009). This is in line with research showing a number of interpretation problems with error bar visualizations in general (Correll and Gleicher 2014). Nonetheless, in this (Savelli and Joslyn, 2013) and other experiments in our lab (Joslyn et al., 2013; Grounds et al., 2017), participants demonstrated substantial practical understanding in that the predictive interval successfully informed their decisions. Interestingly, there were no differences in terms of decision quality between a bracket visualization and the text/numeric version (see Figure 1B) of this information, although there were significant misunderstandings with the bracket (See Deterministic Construal Error below).
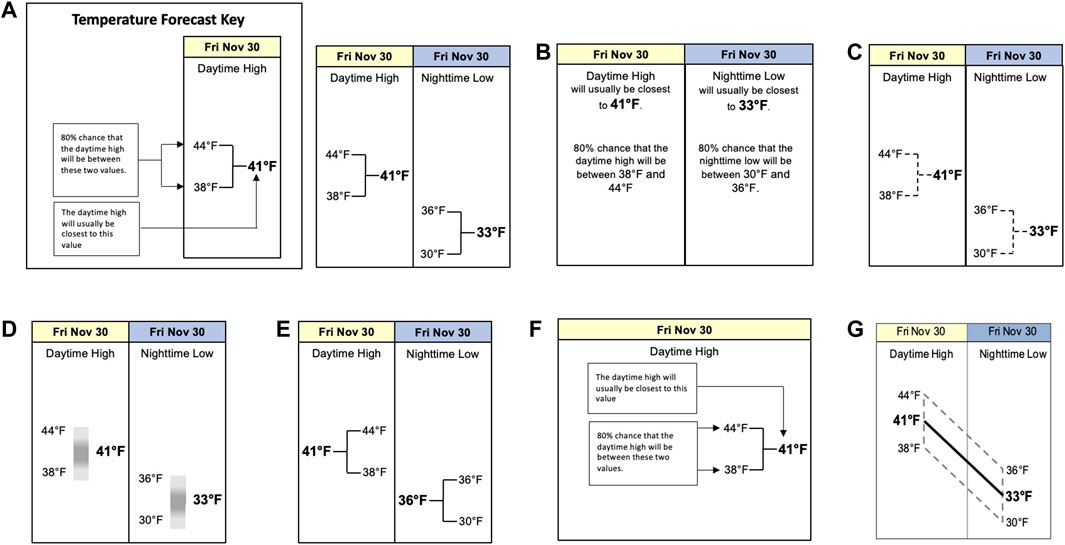
FIGURE 1. Predictive intervals, each accompanied by a key (shown in a) describing “41°F” as the “best forecast”. Note: Font and figure sizes are slightly smaller than they were in the original experiments to conform to journal requirements.
While we do not provide a comprehensive review here, the evidence suggests that there are definite advantages for uncertainty information, including uncertainty visualizations, over deterministic forecasts. However, there may be situations, especially when protective action is required at lower probabilities, where the advantage is less clear (e.g., Miran et al., 2019). Also less clear, are the advantages of visualizations over numeric/text representations. Sometimes visualizations are better (e.g., Cheong et al., 2016), and sometimes there are no differences (e.g., Miran et al., 2019). Indeed, advantages for visualizations are more often seen in specific situations. For instance, there is some evidence that icon arrays are more effective in communicating risk information based on disease prevalence especially among those with low numeracy (Garcia-Retamero and Galesic, 2010; Garcia-Retamero and Hoffrage, 2013). Indeed, these tend to be more complex problems than what we have discussed so far, involving understanding the combination of test accuracy and disease prevalence, risk reduction with specific treatments and Bayesian reasoning. Such visualizations are likely effective because they promote a mental representation that is compatible with the normative response (Evans et al., 2000). Indeed, there is evidence that adding information to a text-only representation of conditional reasoning problems can elicit performance comparable to that of icon arrays (Ottley et al., 2016).
Interpretation Biases Arising From Uncertainty Visualizations
It is also important to note that there are systematic biases in interpretation that arise from some visualizations. For example, in the experiment reviewed above (Mulder et al., 2019), spaghetti plots gave rise to the impression of greater uncertainty than other visualizations despite the fact that all were intended to display the same amount of uncertainty. Similar biases were reported by Tak et al. (2014) for a gradient visualization.
In addition, people tend to make assumptions about the values not depicted in visualizations, such as those within predictive ranges. As noted above, sometimes users assume a normal distribution (Tak et al., 2014; Tak et al., 2015), although this information is not explicit in the visualization. Whether or not a normal distribution is accurate depends on the statistic being reported. However, other evidence suggests that people tend to assume a relatively flat distribution within the range (Rinne and Mazzocco, 2013; Grounds et al., 2017) which is usually not the case. A similar assumption is made about the area within tornado polygons. Unless otherwise specified, people tend to think that the likelihood of a tornado is relatively uniform within the polygon boundary (Ash et al., 2014). This is definitely not the case, due to the typical movement of tornados. The likelihood tends to be less near the southwestern boundaries of the polygon and increase in the northeastern corner (Ash et al., 2014).
Deterministic Construal Error
Thus, it is clear that users of visualizations sometimes interpret them in ways that were not intended. Sometimes misinterpretations are outright errors, contradicting the intended message (e.g., Miran et al., 2019). However, sometimes users infer additional information that was not intentionally specified in the visualization (e.g., Tak et al., 2014; Tak et al., 2015). Perhaps the most serious error in interpretation however is one that most studies are not designed to detect. Sometimes people do not realize that uncertainty is what is being expressed by the visualization. Instead they interpret the image as representing some deterministic quantity, such as the amount of precipitation or the windspeed. This is known as deterministic construal error (Savelli and Joslyn, 2013; Padilla et al., 2020) and is most likely to occur in extra-experimental settings in which users have not already been alerted to the fact that the visualization depicts uncertainty.
A classic example is the cone of uncertainty showing the possible path of a hurricane. Evidence suggests that it is widely misunderstood as the extent of the storm with the central line indicating the main path of the hurricane (Broade et al., 2008; Boone et al., 2018; Bostrom et al., 2018). Indeed, participants tend to indicate that the hurricane will be larger and produce more damage when using the classic cone compared to the same information represented as ensemble or spaghetti plots, showing multiple possible paths (Ruginski et al., 2016; Liu et al., 2017; Padilla et al., 2017). It may be that the border, showing the diameter of the cone which increases with time as the uncertainty increases, suggests to users that the storm is growing over time. In other words, instead of uncertainty in the hurricane path, users interpreted the graphic as indicating a deterministic prediction for a single hurricane path with additional information about storm size that was increasing over time. This error has even been detected among emergency managers (Jennings, 2010). In addition, although spaghetti plots, without the border, attenuate this misinterpretation, it persists to some extent in spaghetti plots as well: Participants tend to think that the damage will be greater if their location is intersected by one of the randomly placed lines of the spaghetti plot (Padilla et al., 2019).
We first noticed the DCE when testing the bracket visualization of the upper and lower bound of the 80% predictive interval mentioned above (see Figure 1A; Savelli and Joslyn, 2013). Although the visualization was accompanied by a prominent key containing a simple, straightforward definition of each number, 36% of participants misinterpreted the upper bound as the daytime high temperature and the lower bound as the nighttime low. In other words, they thought that the bracket was depicting a deterministic forecast for diurnal fluctuation. We discovered this when we asked participants to indicate the “most likely” value, actually shown at the middle of the bracket (see Figure 1A). Instead of providing an approximation of that number, some participants answered with the value at the upper bound when we requested daytime high and the lower bound when we requested nighttime low temperature. In retrospect, this was not surprising, diurnal fluctuation is often included on weather websites. In other words, participants were expecting to see it. However, it was a gross misinterpretation of the single-value forecast, much higher (or lower) than what was intended, and it negatively affected the decisions participants made (e.g., to issue a heat or freeze warning) based on the forecast.
Initially we thought that we had simply done an inadequate job of visualizing uncertainty. So we ran a subsequent study in which we incorporated features recommended by visualization experts to convey uncertainty, such as broken instead of solid lines (Figure 1C) for the bracket (Tufte, 2006) and a bar with blurry, transparent ends (Figure 1D) where the upper and lower bounds were located (MacEachren, 1992). These were also accompanied by the same explicit key. However, again the errors were made at approximately the same rate. In other words, these classic uncertainty features did not help at all.
We tried a number of other adjustments including turning the bracket around so that the single-value forecast was on the left (presumably read first) and the less likely upper and lower bounds on the right (Figure 1E). In another version we put the key inside of the forecast, thinking it could not be ignored in that format (Figure 1F). But still the errors were made at approximately the same rate.
Then we decided we needed to point out the actual location of diurnal fluctuation in the forecast by including a line connecting the daytime high and nighttime low temperatures (see Figure 1G). Perhaps when viewers realized that diurnal fluctuation was represented by the line, they would not attribute the same meaning to the bracket. In other words, this graphic may serve to block DCEs. Participants still made the error.
We even tested a version in which the single-value forecast was accompanied by a plus/minus sign and a number indicating the amount of error to expect. Although not really a “visualization,” we were sure it would lead to fewer misinterpretations, because the only temperature value shown was the “correct” answer, the single-value temperature. Obtaining the upper- and lower-bound values required adding or subtracting the error amount. However, participants made DCEs with this format as well. This was particularly discouraging because it was clear that participants were willing to go to considerable effort to interpret the forecast as deterministic.
At that point, it was clear that we were dealing with a much deeper problem than expectations derived from other websites. In one final effort, we removed the visualization altogether and presented the information in a text format (See Figure 1B). With this format, the misinterpretation all but disappeared. Nearly everyone (94%) was able to correctly identify the numbers intended as the daytime high and nighttime low temperatures. This suggested that the previous errors were at least partially due to the fact that a visualization was used, rather than the particular type of visualization. Perhaps visualizing the information made the forecast seem more concrete and as a result, more certain. Perhaps after initially seeing the visualization, participants assumed they knew what the image meant and ignored the key altogether, regardless of where it was placed.
Indeed, there is growing evidence for DCEs with other forms of likelihood statistics and other uncertainty visualizations. For instance, color-coded uncertainty, whether spectral or monochromatic, may encourage DCEs, in part because color is often used to indicate variation in deterministic quantities, again setting up expectations based on past experience. This may be partly due to the intentional confounding of likelihood and severity in a long history of color-coded risk scales (see Comparison Between Visualizations above). What is particularly striking about color-coded uncertainty visualizations is that there is considerable evidence that experts are susceptible to DCEs with this format. For example, one study investigated professional weather forecasters understanding of a chart color-coded in shades of red and blue, indicating probability of accumulated rainfall greater than 0.01 inch. A full third of forecasters interpreted the increased color intensity (red in this case) as greater accumulation rather than greater likelihood (Wilson et al., 2019). Another example is a study of color-coded climate outlook graphics for temperature (Gerst et al., 2020), intended for use by the U.S. National Oceanic and Atmospheric Administration (NOAA). In these visualizations, hue indicated whether the value would be above normal (e.g., orange), near normal (gray) or below normal (e.g., blue). Uncertainty was indicated by variation in saturation. Expert users from emergency management, agriculture, water resource management, and energy sectors were first asked to explain the meaning of graphics, the relationship to normal temperatures (increase, decrease, near normal) and the probability. Almost half of them thought that a gray sector, intended to indicate the probability of near normal temperatures, meant simply “normal temperatures” (completely overlooking the notion of probability). Similar results were reported for color-coded probability of precipitation outlooks in an earlier study (Pagano et al., 2001). Greater saturation was intended to represent greater probability of wetter (or dryer) than normal conditions. Instead most emergency managers and water management experts interpreted greater saturation as indicating extremely high precipitation. It is interesting to note that these last two visualizations overlaid uncertainty onto other quantities (Category 2 as described by Tak et al., 2014, mentioned above). Thus, this strategy may be particularly conducive to DCEs. Indeed, this is an area where more research is necessary.
In sum, there is growing evidence for DCEs with visualized uncertainty, even among experts. Here we have shown examples of predictive intervals, possible hurricane paths as well as color-coded precipitation likelihood and climate temperature outlooks. However, people are capable of making the same error when no visualization is involved. People often think that probability of precipitation is a deterministic forecast for precipitation with additional information about the percentage area or time precipitation will be observed (Murphy et al., 1980; Joslyn et al., 2009). Similar results were reported in a recent study. When shown a probability of precipitation forecast, the majority of German respondents selected either “It will rain tomorrow in 30 percent of the area for which this forecast is issued” or “It will rain tomorrow for 30 percent of the time” (Fleischhut et al., 2020).
Psychological Explanation
Thus, it is clear that the DCE is fairly attractive to users. Although the examples provided here reside in the domains of weather and climate, we do not think that it is specific to these domains. Instead, we suspect that the DCE is the result of a more general propensity toward reasoning efficiency or heuristic reasoning (Tversky and Kahneman, 1975) that could be observed in any domain. Human reasoners have a tendency to take mental shortcuts that reduce the amount of information they must process at any given time, referred to as “cognitive load.” It has long been known that people tend to opt for a simpler interpretation if one is available, to reduce cognitive load (Kahneman, 2003). In this case, the deterministic interpretation, implying a single outcome, replaces the more complex but accurate interpretation in which one must consider multiple possible outcomes and their associated likelihoods. As such, the DCE may be a form of attribute substitution (Kahneman and Frederick, 2002), the tendency to substitute an easy for a hard interpretation. The deterministic interpretation is easier because it requires considering only one outcome at the choice point instead of many.
This is not to say that it is necessarily a conscious decision in which one considers both interpretations and deliberately selects one. Rather, the DCE likely occurs on an unconscious level, before one is even aware that there is an alternative interpretation. Indeed, cognitive and behavioral scientists who ascribe to the dual processes or dual systems accounts of human reasoning (Carruthers, 2009; see; Keren and Schul, 2009; Keren, 2013) attribute preconscious assumptions such as this to “System 1” (Kahneman and Frederick, 2002; Kahneman, 2011). System 1 includes reasoning that is fast, automatic, largely unconscious, and based on heuristics. The other, System 2, includes reasoning that is conscious, slow, deliberate and effortful. Although System 2 supports logical step-by-step reasoning, there are definite limitations to the amount of information that can be managed (Baddeley, 2012). Therefore, when people encounter complex information, System 1 simplifications, reducing cognitive load, are almost inevitable and take place rapidly prior to awareness (See Padilla et al., 2019, for a broader application of dual process theories to decisions and visualizations). In the case of DCEs people may be inclined to assume (System 1) that the message is deterministic. In a sense this is practical because most decision making is eventually binary in that one must choose between taking action or not. Thus, at some point one must act upon the outcome one judges to be more likely. In other words, because of the increase in cognitive load that accompanies uncertainty and the practical necessity of making a binary choice, perhaps the deterministic interpretation is “preferred” by the human information processing system. As such, the deterministic construal error may be related to a general psychological “desire for certainty” (Slovic et al., 1979).
Nonetheless there are clearly situations in which DCEs are more likely to occur. In particular those in which the same information is often presented as deterministic (i.e., diurnal fluctuations) or the same conventions have been used to express variation in deterministic quantities, such as color-coding in context of weather. In other words, DCEs are more likely to occur when prior experience leads to the expectation that expressions quantify deterministic information. This may be particularly likely with visualizations, which also tend to be highly salient. Usually a small text key is the only thing that specifies the quantity. Users may or may not be willing to read it, especially if they are convinced that they already know what the visualization means.
Ask the Right Question
It is important to understand however, that in order to detect DCEs participants must be asked the right question. Although experts have been warning against this possible error for some time (Kootval, 2008), few studies have reported it directly, mainly because in most studies participants are told that the visualization contains uncertainty before any questions are asked of them. We discovered the DCE by accident when asking about the deterministic quantity depicted in the visualization that also contained uncertainty. A more direct approach would be to begin by asking participants an open-ended question about what the visualization means, as was done by Gerst et al. (2020) above. This is important to do prior to providing participants additional information that may reveal the fact that uncertainty is the subject. This also means that most such comparisons will have to be done between groups. In other words, the same participant should not be asked to respond to more than one format. That is because, once the participant has been alerted to the fact that uncertainty is an issue by more specific questions or well-designed graphics, this knowledge may well influence responses to subsequent visualizations, known as “carryover effects.” The point is that many of the studies reviewed above did not detect this fundamental interpretation error, largely because they were not designed to do so. Participants were simply asked questions about uncertainty directly, revealing in the question itself that the visualization contained uncertainty. In a natural setting, the cues included in such leading questions would not be available to users and they may be more likely to make the deterministic assumption.
Solutions
The bottom line is that people may have a strong propensity to commit DCEs that is built into their cognitive architecture. In the vast majority of cases this is probably a fair assumption and a useful strategy. However, when applied to uncertainty visualizations, the consequences can be serious. The DCE prevents people from benefitting from likelihood information, which as we saw from the work reviewed above can increase trust and improve decision quality. Moreover, DCEs can give users a gross misunderstanding of the single value forecast as was the case with the predictive interval when participants mistook the upper bound for the daytime high and the lower bound for the nighttime low (Savelli and Joslyn, 2013). This is clearly a serious problem for uncertainty communication.
What do we do about it? The first step of course, is to understand it. More research is required that is capable of detecting this error to ascertain the conditions under which people are most prone to make it. Evidence to date suggests that some formats, such as color-coded visualizations, the cone of uncertainty, and brackets, may encourage DCEs. This may be due in part to the facts that visualizations are salient and it is not clear that they indicate uncertainty until the key or caption is read, that visualizations may serve to concretize the quantity, and that prior experience may lead users to assume the deterministic meaning initially. At that point, some users may be convinced that they understand what is being depicted and fail to make an effort to fully grasp any additional explanations that are provided. This might be particularly problematic in situations in which both kinds of information are included in the same graphic. That is, when uncertainty information is overlaid on visualizations of some other quantity such as above normal temperatures. In those cases, it may be particularly challenging even for experts to decode the true meaning of specific aspects of the visualization, even when they take the time to read the key. At the very least, it may help to separate uncertainty and other quantities in graphics, although again, more of the right kind of research is needed to fully understand this issue.
When these issues are better understood, we can begin to think about solutions. Indeed, there have already been some interesting suggestions for overcoming the DCE in the context of visualizations, such as avoiding the use of colors already associated with warnings (yellow, orange, red and violet) and not emphasizing particular points on a graph, such as medians, as they “may inappropriately withdraw attention from the uncertainty” (Fundel et al., 2019). Another potential solution, in some cases, is hypothetical outcome plots in which animation shows different possible outcomes in rapid sequence (see Comparison Between Visualizations above). In this format, the uncertainty becomes “implicit,” rather than a property of something else like color, size, or saturation that usually maps onto deterministic data (Hullman et al., 2015; Kale et al., 2019). Ensembles, such as those discussed in Comparison Between Visualizations and Deterministic Formats in context of hurricane paths, provide a similar but static solution. In fact, the evidence reviewed above (Ruginski et al., 2016) suggests that ensembles, showing a subset of possible hurricane paths reduce DCEs as compared to the conventional cone of uncertainty. Another suggestion for depicting uncertainty with error bars, is to employ gradation with lighter colors indicating lower likelihood, at the ends (Wilke, 2019). However, as of this writing, few of these suggestions have been tested using a procedure capable of detecting DCEs in a situation known to produce them, showing a reduction when they are employed. We do know based on our own work that in situations where DCEs are likely, such as when users have expectations based on prior experience (e.g., diurnal fluctuation), many of the known conventions for visualizing uncertainty failed to eliminate the DCE (Savelli and Joslyn, 2013).
Indeed, because of the need to reduce cognitive load and the fact that most predictions available to members of the public have historically been deterministic, people may automatically assume that they are receiving a deterministic message, unless that interpretation is somehow blocked. As a matter of fact, there is some evidence that blocking DCEs is possible when the specific psychological mechanism that leads to them is understood. DCEs were reduced when probability of precipitation included the probability of “no rain” (70% chance of rain and 30% chance of no rain) specifying both possible outcomes and blocking the percent area/time interpretation (Joslyn et al., 2009). However, the attempt at blocking DCEs in response to the predictive interval bracket (Savelli and Joslyn, 2013), by adding connecting lines to point out the actual diurnal fluctuation (Figure 1G), was not effective. The only thing that eliminated the DCE in that case, was removing the visualization altogether and providing the same information in a text format. On the other hand, information instructing participants that the width of the cone of uncertainty “tells you nothing about the size or intensity of the storm” reduced this impression among participants compared to a control condition in which it was not presented (Boone et al., 2018). Thus, instructions that focus on bocking psychological mechanisms known to produce DCEs, may be an important strategy to test in future research.
There is also some evidence that the DCE can be overcome with experience. We found in our own work with the predictive interval bracket visualization that participants were less likely to commit a DCE on subsequent trials after the first trial (Experiment 1; Joslyn et al., 2013). This suggests that participants came to understand the probabilistic meaning of the forecast after using it. It is important to note however, that explicit instructions did not help in this case. In the second study, the experimenter read the key information aloud, explaining the probabilistic meaning of the upper and lower bound on the bracket, to ensure that all participants were exposed to this information at the beginning of the experiment. This did not reduce DCEs. In other words, we did not see an equal reduction in errors with read-aloud instructions on trial 1, in Experiment 2 as was seen in Experiment 1 on the second trial. Perhaps participants must deliberately interact with the forecast, using it to answer specific questions, to reach this level of understanding. Again, more research is needed to fully understand these processes.
However, in many cases it may be that uncertainty visualizations should be avoided altogether as some have suggested (Savelli and Joslyn, 2013; Fernandes et al., 2018) because they may encourage DCEs and because people are likely to encounter them in novel situations, such as on an internet website, where little or no support is available. As we saw in our own study (Savelli and Joslyn, 2013), omitting the visualization and providing a simple text based numerical representation of the 80% predictive interval instead (Figure 1B) eliminated the error. Moreover, the text format was equally advantageous in terms of forecast understanding, trust in the forecast and decision quality as were the visualizations. In other words, omitting the visualization reduced DCEs with no costs. Moreover, participants were able to understand and use the text predictive interval forecast with absolutely no special training.
Discussion
To reiterate, it is clear that this is an important issue that needs more research specifically designed to address it. The scientific community has long assumed that visualizations facilitate understanding, especially for statistically complex information. However, this assumption has only recently been put to the test with regard to visualized uncertainty and may well be ill advised in some cases. Therefore, we need to better understand whether there are situations in which uncertainty visualizations have advantages over other communication strategies (when they are an option), such as text and or numeric formats. In order to do that, experimental designs must be employed that make the right comparisons, between visualizations and non-visualized representations of the same information as well as comparisons to deterministic controls. Indeed, there may be some contexts in which visualizations are particularly helpful, such as with icon arrays used to communicate risk information based on disease prevalence and test accuracy among those with low numeracy (Garcia-Retamero and Galesic, 2010; Garcia-Retamero and Hoffrage, 2013). In addition, there are some situations in which visualizations may be the only option, such as when the judgment requires appreciating variation across geographic locations (Nadav-Greenberg et al., 2008). When those situations are identified, efforts can be focused on detecting and, if necessary, reducing interpretation errors. To do that however, researchers must ask questions that are capable of detecting fundamental interpretation errors such as the deterministic construal error. Participant should be asked what they think the graphic means prior to being told that it represents uncertainty.
We wish to stress that we firmly believe that more uncertainty information should be made available to members of the public. People have individual concerns and risk tolerances that are not well served by one-size fits-all warnings, single-value estimates, or verbally described risk categories. Furthermore, people have well-founded intuitions about the uncertainties in such situations that may prevent them from trusting deterministic predictions or advice that does not make the uncertainty explicit. At the same time, these intuitions may prepare users to understand uncertainty expressions that are carefully presented in a manner that takes into account how people process and understand uncertainty information in specific contexts. We do not claim that most users understand uncertainty on a theoretical level, but rather that they understand uncertainty expressions on a practical level. It is becoming increasingly clear that members of the public can use carefully presented uncertainty information to make better decisions and decisions that are tailored to their own risk tolerance. Our view is that, not only do people need explicit uncertainty information to make better, more individualized decisions, but also, they can understand it, at least in a practical sense. Many important choices made by non-expert end users, such as those involving financial planning, health issues, and weather-related decisions, could benefit from the consideration of reliable uncertainty estimates. Thus, learning how people interpret uncertainty information and how visualizations impact user decisions is crucial. To quote a prominent risk scientist, “One should no more release untested communications than untested pharmaceuticals” (Fischhoff, 2008).
Author Contributions
SS Conducted literature review. Summarized all research included in the manuscript. SJ Reviewed summaries of all research in the manuscript. Wrote the manuscript.
Funding
The research of Susan Joslyn and Sonia Savelli is based on work supported by: National Science Foundation 1559126, National Science Foundation #1559126, National Science Foundation #724721, Office Of Naval Research #N00014-C-0062.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ash, K. D., Schumann, R. L., and Bowser, G. C. (2014). Tornado warning trade-offs: evaluating choices for visually communicating risk. Weather Clim. Soc. 6 (1), 104–118. doi:10.1175/WCAS-D-13-00021.1
Baddeley, A. (2012). Working memory: theories, models, and controversies. Annu. Rev. Psychol. 63, 1–29. doi:10.1146/annurev-psych-120710-100422
Bisantz, A. M., Stone, R. T., Pfautz, J., Fouse, A., Farry, M., Roth, E., et al. (2009). Visual representations of meta-information. J. Cogn. Eng. Decis. Mak. 3 (1), 67–91. 10.1518/155534309X433726
Boone, A. P., Gunalp, P., and Hegarty, M. (2018). Explicit versus actionable knowledge: the influence of explaining graphical conventions on interpretation of hurricane forecast visualizations. J. Exp. Psychol. Appl. 24 (3), 275–295. doi:10.1037/xap0000166
Borade, A. B., Bansod, S. V., and Gandhewar, V. R. (2008). Hazard perception based on safety words and colors: an Indian perspective. Int. J. Occup. Saf. Ergon. 14 (4), 407–416. doi:10.1080/10803548.2008.11076777
Bornstein, R. F. (1989). Exposure and affect: overview and meta-analysis of research, 1968–1987. Psychol. Bull. 106, 265–289. doi:10.1037/0033-2909.106.2.265
Bostrom, A., Morss, R. E., Lazo, J. K., Demuth, J. L., and Lazrus, H. (Forthcoming 2018). Eyeing the storm: how residents of coastal Florida see hurricane forecasts and warnings. Int. J. Dis. Risk Reduct. 30, 105–119. doi:10.1016/j.ijdrr.2018.02.027
Carruthers, P. (2009). “An architecture for dual reasoning,” in Two minds: dual processes and beyond. Editors J. S. B. T. Evans, and K. Frankish (New York, NY: Oxford University Press), 109–127.
Chapanis, A. (1994). Hazards associated with three signal words and four colours on warning signs. Ergonomics 37 (2), 265–275. doi:10.1080/00140139408963644
Cheong, L., Bleisch, S., Kealy, A., Tolhurst, K., Wilkening, T., and Duckham, M. (2016). Evaluating the impact of visualization of wildfire hazard upon decision-making under uncertainty. Int. J. Geogr. Inf. Sci. 30 (7), 1377–1404. doi:10.1080/13658816.2015.1131829
Correll, M., and Gleicher, M. (2014). Error bars considered harmful: exploring alternate encodings for mean and error. IEEE Trans. Visual. Comput. Graph. 20 (12), 2142–2151. doi:10.1109/TVCG.2014.2346298
Eiser, J. R., Bostrom, A., Burton, I., Johnston, D. M., McClure, J., Paton, D., et al. (2012). Risk interpretation and action: a conceptual framework for responses to natural hazards. Int. J. Dis. Risk Reduct. 1, 5–16. doi:10.1016/j.ijdrr.2012.05.002
Evans, B. J. (1997). Dynamic display of spatial data-reliability: does it benefit the map user? Comput. Geosci. 23 (4), 409–422. doi:10.1016/S0098-3004(97)00011-3
Evans, J. S., Handley, S. J., Perham, N., Over, D. E., and Thompson, V. A. (2000). Frequency versus probability formats in statistical word problems. Cognition 77, 197–213. doi:10.1016/s0010-0277(00)00098-6
Fernandes, M., Walls, L., Munson, S., Hullman, J., and Kay, M. (2018). “Uncertainty displays using quantile dotplots or CDFs Improve transit decision making,” in Proceeding of the 2018 CHI, Montreal, Canada, April 21–26, 2018.
Fischhoff, B. (2008). Assessing adolescent decision-making competence. Dev. Rev. 28, 12–28. 10.1016/j.dr.2007.08.001
Fleischhut, N., Herzog, S. M., and Hertwig, R. (2020). Weather literacy in times of climate change. Weather Clim. Soc. 12, (3), 435–452. doi:10.1175/WCAS-D-19-0043.1
Fundel, V. J., Fleischhut, N., Herzog, S. M., Gober, M., and Hagedorn, R. (2019). Promoting the use of probabilistic weather forecasts through a dialogue between scientists, developers, and end-users. Q. J. R. Meteorol. Soc. 145 (Suppl. 1), 210–231. doi:10.1002/qj.3482
Garcia-Retamero, R., and Galesic, M. (2010). Who profits from visual aids: overcoming challenges in people's understanding of risks [corrected]. Soc. Sci. Med. 70 (7), 1019–1025. doi:10.1016/j.socscimed.2009.11.031
Garcia-Retamero, R., and Hoffrage, U. (2013). Visual representation of statistical information improves diagnostic inferences in doctors and their patients. Soc. Sci. Med. 83 (0), 27–33. doi:10.1016/j.socscimed.2013.01.034
Gershon, N. (1998). Visualization of an imperfect world. IEEE Trans. Comput. Graph. Appl. 18 (4), 43–45.
Gerst, M. D., Kenney, M. A., Baer, A. E., Speciale, A., Wolfinger, J. F., Gottschalck, J., et al. (2020). Using visualization science to improve expert and public understanding of probabilistic temperature and precipitation outlooks. Am. Meteorol. Soc. 12, 117–133. doi:10.1175/WCAS-D-18-0094.1
Gneiting, T., and Raftery, A. E. (2005). Atmospheric science. Weather forecasting with ensemble methods. Science 310 (5746), 248–249. doi:10.1126/science.1115255
Greis, M. (2017). A systematic exploration of uncertainty in interactive systems. Available at: https://elib.uni-stuttgart.de/handle/11682/9770 (Accessed January 2020).
Greis, M., Joshi, A., Singer, K., Schmidt, A., and Machulla, T. (2018). “Uncertainty visualization influences how humans aggregate discrepant information,” in Proceedings of the 2018 CHI conference on human factors in computing systems, Montreal, Canada, April 21–26, 2018, 1–12.
Grounds, M. A., Joslyn, S., and Otsuka, K. (2017). Probabilistic interval forecasts: an individual differences approach to understanding forecast communication. Adv. Meteorol. 2017, 1–18. doi:10.1155/2017/3932565
Grounds, M., and Joslyn, S. (2018). Communicating weather forecast uncertainty: do individual differences matter? J. Exp. Psychol. Appl. 24 (1), 18–33. doi:10.1037/xap0000165
Hellier, E., Tucker, M., Kenny, N., Rowntree, A., and Edworthy, J. (2010). Merits of using color and shape differentiation to improve the speed and accuracy of drug strength identification on over-the-counter medicines by laypeople. J. Patient Saf. 6 (3), 158. doi:10.1097/PTS.0b013e3181eee157
Hullman, J., Resnick, P., and Adar, E. (2015). Hypothetical outcome plots outperform error bars and violin plots for inferences about reliability of variable ordering. PloS One 10, e0142444. doi:10.1371/journal.pone.0142444
Hullman, J. (2016). “Why evaluating uncertainty visualization is error prone,” in Proceedings of the sixth workshop on beyond time and errors on novel evaluation methods for visualization, Baltimore, Maryland, October 24, 2016, 143–151.
Hullman, J., Qiao, X., Correll, M., Kale, A., and Kay, M. (2019). In pursuit of error: a survey of uncertainty visualization evaluation. IEEE Trans. Visual. Comput. Graph. 25 (1), 903–913. doi:10.1109/TVCG.2018.2864889
Jennings, R. (2010). Emergency managers and probabilistic forecast products: end users, their needs & requirements. Presented at the NOAA Hurricane Forecast Improvement. Project-THORPEX Ensemble Product Development Workshop, Boulder, CO. Available at: http://www.ral.ucar.edu/jnt/tcmt/events/2010/hfip_ensemble_workshop/presentations/jennings_hfip.pdf (Accessed June 2020).
Joslyn, S., and LeClerc, J. (2012). Uncertainty forecasts improve weather-related decisions and attenuate the effects of forecast error. J. Exp. Psychol. Appl. 18 (1), 126–140. doi:10.1037/a0025185
Joslyn, S., Nadav-Greenberg, L., and Nichols, R. M. (2009). Probability of precipitation. Am. Meteorol. Soc. 185–193. doi:10.1175/2008BAMS2509.1
Joslyn, S., Nemec, L., and Savelli, S. (2013). The benefits and challenges of predictive interval forecasts and verification graphics for end-users. Weather Forecast. 5, 133–147. 10.1175/WCAS-D-12-00007.1
Joslyn, S., and Savelli, S. (2010). Communicating forecast uncertainty: public perception of weather forecast uncertainty. Meteorol. Appl. 17, 180–195. 10.1002/met.190
Kahneman, D. (2003). A perspective on judgment and choice: mapping bounded rationality. Am. Psychol. 58 (9), 697–720. doi:10.1037/0003-066X.58.9.697
Kahneman, D., and Frederick, S. (2002). “Representativeness revisited: attribute substitution in intuitive judgment,” in Heuristics and biases. Editors T. Gilovich, D. Griffin, and D. Kahneman (New York: Cambridge University Press), 49–81.
Kale, A., Nguyen, F., Kay, M., and Hullman, J. (2019). Hypothetical outcome plots help untrained observers judge trends in ambiguous data. IEEE Trans. Visual. Comput. Graph. 25 (1), 892–902. doi:10.1109/TVCG.2018.2864909
Kaplan, S., and Garrick, B. J. (1991). On the quantitative definition of risk. Risk Anal. 1(1), 11–27. 10.1111/j.1539-6924.1981.tb01350.x
Keren, G., and Schul, Y. (2009). Two is not always better than one: a critical evaluation of two-system theories. Perspect. Psychol. Sci. 4 (6), 533–550. doi:10.1111/j.1745-6924.2009.01164.x
Keren, G. (2013). A tale of two systems: a scientific advance or a theoretical stone soup? Commentary on Evans & stanovich (2013). Perspect. Psychol. Sci. 8 (3), 257–262. doi:10.1177/1745691613483474
Kinkeldey, C., MacEachren, A. M., Riveiro, M., and Schiewe, J. (2015). Evaluating the effect of visually represented geodata uncertainty on decision-making: systematic review, lessons learned, and recommendations. Cartogr. Geogr. Inf. Sci. 44, 1–21. doi:10.1080/15230406.2015.1089792
Kinkeldey, C., MacEachren, A. M., and Schiewe, J. (2014). How to assess visual communication of uncertainty? A systematic review of geospatial uncertainty visualisation user studies. Cartogr. J. 51 (4), 372–386. 10.1179/1743277414Y.0000000099
Klockow-McClain, K. E., McPherson, R. A., and Thomas, R. P. (2020). Cartographic design for improved decision making: trade-offs in uncertainty visualization for tornado threats. Ann. Assoc. Am. Geogr. 110 (1), 314–333. doi:10.1080/24694452.2019.1602467
Kootval, H. (2008). Guidelines on communicating forecast uncertainty. World Meteorological OrganizationWMO/TD No, 1422.
LeClerc, J., and Joslyn, S. (2015). The cry wolf effect and weather-related decision making. Risk Anal. 35, 385. doi:10.1111/risa.12336
Liu, L., Boone, A. P., Ruginski, I. T., Padilla, L., Hegarty, M., Creem-Regehr, S. H., et al. (2017). Uncertainty visualization by representative sampling from prediction ensembles. IEEE Trans. Visual. Comput. Graph. 23 (9), 2165–2178. doi:10.1109/TVCG.2016.2607204
Lorenz, S., Dessai, S., Forster, P. M., and Paavola, J. (2015). Tailoring the visual communication of climate projections for local adaptation practitioners in Germany and the UK. Philos. Trans. A Math Phys. Eng. Sci. 373, 20140457. doi:10.1098/rsta.2014.0457
Mayhorn, C. B., Wogalter, M. S., Bell, J. L., and Shaver, E. F. (2004). What does code red mean? Ergon. Des. Quart. Human Factors Appl. 12 (4), 12–14. doi:10.1177/106480460401200404
Miran, S. M., Ling, C., Gerard, A., and Rothfusz, L. (2019). Effect of providing the uncertainty information about a tornado occurrence on the weather recipients' cognition and protective action: probabilistic hazard information versus deterministic warnings. Risk Anal. 39 (7), 1533–1545. doi:10.1111/risa.13289
Morss, R. E., Demuth, J. L., and Lazo, J. K. (2008). Communicating uncertainty in weather forecasts: a survey of the US public. Weather Forecast. 23 (5), 974–991. 10.1175/2008WAF2007088.1
Mulder, K. J., Lickiss, M., Black, A., Charlton-Perez, A. J., McCloy, R., and Young, J. S. (2019). Designing environmental uncertainty information for experts and non-experts: does data presentation affect users’ decisions and interpretations? Meteorol. Appl. 27, 1–10. doi:10.1002/met.1821
Murphy, A. H., Lichtenstein, S., Fischoff, B., and Winkler, R. L. (1980). Misinterpretations of precipitation probability forecasts. Bull. Am. Meteorol. Soc. 61, 695–701.
Nadav-Greenberg, L., and Joslyn, S. (2009). Uncertainty forecasts improve decision-making among non-experts. J. Cogn. Eng. Decis. Mak. 2, 24–47. 10.1518/155534309X474460
Nadav-Greenberg, L., Joslyn, S., and Taing, M. U. (2008). The effect of weather forecast uncertainty visualization on decision-making. J. Cogn. Eng. Decis. Mak. 2 (1), 24–47.
Ottley, A., Peck, E. M., Harrison, L. T., Afergan, D., Ziemkiewicz, C., Taylor, H. A., et al. (2016). Improving Bayesian reasoning: the effects of phrasing, visualization, and spatial ability. IEEE Trans. Visual. Comput. Graph. 22 (1), 529–538. doi:10.1109/TVCG.2015.2467758
Padilla, L. M., Ruginski, I. T., and Creem-Regehr, S. H. (2017). Effects of ensemble and summary displays on interpretations of geospatial uncertainty data. Cogn. Res. Princ. Implic. 2, 40. doi:10.1186/s41235-017-0076-1
Padilla, L. M. K., Creem-Regehr, S. H., and Thompson, W. (2019). The powerful influence of marks: visual and knowledge-driven processing in hurricane track displays. J. Exp. Psychol. Appl. doi:10.1037/xap0000245
Padilla, L. M., Kay, M., and Hullman, J. (2020). Uncertainty visualization. To appear in, handbook of computational statistics and data science. Available at: https://psyarxiv.com/ebd6r (Accessed October 2020).
Pagano, T. C., Hartmann, H. C., and Sorooshian, S. (2001). Using climate forecasts for water management: Arizona and the 1997-1998 El Nino. J. Am. Water Resour. Assoc. 37 (5), 1139–1153. 10.1111/j.1752-1688.2001.tb03628.x
Parrott, R., Silk, K., Dorgan, K., Condit, C., and Harris, T. (2005). Risk comprehension and judgments of statistical evidentiary appeals. Hum. Commun. Res. 31, 423–452. doi:10.1093/hcr/31.3.423
Patt, A. (2001). Understanding uncertainty: forecasting seasonal climate for farmers in Zimbabwe. Risk Decis. Pol. 6, 105–119.
Radford, L. M., Senkbeil, J. C., and Rockmanm, M. S. (2013). Suggestions for alternative tropical cyclone warning graphics in the USA. Disaster Prev. Manag. 22, 3–209. doi:10.1108/DPM-06-2012-0064.192
Rashid, R., and Wogalter, M. S. (1997). Effects of warning border color, width, and design on perceived effectiveness. Adv. Occup. Ergon. Saf. 455–458.
Reagan, R. T., Mosteller, F., and Youtz, C. (1989). Quantitative meanings of verbal probability expressions. J. Appl. Psychol. 74 (3), 433–442. doi:10.1037/0021-9010.74.3.433
Rinne, L. F., and Mazzocco, M. M. M. (2013). Inferring uncertainty from interval estimates: effects of alpha level and numeracy. Judgm. Decis. Mak. 8 (3), 330–344.
Ruginski, I. T., Boone, A. P., Padilla, L. P., Kramer, H. S., Hegarty, M., Thompson, W. B., et al. (2016). “Non-expert interpretations of hurricane forecast uncertainty visualizations,” in Special issue on visually-supported spatial reasoning with uncertainty. 16 (2), 154–172.
Savelli, S., and Joslyn, S. (2012). Boater safety: communicating weather forecast information to high stakes end users. Weather Clim. Soc. 4, 7–19. 10.1175/WCAS-D-11-00025.1
Savelli, S., and Joslyn, S. (2013). The advantages of predictive interval forecasts for non-expert users and the impact of visualizations. Appl. Cognit. Psychol. 27, 527–541. doi:10.1002/acp.2932
Slovic, P., Fischhoff, B., and Lichtenstein, S. (1979). Rating the risks. Environment. 21 (14–20), 36–39. doi:10.1080/00139157.1979.9933091
Tak, S., Toet, A., and van Erp, J. (2014). The perception of visual UncertaintyRepresentation by non-experts. IEEE Trans. Visual. Comput. Graph. 20 (6), 935–943. doi:10.1109/TVCG.2013.247
Tak, S., Toet, A., and van Erp, J. (2015). Public understanding of visual representation of uncertainty in temperature forecasts. J. Cogn. Eng. Decis. Mak. 9 (3), 241–262. doi:10.1177/1555343415591275
Taylor, A., Dessai, S., and de Bruin, W. B. (2015). Communicating uncertainty in seasonal and interannual climate forecasts in Europe. Philos. Trans. A Math Phys. Eng. Sci. 373, 20140454. doi:10.1098/rsta.2014.0454
Tversky, A., and Kahneman, D. (1975). “Judgment under uncertainty: heuristics and biases,” in Utility, probability, and human decision making, 141–162.
van der Bles, A. M., van der Linden, S., Freeman, A. L. J., Mitchell, J., Galvao, A. B., Zaval, L., et al. (2019). Communicating uncertainty about facts, numbers and science. R Soc. Open. Sci. 6. 181870. doi:10.1098/rsos.181870
Wallsten, T., Budescu, D., Rapoport, A., Zwick, R., and Forsyth, B. (1986). Measuring the vague meaning of probability terms. J. Exp. Psychol. Gen. 115, 348–365. 10.1037/0096-3445.115.4.348
Wilke, C. O. (2019). “Fundamentals of data visualizations. National academies of sciences, engineering, and medicine 2017,” in Communicating science effectively: a research agenda. (Washington, DC: The National Academies Press).
Wilson, K. A., Heinselman, P. L., Skinner, P. S., Choate, J. J., and Klockow-McClain, K. E. (2019). Meteorologists’ interpretations of storm-scale ensemble-based forecast guidance. Am. Meteorol. Soc. 11, 337–354. doi:10.1175/WCAS-D-18-0084.1
Windschitl, P. D., and Wells, G. L. (1996). Measuring psychological uncertainty: verbal versus 578 numerical methods. J. Exp. Psychol. Appl. 2 (4), 343–364. doi:10.1037//1076-898x.2.4.343
Wogalter, M. S., Magurno, A. B., Carter, A. W., Swindell, J. A., Vigilante, W. J., and Daurity, J. G. (1995). Hazard associations of warning header components. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 39 (15), 979–983. doi:10.1177/154193129503901503
Zajonc, R. B. (1968). Attitudinal effects of mere exposure. J. Pers. Soc. Psychol. Monogr. Suppl. 9, 1–27. 10.1037/H0025848
Keywords: visualizations, uncertainty, decision making, risk perception, judgment, experimental psychology
Citation: Joslyn S and Savelli S (2021) Visualizing Uncertainty for Non-Expert End Users: The Challenge of the Deterministic Construal Error. Front. Comput. Sci. 2:590232. doi: 10.3389/fcomp.2020.590232
Received: 31 July 2020; Accepted: 14 December 2020;
Published: 18 January 2021.
Edited by:
Lace M. K. Padilla, University of California, United StatesReviewed by:
Michael Correll, Tableau Research, United StatesIan Ruginski, University of Zurich, Switzerland
Copyright © 2021 Joslyn and Savelli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Susan Joslyn, c3VzYW5qQHV3LmVkdQ==
 Susan Joslyn
Susan Joslyn Sonia Savelli
Sonia Savelli