- CAPE-Lab – Computer Aided Process Engineering Laboratory, Department of Industrial Engineering, University of Padova, Padova, Italy
The development of cell cultures to produce monoclonal antibodies is a multi-step, time-consuming, and labor-intensive procedure which usually lasts several years and requires heavy investment by biopharmaceutical companies. One key aspect of process optimization is improving the feeding strategy. This step is typically performed though design of experiments (DoE) during process development, in such a way as to identify the optimal combinations of factors which maximize the productivity of the cell cultures. However, DoE is not suitable for time-varying factor profiles because it requires a large number of experimental runs which can last several weeks and cost tens of thousands of dollars. We here suggest a methodology to optimize the feeding schedule of mammalian cell cultures by virtualizing part of the experimental campaign on a hybrid digital model of the process to accelerate experimentation and reduce experimental burden. The proposed methodology couples design of dynamic experiments (DoDE) with a hybrid semi-parametric digital model. In particular, DoDE is used to design optimal experiments with time-varying factor profiles, whose experimental data are then utilized to train the hybrid model. This will identify the optimal time profiles of glucose and glutamine for maximizing the antibody titer in the culture despite the limited number of experiments performed on the process. As a proof-of-concept, the proposed methodology is applied on a simulated process to produce monoclonal antibodies at a 1-L shake flask scale, and the results are compared with an experimental campaign based on DoDE and response surface modeling. The hybrid digital model requires an extremely limited number of experiments (nine) to be accurately trained, resulting in a promising solution for performing in silico experimental campaigns. The proposed optimization strategy provides a 34.9% increase in the antibody titer with respect to the training data and a 2.8% higher antibody titer than the optimal results of two DoDE-based experimental campaigns comprising different numbers of experiments (i.e., 9 and 31), achieving a high antibody titer (3,222.8 mg/L) —very close to the real process optimum (3,228.8 mg/L).
1 Introduction
Monoclonal antibodies (mAbs) are biological drugs which have attracted attention for the treatment of autoimmune, oncological, and infectious diseases (Castelli et al., 2019). In 2018, they represented 53% of overall biopharmaceutics approvals by regulatory agencies and 65.6% of entire biopharmaceutical sales (Walsh, 2018). At the industrial scale, mAbs are produced in fed-batch cultures of mammalian cells which are appositely generated to secrete the desired product (O’Flaherty et al., 2020; Wurm, 2004).
The development of mAbs is a multi-step process which requires a lot of resources, both of time and capital investment, because it usually lasts several years and costs billions of dollars (Epifa, 2021; Farid et al., 2020). The upstream development of mAbs starts with cell line generation, screening and selection, and process characterization. At these stages, a large pool of cell lines is generated and tested at different process scales (Barberi et al., 2022; Facco et al., 2020) to identify those that meet the desired performance in terms of growth, productivity, and product quality (Gronemeyer et al., 2014; Tripathi and Shrivastava, 2019). Furthermore, the relationship between critical process parameters (CPP) and critical quality attributes (CQA) is studied for regulatory compliance and for process optimization. During process optimization, bioreactor operating parameters—such as temperature, pH, agitation, and dissolved oxygen—are adapted to the specific host system to enhance cell growth and specific productivity (Gronemeyer et al., 2014; Li et al., 2010; Tripathi and Shrivastava, 2019). Similarly, an appropriate optimization of the medium and feeding strategy is required to balance cell growth, productivity, and product quality (Kim and Lee, 2009; Ling et al., 2015; Tripathi and Shrivastava, 2019).
High-throughput scaled-down equipment and statistical design of experiments (DoE) are the most common methodologies for systematically optimizing media and feeding strategy (Li et al., 2010; Mora et al., 2019; Zhou et al., 1997). Typically, cell cultures are fed with frequent boluses of glucose and glutamine to maintain a low concentration and minimize the production of by-products such as lactate and ammonia (Li et al., 2010). Hence, the optimization of the feeding strategy requires determining the best way of providing feed boluses over time. However, DoE only deals with “static” factors. To deal with the batch process dynamics, DoE can be exploited by assigning a different DoE factor to the feeding action at each day (Mora et al., 2019); however, this results in a design with too many factors that requires several dozen experiments. An appropriate solution to this issue is the adoption of design of dynamic experiments (DoDE), which guarantees the optimization of time-varying factors while minimizing the number of experimental runs (Georgakis, 2013). In fact, DoDE utilizes dynamic subfactors to code the profiles of the time-varying factors and then build a response surface model (RSM) to correlate the factors’ dynamic profile to the CQA. Research on DoDE applied to the bioprocessing field is still ongoing, with few examples of application. Specifically, DoDE has been used to optimize process conditions in 200 L bioreactors for producing monoclonal antibodies (Luo et al., 2023) and on simulated fermentation processes (Klebanov and Georgakis, 2016) and mammalian cell cultures (Wang and Georgakis, 2017).
However, despite being designed to maximize the content of information obtained by experiments while minimizing the number experimental runs, the number of experiments designed by DoDE rapidly increases with the number of dynamic variables and the complexity of their dynamic profiles, leading to high numbers of required experimental runs. Since each experimental run lasts several weeks and costs tens of thousands of dollars, the duration and cost of large experimental campaigns limits the applicability of DoDE in the biopharmaceutical industry. Accordingly, strategies to limit the allocation of resources for experimental campaigns are of paramount importance.
First-principles models are extremely effective tools for digitally representing biological systems since they incorporate fundamental physical and biological phenomena. However, first-principles model identification requires a long trial-and-error procedure, which can be supported by model-based optimal experiment design (Abt et al., 2018; Huang et al., 2020). Furthermore, both the model complexity and the requirement of training data strongly increase when representing complex dynamics, as in the case of mAbs cultures. This leads to model over-parametrization, difficult estimation of model parameters, and thus to the inability to correctly simulate the system under study (Mahanty, 2023).
Hybrid semi-parametric digital models, instead, represent an innovative solution to reducing experimental requirements and development timelines while improving robustness and extrapolation. Such models combine first principles models, embedding the mechanistic knowledge of the system under investigation with data-driven methods which learn complex and possibly unknown relationships among the system variables from experimental data (Sansana et al., 2021; von Stosch et al., 2014; Yang et al., 2020). The data-driven aspect often limits the applicability of the model-based optimal DoE in hybrid modeling. In fact, these methodologies are extremely sensitive to uncertainty in model parameters (Galvanin et al., 2013), which is typical of certain data-driven methods (e.g., artificial neural networks—ANN).
Hybrid semi-parametric models have been widely applied to the bioprocess development of tasks such as prediction, process understanding, and process and quality monitoring. For example, an improved understanding of the relationship between biomass and productivity with the process parameters in microbial cell culture was achieved through hybrid semi-parametric models (von Stosch et al., 2016), while good prediction accuracy was attained by hybrid models trained on intensified DoE data (von Stosch and Willis, 2017), allowing the acceleration of upstream process characterization (Bayer et al., 2020). In mammalian cell cultures, the prediction performance of hybrid models was tested in interpolation and extrapolation scenarios (Narayanan et al., 2021), while, compared to purely multivariate techniques, the prediction of the main culture variables through hybrid models resulted in greater accuracy (Narayanan et al., 2019). In the same context, hybrid semi-parametric models coupled with the extended Kalman filter were used to monitor glucose concentration in bioreactors, suggesting the appropriate timing of feeding action to avoid cell starvation (Narayanan et al., 2020).
Hybrid semi-parametric models were also used for bioprocess optimization. For example, the optimal processing conditions (Ferreira et al., 2014) and glucose feeding strategy (Teixeira et al., 2006) for microbial cell cultures were identified through an iterative batch-to-batch strategy based on hybrid models: the optimal condition identified by the hybrid model at each step was used to retrain the model for further optimizations. A similar strategy identified static process parameters to improve product yield in E. Coli cultures by means of nine experimental runs, with only five from the initial exploratory campaign and four suggested in the batch-to-batch optimization (Bayer et al., 2021). Furthermore, the feeding schedule of mammalian cell culture was optimized by means of hybrid semi-parametric models (Teixeira et al., 2005; 2007), showing the applicability of these methodologies in optimizing mammalian cell culture. In many cases, dynamic feeding optimization is performed by a direct parametrization of the control vector (Banga et al., 2005), where the feeding strategy over the entire culture duration is discretized in several segments using a predefined basis function (e.g., piecewise constant parametrization). For example, such direct dynamic optimization was conducted to optimize the feeding strategy in mAbs production using a fully mechanistic model setup (Kaysfeld et al., 2023). However, in this approach, the number of optimization variables rapidly increases together with the complexity of the optimization problem because one control variable is required for each nutrient and control interval. Instead, conducting optimization in the DoDE framework, where dynamic profiles are represented using specific polynomials controlled by a reduced set of subfactors, can reduce the overall number of optimization variables and the complexity of the problem (Rodrigues and Bonvin, 2020).
Furthermore, although hybrid models have been applied for bioprocess optimization and their added value for the optimization of mammalian feeding schedule has been proven, the advantages of using hybrid semi-parametric models in feeding schedule optimization during bioprocess development is underexplored, and research is still needed to allow a consistent applicability of hybrid models in bioprocess optimization.
This study compares an in silico experimental campaign for the optimization of the feeding schedule in mammalian cell cultures through hybrid digital models with an experimental campaign on the process to evaluate whether the in silico experiments can accelerate experimentation and reduce the experimental burden in the process development. In particular, we use a hybrid semi-parametric model calibrated on the experiments designed through DoDEs in such a way as to identify the time profiles of fed glucose and glutamine, which maximize the antibody titer. The proposed methodology is tested on a well-established simulated process for the production of mAbs at a shake flask scale (Kontoravdi et al., 2010).
2 Materials and methods
2.1 Proposed methodology
In this work, an in silico experimental campaign (strategy #1) for optimizing the feeding schedule of mammalian cell cultures is proposed (Figure 1A). The adopted procedure comprises five steps.
1. DoDE planning: initially, experiments are planned according to a DoDE (Section 2.1.1) on two dynamic factors: the time profiles of glucose and glutamine concentrations; and as response, the antibody titer at harvest.
2. Experiment execution: planned experiments are executed on the process under study, which in this study is a simulated process for producing monoclonal antibodies at 1-L shake flask scale (Kontoravdi et al., 2010; Section 2.2). This study used a simulated process because it allows: i) knowing the exact relationship between nutrients and antibody titer which can be exploited to identify the optimal feeding schedule to use as reference for the performance of the proposed optimization strategy; ii) following in real-time the entire time evolution of the culture variables, whose measurements are available only at a much lower frequency (every few hours) in real processes.
3. Training the hybrid model: a hybrid semi-parametric model (Section 2.1.2) is trained on the data collected from the experiments executed at step 2.
4. Optimization: a genetic algorithm (Section 2.1.3) is used to identify the feeding schedule that maximizes the antibody titer at harvest. This algorithm exploits the hybrid model to simulate in silico experiments and predict the resulting antibody titer, given the profiles of both glucose and glutamine.
5. Execution of the confirmatory experiment at the optimal conditions: once the optimal nutrient profiles (i.e., feeding schedule) are identified, they are executed in the process to assess the antibody titer that the process can achieve and the reliability of the predicted values.
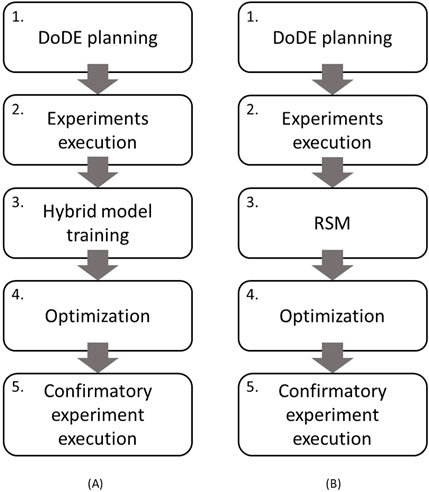
Figure 1. Proposed methodology: (A) optimization strategy #1 (in silico) and (B) optimization strategy #2 (experimental).
Optimization strategy #1 is compared with a standard experimental campaign for optimizing the feeding schedule carried out directly on the process (strategy #2, Figure 1B). Although steps 1, 2, and 5 are the same as those of strategy #1, steps 3 and 4 are as follows.
3. Response surface modeling: RSM is built with the data collected from the experiments executed at step 2 according to the DoDE theory. The model is used to predict the antibody titer at harvest from the DoDE dynamic subfactors after being updated by excluding those effects with low influence on the response (Section 2.1.1.2);
4. Optimization: in this case, the genetic algorithm exploits the RSM to predict the antibody titer given the profiles of glucose and glutamine.
The confirmatory experiments performed at step 5 of both optimization strategies are then compared with the process optimum, which is known in this study because the process is simulated. In the next sections, details on the DoDE, the process, the hybrid model, and the techniques used for experimentation and optimization are presented.
2.1.1 Design of dynamic experiments
Design of dynamic experiments (DeDE) (Georgakis, 2013) is used in this study to plan the experimental campaign for optimizing the glucose and glutamine profiles in the cell culture.
2.1.1.1 Design of dynamic experiment fundamentals and applications
In DoDE, the time-varying factors (i.e., manipulated variables) are expressed as normalized dynamic variables
where
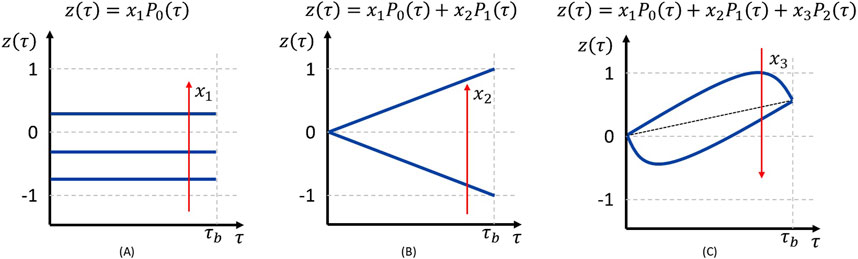
Figure 2. Effect of dynamic subfactors on the normalized dynamic variable
To ensure that
and the value of each subfactor must also be bounded:
The glucose and glutamine concentration profiles
where
being
Since the nutrients are both manipulated and observed, their concentrations vary because of both cell consumption and feeding. Here, we simulate off-line measurements because advanced monitoring strategies, such as on-line monitoring and control systems, are not yet standard in industrial mammalian cell cultures, especially in the small scales for the early stages of product development. Furthermore, the measurements and feeding actions are performed in boluses once every 24 h. Consequently, the nutrient profile cannot precisely follow that proposed by the DoDE. To deal with this issue, we introduce a specific procedure to replicate as precisely as possible the profiles indicated by the DoDE during the experiments, which is schematically represented in Figure 3. The proposed procedure consists of:
• defining a 10% band around the DoDE profile which is used to control the feeding actions (Figure 3A, black dashed lines);
• performing the feeding action only if the nutrient concentration in the culture at the sampling time is
• performing the feeding of a predefined amount (i.e., constant) of fresh medium with a nutrient concentration calculated to achieve 110% of the concentration defined by the designed experiment (Figure 3A, upper black dashed line).
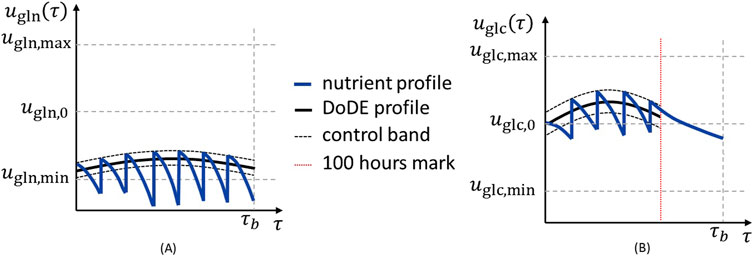
Figure 3. Schematic representation of (A) glutamine and (B) glucose profiles (blue lines), with the profile determined by DoDE (black line), the 110/90% control band (black dashed lines), and the 100-h limit for glucose feeding (red dotted line).
The feeding actions are visible in the nutrient profiles (Figure 3A) as the vertical jumps in the blue line where the nutrient concentration is brought to 110% of that defined by the designed experiment. Furthermore, since the glucose consumption is slow and hardly decreases in the final part of the batch, the glucose cannot follow sharply decreasing profiles; hence it is controlled (and, accordingly, feeding performed) only in the first 100 h of the batch (Figure 3B, red dotted line). After this point, the glucose is fed only to compensate for any dilution effect due to glutamine addition. This is shown in Figure 3B, where after 100 h (red dotted line) the feeding is not performed and nutrient concentration decreases because of cell consumption. Accordingly, the glucose profile after 100 h has no controllable effect on the antibody titer and is not considered in the analysis.
2.1.1.2 Design of dynamic experiments response surface modeling
In this study, the DoDE nutrient profiles are designed by means of a D-optimal DoE (de Aguiar et al., 1995) applied to the
where
The RSM is affected by uncertainty. The uncertainty of the estimated parameter
where
The uncertainty on the parameter propagates in the uncertainty of the predictions, which, for a validatory experiment with subfactors
where
To assess the extent of process improvement that can be achieved when planning a different number of experiments, DoDE is adopted to design the alternative experimental campaigns A and B. Experimental campaign A is a complete campaign for process optimization and is used to assess the process improvement that can be achieved with an extended experimental campaign. A second-order with pairwise interaction RSM (as Equation 6) is fitted with data from 31 experiments planned by assigning the values of the dynamic subfactors through a D-optimal DoE (Supplementary Table S1). Among the 31 experiments, 28 are required to fit the RSM for the six dynamic subfactors, while the three remaining experiments are used to estimate the model’s lack-of-fit (Georgakis, 2013). Experimental campaign B is used to assess the process improvement that can be achieved through a small number of experiments. Data from nine experiments planned by assigning the values of the dynamic subfactors through a D-optimal DoE (Supplementary Table S2) are used to fit a first-order RSM:
Among the nine experimental runs, seven are used to fit the RSM for the six dynamic subfactors while the two remaining experiments are used to estimate the model’s lack-of-fit (Georgakis, 2013).
2.1.2 Hybrid model
A serial hybrid semi-parametric model is used (Oliveira, 2004; Teixeira et al., 2005; von Stosch et al., 2014) to capture the behavior of mammalian cell cultures producing mAbs (Figure 4). This digital model combines a mechanistic model, which embeds the knowledge of the system, and an ANN, which accounts for the unknown dependencies in the system under study.
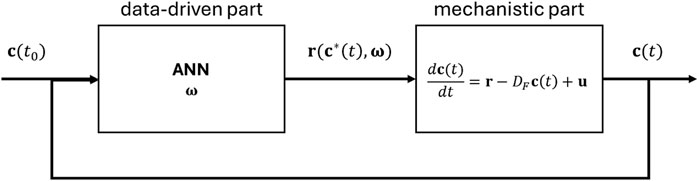
Figure 4. Schematic representation of the serial hybrid model structure, which comprises the culture material balances and the data-driven part (i.e., an artificial neural network—ANN), capturing the complex and unknown relationship between the concentrations and reaction rates.
The mechanistic knowledge of the cell culture is described by the concentration balances of the main culture variables (Equation 10), organized in the column vector
where
where
The relationship between specific production/consumption rates and culture variables,
where
The hybrid model is trained with the nine experiments of experimental campaign B (Section 2.1.1.2) with a stepwise decreasing learning rate (from 0.005 to 0.0001). The model parameters
The hybrid model is used to perform an in silico experimental campaign. It receives as input both the initial viable cell concentration and the culture volume, which are required to simulate the entire experimental run. Feeding is simulated by adjusting the appropriate value of the controlled input vector
2.1.3 Feeding optimization
The optimal profile for glucose and glutamine is determined as that which maximizes the antibody titer at harvest through an optimization problem. Since the shape of the nutrient profiles is defined by the value of the dynamic subfactors according to Equation 1, the optimization problem is formulated considering the DoDE dynamic subfactors
subject to the constraints of Equations 2–4. These constraints on the subfactor values
The antibody titer at harvest
All the simulations described in this work are performed in Matlab® 2020b through the optimization toolbox and in-house developed routines.
2.2 Case study: simulated process for the production of monoclonal antibodies at 1-L shake flask scale
A simulated process for producing monoclonal antibodies at 1-L shake flask scale (Kontoravdi et al., 2010) is considered in this study; we will refer to it as “the process” for the reminder of the manuscript. It models the dynamic behavior of the viable cell density (VCD,
The total duration of a batch is set to
3 Results
The results of optimization strategy #2 for experimental campaigns A and B followed by optimization strategy #1 are presented here. These results are then compared with the process optimum.
3.1 Nutrient profile optimization through full experimental campaign on the process
This section aims to identify the optimal nutrient profile that maximizes the antibody titer at harvest by performing an extended experimental campaign on the process through DoDE.
To this purpose, experimental campaign A with 31 experiments planned through DoDE is performed on the process. The values of the dynamic subfactors
The RSM shows a very high coefficient of determination
Recalling that the subfactors define the shape of the nutrient profile and, specifically, that
According to these results, the antibody titer will not change much in response to different glucose profiles when set within the factor ranges. Instead, the glutamine profile is extremely important for achieving high antibody titer and must be carefully optimized.
The RSM is then used for process optimization through a genetic algorithm (Section 2.1.1.2) to determine the nutrient profile that provides the highest possible antibody titer at harvest. The optimal nutrient profiles (black line) and the confirmatory experiment at the optimal conditions executed on the process (red points—process measurements) are shown in Figure 5. There, the continuous measurement (blue line) of the nutrient profile is also reported. Considering that, at shake flask scale, this profile is typically not available, in this case it is because the process is simulated. In general: i) the optimal glucose profile (Figure 5A) starts at around half (33.6 mM) of the range of possible values and follows a decreasing profile with a very small downward concavity; ii) the optimal glutamine profile (Figure 5B) starts at the minimum value (2 mM) of its possible range and follows an almost constant profile for the entire culture. The optimal values of the glucose and glutamine subfactors are
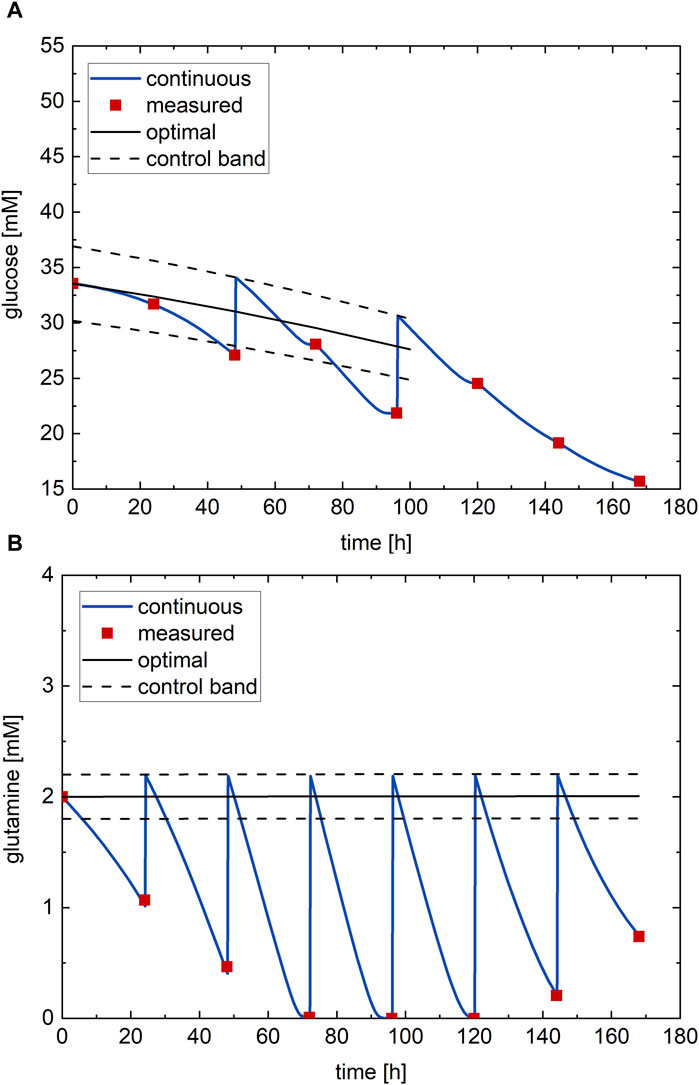
Figure 5. Optimal nutrient profile, determined from DoDE experimental campaign A with 31 experiments, performed on the process: (A) glucose and (B) glutamine. Red dots—process measurements; black line—optimal nutrient profile; black dashed line—control band; blue line–continuous measurement.
The optimal antibody titer at harvest predicted by the RSM with the optimal nutrient profiles is
3.2 Nutrient profile optimization through reduced experimental campaign on the process
This section aims to identify the optimal nutrient profile that maximizes the antibody titer at harvest using a limited set of experiments planned through the DoDE. This is intended to describe how the optimal nutrient profiles identified through DoDE change when the number of performed experimental runs is low.
Therefore, experimental campaign B with nine experiments planned through the DoDE is used. The values of the dynamic subfactors
The RSM fitted onto the process data shows a coefficient of determination of
The RSM is then used for process optimization to determine the nutrient profile that achieves the highest possible antibody titer at harvest by means of a genetic algorithm.
The resulting optimal nutrient profiles (black lines) and the confirmatory experiment executed on the process (red points–process measurements) are shown in Figure 6 with the continuous measurement (blue lines). The optimal glucose profile (Figure 6A) starts at around half its possible range and follows a linearly increasing profile with almost no concavity. The optimal glutamine profile (Figure 6B) instead shows a constant profile along the culture at the minimum value of its possible range. The optimal values of the glucose and glutamine subfactors are
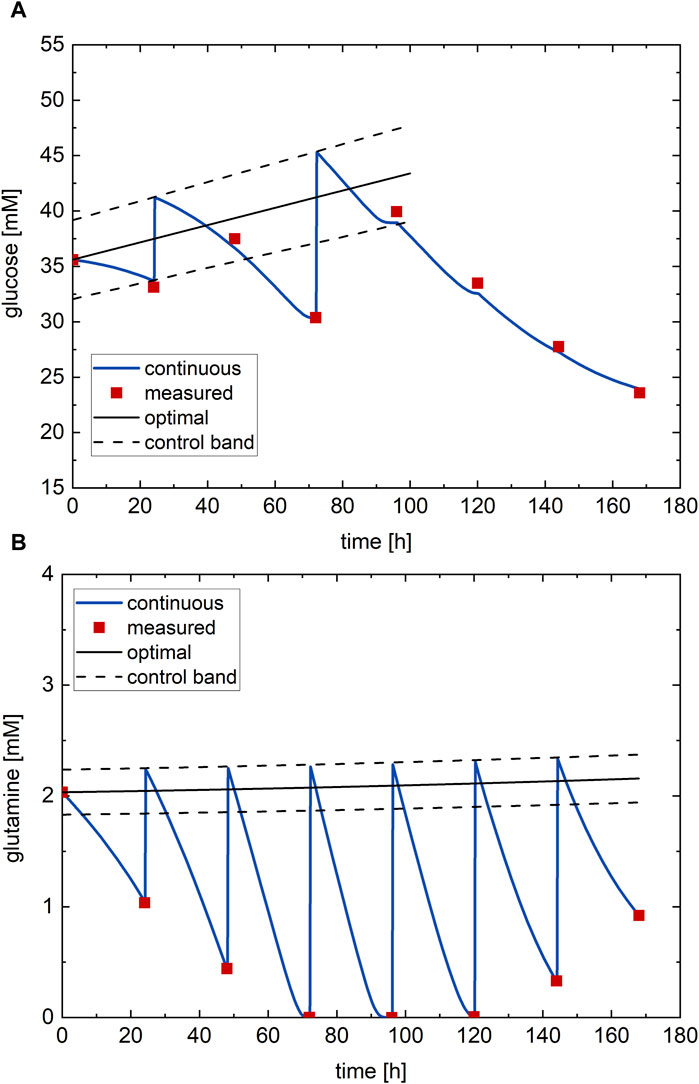
Figure 6. Optimal nutrient profile, determined from DoDE experimental campaign B with nine experiments, tested on the process: (A) glucose and (B) glutamine. Red dots—process measurements; black line—optimal nutrient profile; black dashed line—control band; blue line–continuous measurement.
The RSM predicts with the optimal nutrient profiles an antibody titer at harvest of
3.3 Nutrient profile optimization through an in silico experimental campaign on the hybrid model
This section shows the optimization of the nutrient profiles by performing an in silico experimental campaign through a hybrid model. This will serve as proof of concept to understand the applicability and advantage of conducting virtual experimental campaigns for optimizing cell culture quality attributes through hybrid models.
Consequently, a hybrid model (Section 2.1.2) is trained on the data collected during experimental campaign B planned through the DoDE (Section 3.2), comprising nine experiments. The hybrid model is exploited to perform an in silico experimental campaign, where a genetic algorithm guides the experiments by suggesting the values of the dynamic subfactors defining the nutrient profiles.
The optimal nutrient profiles (black lines), those simulated though the hybrid model (green dashed lines), and the profiles at the optimal conditions executed on the process (blue lines) are shown in Figure 7. The initial value of the optimal glucose profile (Figure 7A) is close to the upper bound of the glucose range (47.7 mM) and follows a monotonically decreasing profile with slight downward concavity, while the initial value of the optimal glutamine profile (Figure 7B) starts at the lower bound of its span range and follows an increasing profile with a small slope and almost no concavity. The optimal values of the glucose and glutamine subfactors are
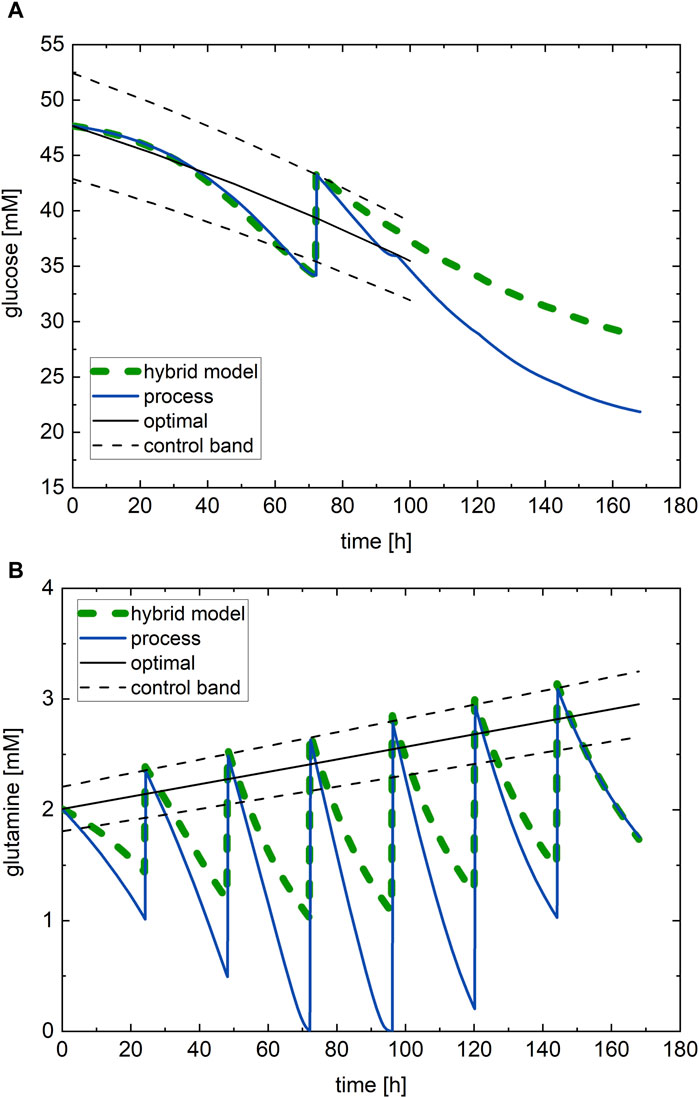
Figure 7. Optimal nutrient profile, determined from the in silico experimental campaign through the hybrid model trained on the nine experiments of experimental campaign B: (A) glucose and (B) glutamine. Green dashed line—hybrid model simulation; black line—optimal nutrient profile; black dashed line—control band; blue line—process continuous measurement.
The hybrid model predicts with the optimal nutrient profiles an antibody titer at harvest of
3.4 Optimal nutrient profile
This section presents the real optimum of the process to understand how well the investigated methodologies can identify the optimal feeding schedule for the cell cultures. The optimum of the process is known because a simulated process is considered; this information would not be available in a real scenario. The genetic algorithm presented in Section 2.1.3 is applied to the process to determine the optimal feeding conditions.
The optimal values of the glucose and glutamine subfactors are
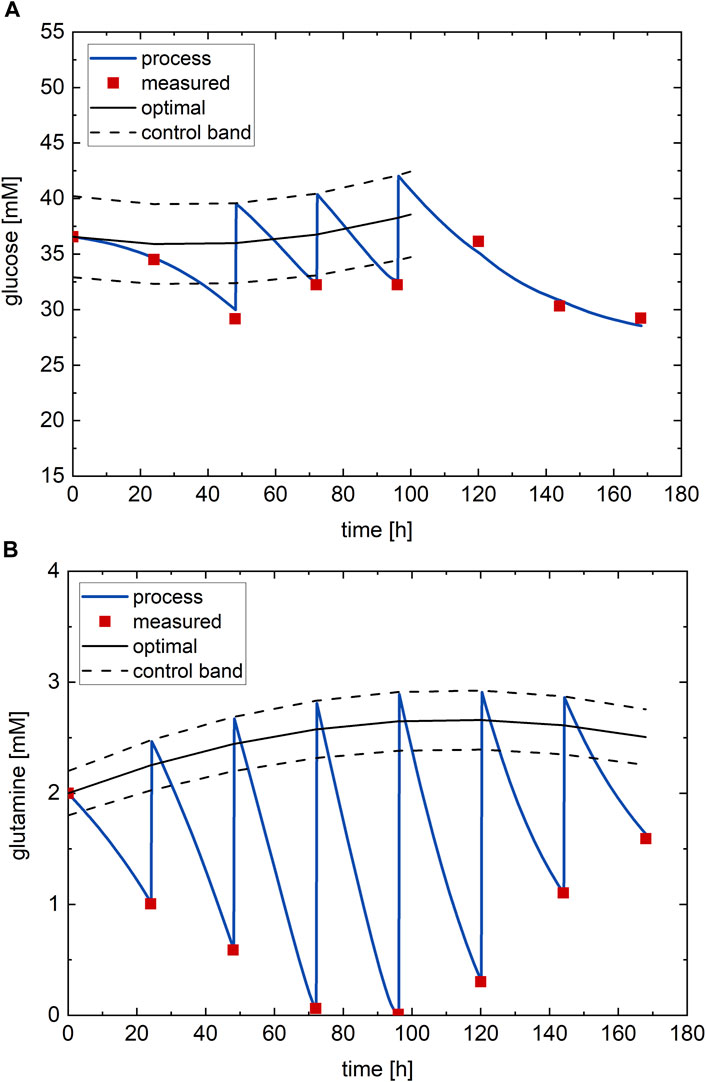
Figure 8. Optimal nutrient profile of the process: (A) glucose and (B) glutamine. Blue line—continuous process measurement; red dots—process measurements; black line—optimal profile; black dashed line—control band.
The optimal nutrient profiles allow the process to achieve an antibody titer
4 Discussion
This section compares the optimal feeding schedule of the process with those obtained through optimization strategies #1 and #2. At its end, the antibody titer in the confirmatory experiment at the optimal conditions is used to identify the best optimization strategy.
4.1 Optimal feeding schedule
The optimal feeding schedule of the process (Section 3.4) is characterized by an initial glucose concentration at approximately the average value in the range of possible concentrations, which allows sustained cell growth in the initial part of the culture, and an increasing profile, which maintains high cell growth even at high viable cell concentration. The low initial glutamine concentration provides enough nutrient for sustained growth and at the same time determines reduced ammonia formation, which is detrimental because it limits cell growth and favors cell death. Furthermore, the downward concavity of the glutamine profile is coherent with the necessity of providing more glutamine when the viable cell concentration is higher (i.e., in the central part of the culture) while also limiting ammonia formation. These results are coherent with previous studies (Teixeira et al., 2005), which recommended limiting the availability of glutamine in the initial growth phase and increasing it later in the culture. Unlike here, previous studies have recommended a low concentration of glucose along the entire culture, possibly decreasing it later in the culture (Teixeira et al., 2007). Even if low glucose concentration is reasonable for limiting lactate production, feeding enough glucose (as in our case) is of paramount importance for avoiding cell starvation, which negatively affects cell growth, productivity, and product quality (Narayanan et al., 2020; Sen et al., 2015).
4.2 Comparison among optimal feeding schedules
In optimization strategy #2 (experimental campaign planned through DoDE), the optimal low level of glutamine throughout the entire duration of the culture is identified in both experimental campaigns A and B. However, the increased amount required in the central part of the culture to compensate for the increased viable cell concentration is not identified in both approaches (that is, experimental campaign A, with 31 experiments, and B, with nine experiments). Regarding glucose, a profile similar to the process optimum is identified only in experimental campaign B (with nine experiments). However, in experimental campaign A, the identified glucose profile with high initial concentration and a decreasing profile leads to a more sustained production of lactate, especially in the initial part of the culture.
In optimization strategy #1 (in silico experimental campaign), correct behavior of the glutamine concentration, which starts at a low level and increases along the culture, is identified. The optimal glucose profile instead has a high initial concentration and decreases along the culture, showing some similarity with experimental campaign A of optimization strategy #2.
These differences in the optimal glucose profiles are due to the small influence that glucose has on the antibody titer in the process. In fact, if glucose is not limited, the growth rate (which also determines the productivity) is only controlled by the glutamine level and by the ammonia produced, leading to a reduced effect of glucose on antibody productivity. For this reason, both modeling strategies effectively capture the glucose behavior. In particular, the second-order RSM is not affected by glucose and does not capture the relationship between glucose, lactate, and a lower cell growth, while the hybrid model underestimates the impact that lactate has on cell growth. This leads both modeling strategies to suggest high levels of glucose at the beginning of the culture.
The predicted antibody titer by the two optimization strategies is compared to that achieved in the process (Section 3.4), with results summarized in Table 1.

Table 1. Optimal nutrient profiles obtained with different strategies: subfactor value, simulated experimental antibody titer, predicted antibody titer, and 95% confidence interval of the predicted antibody titer.
DoDE is thus demonstrated to be applicable in mammalian cell cultures to optimize the feeding schedule, providing a simple and robust science-based strategy to improve antibody yield. In fact, in optimization strategy #2, experimental campaigns A (3,118.2 mg/L) and B (3,136.3 mg/L) both achieved an improved yield of antibodies in the confirmatory experiments at the optimal conditions. In particular, experimental campaign B achieved with only nine experiments a higher yield than experimental campaign A with 31 experiments. However, optimization strategy #2 achieved antibody titer consistently lower than the real process optimum
Hybrid semi-parametric models are promising tools which allow performing of in silico experimental campaigns since they provide a very good representation of the system even when built on a reduced number of runs. In fact, the confirmatory experiment with the optimal feeding schedule identified by optimization strategy #1 achieved a very high antibody titer (3,222.8 mg/L), with results very close to the real process optimum
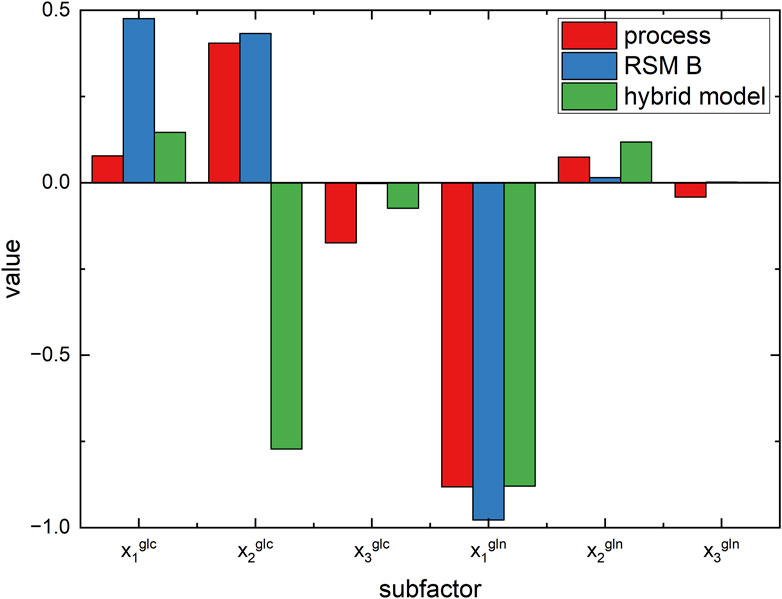
Figure 9. Comparison of values of the optimal subfactors for process, RSM of experimental campaign B, and hybrid model.
It is extremely important to point out that in optimization strategy #1, an antibody titer so close to the real optimal value is identified by only nine experiments (i.e., used to train the hybrid model) on the process. Accordingly, the hybrid model correctly learns and generalizes the relationship between nutrients and antibody titer and captures the cross-correlation between them, even if it is trained from a limited number of experiments. This is somehow expected because hybrid models combine the knowledge of the biological phenomena involved in cell cultures with the capability of learning the complex relationships of data-driven models.
It is also notable that the selected hybrid model structure is the best in terms of the number of samples required for training and extrapolation with a different feeding schedule (Narayanan et al., 2021). In fact, the improvement of the model structure by introducing additional mechanistic knowledge improves the description of the system but requires a larger number of training samples to achieve comparable prediction performance. Accordingly, a trade-off is required between model effectiveness and complexity (which requires a higher number of training samples).
5 Conclusion
This study has compared different strategies of experimentation to optimize the feeding schedule of a mammalian cell culture. In particular, in silico experimentation was compared with an experimental campaign on the process to assess if in silico experimentation can accelerate process development and reduce experimental burden. To conduct in silico experiments, we used a combination of design of dynamics experiments (DoDE) and a hybrid semi-parametric model to virtually identify the optimal shape of glucose and glutamine profile. The optimal nutrient profiles were compared with those obtained through two experimental campaigns planned with DoDE: an extended campaign with 31 experiments (experimental campaign A) and a more parsimonious campaign with nine experiments (experimental campaign B).
Experimental campaign B reached an improved antibody titer of 3,136.3 mg/L, while experimental campaign A provided a smaller antibody titer than experimental campaign B had achieved with nine experiments. Despite being able to improve the antibody titer, the experimental campaigns planned with DoDE could not achieve titer values similar to the real process optimum.
The in silico campaign, which required only nine experimental runs to train the hybrid digital model, provided a 34.9% overall improvement in the antibody titer with respect to training data and a 2.8% improvement with respect to experimental campaigns A and B, reaching a titer very close to the process optimum. The hybrid model accurately captures the relationship between nutrient profiles and antibody titer but underpredicts the numerical value of the antibody titer. Accordingly, hybrid semi-parametric models are promising tools and can be used to conduct in silico experimental campaigns, providing very high performance and reducing the experimental burden and time required to perform feeding schedule optimization in the real world.
A simulated process to produce monoclonal antibodies at 1-L shake flask scale was considered as a case study. In future research, the proposed framework will be checked on a real process to confirm our findings. Furthermore, a thorough comparison of the proposed framework with dynamic optimization methods will be conducted in future studies.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
GB: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Supervision, Visualization, Writing–original draft, Writing–review and editing. CG: Data curation, Formal Analysis, Software, Writing–review and editing. PF: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Writing–original draft, Writing–review and editing.
Funding
The authors declare that financial support was received for the research, authorship, and/or publication of this article. Open Access funding was provided by University of Padova, Open Science Committee.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2024.1456402/full#supplementary-material
References
Abt, V., Barz, T., Cruz-Bournazou, M. N., Herwig, C., Kroll, P., Möller, J., et al. (2018). Model-based tools for optimal experiments in bioprocess engineering. Curr. Opin. Chem. Eng. 22, 244–252. doi:10.1016/j.coche.2018.11.007
Banga, J. R., Balsa-Canto, E., Moles, C. G., and Alonso, A. A. (2005). Dynamic optimization of bioprocesses: efficient and robust numerical strategies. J. Biotechnol. 117, 407–419. doi:10.1016/j.jbiotec.2005.02.013
Barberi, G., Benedetti, A., Diaz-Fernandez, P., Sévin, D. C., Vappiani, J., Finka, G., et al. (2022). Integrating metabolome dynamics and process data to guide cell line selection in biopharmaceutical process development. Metab. Eng. 72, 353–364. doi:10.1016/j.ymben.2022.03.015
Bayer, B., Diaz, R. D., Melcher, M., Striedner, G., and Duerkop, M. (2021). Digital twin application for model-based doe to rapidly identify ideal process conditions for space-time yield optimization. Processes 9, 1109. doi:10.3390/pr9071109
Bayer, B., Striedner, G., and Duerkop, M. (2020). Hybrid modeling and intensified DoE: an approach to accelerate upstream process characterization. Biotechnol. J. 15, 2000121. doi:10.1002/biot.202000121
Castelli, M. S., McGonigle, P., and Hornby, P. J. (2019). The pharmacology and therapeutic applications of monoclonal antibodies. Pharmacol. Res and Perspec 7, e00535. doi:10.1002/prp2.535
de Aguiar, P. F., Bourguignon, B., Khots, M. S., Massart, D. L., and Phan-Than-Luu, R. (1995). D-optimal designs. Chemom. Intelligent Laboratory Syst. 30, 199–210. doi:10.1016/0169-7439(94)00076-X
Facco, P., Zomer, S., Rowland-jones, R. C., Marsh, D., Diaz-fernandez, P., Finka, G., et al. (2020). Using data analytics to accelerate biopharmaceutical process scale-up. Biochem. Eng. J. 164, 107791. doi:10.1016/j.bej.2020.107791
Farid, S. S., Baron, M., Stamatis, C., Nie, W., and Coffman, J. (2020). Benchmarking biopharmaceutical process development and manufacturing cost contributions to R&D. mAbs 12, 1754999. doi:10.1080/19420862.2020.1754999
Ferreira, A. R., Dias, J. M. L., Von Stosch, M., Clemente, J., Cunha, A. E., and Oliveira, R. (2014). Fast development of Pichia pastoris GS115 Mut+ cultures employing batch-to-batch control and hybrid semi-parametric modeling. Bioprocess Biosyst. Eng. 37, 629–639. doi:10.1007/s00449-013-1029-9
Galvanin, F., Ballan, C. C., Barolo, M., and Bezzo, F. (2013). A general model-based design of experiments approach to achieve practical identifiability of pharmacokinetic and pharmacodynamic models. J. Pharmacokinet. Pharmacodyn. 40, 451–467. doi:10.1007/s10928-013-9321-5
Georgakis, C. (2013). Design of dynamic experiments: a data-driven methodology for the optimization of time-varying processes. Industrial Eng. Chem. Res. 52, 12369–12382. doi:10.1021/ie3035114
Gronemeyer, P., Ditz, R., and Strube, J. (2014). Trends in upstream and downstream process development for antibody manufacturing. Bioeng. (Basel). 1, 188–212. doi:10.3390/bioengineering1040188
Huang, Y., Gilmour, S. G., Mylona, K., and Goos, P. (2020). Optimal design of experiments for hybrid nonlinear models, with applications to extended michaelis–menten kinetics. JABES 25, 601–616. doi:10.1007/s13253-020-00405-3
Kaysfeld, M. W., Kumar, D., Nielsen, M. K., and Jørgensen, J. B. (2023). Dynamic optimization for monoclonal antibody production. IFAC-PapersOnLine 56, 6229–6234. doi:10.1016/j.ifacol.2023.10.747
Kim, S. H., and Lee, G. M. (2009). Development of serum-free medium supplemented with hydrolysates for the production of therapeutic antibodies in CHO cell cultures using design of experiments. Appl. Microbiol. Biotechnol. 83, 639–648. doi:10.1007/s00253-009-1903-1
Kingma, D. P., and Ba, J. L. (2015). ADAM: a method for stochastic optimization. arXiv. doi:10.48550/arXiv.1412.6980
Klebanov, N., and Georgakis, C. (2016). Dynamic response surface models: a data-driven approach for the analysis of time-varying process outputs. Industrial Eng. Chem. Res. 55, 4022–4034. doi:10.1021/acs.iecr.5b03572
Kontoravdi, C., Pistikopoulos, E. N., and Mantalaris, A. (2010). Systematic development of predictive mathematical models for animal cell cultures. Comput. Chem. Eng. 34, 1192–1198. doi:10.1016/j.compchemeng.2010.03.012
Li, F., Vijayasankaran, N., Shen, A., Kiss, R., and Amanullah, A. (2010). Cell culture processes for monoclonal antibody production. mAbs 2, 466–479. doi:10.4161/mabs.2.5.12720
Ling, W. L. W., Bai, Y., Cheng, C., Padawer, I., and Wu, C. (2015). Development and manufacturability assessment of chemically-defined medium for the production of protein therapeutics in CHO cells. Biotechnol. Prog. 31, 1163–1171. doi:10.1002/btpr.2108
Luo, Y., Stanton, D. A., Sharp, R. C., Parrillo, A. J., Morgan, K. T., Ritz, D. B., et al. (2023). Efficient optimization of time-varying inputs in a fed-batch cell culture process using design of dynamic experiments. Biotechnol. Prog. 39, e3380. doi:10.1002/btpr.3380
Mahanty, B. (2023). Hybrid modeling in bioprocess dynamics: structural variabilities, implementation strategies, and practical challenges. Biotech and Bioeng. 120, 2072–2091. doi:10.1002/bit.28503
Montgomery, D. C. (2007). Design and analysis of experiments. Fifth Ed. New York (USA): John Wiley and Sons, Inc.
Mora, A., Nabiswa, B., Duan, Y., Zhang, S., Carson, G., and Yoon, S. (2019). Early integration of Design of Experiment (DOE) and multivariate statistics identifies feeding regimens suitable for CHO cell line development and screening. Cytotechnology 71, 1137–1153. doi:10.1007/s10616-019-00350-1
Narayanan, H., Behle, L., Luna, M. F., Sokolov, M., Guillén-Gosálbez, G., Morbidelli, M., et al. (2020). Hybrid-EKF: hybrid model coupled with extended Kalman filter for real-time monitoring and control of mammalian cell culture. Biotechnol. Bioeng. 117, 2703–2714. doi:10.1002/bit.27437
Narayanan, H., Luna, M., Sokolov, M., Arosio, P., Butté, A., and Morbidelli, M. (2021). Hybrid models based on machine learning and an increasing degree of process knowledge: application to capture chromatographic step. Industrial and Eng. Chem. Res. 60, 10466–10478. doi:10.1021/acs.iecr.1c01317
Narayanan, H., Sokolov, M., Morbidelli, M., and Butté, A. (2019). A new generation of predictive models: the added value of hybrid models for manufacturing processes of therapeutic proteins. Biotechnol. Bioeng. 116, 2540–2549. doi:10.1002/bit.27097
O’Flaherty, R., Bergin, A., Flampouri, E., Mota, L. M., Obaidi, I., Quigley, A., et al. (2020). Mammalian cell culture for production of recombinant proteins: a review of the critical steps in their biomanufacturing. Biotechnol. Adv. 43, 107552. doi:10.1016/j.biotechadv.2020.107552
Oliveira, R. (2004). Combining first principles modelling and artificial neural networks: a general framework. Comput. Chem. Eng. 28, 755–766. doi:10.1016/j.compchemeng.2004.02.014
Rodrigues, D., and Bonvin, D. (2020). On reducing the number of decision variables for dynamic optimization. Optim. Control Appl. Methods 41, 292–311. doi:10.1002/oca.2543
Sansana, J., Joswiak, M. N., Castillo, I., Wang, Z., Rendall, R., Chiang, L. H., et al. (2021). Recent trends on hybrid modeling for Industry 4.0. Comput. Chem. Eng. 151, 107365. doi:10.1016/j.compchemeng.2021.107365
Schwarz, G. (1978). Estimating the dimension of a model. Ann. Statistics 6, 461–464. doi:10.1214/aos/1176344136
Sen, J. W., Fan, Y., Jimenez, I., Val, D., Mu, C., Rasmussen, S. K., et al. (2015) Amino acid and glucose metabolism in fed-batch CHO cell culture affects antibody production and glycosylation, 112, 521–535. doi:10.1002/bit.25450
Sivanandam, S. N., and Deepa, S. N. (2008). Introduction to genetic algorithms. Springer Berlin Heidelberg.
Teixeira, A., Cunha, A. E., Clemente, J. J., Moreira, J. L., Cruz, H. J., Alves, P. M., et al. (2005). Modelling and optimization of a recombinant BHK-21 cultivation process using hybrid grey-box systems. J. Biotechnol. 118, 290–303. doi:10.1016/j.jbiotec.2005.04.024
Teixeira, A. P., Alves, C., Alves, P. M., Carrondo, M. J. T., and Oliveira, R. (2007). Hybrid elementary flux analysis/nonparametric modeling: application for bioprocess control. BMC Bioinforma. 8, 30–15. doi:10.1186/1471-2105-8-30
Teixeira, A. P., Clemente, J. J., Cunha, A. E., Carrondo, M. J. T., and Oliveira, R. (2006). Bioprocess iterative batch-to-batch optimization based on hybrid parametric/nonparametric models. Biotechnol. Prog. 22, 247–258. doi:10.1021/bp0502328
Tripathi, N. K., and Shrivastava, A. (2019). Recent developments in bioprocessing of recombinant proteins: expression hosts and process development, Front. Bioeng. Biotechnol. 7. 420. doi:10.3389/fbioe.2019.00420
von Stosch, M., Hamelink, J. M., and Oliveira, R. (2016). Hybrid modeling as a QbD/PAT tool in process development: an industrial E. coli case study. Bioprocess Biosyst. Eng. 39, 773–784. doi:10.1007/s00449-016-1557-1
von Stosch, M., Oliveira, R., Peres, J., and Feyo de Azevedo, S. (2014). Hybrid semi-parametric modeling in process systems engineering: past, present and future. Comput. Chem. Eng. 60, 86–101. doi:10.1016/j.compchemeng.2013.08.008
von Stosch, M., and Willis, M. J. (2017). Intensified design of experiments for upstream bioreactors. Eng. Life Sci. 17, 1173–1184. doi:10.1002/elsc.201600037
Walsh, G. (2018). Biopharmaceutical benchmarks 2018. Nat. Biotechnol. 36, 1136–1145. doi:10.1038/nbt.4305
Wang, Z., and Georgakis, C. (2017). An in silico evaluation of data-driven optimization of biopharmaceutical processes. AIChE J. 63, 2796–2805. doi:10.1002/aic.15659
Wang, Z., and Georgakis, C. (2019). A dynamic response surface model for polymer grade transitions in industrial plants. Industrial Eng. Chem. Res. 58, 11187–11198. doi:10.1021/acs.iecr.8b04491
Wurm, F. M. (2004). Production of recombinant protein therapeutics in cultivated mammalian cells. Nat. Biotechnol. 22, 1393–1398. doi:10.1038/nbt1026
Yang, S., Navarathna, P., Ghosh, S., and Bequette, B. W. (2020). Hybrid modeling in the era of smart manufacturing. Comput. Chem. Eng. 140, 106874. doi:10.1016/j.compchemeng.2020.106874
Keywords: cell cultures, hybrid models, DoDE, feeding schedule optimization, artificial neural networks
Citation: Barberi G, Giacopuzzi C and Facco P (2024) Bioprocess feeding optimization through in silico dynamic experiments and hybrid digital models—a proof of concept. Front. Chem. Eng. 6:1456402. doi: 10.3389/fceng.2024.1456402
Received: 28 June 2024; Accepted: 30 September 2024;
Published: 25 October 2024.
Edited by:
René Schenkendorf, Harz University of Applied Sciences, GermanyReviewed by:
Zhonggai Zhao, Jiangnan University, ChinaSatyajeet Sheetal Bhonsale, KU Leuven, Belgium
Copyright © 2024 Barberi, Giacopuzzi and Facco. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pierantonio Facco, cGllcmFudG9uaW8uZmFjY29AdW5pcGQuaXQ=
 Gianmarco Barberi
Gianmarco Barberi Christian Giacopuzzi
Christian Giacopuzzi Pierantonio Facco
Pierantonio Facco