Enhancing the assessment of in situ beam–column strength through probing and machine learning

Beam–columns are designed to withstand the concurrent action of both axial and bending stresses. Therefore, when assessing the structural health of an in situ beam–column, both of these load effects must be considered. Probing, having been shown recently to be an effective methodology for predicting the in situ health of prestressed stayed columns under axial compression, is applied currently for predicting the in situ health of beam–columns. Although probing stiffness was sufficient for predicting the health of prestressed stayed columns, additional data are required to predict both the moment and axial utilisation ratios. It is shown that the initial lateral deflection is a suitable measure considered alongside the probing stiffness measured at various probing locations within a revised machine learning (ML) framework. The inclusion of both terms in the ML framework produced an almost exact prediction of both the aforementioned utilisation ratios for various design combinations, thereby demonstrating that the probing framework proposed herein is an appropriate methodology for evaluating the structural strength reserves of beam–columns.

1 Introduction

Structural members within buildings and civil infrastructure are typically designed considering a pre-defined “serviceable design life,” in accordance with the respective national building codes and standards. Throughout this stipulated design lifetime, the structure will naturally face a variety of scenarios that may affect the intrinsic structural load-carrying capacity, such as the deterioration of the structural members through corrosion (Doebling et al., 1998) or, perhaps, owing to a change in the design requirements that results in additional loading caused by changes in use or increased occupancy (Ross et al., 2016; Askar et al., 2021; Slaughter, 2001). With the construction industry contributing about 30% of greenhouse gas emissions and energy consumption globally (UNEP, 2020), from which a substantial amount of demolition waste is generated (Publications Office of the European Union, 2017), the industry needs to focus on efforts to reduce its impact. The rehabilitation of existing structures is one such effective method to reduce the embodied carbon of a structure, thereby reducing its environmental impact (Alba-Rodríguez et al., 2017). However, rehabilitating a structure for reuse requires an assessment of the in situ health of the constituent structural members and components such that strategies for strengthening and rehabilitation may be developed.

Structural health monitoring (SHM) covers a wide spectrum of techniques, where essentially the response of structures and their individual components to applied actions is recorded to determine their mechanical state and current health (Gharehbaghi et al., 2022; Katam et al., 2023; Amafabia et al., 2017). SHM techniques can be classified into four categories of increasing levels of complexity, namely, “detection,” “localization,” “quantification,” and “prediction of the remaining life” (Rytter, 1993). The SHM techniques can be further distinguished by the nature of the actions applied, where “static-based methods” measure the response of a structure to quasi-static loads (such as stiffness, strains, and stresses) and “dynamic-based methods” measure the structural response to dynamic loading (such as the frequency response to dynamic loading) (Gharehbaghi et al., 2022; Shokravi et al., 2020). In essence, both classes of methods aim to evaluate the current mechanical state, or health, of a structure, given its response to an applied action, be it a static or dynamic perturbation. Static-based methods have been used in civil infrastructure, such as bridges, where parameters such as displacements, strains, and strut and cable stresses can be measured for identifying structural damage (Chen et al., 2016; Martínez et al., 2016; Wu et al., 2018). Dynamic-based methods are also used extensively in the industry for damage identification through the vibrational characteristics of a structure (Koh and Dyke, 2007; Fan and Qiao, 2011; Hakim et al., 2014; Favarelli et al., 2021). Gharehbaghi et al. (2022) noted that the measurements of static responses were much more straightforward than those of dynamic-based responses since the dynamic-based responses require the meticulous management of operational and environmental effects for obtaining accurate data.

Beam–columns are ubiquitous structural members within steel-framed buildings, transferring the vertical and lateral loads acting on the building to the foundation (Lindner, 1997). Their importance in providing stability to the overall frame underscores the critical need for developing a robust, practical, and cost-effective SHM technique as being an essential precursor for extending the design service life of existing structures (Liu and Nayak, 2012; Thomson, 2013; Sumitro and Wang, 2005). For the outcomes of an SHM procedure to achieve this goal, it must be able to determine the “current” (in situ) structural capacity of the structural member or, at least, be able to provide sufficient information to predict its current proximity to failure. The current paper investigates the feasibility of using the probing SHM procedure, introduced by Shen et al. (2023), to evaluate the health of simply supported beam–columns subjected to axial compression and uniform bending.

Considering first the design of slender steel columns under a purely axial load, these are typically governed by buckling instabilities (Timoshenko and Gere, 1963; Allen and Bulson, 1980), where the ultimate axial load capacity $(P_{\text{ult}})$ is equal to the Euler buckling load, $P_{\text{E}}={\pi }^{2}EI/L_e^2$, where $E$ and $I$ are the Young’s modulus of the material and the second moment of the area of the cross section, respectively, while $L_e$ is the effective buckling length of the column that varies with the boundary conditions at the supports. Considering next the design of slender members subjected to uniaxial bending, the ultimate bending moment capacity $(M_{\text{ult}})$ is typically governed by lateral torsional buckling (LTB). The effects of LTB can be mitigated by restraining the beam to prohibit the lateral deformation or by using cross sections with high torsional and warping stiffness such as closed sections (Kitipornchai and Trahair, 1980; Trahair et al., 2008). The ultimate bending moment for members that are designed to be laterally restrained is typically governed by plasticity and is, hence, dependent on the cross-sectional geometry and material properties.

The current study considers members that are subjected to a combination of both axial and bending forces simultaneously, wherein the effects of LTB are restrained, and henceforth referred to as “beam–columns.” This is achieved by considering a beam–column with a circular hollow section (CHS). In practice, LTB can also be restrained in beams that support a floor slab since the slab restrains the compression flanges of the beam. Hence, the study of laterally restrained beam–columns represents a more straightforward, yet practically realistic, design scenario faced within the industry; the explicit consideration of laterally unrestrained beam–columns is left for future work. Furthermore, the effects of the local–global buckling interaction are not presently considered. The failure criterion for laterally restrained beam–columns is more intricate since it is determined by the member response to both bending and compression actions (EN, 2014; Liew and Gardner, 2015; Arrayago et al., 2015; Cavajdová and Vican, 2023). This response is best demonstrated by the interaction plot shown in Figure 1, where $\widehat{P}$ is the applied axial compression force $P$ normalised by the ultimate axial capacity of the member $P_{\text{ult}}$, and hence, $\widehat{P}=P/P_{\text{ult}}$, while $\widehat{M}$ is the applied moment $M$ normalised by the ultimate bending capacity of the member $M_{\text{ult}}$, and hence, $\widehat{M}=M/M_{\text{ult}}$. In Figure 1, the solid line indicates the failure boundary envelope, i.e., the combinations of ${\widehat{M}}_{\text{b}}$ and ${\widehat{P}}_{\text{b}}$ that would induce the onset of failure within the member. Hence, combinations of $\widehat{M}$ and $\widehat{P}$ that lie below the curve are safe-sided, as depicted by the coordinate $\left({\widehat{M}}_{\text{safe}},{\widehat{P}}_{\text{safe}}\right)$ in Figure 1; conversely, points that lie above the interaction boundary cause failure and are unsafe, as depicted by the coordinate $\left({\widehat{M}}_{\text{unsafe}},{\widehat{P}}_{\text{unsafe}}\right)$. Obtaining $\widehat{M}$ and $\widehat{P}$ for an in situ structure would provide designers with a metric that can inform the potential structural strength reserve of the beam–columns, i.e., addressing the criteria for SHM mentioned above. Previous work has stated that this is a critically important area of research for present SHM methodologies (Gharehbaghi et al., 2022). Consequently, any structural health monitoring index for beam–columns must be evaluated in relation to this boundary, which is discussed in Sections 3,4. Once the results from the probing–machine learning framework are presented and analysed, a brief discussion on the prospects of future developments is presented, and then, conclusions are drawn.

Figure 1

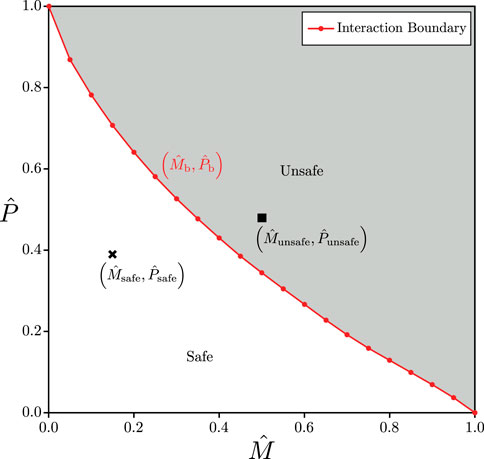
Figure 1. Failure envelope for a beam–column under a combination of normalised uniaxial bending moment $\widehat{M}$ and normalised axially compressive force $\widehat{P}$.

2 Probing SHM methodology for beam–columns

The probing methodology was originally developed by Thompson (2015) to assess the buckling resistance of shells using a non-destructive technique. The process involved loading a cylindrical shell to a prescribed axial compression load and is subsequently probed laterally with a small probing force $F_{\text{p}}$ while recording the corresponding probing lateral deflection ${\delta }_{\text{p}}$. The prescribed axial compression load is then increased, once again recording the response to probing, until all the probing responses for each normalised axial compression level are recorded. The results are plotted, which enables the notoriously difficult-to-predict buckling load of the cylindrical shell to be obtained (Shen et al., 2023). The concept of using probing as a monitoring technique was devised by Shen et al. (2023) by considering the case of axially loaded prestressed stayed columns (PSCs). In their study, the normalised axial utilisation ratios, equivalent to $\widehat{P}$ currently, alongside the degree of cable erosion, were successfully inferred from the probing response of the PSC. This methodology, again, is non-destructive, can be executed with minimal interruption, and may be classified as a periodic visit-based monitoring (PVM) technique since continuous monitoring via sensors is not required. The current work extends the developed probing SHM methodology to predict the utilisation ratio of simply supported beam–columns subjected to combined axial and bending loads.

The procedure adopted here is similar to that implemented for the study of PSCs (Shen et al., 2023), where the more generic steel beam–column is modelled within the commercial finite element (FE) analysis software application Abaqus (Dassault Systèmes Simulia Corp, 2021). The modelled beam–columns, under a specified combination of axial force $(P)$ and uniform bending moment $(M)$, are probed laterally at a prescribed location $L_{\text{p}}$ with a nominal probing force $F_{\text{p}}$; in the present study, $F_{\text{p}}=100\mathrm{N}$. The probing response for the beam–columns is then recorded by measuring the corresponding displacement ${\delta }_{\text{p}}$, as shown in Figure 2, with this procedure being repeated for varying combinations of $\widehat{M}$ and $\widehat{P}$ to generate the dataset for the study presented later. Throughout the parametric study, it is observed that the probing response is typically linear, as reported for PSCs by Shen et al. (2023). However, it is noted that certain combinations of $\widehat{M}$ and $\widehat{P}$ considered within the parametric study exhibit a nonlinear response to probing. This is owing to $M_{\text{ult}}$ being governed by material plasticity for a laterally restrained beam; hence, probing potentially causes the member to be loaded beyond its elastic limit. A fundamental principle of probing in the structural health assessment methodology is that the structure must remain elastic during the probing process to ensure that any of its effects are transient and reversible (Shen et al., 2023). Therefore, combinations of $\widehat{M}$ and $\widehat{P}$ that undergo permanent deformation through plasticity, presently termed “plastic points,” are considered to be beyond the applicability of the probing procedure and are hence excluded from the study. The probing stiffness $k_{\text{p}}$ is evaluated for each loading combination considered using the relationship $k_{\text{p}}=\mathrm{d}{F}_{\text{p}}/\mathrm{d}{\delta }_{\text{p}}$. The evaluated $k_{\text{p}}$ is subsequently used as an input for the artificial neural network (ANN) surrogate machine learning (ML) model to infer the utilisation ratios, $\widehat{M}$ and $\widehat{P}$, of the beam–column; hence, the ANN ML model aims to solve the “inverse” problem to that of the FE analyses. The use of ML surrogate models provides a powerful solution for capturing complex structural behaviours that are difficult to model with traditional methods (Wu et al., 2022; Xing et al., 2023). In theory, with sufficient training, the surrogate ANN ML model should be able to infer both $\widehat{M}$ and $\widehat{P}$ when the beam–column is probed laterally in situ. Details of the surrogate ANN ML model are given in Section 4.

Figure 2

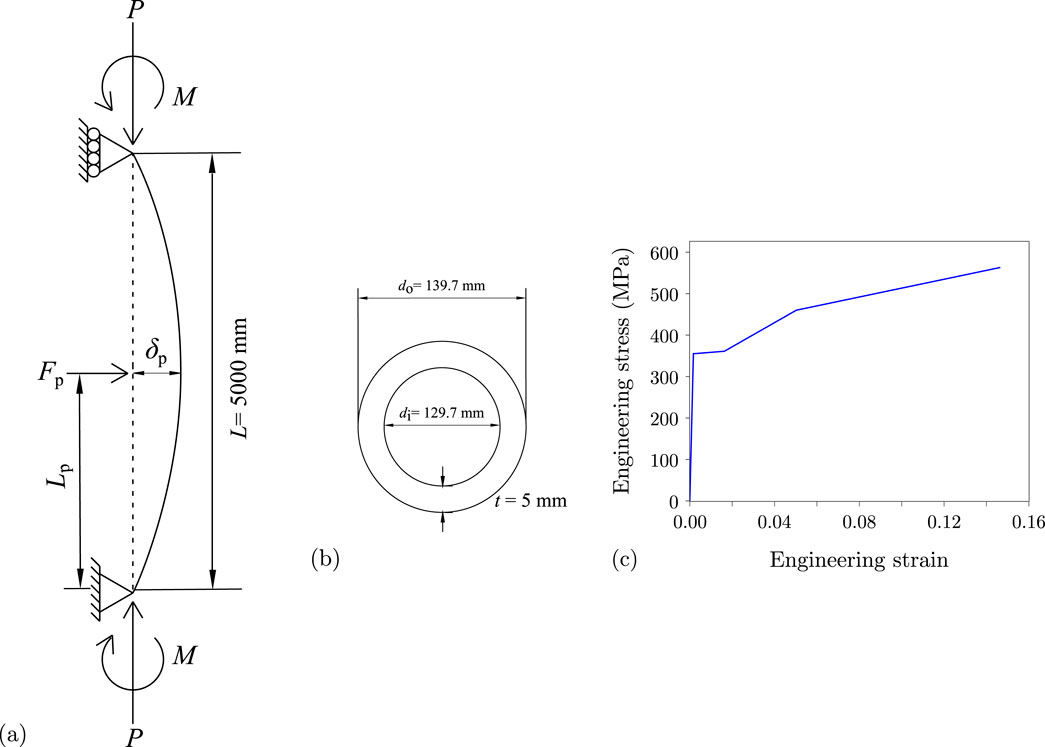
Figure 2. (A) Geometry, loading setup, and boundary conditions of the probing procedure modelled in Abaqus, where the dotted line shows the original state and the solid line depicts the deflected shape during probing; (B) cross section of the beam–column member; (C) engineering stress–strain relationship for the material model used to generate the interaction plot and for the parametric study, as detailed in Table 1.

2.1 FEA model description

An important part of this framework is the FE model of the beam–column. The beam–column considered here is modelled as a simply supported member, as shown in Figure 2. The axial load is applied as a concentrated force at the top of the member, while the uniform uniaxial bending moment is applied as a pair of equal and opposite external moments at its ends, as shown in Figure 2. The geometrical and material properties of the beam–column are given in Table 1.

Table 1

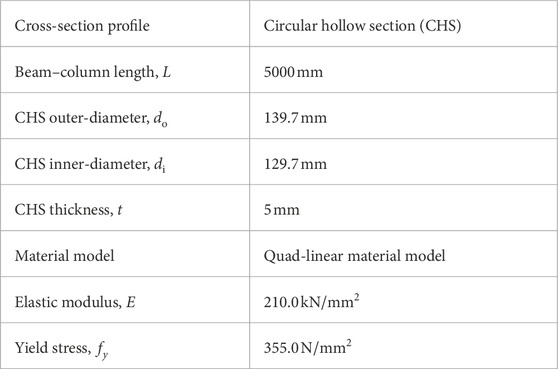
Table 1. Geometrical and material properties used in the parametric study. Note that the “quad-linear material” (QLM) model is defined by Yun and Gardner (2017).

The commercial FE software application Abaqus is used to model the beam–columns, where Timoshenko beam elements with linear interpolation functions (“B21” in the Abaqus element library) are utilised. This choice is appropriate since the interaction between local and global buckling was not within the scope of the current study. Following a mesh sensitivity study, an arrangement comprising 200 beam elements along the main column member is demonstrated to be sufficiently accurate, when verified by comparing the elastic critical buckling load evaluated in FE with the theoretical value from the Euler buckling load $P_{\text{E}}$. The probing response of the structure is expected to remain within the elastic regime, but for the sake of realism, the well-established quad-linear material (QLM) model is implemented here (Yun and Gardner, 2017), using the nominal material properties given in Table 1 and shown in Figure 2C. Unlike the traditional elastic–perfectly plastic material models, the QLM model captures the strain-hardening response of steel, as well as the gradual loss of stiffness near the strain-hardening regions, making it a more accurate representation of the structural material. The static solver accounting for nonlinear geometry is implemented in the pre-loading stage, while the arc length solver presented by Riks (1979) is used for the probing load step.

2.2 Beam–column probing parametric study framework

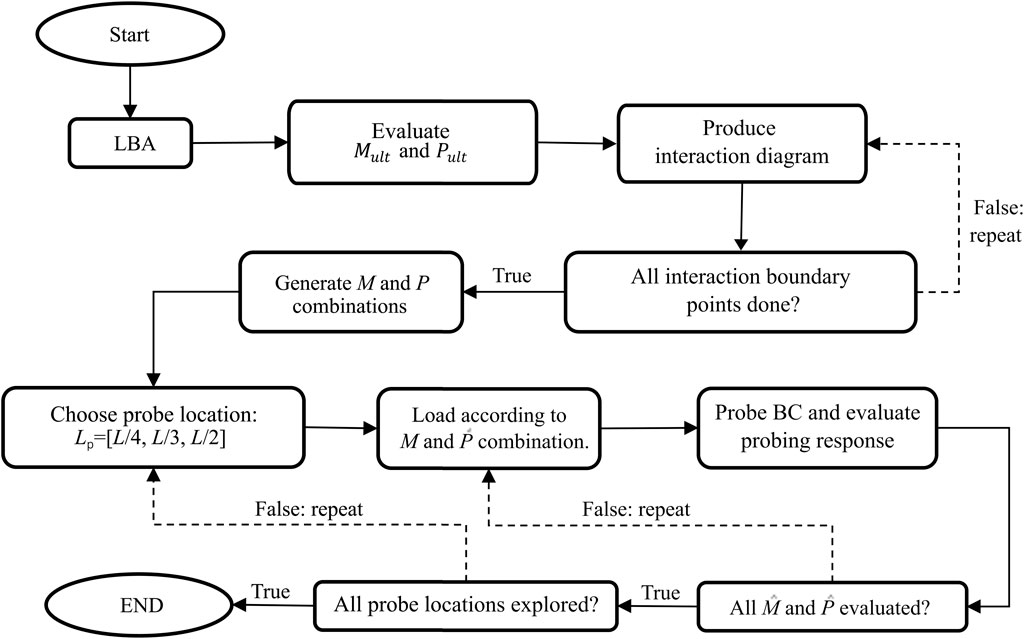
A parametric study was conducted on the presented beam–column by varying the applied moment, applied axial force, and location at which the probe is applied, and the corresponding displacement is measured, as shown in Figure 3. First, a linear buckling analysis (LBA) was executed to obtain the buckling loads and modes of the beam–column. Imperfections were subsequently introduced to the FE model through scaling the first buckling mode by an amplitude of $L/10000$ to introduce a small perturbation to the numerical model that can consistently initiate the initial instability while effectively simulating the behaviour of “perfect” structural members (Saito and Wadee, 2008; Lapira et al., 2017). Since the present aim is to provide a demonstrable enhancement of the original probing concept published by Shen et al. (2023), a comprehensive study focussing on the influence of different imperfection profiles with practically significant magnitudes on the ML model is not within the scope of this study and is earmarked for a future study. The ultimate axial load capacity $P_{\text{ult}}$ and ultimate moment capacity $M_{\text{ult}}$ of the beam–column were then determined by loading the member with the respective forces, in isolation, to failure. In these analyses, the nonlinear arc-length method presented by Riks (1979), as implemented in Abaqus, was utilised, accounting for both geometric and material nonlinearity in the FE analysis procedure. For the member subjected to pure axial compression, $P_{\text{ult}}$ was determined by considering the ultimate load taken at the peak value that is observed in the equilibrium path of load versus deflection, as shown in Figure 4A. For members subject only to uniform bending, a similar peak was not observed in the post-buckling equilibrium path, as shown in Figure 4B, and hence, the approach presented by dos Santos et al. (2018) was used to obtain $M_{\text{ult}}$.

Figure 3

Figure 3. Framework for the parametric study on the probing response of the beam–column.

Figure 4

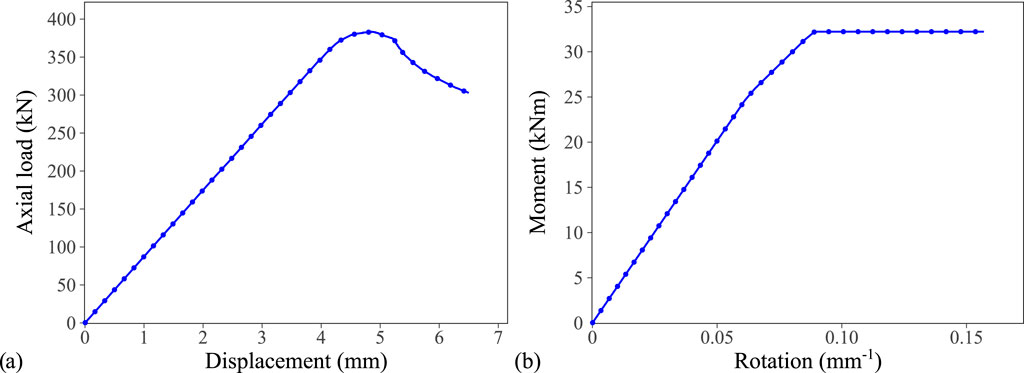
Figure 4. (A) Load–deflection curve of the pure axial case with a peak ultimate load and (B) moment–rotation curve for the pure bending case with no distinct peak.

Having established the values for $P_{\text{ult}}$ and $M_{\text{ult}}$, the interaction boundary of the beam–column was determined; the goal of this procedure was to obtain coordinates $\left({\widehat{M}}_{\text{b}},{\widehat{P}}_{\text{b}}\right)$ that define the interaction boundary, as shown in Figure 1. This was performed by implementing a two-step process within Abaqus, where the beam–column was first subjected to ${\widehat{M}}_{\text{b}}$, i.e., an applied moment as a fraction of $M_{\text{ult}}$, through a *Static load-step that accounts for geometric nonlinearity. Subsequently, the axial force $P$ was applied within a *Static, Riks load-step that also accounts for geometric nonlinearity, until failure occurred. The value for ${\widehat{P}}_{\text{b}}$ is then established by normalising the resulting axial load with $P_{\text{ult}}$. This “two-step process” is shown graphically in Figure 5, and the procedure is repeated until the interaction boundary is defined. Having determined the interaction boundary, “safe-sided” (or structurally viable) combinations of $\widehat{M}$ and $\widehat{P}$ are obtained using a rejection sampling method, executed using the GeoPandas module within Python (GeoPandas, 2023). This was achieved by first generating sample points, with a mesh-size interval of 0.05 by 0.05 on both the $\widehat{M}$ and $\widehat{P}$ axes, while points lying beyond the boundary shown in Figure 5B were rejected. This essentially creates a uniform grid of combinations for $\widehat{M}$ and $\widehat{P}$.

Figure 5

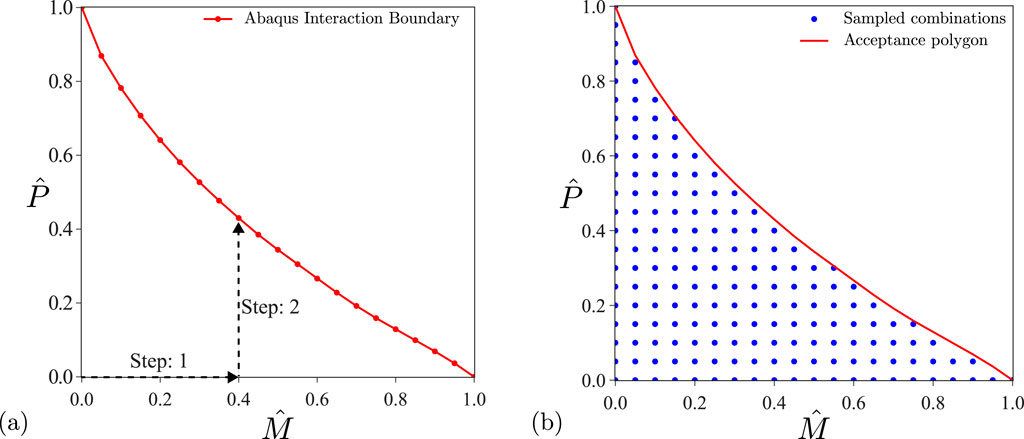
Figure 5. (A) Two-step procedure used to obtain the interaction boundary; (B) combinations of $\widehat{M}$ and $\widehat{P}$ to be examined in the SHM procedure.

Finally, the probing study was conducted on the obtained structurally viable combinations of $\widehat{M}$ and $\widehat{P}$. The probing analysis in Abaqus was conducted in two steps. In the first step, the stipulated loading values of $\widehat{M}$ and $\widehat{P}$ were applied within a *Static step accounting for geometric nonlinearity. Subsequently, a probing force of $F_{\text{p}}=100\mathrm{N}$ was applied at $L_{\text{p}}$ and analysed within the arc-length method load step presented by Riks (1979), where the probing force–displacement response was recorded such that plots of $F_{\text{p}}$ versus ${\delta }_{\text{p}}$, shown in Figure 6A, could be generated. Owing to the linear probing force–deflection response of the beam–column, the probing stiffness $k_{\text{p}}$ was obtained by computing the gradient $\mathrm{d}{F}_{\text{p}}/\mathrm{d}{\delta }_{\text{p}}$, as shown in Figure 6. Moreover, it was noted in Figure 6B that owing to the curvature caused by $\widehat{M}$, there is an initial lateral deflection, $w_{\text{ini}}$, at the intercept of the abscissa on the load–deflection curve; hence, $w_{\text{ini}}$ was also recorded alongside $k_{\text{p}}$. This procedure was then repeated at different probe locations, i.e., $L_p=\left\{L/4,L/3,L/2\right\}$, for each of the aforementioned structurally viable combinations of $\widehat{M}$ and $\widehat{P}$. It should be noted that owing to the symmetrically applied bending moments, the probing response of the beam–column is the same for both the top and lower halves of the column. Therefore, probing was only considered in the lower half of the column. The data from the probing procedure were then organised into a pivot table, where each column of the table corresponded to the probing response ($k_{\text{p}}$ or $w_{\text{ini}}$) at a given probe location such that the results were ready for use within the ML framework.

Figure 6

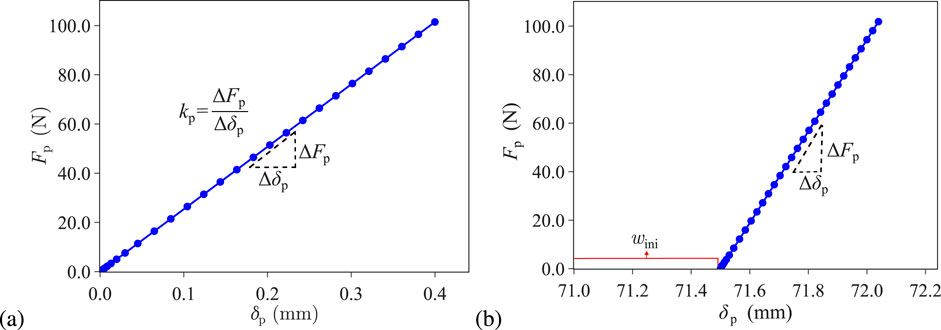
Figure 6. (A) Linear probing response with only $P$, with the abscissa intercept at ${\delta }_{\text{p}}=0$; (B) linear probing response under $M$ and $P$, with the abscissa intercept at ${\delta }_{\text{p}}=w_{\text{ini}}$ due to the curvature induced by $M$.

3 Behaviour and probing response of the beam–column

The presence of the in-service bending moment $M$, along with the axial load $P$, induces a curvature in the beam–column. The deflected profile of this beam–column can be found by considering the differential equation of equilibrium, given by Timoshenko and Gere (1963):

$EI{w}^{″}+Pw=-M,(1)$

where $w$ describes the deflected profile as a function of the longitudinal coordinate $x$, as shown in Figure 7, while primes $(\prime )$ denote derivatives with respect to $x$. The general solution to Equation 1 is known to be of the form

$w\left(x\right)=C_1\sin \beta x+C_2\cos \beta x-\frac{M}{P},(2)$

where $C_1$ and $C_2$ are constants that depend on the structural boundary conditions, while β is defined in Equation 3 as:

$\beta =\sqrt{\frac{P}{EI}}.(3)$

Figure 7

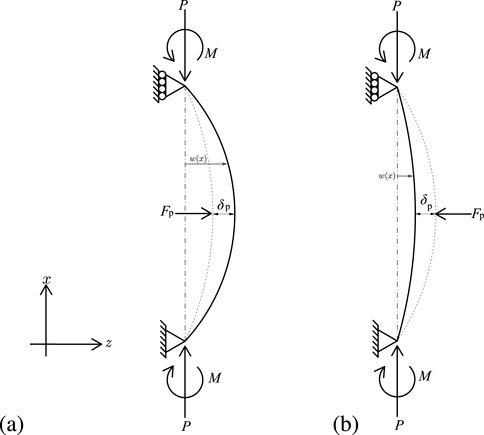
Figure 7. (A) Probing in the direction of deflection (positive direction) exacerbates the deflected shape, leading to a larger curvature, while (B) probing against the direction of deflection (negative direction) leads to a smaller curvature; here, $w(x)$ and solid lines represent the deflected shape of the member after probing, and dashed lines represent the deflected shape before probing.

For a beam–column with uniform bending moment $M$, the boundary conditions are

$-EI{w}^{″}\left(0\right)=-EI{w}^{″}\left(L\right)=M.(4)$

Thus, by substituting the conditions in Equation 4 into Equation 2, the constants $C_1$ and $C_2$ can be determined, which yields

$w\left(x\right)=\frac{M}{P}\left\{\left[\frac{1-\cos \beta L}{\sin \beta L}\right]\sin \beta x+\cos \beta x-1\right\}.(5)$

The deflected profile in Equation 5 is therefore dependent on $M$ and $P$. Note that as $P\to 0$, and thereby, $\beta \to 0$, the deflection function $w$ converges to a parabola in $x$, as described by Euler–Bernoulli bending theory.

Owing to the complex behaviour of beam–columns under combined bending and axial loading, the direction of the probing force $F_{\text{p}}$ is important. For load combinations that are close to the interaction boundary, probing the beam–column in the positive direction, as shown in Figure 7A, leads to a nonlinear probing response, as shown by the solid line in Figure 8A for the load combination ($\widehat{M}=0.45$, $\widehat{P}=0.35$). This behaviour was not observed for load combinations that were remote from the interaction boundary, as shown by the dashed line in Figure 8A, which represents the probing response for load combination ($\widehat{M}=0.15$, $\widehat{P}=0.05$). This nonlinear probing response was caused by the positive probing force $F_{\text{p}}$, triggering an inelastic response that violated one of the principal aims of the probing procedure for structural health assessment, i.e., ensuring that the probing intervention must trigger an elastic (hence reversible) response from the structure, as described in Section 2. One potential strategy to avoid triggering an inelastic response is to probe the member in the “negative” direction, i.e., in the opposing direction to the deflected shape, as shown in Figure 7B. This ensures that a linear and elastic probing response of the beam–column is maintained, as shown by the dashed line in Figure 8B, where a linear probing force–displacement response is observed when probing in the “negative” direction. This is currently attributed to the fact that probing in the negative direction is equivalent to applying a negative moment $(-M)$ to the member, which, in effect, unloads the member, and hence, the probing equilibrium path follows a linear elastic response.

Figure 8

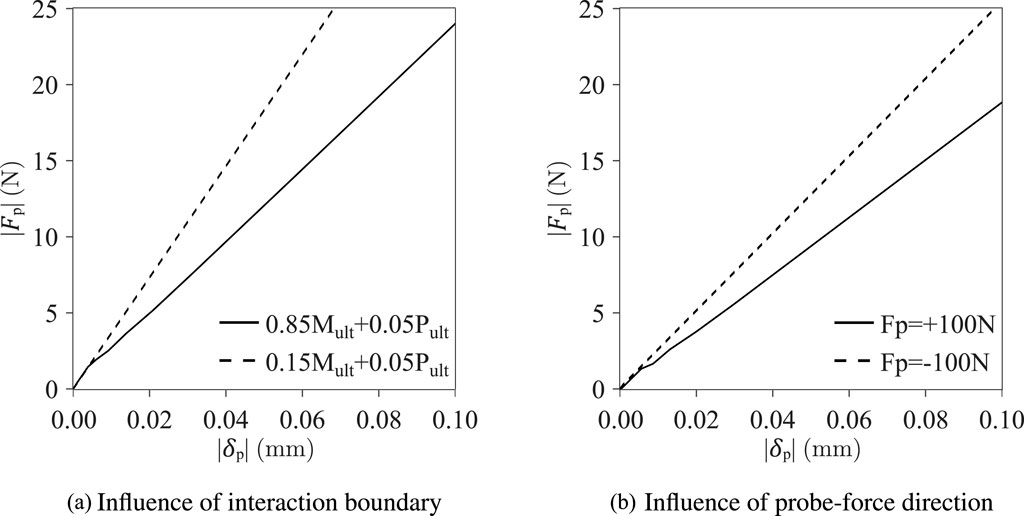
Figure 8. Probing force–displacement response at $L_{\text{p}}=0.5L$ for (A) $F_{\text{p}}=+100\mathrm{N}$ for the load combinations ($\widehat{M}=0.85$, $\widehat{P}=0.05$) and ($\widehat{M}=0.15$, $\widehat{P}=0.05$), which are close to and remote from the interaction boundary, respectively, and (B) $F_{\text{p}}$ for load combination ($\widehat{M}=0.45$, $\widehat{P}=0.35$), which is close to the interaction boundary. In (B), the positive probing response changes the gradient after $F_{\text{p}}=2\mathrm{N}$. In both sub-figures, the probing responses were shifted in the abscissa by $-w_{\text{ini}}$.

A simplified and safe method for identifying the aforementioned “plastic points” is to determine the “elastic boundary” by considering the linear addition of the absolute stress blocks from the applied moment $M$ and the axial compression $P$ while limiting the peak stresses to be less than the yield stress of $f_{\text{y}}$. Mathematically, the addition of the absolute stress blocks can be expressed as

$\left|\frac{P}{A}\right|+\left|\frac{Mz}{I}\right|<f_{\text{y}},(6)$

where $A$ and $I$ are the cross-sectional area and the second moment of the area of the beam–column, respectively, while $z$ is the distance from the geometrical centroid of the cross section to its extreme fibre. Using the definitions of $\widehat{P}$ and $\widehat{M}$, respectively, and substituting them into Equation 6, yields Equation 7:

$\left|\frac{\widehat{P}\left(P_{\text{ult}}\right)}{A}\right|+\left|\frac{\widehat{M}\left(M_{\text{ult}}\right)z}{I}\right|<f_{\text{y},},(7)$

which can be used to eliminate combinations of $\widehat{M}$ and $\widehat{P}$ that experience plasticity, as shown in Figure 9. It was found that points that lie above the elastic boundary exhibit a nonlinear probing response, confirming the accuracy of the derived boundary. Therefore, the present study considers load combinations that lie within the interaction and elastic boundary to avoid triggering plasticity during probing. Moreover, combinations of $\widehat{M}$ and $\widehat{P}$ that are excessively close to the interaction boundary are also excluded from the analysis. This was achieved by bringing the interaction boundary inwards towards the origin by $0.05\widehat{M}$ and $0.05\widehat{P}$; this is presently termed the “offset boundary.” Therefore, the loading combinations of $\widehat{M}$ and $\widehat{P}$ that lie within these established boundaries are considered here and are indicated by blue dots in Figure 9.

Figure 9

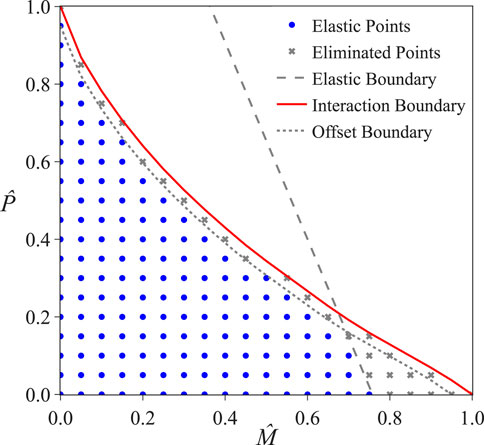
Figure 9. Final combinations of $\widehat{M}$ and $\widehat{P}$ showing the acceptable region and those that exceed both the offset and elastic boundaries are indicated by grey crosses.

The probing response for all combinations of $\widehat{M}$ and $\widehat{P}$ is considered in the parametric study conducted in Abaqus; the results showing the variation in $k_{\text{p}}$ and $w_{\text{ini}}$ alongside $\widehat{M}$ and $\widehat{P}$ are shown in Figures 10A, B. A direct correlation between $\widehat{P}$ and $k_{\text{p}}$ is readily observed by the linear variation in the $\widehat{P}$-axis direction in Figure 10A, echoing the findings obtained by Shen et al. (2023). However, a similar correlation between $\widehat{M}$ and $k_{\text{p}}$ is not readily found since the response is practically constant for different $\widehat{M}$ values, while $\widehat{P}$ is constant. However, a variation in $w_{\text{ini}}$ with both $\widehat{M}$ and $\widehat{P}$ is found, as shown in Figure 10, which strongly suggests that $w_{\text{ini}}$ is a suitable parameter to consider in the ML framework.

Figure 10

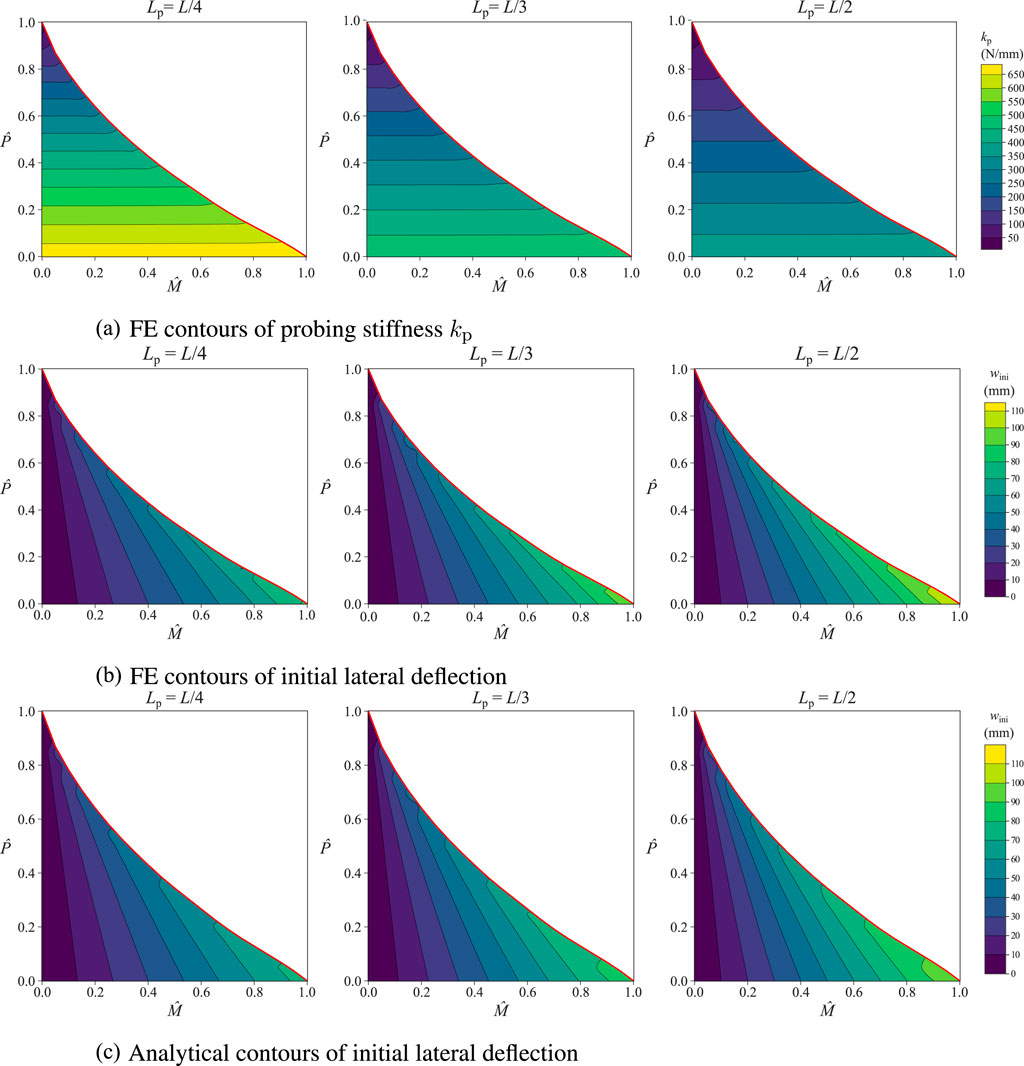
Figure 10. Contours of (A) probing stiffness $k_{\text{p}}$and (B) initial lateral deflection derived from Abaqus, and (C) initial lateral deflection derived from analytical formulations. In each sub-figure, the response is calculated at different probing locations $L_{\text{p}}=L/4$, $L/3$, and $L/2$ (from left to right).

Using Equation 5, the FE results can be verified against $w(x)$ by substituting the probe location into $x$, with the resulting analytical values shown in Figure 10C. It is shown that the calculated values for $w(x)$ agree reasonably well with $w_{\text{ini}}$ obtained from Abaqus as long as the response remains elastic. This is shown in Figure 11, which depicts the ratio of the analytical deflection value to that determined from Abaqus, where values equal to unity denote perfect agreement. It is shown in Figure 11 that all the results lie within the range $\left[0.9,1.0\right]$, with the vast majority lying in the range $\left[0.99,1.00\right]$, which implies that the probing response generated by Abaqus is sufficiently accurate to be utilised as the training data in the ANN ML model to predict $\widehat{M}$ and $\widehat{P}$.

Figure 11

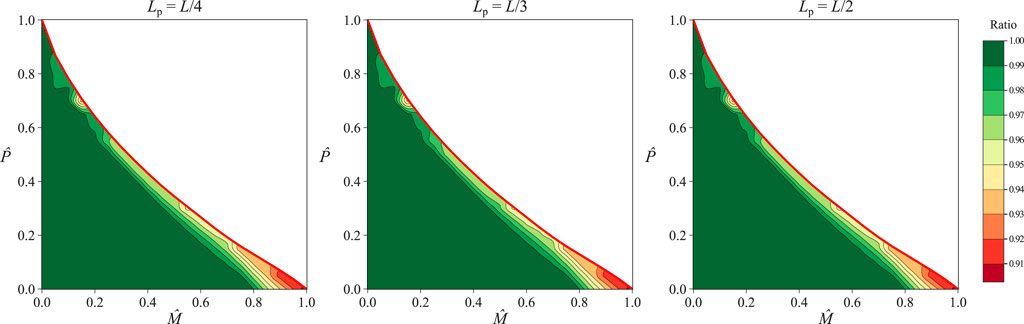
Figure 11. Ratio of analytical to Abaqus $w_{\text{ini}}$ predictions for different $L_{\text{p}}$ values; ratios equal to unity imply exact agreement. The mean ratio is 0.991 for all three cases, while the coefficients of variation ratios are 0.017 for the cases where $L_{\text{p}}=\{L/4,L/3\}$ and 0.018 for the case where $L_{\text{p}}=L/2$.

4 Machine learning framework and results

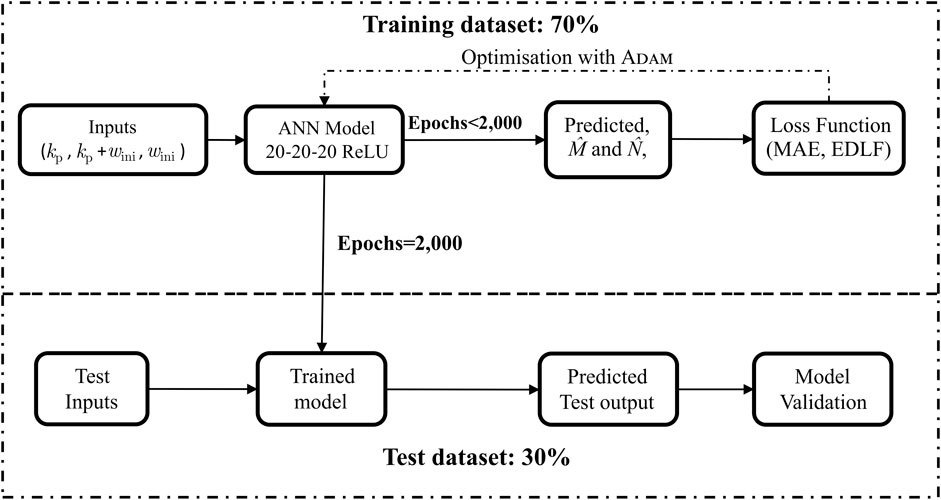
Following the framework developed by Shen et al. (2023), an ANN is implemented for the machine learning framework in the current study to determine whether this can be used to predict $\widehat{M}$ and $\widehat{P}$ for beam–columns. Here, the ANN is developed using TensorFlow (Abadi et al., 2016) with the high-level application programming interface Keras (Chollet, 2015).

As discussed in Section 3, the probing stiffness response $k_{\text{p}}$ alone may be insufficient to determine $\widehat{M}$ and $\widehat{P}$, owing to the lack of variation in the former with $k_{\text{p}}$. Consequently, it was hypothesised that different input cases are required to generate a good prediction of $\widehat{M}$ and $\widehat{P}$ in the ANN. Hence, the suitability of $k_{\text{p}}$ and $w_{\text{ini}}$ measured at different probing locations as ANN input parameters is explored in different scenarios, which are outlined in Table 2. Owing to the symmetry of the loading conditions and geometry, probe locations are limited to the lower half of the member, i.e., $L_p=\left\{L/4,L/3,L/2\right\}$, to avoid duplicating data responses in the ANN. The inputs $(k_{\text{p}},u_{\text{ini}})$ are then normalised using the MinMaxScaler function within the sklearn.preprocessing package, which is known to assist in achieving convergence by reducing scaling effects when training the ANN model (Montavon et al., 2012). The total number of data points used varies according to the input cases, as shown in Table 2.

Table 2

Table 2. Input cases for the ML model and corresponding number of data points.

The ANN model predicts two outputs, ${\widehat{M}}_{\text{pred}}$ and ${\widehat{P}}_{\text{pred}}$, which can be presented as coordinates in the $\widehat{M}$–$\widehat{P}$ space. Following an initial hyperparameter optimisation study, the structure of the ANN is formed of three hidden layers, each having 20 neurons, which produces sufficiently accurate predictions without excessive computational effort. The activation function used for the neurons in the internal layers is chosen to be the rectified linear unit (ReLU) (Agarap, 2018), while for the output layer, a sigmoid function was used to ensure that ${\widehat{M}}_{\text{pred}}$ and ${\widehat{P}}_{\text{pred}}$ lie in the range $\left[\mathrm{0,1}\right]$. The framework for the ANN is shown in Figure 12, which depicts the “70–30” split of the training data, i.e., 70% of the probing results are used as the training dataset, and the remaining 30%, termed the “evaluation dataset,” are set aside as an “unseen and unbiased” dataset to evaluate the accuracy of the trained ANN. From the initial hyperparameter study, the optimum number of epochs was determined to be 2,000.

Figure 12

Figure 12. Framework for testing and training the developed ANN.

In the ML framework, loss functions are used to quantify the model error in the training space, and they are used to optimise the weights and bias between each layer in the ANN (Kerkhof et al., 2023). Currently, two types of loss functions are explored, namely, the mean absolute error (MAE) and a bespoke loss function termed “Euclidean distance-loss function” (EDLF) developed by Sung Lee et al. (2020). The difference between the MAE and EDLF is that the MAE computes the average absolute error between the predicted and actual outputs, averaging both the errors of $\widehat{M}$ and $\widehat{P}$ together (Hodson, 2022), whereas EDLF calculates the distance in the Euclidean space between the ML-predicted coordinate points against the training dataset true coordinate points in the $\widehat{M}$–$\widehat{P}$ two-dimensional space (Sung Lee et al., 2020). The evaluated loss values, calculated using either the MAE or EDLF, are back-propagated into the ANN model (Larochelle et al., 2009) in a manner that minimises subsequent training losses using the Adam optimisation algorithm (Kingma and Ba, 2015). This optimisation procedure is repeated until the training epoch is completed. Subsequently, upon completing the training loop, the test dataset, which was initially set aside, was used to evaluate the performance of the trained ANN model, thus evaluating the model against “unseen” data, thereby preventing potential bias in the results. The results obtained from the evaluation dataset fed into the trained ANN model are then plotted in Figures 13–15.

Figure 13

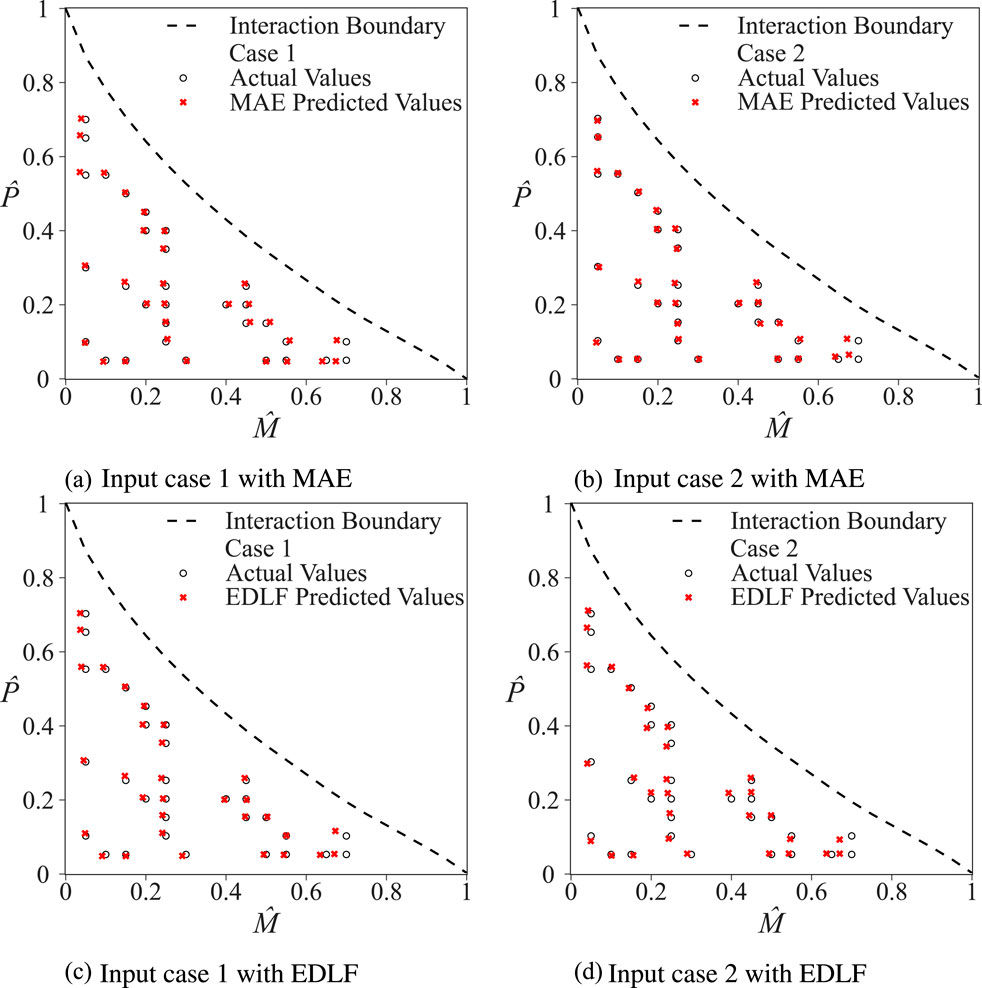
Figure 13. Comparison of the predicted values (ANN results) and the actual values (FE results) on plots of $\widehat{M}$ versus $\widehat{P}$ for input cases 1–2 with (A, B) MAE and (C, D) EDLF. (A) Input case 1 with MAE. (B) Input case 2 with MAE. (C) Input case 1 with EDLF. (D) Input case 2 with EDLF.

Figure 14

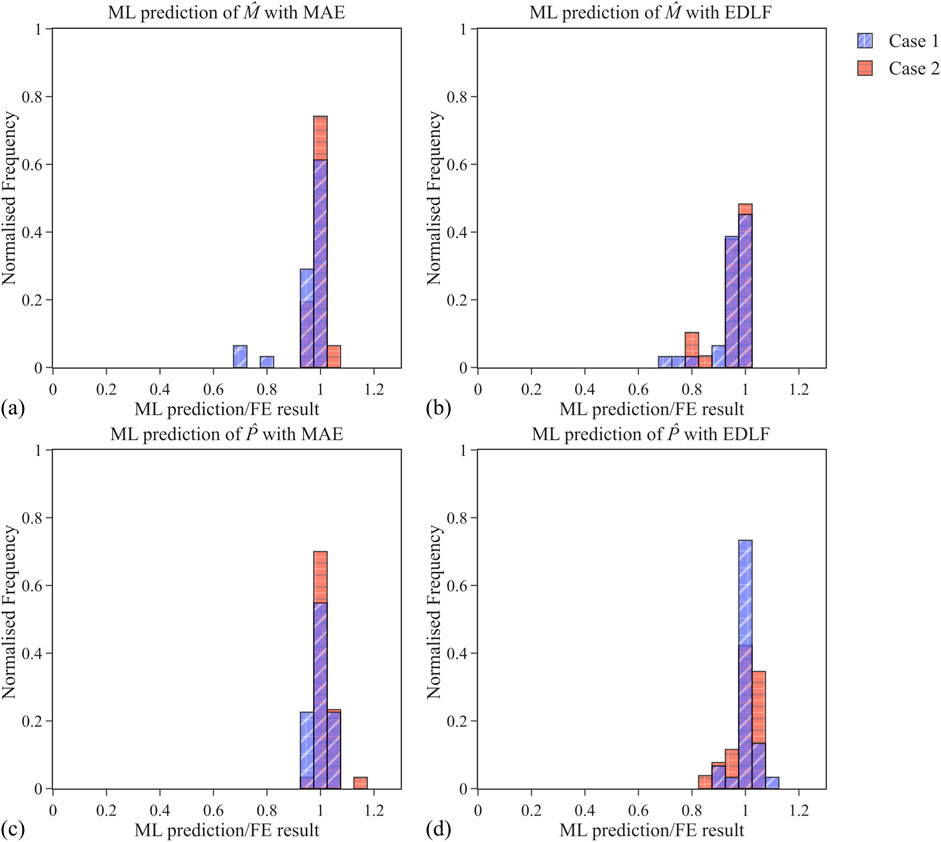
Figure 14. Normalised frequency plots of ML/FE for input cases 1 and 2 with loss functions (A) MAE and (B) EDLF for $\widehat{M}$ and (C) MAE and (D) EDLF for $\widehat{P}$.

Figure 15

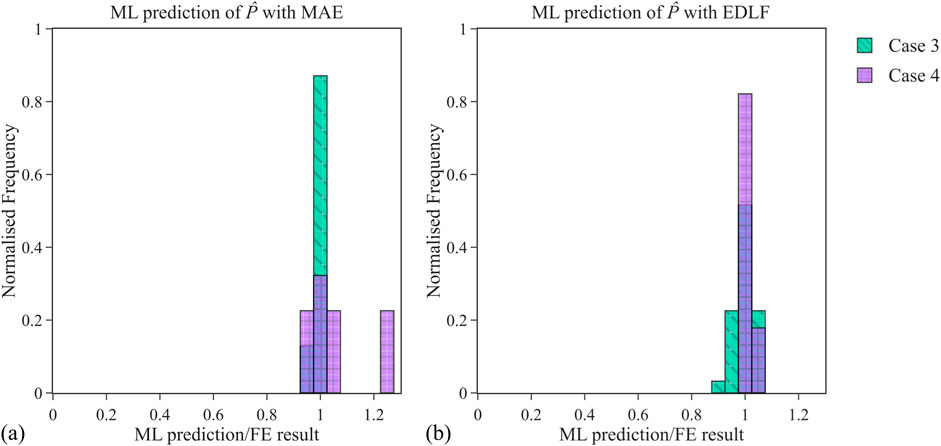
Figure 15. Normalised frequency plots of ML/FE for $\widehat{P}$ for input cases 3 and 4 with loss functions (A) MAE and (B) EDLF.

4.1 Results

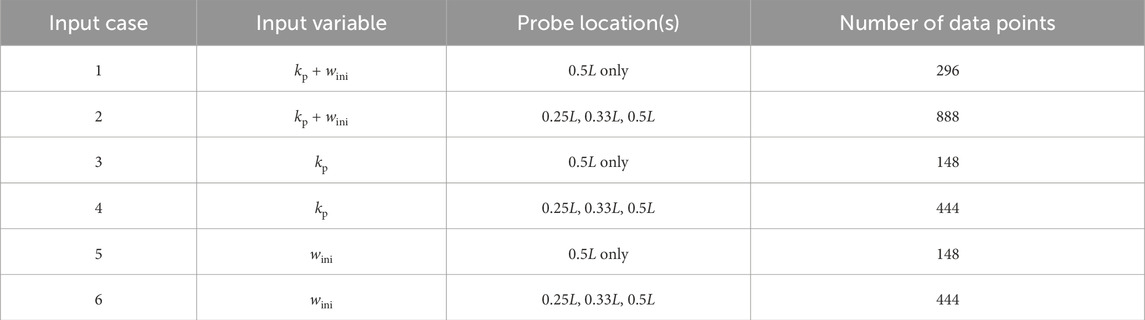
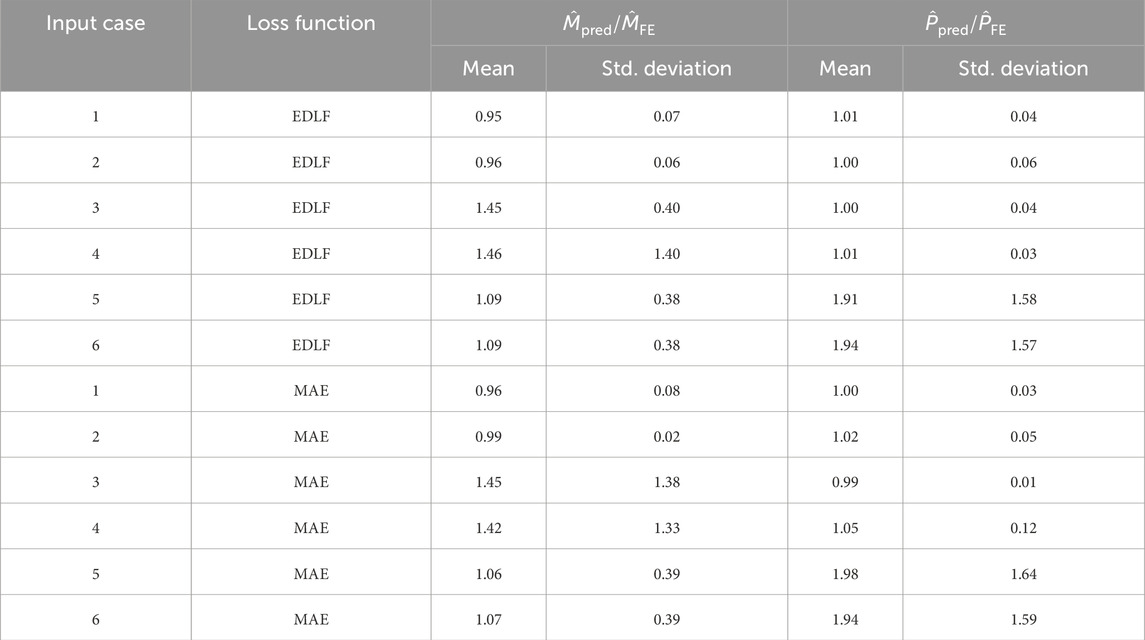
Six input cases and two different loss functions were studied presently, as shown in Table 2. Following the completion of the ANN training procedure presented in Section 4, the evaluation dataset was then used to predict $\widehat{M}$ and $\widehat{P}$ from the “unseen” probing results as an input. The results from the predictions for input cases 1 and 2, with different loss functions, are shown in Figure 13. The accuracy of the prediction is evaluated by comparing the ratio of the predicted to the actual values, i.e., the “ML/FE” ratio. For each input case, the resulting ML/FE ratios are averaged, and the statistical data are given in Table 3, which provides an overview of the performance of all the models. In Table 3, a ML/FE ratio above 1 implies that the ANN model has over-predicted the indicated utilisation ratio, whether for $\widehat{M}$ or $\widehat{P}$.

Table 3

Table 3. Summary of results of ${\widehat{M}}_{\text{pred}}/{\widehat{M}}_{\text{FE}}$ and ${\widehat{P}}_{\text{pred}}/{\widehat{P}}_{\text{FE}}$ with different input cases and loss functions.

Following the discussion presented in Section 3, it is not surprising that input cases 1 and 2 are determined to be the best performing ANN models, as shown in Table 3, since they utilise data points from both the contours of Figures 10A,B as inputs. Consequently, the model captured the variation in probing responses from both $w_{\text{ini}}$ and $k_{\text{p}}$ against both $\widehat{M}$ and $\widehat{P}$. Although it is noted that the results given in Table 3 only evaluate the model performance in summary and in aggregate, the results also suggest some input models may be better at predicting only one of the outputs, i.e., either $\widehat{P}$ or $\widehat{M}$. For instance, input cases 3 and 4 produce accurate predictions for $\widehat{P}$, while input cases 5 and 6 produce accurate predictions for $\widehat{M}$. In the subsequent sections, the different input cases are discussed in more detail.

4.2 Input cases 1 and 2

When comparing the different loss functions for input cases 1 and 2, there is no notable difference in terms of the predicted coordinate and actual coordinate. Both cases predict $\widehat{M}$ and $\widehat{P}$ with very good accuracy, as shown in Figure 13, which was evidenced by the close proximity of the predicted points with the FE results, depicted using the “$\times$” and “$◦$” symbols, respectively. The best performing model among the four cases shown in Figure 13 is case 2, i.e., implementing the MAE loss function and using both $w_{\text{ini}}$ and $k_{\text{p}}$ at three probe locations as inputs. This behaviour is expected since the ANN is trained on a more diverse training dataset, which includes multiple probing locations and two input variables, that is utilised to generate more accurate predictions. This is clearly shown in Figure 14, where the normalised frequency distributions of ${\widehat{M}}_{\text{pred}}/{\widehat{M}}_{\text{FE}}$ and ${\widehat{P}}_{\text{pred}}/{\widehat{P}}_{\text{FE}}$ are presented. The distribution of the ML/FE ratio for both $\widehat{M}$ and $\widehat{P}$ in both cases are centred around a normalised value of 1, with very little spread, indicating an overall encouraging model performance.

Furthermore, the normalised frequency plots shown in Figure 14 suggest that the MAE loss function outperforms EDLF when predicting $\widehat{M}$, as indicated by the normalised frequency ML/FE ratios being more focused around a value of 1.0 in Figure 14A compared with the EDLF results shown in Figure 14B. The same trend is also observed for the predictions of $\widehat{P}$, shown in Figures 14C, D for the MAE and EDLF loss functions, respectively.

4.3 Performance of input cases 3–6

In general, the performance of input cases 3–6 is sub-optimal compared with the results of input cases 1–2, regardless of the loss functions or the number of probe locations considered, as shown in Table 3. Input cases 5–6 are the worst-performing models, regardless of the loss functions used, and are, therefore, not examined further in this study. For input cases 3 and 4, the ML model appears to predict $\widehat{P}$ with some level of accuracy, as shown in Figure 15. This behaviour is expected since input cases 3 and 4 comprise only $k_{\text{p}}$ as the inputs, which was shown to be only sensitive to a change in $\widehat{P}$ in Figure 10A. Although it was noted that most of the $\widehat{P}$ predictions were centred around the ML/FE ratio of unity in Figure 15, the spread in the normalised frequency plots is excessively large, which implies that input cases 3 and 4 are relatively inconsistent in their predictions.

4.4 Discussion of future developments of the probing ML framework

As noted in Section 3, a key finding from the current work is the recognition that owing to the curvature of the column, which is induced by the applied bending moment, the direction in which the probing force is applied becomes an important parameter in ensuring that the beam–column remains elastic. Therefore, for the probing methodology to be extended to include structural members that also experience bending, $w_{\text{ini}}$ needs to be considered an input parameter within the ANN model framework. Moreover, the current study is deliberately limited in scope to consider the beam–column as a planar element; therefore, further work is necessary to consider more complex and realistic scenarios involving major and minor axes bending in three dimensions. This can be further extended to asymmetrical cross sections and open cross sections that are also susceptible to LTB. The current work has also focused on the behaviour of perfect beam–columns, i.e., without considering the effects of imperfections or damage. In theory, damage prediction based on this probing framework is possible, as indicated by Shen et al. (2023).

A comprehensive over-fitting study was not performed in the ML model proposed in the current study since the predictions generated by the ML model were sufficiently accurate for input cases 1 and 2, despite the low number of epochs used. Future work can use techniques such as early stopping and $k$-fold cross-validation (Jung and Hu, 2015) to ensure that the ML model is sufficiently regularised. Moreover, the use of physics-informed neural networks (PINNs) can also be implemented by defining a custom loss function within the ANN. The use of PINNs in ANNs, as a means of buckling analysis, was explored by Tao et al. (2020), where an inequality constraint was used to ensure that the ANN predicts the buckling load of an axially compressed cylindrical shell to be lower than the experimental value. Therefore, through the enforcement of a corresponding inequality, the ANN model for the probing methodology should allow the predicted utilisation ratios to provide safe-sided predictions (Shen et al., 2023). This would inevitably lead to a more conservative estimate of the in situ utilisation ratios of the beam–columns when deployed in the industry, but any degree of conservatism could be controlled through a user-defined tolerance level.

5 Concluding remarks

The probing response of a perfect beam–column that is restrained against the effects of LTB was explored in the current work using the commercial FE software application Abaqus. Owing to a more complex response for probing a beam–column, when compared to a member under pure compression, it is shown that the probing stiffness $k_{\text{p}}$ provides sufficient data to predict $\widehat{P}$, but in isolation, it is insufficient for predicting $\widehat{M}$ since $k_{\text{p}}$ is essentially invariant with the applied moment. However, this is remedied by including a measurement of the initial deflection before probing, $w_{\text{ini}}$, which restores accuracy to the developed ANN. Subsequently, the developed ANN is demonstrated to predict $\widehat{M}$ and $\widehat{P}$ accurately when $k_{\text{p}}$ and $w_{\text{ini}}$ at different probing locations are used as inputs.

The present study also highlights a potential risk associated with the implementation of probing as a structural health assessment tool for beam–columns designed to fail with a plastic ultimate moment of resistance, $M_{\text{ult}}$. To mitigate the risk of damaging the member during the probing process, the member should be probed such that the local deflection is reduced, which would ensure that the probing response of the column remains linear. A further recommendation is that the probing procedure is not conducted within 5% of the elastic limit. Future research will elaborate on the current findings by exploring different scenarios, such as laterally unrestrained beams while also focussing on experimental studies to validate the current findings while ascertaining the practicality of in situ probing as a methodology for assessing structural health.

Data availability statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Author contributions

JM: data curation, formal analysis, investigation, validation, visualization, and writing–original draft. LL: conceptualization, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. MW: conceptualization, methodology, project administration, resources, supervision, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2016). Tensorflow: large-scale machine learning on heterogeneous distributed systems. CoRR abs/1603.04467

Google Scholar

Agarap, A. F. (2018). Deep learning using rectified linear units (relu). CoRR abs/1803.08375

Google Scholar

Alba-Rodríguez, M. D., Martínez-Rocamora, A., González-Vallejo, P., Ferreira-Sánchez, A., and Marrero, M. (2017). Building rehabilitation versus demolition and new construction: economic and environmental assessment. Environ. Impact Assess. Rev. 66, 115–126. doi:10.1016/j.eiar.2017.06.002

CrossRef Full Text | Google Scholar

Allen, H. G., and Bulson, P. S. (1980). Background to buckling. London, UK: McGraw-Hill.

Google Scholar

Amafabia, D. A., Montalvão, D., David-West, O., and Haritos, G. (2017). A review of structural health monitoring techniques as applied to composite structures. SDHM Struct. Durab. Health Monit. 11, 91–147. doi:10.3970/sdhm.2017.011.091

CrossRef Full Text | Google Scholar

Arrayago, I., Picci, F., Mirambell, E., and Real, E. (2015). Interaction of bending and axial load for ferritic stainless steel RHS columns. Thin-Walled Struct. 91, 96–107. doi:10.1016/j.tws.2015.02.012

CrossRef Full Text | Google Scholar

Askar, R., Bragança, L., and Gervásio, H. (2021). Adaptability of buildings: a critical review on the concept evolution. Appl. Sci. Switz. 11, 4483. doi:10.3390/app11104483

CrossRef Full Text | Google Scholar

Cavajdová, K., and Vican, J. (2023). Resistance of beam-column subjected to compression and bending. Transp. Res. Procedia 74, 983–990. doi:10.1016/j.trpro.2023.11.234

CrossRef Full Text | Google Scholar

Chen, C. C., Wu, W. H., Liu, C. Y., and Lai, G. (2016). Damage detection of a cable-stayed bridge based on the variation of stay cable forces eliminating environmental temperature effects. Smart Struct. Syst. 17, 859–880. doi:10.12989/SSS.2016.17.6.859

CrossRef Full Text | Google Scholar

Chollet, F. (2015). Keras. Available at: https://keras.io (Accessed June 3, 2024).

Google Scholar

Dassault Systèmes Simulia Corp (2021). ABAQUS/Standard version 2021. RI, USA: Providence.

Google Scholar

Doebling, S. W., Farrar, C. R., and Prime, M. B. (1998). A summary review of vibration-based damage identification methods. Shock Vib. Dig. 30, 91–105. doi:10.1177/058310249803000201

CrossRef Full Text | Google Scholar

dos Santos, G. B., Gardner, L., and Kucukler, M. (2018). A method for the numerical derivation of plastic collapse loads. Thin-Walled Struct. 124, 258–277. doi:10.1016/j.tws.2017.11.055

CrossRef Full Text | Google Scholar

EN (2014). 1993-1-1:2005+A1:2014 Eurocode 3 – design of steel structures – Part 1-1: general rules and rules for buildings. Brussels, Belgium: European Committee for Standardisation CEN.

Google Scholar

Fan, W., and Qiao, P. (2011). Vibration-based damage identification methods: a review and comparative study. Struct. Health Monit. 10, 83–111. doi:10.1177/1475921710365419

CrossRef Full Text | Google Scholar

Favarelli, E., Testi, E., and Giorgetti, A. (2021). Data management in structural health monitoring. Lect. Notes Civ. Eng. 156, 809–823. doi:10.1007/978-3-030-74258-4_51

CrossRef Full Text | Google Scholar

GeoPandas (2023). GeoPandas 0.13.2 — GeoPandas 0.13.2+0.gd5add48.dirty documentation.

Google Scholar

Gharehbaghi, V. R., Noroozinejad Farsangi, E., Noori, M., Yang, T. Y., Li, S., Nguyen, A., et al. (2022). A critical review on structural health monitoring: definitions, methods and perspectives. Archives Comput. Methods Eng. 29, 2209–2235. doi:10.1007/s11831-021-09665-9

CrossRef Full Text | Google Scholar

Hakim, S. J., Abdul Razak, H., Ravanfar, S. A., and Mohammadhassani, M. (2014). Structural damage detection using soft computing method. Conf. Proc. Soc. Exp. Mech. Ser. 5, 143–151. doi:10.1007/978-3-319-04570-2_16

CrossRef Full Text | Google Scholar

Hodson, T. O. (2022). Root-mean-square error (RMSE) or mean absolute error (MAE): when to use them or not. Geosci. Model Dev. 15, 5481–5487. doi:10.5194/gmd-15-5481-2022

CrossRef Full Text | Google Scholar

Jung, Y., and Hu, J. (2015). A K-fold averaging cross-validation procedure. J. Nonparametric Statistics 27, 167–179. doi:10.1080/10485252.2015.1010532

CrossRef Full Text | Google Scholar

Katam, R., Pasupuleti, V. D. K., and Kalapatapu, P. (2023). A review on structural health monitoring: past to present. Innov. Infrastruct. Solutions 8, 248–320. doi:10.1007/s41062-023-01217-3

CrossRef Full Text | Google Scholar

Kerkhof, M., Wu, L., Perin, G., and Picek, S. (2023). No (good) loss no gain: systematic evaluation of loss functions in deep learning-based side-channel analysis. J. Cryptogr. Eng. 13, 311–324. doi:10.1007/s13389-023-00320-6

CrossRef Full Text | Google Scholar

Kingma, D. P., and Ba, J. L. (2015). “Adam: a method for stochastic optimization,” in 3rd international conference on learning representations, ICLR 2015 - conference track proceedings, 1–15.

Google Scholar

Kitipornchai, S., and Trahair, N. S. (1980). Buckling properties of monosymmetric I-beams. ASCE J. Struct. Div. 106, 941–957. doi:10.1061/jsdeag.0005441

CrossRef Full Text | Google Scholar

Koh, B. H., and Dyke, S. J. (2007). Structural health monitoring for flexible bridge structures using correlation and sensitivity of modal data. Comput. and Struct. 85, 117–130. doi:10.1016/J.COMPSTRUC.2006.09.005

CrossRef Full Text | Google Scholar

Lapira, L., Wadee, M. A., and Gardner, L. (2017). Stability of multiple-crossarm prestressed stayed columns with additional stay systems. Structures 12, 227–241. doi:10.1016/J.ISTRUC.2017.09.010

CrossRef Full Text | Google Scholar

Larochelle, H., Bengio, Y., Louradour, J., and Lamblin, P. (2009). Exploring strategies for training deep neural networks. J. Mach. Learn. Res. 10, 1–40. doi:10.5555/1577069.1577070

CrossRef Full Text | Google Scholar

Liew, A., and Gardner, L. (2015). Ultimate capacity of structural steel cross-sections under compression, bending and combined loading. Structures 1, 2–11. doi:10.1016/j.istruc.2014.07.001

CrossRef Full Text | Google Scholar

Lindner, J. (1997). Design of steel beams and beam columns. Eng. Struct. 19, 378–384. doi:10.1016/S0141-0296(96)00095-8

CrossRef Full Text | Google Scholar

Liu, Y., and Nayak, S. (2012). Structural health monitoring: state of the art and perspectives. Jom 64, 789–792. doi:10.1007/s11837-012-0370-9

CrossRef Full Text | Google Scholar

Martínez, D., Obrien, E. J., and Sevillano, E. (2016). “Damage detection by drive-by monitoring using the vertical displacements of a bridge,” in Insights and innovations in structural engineering, mechanics and computation - proceedings of the 6th international conference on structural engineering (Boca Raton, USA: Mechanics and Computation), 1915–1918. SEMC 2016. doi:10.1201/9781315641645-316

CrossRef Full Text | Google Scholar

Montavon, G., Orr, G., and Müller, K. (2012). Neural networks: tricks of the trade. 2 edn. Berlin, Heidelberg: Springer. doi:10.1007/978-3-642-35289-8

CrossRef Full Text | Google Scholar

Publications Office of the European Union (2017). Resource efficient use of mixed wastes improving management of construction and demolition waste: final report. Tech. rep. Publ. Office Eur. Union. doi:10.2779/99903

CrossRef Full Text | Google Scholar

Riks, E. (1979). An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 15, 529–551. doi:10.1016/0020-7683(79)90081-7

CrossRef Full Text | Google Scholar

Ross, B. E., Chen, D. A., Conejos, S., and Khademi, A. (2016). Enabling adaptable buildings: results of a preliminary expert survey. Procedia Eng. 145, 420–427. doi:10.1016/j.proeng.2016.04.009

CrossRef Full Text | Google Scholar

Rytter, A. (1993). Vibration based inspection of civil engineering structures. Denmark: Aalborg University. Ph.D. thesis.

Google Scholar

Saito, D., and Wadee, M. A. (2008). Post-buckling behaviour of prestressed steel stayed columns. Eng. Struct. 30, 1224–1239. doi:10.1016/J.ENGSTRUCT.2007.07.012

CrossRef Full Text | Google Scholar

Shen, J., Lapira, L., Wadee, M. A., Gardner, L., Pirrera, A., and Groh, R. M. (2023). Probing in situ capacities of prestressed stayed columns: towards a novel structural health monitoring technique. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 381, 20220033. doi:10.1098/rsta.2022.0033

CrossRef Full Text | Google Scholar

Shokravi, H., Shokravi, H., Bakhary, N., Rahimian Koloor, S. S., and Petrů, M. (2020). Health monitoring of civil infrastructures by subspace system identification method: an overview. Appl. Sci. Switz. 10, 2786. doi:10.3390/APP10082786

CrossRef Full Text | Google Scholar

Slaughter, E. S. (2001). Design strategies to increase building flexibility. Build. Res. Inf. 29, 208–217. doi:10.1080/09613210010027693

CrossRef Full Text | Google Scholar

Sumitro, S., and Wang, M. L. (2005). Sustainable structural health monitoring system. Struct. Control Health Monit. 12, 445–467. doi:10.1002/STC.79

CrossRef Full Text | Google Scholar

Sung Lee, B., Phattharaphon, R., Yean, S., Liu, J., and Shakya, M. (2020). “Euclidean distance based loss function for eye-gaze estimation,” in IEEE Sensors Applications Symposium, SAS 2020 - Proceedings, Kuala Lumpur, Malaysia, 09-11 March 2020, 1–5. doi:10.1109/SAS48726.2020.9220051

CrossRef Full Text | Google Scholar

Tao, F., Liu, X., Du, H., and Yu, W. (2020). Physics-informed artificial neural network approach for axial compression buckling analysis of thin-walled cylinder. AIAA Scitech 2020 Forum 1 PartF, 1–18. doi:10.2514/6.2020-0398

CrossRef Full Text | Google Scholar

Thompson, J. M. T. (2015). Advances in shell buckling: theory and experiments. Int. J. Bifurcation Chaos 25, 1530001–1530025. doi:10.1142/S0218127415300013

CrossRef Full Text | Google Scholar

Thomson, D. J. (2013). The economic case for service life extension of structures using structural health monitoring based on the delayed cost of borrowing. J. Civ. Struct. Health Monit. 3, 335–340. doi:10.1007/s13349-013-0057-0

CrossRef Full Text | Google Scholar

Timoshenko, S. P., and Gere, J. M. (1963). Theory of elastic stability. New York, USA: McGraw-Hill.

Google Scholar

Trahair, N. S., Bradford, M. A., Nethercot, D. A., and Gardner, L. (2008). The behaviour and design of steel structures to EC3. Abingdon, UK: CRC Press.

Google Scholar

UNEP (2020). Towards a zero-emissions, efficient and resilient buildings and construction sector. Glob. Status Rep. Build. Constr. 2020, 9–10.

Google Scholar

Wu, B., Wu, G., Yang, C., and He, Y. (2018). Damage identification method for continuous girder bridges based on spatially-distributed long-gauge strain sensing under moving loads. Mech. Syst. Signal Process. 104, 415–435. doi:10.1016/J.YMSSP.2017.10.040

CrossRef Full Text | Google Scholar

Wu, K., Qiang, X., Xing, Z., and Jiang, X. (2022). Buckling in prestressed stayed beam–columns and intelligent evaluation. Eng. Struct. 255, 113902. doi:10.1016/j.engstruct.2022.113902

CrossRef Full Text | Google Scholar

Xing, Z., Wu, K., Su, A., Wang, Y., and Zhou, G. (2023). Intelligent local buckling design of stainless steel I-sections in fire via Artificial Neural Network. Structures 58, 105356. doi:10.1016/j.istruc.2023.105356

CrossRef Full Text | Google Scholar

Yun, X., and Gardner, L. (2017). Stress-strain curves for hot-rolled steels. J. Constr. Steel Res. 133, 36–46. doi:10.1016/j.jcsr.2017.01.024

CrossRef Full Text | Google Scholar