Predicting the impact of adding metakaolin on the flexural strength of concrete using ML classification techniques – a comparative study

The structural design standards, particularly in concrete technology, heavily rely on the mechanical attributes of concrete. Utilizing dependable predictive models for these properties can minimize the need for extensive laboratory testing, evaluations, and experiments to acquire essential design data, thereby conserving time and resources. Metakaolin (MK) is frequently incorporated as an alternative to Portland cement in the production of sustainable concrete, owing to its technical advantages and positive environmental impact, aligning with the United Nations Sustainable Development Goals (UNSDGs) aimed at achieving net-zero objectives. However, this research presents a comparative study between eight (8) ML classification techniques namely, gradient boosting (GB), CN2, naïve bayes (NB), support vector machine (SVM), stochastic gradient descent (SGD), k-nearest neighbor (KNN), Tree and random forest (RF) to estimate the impact of adding metakaolin to concrete on its flexural strength considering mixture components contents and concrete age. The collected data entries for the prediction of the flexural strength (Ft) containing the following concrete components; contentof cement (C), content of metakaolin (MK), content of water (W), content of fine aggregates (FAg), content of coarse aggregates (CAg), content of super-plasticizer (P), and the concrete curing age at testing (Age) were partitioned into 80% and 20% for training and validation sets respectively. At the end of the model protocol, it was found that the GB, SVM, and KNN models which produced an average MSE value of zero (0) showed their decisive ability to predict the flexural strength of the metakaolin (MK) mixed concrete (Ft). This outcome agrees with the previous reports in the literatures; however the work of Shah et al. happens to be the closest in terms of concrete components used in the production of the mixes and the application of machine learning techniques. It was found that the present research work’s models outperformed those presented by Shah et al. Hence the decisive models reported in this research paper show potentials to be applied in the design and production of MK concrete with optimal flexural strength.

1 Introduction

The flexural strength of concrete plays a crucial role in its structural performance, especially in applications where the concrete is subjected to bending or tensile stresses (Shah et al., 2022). In structural elements such as beams, slabs, and cantilevers, concrete is often subjected to bending moments (Koçak et al., 2020). The flexural strength of concrete determines its ability to resist these bending forces without failing (Mane et al., 2019). Higher flexural strength implies that the concrete can withstand greater bending moments before experiencing cracking or failure (Al-alaily and Hassan, 2016). Flexural strength is closely related to the ability of concrete to control cracking under bending loads (Yerramala et al., 2013). Concrete with higher flexural strength will exhibit greater resistance to cracking and can maintain structural integrity over time (Patil and Sangle, 2013). This is particularly important in applications where aesthetic considerations or serviceability requirements necessitate minimal cracking (Amin et al., 2023). The flexural strength of concrete directly affects the serviceability of structures by influencing factors such as deflection and deformation under load (El-Sayed et al., 2023). Concrete with higher flexural strength will experience less deflection and deformation, leading to improved serviceability and user comfort in buildings and other structures (Mohanram and Ramesh, 2022). In reinforced concrete structures, such as beams and slabs, the flexural strength of concrete governs the distribution of loads between the concrete and reinforcing steel (El-Sayed et al., 2023). Higher flexural strength allows for more efficient load transfer from the concrete to the reinforcement, resulting in a more balanced and robust structural system (Saini and Singh, 2020). Flexural strength is a critical parameter considered in the design of concrete structures to ensure adequate safety margins (Zhang et al., 2022). Design codes and standards specify minimum requirements for flexural strength based on factors such as structural loads, material properties, and desired levels of safety (Onyelowe et al., 2022a). Concrete with sufficient flexural strength helps meet these safety requirements and ensures structural stability under design conditions (Onyelowe et al., 2022b). The flexural strength of concrete is also linked to its durability performance (Onyelowe et al., 2022c). Concrete with higher flexural strength tends to have a denser microstructure and lower permeability, which can enhance resistance to environmental factors such as freeze-thaw cycles, chemical attack, and abrasion (Mane et al., 2019). This improved durability contributes to the long-term structural performance and service life of concrete elements (Onyelowe et al., 2022d). In summary, the flexural strength of concrete significantly influences its structural performance by governing bending resistance, crack control, serviceability, load distribution, safety factors, and durability (Onyelowe et al., 2022e). Designers and engineers carefully consider flexural strength requirements to ensure the safe and reliable performance of concrete structures throughout their service life (Onyelowe et al., 2023a). The addition of supplementary cementitious materials (SCMs) such as metakaolin, fly ash, slag, and silica fume to concrete offers numerous benefits, including improved strength and durability (Onyelowe et al., 2023b). SCMs react with calcium hydroxide and other byproducts of cement hydration to form additional hydration products, such as calcium silicate hydrate (C-S-H) gel (Onyelowe and Ebid, 2023). These results in denser and more compact concrete, leading to improved compressive strength, flexural strength, and durability (Akin et al., 2020). SCMs can mitigate the heat generated during concrete hydration, which is particularly beneficial in large pours or mass concrete applications (Qian and Li, 2001). By reducing the peak temperature and thermal gradients, the risk of thermal cracking is minimized, enhancing the long-term durability of the structure. Incorporating SCMs can improve the workability and pumpability of concrete mixes, allowing for easier placement and consolidation (Dinakar et al., 2013). This is especially advantageous in high-performance concrete applications or in situations where concrete needs to be pumped over long distances or to elevated locations. Many SCMs, such as fly ash and slag, are byproducts of industrial processes, which reduces the need for virgin materials and lowers the carbon footprint of concrete production (Poon et al., 2006). By replacing a portion of cement with SCMs, the overall environmental impact of concrete production can be reduced, contributing to sustainability goals. SCMs can enhance the chemical resistance of concrete by reducing permeability and increasing the density of the concrete matrix (Madandoust and Mousavi, 2012). This makes concrete more resistant to chemical attack from sulfates, chlorides, and other aggressive substances, resulting in longer service life and reduced maintenance requirements (El-Sayed et al., 2023). Certain SCMs, such as fly ash, can mitigate the risk of alkali-silica reaction, a chemical reaction that can cause expansion and cracking in concrete due to the presence of reactive aggregates and alkalis from cement (Onyelowe et al., 2022a; Onyelowe et al., 2022b; Onyelowe et al., 2022c; Onyelowe et al., 2022d). By incorporating SCMs, the availability of alkalis is reduced, helping to prevent ASR and preserve the integrity of the concrete (Onyelowe et al., 2022c). In addition to the technical advantages, the use of SCMs in concrete can offer economic benefits by potentially reducing material costs, improving construction efficiency, and extending the service life of structures, leading to lower life-cycle costs (Onyelowe et al., 2022e). Overall, the addition of supplementary cementitious materials like metakaolin, fly ash, slag, and silica fume in concrete can result in enhanced performance, increased sustainability, and cost savings, making them valuable components in modern concrete mixes (Ramezanianpour and Jovein, 2012).

Metakaolin is a pozzolanic material commonly used as a supplementary cementitious material in concrete (Shah et al., 2022). When added to concrete mixes, metakaolin can have several effects on the properties of the resulting concrete, including its flexural strength (Mane et al., 2019). Metakaolin can improve the flexural strength of concrete by enhancing the pozzolanic reaction (Al-alaily and Hassan, 2016). Pozzolanic materials like metakaolin react with calcium hydroxide (a byproduct of cement hydration) to form additional calcium silicate hydrate (C-S-H) gel, which fills in pores and voids in the concrete matrix, leading to increased strength (Madandoust and Mousavi, 2012). The addition of metakaolin can lead to a denser microstructure due to the pozzolanic reaction (Güneyisi et al., 2008). This densification can improve the interfacial transition zone (ITZ) between the cement paste and aggregates, resulting in better load transfer and enhanced flexural strength (Ahmad et al., 2022). Metakaolin incorporation can decrease the porosity of concrete by filling in the voids and capillary pores within the concrete matrix (Khatib, 2008). This reduction in porosity can increase the concrete’s resistance to cracking under flexural loading, thereby improving its flexural strength (Gill and Siddique, 2017). The denser microstructure and reduced porosity achieved with metakaolin can enhance the durability of concrete by reducing permeability to harmful substances such as chloride ions and sulfate ions (El-Din et al., 2017). This improved durability can indirectly contribute to maintaining higher flexural strength over the service life of the concrete (Rashad, 2013). The impact of metakaolin on flexural strength can vary depending on factors such as the dosage of metakaolin, the characteristics of other materials in the concrete mix, and curing conditions (Siddique and Kadri, 2011). Therefore, optimization of mix proportions is essential to maximize the benefits of metakaolin on flexural strength (Khatib, 2008). Overall, the addition of metakaolin to concrete mixes has the potential to enhance the flexural strength of concrete by improving its microstructure, reducing porosity, and enhancing durability (Onyelowe et al., 2022c). However, the specific impact will depend on various factors and should be evaluated through testing and optimization for each application.

Replacing a portion of cement with metakaolin in concrete production can offer several net-zero benefits in terms of sustainability (Rashad, 2013). Cement production is a significant source of carbon dioxide emissions due to the calcination of limestone and the energy-intensive nature of the process (Koçak et al., 2020). By partially replacing cement with metakaolin, which typically requires lower temperatures for production compared to cement, the overall carbon footprint of concrete production can be reduced, contributing to net-zero carbon emissions goals (Wang et al., 2014). Metakaolin is often produced as a by-product of industrial processes, such as the calcination of kaolin clay (Dinakar and Manu, 2014). By incorporating metakaolin into concrete mixes, it provides a beneficial use for this by-product material, reducing waste and promoting circular economy principles (Zhang et al., 2022). As discussed earlier, metakaolin can enhance the performance of concrete by improving strength, durability, and reducing permeability (Onyelowe et al., 2022a). This can lead to longer service life and reduced maintenance requirements for concrete structures, which align with sustainability goals by extending the lifespan of infrastructure (Onyelowe et al., 2022e). Cement production requires significant quantities of raw materials, including limestone and clay. By partially replacing cement with metakaolin, natural resources can be conserved, reducing the environmental impact associated with quarrying and extraction processes (Kavitha et al., 2015). The production of metakaolin typically requires lower energy consumption compared to cement production. By using metakaolin as a supplementary cementitious material, energy savings can be realized, contributing to overall energy efficiency and sustainability in concrete production (Muduli and Mukharjee, 2019). Cement production is associated with various environmental impacts beyond carbon emissions, including quarrying, habitat destruction, and water consumption (Wang et al., 2014). By reducing the demand for cement through the use of metakaolin, these environmental impacts can be mitigated, promoting more sustainable practices in the construction industry (Akin et al., 2020). Overall, replacing cement with metakaolin in concrete production offers net-zero benefits by reducing carbon emissions, utilizing industrial by-products, improving performance, conserving resources, saving energy, and mitigating environmental impacts (Patil and Sangle, 2013). This makes it a promising approach for achieving sustainability goals in the construction sector. In this research, the flexural strength of MK mixed concrete has been evaluated with a view to proposing multiple machine learning models to produce MK-based concrete with optimal strength and with the most impactful MK content.

2 Literature review

Shah et al. (2022) developed models for predicting the mechanical properties of concrete containing metakaolin (MK) utilizing four different machine learning techniques: gene expression programming (GEP), artificial neural network (ANN), M5P model tree algorithm, and random forest (RF). The study collected data from peer-reviewed documents and discovered that RF exhibits superior predictive and generalization capabilities compared to GEP, ANN, and M5P model tree method. The study additionally discovered that the optimal quantities of MK as a partial replacement for cement are 10% for flexural strength (FS) and 15% for both. Koçak et al. (2020) presented the application of Fuzzy Logic models for predicting the flexural strength of cement mortars. The models are developed using combinations of Portland-composite cement and metakaolin. The models employed fuzzy triangular number coefficients and Gauss membership function, with correlation values of 0.84 and 0.87, respectively. The results demonstrated a strong correlation between the experimental and fuzzy outcomes, making them well-suited for applications in civil engineering. The utilization of natural fine aggregate and cement in civil construction has resulted in ecological concerns. Industrial waste such as blast furnace slag, fly ash, metakaolin, and silica fume can serve as a partial substitute for cement. Additionally, fine aggregate can be obtained by using manufactured sand produced by a crusher. Mane et al. (2019) created neural network utilizing MATLAB software model to forecast the flexural strength of concrete produced with pozzolanic ingredients and partially substituted with synthetic sand. The model employed 131 outcomes, allocating 30% for testing purposes and 70% for training purposes. The results demonstrated a high level of precision in forecasting the flexural strength of concrete. Al-alaily and Hassan (2016) enhanced the strength and reduce the chloride permeability of concrete by using metakaolin. This study employed the increased response surface method (RSM) to examine 53 different concrete compositions. The elements taken into account were the overall amount of binder, the proportion of metakaolin, and the ratio of water to binder. The models and design charts were applicable to concrete with water-to-binder (W/B) ratios ranging from 0.3 to 0.5, metakaolin content ranging from 0% to 25%, and total binder content ranging from 350 kg/m3 to 600 kg/m3. The findings indicated that these models and charts can assist in forecasting and choosing the most favorable combination ratios for particular uses, especially for designers contemplating the use of MK in structural applications. Yerramala et al. (2013) assessed the flexural strength of metakaolin Ferro cements by comparing them to reference mortar and mortars containing 5%–25% metakaolin substitution. The mortars underwent a water-curing process for durations of 7, 28, 90, and 180 days. The results indicated that flexural strengths were consistently higher than the control Ferro cement at all curing ages and mesh layers when up to 15% metakaolin substitution was used. Nevertheless, substitutions that were equivalent to or greater than 20% exhibited reduced levels of strength. According to the study, a metakaolin concentration of 10% was determined to be the most effective for achieving the highest flexural strength. Also, Patil and Sangle (2013) examined the influence of mineral admixtures, specifically Metakaolinand Fly ash, on the compressive and flexural strengths as well as the durability of prestressed concrete beams. A total of 90 cube samples were subjected to testing, varying the proportions of MK and FA, in order to identify the optimal ratio that would yield the highest compressive strength. The findings indicated that the combination of 10% MK and FA yielded the most advantageous results for casting prestressed concrete flexural components. Subsequently, the optimal combination of ingredients was employed to evaluate the flexural strength of prestressed beam specimens. After a curing period of 28 days, the beams underwent testing on a universal testing equipment to evaluate the strains on the prestressed tendons. The results were compared with beams exhibiting different levels of strains for prestressed losses and flexural strength. Amin et al. (2023) investigated the comparative analysis of the compressive and flexural strength of concrete when various admixtures are utilized as partial substitutes for cement. The study employs industrial waste materials such as Silica Fume, Rice Husk Ash, and Iron Slag, which possess a significant amount of silica and exhibit pozzolanic characteristics. These materials have the ability to successfully substitute cement in High Performance Concrete, allowing for the evaluation of load bearing capacity for the purpose of design. The study offered significant information for identifying the most appropriate mineral admixture variety. Another, (El-Sayed et al., 2023) presented research conducted on the behaviour of reinforced GPC flexural members cured at ambient temperature. A total of twelve beams were subjected to two-point static loads, with several combinations of GGBS and Metakaolin in the binder phase being considered. The findings indicated that GPC beams exhibited somewhat greater load-bearing capability compared to typical OPC beams, along with increased deflections at various stages. The traditional RC theory is applicable to reinforced GPC flexural beams. Geopolymers are emerging as a viable substitute for conventional portland cement, primarily because of their superior energy efficiency and environmental safeguards. This study examines the mechanical characteristics and flexural performance of geopolymer-reinforced concrete beams including varying proportions of fly ash, GGBS, and MK. Mohanram and Ramesh (2022) revealed that the combination resulted in a significant enhancement in compressive, split tensile, and flexural strength, with increases of 147.75%, 57.21%, and 36.08%, respectively, as compared to the standard sample. The geopolymer reinforced concrete beam exhibited a significant increase in its ultimate load-carrying capacity, reaching up to a 30.43% enhancement. The study also discovered a strong correlation with the loads anticipated by theory, indicating that alternative cement-like materials could be employed to explore the mechanical characteristics of GPC. El-Sayed et al. (2023) examined the utilization of fly ash as a substitute for Ordinary Portland Cement (OPC) in the manufacturing of concrete, emphasizing its capacity to improve compressive strength and decrease porosity. The study examines the flexural characteristics of Geopolymer Concrete (GPC) beams in comparison to control cement concrete beams. The results demonstrated that using 25% GGBS enhances the flexural strength, service load, and peak load. Saini and Singh (2020) investigated the flexural fatigue strength of Self Compacting Concrete (SCC) using 50% Coarse Recycled Concrete Aggregates (RCA) and blended cements Silica Fume (SF) and Metakaolin. Data on the fatigue life of 224 beams subjected to four-point loading at different stress levels was collected. This work presented the notion of failure probability and produced S-N-Pf curves. The inclusion of recycled concrete aggregate (RCA) was seen to result in a reduction in both the theoretical fatigue life and endurance limit. Zhang et al. (2022) investigated the influence of metakaolin (MK) and magnesium oxide (MgO) on the bending strength of ultra-high performance concrete (UHPC). The study revealed that the flexural strength of UHPC exhibits an initial rise as the MM replacement ratios increase. Specifically, at 60 days, UHPC with a 10% MM replacement ratio demonstrated the maximum strength. MM enhances the creation of C-(A-)S–H and LDHs, whereas MgO raises pH levels and facilitates the release of Al. An excessive amount of mineral mixture (MM) leads to a higher level of clinker dilution, which in turn decreases the flexural strength of ultra-high-performance concrete (UHPC). The reviewed previous research works have presented different results from different machine learning techniques and different application of the concrete component materials, the closest to this research work being Shah et al. (2022), which had applied the ANN, GEP and the RF to predict the Ft of the MK mixed concrete. In the present research work, multiple machine learning techniques up to eight (8) have been reported, which allows a more robust application of the flexural strength prediction of different performance abilities especially the use closed-form equations.

3 Methodology of the research

3.1 Statistical appraisal of the collected database

A total of sixty-three (63) records were collected from literature (Shah et al., 2022) forflexural strength for different mixing ratios of metakaolin with concrete at different ages. Each record contains the following data:

• C The contentof cement (kg/m³)

• MK The content of metakaolin (kg/m³)

• W The content of water (kg/m³) or (L/m³)

• FAg The content of fine aggregates (kg/m³)

• CAg The content of coarse aggregates (kg/m³)

• P The content of super-plasticizer (kg/m³)

• Age The concrete age at testing (days)

• Ft Flexuralstrength (MPa)

The research framework is presented in Figure 1 for guidance, which fully shows the steps leading to the data gathering from literature study, data sorting, deployment of the data to be learned by machine methods and the performance analysis of the models towards the prediction of the flexural strength (Ft) of concrete mixed with metakaolin (MK).

Figure 1

Figure 1. Flowchart of research.

The collectedrecords were divided into training set (50 records≈80%) and validation set (13 records≈ 20%). Table 1 summarizes their statistical characteristics. Finally, Figure 2 shows the Pearson correlation matrix, histograms, and the relations between variables. This illustrates the internal consistency between the input variables and the output in both figurative and distribution charts. Concrete curing age (Age) showed the highest consistency with a 0.73 index with the output (Ft), which is followed by MK with a 0.33 index, while others showed very poor relationship.

Table 1

Table 1. Statistical analysis of collected database.

Figure 2

Figure 2. Correlation, Distribution and Interpreting chart.

3.2 Sensitivity analysis

A preliminary sensitivity analysis was carried out on the collected database to estimate the impact of each input on the (Y) values. “Single variable per time” technique is used to determine the “Sensitivity Index” (SI) for each input using Hoffman and Gardener’s formula (Hoffman et al., 1983) as shown in Equation 1.

$SI\left(X_n\right)=\frac{Y\left(X_{\mathit{max}}\right)-Y\left(X_{\mathit{min}}\right)}{Y\left(X_{\mathit{max}}\right)}(1)$

A sensitivity index of 1.0 indicates complete sensitivity, a sensitivity index less than 0.01 indicates that the model is insensitive to changes in the parameter. Figure 3 shows the sensitivity analysis with respect to Ft. The result has shown that cement (C) is the most influential parameter on the flexural strength of the MK mixed concrete, which is followed in order by the aggregates (CAg and FAg), plasticizer (P) and curing age (A). Meanwhile, MK is the least impactful on the behavior of the MK-concrete flexural strength. A 5% degree of influence produced by a supplementary cementitious material such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions.

Figure 3

Figure 3. Sensitivity analysis with respect to Ft.

3.3 Research program

Eight different MLclassification techniques were used to predict the flexural strength of concrete mixed with meta-kaolin using the collected database. These techniques are “Gradient Boosting (GB)”, “CN2 Rule Induction (CN2)”, “Naive Bayes (NB)”, “Support vector machine (SVM), “Stochastic Gradient Descent (SGD)”, “K-Nearest Neighbors (KNN)”, “Tree Decision (Tree)” and “Random Forest (RF)”. Thedeveloped models were used to predict (Ft) using the concrete mixture contents (C, MK, W, FAg, CAg, P) and the concrete age (Age). All the developed models were created using “Orange Data Mining” software version 3.36. The considered data flow diagram is shown in Figure 4.

Figure 4

Figure 4. The considered data flow in “Orange” software.

3.4 Theory of the learning techniques

Ensemble machine learning and symbolic regression are two different approaches to solving machine learning problems, each with its own principles and methodologies. Ensemble learning involves combining multiple individual models to improve predictive performance over any single model. The idea is that by aggregating the predictions of multiple models, the weaknesses of individual models can be mitigated, leading to better overall performance. Bagging (Bootstrap Aggregating) method involves training multiple instances of the same model on different subsets of the training data and combining their predictions, often reducing overfitting. Boosting algorithms build models sequentially, where each subsequent model focuses on the examples that the previous models have struggled with, effectively learning from their mistakes. Ensemble methods are widely used in practice and often achieve state-of-the-art performance in various machine learning tasks, including classification, regression, and clustering. Symbolic regression is a specific type of regression analysis that aims to find mathematical expressions or formulas that best describe the relationship between input variables and output targets. Instead of fitting a predefined model (like linear regression or polynomial regression), symbolic regression algorithms search for mathematical expressions within a predefined function set (such as addition, multiplication, exponentiation, trigonometric functions, etc.). Symbolic regression algorithms often use techniques like genetic programming (GP) or evolutionary algorithms to search the space of possible mathematical expressions iteratively, trying to find the expression that minimizes a chosen objective function (typically a measure of fit or error). Symbolic regression is particularly useful when the underlying relationship between variables is complex and cannot be adequately captured by traditional regression models, or when the goal is to discover interpretable mathematical relationships from data. In summary, while ensemble machine learning focuses on combining multiple models to improve predictive performance, symbolic regression aims to discover mathematical expressions that describe the relationships within the data. Both approaches have their strengths and are applicable in different contexts, depending on the nature of the problem and the desired outcomes. Gradient Boosting (GB) is a machine learning technique for regression and classification problems that builds an ensemble of weak prediction models, typically decision trees, sequentially. Each subsequent model corrects the errors made by the previous one. CN2 Rule Induction (CN2) isan algorithm used for rule-based classification, which iteratively constructs a set of rules to describe the data. It uses statistical significance tests and a covering algorithm to generate rules. Naive Bayes (NB) is a simple probabilistic classifier based on applying Bayes’ theorem with strong independence assumptions between the features. It's often used for text classification and other domains where feature independence assumptions are reasonable. Support Vector Machine (SVM) is a supervised learning algorithm used for classification and regression tasks. SVMs find the optimal hyperplane that separates classes in the feature space by maximizing the margin between the classes. Stochastic Gradient Descent (SGD) isan optimization algorithm used to train machine learning models, particularly in large-scale settings. It updates the model parameters iteratively using a subset of training data at each step. K-Nearest Neighbors (KNN) is a simple algorithm used for classification and regression tasks. KNN makes predictions by identifying the K closest training examples in the feature space and averaging their labels for regression or taking a majority vote for classification. Decision Tree (Tree) isa popular supervised learning algorithm used for classification and regression tasks. Decision trees recursively partition the feature space into regions, with each region corresponding to a prediction. Random Forest (RF) is an ensemble learning method that constructs a multitude of decision trees during training and outputs the mode or mean prediction of the individual trees for classification or regression tasks, respectively. Response Surface Methodology (RSM) is a statistical technique for modeling and optimizing processes. It involves designing experiments to understand the relationship between input variables and the output response of a system, typically using polynomial regression models. The working theoretical frameworks of these machine learning techniques are illustrated in Figure 5. Each of these algorithms and methodologies has its own strengths, weaknesses, and specific use cases. The choice of which one to use depends on factors such as the nature of the problem, the characteristics of the data, computational resources available, and the desired interpretability of the model.

Figure 5

Figure 5. The framework of the ensemble machine learning techniques .

3.5 Performance accuracy checks

Each of the accuracy check metrics provides different insights into the performance of a machine learning model, and the choice of which to use depends on the specific task and goals. For regression tasks, SSE, MAE, MSE, and RMSE are commonly used, while for classification tasks, accuracy is more appropriate. R² can be used in regression tasks to assess the goodness of fit of the model. It's often a good practice to evaluate models using multiple metrics to gain a comprehensive understanding of their performance. The accuracies of developed models were evaluated by comparing SSE, MAE, MSE, RMSE, Error %, Accuracy % and R² between predicted and calculated shear strength parameters values. The definition of each used measurement is presented in Equations 2–7. The results of all developed models are summarized in Table 2.

$MAE=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\left|y_i-\widehat{y}\right|(2)$

$MSE=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_i-\widehat{y}\right)}^2(3)$

$RMSE=\sqrt{MSE}(4)$

$Error\%=\frac{RMSE}{\widehat{y}}(5)$

$Accurcy\%=1-Error\%(6)$

$R^2=1-\frac{\sum {\left(y_i-\widehat{y}\right)}^2}{\sum {\left(y_i-\overline{y}\right)}^2}(7)$

Table 2

Table 2. Performance measurements of developed models for (Ft).

4 Results and discussion

4.1 GB model results

The developed (GB) model was based on (Scikit-learn) method with learning rate of 0.1 and minimum tensile subset of 2. Nine trials were conducted for each model started with two trees and two tree levels and increased gradually to four trees and four tree levels. The reduction of the prediction Error, % for each trail is presented in Figure 6. Accordingly, the models with four trees and four tree levels are considered the optimum ones. Performance metrics of the developed model for both training and validation dataset are listed in Table 2. The average achieved accuracy was 97%. The relations between calculated and predicted values are shown in Figure 7.It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions.

Figure 6

Figure 6. Reduction in Error % with increasing the number of trees and levels.

Figure 7

Figure 7. Relation between predicted and calculated strength using (GB).

4.2 CN2 model results

Similarly, five (CN2) models were developed considering “Laplace accuracy” as evaluation measurement with beam width of 1.0 and minimum rule coverage of 1.0. The maximum rule length was started by 1.0 and increased up to 9.0. Figure 8 shows the reduction in Error % with increasing the rule length. Accordingly, rule length of 7.0 is considered. The developed models contain 39 “IF condition” rules, Figure 9 presents some of these rules. Performance metrics of the developed model for both training and validation dataset are listed in Table 2. The average achieved accuracy was (91%). The relations between calculated and predicted values are shown in Figure 10.It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions.

Figure 8

Figure 8. Reduction in Error % with increasing the rule length.

Figure 9

Figure 9. Sample of the developed CN2 “If condition”.

Figure 10

Figure 10. Relation between predicted and calculated strength using (CN2).

4.3 NB model results

Traditional Naive Bayes classifier technique considering the concept of “Maximum likelihood” was used to develop the nine models. Although this type of classifier is highly scalable and are used in many applications, but it showed a very low performance as shown in Table 2. The relations between calculated and predicted values are shown in Figure 11. The achieved average accuracy was72%.It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions.

Figure 11

Figure 11. Relation between predicted and calculated strength using (NB).

4.4 SVM model results

The developed (SVM) model was based on “polynomial” kernel with cost value of 100, regression loss of 0.10 and numerical tolerance of 1.0. The kernel started with one-degree polynomial (linear) and increased up to three-degree polynomial (cubic). The reduction in the error % with increasing the polynomial degree is illustrated in Figure 12. Accordingly (cubic) kernel is considered. Performance metrics of the three developed models for both training and validation dataset are listed in Table 2. The average achieved accuracy was (98%). The relations between calculated and predicted values are shown in Figure 13. It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions. Therefore, the accuracy of 98% has been recorded with the 5% impact contribution from the addition of MK.

Figure 12

Figure 12. Reduction in Error % with increasing the polynomial degree.

Figure 13

Figure 13. Relation between predicted and calculated strength using (SVM).

4.5 SGD model results

These three models were developed considering modified Huber classification function and “Elastic net” re-generalization technique with mixing factor of 0.01 and strength factor of 0.001. The learning rate starts with 0.01, then gradually decreased to 0.001. The reduction in error% with reducing the learning rate is presented in Figure 14. Performance metrics of the three developed models for both training and validation dataset are listed in Table 2. The average achieved accuracy was (86%). The relations between calculated and predicted values are shown in Figure 15. It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions. Therefore, the 86% accuracy has been recorded under the impactful addition of MK in its model protocol.

Figure 14

Figure 14. Reduction in Error % with reducing the learning rate.

Figure 15

Figure 15. Relation between predicted and calculated strength using (SGD).

4.6 KNN model results

Considering number of neighbors of 1.0, Euclidian metric method and weights were evaluated by distances, the developed (KNN) models showed the best accuracy. (KNN) model showed the best performance where the average error% was (98%). The relations between calculated and predicted values are shown in Figure 16. It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions. Therefore, a 98% accuracy from the KNN model has been recorded considering the impact of MK as an important factor functioning as an SCM in sustainable concrete production.

Figure 16

Figure 16. Relation between predicted and calculated strength using (KNN).

4.7 Tree model results

These five models were developed considering minimum number of instants in leaves of 2.0 and minimum split subset of 5.0. The models began with only two tree levels and gradually increased to six levels. Figure 17 illustrates the reduction in Error % with increasing the number of layers. The layouts of the generated modelsare presented in Figure 18. Performance metrics of the last developed model for both training and validation dataset are listed in Table 2. The average achieved accuracy was (91%). The relations between calculated and predicted values are shown in Figure 19. It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions. An accuracy index of 91% produced by the Tree model has considered the 5% impact degree from the addition of the MK in the concrete production.

Figure 17

Figure 17. Reduction in Error % with increasing the No. of layers.

Figure 18

Figure 18. The layout of the developed (Tree).

Figure 19

Figure 19. Relation between predicted and calculated strength using (Tree).

4.8 RF model results

Finally, nine (RF) models were generated. The models began with only two trees and two levels and increased up to four trees and four levels. Figure 20 shows the reduction in Error % with increasing number of Tress and layers. Accordingly, the models with four trees and four layers are considered. The developed modelsare graphically presented using Pythagorean Forest in Figure 21. These arrangements leaded to a goodaverage accuracy of (88%). The relations between calculated and predicted values are shown in Figure 22. It is important to note that the impact of the addition of metakaolin (MK) has been considered in the model protocol. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions.

Figure 20

Figure 20. Reduction in Error % with increasing the No. of Tress and layers.

Figure 21

Figure 21. Pythagorean Forest diagram for the developed (RF) models.

Figure 22

Figure 22. Relation between predicted and calculated strength using (RF).

4.9 Summary discussion of the results

Overall, the eight (8) models have presented their strengths and weaknesses in their robust analysis of the collected database representing the behavior of the flexural strength of concrete mixed with metakaolin (MK). The developed (GB) model, which applied a learning rate of 0.1 and minimum tensile subset of 2 with nine (9) trials with the most reliable iteration of four trees and four tree levels produced a reduction of the prediction error. The GB produced fit line equations of 1.00x and 0.99x for the training and validation sets giving accuracies of 97% and 98%, respectively. From the five (CN2) modelsdeveloped with “Laplace accuracy” as the evaluation measurement with beam width of 1.0 and minimum rule coverage of 1.0, the model produced an average achieved accuracy of 91% from a representative line of fit relation of 0.97x and 0.97x, respectively. The Naive Bayes classifier technique which employed the “Maximum likelihood” hyperparameter showed a very low performance with achieved average accuracy of 72%from a representative line of fit relation of 1.09x and 1.16x, respectively. The SVM model which was based on “polynomial” kernel with cost value of 100, regression loss of 0.10 and numerical tolerance of 1.0 had its kernel start with one-degree polynomial (linear) and increased up to three-degree polynomial (cubic). The reduction in the error % with increasing the polynomial degree shows the advantage of the polynomial model over linear. The average achieved accuracy was 98%from a representative line of fit relation of 1.00x and 0.99x, respectively. The SGD models were developed considering modified Huber classification function and “Elastic net” re-generalization technique with mixing factor of 0.01 and strength factor of 0.001. The learning rate starts with 0.01, then gradually decreased to 0.001. The average achieved accuracy was (86%), from a representative line of fit relation of 0.95x and 0.90x, respectively. Considering number of neighbors of 1.0, Euclidian metric method and weights were evaluated by distances, the developed (KNN) models showed the best accuracy. (KNN) model showed the best performance where the average error% was (98%) from a representative line of fit relation of 1.00x and 0.99x, respectively. Thefive Tree models were developed considering minimum number of instants in leaves of 2.0 and minimum split subset of 5.0. The models began with only two tree levels and gradually increased to six levels. The reduction in Error % with increasing the number of layers shown by the models illustrates the models’ ability to apply the hyperparameters to enhance performance. Performance metrics of the last developed model for both training and validation dataset are listed in Tables 2. The average achieved accuracy was (91%) from a representative line of fit relation of 0.96x and 0.99x, respectively. Finally, from the RF application, the models began with only two trees and two levels and increased up to four trees and four levels. Accordingly, the models with four trees and four layers are considered. These arrangements led to a good average accuracy of 88%from a representative line of fit relation of 1.01x and 1.00x, respectively. Finally, the GB, SVM, and KNN models which produced an average MSE value of zero (0) showed their decisive ability to predict the flexural strength of the metakaolin (MK) mixed concrete (Ft). This outcome agrees with the previous reports in the literatures (Yerramala et al., 2013; Patil and Sangle, 2013; Rosa et al., 2024), however the work of Shah et al. (2022) happens to be the closest in terms of concrete components used in the production of the mixes and the application of machine learning techniques. It was found that the present research work’s models outperformed those presented by Shah et al. (2022). These previous works had suggested the use of 10% MK to achieve optimal Ft but these decisive models with their dependable accuracy have proposed models that allow the calibration of the optimal Ft considering other mix options to producing a more sustainable MK mixed concrete. Again, the machine learning performance in this work agrees with other reports (Rosa et al., 2024; Silva et al., 2024). Summarily, it is important to note that the impact of the addition of metakaolin (MK) has been considered in the above metaheuristic model protocols. As such, a 5% degree of influence produced by a supplementary cementitious material (SCM) such as metakaolin on the flexural behavior of concrete is of important consideration due to the concrete admixtures’ requirement allowed by design conditions. The summary of the models’ performance is presented in Table 2 and Figure 23.

Figure 23

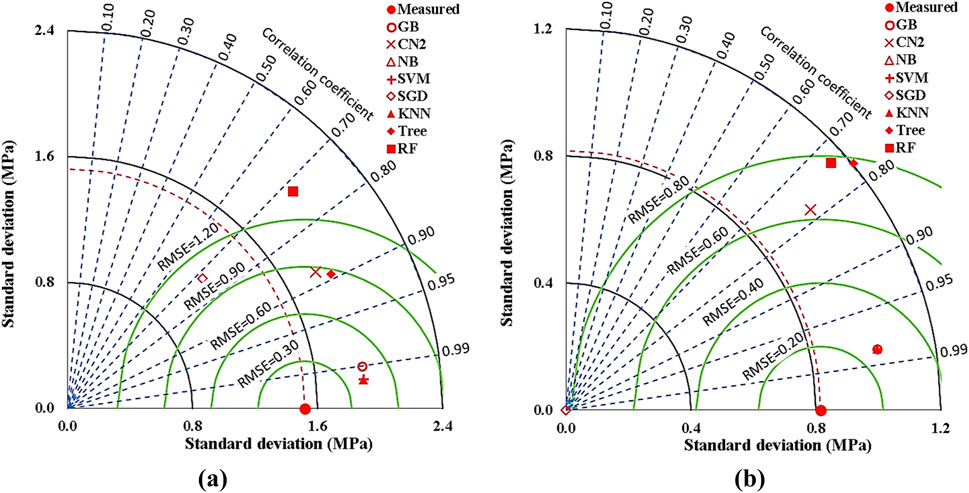
Figure 23. Comparing the accuracies of the developed models for (Ft) using Taylor charts, (A) Training dataset, (B) Validation dataset.

5 Conclusion

This research presents a comparative study between 8 ML classification techniques namely, GB, CN2, NB, SVM, SGD, KNN, Tree and RF to estimate theimpact of adding metakaolin to concrete on its tensile strength considering mixture components contents and concrete age. The outcomes of this study could be concluded as follows:

- GB, SVM, and KNN models showed an excellent accuracy of about 98%, while (CN2, Tree, RF) models showed very good accuracies of about 90% (SGD, NB) models showed fair accuracy level of about 72%–86%.

- Sensitivity analysis indicated that cement content (C) is the major impact on the tensile strength, followed by aggregate contents (CAg, FAg) and super-plasticizer (P), then concrete age, meta-kaolin and water contents (Age, MK, W). On the other hand, the correlation analysis showed that concrete age in the most important factor, then both cement and metakaolin (MK) contents, while the impact of other factors is neglected.

- The impact of MK on the flexural strength of concrete behavior showed a 5% degree of influence as cementing contribution from a supplementary cementitious material (SCM) within the required measurement allowed for its addition in concrete production.

- All the developed models are too complicated to be used manually, which may be considered as the main disadvantage of the ML classification techniques compared with other symbolic regression ML techniques such as (GP) and (EPR).

- The developed models are valid within the considered range of parameter values, beyond this range; the prediction accuracy should be verified.

6 Further/Action plan for the study

Future studies could expand on the original research in several directions. These studies can address limitations, explore new methodologies, and increase the practical applications of machine learning (ML) models in predicting the properties of metakaolin (MK) concrete. Potential areas for future research may include extending the scope of ML models to predict other critical properties of MK concrete beyond flexural strength. This may include investigating how ML models perform in predicting the compressive strength of MK concrete mixes. Also to predict the durability-related properties, such as resistance to chloride ion penetration, sulfate attack, carbonation, and freeze-thaw cycles. Use ML models to predict time-dependent properties like shrinkage and creep of MK concrete, which are crucial for long-term performance in structures. By expanding ML predictions to other concrete properties, future studies can develop comprehensive models to help engineers optimize MK concrete mixes for various applications. To investigate the combined effects of metakaolin and other SCMs on concrete properties using ML models is also an important consideration. SCMs are increasingly used for sustainability, cost savings, and enhanced performance in concrete. ML models can be trained to predict the synergy between MK and these materials for more optimized concrete mixes. Also to explore advanced ML techniques to improve the accuracy and interpretability of predictions such deep neural networks (DNN) or convolutional neural networks (CNN) and Explainable AI (XAI): such as LIME (Local Interpretable Model-agnostic Explanations) or SHAP (SHapley Additive exPlanations) to make predictions more understandable for engineers and practitioners. Future studies on this topic can explore a wide range of directions, from predicting other material properties and integrating advanced ML techniques to real-world validation and automation. By expanding the scope of ML applications and improving prediction accuracy, these studies will enhance the understanding of metakaolin’s role in concrete performance and make significant contributions to both material science and civil engineering practices.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LV: Data curation, Funding acquisition, Investigation, Methodology, Project administration, Software, Writing–review and editing. NV: Data curation, Funding acquisition, Investigation, Methodology, Project administration, Writing–review and editing. HS: Investigation, Methodology, Project administration, Resources, Writing–review and editing. FB: Investigation, Methodology, Project administration, Resources, Writing–review and editing. KO: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. SH: Investigation, Methodology, Project administration, Visualization, Writing–original draft. AE: Data curation, Methodology, Project administration, Resources, Software, Writing–original draft. TJ: Data curation, Investigation, Project administration, Resources, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmad, J., Majdi, A., Arbili, M. M., Deifalla, A. F., and Naqash, M. T. (2022). Mechanical, durability and microstructure analysis overview of concrete made with Metakaolin (MTK). Buildings 12 (9), 1401. doi:10.3390/buildings12091401

CrossRef Full Text | Google Scholar

Akin, O. O., Ocholi, A., Abejide, O. S., and Obari, J. A. (2020). Prediction of the compressive strength of concrete admixed with metakaolin using gene expression programming. Adv. Civ. Eng. 2020, 8883412. doi:10.1155/2020/8883412

CrossRef Full Text | Google Scholar

Al-alaily, H. S., and Hassan, A. A. A. (2016). Refined statistical modeling for chloride permeability and strength of concrete containing metakaolin. Constr. Build. Mater. 114, 564–579. doi:10.1016/j.conbuildmat.2016.03.187

CrossRef Full Text | Google Scholar

Amin, M. N., Ahmad, W., Khan, K., and Deifalla, A. F. (2023). Optimizing compressive strength prediction models for rice husk ash concrete with evolutionary machine intelligence techniques. Case Stud. Constr. Mater. 18, e02102. doi:10.1016/j.cscm.2023.e02102

CrossRef Full Text | Google Scholar

Dinakar, P., and Manu, S. (2014). Concrete mix design for high strength self-compacting concrete using metakaolin. Mater. Des. 60, 661–668. doi:10.1016/j.matdes.2014.03.053

CrossRef Full Text | Google Scholar

Dinakar, P., Sahoo, P. K., and Sriram, G. (2013). Effect of metakaolin content on the properties of high strength concrete. Int. J. Concr. Struct. Mater. 7, 215–223. doi:10.1007/s40069-013-0045-0

CrossRef Full Text | Google Scholar

El-Din, H. K. S., Eisa, A. S., Aziz, B. H. A., and Ibrahim, A. (2017). Mechanical performance of high strength concrete made from high volume of Metakaolin and hybrid fibers. Constr. Build. Mater. 140, 203–209. doi:10.1016/j.conbuildmat.2017.02.118

CrossRef Full Text | Google Scholar

El-Sayed, T. A., Deifalla, A. F., Shaheen, Y. B., Ahmed, H. H., and Youssef, A. K. (2023). Experimental and numerical studies on flexural behavior of GGBS-based geopolymer ferrocement beams. Civ. Eng. J. 9 (3), 629–653. doi:10.28991/CEJ-2023-09-03-010

CrossRef Full Text | Google Scholar

Gill, A. S., and Siddique, R. (2017). Strength and micro-structural properties of self-compacting concrete containing metakaolin and rice husk ash. Constr. Build. Mater. 157, 51–64. doi:10.1016/j.conbuildmat.2017.09.088

CrossRef Full Text | Google Scholar

Güneyisi, E., Gesoğlu, M., and Mermerdaş, K. (2008). Improving strength, drying shrinkage, and pore structure of concrete using metakaolin. Mater. Struct. 41, 937–949. doi:10.1617/s11527-007-9296-z

CrossRef Full Text | Google Scholar

Hoffman, F. O., and Gardner, R. H. (1983). “Evaluation of uncertainties in environmental radiological assessment models,” in Radiological assessments: a textbook on environmental dose assessment. Editors J. E. Till, and H. R. Meyer (Washington, DC: U.S. Nuclear Regulatory Commission). Report No. NUREG/CR-3332.

Google Scholar

Kavitha, O., Shanthi, V., Arulraj, G. P., and Sivakumar, P. (2015). Fresh, micro-and macrolevel studies of metakaolin blended self-compacting concrete. Appl. Clay Sci. 114, 370–374. doi:10.1016/j.clay.2015.06.024

CrossRef Full Text | Google Scholar

Khatib, J. (2008). Metakaolin concrete at a low water to binder ratio. Constr. Build. Mater. 22, 1691–1700. doi:10.1016/j.conbuildmat.2007.06.003

CrossRef Full Text | Google Scholar

Koçak, B., Koçak, Y., and Yücedağ, İ. (2020). Prediction of flexural strength of portland–composite cement mortars substituting metakaolin using fuzzy logic. Derg. 8, 2377–2387. doi:10.29130/dubited.798315

CrossRef Full Text | Google Scholar

Kumar, B. S. C., Ramesh, K., and Poluraju, P. (2017). An experimental investigation on flexural behavior of GGBS and metakaolin based geopolymer concrete. ARPN J. Eng. Appl. Sci. 12, 2052–2062.

Google Scholar

Madandoust, R., and Mousavi, S. Y. (2012). Fresh and hardened properties of self-compacting concrete containing metakaolin. Constr. Build. Mater. 35, 752–760. doi:10.1016/j.conbuildmat.2012.04.109

CrossRef Full Text | Google Scholar

Mane, K. M., Kulkarni, D. K., and Prakash, K. B. (2019). Prediction of flexural strength of concrete produced by using pozzolanic materials and partly replacing NFA by MS. J. Soft Comput. Civ. Eng. 3, 65–75. doi:10.22115/scce.2019.197000.1121

CrossRef Full Text | Google Scholar

Mohanram, B. B. K., and Ramesh, K. (2022). Effect of metakaolin on mechanical properties and flexural behavior of geopolymer-reinforced concrete beams. Pract. Period. Struct. Des. Constr. 27, 4022021. doi:10.1061/(ASCE)SC.1943-5576.0000695

CrossRef Full Text | Google Scholar

Muduli, R., and Mukharjee, B. B. (2019). Effect of incorporation of metakaolin and recycled coarse aggregate on properties of concrete. J. Clean. Prod. 209, 398–414. doi:10.1016/j.jclepro.2018.10.221

CrossRef Full Text | Google Scholar

Onyelowe, K. C., and Ebid, A. M. (2023). The influence of fly ash and blast furnace slag on the compressive strength of high-performance concrete (HPC) for sustainable structures. Asian J. Civ. Eng. 25, 861–882. doi:10.1007/s42107-023-00817-9

CrossRef Full Text | Google Scholar

Onyelowe, K. C., Ebid, A. M., and Ghadikolaee, M. R. (2023b). GRG-optimized response surface powered prediction of concrete mix design chart for the optimization of concrete compressive strength based on industrial waste precursor effect. Asian J. Civ. Eng. 25, 997–1006. doi:10.1007/s42107-023-00827-7

CrossRef Full Text | Google Scholar

Onyelowe, K. C., Ebid, A. M., Mahdi, H. A., Onyelowe, F. K. C., Shafieyoon, Y., Onyia, M. E., et al. (2023a). AI mix design of fly ash admixed concrete based on mechanical and environmental impact considerations. Civ. Eng. J. 9, 27–45. doi:10.28991/CEJ-SP2023-09-03

CrossRef Full Text | Google Scholar

Onyelowe, K. C., Ebid, A. M., Mahdi, H. A., Soleymani, A., Jahangir, H., and Dabbaghi, F. (2022d). Optimization of green concrete containing fly ash and rice husk ash based on hydro-mechanical properties and life cycle assessment considerations. Civ. Eng. J. 8 (12), 3912–3938. doi:10.28991/CEJ-2022-08-12-018

CrossRef Full Text | Google Scholar

Onyelowe, K. C., Ebid, A. M., Riofrio, A., Soleymani, A., Baykara, H., Kontoni, D.-P. N., et al. (2022c). Global warming potential-based life cycle assessment and optimization of the compressive strength of fly ash-silica fume concrete; environmental impact consideration. Front. Built Environ. 8, 992552. doi:10.3389/fbuil.2022.992552

CrossRef Full Text | Google Scholar

Onyelowe, K. C., Gnananandarao, T., Ebid, A. M., Mahdi, H. A., Razzaghian-Ghadikolaee, M., and Al-Ajamee, M. (2022b). Evaluating the compressive strength of recycled aggregate concrete using novel artificial neural network. Civ. Eng. J. 8 (8), 1679–1693. doi:10.28991/CEJ-2022-08-08-011

CrossRef Full Text | Google Scholar

Onyelowe, K. C., Gnananandarao, T., Jagan, J., Ahmad, J., and &Ebid, A. M. (2022e). Innovative predictive model for flexural strength of recycled aggregate concrete from multiple datasets. Asian J. Civ. Eng. 24, 1143–1152. doi:10.1007/s42107-022-00558-1

CrossRef Full Text | Google Scholar

Onyelowe, K. C., Kontoni, D.-P. N., Ebid, A. M., Dabbaghi, F., Soleymani, A., Jahangir, H., et al. (2022a). Multi-objective optimization of sustainable concrete containing fly ash based on environmental and MechanicalConsiderations. Buildings 12, 948. doi:10.3390/buildings12070948

CrossRef Full Text | Google Scholar

Patil, S. P., and Sangle, K. K. (2013). Flexural strength evaluation of prestressed concrete beams with partial replacement of cement by Metakaolin and Flyash. Am. Int. J. Res. Sci. Technol. Eng. Math. 3, 187–194.

Google Scholar

Poon, C.-S., Kou, S., and Lam, L. (2006). Compressive strength, chloride diffusivity and pore structure of high performance metakaolin and silica fume concrete. Constr. Build. Mater. 20, 858–865. doi:10.1016/j.conbuildmat.2005.07.001

CrossRef Full Text | Google Scholar

Qian, X., and Li, Z. (2001). The relationships between stress and strain for high-performance concrete with metakaolin. Cem. Concr. Res. 31, 1607–1611. doi:10.1016/s0008-8846(01)00612-3

CrossRef Full Text | Google Scholar

Ramezanianpour, A., and Jovein, H. B. (2012). Influence of metakaolin as supplementary cementing material on strength and durability of concretes. Constr. Build. Mater. 30, 470–479. doi:10.1016/j.conbuildmat.2011.12.050

CrossRef Full Text | Google Scholar

Rashad, A. M. (2013). A preliminary study on the effect of fine aggregate replacement with metakaolin on strength and abrasion resistance of concrete. Constr. Build. Mater. 44, 487–495. doi:10.1016/j.conbuildmat.2013.03.038

CrossRef Full Text | Google Scholar

Rosa, A. C., Elomari, Y., Calderón, A., Mateu, C., Haddad, A., and Boer, D. (2024). Methodology for the prediction of the thermal conductivity of concrete by using neural networks. Appl. Sci. 14, 7598. doi:10.3390/app14177598

CrossRef Full Text | Google Scholar

Saini, B. S., and Singh, S. P. (2020). Flexural fatigue strength prediction of self compacting concrete made with recycled concrete aggregates and blended cements. Constr. Build. Mater. 264, 120233. doi:10.1016/j.conbuildmat.2020.120233

CrossRef Full Text | Google Scholar

Shah, H. A., Yuan, Q., Akmal, U., Shah, S. A., Salmi, A., Awad, Y. A., et al. (2022). Application of machine learning techniques for predicting compressive, splitting tensile, and flexural strengths of concrete with metakaolin. Mater. (Basel) 15, 5435. doi:10.3390/ma15155435

CrossRef Full Text | Google Scholar

Siddique, R., and Kadri, E.-H. (2011). Effect of metakaolin and foundry sand on the near surface characteristics of concrete. Constr. Build. Mater. 25, 3257–3266. doi:10.1016/j.conbuildmat.2011.03.012

CrossRef Full Text | Google Scholar

Silva, L. S., Najjar, M. K., Stolz, C. M., Haddad, A. N., Amario, M., and Boer, D. T. (2024). Multiple dimensions of energy efficiency of recycled concrete: a systematic review. Energies 17, 3809. doi:10.3390/en17153809

CrossRef Full Text | Google Scholar

Wang, G., Kong, Y., Shui, Z., Li, Q., and Han, J. (2014). Experimental investigation on chloride diffusion and binding in concrete containing metakaolin. Corros. Eng. Sci. Technol. 49, 282–286. doi:10.1179/1743278213y.0000000134

CrossRef Full Text | Google Scholar

Yerramala, A., Ramachandurdu, C., and Bhaskar Desai, V. (2013). Flexural strength of metakaolin ferrocement. Compos. Part B Eng. 55, 176–183. doi:10.1016/j.compositesb.2013.06.029

CrossRef Full Text | Google Scholar

Zhang, B., Ji, T., Ma, Y., and Zhang, Q. (2022). Effect of metakaolin and magnesium oxide on flexural strength of ultra-high performance concrete. Cem. Concr. Compos. 131, 104582. doi:10.1016/j.cemconcomp.2022.104582

CrossRef Full Text | Google Scholar