
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Bioeng. Biotechnol. , 22 July 2022
Sec. Industrial Biotechnology
Volume 10 - 2022 | https://doi.org/10.3389/fbioe.2022.957694
This article is part of the Research Topic Biocatalysis and Biotransformation Guided by Protein Engineering View all 12 articles
Laccases are regarded as versatile green biocatalysts, and recent scientific research has focused on improving their redox potential for broader industrial and environmental applications. The density functional theory (DFT) quantum mechanics approach, sufficiently rigorous and efficient for the calculation of electronic structures, is conducted to better comprehend the connection between the redox potential and the atomic structural feature of laccases. According to the crystal structure of wild type laccase CueO and its variant, a truncated miniature cluster model method was established in this research. On the basic of thermodynamic cycle, the overall Gibbs free energy variations before and after the one-electron reduction were calculated. It turned out that the trends of redox potentials to increase after variant predicted by the theoretical calculations correlated well with those obtained by experiments, thereby validating the feasibility of this cluster model method for simulating the redox potentials of laccases.
Laccases (EC 1.10.3.2) are oxidoreductases with cupredoxin-like domains that can catalyze various substrates oxidized and simultaneously reduce oxygen to water (Madhavi and Lele, 2009; Janusz et al., 2020; Shiroya, 2021). Laccases contain at least four copper atoms comprising one type 1 copper (T1 Cu) serving as the electron entry position to the protein, and one type 2 copper (T2 Cu) and two type 3 coppers (T3 Cu) that compose a trinuclear cluster (TNC) (Sakurai and Kataoka, 2007; Solomon et al., 2008; Liu et al., 2014; Giacobelli, 2017). Given the apparent stability and eco-friendliness of laccases, scientific efforts have been diverted these days to exploit such enzymes in emerging fields such as enzymatic biofuel cells and the degradation of noxious contaminants (Bilal et al., 2019; Li et al., 2020; Moreno et al., 2020). The redox potentials of laccases generally range from 0.43 to 0.79 V versus the normal hydrogen electrode (NHE) (Mateljak et al., 2019). Through directed evolution of laccases, the redox potential value is expected to be improved to fulfill the requirement for many biotechnological and environmental applications.
The copper efflux oxidase (CueO) has conspicuously superior stability in high temperature or alkaline environment when compared to other bacterial laccases. Nevertheless, its relatively low redox potential is detrimental to catalytic activity from a thermodynamic perspective (Santhanam et al., 2011; Martins et al., 2015; Chauhan et al., 2017). Two beneficial substitutions D439T and L502K were found to improve the onset potential up to 0.42 and 0.44 V, respectively (Zhang et al., 2019). The crystal structure of CueO revealed that D439 and L502 form hydrogen bonds with coordinated residues of T1 Cu, H443 and C500, respectively. The redox potential of CueO is mostly governed by the T1 Cu site (Hong et al., 2011; Vázquez-Lima et al., 2012). Computational simulation of the redox potential variation influenced by single-site variants adjoining the T1 Cu site is one interesting avenue of investigation.
Selecting appropriate methods and developing a computational scheme for catalytic processes associated with redox-active metalloenzymes is a challenging task. With the rapid development of computing science, numerous multiscale modeling approaches for enzymes have been adopted, including molecular dynamics (MD), free energy perturbation (FEP), empirical valence bond (EVB), hybrid quantum mechanics/molecular mechanics (QM/MM), and the quantum mechanics (QM) cluster approach (Ahmadi et al., 2018; Sheng et al., 2020). Supposing that the selected QM region is reasonable, the same consequences will be given by QM cluster and QM/MM approaches essentially (Siegbahn, 2006; Liao and Thiel, 2012). The cluster approach is the simple and efficient method for elucidating mechanisms of redox-active metalloenzymes, dealing with the crucial active site region of the metalloenzymes in a QM manner, proved fruitful in reproducing high-precision energy calculations. Lately, Mina Ghiasi et al. (2021) carried out a DFT research on the activation mechanism of the human carbonic anhydrase VII cluster model and demonstrated that the activator molecule participates in proton transfer reactions, enhancing the formation of the active zinc hydroxide species.
In this work, we developed a T1 Cu site active center cluster model protocol for calculating the redox potentials of WT CueO and its variant L502K. The dynamics simulations were carried out, and according to the obtained equilibrium structures, the target cluster model structures were designed, whose oxidized and reduced states were geometrically optimized separately in the solvated environment at the B3LYP-D3(BJ)/6-311G* level. Their vapor phase and solvation Gibbs free energies were calculated at the M062X/def2TZVP and M06X/6-311G* level, respectively, to achieve the redox potentials. Several different DFT and solvation approaches were attempted during the simulation to achieve more accurate results.
The QM cluster model approach, which uses finite models to investigate the active sites of metalloenzymes, is an important tool to elucidate enzymatic reaction mechanisms. Many aspects of the metalloenzyme mechanisms have been understood, employing a relatively small model (Blomberg et al., 2014).
Density functional theory (DFT), a currently used QM atomistic simulation method, can be utilized to describe the electronic structure of the enzyme cluster model system (Himo, 2017). The hybrid functional B3LYP has dominated in the geometric optimization applications, accounting for its simple form, low dependence on the integration lattice point, fast calculation speed, and moderate accuracy. Nonetheless, the B3LYP functional is not suitable for describing weak interactions caused by dispersion (Grimme et al., 2016). In this respect, the recent developed technique, adding an empirical dispersion correction, known as DFT-D, has been shown to dramatically improve the energies in the field of homogeneous catalysis (Witte et al., 2015). When it comes to energy calculations, the M06 functional appears to offer better performance in predicting the overall trends of relative energies than the B3LYP functional (Walker et al., 2013).
Since the cluster approach contains only an enzyme fraction, namely, the active site and its surroundings, when the structures are designed, environment influences need to be taken into account. This environment impact is usually simulated by two simple approximations: steric hindrance and static electricity. To prevent the overall structure of the model from unraveling during optimization, some atoms at the model boundary are fixed. The electrostatic effect of solvent contribution is approximated by the implicit solvation model. The implicit solvation model treats the solvent as a dielectric continuum, in which different solvation environment can be represented by regulating permittivity ε. Furthermore, it should be noted that as the model size increases, the approximation improves. With these two approximations, a cluster model suitable for the T1 Cu site active center of WT CueO and its variant can be constructed.
The theoretical estimate for the concerned potential of the redox reaction (
where
where
The crystal structure of CueO resolved at an atomic resolution of 1.1 Å (PDB code: 3OD3) was used as a starting point of MD simulations (Singh et al., 2011). The structure of the L502K variant was generated using the WT CueO structure as a template by YASARA software version 17.8.15 (Krieger and Vriend, 2014). Molecular dynamics (MD) simulation and analysis were performed with NAMD software version 2.14 (Phillips et al., 2020). Protonation statuses of residues were determined by the H++ online program and checked manually (Anandakrishnan et al., 2012). A cubic box with a protein-to-border distance of 10 Å was established and filled with TIP3P water molecules. The systems were minimized and equilibrated for 20 ns with the T1 Cu site kept fixed. Root mean square deviation (RMSD) was calculated by VMD package tools (Phillips et al., 2020).
The quantum chemical calculations for optimization and vibration analysis of the system were performed at the B3LYP-D3(BJ)/6-311G* level of theory combined with the SMD solvent model. The total charge of oxidized and reduced was 1 and 0, respectively, because the amino acid ligands are neutral, while the SG atom in C500 is coordinated with copper ions, leading to the HG atom originally attached to the SG atom deprotonated. The spin multiplicity of oxidized and reduced was 2 and 1, respectively. More precise electron energies in vacuum were calculated at the M062X/def2TZVP level dependent on the optimized structures. Simultaneously, the M062X/6-311G* level was selected for calculating the solvation free energy difference. All quantum mechanical calculations were carried out using the Gaussian 16 program package (Frisch et al., 2016).
Molecular dynamic simulations testing on both structures (WT CueO L502K variant) showed good results in Figure 1. The backbone RMSD of the equilibrated structures relative to the original structures range from 0.63 to 2.38 Å and 0.69 to 2.46 Å for WT CueO and the L502K variant, respectively.
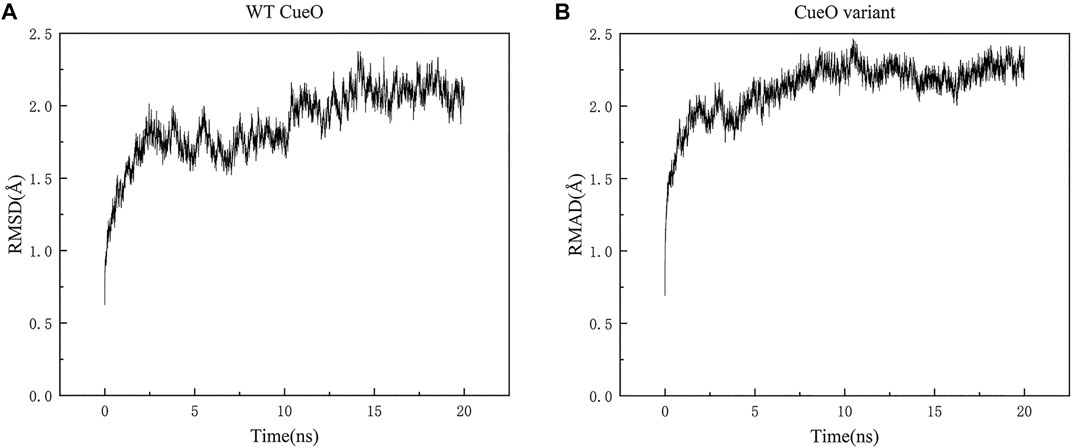
FIGURE 1. Backbone RMSD for (A) WT CueO and (B) the L502K variant during 20 ns course of the MD simulations.
The cluster models for QM research studies were constructed with the residues involved in the biocatalysis active site. The copper ion (Cu2+ or Cu1+) in the core and its ligands (H443, C500, and H505) and L502 for the WT or K502 for the variant, as well as the hydrophobic residues M510, were considered in the enzyme cluster model as shown in Figure 2. After a consolidating procedure in the cluster model, the α carbon atoms of all residues were fixed in their positions at molecular dynamic equilibrium dependent on the crystal structure during the geometry optimization for the sake of avoiding cluster model discretization inconsistent with actuality.
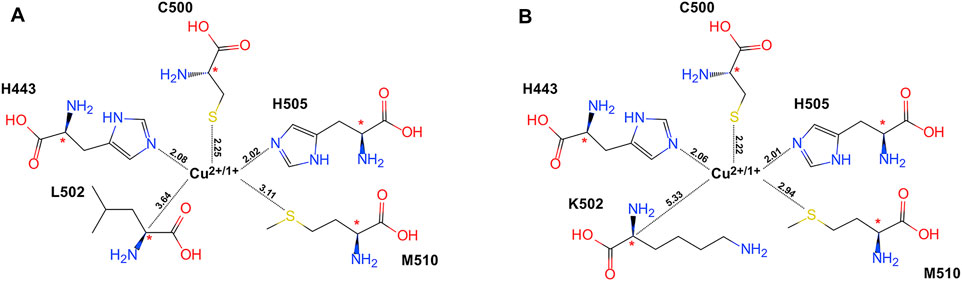
FIGURE 2. Schematic illustration of the cluster model system based on equilibrated crystallographic data collected by molecular dynamic simulation, with key atoms labeled. The stars indicate the atoms that were frozen during the optimization procedure. (A) WT CueO and (B) the L502K variant. The key distances between cupper atom and amino acids were drawn with dotted lines, and the values were labeled (the unit is Å).
The optimized structures of the WT CueO and its variant cluster models are displayed in Figure 3. Owing to the conserved cupredoxin-like domain, the changes of bond distances between copper ion and coordination atom were small (less than 0.1 Å), and it was speculated that the changes of electron density around the T1 Cu site stemmed from capturing an electron majorly affected redox potentials.
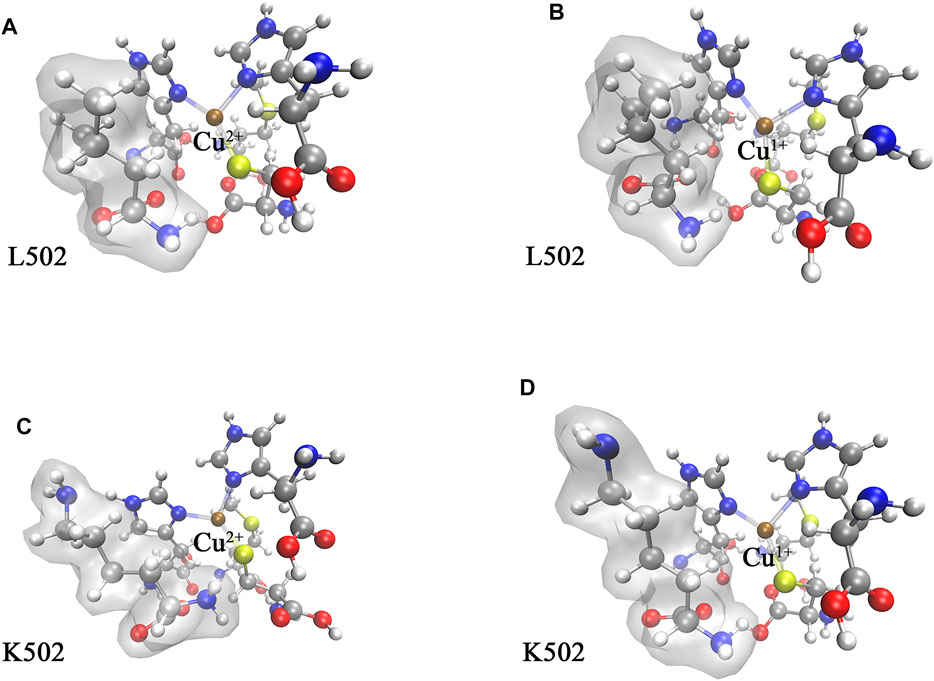
FIGURE 3. The optimized structure of CueO T1 Cu active site cluster models in the water phase: (A) WT in the oxidation state, (B) WT in the reduction state, (C) L502K variant in the oxidation state, and (D) L502K in the reduction state. The colors correspond to atoms: brown for copper, yellow for sulfur, red for oxygen, blue for nitrogen, dark gray for carbon, and light gray for hydrogen. The amino acid residue 502 was highlighted by adding a transparent molecular surface.
Table 1 summarizes the crucial energies involved calculating the redox potential. The gas phase Gibbs free energy changes of the redox processes were calculated using the Shermo software (Lu and Chen, 2021). The gas phase free energy difference of WT and variant is −132.35 and −118.69 kcal/mol, respectively. In solution, according to the electric field intensity near the copper complexes, the copper complexes were solvated, thus exhibiting different solvation free energies. The final results showed that the Gibbs free energy variation of variant gaining one electronic is 22.92 kcal/mol higher than WT.
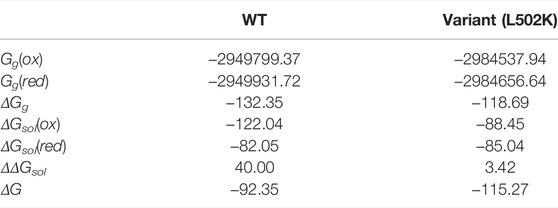
TABLE 1. DFT-calculated energetics for the WT CueO and L502K active sites and for the redox reactions (the unit is kcal/mol).
To obtain theoretical values that could be compared with experimental values, the computed
When compared to earlier results, this DFT research estimated redox potentials qualitatively match with the experiment. It has previously been presented that the redox potential values of copper-containing oxidases depend on the T1 Cu pocket (Kojima et al., 1990). Depending on the structure of the native high potential laccase (T. versicolor), Klaus Piontek et al. (2002) proposed a mechanism that assumes a decrease in electron density contribution at the metal cation through a stretching of the bond between the metal and the ligating amino acid. This mechanism could possibly explain why redox potential increased after the L502K variant. Furthermore, variant-induced structural perturbations on the electron transfer pathway were interpreted as an additional structural determinant (Xu et al., 1998).
In the present work, we investigated the feasibility of cluster models to calculate the redox potential of WT laccase CueO and its variant L502K based on the Gibbs free energy. The redox potential of WT CueO was 0.79 V lower than the experimental values, while the redox potential of L502K was 0.12 V higher than the experimental values. Although the cluster method is not sufficiently accurate for determining absolute redox potentials, the trend of variant-induced redox potential changes is consistent with experimental data. Gibbs free energy variation is a function of state; from the perspective of the structures, the structural changes caused by the variant eventually led to a change in the Gibbs free energy, which led to changes in the redox potential.
Due to the atomic range limitation of the quantitative calculation, the variant sites slightly far from the active site cannot be predicted using the cluster model. With the development of computational methods, the cluster model or the QM/MM method will be able to investigate a broader range of simulations in the future, yielding more accurate results.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: http://www.wwpdb.org/, 3OD3.
Conceptualization, LL and HX; methodology, QJ; formal analysis, ZC; writing—original draft preparation, LL and QJ; writing—review and editing, RW and KN; supervision, LL and HX; and funding acquisition, LL and HX. All authors have read and agreed to the published version of the manuscript.
This study was funded by the National Key Research and Development Program of China (grant number 22021YFC2101004). This study was funded by the National Natural Science Foundation of China (grant numbers 31961133017, 52073022, and 21978017). These grants are part of the MIX-UP project that received funding within the framework of a joint NSFC and EU H2020 collaboration. In Europe, MIX-UP has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 870294.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ahmadi, S., Barrios Herrera, L., Chehelamirani, M., Hostaš, J., Jalife, S., and Salahub, D. R. (2018). Multiscale Modeling of Enzymes: QM-Cluster, QM/MM, and QM/MM/MD: A Tutorial Review. Int. J. Quantum Chem. 118 (9), e25558. doi:10.1002/qua.25558
Anandakrishnan, R., Aguilar, B., and Onufriev, A. V. (2012). H++ 3.0: Automating pK Prediction and the Preparation of Biomolecular Structures for Atomistic Molecular Modeling and Simulations. Nucleic Acids Res. 40 (W1), W537–W541. doi:10.1093/nar/gks375
Bilal, M., Rasheed, T., Nabeel, F., Iqbal, H. M. N., and Zhao, Y. (2019). Hazardous Contaminants in the Environment and Their Laccase-Assisted Degradation - A Review. J. Environ. Manag. 234, 253–264. doi:10.1016/j.jenvman.2019.01.001
Blomberg, M. R. A., Borowski, T., Himo, F., Liao, R.-Z., and Siegbahn, P. E. M. (2014). Quantum Chemical Studies of Mechanisms for Metalloenzymes. Chem. Rev. 114 (7), 3601–3658. doi:10.1021/cr400388t
Bruschi, M., Breglia, R., Arrigoni, F., Fantucci, P., and De Gioia, L. (2016). Computational Approaches to the Prediction of the Redox Potentials of Iron and Copper Bioinorganic Systems. Int. J. Quantum Chem. 116 (22), 1695–1705. doi:10.1002/qua.25228
Chauhan, P. S., Goradia, B., and Saxena, A. (2017). Bacterial Laccase: Recent Update on Production, Properties and Industrial Applications. 3 Biotech 7 (5), 323–420. doi:10.1007/s13205-017-0955-7
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16 Rev. C.01. Wallingford, CT: Gaussian, Inc.
Ghiasi, M., Shahabi, P., and Supuran, C. T. (2021). Quantum Mechanical Study on the Activation Mechanism of Human Carbonic Anhydrase VII Cluster Model with Bis-Histamine Schiff Bases and Bis-Spinaceamine Derivatives. Bioorg. Med. Chem. 44, 116276. doi:10.1016/j.bmc.2021.116276
Giacobelli, V. G. (2017). Wild-Type and Mutated Laccases for a Green Industry. Campania: Fedoa.unina.it.
Grimme, S., Hansen, A., Brandenburg, J. G., and Bannwarth, C. (2016). Dispersion-corrected Mean-Field Electronic Structure Methods. Chem. Rev. 116 (9), 5105–5154. doi:10.1021/acs.chemrev.5b00533
Himo, F. (2017). Recent Trends in Quantum Chemical Modeling of Enzymatic Reactions. J. Am. Chem. Soc. 139 (20), 6780–6786. doi:10.1021/jacs.7b02671
Holland, J. P., Green, J. C., and Dilworth, J. R. (2006). Probing the Mechanism of Hypoxia Selectivity of Copper Bis(thiosemicarbazonato) Complexes: DFT Calculation of Redox Potentials and Absolute Acidities in Solution. Dalton Trans. 4 (6), 783–794. doi:10.1039/b512656h
Hong, G., Ivnitski, D. M., Johnson, G. R., Atanassov, P., and Pachter, R. (2011). Design Parameters for Tuning the Type 1 Cu Multicopper Oxidase Redox Potential: Insight from a Combination of First Principles and Empirical Molecular Dynamics Simulations. J. Am. Chem. Soc. 133 (13), 4802–4809. doi:10.1021/ja105586q
Isse, A. A., and Gennaro, A. (2010). Absolute Potential of the Standard Hydrogen Electrode and the Problem of Interconversion of Potentials in Different Solvents. J. Phys. Chem. B 114 (23), 7894–7899. doi:10.1021/jp100402x
Janusz, G., Pawlik, A., Świderska-Burek, U., Polak, J., Sulej, J., Jarosz-Wilkołazka, A., et al. (2020). Laccase Properties, Physiological Functions, and Evolution. Int. J. Mol. Sci. 21 (3), 966. doi:10.3390/ijms21030966
Kojima, Y., Tsukuda, Y., Kawai, Y., Tsukamoto, A., Sugiura, J., Sakaino, M., et al. (1990). Cloning, Sequence Analysis, and Expression of Ligninolytic Phenoloxidase Genes of the White-Rot Basidiomycete Coriolus Hirsutus. J. Biol. Chem. 265 (25), 15224–15230. doi:10.1016/s0021-9258(18)77245-1
Krieger, E., and Vriend, G. (2014). YASARA View-Molecular Graphics for All Devices-From Smartphones to Workstations. Bioinformatics 30 (20), 2981–2982. doi:10.1093/bioinformatics/btu426
Li, Z., Wei, R., Gao, M., Ren, Y., Yu, B., Nie, K., et al. (2020). Biodegradation of Low-Density Polyethylene by Microbulbifer Hydrolyticus IRE-31. J. Environ. Manag. 263, 110402. doi:10.1016/j.jenvman.2020.110402
Liao, R.-Z., and Thiel, W. (2012). Comparison of QM-Only and QM/MM Models for the Mechanism of Tungsten-dependent Acetylene Hydratase. J. Chem. Theory Comput. 8 (10), 3793–3803. doi:10.1021/ct3000684
Liu, J., Chakraborty, S., Hosseinzadeh, P., Yu, Y., Tian, S., Petrik, I., et al. (2014). Metalloproteins Containing Cytochrome, Iron-Sulfur, or Copper Redox Centers. Chem. Rev. 114 (8), 4366–4469. doi:10.1021/cr400479b
Lu, T., and Chen, Q. (2021). Shermo: A General Code for Calculating Molecular Thermochemistry Properties. Comput. Theor. Chem. 1200, 113249. doi:10.1016/j.comptc.2021.113249
Madhavi, V., and Lele, S. (2009). Laccase: Properties and Applications. BioResources 4 (4), 1694–1717. doi:10.1016/B978-0-12-805419-2.00007-1
Marenich, A. V., Ho, J., Coote, M. L., Cramer, C. J., and Truhlar, D. G. (2014). Computational Electrochemistry: Prediction of Liquid-phase Reduction Potentials. Phys. Chem. Chem. Phys. 16 (29), 15068–15106. doi:10.1039/c4cp01572j
Martins, L. O., Durão, P., Brissos, V., and Lindley, P. F. (2015). Laccases of Prokaryotic Origin: Enzymes at the Interface of Protein Science and Protein Technology. Cell Mol. Life Sci. 72 (5), 911–922. doi:10.1007/s00018-014-1822-x
Mateljak, I., Monza, E., Lucas, M. F., Guallar, V., Aleksejeva, O., Ludwig, R., et al. (2019). Increasing Redox Potential, Redox Mediator Activity, and Stability in a Fungal Laccase by Computer-Guided Mutagenesis and Directed Evolution. ACS Catal. 9 (5), 4561–4572. doi:10.1021/acscatal.9b00531
Moreno, A. D., Ibarra, D., Eugenio, M. E., and Tomás‐Pejó, E. (2020). Laccases as Versatile Enzymes: from Industrial Uses to Novel Applications. J. Chem. Technol. Biotechnol. 95 (3), 481–494. doi:10.1002/jctb.6224
Phillips, J. C., Hardy, D. J., Maia, J. D. C., Stone, J. E., Ribeiro, J. V., Bernardi, R. C., et al. (2020). Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD. J. Chem. Phys. 153 (4), 044130. doi:10.1063/5.0014475
Piontek, K., Antorini, M., and Choinowski, T. (2002). Crystal Structure of a Laccase from the FungusTrametes Versicolor at 1.90-Å Resolution Containing a Full Complement of Coppers. J. Biol. Chem. 277 (40), 37663–37669. doi:10.1074/jbc.m204571200
Sakurai, T., and Kataoka, K. (2007). Basic and Applied Features of Multicopper Oxidases, CueO, Bilirubin Oxidase, and Laccase. Chem. Rec. 7 (4), 220–229. doi:10.1002/tcr.20125
Santhanam, N., Vivanco, J. M., Decker, S. R., and Reardon, K. F. (2011). Expression of Industrially Relevant Laccases: Prokaryotic Style. Trends Biotechnol. 29 (10), 480–489. doi:10.1016/j.tibtech.2011.04.005
Sheng, X., Kazemi, M., Planas, F., and Himo, F. (2020). Modeling Enzymatic Enantioselectivity Using Quantum Chemical Methodology. ACS Catal. 10 (11), 6430–6449. doi:10.1021/acscatal.0c00983
Shiroya, A. J. (2021). Recent Advances of Laccase Enzyme in Industrial Biotechnology: A Review. Surat: Pharma News.
Siegbahn, P. E. M. (2006). The Performance of Hybrid DFT for Mechanisms Involving Transition Metal Complexes in Enzymes. J. Biol. Inorg. Chem. 11 (6), 695–701. doi:10.1007/s00775-006-0137-2
Singh, S. K., Roberts, S. A., McDevitt, S. F., Weichsel, A., Wildner, G. F., Grass, G. B., et al. (2011). Crystal Structures of Multicopper Oxidase CueO Bound to Copper (I) and Silver (I): Functional Role of a Methionine-Rich Sequence. J. Biol. Chem. 286 (43), 37849–37857. doi:10.1074/jbc.m111.293589
Solomon, E. I., Augustine, A. J., and Yoon, J. (2008). O2 Reduction to H2O by the Multicopper Oxidases. Dalton Trans. 6 (30), 3921–3932. doi:10.1039/b800799c
Uudsemaa, M., and Tamm, T. (2003). Density-functional Theory Calculations of Aqueous Redox Potentials of Fourth-Period Transition Metals. J. Phys. Chem. A 107 (46), 9997–10003. doi:10.1021/jp0362741
Vázquez-Lima, H., Guadarrama, P., and Martínez-Anaya, C. (2012). Geometric Distortions on a Three-Coordinated T1 Cu Site Model as a Potential Strategy to Modulate Redox Potential. A Theoretical Study. J. Mol. Model 18 (2), 455–466. doi:10.1007/s00894-011-1063-y
Walker, M., Harvey, A. J. A., Sen, A., and Dessent, C. E. H. (2013). Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions. J. Phys. Chem. A 117 (47), 12590–12600. doi:10.1021/jp408166m
Witte, J., Goldey, M., Neaton, J. B., and Head-Gordon, M. (2015). Beyond Energies: Geometries of Nonbonded Molecular Complexes as Metrics for Assessing Electronic Structure Approaches. J. Chem. Theory Comput. 11 (4), 1481–1492. doi:10.1021/ct501050s
Xu, F., Berka, R. M., Wahleithner, J. A., Nelson, B. A., Shuster, J. R., Brown, S. H., et al. (1998). Site-Directed Mutations in Fungal Laccase: Effect on Redox Potential, Activity And pH Profile. Biochem. J. 334 (1), 63–70. doi:10.1042/bj3340063
Yan, L., Lu, Y., and Li, X. (2016). A Density Functional Theory Protocol for the Calculation of Redox Potentials of Copper Complexes. Phys. Chem. Chem. Phys. 18 (7), 5529–5536. doi:10.1039/c5cp06638g
Keywords: cluster model, redox potential, quantum mechanics, laccase, molecular simulation
Citation: Jiang Q, Cui Z, Wei R, Nie K, Xu H and Liu L (2022) Feasible Cluster Model Method for Simulating the Redox Potentials of Laccase CueO and Its Variant. Front. Bioeng. Biotechnol. 10:957694. doi: 10.3389/fbioe.2022.957694
Received: 31 May 2022; Accepted: 20 June 2022;
Published: 22 July 2022.
Edited by:
Hui-Min Qin, Tianjin University of Science and Technology, ChinaReviewed by:
Changzhu Wu, University of Southern Denmark, DenmarkCopyright © 2022 Jiang, Cui, Wei, Nie, Xu and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haijun Xu, hjxu@mail.buct.edu.cn; Luo Liu, liuluo@mail.buct.edu.cn
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.