- 1School of Computer and Information, Anqing Normal University, Anqing, China
- 2Jiangsu Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Suzhou, China
- 3School of Information Engineering, Nanjing Xiaozhuang University, Nanjing, China
- 4School of Computer Science and Technology, Soochow University, Suzhou, China
The dihedral angle of the protein backbone can describe the main structure of the protein, which is of great significance for determining the protein structure. Many computational methods have been proposed to predict this critically important protein structure, including deep learning. However, these heavyweight methods require more computational resources, and the training time becomes intolerable. In this article, we introduce a novel lightweight method, named dilated convolution and multi-head attention (DCMA), that predicts protein backbone torsion dihedral angles
1 Introduction
Proteins play important roles in biological activities and often fold into unique three-dimensional structures to perform their biological functions. However, experimentally determining protein tertiary structures is costly and time consuming. Predicting protein tertiary structures from their corresponding sequences is still a challenging problem in computational biology. An integral part of predicting tertiary structures is to predict interval structural properties, such as secondary structures, solvent-accessible surface area, backbone dihedral angles, and contact maps. The backbone structure of a protein can be described continuously by backbone dihedral angles
In 1993, a discrete approach was used to predict backbone dihedral angles that removed any approximations, including the assumption that the effects of adjacent residues were uncorrelated (Kang et al., 1993). In 2005, a continuous neural network-based method was proposed to predict protein secondary structure and backbone dihedral angles (Wood and Hirst, 2005). Other machine learning methods have also been applied to the prediction of protein dihedral angles, such as ANGLOR (Wu and Zhang, 2008) and TANGLE (Song et al., 2012) using support vector machines and neural networks, TALOS+ (Shen et al., 2009), SPINE X, and Real-SPINE3.0 using neural networks, DANGLE (Cheung et al., 2010) using Bayesian, conditional random field (Zhang et al., 2013), and so on.
In recent years, deep learning methods have been successfully applied to the prediction of protein structural properties, including protein backbone dihedral angles. A deep recurrent restricted Boltzmann machine (DReRBM) was developed to research protein dihedral angles (Li et al., 2017). RaptorX-angle combines K-means clustering and deep learning techniques to predict dihedral angles (Gao et al., 2018). Spider 3 (Heffernan et al., 2017), which eliminates the effect of the sliding window, used the machine learning model of the bidirectional long short-term memory (BLSTM) (Hochreiter and Schmidhuber, 1997) recurrent neural network (Schuster and Paliwal, 1997; Graves et al., 2014). The DeepRIN (Fang et al., 2018b) was designed based on the combination of the inception (Szegedy et al., 2016) and the ResNet (He et al., 2016) networks. SPOT-1D used an ensemble of BLSTM and ResNet to improve the prediction of protein secondary structure, backbone dihedral angles, solvent accessibility, etc. (Hanson et al., 2019). SPOT-1D integrated three LSTM models, three LSTMResNet models, and three ResNet-LSTM models and integrated contact maps as model input and to boost its performance. Klausen and colleagues proposed the NetSurfP-2.0 model, which used an architecture consisting of a convolutional neural network (CNN) and LSTM Networks (Klausen et al., 2019). Xu and colleagues proposed OPUS-TASS, a protein backbone dihedral angles and secondary structure predictor (Xu et al., 2020). It is an ensemble model; its individual model parts consist of CNN, LSTM, and modified transformer networks. Zhang and colleagues proposed CRRNN2, which introduced a multi-task deep learning method based on BRNNs, one-dimensional (1D) CNN, and an inception network, which can concurrently predict protein secondary structure, solvent accessibility, and backbone dihedral angles (Zhang et al., 2021). As an upgraded version of OPUS-TASS, OPUS-TASS2 integrated global structure information generated by trRosetta (Du et al., 2021) and achieves SOTA performance. OPUS-TASS2 adopts an ensemble strategy as OPUS-TASS and SPOT-1D, and it consists of nine models (Xu et al., 2022).
Recently, AlphaFold2 has achieved great success in predicting protein monomer structures (Jumper et al., 2021; Ismi et al., 2022). However, accuracy for single-sequence-based prediction of secondary structures is far from the theoretical limit of 86%–90% (Zhou et al., 2023). The bottleneck resides in the immense computational demands of running the AlphaFold2 model, both in terms of computing power and runtime. Therefore, there is still a need for prediction tools that can predict protein backbone angles in a faster and more accurate manner. A recurrent neural network (RNN) maintains a vector of activations for each timestep that can remember prior input to influence the current input and output. RNNs can be easily used for sequential or time series data (Jozefowicz et al., 2015). The best-so-far deep learning methods are essentially constructed by RNNs like SPOT-1D (Hanson et al., 2019), OPUS-TASS (Xu et al., 2020), OPUS-TASS2 (Xu et al., 2022), NetSurfP-2.0 (Klausen et al., 2019), and CRRNN2 (Zhang et al., 2021). Because the computation of each step in an RNN depends on the previous step, the recurrent computations are less amenable to parallelization. In contrast to the models built by convolution or attention networks, RNN-based models need more training and running times. Moreover, these heavyweight models consume more computing resources, which is not conducive to training or inference.
In this article, we designed a new hybrid inception block consisting of 1D CNNs and dilated CNNs (Yu and Koltun, 2016). As an alternative to an RNN, a novel architecture with two hybrid inception blocks and one multi-head attention (Vaswani et al., 2017) block called an I2A1 module is intended to capture local and long-range features, which are comprised of two hybrid inception blocks and augmented by one multi-head attention network. The dilated convolution and multi-head attention (DCMA) novel protein backbone dihedral angle predictor is mainly constructed from I2A1 modules. Hence, we have made the following outstanding contributions: 1) proposed a faster method that can substitute for RNNs and offers comparable performance, and 2) provided a more lightweight tool for predicting dihedral angles that is more friendly to biological or medical researchers.
2 Materials and methods
2.1 Datasets
We used the same training (Hanson et al., 2019) and validation sets as SPOT-1D and OPUS-TASS 1/2 for a fair comparison with most state-of-the-art methods. The sequences were culled from the PISCES server (Wang et al., 2003) by SPOT-1D in February 2017, with the following constraints: resolution
To evaluate the performance of different methods, we performed the method on six public independent test sets: (1) The CASP12 dataset contains 40 proteins; (2) CASP13, which contains 32 proteins; (3) CASP-FM (56), collected by SAINT (Uddin et al., 2020), which contains 10 template free modeling (FM) targets from CASP13, 22 FM targets from CASP12, 16 FM targets from CASP11, and 8 FM targets from CASP10; (4) the CASP12-FM dataset, collected by Singh et al. (2021a), which contains 22 FM proteins from CASP12; (5) the CASP13-FM dataset, collected by Singh et al. (2021a), which contains 17 FM proteins from CASP13; and the (6) CASP14-FM dataset, collected by Xu et al. (2022), which contains 15 FM proteins from CASP14.
2.2 Input features
DCMA takes three groups of sequence-based features as input: a position-specific scoring matrix (PSSM) profile, a hidden Markov model (HMM) profile, and residues coding. As SPOT-1D reported, each 20-dimensional protein PSSM was generated by three iterations of PSI-BLAST (Altschul et al., 1997) against the UniRef90 sequence database updated in April 2018. The 30-dimensional HMM sequence profiles are re-generated by HHBlits (v3.1.0) (Steinegger et al., 2019) with default parameters based on the UniRef30 database updated in June 2020. Similarly to CRRNN’s schema (Zhang et al., 2018), a one-hot vector of residues coding is mapped to a 22-dimensional dense vector.
2.3 Outputs
To remove the effect of the angle’s periodicity, we employ a pair of sine and cosine values for each torsion angle as the output instead of directly predicting
The multi-task learning strategy of predicting protein structural properties concurrently has been proven to be effective by CRRNN2 (Zhang et al., 2021). We also adopted the same multi-task learning schema as CRRNN2, in which the auxiliary output during the training period is protein secondary structure (Q3 and Q8) and solvent accessibility. The loss function and respective output ratio in DCMA are the same as in CRRNN2.
2.4 DCMA model
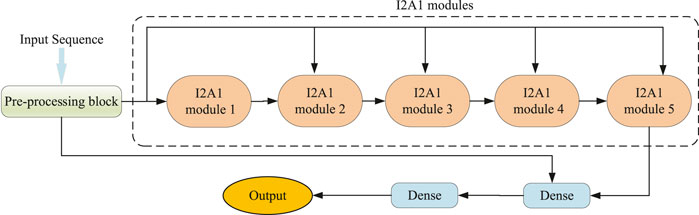
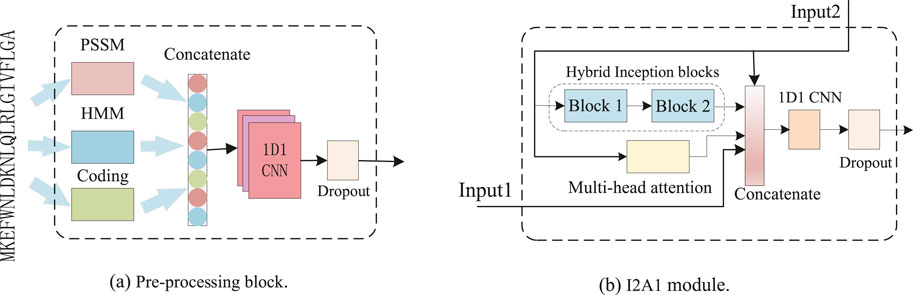
As illustrated in Figure 1, our DCMA model consists of three parts: a pre-processing block, five stacked I2A1 modules, and two fully connected layers. The input features are transformed in the pre-processing block, and its structure is demonstrated in Figure 2A. The I2A1 module is mainly constructed by two cascaded hybrid inception blocks and one multi-head attention block, as Figure 2B shows. The details of these blocks will be introduced below.
2.4.1 Pre-processing block
As Figure 2A and Equation 1 show, the representing residue features, including 20-dimension (D) PSSM, 22-D residue coding, and 30-D HMM, are aggregated and transformed into 256-D tensors by one dimension and one kernel (1D1) CNN (Zhang et al., 2018). The weight constraint of dropout (p = 0.5) used to avoid overfitting was applied to the output of 1D1 CNN. Then, the tensors denoted as input are fed to each I2A1 module and the first dense layer.
2.4.2 Hybrid inception block
CNNs provide the property (Strubell et al., 2017) that parallelizes runtime independent of the sequence length maximizes GPU resource usage and minimizes the training and evaluating time. However, a CNN’s perception is limited by the input size. As Strubell’s description notes (Strubell et al., 2017), the maximum perception length r of CNN is expressed as
Motivated by the effectiveness of the inception (Szegedy et al., 2015; Szegedy et al., 2016) network based on CNNs (Fang et al., 2018b; Fang et al., 2018a; Uddin et al., 2020), we proposed a newly hybrid inception block, as shown in Figure 3. Four types of local features are aggregated from 1D CNNs with 64 filters and kernel size [1, 3, 5, 7] respectively, for the minimum length of protein secondary structures is three, and 1D CNN with kernel size one (1D1 CNN) is used to data dimension transformation. Another four groups of long-range features are perceived from hybrid dilation rates (d_rate) CNNs with 64 filters and kernel size 2. Similar to DeepLabv3’s (Chen et al., 2017) configuration, dilation rates [2, 4, 8, 16] are applied. For better perceptive capability, four channels with stacked [1, 2, 3, 4] dilated CNNs, respectively, are combined. Multi-scale dilation rates { [2], [2, 4], [2, 4, 8], [2, 4, 8, 16]} are used in corresponding channels, respectively. When the eight parallel outputs are concatenated as a 512-dimensional tensor, the data dimension is transformed into 256 by a 1D1 CNN for model weight reduction.
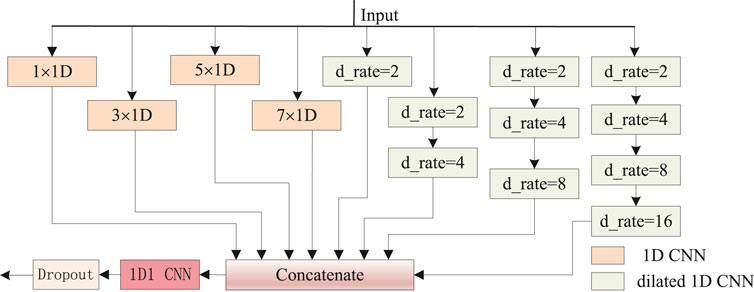
Figure 3. Newly hybrid inception block. The 1D CNNs with 64 filters and kernel size [1, 3, 5, 7] are intended to capture sequence local futures. Dilated 1D CNNs with 64 filters, kernel size 2, and multi-scale dilation rates (d_rate) are used to capture sequence long-range dependencies.
2.4.3 Multi-head attention
The attention mechanism (Tay et al., 2020) can be viewed as a graph-like inductive bias that connects all tokens in a sequence with a relevance-based pooling operation. Multi-head attention (Vaswani et al., 2017) allows the model to jointly attend to information from different representations and focus on different aspects of information. The advantage of attention is that it can capture long-term dependencies without being limited by sequence length. Because the result of each step does not depend on the previous step, steps can be done in parallel mode. We use a multi-head attention mechanism as a complement to the hybrid inception block. Eight heads are employed. In the DCMA model, we use multi-head attention as Equations 2–4, the most popular attention in recent years, which combines multiple self-attention networks to divide the model into multiple heads to form multiple subspaces and can make models focus on different aspects of information. In our model, we employ eight heads, and tanh activated function is added to the output for smooth variation. In order to control model weight, the dimension of
2.4.4 I2A1 module
The input data is fed parallel to one multi-headed attention block and two cascaded hybrid inception blocks, as Figure 2B and Equations 5–10 show. The proposed module can effectively capture both the short-range and long-range dependencies. In the first I2A1 module (i = 1), Input2 is the output of the pre_processing block, and Input1 is null. In other I2A1 modules, Input2 is the output of the previous I2A1 module, and Input1 is the output of the pre_processing block. For a better balance between the ability to model long-range dependencies and computational efficiency, only one attention block is joined with two cascaded hybrid inception blocks, and the dimension of concatenated data is also reduced from 1,024 (768, when in the first module) to 256 by 1D1 CNN.
3 Results
3.1 Experimental settings
The developed DCMA model was implemented in Keras, and the weights in DCMA were initialized using default values. The implementation was trained on a NVIDIA P6000 GPU. Adam optimization with an initial learning rate of 0.0004 was used to optimize the networks.
For training the model on GPU with batch input, proteins shorter than 700 AA are padded with all-zeros. Similar to the CRRNN2 experiment, the strategy of deep multi-task learning is also applied in the DCMA training period. In the inference period, only the backbone angle output is retained.
3.2 Evaluation metrics
To evaluate the predictive performance of protein backbone dihedral angles, the mean absolute error (MAE) (Sunghoon et al., 2011) and Pearson correlation coefficient (PCC) were used to measure the relevance between the native values and predicted ones. Here, the value of a protein dihedral angle is in the range of [
where
Among them,
3.3 Evaluation on independent test datasets
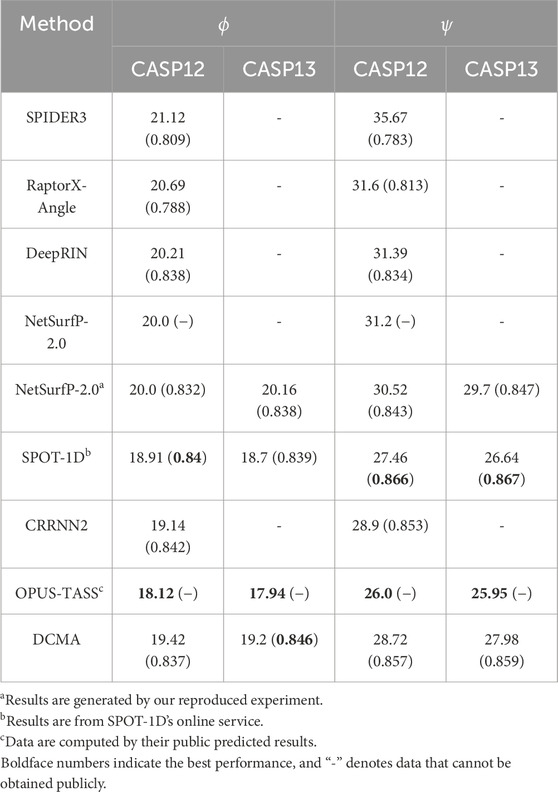
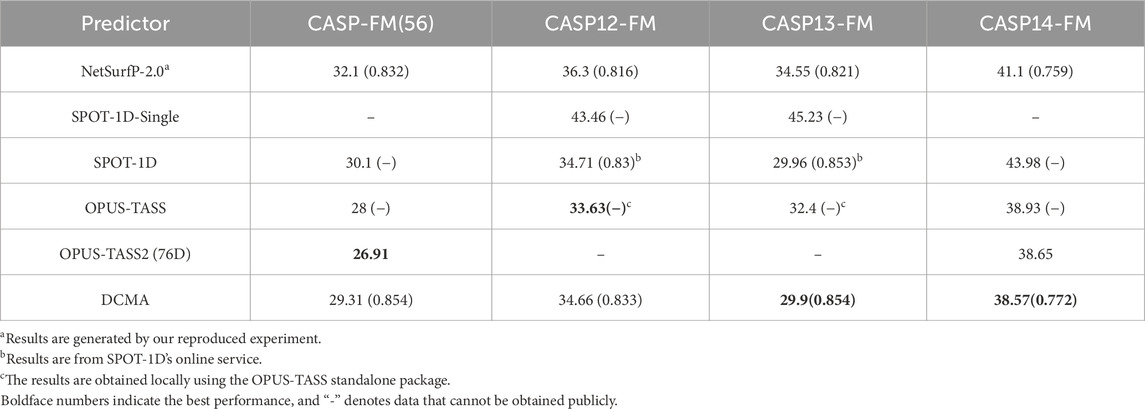
In order to better evaluate the performance of our model, we compare the DCMA model with other representative methods on public independent CASP sets. We compared the performance of DCMA with SPOT-1D, Netsurfp-2.0, DeepRIN, CRNN2, etc., on the CASP12 and CASP13 datasets, as shown in Table 1. Values in brackets are PCC, and “-” denotes data that cannot be obtained publicly. We re-implemented the model of Netsurfp-2.0 and used the same datasets and features as DCMA. DCMA achieved (19.42, 28.72) of
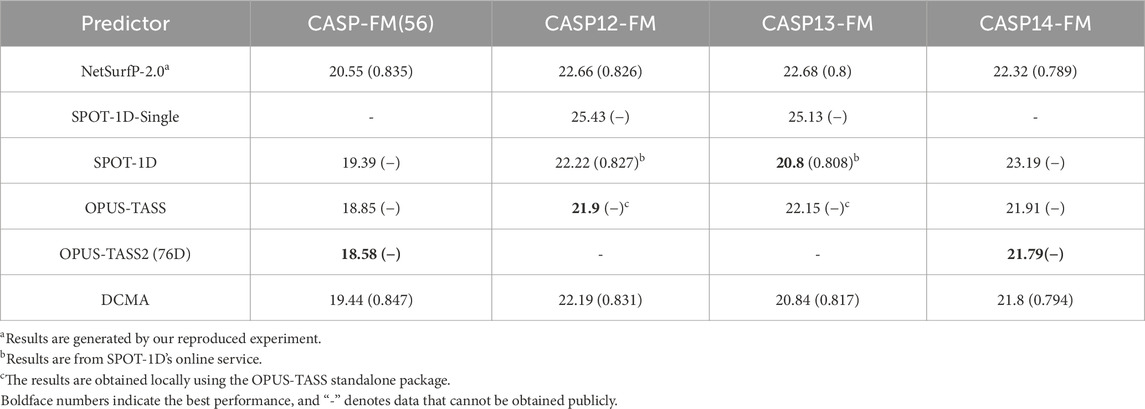
The comparison between state-of-the-art models, including SPOT-1D, OPUS-TASS, OPUS-TASS2, and DCMA, is further analyzed on free modeling targets in Table 2, 3. The prediction results of OPUS-TASS2 based on sequence features are compared. The sequence features of OPUS-TASS2 are 20-D PSSM, 30-D HMM, 7-D physicochemical properties, and 19-D PSP19 features, which are denoted as “OPUS-TASS2 (76D).” Predicting results on the CASP12-FM dataset show that the performance of SPOT-1D and OPUS-TASS is similar and better than others. The performance of OPUS-TASS2 is best on the CASP-FM (56) dataset. DCMA achieved better prediction performance on the more difficult CASP13-FM dataset. On the most difficult CASP14-FM dataset, the prediction performance of OPUS-TASS2 and DCMA is comparable and better than other predictors.
The latest benchmark dataset CASP15 (removing four similar sequences) was also used for evaluating the model generalization and achieved (19.78, 29.53) of MAE metrics and (0.83, 0.847) of PCC metrics on
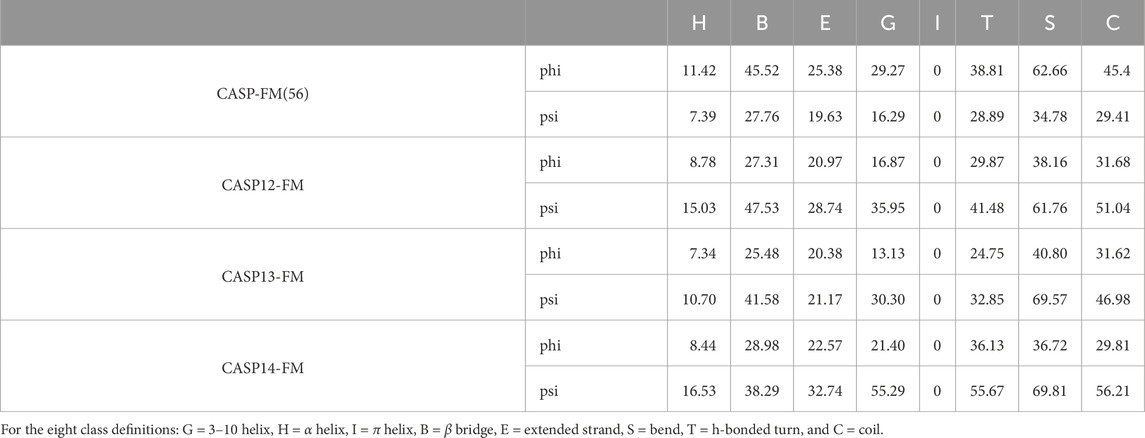
Table 4. MAE of torsion angles on the 8-class secondary structures for the free modeling targets of the CASP datasets.
The prediction performance at the sequence level is further analyzed. The absolute error on the
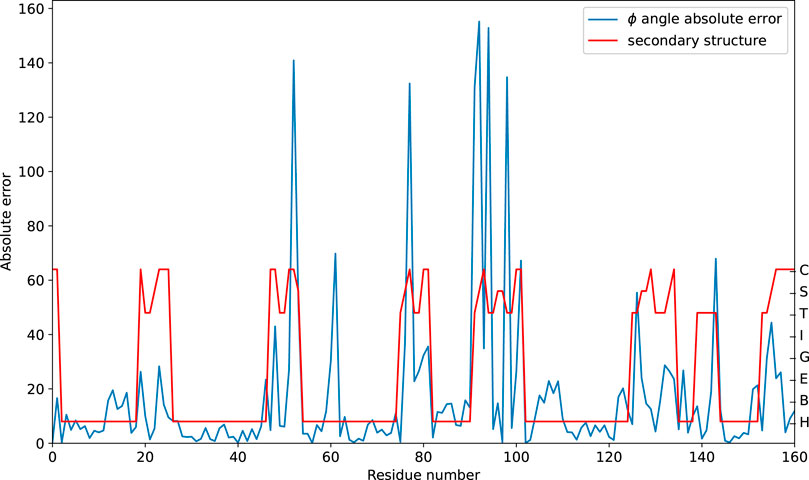
Figure 5. Predicting the absolute error of the
3.4 Ablation study
The impact of different groups of input features is first analyzed. The loss variation on the validation dataset is compared when the model was trained by using different combinations of input features. The experimental results are shown in Figure 4. Compared to the models trained by the input of a single feature, the features of pairwise combinations are more efficient in reducing losses. When three groups of features, PSSM profile, HHM profile, and residue coding, are combined, the effect of reducing loss is best.
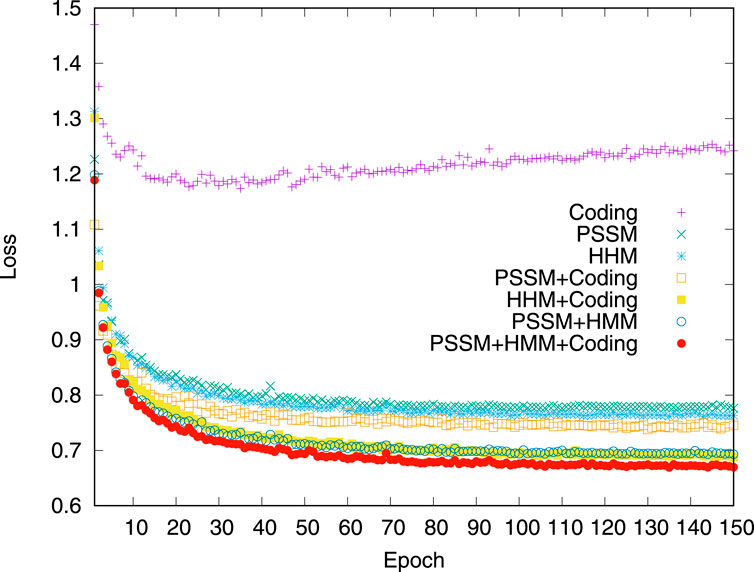
Figure 4. Model loss variation in the validation dataset. The comparison of the dihedral angle prediction performance of the iterative procedure using different input features on the validation dataset.
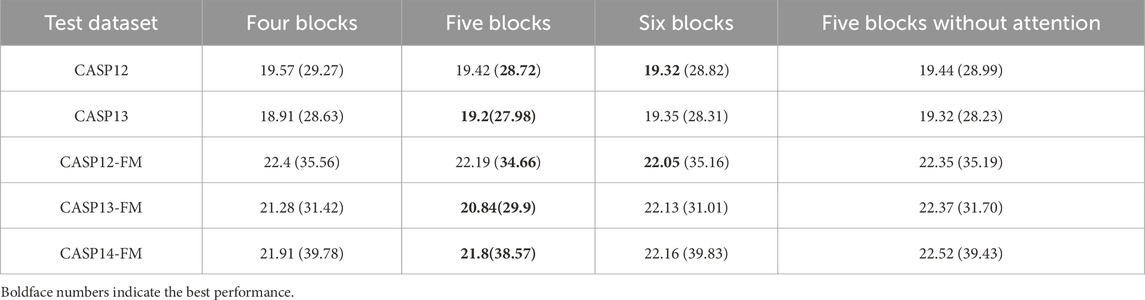
We further analyzed the DCMA model structure. The results of the ablation experiment are shown in Table 5, where values in the cell and the bracket are the MAEs of (
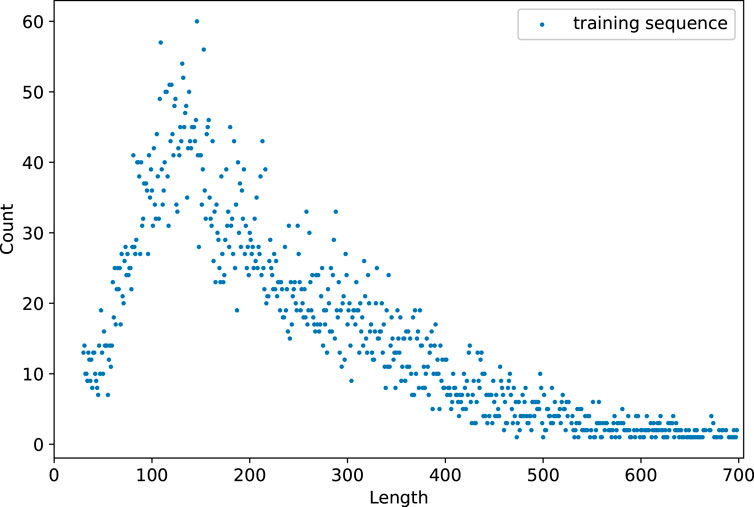
The length distributions of training and validation datasets are shown in Figure 6. The data statistics show a total of 2022 sequences ranging in length from 102 to 213. In addition, there are 7,326 sequences with lengths ranging from 50 to 300. The recommended length of input sequence ranges from 50 to 300.
4 Conclusion
Predicting protein 3D structures is an important and challenging task. Predicting protein backbone torsion dihedral angles helps solve the problem. Heavy models are unfriendly and unsuitable for running on edge computing devices. In particular, the file size of the SPOT-1D model is larger than 10 GB. In this article, a lightweight, faster, and individual model named DCMA is proposed. The model file of DCMA is less than 50 MB. We use hybrid dilated CNN and multi-head attention to design a new deep network structure, I2A1, that substitutes for RNN. The I2A1 block balanced the model generalization and computational efficiency well. Thus, our model mechanism can be applied to predicting various other protein attributes as well.
In future work, input residues will be characterized with more structural information, including physicochemical properties and protein domains (Guo et al., 2003; Yu et al., 2023), to improve the performance of discontinuous or isolated secondary structures. Although DCMA is more lightweight and faster, its input still relies on multi-sequence alignment information such as a PSSM profile. A single-sequence-based method that did not use evolutionary features would be more friendly.
Pre-trained protein language models (pLMs) can generate information-rich representations of sequences. Combined with sequence embedding generated by pLMs, a downstream predictor of backbone dihedral angles and other 1D structural properties can be exploited without generating multi-sequence alignment information.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author/s.
Author contributions
BZ: conceptualization, methodology, software, and writing–original draft. MZ: conceptualization, methodology, and writing–original draft. YZ: conceptualization, data curation, and writing–review and editing. LQ: conceptualization, data curation, and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported in part by the Excellent Youth Scholars Project of Anhui Provincial Universities of China under grant no. gxyq2020029 and the Project of Provincial Key Laboratory for Computer Information Processing Technology, Soochow University of China, under grant no. KJS1934.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Altschul, S. F., Madden, T. L., Schffer, A. A., Zhang, J., Zhang, Z., Webb, M., et al. (1997). Gapped blast and psi-blast: a new generation of protein database search programs. Nucleic acids Res. 25, 3389–3402. doi:10.1093/nar/25.17.3389
Chen, L., Papandreou, G., Schroff, F., and Adam, H. (2017). Rethinking atrous convolution for semantic image segmentation. CoRR abs/1706.05587.
Cheung, M.-S., Maguire, M. L., Stevens, T. J., and Broadhurst, R. W. (2010). Dangle: a bayesian inferential method for predicting protein backbone dihedral angles and secondary structure. J. magnetic Reson. 202, 223–233. doi:10.1016/j.jmr.2009.11.008
Du, Z., Su, H., Wang, W., Ye, L., Wei, H., Peng, Z., et al. (2021). The trrosetta server for fast and accurate protein structure prediction. Nat. Protoc. 16, 5634–5651. doi:10.1038/s41596-021-00628-9
Fang, C., Shang, Y., and Xu, D. (2018a). Mufold-ss:new deep inception-inside-inception networks for protein secondary structure prediction. Proteins Struct. Funct. Bioinforma. 86, 592–598. doi:10.1002/prot.25487
Fang, C., Shang, Y., and Xu, D. (2018b). Prediction of protein backbone torsion angles using deep residual inception neural networks. IEEE/ACM Trans. Comput. Biol. Bioinforma. 16, 1020–1028. doi:10.1109/tcbb.2018.2814586
Gao, Y., Wang, S., Deng, M., and Xu, J. (2018). Raptorx-angle: real-value prediction of protein backbone dihedral angles through a hybrid method of clustering and deep learning. BMC Bioinforma. 19, 100–184. doi:10.1186/s12859-018-2065-x
Graves, A., Jaitly, N., and Mohamed, A. R. (2014). “Hybrid speech recognition with deep bidirectional lstm,” in Automatic speech recognition and understanding, 273–278.
Guo, J., Xu, D., Kim, D., and Xu, Y. (2003). Improving the performance of domainparser for structural domain partition using neural network. Nucleic Acids Res. 31, 944–952. doi:10.1093/nar/gkg189
Hanson, J., Paliwal, K., Litfin, T., Yang, Y., and Zhou, Y. (2019). Improving prediction of protein secondary structure, backbone angles, solvent accessibility and contact numbers by using predicted contact maps and an ensemble of recurrent and residual convolutional neural networks. Bioinformatics 35, 2403–2410. doi:10.1093/bioinformatics/bty1006
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in 2016 IEEE conference on computer vision and pattern recognition (CVPR) (Los Alamitos, CA, USA: IEEE Computer Society), 770–778.
Heffernan, R., Yang, Y., Paliwal, K., and Zhou, Y. (2017). Capturing non-local interactions by long short-term memory bidirectional recurrent neural networks for improving prediction of protein secondary structure, backbone angles, contact numbers and solvent accessibility. Bioinformatics 33, 2842–2849. doi:10.1093/bioinformatics/btx218
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
Ismi, D. P., Pulungan, R., and Afiahayati, (2022). Deep learning for protein secondary structure prediction: pre and post-alphafold. Comput. Struct. Biotechnol. J. 20, 6271–6286. doi:10.1016/j.csbj.2022.11.012
Jozefowicz, R., Zaremba, W., and Sutskever, I. (2015). “An empirical exploration of recurrent network architectures,” in Proceedings of the 32nd international converenfe on machine learning (ICML), 171–180.
Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., et al. (2021). Highly accurate protein structure prediction with alphafold. Nature 596, 583–589. doi:10.1038/s41586-021-03819-2
Kang, H. S., Kurochkina, N. A., and Lee, B. (1993). Estimation and use of protein backbone angle probabilities. J. Mol. Biol. 229, 448–460. doi:10.1006/jmbi.1993.1045
Klausen, M. S., Jespersen, M. C., Nielsen, H., Jensen, K. K., Jurtz, V. I., Soenderby, C. K., et al. (2019). Netsurfp-2.0: improved prediction of protein structural features by integrated deep learning. Proteins Struct. Funct. Bioinforma. 87, 520–527. doi:10.1002/prot.25674
Li, H., Hou, J., Adhikari, B., Lyu, Q., and Cheng, J. (2017). Deep learning methods for protein torsion angle prediction. BMC Bioinforma. 18, 417–513. doi:10.1186/s12859-017-1834-2
Schuster, M., and Paliwal, K. K. (1997). Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 45, 2673–2681. doi:10.1109/78.650093
Shen, Y., Delaglio, F., Cornilescu, G., and Bax, A. (2009). Talos+: a hybrid method for predicting protein backbone torsion angles from nmr chemical shifts. J. Biomol. NMR 44, 213–223. doi:10.1007/s10858-009-9333-z
Singh, H., Singh, S., and Raghava, G. P. S. (2014). Evaluation of protein dihedral angle prediction methods. PLOS ONE 9, e105667–e105669. doi:10.1371/journal.pone.0105667
Singh, J., Litfin, T., Paliwal, K., Singh, J., Hanumanthappa, A. K., and Zhou, Y. (2021a). Spot-1d-single: improving the single-sequence-based prediction of protein secondary structure, backbone angles, solvent accessibility and half-sphere exposures using a large training set and ensembled deep learning. Bioinformatics 37, 3464–3472. doi:10.1093/bioinformatics/btab316
Singh, J., Paliwal, K., Singh, J., and Zhou, Y. (2021b). Rna backbone torsion and pseudotorsion angle prediction using dilated convolutional neural networks. J. Chem. Inf. Model. 61, 2610–2622. doi:10.1021/acs.jcim.1c00153
Song, J., Tan, H., Wang, M., Webb, G. I., and Akutsu, T. (2012). Tangle: two-level support vector regression approach for protein backbone torsion angle prediction from primary sequences. PloS one 7, e30361. doi:10.1371/journal.pone.0030361
Steinegger, M., Meier, M., Mirdita, M., Vöhringer, H., Söding, J., and Söding, J. (2019). HH-suite3 for fast remote homology detection and deep protein annotation. BMC Bioinforma. 20, 473. doi:10.1186/s12859-019-3019-7
Strubell, E., Verga, P., Belanger, D., and Mccallum, A. (2017). “Fast and accurate entity recognition with iterated dilated convolutions,” in Proceedings of the 2017 conference on empirical methods in natural language processing (EMNLP), 2670–2680. doi:10.18653/v1/D17-1283
Sunghoon, J., Se-Eun, B., and Hyeon, S. S. (2011). Validity of protein structure alignment method based on backbone torsion angles. J. Proteomics Bioinforma. 4, 218–226. doi:10.4172/jpb.1000190
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., et al. (2015). “Going deeper with convolutions,” in 2015 IEEE conference on computer vision and pattern recognition (CVPR), 1–9. doi:10.1109/CVPR.2015.7298594
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna, Z. (2016). “Rethinking the inception architecture for computer vision,” in 2016 IEEE conference on computer vision and pattern recognition (CVPR) (IEEE Computer Society), 2818–2826.
Tay, Y., Dehghani, M., Bahri, D., and Metzler, D. (2020). Efficient transformers: a survey. CoRR abs/2009.06732.
Uddin, M. R., Mahbub, S., Rahman, M. S., and Bayzid, M. S. (2020). SAINT: self-attention augmented inception-inside-inception network improves protein secondary structure prediction. Bioinformatics 36, 4599–4608. doi:10.1093/bioinformatics/btaa531
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention is all you need. CoRR abs/1706.03762. doi:10.48550/arXiv.1706.03762
Wang, G., Dunbrack, J., and Roland, L. (2003). Pisces: a protein sequence culling server. Bioinformatics 19, 1589–1591. doi:10.1093/bioinformatics/btg224
Wang, P., Chen, P., Yuan, Y., Liu, D., Huang, Z., Hou, X., et al. (2018). “Understanding convolution for semantic segmentation,” in 2018 IEEE winter conference on applications of computer vision (WACV), 1451–1460. doi:10.1109/WACV.2018.00163
Wood, M. J., and Hirst, J. D. (2005). Protein secondary structure prediction with dihedral angles. PROTEINS Struct. Funct. Bioinforma. 59, 476–481. doi:10.1002/prot.20435
Wu, S., and Zhang, Y. (2008). Anglor: a composite machine-learning algorithm for protein backbone torsion angle prediction. PloS one 3, e3400. doi:10.1371/journal.pone.0003400
Wu, Z., Shen, C., and van den Hengel, A. (2016). Bridging category-level and instance-level semantic image segmentation. CoRR abs/1605.06885.
Xu, G., Wang, Q., and Ma, J. (2020). Opus-tass: a protein backbone torsion angles and secondary structure predictor based on ensemble neural networks. Bioinformatics 36, 5021–5026. doi:10.1093/bioinformatics/btaa629
Xu, G., Wang, Q., and Ma, J. (2022). OPUS-X: an open-source toolkit for protein torsion angles, secondary structure, solvent accessibility, contact map predictions and 3D folding. Bioinformatics 38, 108–114. doi:10.1093/bioinformatics/btab633
Yu, F., and Koltun, V. (2016). “Multi-scale context aggregation by dilated convolutions,” in Conference Track Proceedings 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, May 2-4, 2016. Editors Y. Bengio, and Y. LeCun
Yu, Z.-Z., Peng, C.-X., Liu, J., Zhang, B., Zhou, X.-G., and Zhang, G.-J. (2023). Dombpred: protein domain boundary prediction based on domain-residue clustering using inter-residue distance. IEEE/ACM Trans. Comput. Biol. Bioinforma. 20, 912–922. doi:10.1109/TCBB.2022.3175905
Zhang, B., Li, J., and Lü, Q. (2018). Prediction of 8-state protein secondary structures by a novel deep learning architecture. BMC Bioinforma. 19, 293–313. doi:10.1186/s12859-018-2280-5
Zhang, B., Li, J., Quan, L., and Lyu, Q. (2021). Multi-task deep learning for concurrent prediction of protein structural properties. bioRxiv. doi:10.1101/2021.02.04.429840
Zhang, S., Jin, S., and Xue, B. (2013). Accurate prediction of protein dihedral angles through conditional random field. Front. Biol. 8, 353–361. doi:10.1007/s11515-013-1261-3
Keywords: protein dihedral angles, lightweight model, dilated convolution, multi-head attention, hybrid inception blocks
Citation: Zhang B, Zheng M, Zhang Y and Quan L (2024) DCMA: faster protein backbone dihedral angle prediction using a dilated convolutional attention-based neural network. Front. Bioinform. 4:1477909. doi: 10.3389/fbinf.2024.1477909
Received: 08 August 2024; Accepted: 30 September 2024;
Published: 18 October 2024.
Edited by:
Yaan J. Jang, University of Oxford, United KingdomReviewed by:
Fabien Plisson, Center for Research and Advanced Studies (CINVESTAV), MexicoGuijun Zhang, Zhejiang University of Technology, China
Copyright © 2024 Zhang, Zheng, Zhang and Quan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Buzhong Zhang, emhiemhvbmdAYXFudS5lZHUuY24=; Lijun Quan, bGpxdWFuQHN1ZGEuZWR1LmNu
 Buzhong Zhang
Buzhong Zhang Meili Zheng1
Meili Zheng1 Lijun Quan
Lijun Quan