Qualitative analysis of fourth-order hyperbolic equations

We investigate the qualitative properties of weak solutions to the boundary value problems for fourth-order linear hyperbolic equations with constant coefficients in a plane bounded domain convex with respect to characteristics. Our main scope is to prove some analog of the maximum principle, solvability, uniqueness and regularity results for weak solutions of initial and boundary value problems in the space L². The main novelty of this paper is to establish some analog of the maximum principle for fourth-order hyperbolic equations. This question is very important due to natural physical interpretation and helps to establish the qualitative properties for solutions (uniqueness and existence results for weak solutions). The challenge to prove the maximum principle for weak solutions remains more complicated and at that time becomes more interesting in the case of fourth-order hyperbolic equations, especially, in the case of non-classical boundary value problems with data of weak regularity. Unlike second-order equations, qualitative analysis of solutions to fourth-order equations is not a trivial problem, since not only a solution is involved in boundary or initial conditions, but also its high- order derivatives. Other difficulty concerns the concept of weak solution of the boundary value problems with L² – data. Such solutions do not have usual traces, thus, we have to use a special notion for traces to poss correctly the boundary value problems. This notion is traces associated with operator L or L-traces. We also derive an interesting interpretation (as periodicity of characteristic billiard or the John's mapping) of the Fredholm's property violation. Finally, we discuss some potential challenges in applying the results and proposed methods.

1 Introduction

This study is devoted to the problem of proving some analog of maximum principle and its further application to the questions of uniqueness, existence, and regularity for weak solutions of the Goursat, the Cauchy, and the Dirichlet problems for fourth-order linear hyperbolic equations with the constant coefficients and homogeneous non-degenerate symbol in a plane bounded domain Ω ∈ ℝ² convex with respect to characteristics:

$\begin{array}{ll}L(D_x)u=a_0\frac{{\partial }^{4}u}{\partial x_1^4}+a_1\frac{{\partial }^{4}u}{\partial x_1^3\partial x_2}+a_2\frac{{\partial }^{4}u}{\partial x_1^2\partial x_2^2}+a_3\frac{{\partial }^{4}u}{\partial x_1\partial x_2^3}+a_4\frac{{\partial }^{4}u}{\partial x_2^4}=f(x).& (1)\end{array}$

Here, coefficients a_j, j = 0, 1, ..., 4 are constant, f(x) ∈ L²(Ω), ${\partial }_x=\left(\frac{\partial }{\partial x_1},\frac{\partial }{\partial x_2}\right).$ We consider hyperbolic equations that means all roots of the characteristic equation

$\begin{array}{l}L(1,\lambda )=a_0{\lambda }^4+a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4=0\end{array}$

are prime and real and are not equal to ±i or the symbol of Equation 1 is non-degenerate (Equation 1 is a equation of principal type). If roots of characteristics equation of which are multiple and can take the values ±i we will call the equation with degenerate symbol (see Buryachenko [7]).

The main novelty of this study is to establish some analog of the maximum principle for fourth-order hyperbolic equations. This question is very important due to natural physical interpretation and helps to establish the qualitative properties for solutions (uniqueness and existence results for weak solutions). It is well known that even for the simple case of hyperbolic equation (one dimensional wave equation [23]), [1] the maximum principle is quite different from those for elliptic and parabolic cases, for which it is a natural fact. Such a way a role of characteristics curves and surfaces becomes evident for hyperbolic equations.

We call the angle of characteristics slope solution to the equation −tanφ_j = λ_j, and the angle between j− and k− characteristics: φ_k − φ_j ≠ πl, l ∈ ℤ, where λ_j ≠ ±i are real and prime roots of the characteristics equation, j, k = 1, 2, 3, 4.

Most of these equations serve as mathematical models of many physical processes and attract interest of researchers. The most famous of them are elasticity beam equations (Timoshenko beam equations with and without internal damping) [9], short laser pulse equation [12], equations which describe the structures are subjected to moving loads, and equation of Euler-Bernoulli beam resting on two-parameter Pasternak foundation and subjected to a moving load or mass [11, 24].

Due to evident practice application, these models require more precise tools for study, and as a result, attract fundamental knowledge. As usual, most of these models are studied by analytical-numerical methods (Galerkin's methods).

The range of problems studied in this study belongs to a class of quite actual problems of well-posedness of so-called general boundary value problems for higher-order differential equations. These problems originated from the studies of L. Hormander and M. Vishik, who used the theory of extensions to prove the existence of well-posed boundary value problems for linear differential equations of arbitrary order with constant complex coefficients in a bounded domain with smooth boundary. This theory got its present-day development in the studies of G. Grubb [13], Hörmander [14], and Posilicano [22] (see also [16]). Later, the problem of well-posedness of boundary value problems for various types of second-order differential equations was studied by Burskii [2], Burskii and Zhedanov [3], who developed a method of traces associated with a differential operator and applied this method for study the Poncelet, the Abel, and the Goursat problems. In the previous studies of Burskii and Buryachenko [6], there have been developed the qualitative methods for studying the Cauchy problem and non-standard for hyperbolic equations the Dirichlet and the Neumann problems. Moreover, for equation of any even order 2m, m ≥ 2, using operator methods (L-traces, theory of extension, moment problem, method of duality equation domain, and others), the existence and uniqueness results were proved, and the criteria of non-trivial solvability of the Dirichlet and the Neumann problems in a disk for the principal type equations and equations with degenerate symbol were obtained [4, 8]. In particular, the interrelations between multiplicity of roots of the characteristic equation were established, and the existence of a non-trivial solution of the corresponding problems was proved. As a consequence, the Fredholm property for the problems under consideration was established.

As the concern maximum principle, at the present time there are not any results for fourth-order equations even in linear case. As it was mentioned above, maximum principle even for the simplest case of one dimensional wave equation [23] and for second-order telegraph equation [18–21] is quite different from those for elliptic and parabolic cases. In the monograph of Protter and Weinberger [23], there was shown that solutions of hyperbolic equations and inequalities do not exhibit the classical formulation of maximum principle. Even in the simplest case of the wave equation u_tt − u_xx = 0, a maximum of a non-constant solution u = sinxsint in a rectangle domain {(x, t):x ∈ [0, π], t ∈ [0, π]} occurs at the interior point $(\frac{\pi }{2},\frac{\pi }{2})$. In Chapter 4 [23], maximum principle for linear second hyperbolic equations of general type with variable coefficients has also been obtained for the Cauchy problems and boundary value problems on characteristics (the Goursat problem).

Following Ortega and Robles-Perez [21], we introduce the definition of the maximum principle for hyperbolic equations.

Definition 1. [21] Let L be linear differential operator, acting on functions u : D → ℝ in some domain D. These functions will belong to the certain family B, which includes boundary conditions or other requirements. It is said that L satisfies the maximum principle, if

$L\ge 0,u\in B,$

implies u ≥ 0 in D.

In further studies of these authors (see Mawhin et al. [18–20]), the maximum principle for weak bounded twice periodical solutions from the space L^∞ for the telegraph equation with parameter λ in lower term, one-, two-, and -three dimensional spaces was studied. The precise condition for λ under which the maximum principle still valid was font. There was also introduced a method of upper and lower solutions associated with the non-linear equation, which allows to obtain the analogous results (uniqueness, existence, and regularity theorems) for the telegraph equations with external non-linear forcing.

Maximum principle for second-order quasilinear hyperbolic systems with dissipation was proved by De-Xing [17]. There were given two estimates for solution to the general quasilinear hyperbolic system and introduced the concept of dissipation (strong dissipation and weak dissipation); then, some maximum principles for secound-order quasilinear hyperbolic systems with dissipation were derived. As an application of maximum principle, the existence and uniqueness theorems of the global smooth solution to the Cauchy problem for considered quasilinear hyperbolic system were proved. In recent study by Yi and Ying [10], some analog of Equation 1 with lower order terms and non-linear external force was considered. Qualitative properties of solution of the Dirichlet problem with affine data for differential elasticity inclusion were proved by Ruland et al. [25].

The challenge to prove the maximum principle for weak solutions remains more complicated and at that time becomes more interesting in the case of fourth-order hyperbolic equations, especially, in the case of non-classical boundary value problems with data of weak regularity. Unlike second-order equations, qualitative analysis of solutions to fourth-order equations is not a trivial problem, since not only a solution is involved in boundary or initial conditions but also its high- order derivatives. Other difficulty concerns the concept of weak solution of the boundary value problems with L² − data. Such solutions do not have usual traces; thus, we have to use a special notion for traces to poss correctly the boundary value problems. This notion is traces associated with operator L or L− traces. We derive an example (see Remark 1), which shows that for every L²- solution to the Dirichlet problem for the wave equation, its value u|_∂K on the boundary ∂K does not exist, but its “improved” value −x₁x₂u|_∂K on boundary ∂K exists. It means that multiplying by some polynomial we “improve” a solution. This polynomial depends on the equation. In the case of the wave operator $Lu=\frac{{\partial }^{2}u}{\partial x_1\partial x_2}$, this polynomial equals x₁x₂, what is the symbol L(x) = x₁x₂ of the wave operator. Therefore, such “improved” traces are called the traces associated with operator L or simply the L−traces.

At that moment, there are not any results on the maximum principle even for the model case of linear two- dimensional fourth-order hyperbolic equations with constant coefficients and homogeneous symbol (without lower terms), which are under consideration of the present study.

We also derive an interesting interpretation (as periodicity of characteristic billiard or the John's mapping) of the Fredholm's property violation. For second-order hyperbolic equations, the fact that periodicity of the John's algorithm is sufficient for violation of the Fredholm property for the Dirichlet problem was proved by John [15] (for the wave equation) and Burskii and Zhedanov [3] (for general second-order hyperbolic equations with constant complex coefficients). Analogous result is true for fourth-order hyperbolic equations and will be proved in the present study.

Therefore, obtaining such results as the maximum principle, uniqueness, existence and regularity, kernel dimension, the Fredholm property for weak solutions to fourth-order hyperbolic equations and boundary value problems for them is very important for the reason of their further applications and is the main goal of the study.

2 Statement of the problem and auxiliary definitions

Let us start to establish the maximum principle for weak solutions to the Cauchy problem for Equation 1 in some admissible planar domain. It is expected that in the hyperbolic case, characteristics of the equations play a crucial role.

Let C_j, j = 1, 2, 3, 4 be characteristics, Γ₀: = {x₁ ∈ [a, b], x₂ = 0} is initial line, and define Ω as a domain which is restricted by the characteristics C_j, j = 1, 2, 3, 4 and Γ₀ by the following way. We choose some arbitrary point C and draw through this point two characteristics, C₁ and C₂, for instance. Another two characteristics (C₃ and C₄) we draw through the ends a and b of initial line Γ₀. We determine a points O₁ and O₂ as intersections of C₁, C₃ and C₂, C₄ correspondingly: O₁ = C₁ ∩ C₃, O₂ = C₂ ∩ C₄. Such a way, domain Ω is a pentagon aO₁CO₂b. Consider also the Cauchy problem for Equation 1 on Γ₀:

$\begin{array}{ll}u{|}_{{\Gamma }_0}=\phi (x),u_{\nu }^{\prime }{|}_{{\Gamma }_0}=\psi (x),u_{\nu \nu }^{\prime \prime }{|}_{{\Gamma }_0}=\sigma (x),u_{\nu \nu \nu }^{\prime \prime \prime }{|}_{{\Gamma }_0}=\chi (x),& (2)\end{array}$

where φ, ψ, σ, and χ are given weak regular functions on Γ₀, in general case $\phi ,\psi ,\sigma ,\chi \in L^2({\Gamma }_0),\nu -$ is outer normal of Γ₀.

Definition 2. We call a domain D: = {(x₁, x₂): x₁ ∈ (−∞, +∞), x₂ > 0} in the half-plane x₂ > 0 an admissible domain if it has the property that for each point C ∈ D the corresponding characteristic domain Ω is also in D. More generally, D is a admissible if it is the finite or countable union of characteristics 5 angles (in the case of fourth-order equations with constant coefficients, there exist four different and real characteristics lines).

Establishment of the maximum principle allows us to obtain a local properties of solution to the Cauchy problem (Equations 1, 2) on a arbitrary interior point C ∈ D.

We will consider a weak solution to the problem (Equations 1, 2) from the domain of definition D(L) of maximal operator associated with the differential operation L in Equation 1. Following Burskii and Buryachenko [6], Grubb [13], and Hörmander [14], we remind the corresponding definitions.

In a bounded domain Ω, we consider linear differential operation $\mathcal{L}$ of m−th order, m ≥ 2, and formally adjoint ${\mathcal{L}}^{+}$:

$\begin{array}{ll}\mathcal{L}(D_x)={\displaystyle \sum _{\left|\alpha \right|\le m}}{a}_{\alpha }{D}^{\alpha },{\mathcal{L}}^{+}(D_x)={\displaystyle \sum _{\left|\alpha \right|\le m}}{D}^{\alpha }(a_{\alpha }),& (3)\end{array}$

where α = (α₁, α₂, ...α_n), |α| = α₁ + α₂ + ... + α_n is multi-index. Note, that for Equation 1 n = 2, m = 4.

Definition 3. Minimum operator. [6]. Let us consider differential operation $\mathcal{L}$ (Equation 3) on functions from the space $C_0^{\infty }(\Omega ).$ The minimum operator L₀ is called extension of operation $\mathcal{L}$ from $C_0^{\infty }(\Omega )$ to the set $D(L_0):\; =\overline{C_0^{\infty }(\Omega )}.$ The closure is realized in the norm of graph of operator L: $\left|\right|u|{|}_L^2:\; =|\left|u\right|{|}_{L_2(\Omega )}^2+\left|\right|Lu|{|}_{L_2(\Omega )}^2.$

Definition 4. Maximum operator. [6]. The maximum operator L is defined as the restriction of differential operation $\mathcal{L}(D_x)$ to the set D(L): = {u ∈ L²(Ω):Lu ∈ L²(Ω)}.

Definition 5. [6]. The operator $\tilde{L}$ is defined as the extension of minimum operator L₀, to the set $D(\tilde{L}):\; =\overline{C^{\infty }(\bar{\Omega })}.$

Definition 6. Regular operator. [6]. The maximum operator is called regular if $D(L)=D(\tilde{L}).$

It is easy to see that $D(\tilde{L})=H^4(\Omega ),$ $D(L_0)=\stackrel{0}{H^4}(\Omega ),$ the Hilbert Sobolev space of fourthly weak differentiable functions from L²(Ω).

Analogously, we introduce operators $L^{+},{\tilde{L}}^{+},$ and $L_0^{+}$ associated with the formally adjoint operation ${\mathcal{L}}^{+}$.

Definition of a weak solution to problem (Equations 1, 2) from the space D(L) is closely connected with the notion of L−traces, traces associated with the differential operator L.

Definition 7. L-traces. [5]. Assume, that for a function $u\in D(\tilde{L})$, there exist linear continuous functionals L_(p)u over the space H^m−p−1/2(∂Ω), p = 0, 1, 2..., m − 1, such that the following equality is satisfied:

$\begin{array}{ll}{(Lu,v)}_{L^2(\Omega )}-{(u,L^{+}v)}_{L^2(\Omega )}={\displaystyle \sum _{j=0}^{m-1}}(L_{(m-1-j)}u,{\partial }_{\nu }^{(j)}v).& (4)\end{array}$

Functionals L_(p)u are called L_(p) − traces of function $u\in D(\tilde{L}).$ Here, ${(·,·)}_{L^2(\Omega )}$ is a scalar product in the Hilbert space L²(Ω).

For L² − solutions, the notion of L_(p) − traces can be realized by the following way.

Definition 8. Distributions $L_{(p)}u\in H^{-p-\frac{1}{1}}(\partial \Omega ),p=0,...,m-1$ are called the p−th L−traces of a function u ∈ D(L) on ∂Ω, if the following identity is true

$\begin{array}{ll}{\displaystyle \underset{\Omega }{\int }}(Lu·\overline{v}-u·\overline{L^{+}v})dx={\displaystyle \sum _{j=0}^{m-1}}<L_{(m-1-j)}u,{\partial }_{\nu }^{(j)}v{>}_{\partial \Omega }.& (5)\end{array}$

for any functions v ∈ H^m(Ω).

For example, for some solution u ∈ D(L), L−traces have the form:

${\displaystyle \sum _{j=0}^3}<L_{(3-j)}u,{\partial }_{\nu }^{(j)}v{>}_{\partial \Omega }={\displaystyle \underset{\Omega }{\int }}f·\overline{v}dx,$

for all v ∈ KerL⁺ ∩ H^m(Ω).

Finally, we present the definition of a weak solution to problem (Equations 1, 2):

Definition 9. We will call a function u ∈ D(L) a weak solution to the Cauchy problem (Equations 1, 2), if it satisfies to the following integral identity

$\begin{array}{ll}{(f,v)}_{L^2(\Omega )}-{(u,L^{+}v)}_{L^2(\Omega )}={\displaystyle \sum _{j=0}^3}<L_{(3-j)}u,{\partial }_{\nu }^{(j)}v{>}_{\partial \Omega },& (6)\end{array}$

for any functions $v\in C_0^{\infty }(\Omega ).$ The functionals L_(p)u are called L_(p) − traces of function u, p = 0, 1, 2, 3, and completely determined by the initial data φ, ψ, σ, χ by the following way:

$\begin{array}{l}{L}_{(0)}u=-L(x)u{|}_{\partial \Omega }=-L(\nu )\phi ;\end{array}$

$\begin{array}{l}{L}_{(1)}u=L(\nu )\psi +{\alpha }_1{\phi }_{\tau }^{\prime }+{\alpha }_2\phi ;\end{array}$

$\begin{array}{ll}{L}_{(2)}u=-L(\nu )\sigma +{\beta }_1{\psi }_{\tau }^{\prime }+{\beta }_2\psi +{\beta }_3{\phi }_{\tau \tau }^{\prime \prime }+{\beta }_4{\phi }_{\tau }^{\prime }+{\beta }_5\phi ;& (7)\end{array}$

$\begin{array}{l}{L}_{(3)}u=L(\nu )\chi +{\delta }_1{\phi }_{\tau \tau \tau }^{\prime \prime \prime }+{\delta }_2\sigma \\ +{\delta }_3{\psi }_{\tau \tau }^{\prime \prime }+{\delta }_4{\psi }_{\tau }^{\prime }+{\delta }_5\psi +{\delta }_6{\phi }_{\tau \tau }^{\prime \prime }+{\delta }_7{\phi }_{\tau }^{\prime }+{\delta }_8\phi .\end{array}$

Here, α_i, i = 1, 2, β_j, j = 1, 2, ..., 5, and δ_k, k = 1, ..., 9 are smooth functions, completely determined by coefficients a_i, i = 0, 1, ..., 4.

We can use a general form of operators γ_j in left-hand side of identity (Equation 6) instead of operators of differentiation ${\partial }_{\nu }^{(j)}v$. Indeed, we define γ_j = p_jγ, where

$\begin{array}{l}\gamma :u\in H^m(\Omega )\to (u{|}_{\partial \Omega },...,u_{\nu }^{(m-1)}{|}_{\partial \Omega })\in H^{(m)}\\ =H^{m-1/2}(\partial \Omega )\times H^{m-3/2}(\partial \Omega )\times ...\times H^{1/2}(\partial \Omega ),\end{array}$

and $p_j:H^{(m)}\to H^{m-j-1/2}(\partial \Omega )-$ projection.

Remark 1. As it has been mentioned above, some examples show (see Burskii [2]) that for solutions u ∈ D(L) ordinary traces do not exist even in the sense of distributions. Indeed, let $Lu=\frac{{\partial }^{2}u}{\partial x_1\partial x_2}=0$ in the unit disk K:|x| = 1, the solution $u(x)={(1-x_1^2)}^{-\frac{5}{2}}$ belongs to L²(K), but < u|_∂K, 1 > _∂K = ∞, that means ${\displaystyle {lim}_{r\to 1-0}}\underset{\left|x\right|=r}{\int }u(x)d{s}_x=\infty .$ The trace u|_∂K does not exist even as a distribution. However, for every solution u ∈ L²(K) L₍₀₎ − trace $L_{(0)}u:\; =-L(x)u(x){|}_{\left|x\right|=1}=-x_1{x}_{2}u(x){|}_{\left|x\right|=1}\in L^2(\partial K).$ Likewise, L₍₁₎ − trace, L₍₁₎u, exists for every u ∈ L²(K):

$\begin{array}{l}{L}_{(1)}u=\left(L(x)u_{\nu }^{\prime }+L_{\tau }^{\prime }{u}_{\tau }^{\prime }+\frac{1}{2}{L}_{\tau \tau }^{\prime \prime }u\right){|}_{\partial K}\in H^{-\frac{3}{2}}(\partial K).\end{array}$

Here, τ is the angular coordinate and $u_{\tau }^{\prime }$ is the tangential derivative, and L(x) = x₁x₂− symbol of the wave operator $L=\frac{{\partial }^2}{\partial x_1\partial x_2}$.

3 Maximum principle for weak solutions of the Cauchy problem. Existence, uniqueness, and regularity of solution

We prove the maximum principle for weak solutions of the Cauchy problem (Equations 1, 2) in an admissible plane domain Ω restricted by different and non-congruent characteristics C_j, j = 1, 2, ..., 4 and initial line Γ₀.

Theorem 1. Maximum principle. Let u ∈ D(L) satisfies the following inequalities:

$\begin{array}{ll}Lu=f\le 0,x\in D,& (8)\end{array}$

and

$\begin{array}{ll}{L}_{(0)}u{\mid }_{{\Gamma }_0}\ge 0,L_{(1)}u{|}_{{\Gamma }_0}\ge 0,L_{(2)}u{|}_{{\Gamma }_0}\ge 0,L_{(3)}u{|}_{{\Gamma }_0}\ge 0,& (9)\end{array}$

then, u ≤ 0 in D.

Proof. 1. First of all, we prove the statement for smooth solutions $u\in C^{\infty }(\bar{\Omega }).$

Due to the homogeneity of the symbol in Equation 1, $L(\xi )=a_0{\xi }_1^4+a_1{\xi }_1^3{\xi }_2+a_2{\xi }_1^2{\xi }_2^2+a_3{\xi }_1{\xi }_2^3+a_4{\xi }_2^4=(\xi ,a^1)(\xi ,a^2)(\xi ,a^3)(\xi ,a^4),\xi =({\xi }_1,{\xi }_2)\in {ℝ}^2,$ we can rewrite this equation in the following form:

$\begin{array}{ll}(\nabla ,a^1)(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)u=f(x).& (10)\end{array}$

The vectors $a^j=(a_1^j,a_2^j),j=1,2,3,4$ are determined by the coefficients a_i, i = 0, 1, 2, 3, 4, and $(a,b)=a_1{\bar{b}}_1+a_2{\bar{b}}_2$ is a scalar product in ℂ². It is easy to see that vector a^j is the tangent vector of the j−th characteristic, slope φ_j of which is determined by −tanφ_j = λ_j, j = 1, 2, 3, 4. In what follows, we also consider the vectors ${ã}^j=(-{ā}_2^j,{ā}_1^j),j=1,2,3,4.$ It is obvious that (ã^j, a^j) = 0, so ã^j is a normal vector of the j−th characteristic.

Using Definitions 7 and 9 (m = 4), we assume that domain Ω is restricted by the characteristics C_j, j = 1, 2, 3, 4 and Γ₀:

$\begin{array}{c}{\displaystyle \underset{\Omega }{\int }}\left\{Lu·\bar{v}-u·\overline{L^{+}v}\right\}dx={\displaystyle \sum _{k=0}^3}{\displaystyle \underset{\partial \Omega }{\int }}{L}_{(3-k)}u·{\partial }_{\nu }^{(k)}vds=\\ ={\displaystyle \sum _{k=0}^3}{\displaystyle \underset{C_1}{\int }}{L}_{(3-k)}u·{\partial }_{\nu }^{(k)}vds+{\displaystyle \sum _{k=0}^3}{\displaystyle \underset{C_2}{\int }}{L}_{(3-k)}u·{\partial }_{\nu }^{(k)}vds+\\ +{\displaystyle \sum _{k=0}^3}{\displaystyle \underset{C_3}{\int }}{L}_{(3-k)}u·{\partial }_{\nu }^{(k)}vds\\ +{\displaystyle \sum _{k=0}^3}{\displaystyle \underset{C_4}{\int }}{L}_{(3-k)}u·{\partial }_{\nu }^{(k)}vds+{\displaystyle \sum _{k=0}^3}{\displaystyle \underset{{\Gamma }_0}{\int }}{L}_{(3-k)}u·{\partial }_{\nu }^{(k)}vds.& (11)\end{array}$

Using representation (Equation 10), we have

$\begin{array}{c}{\displaystyle \underset{\Omega }{\int }}Lu·\bar{v}dx={\displaystyle \underset{\Omega }{\int }}(\nabla ,a^1)(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)u·\bar{v}dx=\\ {\displaystyle \underset{\partial \Omega }{\int }}(\nu ,a^1)·(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)u·\bar{v}ds\\ -{\displaystyle \underset{\Omega }{\int }}(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)u·\overline{(\nabla ,a^1)v}dx.\end{array}$

Integrating by parts, we obtain:

$\begin{array}{l}{\displaystyle \underset{\Omega }{\int }L}u·\overline{v}dx={\displaystyle \underset{\partial \Omega }{\int }(\nu ,a^1)(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)}u·\overline{v}ds-\\ {\displaystyle \underset{\partial \Omega }{\int }(\nu ,a^2)(\nabla ,a^3)(\nabla ,a^4)}u·\overline{(\nabla ,a^1)v}ds+\\ {\displaystyle \underset{\partial \Omega }{\int }(\nu ,a^3)(\nabla ,a^4)}u·\overline{(\nabla ,a^2)(\nabla ,a^1)v}ds-\\ {\displaystyle \underset{\partial \Omega }{\int }(\nu ,a^4)}·u·\overline{(\nabla ,a^3)(\nabla ,a^2)(\nabla ,a^1)v}ds+\\ {\displaystyle \underset{\Omega }{\int }u}·\overline{(\nabla ,a)(\nabla ,a^3)(\nabla ,a^2)(\nabla ,a^1)v}dx.\end{array}$

Since (∇, a⁴)(∇, a³)(∇, a²)(∇, a¹)v = L⁺v and

$\begin{array}{l}{\tilde{L}}_{(0)}u:\; =(\nu ,a^4)u,{\tilde{L}}_{(1)}u:\; =(\nu ,a^3)(\nabla ,a^4)u,\\ {\tilde{L}}_{(2)}u:\; =(\nu ,a^2)(\nabla ,a^3)(\nabla ,a^4)u,\\ {\tilde{L}}_{(3)}u=L_{(3)}u=(\nu ,a^1)(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)u,\end{array}$

we have

$\begin{array}{ll}{\displaystyle \underset{\Omega }{\int }}\left\{Lu·\bar{v}-u·\overline{L^{+}v}\right\}dx={\displaystyle \underset{\partial \Omega }{\int }}{L}_{(3)}u·\bar{v}ds-{\displaystyle \underset{\partial \Omega }{\int }}{\tilde{L}}_{(2)}u·\overline{(\nabla ,a^1)v}ds+& (12)\end{array}$

$\begin{array}{l}+{\displaystyle \underset{\partial \Omega }{\int }{\tilde{L}}_{(1)}}u·\overline{(\nabla ,a^2)(\nabla ,a^1)v}ds-{\displaystyle \underset{\partial \Omega }{\int }{\tilde{L}}_{(0)}}u·(\nabla ,a^3)(\nabla ,a^2)(\nabla ,a^1)vds.\end{array}$

Difference between Equations 11, 12 is that natural traces in Equation 11 L_(3−k) are multiplied by the k−th derivative of truncated function $v:{\partial }_{\nu }^{(k)}v$ by outer normal ν. On the other hand, we determined by ${\tilde{L}}_{(3-k)}$ in Equation 12 some expressions multiplied by differential operators $L_k^{+}v,$ which can serve as analogous of natural L_(3−k) traces, k = 0, 1, 2, 3. So, in Equation 12:

$\begin{array}{l}{L}_1^{+}v:\; =(\nabla ,a^1)v,L_2^{+}v:\; =(\nabla ,a^2)(\nabla ,a^1)v,\\ L_0^{+}v=v,L_3^{+}v:\; =(\nabla ,a^3)(\nabla ,a^2)(\nabla ,a^1)v.\end{array}$

Let v ∈ KerL⁺ in Equation 12, and calculate L− traces on ∂Ω = C₁ ∪ C₂ ∪ C₃ ∪ C₄ ∪ Γ₀. For instance, for L₍₃₎u we obtain: $L_{(3)}u=(\nu ,a^1)(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)u.$ We use $(\nabla ,a^j)u=(\nu ,a^j)u_{\nu }^{\prime }+(\tau ,a^j)u_{\tau }^{\prime },j=1,2,3,4,$ where ν− normal vector and τ− tangent vector. It is easy to see that L₍₃₎u = 0 (due to presence the product (ν, a¹)) on characteristic C₁, normal vector ã¹ of which is orthogonal to the vector a¹. On the other parts of ∂Ω, there will be vanish terms containing (ν, a^j) on C_j. After that

$\begin{array}{r}{\displaystyle \underset{\partial \Omega }{\int }(\nu ,a^1)(\nabla ,a^2)(\nabla ,a^3)(\nabla ,a^4)}u={\displaystyle \underset{{\Gamma }_0}{\int }{L}_{(3)}}uds+\hfill \\ ({\tilde{a}}^2,a^1)(a^2,a^2)({\tilde{a}}^2,a^3)({\tilde{a}}^2,a^4){\displaystyle \underset{C_2}{\int }{u}_{\nu \nu \tau }}ds+({\tilde{a}}^3,a^1)({\tilde{a}}^3,a^2)(a^3,a^3)({\tilde{a}}^3,a^4){\displaystyle \underset{C_3}{\int }{u}_{\nu \nu \tau }}ds+\\ ({\tilde{a}}^4,a^1)({\tilde{a}}^4,a^2)({\tilde{a}}^4,a^3)(a^4,a^4){\displaystyle \underset{C_4}{\int }{u}_{\nu \nu \tau }}ds+\{({\tilde{a}}^2,a^1)(a^2,a^2)({\tilde{a}}^2,a^3)(a^2,a^4)+\\ ({\tilde{a}}^2,a^1)(a^2,a^2)(a^2,a^3)({\tilde{a}}^2,a^4)\}{\displaystyle \underset{C_2}{\int }{u}_{\tau \tau \nu }}ds+\{({\tilde{a}}^3,a^1)({\tilde{a}}^3,a^2)(a^3,a^3)(a^3,a^4)+\\ ({\tilde{a}}^3,a^1)(a^3,a^2)(a^3,a^3)({\tilde{a}}^3,a^4)\}{\displaystyle \underset{C_3}{\int }{u}_{\tau \tau \nu }}ds+\{({\tilde{a}}^4,a^1)({\tilde{a}}^4,a^2)(a^4,a^3)(a^4,a^4)+\\ ({\tilde{a}}^4,a^1)(a^4,a^2)({\tilde{a}}^4,a^3)(a^4,a^4)\}{\displaystyle \underset{C_4}{\int }{u}_{\tau \tau \nu }}ds+({\tilde{a}}^2,a^1)(a^2,a^2)(a^2,a^3)(a^2,a^4){\displaystyle \underset{C_2}{\int }{u}_{\tau \tau \tau }}ds+\\ ({\tilde{a}}^3,a^1)(a^3,a^2)(a^3,a^3)(a^3,a^4){\displaystyle \underset{C_3}{\int }{u}_{\tau \tau \tau }}ds+({\tilde{a}}^4,a^1)(a^4,a^2)(a^4,a^3)(a^4,a^4){\displaystyle \underset{C_4}{\int }{u}_{\tau \tau \tau }}ds+\\ {\alpha }_{4,1}{\displaystyle \underset{C_2}{\int }{u}_{\nu \nu }}ds+{\alpha }_{4,2}{\displaystyle \underset{C_3}{\int }{u}_{\nu \nu }}ds+{\alpha }_{4,3}{\displaystyle \underset{C_4}{\int }{u}_{\nu \nu }}ds+{\alpha }_{5,1}{\displaystyle \underset{C_2}{\int }{u}_{\nu \tau }}ds+{\alpha }_{5,2}{\displaystyle \underset{C_3}{\int }{u}_{\nu \tau }}ds+{\alpha }_{5,3}{\displaystyle \underset{C_4}{\int }{u}_{\nu \tau }}ds+\\ {\alpha }_{6,1}{\displaystyle \underset{C_2}{\int }{u}_{\tau \tau }}ds+{\alpha }_{6,2}{\displaystyle \underset{C_3}{\int }{u}_{\tau \tau }}ds+{\alpha }_{6,3}{\displaystyle \underset{C_4}{\int }{u}_{\tau \tau }}ds+{\alpha }_{7,1}{\displaystyle \underset{C_2}{\int }{u}_{\nu }}ds+{\alpha }_{7,2}{\displaystyle \underset{C_3}{\int }{u}_{\nu }}ds+{\alpha }_{7,3}{\displaystyle \underset{C_4}{\int }{u}_{\nu }}ds+\\ {\alpha }_{8,1}{\displaystyle \underset{C_2}{\int }{u}_{\tau }}ds+{\alpha }_{8,2}{\displaystyle \underset{C_3}{\int }{u}_{\tau }}ds+{\alpha }_{8,3}{\displaystyle \underset{C_4}{\int }{u}_{\tau }}ds.\end{array}$

Here, the coefficients α_i,j are numerated as follows: the first index i indicates the derivative of u: 1)u_νντ, 2)u_νττ, 3)u_τττ, 4)u_νν, 5)u_ντ, 6)u_ττ, 7)u_ν 8)u_τ, the second index j indicates the j + 1−th characteristic, j = 1, 2, 3. Such a way, Equation 11 has the form:

$\begin{array}{c}{\displaystyle \underset{\Omega }{\int }}Ludx={\displaystyle \underset{{\Gamma }_0}{\int }}{L}_{(3)}uds+{\alpha }_{1,1}{\displaystyle \underset{C_2}{\int }}{u}_{\nu \nu \tau }ds+{\alpha }_{1,2}{\displaystyle \underset{C_3}{\int }}{u}_{\nu \nu \tau }ds+{\alpha }_{1,3}{\displaystyle \underset{C_4}{\int }}{u}_{\nu \nu \tau }ds+\\ {\alpha }_{2,1}{\displaystyle \underset{C_2}{\int }}{u}_{\tau \tau \nu }ds+{\alpha }_{2,2}{\displaystyle \underset{C_3}{\int }}{u}_{\tau \tau \nu }ds+{\alpha }_{2,3}{\displaystyle \underset{C_4}{\int }}{u}_{\tau \tau \nu }ds+{\alpha }_{3,1}{\displaystyle \underset{C_2}{\int }}{u}_{\tau \tau \tau }ds+{\alpha }_{3,2}{\displaystyle \underset{C_3}{\int }}{u}_{\tau \tau \tau }ds+\\ {\alpha }_{3,3}{\displaystyle \underset{C_4}{\int }}{u}_{\tau \tau \tau }ds+{\alpha }_{4,1}{\displaystyle \underset{C_2}{\int }}{u}_{\nu \nu }ds+{\alpha }_{4,2}{\displaystyle \underset{C_3}{\int }}{u}_{\nu \nu }ds+{\alpha }_{4,3}{\displaystyle \underset{C_4}{\int }}{u}_{\nu \nu }ds+\\ {\alpha }_{5,1}{\displaystyle \underset{C_2}{\int }}{u}_{\nu \tau }ds+{\alpha }_{5,2}{\displaystyle \underset{C_3}{\int }}{u}_{\nu \tau }ds+{\alpha }_{5,3}{\displaystyle \underset{C_4}{\int }}{u}_{\nu \tau }ds+{\alpha }_{6,1}{\displaystyle \underset{C_2}{\int }}{u}_{\tau \tau }ds+{\alpha }_{6,2}{\displaystyle \underset{C_3}{\int }}{u}_{\tau \tau }ds+{\alpha }_{6,3}{\displaystyle \underset{C_4}{\int }}{u}_{\tau \tau }ds+\\ {\alpha }_{7,1}{\displaystyle \underset{C_2}{\int }}{u}_{\nu }ds+{\alpha }_{7,2}{\displaystyle \underset{C_3}{\int }}{u}_{\nu }ds+{\alpha }_{7,3}{\displaystyle \underset{C_4}{\int }}{u}_{\nu }ds+{\alpha }_{8,1}{\displaystyle \underset{C_2}{\int }}{u}_{\tau }ds+{\alpha }_{8,2}{\displaystyle \underset{C_3}{\int }}{u}_{\tau }ds+{\alpha }_{8,3}{\displaystyle \underset{C_4}{\int }}{u}_{\tau }ds.\end{array}$

Coefficients α_i,j are constant and depend on only coefficients a₀, a₁, a₂, a₃, a₄. By analogous way, we calculate others L− traces: L₍₀₎u, L₍₁₎u and L₍₂₎u.

To obtain the statement of Theorem 1, we choose some arbitrary point C ∈ D in admissible plane domain D and draw through this point two arbitrary characteristics, C₁ and C₂. Another two characteristics (C₃ and C₄) we draw through the ends a and b of initial line Γ₀. We determine some points O₁ and O₂ as intersections of C₁, C₃ and C₂, C₄ correspondingly: O₁ = C₁ ∩ C₃, O₂ = C₂ ∩ C₄. Such a way, domain Ω is a pentagon aO₁CO₂b. The value of a function u at the point C ∈ D, u(C) we estimate from the last equality, integrating by the characteristics C₁ and C₂ and using conditions (Equations 2, 7–9). Since a chosen point C ∈ D is arbitrary, we arrive at u ≤ 0 in D.

2. For solutions u ∈ D(L), the statement of the theorem follows from the conditions:

$\overline{C^{\infty }(\overline{\Omega }})=D(L),$

and

$\overline{C^{\infty }(\overline{\Omega }})=D(L^{+}).$

These conditions hold true for operators with constant coefficients in domains convex with respect to characteristics (see Hörmander [14]).

Theorem 1 is proved.

Remark 2. The weak form of the maximum principle for u ∈ L²(Ω) can be derived not only for solutions of the Cauchy problem (Equation 2) but also for all linear problems with constant coefficients Lu = F ∈ L²(Ω) under condition $\overline{\text{Im}{L}^{+}}=L^2(\Omega ).$

Indeed, using conditions (Equations 8, 9) and definition 9, we obtain

${\displaystyle \underset{\Omega }{\int }}u·\overline{L^{+}v}dx\le 0,$

for all v ∈ H^m(Ω). If $\overline{\text{Im}{L}^{+}}=L^2(\Omega ),$ then

${\displaystyle \underset{\Omega }{\int }}u·\bar{w}dx\le 0,$

for any w ∈ L²(Ω). The last inequality serves as a weak maximum principle for L² − solutions.

Remark 3. In the case of classical solutions of the Cauchy problem for second-order hyperbolic equations of general form with constant coefficients, the statement of Theorem 1 coincides with the result of Protter and Weinberger [23]. In this case, conditions (Equation 9) have usual form without using the notion of L−traces (see Protter and Weinberger [23]):

$\begin{array}{l}u{|}_{{\Gamma }_0}\le 0,u_{\nu }^{\prime }{|}_{{\Gamma }_0}\le 0.\end{array}$

4 Method of equation-domain duality and its application to the Goursat problem

We develop the method of equation-domain duality (see also Burskii and Buryachenko [6] and Burskii [2]) for study of the Goursat problem. This method allows us to reduce the Cauchy problem (Equation 1, 2) in bounded domain Ω to the equivalent Goursat boundary value problem. We will show that the method of equation-domain duality can be applied also to boundary value problems in the generalized statement. First of all, we consider the method of equation-domain duality for the case of classical (smooth) solutions.

4.1 Method of equation-domain duality for the case of classical (smooth) solutions

Let Ω ∈ ℝⁿ be a bounded domain defined by the inequality P(x) > 0, where P(x) is some real polynomial. The equation P(x) = 0 denotes the boundary ∂Ω. It is assumed that the boundary is non-degenerate for P, that is, |∇P| ≠ 0 on ∂Ω. Consider general boundary value problem with γ conditions on ∂Ω for m− order differential operator L (Equation 13), γ ≤ m:

$\begin{array}{ll}L(D_x)u=f(x),u{|}_{\partial \Omega }=0,u_{\nu }^{\prime }{|}_{\partial \Omega }=0,...,u_{\nu }^{(\gamma -1)}{|}_{\partial \Omega }=0.& (13)\end{array}$

By the equation-domain duality, we mean (see Burskii and Buryachenko [6]) a correspondence (in the sense of Fourier transform) between problem (Equation 13) and equation

$\begin{array}{ll}{P}^{m-\gamma }(-D_{\xi })\left\{L(\xi )w(\xi )\right\}=\widehat{f}(\xi ).& (14)\end{array}$

This correspondence is described by the following lemma.

Lemma 1. For any non-trivial solution of problem (Equation 13) in the space of smooth functions $C^m(\bar{\Omega })$, there exists a non-trivial analytic solution w of Equation 14 from the space ℂⁿ in a class $Z_{\Omega }^m$ of entire functions. The class $Z_{\Omega }^m$ is defined as the space of Fourier transforms of functions θ_Ωη, where η ∈ C^m(ℝⁿ), θ_Ω is the characteristic function of domain Ω, $w(\xi )=\widehat{{\theta }_{\Omega }u}.$ The function f(x) is assumed to be extended by zero beyond the boundary.

Proof. Let m = 4, γ = 2, and consider the following Dirichlet problem for fourth-order operator in Equation 1:

$\begin{array}{ll}L(D_x)u=f,u{|}_{P(x)=0}=f,u_{\nu }^{\prime }{|}_{P(x)=0}=0.& (15)\end{array}$

Let also $u\in C^4(\bar{\Omega })$ be a classical solution to problem (Equation 15). Denote by ũ ∈ C⁴(ℝ²) the extension of u, and apply fourth-order operator L(D_x) in Equation 1 to the product ũθ_Ω, where θ_Ω is a characteristic function of domain Ω: θ_Ω = 1 in Ω, θ_Ω = 0 out of Ω. We have:

$\begin{array}{l}L(D_x)(\tilde{u}{\theta }_{\Omega })={\theta }_{\Omega }L(D_x)\tilde{u}+\tilde{u}L(D_x){\theta }_{\Omega }+\\ L_3^{(1)}(D_x)\tilde{u}(\nabla ,a^1){\theta }_{\Omega }+L_3^{(2)}(D_x)\tilde{u}(\nabla ,a^2){\theta }_{\Omega }+L_3^{(3)}(D_x)\tilde{u}(\nabla ,a^3){\theta }_{\Omega }\\ +L_3^{(4)}(D_x)\tilde{u}(\nabla ,a^4){\theta }_{\Omega }+\\ L_3^{(1)}(D_x){\theta }_{\Omega }(\nabla ,a^1)\tilde{u}+L_3^{(2)}(D_x){\theta }_{\Omega }(\nabla ,a^2)\tilde{u}+L_3^{(3)}(D_x){\theta }_{\Omega }(\nabla ,a^3)\tilde{u}\\ +L_3^{(4)}(D_x){\theta }_{\Omega }(\nabla ,a^4)\tilde{u}+\\ L_2^{(1,2)}(D_x)\tilde{u}(\nabla ,a^1)(\nabla ,a^2){\theta }_{\Omega }+L_2^{(1,3)}(D_x)\tilde{u}(\nabla ,a^1)(\nabla ,a^3){\theta }_{\Omega }+\\ L_2^{(1,4)}(D_x)\tilde{u}(\nabla ,a^1)(\nabla ,a^4){\theta }_{\Omega }+L_2^{(2,3)}(D_x)\tilde{u}(\nabla ,a^2)(\nabla ,a^3){\theta }_{\Omega }+\\ L_2^{(2,4)}(D_x)\tilde{u}(\nabla ,a^2)(\nabla ,a^4){\theta }_{\Omega }+L_2^{(3,4)}(D_x)\tilde{u}(\nabla ,a^3)(\nabla ,a^4){\theta }_{\Omega }+\\ L_2^{(1,2)}(D_x){\theta }_{\Omega }(\nabla ,a^1)(\nabla ,a^2)\tilde{u}+L_2^{(1,3)}(D_x){\theta }_{\Omega }(\nabla ,a^1)(\nabla ,a)\tilde{u}+\\ L_2^{(1,4)}(D_x){\theta }_{\Omega }(\nabla ,a^1)(\nabla ,a^4)\tilde{u}+L_2^{(2,3)}(D_x){\theta }_{\Omega }(\nabla ,a^2)(\nabla ,a^3)\tilde{u}+\\ L_2^{(2,4)}(D_x){\theta }_{\Omega }(\nabla ,a^2)(\nabla ,a^4)\tilde{u}+L_2^{(3,4)}(D_x){\theta }_{\Omega }(\nabla ,a^3)(\nabla ,a^4)\tilde{u}.\end{array}$

Here, $L_3^{(j)}(D_x),$ $L_2^{(j,k)}(D_x),j,k=1,2,3,4$ are some differential operations of third and second order correspondingly, defined by fourth-order differential operator L(D_x) in Equation 1:

$L_3^{(j)}(D_x)=\frac{L(D_x)}{(\nabla ,a^j)},j=1,...,4,$

$L_2^{(j,k)}(D_x)=\frac{L(D_x)}{(\nabla ,a^j)(\nabla ,a^k)},j\ne k,j,k=1,..4.$

Since ũ is a solution of Equation 1, we obtain

$\begin{array}{c}L(D_x)(ũ{\theta }_{\Omega })={\theta }_{\Omega }f+ũL(D_x){\theta }_{\Omega }\\ +A^{(1)}(x){({\delta }_{\partial \Omega })}_{\nu \nu }^{\prime \prime }+A^{(2)}(x){({\delta }_{\partial \Omega })}_{\nu }^{\prime }+A^{(3)}(x){\delta }_{\partial \Omega },& (16)\end{array}$

where A^(j)(x) are some smooth functions depending on coefficients a^k, k = 1, ..., 4 and j− derivatives of function u by outer normal ν: $u_{\nu }^{(j)}$ and tangent direction τ: $u_{\tau }^{(j)},j=1,2,3.$ Taking into account conditions (Equation 15), $<{({\delta }_{\partial \Omega })}_{\nu }^{\prime },\varphi >=-<{\delta }_{\partial \Omega },{\varphi }_{\nu }^{\prime }>=-\underset{\partial \Omega }{\int }\overline{{\varphi }_{\nu }^{\prime }}(s)ds,\forall \psi \in \mathcal{D}({ℝ}^2),$ we have $ũL(D_x){\theta }_{\Omega }+A^{(1)}(x){({\delta }_{\partial \Omega })}_{\nu \nu }^{\prime \prime }=0$, and $A^{(2)}(x){({\delta }_{\partial \Omega })}_{\nu }^{\prime }=-\underset{\partial \Omega }{\int }{(A^{(2)}(s))}_{\nu }^{\prime }ds={Ã}^{(3)}(x){\delta }_{\partial \Omega }.$ From Equation 16, we obtain

$\begin{array}{ll}L(D_x)(ũ{\theta }_{\Omega })={\theta }_{\Omega }f+B^{(3)}(x){\delta }_{\partial \Omega },& (17)\end{array}$

where B⁽³⁾(x) = Ã⁽³⁾(x)+A⁽³⁾(x) is some smooth function depending on coefficients a^k, k = 1, ..., 4 and third derivatives of function u by outer normal ν: $u_{\nu }^{\prime \prime \prime },$ and tangent direction τ: $u_{\tau }^{\prime \prime \prime }.$

Let us multiply (Equation 17) by P²(x): $P^2(x)B^{(3)}(x){\delta }_{\partial \Omega }=0$, due to P(x) = 0 on ∂Ω. We apply the Fourier transform:

$\begin{array}{l}{P}^2(-D_{\xi })(v(\xi ))=\widehat{f}.\end{array}$

Here, $v(\xi )=L(\xi )w(\xi ),w(\xi )=\widehat{ũ{\theta }_{\Omega }}$ is the Fourier transform of function ũθ_Ω. Such a way we have the dual problem (Equation 14). Function $w(\xi )\in Z_{\Omega }^4,$ the space of entire functions (see, for instance, the Paley-Wiener theorem in Hörmander [14]). Lemma is proved.

As an application of Lemma 1, let us consider the Dirichlet problem for fourth-order hyperbolic Equation 1 in the unit disk K = {x ∈ ℝ²:|x| < 1}:

$\begin{array}{ll}u{|}_{\left|x\right|=1}=0,u_{\nu }^{\prime }{|}_{\left|x\right|=1}=0.& (18)\end{array}$

For case m = 4, γ = 2, m−γ = 2 we have the following dual problem:

$\begin{array}{ll}{\Delta }^{2}v=\widehat{f}(\xi ),v{|}_{L(\xi )=0}=0,& (19)\end{array}$

v = L(ξ)w(ξ). Taking into account representation (Equation 10), condition w|_{L(ξ) = 0} = 0 is equivalent to the following four conditions:

$\begin{array}{ll}w{|}_{(\xi ,a^1)=0}=0,w{|}_{(\xi ,a^2)=0}=0,w{|}_{(\xi ,a^3)=0}=0,w{|}_{(\xi ,a^4)=0}=0.& (20)\end{array}$

Since (ξ, a^j) = 0 is a characteristic, j = 1, 2, ..., 4 we conclude that problem (Equation 19) is the Goursat problem. The method of equation-domain duality allows us to reduce the problem of solvability of a boundary value problem for high-order equations (particularly, hyperbolic type) to the equivalent problem for some equation of less complicated structure and of lower order (in particular, for elliptic type equation, see Equation 19). Thus, the Dirichlet problem for fourth-order hyperbolic equation in a unit disk described by second-order curve $P(x)=x_1^2+x_2^2-1$ is equivalent to the Goursat problem for second-order equation P(D_x)u = 0. Because the curve P(x) = 0 is elliptic, we reduced the Dirichlet problem for fourth-order hyperbolic equation to the Goursat problem for second-order elliptic equations P(D_x)u = 0, which are well studied.

4.2 Method of equation-domain duality for the case of weak solutions and solutions from D(L)

We prove the analog of Lemma 1 for solutions u ∈ D(L). For any function u ∈ H^m(Ω), m ≥ 4, L_(p)u− traces can be expressed by the following way (it follows from Definition 8 and Equation 7): $L_{(p)}u={\displaystyle \sum _{k=0}^p}{\alpha }_{p,k}{\partial }_{\nu }^{k}u{|}_{\partial \Omega },p=0,1,2,3.$ For p = 0, L₍₀₎− trace, L₍₀₎u = u|_∂Ω coincides with usual trace.

For u ∈ D(L), we consider the following boundary value problem

$\begin{array}{ll}L(D_x)u=f(x),L_{(0)}u=0,L_{(1)}u=0,...,L_{(\gamma -1)}u=0,\gamma \le m.& (21)\end{array}$

For the Dirichlet problem (Equation 15) and u ∈ D(L), we have

$\begin{array}{ll}L(D_x)u=f(x),L_{(0)}u=0,L_{(1)}u=0,\gamma =2<m=4.& (22)\end{array}$

The principle of equation-domain duality for solutions u ∈ D(L) is assumed as the correspondence (in the sense of Fourier transform) between problem (Equations 21) and Equation 14, which is realized by the following statement. This statement (Lemma 2) is analog of Lemma 1 for u ∈ D(L).

Lemma 2. For any non-trivial solution of problem (Equation 21) in the space D(L), there exists a non-trivial analytic solution w of Equation 14 from the space ℂⁿ in a class Z_Ω of entire functions. The class Z_Ω is defined as the space of Fourier transforms of functions from the set $V=\left\{v:\text{there exists some function }u\in D(L),\text{such that}:v=u\text{ in }\Omega ,v=0,\text{ out of }\bar{\Omega }\right\},$ $w(\xi )=\hat{v}.$ The function f(x) is assumed to be extended by zero beyond the boundary.

The proof follows from Definition 9. Let us substitute the function v(x) = P^m−γ(x)e^i(x,ãj) ∈ ker(L⁺), j = 1, ..., 4, into equality (Equation 6). Function $w(\xi )=\hat{v}\in Z_{\Omega },$ the space of entire functions (see, for instance, the Paley-Wiener theorem in Hörmander [14]).

5 Connection between the Cauchy and the Dirichlet problems. Existence and uniqueness of solutions for hyperbolic equations

The main result of this section is the following existence and uniqueness theorem of the Cauchy problem (Equations 1, 2).

Theorem 2. Let us assume that there exist four functions $L_3,L_2,L_1,L_0\in L^2(\partial \Omega ),$ satisfying the conditions

$\begin{array}{ll}{\displaystyle \underset{\partial \Omega }{\int }}\{L_3(x)Q(-{ã}^j·x)+L_2(x)Q^{\prime }(-{ã}^j·x)+L_1(x)Q^{\prime \prime }(-{ã}^j·x)+& (23)\end{array}$

$\begin{array}{l}+L_0(x)Q^{\prime \prime \prime }(-{\tilde{a}}^j·x)\}d{S}_x={\displaystyle \underset{\Omega }{\int }f}(x)\overline{Q(-{\tilde{a}}^j·x)}dx,\end{array}$

for any polynomial Q ∈ C[z] ∈ KerL⁺, Q(−ã^j · x), j = 1, 2, 3, 4.

Then, there exists a unique solution u ∈ D(L) to the Cauchy problem (Equations 1, 2), whose L− traces are the given functions L₃, L₂, L₁, L₀: L_j = L_(j)− trace, j = 0, 1, 2, 3, which are determined by Equation 7.

Proof. At first, we prove existence of solution u ∈ D(L) to the Cauchy problem (Equations 1, 2).

Let us consider the auxiliary Dirichlet problem for the properly elliptic eight-order operator Δ⁴ with the given boundary conditions φ, ψ, σ, χ:

$\begin{array}{ll}{\Delta }^4\omega =0,\omega {|}_{\partial \Omega }=\phi ,{\omega }_{\nu }{|}_{\partial \Omega }=\psi ,{\omega }_{\nu \nu }{|}_{\partial \Omega }=\sigma ,{\omega }_{\nu \nu \nu }{|}_{\partial \Omega }=\chi .& (24)\end{array}$

It is well known that solution of problem (Equation 24) exists and belongs to the space H^m(Ω), m ≥ 4. We find some solution u to the Cauchy problem in the following form

$\begin{array}{ll}u=\omega +v,& (25)\end{array}$

where v is a solution of the following problem with null boundary data:

$\begin{array}{c}L(D_x)v=-L(D_x)\omega +f(x),v{|}_{\partial \Omega }=0,v_{\nu }{|}_{\partial \Omega }=0,\\ v_{\nu \nu }{|}_{\partial \Omega }=0,v_{\nu \nu \nu }{|}_{\partial \Omega }=0.& (26)\end{array}$

Since all L−traces of a function v are zero and operator L is regular, we conclude that v ∈ D(L₀) and prove resolvability of the operator equation with minimum operator L₀(D_x):

$\begin{array}{ll}{L}_0(D_x)v=-L\omega +f(x)& (27)\end{array}$

in the space D(L₀).

For resolvability of operator Equation 27 with minimum operator L₀(D_x), it is necessary and sufficiently that right-hand part satisfies the following Fredholm condition

$\begin{array}{ll}{\displaystyle \underset{\Omega }{\int }}\left\{-L\omega +f(x)\right\}\overline{Q(x)}dx=0,& (28)\end{array}$

for any Q ∈ KerL⁺.

We use Equation 4 for the case of function ω and fourth-order operator (m = 4), and taking into account boundary conditions (Equation 24), which mean that the functions L₀, L₁, L₂, L₃ are L− traces for a function ω, conditions (Equation 23), we arrive at Equation 28 for any Q ∈ KerL⁺. As consequences, we prove resolvability of Equation 27 in D(L₀). Such a way, taking into account representation (Equation 25), we arrive at the conclusion on existence for a solution u ∈ D(L).

Solution uniqueness follows from established above the maximum principle for solutions of the Cauchy problem. Theorem is proved.

Remark 4. For given boundary data $(L_3,L_2,L_1,L_0)\in H^{m-7/2}(\partial \Omega )\times H^{m-5/2}(\partial \Omega )\times H^{m-3/2}(\partial \Omega )\times H^{m-1/2}(\partial \Omega ),m\ge 4,$ f ∈ H^m−4(Ω), m ≥ 4, and for elliptic Equation 1, solution u ∈ H^m(Ω), m ≥ 4 (see Buryachenko [5]). For hyperbolic equations, it is not true because symbol L(ξ) has four real roots. Using the Fourier transform and Lemma 2, we arrive at regularity decreasing.

Remark 5. The problem of resolvability the Cauchy problem (Equations 1, 2) is reduced to the integral moment problem (Equation 23).

5.1 The Dirichlet problem

In some bounded domain Ω ∈ ℝ² with elliptic boundary ∂Ω = {x:P(x) = 0}, we consider the following Dirichlet problem for fourth-order hyperbolic Equation 1:

$\begin{array}{ll}{L}_{(0)}u{|}_{P(x)=0}=\phi ,L_{(1)}{u}_{\nu }{|}_{P(x)=0}=\psi .& (29)\end{array}$

Connection between the Dirichlet problem (Equations 1, 29) and the corresponding Cauchy problem is assumed by the following way. Let there exists some solution u^* ∈ D(L) of the Dirichlet problem (Equations 1, 29), then we can construct $L_{(j)}{u}^{*}-$traces (functions L₃, L₂, L₁, L₀ from Theorem 2), which are satisfied condition (Equation 23). From Theorem 2, it means that the Cauchy problem is solvable in D(L). To prove solvability of the Dirichlet problem (Equations 1, 29) in D(L), we have to show that there exist functions $L_2,L_3\in L^2(\partial \Omega ),$ which are uniquely determined by L₍₀₎, L₍₁₎− traces of the Dirichlet problem (Equation 29). Such a way we arrive at the following inhomogeneous moment problem:

$\begin{array}{ll}{\displaystyle \underset{\partial \Omega }{\int }}\left\{L_3(x)Q(-{ã}^j·x)+L_2(x)Q^{\prime }(-{ã}^j·x)\right\}d{S}_x={\displaystyle \underset{\Omega }{\int }}f(x)\overline{Q(-{ã}^j·x)}dx-& (30)\end{array}$

$\begin{array}{l}-{\displaystyle \underset{\partial \Omega }{\int }}\left\{L_{(1)}(x)Q^{\prime \prime }(-{ã}^j·x)+L_{(0)}(x)Q^{\prime \prime \prime }(-{ã}^j·x)\right\}d{S}_x\end{array}$

for any polynomial Q ∈ C[z] ∈ KerL⁺, Q(−ã^j · x), j = 1, 2, 3, 4. Thus, solvability of the Dirichlet problem (Equation 29) in D(L) reduces to solvability of moment problem (Equation 30).

Theorem 3. For solvability of the Dirichlet problem (Equations 1, 29) in D(L), it is necessary and sufficiently that there exists some solution $(L_3^{*}(x),L_2^{*}(x))\in L^2(\partial \Omega )\times L^2(\partial \Omega )$ of moment problem (Equation 30). Then $L_3^{*}(x)=L_{(3)}-$ trace, and $L_2^{*}(x)=L_{(2)}-$ trace.

Remark 6. The exact formulas for evaluation of a couple of functions $(L_3^{*}(x),L_2^{*}(x))\in L^2(\partial \Omega )\times L^2(\partial \Omega )$ via known L₍₀₎, L₍₁₎− traces can be found for particular cases of domain Ω. For example, the case of unit disk was considered in Buryachenko [5].

6 Role of characteristic billiard for the Fredholm property

In this section, we consider the case of Fredholm property violation. In Burskii and Buryachenko [6], the Fredholm property violation for the Dirichlet problem in C^m(Ω), m ≥ 4 was proved. Taking into account Lemma 2, we arrive at the analogous result in the L²(Ω).

Theorem 4. The homogeneous Dirichlet problem (Equation 1)⁰, (Equation 29)⁰ has a non-trivial solution in L²(Ω) if and only if

$\begin{array}{ll}{\phi }_j-{\phi }_k=\frac{\pi p_{jk}}{q},& (31)\end{array}$

with some p_jk, q ∈ ℤ, j, k = 1, 2, 3, 4. Under conditions (Equation 31), there exists a countable set of linearly independent polynomial solutions in the form:

$\begin{array}{ll}u(x)={\displaystyle \sum _{j=1}^4}{C}_j\left(\frac{1}{2q}{T}_q(-{ã}^j·x)-\frac{1}{2(q-2)}{T}_{q-2}(-{ã}^j·x)\right).& (32)\end{array}$

Here, $T_q(-{ã}^j·x)$ are Chebyshev's polynomials, and $\frac{1}{2q}{T}_q(-{ã}^j·x)-\frac{1}{2(q-2)}{T}_{q-2}(-{ã}^j·x)\in Ker{L}^{+},j=1,2,3,4.$

The necessity of condition (Equation 31) follows from the equation-domain duality (in the case of unit disk), see Lemma 2; sufficiency is proved by construction of non-trivial polynomial solutions (Equation 32). It is remarkable by the fact that Theorem 4 is true for all types of operator L. Here, we discuss conditions (Equation 31) for hyperbolic equations, in which these conditions mean the periodicity of characteristics billiard or the John's mapping.

6.1 Characteristic billiard

For domain Ω, which is convex with respect to the characteristics, we construct the mappings T_j, j = 1, ..., 4 for fourth-order hyperbolic equations by the following way.

Let M_j be some point on ∂Ω. Passing through a point M_j j−th characteristic, we obtain a point M_j+1 ∈ ∂Ω. Such a way, T_j is a mapping, which transforms M_j into M_j+1 on the j−characteristic direction with angle of slope φ_j, j = 1, 2, 3, 4. We apply the mapping T₁ for a point M₀ ∈ ∂Ω and obtain a point M₁. After that, we apply the mapping T₂ for a point M₁ and obtain a point M₂. We transform M₂ into M₃ on direction of characteristic, in which angle of slope equals φ₃, and, finally, we transform M₃ into M₄ on direction of the fourth characteristic (Figure 2). Denoted by T = T₄ ∘ T₃ ∘ T₂ ∘ T₁ : M₀ ∈ ∂Ω → M₄ ∈ ∂Ω, T is called the John's mapping. Characteristic billiard is understood as a discrete dynamical system on ∂Ω, that is, an action of group ℤ.

See Figures 1, 2 for second (wave equation) and fourth-order equations correspondingly.

Figure 1

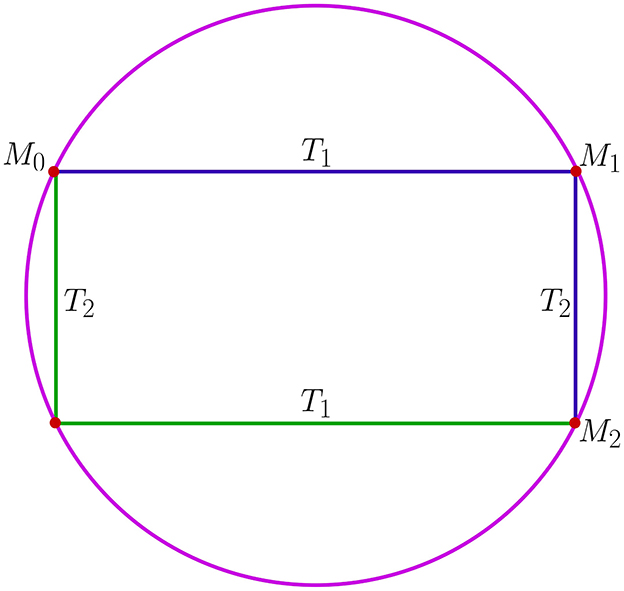
Figure 1. Characteristic billiard or the John's mapping for the wave equation $\frac{{\partial }^{2}u}{\partial x\partial y}=0$ on a disk. Period n = 2 [15].

Figure 2

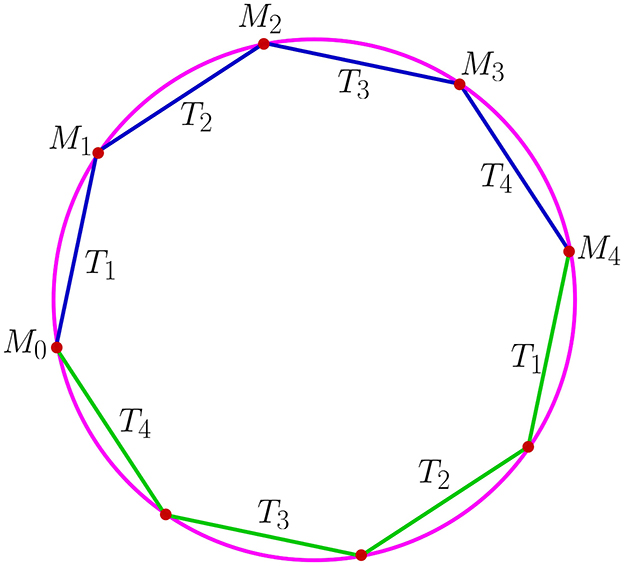
Figure 2. Characteristic billiard for fourth-order equation on a disk with equal angles between characteristics, ${\phi }_i-{\phi }_j=\frac{\pi }{4},i\ne j$, which are π−rational, and the result of Theorem 4 holds true. Period n = 2.

Some point M ∈ ∂Ω is called a periodic point, if there exists some n ∈ ℕ such that Tⁿ(M) = M. Minimal n, for which condition Tⁿ(M) = M holds, is called the period of a point M. For second-order hyperbolic equations, there was proved [3] that periodicity of the John's algorithm is sufficient for violation of the Fredholm property of the Dirichlet problem. Analogous result is true for fourth-order hyperbolic Equation 1. Let us consider domain Ω = K− unit disk in ℝ².

Let us show that conditions (Equation 31) are necessary and sufficient for periodicity of the John's algorithm. It is clear that

$\begin{array}{ll}{T}_j(M(\tau ))=2{\phi }_j-\tau ,& (33)\end{array}$

where τ is angular parameter of a point M ∈ K. From Equation 33, it follows

$T^n(M)=2n({\phi }_4-{\phi }_3+{\phi }_2-{\phi }_1)+\tau =2n({\phi }_4-{\phi }_3+{\phi }_2-{\phi }_1)+2\pi m+\tau ,$

for any m ∈ ℤ. Under conditions (Equation 31), any point M ∈ K is periodical; thus, the John's algorithm is periodical. If now mapping T is periodical for some n ∈ ℕ, then φ₄ − φ₃ + φ₂ − φ₁ ∈ πℚ, which implies that conditions (Equation 31) are satisfied.

Such a way we arrive at the following statement.

Theorem 5. The periodicity of characteristic billiard on the unit disk is necessary and sufficient for violation of the Fredholm property of the Dirichlet problem (Equation 1)⁰, (Equation 29)⁰ in L²(K). Its kernel consists of countable set of linearly independent polynomial solutions (Equation 31).

7 Discussion

In this section, we discuss some potential challenges in applying the results and proposed methods.

The first challenge concerns the presence of some lower terms in many hyperbolic models, for which our results can be applied.

For example, a model of Timoshenko beam with and without internal damping has the form

$EI\frac{{\partial }^{4}u}{\partial x^4}-\left(\rho I+\frac{\rho EI}{kG}\right)\frac{{\partial }^{4}u}{\partial x^2\partial t^2}+\frac{{\rho }^{2}I}{kG}\frac{{\partial }^{4}u}{\partial t^4}+\rho A\frac{{\partial }^{2}u}{\partial t^2}=0.$

Here, u is a deflection of beam due to bending only, G is a modulus of rigidity, A is a constant, cross-sectional area of beam, ρ− mass density of a beam material, E− modulus of elasticity, I- moment of inertia of a beam cross-section with respect to the neutral axis of bending, k- constant, depends on the shape of the cross-section of a beam. Qualitative analysis for initial and boundary value problems is possible via application of maximum principle. For this reason, we need to have an analog of Theorem 1 for fourth-order equations, containing second-order lower terms.

The same situation appears in the case of studying the boundary value problems for fourth-order hyperbolic equation which is connected with response of semi-space to a short laser pulse and belongs to generalized thermoelasticity [12]. The model equation of this process contains third -order lower term and has the form:

$\frac{{\partial }^{4}u}{\partial x^4}-(1+t_0+\epsilon t^0)\frac{{\partial }^{4}u}{\partial x^2\partial t^2}+t_0\frac{{\partial }^{4}u}{\partial t^4}-(1+\epsilon )\frac{{\partial }^{3}u}{\partial x^2\partial t}+\frac{{\partial }^{3}u}{\partial t^3}=f(x,t),$

where $t_0,t^0,$ and ε are constants, $t^0\ge t_0>1,\epsilon >0,{(1+t_0+\epsilon t^0)}^2>4t_0$, f(x, t) is a given function.

Another application of obtained results concerns the cases of non-linear external forces. A lot of models involve external sources f depending on u:f(u), which make the equation under consideration quasilinear. Due to similar principal part, our methods are still applied because L− traces are not changed:

$L(D_x)u=f(u).$

Here, the operator L is the same as in Equation 1.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YA: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft. KB: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Volkswagen Foundation (the project number 9C624). Kateryna Buryachenko was supported by Math+, project AA2-21.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Agmon S, Nirenberg L, Frotter MH. A maximum principle for a class of hyperbolic equations and applications to equations of mixed elliptic–hyperbolic type. Commun Pure Appl Mathem. (1953) 6:455–70. doi: 10.1002/cpa.3160060402

Crossref Full Text | Google Scholar

2. Burskii VP. Methods for Studying Boundary Value Problems for General Differential Equations. Kyiv: Naukova dumka. (2002).

Google Scholar

3. Burskii VP, Zhedanov AS. On Dirichlet, Poncelet and Abel problems. Commun Pure Appl Analysis. (2013) 12:1587–633. doi: 10.3934/cpaa.2013.12.1587

Crossref Full Text | Google Scholar

4. Burskii VP, Buryachenko KO. Some aspects of the nontrivial solvability of homogeneous dirichlet problems for linear equations of arbitrary even order in the disk. Mathem Notes. (2005) 77:461–70. doi: 10.1007/s11006-005-0044-9

Crossref Full Text | Google Scholar

5. Buryachenko KO. Solvability of inhomogeneous boundary value problems for the fourth-order differential equations, Ukr. Math Journal. (2012) 63:1165–76. doi: 10.1007/s11253-012-0570-z

Crossref Full Text | Google Scholar

6. Burskii VP, Buryachenko KO. On the breakdown of the uniqueness of a solution of the dirichlet problem for typeless differential equations of arbitrary even order in a disk. J Mathem Sci. (2013) 190:539–66. doi: 10.1007/s10958-013-1270-4

Crossref Full Text | Google Scholar

7. Buryachenko EA. On the uniqueness of solutions of the Dirichlet problem in a disk for fourth-order differential equations in degenerated cases. Nelin Gran Zad. (2000) 10:44–9.

Google Scholar

8. Buryachenko KO. On the dimension of the kernel of the dirichlet problem for fourth order equations. Differ Equat. (2015) 51:477–86. doi: 10.1134/S0012266115040059

Crossref Full Text | Google Scholar

9. Capsoni A, Vigano GM, Bani-Hani Kh. On damping effects in Timoshenko beams. Int J Mech Sci. (2013) 73:27–39. doi: 10.1016/j.ijmecsci.2013.04.001

Crossref Full Text | Google Scholar

10. Yi C, Ying C. A class of fourth-order hyperbolic equations with strongly damped and nonlinear logarithmic terms. Electr Res Arch. (2021) 29:3867–87. doi: 10.3934/era.2021066

Crossref Full Text | Google Scholar

11. Clain S. Finite volume maximum principle for hyperbolic scalar problems. SIAM J Numer Anal. (2013) 51:467–90. doi: 10.1137/110854278

Crossref Full Text | Google Scholar

12. Fichera G. A boundary value problem connected with response of semi-space to a short laser pulse. Atti della Accad Nazionale dei Lincei Classe di Scienze Fisiche, Matem Naturali Rendiconti Lincei Matem Applic. (1997) 8:197–228.

Google Scholar

13. Grubb G. Distributions and Operators (Graduate Texts in Mathematics). New York: Springer. (2009).

Google Scholar

14. Hörmander L. The Analysis of Linear Partial Differential Operators I-IV. Berlin: Springer (1983).

Google Scholar

15. John F. The Dirichlet problem for a hyperbolic equations. Amer J Math. (1941) 63:141–54. doi: 10.2307/2371285

Crossref Full Text | Google Scholar

16. Kmit I, Recke L. Forced frequency locking for semilinear dissipative hyperbolic PDEs. J Dyn Differ Equat. (2024) 36:2951–97. doi: 10.1007/s10884-022-10236-0

Crossref Full Text | Google Scholar

17. De-Xing K. Maximum principle in nonlinear hyperbolic systems and its applications. Nonl Anal. (1998) 32:871–80. doi: 10.1016/S0362-546X(97)00534-8

Crossref Full Text | Google Scholar

18. Mawhin J, Ortega R, Robles-Pérez AM. Maximum principles for bounded solutions of the telegraph equation in space dimensions two and three and applications. J Differ Equ. (2005) 208:42–63. doi: 10.1016/j.jde.2003.11.003

Crossref Full Text | Google Scholar

19. Mawhin J, Ortega R, Robles-Perez AM. A maximum principle for bounded solutions of the telegraph equations and applications to nonlinear forcing. J Math Anal Appl. (2000) 251:695–709. doi: 10.1006/jmaa.2000.7038

Crossref Full Text | Google Scholar

20. Mawhin J, Ortega R, Robles-Prez AM. A maximum principle for bounded solutions of the telegraph equation in space dimension three. Compt Rendus Mathm. (2002) 334:1089–94. doi: 10.1016/S1631-073X(02)02406-8

Crossref Full Text | Google Scholar

21. Ortega R, Robles-Perez AM. A maximum principle for periodic solutions of the telegraph equation. J Math Anal Appl. (1998) 221:625–51. doi: 10.1006/jmaa.1998.5921

Crossref Full Text | Google Scholar

22. Posilicano A. Self-adjoint extensions of restrictions. arXiv preprint math-ph/0703078. (2007).

Google Scholar

23. Protter MH, Weinberger HF. Maximum Principle in Differential Equations. Berlin: Springer-Verlag. (1984). doi: 10.1007/978-1-4612-5282-5

Crossref Full Text | Google Scholar

24. Uzzal RU, Bhat RB, Ahmed W. Dynamic response of a beam subjected to moving load and moving mass supported by Pasternak foundation. Shock Vibr. (2012) 19:205–20. doi: 10.1155/2012/919512

Crossref Full Text | Google Scholar

25. Ruland A, Zillinger C, Zwicknagl B. Higher sobolev regularity of convex integration solutions in elasticity: the dirichlet problem with affine data in int (K^lc). SIAM J Mathem Anal. (2018) 50:3791–841. doi: 10.1137/17M1149687

Crossref Full Text | Google Scholar