Qualitative analysis of solutions for a degenerate partial differential equations model of epidemic spread dynamics

Compartmental models are widely used in mathematical epidemiology to describe the dynamics of infectious diseases or in mathematical models of population genetics. In this study, we study a time-dependent Susceptible-Infectious-Susceptible (SIS) Partial Differential Equation (PDE) model that is based on a diffusion-drift approximation of a probability density from a well-known discrete-time Markov chain model. This SIS-PDE model is conservative due to the degeneracy of the diffusion term at the origin. The main results of this article are the qualitative behavior of weak solutions, the dependence of the local asymptotic property of these solutions on initial data, and the existence of Dirac delta function type solutions. Moreover, we study the long-term behavior of solutions and confirm our analysis with numerical computations.

1 Introduction

Despite undeniable, vast modern improvements in the development of highly efficient antibiotics and vaccines, infectious diseases still contribute significantly to deaths worldwide. The earlier recognized diseases such as cholera or plague still sometimes pose problems in underdeveloped countries, even erupting occasionally in epidemics. In developed countries, new diseases are emerging, such as the case of AIDS (1981) or hepatitis C and E (1989–1990). New variants are constantly surfacing, such as recent bird flu (SARS) epidemic in Asia, the very dangerous Ebola virus in Africa, and the recent worldwide spread of COVID-19. Overall, infectious diseases continue to be one of the most significant and challenging health problems.

Modeling of epidemiological phenomena has a very long history. The first model for smallpox was formulated by Daniel Bernoulli in 1760. A large number of models have been constructed and analyzed from the early 20th century in response to epidemics of various infectious diseases [see for example [1–6] (and references therein)]. Compartmental models are well established as mathematical modeling techniques. It is often applied to the mathematical modeling of infectious diseases. In this type of modeling, the population is subdivided into compartments or categories such as susceptible, infectious, and recovered in the widely used SIR model or susceptible, infectious, and susceptible like in SIS epidemiological scheme. Here, we are interested in analyzing the SIS model that provides the simplest description of the dynamics of a disease that is contact-transmitted and that does not lead to immunity like it is the case for COVID-19. Discrete-time Markov chain-type SIS models are considered to be a classical approach in modern mathematical modeling in epidemiology. The most recent development in mathematical epidemiology is based on the introduction of continuous modeling based on partial differential equations like in [7, 8].

In our study, for T>0 and Ω = (0, 1), Ω_T = Ω × (0, T), we study a time-dependent Susceptible-Infectious-Susceptible (SIS) model derived in the study mentioned in the reference [9], which is a generalized PDE version of a Kimura model [see [10]] in the unknown function p: = p(x, t): ${\overline{\Omega }}_T\to ℝ$:

$\begin{array}{ll}\frac{\partial p}{\partial t}=\frac{1}{2N}\frac{{\partial }^2}{\partial x^2}(f(x)p)-\frac{\partial }{\partial x}(g(x)p)\text{in\hspace{1em}}{\Omega }_T,& (1.1)\end{array}$

coupled with the boundary condition

$\begin{array}{ll}\frac{1}{2N}[(1-R_0)p(1,t)+\frac{\partial }{\partial x}p(1,t)]+p(1,t)=0,t\in \left[0,T\right],& (1.2)\end{array}$

and initial data

$\begin{array}{ll}p(x,0)=p_0(x)\text{in\hspace{1em}}\overline{\Omega }.& (1.3)\end{array}$

Here, $x\in \overline{\Omega }$ represents the fraction of infected, N is the size of the population of interest, p is the probability to find a fraction x at time t in a population of size N, and R₀≥0 is the basic reproductive factor.

$f(x):=x(R_0(1-x)+1)\text{and }g(x):=x(R_0(1-x)-1)$

are connected with variance and the mean of the change of x in the frame of Kimura model. Note that (1.1) is parabolic equation with non-negative characteristic form, and it is degenerated on the boundary of the domain at x = 0. The corresponding Fichera function for (1.1) [see e. g. [11, (1.1.3), p.17]] is $b(x,t)=\frac{1}{2N}(f^{\prime }(x)-2Ng(x))=\frac{R_0+1}{2N}>0$ on {x = 0} × {t>0}. Hence, according to [11, 12], the problem (1.1–1.3) is well-posed without any boundary conditions at x = 0 for all t>0. Reduced number of boundary conditions required for well-posedness of degenerated problems is a well-known phenomenon, and some interesting examples are shown in the study mentioned in the reference [13, 14]. Imposing zero boundary condition at x = 0 makes the problem to be over-determined, and because some weak solutions have this property, the set of solutions for the over-determined problem will not be empty.

It is worth noting that processes defined by similar models were studied by Feller in the early 1950s and used to great effect by Kimura, et al. in the 1960s and 70s to give quantitative answers to a wide range of questions in population genetics. However, rigorous analysis of the analytic properties of these equations is only the focus of applied mathematicians. The study of initial or/and initial-boundary value problems for degenerated equations, including Kimura-type operators, has a long history. Here, we do not provide a complete survey of the published results pertaining to these degenerated equations. Instead, we survey some of them for the benefit of the interested reader. Indeed, the investigation of elliptic and parabolic problems, leading to degenerated equations containing operators such as

$L:=a(x){\displaystyle \sum _{ij=1}^n}{a}_{ij}(x)\frac{{\partial }^2}{\partial x_i\partial x_j}+{\displaystyle \sum _{i=1}^n}{b}_i(x)\frac{\partial }{\partial x_i}$

with a(x) ≈ |x|^α, α > 0, and a_ij and satisfying ellipticity conditions, are extensively studied by many authors with various analytical approaches [see e.g. [11, 12, 15–26]] including stochastic calculus [27–35].

Under suitable assumptions on the asymptotic behavior of the operator's coefficients at the boundary of the domain, the uniqueness of bounded and unbounded solutions, as well as solutions belonging to the weighted Sobolev spaces, was shown in the study mentioned in the reference [12, 20, 22–24, 36] without prescribing any boundary conditions at the origin. The qualitative properties of the corresponding solutions, including the maximum principle and the Harnack inequality, are discussed in the study mentioned in the reference [31–33, 37–39] (see also references therein). Local asymptotic behavior of solutions for different types of degenerate equations was rigorously studied in the study mentioned in the reference [40–42]. We also refer the reader to the study mentioned in the reference [30–32, 34, 43], where the theories of existence and uniqueness of solutions to stochastic differential equations with degenerate diffusion coefficients are developed. Additionally, the well-posedness of the related problems in the case of α = 1 is discussed in the study mentioned in the reference [27–29]. It is worth noting that degenerate diffusion is examined in the context of measure-valued process [see [44–46]] via the semigroup techniques [47–49].

Finally, for the well-posedness of parabolic degenerate problems, we refer to the study mentioned in the reference [15, 16, 18, 21, 25, 26, 35, 50–52], where the existence of weak and classical solutions is established for different values of α>0. Previous researchers such as Chen and Weth-Wadman [53] and Epstein and Mazzeo [31] restricted their attention to the solutions with the best possible regularity properties, which leads to considerable simplifications and limitations. For real applications, it is important to consider solutions with more complicated behavior, which is the goal of our study.

The outline of the study is as follows: in Section 2, we show the existence of stationary solutions, analyze the dependence of their asymptotic behavior, near the origin, on initial data, confirm numerically their meta-stability, and analyze convergence; in Section 3, we analyze particular classical and weak solutions. We used COMSOL Multiphysics^® software to perform the numerical simulations [54].

2 Weak solutions: convergence to steady state and asymptotic behavior as t → +∞

Throughout the whole article, we encounter the usual spaces W^{1, p}(Ω), L^p(Ω), and $L_{\omega }^2(\Omega )$. It is worth noting that the last class is a weighted space L² with a weight ω and the induced norm

$\Vert v{\Vert }_{L_{\omega }^2(\Omega )}={({\displaystyle \underset{\Omega }{\int }\omega }(x)v^2(x)dx)}^{1/2}.$

Moreover, we use the notations H¹(Ω) and $H_0^1(\Omega )$ for W^{1, 2}(Ω) and $W_0^{1,2}(\Omega )$, respectively.

In this section, as it is mentioned in the introduction, we discuss the long-term behavior of a weak solution to problem (1.1–1.3). To that end, we first construct the explicit stationary solution P_s: = P_s(x): $\overline{\Omega }\to ℝ$ related to (1.1-1.3), and then, we examine a set of initial data which provide the convergence of the weak solution as T → +∞. In particular, we consider a case of convergent p(x, t) to P_s(x).

2.1 Existence of a steady state

First, we start with getting an analytical formula for a stationary solution for (1.1):

$\begin{array}{ll}\frac{1}{2N}\frac{d}{dx}\left(\frac{d}{dx}(f(x)P_s)-2Ng(x)P_s\right)=0\text{in\hspace{1em}}\Omega ,& (2.1)\end{array}$

coupled with the boundary condition:

$\begin{array}{ll}\frac{d}{dx}{P}_s(1)=-(2N-R_0+1)P_s(1).& (2.2)\end{array}$

Integrating (2.1) in x and taking into account (2.2), we get

$\frac{d}{dx}(f(x)P_s)=2Ng(x)P_s.$

It is apparent that this equation has a general solution

$\begin{array}{ll}f(x)P_s(x)=CF(x),& (2.3)\end{array}$

where

$\begin{array}{c}F(x):=e^{2N{\displaystyle \underset{0}{\overset{x}{\int }}\frac{g(s)}{f(s)}ds}}=e^{2Nx}{(\frac{R_0(1-x)+1}{R_0+1})}^{\frac{4N}{R_0}}\text{ if }{R}_0>0,\\ \text{and }F(x)=e^{-2Nx}\text{ if }{R}_0=0,\\ C:=\underset{x\to 0}{\lim }f(x)P_s(x).\end{array}$

As a result, we obtain the explicit form of the classical stationary solution to (1.1–1.3)

$\begin{array}{ll}{P}_s(x)=\frac{C}{\omega (x)}\text{ where }\omega (x):=\frac{f(x)}{F(x)}.& (2.4)\end{array}$

Observe that the changing-sign convection term for R₀ = 2 equals zero at x = 0.5, leading to a wave-like solution that moves toward this point, forming a meta-stable steady-state shape. This illustrates that the solution's short-term behavior is driven by the convection, as shown in Figures 1, 2. It takes a long-time for meta-stable steady state (a wave-like solution that slowly changes its shape) to move mass toward the origin. These long-term dynamics are due to a slow diffusion effect, and eventually, the solution blows up at the origin, which is indeed the case for two different sets of parameter values, as shown in Figures 3, 4. All numerical simulations show high accuracy of the mass conservation property even for long-term computations, which suggests the existence of a solution of Delta function type that acts as a global attractor in this dynamical system.

Figure 1

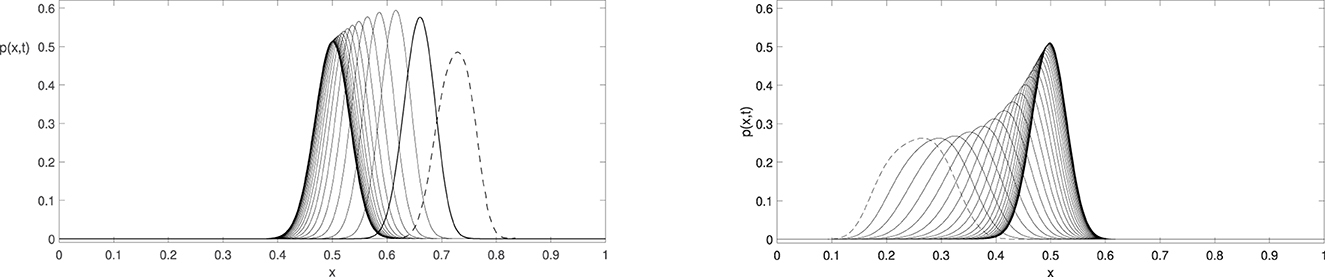
Figure 1. These two pictures illustrate the dominant behavior of convection in the short-term t ∈ [0, 0.1]. (Left) Convection moves the solutions toward the steady state from the right side to the left one for R₀ = 2 and N = 200, (Right) convection moves the solutions toward the steady state from the left side to the right one for the same parameter values. The initial data are plotted with a dashed line.

Figure 2

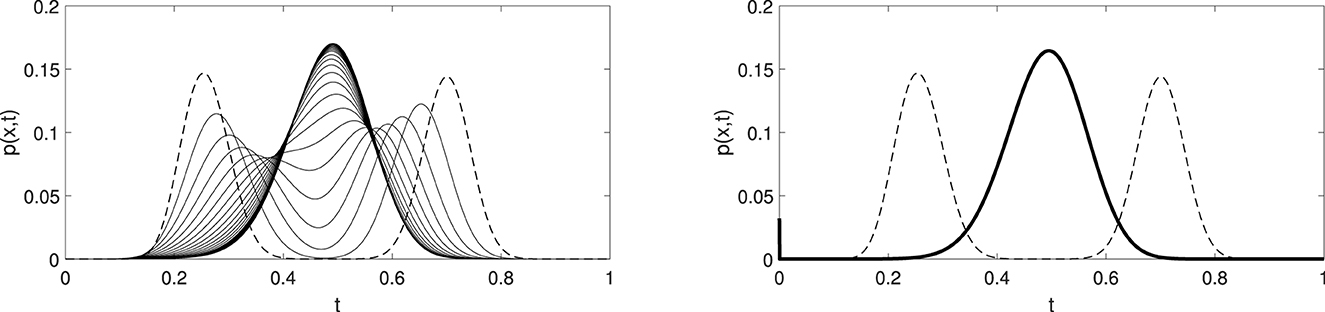
Figure 2. These two pictures illustrate t ∈ [0, 0.1] short-term dynamics for R₀ = 2 and N = 100 (Left) and t ∈ [0, 2000] long-term dynamics with blow up at the origin (Right). The initial data are plotted with a dashed line.

Figure 3

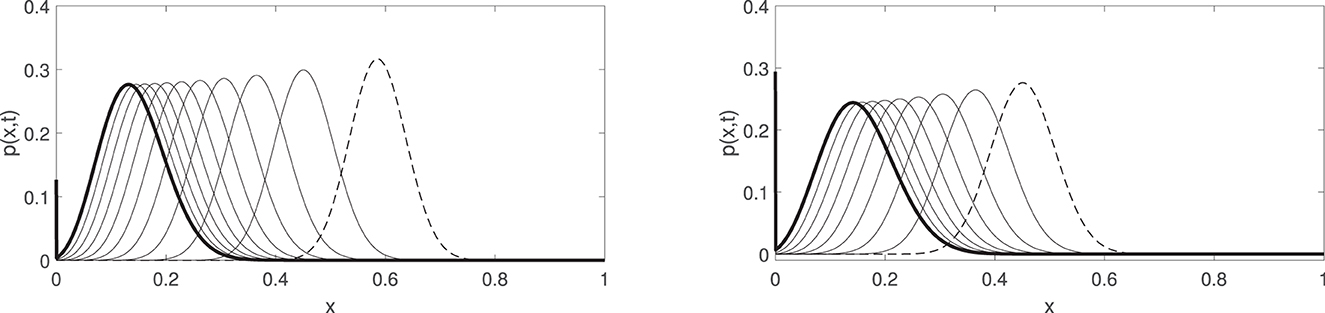
Figure 3. These two pictures illustrate the dominant behavior of convection in the short-term t ∈ [0, 0.1]. (Left) Convection moves solutions toward the origin, here R₀ = 0.5 and N = 100 and where solutions blow up. (Right) Convection again moves solutions toward the origin, here R₀ = 1 and N = 100 and where solutions blow up. The initial data are plotted with a dashed line.

Figure 4

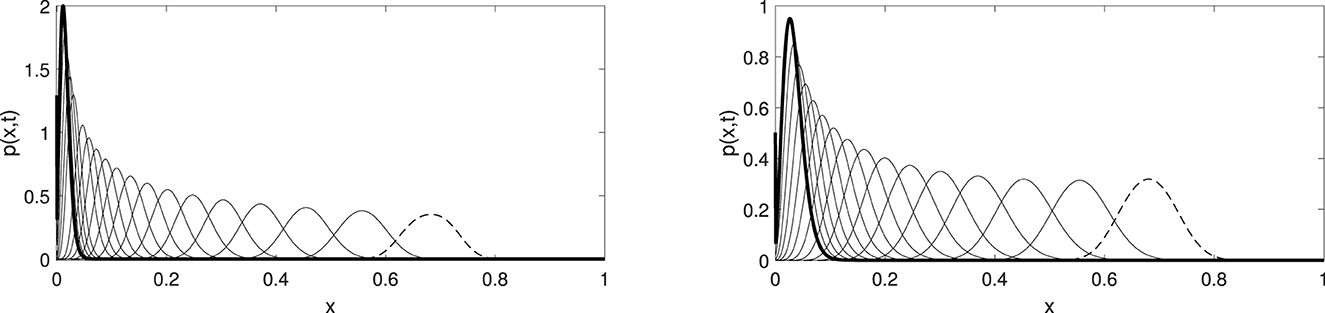
Figure 4. These two pictures illustrate the dominant behavior of convection in the short term t ∈ [0, 0.1]. (Left) Convection moves solutions toward the origin, here R₀ = 0 and N = 100, where the solutions blow up. (Right) Convection again moves solutions toward the origin, here R₀ = 0 and N = 200, where the solutions blow up. The initial data are plotted with a dashed line.

2.2 Long-term behavior of a weak solution

Assuming that ω(x) is defined by Equation (2.4) and that

$N\ge 1,R_0\ge 0\text{and\hspace{1em}}0\le p_0(x)\in L_{\omega }^2(\Omega ).$

We define a weak solution of (1.1–1.3) in the following sense:

Definition 2.1. A non-negative function $p(x,t)\in C(\left[0,T\right];L_{\omega }^2(\Omega ))$ is a weak solution of problem (1.1)–(1.3) for any T>0 if

$p_t\in L^2(0,T;{(H^1(\Omega ))}^{\prime }),{(\omega (x)p)}_x\in L^2({\Omega }_T),$

and p satisfies (1.1) in the sense

${\displaystyle \underset{0}{\overset{T}{\int }}{\langle \frac{\partial p}{\partial t},\psi \rangle }_{{(H^1)}^{\prime },H^1}dt}+{\displaystyle \underset{{\Omega }_T}{\iint }(\frac{1}{2N}\frac{\partial (f(x)p)}{\partial x}-g(x)p)\frac{\partial \psi }{\partial x}dxdt}=0$

for all ψ ∈ L²(0, T; H¹(Ω)), and ψ (0, t) = 0 for allt ∈ [0, T]. Here, ${\langle u,v\rangle }_{{(H^1)}^{\prime },H^1}$ is a dual pair of elements u ∈ (H¹)′ and v ∈ H¹.

Now, we are ready to state our first main result related to the asymptotic behavior of a weak solution to (1.1–1.3).

Theorem 1. (i) Let $0\le p_0(x)\in L_{\omega }^2(\Omega )$ and $\underset{x\to 0}{\lim }\omega (x)p(x,t)=0$, a weak solution p(x, t) satisfies the relation

${\omega }^{\frac{1}{2}}(x)p(x,t)\to 0\text{ strongly in }{L}^2(\Omega )\text{ as }t\to +\infty .$

Moreover, if ${(\omega (x)p_0(x))}_x\in L^2(\Omega )$, ω(x)p(x, t)∈C([0, +∞);H¹(Ω)), and there is convergence

$\begin{array}{ll}\omega (x)p(x,t)\to 0\text{ strongly in }{H}^1(\Omega )\text{ as }t\to +\infty .& (2.5)\end{array}$

(ii) Let ${\omega }^{\frac{1}{2}}(x)p_0(x)\in L_{\omega }^2(\Omega )$, if p(x, t) is a weak solution to (1.1–1.3) and $\underset{x\to 0}{\lim }\omega (x)p(x,t)=\mathcal{C}>0$, where $C$ is the same constant as in Equation (2.3), there exists a constant $C_1>0$, depending on R₀ and N, such that

$\begin{array}{ll}\left|\right|\omega (x)p(x,t)-C|{|}_{L^2(\Omega )}\le C_1||\omega (x)p_0(x)-C|{|}_{L^2(\Omega )}\text{ for all }t\ge 0.& (2.6)\end{array}$

Moreover, if $\omega (x){(\omega (x)p_0(x))}_x\in L^2(\Omega )$, there exist a constant C₁>0 and a time T^*>0, depending on R₀ and N, such that

$\left|\right|\omega (x)\frac{\partial }{\partial x}(\omega (x)p(x,t))|{|}_{L^2(\Omega )}\le C_2||\omega (x)p_0(x)-C|{|}_{L^2(\Omega )}\text{ for all }t\ge T^{*}.$

Numerical simulations in Figures 5, 6 illustrate the convergence result in Equation (2.6).

Figure 5

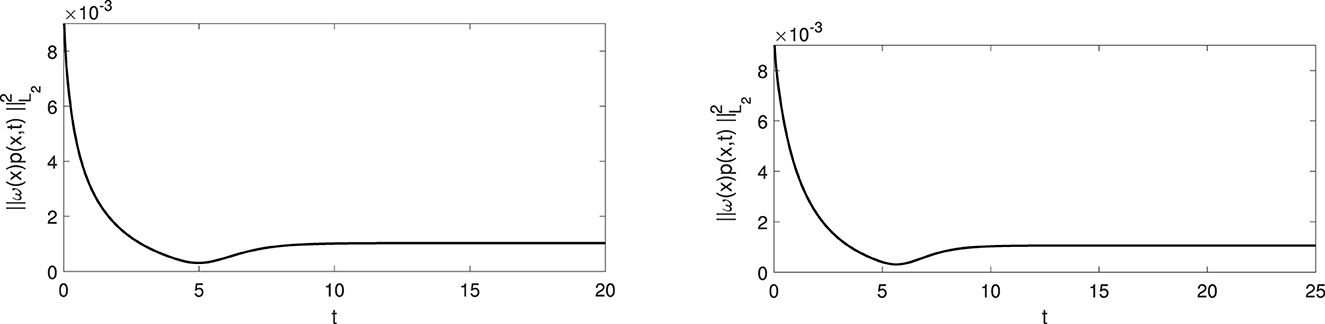
Figure 5. These two pictures illustrate convergence of weighted L²-norm of p(x, t) to a constant for R₀ = 0 and N = 100, $C=4.3*10^{-5}$ (left) and R₀ = 0 and N = 200, $C=1.7*10^{-4}$ (right).

Figure 6

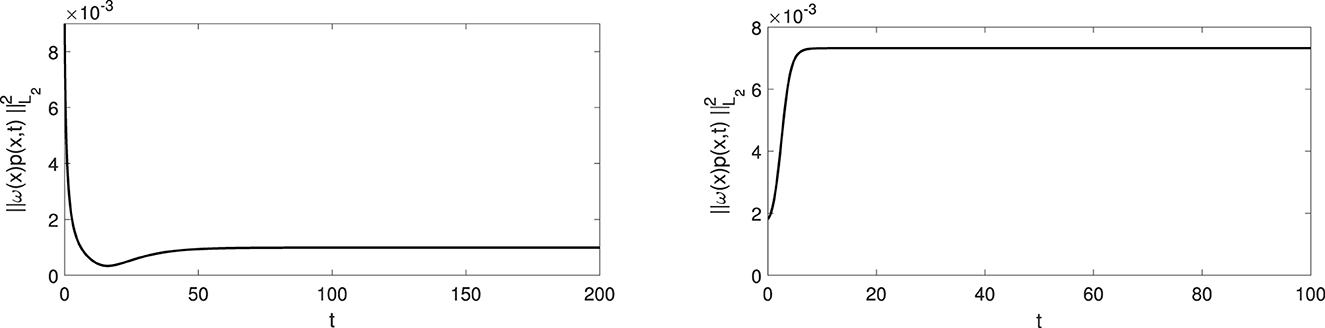
Figure 6. These two pictures illustrate convergence of weighted L²-norm of p(x, t) for R₀ = 0.5 and N = 100, $C=4.2*10^{-5}$ (left) and R₀ = 2 and N = 200, $C=1.6*10^{-4}$ (right).

Note that Theorem 1 describes a behavior of a weak solution to direct well-posed problem (1.1)–(1.3), depending on the different types of behavior ω(x)p(x, t) at x = 0, taking into account two explicit solutions: steady state (subsection 2.1) and Fourier series solutions (subsection 3.1). In other words, our main result has a conditional characteristic via inserting additional assumptions on the term ω(x)p(x, t) as x → 0 in the statement of the Theorem 1 but not to the statement of the problem (1.1)–(1.3). In the context of infectious disease spreading dynamic, Theorem 1 says that a different regularity of the initial data at x = 0 leads to a different rate of the disease extinction, i. e., more regular initial data give us faster decay of infection.

Remark 2.1. In this study, we do not discuss the existence and uniqueness of weak solutions vanishing at the origin. As for these issues, we refer the interested readers to Section 7 in the study mentione4d in the reference [51], where the related questions are analyzed.

Remark 2.2. In particular, Theorem 1 provides the following properties:

(i) (2.5) implies

${\displaystyle \underset{\Omega }{\int }}p(x,t)dx\to 0\text{ as }t\to +\infty ,$

where we deduce that lim_{t → +∞}p(x, t) = 0 a. e. $x\in \overline{\Omega }$;

(ii) (2.6) gives the stability of the steady state P_s.

Proof of Theorem 1. Introducing a new function z: = ω(x)p(x, t) and rewriting problem (1.1)–(1.3) in the more suitable form:

$\begin{array}{ll}\{\begin{array}{l}{\omega }^{-1}(x)\frac{\partial z}{\partial t}=\frac{1}{2N}\frac{\partial }{\partial x}(F(x)\frac{\partial z}{\partial x}),(x,t)\in {\Omega }_T,\hfill \\ \frac{\partial z}{\partial x}{|}_{x=1}=0\text{\hspace{1em} and \hspace{1em}}z{|}_{x=0}=0,t\in [0,T],\hfill \\ z(x,0)=z_0(x):=\omega (x)p_0(x),x\in \overline{\Omega }.\hfill \end{array}& (2.7)\end{array}$

Note that if $z{|}_{x=0}=C>0$, we can define a new function $\tilde{z}=z-C$, and we reduce the case to a problem similar to Equation (2.7). Since the approximation approach is well developed for this type of problem, to avoid technical details, we proceed with formal computations. Our formal computations can be rigorously justified by introducing a sequence of approximate solutions with extra regularity property, taking advantage of the standard approximation arguments, and passing to the limit in the final estimates. The weak solution will be obtained as a limit as ε → 0 of smooth solutions for the corresponding approximating problems. For any ε>0, we consider the approximating problems of Equation (2.7), where instead of ω(x) and z₀(x), we take ${\omega }_{\epsilon }(x)=\frac{f(x)+\epsilon }{F(x)}$ and $z_{\epsilon ,0}(x)\in C^{\infty }(\bar{\Omega })$ such that z_{ε, 0}(x) → z₀(x) strongly in H¹(Ω) as ε → 0. As these approximating problems are uniformly parabolic, by general PDE theory for the second order parabolic equations (see, e.g. [55]), we find a solution $z_{\epsilon }(x,t)\in C^{\infty }({\Omega }_T)$. By going through all routine calculations for z_ε, and then passing to the limit with respect to ε → 0, we arrive at the required estimates for the corresponding limit solution z.

We now verify claim (i) of Theorem 1. To this end, multiplying the equation in (2.7) by z(x, t) and integrating over Ω, we obtain as follows:

$\begin{array}{ll}\frac{1}{2}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }{\omega }^{-1}(x)z^{2}dx}+\frac{1}{2N}{\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z}{\partial x})}^{2}dx}=\frac{1}{2N}F(x)z\frac{\partial z}{\partial x}{|}_0^1=0.& (2.8)\end{array}$

Next, we take advantage of Hardy inequality [56, p. 22, (1.25) with p = q = 2]

${\displaystyle \underset{\Omega }{\int }{\omega }^{-1}(x)z^{2}dx}⩽C_H(R_0){\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z}{\partial x})}^{2}dx}$

with z(0) = 0. Here, the constant C_H(R₀) satisfies the inequalities:

$\begin{array}{r}\hfill A(R_0)⩽C_H(R_0)⩽4A(R_0)\text{\hspace{1em}with\hspace{1em}}A(R_0)=\\ \hfill \underset{r\in (0,1)}{\sup }({\displaystyle \underset{0}{\overset{r}{\int }}\frac{dx}{F(x)}})({\displaystyle \underset{r}{\overset{1}{\int }}\frac{dx}{\omega (x)}}).\end{array}$

Note that

$\begin{array}{c}\left({\displaystyle \underset{0}{\overset{r}{\int }}}\frac{dx}{F(x)}\right)\left({\displaystyle \underset{r}{\overset{1}{\int }}}\frac{dx}{\omega (x)}\right)=\left({\displaystyle \underset{0}{\overset{r}{\int }}}{e}^{-2Nx}{(R_0(1-x)+1)}^{-\frac{4N}{R_0}}dx\right)\\ \left({\displaystyle \underset{r}{\overset{1}{\int }}}{x}^{-1}{e}^{2Nx}{(R_0(1-x)+1)}^{\frac{4N}{R_0}-1}dx\right)\le \\ r^{-1}{e}^{2N}\left({\displaystyle \underset{0}{\overset{r}{\int }}}{(R_0(1-x)+1)}^{-\frac{4N}{R_0}}dx\right)\left({\displaystyle \underset{r}{\overset{1}{\int }}}{(R_0(1-x)+1)}^{\frac{4N}{R_0}-1}dx\right)\\ \le e^{2N}{(R_0(1-r)+1)}^{-\frac{4N}{R_0}}\left({\displaystyle \underset{r}{\overset{1}{\int }}}{(R_0(1-x)+1)}^{\frac{4N}{R_0}-1}dx\right)\le e^{2N},\end{array}$

where it follows that $A(R_0)\le e^{2N}$. Thus, statement (2.8) along with Hardy inequality, see [9], leads to the relation

$\begin{array}{c}{\displaystyle \underset{\Omega }{\int }}{\omega }^{-1}(x)z^2(x,t)dx\le e^{-\frac{t}{N{C}_H(R_0)}}{\displaystyle \underset{\Omega }{\int }}{\omega }^{-1}(x)z_0^2(x)dx\to 0\text{ as }t\to \\ +\infty .\end{array}$

Multiplying the equation in (2.7) by $-\omega (x)\frac{\partial }{\partial x}F(x)\frac{\partial z}{\partial x}$ and integrating over Ω, we obtain the equation

$\begin{array}{c}\frac{1}{2}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z}{\partial x})}^{2}dx}+\frac{1}{2N}{\displaystyle \underset{\Omega }{\int }\omega (x){(\frac{\partial }{\partial x}(F(x)\frac{\partial z}{\partial x}))}^{2}dx}\\ =F(x)\frac{\partial z}{\partial t}\frac{\partial z}{\partial x}{|}_0^1,\end{array}$

which implies

$\frac{1}{2}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z}{\partial x})}^{2}dx}+\frac{1}{2N}{\displaystyle \underset{\Omega }{\int }\omega (x){(\frac{\partial }{\partial x}(F(x)\frac{\partial z}{\partial x}))}^{2}dx}=0.$

To handle the second term in the left-hand side of this equality, we apply to $v=F(x)\frac{\partial z}{\partial x}$ the following inequality:

$\begin{array}{c}{\displaystyle \underset{\Omega }{\int }\frac{v^2}{F(x)}dx}⩽C_P(R_0){\displaystyle \underset{\Omega }{\int }\omega (x){(\frac{\partial v}{\partial x})}^{2}dx}\text{ with }v(1)=0,\\ \text{where\hspace{1em}}{C}_P(R_0)={\displaystyle \underset{\Omega }{\int }\frac{1}{F(x)}({\displaystyle \underset{x}{\overset{1}{\int }}\frac{dy}{\omega (y)}})dx}.\end{array}$

Hence, we end up with the relation

$\begin{array}{ll}{\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z}{\partial x})}^{2}dx}⩽e^{-\frac{t}{N{C}_P(R_0)}}{\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z_0}{\partial x})}^{2}dx}\to 0\text{ as }t\to +\infty .& (2.9)\end{array}$

As a result, we obtain the following convergence:

$z(x,t)\to 0\text{strongly in\hspace{1em}}{H}^1(\Omega )\text{ as }t\to +\infty$

provided the following inequality holds:

${\displaystyle \underset{\Omega }{\int }({\omega }^{-1}(x)z_0^2(x)+F(x){(\frac{\partial z_0}{\partial x})}^2)dx}<+\infty .$

As a simple consequence of this fact and the convergence of (2.9), we obtain an upper bound on z(x, t):

$z(x,t)⩽x^{\frac{1}{2}}{e}^{-\frac{t}{2N{C}_P(R_0)}}{({\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z_0}{\partial x})}^{2}dx})}^{\frac{1}{2}},$

which, in turn, provides the desired relation

$p(x,t)⩽\frac{x^{\frac{1}{2}}}{\omega (x)}{e}^{-\frac{t}{2N{C}_P(R_0)}}{({\displaystyle \underset{\Omega }{\int }F(x){(\frac{\partial z_0}{\partial x})}^{2}dx})}^{\frac{1}{2}}.$

We now proceed by showing that statement (ii) of Theorem 1 is in fact valid. We multiply (2.7) by ω(x)ψ(x)z(x, t) and integrate over Ω to obtain

$\begin{array}{l}\frac{1}{2}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }\psi (x)z^{2}dx}+\frac{1}{2N}{\displaystyle \underset{\Omega }{\int }f(x)\psi (x){(\frac{\partial z}{\partial x})}^{2}dx}=\\ \frac{1}{2N}(f(x)\psi (x)z\frac{\partial z}{\partial x}-\frac{1}{2}(\omega (x)\psi (x){)}^{\prime }F(x)z^2){|}_0^1\\ +\frac{1}{4N}{\displaystyle \underset{\Omega }{\int }{z}^2}\frac{\partial }{\partial x}(F(x)\frac{\partial }{\partial x}(\omega (x)\psi (x)))dx.\end{array}$

Then, choosing here

$\psi (x)={\omega }^{-1}(x){\displaystyle \underset{0}{\overset{x}{\int }}}\frac{dy}{F(y)}=\frac{F(x)}{f(x)}{\displaystyle \underset{0}{\overset{x}{\int }}}\frac{dy}{F(y)}\to \frac{1}{1+R_0}\text{ as }x\to 0,$

we arrive at the equality

$\begin{array}{ll}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }\psi (x)z^{2}dx}+\frac{1}{N}{\displaystyle \underset{\Omega }{\int }f(x)\psi (x){(\frac{\partial z}{\partial x})}^{2}dx}+\frac{1}{2N}{z}^2(1,t)=0,& (2.10)\end{array}$

where

$\begin{array}{l}{\displaystyle \underset{\Omega }{\int }}\psi (x)z^{2}dx\le {\displaystyle \underset{\Omega }{\int }}\psi (x)z_0^2(x)dx.\end{array}$

Thus, we easily conclude that

$\begin{array}{l}{\displaystyle \underset{\Omega }{\int }}{z}^2(x,t)dx\le C_1{\displaystyle \underset{\Omega }{\int }}{z}_0^2(x)dx\text{ for all }t\ge 0,\end{array}$

where $0<C_1=\frac{sup\psi (x)}{inf\psi (x)}<+\infty .$ Now, multiplying the equation in (2.7) by $-\omega (x)\varphi (x)\frac{\partial }{\partial x}(F(x)\frac{\partial z}{\partial x})$ and integrating over Ω, we obtain

$\begin{array}{l}\frac{1}{2}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }\varphi (x)F(x){(\frac{\partial z}{\partial x})}^{2}dx}+\frac{1}{2N}{\displaystyle \underset{\Omega }{\int }\omega }(x)\varphi (x)(\frac{\partial }{\partial x}(F(x)\frac{\partial z}{\partial x}){)}^{2}dx\\ =(\varphi (x)F(x)\frac{\partial z}{\partial t}\frac{\partial z}{\partial x}-\\ \frac{1}{4N}\omega (x){\varphi }^{\prime }(x)F^2(x)(\frac{\partial z}{\partial x}{)}^2){|}_0^1+\frac{1}{4N}{\displaystyle \underset{\Omega }{\int }(}\omega (x){\varphi }^{\prime }(x){)}^{\prime }{F}^2(x)(\frac{\partial z}{\partial x}{)}^{2}dx.\end{array}$

Now, consider ϕ(x) such that (ω(x)ϕ′(x))′F²(x) = 2f(x)ψ(x), i. e.,

$\varphi (x)=2{\displaystyle \underset{0}{\overset{x}{\int }}}\frac{1}{\omega (y)}\left({\displaystyle \underset{0}{\overset{y}{\int }}}\frac{1}{F(v)}\left({\displaystyle \underset{0}{\overset{v}{\int }}}\frac{ds}{F(s)}\right)dv\right)dy~\frac{x^2}{2(R_0+1)}\text{ as }x\to 0,$

we have

$\begin{array}{c}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }\varphi }(x)F(x)(\frac{\partial z}{\partial x}{)}^{2}dx+\frac{1}{N}{\displaystyle \underset{\Omega }{\int }\omega }(x)\varphi (x)(\frac{\partial }{\partial x}(F(x)\frac{\partial z}{\partial x}){)}^{2}dx\\ =\frac{1}{N}{\displaystyle \underset{\Omega }{\int }f}(x)\psi (x)(\frac{\partial z}{\partial x}{)}^{2}dx.\end{array}$

The above equality, along with (2.10), leads to

$\begin{array}{c}\frac{d}{dt}{\displaystyle \underset{\Omega }{\int }(}\varphi (x)F(x)(\frac{\partial z}{\partial x}{)}^2+\psi (x)z^2)dx+\frac{1}{N}{\displaystyle \underset{\Omega }{\int }\omega }(x)\varphi (x)\\ (\frac{\partial }{\partial x}(F(x)\frac{\partial z}{\partial x}){)}^{2}dx+\frac{1}{2N}{z}^2(1,t)=0.& (2.11)\end{array}$

Now, applying to $v=F(x)\frac{\partial z}{\partial x}$, the following estimate

${\displaystyle \underset{\Omega }{\int }\frac{\varphi (x)}{F(x)}}{v}^{2}dx⩽C_P(R_0){\displaystyle \underset{\Omega }{\int }\omega }(x)\varphi (x){(\frac{\partial v}{\partial x})}^{2}dx\text{ with }v(1)=0,$

where

$C_P(R_0)={\displaystyle \underset{\Omega }{\int }}\frac{\varphi (x)}{F(x)}\left({\displaystyle \underset{x}{\overset{1}{\int }}}\frac{dy}{\omega (y)\varphi (y)}\right)dx,$

to (2.11) and conclude that

$\begin{array}{c}{\displaystyle \underset{\Omega }{\int }\varphi (x)F(x){(\frac{\partial z}{\partial x})}^{2}dx}⩽e^{-\frac{t}{N{C}_P(R_0)}}{\displaystyle \underset{\Omega }{\int }\varphi (x)F(x){(\frac{\partial z_0}{\partial x})}^{2}dx}\\ +{\displaystyle \underset{\Omega }{\int }\psi (x)z_0^2(x)dx},\end{array}$

where

$\begin{array}{c}{\displaystyle \underset{\Omega }{\int }{\omega }^2(x){(\frac{\partial z}{\partial x})}^{2}dx}⩽\frac{\sup (\frac{\varphi (x)F(x)}{{\omega }^2(x)})}{\inf (\frac{\varphi (x)F(x)}{{\omega }^2(x)})}{e}^{-\frac{t}{N{C}_P(R_0)}}{\displaystyle \underset{\Omega }{\int }{\omega }^2(x){(\frac{\partial z_0}{\partial x})}^{2}dx}\\ +\frac{\sup \psi (x)}{\inf (\frac{\varphi (x)F(x)}{{\omega }^2(x)})}{\displaystyle \underset{\Omega }{\int }{z}_0^2(x)dx}.\end{array}$

As a result, there exists a time T^*>0 such that

${\displaystyle \underset{\Omega }{\int }{\omega }^2(x){(\frac{\partial z}{\partial x})}^{2}dx}⩽C_2{\displaystyle \underset{\Omega }{\int }{z}_0^2(x)dx}\text{ for all }t⩾T^{*}$

provided the following inequality holds:

${\displaystyle \underset{\Omega }{\int }(\psi (x)z_0^2(x)+\varphi (x)F(x){(\frac{\partial z_0}{\partial x})}^2)dx}<+\infty .$

This completes the proof of assertion (ii) and, as a consequence, of Theorem 1.

3 Solutions in weighted L²-space

In this section, we will illustrate an application of Theorem 1 by constructing solutions, using the spectral decomposition method, in a weighted L²-space. First, we analyze classical solutions to problem (2.7), and then, we discuss some classes of weak solutions.

3.1 Fourier series solutions in a weighted space

Introducing a new variable

$s=\sqrt{2N}{\displaystyle \underset{0}{\overset{x}{\int }}}\frac{dy}{f^{\frac{1}{2}}(y)},$

and denoting by

$\begin{array}{c}l(s):=\sqrt{2N}\frac{g(x)}{f^{\frac{1}{2}}(x)}=\sqrt{\frac{2N}{R_0}}\frac{\sin (\frac{1}{2}\sqrt{\frac{R_0}{2N}}s)[R_0-1-(R_0+1){\sin }^2(\frac{1}{2}\sqrt{\frac{R_0}{2N}}s)]}{|\cos (\frac{1}{2}\sqrt{\frac{R_0}{2N}}s)|},\\ s_1:=2\sqrt{\frac{2N}{R_0}}\arcsin (\sqrt{\frac{R_0}{R_0+1}}),\end{array}$

we rewrite problem (2.7) in the form as follows:

$\begin{array}{ll}\{\begin{array}{l}\frac{\partial z}{\partial t}=\frac{{\partial }^{2}z}{\partial s^2}+l(s)\frac{\partial z}{\partial s},s\in (0,s_1),t\in (0,T),\hfill \\ z(0,t)=0,\frac{\partial z}{\partial s}(s_1,t)=0,t\in [0,T].\hfill \end{array}& (3.1)\end{array}$

It is worth noting that to establish (3.1), we have made use of the following simple and verifiable relations:

$s=\{\begin{array}{l}2\sqrt{\frac{2N}{R_0}}\arcsin (\sqrt{\frac{R_0}{R_0+1}}{x}^{\frac{1}{2}})\text{\hspace{1em} if \hspace{1em}}{R}_0>0,\hfill \\ 2\sqrt{2N}{x}^{\frac{1}{2}}\text{\hspace{1em}\hspace{1em}\hspace{1em} if \hspace{1em}}{R}_0=0,\hfill \end{array}$

or as consequence

$x=\{\begin{array}{l}\frac{R_0+1}{R_0}{\sin }^2(\frac{1}{2}\sqrt{\frac{R_0}{2N}}s)\text{\hspace{1em} if \hspace{1em}}{R}_0>0,\hfill \\ \frac{1}{8N}{s}^2\text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} if \hspace{1em}}{R}_0=0.\hfill \end{array}$

Separating variables in (3.1):

$z(s,t)=T(t)S(s),$

leads to the problems

$\frac{T^{\prime }(t)}{T(t)}=\frac{S^{″}(s)+l(s)S^{\prime }(s)}{S(s)}=-\lambda ,$

where

$\begin{array}{l}{T}^{\prime }(t)=-\lambda T(t),\\ S^{″}(s)+l(s)S^{\prime }(s)=-\lambda S(s)& (3.2)\end{array}$

with

$S(0)=0,S^{\prime }(s_1)=0.$

Now, multiplying (3.2) by $p(s):=e^{\underset{0}{\overset{s}{\int }}l(y)dy}$, we immediately obtain the equation

$-{(p(s)S^{\prime }(s))}^{\prime }=\lambda p(s)S(s).$

Then, setting

$U(s)=p^{\frac{1}{2}}(s)S(s)q(s)=\frac{{(p^{\frac{1}{2}}(s))}^{″}}{p^{\frac{1}{2}}(s)}=\frac{1}{2}\left(l^{\prime }(s)+\frac{1}{2}{l}^2(s)\right),$

we arrive at the classical Sturm–Liouville problem with the continuous potential q(s)

$\begin{array}{ll}\{\begin{array}{l}-U^{″}(s)+q(s)U(s)=\lambda U(s),s\in (0,s_1),\hfill \\ U(0)=0,U^{\prime }(s_1)=0.\hfill \end{array}& (3.3)\end{array}$

From here, we rely on standard computational methods to obtain the following asymptotic behavior of eigenvalues and eigenfunctions to problem 3.3:

${\lambda }_k~{(\frac{\pi }{s_1})}^2{\left(k+\frac{1}{2}\right)}^2,U_k(s)~sin\left(\frac{\pi }{s_1}(k+\frac{1}{2})s\right),$

or returning to (3.2):

${\lambda }_k~{(\frac{\pi }{s_1})}^2{\left(k+\frac{1}{2}\right)}^2,S_k(s)~e^{-\frac{1}{2}{\displaystyle \underset{0}{\overset{s}{\int }}}l(y)dy}sin\left(\frac{\pi }{s_1}(k+\frac{1}{2})s\right).$

Thus, problem (3.1) has a particular solution

$z(s,t)={\displaystyle \sum _{k=0}^{+\infty }}{c}_k{e}^{-{\lambda }_{k}t}{S}_k(s),$

which, in turn, means

$z(x,t)={\displaystyle \sum _{k=0}^{+\infty }}{c}_k{e}^{-{\lambda }_{k}t}{\phi }_k(x),$

where

${\lambda }_k~\frac{{\pi }^2}{N}{\left(k+\frac{1}{2}\right)}^2,{\phi }_k(x)~e^{-N^{\frac{3}{2}}x}sin\left(\pi (k+\frac{1}{2})\frac{arcsin\left(\sqrt{\frac{R_0}{R_0+1}}{x}^{\frac{1}{2}}\right)}{arcsin\left(\sqrt{\frac{R_0}{R_0+1}}\right)}\right).$

Finally, keeping in mind the relation z(x, t) = ω(x)p(x, t), we deduce the formal solution

$p(x,t)=\frac{1}{\omega (x)}{\displaystyle \sum _{k=0}^{+\infty }}{c}_k{e}^{-{\lambda }_{k}t}{\phi }_k(x)$

that is a weak solution in a weighted L²-space in the sense of the Definition 2.1. It is worth noting that the asymptotic behavior of the solution $\frac{C_1}{\sqrt{x}{e}^{C_{2}t}}$ as x → 0⁺ is in agreement with Theorem 1 (i).

3.2 The Dirac delta function solutions

In this section, we show that Dirac delta function type solutions belong to our class of weak solutions. The main problem here is that, with zero on the boundary, the integral $\underset{0}{\overset{a}{\int }}f(z)\delta (z)dz$ is a priori not well defined (over-determined ill-posed problem was previously considered in the study mentioned in the reference [9]). Now, we denote positive and non-negative cut of functions by f(x)χ_{x>0} and f(x)χ_{x≥0}, respectively. This corresponds to integrating δ function against the function f(x)χ_{x>0} (or possibly f(x)χ_{x≥0}), which is not continuous at the origin x = 0, where the support of the Dirac delta function lies. With the Dirac delta function at the boundary of the integration, only formal expressions could be found in the literature: $\underset{0}{\overset{a}{\int }}f(z)\delta (z)dz=\underset{-a}{\overset{0}{\int }}f(z)\delta (z)dz=\frac{1}{2}f(0)$. This is the justification for choosing a symmetrization method by considering a problem of extended domain [−1, 1] for our Dirac delta function type solutions. Now, we look for a solution to a symmetrically extended problem (1.1)–(1.3) on the interval (−1, 1) in the form of p(x, t) = η(t)δ₀(x), where δ₀(x) is the Dirac delta function concentrated at the origin.

Multiplying symmetrized Equation (1.1) by ϕ(x)∈C²[−1, 1] with compact support and ϕ(0)≠0, after integrating by parts in Q_T: = (−1, 1) × (0, T), we have

${\displaystyle \underset{Q_T}{\iint }}\frac{\partial p}{\partial t}\varphi (x)dxdt=\frac{1}{2N}{\displaystyle \underset{Q_T}{\iint }}\left(\tilde{f}(x)p{\varphi }^{″}(x)+2N\tilde{g}(x)p{\varphi }^{\prime }(x)\right)dxdt,$

where $\tilde{f}$ and $\tilde{g}$ are even continuation of f and g, respectively. Taking p(x, t) = η(t)δ₀(x) in the last equality, we deduce that

$(\eta (T)-\eta (0))\varphi (0)=(\frac{1}{2N}f(0){\varphi }^{″}(0)+g(0){\varphi }^{\prime }(0)){\displaystyle \underset{0}{\overset{T}{\int }}}\eta (t)dt=0.$

Due to the inequality ϕ(0)≠0, we have

$\eta (T)=\eta (0)=M>0.$

As a result, symmetrized Equation (1.1) has the following solution:

$p(x,t)=M{\delta }_0(x)\text{ for all }(x,t)\in (-1,1)\times (0,+\infty ).$

Convergence of a weak solution to the Dirac delta function is shown in Figure 7. It is interesting to mention that a non-smooth change of variables $y=2\sqrt{x}$ (for the case R₀ = 0) will remove the degeneracy from the equation. However, the whole long-term dynamics will not be recovered in terms of y as a global attractor-type solution. Ce^t that satisfies no-flux boundary conditions in terms of variable y will not be satisfying no-flux boundary conditions in terms of variable x. Although Ce^t solves the original problem with Neumann boundary conditions (which make the original problem ill-posed), it is unstable. Indeed, a slight perturbation will drive the dynamics toward the Dirac delta function.

Figure 7

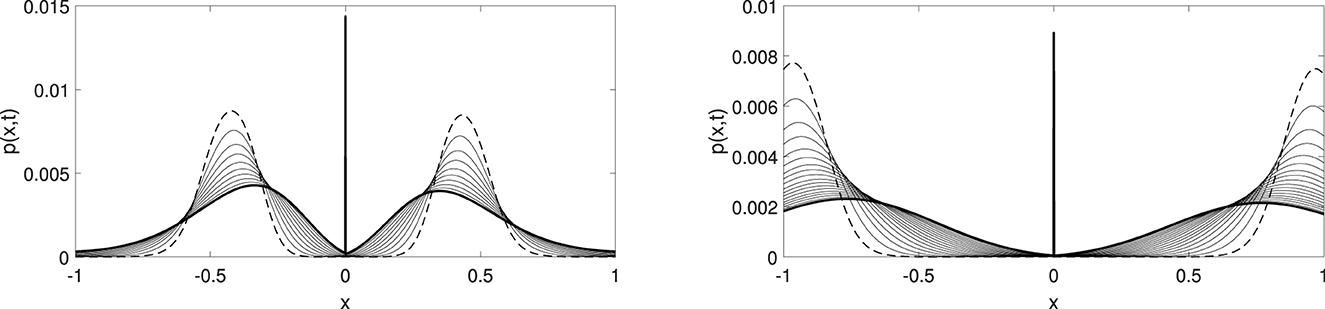
Figure 7. These two pictures illustrate the existence of the Dirac delta function type solutions for symmetrized problems with R₀ = 0 and N = 10. The initial data are plotted with a dashed line.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RT: Writing – original draft. NV: Writing – original draft. BA-A: Writing – original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. RT and NV were partially supported by the Foundation of the European Federation of Academy of Sciences and Humanities (ALLEA), the Grant EFDS-FL2-08.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Allen LJS. Some discrete-time SI, SIR, and SIS epidemic models. Mathemat Biosci. (1994) 124:83–105. doi: 10.1016/0025-5564(94)90025-6

PubMed Abstract | Crossref Full Text | Google Scholar

2. Allen LJS, Burgin AM. Comparison of deterministic and stochastic SIS and SIR models in discrete time. Math Biosci. (2000) 163:1–33. doi: 10.1016/S0025-5564(99)00047-4

PubMed Abstract | Crossref Full Text | Google Scholar

3. Bailey NTJ. The mathematical Theory of Infectious Diseases and its Applications, 2nd Edition. New York: Hafner Press [Macmillan Publishing Co., Inc.] (1975).

Google Scholar

4. Diekmann O, Heesterbeek H, Britton T. Mathematical Tools for Understanding Infectious Disease Dynamics. Princeton, NJ: Princeton University Press (2013).

Google Scholar

5. Ewens WJ. Mathematical Population Genetics, 2nd Edition. New York: Springer (2004).

Google Scholar

6. Feng Z, Huang W. Castillo-Chavez C. Global behavior of a multi- group sis epidemic model with age structure. J Differential Equat. (2005) 218:292–324. doi: 10.1016/j.jde.2004.10.009

PubMed Abstract | Crossref Full Text | Google Scholar

7. Wang Y, Xu K, Kang Y, Wang H, Wang F, Avram A. Regional influenza prediction with sampling twitter data and pde model. Int J Environ Res Public Health. (2020) 17:678. doi: 10.3390/ijerph17030678

PubMed Abstract | Crossref Full Text | Google Scholar

8. Li XZ, Yang J, Martcheva M. Age Structured Epidemic Modeling. Vol. 52. Cham: Springer Nature (2020).

Google Scholar

9. Chalub ACC, Souza MO. Discrete and continuous SIS epidemic models: a unifying approach. Ecol Compl. (2014) 18:83–95. doi: 10.1016/j.ecocom.2014.01.006

Crossref Full Text | Google Scholar

10. Kimura M. On the probability of fixation of mutant genes in a population. Genetics. (1962) 6:713. doi: 10.1093/genetics/47.6.713

PubMed Abstract | Crossref Full Text | Google Scholar

11. Oleinik OA, Radkevic EV. Second-Order Equations with Non-Negative Characteristic form, 1st Edition. Boston: Springer-Verlag US. (1973).

Google Scholar

12. Fichera G. Sulle equazioni differenziali lineri ellittico-paraboliche del secondo ordine. Atti Accad Naz Lincei Mem Cl Sei Fiz Mat Nat Sez I. (1956) 5:1–30.

Google Scholar

13. Chugunova M, Karabash IM, Pyatkov SG. On the nature of ill-posedness of the forward-backward heat equation. Integral Equ Operat Theory. (2009) 65:319–44. doi: 10.1007/s00020-009-1720-z

Crossref Full Text | Google Scholar

14. Chugunova M, Pelinovsky D. Spectrum of a non-self-adjoint operator associated with the periodic heat equation. J Math Analysis Appl. (2008) 342:970–88. doi: 10.1016/j.jmaa.2007.12.036

Crossref Full Text | Google Scholar

15. Bazaliy BV, Krasnoschek NV. Regularity of solutions to multidimensional free boundary problems for the porous medium equation. Math Trudy. (2002) 5:38-91. Available online at: http://mathscinet.ams.org/mathscinet-getitem?mr=1944066

Google Scholar

16. Feehan PMN, Pop CA. A Schauder approach to degenerate-parabolic partial differential equations with unbound coefficients. J Differential Equat. (2013) 254:4401–45. doi: 10.1016/j.jde.2013.03.006

Crossref Full Text | Google Scholar

17. Feehan PMN, Pop CA. On the martingale problem for degenerate-parabolic partial differential operators with unbounded coefficients and a mimicking theorem for Ito processes. Trans Amer Math Soc. (2015) 367:7565–93. doi: 10.1090/tran/6243

Crossref Full Text | Google Scholar

18. Feehan PMN, Pop CA. Boundary-degenerate elliptic operators and Hölder continuity for solutions to variational equations and inequalities. Ann Inst H Poincaré-Anal Nonlin. (2017) 34:1075–129. doi: 10.1016/j.anihpc.2016.07.005

Crossref Full Text | Google Scholar

19. Monticelli DD, Punzo F. Distance from sub-manifolds with boundary and applications to Poincaré inequalities and to elliptic and parabolic problems. J Differential Equat. (2019) 267:4274–92. doi: 10.1016/j.jde.2019.04.038

Crossref Full Text | Google Scholar

20. Nobili C, Punzo F. Uniqueness for degenerate parabolic equations in weighted L¹ spaces. J Evol Equa. (2022) 22:7. doi: 10.1007/s00028-022-00805-7

Crossref Full Text | Google Scholar

21. Pozio MA, Punzo F. Tesei A. Criteria for well-posedness of degenerate elliptic and parabolic problems. J Math Pures Appl. (2008) 90:353–86. doi: 10.1016/j.matpur.2008.06.001

Crossref Full Text | Google Scholar

22. Pozio MA, Punzo F, Tesei A. Uniqueness and non-uniqueness of solutions to parabolic problems with singular coefficients. DCDS-A. (2011) 30:891–916. doi: 10.3934/dcds.2011.30.891

Crossref Full Text | Google Scholar

23. Pozio MA, Tesei A. On the uniqueness of bounded solutions to singular parabolic problems, DCDS-A. (2005) 13:117–37. doi: 10.3934/dcds.2005.13.117

Crossref Full Text | Google Scholar

24. Punzo F. Uniqueness of solutions to degenerate parabolic and elliptic equations in weighted Lebesgue spaces. Math Nachr. (2013) 286:1043–54. doi: 10.1002/mana.201200040

Crossref Full Text | Google Scholar

25. Stroock D, Varadhan SRS. On degenerate elliptic-parabolic operators of second order and their associate diffusion. Commun Pure Appl Math. (1972) 25:651–713. doi: 10.1002/cpa.3160250603

Crossref Full Text | Google Scholar

26. Venni A. Maximal regularity for a singular parabolic problem. Rend Sem Mat Univ Politec Torino. (1994) 52:87–101.

Google Scholar

27. Athreya S, Barlow M, Bass R, Perkins E. Degenerate stochastic differential equations and super-markov chains. Probab Theory Related Fields. (2002) 128:484–520. doi: 10.1007/s004400100191

Crossref Full Text | Google Scholar

28. Bass RE. Perkins Degenerate stochastic differential equations with HI' older continuous coefficients and super-markov chains. Trunsactions Amer Math Society. (2002) 355:373–405. doi: 10.1090/S0002-9947-02-03120-3

PubMed Abstract | Crossref Full Text | Google Scholar

29. Cherny AS. On the uniqueness in law and the path-wise uniqueness for stochastic differential equations. Theory Prob Appl. (2001) 46:483–97. doi: 10.1137/S0040585X97979093

Crossref Full Text | Google Scholar

30. Cherny AS, Engelbert H-J. Singular Stochastic Differential Equations. Cham: Springer, Lecture Notes in Mathematics Series. (2005).

Google Scholar

31. Epstein CL, Mazzeo R. Degenerate Diffusion Operators Arising in Population Biology, v 185 in the series Annals of Mathematics Studies. Princeton: Princeton University Press. (2013). p. 320.

Google Scholar

32. Epstein CL, Mazzeo R. The geometric micro-local analysis of generalized Kimura and Heston diffusion. In: Analysis Topology in Nonlinear Differential Equations Progress and Their Applications. Cham: Springer International Publishing; Birkhäuser (2014). p. 241–266.

Google Scholar

33. Epstein CL, Pop CA. Transition probabilities for degenerate diffusion arising in population genetics. Prob Theory Related Fields. (2019) 173:537–603. doi: 10.1007/s00440-018-0840-2

Crossref Full Text | Google Scholar

34. Kumar KS. A class of degenerate stochastic differential equations with non-Lipshits coefficients. Proc Indian Acad Sci. (2013) 123:443–54. doi: 10.1007/s12044-013-0141-8

Crossref Full Text | Google Scholar

35. Pop CA. Existence, uniqueness and the strong Markov property of solutions to Kimura diffusion with singular drift. Trans Amer Math Soc. (2017) 369:5543–79. doi: 10.1090/tran/6853

Crossref Full Text | Google Scholar

36. Punzo F. Integral conditions for uniqueness of solutions to degenerate parabolic equations. J Diff Equa. (2019) 267:6555–73. doi: 10.1016/j.jde.2019.07.003

Crossref Full Text | Google Scholar

37. Aronson DG, Besala P. Uniqueness of solutions of the Cauchy problem for parabolic equations. J Math Anal Appl. (1966) 13:516–26. doi: 10.1016/0022-247X(66)90046-1

Crossref Full Text | Google Scholar

38. Epstein CL, Mazzeo R. Harnack inequalities and heat-kernel estimates for degenerate diffusion operators arising in population biology. Appl Math Res eXpress. (2016) 2016:217–80. doi: 10.1093/amrx/abw002

Crossref Full Text | Google Scholar

39. Epstein CL, Pop CA. The Feynman-kac formula and Harnack inequality for degenerate diffusion. Annuals Probabil. (2017) 45:3336–84. doi: 10.1214/16-AOP1138

Crossref Full Text | Google Scholar

40. Vespri V. Analytic semigroups, degenerate elliptic operators and applications to nonlinear Cauchy problems. Annali di Matematica Pura ed Applicata. (1989) 155:353–88 doi: 10.1007/BF01765950

Crossref Full Text | Google Scholar

41. Porzio MM, Vespri V. Hölder estimates for local solutions of some doubly nonlinear degenerate parabolic equations. J Differ Equ. (1993) 103:146–78 doi: 10.1006/jdeq.1993.1045

Crossref Full Text | Google Scholar

42. DiBenedetto E, Urbano JM, Vespri V. Current issues on singular and degenerate evolution equations. In: Handbook of Differential Equations: Evolutionary Equations 1. North-Holland: Elsevier (2002). p. 169–286.

Google Scholar

43. Ethier SN. A class of degenerate diffusion processes occurring in population genetics. Commun Pure Appl Math. (1976) 29:483–93. doi: 10.1002/cpa.3160290503

Crossref Full Text | Google Scholar

44. Cerrai S., Clément P. Well-posedness of the martingale problem for some degenerate diffusion processes occurring in dynamics of populations. Bul Sci Math. (2004) 128:355–89. doi: 10.1016/j.bulsci.2004.03.004

Crossref Full Text | Google Scholar

45. Dawson DA, March P. Resolvent estimates for Fleming-Viot operators and uniqueness of solutions to related martingale problems. J Func Anal. (1995) 132:417–74. doi: 10.1006/jfan.1995.1111

Crossref Full Text | Google Scholar

46. Perkins E. Dawson-watanable super-processes and measure-valued diffusion. In: Lecture Notes in Mathematics. Berlin: Spring-Velag (2001).

Google Scholar

47. Barbu V, Favini A, Romanelli S. Degenerate evolution equations and regularity of their associated semigroups. Funkcialaj Ekvacioj. (1996) 39:421-448.

Google Scholar

48. Goldstein JA, Cin CY. Degenerate parabolic problems and wentzel boundary condition, semigroup theory applications. Lecture Notes Pure Appl Math. (1989) 116:189–99.

Google Scholar

49. Pop CA. C⁰− estimates and smoothness of solutions to the parabolic equation defined by Kimura operators. J Functional Anal. (2017) 272:47–82. doi: 10.1016/j.jfa.2016.10.014

Crossref Full Text | Google Scholar

50. Bazaliy BV, Degtyarev SP. On a boundary-value problem for a strongly degenerate second-order elliptic equation in an angular domain. Ukrain Math J. (2007) 59:955–75. doi: 10.1007/s11253-007-0062-8

Crossref Full Text | Google Scholar

51. Chugunova M, Taranets R, Vasylyeva N. Initial-boundary value problems for conservative Kimura-type equations solvability asymptotic and conservation law. J Evol Equ. (2023) 23:17. doi: 10.1007/s00028-023-00869-z

Crossref Full Text | Google Scholar

52. Degtyarev SP. Solvability of the first initial-boundary value problem to degenerate parabolic equations in the domains with a singular boundary. Ukr Math Bull. (2008) 5:59–82. Available online at: http://dspace.nbuv.gov.ua/handle/123456789/124297

Google Scholar

53. Chen L, Weth-Wadman I. Fundamental solution to 1D degenerate diffusion equation, with locally bounded coefficients. J Math Anal and Appl. (2022) 510:125979. doi: 10.1016/j.jmaa.2021.125979

Crossref Full Text | Google Scholar

54. COMSOL Multiphysics. COMSOL AB. COMSOL Multiphysics^® v. 6.2. Stockholm (2024). Available online at: www.comsol.com

Google Scholar

55. Ladyzhenskaia OA, Solonnikov VA, Uraltseva NN. Linear and Quasilinear Parabolic Equations. New York: Academic Press (1968).

Google Scholar

56. Kufner A, Persson L-E. Weighted Inequalities of Hardy Type. New Jersey/London/Singapore/Hong Kong: World Scientific. (2003).

Google Scholar