- Department of Economics and Finance, Universidad de Castilla-La Mancha, Albacete, Spain
Throughout the financial literature, there is a great deal of debate about the nature of investors’ risk preferences. In an ever-changing world, the main schools of knowledge discuss the constant or dynamic basis of these preferences. Based on an exhaustive review of the subject of risk aversion, this paper contributes to filling the gap that exists in the literature on the risk aversion parameter that best fits the investors’ behavior toward risk. The main determinants of risk attitude are examined and the different and most novel methodologies and perspectives are carefully analyzed.
Introduction
Risk aversion is one of the pillars of the theories used by economists. The theory of choice is also extensively analyzed by social sciences such as anthropology, psychology, political science, sociobiology, and sociology. Investor choice theory analyzes the behavior of individuals when confronted with the task of ranking risky alternatives and the assumption of nonsatiation. Markowitz (1952) considers that an investor is risk averse when she\he receives more utility from the actuarial value of a gamble obtained with certainty than from taking the gamble itself. Markowitz (1952) and later Tobin (1958) consider risk attitude in the portfolio selection process, implementing the theory of games and economic behavior described by Von Neumann and Morgenstern (1944). Beyond the characterization of a risk-averse utility function and how to measure a risk premium, Pratt (1964) and Arrow (1965) provide a specific definition of risk aversion. The Pratt-Arrow definition of risk aversion is useful because it provides much more insight into people’s behavior in the face of risk.
Risk preferences depend on a great deal of determinants; but, in order to make their implementation easier, the classical literature summarizes them by a single risk aversion coefficient. However, fixed risk attitude coefficients could yield strategies that do not consider the variability in the agents’ expectations. The financial literature considers risk aversion through a constant parameter or, alternatively, through a time-dependent parameter with respect to different macroeconomic and financial variables. As an additional component, recent developments take advantage of growing data processing capacity to reduce uncertainty and estimate ever more accurate changing risk aversion. The use of big data in financial markets enables faster and faster processing of data on many macro and financial variables. This better quality information provides insight into the expectations of modern investors and reduces their uncertainty about investment outcomes. In this context, the aim of this paper is to review the risk aversion literature by comparing the invariant and dynamic nature of risk preferences.
Background
Individual preferences are complex, depending on a variety of economic, political, human, or even cultural factors. Risk aversion plays a key role to understand the behavior of different economic periods and, above all, economic recessions. This parameter amplifies the response of the most relevant macroeconomic variables to shocks of uncertainty and is, in short, the point of conciliation that makes it possible to relate finance, macroeconomics, and uncertainty. An extensive literature analyzes how fluctuations in economic uncertainty influence the dynamics of the economic cycle (see, e.g., Bernanke, 1983; Bertola and Caballero, 1994; Abel and Eberly, 1994, 1996; Caballero and Pindyck, 1996; Bloom, 2009; Bachmann and Bayer, 2013) and help explain the countercyclical behavior of major economic variables (e.g., Campbell and Taksler, 2003; Storesletten et al., 2004; Eisfeldt and Rampini, 2006; Bloom, 2009). However, the traditional way in which macroeconomists explained economic fluctuations largely ignored the importance of risk aversion in understanding economic cycles. Thereunder, the new macroeconomy recognizes that financial shocks are relevant to the real economy. Jurado et al. (2015) observe a time-varying relationship between uncertainty and real activity based on a new measure of uncertainty linking financial risk aversion coefficients with macroeconomic variables. In this sense, market risk premium and volatility reach their highest values in financial crises rather than in times of economic recession or war (Muir, 2016). Guiso et al. (2018) link changes in investor risk aversion to changes in wealth, expected income, and perceived probabilities and emotional changes in the utility function. Several authors highlight the interaction between political uncertainty and individual risk aversion. In this sense, Pástor and Veronesi (2013) incorporate this relationship into a general equilibrium model, while Brogaard and Detzel (2015) and Baker et al. (2016) examine this interaction by fitting political uncertainty through an index based on press reports.
Numerous studies show that risk aversion increases with age (e.g., Jianakoplos and Bernasek, 2006; Bucciol and Miniaci, 2011; Boyle et al., 2012; Brooks et al., 2018). Hansen et al. (1999) and Ilut and Schneider (2014) consider that consumers have pessimistic beliefs and, faced with a range of possible outcomes, act as if the worst outcomes occurred, displaying a behavior known as “ambiguity aversion.” This concept explains why many households do not invest in the stock market since the return on this investment is more ambiguous (i.e., they are not able to assign probabilities to possible outcomes) than the return on a bank deposit or a Treasury Bill (Dow and Werlang, 1992). Zhang et al. (2019) relate risk aversion with pessimism and rare disasters. Goetzmann et al. (2016) propose the availability heuristic theory in which the most recent observations have the greatest impact on an individual’s decision-making. Investors assign more probability to future stock market falls after a stock market crash. Kamstra et al. (2003) relate risk aversion to seasonal affective disorder, a depressive disorder associated with declining daylight hours. Nofsinger et al. (2018) examine the influence of behavioral biases as testosterone or stress on the individual’s risk aversion. Hoffmann and Post (2016, 2017) link up investor return experiences, confidence and investment beliefs and show why confident investors trade more than less confident investors. Falk et al. (2018) and Potrafke (2019) find a positive correlation between patience and intelligence. Suen (2018) suggests a possible discrepancy between individual and aggregate risk aversion in the context of background risk. Finally, a branch of literature proofs the influence of social factors, ethical preferences, or religious beliefs on investor’s risk attitude (e.g., Eisenhauer, 2008; Nielsen et al., 2017; Berrada et al., 2018).
Constant Risk Aversion
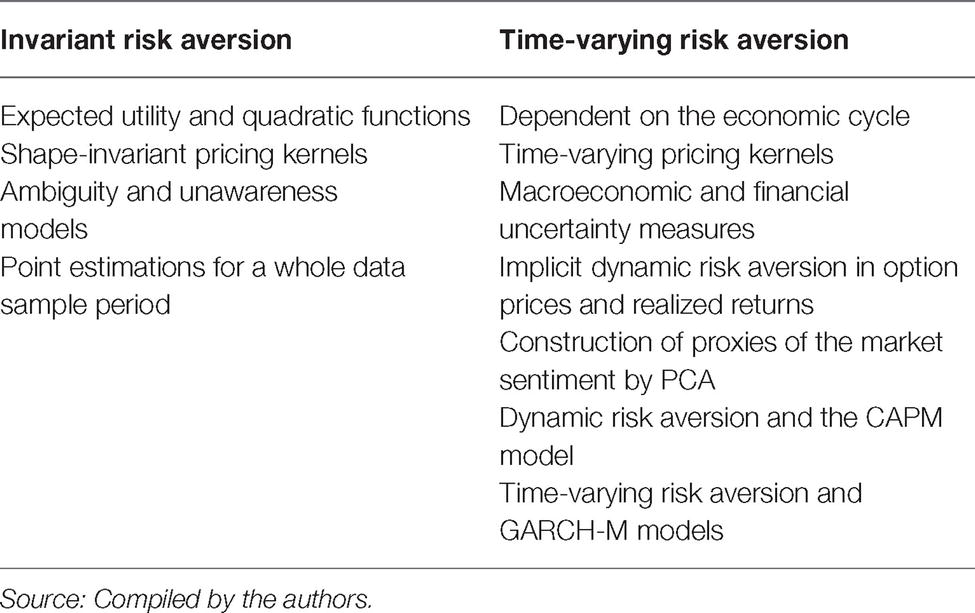
Although risk preferences depend on several factors, most theoretical literature fits the risk aversion as an invariant parameter that represents the personal level of risk attitude. Simple models are very relevant as they help us set ideas. Assuming constant risk aversion allows models to reach precise and relatively simple formulas for relationships between variables. Table 1 shows some applications of constant risk aversion parameters compared to other applications with time-varying coefficients. Empirical studies show contradictory evidence for this invariable parameter over time. For instance, the risk attitude parameter appears as stable for correlative periods of time in Chou (1988), or much more unstable in French et al. (1987).
Safra and Segal (1998) define constant risk aversion as the invariant preference relation between outcomes of two distributions when adding or multiplying them by the same positive number. Quiggin and Chambers (2004) show that risk attitude is strongly linked with the family of generalized expected utility preferences which exhibit constant risk aversion. These expected utility preferences are constant only if the investor’s utility function is quadratic, which is consistent with the capital asset pricing model (CAPM). In addition, these preferences are a generalization of both, invariant risk preferences (e.g., Quiggin and Chambers, 1998; Safra and Segal, 1998) and mean-standard deviation attitude. Other approaches link shape-invariant pricing kernels to the estimation of a constant risk aversion parameter (e.g., Lawton et al., 1972; Grith et al., 2013).
Recently, Dominiak and Tsjerengjimid (2018) generalized the preference structure in Gilboa and Schmeidler (1989) to allow for the decision maker’s ex post preferences to be ambiguity averse, which implies constant risk appetite. Other studies assume that investor’s risk preferences are constant and invariant to changes of unawareness and unforeseen contingencies (e.g., Karni and Vierø, 2013, 2015; Mengel et al., 2016; Ma and Schipper, 2017). Baillon and Placido (2019) demonstrate that most ambiguity models forecast that risk aversion remains constant when individuals improve overall.
Time-Varying Risk Aversion
Considering the variability in agents’ expectations, to model the risk aversion parameter has a cost in terms of complexity. Empirical papers document time-varying risk premia in several financial markets (e.g., Fama, 1984; Hodrick and Srivastava, 1986; Keim and Stambaugh, 1986; Harvey, 1989; Li et al., 2011). There are several studies in financial literature that refer to time-varying risk aversion as a dependent parameter of different macroeconomic and financial variables. In a seminal paper on asset pricing, Campbell and Cochrane (1999) consider that an individual is more or less risk averse according to the economic and political circumstances. Their “habit formation” model incorporates large and frequent variation of the risk aversion parameter. In the same vein, Brandt and Wang (2003) develop a consumption-based asset pricing model in which aggregate risk aversion responses to both consumption growth and inflation news. Eisenbach and Schmalz (2016) consider “anxious” investors, who are more risk averse to an imminent risk than to distant one and propose a theory that leads to a downward-sloping term structure of risk premia. In the same vein, Andries et al. (2018) propose a horizon-dependent risk aversion model involving term structures of risk premium consistent with the evidence that agents are more reluctant to immediate risks than to deferred risks. Behavioral approaches have also incorporated time-varying risk aversion by way of dynamic loss aversion or conditional disappointment aversion (e.g., Barberis et al., 2001; Routledge and Zin, 2010).
As mentioned, risk preferences are closely related to economic cycles. Many studies indicate that risk aversion is countercyclical. This way, Rosenberg and Engle (2002) observe a countercyclical investor risk aversion parameter by fitting a dynamic pricing kernel. Based on the consumption-based model of Campbell and Cochrane (1999), Li (2007) shows the influence of dynamic risk aversion on asset pricing by observing that countercyclical changes in risk attitude lead to a procyclical time-varying risk premium. Furthermore, Cochrane (2017) notes that risk premia are countercyclical over time and are also coordinated across asset classes. Finally, González et al. (2018) observe the key role of time-varying risk aversion as a macroeconomic determinant of stock market betas.
Time-varying risk preferences have been modeled in several ways. A branch of the financial literature focuses on risk aversion implicit in option prices and realized returns. Option contracts offer several advantages when considering risk preferences (e.g., Bliss and Panigirtzoglou, 2004). To price options, it is only necessary to infer a discounted cash flow for a given horizon. In addition, there are options for different maturities. The multiplicity of prices for different payments on the same underlying asset provided by the options makes it possible to construct a density function for the distribution of the possible values of the underlying asset. The risk attitude implicit in option prices contains information of investors’ behavior toward risk and, hence, its variability may be captured by the jumps in risk premia implicit in the market. From option prices and realized returns on the S&P500 index, Jackwerth (2000) derives investor’s risk aversion functions and observes how shapes around financial crises change dramatically. As expected from the economic theory, these functions are positive and diminish in wealth during the pre-crisis period. On the other hand, their behavior is not consistent with the hypotheses after this event. Several authors, such as Aït-Sahalia and Lo (2000), Bedoui and Hamdi (2015), Yoon (2017), Kiesel and Rahe (2017), and Liao and Sung (2018), implement an implicit estimation of the individuals’ risk attitude from the joint observations of the cross-section of option premiums and time series of underlying assets. They examine the risk preference of market participants in different states of the world and find that risk aversion level strongly increases during stressed market conditions.
Other approaches are related to the construction of indices or proxies that represent the time-varying aggregate investor sentiment in a given financial market. The main aversion indicators can be grouped into different types: indicators that use a principal component analysis (PCA) on several financial variables (e.g., Baker and Wurgler, 2006, 2007; Han and Li, 2017; Cheema et al., 2018; Bekaert et al., 2019); indicators based on the correlation between volatilities and changes in asset prices (e.g., Kumar and Persaud, 2002); volatility indices, such as the “VIX” that uses the implied volatility of option prices on the Chicago Board Options Exchange (CBOE); and many others. For instance, Baker and Wurgler (2006) elaborate a composite index of investor sentiment derived from the first principal component of six basic proxies of investor sentiment based on various stock market indicators. On the basis of a dynamic asset pricing model with stochastic risk aversion, Bekaert et al. (2019) propose a measure of a time-varying risk aversion computed at a daily frequency that distinguishes the time variation in economic uncertainty (the amount of risk) from time variation in risk aversion (the price of risk). Most of these risk aversion indicators are used by other authors to test their ability to forecast financial crises. For example, Coudert and Gex (2008) use logit and multilogit models and observe that risk aversion indicators are good leading indicators of stock market crises.
There is a line of research linking investor risk aversion with the market risk premium derived from conditional heteroscedasticity models. The mean-variance Capital Asset Pricing Model (CAPM) of Sharpe (1964) and Lintner (1965) assumes constant second-order moments to arrive at its valuation expression, which is based on a linear relationship between expected return and risk. However, an extensive empirical evidence shows a conditional heteroscedasticity in the stock markets (e.g., Christie, 1982; Poterba and Summers, 1986; French et al., 1987)1. In parallel, models of Autoregressive Conditional Heteroscedasticity (ARCH) are developed (Engle, 1982) with a multitude of subsequent extensions (e.g., Bollerslev, 1986; Ding et al., 1993; Engle and Ng, 1993). Authors such as Giovannini and Jorion (1987, 1989) analyze the effects of conditional risk aversion and ARCH models for both market risk premium and performance in the static CAPM model. Given the instability of risk aversion coefficients and risk premiums over different time periods, Chou et al. (1992) improve the ARCH-in-mean (ARCH-M) model of Engle et al. (1987) with a rolling estimation procedure in which the time-varying risk aversion is integrated by a Kalman filter method. This methodology is widely applied and expanded by the use of Generalized Autoregressive Conditional Heteroskedasticity in-mean models (GARCH-M) to test the validity of dynamic risk aversion parameters in the estimation of the market risk premium (e.g., Flannery et al., 1997; Elyasiani and Mansur, 1998; Devaney, 2001; Cotter and Hanly, 2010; Dias, 2017).
Recent literature proposes text-processing techniques based on Internet search volume of certain keywords to predict returns, rather than measures based on market trading volumes and returns. There is a debate about whether these high-frequency measures actually measure time-varying risk aversion (e.g., Vlastakis and Markellos, 2012; Kearney and Liu, 2014) or whether, on the contrary, they capture retail investors’ attention toward the stock market (e.g., Da et al., 2011; Jacobs and Weber, 2012; Vlastakis and Markellos, 2012; Dimpfl and Jank, 2016) or even the investor sentiment (e.g., Da et al., 2015; Heston and Sinha, 2017). In any case, social networks can provide information on the collective behavior of investors, their state of mind, and thus allow an estimation of risk aversion at each instant of time. Financial analysis improves by increasing the speed of processing and the amount of data available. Big data and faster processors enhance investors’ forecasts of future returns. As faster and wider access to information about assets reduces uncertainty, investors tend to perceive them as “safer” (Veldkamp, 2006) and makes portfolio selection results more predictable (Kacperczyk et al., 2016; Begenau et al., 2018). Given that traditional literature states that more risk-averse investors demand more information (e.g., Willinger, 1989; Eeckhoudt and Godfroid, 2000), future research can further explore the extent to which the greater current availability of information accessible to all investors could imply a reduction in risk aversion.
Conclusions
This literature review summarizes, critically examines, and clarifies alternative viewpoints of the most relevant contributions in each of the facets that affect the study and use of risk aversion in financial models. We review the literature with a view to providing a clear understanding of both constant or invariable risk aversion and variable risk attitude over time in the context of investor behavior and investment decisions in an environment of uncertainty.
Despite the influence of risk aversion in the investment context, most classical financial literature considers fixed values to reflect common levels of risk aversion over a full sample period. The use of a static estimate of the risk aversion coefficient over large timeframes may be desirable in simplifying models but could lead to investment decisions that do not reflect the investor’s actual attitude toward risk. On this basis, an extensive literature both in economics and in many other disciplines shows the large number of determinants of risk aversion and proofs its changing nature over time. New macroeconomy and financial theory recognize the key role of risk aversion in economic cycles, finding a countercyclical relation between risk preferences and the economic period. Many asset pricing models exhibit countercyclical risk aversion, including a behavioral dimension by way of risk-averse utility functions. Furthermore, several approaches allow the inclusion of dynamic risk aversion, such as volatility or sentiment indices, implied methods based on financial option pricing, the rolling ARCH-M model and the Kalman filter methodology, or information technology and big data analysis.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication. Corresponding author contributed to the design and implementation of the research. Both authors have collaborated in the review of the literature and in the writing of the manuscript.
Funding
This research was supported by MINECO (ECO2017-89715-P) and UCLM (2019-GRIN-27072, co-financed with FEDER funds).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. This evidence is one more of the traditional criticisms of CAPM, such as the unobservability of the market portfolio (Roll, 1977) or the need to incorporate additional risk factors (e.g., Banz, 1981).
References
Abel, A. B., and Eberly, J. C. (1994). A unified model of investment under uncertainty. Am. Econ. Rev. 84, 1369–1384.
Abel, A. B., and Eberly, J. C. (1996). Optimal investment with costly reversibility. Rev. Econ. Stud. 63, 581–593. doi: 10.2307/2297794
Aït-Sahalia, Y., and Lo, A. W. (2000). Nonparametric risk management and implied risk aversion. J. Econ. 94, 9–51. doi: 10.1016/S0304-4076(99)00016-0
Andries, M., Eisenbach, T. M., and Schmalz, M. C. (2018). “Asset pricing with horizon-dependent risk aversion” in FRB of New York staff report. Vol. 703.
Bachmann, R., and Bayer, C. (2013). ‘Wait-and-See’ business cycles? J. Monet. Econ. 60, 704–719. doi: 10.1016/j.jmoneco.2013.05.005
Baillon, A., and Placido, L. (2019). Testing constant absolute and relative ambiguity aversion. J. Econ. Theory. 181, 309–332. doi: 10.1016/j.jet.2019.02.006
Baker, S. R., Bloom, N., and Davis, S. J. (2016). Measuring economic policy uncertainty. Q. J. Econ. 131, 1593–1636. doi: 10.1093/qje/qjw024
Baker, M., and Wurgler, J. (2006). Investor sentiment and the cross-section of stock returns. J. Financ. 61, 1645–1680. doi: 10.1111/j.1540-6261.2006.00885.x
Baker, M., and Wurgler, J. (2007). Investor sentiment in the stock market. J. Econ. Perspect. 21, 129–151. doi: 10.1257/jep.21.2.129
Banz, R. W. (1981). The relationship between return and market value of common stocks. J. Financ. Econ. 9, 3–18. doi: 10.1016/0304-405X(81)90018-0
Barberis, N., Huang, M., and Santos, T. (2001). Prospect theory and asset prices. Q. J. Econ. 116, 1–53. doi: 10.1162/003355301556310
Bedoui, R., and Hamdi, H. (2015). Option-implied risk aversion estimation. J. Econ. Asymmetries 12, 142–152. doi: 10.1016/j.jeca.2015.06.001
Begenau, J., Farboodi, M., and Veldkamp, L. (2018). Big data in finance and the growth of large firms. J. Monet. Econ. 97, 71–87. doi: 10.1016/j.jmoneco.2018.05.013
Bekaert, G., Engstrom, E., and Xu, N. (2019). The time variation in risk appetite and uncertainty (No. 25673).
Bernanke, B. (1983). Non-monetary effects of the financial crisis in the propagation of the great depression. Am. Econ. Rev. 73, 257–276.
Berrada, T., Detemple, J., and Rindisbacher, M. (2018). Asset pricing with beliefs-dependent risk aversion and learning. J. Financ. Econ. 128, 504–534. doi: 10.1016/j.jfineco.2018.03.002
Bertola, G., and Caballero, R. J. (1994). Irreversibility and aggregate investment. Rev. Econ. Stud. 61, 223–246. doi: 10.2307/2297979
Bliss, R. R., and Panigirtzoglou, N. (2004). Option-implied risk aversion estimates. J. Financ. 59, 407–446. doi: 10.1111/j.1540-6261.2004.00637.x
Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. J. Econ. 31, 307–327. doi: 10.1016/0304-4076(86)90063-1
Boyle, P. A., Yu, L., Buchman, A. S., and Bennett, D. A. (2012). Risk aversion is associated with decision making among community-based older persons. Front. Psychol. 3. doi: 10.3389/fpsyg.2012.00205
Brandt, M. W., and Wang, K. Q. (2003). Time-varying risk aversion and unexpected inflation. J. Monet. Econ. 50, 1457–1498. doi: 10.1016/j.jmoneco.2003.08.001
Brogaard, J., and Detzel, A. (2015). The asset-pricing implications of government economic policy uncertainty. Manag. Sci. 61, 3–18. doi: 10.1287/mnsc.2014.2044
Brooks, C., Sangiorgi, I., Hillenbrand, C., and Money, K. (2018). Why are older investors less willing to take financial risks? Int. Rev. Financ. Anal. 56, 52–72. doi: 10.1016/j.irfa.2017.12.008
Bucciol, A., and Miniaci, R. (2011). Household portfolios and implicit risk preference. Rev. Econ. Stat. 93, 1235–1250. doi: 10.1162/REST_a_00138
Caballero, R. J., and Pindyck, R. S. (1996). Uncertainty, investment, and industry evolution. Int. Econ. Rev. 37, 641–662. doi: 10.2307/2527445
Campbell, J. Y., and Cochrane, J. H. (1999). By force of habit: a consumption-based explanation of aggregate stock market behavior. J. Polit. Econ. 107, 205–251. doi: 10.1086/250059
Campbell, J. Y., and Taksler, G. B. (2003). Equity volatility and corporate bond yields. J. Financ. 58, 2321–2349. doi: 10.1046/j.1540-6261.2003.00607.x
Cheema, M. A., Man, Y., and Szulczyk, K. R. (2018). Does investor sentiment predict the near-term returns of the chinese stock market? Int. Rev. Financ. doi: 10.1111/irfi.12202
Chou, R. Y. (1988). Volatility persistence and stock valuations: some empirical evidence using garch. J. Appl. Econ. 3, 279–294. doi: 10.1002/jae.3950030404
Chou, R., Engle, R. F., and Kane, A. (1992). Measuring risk aversion from excess returns on a stock index. J. Econ. 52, 201–224. doi: 10.1016/0304-4076(92)90070-8
Christie, A. A. (1982). The stochastic behavior of common stock variances: value, leverage and interest rate effects. J. Financ. Econ. 10, 407–432. doi: 10.1016/0304-405X(82)90018-6
Cotter, J., and Hanly, J. (2010). Time-varying risk aversion: an application to energy hedging. Energy Econ. 32, 432–441. doi: 10.1016/j.eneco.2009.08.009
Coudert, V., and Gex, M. (2008). Does risk aversion drive financial crises? Testing the predictive power of empirical indicators. J. Empir. Financ. 15, 167–184. doi: 10.1016/j.jempfin.2007.06.001
Da, Z., Engelberg, J., and Gao, P. (2011). In search of attention. J. Financ. 66, 1461–1499. doi: 10.1111/j.1540-6261.2011.01679.x
Da, Z., Engelberg, J., and Gao, P. (2015). The sum of all FEARS investor sentiment and asset prices. Rev. Financ. Stud. 28, 1–32. doi: 10.1093/rfs/hhu072
Devaney, M. (2001). Time varying risk premia for real estate investment trusts: a GARCH-M model. Q. Rev. Econ. Finance 41, 335–346. doi: 10.1016/S1062-9769(00)00074-0
Dias, G. F. (2017). The time-varying GARCH-in-mean model. Econ. Lett. 157, 129–132. doi: 10.1016/j.econlet.2017.06.005
Dimpfl, T., and Jank, S. (2016). Can Internet search queries help to predict stock market volatility? Eur. Financ. Manag. 22, 171–192. doi: 10.1111/eufm.12058
Ding, Z., Granger, C. W. J., and Engle, R. F. (1993). A long memory property of stock market returns and a new model. J. Empir. Financ. 1, 83–106. doi: 10.1016/0927-5398(93)90006-D
Dominiak, A., and Tserenjigmid, G. (2018). Belief consistency and invariant risk preferences. J. Math. Econ. 79, 157–162.
Dow, J., and Werlang, S. R. C. d. (1992). Uncertainty aversion, risk aversion, and the optimal choice of portfolio. Econometrica 60, 197–204. doi: 10.2307/2951685
Eeckhoudt, L., and Godfroid, P. (2000). Risk aversion and the value of information. J. Econ. Educ. 31, 382–388. doi: 10.1080/00220480009596456
Eisenbach, T. M., and Schmalz, M. C. (2016). Anxiety in the face of risk. J. Financ. Econ. 121, 414–426. doi: 10.1016/j.jfineco.2015.10.002
Eisenhauer, J. G. (2008). Ethical preferences, risk aversion, and taxpayer behavior. J. Socio-Econ. 37, 45–63. doi: 10.1016/j.socec.2007.01.030
Eisfeldt, A. L., and Rampini, A. A. (2006). Capital reallocation and liquidity. J. Monet. Econ. 53, 369–399. doi: 10.1016/j.jmoneco.2005.04.006
Elyasiani, E., and Mansur, I. (1998). Sensitivity of the bank stock returns distribution to changes in the level and volatility of interest rate: a GARCH-M model. J. Bank. Financ. 22, 535–563.
Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50, 987–1007. doi: 10.2307/1912773
Engle, R. F., Lilien, D. M., and Robins, R. P. (1987). Estimating time varying risk premia in the term structure: the Arch-M model. Econometrica 55, 391–407. doi: 10.2307/1913242
Engle, R. F., and Ng, V. K. (1993). Measuring and testing the impact of news on volatility. J. Financ. 48, 1749–1778. doi: 10.1111/j.1540-6261.1993.tb05127.x
Falk, A., Becker, A., Dohmen, T., Enke, B., Huffman, D., and Sunde, U. (2018). Global evidence on economic preferences. Q. J. Econ. 133, 1645–1692. doi: 10.1093/qje/qjy013
Fama, E. F. (1984). Forward and spot exchange rates. J. Monet. Econ. 14, 319–338. doi: 10.1016/0304-3932(84)90046-1
Flannery, M. J., Hameed, A. S., and Harjes, R. H. (1997). Asset pricing, time-varying risk premia and interest rate risk. J. Bank. Financ. 21, 315–335. doi: 10.1016/S0378-4266(96)00044-1
French, K. R., Schwert, G. W., and Stambaugh, R. F. (1987). Expected stock returns and volatility. J. Financ. Econ. 19, 3–29. doi: 10.1016/0304-405X(87)90026-2
Gilboa, I., and Schmeidler, D. (1989). Maxmin expected utility with non-unique prior. J. Math. Econ. 18, 141–153. doi: 10.1016/0304-4068(89)90018-9
Giovannini, A., and Jorion, P. (1987). Interest rates and risk premia in the stock market and in the foreign exchange market. J. Int. Money Financ. 6, 107–123. doi: 10.1016/0261-5606(87)90016-7
Giovannini, A., and Jorion, P. (1989). The time variation of risk and return in the foreign exchange and stock markets. J. Financ. 44, 307–325. doi: 10.1111/j.1540-6261.1989.tb05059.x
González, M., Nave, J., and Rubio, G. (2018). Macroeconomic determinants of stock market betas. J. Empir. Financ. 45, 26–44. doi: 10.1016/j.jempfin.2017.10.003
Grith, M., Härdle, W., and Park, J. (2013). Shape invariant modeling of pricing kernels and risk aversion. J. Financ. Economet. 11, 370–399. doi: 10.1093/jjfinec/nbs019
Guiso, L., Sapienza, P., and Zingales, L. (2018). Time varying risk aversion R. J. Financ. Econ. 128, 403–421. doi: 10.1016/j.jfineco.2018.02.007
Han, X., and Li, Y. (2017). Can investor sentiment be a momentum time-series predictor? Evidence from China. J. Empir. Financ. 42, 212–239. doi: 10.1016/j.jempfin.2017.04.001
Hansen, L. P., Sargent, T. J., and Tallarini, T. D. (1999). Robust permanent income and pricing. Rev. Econ. Stud. 66, 873–907. doi: 10.1111/1467-937X.00112
Harvey, C. R. (1989). Time-varying conditional covariances in tests of asset pricing models. J. Financ. Econ. 24, 289–317. doi: 10.1016/0304-405X(89)90049-4
Heston, S. L., and Sinha, N. R. (2017). News vs. sentiment: predicting stock returns from news stories. Financ. Anal. J. 73, 67–83. doi: 10.2469/faj.v73.n3.3
Hodrick, R. J., and Srivastava, S. (1986). The covariation of risk premiums and expected future spot exchange rates. J. Int. Money Financ. 5, 5–21.
Hoffmann, A. O. I., and Post, T. (2016). How does investor confidence lead to trading? Linking investor return experiences, confidence, and investment beliefs. J. Behav. Exp. Financ. 12, 65–78. doi: 10.1016/j.jbef.2016.09.003
Hoffmann, A. O. I., and Post, T. (2017). How return and risk experiences shape investor beliefs and preferences. Account. Finance 57, 759–788. doi: 10.1111/acfi.12169
Ilut, C. L., and Schneider, M. (2014). Ambiguous business cycles. Am. Econ. Rev. 104, 2368–2399. doi: 10.1257/aer.104.8.2368
Jackwerth, J. C. (2000). Recovering risk aversion from option prices and realized returns. Rev. Financ. Stud. 13, 433–451. doi: 10.1093/rfs/13.2.433
Jacobs, H., and Weber, M. (2012). The trading volume impact of local bias: evidence from a natural experiment. Rev. Finance 16, 867–901. doi: 10.1093/rof/rfr022
Jianakoplos, N. A., and Bernasek, A. (2006). Financial risk taking by age and birth cohort. South. Econ. J. 72, 981–1001. doi: 10.2307/20111864
Jurado, K., Ludvigson, S. C., and Ng, S. (2015). Measuring uncertainty. Am. Econ. Rev. 105, 1177–1216. doi: 10.1257/aer.20131193
Kacperczyk, M., Van Nieuwerburgh, S., and Veldkamp, L. (2016). A rational theory of mutual funds’ attention allocation. Econometrica 84, 571–626. doi: 10.3982/ECTA11412
Kamstra, M. J., Kramer, L. A., and Levi, M. D. (2003). Winter blues: a SAD stock market cycle. Am. Econ. Rev. 93, 324–343. doi: 10.1257/000282803321455322
Karni, E., and Vierø, M.-L. (2013). “Reverse Bayesianism”: a choice-based theory of growing awareness. Am. Econ. Rev. 103, 2790–2810. doi: 10.1257/aer.103.7.2790
Karni, E., and Vierø, M.-L. (2015). Probabilistic sophistication and reverse Bayesianism. J. Risk Uncertain. 50, 189–208. doi: 10.1007/s11166-015-9216-5
Kearney, C., and Liu, S. (2014). Textual sentiment in finance: a survey of methods and models. Int. Rev. Financ. Anal. 33, 171–185. doi: 10.1016/j.irfa.2014.02.006
Keim, D. B., and Stambaugh, R. F. (1986). Predicting returns in the stock and bond markets. J. Financ. Econ. 17, 357–390. doi: 10.1016/0304-405X(86)90070-X
Kiesel, R., and Rahe, F. (2017). Option pricing under time-varying risk-aversion with applications to risk forecasting. J. Bank. Financ. 76, 120–138. doi: 10.1016/j.jbankfin.2016.11.006
Kumar, M. S., and Persaud, A. (2002). Pure contagion and investors’ shifting risk appetite: analytical issues and empirical evidence. Int. Finance 5, 401–436. doi: 10.1111/1468-2362.00102
Lawton, W. H., Sylvestre, E. A., and Maggio, M. S. (1972). Self modeling nonlinear regression. Technometrics 14, 513–532. doi: 10.1080/00401706.1972.10488942
Li, G. (2007). Time-varying risk aversion and asset prices. J. Bank. Financ. 31, 243–257. doi: 10.1016/j.jbankfin.2006.02.005
Li, D., Ghoshray, A., and Morley, B. (2011). “Uncovered interest parity and the risk premium” in Department of Economics Working Papers (No. 24072) (University of Bath, Department of Economics).
Liao, W. J., and Sung, H.-C. (2018). Implied risk aversion and pricing kernel in the FTSE 100 index. North Am. J. Econ. Finance. doi: 10.1016/j.najef.2018.08.009
Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Rev. Econ. Stat. 47, 13–37. doi: 10.2307/1924119
Ma, W., and Schipper, B. C. (2017). Does exposure to unawareness affect risk preferences? A preliminary result. Theor. Decis. 83, 245–257. doi: 10.1007/s11238-017-9594-z
Mengel, F., Tsakas, E., and Vostroknutov, A. (2016). Past experience of uncertainty affects risk aversion. Exp. Econ. 19, 151–176. doi: 10.1007/s10683-015-9431-6
Muir, T. (2016). Financial crises and risk premia. Q. J. Econ. 132, 765–809. doi: 10.1093/qje/qjw045
Nielsen, J. S., Bech, M., Christensen, K., Kiil, A., and Hvidt, N. C. (2017). Risk aversion and religious behaviour: analysis using a sample of Danish twins. Econ. Hum. Biol. 26, 21–29. doi: 10.1016/j.ehb.2017.01.004
Nofsinger, J. R., Patterson, F. M., and Shank, C. A. (2018). Decision-making, financial risk aversion, and behavioral biases: the role of testosterone and stress. Econ. Hum. Biol. 29, 1–16. doi: 10.1016/j.ehb.2018.01.003
Pástor, Ľ., and Veronesi, P. (2013). Political uncertainty and risk premia. J. Financ. Econ. 110, 520–545. doi: 10.1016/j.jfineco.2013.08.007
Poterba, J. M., and Summers, L. H. (1986). The persistence of volatility and stock market fluctuations. Am. Econ. Rev. 76, 1142–1151.
Potrafke, N. (2019). Risk aversion, patience and intelligence: evidence based on macro data. Econ. Lett. 178, 116–120. doi: 10.1016/j.econlet.2019.02.026
Pratt, J. W. (1964). Risk aversion in the small and in the large. Econometrica 32, 122–136. doi: 10.2307/1913738
Quiggin, J., and Chambers, R. G. (1998). Risk premiums and benefit measures for generalized-expected-utility theories. J. Risk Uncertain. 17, 121–137. doi: 10.1023/A:1007767512327
Quiggin, J., and Chambers, R. G. (2004). Invariant risk attitudes. J. Econ. Theory 117, 96–118. doi: 10.1016/j.jet.2003.09.006
Roll, R. (1977). A critique of the asset pricing theory’s tests; part i: on past and potential testability of the theory. J. Financ. Econ. 4, 129–176.
Rosenberg, J. V., and Engle, R. F. (2002). Empirical pricing kernels. J. Financ. Econ. 64, 341–372. doi: 10.1016/S0304-405X(02)00128-9
Routledge, B. R., and Zin, S. E. (2010). Generalized disappointment aversion and asset prices. J. Financ. 65, 1303–1332. doi: 10.1111/j.1540-6261.2010.01571.x
Safra, Z., and Segal, U. (1998). Constant risk aversion. J. Econ. Theory 83, 19–42. doi: 10.1006/jeth.1997.2457
Sharpe, W. F. (1964). Capital asset prices: a theory of market equilibrium under conditions of risk. J. Financ. 19, 425–442.
Storesletten, K., Telmer, C. I., and Yaron, A. (2004). Cyclical dynamics in idiosyncratic labor market risk. J. Polit. Econ. 112, 695–717. doi: 10.1086/383105
Suen, R. M. H. (2018). Standard risk aversion and efficient risk sharing. Econ. Lett. 173, 23–26. doi: 10.1016/j.econlet.2018.09.005
Veldkamp, L. L. (2006). Media frenzies in markets for financial information. Am. Econ. Rev. 96, 577–601. doi: 10.1257/aer.96.3.577
Vlastakis, N., and Markellos, R. N. (2012). Information demand and stock market volatility. J. Bank. Financ. 36, 1808–1821. doi: 10.1016/j.jbankfin.2012.02.007
Von Neumann, J., and Morgenstern, O. (1944). Theory of games and economic behavior. (Princeton, New Jersey: Princeton University Press).
Willinger, M. (1989). Risk aversion and the value of information. J. Risk Insur. 56, 104–112. doi: 10.2307/253017
Yoon, S.-J. (2017). Time-varying risk aversion and return predictability. Int. Rev. Econ. Finance 49, 327–339. doi: 10.1016/j.iref.2017.02.006
Keywords: risk aversion, economic cycles, market risk premium, pricing models, big data
Citation: Díaz A and Esparcia C (2019) Assessing Risk Aversion From the Investor’s Point of View. Front. Psychol. 10:1490. doi: 10.3389/fpsyg.2019.01490
Edited by:
Alicia Izquierdo-Yusta, University of Burgos, SpainReviewed by:
Inés González, Escuela de Negocios de Navarra, SpainLars Tegtmeier, Merseburg University of Applied Sciences, Germany
Copyright © 2019 Díaz and Esparcia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Carlos Esparcia, Y2FybG9zLmVzcGFyY2lhQHVjbG0uZXM=
 Antonio Díaz
Antonio Díaz Carlos Esparcia
Carlos Esparcia