- 1School of Cybersecurity, Chengdu University of Information Technology, Chengdu, China
- 2Department of Mathematics, COMSATS University Islamabad, Vehari, Pakistan
- 3School of Information Science and Engineering, Chengdu University, Chengdu, China
For the graphs G1, G2, and G, if every 2-coloring (red and blue) of the edges of G results in either a copy of blue G1 or a copy of red G2, we write G → (G1, G2). The size Ramsey number is the smallest number e such that there is a graph G with size e satisfying G → (G1, G2), i.e., . In this paper, by developing the procedure and algorithm, we determine exact values of the size Ramsey numbers of some paths and cycles. More precisely, we obtain that , , , , , , and .
1. Introduction
We use standard notions and symbols from the field of graph theory, see [1]. By G = G(V, E), we denote a simple graph with vertex and edge sets V and E having cardinalities |V(G)| and |E(G)|, respectively. For S1, S2 ⊆ V(G), we denote E(S1) = {uv ∈ E(G)|v, u ∈ S1} and E(S1, S2) = {uv ∈ E(G)|u ∈ S1, v ∈ S2}. Moreover, we denote: the degree of a vertex v in G by d(v|G) (or d(v)), the minimum degree among the vertices of G by δ(G), a path and a cycle having i vertices by Pi and Ci, respectively. For the graphs G1, G2, and G, if every 2-coloring (red and blue) of the edges of G results in either a copy of blue G1 or a copy of red G2, we call it Ramsey property of G and write G → (G1, G2). The size Ramsey number is the smallest number e such that there is a graph G with size e satisfying G → (G1, G2), i.e., . For k ∈ ℕ, a non-complete graph G is called k-connected if |V(G)| > k and G − X is connected for every set X ⊆ V with |X| < k. The greatest integer k such that G is k-connected is the connectivity κ(G) of G. For the complete graph Kn, we define κ(Kn) = n − 1.
In 1978, Erdös et al. initiated the study of the size Ramsey number, and later it was continued by Faudree [2, 3], Lortz and Mengersen [4], and Pikhurko [5]. From these studies, we can see that the size Ramsey number exists for the graphs G1 and G2. Su and Shao applied a backtracking algorithm to find some upper bounds for the size Ramsey numbers. The study of the size Ramsey numbers based on the graph coloring is implicitly connected to several branches of science, such as: the energies of the status level “fully functional nodes,” “partially functional nodes,” and “non-functional nodes” can be interpreted by the way of graph coloring [6], frequency channel assignment [7, 8], time tabling [9], and CAD problems [10, 11]. For more literature regarding the Ramsey numbers, we refer [12–16] to the readers. This paper is devoted to study the properties of the graphs G with the smallest size for which G → (G1, G2) for given graphs G1 and G2. Moreover, by developing the procedure and algorithm, we determined size Ramsey numbers of some paths and cycles.
2. The Approach
LEMMA 1. Let G be a graph with the smallest size for which G → (G1, G2). Then any G′, obtained by removing all the isolated vertices of G, is connected.
PROOF: By the definition of G′, we have . Suppose to the contrary that there are at least two components H1, H2 in G′. Let with n ≥ 2. Since Hi is not an isolated vertex for any i, we have for any i. Then there is a 2-coloring (red and blue) fi of the edges of Hi such that Hi contains neither red G1 nor blue G2. Now, consider a 2-edge coloring f of the edges of G′ with f(e) = fi(e) for any e ∈ Hi for i = 1, 2, ⋯ , n. Then G contains neither red G1 nor blue G2 under f, and so , a contradiction.
Remark 1: Given the graphs G, G1, G2 with G → (G1, G2), by the Lemma 1, we only need to consider the connected graphs for G.
LEMMA 2. If G is a graph with the smallest size for which G → (G1, G2), and G is a connected graph, then κ(G) ≥ min{κ(G1), κ(G2)}.
PROOF: Assume on contrary that we have κ(G) < min{κ(G1), κ(G2)}. Let S ⊆ V(G) such that |S| = κ(G) and G − S is disconnected and assume G − S = H1 ∪ H2 ∪ … ∪ Hn with n ≥ 2. Let V(Ti) = V(Hi) ∪ S and E(Ti) = E(Hi) ∪ E(Hi, S). Since G is a graph with the smallest size for which G → (G1, G2), there is a red-blue coloring fi of the edges of Ti such that Ti contains neither red G1 nor blue G2 for any i. Let E(S) = {e1, e2, ⋯ , ek} for some k. Now consider a 2-edge coloring f of the edges of G with f(e) = fi(e) for any e ∈ Hi for i = 1, 2, ⋯ , n, f(e1) = red, f(ei) = blue for any i = 2, 3, ⋯ , k. Then G contains neither red G1 nor blue G2 under f, and so . Now, we consider the following two cases:
Case 1: If there is a red copy of G1 as a subgraph of G.
Subcase 1.1: E(G1) ⊆ E(Ti) ∪ E(S) with i ∈ {1, …, n}.
Since fi is a red-blue coloring of the edges of Ti such that Ti contains no red G1. Then E(G1) ∩ E(S) ≠ ∅. Since G1[E(G1) ∩ E(S)] is not a clique with |S| vertices, there is a cut-set S1 of G1 with S1 ⊆ S. Then |S1| ≤ |S| < κ(G1) by the assumption, a contraction.
Subcase 1.2: E(G1) ∩ E(Hi) ≠ ∅, E(G1) ∩ E(Hj) ≠ ∅ with i ≠ j.
Then S is a cut-set of G1 with |S| < κ(G1) by the assumption, a contraction.
Case 2: If there is a blue copy of G2 as a subgraph of G.
Subcase 2.1: E(G2) ⊆ E(Ti) ∪ E(S) with i ∈ {1, …, n}.
Since fi is a red-blue coloring of the edges of Ti such that Ti contains no blue G2. Then E(G2) ∩ E(S) ≠ ∅. Since G2[E(G2) ∩ E(S)] is not a clique with |S| vertices, there is a cut-set S2 of G2 with S2 ⊆ S. Then |S2| ≤ |S| < κ(G2) by the assumption, a contraction.
Subcase 2.2: E(G2) ∩ E(Hi) ≠ ∅, E(G2) ∩ E(Hj) ≠ ∅ with i ≠ j.
Then S is a cut-set of G2 with |S| < κ(G2) by the assumption, a contraction.
LEMMA 3. For the graphs G, G1 and G2, if there exist vertices v1, …, vt for some 1 ≤ t ≤ |V(G)| satisfying that for any i = 1, 2, ⋯ , t and Gt ↛ (G1, G2), where and G0 = G. Then G ↛ (G1, G2).
PROOF: We apply induction on t to prove it. Firstly, it is clear that the lemma holds if t = 1. Now, we suppose the stated result holds for t = i, we need to prove it for t = i + 1. Since the lemma holds if t = i, we have . Then there is a red-blue coloring g of the edges of G1 such that there is neither a red copy of G1 nor a blue copy of G2 in G1. Let E(w) = {uv ∈ E(G)|u = w or v = w}. Since , we can divide E(v1) into E1, E2 with |E1| < δ(G1), |E2| < δ(G2). Let f be a coloring of G obtained by assigning red to E1, blue to E1 based on g.
Case 1: If there is a red copy of G1 as a subgraph of G under f, then v1 ∈ V(G1). Since |E1| < δ(G1), then d(v1|G1) < δ(G1), a contraction.
Case 2: If there is a blue copy of G2 as a subgraph of G under f, then v1 ∈ V(G2). Since |E2| < δ(G2), then d(v1|G2) < δ(G2), a contraction.
There is neither a red copy of G1 nor a blue copy of G2 in G under f. Therefore, G ↛ (G1, G2).
The contrapositive of the Lemma 3 for t = 1 produces the following corollary:
COROLLARY 1. For any graphs G1 and G2, if G is any graph with the smallest size for which G → (G1, G2), then δ(G) ≥ δ(G1) + δ(G2) − 1.
LEMMA 4. For any graphs G1 and G2, if G is any graph with order n and size m such that G ↛ (G1, G2), then for any graph G′ with order at most n and size , we have .
PROOF: First, we have G′ is not a complete graph, then there are two vertices u, v with uv ∉ E(G′). Now, we insert the edge uv to obtain a graph G″ based on G′. Then G″ is a graph with m edges and n vertices and so . Therefore, there is a red − blue coloring f of G″ such that there is neither a red copy of G1 nor a blue copy of G2 in G″ under f. Then, there is also neither a red copy of G1 nor a blue copy of G2 in G′ under . Then .
By applying the Lemma 1 and the Corollary 1, we only need to consider the connected graphs, and then propose the following algorithm (FindSizeRamseynumber) to find the size Ramsey number of G1 and G2. We will use the software nauty [17] to generate non-isomorphic graphs with necessary properties. If G1 and G2 are k-connected graphs, we further apply the Lemma 2 to reduces the number of graphs needed to be processed. For testing if G → (G1, G2), we applying the backtracking procedure proposed in [18].
Procedure Find(m,n,G1,G2);
input: m, n be integers;
graphs G1 and G2.
begin
generate the family of all the non-isomorphic connected graphs with size m and
order n with minimum degree δ(G1) + δ(G2) − 1; (Apply Lemma 1 and Corollary 1);
foreach G in
if (G → (G1, G2))
return true;
end if
end for
return true;
end.
Algorithm FindSizeRamseynumber(G1,G2);
input: graphs G1 and G2.
begin
1 : Find a graph G such G → (G1, G2);
2 : m = |E(G)| − 1;
3 : ;
4 : while Find(m, n, G1, G2) do;
5 : n = n − 1;
6 : if do
7 : m = m − 1;
8 : ;
9 : end if
10: end while
11: return m + 1.
end.
3. Results
EXAMPLE 1. .
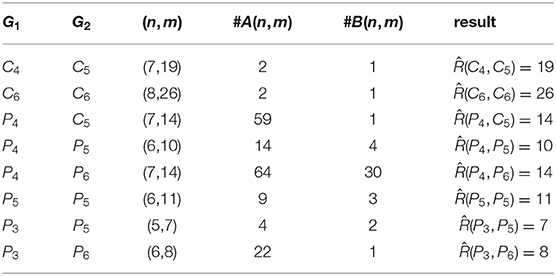
PROOF: Consider G1 = C4, G2 = C5. By Algorithm FindSizeRamseynumber, we first find the graph H satisfying H → (C4, C5) (line 1). Therefore, . Then, we consider the edge number less than 19 (i.e., m ≤ 18, by line 2), and the order of graph at most . Now, the procedure will check if there is no graph G with minimum degree 3, size at most and order from 7 to 12 satisfying G → (C4, C5) (line 3-10). In this case, by applying Procedure Find, we find that there is no such graph. Therefore, .
By applying Algorithm FindSizeRamseynumber, we obtain many size Ramsey numbers presented in Table 1, where #A(n, m) denote the number of non-isomorphic connected graphs with minimum degree δ(G1) + δ(G2) − 1 with size m and order n, and #B(n, m) denote the number of such graphs G with G → (G1, G2). An application of the algorithm can be used in some other graph problems, see [19].
4. Conclusion
It is a very hard task to determine the size Ramsey number even for small graphs. Faudree and Sheehan gave a table of the size Ramsey numbers for graphs with order not more than four [3]. Su and Shao [18] provide upper bounds for the size Ramsey numbers of some paths and cycles. Until now, very limited results on the size Ramsey numbers are known. In this paper, we have developed some computational techniques to determine many of those size Ramsey numbers. There are numerous variants of the Ramsey numbers such as ordered Ramsey numbers, size Ramsey numbers and zero-sum Ramsey numbers, see [20]. It is also very difficult to compute each variant of these Ramsey numbers. In order to compute some possible Ramsey numbers, we need to obtain the structure of the graphs by studying their mathematical properties. So, the approach of this paper may be considered to compute some challenging Ramsey numbers.
Author Contributions
All authors contributed equally in completing the current work.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Bondy JA, Murty USR. Graph Theory with Applications. London; Basingstoke: The Macmillan Press Ltd. (1976).
2. Faudree RJ, Rousseau CC, Sheehan J. A class of size Ramsey problems involving stars. In: Bollobas B, editor. Graph Theory and Combinatorics. Cambridge: Cambridge Univ Press (1983). p. 273–81.
3. Faudree RJ, Sheehan J. Size Ramsey Numbers for small-order graphs. J Graph Theory. (1983) 7:53–5.
4. Lortz R, Mengersen I. Size Ramsey results for paths versus stars. Australas J Comb. (1998) 18:3–12.
5. Pikhurko O. Asymptotic size Ramsey results for bipartite graphs. SIAM J Discr Math. (2002) 16:99–113. doi: 10.1137/S0895480101384086
6. Shang Y. Vulnerability of networks: fractional percolation on random graphs. Phys Rev E. (2014) 89:12813. doi: 10.1103/PhysRevE.89.012813
7. Ramanathan S, Lloyd EL. Scheduling broadcasts inmultihop radio networks. IEEE/ACM Trans Network. (1993) 1:166–72.
8. Smith K, Palaniswami M. Static and dynamic channel assignment using neural networks. IEEE J Select Areas Commun. (1997) 15:238–49.
11. Gajski D, Dutt N, Wu A, Lin S. High-Level Synthesis: Introduction to Chip and System Design. Boston, MA: Kluwer (1992).
12. Erdös P, Rousseau CC, Faudree RJ, Schelp RH. The size Ramsey number. Period Math Hung. (1978) 9:145–61.
14. Pikhurko O. Size Ramsey numbers of stars versus 3-chromatic graphs. Combinatorica. (2001) 21:403–12. doi: 10.1007/s004930100004
15. Shao Z, Shi X, Xu X, Pan L. Some three-color Ramsey numbers R(P4, P5, Ck) and R(P4, P6, Ck). Eur J Combinatorics. (2009) 30:396–403. doi: 10.1016/j.ejc.2008.05.008
16. Shao Z, Xu J, Pan L. Lower bounds on Ramsey numbers R(6, 8), R(7, 9) and R(8, 17). Ars Combinatoria. (2010) 94:55–59.
17. McKay BD. Nauty User Guide (version 26). Australian National University. Available online at: http://userscecsanueduau/~bdm/
18. Shao Z, Su C. On upper bounds for some size Ramsey numbers. J Chongqing Univers Posts Telecommun. (2011) 23:770–2.
19. Shang Y. On the number of spanning trees, the Laplacian eigenvalues, and the Laplacian Estrada index of subdivided-line graphs. Open Math. (2016) 14:641–8. doi: 10.1515/math-2016-0055
Keywords: size Ramsey number, 2-coloring, connected graphs, connectivity, paths, cycles
Citation: Li X, Fahad A, Zhou X and Yang H (2020) Exact Values for Some Size Ramsey Numbers of Paths and Cycles. Front. Phys. 8:350. doi: 10.3389/fphy.2020.00350
Received: 01 May 2020; Accepted: 23 July 2020;
Published: 18 September 2020.
Edited by:
Muhammad Javaid, University of Management and Technology, Lahore, PakistanReviewed by:
Kashif Ali, COMSATS Institute of Information Technology, PakistanYilun Shang, Northumbria University, United Kingdom
Copyright © 2020 Li, Fahad, Zhou and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Asfand Fahad, YXNmYW5kZmFoYWQxJiN4MDAwNDA7eWFob28uY29t
 Xiangmei Li1
Xiangmei Li1 Asfand Fahad
Asfand Fahad Hong Yang
Hong Yang