- 1Faculty of Engineering Technology, Amol University of Special Modern Technologies, Amol, Iran
- 2Department of Mathematics, Science Faculty, Firat University, Elâzig, Turkey
- 3Department of Mathematics, Faculty of Art and Sciences, Cankaya University, Ankara, Turkey
- 4Institute of Space Sciences, Măgurele, Romania
- 5Department of Medical Research, China Medical University Hospital, China Medical University, Taichung City, Taiwan
We solve distinct forms of (3+1)-Dimensional Wazwaz-Benjamin-Bona-Mahony [(3+1)-Dimensional WBBM] equations by employing the method of Sardar-subequation. When parameters involving this approach are taken to be special values, we can obtain the solitary wave solutions (sws) which is concluded from other approaches such as the functional variable method, the trail equation method, the first integral method and so on. We obtain new and general solitary wave solutions in terms of generalized hyperbolic and trigonometric functions. The results demonstrate the power of the proposed method for the determination of sws of non-linear evolution equations (NLEs).
Introduction
Exact solutions and solitary wave solutions of NLEs have a high importance in non-linearity theory. It is a well-known fact that numerous complex events in various fields of engineering application and non-linear science such as chemistry, mathematical physics, mechanics, hydrodynamics, biology, cosmology, and mechanics are explained by NLEs. Exact solutions produce corporal information to describe the physical behavior of system connected with these NLEs. In recent years, several efficient methods including method of extended tanh [1, 2], tanh-coth [3, 4], Hirota's direct [5, 6], sine-cosine [7, 8], extended direct algebraic [9, 10], extended trial approach [11, 12], Exp [-φ(ξ)]-Expansion [13, 14], a new auxiliary equation [15, 16], Jacobi elliptic ansatz [17, 18], generalized Bernoulli sub-ODE [19, 20], functional variable [21, 22], sub equation [23, 24], and so on [25–39], have been established for efficient solutions of NLEs.
In this paper, we utilize of an effective and efficient technique for manufacturing a range of solitary wave solutions for the variants of the (3+1)-dimensional WBBM equations.
The Benjamin-Bona-Mahony (BBM) equation
proposed in [40] as a model to study the approximately the unidirectional propagation of small-amplitude long waves on certain non-linear dispersive systems as a good alternative to the KdV [41]. It is used in modeling surface waves of long wavelength in liquids; it covers hydro-magnetic waves in cold plasma, acoustic waves in anharmonic crystals, and acoustic gravity waves in compressible fluids. Many efforts have been offered to modified forms of this equation such as
known as the modified Benjamin-Bona-Mahoney (mBBM) equation [42]. Furthermore, as higher dimensional samples convert to be more realistic; various modifications to Equation (2) have been proposed in the literature among which the (3+1)-dimensional mBBM equation given in Equations (3–5) by Wazwaz [43]. Using the tanh/sech method, Wazwaz obtained soliton, kink, and periodic solutions for the following three different types of Equation (2)
and
Based on these ideas, this paper is organized as follows. Section The Sardar-Subequation Method introduces a brief description of the Sardar-sub-equation method. Section The (3+1)-Dimensional WBBM Equation discusses the application of the Sardar-subequation method to variants of (3+1)-dimensional WBBM equations represent by (3)–(5). The graphical presentation for the acquired solution is given in section Exact Solutions of the (3+1)-Dimensional WBBM Equation. We complete the paper with conclusions part.
The Sardar-Subequation Method
We consider the following NLEs
where u = u(x, t) is an unknown function and G is a polynomial in u and its partial derivatives.
To solve (Equation 6), we take the traveling wave transformation (twt)
where c ≠ 0 is constants to be determined later.
By using (7), Equation (6) is turned into following ODE w.r.t. η
in which
Suppose that the Equation (8) has a solution of the form
where ϖi, (i = 0, 1, …, s) are coefficients to be determined with (ϖs ≠ 0) and φ(η) satisfies the ODE in the form
where a and ρ are real constants. The solutions of ODE (10) are
Case I: If a > 0 and ρ = 0 then
where
Case II: If a < 0 and ρ = 0 then
where
Case III: If a < 0 and then
where
Case IV: If a > 0 and then
where
The procedure starts by determining s by the assistance of the classical balance rule. When s is determined the predicted solution (8) is substituted into (Equation 7). Since we seek a non-zero solution that is φ(η) ≠ 0, all the coefficient of power of φ(η) are equated to zero. Thus, the resultant algebraic system is solved for ϖis and c. One should note that ϖs ≠ 0 and c ≠ 0 both have to be satisfied in the solution sets. Whenever ϖis and c are determined the solutions are constructed by using these parameters explicitly. The procedure ends by substitution of η = x − ct into the solutions satisfying (Equation 7).
Remark 1. The Sardar-subequation method is considered among those general ones from which, under certain cases, various methods can be deduced such as the functional variable method [44], the first integral method [45], and so on.
The (3+1)-Dimensional WBBM Equation
To solve the (3+1)-Dimensional (3+1)-Dimensional WBBM equations (3), (4), and (5) by using the Sardar-sub-equation method, we make the following subsection.
The First (3+1)-Dimensional WBBM Equation
We next study the first (3+1)-dimensional WBBM equation (3). The twt u(x, t) = U(η), η = kx + λy + μz − ct, reduces (Equation 3) to the following ordinary differential equation
Integrating (Equation 11), we get
Then, Equation (12) can be written as.
where
The Second (3+1)-Dimensional WBBM Equation
We next study the second (3+1)-dimensional WBBM equation (4). The twt u(x, t) = U(η), η = kx + λy + μz − ct, reduces (Equation 4) to the following ordinary differential equation
Integrating (Equation 15), we get
Then, Equation (16) can be written as.
where.
The Third (3+1)-Dimensional WBBM Equation
We next study the third (3+1)-dimensional WBBM equation (5). By making the traveling wave transformation
(Equation 5) becomes
Integrating (Equation 20) twice and setting the integration constants to zero yield
Then, Equation (21) can be written as.
where
Exact Solutions of the (3+1)-Dimensional WBBM Equation
Balancing U with U″ in Equations (13, 17, 22), we get s = 1. Therefore, the solutions form of Equations (13, 17, 22) has the following expression
Substituting Equation (24) into (13) [or (17) or (22)] with along (Equation 10) and equating all the coefficients of φ(η) to zero, we obtain a highly complicated system of algebraic equations. A set of algebraic equations is obtained in ϖ0, ϖ1, and a as follows:
Solving these algebraic equations with Maple, we acquire:
The First (3+1)-Dimensional WBBM Equation
Substituting (Equation 14) into (Equation 25), we have
The solutions of (3) corresponding to (26), along with solution (10) are
Case I: If and ρ = 0 then
Case II: If and ρ = 0 then
Case III: If and then
Case IV: If and then
The Second (3+1)-Dimensional WBBM Equation
Substituting (Equation 18) into (Equation 25), we have
The solutions of (4) corresponding to (27), along with solution (10) are
Case I: If and ρ = 0 then
Case II: If and ρ = 0 then
Case III: If and then
Case IV: If and then
The Third (3+1)-Dimensional WBBM Equation
Substituting (Equation 23) into (Equation 25), we have
The solutions of (5) corresponding to (28), along with solution (10) are
Case I: If and ρ = 0 then
Case II: If and ρ = 0 then
Case III: If and then
Case IV: If and then
Graphical Presentation
Graph is a strong tool for relationship describing clarity the solutions of the challenges. Therefore, some graphs of the solutions are given in each subsection above with different parameters. The graphs easily have shown the solitary wave form of the modulus solution ,,,,, and in Figures 1–6 [(a) 3D plot, (b) cp, and (c) 2D plot], respectively. We see in Figures 1, 6 that the absolute value of and are singular periodic wave solutions and, in Figures 2, 5 that the absolute value of and are bright solitary wave solutions and in Figures 3, 4 that the absolute value of and are singular solitary wave solutions.
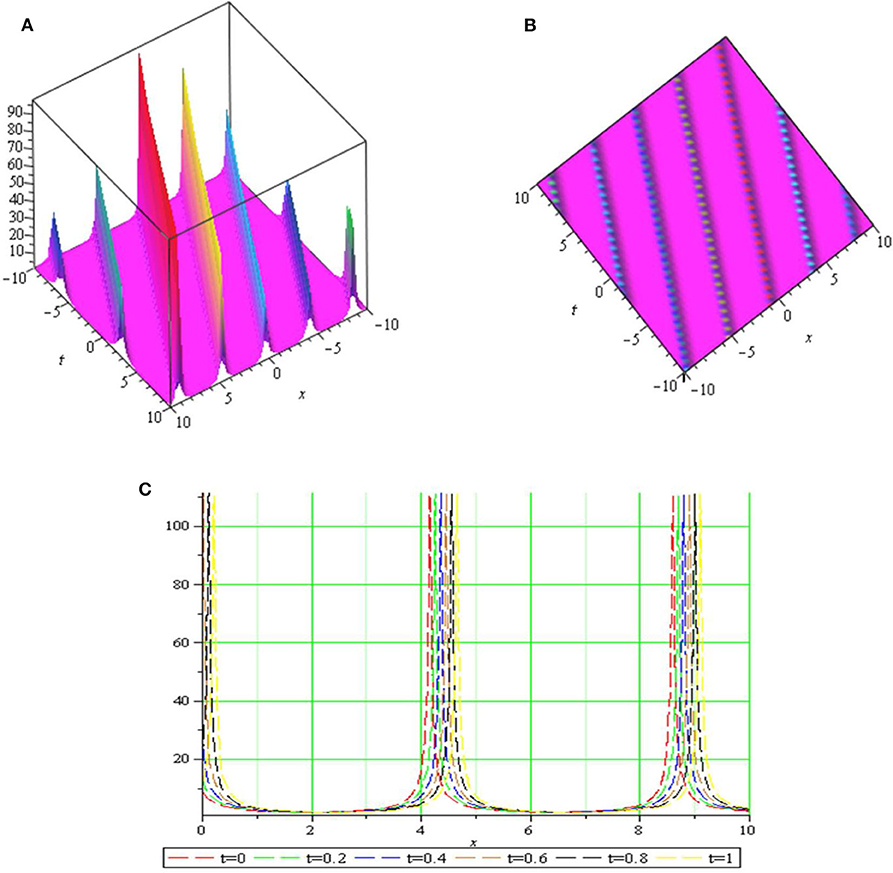
Figure 1. The sws with parameters μ = 1, k = 1, c = 0.5, λ = 1, p = 0.98, q = 0.95, y = 0.5, z = 1 and (A) 3D plot, (B) contour plot (cp), and (C) 2D plot.
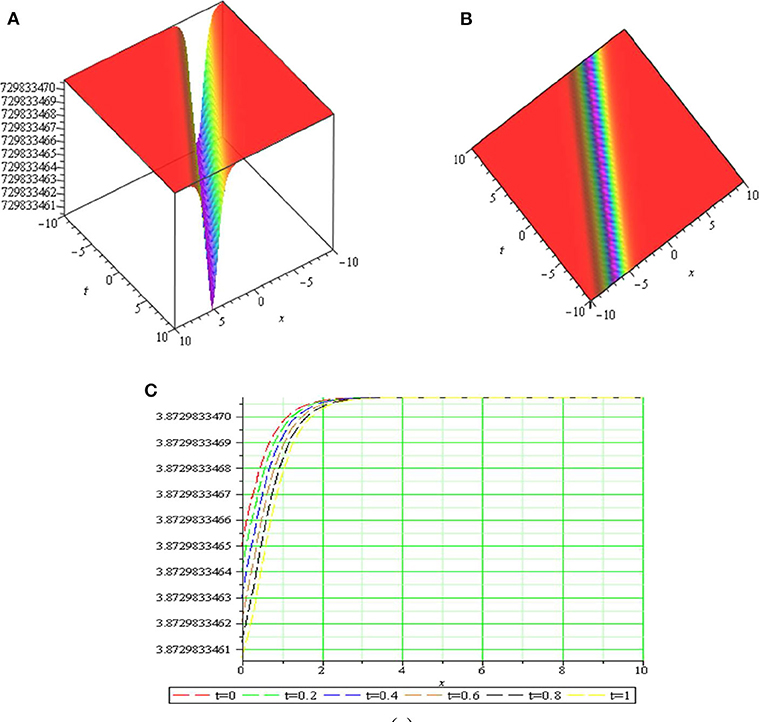
Figure 2. The sws with parameters μ = 3, k = 2.5, c = 1.5, λ = 0.2, p = 1.2, q = 1.1, y = 1.5, z = 0.5 and (A) 3D plot, (B) cp, and (C) 2D plot.
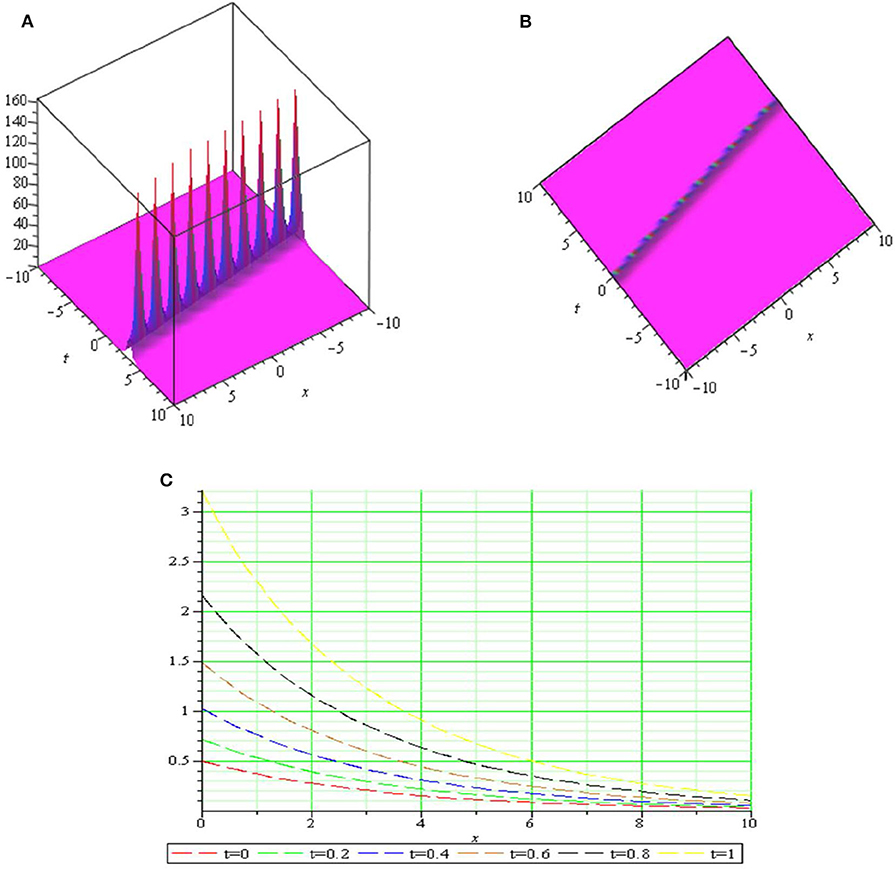
Figure 3. The sws with μ = 0.3, k = 0.5, c = 3, λ = 5, p = 1.1, q = 1.2, y = 1, z = 1 (A) 3D plot, (B) cp, and (C) 2D plot.
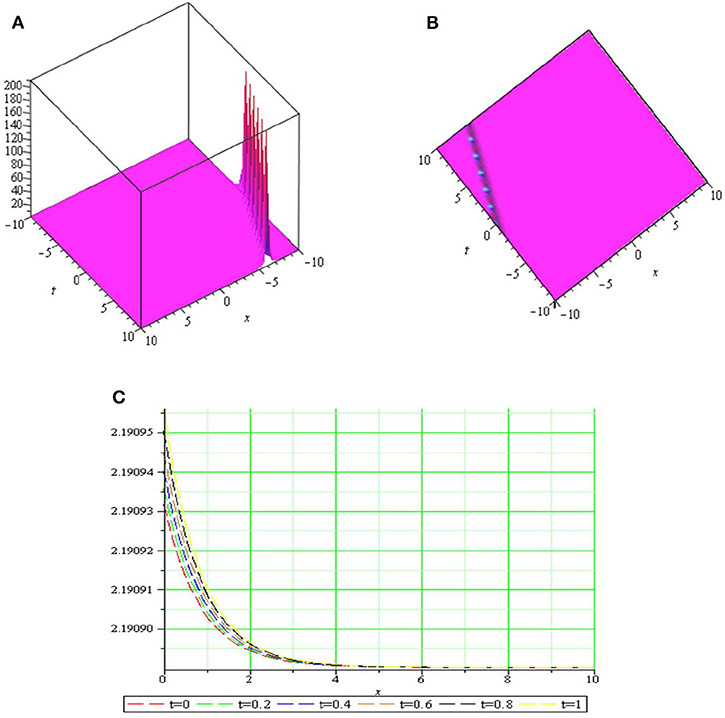
Figure 4. The sws withμ = 1, k = 0.5, c = 0.2, λ = 3, p = 0.97, q = 0.95, y = 1.5, z = 0.5 and (A) 3D plot, (B) cp, and (C) 2D plot.
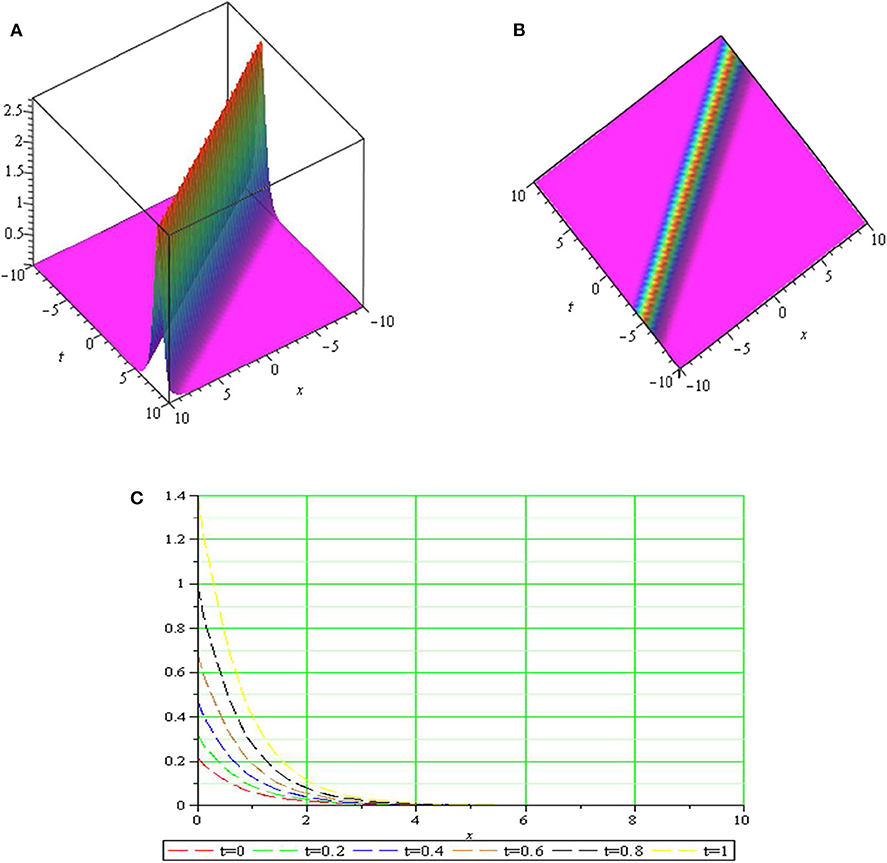
Figure 5. The sws with parameters μ = 2, k = 1, c = 1.5, λ = −1, p = 1, q = 1, y = 1.5, z = 2 and (A) 3D plot, (B) cp, and (C) 2D plot.
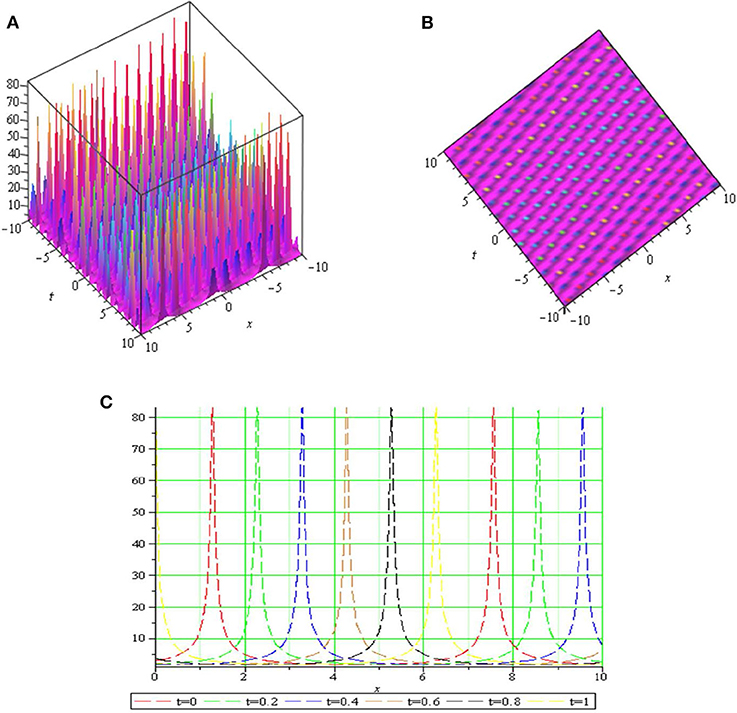
Figure 6. The sws with parameters μ = 0.5, k = 0.2, c = 1, λ = 0.5, p = 0.97, q = 0.95, y = 1, z = 1 and (A) 3D plot, (B) cp, and (C) 2D plot.
Conclusions
We have proposed a method, namely Sardar-subequation method to solve NLEs with the help of Maple Software. Distinct forms of (3+1)-dimensional WBBM equations are handled to display the effectiveness of the suggested method. From our results, some sws are obtained including the generalized hyperbolic and trigonometric function solutions. As far as we know, for the first time, we describe and introduce Sardar-subequation method which is a new method for solving NLEs. Thus, all the solutions distinct forms of (3+1)-dimensional WBBM equations are new, which cannot be found in literature to our best knowledge. We can also see that the approach used in this letter is very effective, powerful and convenient and can be steadily applied to NLEs. We will extend the proposed method for some fractional models [46–48] in a future work.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
HR, MI, and DB contributed conception and design of the study. HR organized the database. MI performed the statistical analysis. DB wrote the first draft of the manuscript. HR, MI, and DB wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Wazwaz AM. The tan h method: solitons and periodic solutions for the Dodd-Bullough-Mikhailov and the Tzitzeica-Dodd-Bullough equations. Chaos Solitons Fractals. (2005) 25:55–63. doi: 10.1016/j.chaos.2004.09.122
2. Wazwaz AM. The tanh method for traveling wave solutions of nonlinear equations. Appl Math Comput. (2004) 154:713–23. doi: 10.1016/S0096-3003(03)00745-8
3. Wazwaz AM. The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations. Appl Math Comput. (2007) 188:1467–75. doi: 10.1016/j.amc.2006.11.013
4. Wazwaz AM. The tanh-coth method for new compactons and solitons solutions for the K (n,n) and the K (n+1, n+1) equations. Appl Math Comput. (2007) 188:1930–40. doi: 10.1016/j.amc.2006.11.076
5. Wazwaz AM. The Hirota's direct method and the tanh-coth method for multiple-soliton solutions of the Sawada-Kotera-Ito seventh-order equation. Appl Math Comput. (2008) 199:133–8. doi: 10.1016/j.amc.2007.09.034
6. Wazwaz AM. The Hirota's direct method for multiple-soliton solutions for three model equations of shallow water waves. Appl Math Comput. (2008) 201:489–503. doi: 10.1016/j.amc.2007.12.037
7. Wazwaz AM. The sine-cosine method for obtaining solutions with compact and noncompact structures. Appl Math Comput. (2004) 159:559–76. doi: 10.1016/j.amc.2003.08.136
8. Wazwaz AM. A sine-cosine method for handlingnonlinear wave equations. Math Comput Model. (2004) 40:499–508. doi: 10.1016/j.mcm.2003.12.010
9. Gao W., Rezazadeh H, Pinar Z, Baskonus HM, Sarwar S, Yel G. Novel explicit solutions for the nonlinear Zoomeron equation by using newly extended direct algebraic technique. Optic Quant Electron. (2020) 52:1–13. doi: 10.1007/s11082-019-2162-8
10. Rezazadeh H. New solitons solutions of the complex Ginzburg-Landau equation with Kerr law nonlinearity. Optik. (2018) 167:218–27. doi: 10.1016/j.ijleo.2018.04.026
11. Raza N, Aslam MR, Rezazadeh H. Analytical study of resonant optical solitons with variable coefficients in Kerr and non-Kerr law media. Optic Quant Electron. (2019) 51:59. doi: 10.1007/s11082-019-1773-4
12. Raza N, Javid A. Optical dark and dark-singular soliton solutions of (1+2)-dimensional chiral nonlinear Schrodinger's equation. Waves Random Comp Media. (2019) 29:496–508. doi: 10.1080/17455030.2018.1451009
13. Raza N, Abdullah M, Butt AR. Analytical soliton solutions of Biswas-Milovic equation in Kerr and non-Kerr law media. Optik. (2018) 157:993–1002. doi: 10.1016/j.ijleo.2017.11.043
14. Raza N, Afzal U, Butt AR, Rezazadeh H. Optical solitons in nematic liquid crystals with Kerr and parabolic law nonlinearities. Optic Quant Electron. (2019) 51:107. doi: 10.1007/s11082-019-1813-0
15. Khater MM, Seadawy AR, Lu D. Dispersive optical soliton solutions for higher order nonlinear Sasa-Satsuma equation in mono mode fibers via new auxiliary equation method. Superlattices Microstruct. (2018) 113:346–58. doi: 10.1016/j.spmi.2017.11.011
16. Rezazadeh H, Korkmaz A, Eslami M, Mirhosseini-Alizamini SM. A large family of optical solutions to Kundu-Eckhaus model by a new auxiliary equation method. Optic Quant Electron. (2019) 51:84. doi: 10.1007/s11082-019-1801-4
17. Aslan EC., Inc M. Optical soliton solutions of the NLSE with quadratic-cubic-Hamiltonian perturbations and modulation instability analysis. Optik. (2019) 196:162661. doi: 10.1016/j.ijleo.2019.04.008
18. Korpinar Z, Inc M, Bayram M, Hashemi MS. New optical solitons for Biswas–Arshed equation with higher order dispersions and full nonlinearity. Optik. (2019) 206:163332. doi: 10.1016/j.ijleo.2019.163332
19. Yusuf A, Inc M, Aliyu AI, Baleanu D. Optical solitons possessing beta derivative of the Chen-Lee-Liu equation in optical fiber. Front Phys. (2019) 7:34. doi: 10.3389/fphy.2019.00034
20. Yusuf A, Inc M, Baleanu D. Optical solitons with M-truncated and beta derivatives in nonlinear optics. Front Phys. (2019) 7:126. doi: 10.3389/fphy.2019.00126
21. Çenesiz Y, Tasbozan O, Kurt A. Functional Variable Method for conformable fractional modified KdV-ZK equation and Maccari system. Tbilisi Math J. (2017) 10:117–25. doi: 10.1515/tmj-2017-0010
22. Eslami M, Rezazadeh H, Rezazadeh M, Mosavi SS. Exact solutions to the space-time fractional Schrödinger-Hirota equation and the space-time modified KDV-Zakharov-Kuznetsov equation. Optic Quant Electron. (2017) 49:279. doi: 10.1007/s11082-017-1112-6
23. Kurt A. New analytical and numerical results for fractional Bogoyavlensky-Konopelchenko equation arising in fluid dynamics. Appl Math A J Chin Univ. (2020) 35:101–12. doi: 10.1007/s11766-020-3808-9
24. Atilgan E, Senol M, Kurt A, Tasbozan O. New wave solutions of time-fractional coupled Boussinesq-Whitham-Broer-Kaup equation as a model of water waves. China Ocean Eng. (2019) 33:477–83. doi: 10.1007/s13344-019-0045-1
25. Nestor S, Houwe A, Rezazadeh H., Bekir A, Betchewe G, Doka SY. New solitary waves for the Klein-Gordon-Zakharov equations. Modern Phys Lett B. (2020) 60:324–343. doi: 10.1142/S0217984920502462
26. Nestor S, Abbagari S, Houwe A, Betchewe G, Doka SY. Diverse chirped optical solitons and new complex traveling waves in nonlinear optical fibers. Commun Theor Phys. (2020) 72:065501. doi: 10.1088/1572-9494/ab7ecd
27. Houwe A, Abbagari S, Salathiel Y, Inc M, Doka SY, Crépin KT, et al. Complex traveling-wave and solitons solutions to the Klein-Gordon-Zakharov equations. Results Phys. (2020) 17:103127. doi: 10.1016/j.rinp.2020.103127
28. Houwe A, Abbagari S, Inc M, Betchewe G, Doka SY, Crépin, et al. Chirped solitons in discrete electrical transmission line. Results Phys. (2020) 18:103188. doi: 10.1016/j.rinp.2020.103188
29. Park C, Khater MM, Abdel-Aty AH, Attia RA, Rezazadeh H, Zidan AM, et al. Dynamical analysis of the nonlinear complex fractional emerging telecommunication model with higher-order dispersive cubic-quintic. Alexandria Eng J. (2020) 59:1425–33. doi: 10.1016/j.aej.2020.03.046
30. Alquran M, Jarrah A. Jacobi elliptic function solutions for a two-mode KdV equation. J King Saud Univ Sci. (2019) 31:485–9. doi: 10.1016/j.jksus.2017.06.010
31. Jaradat HM, Syam M, Alquran M. A two-mode coupled Korteweg-de Vries: multiple-soliton solutions and other exact solutions. Nonlinear Dyn. (2017) 90:371–7. doi: 10.1007/s11071-017-3668-x
32. Alquran M, Jaradat HM, Syam MI. A modified approach for a reliable study of new nonlinear equation: two-mode Korteweg-de Vries-Burgers equation. Nonlinear Dyn. (2018) 91:1619–26. doi: 10.1007/s11071-017-3968-1
33. Jaradat HM, Awawdeh F, Al-Shara S, Alquran M, Momani S. Controllable dynamical behaviors and the analysis of fractal burgers hierarchy with the full effects of inhomogeneities of media. Rom. J. Phys. (2015) 60:324–43.
34. Syam M, Jaradat HM, Alquran M. A study on the two-mode coupled modified Korteweg-de Vries using the simplified bilinear and the trigonometric-function methods. Nonlinear Dyn. (2017) 90:1363–71. doi: 10.1007/s11071-017-3732-6
35. Alquran M, Jaradat HM, Al-Shara S, Awawdeh F. A new simplified bilinear method for the N-soliton solutions for a generalized FmKdV equation with time-dependent variable coefficients. Int J Nonlinear Sci Numer Simul. (2015) 16:259–69. doi: 10.1515/ijnsns-2014-0023
36. Rezazadeh H, Vahidi J, Zafar A, Bekir A. The functional variable method to find new exact solutions of the nonlinear evolution equations with dual-power-law nonlinearity. Int J Nonlinear Sci Numer Simul. (2020) 21:249–57. doi: 10.1515/ijnsns-2019-0064
37. Yépez-Martínez H, Gómez-Aguilar JF. Fractional sub-equation method for Hirota-Satsuma-coupled KdV equation and coupled mKdV equation using the Atangana's conformable derivative. Waves Ran Comp Med. (2019) 29:678–93. doi: 10.1080/17455030.2018.1464233
38. Yépez-Martínez H, Gómez-Aguilar JF, Baleanu D. Beta-derivative and sub-equation method applied to the optical solitons in medium with parabolic law nonlinearity and higher order dispersion. Optik. (2018) 155:357–65. doi: 10.1016/j.ijleo.2017.10.104
39. Yépez-Martínez H, Gómez-Aguilar JF. M-derivative applied to the soliton solutions for the Lakshmanan-Porsezian-Daniel equation with dual-dispersion for optical fibers. Optical Quant Electron. (2019) 51:31. doi: 10.1007/s11082-018-1740-5
40. Benjamin TB, Bona JL, Mahony JJ. Model equations for long waves in nonlinear dispersive systems. Philos Trans R Soc Lond Ser A Math Phys Sci. (1972) 272:47–78. doi: 10.1098/rsta.1972.0032
41. Bona JL, Pritchard WG, Scott LR. An evaluation of a model equation for water waves. Philos Trans R Soc Lond Ser A Math Phys Sci. (1981) 302:457–510. doi: 10.1098/rsta.1981.0178
42. Yusufoglu E. New solitonary solutions for the MBBM equations using Exp-function method. Phys Lett A. (2008) 372:442–6. doi: 10.1016/j.physleta.2007.07.062
43. Wazwaz AM. Exact soliton and kink solutions for new (3+1)-dimensional nonlinear modified equations of wave propagation. Open Eng. (2017) 7:169–74. doi: 10.1515/eng-2017-0023
44. Eslami M, Mirzazadeh M. Functional variable method to study nonlinear evolution equations. Open Eng. (2013) 3:451–8. doi: 10.2478/s13531-013-0104-y
45. Mirzazadeh M, Eslami M. Exact solutions of the Kudryashov-Sinelshchikov equation and nonlinear telegraph equation via the first integral method. Nonlinear Analy Model Control. (2012) 17:481–8. doi: 10.15388/NA.17.4.14052
46. Memon Z, Qureshi S, Memon BR. Mathematical analysis for a new nonlinear measles epidemiological system using real incidence data from Pakistan. Eur Phys J Plus. (2020) 135:378. doi: 10.1140/epjp/s13360-020-00392-x
47. Atangana A, Qureshi S. Mathematical analysis of dengue fever outbreak by novel fractional operators with field data. Phys A. (2019) 526:121127. doi: 10.1016/j.physa.2019.121127
Keywords: Sardar-subequation method, (3+1)-dimensional WBBM equations, solitary wave solutions, NLEs, simulations
Citation: Rezazadeh H, Inc M and Baleanu D (2020) New Solitary Wave Solutions for Variants of (3+1)-Dimensional Wazwaz-Benjamin-Bona-Mahony Equations. Front. Phys. 8:332. doi: 10.3389/fphy.2020.00332
Received: 13 April 2020; Accepted: 17 July 2020;
Published: 04 September 2020.
Edited by:
Francisco Gomez, Centro Nacional de Investigación y Desarrollo Tecnológico, MexicoReviewed by:
Sania Qureshi, Mehran University of Engineering and Technology, PakistanHaci Mehmet Baskonus, Harran University, Turkey
Marwan Alquran, Jordan University of Science and Technology, Jordan
Copyright © 2020 Rezazadeh, Inc and Baleanu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dumitru Baleanu, ZHVtaXRydUBjYW5rYXlhLmVkdS50cg==
 Hadi Rezazadeh
Hadi Rezazadeh Mustafa Inc
Mustafa Inc Dumitru Baleanu
Dumitru Baleanu