An Efficient Computational Method for the Time-Space Fractional Klein-Gordon Equation

In this paper, we present a computational method to solve the fractional Klein-Gordon equation (FKGE). The proposed technique is the grouping of orthogonal polynomial matrices and collocation method. The benefit of the computational method is that it reduces the FKGE into a system of algebraic equations which makes the problem straightforward and easy to solve. The main reason for using this technique is its high accuracy and low computational cost compared to other methods. The main solution behaviors of these equations are due to fractional orders, which are explained graphically. Numerical results obtained by the proposed computational method are also compared with the exact solution. The results obtained by the suggested technique reveals that the method is very useful for solving FKGE.

Introduction

The standard Klein-Gordon equation (KGE) is written as

$\begin{array}{ll}\frac{{\partial }^{2}v}{\partial t^2}-\frac{{\partial }^{2}v}{\partial x^2}+v=h(x,t),x\ge 0,t\ge 0& (1)\end{array}$

where v indicates an unknown function in variables x and t, and h(x, t) stands for the source term. Due to the non-local nature and real-life applications of fractional derivatives, the fractional extension of this equation is very useful [1–12]. The fractional extension of this model handles the initial and boundary conditions of the model very accurately. The non-integer derivative helps in understanding the complete memory effect of the system. A broad literature of models with fractional derivatives can be found in [13–17]. Therefore, motivated by our ongoing research work into this special branch of mathematics (namely, fractional calculus), we study non-integer KGE by changing integer order derivative in both time and space using the Liouville-Caputo derivative of fractional order in the following manner:

$\begin{array}{l}\frac{{\partial }^{\beta }v(x,t)}{\partial t^{\beta }}-\frac{{\partial }^{\gamma }v(x,t)}{\partial x^{\gamma }}+v(x,t)\\ =h(x,t),1<\beta \le 2,1<\gamma \le 2& (2)\end{array}$

having the initial conditions:

$\begin{array}{ll}v(x,0)=h_1(x),\frac{\partial v(x,0)}{\partial t}=h_2(x),\text{for }0\le x,t\le 1& (3)\end{array}$

and boundary conditions:

$\begin{array}{ll}v(0,t)=g_1(t),v(1,t)=g_2(t)& (4)\end{array}$

The KGE is used in science, plasma (especially in quantum field theory), optical fibers, and dispersive wave-phenomena. Due to the great importance of KGE, many authors have studied it using various numerical and analytical schemes [18–27], each with their own limitations and shortcomings. The operational matrix method [28–38] is also applied to solve problems in fractional calculus. There are several other numerical and analytical methods which have been used to solve non-linear problems pertaining to fractional calculus, which can be found in [39, 40]. Some other applications of orthogonal polynomials-based solutions can be found in [41, 42].

In this paper, we present a computational technique which is a combination of the operational matrix and collocation method. We have used Chebyshev polynomials as a basis function for the construction of operational matrices of differentiations and integrations. In our proposed method, first the unknown function and their derivatives are approximated by taking finite dimensional approximations. Then, by using these approximations along with operational matrices of differentiations and integrations in the FKGE, we obtain a system of equations. Finally, by collocating this system, we get an approximate solution for the FKGE. The efficiency and accuracy of the used technique is shown by making a comparison amongst the results derived by our technique, exact solutions, and numerical results by some existing methods.

Some Basic Definitions

In this paper, we use non-integer order integrals and derivatives in the Riemann-Liouville and Caputo sense, respectively, which are given as:

Definition 2.1: The Riemann-Liouville non-integer integral operator of order α is presented as

$\begin{array}{l}{I}^{\alpha }f(x)=\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^x}{(x-t)}^{\alpha -1}f(t)dt,\alpha >0,x>0,\end{array}$

I⁰f(x) = f(x).

Definition 2.2: The Liouville-Caputo non-integer derivative of order β are defined as [1–3]

$D^{\beta }f(x)=I^{l-\beta }{D}^{l}f(x)=\frac{1}{\Gamma (l-\beta )}{\int }_0^x{(x-t)}^{l-\beta -1}\frac{d^l}{d{t}^l}f(t)dt$, l − 1 < β < l, x > 0 and l is a natural number.

Chebyshev polynomial of the third kind of degree i on [0, 1] is given as,

$\begin{array}{ll}{H}_i(t)={\displaystyle \sum _{k=0}^i}{(-1)}^{i-k}\frac{\Gamma (i+\frac{3}{2})\Gamma (i+k+1)}{\Gamma \left(k+\frac{3}{2}\right)\Gamma (i+1)\left(i-k\right)!k!}{t}^k& (5)\end{array}$

The orthogonal property of these polynomials is given as:

$\begin{array}{ll}{\displaystyle {\int }_0^1}{H}_n(t)H_m(t)w(t)dt=\{\begin{array}{c}\frac{\pi }{2},n=m\\ 0,n\ne m\end{array}& (6)\end{array}$

where, $w(t)=\sqrt{\frac{t}{1-t}}$, is a weight function and n and m are the degrees of polynomials.

A function $g(x,t)\in L_{w(t)}^2(\left[0,1\right]\times \left[0,1\right])$ can be approximated as

$\begin{array}{ll}g(x,t)\cong {\displaystyle \sum _{i_1=0}^{n_1}}{\displaystyle \sum _{i_2=0}^{n_2}}{c}_{i_1,i_2}{H}_{i_1,i_2}(x,t)=C^T{\theta }_{n_1,n_2}(x,t)& (7)\end{array}$

where, $C={\left[c_{0,0},\dots ,c_{0,n_2},\dots ,c_{n_1,1},\dots ,c_{n_1,n_2}\right]}^T$ and

$\begin{array}{l}{\theta }_{n_1,n_2}\left(x,t\right)=[H_{0,0}\left(x,t\right),\dots ,H_{0,n_2}\left(x,t\right),\\ \dots .H_{n_1,0}\left(x,t\right),\dots H_{n_1,n_2}\left(x,t \right){]}^T.\end{array}$

For any approximation taking n₁ = n₂ = n then Equation (6), can be written as,

$\begin{array}{ll}g(x,t)\cong {\theta }_n^T(x)C{\theta }_n(t)& (8)\end{array}$

The matrix C in Equation (8), is given as:

$\begin{array}{ll}C=P^{-1}\left({\displaystyle {\int }_0^1}{\displaystyle {\int }_0^1}{\theta }_n(x)C{\theta }_n^T(t)w(x)w(t)dxdt\right)P^{-1}& (9)\end{array}$

where, $P={\int }_0^1{\theta }_n(x){\theta }_n^T(x)w(x)dx$, is called the matrix of dual.

Theorem 1. If ${\theta }_n(t)={\left[H_0,H_1,\dots .,H_n\right]}^T$, is Chebyshev vector and we consider v > 0, then

$\begin{array}{ll}{I}^v{H}_i(t)=I^{(v)}{\theta }_n(t)& (10)\end{array}$

where, I^(v) = (e(i, j)), is (n + 1) × (n + 1) matrix of integral of non-integer order v and its entries are given by

$\begin{array}{l}e\left(i,j\right)={\displaystyle \sum _{k=0}^i}{\displaystyle \sum _{l=0}^j}{\left(-1\right)}^{i+j-k-l}\\ \times \frac{\Gamma \left(\frac{1}{2}\right)\Gamma \left(i+\frac{3}{2}\right)\Gamma \left(i+k+1\right)\Gamma \left(j+l+1\right)\Gamma \left(v+k+l+\frac{3}{2}\right)\left(2j+1\right)j!}{\left(i-k\right)!\left(j-l\right)!\left(l\right)!\Gamma \left(k+\frac{3}{2}\right)\Gamma \left(i+1\right)\Gamma \left(v+k+1\right)\Gamma \left(j+\frac{1}{2}\right)\Gamma \left(l+\frac{3}{2}\right)\Gamma \left(k+l+v+2\right)}.\end{array}$

Proof. Please see [30, 32, 38].

Theorem 2. If ${\theta }_n(t)={\left[H_0,H_1,\dots .,H_n\right]}^T$, is Chebyshev vector and we consider β > 0, then

$\begin{array}{ll}{D}^{\beta }{H}_i(t)=D^{(\beta )}{\theta }_n(t)& (11)\end{array}$

where, D^(β) = (s(i, j)), is (n + 1) × (n + 1) matrix of differentiation of non-integer order β and its entries are given by

$\begin{array}{l}s\left(i,j\right)={\displaystyle \sum _{k=\lceil \beta \rceil }^i}{\displaystyle \sum _{l=0}^j}{\left(-1\right)}^{i+j-k-l}\\ \times \frac{\Gamma \left(\frac{1}{2}\right)\Gamma \left(i+\frac{3}{2}\right)\Gamma \left(i+k+1\right)\Gamma \left(j+l+1\right)\Gamma \left(k+l-\beta +\frac{3}{2}\right)\left(2j+1\right)j!}{\left(i-k\right)!\left(j-l\right)!\left(l\right)!\Gamma \left(k+\frac{3}{2}\right)\Gamma \left(i+1\right)\Gamma \left(k-\beta +1\right)\Gamma \left(j+\frac{1}{2}\right)\Gamma \left(l+\frac{3}{2}\right)\Gamma \left(k+l-\beta +2\right)}.\end{array}$

Proof. Please see [38].

Method of Solution

In this section, we apply our proposed algorithm to solve a fractional model of KGE. We use equal number basis elements i.e. n₁ = n₂ = n, for any approximations of space and time variables. We initially approximate the time derivative of the unknown function as follows:

$\begin{array}{ll}\frac{{\partial }^{\beta }v(x,t)}{\partial t^{\beta }}={\theta }_n^T(x)C{\theta }_n(t)& (12)\end{array}$

Taking integral of order β with respect to t on both sides of Equation (12), we have

$\begin{array}{l}v(x,t)={\theta }_n^T(x)C{I}^{(\beta )}{\theta }_n(t)+{\theta }_n^T(x)A{I}^{(1)}{\theta }_n(t)\\ +{\theta }_n^T(x)B{\theta }_n(t)& (13)\end{array}$

where I^(β)and I⁽¹⁾ are operational matrices of integration of order β and 1, respectively, and are given by Equation (10) and

$\begin{array}{ll}\frac{\partial v(x,0)}{\partial t}=h_2(x)={\theta }_n^T(x)A{\theta }_n(t)& (14)\end{array}$

$\begin{array}{ll}v(x,0)=h_1(x)={\theta }_n^T(x)B{\theta }_n(t)& (15)\end{array}$

where A and B are known square matrices and can be calculated using Equation (9).

Taking the differentiation of order γ on both sides of Equation (13), we get

$\begin{array}{l}\frac{{\partial }^{\gamma }v(x,t)}{\partial x^{\gamma }}={\theta }_n^T(x)D^{(\gamma ),T}C{I}^{(\beta )}{\theta }_n(t)+{\theta }_n^T(x)D^{(\gamma ),T}A{I}^{(1)}{\theta }_n(t)\\ +{\theta }_n^T(x)D^{(\gamma ),T}B{\theta }_n(t)& (16)\end{array}$

where, D^(γ)is the operational matrix of differentiation of order γ and is given by Equation (11). Further, the inhomogeneous term can be approximated as

$\begin{array}{ll}h(x,t)={\theta }_n^T(x)E{\theta }_n(t)& (17)\end{array}$

where E is the known square matrix and can be calculated using Equation (9).

Grouping Equations (12), (13), (16), (17), and (2), we get

$\begin{array}{l}{\theta }_n^T\left(x\right)C{\theta }_n\left(t\right)-({\theta }_n^T\left(x\right)D^{\left(\gamma \right),T}C{I}^{\left(\beta \right)}{\theta }_n\left(t\right)\\ +{\theta }_n^T\left(x\right)D^{\left(\gamma \right),T}A{I}^{\left(1\right)}{\theta }_n\left(t\right)+{\theta }_n^T\left(x\right)D^{\left(\gamma \right),T}B{\theta }_n\left(t\right))\\ +{\theta }_n^T\left(x\right)C{I}^{\left(\beta \right)}{\theta }_n\left(t\right)+{\theta }_n^T\left(x\right)A{I}^{\left(1\right)}{\theta }_n\left(t\right)\\ +{\theta }_n^T\left(x\right)B{\theta }_n\left(t\right)={\theta }_n^T(x)E{\theta }_n(t)& (18)\end{array}$

Equation (18), can be written as

$\begin{array}{l}C-D^{(\gamma ),T}C{I}^{(\beta )}-D^{(\gamma ),T}A{I}^{(1)}-D^{(\gamma ),T}B+C{I}^{(\beta )}\\ +A{I}^{(1)}+B=E& (19)\end{array}$

Equation (19) is a system of equations which is easy to handle using the collocation method to determine the unknown matrix. By making use of the value of C in Equation (13), we can obtain an approximate solution for FLGE.

Numerical Experiments and Discussion

Example 1. Firstly, we take the time fractional KGE [26] given as

$\frac{{\partial }^{\beta }v(x,t)}{\partial t^{\beta }}-\frac{{\partial }^{2}v(x,t)}{\partial x^2}-v(x,t)=0,1<\beta \le 2$, having the ICs:

v(x, 0) = 1+sin(x), $\frac{\partial v(x,0)}{\partial t}=0$, for 0 ≤ x, t ≤ 1, and boundary conditions:

v(0, t) = cosh(t), v(1, t) = sin(1)+ cosh(t).

The exact solution is v(x, t) = sin(x)+ cosh(t).

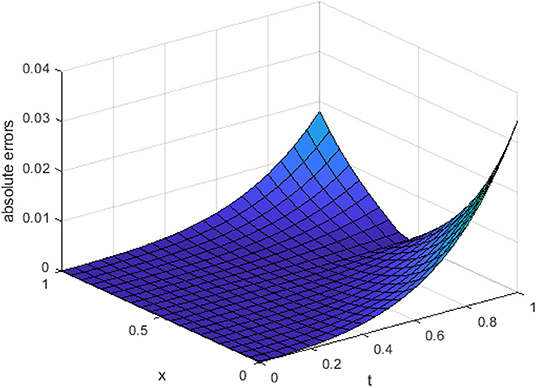
In Figure 1, we have shown the three-dimensional trajectory of the approximate solution obtained by our used technique for integer KGE. In Figure 2, we have shown absolute errors by our proposed method for integer order KGE at n = 4.

FIGURE 1

Figure 1. Approximate solution at β = 2.

FIGURE 2

Figure 2. Absolute errors at β = 2.

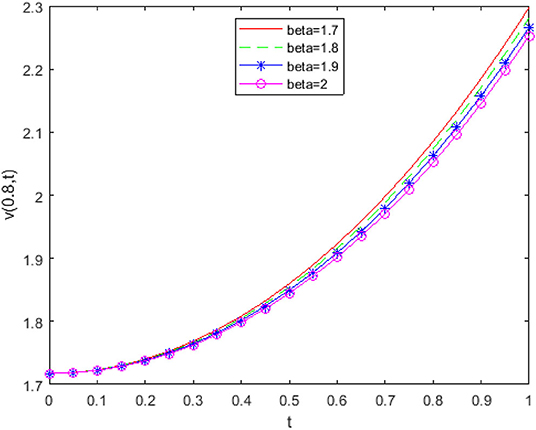
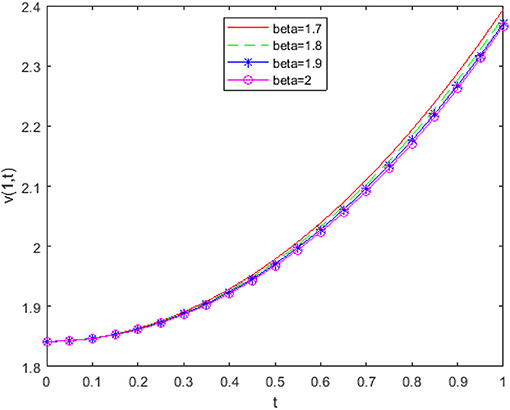
From Figure 2 it is detected that absolute errors are very low, showing good agreement between the exact and approximate solution. In Figure 3, we have plotted fractional order KGE by changing the values of β and t at x = 0.8. In Figure 4, we have plotted fractional order KGE by changing the values of β and t at x = 1.

FIGURE 3

Figure 3. Approximate solution at different values of t and β at x = 0.8.

FIGURE 4

Figure 4. Approximate solution at different values of t and β at x = 1.

From Figures 3, 4, it can be seen that the solution changes consistently from fractional order to integer solution, showing the consistency of the proposed algorithm for time fractional order models.

Example 2. Secondly, taking the space fractional KGE [26] given as

$\frac{{\partial }^{2}v(x,t)}{\partial t^2}-\frac{{\partial }^{\gamma }v(x,t)}{\partial x^{\gamma }}=h(x,t),1<\gamma \le 2$, having the ICs:

v(x, 0) = x^γ(1 − x), $\frac{\partial v(x,0)}{\partial t}=x^{\gamma }(x-1)$, for 0 ≤ x, t ≤ 1, and boundary conditions:

v(0, t) = 0, v(1, t) = 0, with source function h(x, t) = x^γ(1 − x) exp (−t) − [(γ + 1) −(γ + 2) x] exp (−t) and the exact solution v(x, t) = x^γ(1 − x) exp (−t).

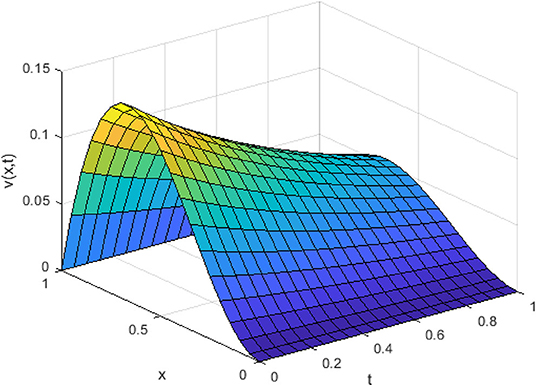
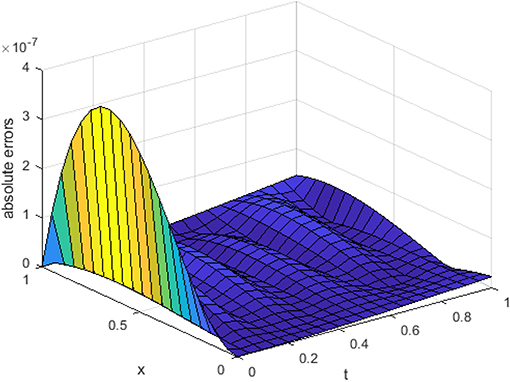
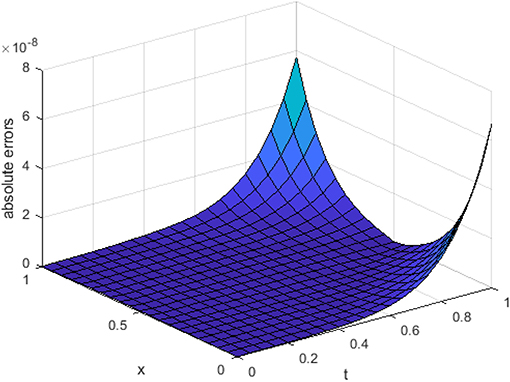
In Figure 5, we have shown the three-dimensional trajectory of the approximate solution obtained by our proposed method for integer KGE. In Figures 6–8, we have shown absolute errors by our proposed method for integer order KGE at different values of n = 3, 5, and 7, respectively.

FIGURE 5

Figure 5. Approximate solution at γ = 2.

FIGURE 6

Figure 6. Absolute errors at n = 3 and γ = 2.

FIGURE 7

Figure 7. Absolute errors at n = 5 and γ = 2.

FIGURE 8

Figure 8. Absolute errors at n = 7 and γ = 2.

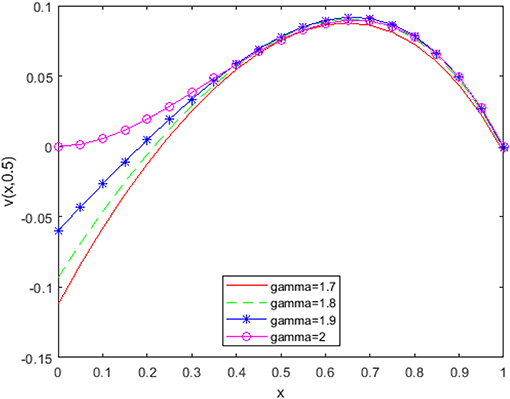
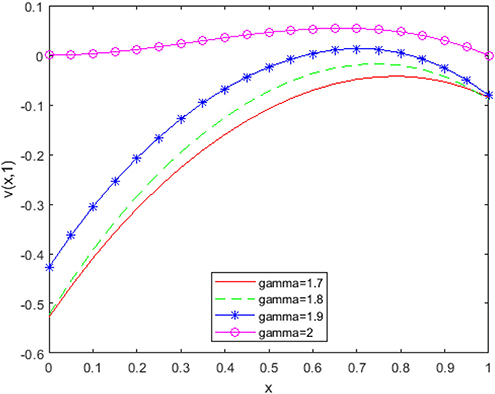
From Figures 6–8, it is detected that absolute errors are very low and show good agreement between the exact and approximate solution. It is also observed that absolute errors decrease when increasing the basis elements. In Figure 9, we have plotted fractional order KGE by changing the values of γ and x at t = 0.5. In Figure 10, we have plotted fractional order KGE by changing the values of γ and x at t = 1.

FIGURE 9

Figure 9. Approximate solution at different values of x and γ at t = 0.5.

FIGURE 10

Figure 10. Approximate solution at different values of x and γ at t = 1.

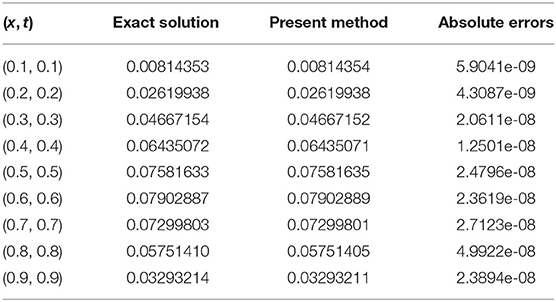
From Figures 9, 10, it can be seen that the solution changes consistently from fractional order to integer solution, showing the consistency of the proposed algorithm for space fractional order models. In Table 1, we have compared absolute errors by our method and the method used in [26] and observed that our used technique is more accurate in comparison to the technique used in [26].

TABLE 1

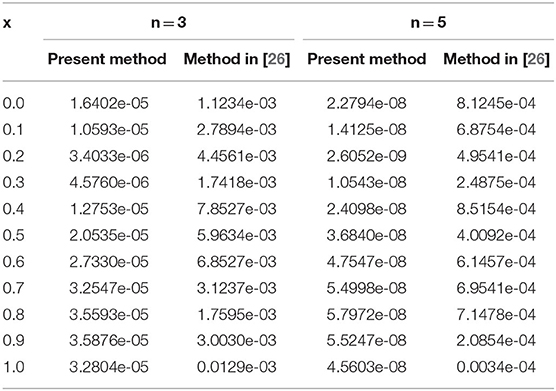
Table 1. Comparison of absolute errors by our method and the method in [26] at t = 1, Example 2.

In Table 2, we have compared our solution with the exact solution for different values of x and t at γ = 2.

TABLE 2

Table 2. Comparison approximate and exact solution at γ = 2 and n = 5, Example 2.

Concluding Remarks

The key benefit of the used algorithm is that it works for both time and space FKGE. Using the proposed algorithm, we can derive an approximate solution for FKGE when the analytical solutions are not possible. It is also easy for computational purposes because FKGE is reduced into algebraic equations. We can apply this method together for time and space fractional, which reduces the time period of computation. Integer and fractional order behavior of KGE is shown. The outcomes of the present study are very helpful for scientists and engineers working in the mathematical modeling of natural phenomena. In a nutshell, we can say that with the aid of this scheme we can examine FKGE for use in quantum field theory, plasma, optical fibers, and dispersive wave-phenomena.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors have worked equally on this manuscript and have read and approved the final manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Podlubny I. Fractional Differential Equations. San Diego, CA: Academic Press. (1999). p. 340.

Google Scholar

2. Caputo M. Elasticita e Dissipazione. Bologna: Zani-Chelli (1969).

3. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier (2006). p. 540.

Google Scholar

4. Hristov J. Transient heat diffusion with a non-singular fading memory: from the cattaneo constitutive equation with Jeffrey's kernel to the Caputo-Fabrizio time-fractional derivative. Thermal Sci. (2016) 20:765–70. doi: 10.2298/TSCI160112019H

CrossRef Full Text | Google Scholar

5. Baskonus HM, Mekkaoui T, Hammouch Z, Bulut H. Active control of a Chaotic fractional order economic system. Entropy. (2015) 17:5771–83. doi: 10.3390/e17085771

CrossRef Full Text | Google Scholar

6. Singh H. A new stable algorithm for fractional Navier-Stokes equation in polar coordinate. Int J Appl Comput Math. (2017) 3:3705–22. doi: 10.1007/s40819-017-0323-7

CrossRef Full Text | Google Scholar

7. Yang XJ, Machado JAT, Cattani C, Gao F. On a fractal LC-electric circuit modeled by local fractional calculus. Commun Nonlin Sci Numeric Simul. (2017) 47:200–6. doi: 10.1016/j.cnsns.2016.11.017

CrossRef Full Text | Google Scholar

8. Yang XJ. A new integral transform operator for solving the heat-diffusion problem. Appl Math Lett. (2017) 64:193–7. doi: 10.1016/j.aml.2016.09.011

CrossRef Full Text | Google Scholar

9. Srivastava HM, Kumar D, Singh J. An efficient analytical technique for fractional model of vibration equation. Appl Math Model. (2017) 45:192–204. doi: 10.1016/j.apm.2016.12.008

CrossRef Full Text | Google Scholar

10. Kumar D, Singh J, Baleanu D. A new analysis for fractional model of regularized long-wave equation arising in ion acoustic plasma waves. Math Methods Appl Sci. (2017) 40:5642–53. doi: 10.1002/mma.4414

CrossRef Full Text | Google Scholar

11. Kumar D, Agarwal RP, Singh J. A modified numerical scheme and convergence analysis for fractional model of Lienard's equation. J Comput Appl Math. (2018) 339:405–13. doi: 10.1016/j.cam.2017.03.011

CrossRef Full Text | Google Scholar

12. Singh H, Srivastava HM. Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Appl Sci. (2020) 10:2850. doi: 10.3390/app10082850

CrossRef Full Text | Google Scholar

13. Singh H. A new numerical algorithm for fractional model of Bloch equation in nuclear magnetic resonance. Alex Engl J. (2016) 55:2863–9. doi: 10.1016/j.aej.2016.06.032

CrossRef Full Text | Google Scholar

14. Sumelka W. Non-local Kirchhoff–Love plates in terms of fractional calculus. Arch Civil Mech Eng. (2015) 15:231–42. doi: 10.1016/j.acme.2014.03.006

CrossRef Full Text | Google Scholar

15. Singh H. Solution of fractional Lienard equation using Chebyshev operational matrix method. Nonlin Sci Lett A. (2017) 8:397–404.

Google Scholar

16. Lazopoulos AK. On fractional peridynamic deformations. Arch Appl Mech. (2016) 86:1987–94. doi: 10.1007/s00419-016-1163-3

CrossRef Full Text | Google Scholar

17. Ying YP, Lian YP, Tang SQ, Liu WK. High-order central difference scheme for Caputo fractional derivative. Comput Methods Appl Mech Eng. (2017) 317:42–54. doi: 10.1016/j.cma.2016.12.008

CrossRef Full Text | Google Scholar

18. Abbasbandy S. Numerical solutions of nonlinear Klein-Gordon equation by variational iteration method. Int J Num Meth Engg. (2007) 70:876–81. doi: 10.1002/nme.1924

CrossRef Full Text | Google Scholar

19. Mohyud-Din ST, Noor MA, Noor KI. Some relatively new techniques for nonlinear problems. Math Porb Engg. (2009) 2009:234849. doi: 10.1155/2009/234849

CrossRef Full Text | Google Scholar

20. Wazwaz AM. The modified decomposition method for analytic treatment of differential equations. Appl Math Comput. (2006) 173:165–76. doi: 10.1016/j.amc.2005.02.048

CrossRef Full Text | Google Scholar

21. Kumar D, Singh J, Kumar S, Sushila. Numerical computation of Klein-Gordon equations arising in quantum field theory by using homotopy analysis transform method. Alexandria Eng J. (2014) 53:469–74. doi: 10.1016/j.aej.2014.02.001

CrossRef Full Text | Google Scholar

22. Golmankhaneh AK, Baleanu D. On nonlinear fractional Klein-Gordon equation. Signal Proc. (2011) 91:446–51. doi: 10.1016/j.sigpro.2010.04.016

CrossRef Full Text | Google Scholar

23. Kurulay M. Solving the fractional nonlinear Klein-Gordon equation by means of the homotopy analysis method. Adv Diff Eqs. (2012) 13:529–39. doi: 10.1186/1687-1847-2012-187

CrossRef Full Text | Google Scholar

24. Gepreel KA, Mohamed MS. Analytical approximate solution for nonlinear space-time fractional Klein-Gordon equation. Chin Phys B. (2013) 22:010201. doi: 10.1088/1674-1056/22/1/010201

CrossRef Full Text | Google Scholar

25. Kumar D, Singh J, Baleanu D. A hybrid computational approach for Klein- Gordon equations on Cantor sets. Nonlin Dyn. (2017) 87:511–7. doi: 10.1007/s11071-016-3057-x

CrossRef Full Text | Google Scholar

26. Khader MM, Kumar S. An accurate numerical method for solving the linear fractional Klein–Gordon equation. Math Meth Appl Sci. (2013) 37:2972–9. doi: 10.1002/mma.3035

CrossRef Full Text | Google Scholar

27. Yousif MA, Mahmood BA. Approximate solutions for solving the Klein-Gordon sine-Gordon equations. J Assoc Arab Univ Bas Appl Sci. (2017) 22:83–90. doi: 10.1016/j.jaubas.2015.10.003

CrossRef Full Text | Google Scholar

28. Singh H, Srivastava HM, Kumar D. A reliable numerical algorithm for the fractional vibration equation. Chaos Solitons Fractals. (2017) 103:131–8. doi: 10.1016/j.chaos.2017.05.042

CrossRef Full Text | Google Scholar

29. Singh CS, Singh H, Singh VK, Om Singh P. Fractional order operational matrix methods for fractional singular integro-differential equation. Appl Math Model. (2016) 40:10705–18. doi: 10.1016/j.apm.2016.08.011

CrossRef Full Text | Google Scholar

30. Singh H, Srivastava HM. Jacobi collocation method for the approximate solution of some fractional-order Riccati differential equations with variable coefficients. Phys A. (2019) 523:1130–49. doi: 10.1016/j.physa.2019.04.120

CrossRef Full Text | Google Scholar

31. Singh CS, Singh H, Singh S, Kumar D. An efficient computational method for solving system of nonlinear generalized Abel integral equations arising in astrophysics. Phys A. (2019) 525:1440–8. doi: 10.1016/j.physa.2019.03.085

CrossRef Full Text | Google Scholar

32. Singh H, Pandey RK, Baleanu D. Stable numerical approach for fractional delay differential equations. Few Body Syst. (2017) 58:156. doi: 10.1007/s00601-017-1319-x

CrossRef Full Text | Google Scholar

33. Singh H, Singh CS. Stable numerical solutions of fractional partial differential equations using Legendre scaling functions operational matrix. Ain Shams Eng J. (2018) 9:717–25. doi: 10.1016/j.asej.2016.03.013

CrossRef Full Text | Google Scholar

34. Singh H. Operational matrix approach for approximate solution of fractional model of Bloch equation. J King Saud Univ Sci. (2017) 29:235–40. doi: 10.1016/j.jksus.2016.11.001

CrossRef Full Text | Google Scholar

35. Wu JL. A wavelet operational method for solving fractional partial differential equations numerically. Appl Math Comput. (2009) 214:31–40. doi: 10.1016/j.amc.2009.03.066

CrossRef Full Text | Google Scholar

36. Singh H. An efficient computational method for the approximate solution of nonlinear Lane-Emden type equations arising in astrophysics. Astrophys Space Sci. (2018) 363:71. doi: 10.1007/s10509-018-3286-1

CrossRef Full Text | Google Scholar

37. Singh H, Sahoo MR, Singh OP. Numerical method based on Galerkin approximation for the fractional advection-dispersion equation. Int J Appl Comput Math. (2016) 3:2171–87. doi: 10.1007/s40819-016-0233-0

CrossRef Full Text | Google Scholar

38. Singh H. Approximate solution of fractional vibration equation using Jacobi polynomials. Appl Math Comput. (2018) 317:85–100. doi: 10.1016/j.amc.2017.08.057

CrossRef Full Text | Google Scholar

39. Bhatter S, Mathur A, Kumar D, Singh J. A new analysis of fractional Drinfeld–Sokolov–Wilson model with exponential memory. Physi A. (2020) 537:122578. doi: 10.1016/j.physa.2019.122578

CrossRef Full Text | Google Scholar

40. Dubey VP, Kumar R, Kumar D, Khan I, Singh J. An efficient computational scheme for nonlinear time fractional systems of partial differential equations arising in physical sciences. Adv Diff Equat. (2020) 2020:46. doi: 10.1186/s13662-020-2505-6

CrossRef Full Text | Google Scholar

41. Shiri B, Perfilieva I, Alijani Z. Classical approximation for fuzzy Fredholm integral equation, fuzzy sets and systems. (2020). doi: 10.1016/j.fss.2020.03.023

CrossRef Full Text | Google Scholar

42. Alijani Z, Shiri B, Baleanu D. A Chebyshev based numerical methods for solving fractional fuzzy differential equations (2019).