- 1Department of Mathematics, Faculty of Science, Taif University, Taif, Saudi Arabia
- 2Department of Mathematics, Faculty of Science, Al-Azhar University, Nasr City, Egypt
- 3Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt
- 4Department of Physics, Faculty of Science, Taif University, Taif, Saudi Arabia
- 5Department of Mathematics, Faculty of Science, South Valley University, Qena, Egypt
- 6Department of Physics, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia
This paper examines the squeezing on information entropy and entanglement on the basis of a quantum scheme that contains two-mode interaction with time dependence of a two-level atom, including the external field. The proposed model is formulated by eliminating the external field after applying a certain transformation. The dynamics of information entropy squeezing and non-local correlation information for the system Hamiltonian are investigated. The effect of the evolution of the squeezing and entanglement by the classical field are estimated. Based on the results, the obtained dynamic behavior of squeezing and entanglement is controlled using the external field.
Introduction
The NLC (non-local correlations) between bipartite systems, such as the atom field, performs different tasks in quantum information [1–6]. In this way, the atomic von Neumann entropy (ANE) has usually been measured by the NLC between two-partite systems [7]. The measure of NLC for the complex physical systems cannot be achieved by the ANE. Therefore, different investigations have been done to quantify the NLC for different quantum schemes. The correlation function for a TLA that interacts with a field mode prepared at the coherent state within the evoluting Wehrl space entropy has been investigated [8]. Additionally, the classical field's influence in the quantum scheme belonging to a two TLA based on the evolution of quantum correlations between two TLA through quantum discord (QD) has been studied [9]. On the contrary, the study of the dynamics of NLC of a two-TLA Interaction, which leads to the exploration of many useful phenomena within quantum information, such as sudden death (ESD) and sudden birth (ESB), has been carried out [10]. For example, the ESD and ESB of two TLA for many conditions for the atomic state's position have been examined [11]. In addition, two-level atoms that were expanded into three two-level atoms prepared in a squeezed state has been presented [12]. This work has been extended to include the ESD of su(1,1) set with two non-linear qubits [13].
Recently, different effects on the quantum schemes have been established based on the JCM (Jaynes-Cummings model). These schemes have been modified by examining different effects, such as atomic motion, intrinsic damping, and the external classical field [14]. Also, the effect of the cavity damping on the model described by the JCM based on approximation has been studied based on dispersive Approximation [15]. It has been shown that the system is sensitive to the decay and Stark-shift parameters. Furthermore, the type of interaction between two TLA and the N-level atom has been explored [16]. The results show that the non-local correlation depends crucially on the detuning.
Measuring the squeezing on the quantum system assumed from information entropy fulfills diverse tasks in quantum information processing (QIP). It employs the density matrix and entropic uncertainty relation (EUR) of the suggested model [17, 18]. The EURs were introduced as the basic component in the quantum key distribution, quantum cryptographic protocols, and quantum memory [19]. The Shannon entropy-a classical measure on the point of view of QIP-has been employed to quantify the squeezing based on the EUR. Further directions include efforts to quantify entropy squeezing with multi-level atomic models because it is hard to get an analytical formula of the density matrix. The atomic entropy squeezing for a quantum scheme of TLA that interacts with field mode in the coherent state [20] when having non-linear medium [21, 22] and two coupled modes under frequency converter type has been explored [23]. More recently, the effects of decaying terms and external fields on the performance of entropy squeezing have been explored [15, 24].
It is known that adding the classical field gives us the permittivity of exploring the way a strong field affects the interacting one or two atoms with it. The effect of the strong field on two atoms in a time-independent fashion was studied [25]. Furthermore, it was concluded that the dynamical performance of AFI is organized by the NLC of time-dependent coupling [26]. In this paper, we consider a two-level atom dependent on time. We obtain a solution through the condition of integration. This gives us the opportunity to study and compare the state of time dependence and independence.
Our main goal in this paper is to determine the dynamics of the concurrence and skew information correlations for the interaction between two qubits with a pair of fields of the amplifier type. The paper is ordered as follows: the physical scheme and its solution of the field that interact with two TLA are presented in section II; the atomic population is discussed in section III; the TLA degree of entanglement is provided in section IV; the entropy squeezing is discussed in section V; and our main results are presented in the final section.
Quantum Scheme and Solution
This section introduces a quantum scheme of a TLA that interacts with a field of two modes in a cavity containing a classical field. The system Hamiltonian takes the form
with â denoting annihilation operator, whereas ↠denotes creation operator and obeys the commutations relations:
such that δjk suggests the Kronecker delta, which satisfies that δjk = 1 ∀ j = k, δjk = 0. Otherwise, ωi and ω0 denote the frequencies of the field and atomic transition, respectively. But , and are the Pauli matrix. They are given by existing state (|e〉) and ground state (|g〉), such as , , and , where and . ξ(t) is the coupling parameter for the atom and is the coupling constant for the electromagnetic field λ is the coupling constant for the electromagnetic field. λ3 is the external classical field coupling.
We are currently going to make a detuning to remove the last two terms in the last equation. In their presence, we cannot obtain a general solution to this system. Therefore, a conversion must be made in the atomic space as follows
If we define the operators Ŝ±,z where Ŝz = |+〉〈+|−|−〉〈−|, Ŝ+ = |+〉〈−|, Ŝ− = |−〉〈+|, they have the same properties of commutation relation, such as , , and . Through previous transformations, we can calculate the connection between operators and Ŝ, s operators as follows
At λ3 = 0, i.e., θ = 0, it is easy to see 〈+| = 〈e| and 〈−| = 〈g|. After preforming the transformation (6) and using the rotating wave approximation, the system (1) becomes
where . We note that the effective external field is introduces the frequency definition for the atom Ω0.
For the calculation of the wave function, it is necessary to calculate the constant of motion by writing the equations of motion by using the Heisenberg equation as follows
Consequently, the operators' motion equations in the model (7) are calculated as follows:
Thus, we deduce that operators , j = 1, 2 is the constant of motion. The Hamiltonian (7) turns into:
where Δ = (Ω0 − ω1 − ω2)
Wave Function
We are now calculating the wave function to describe the features of this physical model. The initial state of the atom in superposition from the atomic states:
The field prepared in pair coherent states,
where Bq(2η) is the modified Bessel function. So the formula of the wave function becomes,
Some techniques have been introduced for solving the Schrödinger equation [27]. For calculating factors A(n, t) and B(n, t) as follows,
where . Suppose that
using the integrability condition , where c is constant, the general solution of the aforementioned equations (16) is
It should be noted that this solution is general, and we will allocate time dependence in the case of velocity and acceleration as follows:
After solving the problem generally, we may calculate some of the statistical quantities, which explain and analyze the performance of the system in the presence and absence of the external field. This task can be accomplished in the next sections.
Atomic Inversion
Studying the phenomena of collapse and revival provides us with more details about the behavior of the physical system during periods of strong and weak interaction between the parts of the system. The study of atomic populations is therefore an important quantity in quantum information. It may be perceived as
where B* is the complex conjugate of B.
For plotting the atomic inversion, consider the parameters , Δ = 0.9λ, c = α = 1, β = 0.3, η = 25. First, neglect the external field (λ3 = 0) and c+ = 0; the function shows symmetric oscillation around the horizontal axis, and the phenomena of revivals and collapses are achieved in many intervals (see Figure 1A). Note that the collapses almost occur in consideration of the time interaction except for some squeezed intervals for the revivals. We note that the symmetry around the horizontal axis in the aforementioned case fades after adding the external field of the interaction cavity. The fluctuations among the ground and excited states are increased. Therefore, the interactive atom and the field become sturdier (see Figure 1B). We also find that the period of collapse oscillates among the ground and excited conditions, which reflect the impact of the external field terms. For case c+ = 0.5 and (λ3 = 0), the phenomena of collapse and revival occur occasionally when reducing the amplitude of oscillations as seen in Figure 1C. After putting the parameter λ3 = 0.3λ, we see that the amplitude of oscillations increased and the collapses phenomena never occurred, while the revivals occurred periodically within a period as seen in Figure 1D.
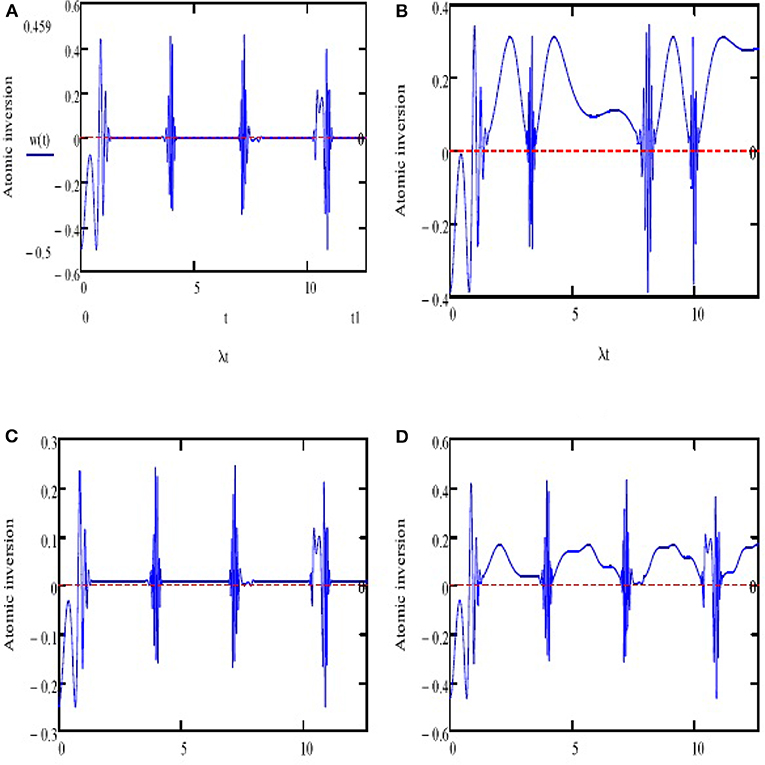
Figure 1. W(t) for the parameters η = 25, ϕ = π/2 and Δ = 0.9, c = α = 1, β = 0.3. The atom is initially in the upper state c+ = 0 in (A,B) and in a superposition state c+ = 0.5 in (C,D). The classical field effect is ignored λ3 = 0 in (A,C) and is considered for λ3 = 0.3λ in (B,D).
TLA-Field Degree of Entanglement
The field or atomic entropy is one of the most important criteria used to measure the entanglement of the parts of a closed system (no external effects). We therefore calculate the atomic entropy of the previously obtained condition (14).
We consider the ANE formula concerning the eigenvalues of the atomic density matrix as
The degree of NLC is obtained according to the value of S(t) when the ANE has a zero value for the atom-field system in the separable state, while the system takes a maximally entangled state for S = ln (2). The same conditions are used. In the first case, in absence of the classical external field and fixing the parameter c+ = 0, the entanglement function S(t) shows periodical weak entanglement with a higher value, but the lower value is almost the pure state at nπ (Figure 2A). In the second case, consider the classical external field λ3 = 0.3λ, the function displays consistent fluctuations, and the minimum values reduce (see Figure 2B). The function shows a different behavior when we take λ3 = 0 and c+ = 0.5. The function shows more regular oscillations and reaches pure states at nπ, as shown in Figure 2C). When the parameter λ3 is added to the cavity interaction, the function has the minimum values for the intervals of revivals (see Figure 2D).
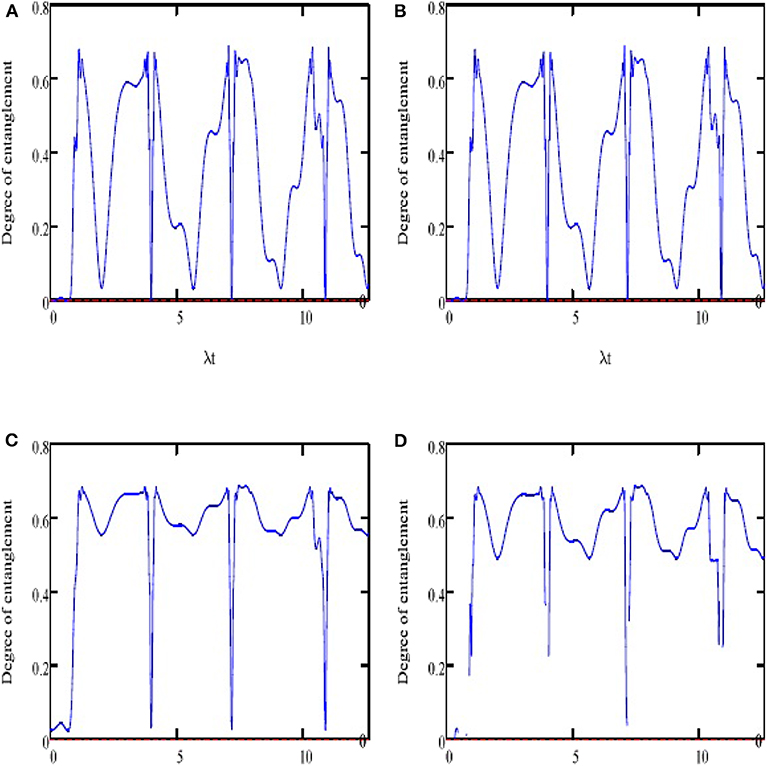
Figure 2. (A–D) Variation of degree of entanglement quantified by the ANE for with the same parameters and conditions as in Figure 1.
Phenomena of Information Entropy Squeezing
This section investigates the squeezing of classical entropy of the atomic system based on Shannon information entropy H(Ŝr) with regard to the atomic operator of Pauli matrix as
where indicates the Shannon information entropy [23, 28–30], ρr is the reduced atomic-density matrix. The squeezing is achieved for the component when
the uncertainty relation becomes
Figure 3 shows the entropy squeezing when applying the aforementioned conditions. When A(0) = 0, irregular squeezing achieves both quadratures Ex(t) and Ey(t). The highest squeezing for quadrature is achieved in the center of the areas of collapse. Quadrature Ey(t) is achieved in the center of the areas of revivals (see Figure 3A). In contrast, for λ3 = 0.3λ and c+ = 0, the amount of squeezing rises considerably in this case (see Figure 3B). When we considered the case in which λ3 = 0 and c+ = 0.5, the squeezing is achieved in the quadrature Ey(t) but not on the other. Moreover, the areas of the squeezing reach the lowest values (see Figure 3C). The reduction continues in the intervals of squeezing after considering the acceleration (λ3 = 0.3λ and c+ = 0.5) (see Figure 3D). We thus conclude that the acceleration plays a role in the reduction of the squeezing in Ex(t). In all cases, the squeezing in quadrature Ey(t) is achieved according to the revival intervals.
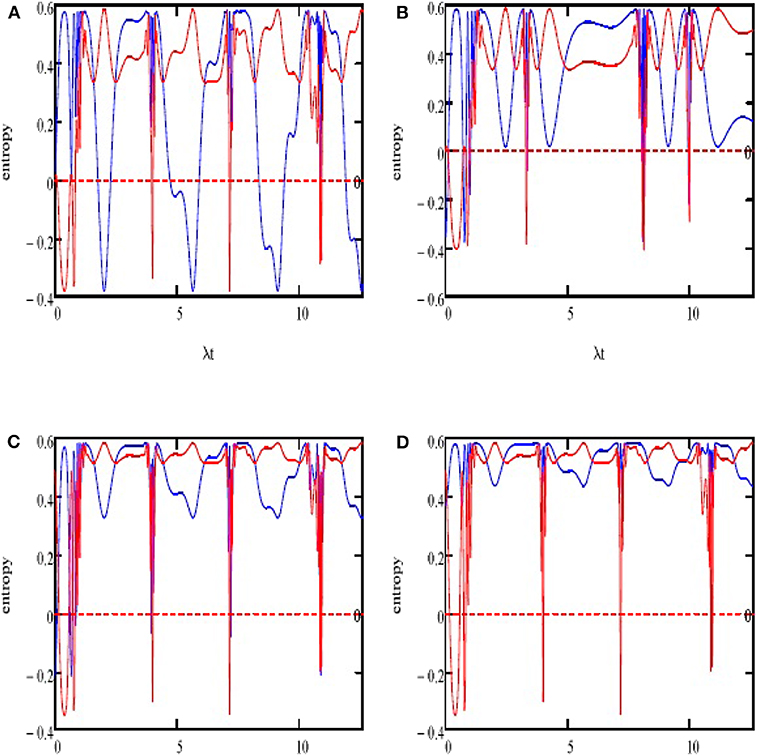
Figure 3. (A–D) Variation of the entropy squeezing components Ex(t) (blue curve) and Ey(t) (red curve) of classical entropy for with the same parameters and conditions as in Figure 1.
Conclusion
In summary, we have used a quantum model of the interaction between a time-dependent two-level atom and two-mode field in the cavity containing an external field. The general solution is obtained after using the integrability condition. The resulting wave function and atomic density matrix are used to investigate atomic inversion and atomic entropy, respectively. We have shown that the amplitude of oscillations is increased, and the collapsed phenomena never occur, while the revivals occur periodically. Furthermore, we have discussed the effect of the external classical field on the phenomenon of the degree of entanglement the function illustrates systematic fluctuations; the minimum values, however, reduce. Finally, we have found that the external classical field does not affect the entropy squeezing phenomena. Such phenomena benefit in various uses of quantum physics and optics.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under Grant no. D-622-130-1441. The authors, therefore, gratefully acknowledge DSR technical and financial support.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information. New York, NY: Cambridge University Press (2000).
2. Jaynes ET, Cummings FW. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc IEEE. (1963) 51:89–109. doi: 10.1109/PROC.1963.1664
3. Bouwmeester D, Ekert A, Zeilinger A. The Physics of Quantum Information. Berlin: Springer-Verlag (2000).
4. Bennett CH, Brassard G, Crepeau C, Jozsa R, Peres A, Wootters WK. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys Rev Lett. (1993) 70:1895. doi: 10.1103/PhysRevLett.70.1895
5. Jung K. Polarization correlation of entangled photons derived without using non-local interactions. Front Phys. (2020) 8:170. doi: 10.3389/fphy.2020.00170
6. Santos E. Local realistic interpretation of entangled photon pairs in the Weyl-Wigner formalism. Front Phys. (2020) 8:191. doi: 10.3389/fphy.2020.00191
7. Fuchs CA, Gisin N, Griffiths RB, Niu CS, Peres A. Optimal eavesdropping in quantum cryptography. I. Information bound and optimal strategy. Phys Rev A. (1997) 56:1163. doi: 10.1103/PhysRevA.56.1163
8. von Neumann J. The Measuring Process in Mathematische Grundlagen Derquantenmechanik. Berlin: Springer V (1932).
9. Abdel-Khalek S, Obada ASF. New features of Wehrl entropy and Wehrl PD of a single Cooper-pair box placed inside a dissipative cavity. Ann Phys. (2010) 325:2542–9. doi: 10.1016/j.aop.2010.05.011
10. Sebawe Abdalla M, Khalil EM, Ali SI. Entanglement and sudden death of a nonlinear two-level-atom pair interacting with a radiation field. J Russ Laser Res. (2014) 35:408–15. doi: 10.1007/s10946-014-9442-3
11. Sebawe Abdalla M, Khalil EM, Obada ASF, Perina J, Krepelka J. Quantum statistical characteristics of the interaction between two two-level atoms and radiation field. Eur Phys Plus J. (2015) 130:227. doi: 10.1140/epjp/i2015-15227-9
12. Obada ASF, Abdel-Khalek S, Abo-Kahla DAM. New features of entanglement and other applications of a two-qubit system. Opt Commun. (2010) 283:4662–70. doi: 10.1016/j.optcom.2010.06.074
13. Abdel-Khalek S, Halawani SHA, Obada ASF. Effect of time dependent coupling on the dynamical properties of the nonlocal correlation between two three-level atoms. Int J Theor Phys. (2017) 56:2898–910. doi: 10.1007/s10773-017-3457-9
14. Haifa Alqannas S, Khalil ME. Quantum interaction of SU(1,1) Lie group with entangled a two 2-level atoms. Phys A. (2018) 489:1–8. doi: 10.1016/j.physa.2017.07.015
15. Al Naim AF, Khan JY, Khalil EM, Abdel-Khalek S. Effects of Kerr medium and Stark Shift parameter on Wehrl entropy and the field purity for two-photon Jaynes Cummings model under dispersive approximation. J Russ Laser Res. (2019) 40:20–9. doi: 10.1007/s10946-019-09764-w
16. Obada ASF, Al Naim AF, Khalil EM, Abdel-Khalek S, Eleuch H. Interaction between two two-level atoms coupled to N-level quantum system. Opt Quant Electron. (2019) 51:259. doi: 10.1007/s11082-019-1952-3
17. Everett H. “Relative state” Formulation of quantum mechanics. Rev Mod Phys. (1957) 29:454–62. doi: 10.1103/RevModPhys.29.454
18. Riccardi A, Macchiavello C, Maccone L. Tight entropic uncertainty relations for systems with dimension three to five. Phys Rev A. (2017) 95:032109. doi: 10.1103/PhysRevA.95.032109
19. Christandl M, Winter A. Uncertainty, monogamy, and locking of quantum correlations. IEEE Trans Inform Theory. (2005) 51:3159–65. doi: 10.1109/TIT.2005.853338
20. El-Shahat TM, Abdel-Khalek S, Obada ASF. Entropy squeezing of a driven two-level atom in a cavity with injected squeezed vacuum. Chaos Solit Fract. (2005) 26:1293–307. doi: 10.1016/j.chaos.2005.03.013
21. Abdalla MS, Obada ASF, Abdel-Khalek S. Entropy squeezing of time dependent single-mode Jaynes Cummings model in presence of non-linear effect. Chaos Solit Fract. (2008) 36:405–17. doi: 10.1016/j.chaos.2006.06.067
22. El-Shahat TM, Abdel-Khalek S, Abdel-Aty M, Obada ASF. Entropy squeezing of a degenerate two-photon process with a nonlinear medium. J Mod Opt. (2003) 50:2013. doi: 10.1080/0950034031000095542
23. Khalil EM, Abdalla MS, Obada ASF. Entropy and variance squeezing of two coupled modes interacting with a two-level atom: frequency converter type. Ann Phys. (2006) 321:421–34. doi: 10.1016/j.aop.2005.09.004
24. Alqannas HS, Abdel-Khalek S. Nonclassical properties and field entropy squeezing of the dissipative two-photon JCM under Kerr like medium based on dispersive approximation. Opt Laser Technol. (2019) 111:523–9. doi: 10.1016/j.optlastec.2018.10.028
25. Abdalla MS, Khalil EM, Obada ASF, Peina J, Kepelka J. Linear entropy and squeezing of the interaction between two quantum system described by su(1,1) and su(2) Lie group in presence of two external terms. AIP Adv. (2017) 7:015013. doi: 10.1063/1.4973916
26. Abu-Zinadah HH, Abdel-Khalek S. Fisher information and quantum state estimation of two-coupled atoms in presence of two external magnetic fields. Results Phys. (2017) 7:4318–23. doi: 10.1016/j.rinp.2017.10.058
27. Irshad A, Ahmed N, Khan U, Mohyud-Din ST, Khan I, Sherif ESM. Optical solutions of Schdinger equation using extended Sinh-Gordon equation expansion method. Front Phys. (2020) 8:73. doi: 10.3389/fphy.2020.00073
28. Fang MF, Zhou P, Swain S. Entropy squeezing for a two-level atom. J Mod Opt. (2000) 47:1043–53. doi: 10.1080/09500340008233404
29. Khalil EM. Generation of a nonlinear two-mode stark shift via nondegenerate Raman transition. Int J Mod Phys B. (2007) 30:5143–58. doi: 10.1142/S0217979207038125
Keywords: external field, non-local correlation, two level atom, information entropy squeezing, two mode
Citation: Khalil EM, Abdel-Khalek S, Albogami W, Bouslimi J, Abo-Dahab SM and Besbes HR (2020) Information Entropy Squeezing and Non-local Correlation Between a Two-Level Atom and Two-Mode Field Under the Classical Field Effect. Front. Phys. 8:278. doi: 10.3389/fphy.2020.00278
Received: 20 April 2020; Accepted: 22 June 2020;
Published: 22 September 2020.
Edited by:
Mustafa Inc, Firat University, TurkeyReviewed by:
Younes Menni, University of Tlemcen, AlgeriaAndreas Gustavsson, University of Seoul, South Korea
Copyright © 2020 Khalil, Abdel-Khalek, Albogami, Bouslimi, Abo-Dahab and Besbes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: E. M. Khalil, ZWllZGtoYWxpbEB5YWhvby5jb20=
 E. M. Khalil
E. M. Khalil Sayed Abdel-Khalek
Sayed Abdel-Khalek Waad Albogami1
Waad Albogami1 Jamel Bouslimi
Jamel Bouslimi Sayed M. Abo-Dahab
Sayed M. Abo-Dahab