Recent Progress in Nuclear Lattice Simulations

We review several recent results on lattice simulations by the Nuclear Lattice Effective Field Theory Collaboration. In the first part we discuss the implementation of nuclear forces on the lattice using chiral effective field theory. The new development we highlight is the use of non-local lattice operators to achieve a simpler spin channel decomposition, in contrast with previous studies that considered only local interactions. In the second part, we present evidence that nuclear physics is close to a quantum phase transition. This development is also linked to the study of the differences between local and non-local interactions. In the final part we further explore the link between the nuclear forces and nuclear structure. We consider the simplest possible nuclear interaction which can accurately reproduce the ground state energies of neutron matter, light nuclei, and medium-mass nuclei. We discuss what these recent developments say about the emergence of nuclear structure from nuclear forces and the road ahead for nuclear lattice simulations.

1. Introduction

In this article we review several recent advances by the Nuclear Lattice Effective Field Theory Collaboration that combine of chiral effective field theory with lattice methods, an approach that we call nuclear lattice effective field theory. See Epelbaum et al. [1] and Machleidt and Entem [2] for reviews of chiral effective field theory (EFT) and Lee [3] and Lähde and Meißner [4] for reviews of nuclear lattice EFT. We begin the article by presenting some technical developments regarding the nuclear lattice interactions. The new technology that makes this possible is the use of non-local smearing for the operator interactions. These are important for producing interactions that can give accurate reproductions of the empirical nucleon-nucleon phase shifts.

In the second part of the article we consider the features of the nuclear interactions which are responsible for the bulk binding properties of atomic nuclei. From ab initio lattice simulations we present numerical data showing that nature sits near a quantum phase transition. It turns out that the differences between local and non-local interactions will again be important. In the last part of the review we continue with our first principles investigations of nuclear forces and nuclear structure. This time we discuss a simple nuclear interaction which gives the correct ground state energies of neutron matter, light nuclei, and medium-mass nuclei with no more than a few percent error. We then conclude by discussing the connection between nuclear structure and nuclear forces and some possible future directions for nuclear lattice simulations.

2. Improved Lattice Interactions

Simulations using lattice chiral EFT have been applied to predict the scattering and structure of nuclei [5–7]. The application of nuclear forces at higher chiral orders are problematic on the lattice due to the breaking of rotational invariance produced by the lattice regularization [8, 9]. In this review we focus only on the short-range interactions since this is where the new developments have been made. We use the terms leading order (LO), next-to-leading order (NLO), next-to-next-to-leading order (N²LO), and next-to-next-to-next-to-leading order (N³LO) for the successive orders in chiral EFT.

In Li et al. [10], we introduce a set of short-range interactions in lattice chiral EFT that decompose more naturally into spin channels. In the following we explain how to construct two-nucleon operators on the lattice with intrinsic spin S, S_z, orbital angular momentum L, L_z, and isospin I, I_z. Since orbital angular momentum is not exactly conserved on the lattice, we enforce the required orbital angular momentum projection by hand using smeared distributions of annihilation and creation operators whose angular dependence are given by spherical harmonics. The use of these smeared annihilation and creation operators has the effect of controlling the range of the interaction as well as reducing lattice artifacts. Since the annihilation and creation operators are no longer at the same point in space, the resulting interaction depends on the particle velocities and is therefore a non-local interaction. This is in contrast with local interactions, where the annhiliation and creation operators are at the same point in space. Previous lattice studies had only considered local interactions [8].

We will work with lattice units where quantities are multiplied by the corresponding power of the spatial lattice spacing a to make the object dimensionless. Let 〈n′n〉 denote the nearest neighbors n′ of lattice site n. Our starting point is a_i,j(n), the nucleon annihilation operator for lattice site n with spin i and isospin j. We then add lattice operators on neighboring lattice sites with coefficient, s_NL. This defines the smeared annihilation operator

$\begin{array}{ll}{a}_{\text{NL},i,j}(\text{n})=a_{i,j}(\text{n})+s_{\text{NL}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}{a}_{i,j}({\text{n}}^{\prime }).& (1)\end{array}$

The overall normalization of the smeared annihilation operators is not important since any normalization factors can be absorbed into the definition of the interaction coefficients that we build with these smeared operators.

This process can easily be extended to lattice sites beyond the nearest neighbors of n. After this we construct combinations with spin S, S_z, and isospin I, I_z,

$\begin{array}{l}{\left[a(\text{n})a({\text{n}}^{\prime })\right]}_{S,S_z,I,I_z}^{s_{\text{NL}}}\\ ={\displaystyle \sum _{i,j,i^{\prime },j^{\prime }}}{a}_{\text{NL},i,j}(\text{n})M_{i{i}^{\prime }}(S,S_z)M_{j{j}^{\prime }}(I,I_z)a_{\text{NL},i^{\prime },j^{\prime }}({\text{n}}^{\prime }).& (2)\end{array}$

Let us define the lattice derivative ∇_l along the l spatial direction as

$\begin{array}{ll}{\nabla }_{l}f(\text{n})=\frac{1}{2}f(\text{n}+\widehat{\text{l}})-\frac{1}{2}f(\text{n}-\widehat{\text{l}}).& (3)\end{array}$

We can also define the lattice derivative ∇_1/2,l with half steps in the forward and backward directions,

$\begin{array}{ll}{\nabla }_{1/2,l}f(\text{n})=f(\text{n}+\frac{1}{2}\widehat{\text{l}})-f(\text{n}-\frac{1}{2}\widehat{\text{l}}).& (4)\end{array}$

This yields a well-defined function on the lattice sites when we take double derivatives,

$\begin{array}{ll}{\nabla }_{1/2,l}^{2}f(\text{n})=f(\text{n}+\widehat{\text{l}})-2f(\text{n})+f(\text{n}-\widehat{\text{l}}).& (5)\end{array}$

The lattice Laplacian operator is defined as

$\begin{array}{ll}{\nabla }_{1/2}^{2}f(\text{n})={\displaystyle \sum _l}{\nabla }_{1/2,l}^{2}f(\text{n}).& (6)\end{array}$

We select orbital angular momenta with the help of solid spherical harmonics,

$\begin{array}{ll}{R}_{L,L_z}(\text{r})=\sqrt{\frac{4\pi }{2L+1}}{r}^L{Y}_{L,L_z}(\theta ,\varphi ).& (7)\end{array}$

We work with polynomials of the lattice derivatives that act on one of the annihilation operators, with coefficients prescribed by the solid spherical harmonics,

$\begin{array}{ll}{P}_{S,S_z,L,L_z,I,I_z}^{2M,s_{\text{NL}}}(\text{n})={[a(\text{n}){\nabla }_{1/2}^{2M}{R}_{L,L_z}^{*}(\nabla )a(\text{n})]}_{S,S_z,I,I_z}^{s_{\text{NL}}}.& (8)\end{array}$

This ensures the lattice operators have the correct rotational properties in the continuum limit. We use Clebsch-Gordan coefficients to put together the required spin and orbital angular momentum combinations,

$\begin{array}{l}{O}_{S,L,J,J_z,I,I_z}^{2M,s_{\text{NL}}}(\text{n})\\ ={\displaystyle \sum _{S_z,L_z}}\langle S{S}_{z}L{L}_z|J{J}_z\rangle P_{S,S_z,L,L_z,I,I_z}^{2M,s_{\text{NL}}}(\text{n}).& (9)\end{array}$

In Li et al. [10], we consider the neutron-proton system up to N³LO. The chosen lattice spacings are 1.97, 1.64, 1.32, and 0.99 fm. In Figure S1 we show the phase shifts and mixing angles for neutron-proton scattering vs. relative momenta for lattice spacing a = 1.32 fm. In Figure S2 we show the phase shifts and mixing angles for neutron-proton scattering for lattice spacing a = 0.99 fm. The estimated uncertainties at NLO, N²LO, and N³LO are labeled with the blue, green, and red bands, respectively. The Nijmegen partial wave analysis results are shown with black solid lines, and the lattice results at N³LO are shown with diamonds. These results show marked improvement over previous studies of the lattice chiral EFT interactions [8]. We see that in most cases the error bands at LO, NLO, N²LO, and N³LO are overlapping with each other and decreasing in width with each successive order. This indicates the consistency of the effective field theory expansion as well as its convergence rate. There are however some exceptions such as the high-momentum region of the ³P₂ and ³D₂ phase shifts where the convergence is not yet optimal. We have work in progress now that indicates these problems are resolved with a better lattice treatment of the tensor force in the one-pion exchange potential and will be discussed in a forthcoming publication. As one would expect, we also see a general improvement of the lattice phase shifts as we decrease the lattice spacing. We see both better agreement with the empirical data as well as smaller error bands.

3. Nuclear Physics Near a Quantum Phase Transition

In Elhatisari et al. [11], we investigate two different LO interactions in chiral EFT, which we call interactions A and B. Both are defined with lattice spacing a = 1.97 fm and have nearly the same nucleon-nucleon scattering phase shifts and binding energies for the three- and four-nucleon systems. However, for heavier nuclei the binding energies are very different. Interactions A and B each have the same one-pion exchange interaction as well as the same Coulomb potential between protons. The only distinction between the interactions A and B is the form of the short-range interactions, and we limit our discussion here to the short-range interactions.

We write σ_S with S = 1, 2, 3 for the spin Pauli matrices, and τ_I with I = 1, 2, 3 for the isospin Pauli matrices. We will write a(n) for the column vector of annihilation operators a_i,j(n), and we will write a^†(n) for the row vector of creation operators $a_{i,j}^{†}(\text{n})$. For our chosen non-local smearing parameter s_NL, we construct the smeared operators as in Equation (1),

$\begin{array}{ll}{a}_{\text{NL}}(\text{n})=a(\text{n})+s_{\text{NL}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}a({\text{n}}^{\prime }),& (10)\end{array}$

$\begin{array}{ll}{a}_{\text{NL}}^{†}(\text{n})=a^{†}(\text{n})+s_{\text{NL}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}{a}^{†}({\text{n}}^{\prime }).& (11)\end{array}$

The point-like density operators are defined as

$\begin{array}{ll}\rho (\text{n})=a^{†}(\text{n})a(\text{n}),& (12)\end{array}$

$\begin{array}{ll}{\rho }_S(\text{n})=a^{†}(\text{n})\left[{\sigma }_S\right]a(\text{n}),& (13)\end{array}$

$\begin{array}{ll}{\rho }_I(\text{n})=a^{†}(\text{n})\left[{\tau }_I\right]a(\text{n}),& (14)\end{array}$

$\begin{array}{ll}{\rho }_{S,I}(\text{n})=a^{†}(\text{n})\left[{\sigma }_S\otimes {\tau }_I\right]a_{}(\text{n}).& (15)\end{array}$

The smeared non-local densities are defined as

$\begin{array}{ll}{\rho }_{\text{NL}}(\text{n})=a_{\text{NL}}^{†}(\text{n})a_{\text{NL}}(\text{n}),& (16)\end{array}$

$\begin{array}{ll}{\rho }_{S,\text{NL}}(\text{n})=a_{\text{NL}}^{†}(\text{n})\left[{\sigma }_S\right]a_{\text{NL}}(\text{n}),& (17)\end{array}$

$\begin{array}{ll}{\rho }_{I,\text{NL}}(\text{n})=a_{\text{NL}}^{†}(\text{n})\left[{\tau }_I\right]a_{\text{NL}}(\text{n}),& (18)\end{array}$

$\begin{array}{ll}{\rho }_{S,I,\text{NL}}(\text{n})=a_{\text{NL}}^{†}(\text{n})\left[{\sigma }_S\otimes {\tau }_I\right]a_{\text{NL}}(\text{n}),& (19)\end{array}$

while the smeared local densities for local smearing parameter s_L are

$\begin{array}{ll}{\rho }_{\text{L}}(\text{n})=a^{†}(\text{n})a(\text{n})+s_{\text{L}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}{a}^{†}({\text{n}}^{\prime })a({\text{n}}^{\prime }),& (20)\end{array}$

$\begin{array}{ll}{\rho }_{S,\text{L}}(\text{n})=a^{†}(\text{n})\left[{\sigma }_S\right]a(\text{n})+s_{\text{L}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}{a}^{†}({\text{n}}^{\prime })\left[{\sigma }_S\right]a({\text{n}}^{\prime }),& (21)\end{array}$

$\begin{array}{ll}{\rho }_{I,\text{L}}(\text{n})=a^{†}(\text{n})\left[{\tau }_I\right]a(\text{n})+s_{\text{L}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}{a}^{†}({\text{n}}^{\prime })\left[{\tau }_I\right]a({\text{n}}^{\prime }),& (22)\end{array}$

$\begin{array}{ll}{\rho }_{S,I,\text{L}}(\text{n})=a^{†}(\text{n})\left[{\sigma }_S\otimes {\tau }_I\right]a(\text{n})+s_{\text{L}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}{a}^{†}({\text{n}}^{\prime })\left[{\sigma }_S\otimes {\tau }_I\right]a({\text{n}}^{\prime }).& (23)\end{array}$

The non-local short-range interactions have the form

$\begin{array}{ll}{V}_{\text{NL}}=\frac{c_{\text{NL}}}{2}{\displaystyle \sum _{\text{n}}}:{\rho }_{\text{NL}}(\text{n}){\rho }_{\text{NL}}(\text{n}):+\frac{c_{I,\text{NL}}}{2}{\displaystyle \sum _{\text{n},I}}:{\rho }_{I,\text{NL}}(\text{n}){\rho }_{I,\text{NL}}(\text{n}):,& (24)\end{array}$

while the local short-range interactions are given by

$\begin{array}{l}{V}_{\text{L}}=\frac{c_{\text{L}}}{2}{\displaystyle \sum _{\text{n}}}:{\rho }_{\text{L}}(\text{n}){\rho }_{\text{L}}(\text{n}):+\frac{c_{S,\text{L}}}{2}{\displaystyle \sum _{\text{n},S}}:{\rho }_{S,\text{L}}(\text{n}){\rho }_{S,\text{L}}(\text{n}):\\ +\frac{c_{I,\text{L}}}{2}{\displaystyle \sum _{\text{n},I}}:{\rho }_{I,\text{L}}(\text{n}){\rho }_{I,\text{L}}(\text{n}):+\frac{c_{S,I,\text{L}}}{2}{\displaystyle \sum _{\text{n},S,I}}:{\rho }_{S,I,\text{L}}(\text{n}){\rho }_{S,I,\text{L}}(\text{n}):.& (25)\end{array}$

The :: symbol indicates normal ordering where the annihilation operators are pushed to the right and the creation operators are pulled to the left.

For interaction A we take the short-range interaction to have the purely non-local form described in Equation (24). For interaction B we take the short-range interaction to have a combination of the non-local and local forms described in Equations (24), (25), respectively. In Table 1, we show results for the ground state energies of ⁸Be, ¹²C, ¹⁶O, and ²⁰Ne. We present results for interactions A and B at LO, including Coulomb interactions, and the comparison with experimental data. While the ground state energies for B are close to the experimental data, the binding energies for A are not.

TABLE 1

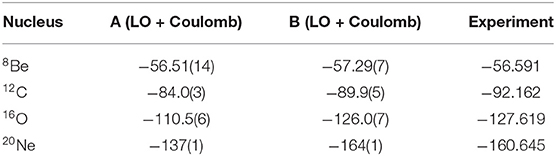
Table 1. Results for the ground energies of ⁸Be, ¹²C, ¹⁶O, and ²⁰Ne using interactions A and B at LO with Coulomb interactions and the comparison with experimental data.

To identify the reason for the disagreement, we compute the ground state energies of ⁸Be, ¹²C, ¹⁶O, and ²⁰Ne for interaction A with the Coulomb interactions turned off. When we turn off Coulomb and divide the ground state energy for each nucleus with that of ⁴He, we find the ratios

$\begin{array}{ll}\frac{E_{{}^8\text{Be}}}{E_{{}^4\text{He}}}=1.997(6),\frac{E_{{}^{12}\text{C}}}{E_{{}^4\text{He}}}=3.00(1),& (26)\end{array}$

$\begin{array}{ll}\frac{E_{{}^{16}\text{O}}}{E_{{}^4\text{He}}}=4.00(2),\frac{E_{{}^{20}\text{Ne}}}{E_{{}^4\text{He}}}=5.03(3).& (27)\end{array}$

These consecutive integer numbers are an indication of a Bose condensate of alpha particles filling the periodic box. In Elhatisari et al. [11] this interpretation is confirmed by showing that the alpha-alpha interactions are indeed very weak for interaction A.

These results shows that nature sits near a quantum phase transition. Along the N = Z line where the number of neutrons equals the number of protons, there is a first-order quantum transition separating a Bose gas of alpha particles from a nuclear liquid. The strength of the alpha-alpha interactions determines whether one has a Bose gas of alpha particles or a nuclear liquid. In turn, the alpha-alpha interactions are impacted by the strength and range of the local part of the nucleon-nucleon interactions. The local part of interaction B is stronger than the local part of interaction A, and hence the different behaviors that we see.

The phase diagram of nuclear matter at zero temperature is in Figure S3. The parameter λ indicates the strength of the local part of the nucleon-nucleon interactions. This can be constructed explicitly by taking a linear combination of the interactions used for interactions A and B. Nuclear matter is in a Bose gas phase of alpha particles when λ is below the critical value, and nuclear matter is in a nuclear liquid phase if λ crosses above the critical value. When λ increases even further, finite A-body nuclei become stable as their energy fall below the threshold value E_αA/4 associated with multi-alpha continuum states.

4. Essential Elements for Nuclear Binding

In Lu et al. [12], we investigate a basic question connecting nuclear forces and nuclear structure. What are the essential elements for nuclear binding? For this analysis we work with a simple leading order effective field theory without pions. This simple pionless EFT theory is SU(4)-invariant, where the SU(4) is Wigner's approximate symmetry where the four nucleon degrees of freedom can be rotated into each other [13]. The lattice Hamiltonian has the form

$\begin{array}{ll}{H}_{\text{SU}(4)}=H_{\text{free}}+\frac{1}{2!}{C}_2{\displaystyle \sum _n}{\tilde{\rho }}^2(\text{n})+\frac{1}{3!}{C}_3{\displaystyle \sum _{\text{n}}}{\tilde{\rho }}^3(\text{n}),& (28)\end{array}$

where H_free is the free nucleon Hamiltonian and

$\begin{array}{ll}\tilde{\rho }(\text{n})={\rho }_{\text{NL}}(\text{n})+s_{\text{L}}{\displaystyle \sum _{\langle {\text{n}}^{\prime }\text{n}\rangle }}{\rho }_{\text{NL}}(\text{n}),& (29)\end{array}$

and ρ_NL(n) was defined in Equation (16). The local part of the interaction is adjusted using the parameter s_L, while the non-local part of the interaction is controlled by the parameter s_NL, which appears implicitly in the definition of ρ_NL(n). The parameter C₂ controls the strength of the two-nucleon interaction, and C₃ controls the three-nucleon interaction. For these calculations the lattice spacing is a = 1.32 fm.

The two-nucleon interaction coefficient C₂ and interaction range, controlled jointly by s_NL and s_L, are set by fitting the scattering length a₀ and effective range r₀ averaged over the two S-wave channels, ${}^1{S}_0$ and ${}^3{S}_1$. The three-nucleon coupling strength C₃ is set according to the binding energy of ³H. At the empirical binding energy B(³H) = 8.48 MeV, the ⁴He binding energy is 28.9 MeV, and this is near the empirical value B(⁴He) = 28.3 MeV. This fitting process is carried out for several pairs of values for s_NL and s_L. We calculate several nuclear ground states for each pair using auxiliary-field lattice Monte Carlo simulations. We find that s_NL = 0.5 and s_L = 0.061 gives the best agreement overall. We note that the rather large value of s_L as compared with s_NL is an indication that the local interaction plays an important role in nuclear binding. The corresponding couplings are $C_2=-3.41\times 10^{-7}$ MeV⁻² and $C_3=-1.4\times 10^{-14}$ MeV⁻⁵. Overall about 20% of the binding is coming from the three-body interaction. This is consistent with the expected hierarchy of forces in effective field theory, with three-body forces being less important than two-body forces.

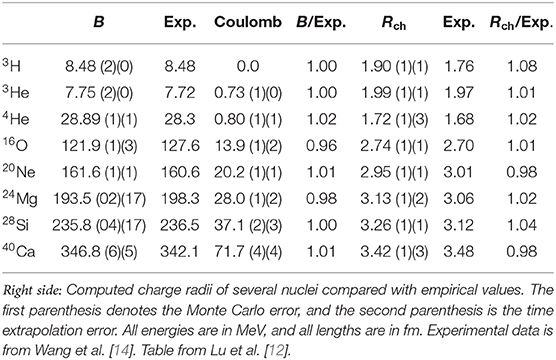
We present binding energies and charge radii in Table 2 for selected nuclei together with the experimental values and the computed Coulomb energy. Although the ³H energy is a constraint in the fitting process, the other values are predictions. We have included the charge radius of the proton for calculations of the nuclear charge radii, but have not included smaller effects arising from the charge distribution of the neutron, relativistic corrections, and spin-orbit terms. In Figure S4 we show the binding energies for 86 bound nuclei with up to A = 48 nucleons in comparison with empirical data. The Monte Carlo error bars are not visible as they are smaller than the symbol size. The errors associated with Euclidean time extrapolation and volume extrapolation are less than 1% relative error, and these errors are not shown. In Figure S4 one can see that the agreement with empirical results is fairly good. The remaining discrepancies are a sign of missing effects such as interactions which are spin dependent.

TABLE 2

Table 2. Left side: Computed binding energies of several nuclei compared with experimental values.

In Figure S5 we show the charge densities of ¹⁶O and ⁴⁰Ca. These densities are calculated using the pinhole algorithm [16] where a barrier is placed in the middle of the Euclidean time evolution, and the amplitude vanishes unless each nucleon passes through a pinhole. As the number of pinholes are set to equal the number of nucleons, the sampling over pinholes yields a classical distribution of the nucleon positions. We show the comparison with electron scattering data, as well as the lattice results with the Coulomb interaction included via first order perturbation theory. The Coulomb force suppresses the densities near the nucleus center, bringing the results in better agreement with the experimental data. The results are surprisingly accurate in view of the simple nuclear interaction.

The ground state energy of pure neutron matter is shown in Figure S6 as a function of the neutron density. We show the results of several other calculations for comparison. For the lattice results the number of neutrons ranges from 14 to 66. The calculations are done with three box sizes L = 5, 6, 7. Our lattice results, shown as the filled red polygons, are generally in good agreement with the other calculations for densities higher than 0.05 fm⁻³. For lower densities the disagreement is larger due to the neutron-neutron scattering length being incorrect. The open red polygons correspond to an improved calculation where a contact interaction is included to give the correct neutron-neutron scattering length. There is also a correction included to restore invariance with respect to Galilean boosts [17]. In spite of the simplicity of the interaction, the results are quite good.

5. Discussion

We have reviewed several recent results by the Nuclear Lattice EFT Collaboration. We presented the improved description of scattering phase shifts in chiral effective field theory up to N³LO. We then showed evidence that nuclear physics is close to a quantum phase transition. After this we described the minimal nuclear interaction that can accurately reproduce the ground state energies of neutron matter, light nuclei, and medium-mass nuclei. A common theme flowing through all aspects of our review was the notable difference between local and non-local interactions. We now put some of these findings into context.

Numerous calculations show the reliability of chiral EFT for the properties of light nuclei [18–22]. However, the binding energies as well as the charge radii of medium mass nuclei are sometimes not well reproduced [20, 23–29]. One notable case is that the charge radius of ¹⁶O, which is often too small [23, 25–28]. Without further input, chiral EFT calculations do not yet provide accurate predictions at higher nuclear densities.

One practical approach is to put constraints on the nuclear force by fitting the properties of medium mass nuclei and nuclear matter saturation [29]. This strategy has been used in several calculations [30–33]. The approach we have pursued in nuclear lattice studies is to focus on the microscopic origins of the problem. In Elhatisari et al. [11], we find that nuclear matter resides near a quantum phase transition that lies at the boundary between a Bose condensate of alpha particles and a nuclear liquid. There we show that local interactions are especially important for nuclear binding. In Lu et al. [12], we construct a simple nuclear interaction that can produce, with no more than a few percent error, the ground state energies of neutron matter, light nuclei, and medium-mass nuclei. From that analysis we see the importance of the range and locality of the SU(4)-invariant forces in determining the bulk properties of nuclei.

The dominance of SU(4)-invariant interactions can be explained in terms of coherent enhancement. Upon summation over nucleonic spin configurations, much of the effect of spin-dependent forces cancel. In a similar manner, isospin-dependent forces will cancel in symmetric nuclear matter due to the protons and neutrons being equal in number. One important exception though is the Coulomb interaction. SU(4) symmetry and large scattering length universality have a long history in nuclear physics. It is well-known that the Tjon line connecting ³H and ⁴He binding energies is a manifestation of universality in nuclear systems [9, 34–36].

SU(4)-symmetric short-range interactions are now being used with local and non-local smearing and one-pion exchange. These improved calculations of light and medium-mass nuclei will use chiral forces up to N³LO. One of the central questions that we seek to address is why the straightforward application of chiral EFT does not give reliable and accurate predictions at higher nuclear densities. While more investigations are needed, it seems that part of the answer to this question is related to the emergence of a physical length scale relevant to many-body nuclear systems, the size of the alpha particle. The amount of fine tuning needed to reproduce the alpha-alpha and alpha-nucleon scattering phase shifts can be understood as the competition between Pauli repulsion and attractive nucleon-nucleon interactions. This important and delicate balance is amplified by the fact that the range of the nucleon-nucleon interaction is comparable to the size of the alpha particle. Hence small differences in the range or locality of the interaction can have a large impact on the interactions of the alpha particle. This is turn has consequences for nuclear systems with increasing numbers of nucleons.

Data Availability Statement

The datasets analyzed in this article are not publicly available. Requests to access the datasets should be directed to leed@frib.msu.edu.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank my wonderful collaborators Serdar Elhatisari, Evgeny Epelbaum, Hermann Krebs, Timo A. Lähde, Ning Li, Bing-Nan Lu, Thomas Luu, Ulf-G. Meißner, Gautam Rupak, for their insight, work, and determination that made on the collaborative work reported here possible. Partial support provided by the U.S. Department of Energy (DE-SC0018638 and DE-AC52-06NA25396). The computational resources were provided by the Julich Supercomputing Centre at Forschungszentrum Jülich, Oak Ridge Leadership Computing Facility, RWTH Aachen, and Michigan State University.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00174/full#supplementary-material

Figure S1. Results for the neutron-proton scattering phase shifts and mixing angles vs. the relative momenta for lattice spacing a = 1.32 fm. The blue, green and red bands show the estimated uncertainties at NLO, N²LO and N³LO respectively. The black solid line and diamonds denote phase shift or mixing angle from the Nijmegen partial wave analysis and lattice calculation at N³LO, respectively. Figure from Li et al. [10].

Figure S2. Results for the neutron-proton scattering phase shifts and mixing angles vs. the relative momenta for lattice spacing a = 0.99 fm. The blue, green and red bands show the estimated uncertainties at NLO, N²LO and N³LO respectively. The black solid line and diamonds denote phase shift or mixing angle from the Nijmegen partial wave analysis and lattice calculation at N³LO, respectively. Figure from Li et al. [10].

Figure S3. Phase diagram of nuclear matter at zero temperature. λ controls the strength of the local part of the interactions. Figure from Elhatisari et al. [11].

Figure S4. Calculated binding energies from ³H to ⁴⁸Ca. The solid symbols are lattice results and the open symbols are experimental values. The experimental values are from Wang et al. [14]. Figure adapted from Lu et al. [12].

Figure S5. Computed ¹⁶O and ⁴⁰Ca charge densities compared with experimental results. The circles denote the results without Coulomb interaction. The squares are the results with the Coulomb interaction included perturbatively. Experimental results are from De Vries et al. [15]. Figure adapted from Lu et al. [12].

Figure S6. Ground state energy of pure neutron matter as a function of neutron density for box sizes L = 5 (upright triangles), L = 6 (squares), L = 7 (right-pointing triangles). The filled red polygons are results for the leading-order interaction. The open red polygons show an improved calculation with a short-range interaction tuned to the physical neutron-neutron scattering length as well as a correction to restore Galilean invariance. Also shown are results calculated with N³LO chiral interactions (EM 500 MeV, EGM 450/500 MeV and EGM 450/700 MeV) [37], as well as results from variational (APR) [38] and auxiliary-field diffusion MC calculations (GCR) [39]. Figure adapted from Lu et al. [12].

References

1. Epelbaum E, Hammer HW, Meißner U-G. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773. doi: 10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

2. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

3. Lee D. Lattice simulations for few- and many-body systems. Prog Part Nuclear Phys. (2009) 63:117–74. doi: 10.1016/j.ppnp.2008.12.001

CrossRef Full Text | Google Scholar

4. Lähde TA, Meißner UG. Nuclear Lattice Effective Field Theory : An Introduction. Cham: Springer (2019).

Google Scholar

5. Epelbaum E, Krebs H, Lee D, Meißner UG. Ab initio calculation of the Hoyle state. Phys Rev Lett. (2011) 106:192501. doi: 10.1103/PhysRevLett.106.192501

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Epelbaum E, Krebs H, Lähde TA, Lee D, Meißner UG. Structure and rotations of the Hoyle state. Phys Rev Lett. (2012) 109:252501. doi: 10.1103/PhysRevLett.109.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Elhatisari S, Lee D, Rupak G, Epelbaum E, Krebs H, Lähde TA, et al. Ab initio alpha-alpha scattering. Nature (2015) 528:111. doi: 10.1038/nature16067

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Alarcón JM., Du D, Klein N, Lähde TA, Lee D, Li N, et al. Neutron-proton scattering at next-to-next-to-leading order in Nuclear Lattice Effective Field Theory. Eur Phys J A. (2017) 53:83. doi: 10.1140/epja/i2017-12273-x

CrossRef Full Text | Google Scholar

9. Klein N, Elhatisari S, Lähde TA, Lee D, Meißner UG. The Tjon band in nuclear lattice effective field theory. Eur Phys J A. (2018) 54:121. doi: 10.1140/epja/i2018-12553-y

CrossRef Full Text | Google Scholar

10. Li N, Elhatisari S, Epelbaum E, Lee D, Lu BN, Meißner UG. Neutron-proton scattering with lattice chiral effective field theory at next-to-next-to-next-to-leading order. Phys Rev C. (2018) 98:044002. doi: 10.1103/PhysRevC.98.044002

CrossRef Full Text | Google Scholar

11. Elhatisari S, Li N, Rokash A, Alarcón JM, Du D, Klein N, et al. Nuclear binding near a quantum phase transition. Phys Rev Lett. (2016) 117:132501. doi: 10.1103/PhysRevLett.117.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lu BN, Li N, Elhatisari S, Lee D, Epelbaum E, Meißner UG. Essential elements for nuclear binding. Phys Lett B. (2019) 797:134863. doi: 10.1016/j.physletb.2019.134863

CrossRef Full Text | Google Scholar

13. Wigner E. On the consequences of the symmetry of the nuclear Hamiltonian on the spectroscopy of nuclei. Phys Rev. (1937) 51:106. doi: 10.1103/PhysRev.51.106

CrossRef Full Text | Google Scholar

14. Wang M, Audi G, Kondev FG, Huang WJ, Naimi S, Xu X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin Phys C. (2017) 41:030003. doi: 10.1088/1674-1137/41/3/030003

CrossRef Full Text | Google Scholar

15. De Vries H, De Jager CW, De Vries C. Nuclear charge-density-distribution parameters from elastic electron scattering. Atom Data Nuclear Data Tabl. (1987) 36:495–536. doi: 10.1016/0092-640X(87)90013-1

CrossRef Full Text | Google Scholar

16. Elhatisari S, Epelbaum E, Krebs H, Lähde TA, Lee D, Li N, et al. Ab initio calculations of the isotopic dependence of nuclear clustering. Phys Rev Lett. (2017) 119:222505. doi: 10.1103/PhysRevLett.119.222505

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li N, Elhatisari S, Epelbaum E, Lee D, Lu B, Meißner UG. Galilean invariance restoration on the lattice. Phys Rev C. (2019) 99:064001. doi: 10.1103/PhysRevC.99.064001

CrossRef Full Text | Google Scholar

18. Hupin G, Quaglioni S, Navrátil P. Unified description of ⁶Li structure and deuterium-⁴He dynamics with chiral two- and three-nucleon forces. Phys Rev Lett. (2015) 114:212502. doi: 10.1103/PhysRevLett.114.212502

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Navrátil P, Gueorguiev VG, Vary JP, Ormand WE, Nogga A, Quaglioni S. Light nuclei from chiral EFT interactions. Few Body Syst. (2008) 43:129–35. doi: 10.1007/s00601-008-0221-y

CrossRef Full Text | Google Scholar

20. Lonardoni D, Carlson J, Gandolfi S, Lynn JE, Schmidt KE, Schwenk A, et al. Properties of nuclei up to A = 16 using local chiral interactions. Phys Rev Lett. (2018) 120:122502. doi: 10.1103/PhysRevLett.120.122502

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Epelbaum E, Golak J, Hebeler K, Hüther T, Kamada H, Krebs H, Maris P, et al. Few- and many-nucleon systems with semilocal coordinate-space regularized chiral two- and three-body forces. Phys Rev C. (2019) 99:024313. doi: 10.1103/PhysRevC.99.024313

CrossRef Full Text | Google Scholar

23. Wloch M, Dean DJ, Gour JR, Hjorth-Jensen M, Kowalski K, Papenbrock T, et al. Ab initio coupled-cluster study of O-16. Phys Rev Lett. (2005) 94:212501. doi: 10.1103/PhysRevLett.94.212501

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Hagen G, Papenbrock T, Dean DJ, Hjorth-Jensen M. Medium-mass nuclei from chiral nucleon-nucleon interactions. Phys Rev Lett. (2008) 101:092502. doi: 10.1103/PhysRevLett.101.092502

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Hagen G, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Continuum effects and three-nucleon forces in neutron-rich oxygen isotopes. Phys Rev Lett. (2012) 108:242501. doi: 10.1103/PhysRevLett.108.242501

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Binder S, Langhammer J, Calci A, Roth R. Ab initio path to heavy nuclei. Phys Lett B. (2014) 736:119. doi: 10.1016/j.physletb.2014.07.010

CrossRef Full Text | Google Scholar

27. Epelbaum E, Krebs H, Lähde TA, Lee D, Meißner UG, Rupak G. Ab initio calculation of the spectrum and structure of ¹⁶O. Phys Rev Lett. (2014) 112:102501. doi: 10.1103/PhysRevLett.112.102501

CrossRef Full Text | Google Scholar

28. Cipollone A, Barbieri C, Navrátil P. Chiral three-nucleon forces and the evolution of correlations along the oxygen isotopic chain. Phys Rev C. (2015) 92:014306. doi: 10.1103/PhysRevC.92.014306

CrossRef Full Text | Google Scholar

29. Ekström A, Jansen JR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

30. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the ⁴⁸Ca nucleus. Nat Phys. (2015) 12:186–90. doi: 10.1038/nphys3529

CrossRef Full Text | Google Scholar

31. Hagen G, Jansen GR, Papenbrock T. Structure of ⁷⁸Ni from first principles computations. Phys Rev Lett. (2016) 117:172501. doi: 10.1103/PhysRevLett.117.172501

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Simonis J, Stroberg SR, Hebeler K, Holt JD, Schwenk A. Saturation with chiral interactions and consequences for finite nuclei. Phys Rev C. (2017) 96:014303. doi: 10.1103/PhysRevC.96.014303

CrossRef Full Text | Google Scholar

33. Morris TD, Simonis J, Stroberg SR, Stumpf C, Hagen G, Holt JD, et al. Structure of the lightest tin isotopes. Phys Rev Lett. (2018) 120:152503. doi: 10.1103/PhysRevLett.120.152503

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Platter L, Hammer HW, Meißner UG. On the correlation between the binding energies of the triton and the alpha-particle. Phys Lett B. (2005) 607:254. doi: 10.1016/j.physletb.2004.12.068

CrossRef Full Text | Google Scholar

35. König S, Grießhammer HW, Hammer HW, van Kolck U. Nuclear physics around the unitarity limit. Phys Rev Lett. (2017) 118:202501. doi: 10.1103/PhysRevLett.118.202501

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kievsky A, Gattobigio M. Efimov physics with 1/2 spin-isospin fermions. Few Body Syst. (2016) 57:217–27. doi: 10.1007/s00601-016-1049-5

CrossRef Full Text | Google Scholar

37. Tews I, Krüger T, Hebeler K, Schwenk A. Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory. Phys Rev Lett. (2013) 110:032504. doi: 10.1103/PhysRevLett.110.032504

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Akmal A, Pandharipande VR, Ravenhall DG. The Equation of state of nucleon matter and neutron star structure. Phys Rev C. (1998) 58:1804. doi: 10.1103/PhysRevC.58.1804

CrossRef Full Text | Google Scholar

39. Gandolfi S, Carlson J, Reddy S. The maximum mass and radius of neutron stars and the nuclear symmetry energy. Phys Rev C. (2012) 85:032801. doi: 10.1103/PhysRevC.85.032801

CrossRef Full Text | Google Scholar