
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 23 September 2020
Sec. Educational Psychology
Volume 5 - 2020 | https://doi.org/10.3389/feduc.2020.533998
This article is part of the Research Topic Psychology and Mathematics Education View all 40 articles
Research on Bayesian reasoning suggests that humans make good use of available information. Similarly, research on human information acquisition suggests that Optimal Experimental Design models predict human queries well. This perspective contrasts starkly with educational research on help seeking, which suggests that many students wait excessively long to ask for help, or even decline help when it is offered. We bring these lines of work together, exploring when people seek help as a function of problem state in the Entropy Mastermind code breaking game. The Entropy Mastermind game is a probabilistic version of the classic code breaking game, involving inductive, deductive and scientific reasoning. Whether help in the form of a hint was available was manipulated within subjects. Results showed that participants tended to ask for help late in the game play, often when they already had all the necessary information needed to crack the code. These results pose a challenge for some versions of Bayesian and Optimal Experimental Design frameworks. Possible theoretical frameworks to understand the results, including from computer science approaches to the Mastermind game, are considered.
Help seeking is an important aspect of the learning process in allowing an individual to advance their understanding (Nelson-Le Gall, 1985), and develop their independent skill and abilities (Newman, 1994). Once an individual reaches an impasse – a situation where no progress is possible – the initiation of help seeking behavior can be valuable for allowing them to move beyond their impasse (Price et al., 2017).
Interestingly, research also suggests that people often do not effectively utilize opportunities for help or even ignore them altogether (Aleven et al., 2003). Educational research has suggested that many students do not know when to ask for help and tend to wait, trying to work something out for themselves for a relatively long time before asking for hints (Aleven and Koedinger, 2000). In an analysis of students’ help seeking behavior through completing computer tasks, a clear pattern emerged: students would attempt a task, they would be provided with feedback and the offer of help, and then they would decline the help (du Boulay et al., 1999). These findings highlight the importance of establishing when people ask for help and what factors may influence the help seeking process.
In this paper, we bring the phenomena of help-seeking and theoretical models of cognition together, in the context of a mathematical game. Although many types of models of reasoning and decision making processes exist (Roberts, 1993; Smith, 2001), we largely focus on probabilistic Bayesian models. Bayesian models posit that humans make sense of the world by reasoning inductively about how alternative hypotheses give rise to observable data. A common assumption is that people are motivated to find the best explanation to explain the available data (Chater et al., 2006; Kharratzadeh and Shultz, 2016). In studies of human information acquisition in this framework, it has frequently been found that people have good intuitions about which pieces of information are most informative (Oaksford and Chater, 1994; Nelson, 2005; Coenen et al., 2018). It is also important to keep in mind that people are constantly presented with large amounts of information, of which only some is useful, and must appropriately identify what information is useful in order to respond and act appropriately (Hopfinger and Mangun, 2001).
In psychology, mathematics style games and game-like experimental designs have been influential in models of human decision making and reasoning. Chess (Burgoyne et al., 2016) is perhaps the most famous example. One game that has been suggested for use in teaching scientific reasoning is the popular code breaking game Mastermind (Strom and Barolo, 2011). The game was originally designed as a two-player board game in 1970 by Mordecai Meirowitz. Theoretically, Mastermind can be viewed as a kind of concept learning game, with connections to work by Bruner et al. (1956), Wason (1960) and others. One might also relate the deductive logical aspects of the game to logical reasoning tasks such as Wason’s (1968) Selection Task and THOG (Wason, 1977) experimental paradigms. Recent work on Deductive Mastermind (Gierasimczuk et al., 2012, 2013; Zhao et al., 2018) uses versions of the game in which the participant is given all the information to uniquely infer the hidden code. Mastermind can also be viewed as a problem-solving task (e.g., Simon and Newell, 1971; Newell and Simon, 1988) and analyzed accordingly.
Here we use a computer-based, single-player version of the Mastermind game. In the computer-based game, the aim is to guess the secret code generated by the computer using as few guesses as possible. For each guess made by the player they receive feedback regarding the colors and positions of the items in their guess. The player is then expected to learn from the feedback and to use that feedback to make another guess which will add to the amount of information they have about the code. From their guesses the player then tries to deduce the correct color and position of every item in the code. We use an app-based version of Entropy Mastermind, a recently developed, customizable computer-based version of the game (Schulz et al., 2019). Figure 1 displays the gameplay and feedback in more detail.

Figure 1. Example of the app version of the Entropy Mastermind game. Participants make guesses by dragging the colors into the gray circles in the order they choose and then click the make guess button. This generates the feedback displayed on the right-hand side in the form of either a black circle, white circle or cross. A cross means that the item in the code is wrong in both position and color, a white circle means that the item is correct in color but not position and a black circle means that the item is correct in both position and color. The position of the feedback does not correspond with the position of the items in the guess. The first three lines of this example demonstrates that there are no orange colors in the code but there are two green and two blue. Guess number four shows that only two of the colors are in the right place and guess number five shows that none of the items are placed correctly. This information was used to decipher the correct position of the colors as shown in guess six.
Can probabilistic models explain how people’s knowledge and beliefs develop when they play Mastermind? Are people’s queries optimal, or at least highly informative? Bayesian models suggest that humans are rational about learning and inference and will use information to ask questions that will maximize their knowledge (Eberhardt and Danks, 2011). However, Bayesian models have been criticized on a number of theoretical and practical points (Jones and Love, 2011), and human probabilistic reasoning can deviate from Bayesian accounts (Eddy, 1982). One perplexing phenomenon, not yet related in the literature to Bayesian reasoning, is that when acquiring and processing information, people can feel they are at an impasse, are “stuck” (Weisberg, 2015), and be unsure of how to proceed.
The primary aim of this study was to provide the first quantitative empirical investigation of help-seeking as a function of problem state, using the Mastermind code-breaking game. Theoretically, from a purely information-theoretic perspective, help would be most informative at the beginning of the game, when the largest number of codes are possible, and the underlying entropy in the probability distribution corresponding to the true code is highest. In other words, in the beginning of the game, help (in the form of a hint, as we describe below) would tend to provide much more information, as quantified in bits or otherwise, than help later in the game. On the other hand, alternate models that are not purely information-theoretic– for instance, because they take into account the agent’s resource limitations– may find help more valuable later on in the game. This applies to both resource-rational models that operate within the Bayesian framework (Griffiths et al., 2015) as well as heuristic models in computer science (e.g., see Cotta et al., 2010, for an evolutionary algorithm-based approach that maintain less than a complete representation of the problem state).
When will people ask for help when playing Mastermind? Will people ask for help when from a mathematical perspective help is most needed, i.e., early on in the game? Or will people first seek help when they feel stuck (at an impasse), perhaps late in the game? We also consider the points at which people ask for help, and how receiving help influences game play. To investigate these issues across a variety of experimental conditions, the difficulty of the game (1296 possible codes, with 4 items and 6 colors; or 4096 possible codes, with 6 items and 4 colors) and whether or not it was possible to obtain extra help were manipulated within participants.
Two specific research hypotheses were examined:
Hypothesis (1): The point at which an individual will ask for help will be predicted by the number of possible codes remaining, and the number of previous guesses made.
Hypothesis (2): Participants will need fewer guesses to complete the code in the help condition compared to the normal gameplay condition.
We aimed to recruit 20 participants through the University of Surrey’s participation website SONA. The experiment was expected to take around 60 min to complete, thus participants were each compensated two lab tokens for their time (if applicable) and entered into a prize draw for one of two £50 Amazon vouchers. (University of Surrey Psychology students can earn lab tokens by participating in experiments, which they can then spend to obtain participation in their own experiments). Participants gave informed consent, following University of Surrey procedures.
The experiment took place in a laboratory room at the University of Surrey. The participant was given a laptop on which the Mastermind app was installed and displayed. The laptop was connected to a second screen so that the experimenter could observe game play and also had access to a statistics output box showing the number of possible codes remaining, the entropy of the set after each guess, and the true code. Next to the computer was a bell that participants were asked to ring in the help condition, when they felt stuck and would like to receive a hint.
The experiment used a within-subjects design with two experimental conditions: normal game play and help offered. Some participants completed the “normal game play” condition first before being offered a short break and were then asked to complete the “help offered” condition of the experiment. The remaining participants completed the conditions in reverse order.
In each condition participants played four games. The first two games involved completing an easy (4-item) code made up of six equally probable colors (thus containing 6^4 = 1296 possible codes), and the second two games involved completing a difficult (6-item) code made up of four equally probable colors (thus containing 4^6 = 4096 possible codes). Uniform probability distributions across the possible colors were used in all games; each item in the code was drawn with replacement. Note that from one game to the next, for a particular (e.g., 4-item) code length, the difficulty– with respect to any particular guessing strategy– may vary. However, because games are generated at random with equal probability, experimental condition (help available or not) should not be confounded with idiosyncracies of individual games’ difficulty.
Before the experiment, the experimenter showed the participant the Entropy Mastermind game and explained the rules and gameplay. Participants were asked to complete a short quiz to ensure that they understood the rules and were then asked to play a simple version of the game (3-item code generated with white, blue, and green appearing with equal probability) to ensure that they understood.
After this, the experimenter explained that the aim of the game was to complete the code with the smallest possible number of guesses. For each game the experimenter recorded: the true code, how many guesses the participant needed to complete the code, and the point at which the code could have been deciphered according to the participant’s guesses and the feedback given. Participants had up to 18 guesses to break the code in each game. If the participant was unable to decipher the code within the 18 guesses available, the total number of guesses needed was recorded as 19 guesses, for the purposes of statistical analyses.
In the “help” condition, participants were told to ring the bell when they felt stuck, and that the experimenter would offer them help, by telling them the color and position of one item in the code of their choice. There was no limit on the number of times participants could ask for help per game. Thus, it would be allowed, if a participant wished, to ask for help multiple times, from the beginning until the code was solved. In each instance that help was asked for, the experimenter recorded: the guess number, the specific guess and feedback of the previous line, the number of possible codes remaining, the Shannon entropy of the probabilities of the possible codes at that time, and which item of the code the participant asked the experimenter to tell them.
Seventeen participants (13 female, 4 male) completed the experiment. Fifteen of these participants reported their ages as ranging from 18 to 52 (median 22, mean 20). Full demographic information is provided together with the study data at https://osf.io/q5rct/.
Each participant had both help available and easy conditions. In each condition each participant played four games: two games involved looking for an easy (4-item) code and two games involved a difficult (6-item) code. Therefore a total of 136 games of Mastermind were played, including 68 games each in the help available and normal gameplay conditions, by the 17 participants. Note that due to experimenter error the order of conditions– within a particular game length– in which help was offered was not randomized throughout the experiment. Rather, the first ten participants completed two games of each code length of normal gameplay, followed by two games of each code length of help-available game play. The remaining participants completed the help offered games first followed by the games of normal gameplay. Visual inspection of the data suggested no differences according to the order in which conditions were completed.
The number of guesses needed to complete the code aggregating across four and six item codes in each condition were as follows: normal game play condition (M = 10.66, SD = 2.51); help condition (M = 9.28, SD = 2.15). A paired samples t-test shows a marginally significant difference for the number of guesses needed to complete the code in the help condition vs. the normal gameplay condition [t(16) = −2.05, two-tail p = 0.056]. A 95% bootstrap confidence interval for the difference in number of queries suggested that the availability of help reduced the number of queries between [0.12, 2.68] guesses per game.
Of the 68 games where help was available to participants, help was accepted in 25 games a total of 38 times. Help was requested much more frequently in the six-item-code games, as in the four-item-code games. For a four-item code, help was accepted in 8 games a total of 8 times; for a six-item code help was accepted in 17 games a total of 30 times. A paired t-test confirmed that participants had a greater tendency to ask for help in 6-item games than in 4-item games [t(16) = 3.10, two-tail p = 0.007]. A bootstrap 95% confidence interval for the difference in number of times each participant requested help in the 6-item games, minus in the 4-item games, was [0.53, 2.12], corroborating the descriptive statistics and the t-test results.
For the 4-item code, participants always guessed the true code within the 18 guesses. In 14 of the games with the 6-item code, participants did not guess the code within the 18 guesses allowed. The 14 instances of not being able to complete the 6-item code were split across 8 participants; the maximum number of games a single participant was unable to complete was 4. In all games where the participant was unable to complete the code, the code had already been mathematically determined based on the feedback from the prior 18 guesses.
Histograms were produced to relate the points when help was asked for to the number of possible codes remaining (Figure 2) and the number of previous guesses made so far (Figure 3) at the point when help was asked for. Visual inspection of the histogram displaying the number of possible codes remaining (Figure 2) showed that participants had a strong tendency to ask for help when the code was already determined, and they had already received the necessary information to decipher the code. Interpreting the relationship between the number of guesses made so far to the tendency to ask for help (Figure 3) is more difficult, because help tended to be asked for only very late in the game, and the number of guesses varied by game and code length. Figure 3 does however suggest that people did not tend to ask for help early in the game, at which point (from a purely mathematical standpoint) help would be most valuable. To test whether help is asked for at a random point in the game, the point at which help was asked for was coded in terms of the quartile of the total number of queries in each individual game. Figure 4 shows a histogram displaying this analysis. Visual inspection of this histogram (Figure 4) showed that participants tended to ask for help late in the game, with most help being asked for in the fourth quartile of gameplay.
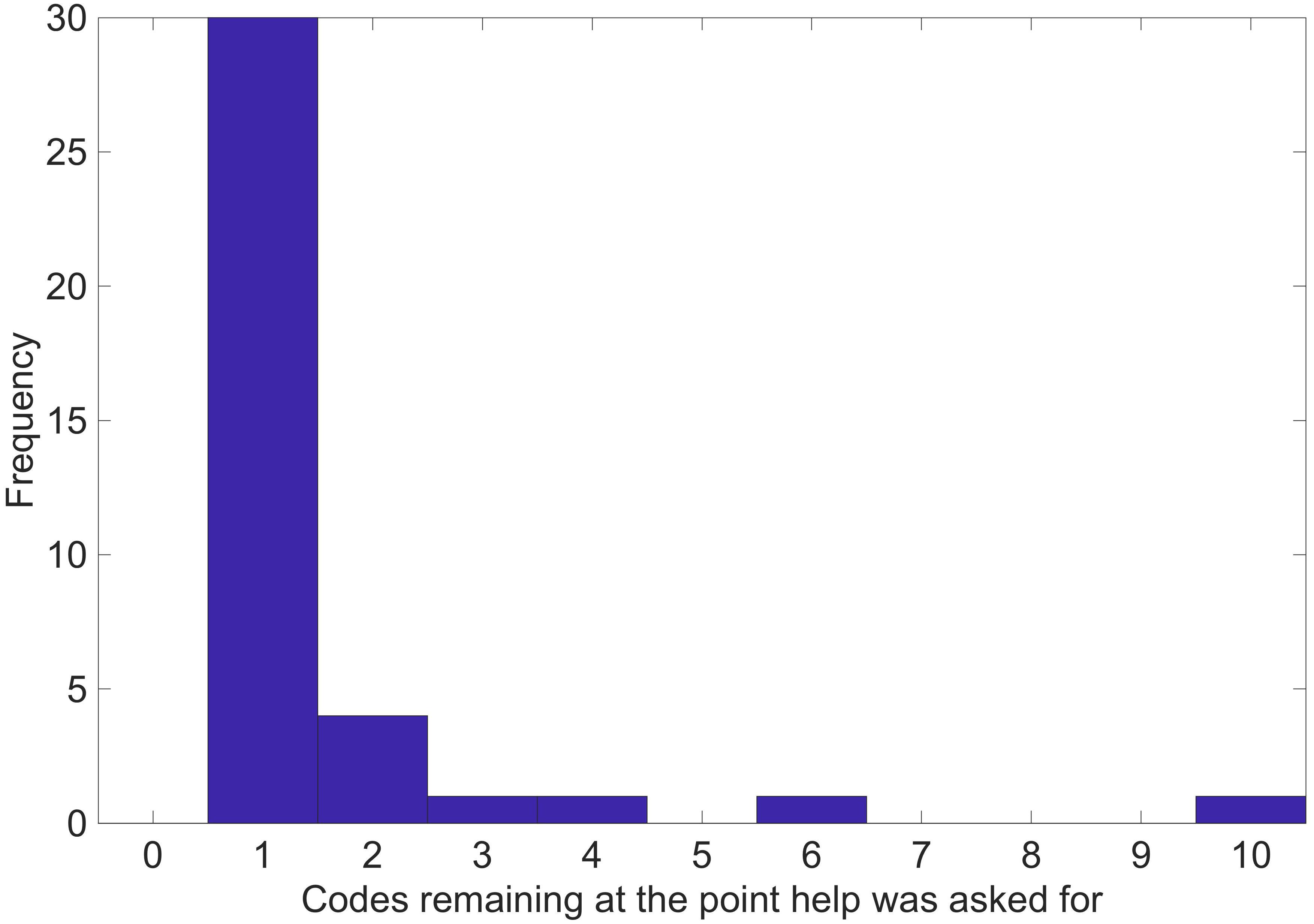
Figure 2. Histogram showing the distribution of the number of remaining possible codes at the points in which help was asked for. For purposes of plotting this histogram, if there were more than 10 possible codes remaining, the number was truncated to 10.
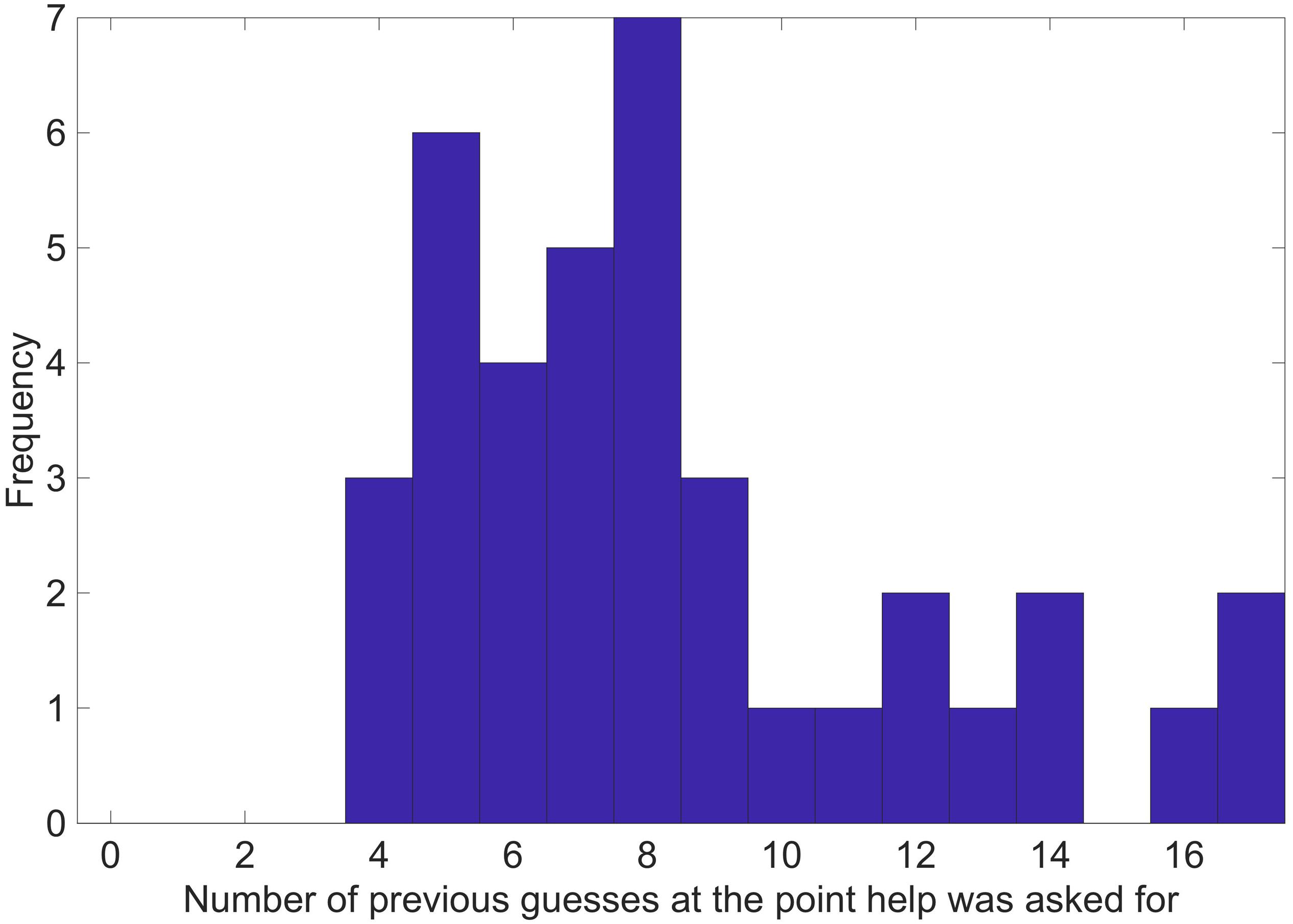
Figure 3. Histogram showing the distribution of the number of guesses made so far at the points in which help was asked for.
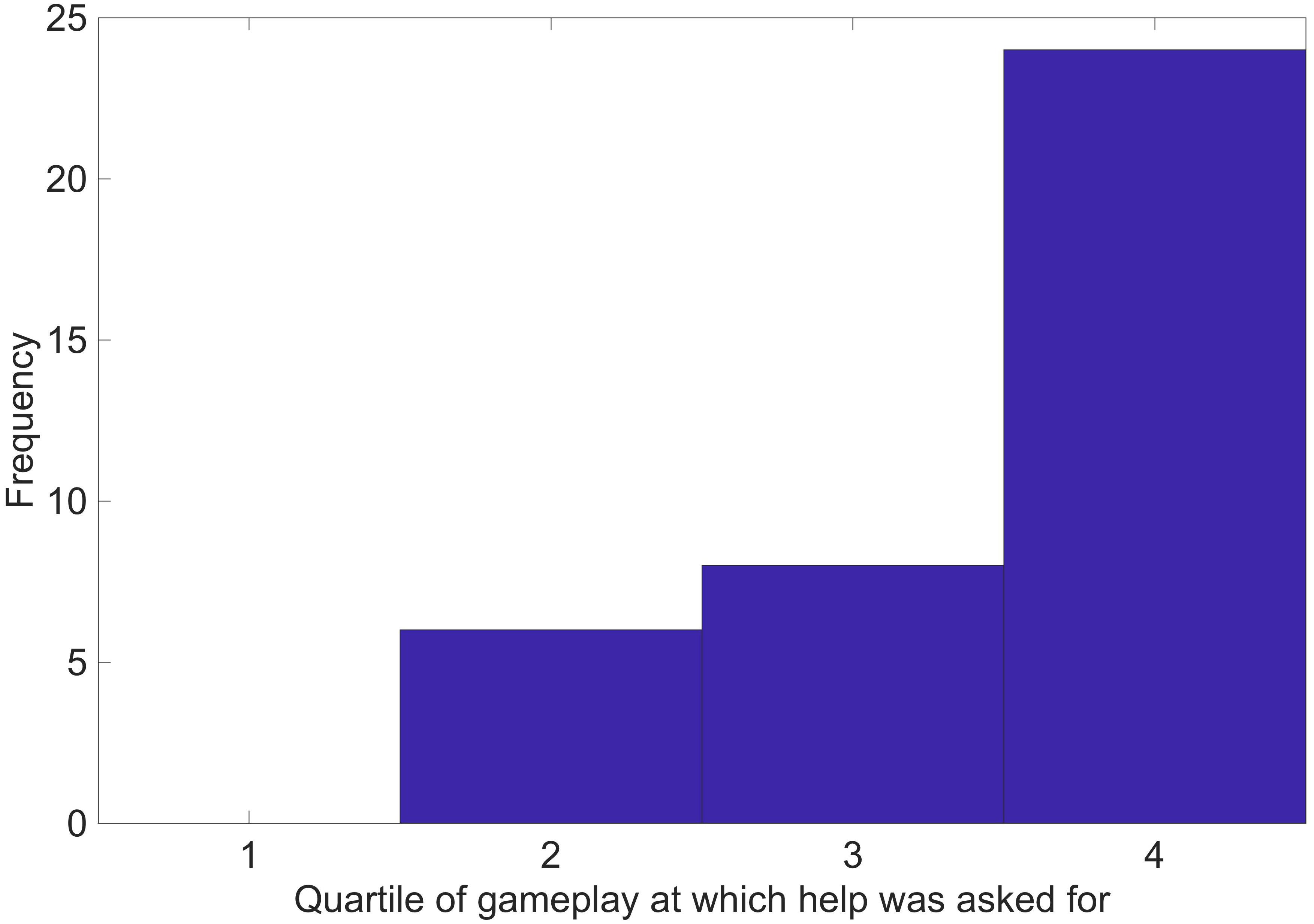
Figure 4. Histogram showing the distribution of the number of previous guesses as represented by quartile of game play at the point that help was asked for.
A chi square test of independence was conducted to assess whether the quartile of gameplay was a statistically significant predictor of when people asked for help. This test compared the observed number of times help was asked for in each quartile of gameplay with the number of times we would expect help to be asked for in each quartile of gameplay if participants asked for help with equal probability in each quartile. The chi square was conducted on the combined data for both four and six item codes to ensure that the assumption of cell frequencies above five was met. The analysis showed a strong association between quartile of gameplay and when help was asked for, χ2(3) = 30.29, p < 0.001, suggesting that the stage of gameplay is a significant predictor of when people ask for help when playing the mastermind game.
Participants appeared to adopt one of two qualitatively different strategies when playing the mastermind game. We think of these strategies as the “systematic strategy” and the “random strategy.” The systematic strategy involved testing each color to find out how many items of the code consisted of that color. (Note that participants’ frequent use of the systematic strategy effectively rules out chance responding, despite the fact that people needed more queries than strategies characterized in the computer science literature). After the first query, in the systematic strategy, the participant would then either use a color not included in the code (if applicable) or another color to decipher the position of all the items of one color in the code. This strategy was used until all items in the code had been deciphered; a stylized example is displayed in Figure 5. The other strategy appears to be much more random; a stylized example is displayed in Figure 6. In this strategy participants would test a number of colors in each guess and did not appear to have any set ways of deciphering the specific position of each color.

Figure 5. Stylized example (not from actual gameplay) of the systematic strategy when playing the Mastermind game.

Figure 6. Stylized example (not from actual gameplay) of the random strategy when playing the Mastermind game.
To address this quantitatively, we (NT) went through the dataset and classified each of the 136 games according to whether it seemed qualitatively closer to the “systematic” or “random” strategy. It turns out that our qualitative understanding was almost perfectly predicted by whether the first query was all the same color (systematic strategy) or not (random strategy). Therefore, we operationally defined the systematic strategy as starting with all the same color in the first query, and the random strategy as everything else. Of the 136 games played, 71 were thus classified as random and 65 as systematic.
There was no meaningful difference between the average of 9.74 queries required to identify the true code with a systematic strategy, vs. the average of 10.12 queries for a random strategy [t(134) = 0.54, n.s., two-tailed t-test]. However, because the code length 4 games always occurred in the first part of the experiment, and there was a slightly greater tendency to use a random strategy with the code length 4 games, any harm from using the random strategy might have been counterbalanced by the intrinsically easier nature of the 4-item games.
A more meaningful measure may be the number of additional queries required, beyond when the true code was mathematically determined, for a person to identify the true code. We can in turn ask whether this additional number of (zero-information-gain) queries differed according to the strategy used. By this measure, the code was more quickly identified by the participant when a systematic strategy was used than when a random strategy was used [t(134) = 2.27, p = 0.025, two-tailed t-test; 95% CI for difference 0.23–3.13, by bootstrap sampling].
Interestingly, however, from a purely information-theoretical mathematical standpoint, it appears that the random strategy is more efficient than the systematic strategy. (Here it is important to keep in mind that we mean the participants’ queries in games in which the first query was not all of a single item, which could differ from a theoretical strategy of picking among all feasible codes with equal probability). The code was mathematically determined with a smaller number of queries in games with the random strategy, as compared to the systematic strategy [t(134) = −4.17, p < 0.0001, two-tailed t-test; 95% CI for difference 0.66 to 1.83, by bootstrap sampling].
It is thus something of a paradox that the most informative queries for people are not those that lead mathematically to identifying the true code in the most efficient manner. We consider possible explanations below.
Of the 68 games in which help was offered, help was accepted in only 30 games. This supports the findings of previous research that students don’t always utilize opportunities for help (Aleven and Koedinger, 2000) or even recognize that help would be beneficial (Aleven et al., 2003).
Some possible explanations for this finding draw upon research around threat to identity and self-concept. For some participants asking for or accepting help may be harmful to their self-concept (Delacruz, 2011), thus discouraging them from engaging in help seeking strategies, to the detriment of their learning (Nelson-Le Gall, 1985). It is often the most able learners who seek help when they reach an impasse, perhaps as their academic self-concept is more robust, whereas those with lower abilities appear to have a lower academic self-concept and subsequently, less awareness of their need for help and/or less willingness to accept help when offered (Wood and Wood, 1999).
Alternatively, stereotype threat should also be considered as a possible explanation for the paucity of help seeking we observed. It is possible that participants may have associated the Mastermind game with mathematics, either through previous knowledge, or through the language used by the experimenter, for instance when mentioning “probabilities” while explaining the game. It is thought that girls perform more poorly at tasks associated with maths due to the activation of the stereotype that boys are more competent at maths (Casad et al., 2017). Our participants were mostly female; therefore, it is possible that their help seeking behaviors were blocked due to believing that Mastermind was a maths game.
A caveat is that in the present study, although participants were told that the aim of the game is to complete the code in as few guesses as possible, there was no explicit external incentive for doing so. It is thus possible that participants may have chosen to continue figuring the code out for themselves because they enjoyed playing the game.
A further consideration is that participants may have been primed to ask for help due to the experimenter telling them help was available if they felt stuck in the help condition. Participants were allowed to ask for help at any point, however, and our results are consistent with prior help seeking research.
Due to the strong links between help seeking behavior and learning and educational attainment (Ryan et al., 1998), our findings have strong implications for educational practice. The findings show that when help is asked for, in many situations all the necessary information had been obtained. Thus, help is not needed for acquiring the necessary information but rather for deciphering the information that had already been obtained. An interesting direction for further research would be to investigate the effects of different types of help. One possibility would be to offer help in the form of highlighting aspects of previous queries and feedback to help the participant decipher the information, rather than giving the position of a specific item in the code. Another possibility would be to have help available from a computer, rather than from a person.
The present study also supported previous research that highlights that help is not always taken advantage of by students, even though it would be beneficial to advance their learning. Further research is needed to determine the influence of stereotype threat, threat to self-concept, and other variables on help-seeking behavior and to identify other factors that may also be important. One idea for further studies is to investigate whether rewarding participants for completing the code in the fewest number of guesses (e.g., paying them according to performance, or giving the participant with the fewest average number of guesses £50) may lead to different patterns of help seeking. These manipulations would clarify whether willingness to ask for help can be increased if the stakes are high enough, thus informing educational practices to improve help seeking and overall student attainment.
One theme in Bayesian modeling is that people will find the best fitting hypothesis for the data available to them. When our participants asked for help they typically already had all the necessary information to complete the code. Why is this? It is something of a paradox that despite being in possession of all of the information needed to decipher the code, participants were in many cases unable to do so.
Research on human queries and human assessments of queries’ expected usefulness, in the Optimal Experimental Design perspective (Baron et al., 1988; Oaksford and Chater, 1994; Coenen et al., 2018) has usually found that people have a very good, if not necessarily a perfect, sense of the relative usefulness of possible queries. From this standpoint it is surprising that participants tended to ask for help late in the game, rather than early in the game, when help would– from a mathematical standpoint– provide the most information. One crucial point is that this research, in the vast majority of experimental tasks, including Schulz et al.’s (2019) information-theoretic model of Entropy Mastermind, uses the complete probability distribution when modeling human behavior.
Interestingly, computer science approaches to Mastermind, except for fairly small versions of the task (e.g., Knuth, 1976), do not attempt to represent the full probability distribution over possible codes. Here we focus on computer-science approaches; for a more mathematical treatment of bounds on the efficiency of possible solutions, see Doerr et al. (2013). Computer science approaches typically focus on finding one or more possible codes from the feasible set of codes that are consistent with the queries and feedback to date. Berghman et al. (2009) use genetic algorithms to find codes in the feasible set. Cotta et al. (2010) use a similar approach, but specifically attempt to find feasible codes that will maximize obtained information, thus building on Bestavros and Belal’s (1986) ideas. Merelo et al. (2011) further introduce the idea of endgames, namely looking for particular game situations in which known strategies can be used. Merelo-Guervós et al. (2013) combine an improved genetic algorithm with an entropy-based fitness score to evaluate the usefulness of possible queries.
If people (as we strongly suspect) are not fully representing the possible codes in smaller versions (e.g., with 6^4 = 1296 possible codes) of the game, it would be sensible in the future to see whether these computer science approaches might offer good insight into human behavior. For instance, unless guesses are repeated, the proportion of feasible codes relative to possible codes is guaranteed to decrease over the course of a game. Of particular note will be to check whether these approaches therefore take longer to find items to test in later stages of the game, thus providing a possible resolution to the paradox of humans’ greater tendency to ask for help when there is less information (in terms of bits) to be obtained.
Model variants along these lines would very much be in the spirit of boundedly Bayesian models (Griffiths et al., 2015; Lieder and Griffiths, 2019), in which the focus is on keeping models within the broadly probabilistic framework but incorporating computational resource limitations. On other concept learning tasks, for instance the Shepard et al. (1961) task, participants also need many more learning trials than would be mathematically required if they have perfect memory (Rehder and Hoffman, 2005); some models (Nelson and Cottrell, 2007) use conservative (Edwards, 1968) belief updating to model this process. If Mastermind is viewed as a concept learning task, then the fact that some participants require additional queries, beyond those mathematically necessary to infer the code, is not necessarily surprising. As a point of comparison, Merelo-Guervós et al. (2013) report a variety of algorithms that can solve a larger version of the game than we used, namely with codelength 6 and 9 possible colors (i.e., with 9^6 = 531,441 possible codes), with a mean of less than 7 queries, achieving much better performance than our participants.
A further potential connection between human psychology and computer science approaches starts with research on information foraging (Pirelli and Card, 1999). Information foraging describes the decision-making process in problem solving when the information is incomplete and the probabilities are unclear (Murdock et al., 2017). Attempts to solve these types of cognitive problems involve tradeoffs between “exploration” of novel information and using or “exploiting” knowledge to improve performance (Berger-Tal et al., 2014). How does this relate to Mastermind? Mastermind, from a purely mathematical standpoint involves a well-defined problem: both how the hidden code is generated, and the processes by which one can find the code, are known and disclosed to the player. (We refer here to non-strategic versions of Mastermind). However, people may not have this full information (such as a probability distribution over several thousand possible codes) ready at hand. One possible point of connection to information foraging theory is in the search for new items to possibly test. Many computer science models use genetic algorithms with populations of possible query items which are thought or known to be in the feasible set. An issue in the computer science literature is when to try to improve the population of known query items through genetic algorithms, and when to search for new items altogether. This parallels issues of search in human memory (Hills et al., 2008), when people either try to exploit a current semantic region (e.g., to continue finding feline animals, after they have found cat, lion, tiger, lynx) or to explore for a new region altogether.
Then there is the paradox that among the two qualitative strategies that we identified, namely the systematic strategy and the random strategy, the systematic strategy was perhaps more useful for human participants, but the random strategy was clearly more useful from a purely information-theoretic standpoint, leading to the true code being determined with fewer queries. Our finding on this parallels earlier work by Laughlin et al. (1982), who studied a reduced version of Mastermind with 3 possible colors and 4 positions, entailing 3^4 = 81 possible codes. They found that human players did better when their first query was all of a single color, even though computers could solve the game more quickly when the first query had two items of one color, and one item of each of two other colors. Why do we find these discrepancies between theoretical usefulness (for computers) of particular strategies, and those strategies’ actual usefulness to human game players? What makes particular queries– or more precisely, particular query-feedback combinations– easier or harder for people to assimilate? Are there parallels between what queries are easier or harder for people to assimilate, and what is easier or harder for particular computer science approaches to the task? One possibility to consider is that people may have their beliefs in a psychological feature space, and may best assimilate query-feedback combinations that are directly relevant to that feature space. A prominent possibility here would be that people appear to focus on figuring out the counts of each color (or type of item), and all-same-color queries are easily suited to this kind of belief update. A focus on psychological feature spaces would be analogous to the successful (Bramley et al., 2017) approach to causal learning. It would also be worthwhile to investigate whether the epistemic logical model of inference in Deductive Mastermind (Zhao et al., 2018), in which participants are given a game state that uniquely identifies the true code, also finds the random strategy to be more difficult than the systematic strategy.
Finally, why is it that many (but not all) participants tended to need several additional queries, beyond the point where the code was mathematically determined? This is a kind of opposite result to Wason’s (1960) finding that participants tended to prematurely announce that they had figured out the hidden rule in his “2-4-6” scientific inference task, suggesting that participants on that task overestimated the information value of the information they had received. For Mastermind, it seems that imperfect memory or conservative belief updating (Edwards, 1968; Dasgupta et al., 2020) needs to be incorporated into probabilistic task models.
Ultimately, whereas the focus of the present work was on empirically characterizing help-seeking behavior in Entropy Mastermind, we hope that it will be possible to build probabilistic or other cognitively meaningful models of people’s behavior on this task. Such models may also serve development of individually customized, adaptive tutoring systems, which is a pressing issue in cognitive science and educational research alike (Anderson et al., 1995; Bertram, in press).
The dataset for this study is posted on the Open Science Framework, https://osf.io/q5rct/, 10.17605/OSF.IO/Q5RCT.
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. The patients/participants provided their written informed consent to participate in this study.
NT, MH, and JN conceptualized and designed the experiment, and wrote the manuscript. NT conducted the experiment. NT and JN analyzed the data. All authors contributed to the article and approved the submitted version.
This research was supported by the grant NE 1713/1–2 from the Deutsche Forschungsgemeinschaft (DFG) as part of the priority program New Frameworks of Rationality (SPP 1516), and by a University of Surrey Faculty Development grant to JN.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Anselm Rothe, Bonan Zhao, Elif Özel, Eric Schulz, Lara Bertram, Laura Martignon, and Neil Bramley provided very helpful ideas on this work.
Aleven, V., and Koedinger, K. R. (2000). “Limitations of student control: Do students know when they need help?,” in Proceedings of the 5th International Conference on Intelligent Tutoring Systems, ITS 2000, eds C. F. G. Gauthier and K. VanLehn, (Berlin: Springer-Verlag), 292–303.
Aleven, V., Stahl, E., Schworm, S., Fischer, F., and Wallace, R. (2003). Help seeking and help design in interactive learning environments. Rev. Educat. Res. 73, 277–320.
Anderson, J. R., Corbett, A. T., Koedinger, K. R., and Pelletier, R. (1995). Cognitive tutors: lessons learned. J. Learn. Sci. 4, 167–207.
Baron, J., Beattie, J., and Hershey, J. C. (1988). Heuristics and biases in diagnostic reasoning: II. Congruence, information, and certainty. Organ. Behav. Hum. Decis. Proc. 42, 88–110.
Berger-Tal, O., Nathan, J., Meron, E., and Saltz, D. (2014). The exploration-exploitation dilemma: a multidisciplinary framework. PLoS One 9:e95693. doi: 10.1371/journal.pone.0095693
Berghman, L., Goossens, D., and Leus, R. (2009). Efficient solutions for Mastermind using genetic algorithms. Comput. Operat. Res. 36, 1880–1885.
Bertram L. (in press). Digital learning games for mathematics and computer science education: the need for preregistered RCTs, standardized methodology and advanced technology. Front. Educ.
Bestavros, A., and Belal, A. (1986). “Mastermind: a game of diagnosis strategies,” in Bulletin of the Faculty of Engineering, (Alexandria: Alexandria University).
Bramley, N. R., Dayan, P., Griffiths, T. L., and Lagnado, D. A. (2017). Formalizing Neurath’s ship: Approximate algorithms for online causal learning. Psychol. Rev. 124, 301–338. doi: 10.1037/rev0000061
Bruner, J. S., Goodnow, J. J., and Austin, G. A. (1956). A Study of Thinking. New York, NY: John Wiley and Sons, Inc.
Burgoyne, A. P., Sala, G., Gobet, F., Macnamara, B. N., Campitelli, G., and Hambrick, D. Z. (2016). The relationship between cognitive ability and chess skill: a comprehensive meta-analysis. Intelligence 59, 72–83.
Casad, B. J., Hale, P., and Wachs, F. L. (2017). Stereotype threat among girls: differences by gender identity and math education context. Psychol. Women Q. 41, 513–529.
Chater, N., Tenenbaum, J. B., and Yuille, A. (2006). Probabilistic models of cognition: conceptual foundations. Trends Cogn. Sci. 10, 287–291.
Coenen, A., Nelson, J. D., and Gureckis, T. M. (2018). Asking the right questions about the psychology of human inquiry: nine open challenges. Psychon. Bull. Rev. 26, 1548–1587. doi: 10.3758/s13423-018-1470-5
Cotta, C., Merelo Guervós, J. J., Mora Garćia, A. M., and Runarsson, T. P. (2010). “Entropy-driven evolutionary approaches to the mastermind problem,” in Parallel Problem Solving from Nature, PPSN XI. PPSN 2010. Lecture Notes in Computer Science, eds R. Schaefer, C. Cotta, J. Kołodziej, and G. Rudolph (Berlin: Springer), 6239, 421–431. doi: 10.1007/978-3-642-15871-1_43
Dasgupta, I., Schulz, E., Tenenbaum, J. B., and Gershman, S. J. (2020). A theory of learning to infer. Psychol. Rev. 127, 412–441.
Delacruz, G. C. (2011). Games as formative assessment environments: Examining the impact of explanations of scoring and incentives on math learning, game performance, and help seeking. Dissert. Abstr. Int. A 72, 1170.
Doerr, B., Doerr, C., Spöhel, R., and Thomas, H. (2013). Playing Mastermind with Many Colors. Available at: https://arxiv.org/abs/1207.0773
du Boulay, B., Luckin, R., and del Soldato, T. (1999). “The plausibility problem: Human teaching tactics in the ‘hands’ of a machine,” in Artificial Intelligence in Education, Open Learning Environments: New Computational Technologies to Support Learning, Exploration, and Collaboration, Proceedings of AIED-99, eds S. P. Lajoie and M. Vivet, (Amsterdam: IOS Press), 225–232.
Eberhardt, F., and Danks, D. (2011). Confirmation in the cognitive sciences: the problematic case of Bayesian models. Minds Machin. 21, 389–410.
Eddy, D. M. (1982). “Probabilistic reasoning in clinical medicine: problems and opportunities,” in Judgment Under Uncertainty: Heuristics and Biases, eds D. Kahneman, P. Slovic, and A. Tversky, (Cambridge: Cambridge University Press).
Edwards, W. (1968). “Conservatism in human information processing,” in Formal Representation of Human Judgment, ed. B. Kleinmuntz, (New York, NY: John Wiley), 17–52.
Gierasimczuk, N., van der Maas, H. L., and Raijmakers, M. E. (2012). “Logical and psychological analysis of deductive mastermind,” in ESSLLI Logic & Cognition Workshop, Opole, 1–13.
Gierasimczuk, N., van der Maas, H. L., and Raijmakers, M. E. (2013). An analytic tableaux model for deductive mastermind empirically tested with a massively used online learning system. J. Logic Lang. Inf. 22, 297–314.
Griffiths, T. L., Lieder, F., and Goodman, N. D. (2015). Rational use of cognitive resources: levels of analysis between the computational and the algorithmic. Top. Cogn. Sci. 7, 217–229. doi: 10.1111/tops.12142
Hills, T. T., Todd, P. M., and Goldstone, R. L. (2008). Search in external and internal spaces: evidence for generalized cognitive search processes. Psychol. Sci. 19, 802–808.
Hopfinger, J. B., and Mangun, G. R. (2001). Electrophysiological studies of reflexive attention. Adv. Psychol. 133, 3–26.
Jones, M., and Love, B. C. (2011). Bayesian fundamentalism or enlightenment? On the explanatory status and theoretical contributions of Bayesian models of cognition. Behav. Brain Sci. 34, 169–188.
Kharratzadeh, M., and Shultz, T. (2016). Neural implementation of probabilistic models of cognition. Cogn. Syst. Res. 40, 99–113.
Laughlin, P. R., Lange, R., and Adamopoulos, J. (1982). Selection strategies for “mastermind” problems. J. Exp. Psychol. 8, 475–483.
Lieder, F., and Griffiths, T. L. (2019). Resource-rational analysis: understanding human cognition as the optimal use of limited computational resources. Behav. Brain Sci. 43:e1. doi: 10.1017/S0140525X1900061X
Merelo, J. J., Cotta, C., and Mora, A. (2011). “Improving and scaling evolutionary approaches to the mastermind problem,” in Applications of Evolutionary Computation. EvoApplications 2011. Lecture Notes in Computer Science, eds C. Di Chio et al. (Berlin: Springer), 6624, 103–112. doi: 10.1007/978-3-642-20525-5_11
Merelo-Guervós, J. J., Castillo, P., Mora García, A. M., and Esparcia-Alcázar, A. I. (2013). “Improving evolutionary solutions to the game of MasterMind using an entropy-based scoring method,” in Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam, 829–836.
Murdock, J., Allen, C., and DeDeo, S. (2017). Exploration and exploitation of Victorian science in Darwin’s reading notebooks. Cognition 159, 117–126.
Nelson, J. D. (2005). Finding useful questions: on Bayesian diagnosticity, probability, impact, and information gain. Psychol. Rev. 112, 979–999. doi: 10.1037/0033-295X.112.4.979
Nelson, J. D., and Cottrell, G. W. (2007). A probabilistic model of eye movements in concept formation. Neurocomputing 70, 2256–2272.
Newell, A., and Simon, H. A. (1988). “Problem solving,” in Readings in Cognitive Science: A Perspective from Psychology and Artificial Intelligence, eds A. Collins and E. E. Smith, (San Mateo, CA: Morgan Kaufmann).
Newman, R. S. (1994). “Adaptive help seeking: a strategy of self-regulated learning,” in Self-regulation of Learning and Performance: Issues and Educational Applications, eds D. H. Schunk and B. J. Zimmerman, (Hillsdale, NJ: Lawrence Erlbaum Associates, Inc), 283–301.
Oaksford, M., and Chater, N. (1994). A rational analysis of the selection task as optimal data selection. Psychol. Rev. 101:608.
Price, T. W., Catete, V., Liu, Z., and Barnes, T. (2017). “Factors influencing students’ help-seeking behavior while programming with human and computer tutors,” in Proceedings of the International Computing Education Research Conference, Tacoma, WA.
Rehder, B., and Hoffman, A. B. (2005). Eyetracking and selective attention in category learning. Cognit. Psychol. 51, 1–41.
Roberts, M. J. (1993). Human reasoning: deduction rules or mental models, or both? Q. J. Exp. Psychol. A 46A, 569–589.
Ryan, A. M., Gheen, M. H., and Midgley, C. (1998). Why do some students avoid asking for help? An examination of the interplay among students’ academic efficacy, teachers’ social-emotional role, and the classroom goal structure. J. Educ. Psychol. 90, 528–535.
Schulz, E., Bertram, L., Hofer, M., and Nelson, J. D. (2019). “Exploring the space of human exploration using Entropy Mastermind,” in Proceedings of the 41st Annual Conference of the Cognitive Science Society, Montreal, QC, doi: 10.1101/540666
Shepard, R. N., Hovland, C. I., and Jenkins, H. M. (1961). Learning and memorization of classifications. Psychol. Monogr. 75, 1–42.
Simon, H. A., and Newell, A. (1971). Human problem solving: the state of the theory in 1970. Am. Psychol. 26, 145–159.
Smith, E. E. (2001). “Cognitive psychology: history,” in International Encyclopaedia of the Social and Behavioral Sciences, eds N. J. Smelser and P. B. Baltes, (Oxford: Pergamon), 2140–2147.
Strom, A. R., and Barolo, S. (2011). Using the game of mastermind to teach, practise and discuss scientific reasoning skills. PLoS Biol. 9:e10000578. doi: 10.1371/journal.pbio.1000578
Wason, P. C. (1960). On the failure to eliminate hypotheses in a conceptual task. Q. J. Exp. Psychol. 12, 129–140.
Wason, P. C. (1977). “Self-contradictions,” in Thinking: Readings in Cognitive Science, eds P. N. Johnson- Laird and P. C. Wason, (Cambridge: Cambridge University Press).
Weisberg, R. W. (2015). Toward an integrated theory of insight in problem solving. Think. Reason. 21, 5–39.
Wood, H., and Wood, D. (1999). Help seeking, learning and contingent tutoring. Comput. Educ. 33, 153–169.
Zhao, B., van de Pol, I., Raijmakers, M., and Szymanik, J. (2018). “Predicting cognitive difficulty of the deductive mastermind game with dynamic epistemic logic models,” in Proceedings of the 40th Annual Conference of the Cognitive Science Society, eds C. Kalish, M. Rau, J. Zhu, and T. Rogers (Austin: Cognitive Science Society), 2789–2794.
Keywords: help-seeking, Bayesian reasoning, mathematical games, Optimal Experimental Design theory, information-seeking behavior
Citation: Taylor N, Hofer M and Nelson JD (2020) The Paradox of Help Seeking in the Entropy Mastermind Game. Front. Educ. 5:533998. doi: 10.3389/feduc.2020.533998
Received: 10 February 2020; Accepted: 24 August 2020;
Published: 23 September 2020.
Edited by:
Karin Binder, University of Regensburg, GermanyReviewed by:
Juan Julián Merelo, University of Granada, SpainCopyright © 2020 Taylor, Hofer and Nelson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jonathan D. Nelson, bmVsc29uQG1waWItYmVybGluLm1wZy5kZQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.