- 1Department of Early Childhood and Elementary Education, Murray State University, Murray, KY, United States
- 2Department of Educational Studies, Leadership and Counseling, Murray State University, Murray, KY, United States
Supporting growth in problem solving is key to capacity development for both teachers and students. When teachers engage in rich academic conversations that inquire deeply into content and pedagogy, they have an opportunity to cultivate student capacity to engage in rich academic discourse, problem solving and mathematical learning. In this study, we examined an intensive professional development training intervention in which teacher participants learned to use and understand the Teaching Learning Community (TLC) approach, design and connect standards-based lessons, and nurture a mindset of learning and thinking like a problem solver among students and teachers alike. We further examined whether there were any differences in students' MAP test scores over time among students whose teachers participated in the intervention and students whose teachers did not participate. Findings from the Analysis of Variance of students' MAP test scores indicated that students whose teachers participated in the intervention demonstrated more growth in mathematical proficiency, particularly in Grade 3. Thus, implementing an intervention like the one described herein that provides the appropriate resources to teachers, education in the form of high-quality professional development, and an opportunity to collaborate with peers and experts can result in direct improvement to student achievement in math.
Introduction
Is it possible to create change in a school mathematics curriculum delivery? What interventions can be provided for teachers to build their own capacity and support their students' building numeracy skills all at the same time? In this study, interviews with four elementary principals revealed a need to build strong student numeracy skills including problem solving in order to provide a smooth transition to fourth grade with higher stakes testing. Vygotsky's (1978) sociocultural theory contends that children grow into the intellectual community that surrounds them. In order to prepare students for life-long learning, the focus of education needs to be on learning to acquire knowledge, create, innovate, communicate, and discern. For teachers, that means facilitating robust learning habits in their students. When teachers engage in rich academic conversations that inquire deeply into content and pedagogy, they have a better shot at cultivating student capacity to engage in rich academic discourse (West and Cameron, 2013). In order to build such capacity, teachers are ideally charged with having deep and flexible knowledge about the content they teach and how their students learn that content.
Ma (2010) describes the development of teachers' understanding of school mathematics as “a process with a series of interactions: between considerations of what one should teach and how to teach it; among colleagues; between teachers and students; and between one's interest in mathematics as a teacher and as a layperson or mathematician” (p. 41). Additionally, building number sense in children is fundamental for their growth in mathematical reasoning. But the extent to which building number sense “becomes an individual's major talent still rests with the type and strength of genetic input and the environment in which the individual grows and learns” (Sousa, 2015, p. 12). Number sense is often discussed in math education, but what is it? Fennell and Landis (1994) state, “Number sense is an awareness and understanding about what numbers are, their relationships, their magnitude, the relative effect of operating on numbers, including the use of mental mathematics and estimation” (Parrish, 2010, p. 35–36). Developing a healthy sense of numbers is essential to building a confident mathematical learner in grades K-3 while connecting with future mathematical productivity.
What about the role of mathematical proficiency? In order to build capacity through building numeracy mathematical proficiency is key. In their book, Kipatrick et al. (2001) reported five “interwoven and interdependent” stands, which have implications for “how students acquire mathematical proficiency, how teachers develop that proficiency in their students, and how teachers are educated to achieve that goal” (p. 5). The five stands are “conceptual understanding,” “procedural fluency,” “strategic competence,” “adaptive reasoning,” and “productive disposition” (Kipatrick et al., 2001, p. 5). Furthermore, when children are in classrooms where these strands of proficiency are developed together, they are able to build a stronger understanding of both mathematical concepts and procedures (Walle et al., 2018). When supported by knowledgeable and caring teachers, mathematical proficiency builds capacity for future learning and connections.
To explore the development of an intervention for building students' numeracy and mathematical proficiency, a Midwestern university implemented a 2-years project, entitled “Supporting Strategies for Building Numeracy in Grades K-3,” that focused on building capacity of educators to identify and support high-level instructional practices that result in improved mathematical learning in the elementary grades. Specifically, the project sought to prepare teachers and students in building numeracy. The 2-years grant project targeted four elementary schools in two rural school districts in the United States. Participants included four administrators and 26 teachers of Grades K-3 in Year 1 of the grant. Year 2 of the grant project included three of the same administrators and one new administrator. Year 2 of the grant retained 17 of the teachers from Year 1 and added eight new teachers.
The focus of the project was initially established through interviews with principals at four schools that revealed patterns of concern regarding a lack of problem-solving skills and a decrease in state testing scores between third and fourth grades. From this, the project investigators identified the following patterns of needs in mathematics education: focusing on number sense in the early grades; preparing K-3 students and their teachers to be problem solvers; and supporting and guiding students in formulating their own mathematical questions. The investigators then designed and implemented the project to meet these needs.
During the 2015 through 2017 school years, teacher participants took part in an intensive training process to acquire and then apply knowledge and skills in mathematics to build numeracy and capacity for productive, meaningful, and successful teaching and learning. Interventions for the teachers included full- and half-day professional development seminars with experts in the mathematical education field. As part of the training, participating teachers experienced co-teaching with mathematics teaching experts, mathematics professors from state universities and their own colleagues. They also took time to slow down and meet in reflective focus groups twice each school year. Substitute teachers were provided for collaborations, allowing the participating teachers to meet and talk, observe each other in the classroom settings, and work in small groups with a mathematical expert to develop and connect strategies to build capacity.
Components of the Intervention
The training intervention involved several important components. The first was helping teachers develop an understanding of the Teaching Learning Community (TLC) approach to building numeracy. The content coaching model of Plan, Teach, and Debrief was utilized. Content coaching is a process designed to cultivate rigorous, collaborative, professional learning habits among adults (West and Cameron, 2013). Throughout the span of the project, participating teachers interacted and processed their new learning through content coaching in their own classrooms with experts. Additionally, the teachers observed colleagues and experts, wrote collaborative lesson plans, shared on a teacher-initiated Facebook page, and completed various formative evaluations. Feedback was provided throughout from the math expert, debriefings, pre-planning collaborative sessions, and the actual collaborating teaching experiences both formal and informal. Timely, specific feedback is one of the most effective ways to ensure learning at any age (Hattie and Timperly, 2007). Providing feedback in non-threatening settings such as small expert groups and in the classroom supports teacher growth in implementing new strategies.
A second component is the mathematical landscape. The mathematical landscape provided many new teaching opportunities for both teachers and their students including teaching with mini-lessons, using new models, landmark strategies, and focusing on the big ideas. Teachers found more opportunities to discuss the math with their colleague and their own students. Teachers began to understand the value of teaching in small groups. These small group lessons provided opportunities to directly see how their students actually interacted and responded to the math questions. Teachers noticed error patterns in these small groups that they had not noticed before in the traditional whole class settings. Teachers could address misconceptions “in the moment” not when they were grading paper later. A few of the strategies that were new to the teachers included bead-strings for counting and grouping, problem solving situations, the use of thinking strategies such as “true or not true,” using “number strings,” use of the open number line, using small group focused mini-lessons, and many more. For example, repetitive drill and practice are typically used to help students master the operations of multiplication. Students need to understand “what it means to multiply and divide before the facts can become automatic, but understanding does not necessary lead to this automaticity” (Uittenbogaard and Fosnot, 2007, p. 6–7). To somewhat counter and support at the same time what Uittenbogarrd stated, Boaler stated, “My lack of memorization has never held me back at any time or place in my life, even though I am a mathematics professor, because I had number sense, which is more important for students to learn and includes learning of math facts along with deep understanding of numbers and the ways they relate to each other” (Boaler, 2016, p. 38). She goes on the say that “for about one-third of students, the onset of timed testing is the beginning of math anxiety” (Boaler, 2016, p. 38). Slowing down in the math process was supported by both teachers and students as they solved problems together.
A third component is standard-based lesson planning. Teacher participants were taught to design and connect standards-based lessons to mathematical learning using the National Council of Teachers of Mathematics (National Council of Teachers of Mathematics, 2014) Process Standards. These standards, which outline the mathematical processes through which pre-K-12 students acquire and use mathematical knowledge, should not be regarded as separate content or strands in the mathematics curriculum; rather, they are integral components of all mathematics learning and teaching (Walle et al., 2016). These direct classroom interventions provided valuable models for the teachers to connect to their own future lessons. Participants then wrote practice lesson plans and submitted them for program evaluation and formative feedback that included the process standards. Not only did they write the plans, but they collaborated in their planning within schools, between schools, and with the experts. This model parallels Schmoker's school reform recommendation: small groups of teachers working in collaborative learning communities focused on day-to-day instruction that leads to short-term goals of student improvement (Stewart and Brendefur, 2005). Teacher participants focused upon incorporating the NCTM's Standards for Mathematical Practice (SMP) into their daily mathematical routines for teaching and learning. The SMP go beyond specifying mathematics content expectations to also outline proficiencies. These tenets are based on the underlying frameworks of the NCTM process standards and the components of mathematical proficiency identified by the National Research Council (Walle et al., 2016). Unfortunately, the SMP are often overlooked because they are not directly embedded into any grade-level standards. They are intended to be overarching standards used and taught throughout all grades (Aungst, 2016). In the intervention project, teacher participants incorporated the SMP in every lesson plan created either solely by the teachers or in collaboration with experts and colleagues. The SMP supported the development and the depth of learning by both teachers and their students.
Building Students' Mathematical Thinking
Teacher participants benefitted from learning to nurture students in developing a mindset of learning and thinking like a problem solver. According to Burns (2015), solving problems is the ultimate reason for students to study mathematics. It is likely that all of today's students will face problems to solve “that call for reasoning mathematically” (Burns, 2015, p. 41). Mathematical learning should focus on “developing understanding of concepts and procedures through problem solving, reasoning, and discourse” (Leinwant et al., 2014, p. 11). The intervention aimed at supporting teacher participants in helping their student to be a lifelong problem solver. Teacher participants were guided in applying mathematical thinking mindset as defined by Dweck (2006) and Boaler (2016) in their own classrooms. A shift in the teacher participants' own willingness to share their mathematical thinking processes through the 2-years period of the grant project was positively noticed in the focus groups with the teachers and in professional development events. In the present study, we examined the effect of enhancing teachers' competence in building numeracy on their students' mathematical thinking as measured by test scores. Our specific research question is as follows: Are there any differences in students' mathematical thinking test scores over time among students whose teachers participated in the intervention and students whose teachers did not participate?
Methods
Data Source
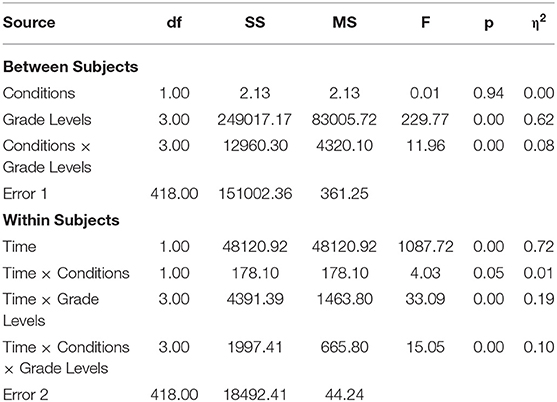
The project was conducted and reviewed in accordance with the rules and regulations of the funding agency (Kentucky Department of Education). All teacher and administrator participants reviewed the proposed activities related to the project and evaluation, and gave written informed consent to participation, including providing access to student assessment data (anonymous and non-identifiable to project staff). Student assessment was planned and administered by schools independent of their participation in the project. One type of student assessments used by the four participating schools is Measures of Academic Progress (MAP) testing. The MAP is a standardized test used by the participating school districts during the fall, winter, and spring of every school year except one school's kindergarten. Student MAP data was used for the present study. The use of student data did not require further consent to be obtained as these data were provided by the schools to the authors in an anonymous and non-identifiable format. The separate files from each participating school were then merged together using SPSS version 23.0 for further analyses. The merged dataset had 343 students whose teachers participated in the intervention and 53 students whose teachers did not participate in the intervention. Out of the 343 students, 53 students were in kindergarten; 110 first grade; 64 second grade; and 116 third grade. For the 53 students whose teachers did not participate in the intervention (the control group), 18 students were in kindergarten; 21 first grade; 21 second grade; and 23 third grade.
Variables
Student MAP test score. MAP testing is developed by Northwest Evaluation Association (NWEA), a not-for-profit organization that produces assessment solutions that precisely measure growth and proficiency. The student MAP test score ranges from about 100 to 300. The MAP testing is known for its validity and reliability in measuring student mathematical proficiency.
Condition. Students whose teachers participated in the year-long training were placed in the intervention group while students whose teachers did not participate were placed in the control group.
Time. Student MAP test scores (anonymous and non-identifiable) from Fall 2016, Winter 2016, and Spring 2017 were analyzed.
Results
The means and standard deviations of student MAP test scores arranged by grade level (K, 1, 2, and 3) in two different conditions (intervention and control) at the three testing times (fall, winter, and spring) are shown in Table 1. The third-grade treatment group showed more growth in mathematical achievement than its respective control group. The kindergarten and second-grade treatment groups did not show much difference when compared to their control groups. The first-grade treatment group showed a slight advantage over its control group.
Table 1. Means and standard deviations for student MAP test scores by grade levels in intervention and control conditions at three testing times.
A mixed-method ANOVA was conducted with time (Time 1, Time 2, and Time 3) as a within-subjects factor and conditions (intervention vs. control) and grade levels (K, 1, 2, and 3) as between-subjects factors. Table 2 summarizes analysis of variance (ANOVA) results.
The ANOVA revealed that the main effect for time was statistically significant: F(1,418) = 1087.72, p < 0.001, η2 = 0.72. The main effect of grade level was also statistically significant: F(31,418) = 229.77, p < 0.001, η2 = 0.62. Further, the within-subjects Time × Grade Levels interaction was statistically significant: F(3,418) = 33.09, p < 0.001, η2 = 0.19. Moreover, the within-subjects Time × Conditions × Grade Levels interaction was statistically significant: F(3,418) = 15.05, p < 0.001, η2 = 0.10. Finally, the between-subjects Conditions × Grade Levels was statistically significant: F(3,418) = 11.96, p < 0.001, η2 = 0.08. All other main effects and interactions were non-significant.
Discussion
In this study, we examined whether there were any differences in students' MAP test scores over time among K-3 students whose teachers participated in the intervention and students whose teachers did not participate. The sample number in each grade groups are not the same. The sample number in the third-grade groups was the highest. Our findings indicated students whose teachers participated in the intervention demonstrated more growth in mathematical proficiency, particularly in Grade 3. One plausible explanation is that the third-grade groups and their teachers had more at stake than the K, 1, or 2 groups since mandated testing and comparisons begin at grade 3 at the state level in the area of mathematics. In a way, testing, especially high-stake testing affects teaching and learning. It could be true that compared with K-2 teachers in our study, the third grade teachers in our study had a higher motivation to help their students in mastering mathematics. However, research also indicated that high-stake testing may lead to negative and undesirable outcomes as well. Possible negative impact includes “the superficial coverage of subject matters, the emphasis on basic skills that are arbitrarily defined and seldom add up to more complex learning, the focus on outcomes and evaluation rather than on assessing for promoting further learning, and the loss of professional standing for teachers and educators, as the provision of external information on students' achievement is prioritized over educators' knowledge and skills (e.g., Darling-Hammond, 1997; Elmore, 2004; Fuhrman, 2004; Afflerbach, 2005)” (Kontovourki and Campis, 2010, p. 236). Informal observations and focus group transcripts seemed to suggest a different explanation. Informal observations and focus group transcripts indicated a higher-level of engagement and collaboration from the third grade teachers overall. it is the authors' perspective that teachers who learned to fluently use the TLC approach, design and connect standards-based lessons, and nurture a mindset of learning and thinking like a problem solving mathematician are more likely to be able to build their students' numeracy.
Providing the appropriate resources and supports to teachers' education in the form of high-quality professional development, and an opportunity to collaborate with peers and experts has potential to make a difference. To replicate the training intervention designed in this project, the authors recommend the following: train teachers in the TLC approach or another Professional Learning Community approach to building numeracy; use the co-teaching model of Plan, Teach, and Debrief as suggested by the TLC approach; provide direct content coaching and side-by-side teaching experiences in an authentic classroom setting; create standards-based lessons incorporating the SMP including collaborative pre-planning, co-teaching, and then debriefing; provide opportunities for teachers to visit the classrooms of other teachers in their schools for math collaborations by placing substitute teachers in classroom for release time; and promote opportunities for teachers to participate in their own math problem solving and mathematical discourse with their peers and math experts. School administrators can support teachers by arranging times for teachers to meet informally to collaborate and have mathematical discourse; and nurture a mindset of thinking like a mathematician for teachers, students, and administrators. Creating a mathematical community of learners working together benefits all.
Limitations
We utilized non-equivalent control group pretest-posttest quasi-experimental design in the current study. One limitation of this quasi-experimental research design is that it is likely affected by the selection threat to the validity. In the study, teachers and students were not randomly assigned to intervention (the TLC approach) and control groups. Preexisting differences in teachers and students could have contributed to the difference in the MAP test scores in the third grade or the non-significant differences in the MAP test scores in the K-2 grades. Second, students' numeracy in grades K-3 was measured by student MAP test score in this study. Additional instruments could be used to further corroborate the findings of this study. Third, the current study included only K-3 students in two rural school districts in the United States, results on the TLC approach may not be generalized to a larger population elsewhere. For future research, it is recommended that a more diverse sample, coupled with random assignment, could be used to further investigate the effect of the use of the TLC approach on enhancing teachers' competence in building students' numeracy. Moreover, it would be necessary to develop and use other valid and reliable instrument to measure students' numeracy.
Data Availability Statement
The datasets analyzed in this article are not publicly available. Requests to access the datasets should be directed to Yuejin Xu,eXh1QG11cnJheXN0YXRlLmVkdQ==.
Ethics Statement
The project was conducted and reviewed in accordance with the rules and regulations of the funding agency (Kentucky Department of Education). All teacher and administrator participants reviewed the proposed activities related to the project and evaluation, and gave written informed consent to participation, including providing access to student assessment data (anonymous and non-identifiable to project staff). Student assessment was planned and administered by schools independent of their participation in the project. The project used those existing student assessment data for project evaluation. The project evaluation study was reviewed and approved by the Murray State University Institutional Review Board. The use of student data did not require further consent to be obtained as these data were provided by the schools to the authors in a de-identifiable format.
Author Contributions
LP and YX made equal contributions to the funded research project on which this article is based. LP wrote the introduction and discussion section. YX wrote the method and results section. Both reviewed the paper.
Funding
This project was funded by Mathematics and Science Partnership, Kentucky Department of Education (PON2 540 1600000517 1), U.S.A.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We greatly acknowledge and appreciate our partnerships Northern Kentucky University, Western Kentucky University, Kentucky Center for Mathematics.
References
Afflerbach, P. (2005). National reading conference policy brief: high stakes testing and reading assessment. J. Lit. Res. 37, 151–162. doi: 10.1207/s15548430jlr3702_2
Aungst, G. (2016). 5 Principles of the Modern Mathematics Classroom: Creating a Culture of Innovative Thinking. Thousand Oaks, CA: Corwin.
Darling-Hammond, L. (1997). The Right to Learn: A Blueprint for Creating Schools that Work. San Francisco, CA: Jossey-Bass.
Dweck, C. S. (2006). Mindset: The New Psychology of Success: How we can Learn to Fulfill our Potential. New York, NY: Random House.
Elmore, R. F. (2004). “Conclusion: the problem of stakes in permanance-based accontability systems,” in Redesigning Accountabilit Sysems for Edcuation. eds S. H. Fuhrman and R.F. Elmore (New York, NY: Teachers College Press), 274–296.
Fennell, F., and Landis, T. (1994). Number Sense and Operation Sense, Windows of Opportunity: Mathematics for Students with Special Needs. Reston, VA: National Council of Teachers of Mathematics.
Fuhrman, S. H. (2004). “Introduction,” in Redesigning Accountability Systems for Education, eds S. H. Fuhrman and R. F. Elmore (New York, NY: Teachers College Press), 1–2.
Hattie, J., and Timperly, H. (2007). The power of feedback. Rev. Educ. Res. 77, 81–112. doi: 10.3102/003465430298487
Kipatrick, J., Swafford, J., and Findell, B. (2001). Adding it up: Helping Children Learn Mathematics. Washington, DC: National Academy Press.
Kontovourki, S., and Campis, C. (2010). Meaningful practice: test prep in a third-gade public school cassroom. Read. Teacher 64, 236–245. doi: 10.1598/RT.64.4.2
Leinwant, S., Brahier, D., and Huinker, D. (2014). Principles to Action: Ensuring Mathematical Success for All. Reston, VA: The National Council of Techers of Mathematics.
Ma, L. (2010). Knowing and Teaching Elementary Mathematics: Fundamental Mathematics in China and the United States. Abington, Oxon: Routledge.
National Council of Teachers of Mathematics. (2014). Principles to Actions: Ensuring Mathematical Success for all. Reston, VA: Author.
Parrish, S. (2010). Number Talks: Helping Children Build Mental Math and Computation Strategies. Sausalito, CA: Math Solutions.
Stewart, R. A., and Brendefur, J. (2005). Fusing lesson study and authentic achievement: a model for teacher collaboration. Phi Delta Kappan 86, 681–687. doi: 10.1177/003172170508600912
Uittenbogaard, W., and Fosnot, C. (2007). Minilessons for Early Multiplication and Division: A Yearlong Resource. Portsmouth, NH: Heinemann.
Vygotsky, L. S. (1978). Mind in Society: The Development of Higher Psychological Processes. Cambridge, MA: Harvard University Press.
Walle, J. A., Karp, K. S., and Bay-Williams, J. M. (2016). Elementary and Middle School Mathematics: Teaching Developmentally. Upper Saddle River, NJ: Pearson Education.
Walle, J. A., Lovin, L., Karp, K. S., and Bay-Williams, J. M. (2018). Teaching Student-Centered Mathematics: Developmentally Appropriate Instruction for Grades preK-2. 330. Hudson Street, NY: Pearson Education.
Keywords: elementary mathematics, mathematics education, content coaching, teacher learning community, mathematical thinking, numeracy
Citation: Patterson L and Xu Y (2020) Enhancing Teachers' Competence in Building Students' Numeracy in Grades K-3. Front. Educ. 5:31. doi: 10.3389/feduc.2020.00031
Received: 30 November 2019; Accepted: 12 March 2020;
Published: 03 April 2020.
Edited by:
Laura Macchi, University of Milan-Bicocca, ItalyReviewed by:
Paraskevi Papadopoulou, American College of Greece, GreeceEvangelia Karagiannopoulou, University of Ioannina, Greece
Copyright © 2020 Patterson and Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuejin Xu, eXh1QG11cnJheXN0YXRlLmVkdQ==
 Lynn Patterson
Lynn Patterson Yuejin Xu
Yuejin Xu