Corrigendum: Spatial Continuity Effect vs. Spatial Contiguity Failure. Revising the Effects of Spatial Proximity Between Related and Unrelated Representations
- 1Faculty of Humanities, Technische Universität Chemnitz, Chemnitz, Germany
- 2Max Planck Research Group “Rationality Enhancement”, Max Planck Institute for Intelligent Systems, Tübingen, Germany
The split-attention effect refers to learning with related representations in multimedia. Spatial proximity and integration of these representations are crucial for learning processes. The influence of varying amounts of proximity between related and unrelated information has not yet been specified. In two experiments (N1 = 98; N2 = 85), spatial proximity between a pictorial presentation and text labels was manipulated (high vs. medium vs. low). Additionally, in Experiment 1, a control group with separated picture and text presentation was implemented. The results revealed a significant effect of spatial proximity on learning performance. In contrast to previous studies, the medium condition leads to the highest transfer, and in Experiment 2, the highest retention score. These results are interpreted considering cognitive load and instructional efficiency. Findings indicate that transfer efficiency is optimal at a medium distance between representations in Experiment 1. Implications regarding the spatial contiguity principle and the spatial contiguity failure are discussed.
Introduction
A look at popular educational material reveals that diverse media are combined to teach a curriculum of learning content. Thereby, multiple representations of information are implemented to create a more varied and interesting learning environment. However, this implementation is often problematic. For example, graphics are presented separately in additional sections, and important notes are placed below these pictorial representations. This design refers to a broad spectrum of educational material, including schoolbooks and lecture notes. Furthermore, educational videos use a wide spectrum of information sources such as audio comments, textual information, and dynamic visualizations. These different representations need to be continuously analyzed and mentally integrated by learners in order to completely understand the learning content (e.g., Chandler and Sweller, 1991). Therefore, spatial arrangement of the representations of information must be considered, especially in a learning context. Information processing, integration and in consequence, learning is fostered when related representations are spatially integrated by the designer and/or close to each other (Clark and Mayer, 2008). This split-attention effect is an often-studied phenomenon in multimedia learning (e.g., Chandler and Sweller, 1992; Ginns, 2006; Owens and Sweller, 2008; Florax and Plötzner, 2010). Until now, it is difficult to give concrete design recommendations because investigations regarding the split-attention effect provide mixed results (Florax and Plötzner, 2010), cannot replicate the split-attention effect (Schmidt-Weigand et al., 2010), or highlight the benefits of a low spatial proximity between representations (Jarodzka et al., 2015). In order to determine boundary conditions for the split attention effect and to explain these mixed results, the current investigation focused on the spatial integration of texts and pictures. By manipulating spatial distance and integration of text-picture information, the aim of this study is to gain further insights into the emergence, expression, and boundary conditions of the split-attention effect.
Split-Attention and Cognitive Load Theory
Fundamental explanations for the split-attention effect are provided by the Cognitive Load Theory (Sweller, 1988; Kalyuga, 2011; Sweller et al., 2011; Kalyuga and Singh, 2016). The Cognitive Load Theory is an instructional framework theory for learning with multimedia and is based upon a memory system, postulated by Atkinson and Shiffrin (1968). The overall cognitive load during learning with media can be separated into three additive load facets (Sweller, 2011). First, the intrinsic cognitive load (ICL) comprises the complexity of the used learning material as well as learners' prior knowledge. The extraneous cognitive load (ECL) arises from the sub-optimal designs of the instructional material, such as the demand on learners to spread their attention across different information. These two facets provide the basis for element interactivity. According to Sweller (2010), in instructional materials with low element interactivity, elements can be learned with minimal reference to other elements. This results in a low working memory load (e.g., learning vocabularies). In materials with high element interactivity, elements heavily interact and cannot be learned in isolation (e.g., learning the grammar of a language). The more elements that interact, the higher the working memory load. Element interactivity is related to both ICL and ECL if the respective aspect of the learning material is relevant for learning (Beckmann, 2010; Sweller, 2010). Relevant learning processes of schema acquisition and automation are assigned to the germane cognitive load (GCL).
With respect to the Cognitive Load Theory, increased ECL is used as an explanation for the split-attention effect in learning environments with text and pictures. When related representations are not spatially integrated, related information must be searched and maintained contemporaneously in working memory (Sweller et al., 2011). Additionally, after switching the visual focus, reorientation processes inhibit learning processes (Huff et al., 2012). In consequence, learning is inhibited because obstructive design depletes the resources needed for schema acquisition. In contrast, if related representations are presented in a spatially integrated way, learners are under less demand, and more cognitive resources can be dedicated to processes of learning. Ginns (2006) supported the split-attention effect in a meta-analysis (weighted mean effect size: d = 0.85; 95% confidence interval: 0.68–1.02). Furthermore, disadvantages and benefits of spatially separated in contrast to spatially integrated information depend on the complexity of learning materials. In the case of high complexity, spatial integration can be characterized as effective for instructional quality, which results in high effect sizes (d = 0.78) (Cohen, 1988). When complexity is low, only small effect sizes (d = 0.28; p > 0.05) could be observed. These results refer to the element interactivity effect (e.g., Sweller and Chandler, 1994). Learners who experienced high ICL and an additional high ECL through split attention (e.g., differentiating between individual information and searching for matching information between related representations) are hindered in their learning process. In contrast, if experienced ICL is low, the induced ECL does not inhibit learning because enough cognitive resources are still available (Ginns, 2006). A recent meta-analysis (Schroeder and Cenkci, 2018) supports these results. In order to replicate the split-attention effect, a stimulus material with high complexity was chosen for the current experiments.
Split-Attention and Cognitive Theory of Multimedia Learning
A further important approach in explaining the split-attention effect is the Cognitive Theory of Multimedia Learning (Mayer, 2014). The Cognitive Theory of Multimedia Learning considers limitations in working memory capacity as a crucial aspect of instructional settings. Such limitations apply to two information-processing channels (auditory/verbal vs. visual/pictorial) that can only store a defined amount of information entities (Miller, 1956; Cowan et al., 2007; Cowan, 2010). Furthermore, information processing is assumed to occur in an active manner, dedicated to constructing a coherent verbal and pictorial mental model. In correspondence with the previously described facets of cognitive load (Sweller et al., 2011), the related amount of cognitive processing arises from different sources. While extraneous cognitive processing usually interferes with the instructional goal and arises from an inappropriate instructional design, intrinsic cognitive processing is caused by the complexity of the learning material.
With respect to the Cognitive Theory of Multimedia Learning, the mental integration of text-picture information requires mapping between corresponding elements (Schnotz and Bannert, 2003). The interrelations between the conceptual structure of information must be recognized in order to build a coherent mental model (Schnotz and Baadte, 2015). Information that is related has to be identified and discriminated from unrelated textual or pictorial information. These identification processes and discriminating processes are essential for integrating all information in a complete mental model. A disadvantageous spatial arrangement of pictorial and textual information means that an additional visual search is necessary. This is a further explanation for the split-attention effect (Mayer and Moreno, 2003). If related information is presented as being spatially distant, learners have to switch dynamically between visual information. This causes an additional extraneous cognitive load (Hegarty et al., 1996) and decreases learning performance (e.g., Wirzberger et al., 2016). An increased distance between related information leads to a decreased amount of gaze shifts, which are indicators of an enhanced working memory load (Bauhoff et al., 2012). Therefore, related representations should be presented close to each other (spatial contiguity effect; Mayer, 2014). This allows the learner to build an accurate mental model in real time because of the efficient process of micro-switching between related representations (Ganier, 2004). In contrast, spatial proximity might be harmful as well. Spatial contiguity between unrelated representations induces an incidental cognitive load (Moore and Fitz, 1993) since unrelated information should not be processed simultaneously. This spatial contiguity failure is based on the process of micro-switching between unrelated representations which takes place with increasing proximity (Doherty, 2016). According to Moore and Fitz (1993), this additional micro-switching hinders visual orientation processes and therefore, learning. Schüler (2017) supports these assumptions by investigating the gaze behavior of learners with inconsistent representations. A simultaneous presentation of inconsistent and therefore unrelated information leads to an increased switching between information because the information-coherence is broken. This increased switching between unrelated representations can be interpreted as a symptom of the inhibition of the ongoing integration process. Information cannot be mentally integrated, and learners try to reestablish coherence.
Current Research
Current research focuses on self-management strategies (Roodenrys et al., 2012; Tindall-Ford et al., 2015), spatial distributed instructions (Jang et al., 2011), and the benefits of a spatially separated format in contrast to a spatially integrated format (spatial proximity failure; Jarodzka et al., 2015). Furthermore, several studies cannot replicate the split-attention effect or can only partly confirm previous findings in terms of spatial proximity and integration (Florax and Plötzner, 2010; Schmidt-Weigand et al., 2010). Thus, the split-attention effect cannot be determined without boundary conditions, and the basic idea of the spatial contiguity failure may be the key to understanding these heterogeneous results. Spatially integrated material or a high proximity between different sources of information do not only increase the proximity of related representations but also lead to an increased proximity of unrelated representations. Especially, labeled pictures struggle with this problem. When the learning material becomes more complex and more text is necessary to fully explain the pictorial visualization, it becomes increasingly difficult to enhance the proximity between related information without affecting the proximity between unrelated information. In this special scenario, by increasing the proximity between labels and pictures, the different labels also become closer to each other (see Figure 1).
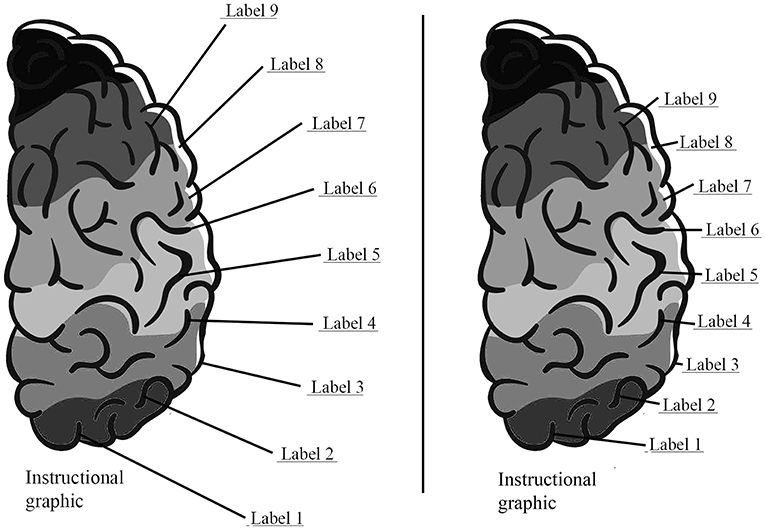
Figure 1. A high distance between labels and the graphic leads to a higher distance between the labels (Left) and a low distance between the graphic and the labels leads to a high proximity between the labels (Right).
As a result, irrelevant micro-switching becomes more frequent. In this vein, the current study aims to determine if the benefits of an increased spatial proximity between related information only dominate up to a specific point. The further increasing of relevant information may lead to a too-high proximity of unrelated information, and the spatial contiguity failure may dominate. An optimal, medium distance between related and unrelated information is assumed, and a precise distance should be explored.
In order to determine the adequate distance between the text and visual representation, findings from eye-tracking studies were obtained. Eye-tracking studies revealed that spatial distance between information results in lower processing speeds and longer processing time (Bai et al., 2008). Information must be mentally integrated and thus, the need for eye movements may be harmful for cognitive processing (Rayner, 1995). Certainly, no data can be found regarding an optimal spatial “distance” between related or unrelated representations. Eye-tracking investigations use the term “saccade” to describe jumps in eye fixations between different information (e.g., Bai et al., 2008; Castelhano and Henderson, 2008). Saccade sizes describe the angle between fixation points and the eye and measure the extent of eye movement. This measure can be used to describe the distance between the information and the cognitive processes that occur during eye movement. Altered attention processes are already measurable at an angle of 0.5° to 1° (Rayner, 1995; Liversedge and Findlay, 2000). A higher saccade amplitude (2° to 3°) leads to shorter fixations on the information itself (Unema et al., 2005). Thus, jumps in eye movements over a greater distance may inhibit learning because the processing time of the individual information is shortened. Furthermore, long saccade paths are an indicator of inefficient search behavior (Goldberg and Kotval, 1999). In sum, high saccade angles are associated with badly designed visualizations (Fu et al., 2017) because the fixation point of the saccade might slightly fail. Therefore, corrective eye-movements are necessary until the searched information is found (Huff et al., 2012). Based on these previous findings, the approximate differences in saccade angles of 2° are adapted for the current investigation in order to manipulate the distance between the text and visual representation.
A review of several studies regarding the split-attention effect revealed that the characteristics of spatially integrated conditions are not reported. Data concerning the distance between different representations are often lacking. As a consequence, the spatially integrated conditions differ between various studies. It may be problematic to compare the results of various experiments because graphical representations and textual representations had a different distance from each other. This inconsistency may result in the fact that some studies support and some studies do not support a split-attention effect.
Experiment 1
Experiment 1 was based on the investigation of Florax and Plötzner (2010) and provided additional insights in learning with several visual representations. As such, the learning material was obtained from Florax and Plötzner (2010). This material consisted of static graphics showing synaptic activity. The level of spatial proximity in these labeled pictures was systematically manipulated by varying the distance between the pictorial representation and the associated text labels. Furthermore, a non-integrated (separated) presentation was designed as a control condition. Following previous empirical findings (e.g., Ginns, 2006; Clark and Mayer, 2008; Florax and Plötzner, 2010), a spatially integrated presentation should lead to higher learning performances than a non-integrated presentation of learning materials (replication of the split-attention effect). In addition, a higher proximity should lead to higher learning outcomes, as learners do not have to split their attention between related representations (spatial contiguity principle; Mayer, 2014). However, unrelated representations should not be presented too close to each other, because the probability of micro-switches between unrelated representations increases with a high proximity (spatial contiguity failure) (Doherty, 2016; Schüler, 2017). Therefore, a medium proximity should be ideal for learning.
H1a: Learners receiving a spatially integrated format achieve higher learning outcomes than learners receiving a separated format.
H1b: A medium spatial proximity between pictorial representation and associated text labels results in higher learning outcomes than a high or low proximity between pictorial representation and associated text labels.
With respect to Cognitive Load Theory and Cognitive Theory of Multimedia Learning, the split-attention effect can be explained by an increased ECL (Sweller et al., 2011). Therefore, less cognitive resources should be available for schema acquisition, and GCL should be decreased. The following hypotheses were formulated to clarify the influence of cognitive load on learning outcomes in spatially integrated presentations with different spatial proximity and a non-integrated format.
H2a: Learners receiving a spatially integrated format report a lower extraneous cognitive load than learners receiving a separated format.
H2b: A medium spatial proximity between pictorial representation and associated text labels results in a lower extraneous cognitive load than a presentation with a high or low proximity between pictorial representation and associated text labels.
H3a: Learners receiving a spatially integrated format report a higher germane cognitive load than learners receiving a separated format.
H3b: A medium spatial proximity between pictorial representation and associated text labels results in a higher germane cognitive load than a presentation with a high or low proximity between pictorial representation and associated text labels.
Additionally, investigating cognitive load in combination with learning results indicates the quality of learning in terms of efficiency (Van Gog and Paas, 2008). Instructional efficiency is described as the extent of cognitive load invested by a learner to reach a certain level of learning performance. A high efficiency describes a relatively high performance compared to the cognitive load investment. A low efficiency refers to a low performance in combination with a high investment of cognitive resources. Therefore, learners receiving the spatially integrated format with medium proximity should be able to achieve a higher instructional efficiency than students receiving the spatially integrated format with high proximity, low proximity, or a non-integrated format.
Hypothesis 4a: Learners receiving a spatially integrated format archive higher efficiency scores than learners receiving a separated format.
Hypothesis 4b: A medium spatial proximity between pictorial representation and associated text labels results in higher instructional efficiency than a presentation with a high or low proximity between pictorial representation and associated text labels.
Because numerous studies have demonstrated that spatial ability impacts learning processes from graphics or pictures (e.g., Hegarty et al., 2003), spatial ability was implemented as a covariate for statistical analyses. Since prior knowledge is the strongest positive or even negative determinant of learning (Simonsmeier et al., 2018), prior knowledge was included as additional covariate.
Method
Participants and Design
Overall, 101 students could be acquired for this experiment. Three students had to be excluded because they did not complete the retention or prior knowledge questionnaire. The remaining 98 students (74.5% female; age: M = 22.73; SD = 3.59) from the Chemnitz University of Technology were in the first (n = 22), second (n = 16), third (n = 40), forth (n = 10), or higher (n = 10) semester. Students were enrolled in media and communication studies (59.2%), instructional and media psychology (25.5%), or other fields of study (15.3%). Each participant received a 2-h course credit or €7. The domain-specific prior knowledge of the participants was rather low (mean percentage of correct answers in the prior knowledge test: M = 0.33; SD = 0.13). The mean spatial ability score was 3.99 (SD = 2.37 on a scale from 1 to 17). No significant differences existed in terms of age, number of semesters, spatial ability, prior knowledge, F(1, 97) = (0.30–2.18); p = (0.07–0.24), gender, or subject of study, χ2 = (5.39–7.42); p = (0.11–0.15).
Each student was randomly assigned to an experimental condition of a between-subjects design. The four experimental conditions differed in terms of spatial proximity and the integration of related and unrelated representations. The conditions comprised a spatially integrated format with high spatial proximity (n = 25), a spatially integrated format with medium spatial proximity (n = 25), a spatially integrated format with low spatial proximity (n = 24), and a separated text-picture presentation (n = 24).
Materials
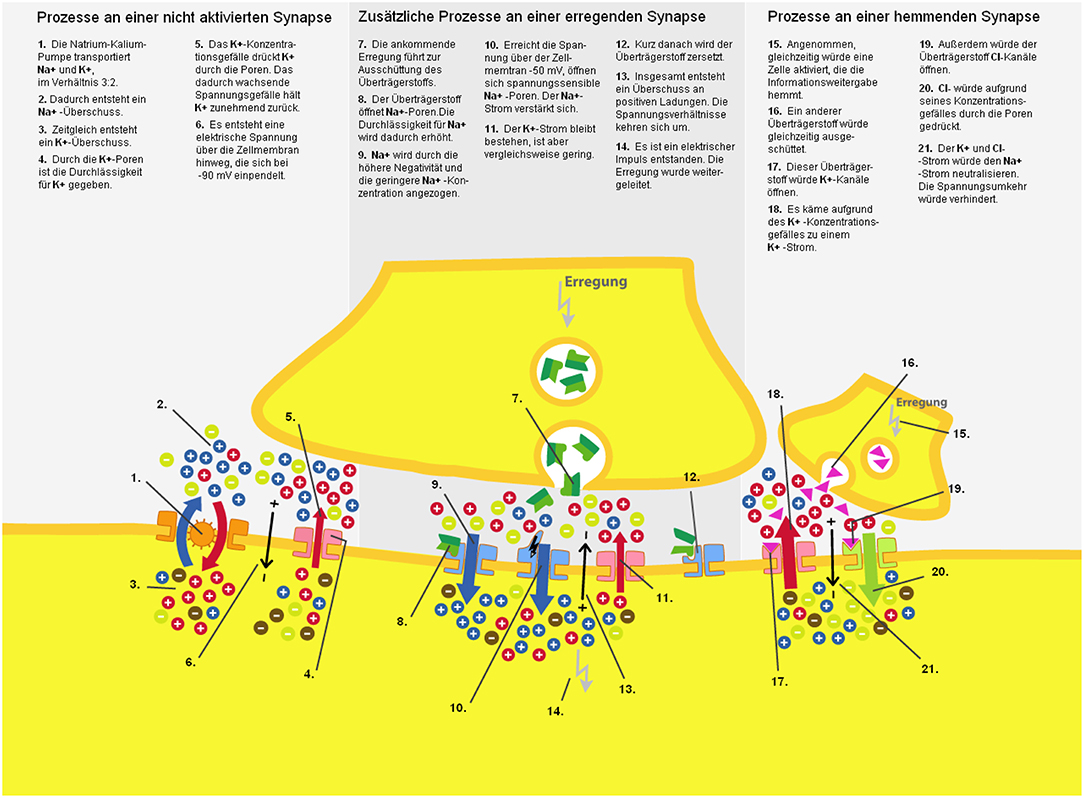
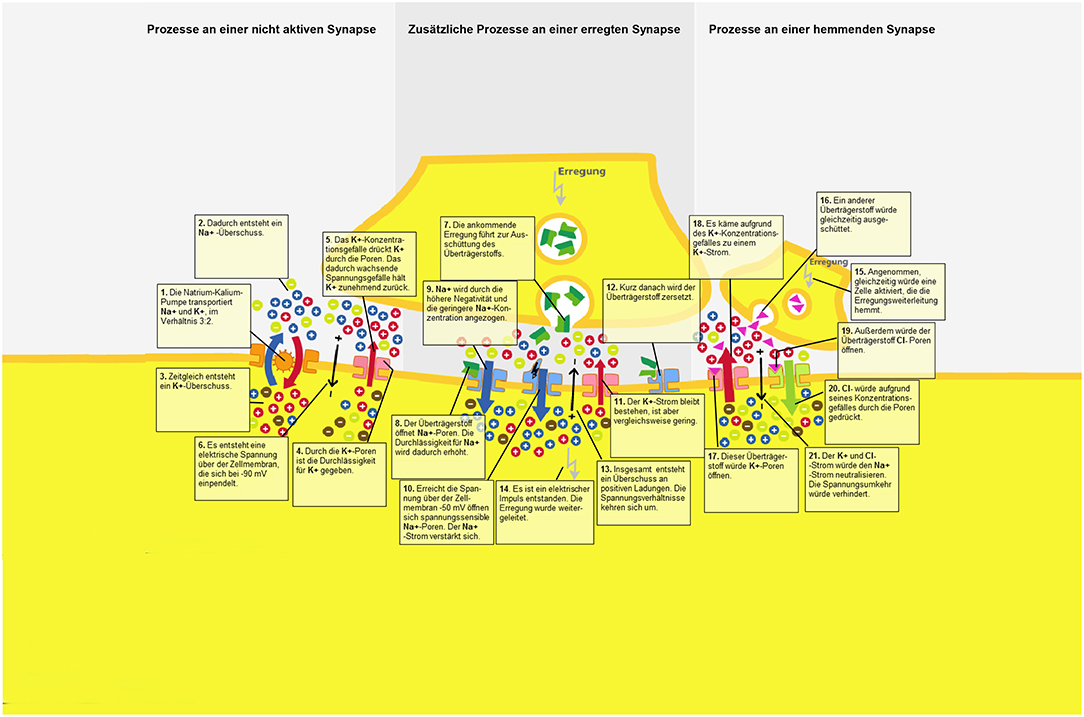
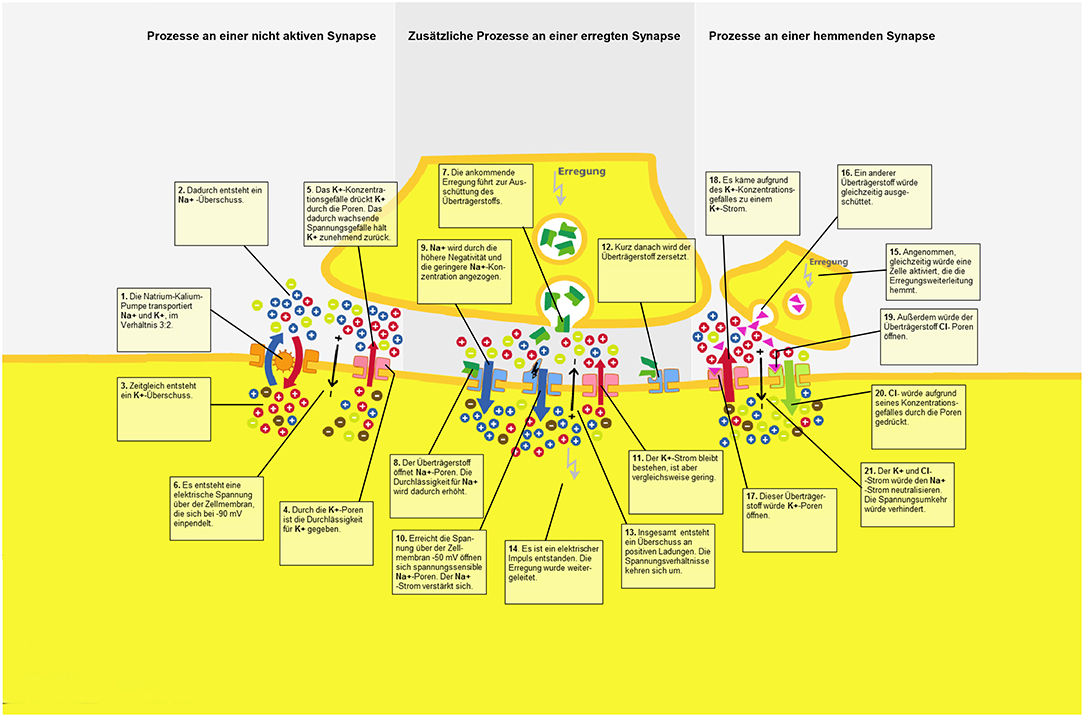
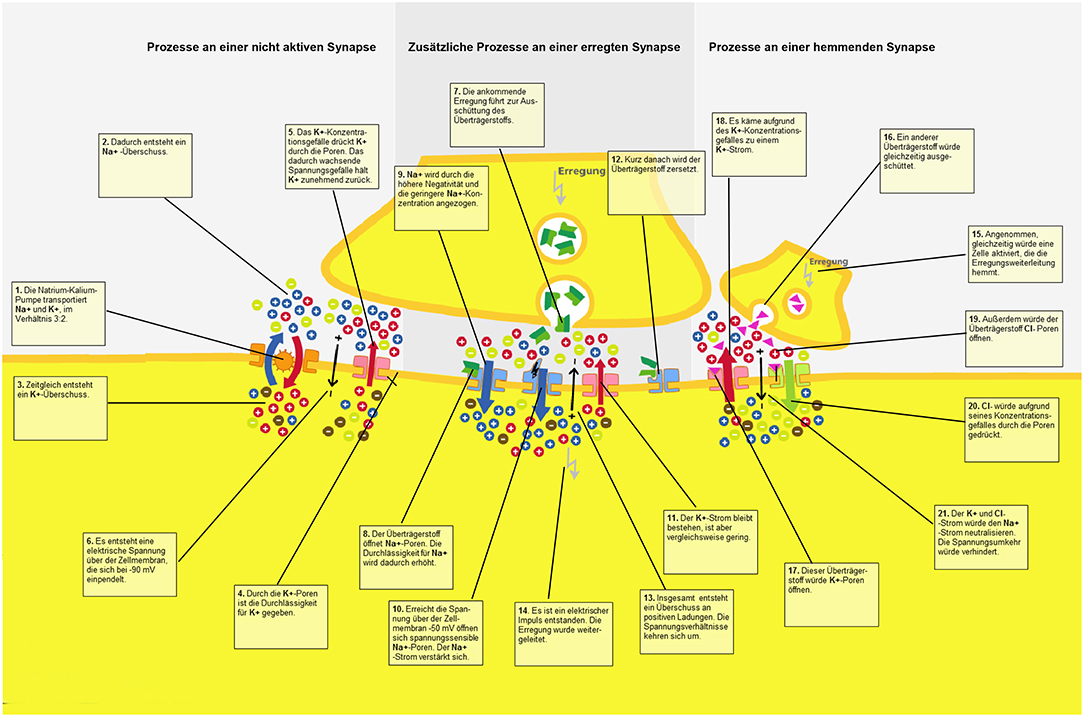
In order to introduce the participants to the learning topic, an introductory text discussing the nervous system and its components (e.g., neurons, synapses, chemical concentration gradient, electrical gradient, permeability of the cell membrane) was obtained from Florax and Plötzner (2010). The learning material consisted of a static graphic that displayed the functioning of a synapse. Resting potential, an activated and inhibited synapse, as well as the role of electric charges, ion currents, and transmitter currents were illustrated in detail. The graphic was shown on a computer screen. It was not possible for students to manipulate the presentation. Twenty-one synaptic sub-processes were displayed within the graphic, and every subprocess had an associated text label. The separated and unrevised material was taken for the control group (Figure 2).
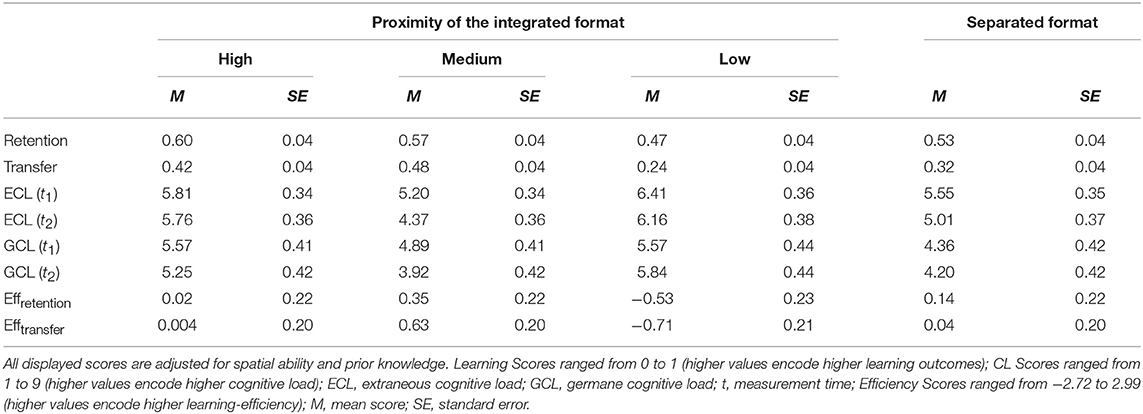
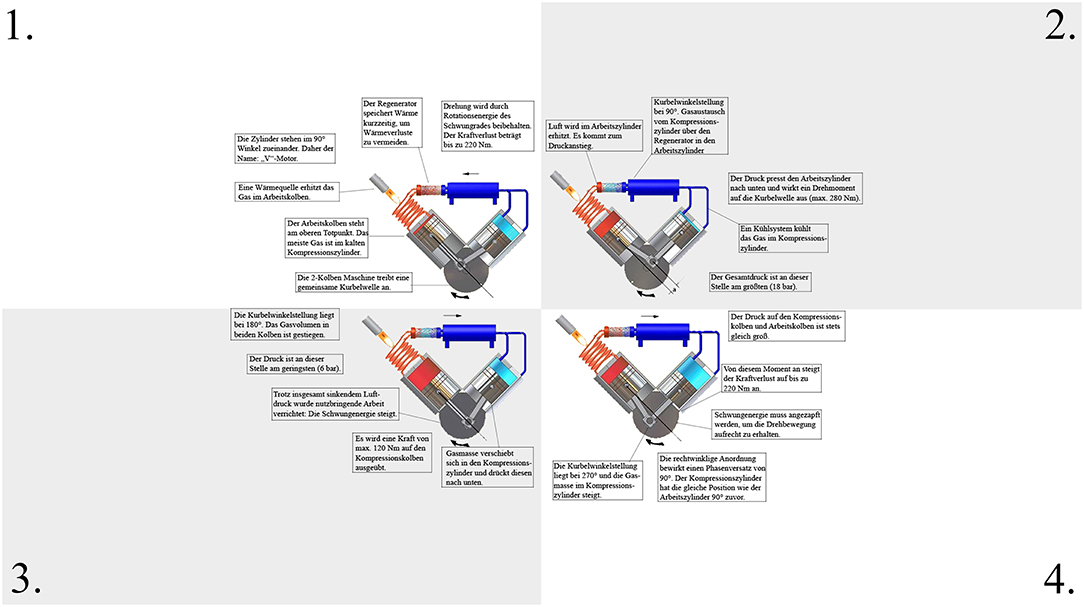
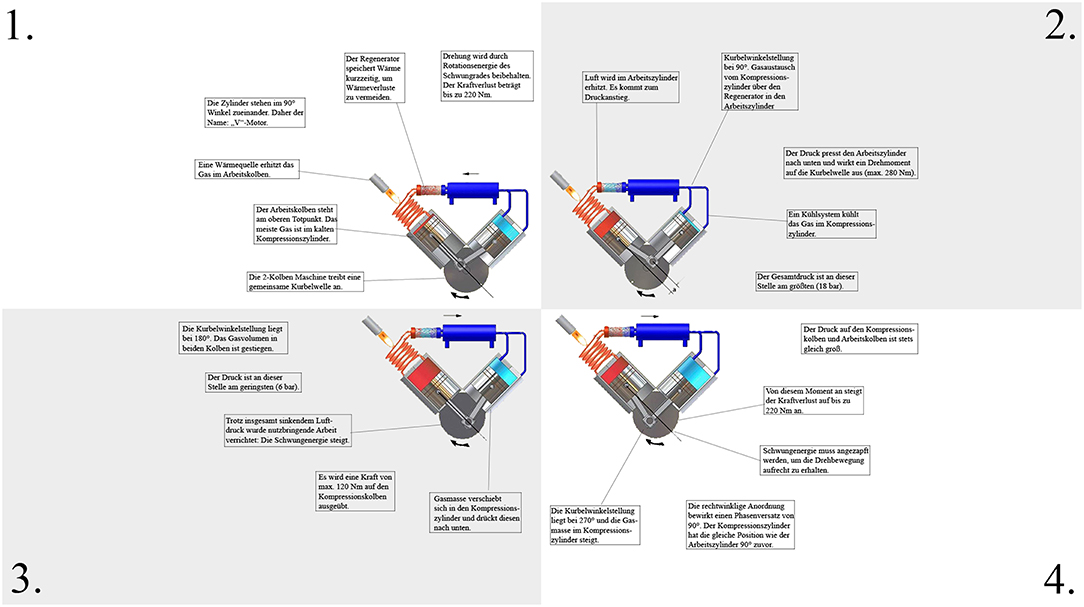
To analyze the effect of spatial proximity, the text was spatially integrated into the picture and the distance between text segments and the corresponding part in the pictorial representation was manipulated. For this purpose, the connecting lines between text segments and the picture in the integrated material used in Florax and Plötzner (2010) study were adjusted for a high spatial proximity condition (Figure 3), a medium spatial proximity condition (Figure 4), and a low spatial proximity condition (Figure 5).
As mentioned, the distance between the pictorial representation and the associated text labels was manipulated by using findings from eye-tracking studies. The approximate differences in saccade angles of 2° were adapted for the current investigation in order to manipulate the distance between the text and the visual representation.
To avoid confusion due to the overlapping of text labels or the overlapping of text labels and relevant pictorial representation, the lines could not be kept at exactly the same length within each of the three experimental conditions. Particularly in the low proximity condition, it was emphasized that text labels did not overlap and that the pictorial information was not covered. In the high spatial proximity condition, the length of the connecting lines had a mean of 1.88 cm (range: 0.5–3.9 cm); in the medium spatial proximity condition, the lines had a mean of 4.26 cm (range: 2.5–5.8 cm); and in the low spatial proximity condition, the lines had a mean of 6.72 cm (range: 5.2–8.7 cm). These distances were measured from the point where the line bordered the frame around the text labels to the point where the line ended in the pictorial representation. The deviations of the different lengths from the medium length occur to the same extent in all of the conditions (high proximity: M = 0.77 cm; SD = 0.51 cm; medium proximity: M = 0.85; SD = 0.51 cm; low proximity: M = 0.88 cm; SD = 0.62 cm) and did not differ between the experimental conditions [F(2, 63) = 0.06; p = 0.81; = 0.01]. Participants sat an average of 70 cm (range 60–80 cm) away from the 24″ monitor. No head fixation was used in order to strengthen the external validity. This resulted in an average saccade angle between graphic and associated text label of 1.5° (SD = 0.41°) for the high proximity condition, an average saccade angle of 3.5° (SD = 0.41°) for the medium proximity condition, and an average saccade angle of 5.5° (SD = 0.51°) for the low proximity condition.
Measures
Because of the ongoing criticism of Cronbach's α (for an overview, see McNeish, 2017), the coefficient Revelle's omega (ω; McDonald, 1999; Revelle and Zinbarg, 2009) was chosen in order to calculate reliability estimates for all measures.
Learning
In order to increase the compatibility to the work of Florax and Plötzner (2010), many measures from the former experiment served as a template for current measures. Thus, learning measures were created using the same learning scales as the foundation. A 12-item questionnaire (ω = 0.68) was used to measure prior knowledge, with questions on dendrites, synapses, chemical concentration, electrical gradients, and ions. Each question had a choice of four answers, and only one option was correct and rewarded with one point. Additionally, an “I don't know” category was provided in order to prevent arbitrary guessing. If the participants chose this category or gave the wrong answer, they received no points. The same question format was used to gather retention scores. A 19-item questionnaire was created in order to measure retention knowledge (ω = 0.90). The questions covered information that was explicitly presented in the learning material (e.g., “What is the correct statement about chloride?”) In order to measure transfer knowledge, a 9-item scale (ω = 0.68) with the same question format as the other knowledge questions was created. Transfer is defined as “understanding.” Learners need a coherent mental model to solve novel problems that are not explicitly presented in the learning material (Mayer, 2014). For example, the question “Which consequences would occur when a person suffers from sodium depletion?” was used. Learning scores ranged from 0 (no correct answers) to 1 (all answers correct).
Spatial ability
In contrast to Florax and Plötzner (2010), spatial ability was measured with the German standardized inventory “Schnitte” of Fay and Quaiser-Pohl (1999) to reduce the overall test time. This questionnaire consisted of 17 single-choice items in which statements about patterns in geometric figures in multidimensional space had to be assessed. Participants could choose between five possible answers. Sum scores were conducted which ranged from 0 to 17 (higher values encode higher spatial ability).
Cognitive load
Cognitive load was assessed by the cognitive load questionnaire from Eysink et al. (2009). The questionnaire includes three items addressing ECL and one item for each measurement of ICL, GCL, and overall load (OL). The OL is considered a mental effort (ME), in accordance with Nebel et al. (2016). The participants had to rate a question regarding ECL (e.g., “How easy or difficult is it for you to work with the learning environment?”) on 9-point Likert scales ranging from very easy to very hard. In order to check for a possible exhaustion of the participants in a 2-h experiment and gather more detailed information about the learning process, the cognitive load scale was implemented twice in the current experiment (during leaning and after learning). Because CL was measured twice, the ECL reliabilities were conducted separately for each measurement time (t1: ω = 0.84; t2: ω = 0.89). Mean scores were conducted which ranged from 1 to 9 (higher values encode a higher cognitive load). Since ICL and ME were not the focus of the current investigations, the results regarding these variables are displayed in Appendix A.
Instructional efficiency
Instructional efficiency was calculated with the following formula (Paas and van Merriënboer, 1993; Van Gog and Paas, 2008):
The z-standardized test performance (P) was calculated for each learning measure (Pretention & Ptransfer). The z-standardized effort (E) was calculated using the cognitive load measure (ECL). For ECL, the cognitive load facets were aggregated, and a mean cognitive load score was conducted over time (the OL/ME sitem was not included). In order to obtain a detailed insight, two efficiency measures were calculated: retention-efficiency (Effretention) and transfer-efficiency (Efftransfer). After calculation, the efficiency scores ranged from −1.72 to 2.99 (higher values encode a higher learning efficiency).
Procedure
The study was conducted in a computer lab consisting of 10 workstations. The workstations were prepared with partition walls in order to ensure that the participants stayed focused on their screens. The number of students within 1 experimental run ranged between two and ten. Each workplace was prepared with paper materials (instructional and test materials), and pre-opened versions of the experimental pictures on the computer desktops. However, monitors were switched off prior to the experiment. At the beginning of the experiment, all of the students completed the demographic, spatial ability, and prior knowledge questionnaire autonomously within 55 min. After each participant finished these materials, they were told to switch on their monitors and learn the presented materials for 7 min. The learning phase was stopped after this time so that the students could fill out the cognitive load questionnaire for the first time. Then they were given 7 min to study their illustrations with a repeated cognitive load measurement at the end. Overall, this learning phase lasted 15 min. The cognitive load questionnaire was implemented before the learning scales in order to minimize interferences between the cognitive processes during learning and the subjective assessment of cognitive load during learning. Afterwards, students were instructed to complete the retention and transfer questionnaire. This phase lasted 30 min and, overall, the experiment required 1 h and 40 min.
Results
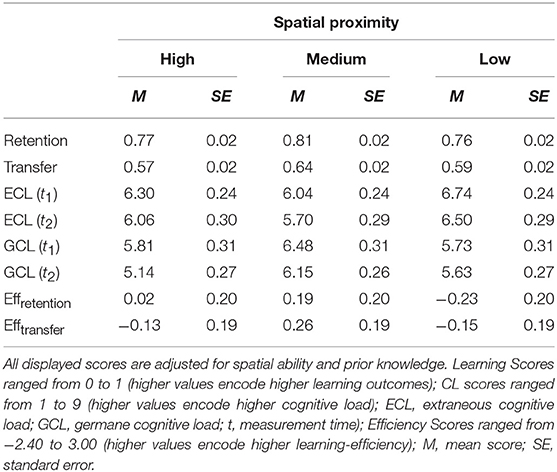
In order to investigate the differences between the experimental groups, multivariate analyses of covariance (MANCOVAs), mixed methods MANCOVAs and contrast analyses were conducted. For all analyses, the spatial manipulation (high proximity vs. medium proximity vs. low proximity vs. separated; defined as “condition” in the following) was used as the independent variable. As described, the spatial ability and prior knowledge of the participants were used as a covariate for all analyses. For contrast analyses, contrast weights were chosen with respect to our hypotheses. According to the Hypotheses Xa, the separated format should achieve the lowest learning scores, GCL, efficiency, and the highest ECL. According to the Hypotheses Xb, students in the medium condition should report the highest learning outcomes, GCL, efficiency, and the lowest ECL. Test assumptions were examined and only reported if these assumptions were significantly violated. Descriptive results for all dependent variables are outlined in Table 1.
Learning
A MANCOVA was conducted with the condition as the between-subject factor and the retention and transfer (r = 0.57; p < 0.001) scores as dependent measures. Prior knowledge [Wilk's Λ = 0.81; F(2, 91) = 10.58; p < 0.001; = 0.19] and spatial ability [F(2, 91) = 3.11; p = 0.05; = 0.06] were significant covariates. Overall, the experimental condition had a significant effect on learning scores [Wilk's Λ = 0.82; F(6, 182) = 3.24, p = 0.005, = 0.10].
With respect to H1a, follow-up contrast analyses (high proximity: λ = 1; medium proximity: λ = 1; low proximity: λ = 1; separated condition: λ = −3) were conducted in order to test our postulated results pattern. In terms of retention, the results pattern could not be supported t = 0.66, SE = 0.26, p = 0.51, r = 0.07. In terms of transfer, the contrast analysis also revealed a non-significant result (t = 1.47, SE = 0.15, p = 0.15, r = 0.15). The separated condition did not generally score lower than the spatially integrated conditions.
With respect to H1b, quadratic contrast analyses (high proximity: λ = −0.5; medium proximity: λ = 1; low proximity: λ = −0.5) revealed no significant results for retention (t = −0.09, SE = 0.06; p = 0.93, r = −0.01) but a significant result for transfer (t = 2.19; SE = 0.05, p = 0.03, r = 0.57).
Cognitive Load
In order to investigate the cognitive load effects over time and to examine the differences between experimental conditions, a mixed methods MANCOVA was conducted. The condition was used as a between-subject factor, and the measurement time (t1 = during learning; t2 = after learning) was used as a within-subject factor. ECL and GCL (r = 0.73; p < 0.001) were implemented as dependent variables.
The covariates of spatial ability [Wilk's Λ = 0.96; F(2, 91) = 2.06, p = 0.13, = 0.04] and prior knowledge [Wilk's Λ = 0.97, F(2, 91) = 1.63, p = 0.20, = 0.04] were non-significant. There was a significant effect for the between-subject factor condition [Wilk's Λ = 0.85, F(6, 182) = 2.49, p = 0.02, = 0.08], no main effect for the within-subject factor measurement time [Wilk's Λ = 0.98, F(2, 91) = 0.75, p = 0.47, = 0.02], and no interaction between the factors [Wilk's Λ = 0.90, F(6, 182) = 1.62, p = 0.14, = 0.05].
For follow-up contrast analyses regarding the between-subject factor condition, ECL and GCL scores were aggregated over time.
ECL
With regard to H2a, a contrast analysis (high proximity: λ = −1; medium proximity: λ = −1; low proximity: λ = −1; separated condition: λ = 3) was non-significant (t = −0.57, SE = 1.17, p = 0.57, r = −0.06). The results revealed that the separated condition did not generally lead to higher ECL scores than the spatially integrated conditions. With respect to H2b3, a quadratic contrast analysis (high proximity: λ = 0.5; medium proximity: λ = −1; low proximity: λ = 0.5) revealed a significant result (t = 2.88, SE = 0.38, p = 0.01, r = 0.32).
GCL
Regarding H3a, a contrast analysis (high proximity: λ = 1; medium proximity: λ = 1; low proximity: λ = 1; separated condition: λ = −3) was non-significant (t = 1.81, SE = 1.35, p = 0.07, r = 0.18). The results revealed that the separated condition did not generally lead to lower scores than the spatially integrated conditions. With respect to H3b, a quadratic contrast analysis (high proximity: λ = −0.5; medium proximity: λ = 1; low proximity: λ = −0.5) revealed a significant result (t = −2.28, SE = 0.44, p = 0.03, r = −0.26), but the results pattern is exactly reversed. Descriptively, GCL is reduced in the medium condition in contrast to the high and low condition.
Retention negatively correlated with the aggregated ECL (r = −0.36, p < 0.001) and GCL score (r = −0.37, p < 0.001). Transfer negatively correlated with the aggregated ECL (r = −0.22, p = 0.03) and GCL score (r = −0.24, p = 0.02).
Instructional Efficiency
In order to investigate the effects of proximity and spatial integration on efficiency scores, a MANCOVA was conducted with the condition as a between-subject factor and the learning efficiency scores (r = 0.84, p < 0.001) as dependent measures.
Spatial ability [Wilk's Λ = 0.93, F(2, 91) = 4.03, p = 0.03, = 0.07] and prior knowledge [Wilk's Λ = 0.89, F(2, 91) = 5.78, p = 0.004, = 0.11] were significant covariates. There was a significant effect for the condition [Wilk's Λ = 0.79, F(6, 182) = 3.87, p = 0.001, = 0.11].
Effretention
With regard to H4a, a contrast analysis (high proximity: λ = 1; medium proximity: λ = 1; low proximity: λ = 1; separated condition: λ = −3) was non-significant (t = −0.14, SE = 0.84; p = 0.89, r = −0.01). The results revealed that spatially integrated conditions did not generally lead to a higher efficiency than the separated condition. With respect to H4b, a quadratic contrast analysis (high proximity: λ = −0.5; medium proximity: λ = 1; low proximity: λ = −0.5) revealed a non-significant result (t = 1.52, SE = 0.28, p = 0.13, r = 0.18) but descriptively, the effect size increased.
Efftransfer
With regard to H4a, a contrast analysis (high proximity: λ = 1; medium proximity: λ = 1; low proximity: λ = 1; separated condition: λ = −3) was non-significant (t = 0.33, SE = 0.77, p = 0.74, r = 0.04). Results revealed that spatially integrated conditions did not generally lead to a higher efficiency than the separated condition. With respect to H4b, a quadratic contrast analysis (high proximity: λ = −0.5; medium proximity: λ = 1; low proximity: λ = −0.5) revealed a significant result (t = 3.23, SE = 0.25, p = 0.002, r = 0.35).
Discussion
The aim of this experiment was to explore the boundary conditions regarding the emergence and expression of the split-attention effect. With respect to the Cognitive Load Theory and the Cognitive Theory of Multimedia Learning learners receiving the spatially integrated material, they should outperform the learners receiving the separated material (H1a). In contrast, the contrast analysis revealed that students in the separated condition did not score worse in the learning tests than students in the integrated conditions. H1a had to be rejected. The same results pattern could be observed for all the other depended variables. The separated condition did not lead the changes in perceived cognitive load and efficiency. Thus, H2a, H3a, and H4a had to be rejected.
Regarding the spatial contiguity effect and the spatial contiguity failure, learners receiving learning material with medium distance should outperform learners receiving the high or low proximity condition (H1b). H1b was partially supported based on the current results. Students in the medium condition achieved the best transfer scores, but the retention score did not differ between the experimental conditions. Learners in the medium proximity condition should report the lowest ECL (H2b) and the highest GCL (H3b). Students in the medium condition showed the lowest cognitive load regarding all facets. Therefore, H2b could be supported, but H3b had to be rejected. Instructional efficiency should be increased in the medium proximity condition (H4b). Learners receiving the material with medium proximity descriptively showed the highest efficiency regarding transfer but not in terms of retention performance. Thus, H4b could be supported partially.
Even if this exploratory experiment provided insights into the benefits of a medium spatial proximity in contrast to a high and low spatial proximity, four major limitations were detected. The first limitation was rooted in the organization of the learning material. The text segments from the material were marked with numbers to structure the pictured processes. Consecutive text segments could not be presented spatially close to each other because they had to be integrated in the associated parts of the picture. In consequence, associated text labels in the spatially integrated conditions were not shown in the correct order of the synaptic processes. Thus, separating text labels from the picture and organizing them in their natural order might positively influence learning outcomes. Thus, students receiving the separated material might not score worse than students in most of the spatially integrated conditions. This result is in line with the study of Florax and Plötzner (2010), which could not outline a significant difference between a separated and labeled presentation in learning performances.
The second major limitation of the current study lay within the control group. When spatially integrating or separating different representations, proximity was unavoidably modified. Separating (dis-labeling) text blocks from the picture and displaying them at the top of the pictures led to the lowest spatial proximity of all conditions. Therefore, the separated condition was not technically a clean control condition. The effects of spatial integration and distance were confounded concerning the comparison of the experimental groups with the control group. This is especially important because this research showed the impact of distance on learning outcomes.
The third limitation lay within the manipulation of the distance of the text segments and the picture. Within the conditions, the range of the distance was quite large, and the intervals were overlapping between the conditions (e.g., high: 0.5–3.9 cm, medium: 2.5–5.8 cm).
Fourth, retention performance was not influenced by the current manipulation. A possible explanation for this might lie within the construction of the questions. A lot of questions (19) were created to assess simple information that was explicitly presented in the material. According to Mayer et al. (2003), representations of learning materials interconnected with each other and the prior knowledge of the learners. Because of the conducive and demanding learning environment, deeper cognitive processing resulted in meaningful knowledge, which was required for the transfer test. Element-interactivity in the used retention items was too low, and therefore the manipulation did not affect the outcomes. More difficult questions have to be created in order to raise element-interactivity. Therefore, an additional experiment was conducted in order to tackle these issues.
Experiment 2
Experiment 2 was conducted in order to sharpen the findings and resolve the mentioned limitations from Experiment 1. Therefore, static graphics were created, showing the functionality of a Stirling engine (i.e., a heat engine that generates power by the expansion and compression of a medium). The level of spatial proximity in these labeled pictures was systematically manipulated by varying the distance between the pictorial representation and the associated text labels. A spatially non-integrated (separated) presentation was not included because of the problems mentioned in Experiment 1.
In line with Experiment 1, a medium spatial proximity should be beneficial for learning because of the effects of the spatial contiguity principle (Mayer, 2014) and the spatial contiguity failure (Doherty, 2016; Schüler, 2017).
H1: A medium spatial proximity between pictorial representation and associated text labels results in higher learning outcomes than a high or low proximity between pictorial representation and associated text labels.
With respect to the results of current literature, an optimal instructional design should lead to an enhanced GCL and reduced ECL. According to Experiment 1, a medium proximity between the two representations might be the optimal design recommendation. Furthermore, a medium proximity should lead to the highest efficiency scores. The following hypotheses are formulated:
H2: A medium spatial proximity between pictorial representation and associated text labels results in a lower extraneous cognitive load than a presentation with a high or low proximity between pictorial representation and associated text labels.
H3: A medium spatial proximity between pictorial representation and associated text labels results in a higher germane cognitive load than a presentation with a high or low proximity between pictorial representation and associated text labels.
H4: A medium spatial proximity between pictorial representation and associated text labels results in higher instructional efficiency than a presentation with a high or low proximity between pictorial representation and associated text labels.
Method
Participants and Design
Overall, 92 students could be acquired for this Experiment. Seven students had to be excluded due to technical problems. The remaining 85 students (75.6% female; age: M = 23.45; SD = 4.25) from the Chemnitz University of Technology were enrolled in media and communication studies (64.3%), instructional and media psychology (26.2%), or other fields of study (9.5%). Each participant received a 1-h course credit or €5. The domain-specific prior knowledge of the participants was rather high (mean percentage of correct answers in the prior knowledge test: M = 0.72; SD = 0.19). The mean spatial ability score was 8.38 (SD = 3.62 on a scale from 1 to 20). No significant differences existed in terms of age, spatial ability, or prior knowledge, F(1, 84) = (0.23–1.02); p = (0.37–0.80), gender, or subject of study, χ2 = (3.91–5.87); p = (0.14–0.21).
Each student was randomly assigned to an experimental condition of a between-subjects design. The three experimental conditions differed in terms of spatial proximity: high spatial proximity (n = 29), medium spatial proximity (n = 29), and low spatial proximity (n = 27).
Materials
In order to introduce the participants to the learning topic, an introductory text discussing thermodynamics and the basic structure of a Stirling engine was created. Learning material consisted of a static graphic that displayed the functioning of a Stirling engine in 4 steps, depending on the position of the pistons. The resulting power, pressure conditions, and the floating gas was described in detail in order to extensively explain the functionality of the engine. The presentation and manipulation of the learning material were similar to Experiment 1. The connection lines were adjusted for a high spatial proximity condition (Figure 6), a medium spatial proximity condition (Figure 7), and a low spatial proximity condition (Figure 8).
In contrast to Experiment 1, the length of the lines could be controlled in order to strengthen the internal validity. In the high spatial proximity condition, the length of the connecting lines had a mean of 1.84 cm or 1.5° (range: 1.6–1.9 cm), in the medium spatial proximity condition a mean of 4.28 cm or 3.5° (range: 4.2–4.3 cm), and in the low spatial proximity condition a mean of 6.71 cm or 5.5° (range: 6.6–6.8 cm).
Measures
In line with Experiment 1, Revelle's omega was conducted for all scales.
Learning
A 5-item questionnaire was used to measure prior knowledge, with questions on the basic structure of a Stirling engine and the basics of thermodynamics. Four single-choice questions were implemented (ω = 0.70). The same answer format as in Experiment 1 was used. Furthermore, an item with open-answer format (i.e., “Please write down everything you know about Stirling engines”) was implemented in order to gather additional prior knowledge. Students could reach up to two points on the open-answer question, depending on the quality of the answers. To summarize, students could reach up to six points in the prior knowledge test.
The same question format as in Experiment 1 was used in order to gather retention and transfer scores. Retention knowledge was measured with a 10-item questionnaire (ω = 0.67). “What is the maximum torque of the Stirling engine?” was used as an item. In contrast to Experiment 1, more complex questions covering several aspects were included. This resulted in a smaller number of questions. In order to measure transfer knowledge, an 8-item scale, addressing knowledge gained from drawn inferences, was created (ω = 0.67). One of the questions used was “What would happen if the regenerator was omitted?”
Spatial ability
In contrast to Experiment 1, the mental rotation test from Vandenberg and Kuse (1978) was chosen in order to assess spatial ability because the overall test time was much lower than the test time of “Schnitte.” Thus, the economy of Experiment 2 was raised. This questionnaire consisted of 20 multiple-choice items in which the spatial rotation of figures had to be assessed (ω = 0.91). For each item, students could choose between four possible answers, where two answers were always correct. Students received only one 1 point per item if both correct answers were identified. The sum score ranged from 0 to 20 (higher scores encode higher spatial ability).
Cognitive load
Again, cognitive load was assessed by the cognitive load questionnaire from Experiment 1 (Eysink et al., 2009). Since CL was measured twice during the investigation (during and after learning), ECL reliabilities were conducted separately for each measurement time (t1: ω = 0.67; t2: ω = 0.80). In contrast to Experiment 1, the OL (ME) item was not included. Results regarding ICL are displayed in Appendix B.
Instructional efficiency
The same calculation was used as in Experiment 1.
Procedure
The procedure was nearly identical to Experiment 1. The experiments differed slightly in that Experiment 2 was fully computerized, and no paper-pencil questionnaires were used. Since another spatial-ability-test was used, Experiment 2 only lasted for roughly 1 h.
Results
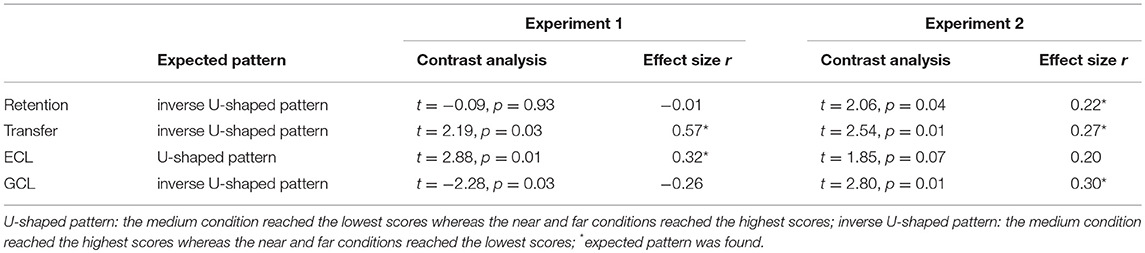
In line with Experiment 1, MANCOVAs, repeated measures MANCOVAs, and contrast analyses were conducted. For all analyses, spatial proximity (high vs. medium vs. low) was used as an independent variable. Spatial ability and prior knowledge of the participants were used as covariates for all analyses. According to the hypotheses, students in the medium condition should achieve the highest learning outcomes, GCL, efficiency, and the lowest ECL. Test assumptions were examined and only reported if these assumptions were significantly violated. Descriptive results for all dependent variables are outlined in Table 2.
Learning
A MANCOVA was conducted with spatial proximity as the between-subject factor and retention and transfer (r = 0.38, p < 0.001) scores as the dependent measures. Prior knowledge [Wilk's Λ = 0.85, F(2, 79) = 7.15, p = 0.001; = 0.15] but not spatial ability [F(2, 79) = 1.98, p = 0.15, = 0.05] was a significant covariate. Overall, the experimental spatial proximity had a significant effect on learning scores [Wilk's Λ = 0.89, F(4, 158) = 2.46, p = 0.048, = 0.06].
With respect to H1, follow-up quadratic contrast analyses (high proximity: λ = −0.5; medium proximity: λ = 1; low proximity: λ = −0.5) were conducted in order to test our postulated results pattern. In terms of retention, the results pattern could be supported (t = 2.06, SE = 0.79, p = 0.04, r = 0.22). In terms of transfer, the contrast analysis was significant (t = 2.54, SE = 0.69, p = 0.01, r = 0.27).
Cognitive Load
In order to investigate cognitive load over time and to examine differences between the experimental conditions, a mixed methods MANCOVA was conducted. Spatial proximity was used as a between-subject factor, and measurement time (t1 = during learning; t2 = after learning) was used as within-subject factor. ECL and GCL (r = 0.54, p < 0.001) were implemented as dependent variables.
Spatial ability [Wilk's Λ = 0.99, F(2, 76) = 0.31, p = 0.74, = 0.01] and prior knowledge [Wilk's Λ = 0.96, F(2, 76) = 1.74, p = 0.18, = 0.04] were not significant covariates. There was a significant effect for the between-subject factor spatial proximity with a high effect size [Wilk's Λ = 0.75, F(4, 152) = 6.01, p < 0.001, = 0.14]. There was no main effect for the within-subject factor measurement time [Wilk's Λ = 0.96; F(2, 76) = 1.51, p = 0.23, = 0.04] and no interaction between the levels [Wilk's Λ = 0.98; F(4, 152) = 0.47, p = 0.76, = 0.01].
With respect to H2 and H3, follow-up quadratic contrast analyses were conducted in order to test our postulated results pattern. In terms of ECL, the contrast analysis (high proximity: λ = 0.5; medium proximity: λ = −1; low proximity: λ = 0.5) was non-significant (t = 1.85, SE = 0.60, p = 0.07, r = 0.20), but there was a descriptive hint for the postulated pattern. In terms of GCL, the quadratic contrast analysis (high proximity: λ = −0.5; medium proximity: λ = 1; low proximity: λ = −0.5) revealed a significant result (t = 2.80, SE = 0.58, p = 0.01, r = 0.30).
Retention negatively correlated with the aggregated ECL (r = −0.38; p < 0.001) but not with the aggregated GCL score (r = −0.16, p = 0.15). Transfer did not correlate with the aggregated ECL (r = −0.07, p = 0.52), or GCL score (r = −0.09, p = 0.40).
Instructional Efficiency
In order to investigate effects of proximity on efficiency scores, a MANCOVA was conducted with spatial proximity as a between-subject factor, learning efficiency scores (r = 0.73, p < 0.001) were dependent measures.
Prior knowledge was a significant covariate [Wilk's Λ = 0.88, F(2, 76) = 5.01, p = 0.01, = 0.12] but spatial ability was not [Wilk's Λ = 0.97, F(2, 76) = 1.33, p = 0.27, = 0.03]. There was no significant effect for spatial proximity [Wilk's Λ = 0.95, F(4, 152) = 1.07, p = 0.37, = 0.03]. Descriptively, the efficiency scores were enhanced in the medium condition.
Comparison Between Experiment 1 and Experiment 2
Comparisons between the results of both experiments are displayed in Table 3. For consistency reasons, the separated condition of experiment is not included. Efficiency scores are not included because of the non-significant MANOVAs.
Discussion
The aim of this experiment was to clarify the findings of Experiment 1. Furthermore, the boundary conditions regarding the emergence and expression of the split-attention effect should be specified. The influence of spatial proximity of related and unrelated representations of the text-picture combination was manipulated systematically, and methodical problems from Experiment 1 were eliminated. In line with H1, learners receiving learning material with medium distance outperformed learners receiving the high or low proximity condition regarding transfer and retention performance. H1 could be supported. No differences could be detected regarding ECL. Therefore, H2 had to be rejected. H3 could be supported since GCL increased in the condition with medium proximity. Regarding H4, learners receiving the material with medium proximity descriptively showed the highest efficiency regarding retention and transfer, but results did not reach significance. Therefore, H4 had to be rejected.
There were several differences in the results between both experiments. At first, in the second experiment, the results regarding both learning scales reached significance. This can be explained by considering the cleaner manipulation of spatial proximity in Experiment 2. The results of ECL and GCL strongly differed. In the second experiment, GCL increased in the medium condition, whereas GCL decreased in the medium condition of Experiment 1. This also led to differences in the results regarding the efficiency scores. This might be explained by two factors. At first, the learning topic differed. Since the participants were recruited from a technical university, the technical topic of a Stirling engine, which was used as learning material in Experiment 2, might be more familiar to the students which is reflected in a higher prior knowledge score in Experiment 2. This might result in different perceptions of the learning material and different learning strategies. Since the cognitive load was assessed with a subjective rating scale, the perceived germane load might be influenced differently by our manipulation. Second, the used questionnaire might be problematic. Since GCL was measured with only one item, it was difficult to state if the measurement was reliable.
General Discussion
In line with previous findings regarding the spatial proximity of information in learning media, a medium proximity between information led to higher learning scores than a low proximity between information (with exception of retention in Experiment 1). Therefore, the results of the current experiments support the spatial contiguity effect. According to the Cognitive Load Theory and Cognitive Theory of Multimedia Learning, a lower spatial proximity between related representations reduces the capacity available for relevant learner involvement (Mayer, 2014). Thus, an average saccade angle of 5.5° between related representations lead to longer saccade paths. This might result in inefficient search behavior, which is an indicator of a lower processing speed. The results of the current studies supported these explanations. ECL was enhanced in the low proximity condition in contrast to the medium proximity condition in Experiment 1 and descriptively in Experiment 2. As a consequence, learning processes were inhibited.
With respect to these arguments, learners in the condition with the highest proximity between related representations should outperform learners in the medium and low condition. In contrast, in the current investigation, students in the high proximity condition scored significantly worse than the students in the medium condition (with exception of retention in Experiment 1). This result supports the spatial contiguity failure. An explanation can be provided by Wickens and Carswell (1995). High proximity and a too-large amount of information in limited space was confusing. High spatial proximity might cause interference (Wickens and McCarley, 2008) and lead to micro-switching between unrelated information, which was presented too closely together (Ganier, 2004; Doherty, 2016; Schüler, 2017). Learners might have problems in finding corresponding text fragments for the relevant parts of the picture and often switched inadvertently between information that was not needed for schema construction at a specific time. The high proximity between related and unrelated representations induced an incidental cognitive load, and therefore element-interactivity was increased (Moore and Fitz, 1993). This was particularly reflected in the ECL measure of Experiment 1. Thus, a medium proximity led to higher performance because, subsequently, a designed distance with an average saccade angle of 1.5° between related and unrelated representations hindered learning. In line with recent literature (e.g., Fu et al., 2017), a poorly designed visualization with a lot of (partly unrelated) information on a small spatial area led to inaccurate search behavior. It is important to state that these explanations have to be viewed with caution, since no eye-tracking data were recorded. However, hints for these explanations could be found in the results regarding cognitive load and instructional efficiency of the current experiments. ECL reached its minimum in the medium condition in Experiment 1, and students within this condition reached the highest transfer score as well as the highest retention score in Experiment 2. According to the current results, spatial proximity is an important design factor for fostering the acquisition of a coherent mental model that contains information from the text and pictorial representation. Thus, the current investigation provides a contribution to the discussion on the spatial integration of multiple representations of information (e.g., Schüler et al., 2015) and spatial contiguity (e.g., Paek et al., 2017).
Implications
On the theoretical side, it can be shown that learning with different representations of information can only be partially explained with respect to Cognitive Load Theory and Cognitive Theory of Multimedia Learning. A higher spatial proximity can also cause various problems, which can act against current design recommendations. Thus, the relationship between proximity and learning outcomes may not be linear but rather an inverse U-shaped relationship with greater benefits to medium distances. The spatial contiguity principle may almost always be restricted by mechanisms of the spatial contiguity failure. It is almost impossible to spatially integrate different representations without presenting information closely, which is obstructive for schema acquisition. This may be a significant contribution to the discussion about the spatial integration of multiple representations. It is important to clarify the boundaries of spatial contiguity to further improve the design of the instructional material.
Therefore, on the practical side, instructional designers should realize which information is necessary and which information is unnecessary at a specific time in order to fully understand the instructional material. Unrelated information should not be presented too closely on limited space. Additionally, relevant information should not be presented too far away, because split attention also hinders learning. It is difficult to postulate a concrete design principle because the saccades do not depend solely on the proximity of information within the learning material but also on the distance of the viewer. This should be considered if learning material is produced for textbooks, monitors, or projector presentations in classes, because the distance from the learners to the learning material varies. Depending on the context and field of application, different designs may be useful.
Limitations
The current investigation provides an insight into the benefits and disadvantages of spatial proximity, but further studies must specify the role of distance and examine proximity in more detail. Limitations must be mentioned regarding certain parts of the measurement. The momentary perception of cognitive load was measured with the questionnaire of Eysink et al. (2009); this might capture the construct insufficient. The questionnaire was chosen because the questions regarding ECL especially referred to distinguishing and collecting information. Nevertheless, GCL was measured with only 1 item. Furthermore, students in the medium condition reported lower ICL than students in the high or low condition in both experiments, although the learning content was not part of the manipulation. These are indications that the cognitive load questionnaire might be inappropriate. The negative correlations between the learning scales and GCL in Experiment 1 and the missing correlations between the learning scales and GCL in Experiment 2 are an additional indication. Alternative questionnaires (Leppink et al., 2013, 2014) could capture the construct more adequately. Another limitation is the variable distance of the participants to the monitor. Since students could move freely in front of the monitor, the saccades might change during the investigation. As mentioned, the current study only addresses short-term learning effects through the spatial integration of multiple representation. Even if it can be positively stated that transfer results were significant in a 1- or 2-h experiment, deeper understanding of the learning material might need a longer learning period. This should be taken into account when interpreting the results. The proximity between related and unrelated information was studied one-dimensionally. The current experiments did not separately investigate the proximity between related and unrelated information. Therefore, the current investigation cannot postulate if the distance between related or unrelated information is more important for learning materials with multiple representations of information. Finally, this investigation cannot specify the exact curve of the function of the relationship between proximity and learning outcomes. The manipulation of the current experiment cannot specify, if the best proximity is at an angle of 3.5° or if another angle between 1.5° and 5.5° since no data is available. The terms “low,” “medium,” or “high” proximity were chosen to describe the manipulation. Future research should specify, if a “medium” distance is actually beneficial, or if a high proximity is beneficial until the proximity of unrelated information gets too high.
Conclusions and Future Directions
Spatial proximity between two different representations can foster or hinder learning. Now it is necessary to investigate what proximity is ideal for learning processes and at which proximity learning is affected negatively. Future research with a more differentiated design in terms of distance between the pictorial representation and the associated text labels can provide further insights as to the beneficial and harmful effects of proximity. Furthermore, more extreme distances between related and unrelated representations may produce bigger effects. The current investigation focused on distances from 1.5° to 5.5°, but distances of, for example, 0.5° or 6°, may also be interesting and relevant. Furthermore, future studies should separately investigate proximity between related and unrelated information separately in one or multiple many experimental designs. This could result in concrete distance references, depending on the presentation format, and a concrete recommendation on which saccade angles should be used for specific learning material. Further, it is possible that the distance between the information is not the only central variable which should be investigated. Thus, the related construct of information density (e.g., Ziefle, 2010) should be considered in future work as well. This can be enriched by investigating different types of learning content, modalities, and presentations. Furthermore, the amount of information should be analyzed. It has to be examined how spatial proximity interacts with the amount of information presented, especially as the complex and assumed inverse U-shaped relationship may be influenced by further, yet not sufficiently analyzed, variables. Future investigations should examine the effect of the distance of the learner from the material. Often, learners vary their distance toward the learning material, and an altered distance changes the subjective distance of representations of information as well as the size and visual clarity of information. Incorporating the signaling of related information might reduce micro-switching between unrelated information. Thus, manipulating signaling and spatial proximity between information are relevant for future studies.
In sum, the current investigation could be a cornerstone in clarifying the role of spatial proximity in multimedia learning. Various sources of information are predominantly in multimedia learning environments and therefore, spatial presentation could be further optimized through future research. This study could serve as the foundation for a deeper conceptualization of the split attention effect and the spatial contiguity principle.
Data Availability
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
All procedures were performed in full accordance with the ethical guidelines of the German Psychological Society (DGPs, https://www.dgps.de/index.php?id=85) and the APA Ethics code with written informed consent from all subjects. Since the experiments constitutes non-medical low risk research, no special permission by an ethics committee is required for psychological research in Germany. At the beginning of the study, participants were informed that the data of this study will be used for research purposes only and that all data are collected anonymously. Thus, no identifying information was collected. Participants who prematurely stopped the survey were not included in the analyses and all of their data were deleted from the dataset.
Author Contributions
MB: conducted experiments, statistical analyses, and wrote major parts of manuscript. SN and SS: wrote minor parts, proofreading. MW: conducted experiments and wrote minor parts. NS: created experimental materials and wrote minor parts. GR: proofreading.
Funding
The publication costs of this article were funded by the German Research Foundation/DFG-392676956 and the Technische Universität Chemnitz in the funding programme Open Access Publishing. Both funders were involved in paying the publication costs and were not involved in the conduction of the experiments.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We want to thank Rolf Plötzner for the permission to use the experimental material and publish the figures. Since the figures were already published in an ELSEVIER journal (https://doi.org/10.1016/j.learninstruc.2009.02.021), rights for the publication have been obtained (license number: 4594730874590). Furthermore, we want to thank Shirin Esmaeili Bijarsari for programming the online environment for the second experiment and Freepik for designing the basis of Figure 1.
References
Atkinson, R. C., and Shiffrin, R. M. (1968). “Human memory: a proposed system and its control processes,” in The Psychology of Learning and Motivation, Vol. 2, ed K. W. Spence (New York, NY: Academic Press), 89–195. doi: 10.1016/S0079-7421(08)60422-3
Bai, X., Yan, G., Liversedge, S. P., Zang, C., and Rayner, K. (2008). Reading spaced and unspaced Chinese text: evidence from eye movements. J. Exp. Psychol. 34, 1277–1287. doi: 10.1037/0096-1523.34.5.1277
Bauhoff, V., Huff, M., and Schwan, S. (2012). Distance matters: spatial contiguity effects as trade-off between gaze switches and memory load. Appl. Cogn. Psychol. 26, 863–871. doi: 10.1002/acp.2887
Beckmann, J. F. (2010). Taming a beast of burden – On some issues with the conceptualisation and operationalisation of cognitive load. Learn. Instruct. 20, 250–264. doi: 10.1016/j.learninstruc.2009.02.024
Castelhano, M. S., and Henderson, J. M. (2008). Stable individual differences across images in human saccadic eye movements. Can. J. Exp. Psychol. 62, 1–14. doi: 10.1037/1196-1961.62.1.1
Chandler, P., and Sweller, J. (1991). Cognitive load theory and the format of instruction. Cogn. Instr. 8, 293–332. doi: 10.1207/s1532690xci0804_2
Chandler, P., and Sweller, J. (1992). The split-attention effect as a factor in the design of instruction. Br. J. Educ. Psychol. 62, 233–246. doi: 10.1111/j.2044-8279.1992.tb01017.x
Clark, R. C., and Mayer, R. E. (2008). E-Learning and the Science of Instruction, 2nd Edn. San Francisco, CA: Jossey-Bass/Pfeiffer.
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences, 2nd Edn. Hillsdale, NJ: Erlbaum.
Cowan, N. (2010). The magical mystery four: how is working memory capacity limited, and why? Curr. Dir. Psychol. Sci. 19, 51–57. doi: 10.1177/0963721409359277
Cowan, N., Morey, C. C., and Chen, Z. (2007). “The legend of the magical number seven,” in Tall Tales About the Mind and Brain: Separating Fact From Fiction, ed S. Della Sala (Oxford: Oxford University Press), 45–59. doi: 10.1093/acprof:oso/9780198568773.003.0005
Doherty, P. E. (2016). A study of the effects of spatial contiguity and hierarchically structured headings in a shipboard operating and maintenance manual. WMU J. Maritime Affairs 15, 97–125. doi: 10.1007/s13437-015-0090-4
Eysink, T. H., de Jong, T., Berthold, K., Kollöffel, B., Opfermann, M., and Wouters, P. (2009). Learner performance in multimedia learning arrangements: an analysis across instructional approaches. Am. Educ. Res. J. 46, 1107–1149. doi: 10.3102/0002831209340235
Fay, E., and Quaiser-Pohl, C. (1999). “Schnitte”- Ein Test zur Erfassung des Räumlichen Vorstellungsvermögens. Frankfurt: Swets Test Services.
Florax, M., and Plötzner, R. (2010). What contributes to the split-attention effect? The role of text segmentation, picture labelling, and spatial proximity. Learn. Instruct. 20, 216–224. doi: 10.1016/j.learninstruc.2009.02.021
Fu, B., Noy, N. F., and Storey, M. A. (2017). Eye tracking the user experience–an evaluation of ontology visualization techniques. Semant. Web 8, 23–41. doi: 10.3233/SW-140163
Ganier, F. (2004). Factors affecting the processing of procedural instructions: implications for document design. IEEE Transact Profess. Commun. 47, 15–26. doi: 10.1109/TPC.2004.824289
Ginns, P. (2006). Integrating information: a meta-analysis of the spatial contiguity and temporal contiguity effects. Learn. Instruct. 16, 511–525. doi: 10.1016/j.learninstruc.2006.10.001
Goldberg, J. H., and Kotval, X. P. (1999). Computer interface evaluation using eye movements: methods and constructs. Int. J. Ind. Ergon. 24, 631–645. doi: 10.1016/S0169-8141(98)00068-7
Hegarty, M., Carpenter, P. A., and Just, M. A. (1996). “Diagrams in the comprehension of scientific texts,” in Handbook of Reading Research, Vol. 2, eds T. Barr, M. L. Kamil, P. Mosenthal, and P. D. Pearson (Mahwah, NJ; New York, NY: Erlbaum, 641–648.
Hegarty, M., Kriz, S., and Cate, C. (2003). The roles of mental animations and external animations in understanding mechanical systems. Cogn. Instr. 21, 209–249. doi: 10.1207/s1532690xci2104_1
Huff, M., Bauhoff, V., and Schwan, S. (2012). Effects of split attention revisited: a new display technology for troubleshooting tasks. Comput. Human Behav. 28, 1254–1261. doi: 10.1016/j.chb.2012.02.008
Jang, J., Schunn, C. D., and Nokes, T. J. (2011). Spatially distributed instructions improve learning outcomes and efficiency. J. Educ. Psychol. 103, 60–72. doi: 10.1037/a0021994
Jarodzka, H., Janssen, N., Kirschner, P. A., and Erkens, G. (2015). Avoiding split attention in computer-based testing: is neglecting additional information facilitative? Br. J. Educ. Technol. 46, 803–817. doi: 10.1111/bjet.12174
Kalyuga, S. (2011). Cognitive load theory: how many types of load does it really need? Educ. Psychol. Rev. 23, 1–19. doi: 10.1007/s10648-010-9150-7
Kalyuga, S., and Singh, A. M. (2016). Rethinking the boundaries of cognitive load theory in complex learning. Educ. Psychol. Rev. 28, 831–852. doi: 10.1007/s10648-015-9352-0
Leppink, J., Paas, F., Van der Vleuten, C. P., Van Gog, T., and Van Merriënboer, J. J. (2013). Development of an instrument for measuring different types of cognitive load. Behav. Res. Methods 45, 1058–1072. doi: 10.3758/s13428-013-0334-1
Leppink, J., Paas, F., Van Gog, T., van Der Vleuten, C. P., and Van Merriënboer, J. J. (2014). Effects of pairs of problems and examples on task performance and different types of cognitive load. Learn. Instruct. 30, 32–42. doi: 10.1016/j.learninstruc.2013.12.001
Liversedge, S. P., and Findlay, J. M. (2000). Saccadic eye movements and cognition. Trends Cogn. Sci. 4, 6–14. doi: 10.1016/S1364-6613(99)01418-7
Mayer, R. E. (2014). The Cambridge Handbook of Multimedia Learning, 2nd Edn. Cambridge, MA: Cambridge University Press. doi: 10.1017/CBO9781139547369
Mayer, R. E., and Moreno, R. (2003). Nine ways to reduce cognitive load in multimedia learning. Educ. Psychol. 38, 43–52. doi: 10.1207/S15326985EP3801_6
Mayer, R. E., Sobko, K., and Mautone, P. D. (2003). Social cues in multimedia learning: role of speaker's voice. J. Educ. Psychol. 95, 419–425. doi: 10.1037/0022-0663.95.2.419
McNeish, D. (2017). Thanks coefficient alpha, we'll take it from here. Psychol. Methods 23, 412–433. doi: 10.1037/met0000144
Miller, G. A. (1956). The magical number seven plus or minus two: some limits on our capacity for processing information. Psychol. Rev. 63, 81–97. doi: 10.1037/h0043158
Moore, P., and Fitz, C. (1993). Using Gestalt theory to teach document design and graphics. Tech. Commun. Q. 2, 389–410. doi: 10.1080/10572259309364549
Nebel, S., Schneider, S., and Rey, G. D. (2016). From duels to classroom competition: social competition and learning in educational videogames within different group sizes. Comput. Human Behav. 55, 384–398. doi: 10.1016/j.chb.2015.09.035
Owens, P., and Sweller, J. (2008). Cognitive load theory and music instruction. Educ. Psychol. 28, 29–45. doi: 10.1080/01443410701369146
Paas, F. G. W. C., and van Merriënboer, J. J. G. (1993). The efficiency of instructional conditions: an approach to combine mental effort and performance measures. Hum. Factors 35, 737–743. doi: 10.1177/001872089303500412
Paek, S., Hoffman, D. L., and Saravanos, A. (2017). Spatial contiguity and incidental learning in multimedia environments. Br. J. Educ. Technol. 48, 1390–1401. doi: 10.1111/bjet.12488
Rayner, K. (1995). Eye movements and cognitive processes in reading, visual search, and scene perception. Stud. Vis. Inform. Process. 6, 3–22. doi: 10.1016/S0926-907X(05)80003-0
Revelle, W., and Zinbarg, R. E. (2009). Coefficients alpha, beta, omega, and the glb: comments on Sijtsma. Psychometrika 74, 145–154. doi: 10.1007/s11336-008-9102-z
Roodenrys, K., Agostinho, S., Roodenrys, S., and Chandler, P. (2012). Managing one's own cognitive load when evidence of split attention is present. Appl. Cogn. Psychol. 26, 878–886. doi: 10.1002/acp.2889
Schmidt-Weigand, F., Kohnert, A., and Glowalla, U. (2010). Explaining the modality and contiguity effects: new insights from investigating students' viewing behaviour. Appl. Cogn. Psychol. 24, 226–237. doi: 10.1002/acp.1554
Schnotz, W., and Baadte, C. (2015). Surface and deep structures in graphics comprehension. Mem. Cogn. 43, 605–618. doi: 10.3758/s13421-014-0490-2
Schnotz, W., and Bannert, M. (2003). Construction and interference in learning from multiple representation. Learn. Instruct. 13, 141–156. doi: 10.1016/S0959-4752(02)00017-8
Schroeder, N. L., and Cenkci, A. T. (2018). Spatial contiguity and spatial split-attention effects in multimedia learning environments: a meta-analysis. Educ. Psychol. Rev. 30, 679–701. doi: 10.1007/s10648-018-9435-9
Schüler, A. (2017). Investigating gaze behavior during processing of inconsistent text-picture information: evidence for text-picture integration. Learn. Instruct. 49, 218–231. doi: 10.1016/j.learninstruc.2017.03.001
Schüler, A., Arndt, J., and Scheiter, K. (2015). Processing multimedia material: does integration of text and pictures result in a single or two interconnected mental representations? Learn. Instruct. 35, 62–72. doi: 10.1016/j.learninstruc.2014.09.005
Simonsmeier, B. A., Flaig, M., Deiglmayr, A., Schalk, L., and Schneider, M. (2018). Domain-Specific Prior Knowledge and Learning: A Meta-Analysis. Research Synthesis 2018. Trier. Available online at: https://www.researchgate.net/publication/323358056_Domain-Specific_Prior_Knowledge_and_Learning_A_Meta-Analysis
Sweller, J. (1988). Cognitive load during problem solving: effects on learning. Cogn. Sci. 12, 257–285. doi: 10.1207/s15516709cog1202_4
Sweller, J. (2010). Element interactivity and intrinsic, extraneous and germane cognitive load. Educ. Psychol. Rev. 22, 123–138. doi: 10.1007/s10648-010-9128-5
Sweller, J. (2011). Cognitive load theory. Psychol. Learn. Motivat. Cogn. Educ. 55, 37–76. doi: 10.1016/B978-0-12-387691-1.00002-8
Sweller, J., Ayres, P., and Kalyuga, S. (2011). Cognitive load Theory. New York, NY: Springer Science + Business Media. doi: 10.1007/978-1-4419-8126-4
Sweller, J., and Chandler, P. (1994). Why some material is difficult to learn. Cogn. Instr. 12, 185–233. doi: 10.1207/s1532690xci1203_1
Tindall-Ford, S., Agostinho, S., Bokosmaty, S., Paas, F., and Chandler, P. (2015). Computer-based learning of geometry from integrated and split-attention worked examples: the power of self-management. J. Educ. Technol. Soc. 18:89–99. Available online at: http://www.jstor.org/stable/jeductechsoci.18.4.89
Unema, P. J., Pannasch, S., Joos, M., and Velichkovsky, B. M. (2005). Time course of information processing during scene perception: the relationship between saccade amplitude and fixation duration. Vis. Cogn. 12, 473–494. doi: 10.1080/13506280444000409
Van Gog, T., and Paas, F. (2008). Instructional efficiency: revisiting the original construct in educational research. Educ. Psychol. 43, 16–26. doi: 10.1080/00461520701756248
Vandenberg, S. G., and Kuse, A. R. (1978). Mental rotations, a group test of three-dimensional spatial visualization. Percept. Mot. Skills 47, 599–604. doi: 10.2466/pms.1978.47.2.599
Wickens, C. D., and Carswell, C. M. (1995). The proximity compatibility principle: its psychological foundation and relevance to display design. Hum. Factors 37, 473–494. doi: 10.1518/001872095779049408
Wickens, C. D., and McCarley, J. S. (2008). Applied Attention Theory. Boca-Raton, FL: Taylor and Francis. doi: 10.1201/9781420063363
Wirzberger, M., Beege, M., Schneider, S., Nebel, S., and Rey, G. D. (2016). One for all?! Simultaneous examination of load-inducing factors for advancing media-related instructional research. Comput. Educ. 100, 18–31. doi: 10.1016/j.compedu.2016.04.010
Ziefle, M. (2010). Information presentation in small screen devices: the trade-off between visual density and menu foresight. Appl. Ergon. 41, 719–730. doi: 10.1016/j.apergo.2010.03.001
Appendix A
Results Regarding ICL ME of Experiment
In order to investigate cognitive load and mental effort effects over time and to examine differences between the experimental conditions, a repeated measures MANCOVA was conducted. The condition was used as between-subject factor and measurement time (t1 = during learning, t2 = after learning) as within-subject factor. ICL and ME were implemented as dependent variables and prior knowledge and spatial ability was used as a covariate.
Spatial ability [Wilk's Λ = 0.93; F(2, 91) = 3.61; p = 0.03; = 0.07] and prior knowledge [Wilk's Λ = 0.92; F(2, 91) = 3.51; p = 0.03; = 0.07], were significant covariates. There was a significant effect for the between-subject factor condition [Wilk's Λ = 0.81; F(6, 182) = 3.45; p = 0.003;, = 0.10], no main effect for the within subject factor measurement time [Wilk's Λ = 0.98; F(2, 91) = 0.77; p = 0.47; = 0.02], and no interaction between the factors [Wilk's Λ = 0.92; F(6, 182) = 1.24; p = 0.29; = 0.04].
Follow up ANCOVAs regarding the between-subject factor condition and additional Sidak-corrected post-hoc tests revealed a significant effect with a high effect size for ICL [F(3, 92) = 5.60; p = 0.001; = 0.15]. Students in the medium condition reported a significant lower ICL than students in the high (Mdiff = −1.34; p = 0.03) and low condition (Mdiff = −1.88; p = 0.001). The other conditions did not differ from each other significantly. A significant effect with a high effect size was found for ME [F(3, 92) = 2.81; p = 0.04; = 0.08]. None of the Sidak-corrected post-hoc comparisons reached significance.
Appendix B
Results Regarding ICL of Experiment 2
In order to investigate cognitive load and mental effort effects over time and to examine differences between the experimental conditions, a repeated measures ANCOVA was conducted. The condition was used as between-subject factor and measurement time (t1 = during learning, t2 = after learning) as within-subject factor. ICL was implemented as dependent variable and prior knowledge and spatial ability was used as a covariate.
Spatial ability [F(1, 80) = 2.57; p = 0.11; = 0.03], and prior knowledge [F(1, 80) = 0.90; p = 0.35; = 0.01] were no significant covariates. There was a significant effect with a medium to high effect size for the between-subject factor condition [F(2, 80) = 5.36; p = 0.01; = 0.12]. Sidak-corrected post-hoc tests revealed that students in the medium condition reported a significant lower ICL than students in the high (Mdiff = −0.88; p = 0.02) and low condition (Mdiff = −0.86; p = 0.02). There was no main effect for the within subject factor measurement time [F(1, 80) = 2.50; p = 0.12; = 0.03] and no interaction between the factors [F(1, 80) = 0.44; p = 0.65; = 0.01].
Keywords: split-attention effect, proximity, integration, spatial contiguity principle, spatial contiguity failure
Citation: Beege M, Wirzberger M, Nebel S, Schneider S, Schmidt N and Rey GD (2019) Spatial Continuity Effect vs. Spatial Contiguity Failure. Revising the Effects of Spatial Proximity Between Related and Unrelated Representations. Front. Educ. 4:86. doi: 10.3389/feduc.2019.00086
Received: 09 April 2019; Accepted: 31 July 2019;
Published: 16 August 2019.
Edited by:
Monika Akbar, The University of Texas at El Paso, United StatesReviewed by:
Eric Fouh, University of Pennsylvania, United StatesClifford A. Shaffer, Virginia Tech, United States
Copyright © 2019 Beege, Wirzberger, Nebel, Schneider, Schmidt and Rey. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maik Beege, bWFpay5iZWVnZUBwaGlsLnR1LWNoZW1uaXR6LmRl
 Maik Beege
Maik Beege Maria Wirzberger
Maria Wirzberger Steve Nebel1
Steve Nebel1 Sascha Schneider
Sascha Schneider