Dynamic Deep Networks for Retinal Vessel Segmentation

Deep learning has recently yielded impressive gains in retinal vessel segmentation. However, state-of-the-art methods tend to be conservative, favoring precision over recall. Thus, they tend to under-segment faint vessels, underestimate the width of thicker vessels, or even miss entire vessels. To address this limitation, we propose a stochastic training scheme for deep neural networks that robustly balances precision and recall. First, we train our deep networks with dynamic class weights in the loss function that fluctuate during each training iteration. This stochastic approach–which we believe is applicable to many other machine learning problems–forces the network to learn a balanced classification. Second, we decouple the segmentation process into two steps. In the first half of our pipeline, we estimate the likelihood of every pixel and then use these likelihoods to segment pixels that are clearly vessel or background. In the latter part of our pipeline, we use a second network to classify the ambiguous regions in the image. Our proposed method obtained state-of-the-art results on five retinal datasets—DRIVE, STARE, CHASE-DB, AV-WIDE, and VEVIO—by learning a robust balance between false positive and false negative rates. Our novel training paradigm makes a neural network more robust to inter-sample differences in class ratios, which we believe will prove particularly effective for settings with sparse training data, such as medical image analysis. In addition, we are the first to report segmentation results on the AV-WIDE dataset, and we have made the ground-truth annotations for this dataset publicly available. An implementation of this work can be found at https://github.com/sraashis/deepdyn.

1. Introduction

Retinal vessels provide the only non-invasive view of the cardiovascular system. Thus, they are a key diagnostic feature for a number of diseases, including diabetic retinopathy (Kondermann et al., 2007), coronary heart disease (Rochtchina et al., 2007), and atherosclerosis (Ikram et al., 2004). However, the current standard of care requires manual inspection by an ophthalmologist, which makes it more challenging for people in developing nations and low-income communities to receive care. For example, only 30% of African Americans in southern Los Angeles reported being screened for diabetic retinopathy, despite being the most at-risk ethnicity (Lu et al., 2016). Therefore, it is vital to develop automatic retinal analysis methods to improve screening rates and public health outcomes.

The first step in a retinal analysis pipeline is to segment the regions in the image that correspond to the vasculature. Formally, vessel segmentation is a binary classification problem, but it presents unique challenges. First, existing datasets are small—typically on the order of 20–40 images—because an ophthalmologist has to manually trace every vessel in each fundus image. In addition, we need to classify hundreds of thousands or even millions of pixels per image, and the labels of nearby pixels are correlated.

Deep neural networks are the state of the art for a wide range of classification problems, but, due to the aforementioned challenges, training a deep network to segment retinal images is not straightforward. The two main strategies for applying deep learning to this domain are: (1) dividing each image into small patches to maximize the number of training samples (Ciresan et al., 2012) or (2) combining traditional convolutional layers with upsampling to learn both local and global features (Ronneberger et al., 2015). In particular, the U-net architecture (Ronneberger et al., 2015) and its extensions (e.g., Recurrent U-net, Alom et al., 2018) have achieved state-of-the-art results by applying the latter strategy.

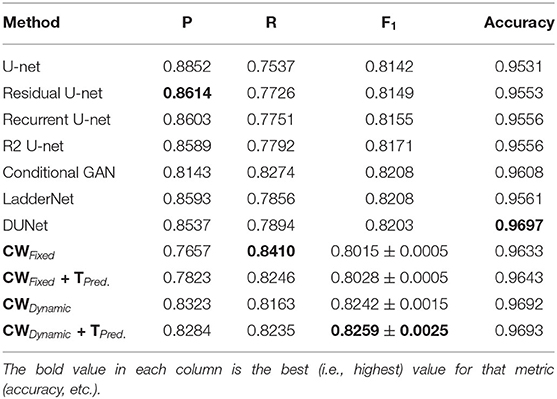
However, U-net and other deep learning-based methods favor precision over recall. As our experimental results in Tables 1–6 show, almost all state-of-the-art techniques have notably lower false-positive vs. false-negative rates. One reason these techniques tend to classify ambiguous vessels as background is because true positives (i.e., vessel pixels) typically constitute only around 10% of the image. However, under-segmenting the retinal vasculature can lead to missing faint vessels or underestimating the thickness of larger vessels. This, in turn, can compromise later diagnoses since many crucial bio-markers—including the artery-vein (AV) ratio, branching angles, number of bifurcation, fractal dimension, tortuosity, vascular length-to-diameter ratio and wall-to-lumen length—require precise measurements of individual vessels. In this work, we address this pitfall by using a dynamic, class-weighted loss function during training. As our results show, our proposed approach achieves both higher accuracy and more balanced precision and recall than prior methods. In other words, networks trained with dynamic weights can better classify fainter or ambiguous vessels.

TABLE 1

Table 1. Results on DRIVE dataset.

TABLE 2

Table 2. Results on STARE dataset.

TABLE 3

Table 3. Results on CHASE-DB dataset.

TABLE 4

Table 4. Results on AV-WIDE dataset.

TABLE 5

Table 5. Results on VEVIO dataset (Mosaics).

TABLE 6

Table 6. Results on VEVIO dataset (Frames).

More concretely, we propose a two-stage segmentation method that combines both upsampling and patch-based processing. Our approach also leverages loss functions with stochastic weights to better balance precision and recall. As our experiments show, our proposed pipeline achieves state-of-the-art results on five vessel segmentation datasets, including conventional fundus images (Hoover et al., 2000; Staal et al., 2004; Fraz et al., 2012), wide field-of-view (FOV) images (Estrada et al., 2015), and low-resolution video stills and mosaics (Estrada et al., 2012).

As Figure 1 shows, we separate the overall vessel segmentation problem into two stages: (1) likelihood estimation and (2) targeted prediction. In the first half of our pipeline, we train a U-net architecture to estimate the vessel likelihood of each pixel using a stochastic cross entropy loss. That is, we randomly assign a weight to each class on each training iteration, which forces the network to alternate between higher false positive vs. higher false negative rates during training, preventing it from getting stuck in a single minimum. In the second half of our pipeline, we first separate potential vessel pixels into two categories—easy and ambiguous—and then train a patch-based network to classify the latter. (Easy pixels can be classified with a simple threshold.) This second network, which we refer to as mini-U-net, is a scaled-down version of the network used in the first stage. To the best of our knowledge, we are the first to apply stochastic weights for vessel segmentation, as well as the first to combine both upsampling and patch-based learning into a single pipeline.

FIGURE 1

Figure 1. Dynamic Vessel Segmentation Pipeline: We separate vessel segmentation into simpler tasks. The steps in gray boxes are fixed, while the ones in blue require training. In (A), we first extract the green channel and preprocess it with contrast adaptive histogram equalization. Then, in (B) we train a U-net architecture using a dynamic loss function. This network outputs a likelihood map across the entire image. In (C), we use two thresholds, support and resistance, (SRS) to separate easy (top image) from ambiguous (bottom image) pixels. We assign the final labels to easy pixels at this stage. To classify ambiguous pixels, in (D) we use the support threshold to generate a high-recall estimate of the vascular structure (left image) and then skeletonize this mask (right image). We then intersect this skeleton with a lattice mask (shown in E) to find a set of seed points (shown in F). The left image in (F) shows the seed locations for the entire image, while the right image is a close-up of the square shown in red. We then define a small patch around each seed point and train a small network (mini-U-net) on these patches (G). Each patch has two channels. The channel highlighted with the purple border is extracted from the original likelihood map, while the channel with the green border includes only the ambiguous pixels in that region. In (H), we merge the mini-U-net predictions for ambiguous pixels with the labels for the easy pixels to obtain our complete segmentation result (shown in I). Figure best viewed on-screen.

The rest of this paper is organized as follows. First, we discuss related work on vessel segmentation, particularly deep learning-based approaches. Then, we detail our complete methodology, including our stochastic loss function and targeted prediction steps. We then present and discuss experimental results on five datasets and explore avenues for future work.

2. Related Work

Vessel segmentation has a long history, although the advent of deep neural networks has yielded significant improvements in recent years. Earlier techniques relied primarily on handcrafted features, including matched filters (Chaudhuri et al., 1989), quadrature filters (Läthén et al., 2010), and Gabor filters (Yavuz and Köse, 2011; Farokhian and Demirel, 2013). The latter approach, in particular, uses a predefined kernel bank to incorporate all vessel widths and orientations. However, handcrafted features are limited by our ability to analytically model the segmentation process. Other classic techniques, as surveyed further in Kaur and Kaur (2014), include piece-wise thresholding (Hoover et al., 2000), region growing (Martínez-Pérez et al., 1999), and concavity measurements (Lam et al., 2010). In addition to handcrafted features, some prior approaches used graph-theoretic techniques to trace the vascular structure, including shortest-path tracking (Estrada et al., 2012) and the fast marching algorithm (Benmansour and Cohen, 2011).

Since the breakthrough by convolutional neural networks (CNNs) on the ImageNet dataset in 2012 (Krizhevsky et al., 2012), deep learning has achieved tremendous success across a wide array of machine learning tasks (Krizhevsky et al., 2012; He et al., 2017; Alom et al., 2018; Jiang and Tan, 2018). Currently, deep networks are the state of the art in vessel segmentation. In particular, the most successful deep architecture in this domain—U-net (Ronneberger et al., 2015)—combines traditional convolutional layers with feature upsampling to estimate both local and global image features. As noted above, earlier deep learning approaches (Ciresan et al., 2012; Dasgupta and Singh, 2017) divided an image into a series of patches and applied a classifier to each patch independently. For instance, Dasgupta and Singh (2017) divided the full image into small patches to train a CNN, while Ciresan et al. (2012) defined a patch around each pixel and used those patches to train their network. One of the drawbacks of patch-based approaches is that we need to train a CNN with a large number of small patches, which have redundant information and little context. The upsampling in U-net, on the other hand, allows a network to train with fewer, significantly larger patches.

There are numerous extensions to the original U-net architecture. Alom et al. increased the performance of U-net by introducing residual connections and a recursive training strategy (Alom et al., 2018), albeit at the expense of increased training time due to the extra connections and recursion. Zhuang et al. arranged two U-net architectures in serial fashion, enabling the architecture to learn more abstract features (Zhuang, 2018). This serialization significantly increases the training time and requires heavy computational infrastructure to be able to train well. Jin et al. used deformable CNNs to construct better vascular features (Jin et al., 2018), but also with added training complexity. Finally, Jiang and Tan combined conditional generative adversarial networks (GANs) with U-net (Jiang and Tan, 2018); their approach achieved more balanced results than the other U-net extensions but at the cost of significant additional complexity (GANs are notoriously hard to train; Mescheder et al., 2018). In contrast, our approach not only yielded better results, but is simpler and faster to train, as detailed in the following section.

3. Methodology

As noted above, we separate vessel segmentation into two stages. Figure 1 details each step of our pipeline. In the first stage, we use a stochastic loss function to obtain an overall likelihood map for every pixel in the image. Then, we identify those pixels that are most likely to be misclassified—generally faint vessels and pixels at the periphery of thick vessels—and apply a second, smaller network to these ambiguous regions. Below, we first present and motivate the use of stochastic loss functions and then discuss each step in our pipeline in turn.

3.1. Dynamic Loss Functions

A weighted loss function penalizes some types of errors more than others. They are useful for problems with unbalanced datasets or in which we want to prioritize certain outcomes (e.g., minimize false positives for a particular class). Traditionally, these weights are fixed a priori by estimating them using a training set.

In this work, however, we propose using dynamic or stochastic weights. In this case, each weight is defined not as a single value but as a distribution. During training, every time we feed a new mini-batch to the network, we first sample weights for each class and then use those sampled weights to compute the loss. Since the weights will vary for each training iteration, the same error will be penalized more or less heavily at different points during training. Empirically, this forces the network to optimize across all ranges of false positive vs. false negative rates, leading to more robust classification. For concreteness, below we discuss the use of dynamic weights for the cross-entropy loss, but one can randomize any weighted loss function. The cross-entropy loss is a natural choice for binary classification (e.g., it was also used in the original U-net paper; Ronneberger et al., 2015) since it encourages values to converge toward either zero or one by penalizing a network proportionally to how certain it is about its output. Intuitively, a misclassification in which the network is 99% sure of the wrong label is penalized more heavily than one in which the network is only 51% sure. In addition, computing the CE loss is very fast, which speeds up training. This loss is defined as follows:

$\begin{array}{ll}H=-{\displaystyle \sum _x}p(x)logq(x)& (1)\end{array}$

where p is the true distribution and q is the predicted distribution, i.e., the network's outputs. The training process aims to make these two distributions as close as possible. However, when the data is highly skewed, we can trivially obtain a high accuracy by always assigning the most common class to every pixel. In the case of vessel segmentation, very few pixels are part of a vessel, so always assigning a label of background will yield an accuracy of around 90% (but a recall of 0%). A straightforward way to ameliorate this imbalance is by applying different weights to each class:

$\begin{array}{ll}H=-{\displaystyle \sum _x}{w}_{i}p(x)logq(x)& (2)\end{array}$

where w_i are the class weights and i = 1, ..., C are the class labels (C = 2 for binary segmentation). By using weights, we force the network to care about both positive and negative samples equally during training. An easy way to define these weights is to estimate them from the training set, as was done for the original U-net architecture (Ronneberger et al., 2015).

A major drawback of the above strategy is that it imposes a fixed ratio of vessel-to-background. As our experiments show, this ratio is a major determinant of whether ambiguous pixels will be mapped to either vessel or background (Table 8). In other words, when faced with an ambiguous pixel, the network will use this ratio to “guess” which label to assign to it. We can see in Figures 3B,C that a network trained with fixed weights will preferentially over- or under-segment ambiguous pixels.

Instead, we propose using stochastic weights which are randomly generated at each training iteration:

$\begin{array}{ll}H=-{\displaystyle \sum _x}{w}_{rand(1,\alpha ,s)}p(x)logq(x)& (3)\end{array}$

Here, rand(1, α, s) draws two random weights [w_negative, w_positive], for both positive (i.e., vessel pixels) and negative (i.e., background pixels) classes, on each iteration. These weights serve as the costs for false negative and false positive in that iteration, resp. Both the w_negative and w_positive values are randomly drawn from evenly spaced samples in the interval [1, α] with s as the step size between consecutive values. In other words, the possible values that can be sampled are [1, 1 + s, 1 + 2s, ..., α − 2s, α − s, α].

Dynamic weights are both distinct from and compatible with other training schemes that leverage stochasticity (e.g., stochastic gradient descent, SGD). In particular, SGD and related data-shuffling techniques randomize over samples, while our stochastic weights randomize over loss functions. In standard SGD, the error associated with each pixel in each image is always the same; in our approach, on the other hand, this error will vary for the same image over different training epochs.

As noted earlier and as Figures 3B,C show, fixed weights fail to account for fainter vessels and are insensitive to noise. Stochastic costs reduce this bias because the network must vary in how aggressively it segments ambiguous pixels throughout the training process. Even if completely different weights are given in a subsequent iteration, some of the information learned in the previous step is preserved, leading to a more balanced segmentation of ambiguous regions. As Figure 3D shows, dynamic weights capture faint vessels without introducing additional noise.

We now discuss the various steps of our proposed pipeline below.

3.2. Likelihood Map

The first step in our pipeline consists of training a U-net architecture using stochastic weights to derive a likelihood map over the entire image. The goal of this map is not to segment the image directly but to indicate how likely a particular pixel is to be part of a vessel. We do not segment the image at this stage because the up-sampling used by U-net blurs the original vessels, making it difficult to correctly label high-frequency elements (e.g., thin vessels or pixels near the edge of a thick vessel).

Figure 3 contrast the outputs of our stochastic U-net vs. two fixed-weight U-nets on the datasets used in our experiments (see figure for details). Overall, networks trained with fixed weights struggle to balance ambiguous pixels with noisy regions of the image. Our stochastic weights, on the other hand, are better able to ignore vessel-like artifacts, e.g., the rim of a lens as seen in Figure 3.

3.3. Support-Resistance Segmentation (SRS) for Easy Pixels

The likelihood map generated in the previous step ranges from [0,1]. Pixels with a higher probability of being vessels have values closer to one (and closer to zero otherwise). Intuitively, the closer a value is to either extreme, the more confident the network is in its classification. Thus, we use this likelihood map to separate pixels into either easy or ambiguous classes. The top and bottom of Figure 1C show the easy and ambiguous pixels, respectively, of the likelihood map in Figure 1B.

We use two thresholds to classify pixels into these two classes. We refer to the lower threshold as support and the upper threshold as resistance. All pixels between resistance and support are considered ambiguous. Pixels below support (those with values near zero), which account for the majority of pixels, are background pixels whereas pixels above the resistance (those with value near one) are considered vessel pixels.

The choice of support and resistance thresholds affects the trade-off between precision and recall. Thresholds close to one and zero, respectively, lead to higher precision for easy pixels but cause more pixels to fall in the intermediate, ambiguous band. Thresholds closer to the middle lead to higher recall, but affect precision. For our experiments, selected a support of 20 and a resistance of 235 based on empirical evidence. Specifically, we tested a wide range of thresholds on all datasets and chose the pair that worked best across the various validation sets.

3.4. Targeted Prediction for Ambiguous Pixels

The last stage of our pipeline segments ambiguous pixels, i.e., those that fall within the support-resistance band described above. Figures 1D–G illustrate the various steps involved in this targeted prediction. Generally, most vessel pixels will lie above the support threshold, so they have already been predicted with high precision. To classify the pixels with intermediate values, we train a second, patch-based network only on those pixels. We use the same threshold (20 for support and 235 for resistance) for all datasets, which proves that these thresholds can work with wide range of images. As Figure 2 shows, this mini-U-net network is a scaled-down version that uses only the middle layers of the full U-net architecture. Introducing another network significantly reduces the amount of information to be learned for ambiguous pixel classification. Because most of the hard work (e.g., learning vessel patterns, separating the background, etc.) has been done by the full U-net in the first step, the mini-U-net can focus on identifying ambiguous pixels. We use two channels as inputs to this network: the full likelihood map outputted by the first U-net (Figure 1B) and a version of this likelihood map which only contains ambiguous pixels (the bottom image in Figure 1C). Mini-U-net was trained from the scratch because, as mentioned earlier, it is a scaled down version of U-net. If we had reused the full U-net's weights to initialize this second network, we would have had to select a fraction of filters from each layers. However, since neural network learned features are represented collectively, taking a fraction would likely lead to negative transfer, i.e., the network would start closer to a worse local minimum and we would require more data to reach acceptable performance. Using a full U-net for targeted prediction, on the other hand, is very data inefficient since we only require a small region around each pixel to classify it correctly.

FIGURE 2

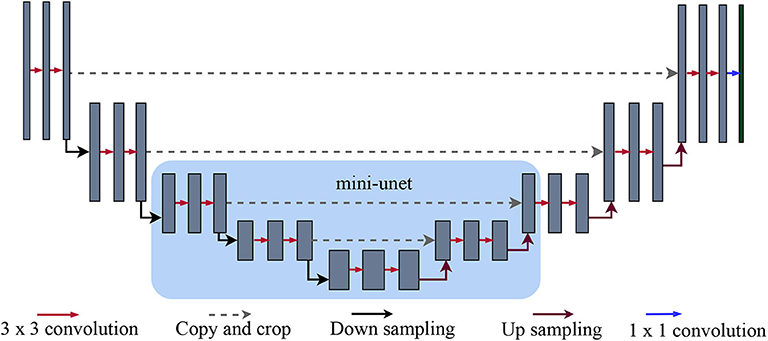
Figure 2. U-net and mini-U-net architectures: As originally detailed in (Ronneberger et al., 2015), the first half of the U-net architecture is a standard sequence of convolution and max-pooling layers. The layers in the second half, on the other hand, receive two inputs: the features from the previous layer and the features from the corresponding layer in the first half of the network (i.e., the one with the same dimensionality). The features from previous layers are upsampled to match the larger dimensions of subsequent layers. Intuitively, the upsampled features provide more global information, while the features transferred from the earlier layer give more local information. Our mini-U-net architecture (highlighted by the light blue square) consists of the middle layers of the full U-net.

Unlike prior patch-based approaches (e.g., Ciresan et al., 2012), we do not extract a patch for every pixel. Instead, we use a sparse set of p × p patches centered at the intersections between ambiguous pixels and a regular lattice, as described below:

1. Raw estimate: We first produce a high-recall binary mask by considering all pixels above the support threshold as vessels. Intuitively, this mask should contain almost no false negatives, but will have numerous false positives. We then skeletonize the largest connected component in this mask (Figure 1D).

2. Patch selection: We then define a regular lattice of width p/2 (Figure 1E) and determine the intersection points between this lattice and the skeleton from the previous step (Figure 1D). We empirically verified that the union of the patches defined by these intersections always covered every ambiguous pixel.

3. Mini-U-net classification: Finally, we classify the ambiguous pixels in each patch using our second network (Figure 1G). For each patch, we extract the corresponding regions in the full likelihood map and the map with only ambiguous pixels, resp. Intuitively, the second channel indicates which pixels are most crucial to classify correctly. Finally, we use the outputs from the second network as the final labels for ambiguous pixels (Figure 1H).

4. Experiments and Results

We carried out experiments on five different retinal vessel datasets to verify the effectiveness of our proposed approach. Below, we first detail our experimental protocol and then discuss our results.

4.1. Materials and Methods

Hardware: All our experiments were conducted on a Dell Precision 7920R server with two Intel Xeon Silver 4110 CPUs, two GeForce GTX 1080 Ti graphics cards, and 128 GBs of RAM.

Datasets: We used five datasets for our experiments (see the first column of Figure 3 for a sample image from each dataset):

• DRIVE (Staal et al., 2004): 40, 565×584 color fundus images centered on the macula. Each image includes a circular field-of-view (FOV) mask. This dataset is pre-divided into 20 training and 20 test images, but we further divided the training set randomly into 15 training and 5 validation images.

• STARE (Hoover et al., 2000): 20, 700× 605 color images with no FOV masks, also centered on the macula. Many images exhibit some degree of pathology (e.g., exudates).

• AV-WIDE (Estrada et al., 2015): 30 wide-FOV images. Image sizes vary, but are around 1300×800 pixels for most images. Images are loosely centered on the macula. As explained below, we used the existing, graph-based annotations to manually segment these images.

• VEVIO (Estrada et al., 2012): This dataset has two types of images: 16, 640×480 frames from 16 different video indirect ophthalmoscopy (VIO) videos and 16 corresponding mosaics (around 600×500 pixels) obtained by fusing different frames into a single image (Estrada et al., 2011). Due to the difficult image acquisition process, these images are blurry and have lens artifacts.

• CHASE-DB (Fraz et al., 2012): 14 left-to-right pairs of color images centered on the optic nerve (28 images total). Images are 999×960 pixels.

FIGURE 3

Figure 3. Dynamic vs. fixed likelihoods maps: (A) Sample DRIVE, STARE, CHASE-DB, AV-WIDE, and VEVIO (Mosaics and Frames) images. (B) Likelihood map using weights estimated from the training data. (C) Likelihood map using equal weights for both classes. (D) Likelihood map using dynamic weights (see text for details). Dynamic weights allow the network to capture more vessels without introducing additional noise (examples highlighted in red circles). The noise in all but the next-to-last row consists of choroidal vessels, a frequent source of false positives in retinal vessel segmentation. The main artifact in the VEVIO frames is the rim of the handheld zooming lens used to capture these images (see Estrada et al., 2011 for details). Figure best viewed on-screen.

DRIVE and STARE are standard datasets in the field of vessel segmentation, while the other three datasets provide different imaging conditions. The VEVIO dataset has lower-resolution images with more artifacts, while AV-WIDE and CHASE-DB consist of higher-resolution images. The AV-WIDE images also have much wider FOV. In addition, different datasets have different ratios of healthy vs. unhealthy images. Overall, we believe that these various datasets provide a good benchmark for assessing a method's general effectiveness.

Data preparation: We used only the green channel of each image. We then applied contrast adaptive histogram equalization (Zuiderveld, 1994) as a preprocessing step to enhance contrast. Given the limited number of images in each dataset, we used image augmentation techniques to increase our data size. Specifically, we flipped the input image horizontally and vertically randomly in each iteration.

Ground truth preparation: All datasets except AV-WIDE had preexisting ground-truth pixel labels. The original AV-WIDE dataset had only graph-based labels, so we manually traced the vessels in Adobe Photoshop CS (Adobe Systems Inc., San Jose, CA) using a Wacom Intuous3 graphics tablet (Wacom Co. Ltd, Kazo-shi, Saitama, Japan) to obtain pixel-level segmentations. The original, graph-based annotations had been carried out by an expert ophthalmologist, so we followed them exactly.

Network architectures: As noted above, we used a full-sized U-net architecture for our initial probability map and a smaller, mini-U-net network for targeted prediction. The U-net architecture consist of a series of down-sampling steps followed by the same number of up-sampling steps. Each up-sampling step receives, crops to match the size, and concatenates the feature map from the down-sample step on the same level, as shown in Figure 2. We used 3×3-pixel kernels except in the last layer; here, we used 1×1 kernels to produce two outputs, which are then passed through a softmax layer to obtain two probabilities: one for that particular pixel being a vessel and another for it being part of the background. Depending on which of the probabilities is higher, a pixel is labeled as either vessel or background. As in the original U-net architecture (Ronneberger et al., 2015), this network receives inputs of size 572×572 pixels, but only predicts values for the internal 388×388 pixels. The outer band of 92×92 pixel allows the U-net a wider view of the vascular structure. As in (Ronneberger et al., 2015), we shift the U-net to obtain a label for every pixel and mirror the 388× 388 region if the outer band extends beyond the image. A single patch size of 388×388 proved suitable for the various datasets (but see section 6 for possible extensions).

Our second network, the mini-U-net architecture, is identical to the middle three layers of the full-size U-net (see Figure 2). Thus, its input size is 140 × 140 and it produces labels for the middle 100×100 pixels. Similar to the first network, we expand and mirror patches as needed. However, we train this network using a dice loss, rather than cross entropy because our goal is to maximize the F1 score of our pipeline. The weighted dice loss is given by the following formula:

$\begin{array}{ll}{F}_{\beta }=(1+{\beta }^2)·\frac{precision·recall}{{\beta }^2·precision+recall},& (4)\end{array}$

where β controls how much we want to favor precision vs. recall. Higher beta yields higher precision and vice versa. As with the full-size U-net, we used a stochastic loss in which we sampled β for each training iteration:

$\begin{array}{ll}{F}_{\beta }=(1+B_{rand}{(1,\alpha ,s)}^2)·\frac{precision·recall}{B_{rand}{(1,\alpha ,s)}^2·precision+recall},& (5)\end{array}$

where B_rand(1, α, s) is picked randomly within range 1 - α with a stepsize of s.

Training parameters: We trained our networks using Adam optimization (Kingma and Ba, 2014) with a learning rate of 0.001 and a mini-batch size of 4. We trained the full U-net for 250 epochs and the mini-U-net for 60 epochs. For the full U-net, we used stochastic weights of w_rand(1, 100, 1), i.e., where weights randomly oscillated within a range of 1 − 100 with a step size of 1. For the mini-U-net, we used a dice loss with stochastic weights of B_rand(1, 2, 0.1), where β randomly oscillated between 1 and 2 with a step size of 0.1.

Model validation: We used five-fold cross validation with training, validation, and test sets on all datasets except DRIVE, since this dataset already had a predefined test set. Five-fold CV proved best for these datasets because of their small size (minimum of 16, maximum of 40 images). Larger folds would have yielded too few images in the validation and test sets and led to overfitting. For each fold, we randomly split the training set into 75% training and 25% validation images. In our tables, we report the performance on the test set across all the folds. Note that, using this protocol, each image is only included once in a test set.

4.2. Pipelines Tested

To better understand the impact of each stage of our pipeline, we tested two versions of our approach, as well as two baseline methods:

• Dynamic weights with targeted prediction: Our proposed approach.

• Dynamic weights only: We trained the full U-net using dynamic class weights, but omitted the targeted prediction step.

• Fixed weights only: We trained the full U-net using fixed class weights based on the ratio of vessel to background pixels in the training set. No targeted prediction step.

• Fixed weights with targeted prediction: We applied both fixed weights and targeted prediction.

The parameters for the Mini-U-net at the end of the full pipelines (variations 1 and 4) were the same for both configurations. For pipelines 2 and 3, we used a threshold of 0.5 to convert the likelihood map into a binary classification. In total, we carried out an ablation study consisting of twenty experiments across five datasets.

4.3. Results

We quantified our method's performance in terms of precision, recall and F1 score (also called F-measure). The softmax threshold for computing these metrics is 0.5. For comparison to the state of the art, we also calculated the accuracy of our model, even though this value can be misleading for unbalanced datasets (Estrada et al., 2012). The precision, recall, and accuracy values in our tables are the mean values across all test images. The reported F1 score is the harmonic average of the corresponding mean precision and recall values. As Forman et al. showed (Forman and Scholz, 2010), if the positive cases constitute around 7% or more of the samples, then this is an unbiased way to calculate the mean F1 score for k-fold cross validation. Across the different datasets, vessel pixels constituted around 10% of all pixels.

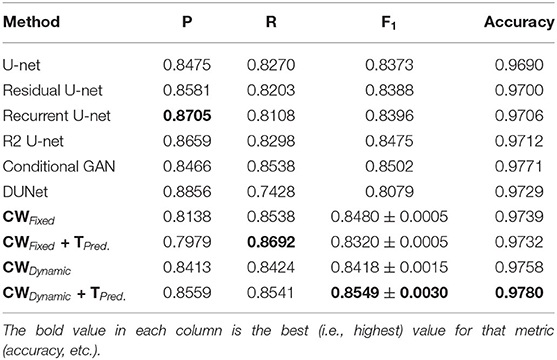
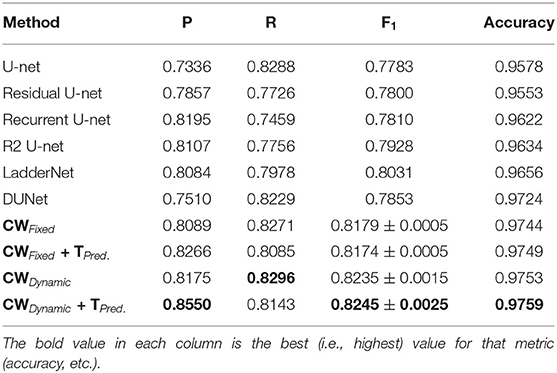
Tables 1–6 summarize our results on the various datasets. For completeness, we included the maximum deviation from the mean for the F1 score. A value in bold represents the best score for that particular column. For convenience, we also included those of current state-of-the-art approaches. Note, though, that we only list methods that reported F1 scores (or, equivalently, both precision and recall values). Due to the strong class imbalance between the two classes, accuracy alone is not an informative measure of performance. As the various tables show, our proposed pipeline consistently outperformed existing methods. To the best of our knowledge, our F1 scores and most of our accuracy values are state-of-the-art results across the five datasets.

Overall, dynamic weights outperformed fixed weights across the various datasets, including the highly studied DRIVE and STARE datasets, and led to more balanced precision and recall scores. Importantly, as the second row in Tables 1–6, shows, the F1 score of just our dynamic, class-weighted U-net (no targeted prediction) is better than the state-of-the-art techniques, demonstrating the usefulness of stochastic weights alone. Applying targeted prediction on the dynamic U-net's likelihood map further improved performance across the various datasets, showing that this second step is also of value for this problem. For example, in the DRIVE dataset, the full, stochastic pipeline obtained a precision of 0.8284, and a recall of 0.8235. The approach using only dynamic class weights, on the other hand, yielded precision of 0.8323, recall of 0.8163, and F1 score of 0.8242, which is already balanced, and better than other state of the art techniques. In contrast, the fixed-weight pipeline gave a more unbalanced results (precision of 0.7823 and recall of 0.8246). This pattern was replicated across datasets. Although the differences in results across the different state-of-the-art methods are not statistically significant, our method consistently achieved better recall with little or no sacrifice in precision.

Furthermore, as noted in section 4.1, we used the Adam optimizer to train our networks, which, like SGD, uses batches of data samples to compute the gradients. Therefore, the difference in performance between the fixed-weight and dynamic-weight variants of our pipeline is roughly the difference between (1) using only mini-batch for data randomization, and (2) combining data randomization with stochastic weights. As these results show, using stochastic weights greatly improves performance relative to shuffling the data alone.

Our method outperformed other extensions of the original U-net architecture, including LadderNet (Zhuang, 2018), R2Unet (Alom et al., 2018), and DUNet (Jin et al., 2018). The difference is particularly large for the CHASE-DB dataset (Table 3). Here, our method F₁ score was 2.66% higher than the previous state of the art (LadderNet).

Table 4 shows our results for the AV-WIDE dataset. Our paper is the first assessment of this dataset as we manually created the ground truth for it. As with the other datasets, we can observe a similar pattern of unbalanced precision and recall for fixed class weights. In contrast, our stochastic technique has more balanced precision and recall. Moreover, the F₁ score and accuracy are significantly higher for our method, particularly for the full pipeline with targeted prediction.

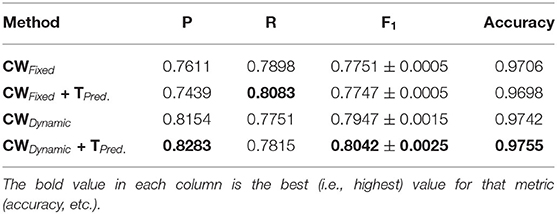
Our method also achieved state-of-the-art results in the highly challenging VEVIO dataset, which has two sets of images: composite mosaics and individual frames taken from a low-resolution video (Estrada et al., 2011). As with the other datasets, fixed class weights gave highly biased scores in terms of precision and recall, while dynamic weights gave more balanced results (Tables 5, 6). In conclusion, by evaluating our method on five different, well-known datasets (Tables 1–6), we have established that our technique yields better, more consistent results than existing state-of-the-art techniques.

5. Discussion

The main contributions of our technique are two-fold. First, we use dynamic, as opposed to fixed, weights on the loss function, which allow our networks to learn a more robust balance between false positives and false negatives. Second, we separate different types of tasks involved in retinal vessel segmentation, which, as we detail in section 5.4, makes the segmentation more robust compared to end-to-end training. The likelihood estimation step only focuses on capturing the vascular structure without worrying about the final segmentation. Conversely, the targeted prediction step relies on having a precomputed likelihood map with which to make the final predictions. We discuss specific properties of our approach below.

5.1. Dynamic Weights Yield Smoother Likelihood Maps

In Figure 3 (columns b and c), we can see that using class weights computed from the training set almost binarizes the image. All the likelihoods are very close to either 0 (background) or 1 (vessel); thus, we have no useful information with which to refine our estimate in the targeted prediction step. Any information about fainter pixels was lost. However, if we use dynamic weights, a higher percentage of pixels will be assigned non-trivial likelihood values (Figure 3D), which will allow our second network to better classify ambiguous pixels.

5.2. Dynamic Weights Yield More Balanced Precision and Recall

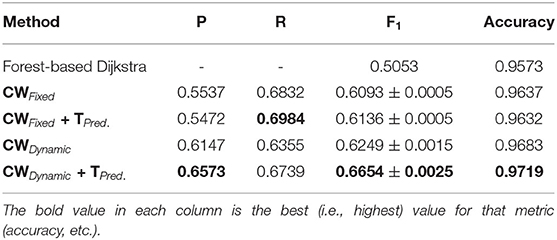
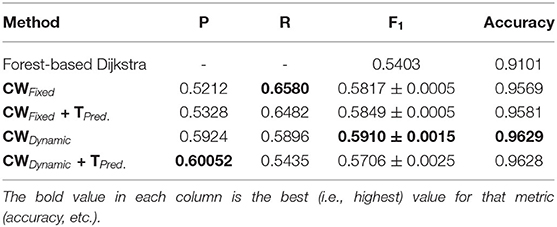
As we can observe from the results (Tables 1–6), our method consistently achieves a good balance between precision and recall. This implies that our approach handles fainter or more ambiguous pixels, rather than ignoring them. In contrast, the state-of-the-art results for the DRIVE dataset (Zhuang, 2018) report precision and recall values of 0.8593 and 0.7896, respectively. Our corresponding, more balanced values were 0.8284 and 0.8163. We can see even more of a difference on the VEVIO dataset (Tables 5, 6). For the mosaics, the precision and recall for the U-net with class weights were 0.5537 and 0.6832, respectively. However, our full, dynamic pipeline yielded values of 0.6573 and 0.6739.

Our dynamic weights on the loss function allow a network to settle on a local optimum that better balances precision and recall. As noted earlier, retinal images have a much higher percentage of background pixels (over 90%). Thus, a network trained on this type of data will be more reticent to label an ambiguous pixel a vessel (since the prior probability is so much lower). This imbalance makes the network settle on a local optimum that is skewed toward high precision and low recall. Previous approaches have ameliorated this effect by assigning fixed class weights in order to re-balance the classification problem. For example, if only 10% of pixels are vessels, then misclassifying those pixels will be penalized by a factor of 9. However, not all faint vessels are similar or distributed equally across different images, so a one-size-fits-all treatment is suboptimal. Our technique, on the other hand, applies stress tests during the training process to ensure that the network is robust across different ratios of precision and recall. As our experiments show, this approach allows the network to settle on a better optimum.

In more detail, Figure 4 illustrates the effects of dynamic vs. fixed weights during training for the DRIVE dataset. Here, each subplot on the left-hand side shows precision vs. recall during training, while the subplots on the right show this value for the validation set. As Figure 4C shows, a network that uses weights calculated from the training set will begin by strongly favoring recall, since a false negative is penalized more heavily than a false positive. An unweighted network (Figure 4E) will favor precision instead, since the probability that an ambiguous pixel is a vessel is very low, a priori. In contrast, We can clearly see that dynamic weights (first row) are balanced with regard to both precision and recall. This is one of the reasons why our technique generalizes more robustly and yields better results. Over time, the class-weighted and equal-weight networks learn to classify the training set, but their initial bias lead to poor results on the validation set (Figures 4D,F). If we look at Figures 4C,D, we see that this network is skewed toward high recall. Similarly, in Figures 4E,F we can see that a network trained with equal weights achieves almost perfect precision and recall at the end of training, which is an instance of overfitting. These network are very confident about easy pixels and therefore settle on an optimum that favors this class of pixels; however, this choice makes them ignore fainter pixels. Our method, on the other hand, (Figures 4A,B), had more balanced scores throughout the training process. The optimum on which it settled was more robust and thus achieved better scores on the validation and test sets. Our results suggest that the network was able to learn features that separate faint vessels from noise in the background.

FIGURE 4

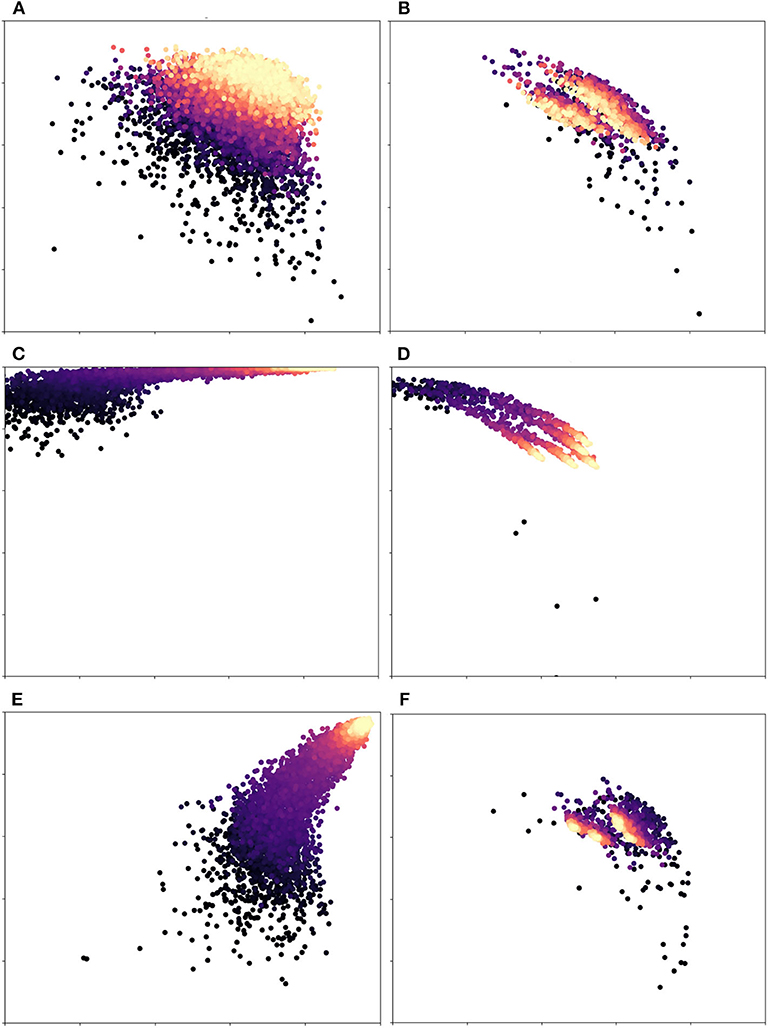
Figure 4. Precision(x-axis) vs. Recall(y-axis) for different weight variations: Each dot represents an iteration of training/validation; darker circles indicate earlier iterations, while lighter/golden ones indicate later iterations. The first row (A,B) is our proposed pipeline, while the second (C,D) and third rows (E,F) are class-based weights (the ones used by the original U-net) and equal weights, resp. The left column is the training set, while the right column corresponds to the validation set. The scale of both axes is [0.5, 1.0] in all plots. Equal weights are biased toward recall and class-based weights overfit to the training set. Dynamic weights, however, achieve a robust balance of precision and recall. Figure best viewed in color.

5.3. Effect of Different Weighing Schemes

Finally, we carried out additional analyses to investigate the impact of different weighing schemes on the final segmentation result. First, we trained a U-net architecture (without targeted prediction) with equal weights for the two classes. In other words, each misclassification, whether false positive or false negative, was weighted equally. Table 7 shows the results of this equal weighing on our different datasets (we also show the class-weighted results for each dataset for comparison). Equal weights yielded better precision but worst recall. Due to the roughly 9 to 1 class imbalance between background and vessel pixels, a network trained with equal weights will tend to label ambiguous pixels as background. We verified this trade-off further by systematically varying the class weights for the DRIVE dataset and recording the resulting precision and recall values. Table 8 lists the results when training with background-to-vessel weights of {1, 5}, {1, 1} (equal weights), {5, 1}, and {10, 1}. For comparison, the class-based weights were roughly 1 to 10. We also tested a U-net with dynamic weights, but with a range of weights spanning only 10 to 1 (our main experiments used a range of 100 to 1). In this case, the dynamic weights has less variance across training epochs.

TABLE 7

Table 7. Equal weights {1, 1} vs. class-based weights.

TABLE 8

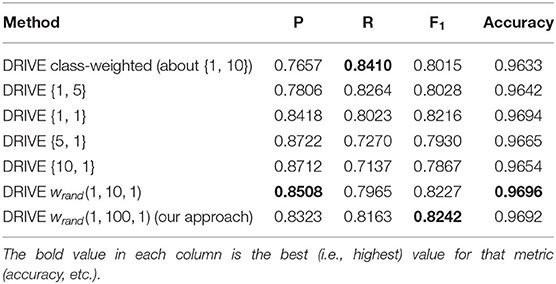
Table 8. Results of different combination of fixed weights in cross entropy loss function without targeted prediction for DRIVE dataset {w₀, w₁}={weight for class 0 or background pixels, and weight for class 1 or vessel pixel}.

Interestingly, the best fixed-weight result for the DRIVE dataset used equal weights (this result was not consistent across datasets, though, as Table 7 shows). Overall, we can see that the trade-off of precision vs. recall is driven by the ratio of class weights. Also, the dynamic weights with a 10-to-1 range did not balance the precision vs. recall as much as the 100-to-1 weights, so their results more closely resembled equal weights. We observed a similar pattern for the other datasets (we omitted these results for conciseness). Skewed weights tend to favor either precision or recall and reduce the other score accordingly. By effectively balancing these two scores, our dynamic weights achieve a better result.

In summary, one of the main contributions of our technique is that it yields a better balance of precision and recall relative to current state-of-the-art techniques. This claim is also supported by Figure 4. In other words, the lower of either precision and recall is higher for our method than for previous methods. This balance not only yields better F1 scores, but it also ensures that our method is not “cheating.” What we mean by that is the following: (1) Precision only factors false positives, so a method can achieve a very high precision score by labeling most ambiguous pixels as background (because background pixels outnumber vessel pixels by a roughly 10-to-1 ratio). (2) Conversely, one can trivially achieve a very high recall by labeling most ambiguous pixels as vessel. Simultaneously achieving both high precision and high recall, though, is much more challenging. Our proposed approach is able to achieve this through both dynamic weights on the loss function and targeted prediction. Depending on which class the dynamic weights on the loss function are skewed toward on a given training epoch, the network will learn to favor either precision or recall under different conditions. This, in turn, makes the network more robust to different ratios of vessel-to-background pixels in novel images.

5.4. Two-Step Segmentation

Our proposed approach has two distinct steps, instead of a single, end-to-end process as is common in deep learning. However, although current state-of-the-art techniques for vessel segmentation (e.g., Alom et al., 2018; Zhuang, 2018) are trained end-to-end, they are more complicated and resource-intensive than our method. For example, Alom et al. (2018) involves recurrent connections making it complex and hard to train, while Zhuang (2018) involves two U-nets stacked together. Our two step, estimation technique, on the other hand, divides the segmentation task into two simple task and optimizes a different network for each one. This partitioning is similar to one of the finest advances in object detection technique He et al. (2017), which uses a region proposal network to propose object regions and a classification network to classify those regions to different classes.

6. Conclusion

Accurately segmenting the retinal vasculature is crucial for retinal disease diagnosis. However, this task is not easy because the quality and features of a retinal image depend on many factors, including the imaging device, lighting conditions, and an individual's anatomy. Thus, trying to enforce a single, static approach for all retinal images is suboptimal. Instead, by separating retinal vessel segmentation into sub-tasks, we have more degrees of freedom with which to adapt our processing to the current image. Furthermore, dynamic weights allow a network to learn to classify all types of vessels, regardless of their color or intensity, which in turn generates a likelihood map with clear distinctions between vessel, background, and noise. Our targeted prediction step then uses this likelihood map to better classify ambiguous pixels. Our technique gives better results than state-of-the-art techniques, many of which are much complex and less intuitive. Instead of optimizing a single, black box, our approach breaks down the problem into more manageable steps and makes these steps more robust by using dynamic weights.

In future work, we plan to apply our pipeline to other medical imaging domains, including CT and MRI scans. We also intend to investigate the theoretical properties of our stochastic weights further. Another important avenue of further work is to make the patch size adaptive. While a single patch size proved adequate for our experiments, it is not optimal across all fundus images. If the vessels in the image are very large, then a 388 × 388 patch size cannot capture enough context around then; conversely, if they're very small, then this patch size will include too much of the vasculature at once (and likely under-segment the smallest vessels). Overall, our goal is to continue developing learning methods that make the most of the relatively small dataset available in the medical imaging domain and that can robustly adapt to novel conditions.

Data Availability Statement

The source code and datasets analyzed for this study can be found in the following GitHub repository: https://github.com/sraashis/deepdyn.

Author Contributions

RE conceived of the original idea. AK wrote the source code, extended the algorithm, and ran the experiments. AK and RE wrote the manuscript.

Funding

This research was funded in part by NSF award 1849946.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This manuscript has been released as a Pre-Print (Khanal and Estrada, 2019) at https://arxiv.org/abs/1903.07803.

References

Alom, M. Z., Hasan, M., Yakopcic, C., Taha, T. M., and Asari, V. K. (2018). Recurrent residual convolutional neural network based on U-net (R2U-net) for medical image segmentation. CoRR abs/1802.06955. doi: 10.1109/NAECON.2018.8556686

PubMed Abstract | CrossRef Full Text | Google Scholar

Benmansour, F., and Cohen, L. D. (2011). Tubular structure segmentation based on minimal path method and anisotropic enhancement. Int. J. Comput. Vis. 92, 192–210. doi: 10.1007/s11263-010-0331-0

CrossRef Full Text | Google Scholar

Chaudhuri, S., Chatterjee, S., Katz, N., Nelson, M., and Goldbaum, M. (1989). Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Trans. Med. Imaging 8, 263–269. doi: 10.1109/42.34715

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciresan, D., Giusti, A., Gambardella, L. M., and Schmidhuber, J. (2012). “Deep neural networks segment neuronal membranes in electron microscopy images,” in Advances in Neural Information Processing Systems 25, eds F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (Lugano: Curran Associates, Inc.), 2843–2851.

Google Scholar

Dasgupta, A., and Singh, S. (2017). “A fully convolutional neural network based structured prediction approach towards the retinal vessel segmentation,” in 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017) (West Bengal), 248–251. doi: 10.1109/ISBI.2017.7950512

CrossRef Full Text | Google Scholar

Estrada, R., Allingham, M. J., Mettu, P. S., Cousins, S. W., Tomasi, C., and Farsiu, S. (2015). Retinal artery-vein classification via topology estimation. IEEE Trans. Med. Imaging 34, 2518–2534. doi: 10.1109/TMI.2015.2443117

PubMed Abstract | CrossRef Full Text | Google Scholar

Estrada, R., Tomasi, C., Cabrera, M. T., Wallace, D. K., Freedman, S. F., and Farsiu, S. (2011). Enhanced video indirect ophthalmoscopy (VIO) via robust mosaicing. Biomed. Opt. Express 2, 2871–2887. doi: 10.1364/BOE.2.002871

PubMed Abstract | CrossRef Full Text | Google Scholar

Estrada, R., Tomasi, C., Cabrera, M. T., Wallace, D. K., Freedman, S. F., and Farsiu, S. (2012). Exploratory Dijkstra forest based automatic vessel segmentation: applications in video indirect ophthalmoscopy (VIO). Biomed. Opt. Express 3, 327–339. doi: 10.1364/BOE.3.000327

PubMed Abstract | CrossRef Full Text | Google Scholar

Estrada, R., Tomasi, C., Schmidler, S. C., and Farsiu, S. (2015). Tree topology estimation. IEEE Trans. Pattern Anal. Mach. Intell. 37, 1688–1701. doi: 10.1109/TPAMI.2014.2382116

PubMed Abstract | CrossRef Full Text | Google Scholar

Farokhian, F., and Demirel, H. (2013). “Blood vessels detection and segmentation in retina using gabor filters,” in 2013 High Capacity Optical Networks and Emerging/Enabling Technologies (Famagusta), 104–108. doi: 10.1109/HONET.2013.6729766

CrossRef Full Text | Google Scholar

Forman, G., and Scholz, M. (2010). Apples-to-apples in cross-validation studies: pitfalls in classifier performance measurement. SIGKDD Explor. Newsl. 12, 49–57. doi: 10.1145/1882471.1882479

CrossRef Full Text | Google Scholar

Fraz, M. M., Remagnino, P., Hoppe, A., Uyyanonvara, B., Rudnicka, A. R., Owen, C. G., et al. (2012). An ensemble classification-based approach applied to retinal blood vessel segmentation. IEEE Trans. Biomed. Eng. 59, 2538–2548. doi: 10.1109/TBME.2012.2205687

PubMed Abstract | CrossRef Full Text | Google Scholar

He, K., Gkioxari, G., Dollár, P., and Girshick, R. B. (2017). Mask R-CNN. CoRR abs/1703.06870. doi: 10.1109/ICCV.2017.322

PubMed Abstract | CrossRef Full Text

Hoover, A. D., Kouznetsova, V., and Goldbaum, M. (2000). Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response. IEEE Trans. Med. Imaging 19, 203–210. doi: 10.1109/42.845178

PubMed Abstract | CrossRef Full Text | Google Scholar

Ikram, M. K., de Jong, F. J., Vingerling, J. R., Witteman, J. C. M., Hofman, A., Breteler, M. M. B., et al. (2004). Are retinal arteriolar or venular diameters associated with markers for cardiovascular disorders? The Rotterdam study. Investig. Ophthalmol. Visual Sci. 45, 2129–2134. doi: 10.1167/iovs.03-1390

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Y., and Tan, N. (2018). Retinal vessel segmentation based on conditional deep convolutional generative adversarial networks. CoRR abs/1805.04224.

Google Scholar

Jin, Q., Meng, Z., Pham, T. D., Chen, Q., Wei, L., and Su, R. (2018). DUNet: a deformable network for retinal vessel segmentation. arXiv preprint arXiv:1811.01206. doi: 10.1016/j.knosys.2019.04.025

CrossRef Full Text | Google Scholar

Kaur, D., and Kaur, Y. (2014). “Various image segmentation techniques: a review,” in International Journal of Computer Science and Mobile Computing (Sahibzada Ajit Singh Nagar), 13, 809–814.

Google Scholar

Khanal, A., and Estrada, R. (2019). Dynamic deep networks for retinal vessel segmentation. arXiv [Preprint] arXiv:1903.07803.

Google Scholar

Kingma, D. P., and Ba, J. (2014). Adam: a method for stochastic optimization. arXiv [Preprint] arXiv:1412.6980.

Google Scholar

Kondermann, C., Kondermann, D., and Yan, M. (2007). Blood vessel classification into arteries and veins in retinal images. Proc. SPIE 6512:1–2. doi: 10.1117/12.708469

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems 25, eds F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (Toronto, ON: Curran Associates, Inc.), 1097–1105.

Google Scholar

Lam, B. S. Y., Gao, Y., and Liew, A. W. (2010). General retinal vessel segmentation using regularization-based multiconcavity modeling. IEEE Trans. Med. Imaging 29, 1369–1381. doi: 10.1109/TMI.2010.2043259

PubMed Abstract | CrossRef Full Text | Google Scholar

Läthén, G., Jonasson, J., and Borga, M. (2010). Blood vessel segmentation using multi-scale quadrature filtering. Pattern Recogn. Lett. 31, 762–767. doi: 10.1016/j.patrec.2009.09.020

CrossRef Full Text | Google Scholar

Lu, Y., Serpas, L., Genter, P., Mehranbod, C., Campa, D., and Ipp, E. (2016). Disparities in diabetic retinopathy screening rates within minority populations: differences in reported screening rates among African American and hispanic patients. Diabetes Care 39, e31–e32. doi: 10.2337/dc15-2198

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-Pérez, M. E., Hughes, A. D., Stanton, A. V., Thom, S. A., Bharath, A. A., and Parker, K. H. (1999). “Retinal blood vessel segmentation by means of scale-space analysis and region growing,” in Medical Image Computing and Computer-Assisted Intervention-MICCAI'99, C. Taylor and A. Colchester (Berlin; Heidelberg: Springer), 90–97. doi: 10.1007/10704282_10

CrossRef Full Text | Google Scholar

Mescheder, L., Geiger, A., and Nowozin, S. (2018). Which training methods for GANs do actually converge? arXiv [Preprint] arXiv:1801.04406.

Google Scholar

Rochtchina, E., Burlutsky, G., Liew, G., Mitchell, P., Wang, J. J., Klein, B. E., et al. (2007). Retinal vessel diameter and cardiovascular mortality: pooled data analysis from two older populations. Eur. Heart J. 28, 1984–1992. doi: 10.1093/eurheartj/ehm221

PubMed Abstract | CrossRef Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-net: convolutional networks for biomedical image segmentation,” in MICCAI (Freiburg im Breisgau). doi: 10.1007/978-3-319-24574-4_28

CrossRef Full Text | Google Scholar

Staal, J., Abramoff, M., Niemeijer, M., Viergever, M., and van Ginneken, B. (2004). Ridge based vessel segmentation in color images of the retina. IEEE Trans. Med. Imaging 23, 501–509. doi: 10.1109/TMI.2004.825627

PubMed Abstract | CrossRef Full Text | Google Scholar

Yavuz, Z., and Köse, C. (2011). “Retinal blood vessel segmentation using gabor filter and top-hat transform,” in 2011 IEEE 19th Signal Processing and Communications Applications Conference (SIU), 546–549. doi: 10.1109/SIU.2011.5929708

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhuang, J. (2018). Laddernet: multi-path networks based on u-net for medical image segmentation. CoRR abs/1810.07810.

Google Scholar

Zuiderveld, K. (1994). “Contrast limited adaptive histogram equalization,” in Graphics Gems IV, ed P. S. Heckbert (San Diego, CA: Academic Press Professional, Inc.), 474–485. doi: 10.1016/B978-0-12-336156-1.50061-6

CrossRef Full Text | Google Scholar