
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Appl. Math. Stat. , 30 January 2019
Sec. Dynamical Systems
Volume 4 - 2018 | https://doi.org/10.3389/fams.2018.00067
This article is part of the Research Topic Chimera States in Complex Networks View all 14 articles
Chimera states are intriguing complex spatio-temporal patterns of coexisting coherent and incoherent domains. They can often be observed in networks with non-local coupling topology, where each element interacts with its neighbors within a fixed range. In small-size non-locally coupled networks, chimera states usually exhibit short lifetimes and erratic drifting of the spatial position of the incoherent domain. This problem can be solved with a tweezer feedback control which can stabilize and fix the position of chimera states. We analyse the action of the tweezer control in two-layer networks, where each layer is a small non-locally coupled ring of Van der Pol oscillators. We demonstrate that tweezer control, applied to only one layer, successfully stabilizes chimera patterns in the other, uncontrolled layer, even in the case of non-identical layers. These results might be useful for applications in multilayer networks, where one of the layers cannot be directly accessed, thus it can be effectively controlled via a neighboring layer.
Networks of coupled oscillators are an intensively studied topic in non-linear science, they have a wide range of applications in physics, biology, chemistry, technology, and social sciences. Special interest has been paid to synchronization and partial synchronization of oscillators, including chimera states which are characterized by a hybrid nature of coexisting spatially coherent and incoherent domains [1–7]. Theoretical studies of chimera states have considered a wide range of networks with different local dynamics and a variety of regular and irregular coupling topologies: rings of phase oscillators with non-local coupling [8–12], interacting globally coupled populations of phase oscillators [13, 14], non-locally coupled maps [15, 16], oscillators with phase-amplitude dynamics [17–21], neural oscillators [22–26], two- and three-dimensional lattices of oscillators [27–31], networks with adaptive topologies [32, 33], fractal complex topologies [34–38], oscillators with local or global interaction [39–42], and networks with multiple layers[43–47]. Experimentally, chimera states were demonstrated in optical [48] and chemical [49, 50] systems, as well as in mechanical [51], electronic [52, 53], optoelectronic [54, 55], electrochemical [56, 57] oscillator systems, and Boolean networks [58]. Possible analytical insights and bifurcation analysis of chimera states have been obtained in the continuum limit, which explains the behavior of very large ensembles of coupled oscillators [59–63]. In contrast, lab experiments are commonly performed with small-size networks, where chimera states are more difficult to observe [64–67].
Ring networks with non-local coupling, where each element interacts with its neighbors within a certain range, are a prominent example of a topology allowing for the observation of chimera states. However, the size of the network is essential. In small-size rings of non-locally coupled oscillators, chimera states are often short-living chaotic transients, which eventually collapse to the synchronized state. Their mean lifetime decreases rapidly with decreasing system size [10]. In addition to this, chimera states exhibit a chaotic spatial motion of the position of the coherent and incoherent domains, which is more pronounced with decreasing of the system size [68]. These two effects are weakly noticeable in large networks, but they strongly impede the observation of chimera states in small systems. Only in some special cases beyond simple non-local topologies, chimera states can be observed. For instance, when phase interaction involves higher order harmonics [69, 70], or oscillators are organized in globally coupled interacting subpopulations, the observation of stable chimeras that are not transients is possible in small phase oscillator networks [64, 70].
Control of non-linear systems is an important topic in applied complex systems science [71]. Some control techniques, which allow to stabilize chimera patterns in non-locally coupled oscillator networks, have been proposed recently. The lifetime of amplitude chimeras can be greatly enhanced by time-delayed coupling [72]. For Kuramoto phase oscillators the lifetime of chimera states can be extended by proportional feedback control based on the measurement of the global order parameter [73]. The spatial position of the coherent and incoherent domains of the chimera states can be fixed by a feedback loop inducing a state-dependent asymmetry of the coupling topology [74], defined by a finite difference derivative for a local mean field. Moreover, in one-dimensional arrays of identical oscillators, a self-feedback control applied to a subpopulation of the array can be used for the stabilization of the spatial positions of the coherent and incoherent domains of the chimeras [75]. Recently, we introduced a tweezer control scheme for stabilization of chimera states [76] in small-size non-locally coupled networks. This control scheme consists of two parts, symmetric and asymmetric, and effectively stabilizes chimera states in small networks of oscillators exhibiting both phase and amplitude dynamics. Note, that in contrast to pure phase oscillators, a simple analytical study for the continuum limit (N → ∞) is not possible for non-linear phase-amplitude oscillators, therefore we concentrated mainly on the numerical stability analysis. In small networks of Van der Pol and FitzHugh-Nagumo oscillators, we demonstrated that tweezer control allows for stabilization of variable chimera patterns with different sizes of coherent domains [77].
Current research in the field of complex systems is moving beyond simple network structures to more complicated, realistic topologies. One of them are multilayer networks, which find a wide range of applications in nature and technology, such as neuronal and genetic networks, social networks, power grids, transportation networks [78–91]. Recent studies have been focused on various synchronization scenarios in multilayer structures, including remote and relay synchronization [92–94]. Moreover, it has been reported that multiplexing can be used to control spatio-temporal patterns in networks [86, 88, 95]. The advantage of control schemes based on multiplexing is that they allow to achieve the desired state in a certain layer without manipulating its parameters, and they can work for weak inter-layer coupling. For example, it has been shown that weak multiplexing can induce coherence resonance [96] as well as chimera states and solitary states [95] in neural networks. However, multiplexing has not been previously combined with tweezer control.
In many real multi-layer networks some of the layers cannot be easily accessed. An urgent issue, therefore, is the question whether it is possible to control or stabilize spatio-temporal patterns in one layer of the network by applying control to the other layer. We aim to answer this question by an analysis of a simple two-layer network of Van der Pol oscillators. We demonstrate that chimera states which are not observable in small isolated networks, can be efficiently stabilized by the combined action of multiplexing and tweezer control.
We consider a network of 2N coupled Van der Pol oscillators, organized in two layers, each of which contains N oscillators, with non-local ring topology within each layer:
where , i = 1, 2 denotes the layer number, k = 1, …, N is the oscillator index within each layer. The scalar parameter ε > 0 determines the internal dynamics of the individual elements. For small ε the oscillation of a single element is sinusoidal, while for large ε it is a strongly non-linear relaxation oscillation. Each element is coupled with Ri nearest neighbors to the left and to the right, we assume that the oscillators within the layers are arranged on a ring (i.e., periodic boundary conditions). The coupling term inside each layer consists of two parts: the coupling constants with respect to position and velocity to the left and to the right are denoted as , and , , respectively. Such a coupling scheme can be associated with biological [97, 98] and technological applications [99]. Interaction between the layers consists of one-to-one bidirectional connections between the corresponding pairs of oscillators and , with inter-layer coupling strength ainter and binter. Figure 1 shows schematically the topology of the considered network: both layers consist of non-locally coupled rings of oscillators, corresponding pairs of oscillators in each layer are connected by inter-layer links shown by dashed lines. This network structure can also be referred to as a multiplex, since only one-to-one inter-layer connections between the layers exist.
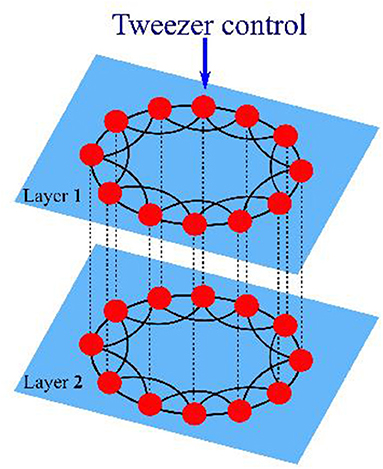
Figure 1. Schematic structure of the two layer networks: red dots denote the oscillators, blue planes correspond to the two layers. Solid lines show intra-layer couplings, dashed lines represent pairwise inter-layer couplings between the oscillators. Tweezer control is applied to layer 1.
For the sake of simplicity we assume
with rescaled coupling parameters a(i), , and .
In order to introduce the tweezer control [76], we define two complex order parameters within each network layer i
where is the geometric phase of the k-th oscillator computed from
The tweezer feedback control [76] for the non-locally coupled ring of oscillators is defined as
The control term has two parts referred to as symmetric and asymmetric controls, with corresponding control gains Ks and Ka. The idea of the symmetric proportional control was suggested for phase oscillators in Sieber et al. [73]. It is defined as a feedback loop between coupling parameters and the global Kuramoto order parameter of the oscillators within one layer . This feedback loop aims to suppress the collapse of small-size chimera states and extend their lifetime.
The asymmetric control part is realized as a second feedback loop between coupling parameters and the difference . It indicates a relative spatial shift of the chimera's incoherent domain with respect to the center of the oscillator array 1, …, N. If the incoherent domain of the chimera state is shifted toward larger indices , then the difference is positive, and as a result . In the opposite case, when the incoherent domain of the chimera state is shifted toward smaller indices , we will obtain . A discrepancy between and introduces asymmetry in the coupling term, and induces the counterbalancing lateral motion of a chimera state toward dynamically preferable centered position.
In Omelchenko et al. [76, 77] we have demonstrated the effective action of the tweezer control in small rings of non-locally coupled Van der Pol and FitzHugh-Nagumo oscillators. When both the symmetric and asymmetric parts of the control are acting (the control gains Ks and the Ka are positive), a stable chimera state can be observed in the system. When we switch off the asymmetric part of the control, Ka = 0, and keep a positive symmetric gain Ks > 0, the chimera state starts to drift on the ring. Its motion becomes stronger for decreasing system size. To switch off both parts of the control, we keep and constant, and after a short transient time the chimera state collapses to the completely synchronized state.
In the present work, the tweezer control acts in the first layer of our network (1) only, while in the second layer the coupling strength is constant. We will compare patterns obtained in both layers in a network of relatively small size. The characteristic signature of a chimera state is a pronounced difference of the average frequencies for oscillators belonging to the coherent and incoherent domains, respectively. The oscillators from the coherent domain are phase-locked having equal frequencies, while the oscillators from the incoherent domain have different average frequencies which typically form an arc-like profile. The mean phase velocities are obtained as
averaged over the time window T0. To visualize the temporal dynamics of the oscillators we plot their mean phase velocities defined by Equation (7) with T0 = 50 for each layer. Throughout this work in our numerical simulations we use random initial conditions.
Figure 2 shows the mean phase velocities for a two-layer network of Van der Pol oscillators with N = 48 oscillators within each layer, coupled to their R1 = R2 = 16 nearest neighbors. Such an intermediate coupling range is the prerequisite of the existence of chimera patterns in non-locally coupled rings. In our earlier work [21] we have demonstrated analytically that in the ring of non-locally coupled Van der Pol oscillators the ratio of the coupling constants of position and velocity (in our case and ) can be associated with the phase lag parameter for a reduced phase oscillator network. In order to observe chimera states, the coupling constant of position should be chosen larger than the coupling constant of velocity. In the following, we will use this property for both intra- and inter-layer couplings. As a first step, we consider very weak inter-layer coupling with constants ainter = 0.002, binter = 0.001 approximately ten times smaller than intra-layer coupling strengths. Figure 2A shows, that in this case the intra-layer coupling dominates, and the two layers perform different dynamics: in the first layer we observe a stable chimera state due to the action of the tweezer control, while in the second, uncontrolled layer after short transient time all oscillators synchronize. Figure 2B shows the mean phase velocities of the oscillators averaged over large time interval T0 = 25,000 (upper panel). In the first layer the typical arc-shape profile is formed (shown red), which is one of the prominent features of chimera states. In the second layer, all oscillators are frequency-locked (shown blue). The middle panel demonstrates snapshots for both layers at fixed time, and the bottom panel depicts the same snapshots in the phase space, where the limit cycle of one uncoupled Van der Pol unit is shown in black. The oscillators from the incoherent domain of the chimera state are scattered around this limit cycle.
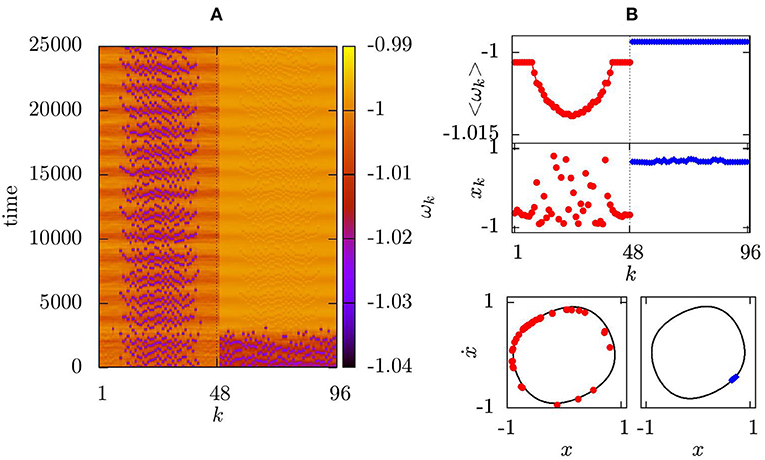
Figure 2. Mean phase velocities for a two-layer system of N = 48 oscillators in each layer with R1 = R2 = 16, ε = 0.2, a(1) = a(2) = 0.02, ainter = 0.002, binter = 0.001. Layer 1 is controlled with Ka = 2, Ks = 0.5, layer 2 is uncontrolled with . Oscillators k = 1…48 represent the first layer, k = 49…96 the second layer; (A) space-time plot; (B) mean phase velocity profile averaged over 25,000 time units for the first layer (red dots) and the second layer (blue diamonds) (top panel); snapshot of variables xk (middle panel) and snapshot in the (xk; ẋk) phase space at t = 25,000 (bottom panel).
With increasing inter-layer coupling strength, we observe successful stabilization of the chimera state in the second layer shown in Figure 3 for ainter = 0.011, binter = 0.0025. Due to the fact that our layers are identical, the mean phase velocities profiles have the same shape, and coherent/incoherent domains of chimera states are synchronized spatially in both layers. Figure 4 presents a diagram in the parameter plane of inter- and intra-layer coupling constants. When the interlayer coupling is too weak, chimera states in the second layer can not be stabilized (blue region). In the red region synchronization of both layers, and thus successful control of the chimera state in the second layer via multiplexing is observed. In the thin hatched region our numerical evidence shows a sensitive dependence on the initial conditions. However, system (1) has numerous parameters which should also be fixed appropriately. For instance, the control gains Ks and Ka can influence the shape of the controlled chimera pattern and the size of its coherent domain [77]. Moreover, in the examples demonstrated in the present manuscript, the non-linearity parameter ε of the individual Van der Pol oscillator is chosen to be small, corresponding to sinusoidal oscillations. The tweezer control acts successfully also in the case of relaxation oscillations when ε is large [76].
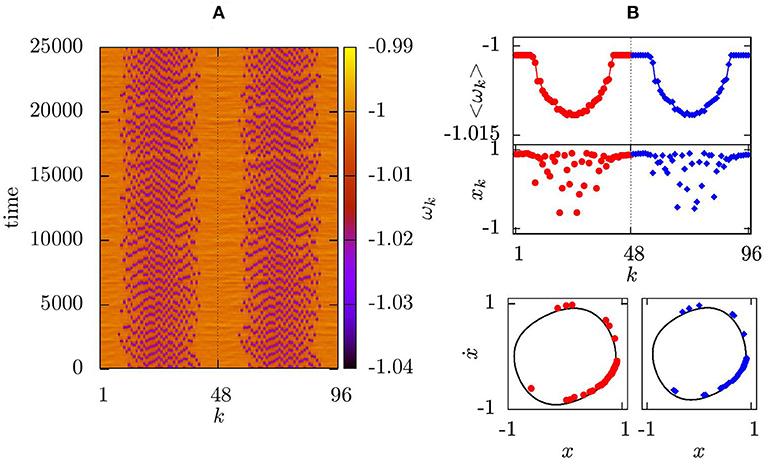
Figure 3. Same as Figure 2 for ainter = 0.011, binter = 0.0025.
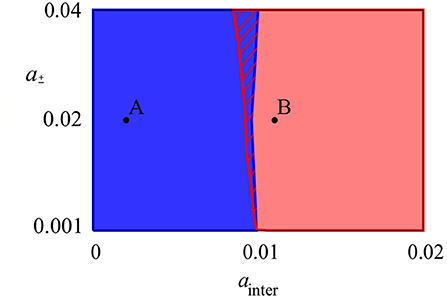
Figure 4. Diagram in the plane of inter-layer ainter and intra-layer a coupling constants for a two-layer system of N = 48 oscillators in each layer with R1 = R2 = 16. The red region corresponds to the successful stabilization of chimera states in both layers, the blue region depicts chimera collapse in the uncontrolled layer. In the hatched region only part of the numerical realizations indicated successful control. Points A and B denote parameter values corresponding to Figures 2 and 3, respectively. Other parameters as in Figure 2.
Figure 5 demonstrates the behavior of chimera patterns within two layers under the action of each part of the control (6) separately. When the asymmetric part is deactivated, Ka = 0, the lifetime of the chimera state is still extended, but it starts to drift, as shown in Figure 5A. The coherent and incoherent domains of the chimera state in the second layer drift along with the chimera in the controlled layer. Thus, extending of lifetime without position control in both layers is possible as well. When we stop to control the lifetime of chimeras, by keeping the coupling coefficients constant in the first layer, after some transient time we observe simultaneous chimera collapse in both layers as depicted in Figure 5B.
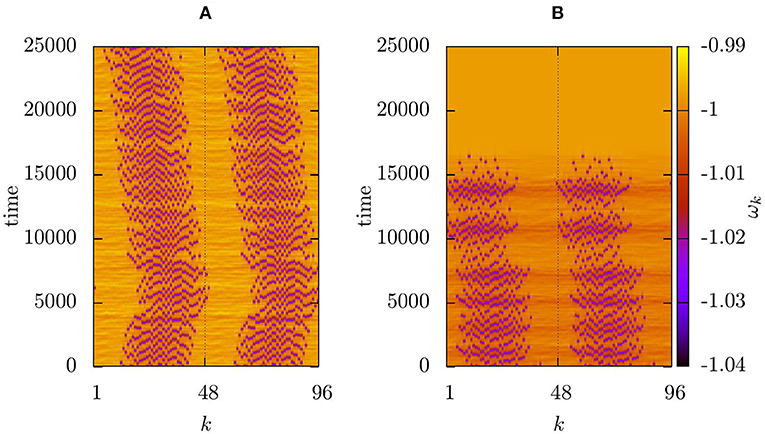
Figure 5. Space-time plot of the mean phase velocities for a two-layer network with one part of the control switched off; (A) drifting chimera state in both layers with Ka = 0; (B) collapse of the uncontrolled chimera state in both layers, with constant coupling coefficients . Other parameters as in Figure 3.
Hence, the combination of tweezer control and multiplexing allows for efficient control of chimera states in multiple layers, with the control applied directly to only one layer.
In real-world networks non-identical layers are more common. Therefore, the analysis of the robustness of the tweezer control in two-layer networks is an important issue. In the following we will consider the topological inhomogeneity of the layers in the network by introducing a coupling range mismatch R1 ≠ R2. In non-locally coupled rings the coupling range is one of the essential parameters for the observation of chimera states. An intermediate coupling range is usually favorable, while too small or too large numbers of coupled neighbors prevent the formation of chimera states. Furthermore, within intermediate values, smaller coupling ranges can cause multiple coherent and incoherent domains of the chimera state. Thus, considering different coupling ranges in two layers will result in competitive patterns formed in each layer. As before, the tweezer control acts only in the first layer of our network.
Figure 6 depicts the stabilization of chimera states in system (1) with N = 48 oscillators in each layer, and slightly inhomogeneous topologies with coupling ranges R1 = 16 and R2 = 18. After a short transient time, the interplay of the tweezer control and inter-layer coupling results in the successful spatial alignment of the coherent and incoherent domains, and their mean phase velocity profiles have similar shapes as well, as shown in Figure 6B.
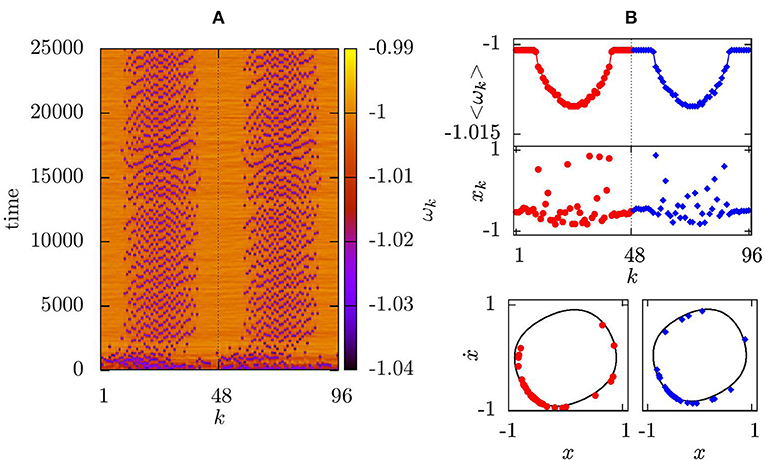
Figure 6. Mean phase velocities for a two-layer system of N = 48 oscillators in the layers and non-identical coupling ranges: R1 = 16, R2 = 18, other parameters:ε = 0.2, a(1) = a(2) = 0.02, ainter = 0.009, binter = 0.0023, Ka = 2, Ks = 0.5, . Oscillators k = 1…48 represent the first layer, k = 49…96 the second layer; (A) space-time plot; (B) mean phase velocity profile averaged over 25,000 time units for the first layer (red dots) and the second layer (blue diamonds) (top panel); snapshot of variables xk (middle panel) and snapshot in the (xk; ẋk) phase space at t = 25,000 (bottom panel).
As a next step, we increase the layer mismatch and choose R1 = 16, R2 = 12. In the isolated case, the second layer would exhibit a chimera state with multiple incoherent domains [21], which collapses to the completely synchronized state. Figure 7 demonstrates that by controlling the first layer, we successfully suppress the collapse, and synchronize the chimera states in both layers. However, due to the bidirectional inter-layer interaction, the dynamics of the second layer has indeed an influence on the first one. The chimera states shown in Figure 7 have larger incoherent domains induced by the smaller coupling range in the second layer. It is worth to note that to stabilize their position, the asymmetric control gain had to be increased (Ka = 6). We have shown numerically that we can stabilize the chimera states in two layers for an even larger topology mismatch, however, the coupling parameters and control gains had to be tuned.
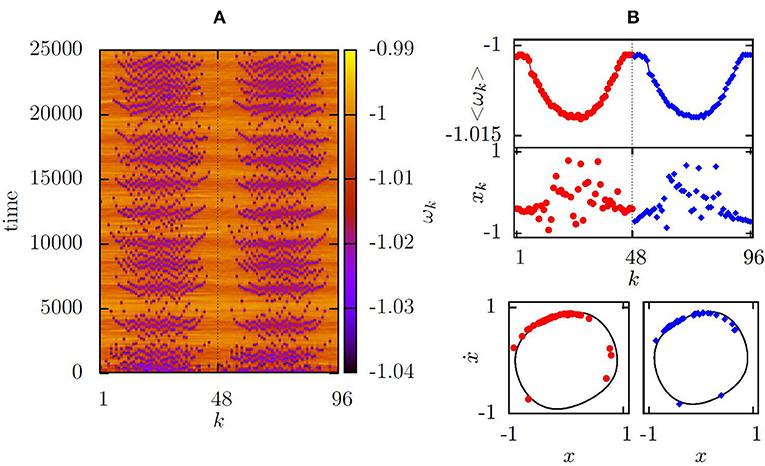
Figure 7. Same as Figure 6 with R1 = 16, R2 = 12, and Ka = 6.
In the present manuscript, we have demonstrated that the combination of the tweezer control for chimera states and multiplexing allows for successful stabilization of chimera states in both layers of two-layer networks of Van der Pol oscillators. Considering a ring topology with non-local interaction between the oscillators within each layer, and one-to-one connections between the corresponding oscillators from the two layers, we have focused on networks of relatively small size, where chimera states are usually hard to observe. Tweezer control, consisting of two parts, extends the lifetime of chimera states, and fixes their spatial position on the ring.
In two-layer networks we have applied the tweezer control to one layer only, and have shown that for sufficiently strong inter-layer coupling the action of the control is transferred to the second layer, where the lifetime of the chimera state is increased and its spatial position if fixed. Without the inter-layer connections, or if their strength is too weak, after a short transient time the chimera state collapses and all oscillators in the second layer synchronize.
We have demonstrated that the combination of tweezer control and multiplexing is robust with respect to the topological inhomogeneity of the layers, and chimera states can be successfully stabilized even in the case of large coupling range mismatch between the layers. Previously, we have demonstrated that tweezer control acts efficiently in non-locally coupled rings consisting of inhomogeneous oscillators [76], therefore the stabilization of chimera states in the two-layer networks with inhomogeneous nodes is plausible as well.
Our results can be useful in real multilayer networks, where the access to some layers is not possible, but there is need to control spatio-temporal patterns. Combination of tweezer control and multiplexing appears to be a powerful and robust tool to solve this problem even for small networks with inhomogeneous layers.
IO, AZ, and ES designed and supervised the study and carried out the analytical work. TH provided numerical simulations and constructed the figures. All authors discussed the results and contributed to writing the manuscript.
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)–Projektnummer 163436311–SFB 910.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. Abrams DM, Strogatz SH. Chimera states for coupled oscillators. Phys Rev Lett. (2004) 93:174102. doi: 10.1103/physrevlett.93.174102
2. Kuramoto Y, Battogtokh D. Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlinear Phenomena Complex Syst. (2002) 5:380–5.
3. Shima S, Kuramoto Y. Rotating spiral waves with phase-randomized core in nonlocally coupled oscillators. Phys Rev E (2004) 69:036213. doi: 10.1103/physreve.69.036213
4. Laing CR. The dynamics of chimera states in heterogeneous Kuramoto networks. Physica D (2009) 238:1569–88. doi: 10.1016/j.physd.2009.04.012
5. Motter AE. Nonlinear dynamics: spontaneous synchrony breaking. Nat Phys. (2010) 6:164–5. doi: 10.1038/nphys1609
6. Panaggio MJ, Abrams DM. Chimera states: coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity (2015) 28:R67. doi: 10.1088/0951-7715/28/3/r67
7. Schöll E. Synchronization patterns and chimera states in complex networks: interplay of topology and dynamics. Eur Phys J Spec Top. (2016) 225:891–919. doi: 10.1140/epjst/e2016-02646-3
8. Sakaguchi H. Instability of synchronized motion in nonlocally coupled neural oscillators. Phys Rev E (2006) 73:031907. doi: 10.1103/physreve.73.031907
9. Wolfrum M, Omel'chenko OE, Yanchuk S, Maistrenko Y. Spectral properties of chimera states. Chaos (2011) 21:013112. doi: 10.1063/1.3563579
10. Wolfrum M, Omel'chenko OE. Chimera states are chaotic transients. Phys Rev E (2011) 84:015201. doi: 10.1103/physreve.84.015201
11. Omel'chenko OE, Wolfrum M, Yanchuk S, Maistrenko Y, Sudakov O. Stationary patterns of coherence and incoherence in two-dimensional arrays of non-locally-coupled phase oscillators. Phys Rev E (2012) 85:036210. doi: 10.1103/physreve.85.036210
12. Wolfrum M, Omel'chenko OE, Sieber J. Regular and irregular patterns of self-localized excitation in arrays of coupled phase oscillators. Chaos (2015) 25:053113. doi: 10.1063/1.4921297
13. Martens EA, Laing CR, Strogatz SH. Solvable model of spiral wave chimeras. Phys Rev Lett. (2010) 104:044101. doi: 10.1103/physrevlett.104.044101
14. Martens EA. Chimeras in a network of three oscillator populations with varying network topology. Chaos (2010) 20:043122. doi: 10.1063/1.3499502
15. Omelchenko I, Maistrenko Y, Hövel P, Schöll E. Loss of coherence in dynamical networks: spatial chaos and chimera states. Phys Rev Lett. (2011) 106:234102. doi: 10.1103/physrevlett.106.234102
16. Omelchenko I, Riemenschneider B, Hövel P, Maistrenko Y, Schöll E. Transition from spatial coherence to incoherence in coupled chaotic systems. Phys Rev E (2012) 85:026212. doi: 10.1103/physreve.85.026212
17. Sethia GC, Sen A, Atay FM. Clustered chimera states in delay-coupled oscillator systems. Phys Rev Lett. (2008) 100:144102. doi: 10.1103/physrevlett.100.144102
18. Sethia GC, Sen A, Johnston GL. Amplitude-mediated chimera states. Phys Rev E. (2013) 88:042917. doi: 10.1063/1.5031804
19. Sethia GC, Sen A. Chimera states: the existence criteria revisited. Phys Rev Lett. (2014) 112:144101. doi: 10.1103/physrevlett.112.144101
20. Zakharova A, Kapeller M, Schöll E. Chimera death: symmetry breaking in dynamical networks. Phys Rev Lett. (2014) 112:154101. doi: 10.1103/physrevlett.112.154101
21. Omelchenko I, Zakharova A, Hövel P, Siebert J, Schöll E. Nonlinearity of local dynamics promotes multi-chimeras. Chaos (2015) 25:083104. doi: 10.1063/1.4927829
22. Omelchenko I, Omel'chenko OE, Hövel P, Schöll E. When nonlocal coupling between oscillators becomes stronger: patched synchrony or multichimera states. Phys Rev Lett. (2013) 110:224101. doi: 10.1103/physrevlett.110.224101
23. Omelchenko I, Provata A, Hizanidis J, Schöll E, Hövel P. Robustness of chimera states for coupled FitzHugh-Nagumo oscillators. Phys Rev E (2015) 91:022917. doi: 10.1103/physreve.91.022917
24. Hizanidis J, Kanas V, Bezerianos A, Bountis T. Chimera states in networks of nonlocally coupled Hindmarsh-Rose neuron models. Int J Bifurcation Chaos (2014) 24:1450030. doi: 10.1142/s0218127414500308
25. Laing CR. Derivation of a neural field model from a network of theta neurons. Phys Rev E (2014) 90:010901. doi: 10.1103/physreve.90.010901
26. Hizanidis J, Panagakou E, Omelchenko I, Schöll E, Hövel P, Provata A. Chimera states in population dynamics: networks with fragmented and hierarchical connectivities. Phys Rev E (2015) 92:012915. doi: 10.1103/physreve.92.012915
27. Panaggio MJ, Abrams DM. Chimera states on a flat torus. Phys Rev Lett. (2013) 110:094102. doi: 10.1103/PhysRevLett.110.094102
28. Xie J, Knobloch E, Kao HC. Multicluster and traveling chimera states in nonlocal phase-coupled oscillators. Phys Rev E (2014) 90:022919. doi: 10.1103/physreve.90.022919
29. Maistrenko Y, Vasylenko A, Sudakov O, Levchenko R, Maistrenko VL. Cascades of multi-headed chimera states for coupled phase oscillators. Int J Bifur Chaos (2014) 24:1440014. doi: 10.1142/S0218127414400148
30. Maistrenko Y, Sudakov O, Osiv O, Maistrenko VL. Chimera states in three dimensions. New J Phys. (2015) 17:073037. doi: 10.1088/1367-2630/17/7/073037
31. Panaggio MJ, Abrams DM. Chimera states on the surface of a sphere. Phys Rev E (2015) 91:022909. doi: 10.1103/physreve.91.022909
32. Kasatkin DV, Yanchuk S, Schöll E, Nekorkin VI. Self-organized emergence of multi-layer structure and chimera states in dynamical networks with adaptive couplings. Phys Rev E (2017) 96:062211. doi: 10.1103/physreve.96.062211
33. Bera BK, Majhi S, Ghosh D, Perc M. Chimera states: effects of different coupling topologies. Europhys Lett. (2017) 118:10001. doi: 10.1209/0295-5075/118/10001
34. Ulonska S, Omelchenko I, Zakharova A, Schöll E. Chimera states in networks of Van der Pol oscillators with hierarchical connectivities. Chaos (2016) 26:094825. doi: 10.1063/1.4962913
35. Sawicki J, Omelchenko I, Zakharova A, Schöll E. Chimera states in complex networks: interplay of fractal topology and delay. Eur Phys J Spec Top. (2017) 226:1883–92. doi: 10.1140/epjst/e2017-70036-8
36. Tsigkri-DeSmedt ND, Hizanidis J, Schöll E, Hövel P, Provata A. Chimeras in leaky integrate-and-fire neural networks: effects of reflecting connectivities. Eur Phys J. B (2017) 90:139. doi: 10.1140/epjb/e2017-80162-0
37. zur Bonsen A, Omelchenko I, Zakharova A, Schöll E. Chimera states in networks of logistic maps with hierarchical connectivities. Eur Phys J B (2018) 91:65. doi: 10.1140/epjb/e2018-80630-y
38. Chouzouris T, Omelchenko I, Zakharova A, Hlinka J, Jiruska P, Schöll E. Chimera states in brain networks: empirical neural vs. modular fractal connectivity. Chaos (2018) 28:045112. doi: 10.1063/1.5009812
39. Yeldesbay A, Pikovsky A, Rosenblum M. Chimeralike states in an ensemble of globally coupled oscillators. Phys Rev Lett. (2014) 112:144103. doi: 10.1103/physrevlett.112.144103
40. Schmidt L, Krischer, K. Clustering as a prerequisite for chimera states in globally coupled systems. Phys Rev Lett. (2015) 114:034101. doi: 10.1103/PhysRevLett.114.034101
41. Laing CR. Chimeras in networks with purely local coupling. Phys Rev E (2015) 92:050904. doi: 10.1103/PhysRevE.92.050904
42. Olmi S, Martens EA, Thutupalli S, Torcini A. Intermittent chaotic chimeras for coupled rotators. Phys Rev E (2015) 92:030901. doi: 10.1103/physreve.92.030901
43. Bogomolov S, Slepnev A, Strelkova G, Schöll E, Anishchenko VS. Mechanisms of appearance of amplitude and phase chimera states in a ring of nonlocally coupled chaotic systems. Commun Nonlinear Sci Numer Simul. (2017) 43:25. doi: 10.1016/j.cnsns.2016.06.024
44. Semenova N, Zakharova A, Anishchenko VS, Schöll E. Coherence-resonance chimeras in a network of excitable elements. Phys Rev Lett. (2016) 117:014102. doi: 10.1103/PhysRevLett.117.014102
45. Kundu S, Majhi S, Bera BK, Ghosh D, Lakshmanan M. Chimera states in two-dimensional networks of locally coupled oscillators. Phys Rev E (2018) 97:022201. doi: 10.1103/PhysRevE.97.022201
46. Majhi S, Ghosh D. Alternating chimeras in networks of ephaptically coupled bursting neurons. Chaos (2018) 28:083113. doi: 10.1063/1.5022612
47. Majhi S, Bera BK, Ghosh D, Perc M. Chimera states in neuronal networks: a review. Phys Life Rev. (2018). doi: 10.1016/j.plrev.2018.09.003
48. Hagerstrom AM, Murphy TE, Roy R, Hövel P, Omelchenko I, Schöll E. Experimental observation of chimeras in coupled-map lattices. Nat Phys. (2012) 8:658–61. doi: 10.1038/nphys2372
49. Tinsley MR, Nkomo S, Showalter K. Chimera and phase cluster states in populations of coupled chemical oscillators. Nat Phys. (2012) 8:662–5. doi: 10.1038/nphys2371
50. Nkomo S, Tinsley MR, Showalter K. Chimera states in populations of nonlocally coupled chemical oscillators. Phys Rev Lett. (2013) 110:244102. doi: 10.1103/physrevlett.110.244102
51. Martens EA, Thutupalli S, Fourriere A, Hallatschek O. Chimera states in mechanical oscillator networks. Proc Natl Acad Sci USA. (2013) 110:10563. doi: 10.1073/pnas.1302880110
52. Larger L, Penkovsky B, Maistrenko Y. Virtual chimera states for delayed-feedback systems. Phys Rev Lett. (2013) 111:054103. doi: 10.1103/physrevlett.111.054103
53. Gambuzza LV, Buscarino A, Chessari S, Fortuna L, Meucci R, Frasca M. Experimental investigation of chimera states with quiescent and synchronous domains in coupled electronic oscillators. Phys Rev E (2014) 90:032905. doi: 10.1103/physreve.90.032905
54. Larger L, Penkovsky B, Maistrenko Y. Laser chimeras as a paradigm for multistable patterns in complex systems. Nat Commun. (2015) 6:7752. doi: 10.1038/ncomms8752
55. Brunner D, Penkovsky B, Levchenko R, Schöll E, Larger L, Maistrenko Y. Two-dimensional spatiotemporal complexity in dual-delayed nonlinear feedback systems: chimeras and dissipative solitons. Chaos (2018) 28:103106. doi: 10.1063/1.5043391
56. Wickramasinghe M, Kiss IZ. Spatially organized dynamical states in chemical oscillator networks: Synchronization, dynamical differentiation, and chimera patterns. PLoS ONE (2013) 8:e80586. doi: 10.1371/journal.pone.0080586
57. Schmidt L, Schönleber K, Krischer K, García-Morales V. Coexistence of synchrony and incoherence in oscillatory media under nonlinear global coupling. Chaos (2014) 24:013102. doi: 10.1063/1.4858996
58. Rosin DP, Rontani D, Haynes N, Schöll E, Gauthier DJ. Transient scaling and resurgence of chimera states in coupled Boolean phase oscillators. Phys Rev E (2014) 90:030902. doi: 10.1103/physreve.90.030902
59. Ott E, Antonsen TM. Low dimensional behavior of large systems of globally coupled oscillators. Chaos (2008) 18:037113. doi: 10.1063/1.2930766
60. Ott E, Antonsen TM. Long time evolution of phase oscillator systems. Chaos (2009) 19:023117. doi: 10.1063/1.3136851
61. Omel'chenko OE. Coherence-incoherence patterns in a ring of non-locally coupled phase oscillators. Nonlinearity (2013) 26:2469. doi: 10.1088/0951-7715/26/9/2469/meta
62. Pazó D, Montbrió E. Low-dimensional dynamics of populations of pulse-coupled oscillators. Phys Rev X (2014) 4:011009. doi: 10.1103/physrevx.4.011009
63. Omel'chenko OE. The mathematics behind chimera states. Nonlinearity (2018) 31:R121. doi: 10.1088/1261-6544/aaaa07
64. Ashwin P, Burylko O. Weak chimeras in minimal networks of coupled phase oscillators. Chaos (2015) 25:013106. doi: 10.1063/1.4905197
65. Panaggio MJ, Abrams DM, Ashwin P, Laing CR. Chimera states in networks of phase oscillators: the case of two small populations. Phys Rev E (2016) 93:012218. doi: 10.1103/physreve.93.012218
66. Böhm F, Zakharova A, Schöll E, Lüdge K. Amplitude-phase coupling drives chimera states in globally coupled laser networks. Phys Rev E (2015) 91:040901. doi: 10.1103/physreve.91.040901
67. Hart JD, Bansal K, Murphy TE, Roy R. Experimental observation of chimera and cluster states in a minimal globally coupled network. Chaos (2016) 26:094801. doi: 10.1063/1.4953662
68. Omel'chenko OE, Wolfrum M, Maistrenko Y. Chimera states as chaotic spatiotemporal patterns. Phys Rev E (2010) 81:065201. doi: 10.1103/physreve.81.065201
69. Suda Y, Okuda K. Persistent chimera states in nonlocally coupled phase oscillators. Phys Rev E (2015) 92:060901. doi: 10.1103/physreve.92.060901
70. Bick C. Heteroclinic switching between chimeras. Phys Rev E (2018) 97:050201. doi: 10.1103/physreve.97.050201
71. Schöll E, Klapp SHL, Hövel P. Control of Self-organizing Nonlinear Systems. Berlin: Springer (2016).
72. Gjurchinovski A, Schöll E, Zakharova A. Control of amplitude chimeras by time delay in dynamical networks. Phys Rev E (2017) 95:042218. doi: 10.1103/physreve.95.042218
73. Sieber J, Omel'chenko OE, Wolfrum M. Controlling unstable chaos: stabilizing chimera states by feedback. Phys Rev Lett. (2014) 112:054102. doi: 10.1103/physrevlett.112.054102
74. Bick C, Martens EA. Controlling chimeras. New J Phys. (2015) 17:033030. doi: 10.1088/1367-2630/17/3/033030
75. Bera BK, Ghosh D, Parmananda P, Osipov GV, Dana SK. Coexisting synchronous and asynchronous states in locally coupled array of oscillators by partial self-feedback control. Chaos(2017) 27:073108. doi: 10.1063/1.4993459
76. Omelchenko I, Omel'chenko OE, Zakharova A, Wolfrum M, Schöll E. Tweezers for chimeras in small networks. Phys Rev Lett. (2016) 116:114101. doi: 10.1103/physrevlett.116.114101
77. Omelchenko I, Omel'chenko OE, Zakharova A, Schöll E. Optimal design of tweezer control for chimera states. Phys Rev E (2018) 97:012216. doi: 10.1103/PhysRevE.97.012216
78. De Domenico M, Solé-Ribalta A, Cozzo E, Kivelä M, Moreno Y, Porter MA, et al. Mathematical formulation of multilayer networks. Phys Rev X (2013) 3:041022. doi: 10.1103/PhysRevX.3.041022
79. Kivelä M, Arenas A, Barthélemy M, Gleeson JP, Moreno Y, Porter MA. Multilayer networks. J Complex Netw. (2014) 2:203–71. doi: 10.1093/comnet/cnu016
80. Kleineberg KK, Boguñá M, Serrano M. Á, Papadopoulos F. Hidden geometric correlations in real multiplex networks. Nat Phys. (2016) 12:1076–81. doi: 10.1038/nphys3812
81. Maksimenko VA, Makarov VV, Bera BK, Ghosh D, Dana SK, Goremyko MV, et al. Excitation and suppression of chimera states by multiplexing. Phys Rev E (2016) 94:052205. doi: 10.1103/physreve.94.052205
82. De Domenico M. Multilayer modeling and analysis of human brain networks. Gigascience (2017) 6:1–8. doi: 10.1093/gigascience/gix004
83. Battiston F, Nicosia V, Chavez M, Latora V. Multilayer motif analysis of brain networks. Chaos (2017) 27:047404. doi: 10.1063/1.4979282
84. Goremyko MV, Maksimenko VA, Makarov VV, Ghosh D, Bera B, Dana SK, et al. Interaction of chimera states in a multilayered network of nonlocally coupled oscillators. Technol Phys Lett. (2017) 43:712–5. doi: 10.1134/s1063785017080077
85. Majhi S, Perc M, Ghosh D. Chimera states in a multilayer network of coupled and uncoupled neurons. Chaos (2017) 27:073109. doi: 10.1063/1.4993836
86. Ghosh S, Kumar A, Zakharova A, Jalan S. Birth and death of chimera: interplay of delay and multiplexing. Europhys Lett. (2016) 115:60005. doi: 10.1209/0295-5075/115/60005
87. Leyva I, Sendiña-Nadal I, Sevilla-Escoboza R, Vera-Avila VP, Chholak P, Boccaletti S. Relay synchronization in multiplex networks. Sci Rep. (2018) 8:8629. doi: 10.1038/s41598-018-26945-w
88. Ghosh S, Zakharova A, Jalan S. Non-identical multiplexing promotes chimera states. Chaos Solitons Fractals (2018) 106:56–60. doi: 10.1016/j.chaos.2017.11.010
89. Andrzejak RG, Ruzzene G, Malvestio I, Schindler K, Schöll E, Zakharova A. Mean field phase synchronization between chimera states. Chaos (2018) 28:091101. doi: 10.1063/1.5049750
90. Sawicki J, Omelchenko I, Zakharova A, Schöll E. Synchronization scenarios of chimeras in multiplex networks. Eur Phys J Spec Top. (2018) 227:1161. doi: 10.1140/epjst/e2018-800039-y
91. Carpi LC, Schieber TA, Pardalos PM, Marfany G, Masoller C, Díaz-Guilera A, et al. Assessing diversity in multiplex networks. arXiv:1805.12350 (2018).
92. Nicosia V, Valencia M, Chavez M, Díaz-Guilera A, Latora V. Remote synchronization reveals network symmetries and functional modules. Phys Rev Lett. (2013) 110:174102. doi: 10.1103/physrevlett.110.174102
93. Zhang L, Motter AE, Nishikawa T. Incoherence-mediated remote synchronization. Phys Rev Lett. (2017) 118:174102. doi: 10.1103/physrevlett.118.174102
94. Sawicki J, Omelchenko I, Zakharova A, Schöll E. Delay controls chimera relay synchronization in multiplex networks. Phys Rev E (2018) 98:062224. doi: 10.1103/PhysRevE.98.062224
95. Mikhaylenko M, Ramlow L, Jalan S, Zakharova A. Weak multiplexing in neural networks: switching between chimera and solitary states. arXiv:1809.07148 (2018).
96. Semenova N, Zakharova A. Weak multiplexing induces coherence resonance. Chaos (2018) 28:051104. doi: 10.1063/1.5037584
97. Low LA, Reinhall PG, Storti DW. An investigation of coupled van der Pol oscillators. J Vib Acoust. (2003) 125:162–9. doi: 10.1115/1.1553469
98. Low LA, Reinhall PG, Storti DW, Goldman EB. Coupled van der Pol oscillators as a simplified model for generation of neural patterns for jellyfish locomotion. Struct Control Health Monit. (2006) 13:417–29. doi: 10.1002/stc.133
Keywords: dynamical systems, synchronization, chimera states, multilayer networks, feedback control, Van der Pol oscillators
Citation: Omelchenko I, Hülser T, Zakharova A and Schöll E (2019) Control of Chimera States in Multilayer Networks. Front. Appl. Math. Stat. 4:67. doi: 10.3389/fams.2018.00067
Received: 30 October 2018; Accepted: 27 December 2018;
Published: 30 January 2019.
Edited by:
Jun Ma, Lanzhou University of Technology, ChinaReviewed by:
Dibakar Ghosh, Indian Statistical Institute, IndiaCopyright © 2019 Omelchenko, Hülser, Zakharova and Schöll. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Iryna Omelchenko, b21lbGNoZW5rb0BpdHAudHUtYmVybGluLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.