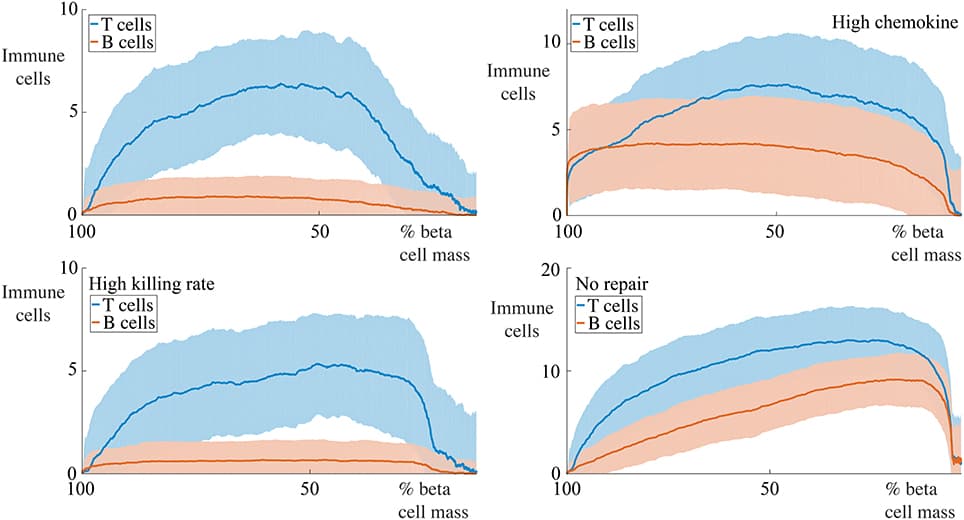
Vaccination programs for childhood diseases, such as measles, mumps and rubella have greatly contributed to decreasing the incidence and impact of those diseases. Nonetheless, despite long vaccination programmes across the world, mumps has not yet been eradicated in those countries: indeed, large outbreaks continue. For example, in Scotland large outbreaks occurred in 2004, 2005, and 2015, despite introducing the MMR (Measles-Mumps-Rubella) vaccine more than 20 years ago. There are indications that this vaccine-preventable disease is re-emerging in highly vaccinated populations. Here we investigate whether the resurgence of mumps is due to waning immunity, and further, could a booster dose be the solution to eradicate mumps or would it just extend the period of waning immunity? Using mathematical modeling we enhance a seasonally-structured disease model with four scenarios: no vaccination, vaccinated individuals protected for life, vaccinated individuals at risk of waning immunity, and introduction of measures to increase immunity (a third dose, or a better vaccine). The model is parameterised from observed clinical data in Scotland 2004–2015 and the literature. The results of the four scenarios are compared with observed clinical data 2004–2016. While the force of infection is relatively sensitive to the duration of immunity and the number of boosters undertaken, we conclude that periodic large outbreaks of mumps will be sustained for all except the second scenario. This suggests that the current protocol of two vaccinations is optimal in the sense that while there are periodic large outbreaks, the severity of cases in vaccinated individuals is less than in unvaccinated individuals, and the size of the outbreaks does not decrease sufficiently with a third booster to make economic sense. This recommendation relies on continuous efforts to maintain high levels of vaccination uptake.
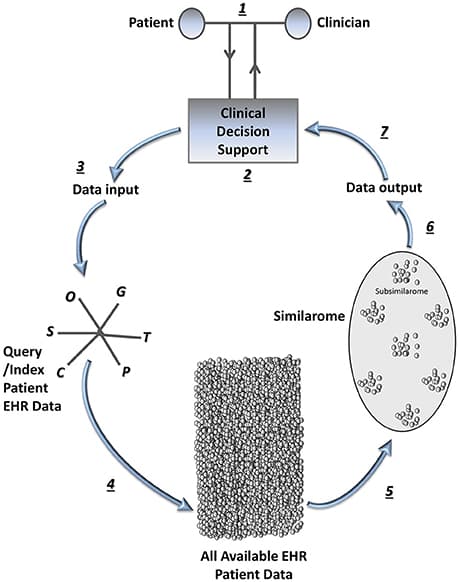
Precision medicine refers to the idea of delivering the right treatment to the right patient at the right time, usually with a focus on a data-centered approach to this task. In this perspective piece, we use the term “precision healthcare” to describe the development of precision approaches that bridge from the individual to the population, taking advantage of individual-level data, but also taking the social context into account. These problems give rise to a broad spectrum of technical, scientific, policy, ethical and social challenges, and new mathematical techniques will be required to meet them. To ensure that the science underpinning “precision” is robust, interpretable and well-suited to meet the policy, ethical and social questions that such approaches raise, the mathematical methods for data analysis should be transparent, robust, and able to adapt to errors and uncertainties. In particular, precision methodologies should capture the complexity of data, yet produce tractable descriptions at the relevant resolution while preserving intelligibility and traceability, so that they can be used by practitioners to aid decision-making. Through several case studies in this domain of precision healthcare, we argue that this vision requires the development of new mathematical frameworks, both in modeling and in data analysis and interpretation.
Issues of parameter identifiability of routinely used pharmacodynamics models are considered in this paper. The structural identifiability of 16 commonly applied pharmacodynamic model structures was analyzed analytically, using the input-output approach. Both fixed-effects versions (non-population, no between-subject variability) and mixed-effects versions (population, including between-subject variability) of each model structure were analyzed. All models were found to be structurally globally identifiable under conditions of fixing either one of two particular parameters. Furthermore, an example was constructed to illustrate the importance of sufficient data quality and show that structural identifiability is a prerequisite, but not a guarantee, for successful parameter estimation and practical parameter identifiability. This analysis was performed by generating artificial data of varying quality to a structurally identifiable model with known true parameter values, followed by re-estimation of the parameter values. In addition, to show the benefit of including structural identifiability as part of model development, a case study was performed applying an unidentifiable model to real experimental data. This case study shows how performing such an analysis prior to parameter estimation can improve the parameter estimation process and model performance. Finally, an unidentifiable model was fitted to simulated data using multiple initial parameter values, resulting in highly different estimated uncertainties. This example shows that although the standard errors of the parameter estimates often indicate a structural identifiability issue, reasonably “good” standard errors may sometimes mask unidentifiability issues.
![The IGT score. (A) Shows the STN network (=50 × 50) with quadrants that receive input from each of the corresponding decks (A–D) (B) The IGT score for three electrode positions [Position 1—in first quadrant with electrode center at lattice point (13,13), Position 2—center of the electrode at the lattice point (25,25), and Position 3- center of the electrode at the lattice point (38,38) in the fourth quadrant]. (C) For the electrode at position-2, the spread of the current (σ) was varied (D) the effect of DBS current amplitude (70, 100, and 300 pA) on IGT scores when the electrode is placed in position 3.](https://www.frontiersin.org/_rtmag/_next/image?url=https%3A%2F%2Fwww.frontiersin.org%2Ffiles%2FArticles%2F226397%2Ffphys-07-00585-HTML%2Fimage_m%2Ffphys-07-00585-g007.jpg&w=3840&q=75)