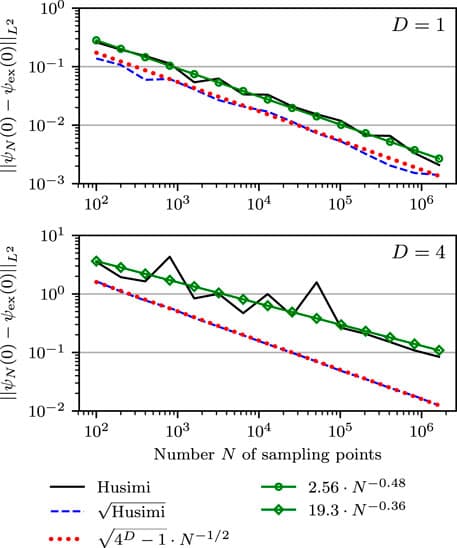
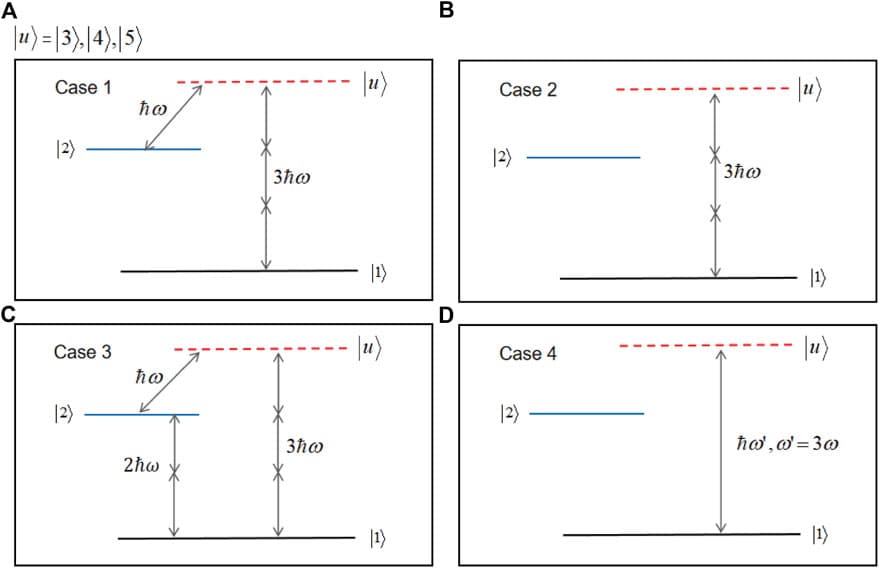
When the semiclassical Herman–Kluk propagator is used for evaluating quantum-mechanical observables or time-correlation functions, the initial conditions for the guiding trajectories are typically sampled from the Husimi density. Here, we employ this propagator to evolve the wavefunction itself. We investigate two grid-free strategies for the initial sampling of the Herman–Kluk propagator applied to the wavefunction and validate the resulting time-dependent wavefunctions evolved in harmonic and anharmonic potentials. In particular, we consider Monte Carlo quadratures based either on the initial Husimi density or on its square root as possible and most natural sampling densities. We prove analytical convergence error estimates and validate them with numerical experiments on the harmonic oscillator and on a series of Morse potentials with increasing anharmonicity. In all cases, sampling from the square root of Husimi density leads to faster convergence of the wavefunction.
We investigate the dynamics of the out-of-time-order correlators (OTOCs) via a non-Hermitian extension of the quantum kicked rotor model, where the kicking potential satisfies -symmetry. The spontaneous -symmetry breaking emerges when the strength of the imaginary part of the kicking potential exceeds a threshold value. We find, both analytically and numerically, that in the broken phase of symmetry, the OTOCs rapidly saturate with time evolution. Interestingly, the late-time saturation value scales as a pow-law in the system size. The mechanism of such scaling law results from the interplay between the effects of the nonlocal operator in OTOCs and the time reversal induced by non-Hermitian-driven potential.
It is known that the dynamics and geometric phase of a quantum system can be simulated by classical coupled oscillators using the quantum−classical mapping method without loss of physics. In this work, we show that this method can also be used to simulate the schemes of quantum shortcuts to adiabaticity, which can quickly achieve the adiabatic effect through a non-adiabatic process. By mapping quantum systems by classical oscillators, two schemes, Berry’s “transitionless quantum driving” and the Lewis−Riesenfeld invariant method, are simulated by a corresponding transitionless classical driving method, which keeps adiabatic phase trajectories and acquires Hannay’s angle and the classical Lewis−Riesenfeld invariant method by manipulating the configurations of classical coupled oscillators. The classical shortcuts to adiabaticity for the two coupled classical oscillators, which is the classical version of a spin-1/2 in a magnetic field, is employed to illustrate our results and compared with quantum shortcuts-to-adiabaticity methods.
Heisenberg guessed, after he established the matrix quantum mechanics, that the non-commutativity of the matrices of position and momentum implied that the position and momentum of a particle could not be precisely simultaneously determined. He consequently conjectured that time and energy should also have a similar relationship. Soon after, Robertson derived an inequality concerning the space coordinate and momentum, which was thought to be the mathematical expression of the uncertainty relation guessed by Heisenberg. Since then, people have tried various devices to prove the correctness of these two relations. However, no one conducted a careful analysis of Heisenberg’s primary paper. In this work, we point out some serious problems in Heisenberg’s paper and the literature talking about the uncertainty relationships: the physical concepts involved in the uncertainty relations are not clear; one physical concept had more than one explanation, i.e., switching concepts; there has never been measurement experiment to support the relations. The conclusions are that the so-called coordinate–momentum uncertainty relation has never been related to actual measurement and there does not exist a time–energy uncertainty relation.
Frontiers in Chemistry
Perovskite Nanocrystals and Bio-related Detection Applications