Subgrid channel formulation in an integrated surface-subsurface hydrologic model

In hydrologic modeling, the assumption of homogeneity within a cell averages all variability finer than the model resolution. This loss of information can impact a model's ability to accurately represent hydrologic processes, especially in highly heterogeneous domains. This study quantified the impact of this loss of information on surface water fluxes by comparing the outputs of a high-resolution and coarse hydrologic model applied to an idealized domain. This study also presented a framework for including subgrid information in the surface water physics of integrated hydrologic models. Channel width was used as a representative subgrid parameter to better characterize surface water flow in cells containing subgrid channels. A new, nonlinear relationship between flux and calculated flow depth was derived based on assumed bathymetry and known channel width. This flux relationship was incorporated into ParFlow, an integrated 3D subsurface flow and 2D surface flow hydrologic model. In all scenarios tested, the subgrid channel formulation applied to a coarse-resolution model produced peak flows that only differed from the high-resolution model by more than 1% in 11/400 of scenarios and never differed by more than 5%. This is a substantial improvement from the baseline formulation applied to a coarse-resolution model, where peak flow differed by more than 1% in 213/400 scenarios and had a maximum difference of 78%.

1 Introduction

Large-scale, integrated hydrology models can represent regional hydrology by capturing surface-subsurface interplay and interactions across watershed boundaries. It is becoming increasingly necessary to quantify the terrestrial water cycle across large spatial scales to understand water availability and flood risk under climate stress. To do this, many studies have applied hydrology models to large-scale real world domains (Bauer et al., 2006; Goderniaux et al., 2009; Shen and Phanikumar, 2010; Sutanudjaja et al., 2011; de Paiva et al., 2013; O'Neill et al., 2021; Yang et al., 2023; Delottier et al., 2024). Physics-based modeling at these scales can be very computationally expensive, so other products and models have been developed based on remote sensing, data aggregation, or machine learning of surface (Miller et al., 2018; Mohanasundaram et al., 2021; Durand et al., 2023) and subsurface hydrology (Cools et al., 2006; Ma et al., 2024). These studies are helpful in defining regional hydrology but typically have the disadvantage of producing relatively coarse outputs. Low-resolution is necessary given the computational cost of high-resolution large-scale hydrologic modeling, but coarse models do not necessarily reflect the same hydrology that high-resolution models would (Foster et al., 2020).

Hydrologic models often assume homogeneity within a cell for both inputs and outputs. Each cell is treated as a representative elementary volume, which is necessary to solve the relevant partial differential equations. This can lead to coarse-resolution model outputs and the loss of natural spatial variability in inputs. Many studies have investigated the impact of subgrid information on the accuracy of hydrologic models and how this lost information can be reincorporated into the modeling process. Specifically, subgrid variability in both land surface processes (Shuttleworth, 1988; Leung et al., 1996; Ghan et al., 1997; Noilhan et al., 1997; Giorgi et al., 2003; Wang and Wang, 2007) and soil characteristics (Wood et al., 1992; Ghan et al., 1997; Kabat et al., 1997; Kreye and Meon, 2016) have been heavily studied. Generally, these studies find that the inclusion of subgrid information is influential on model output and increases model accuracy, yet it is still unclear to what extent subgrid information impacts the large-scale solution.

Subgrid topographic variability ranging in scale from microtopography to subgrid channels can also be impactful on hydrologic fluxes (Jan et al., 2018; Thompson et al., 2010). Subgrid topography has previously been incorporated into overland flow models utilizing a large array of methodologies. This has been done by defining an additional high-resolution grid of topography data within each coarse-grid cell to determine surface storage and flux (Volp et al., 2013; Zhang et al., 2023). The impact of microtopography on surface storage has been represented by developing and modeling storage-outflow curves (Hu et al., 2020). Known anthropogenic impacts on flow paths, such as roads and hedges (Carluer and Marsily, 2004; Gascuel-Odoux et al., 2011) as well as the anisotropic impact of microtopography such as crop rows on overland flow (Viero and Valipour, 2017) have also been incorporated into models. Subgrid topographic information has also been modeled via the use of effective parameters. An effective Manning's n value has been used previously to account for subgrid channels in overland flow calculations (Schalge et al., 2019). Similar to an effective parameter, Moretti and Orlandini (2018) proposed a different methodology to determine the elevation assigned to a cell based on the elevation of the highest Horton-order river within the cell, essentially creating an effective elevation. Additional studies have distilled new subgrid parameters out of subgrid topographic data. These parameters are new values assigned to each grid cell designed to represent lost information and can be used as inputs into the continuity and flux equations (Jan et al., 2018; Li and Hodges, 2019; Ferrari and Viero, 2020).

The issue of accounting for partially inundated cells in hydrologic models has been the subject of many studies (Bates and Hervouet, 1999; Defina, 2000; Casulli, 2009). Recent work has focused on explicitly modeling subgrid channels in 2D hydrologic models to better represent floodplain inundation. Neal et al. (2012) developed a methodology to identify subgrid channel cells and model their fluxes using the dynamic wave equation based on the subgrid parameters of channel width and channel bed elevation in the model LISFLOOD-FP. Viero et al. (2014) used the subgrid method developed by Defina (2000) to model subgrid channel flow in a coupled 2D surface and 2D saturated shallow subsurface model. Other studies have instead modeled channel flow directly as one dimensional stream elements with different geometries. These streams are in one- or two-way communication with other hydrologic processes operating on a regular grid. As an example, David et al. (2011) developed RAPID, an explicit channel network model embedded in a regular grid-based land surface model. Panday and Huyakorn (2004) also modeled channel and reach networks as a separate process from 2D overland flow. The goal of this study is to build on this previous work modeling subgrid channels to further improve the ability to represent surface water accurately across scales. A subgrid approach can increase local accuracy when representing the terrestrial water cycle at large scales without the computational cost of increasing resolution.

The goal of this work was to create a framework to develop and implement subgrid parameterizations in the integrated surface-subsurface hydrologic model ParFlow. The newly implemented subgrid parametrization was evaluated by quantifying the discrepancy in representing channels between coarse-resolution and high-resolution models across an array of input parameters. We then determined when a parameterization of subgrid channels would be most impactful on model accuracy. Channel width was used as a representative topographic subgrid parameter, which is used as an input in the flux equation of the kinematic wave approximation. This formulation is mathematically similar to the effective parameter implementation done by Schalge et al. (2019) but was implemented directly within the surface flux equations in an integrated hydrologic model. This new methodology of directly including subgrid information in the flux formulation allows for nonlinear depth-dependent corrections to the overland flow formulation, which was not possible with effective parameters alone. For example, this subgrid channel formulation was able to account for side-wall friction of subgrid channels while the effective parameter methodology proposed by Schalge et al. (2019) is not. While this is a simple example, this framework paves the way for complex subgrid formulations necessary for regional accuracy in large-scale integrated hydrologic models.

2 Methods

We developed and applied a subgrid parameterization of the kinematic wave equation in the overland flow module of ParFlow, a 3D subsurface and 2D surface flow integrated model which can efficiently be applied at large scales (Ashby and Falgout, 1996; Jones and Woodward, 2001; Kollet and Maxwell, 2006; Maxwell, 2013). This subgrid channel formulation and its derivative are embedded directly into ParFlow's nonlinear solver. We applied this subgrid formulation and the baseline ParFlow overland flow formulation to a coarse idealized model domain. We then compared their outputs to the baseline ParFlow overland flow formulation applied to a high-resolution model domain to determine if using a subgrid formulation resulted in flows that better matched a high-resolution model. Additionally, we compared these model formulation and domain combinations across an array of parameter and precipitation scenarios. This is to determine under what conditions the subgrid formulation increased the accuracy of the coarse-resolution model. Since this study is conducted on an idealized domain, accuracy is defined as how closely a coarse model's outflow matches the high-resolution model's outflow. This allows the accuracy of the baseline coarse model to be assessed as well as the improvements of the subgrid model to be quantified. All models, here defined as a combination of a model domain and an overland flow formulation, used in this study are described in Figure 1 and Table 1.

Figure 1

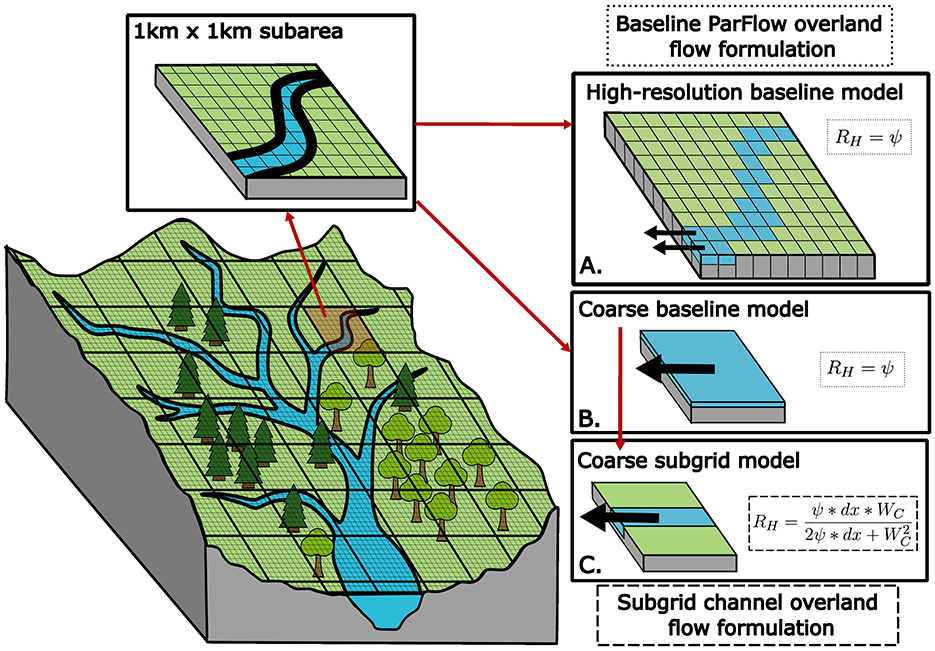
Figure 1. Conceptual overview of modeling domain and the characterization of subgrid channels in the (A) high-resolution baseline model, (B) coarse baseline model, and (C) coarse subgrid model.

Table 1

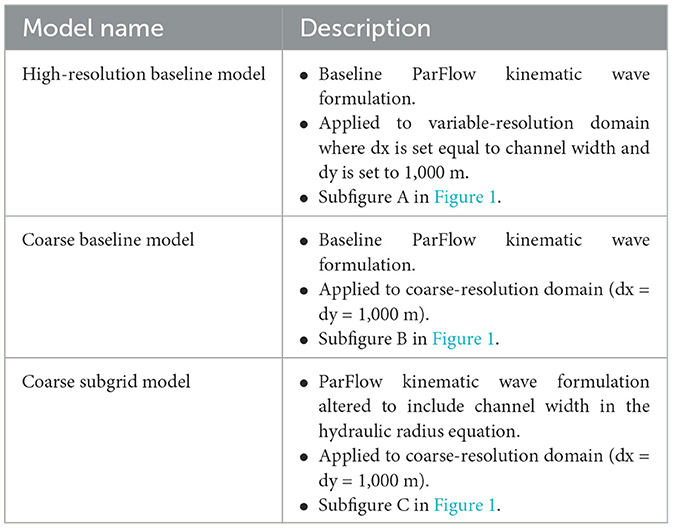
Table 1. Description of all models, defined as a combination of an overland flow formulation and a model domain.

2.1 Overland flow formulations

2.1.1 Baseline ParFlow formulation

ParFlow can calculate overland flux using either the diffusive wave or kinematic wave approximations. The baseline ParFlow overland flow formulation used in this study is based on the cell-centered Kinematic Wave Approximation using Manning's equation with the additional assumption that hydraulic radius is equal to pressure head (Kollet and Maxwell, 2006). This is executed in ParFlow as follows:

$\begin{array}{ll}Q=\frac{\sqrt{S}}{\text{n}}*{\psi }^{5/3}*dx& (1)\end{array}$

where Q is discharge (L³/t), S is bottom slope (L/L), n is Manning's coefficient (t/L^1/3), ψ is surface pressure head (L), and dx is cell size or resolution (L). Setting hydraulic radius equal to pressure head is a common assumption in hydrologic models which holds true when flow depth is much smaller than width, slopes are small and pressure is hydrostatic. Since homogeneity is assumed within each cell, all overland flow is represented as sheet flow across each cell. In this representation, flow depth is equivalent to pressure head within a cell and flow width is equivalent to cell size so the assumption that flow depth is much smaller than flow width holds true (Figure 2). However, in scenarios where flow within a cell is confined to a smaller area, such as a subgrid channel, representing flow as sheet flow can lead to an underestimation of the hydraulic radius and therefore an underestimation of flux.

Figure 2

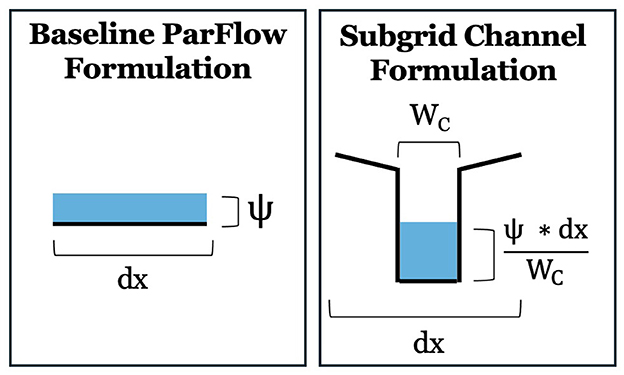
Figure 2. Conceptual representation of baseline (left) and subgrid channel (right) overland flow formulations.

2.1.2 Subgrid channel formulation

The subgrid formulation methodology incorporates channel width as an additional parameter within the kinematic wave equation. This new, nonlinear relationship between flux and calculated flow depth replaces the current flux equation within ParFlow. Channel width in both horizontal directions are used as new inputs into ParFlow and are the basis of this new flux calculation. Flux direction is still determined based on cell slope, which is derived from topography.

Overland fluxes are determined using the same kinematic wave approximation as default ParFlow, but we no longer assume that the hydraulic radius is equal to pressure head. Instead, it is assumed that all flow is confined to a rectangular channel of known width (Figure 2). The hydraulic radius can then be calculated based on the depth and width of flow in the rectangular channel:

$\begin{array}{ll}{R}_H=\frac{\psi *dx*W_C}{2\psi *dx+W_C^2}& (2)\end{array}$

where W_C is channel width (L), a new subgrid parameter. Depth of flow was calculated based on confining the known volume of surface water to the channel. Substituting this hydraulic radius into the kinematic wave equation results in an overland flux formulation of:

$\begin{array}{ll}Q=\frac{\sqrt{S}}{\text{n}}*{\psi }^{5/3}*dx*{\left(\frac{dx*W_C}{2\psi *dx+W_C^2}\right)}^{2/3}& (3)\end{array}$

Given the implicit solution in ParFlow, the derivative of this new flux equation with respect to ψ needs to be included in the Jacobian as well. That derivative is:

$\begin{array}{ll}\begin{array}{r}\hfill \frac{dQ}{d\psi }=\frac{\sqrt{S}}{n}*d{x}^{5/3}*W_C^{2/3}*(\frac{5}{3}{\left(\frac{\psi }{2\psi *dx+W_C^2}\right)}^{2/3}\\ \hfill -\frac{4dx}{3}{\left(\frac{\psi }{2\psi *dx+W_C^2}\right)}^{5/3})\end{array}& (4)\end{array}$

This new overland flow formulation and its derivative are added directly into ParFlow's nonlinear solver. As described in Kollet and Maxwell (2006), the surface and subsurface are directly integrated through a global variable of ψ, or pressure, at the surface-subsurface interface. This proposed overland flow formulation replaces the previous overland flow equation and is used in the overland flow boundary condition to simulate integrated surface-subsurface flows.

This formulation is executed in the positive and negative X and Y directions with channel width in both directions defined independently. This is so that channel width only impacts fluxes through a cell in the direction of a channel and not overland fluxes perpendicular to the channel. All overland fluxes from non-channel cells and from channel cells not in the direction of channel flow set W_C equal to cell size. Since ψ is much smaller than dx in these scenarios, this collapses back down to the baseline ParFlow flux formulation.

2.2 Idealized test case

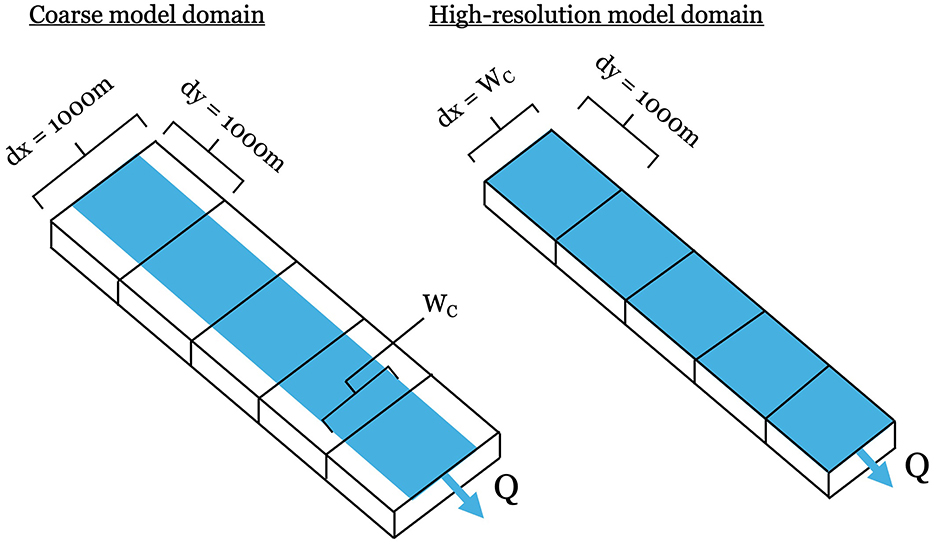
An idealized domain was created to compare all models across a large array of parameters in a controlled environment. This domain is a one cell by five cell rectangle with a channel running down the center of the domain (Figure 3). All models have a cell-size parallel to the channel equal to 1 km and all models except the high-resolution baseline model also have a cell size perpendicular to the channel equal to 1 km. The cell size perpendicular to the channel of the high-resolution baseline model is equal to the width of the rectangular channel. This is so the high-resolution baseline model domain only includes the channel without any overland cells to remove the additional variability associated with the parameterization of those overland cells. Rainfall is scaled for the high-resolution baseline model to account of the lower surface area of each cell. This high-resolution domain will be used as a benchmark to assess performance of the other formulations.

Figure 3

Figure 3. Idealized model domains.

All cells have equal unidirectional slopes downstream. Four hours of spatially invariable rainfall are applied at the beginning of each simulation and then the simulation continues with hourly timesteps until outflow is approaching zero. To simplify the hydrology to allow better comparison of overland flow between models, the impacts of infiltration and groundwater interactions are neglected by setting permeability to nearly zero.

2.3 Parameter scenarios

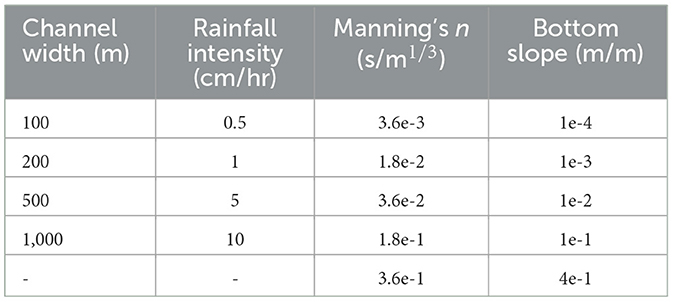
To determine under what conditions the current ParFlow formulation differs from the subgrid channel formulation as well as when the coarse baseline model diverges from the high-resolution baseline model we ran all three ParFlow models across a large array of different input parameters. The Manning's n and bottom slope parameters are varied across ranges of realistic values (Yang et al., 2023). Four values of channel width ranging from 100 m to 1 km were tested to assess performance when channel width is similar to cell size as well as much smaller than cell size. Four values of rainfall intensity are also applied to assess performance across various water depths. Channel width is also used to determine cell size perpendicular to the channel in the high resolution model. All parameter values are listed in Table 2.

Table 2

Table 2. All input parameters varied and their corresponding values.

3 Results

3.1 Coarse baseline model performance

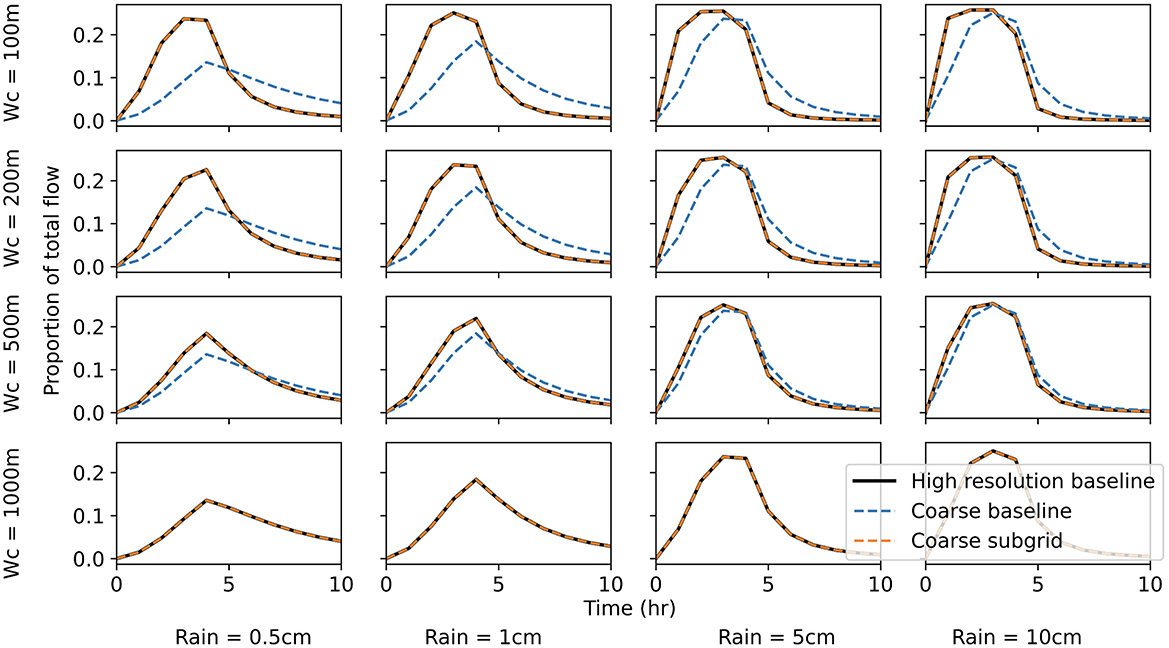
Parameter scenarios in which the coarse baseline model differs from the high-resolution baseline model must first be identified to assess when subgrid formulations would be most applicable. Figure 4 shows how changes in channel width and rainfall intensity impact hydrograph characteristics at the outlet when comparing the coarse baseline model and the high-resolution baseline model. When channel width is equal to cell size, there is no difference between the low- and high-resolution baseline models, which is to be expected since the models are equivalent in this scenario. As channel width decreases, discrepancies in the peak flow volume begin to emerge between the coarse baseline and high-resolution baseline model.

Figure 4

Figure 4. Difference in outflow between all three models based on rainfall and channel width.

The difference in peak flow between the coarse baseline model and the high-resolution baseline model across all parameter and rainfall scenarios is shown in Figure 5. As was seen in Figure 4, there is essentially no difference between the two models when channel width is equal to cell size. At the lowest channel width of 100 m, 1/10 the cell size, 35% of the scenarios result in a difference in peak flow of greater than 50% with 20% of scenarios resulting in a difference of greater than 75%. When channel width is 200 m, 1/5 the cell size, 35% of scenarios still result in a peak difference of greater than 50% and no scenarios have a difference of greater than 75%. When channel width is 500 m, 1/2 the cell size, no scenarios have a peak difference exceeding 50% with the greatest difference being 37.02%. Across all channel widths, peak flow differs by greater than 1% in 213 out of 400 scenarios. As channel width decreases, the number of scenarios which differ and the magnitude of those differences increase.

Figure 5

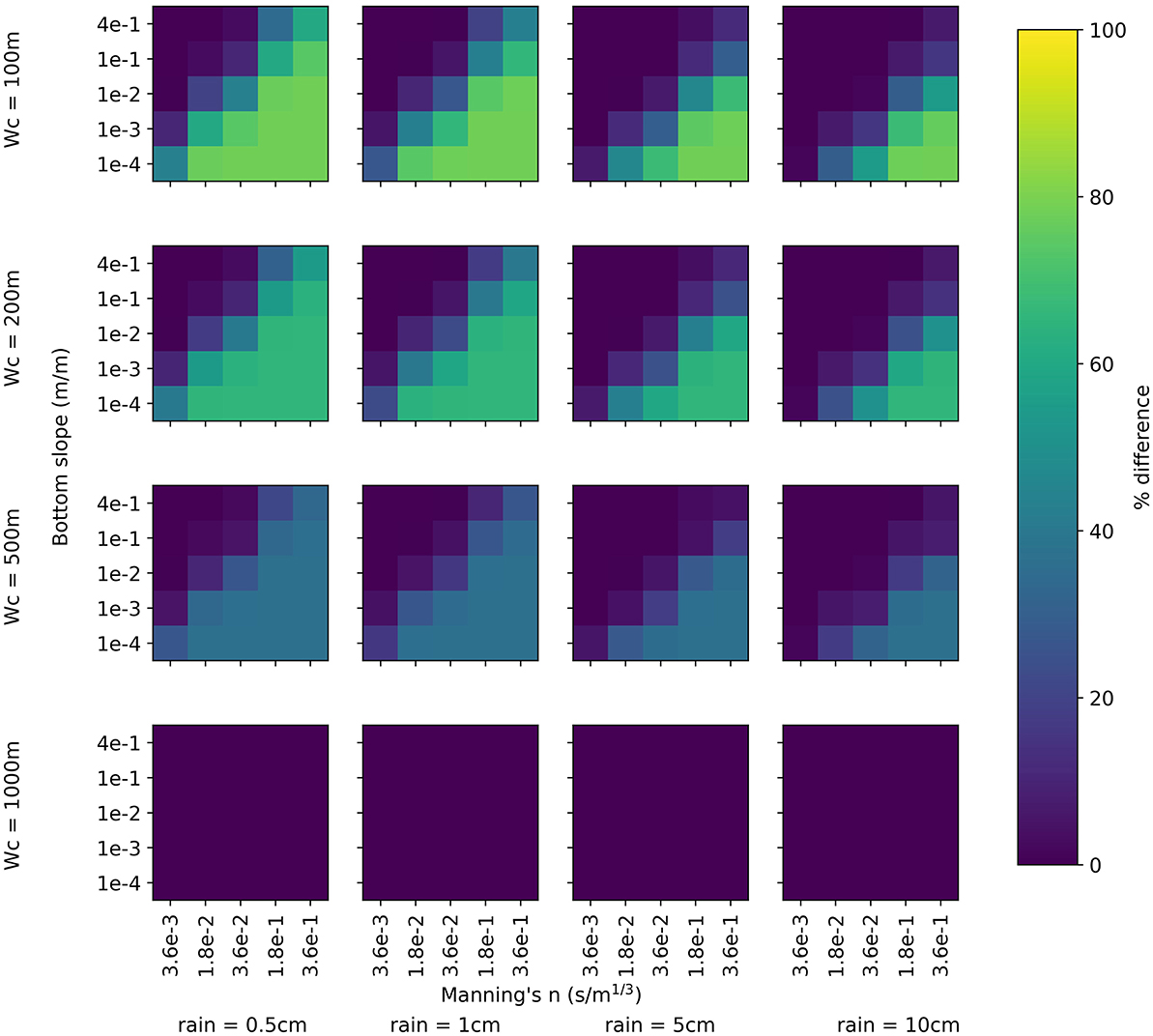
Figure 5. Percentage difference in peak flow between the coarse baseline and high-resolution baseline models. Here channel width is not an input in the coarse baseline model but instead is only used to define the domain resolution of the high-resolution model.

Within each rainfall-channel width scenario, bottom slope and Manning's n are also varied. These two overland flow parameters are influential on the discrepancy in peak flow between the two models when channel width is not equal to cell size. The difference in peak is greatest when Manning's n is high and bottom slope is low. This difference is further exacerbated in lower rainfall conditions, which are representative of when there is lower flow volume in the channel. Overall, the largest discrepancy in peak flow of 78.40% is seen in the scenario where channel width is 100 m, rainfall intensity is 0.5 cm/hr, Manning's n is 6e-3 s/m^1/3, and bottom slope is 1e-4 m/m.

Despite the significant differences in peak flow, peak timing is consistent between the coarse baseline and high-resolution baseline models (Figure 4). While there are some scenarios that result in a single time step difference in the peak timing, these scenarios don't follow any trend relating to the parameters varied in this study. The shape of the rising and falling limb also varied significantly between the coarse baseline and high-resolution baseline models (Figure 4). Qualitatively, hydrograph shape of the coarse baseline and the high-resolution baseline models was most different in the low rainfall and small channel width scenarios.

3.2 Coarse subgrid model performance

The coarse subgrid model performed nearly identically to the high-resolution baseline model across nearly all scenarios (Figure 6). In only 11 of 400 total scenarios are there differences in peak flow greater than 1% and no scenarios exceed 5%. These differences are relatively small when compared to the differences seen between the coarse baseline and high-resolution baseline models of up to 78.40%. The differences in peak flow occur when channel width is small, rainfall is high, and flow is slow. Overall, the coarse subgrid model performed more similarly to the high-resolution model than the coarse baseline model across all parameter scenarios tested.

Figure 6

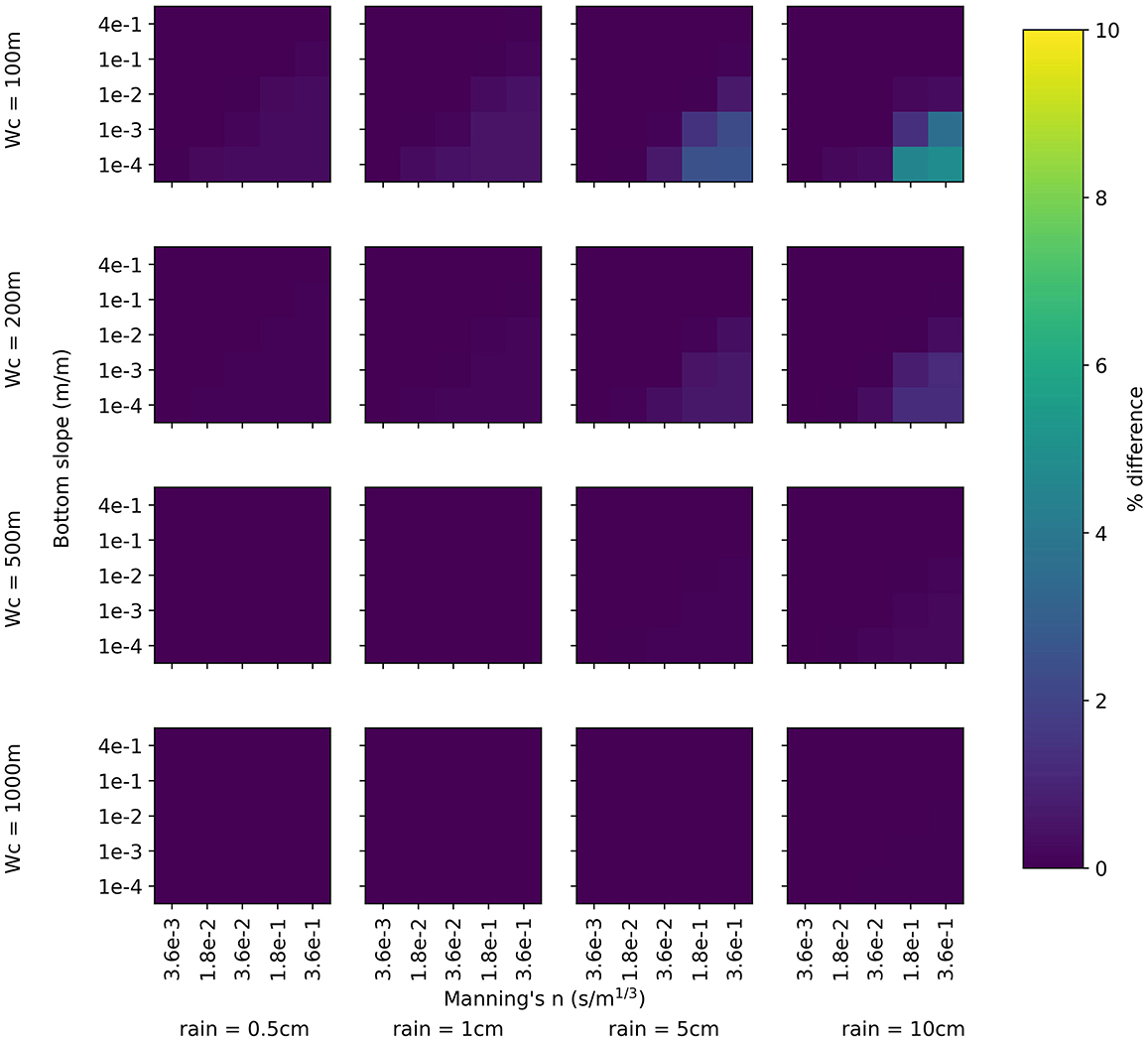
Figure 6. Percentage difference in peak flow between the coarse subgrid formulation and high-resolution baseline models. Here channel width is an input in the coarse subgrid model as well as used to define the domain resolution of the high-resolution model.

Small differences in peak flow are expected, as the high-resolution baseline model and the coarse subgrid model use different formulations for the kinematic wave equation. The subgrid formulation is based on the assumption of a rectangular channel while the coarse baseline formulation is based on the assumption that flow depth is negligible in comparison to flow width. These scenarios where differences arise highlight when the addition of side-wall friction is impactful on model accuracy, as it is included in the subgrid formulation but not the baseline formulation.

4 Discussion

4.1 Impact of subgrid formulation on coarse model accuracy

The coarse baseline model consistently underestimated peak flow across all rainfall scenarios when channel width was less than cell size. The magnitude of this underestimation was dependent on all parameters evaluated. The addition of the subgrid formulation to the coarse model resulted in the coarse model to perform much more similarly to the high resolution model. These results align with what was found by Schalge et al. (2019).

Rainfall volume was very influential on the accuracy of the coarse baseline model compared to the high resolution model. Lower rainfall scenarios resulted in a higher peak difference between the coarse baseline and high-resolution baseline models across all channel widths, slopes, and n values. Since lower rainfall corresponds with lower flow volume, this implies that the difference between coarse and high-resolution baseline models are most pronounced in low-flow conditions. In high rainfall conditions (when flow depth was high), channel width was much less impactful on peak flow than in low rainfall scenarios (Figure 7). Therefore, in these high flow scenarios the addition of a subgrid formulation only resulted in small improvements from the coarse baseline.

Figure 7

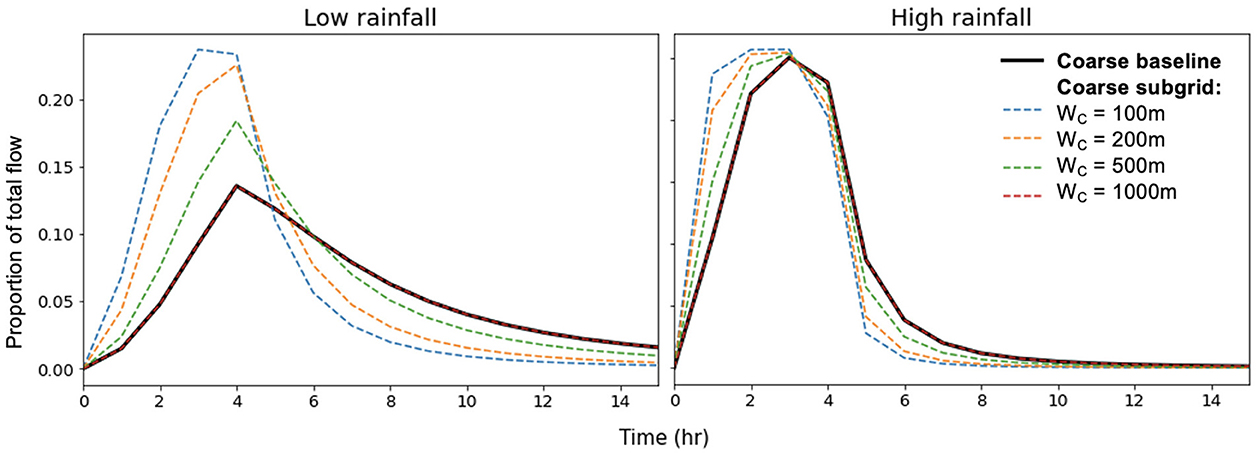
Figure 7. Impact of rainfall and channel width on difference between coarse baseline and subgrid formulation models.

Combinations of high n values and low slopes, resulting in slow flow, also resulted in the greatest differences in peak flow across all rainfall and channel width scenarios. Collectively, this implies that smaller fluxes, such as those from tributaries, in areas with topography and vegetation which result in slow flow would be the most misrepresented by coarse models. These tributaries are likely also small, potentially with widths much smaller than the cell size, which further exacerbates the underestimation of these fluxes. Systematically underestimating tributary fluxes could have a large impact on the overall hydrology of a region. This could compound when there are multiple tributaries with underestimated flows feeding into the same river. The addition of channel width as a subgrid variable was able to mitigate this underestimation and when applied to the coarse model domain resulted in fluxes nearly identical to the high-resolution baseline model.

4.2 Impact of channel length on coarse model accuracy

All three models across all parameter and rainfall scenarios were also applied to a thirty-cell idealized domain to determine if a longer flow length would result in a larger discrepancy in peak flow or peak flow timing between the coarse baseline and high-resolution baseline model. The outflow of the coarse baseline, high-resolution, and coarse subgrid models were all compared at the outlet of the 30 km channel model.

In the 30 km channel length model, there is still very little difference between the high resolution model and the coarse subgrid model. The few scenarios where these two models differed after 5 km of channel still differed after 30 km, but in peak timing as opposed to peak flow. This is because both the high-resolution baseline model and the subgrid model reach the same constant outflow where inflow from upstream cells is equal to discharge, the high-resolution baseline model just reaches this outflow slightly earlier. This illustrates that over longer channels and time frames, the subgrid model output approaches that of the high-resolution baseline model.

The same trends in peak flow difference between the coarse baseline and high-resolution baseline models observed in the five-cell domain were also observed at all locations in the thirty-cell domain but were further exacerbated at longer distances from the origin. Figure 8 shows the percent difference in peak between the coarse baseline and coarse subgrid model at the end of the 30 km channel. When compared to Figure 5, there are more scenarios which have higher peak flow difference between the two models. The increase in peak discrepancy between the coarse baseline model and the high-resolution baseline model as channel length increases shows that the impact of underestimating flux between subgrid channel cells compounds over distance. Therefore longer channels will be most misrepresented when not accounting for subgrid channels. Despite more scenarios having a larger peak difference between the coarse baseline model and the high-resolution baseline model, the maximum percentage difference between peaks does not change and it can be clearly seen that the maximum peak difference is dependent on channel width (Figure 8).

Figure 8

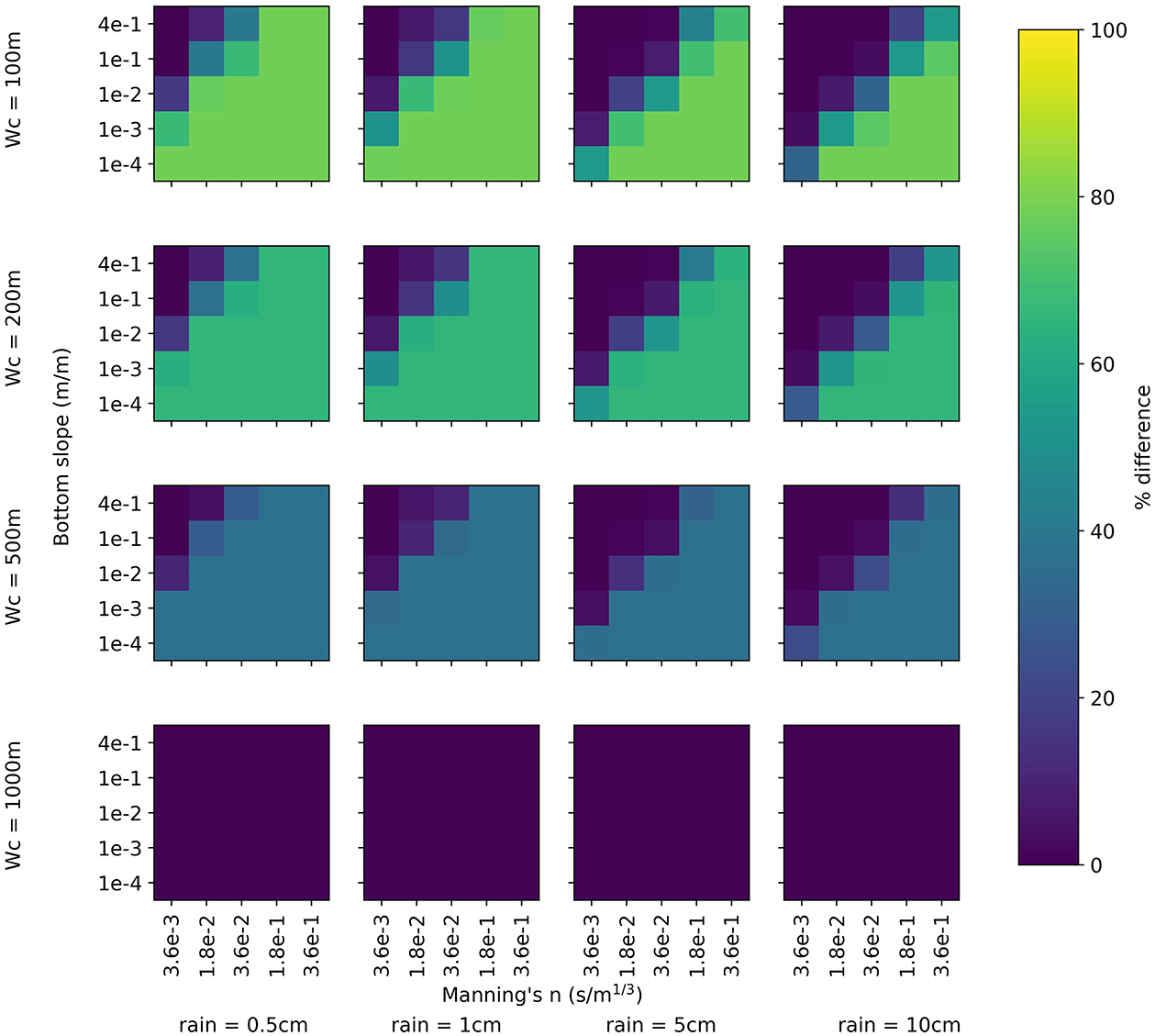
Figure 8. Percentage difference in peak flow between the coarse baseline formulation and high-resolution baseline models at the outlet of the 30 km channel.

4.3 Using nondimensional parameters to define applicability subspace

The Froude Number and the Kinematic Wave Number (KWN) are non-dimensional values based on flow parameters and have been used to define ranges of applicability of the Kinematic Wave Approximation and the Diffusive Wave Approximation (Vieira, 1983). These dimensionless values were used in this study to investigate the relationship between domain parameters and accuracy of a coarse-scale model compared to a high-resolution baseline model. Under the assumption of uniform flow and substituting in the Chezy equation, the Froude number can be calculated by:

$\begin{array}{ll}{F}_0=C{\left(\frac{tan(\theta )}{g}\right)}^{1/2}& (5)\end{array}$

where C is Chezy roughness which is equivalent to 1/n*(R^1/6), θ is the bottom slope angle, and g is gravitational acceleration. The Kinematic Wave Number is defined as:

$\begin{array}{ll}k={\left(\frac{g^{3}Lsin(\theta )}{C^4{q}^2}\right)}^{1/3}& (6)\end{array}$

where L is defined in Vieira (1983) as the length of the channel at which values are measured and q is lateral inflow into the channel. In this study, we define L as cell length parallel to the channel and q as flux through the cell. This definition allows the kinematic wave number to be calculated for any cell in a hydrologic model and will serve as a non-dimensional value which can be used in conjunction with the Froude number to classify conditions in any given cell to determine if a coarse model output will closely match a higher-resolution model. It is useful to classify these scenarios using non-dimensional parameters so this analysis can be applied to other model resolutions or subgrid parameters of interest.

The Froude Number and Kinematic Wave Number were used to determine if there is a non-dimensional pattern where the coarse model performed most differently than the high-resolution baseline model. These cases where differences in peak flow are highest are cases where the subgrid formulation would be most impactful. Figure 9 shows where all 400 parameter combinations fall in the Froude Number and KWN space. The color bar represents the same values as shown in Figure 5, which is the percentage difference between the coarse and high-resolution baseline models for the same parameter values. As seen before, smaller channel width and longer channel length have higher percent differences between the two models. The upper left portion of the sample space, high KWN and low Froude Number, also has higher percent difference between the two models. Low Froude Number and high KWN also corresponds with high Manning's n and low bottom slope across all three models, as was also seen in Figure 5. While there isn't a specific cutoff where a subgrid formulation is necessary, when the Froude Number is less than one is when most large differences between the coarse baseline model and the high-resolution baseline model arise. Analysis of non-dimensional values such as the Froude Number and KWN can be used as guidance regarding when coarse models may not be accurately capturing overland flow in subgrid channel cells and when a subgrid formulation would most improve overland flow accuracy.

Figure 9

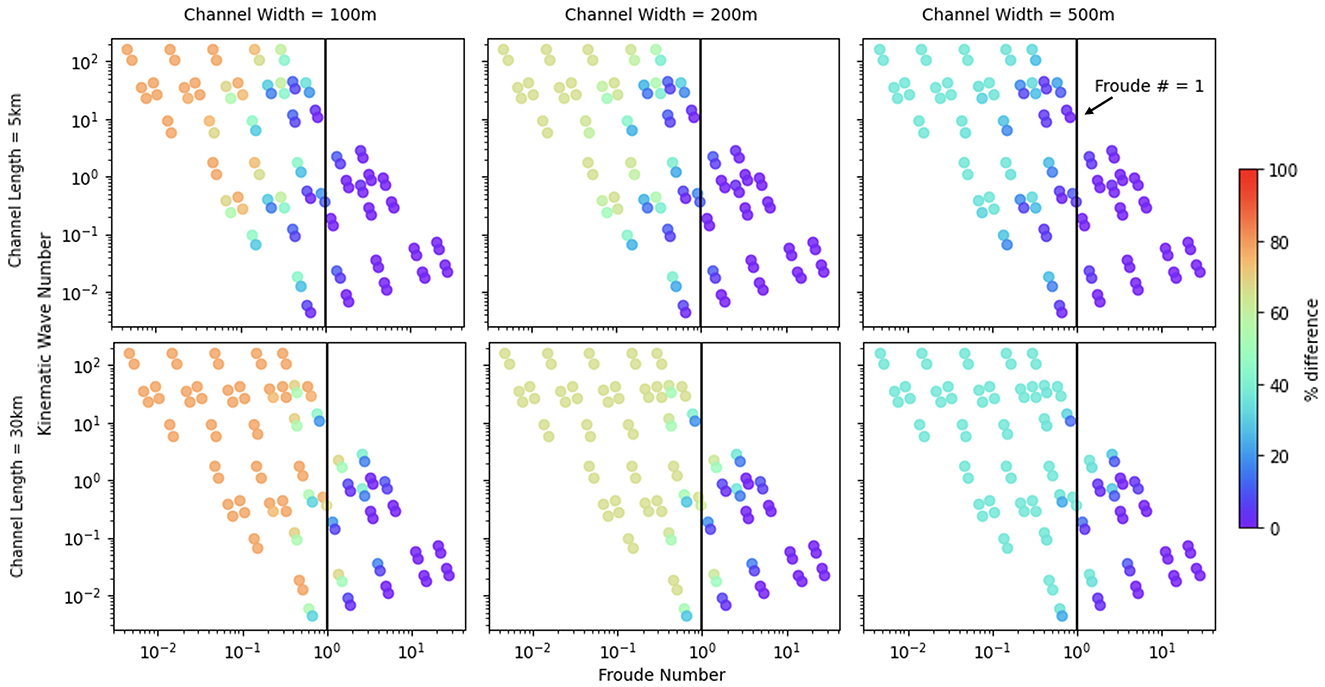
Figure 9. Kinematic Wave Number and Froude Number of coarse model across channel width and channel length scenarios. Color represents the difference in peak between the coarse baseline and high-resolution baseline models.

4.4 Future work to improve accuracy of subgrid formulations

We used an idealized model domain to benchmark the performance of the subgrid channel formulation, but the only subgrid variability this captures is subgrid channels. This was important to verify this formulation against a high-resolution model without additional sources of variability, but doesn't evaluate the accuracy of this formulation when applied to a real domain which also contains subgrid microtopographic variation outside of channels. To understand how this subgrid channel formulation, as well as future subgrid formulations, are able to improve the accuracy of modeled fluxes, they should be tested on real-world domains. This will also help identify which subgrid parameters are most impactful on the accuracy of overland flow.

An additional challenge in applying subgrid formulations to real-world models is determining the values of new subgrid parameters. There are many ways how channel width has been determined in previous studies including using empirical relationships (Schalge et al., 2019) or satellite data (Neal et al., 2012). When new subgrid formulations are derived, methodologies to assign effective values to the real-world parameters values will also need to be developed so they can be applied to real domains.

5 Conclusions

Subgrid formulations and parameterizations are important next steps in increasing accuracy while maintaining efficiency within large-scale hydrologic models. This study has shown that an additional parameter, channel width, can be incorporated into flux formulations in an integrated surface-groundwater model to increase model accuracy without increasing resolution or runtime. This coarse subgrid model performed nearly identically to the high-resolution baseline model in all scenarios tested in an idealized domain.

The scenarios in which the coarse baseline model differed most from the high-resolution baseline model were identified to determine under what conditions a subgrid formulation would be most impactful at improving accuracy. The largest difference between the coarse baseline and high-resolution baseline model occurs when flow velocity is low (i.e. when Manning's n is high and channel slope is low), when flow volume is low, and when channel width is much smaller than cell size. When these three flow conditions are combined, there was up to a 78.4% difference in the peak flow between the coarse baseline model and the high-resolution baseline model. This difference in peak was completely mitigated via the use of a subgrid formulation in the coarse model.

Future studies should build on this framework of implementing subgrid formulations into integrated surface-groundwater models to further increase accuracy in more complex systems. This study focused on assessing the accuracy of a subgrid formulation in an idealized domain to isolate the impact on channel flow, but in real-world domains with additional heterogenities, additional subgrid parameters incorporated into flux formulations could further improve accuracy. Large-scale hydrologic modeling is an important next step in answering pertinent hydrology questions and subgrid formulations are necessary to increase their accuracy at coarse resolutions.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/miapeeples/subgrid_channel_parflow.

Author contributions

AP: Conceptualization, Data curation, Formal analysis, Methodology, Writing – original draft, Writing – review & editing. RMM: Conceptualization, Methodology, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This material was based upon work supported by the National Science Foundation Graduate Research Fellowship Program (grant no. DGE-2039656) and HydroGEN, National Science Foundation Convergence Accelerator (grant no. 2134892).

Acknowledgments

The authors would like to thank Georgios Artavanis and Kenadi Waymire for their contributions to the software development of this work in ParFlow. We also thank the editor, Oliver Schilling, and the three reviewers for their constructive feedback during the review process.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

References

Ashby, S. F., and Falgout, R. D. (1996). A parallel multigrid preconditioned conjugate gradient algorithm for groundwater flow simulations. Nuclear Sci. Eng. 124, 145–159. doi: 10.13182/NSE96-A24230

Crossref Full Text | Google Scholar

Bates, P. D., and Hervouet, J. (1999). A new method for moving boundary hydrodynamic problems in shallow water. Proc. Royal Soc. London. Series A: Mathem. Phys. Eng. Sci. 455, 3107–3128. doi: 10.1098/rspa.1999.0442

Crossref Full Text | Google Scholar

Bauer, P., Gumbricht, T., and Kinzelbach, W. (2006). A regional coupled surface water/groundwater model of the okavango delta, botswana. Water Resour. Res. 42:4. doi: 10.1029/2005WR004234

PubMed Abstract | Crossref Full Text | Google Scholar

Carluer, N., and Marsily, G. (2004). Assessment and modelling of the influence of man-made networks on the hydrology of a small watershed: implications for fast flow components, water quality and landscape management. J. Hydrol. 285, 76–95. doi: 10.1016/j.jhydrol.2003.08.008

Crossref Full Text | Google Scholar

Casulli, V. (2009). A high-resolution wetting and drying algorithm for free-surface hydrodynamics. Int. J. Numer. Methods Fluids 60, 391–408. doi: 10.1002/fld.1896

Crossref Full Text | Google Scholar

Cools, J., Meyus, Y., Woldeamlak, S. T., Batelaan, O., and De Smedt, F. (2006). Large-scale gis-based hydrogeological modeling of flanders: a tool for groundwater management. Environ. Geol. 50, 1201–1209. doi: 10.1007/s00254-006-0292-3

Crossref Full Text | Google Scholar

David, C. H., Maidment, D. R., Niu, G. Y., Yang, Z. L., Habets, F., and Eijkhout, V. (2011). River network routing on the nhdplus dataset. J. Hydrometeorol. 12, 913–934. doi: 10.1175/2011JHM1345.1

PubMed Abstract | Crossref Full Text | Google Scholar

Defina, A. (2000). Two-dimensional shallow flow equations for partially dry areas. Water Resour. Res. 36, 3251–3264. doi: 10.1029/2000WR900167

Crossref Full Text | Google Scholar

Delottier, H., Schilling, O. S., and Therrien, R. (2024). Assessing the impact of surface water and groundwater interactions for regional-scale simulations of water table elevation. J. Hydrol. 639:131641. doi: 10.1016/j.jhydrol.2024.131641

Crossref Full Text | Google Scholar

Durand, M., Gleason, C. J., Pavelsky, T. M., Prata de Moraes Frasson, R., Turmon, M., David, C. H., et al. (2023). A framework for estimating global river discharge from the surface water and ocean topography satellite mission. Water Resour. Res. 59:e2021WR031614. doi: 10.1029/2021WR031614

Crossref Full Text | Google Scholar

de Paiva, R. C. D., Buarque, D. C., Collischonn, W., Bonnet, M.-P., Frappart, F., Calmant, S., et al. (2013). Large-scale hydrologic and hydrodynamic modeling of the Amazon river basin. Water Resour. Res. 49, 1226–1243. doi: 10.1002/wrcr.20067

PubMed Abstract | Crossref Full Text | Google Scholar

Ferrari, A., and Viero, D. P. (2020). Floodwater pathways in urban areas: a method to compute porosity fields for anisotropic subgrid models in differential form. J. Hydrol. 589:125193. doi: 10.1016/j.jhydrol.2020.125193

Crossref Full Text | Google Scholar

Foster, L. M., Williams, K. H., and Maxwell, R. M. (2020). Resolution matters when modeling climate change in headwaters of the colorado river. Environm. Res. Letters 15:104031. doi: 10.1088/1748-9326/aba77f

Crossref Full Text | Google Scholar

Gascuel-Odoux, C., Aurousseau, P., Doray, T., Squividant, H., Macary, F., Uny, D., et al. (2011). Incorporating landscape features to obtain an object?oriented landscape drainage network representing the connectivity of surface flow pathways over rural catchments. Hydrol. Process. 25, 3625–3636. doi: 10.1002/hyp.8089

Crossref Full Text | Google Scholar

Ghan, S. J., Liljegren, J. C., Shaw, W. J., Hubbe, J. H., and Doran, J. C. (1997). Influence of subgrid variability on surface hydrology. J. Clim. 10, 3157–3166.

Google Scholar

Giorgi, F., Francisco, R., and Pal, J. (2003). Effects of a subgrid-scale topography and land use scheme on the simulation of surface climate and hydrology.: Part i: Effects of temperature and water vapor disaggregation. J. Hydrometeorol. 4, 317–333. doi: 10.1175/1525-7541(2003)4<317:EOASTA>2.0.CO;2

Crossref Full Text | Google Scholar

Goderniaux, P., Brouyère, S., Fowler, H. J., Blenkinsop, S., Therrien, R., Orban, P., et al. (2009). Large scale surface-subsurface hydrological model to assess climate change impacts on groundwater reserves. J. Hydrol. 373, 122–138. doi: 10.1016/j.jhydrol.2009.04.017

Crossref Full Text | Google Scholar

Hu, L., Bao, W., Shi, P., Wang, J., and Lu, M. (2020). Simulation of overland flow considering the influence of topographic depressions. Sci. Rep. 10:6128. doi: 10.1038/s41598-020-63001-y

PubMed Abstract | Crossref Full Text | Google Scholar

Jan, A., Coon, E. T., Graham, J. D., and Painter, S. L. (2018). A subgrid approach for modeling microtopography effects on overland flow. Water Resour. Res. 54, 6153–6167. doi: 10.1029/2017WR021898

Crossref Full Text | Google Scholar

Jones, J. E., and Woodward, C. S. (2001). Newton krylov-multigrid solvers for large-scale, highly heterogeneous, variably saturated flow problems. Adv. Water Resour. 24, 763–774. doi: 10.1016/S0309-1708(00)00075-0

Crossref Full Text | Google Scholar

Kabat, P., Hutjes, R. W. A., and Feddes, R. A. (1997). The scaling characteristics of soil parameters: from plot scale heterogeneity to subgrid parameterization. J. Hydrol. 190, 363–396. doi: 10.1016/S0022-1694(96)03134-4

Crossref Full Text | Google Scholar

Kollet, S. J., and Maxwell, R. M. (2006). Integrated surface groundwater flow modeling: A free-surface overland flow boundary condition in a parallel groundwater flow model. Adv. Water Resour. 29, 945–958. doi: 10.1016/j.advwatres.2005.08.006

Crossref Full Text | Google Scholar

Kreye, P., and Meon, G. (2016). Subgrid spatial variability of soil hydraulic functions for hydrological modelling. Hydrol. Earth Syst. Sci. 20, 2557–2571. doi: 10.5194/hess-20-2557-2016

Crossref Full Text | Google Scholar

Leung, L. R., Wigmosta, M. S., Ghan, S. J., Epstein, D. J., and Vail, L. W. (1996). Application of a subgrid orographic precipitation/surface hydrology scheme to a mountain watershed. J. Geophys. Res.: Atmospheres 101, 12803–12817. doi: 10.1029/96JD00441

Crossref Full Text | Google Scholar

Li, Z., and Hodges, B. R. (2019). Modeling subgrid-scale topographic effects on shallow marsh hydrodynamics and salinity transport. Adv. Water Resour. 129, 1–15. doi: 10.1016/j.advwatres.2019.05.004

Crossref Full Text | Google Scholar

Ma, Y., Leonarduzzi, E., Defnet, A., Melchior, P., Condon, L. E., and Maxwell, R. M. (2024). Water table depth estimates over the contiguous united states using a random forest model. Groundwater 62, 34–43. doi: 10.1111/gwat.13362

PubMed Abstract | Crossref Full Text | Google Scholar

Maxwell, R. M. (2013). A terrain-following grid transform and preconditioner for parallel, large-scale, integrated hydrologic modeling. Adv. Water Resour. 53, 109–117. doi: 10.1016/j.advwatres.2012.10.001

Crossref Full Text | Google Scholar

Miller, M. P., Carlisle, D. M., Wolock, D. M., and Wieczorek, M. (2018). A database of natural monthly streamflow estimates from 1950 to 2015 for the conterminous united states. JAWRA J. Am. Water Res. Assoc. 54, 1258–1269. doi: 10.1111/1752-1688.12685

Crossref Full Text | Google Scholar

Mohanasundaram, S., Mekonnen, M. M., Haacker, E., Ray, C., Lim, S., and Shrestha, S. (2021). An application of grace mission datasets for streamflow and baseflow estimation in the conterminous united states basins. J. Hydrol. 601:126622. doi: 10.1016/j.jhydrol.2021.126622

Crossref Full Text | Google Scholar

Moretti, G., and Orlandini, S. (2018). Hydrography-driven coarsening of grid digital elevation models. Water Resour. Res. 54:3654–3672. doi: 10.1029/2017WR021206

Crossref Full Text | Google Scholar

Neal, J., Schumann, G., and Bates, P. (2012). A subgrid channel model for simulating river hydraulics and floodplain inundation over large and data sparse areas. Water Resour. Res. 48:12514. doi: 10.1029/2012WR012514

Crossref Full Text | Google Scholar

Noilhan, J., Lacarrere, P., Dolman, A. J., and Blyth, E. M. (1997). Defining area-average parameters in meteorological models for land surfaces with mesoscale heterogeneity. J. Hydrol. 190, 302-316. doi: 10.1016/S0022-1694(96)03131-9

Crossref Full Text | Google Scholar

O'Neill, M. M. F., Tijerina, D. T., Condon, L. E., and Maxwell, R. M. (2021). Assessment of the parflow-clm conus 1.0 integrated hydrologic model: evaluation of hyper-resolution water balance components across the contiguous united states. Geosci. Model Dev. 14, 7223–7254. doi: 10.5194/gmd-14-7223-2021

Crossref Full Text | Google Scholar

Panday, S., and Huyakorn, P. S. (2004). A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow. Adv. Water Resour. 27, 361–382. doi: 10.1016/j.advwatres.2004.02.016

Crossref Full Text | Google Scholar

Schalge, B., Haefliger, V., Kollet, S., and Simmer, C. (2019). Improvement of surface run-off in the hydrological model parflow by a scale-consistent river parameterization. Hydrol. Process. 33, 2006–2019. doi: 10.1002/hyp.13448

Crossref Full Text | Google Scholar

Shen, C., and Phanikumar, M. S. (2010). A process-based, distributed hydrologic model based on a large-scale method for surface-subsurface coupling. Adva. Water Resour. 33, 1524–1541. doi: 10.1016/j.advwatres.2010.09.002

Crossref Full Text | Google Scholar

Shuttleworth, W. J. (1988). Macrohydrology the new challenge for process hydrology. J. Hydrol. 100, 31–56. doi: 10.1016/0022-1694(88)90180-1

Crossref Full Text | Google Scholar

Sutanudjaja, E. H., van Beek, L. P. H., de Jong, S. M., van Geer, F. C., and Bierkens, M. F. P. (2011). Large-scale groundwater modeling using global datasets: a test case for the rhine-meuse basin. Hydrol. Earth System Sci. 15, 2913–2935. doi: 10.5194/hess-15-2913-2011

Crossref Full Text | Google Scholar

Thompson, S. E., Katul, G. G., and Porporato, A. (2010). Role of microtopography in rainfall-runoff partitioning: an analysis using idealized geometry. Water Resour. Res. 46:8835. doi: 10.1029/2009WR008835

Crossref Full Text | Google Scholar

Vieira, J. H. D. (1983). Conditions governing the use of approximations for the saint-vnant equations for shallow surface water flow. J. Hydrol. 60, 43–58. doi: 10.1016/0022-1694(83)90013-6

PubMed Abstract | Crossref Full Text | Google Scholar

Viero, D. P., Peruzzo, P., Carniello, L., and Defina, A. (2014). Integrated mathematical modeling of hydrological and hydrodynamic response to rainfall events in rural lowland catchments. Water Resour. Res. 50, 5941–5957. doi: 10.1002/2013WR014293

Crossref Full Text | Google Scholar

Viero, D. P., and Valipour, M. (2017). Modeling anisotropy in free-surface overland and shallow inundation flows. Adv. Water Resour. 104, 1–14. doi: 10.1016/j.advwatres.2017.03.007

Crossref Full Text | Google Scholar

Volp, N. D., van Prooijen, B. C., and Stelling, G. S. (2013). A finite volume approach for shallow water flow accounting for high-resolution bathymetry and roughness data. Water Resour. Res. 49, 4126–4135. doi: 10.1002/wrcr.20324

Crossref Full Text | Google Scholar

Wang, D., and Wang, G. (2007). Toward a robust canopy hydrology scheme with precipitation subgrid variability. J. Hydrometeorol. 8, 439–446. doi: 10.1175/JHM585.1

PubMed Abstract | Crossref Full Text | Google Scholar

Wood, E. F., Lettenmaier, D. P., and Zartarian, V. G. (1992). A land-surface hydrology parameterization with subgrid variability for general circulation models. J. Geophys. Res.: Atmosph. 97, 2717–2728. doi: 10.1029/91JD01786

Crossref Full Text | Google Scholar

Yang, C., Tijerina-Kreuzer, D. T., Tran, H. V., Condon, L. E., and Maxwell, R. M. (2023). A high-resolution, 3d groundwater-surface water simulation of the contiguous us: Advances in the integrated parflow conus 2.0 modeling platform. J. Hydrol. 626:130294. doi: 10.1016/j.jhydrol.2023.130294

Crossref Full Text | Google Scholar

Zhang, J., Wu, G., Liang, B., and Chen, Y. (2023). Subgrid modeling of urban flooding incorporating buildings effects. Phys. Fluids 35:127108. doi: 10.1063/5.0178816

Crossref Full Text | Google Scholar