Empirical and thermal resistance approaches for debris thickness estimation on the Hoksar Glacier, Kashmir Himalaya

Supraglacial debris modulates the thermal regime and alters glacial melt rates depending on its thickness. Thus, the estimation of debris thickness becomes imperative for predicting the hydrological response and dynamics of such glaciers. This study tests the performance of empirical and thermal resistance-based debris thickness approaches against field measurements on the Hoksar Glacier, Kashmir Himalaya. The aim of this study was accomplished using thermal imageries (Landsat 8 Operational Land Imager [Landsat-OLI], 2017 and Advanced Spaceborne Thermal Emission and Reflection Radiometer [ASTER] Surface Kinetic Temperature Product [AST08], 2017) and the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA-5) datasets. First, the spatially resolved estimates of debris thickness for the entire debris-covered zone were achieved by establishing an empirical relationship between debris thickness and debris surface temperature (both field and satellite thermal imageries). Second, debris thickness for every pixel of thermal imagery was executed by calculating thermal resistance from the energy balance model incorporating primary inputs from (ERA-5), debris temperature (AST08, Landsat OLI), and thermal conductivity. On comparison with field temperature and thickness measurements with satellite temperature, homogenous debris thickness pixels showed an excellent coherence (r = 0.9; p < 0.001 for T_AST08 and r = 0.88; p < 0.001 for T_{Landsat OLI} for temperature) and (r = 0.9; p < 0.001 for T_AST08 and r = 0.87; p < 0.002 for T_{Landsat OLI} for debris thickness). Both approaches effectively captured the spatial pattern of debris thickness using Landsat OLI and AST08 datasets. However, results specify an average debris thickness of 18.9 ± 7.9 cm from the field, which the empirical approach underestimated by 12% for AST08 and 28% for Landsat OLI, and the thermal resistance approach overestimated by 6.2% for AST08 and 5.1% for Landsat OLI, respectively. Debris thickness estimates from the thermal resistance approach (deviation 11.2% for AST08 and 11.6% for Landsat OLI) closely mirror the field measurements compared to the empirical approach (deviation 26.9% for AST08 and 35% for Landsat OLI). Thus, the thermal resistance approach can solve spatial variability in debris thickness on different heavily debris-covered glaciers globally without adequate knowledge of field measurements.

1 Introduction

Debris-covered glaciers constitute an indispensable component of Earth’s cryospheric system (Scherler et al., 2018; Anderson and Anderson, 2018). Supraglacial debris finds its existence on 7.3% of Earth’s Mountain glaciers with its global increase in the context of changing climate (Scherler et al., 2018; Kirkbride and Deline, 2013; Bhambri et al., 2011; Bolch et al., 2012). High mountain regions such as Himalaya, where a sizeable population is essentially dependent on glacier-driven runoff, can be highly afflicted due to their characterised sensitivity to climate warming (Scherler et al., 2018; Sharma et al., 2016).

Supraglacial debris thickness is closely associated with the thermodynamic system of the glacier (Rowan et al., 2020; Brun et al., 2019; Ali et al., 2017; Pellicciotti et al., 2015). It modifies the impact of atmospheric warming on glacier mass balance by changing the distribution and magnitude of ablation of the underlying ice (Minora et al., 2016). Generally, thin and patchy debris represents higher ablation rates than clean-ice surfaces until reaching critical thickness (Minora et al., 2016; Fyffe et al., 2014; Lejeune et al., 2013; Brock et al., 2010; Nicholson and Benn, 2006; Mihalcea et al., 2006; Østrem, 1959). This is usually attributed to efficient heat transfer through the debris and the lower albedo of rock debris compared to clean ice (Nicholson and Benn, 2006; Mihalcea et al., 2006; Østrem, 1959). However, the insulating effect of thick debris cover suppresses subdebris melting rates compared to clean ice (Minora et al., 2016; Anderson et al., 2021; Immerzeel et al., 2012). The spatial variability in debris thickness distribution thus makes the response of these glaciers strongly non-linear to the changing climate and emphasises their detailed assessment (Minora et al., 2016; Anderson et al., 2021; Nicholson and Benn, 2013). A comprehensive understanding of the spatial pattern of debris thickness facilitates their vulnerability to climate change (Ali et al., 2017; Huss, 2011; Shukla et al., 2010; King et al., 2019). As such, the suitable knowledge of debris thickness simplifies the model predictions of meltwater production and glacier lake outburst flood-like hazards (Benn et al., 2012; Sattar et al., 2022; Harrison et al., 2018; Herreid and Pellicciotti, 2020), which is poorly addressed at both regional and global levels.

Detailed in situ debris thickness measurements remain a challenge for the majority of the glaciers on Earth, with special reference to Himalaya (Scherler et al., 2018; Berthier et al., 2010; McCarthy et al., 2017). Challenging field debris thickness measurements has become possible only for a few Himalayan glaciers (Patel et al., 2016; Soncini et al., 2016; Rounce and McKinney, 2014; Reid et al., 2012; Nicholson and Mertes, 2017). Furthermore, these field debris thickness measurements were mainly achieved manually, either by digging or excavation of the debris (Soncini et al., 2016; Rounce and McKinney, 2014), using a total station and reflector (Immerzeel et al., 2012), terrestrial photography (Nicholson and Benn, 2013), ground penetrating radar (Patel et al., 2016) and ice-cliff extrapolation (Nicholson and Benn, 2013; Foster et al., 2012). Although accurate, the logical complexity and a single debris thickness value representative of the entire sampled area prevents their applicability at mountain-range or basin scales (Nicholson and Benn, 2006; Mihalcea et al., 2008a; Ranzi et al., 2004). Conversely, appropriate resolution remotely sensed data have shown the potential to provide a reasonable estimate of the debris thicknesses at higher spatial and temporal scales (Mihalcea et al., 2008a; Ranzi et al., 2004). Earlier studies have confirmed a good agreement between debris thickness and debris surface temperature for thickness values ranging between >1 and < 40 cm (Rounce and McKinney, 2014; Nicholson and Benn, 2013; Mihalcea et al., 2008a; Ranzi et al., 2004). This known dependence of debris surface temperature for varying debris thickness formed the basis for the empirical debris thickness measurements (Ranzi et al., 2004; Taschner and Ranzi, 2002; Fujita and Sakai, 2014). Such empirical relationships were previously developed by using thermal satellite imagery and extensive field debris thickness measurements concomitant with the acquisition of satellite images (Ranzi et al., 2004; Taschner and Ranzi, 2002; Fujita and Sakai, 2014). Although such progressive attempts assisted in understanding the spatial pattern of debris thickness at a glacier-wide scale, the concern of considerable field debris thickness measurements curtailed their transferability to other glacier sites (Mihalcea et al., 2008a). Addressing this research gap, later studies reconstructed debris thickness from surface energy balance modelling, which solved debris thickness as a function of prevailing meteorological parameters, debris properties, and the corresponding surface temperature from field/satellite imagery (Rounce and McKinney, 2014; Reid et al., 2012; Mihalcea et al., 2008a; Ranzi et al., 2004; Suzuki et al., 2007; Yong et al., 2016). A progression of suggested energy balance models resolved the transferability issue either by (a) solving thermal resistance, which is the debris thickness divided by the thermal conductivity (Zhang et al., 2011; Suzuki et al., 2007; Nakawo and Rana, 1999; Nakawo and Young, 1982; Nakawo and Young, 1981), (b) assuming linear debris-temperature profile within the debris layer (Rounce and McKinney, 2014; Mihalcea et al., 2008a; Ranzi et al., 2004), (c) inverting the Østrem curve (a plot of the melt rate as a function of debris depth) using an energy balance model and surface lowering measurements (Carenzo et al., 2016; Ragettli et al., 2015; Stewart et al., 2021), (d) reversal of subdebris melting rates (Stewart et al., 2021), and (e) by accounting a non-linear temperature gradient within the debris layer (Reid et al., 2012; Schauwecker et al., 2015; Yong et al., 2016). While acknowledging such attempts as a step-change in mitigating transferability issues, they were inherited by several limitations. Inconsistencies in such approaches profoundly arise from prerequisite well-quantified meteorological parameters, complex debris properties, improper validation, and immense data requirements, which are usually unavailable in the Himalayan region. The broader application of such approaches is additionally obstructed by inappropriate validation of unavailable in situ measurements. Earlier attempts to estimate debris thickness were further accomplished by inversion of subdebris melt model using difference-derived elevation change from the digital elevation model (Rounce et al., 2018). The approach accurately estimated thicker debris (>0.5 m) over both actively flowing and stagnant parts of the glacier. However, the uncertainties in the debris thickness estimates emerged due to thermal conductivity and elevation change, which is usually a challenge to determine in the field. To overcome these concerns, mapping debris thickness remains a hot topic in the field of glaciology.

The intended goal of the present research is to estimate debris thickness on the Hoksar Glacier, Kashmir Himalaya, using (a) an empirical approach that establishes a correlation between debris thickness and debris surface temperature using data inputs from AST08/Landsat OLI thermal imageries and field measurements and (b) thermal resistance approach using inputs from European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 (ERA-5) reanalysis data, thermal imageries, and field measurements. The first attempt to introduce thermal resistance as representative of debris thickness was on the Hailuogou Glacier in southern Tibet (Suzuki et al., 2007). The approach worked well throughout the glacier’s length and showed a good agreement with field-derived debris thickness observations. Consequently, the potential to estimate debris thickness effectively with minimum site-specific data requirements encouraged its implementation in other regions (Zhang et al., 2011; Zhang et al., 2013; Ali, 2019). With this advance over previous approaches, for this study, we consider the thermal resistance approach for estimating debris thickness (Suzuki et al., 2007). However, we primarily progress the approach by evaluating its performance in measuring debris thickness using two distinct thermal datasets (AST08 and Landsat OLI). Second, we introduce both thermal conductivity (which principally controls heat conduction to the debris–ice interface) and thermal resistance (debris thickness divided by the thermal conductivity of the debris layer) as representative of debris thickness, unlike previous studies (Suzuki et al., 2007; Zhang et al., 2013; Ali, 2019). We preferred this study to be primarily in the Kashmir Himalayan region where no such work has been adopted. Mainly, it is a necessary first step towards understanding the spatial pattern of debris thickness in the region where meteorological data are scarce, and weather stations are unavailable at altitudes above 3,000 m. Such an analysis is crucial to understand the glaciers’ behavior to climate change and in the assessment of freshwater reserves to satisfy increasing water demands in high mountainous regions.

2 Study area

Hoksar Glacier, Kashmir Himalaya, is a small-sized glacier with an area of 2.1 km² and a length of 2.2 km (Kaul, 1990). The accessibility and small size of the glacier helped in the extensive measurement of debris thickness and temperature. Geographically it extends between 34°17′58″ N to 33°19′54″ N latitude and 75°29′42″ E to 75°30′56″ E longitude (Figure 1). It exists in west Lidder valley between Dudnag and Hoksar Mountains at an altitude of 4,200 m and the snout terminates at 3,200 m (Rashid et al., 2022). The glacier has a northwest orientation (Rashid et al., 2022) with a mean slope of 23° (Kanth et al., 2011). The annual field expeditions from 2013 to 2018 have shown an upwards shift of 40 ± 3 m in ELA, ranging from 4,022 m in 2013 to 4,062 m in 2018 (Romshoo et al., 2022). Approximately 57% of the total area of the glacier is debris covered (Figure 1B) (Kaul, 1990), and a proglacial lake exists near the snout of the glacier (Figure 1C). The glacier is slashed by both longitudinal and transverse crevasses (Figure 1D). Distribution of debris on the surface of the glacier is heterogeneous, and the size of the debris ranges from few millimetres of gravel to several metres of large boulders (Figure 1F). Low lateral moraines flank the snout. These moraines are 0.5 km long (Rashid et al., 2022). It has deposited a vast end moraine of angular blocks in front of the snout, the majority of whose ground mass has been washed away (Rashid et al., 2022). The melt of this glacier predominantly contributes to the drainage flows of the Lidder basin, which additionally forms a vital tributary of the Indus River system.

Figure 1

Figure 1. Location map of the Hoksar Glacier. (A) Broad geographical setup of the Hoksar Glacier (shown by a red rectangle). The background image is False Colour Composite (FCC): 3:2:1 created from LISS IV image (dated 19 September 2013); (B) debris extent shown on the panoramic view of the glacier; (C) location of proglacial lake; (D) existence of crevasses in the middle of the glacier between upper ablation and lower accumulation zones; (E) accumulation zone of the glacier; and (F) spatial variability in debris size found in the ablation zone of the glacier.

The region has a sub-Mediterranean type of climate, with nearly 80% of its annual rainfall in winter and spring seasons (Kanth et al., 2011). The annual minimum and maximum temperatures vary between −10 and 35°C (Romshoo et al., 2022). The glaciers are winter accumulation type and experience snow precipitation predominantly from westerlies during winter seasons (Romshoo et al., 2020; Yadav et al., 2012; Dimri, 2006; Kaul et al., 1977).

Literature review suggests that the interest in glaciers and hydrology of the Kashmir Himalaya has been renewed lately (Benn and Owen, 1998; Marazi and Romshoo, 2018; Shukla and Ali, 2016; Shukla and Yousuf, 2016; Kanth et al., 2011). In addition, these inceptive studies in the region have mainly focused on field mapping (Murtaza and Romshoo, 2017), estimates of retreat (Kanth et al., 2011; Shukla and Yousuf, 2016; Murtaza and Romshoo, 2017; Neve, 1910; Kanth et al., 2011), geomorphology and palaeoglaciation (Rashid et al., 2022; Odell, 1963), and mass balance (Shukla and Yousuf, 2016). However, none of the studies have focussed on debris thickness mapping in the region.

3 Materials and methods

3.1 Data acquisition

A complete list of the repository of datasets used in the study is given in Table 1. Two scenes of Landsat 8 Operational Land Imager (OLI) and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) kinetic temperature product (AST08) were acquired from the U.S. Geological Survey (USGS; http://earthexplorer.usgs.gov/) and NASA’s Earth Observing System Data and Information System¹ under the auspices of the Global Land Ice Measurements from Space (GLIMS) project. Landsat optical and thermal bands, used as input parameters in empirical and thermal resistance approaches, were converted to respective reflectance and brightness temperatures following the procedure suggested in King et al. (2019) and Boxall et al. (2021). In addition, AST08 by Land Processes Distributed Active Archive Center to Level 1 are atmospherically, radiometrically, and geometrically corrected products with temperature resolution of 0.5 K and absolute accuracies of 0.3 and 4 K, respectively (Iwasaki and Fujisada, 2005; Tonooka, 2005). Furthermore, Landsat OLI images were co-registered with AST08 with an acceptable co-registration error limited to one pixel.

Table 1

Table 1. Details of various data sources and their respective application in the current study.

Apart from this, ERA-5 reanalysis data were downloaded from the European Centre for Medium Range Weather Forecasts (ECMWF).² The data are available in netCDF4 format, and each grid point has a horizontal resolution of 31 km (Hersbach, 2018). The primary data variables used in the study are listed in Table 1. It is pertinent to mention that each variable is produced with a 1-h time step corresponding to the nearest time and location of the Landsat 7 overpass (Hersbach, 2018). ERA-5 reanalysis data have widely been used to deduce debris thickness (Schauwecker et al., 2015; Hersbach, 2018; Gök et al., 2023).

As many as 109 debris thicknesses and temperature measurements were accomplished between 18 Sepember 2017 and 20 September 2017 field campaign, especially across the glacier’s altitudinal range of 3,700–4,100 masl. Both debris thickness and temperature measurements recorded during the period were selected to develop the empirical approach and to appraise the thermal resistance approach. The glacier is characterised by deep crevasses and steep moraines, which strongly prohibited the transect-wise field measurements (Figure 1E). As such, for safe access, the thermal and thickness characteristics of the entire debris-covered zone were achieved at different intervals randomly in a north, south, east, and west direction. However, it was ascertained that a minimum of 10 measurements were attained along each direction to investigate the spatial variability of debris thickness over a small scale. From this an average value of debris thickness for the sampled area was calculated to have an acceptable comparison for the estimated debris thickness from both approaches. Debris thickness was measured at each site by digging through the debris layer to the ice beneath. An accurate estimate of debris thickness was primarily accomplished by placing a straight edge across the top of each excavation site, followed by measurement of the vertical height of the debris–ice interface as shown by the red arrow in Figure 2A. The giant boulders and glacier margins above 4.000 masl were deliberately avoided due to apparent unstable glacier flanks. Earlier studies have applied similar procedures for debris thickness profiling of different glaciers at distinct sites (Rounce and McKinney, 2014; Mihalcea et al., 2008a; Suzuki et al., 2007). The debris temperature was recorded simultaneously on the same sites using an infrared thermometer (Figure 2B). The infrared thermometer measures temperature in the range of −30 to 100°C with a resolution of 0.1°C and accuracy of ±0.5% (Suzuki et al., 2007). At each sample point, debris surface temperature was recorded for 5 min with a minimum of 15 readings. The recorded measurements were averaged and were assumed to be more representative of AST08/OLI (90 m × 90 m) pixel than point measurements as suggested by (Foster et al., 2012). The procedure was also targeted to account for spatial variability of debris surface temperature at different time and space intervals to have a precise estimate of debris thickness from thermal imagery (Patel et al., 2016). Furthermore, the debris rock samples from the glacier surface were also collected to identify rock types and geological characteristics.

Figure 2

Figure 2. Field photographs showing the procedure for collection of field data on the Hoksar Glacier’s (A) debris thickness measurements and (B) debris temperature measurements.

3.2 Methodology adopted

Before implementing empirical and thermal resistance approaches for debris thickness estimation, it was essential to map its spatial extent. Debris extent was mapped from Landsat OLI (2017) because a more recent image for the glacier was unavailable due to extensive snow and cloud cover. A hierarchical knowledge-based classification procedure was applied to map debris extent (Ali et al., 2017; Marazi and Romshoo, 2018; Shukla et al., 2016). The classification scheme involved generating numerous input layers from the primary dataset (Landsat OLI, 2017), which were later set to exclusive conditions for the extraction of debris cover (Ali et al., 2017).

A schematic flowchart adopted for estimating debris thickness through both approaches is given in Figure 3, Table 2 and described in the following subsections.

Table 2

Table 2. Main input variables used to estimate debris thickness.

Figure 3

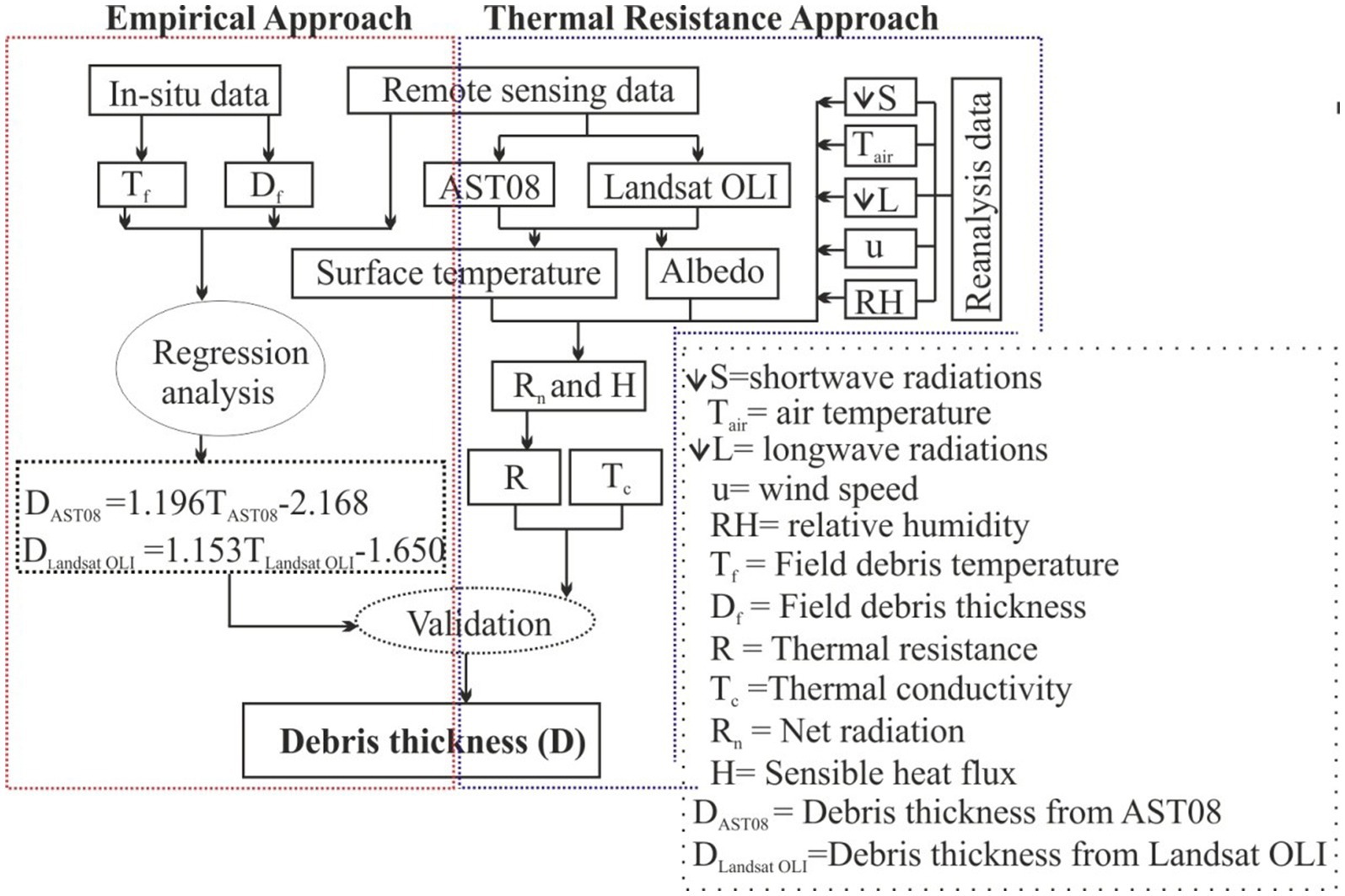
Figure 3. Schematic flowchart adopted for the development of empirical and thermal resistance approaches for mapping debris thickness over the glacier-wide scale of the Hoksar Glacier.

4 Methodology

4.1 Empirical approach

In the first step, debris surface temperature (T_f) and debris thickness (D_f) measured at 109 sites were overlaid on AST08 and Landsat OLI images. Field observations (both T_f and D_f) falling within the (90 m × 90 m) pixel were averaged, resulting in a new set of 26 data points. The resultant observations were considered more reliable and accurate than point measurements (Patel et al., 2016). The spatial distribution of both point and averaged field measurements is given in Figure 4.

Figure 4

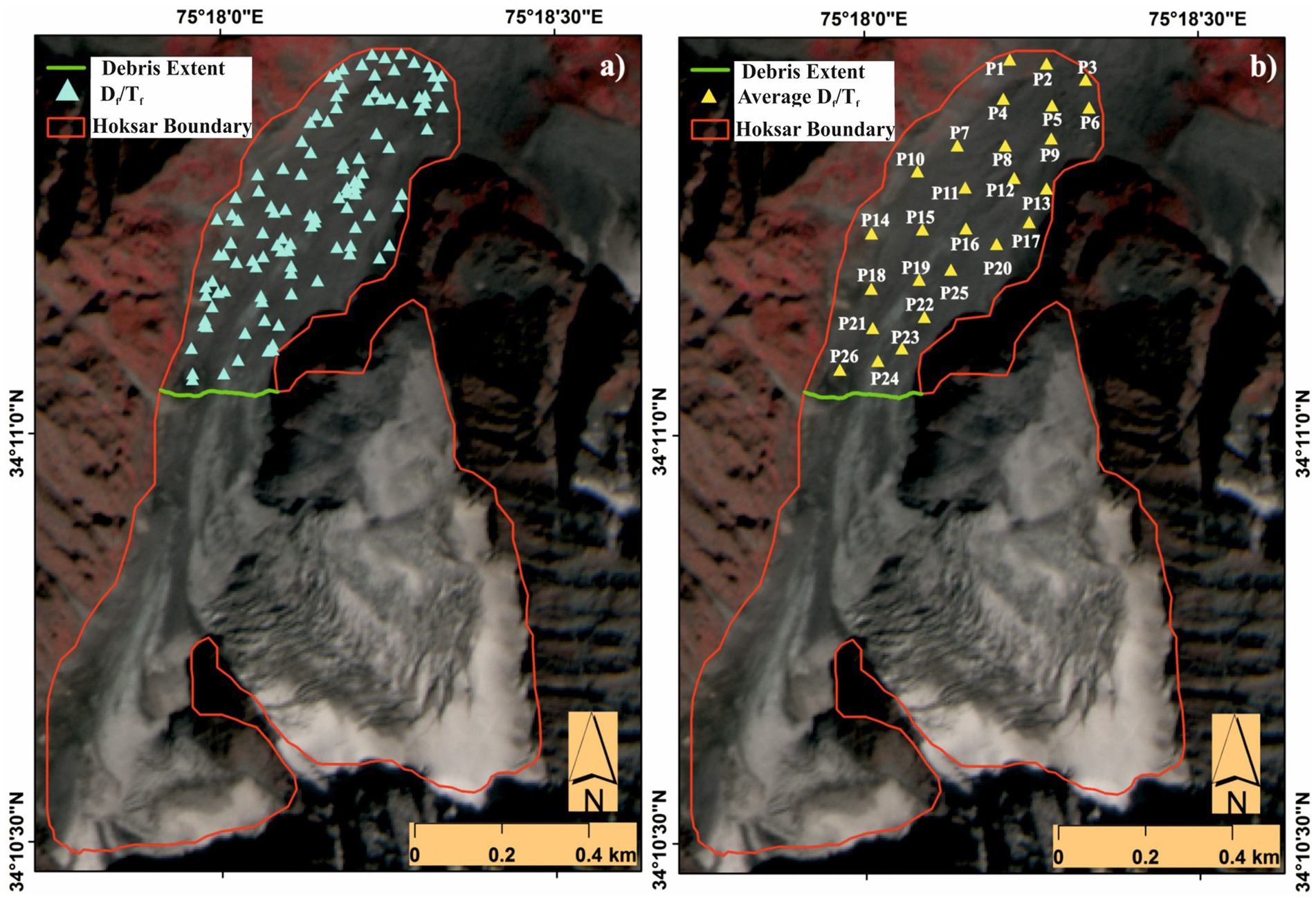
Figure 4. Spatial distribution of the field measurements (September 2017) on the Hoksar Glacier; (A) 109-point debris thickness (D_f) and corresponding debris temperature (T_f) measurements and (B) average debris thickness (D_f) and corresponding debris temperature (T_f) measurements. The base image is FCC: 3:2:1, created from the LISS P6-IV image (dated 13 September 2015).

The empirical approach worked on the premises of higher temperatures associated with thicker debris (Suzuki et al., 2007; Rounce et al., 2021). Following this basic idea, an in-depth analysis of T_f and D_f was performed which emerged in a linear empirical relationship between the parameters. A strong correlation of (r = 0.9; p < 0.001) achieved during the analysis is in agreement with earlier findings, which recorded an empirical relation of R² = 0.82 between debris thickness and temperature on the Miage glacier (Patel et al., 2016). Based on the relationship between T_f and D_f, we developed debris thickness over the entire debris-covered zone of the glacier by substituting the debris surface temperature from AST08 and Landsat OLI according to Equations 1 and 2:

$\begin{array}{ll}{\mathrm{D}}_{\mathrm{A}\mathrm{S}\mathrm{T}08}=1.196{\mathrm{T}}_{\mathrm{A}\mathrm{S}\mathrm{T}08}–2.168& (1)\end{array}$

$\begin{array}{ll}{\mathrm{D}}_{\mathrm{Landsat}\mathrm{O}\mathrm{L}\mathrm{I}}=1.153{\mathrm{T}}_{\mathrm{Landsat}\mathrm{O}\mathrm{L}\mathrm{I}}+1.650& (2)\end{array}$

where D_AST08 and T_AST08 are debris thickness and surface temperature from AST08 and D_{Landsat OLI} and T_{Landsat OLI} are debris thickness and surface temperature from Landsat OLI, respectively. Inevitably, spatial patterns in debris thickness on different Himalayan glaciers were effectively established based on locally derived empirical relationships between debris thickness and surface temperature (Rounce and McKinney, 2014; Mihalcea et al., 2008a; Ranzi et al., 2004; Taschner and Ranzi, 2002; Fujita and Sakai, 2014; Srigyan et al., 2023).

4.2 Thermal resistance approach

This approach estimates debris thickness for every pixel of thermal imagery by calculating thermal resistance from the energy balance model of a debris-covered glacier surface coupling primary inputs from meteorological data (ERA-5), remote sensing surface temperature (AST08, Landsat OLI) and thermal conductivity as shown in Figure 3. Under uniform debris condition, the transfer of energy within the debris layer is governed by thermal resistance (R) which in turn is controlled by thermal conductivity (T_c) (Rounce et al., 2021; Boxall et al., 2021). Consequently, R of the debris layer is defined as the ratio between D and T_c as expressed in Equation 3:

$\begin{array}{ll}\mathrm{R}\mathrm{D}/\mathrm{T}\mathrm{c}& (3)\end{array}$

where D is calculated by solving the relationship of R with T_c of the debris layer (Equation 4) according to the relationship suggested by the study mentioned in Suzuki et al. (2007).

$\begin{array}{ll}\mathrm{D}\mathrm{R}/\mathrm{T}\mathrm{c}& (4)\end{array}$

The determination of R and T_c on the field becomes cumbersome and unrealistic when considering the vast extent of glaciers. Therefore, earlier studies have estimated the spatial variation of thermal resistance using remote sensing data (Zhang et al., 2011; Suzuki et al., 2007; Nakawo and Rana, 1999; Nakawo and Young, 1982). In addition, thermal resistance is independent of the glacier area and topographic parameters which permits it to compute as an isolated parameter. Considering a linear temperature gradient (due to a lack of reliable temperature measurements between the debris layer and ice interface) within the debris layer and ice–debris interface at melting point (Mihalcea et al., 2008a; Suzuki et al., 2007; Yin et al., 2013), conductive heat flux (G) of the debris layer is related to surface temperature (T_s) and R by Equation 5:

$\begin{array}{ll}\mathrm{G}\mathrm{T}\mathrm{S}0/\mathrm{R}& (5)\end{array}$

Earlier studies have verified that the assumption of ice–debris interface at the melting point with a linear vertical temperature gradient within the debris layer stands true for the ablation season (Reid and Brock, 2010). Further investigation regarding the temperature profiles within the debris layer confirmed almost a linear trend at the time of image acquisition and during the middle hours of the day (Reid and Brock, 2010). Even though few studies have incorporated a non-linear approximation factor (G_ratio) as a temperature profile within the debris layer, it is expected to vary from glacier to glacier (Reid et al., 2012; Schauwecker et al., 2015; Yong et al., 2016). Likewise, the value of G_ratio in earlier studies was either measured on the field (Reid et al., 2012) or used based on a previous study (Schauwecker et al., 2015) which apparently may not stand true everywhere. It is noteworthy that G_ratio can cause limited uncertainty to estimated debris thickness for it being least or moderately sensitive to debris thickness (Reid et al., 2012; Schauwecker et al., 2015).

In Equation 5, G was calculated from the general energy-balance equation, according to which the total source of the energy available to the debris surface is summed in Equation 6:

$\begin{array}{ll}{\mathrm{R}}_{\mathrm{n}}+\mathrm{H}+\mathrm{L}\mathrm{E}+\mathrm{P}+\mathrm{G}=0& (6)\end{array}$

where R_n is the net radiation flux; H is the net sensible heat flux, LE is the net latent heat flux, P is the heat flux supplied or consumed by precipitation falling on the surface, and G is the conductive heat flux into the debris layer, which controls the warming or cooling of the snow or icepack, respectively (Suzuki et al., 2007). All these fluxes (Wm⁻²) are considered positive when directed towards the debris surface (Patel et al., 2016; Zhang et al., 2011). Energy contributions from P can be neglected as the debris surface is dry under clear sky conditions in the ablation season except immediately after precipitation, which is unlikely to impact satellite imagery acquired under dry conditions (Brock et al., 2010). The net latent heat flux (LE) includes energy transfer through sources and sinks (e.g., convection, advection, phase changes, or ventilation) which are negligible when considering the neutral atmosphere (Nicholson and Benn, 2006; Reid et al., 2012; Yong et al., 2016). Although a thin debris layer can be saturated at the surface, the vapour pressure gradient between the surface and atmosphere is usually weak owing to the low surface temperature, which further points towards low LH for such areas (Yong et al., 2016). Simplifying for LE = 0 and p = 0, the sources of energy available at the surface are reduced to net radiations (R_n) and sensible heat flux (H) (Kayastha et al., 2000; Takeuchi et al., 2000). This approximation is also in line with previous studies, which concluded that net radiation is the dominant source of heat energy on the Himalayan debris-covered glaciers with negligible uncertainties introduced by omitting latent heat fluxes (Rounce and McKinney, 2014; Suzuki et al., 2007; Nakawo and Rana, 1999; Nicholson et al., 2018; Kayastha et al., 2000). These studies further stressed that the spatial pattern of thermal resistance is least dominated by excluding latent heat fluxes. Although the presence of water in the debris layer influences thermal resistance (Nakawo and Rana, 1999), the acquisition of AST08/Landsat OLI imageries under a clear sky and dry conditions minimise such impacts (Nicholson et al., 2018; Kayastha et al., 2000). In addition, to assess our approach’s effectiveness and certainty in the calculation of R, two Landsat OLI imageries of different dates (dated 8 September 2017 and 17 September 2018) were used. Previous studies have amply demonstrated that the R of the debris layer at a specific site can be considered constant during the melting season (Nakawo and Rana, 1999; Nakawo and Young, 1982; Takeuchi et al., 2000). Comparative analysis of R values from Landsat OLI images of different dates showed minimal differences. The overall correlation coefficient of r = 0.83 (p < 0.001) was obtained between R of two independent Landsat OLI imageries, which were consequently considered to be constant on the glacier during the melting season of 2017. The finding of slight differences in calculated R from two distinct datasets is also corroborated elsewhere (Suzuki et al., 2007).

Subsequently, Equations 5, 6 can be simplified as follows:

$\begin{array}{ll}\mathrm{R}={\mathrm{T}}_{\mathrm{S}}0/{\mathrm{R}}_{\mathrm{n}}+\mathrm{H}& (7)\end{array}$

where R of the debris layer was determined from the surface temperature (T_S°C) of the debris layer obtained from thermal infrared (TIR) bands of AST08 and Landsat OLI (Figure 3), and R_n and LE were calculated following Suzuki et al. (2007), as shown in Equations 8 and 9:

$\begin{array}{ll}{\mathrm{R}}_{\mathrm{n}}=\left(1-\alpha \right){\mathrm{R}}_{\mathrm{S}}+{\mathrm{R}}_{\mathrm{L}}–\epsilon \times \sigma {\left({\mathrm{T}}_{\mathrm{s}}-273.2\right)}^4& (8)\end{array}$

$\begin{array}{ll}\mathrm{T}={\mathrm{K}}_2/ln\left({\mathrm{K}}_1/{\mathrm{L}}_{\mathrm{\lambda }}+1\right)& (9)\end{array}$

where R_S is downwards shortwave radiation, R_L is downwards longwave radiation, α is albedo which was set to 0.3 and kept constant throughout the glacier due to the relative insensitivity of the model to its change (Nicholson and Mertes, 2017; Foster et al., 2012; Suzuki et al., 2007; Schauwecker et al., 2015), ε is the emissivity of the debris surface (taken to be 1) (Suzuki et al., 2007), σ is the Stefan–Boltzmann constant (5.67 × 10⁻⁸ W m⁻² K⁻⁴), T_S is the surface temperature of the debris (°C), K₁ and K₂ are coefficients determined by effective wavelength, and L_λ is top of atmospheric spectral radiance. Likewise, sensible heat flux (H) was calculated by using the bulk method as expressed in Equation 10:

$\begin{array}{ll}\mathrm{H}={\mathrm{c}}_{\mathrm{a}}{\rho }_{\mathrm{a}}\mathrm{C}\mathrm{U}\left({\mathrm{T}}_{\mathrm{air}}-{\mathrm{T}}_{\mathrm{s}}\right)& (10)\end{array}$

where c_a is the specific heat capacity of air (1,006 J kg⁻¹ K⁻¹), ρ_a is the density of air (kg m⁻³), C is the bulk coefficient for sensible heat (0.002), U is wind speed (which was set to 1.41 m s⁻¹), T_air is air temperature (°C). It should be noted that distributed incoming R_S was corrected for the effects of topography using ASTER DEM, as proposed by (Rana et al., 1997). Thus, the R of debris cover was calculated by substituting Equations 8–10 in Equation 7.

Debris conductivity is heterogeneous and depends mainly on rock type, lithology, and water saturation (Rounce and McKinney, 2014; Foster et al., 2012; Yong et al., 2016). All these debris characteristics are spatially variable and impractical to measure on the field. The lack of knowledge of the moisture in the debris and at its surface makes it difficult to estimate the thermal conductivity accurately. The problems are further exacerbated in data-scarce regions (such as Himalaya) where automatic weather stations are unavailable. In these situations, using the thermal conductivity of the rock type found in the region was most convenient. During the field expedition, a mixture of two rock types (mainly granite and basalt) was identified on the glacier surface. Furthermore, the surface of the glacier is dominated by boulders, gravel, and cobbles, however, as observed at the excavation sites, the debris interface was majorly composed of fine sand (Figures 2, 4). The composition and size of the debris on the glacier finds its resemblance with different Himalayan glaciers elsewhere (Rounce and McKinney, 2014; Kayastha et al., 2000). Considering the type and composition of debris, a uniform value of T_c = 1.3 W s⁻¹ K⁻¹ (mean T_c of the two rock types) was found to be more reasonable to match best with the field evidence (Gibson et al., 2017). Interestingly, a small variation in the range of values for T_c on a single glacier (standard deviation of 0.20 W m⁻¹ K⁻¹) has generated an acceptable level of uncertainty in modelled debris thickness, which justifies the use of a single value of T_c for an isolated glacier (Reid and Brock, 2010). Even though earlier studies quantified a wide range of thermal conductivity values from 0.42 (±0.04) to 2.28 (±0.23) W m⁻¹ K⁻¹, which are in agreement with other studies that have found thermal conductivity to vary between 0.60 and 1.29 W m − 1 K − 1in Everest region (Immerzeel et al., 2012; Reid et al., 2012; Nicholson et al., 2018; Kayastha et al., 2000). However, it is worth mentioning that such analysis was specifically accomplished in the Everest region, and we assume that no such investigation has so far been executed on the Kashmir Himalayan glaciers, which further restricts its intercomparison or uncertainty analysis. Nevertheless, a single value for thermal conductivity throughout the glacier was extensively used in previous studies (Immerzeel et al., 2012; Reid et al., 2012; Schauwecker et al., 2015; Kayastha et al., 2000). The wide range of thermal conductivity applied on different glaciers at different sites is given in Table 3.

Table 3

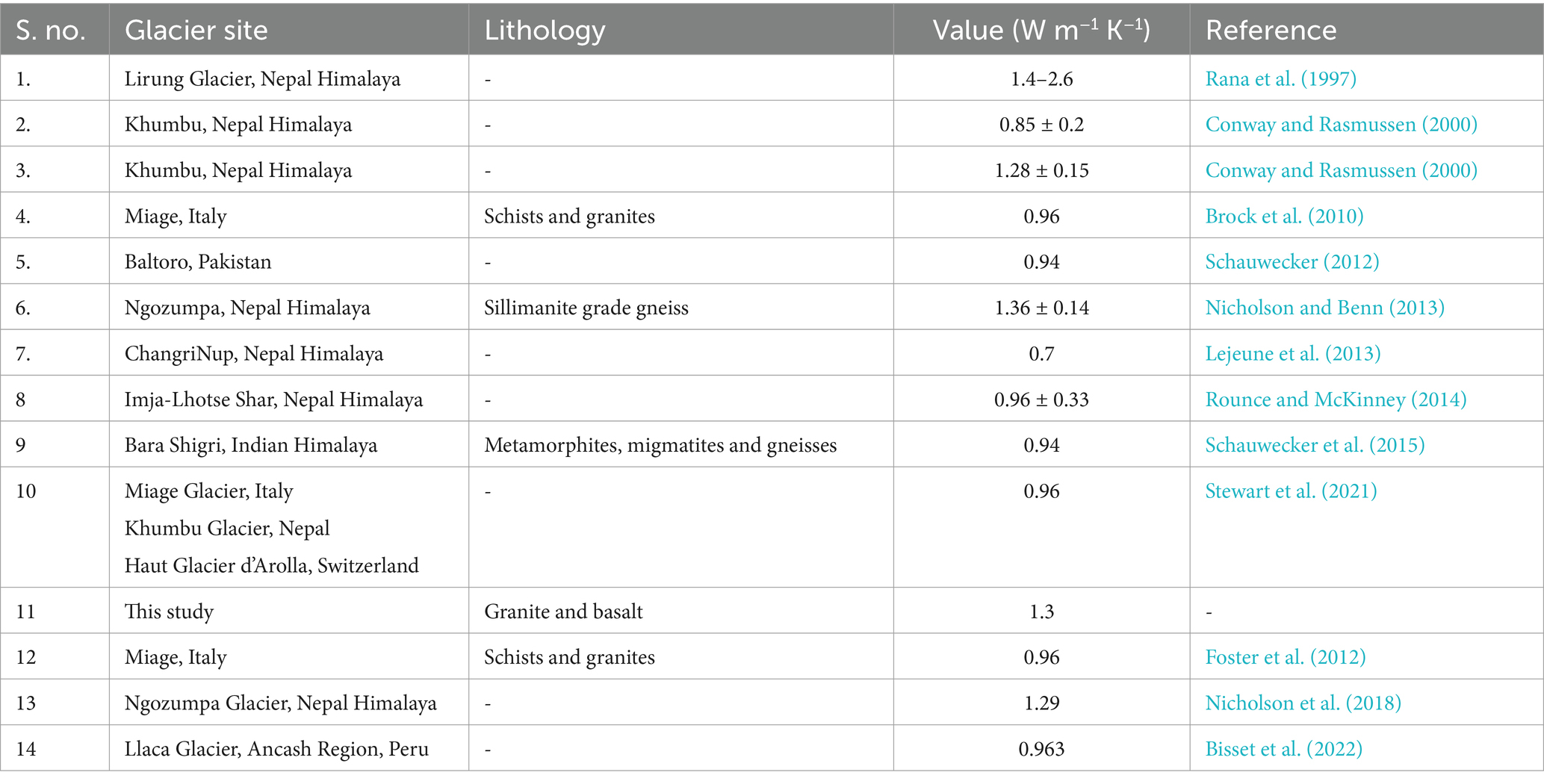
Table 3. Range of values for thermal conductivity (T_c) used on different glaciers situated at different sites.

5 Results and discussions

In this section, a comparative analysis of field measurements (T_f and D_f) and satellite thermal characteristics T_s (both T_AST08 and T_{Landsat OLI}) with T_f and D_f is accomplished, which shall be followed by an investigation of spatial variability in debris thickness estimates as obtained from field, empirical and thermal resistance approaches.

5.1 Spatial variation in T_f and T_s

The spatial distribution of debris thickness on a glacier is computed as a function of debris surface temperature (Nicholson and Benn, 2006; Ranzi et al., 2004; Kirkbride and Warren, 1999). Therefore, an assessment of the consistency of temperature from T_AST08 and T_{Landsat OLI} was performed by its appraisal with T_f observations sampled during the 2017 field expedition (Figure 5). On comparison, we find a statistically significant correlation of (r = 0.85; p < 0.001) for T_f/T_AST08 and (r = 0.87; p < 0.001) for T_f/T_{Landsat OLI}, respectively (Figure 6). The consistency of temperature between T_f/T_AST08 and T_f/T_{Landsat OLI} increased for homogenous debris thickness pixels sampled along the western margins of glacier; however, the correlation decayed as the variability of debris thickness within and between the pixels increased (Figure 6). For homogenous pixels, a correlation of (r = 0.9; p < 0. 001) for T_AST08 and (r = 0.88, p < 0.001) for T_{Landsat OLI} was observed. Overall, we found a close agreement in the spatial pattern of temperature between T_f, T_AST08, and T_{Landsat OLI} (Figure 6). However, on closer inspection, two major temperature differences were noted between T_f, T_AST08, and T_{Landsat OLI}—one in which T_AST08 and T_{Landsat OLI} overestimated T_f, and the other T_AST08 and T_{Landsat OLI} underestimated the other T_f. These two differences were recognised at different glacier elevations with variable debris thickness. We found T_f > T_AST08 and T_{Landsat OLI} along the eastern margins of the glacier (T_AST08 ≥ 8°C at 3,900 m and T_{Landsat OLI} ≥ 6.5°C at 3,970 m). Such temperature differences between T_f and T_AST08 and T_{Landsat OLI} may be likely due to the time difference in image acquisition (10:30 to 10:40 coordinated universal time [UTC]) and field debris measurements (10:30 to 12:30 UTC). Furthermore, T_f is enhanced for sites with single-point temperature measurements that are highly sensitive to microclimatic conditions such as shadow, aspect, and moisture. However, any such temperature variations are averaged out within an AST08 and Landsat OLI pixel. Accordingly, we noted T_f < T_AST08 and T_{Landsat OLI} towards the western part of the glacier closer to the central flowline (T_AST08 > 7.8°C at 3,470 m; T_{Landsat OLI} > 9.2°C at 3,553 m). In particular, local glacial conditions such as microtopography, shading, variable lithology, small ponds, crevasses, and the influence of the Sun and wind principally affect T_f. However, such differences in temperature within a single pixel (90 m × 90 m pixel) are averaged in T_AST08 and T_{Landsat OLI}. Earlier, such magnitude differences in T_f and satellite-derived temperature were noticed by Mihalcea et al. (2008a), which further suggested that the satellite-derived surface temperature is better for use in debris thickness estimations over large spatial scales.

Figure 5

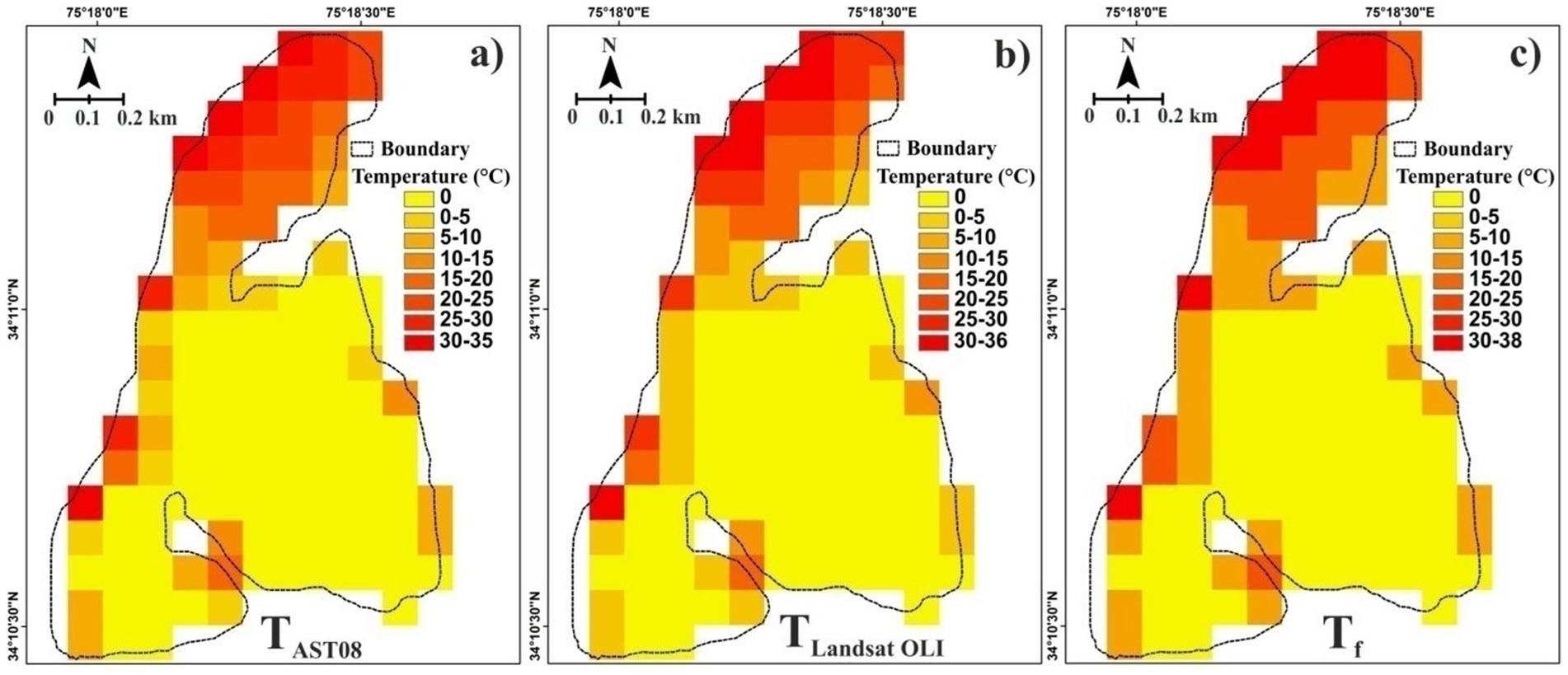
Figure 5. Spatial pattern of surface temperature (90 m pixel and temperature in °C) on the Hoksar Glacier obtained from (A) AST08; (B) Landsat OLI; and (C) field.

Figure 6

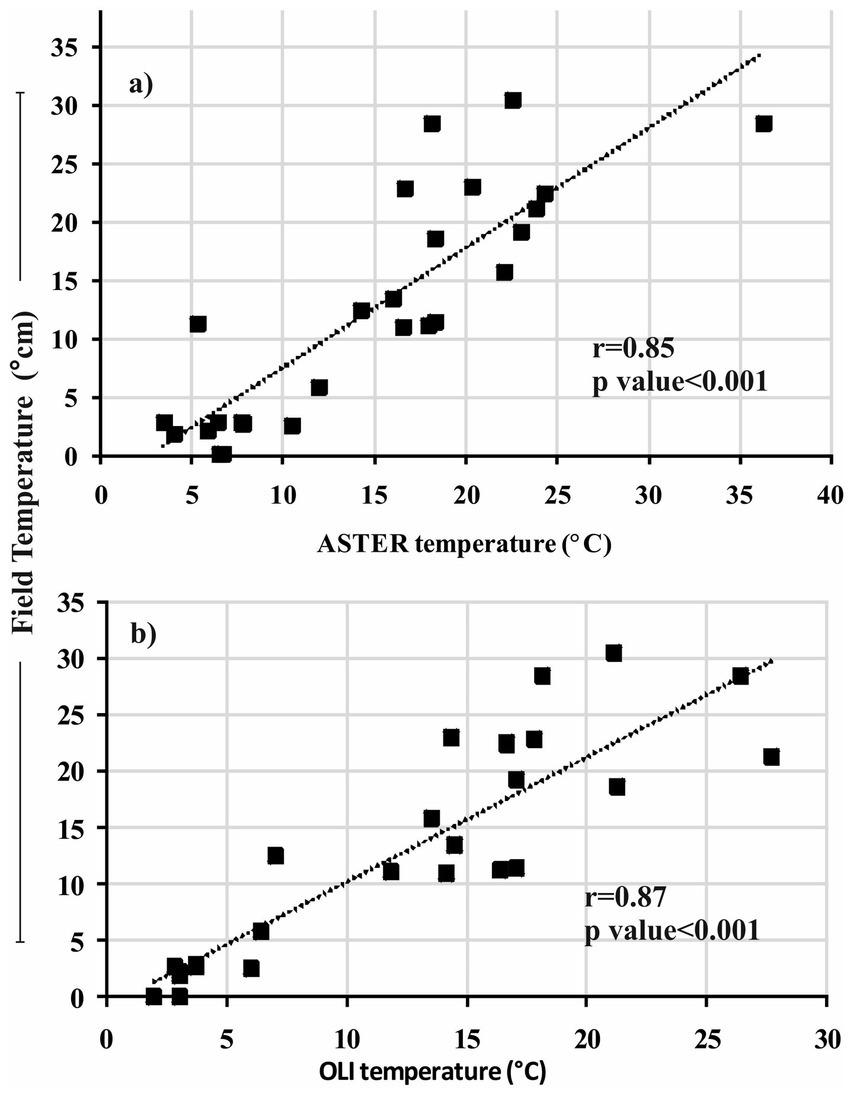
Figure 6. Relationship between field temperature (T_f) measurements with (A) AST08 temperature (T_AST08) and (B) Landsat OLI temperature (T_LandsatOLI).

5.2 Spatial variability in D_f and T_s

As mentioned earlier, D_f depends on the debris surface temperature’s magnitude (Suzuki et al., 2007; Kirkbride and Warren, 1999; Aubry-Wake et al., 2023). Therefore, we analysed the relation of D_f with T_f, T_AST08, and T_{Landsat OLI} to have confidence in accurate estimates of debris thickness. Though, synchronisation of satellite data with field expeditions is better for achieving significant results, as found in previous studies (Ranzi et al., 2004; Mihalcea et al., 2008b). However, aligning field observations with the availability of remote sensing datasets is difficult, especially in the Himalaya (Mihalcea et al., 2008b; Rounce et al., 2018). Accordingly, we compared field observations with satellite imageries of different acquisition dates and attained a reasonable statistically significant correlation. As shown in Figure 7, T_f, T_AST08, and T_OLI showed the influence of debris thickness and correlated strongly. On comparison, D_f showed a stronger correlation with T_f (r = 0.9; p < 0.001) followed by T_AST08 (r = 0.87; p < 0.001) and least with T_{Landsat OLI} (r = 0.8; p < 0.002) (Figure 7). The strongest and most consistent correlation was observed for homogeneous debris thickness pixels (for such pixels, r = 0.91; p < 0.001 for T_f, r = 0.9; p < 0.001 for T_AST08 and r = 0.87; p < 0.002 for T_{Landsat OLI}) which is in agreement to existing literature evidenced elsewhere (Rounce and McKinney, 2014; Mihalcea et al., 2008a; Ranzi et al., 2004). In contrast, correlation sharply deteriorated (r = 0.78; p < 0.02 for T_f, r = 0.66; p < 0.03 for T_AST08 and r = 0.6; p < 0.04 for T_{Landsat OLI}) for thin and dispersed debris at higher elevations towards the upper ablation zone of the glacier. These results emphasise the careful interpretation of the spatial patterns of debris thickness for highly heterogeneous debris thickness environments obtained from an empirical approach. A maximum D_f ≤ 39 cm was found to be quite consistent with the highest T_f ≥ 30°C at an elevation of 3,741 masl near the snout along the western region of the glacier (Figure 7C). We also observed large differences (<3.6°C) in temperature for small variation in debris thickness at different elevations which reflects the influence of microenvironment on temperature. Previous studies have noted a temperature difference of ≥4°C between the recorded and ASTER temperatures and suggested they are acceptable and within the range of error when considering the absolute accuracy of 4 K for ASTER (Suzuki et al., 2007). This motivated us to use both T_AST08 and T_{Landsat OLI} for the estimation of debris thickness over the entire debris-covered zone of the glacier.

Figure 7

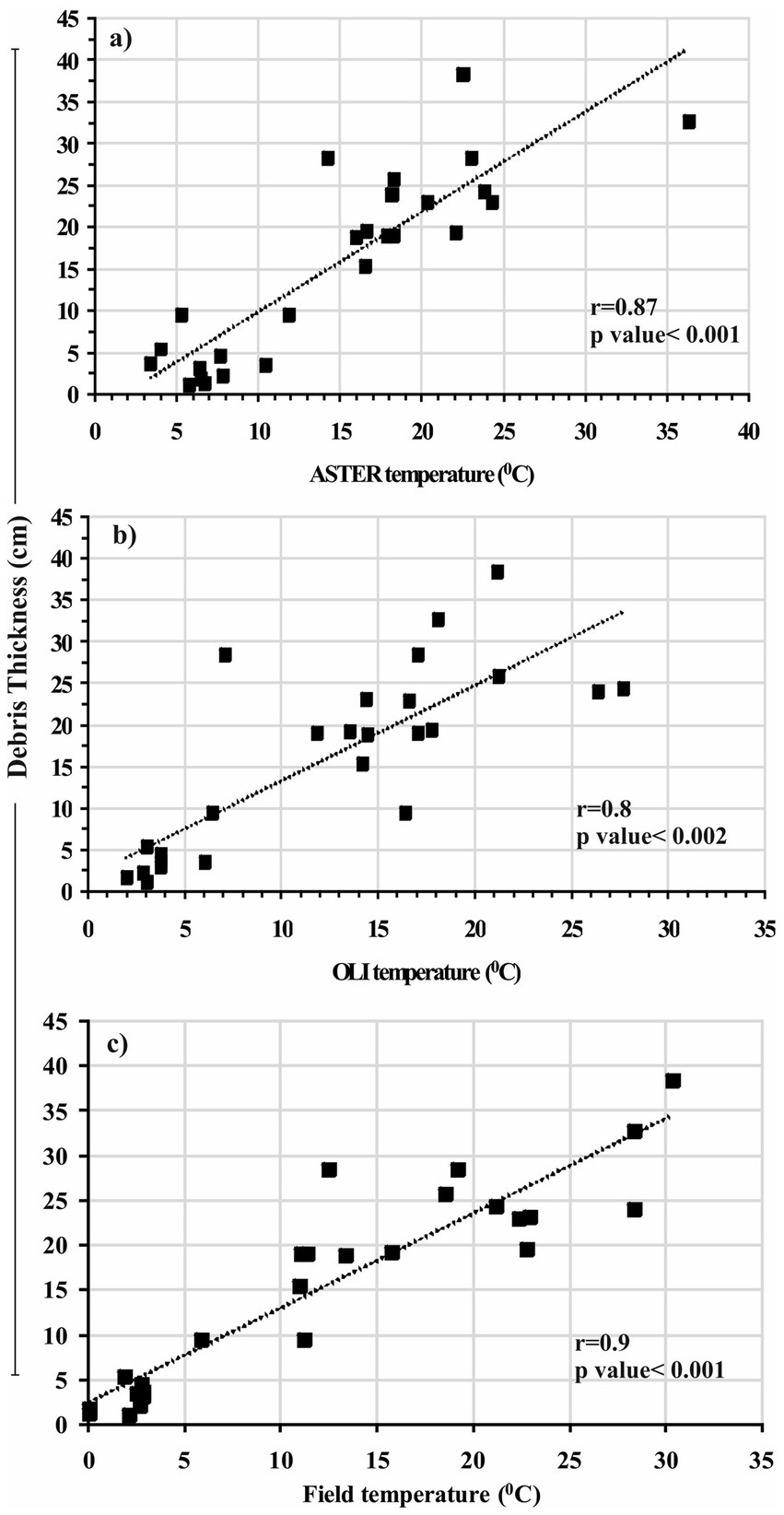
Figure 7. Relationship of field debris thickness (D_f) measurements with corresponding (A) field debris surface temperature (T_f); (B) AST08 debris surface temperature (T_AST08), and (C) Landsat OLI debris surface temperature (T_{Landsat OLI}).

5.3 Spatial pattern of debris thickness from empirical approach

Over an entire debris-covered zone, we noted a general trend of increasing debris thickness towards the snout at lower elevations from both AST08 and Landsat OLI, consistent with field debris thickness measurements (Figure 8). A similar pattern of relatively thicker debris was observed along the lateral and the terminal areas of the glacier which nevertheless decreased continuously along the central flowline (Figure 8). A maximum debris thickness ≤ 39 cm near the snout from field was comparatively higher than Landsat OLI (≤30 cm) and quite consistent with AST08 (≤42 cm) (Figure 8). The mean debris thickness (mean + standard deviation [SD]) of 18.9 ± 7.9 cm, 16.6 ± 9.7 cm, and 12.5 ± 8.9 cm from field, AST08, and Landsat OLI was obtained over an entire 1.2 km² debris-covered zone of the glacier. Thus, the empirical approach using different satellite images for debris thickness estimation could prove useful in gaining knowledge about the spatial pattern of debris thickness distribution at glacier-wide scale. However, the resulting debris thickness cannot be relied upon to give accurate thickness values, particularly in the regions associated with crevasses, water ponds, and ice cliffs. However, it can identify relatively thick/thin debris pixels. Furthermore, the deviation in debris thickness estimates at pixel level from AST08 and Landsat OLI was prominent in the areas where the debris layer was very thin and patchy. The general trend of higher debris thickness values at each pixel from the field compared to AST08 and OLI could be likely due to scanty field debris thickness observations, which does not reflect the average debris thickness for a pixel of AST08 and Landsat OLI. Furthermore, the possible explanation for the deviation in estimated debris thickness from AST08 and Landsat OLI may be related to the difference in image acquisition time; AST08 (10:40 a.m.), OLI (9:16 a.m.) local time in the study area and field data collection. At this time of the day, the low solar elevation (~48°) results in significant topographic shadowing on many south and west-facing slopes (Rounce and McKinney, 2014). This effect could be enough to obscure the thermal signatures exhibited by the glacier, which forms the basis for debris thickness estimation through an empirical approach. Earlier studies on debris-covered studies have also concluded a significant difference in the general trend of debris thickness induced by the characteristic presence of crevasses, water ponds, and ice cliffs on glacier surfaces (Rounce and McKinney, 2014; Juen et al., 2014).

Figure 8

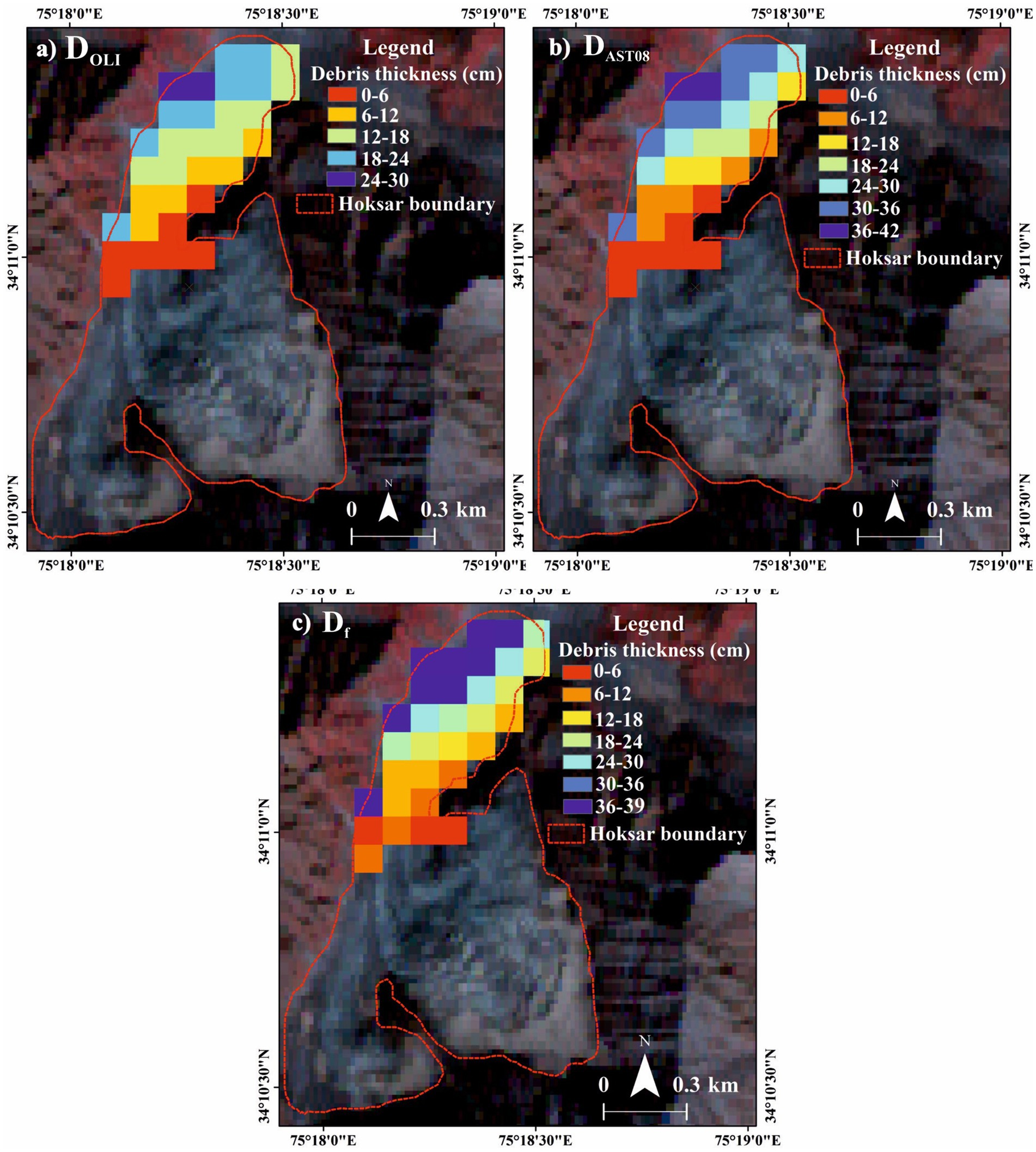
Figure 8. Spatial pattern of debris thickness derived from empirical approach over an entire debris-covered zone of the Hoksar Glacier using (A) Landsat OLI, (B) AST08, and (C) Field. The background image is ASTER (dated 23 October 2015) FCC with band combinations R = near-infrared, G = red, and B = green band, and debris thickness is expressed in (cm). In each panel, D = debris thickness.

5.4 Spatial variability in thermal resistance (R)

Spatial variation of estimated R ranged from (R_AST08 = 0 to 9.8 × 10⁻² m² W K⁻¹ and R_{Landsat OLI} = 0 to 8.7 × 10⁻² m² W K⁻¹) for AST08 and Landsat OLI, respectively (Figure 9). A general trend of relatively higher values of R from both AST08 and Landsat OLI were observed near the snout and along the western margins of the glacier where the debris is thick (Figure 9). However, a gradual decrease in R along the central flowline (CFL) towards the accumulation zone was well distinguished where the debris is comparatively thinner and discontinuous (Figure 9). Thus, it can be perceived that R followed the consistency of measured spatial pattern of debris thickness existing on the glacier (Section 5.5). Thermal resistance correlated well with D_f, and we achieved a significant correlation of (r = 0.89; p < 0.001 for R_AST08 and r = 0.83; p < 0.002 for R_{Landsat OLI}), respectively. Excluding mixed pixels, earlier findings on the spatial distribution of thermal resistance have typically agreed well with field observations (Suzuki et al., 2007). The mixed pixel effect refers to the pixels in the satellite imagery comprising supraglacial ponds, ice cliffs, and bare ice areas (Suzuki et al., 2007). Significantly lower values for calculated thermal resistance were also observed for the areas with exposed ice cliffs having lower temperature (Nakawo and Young, 1982). In contrast, Zhang et al. (2011) did not address the low values of thermal resistances but did attribute the small disagreement between modelled and observed melt rates to the unknown variations in meteorological conditions caused by altitude, aspect, and shading in different areas, as well as the unknown nature of water content in the debris. In addition, earlier findings argued that though the mixed-pixel effect and the spatial variation in meteorological conditions may reduce the thermal resistances, it is unlikely to cause the satellite-derived thermal resistances to be 1 or 2 orders of a magnitude lower than those found in the field (Rounce and McKinney, 2014). However, it has been used in the current study to understand the spatial pattern of debris thickness in combination with thermal conductivity and restricted meteorological inputs. Moreover, we compared the derived thermal resistance with observed debris thickness, and we achieved a significant correlation, which encourages us to use thermal resistance as one variable for estimating debris thickness.

Figure 9

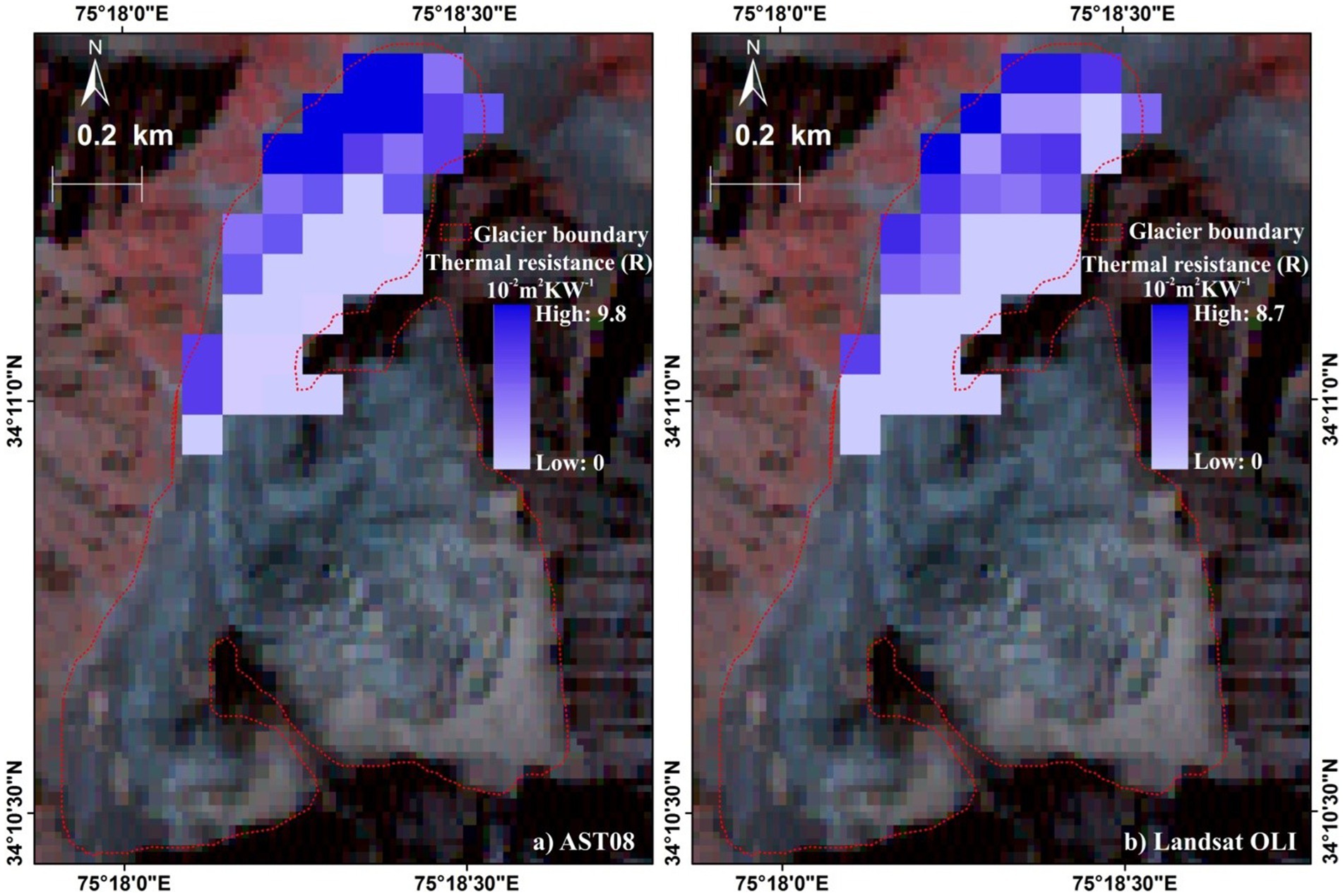
Figure 9. Spatial variability of thermal resistance (R) as achieved from AST08 and Landsat OLI. Note that the thermal resistance was measured in 10⁻² m² W K⁻¹.

5.5 Spatial pattern of debris thickness from thermal resistance approach

Debris thickness estimates using AST08 and Landsat OLI showed a considerable inhomogeneity that thickens towards the snout and thins up-glacier, identical to that obtained from the field (Figure 10). In general, debris thickness from Landsat OLI varied from 0 to 55 cm with a mean debris thickness of ≥23 ± 17 cm. In contrast, a slightly higher debris thickness of 0–57 cm with a mean debris thickness of ≥23 ± 17 cm was observed from AST08. A maximum thickness of 53 ± 7 cm for Landsat OLI and 55 ± 9 cm for AST08 was computed for the regions situated along the western margins near the terminus where the debris had likely accumulated over time due to differential melting and backwasting (Figure 10). Although computed debris thickness from AST08 and Landsat OLI varied at the pixel level, however, we observed a similar and consistent pattern of debris thickness variation which gradually decreased from west to east (Figure 10). Areas of thin debris cover, that is, 22 ± 9 cm for Landsat OLI and 25 ± 11 cm for AST08 were represented along the eastern lateral margins and towards the accumulation zone of the glacier (Figure 9). We could not obtain a wide rage in the spatial variability of debris thickness which could be partially explained by small size (~2.1 km² in the area; debris-covered area ~ 1.2 km²) of the glacier and further by pixel scale (90 m × 90 m) of AST08 and 60 * 60 m of Landsat OLI datasets.

Figure 10

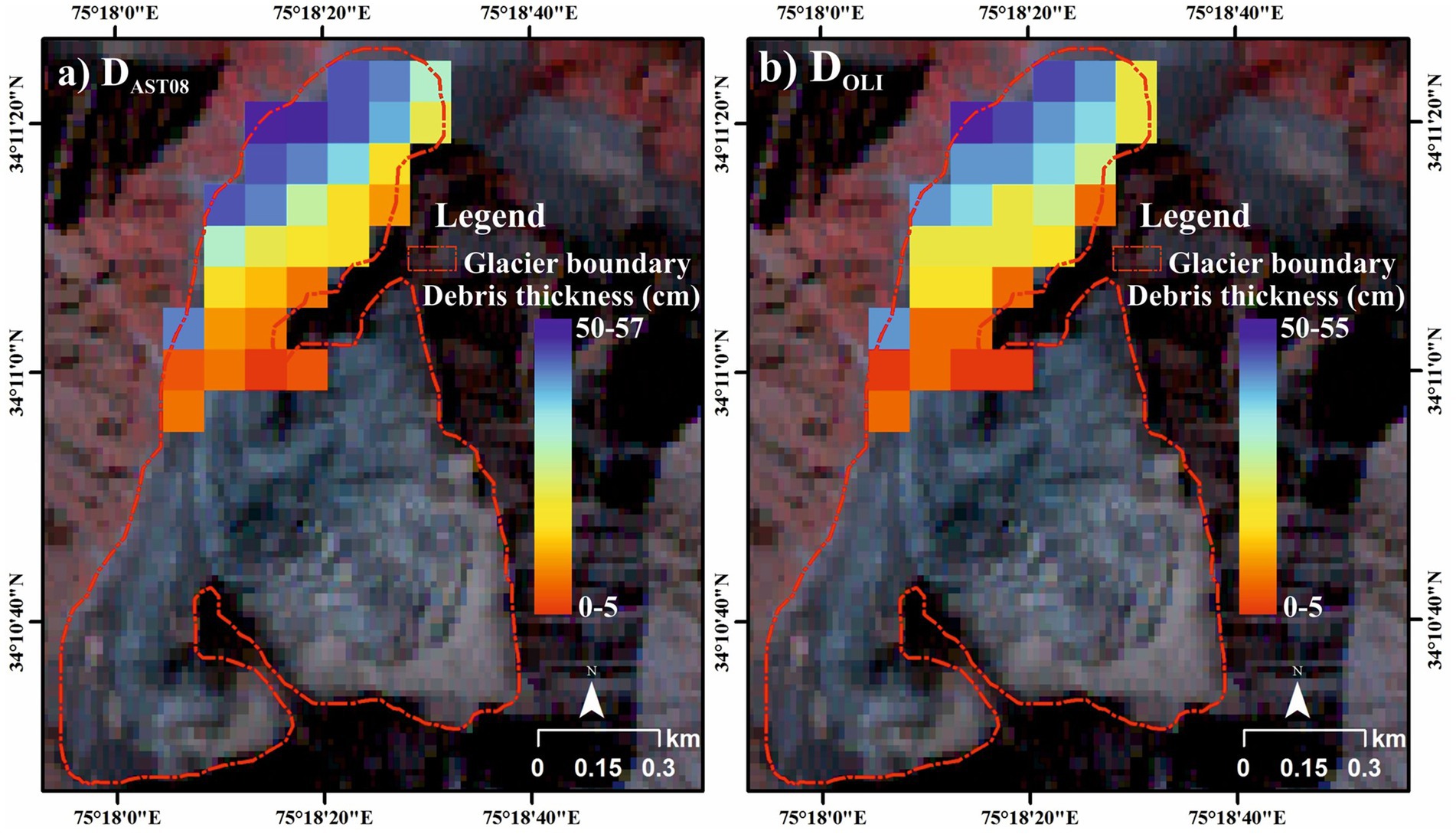
Figure 10. Spatial distribution of debris thickness on the Hoksar Glacier as obtained through thermal resistance approach using (A) Landsat OLI and (B) AST08. In each panel, D_OLI = debris thickness from Landsat OLI and D_AST08 = debris thickness from AST08.

5.6 Comparison of debris thickness estimates on the Hoksar Glacier

We also compared and evaluated debris thickness estimates obtained through empirical and thermal resistance-based approaches along different transects set along the glacier’s central flowline. Starting from the snout, at a regular distance of 90 m, a total of five transects, namely, T1, T2, T3, T4, and T5, were drawn throughout the debris-covered zone of the glacier (Figure 10A). The average debris thickness obtained through these transects is shown in Figure 11B.

Figure 11

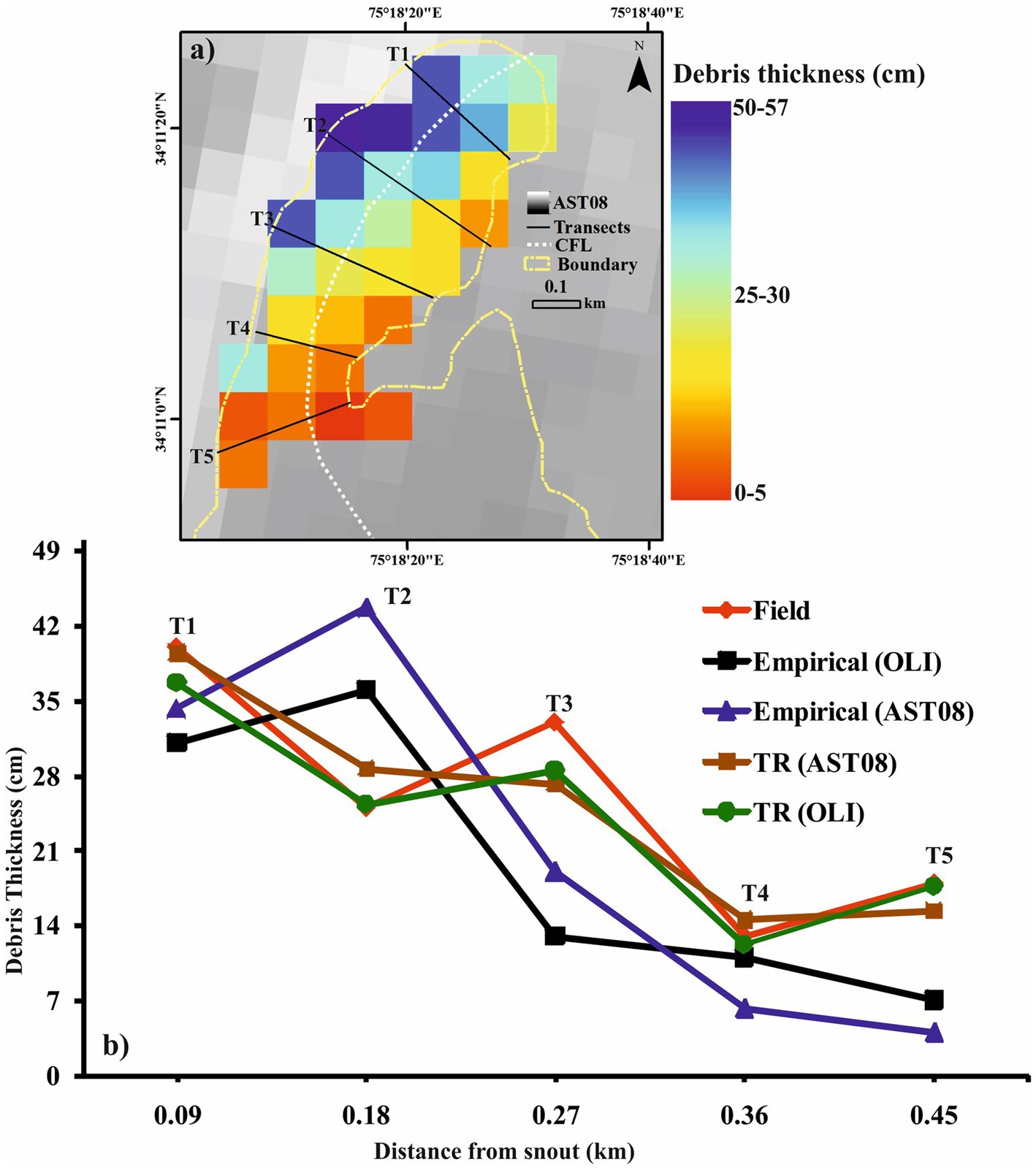
Figure 11. Comparative analysis of debris thickness on the Hoksar Glacier derived through different approaches; (A) represents the location of transects T1, T2, T3, T4, and T5 along the central flowline of the glacier and (B) represents the average debris thickness along transects T1 to T5. In legend, Empirical = Empirical Approach and TR = thermal resistance approach.

From both empirical (AST08 and Landsat OLI) and thermal resistance (AST08 and Landsat OLI) approaches, we observed an identical fluctuating trend in debris thickness along the central flowline, which can be expected for high heterogeneity of thickness over short distances (Patel et al., 2016; Nicholson and Benn, 2013; Ranzi et al., 2004; Suzuki et al., 2007). However, a noticeable deviation was recognised in average debris thickness within each transect (Figure 11). The empirical average debris thickness along these transects was significantly smaller (AST08 = 19.6 ± 5 cm; Landsat OLI = 17.4 ± 8 cm) in comparison to the average field debris thickness (26.8 ± 7.5 cm) yielding a percentage deviation of 26.9 and 35%, respectively. Comparatively, thermal resistance-derived average debris thickness of 23.7 ± 7.8 cm from AST08 and 22.3 ± 4.8 cm from Landsat OLI coincided well with field-derived average debris thickness achieving a smaller deviation of 11.2 and 11.6%, respectively. Since the empirical approach could not capture debris thickness > 50 cm which has influenced an overall estimated debris thickness (Ranzi et al., 2004; Yong et al., 2016; Conway and Rasmussen, 2000).

The thermal resistance approach showed the highest average debris thickness (AST08 = 39.4 ± 7.8 cm; Landsat OLI = 37.6 ± 8.9 cm) in transect T1, which agreed reasonably well with field mean debris thickness (40 ± 6.7 cm) in the same transect (Figure 11B). However, relatively lower mean debris thickness was obtained from empirical approach in transect T1, which is likely due to insensitivity of satellite surface temperature to debris thickness > 50 cm (Figure 11B). The empirical approach estimated relatively higher average debris thickness (AST08 = 42.8 ± 12 cm; Landsat OLI = 37 ± 9.5 cm) in transect T2 compared to 26 ± 5.5 cm and 29.6 ± 7 cm in field and thermal resistance approach, respectively (Figure 11B). Overshoot in transect T2 from empirical approach is possible due to predominant south- and east-facing orientation of pixels which allows them to experience more incoming shortwave radiations throughout morning, thereby enhancing debris surface temperature and resultant debris thickness (Nicholson and Mertes, 2017; Mihalcea et al., 2008a). In transect T3, empirical and thermal resistance approaches mapped debris thickness (AST08 = 60%; Landsat OLI = 42%) and (AST08 = 33%; Landsat OLI = 35%) lower when compared to field debris thickness. This trend in debris thickness in transect T3 can be the impact of microclimate (e.g., shading by surrounding terrain), presence of crevasses (Figure 1E), and north and west-facing slopes (that receive less radiation), which results in reduced net radiations/debris surface temperature, used to derive debris thickness (Mihalcea et al., 2008a; Ranzi et al., 2004). A close approximation in estimated debris thickness from empirical and thermal resistance approaches with the field in transect T4 can be explained as a consequence of the uniform distribution of debris thickness where the thickness/temperature relationship is supposed to be the strongest (Figure 11). In contrast, the spatial variability in temperature which influences debris thickness is pronounced in transect T5 particularly due to patchy and discontinuous debris cover. Thus, the average debris thickness in transect T5 is comparatively underrepresented in the empirical approach compared to the field and thermal resistance approach. These results suggest that the estimated debris thickness from both approaches is reliable in areas with uniform debris cover. Unlike the thermal resistance approach, the method of obtaining debris thickness from the thickness-temperature relationship does not perform well where debris thickness is thin and patchy. In such areas, debris thickness from the empirical approach appears to be relatively lower, indicating that the surface temperature of the debris is independent of the thickness of the underlying debris. Furthermore, the local microclimatic-driven surface temperature differences (which can be the limitation of AST08 and Landsat OLI pixel size to compensate for the small-scale local variations in temperature) are reflected in both approaches where surface temperature-driven debris thickness is obscured. Therefore, we recommend that future studies estimating debris thickness from thermal imagery may collect enough site-specific debris temperature and thickness measurements to ensure that empirical and thermal resistance approaches used are calibrated to account for these differences. In the future, applying the thermal resistance approach at a regional scale and its validation with the existing in-situ measurements would enable its further validation and universal applicability.

5.7 Status of debris thickness on the Hoksar Glacier

Debris thickness estimates from the thermal resistance approach (deviation ~11.2% for AST08 and 11.6% for Landsat OLI) closely approximate to field measurements. We exhibit a typical spatial distribution of debris thickness that decreases from the snout towards the up-glacier but thickens towards margins with increasing distance from the central flowline. This generalisation is also confirmed by field measurements that show a thinly debris-covered central portion of the glacier with a positive trend towards western margins (Figure 8), usually typical of widespread debris-covered glaciers globally (Anderson and Anderson, 2018; Rana et al., 1997; Kraaijenbrink et al., 2018). Such a distribution of debris thickness further reflects the phenomenon of differential melting wherein higher melting has occurred near or along the central flowline and lower at the margins. A constant englacial transport of debris through debris slides and rockfall coupled with the steepness of surrounding topography could explain higher debris thickness in the lower sections (Kirkbride and Deline, 2013; Suzuki et al., 2007; Rana et al., 1997). Earlier studies have investigated net deglaciation with a consequent increase in debris cover in the region (Ali et al., 2017; Gibson et al., 2017). Under such a negative mass balance regime, this pattern of debris thickness is essentially governed by glacier flow, ablation, medial moraine expansion, and englacial transport (Kirkbride and Deline, 2013; Ali et al., 2017). To investigate the effectiveness of the approach, we further compared our thermal resistance-derived debris thickness estimates to global debris thickness data modelled from satellite data. Global debris thickness was earlier produced by using Landsat 8 surface temperature data in combination with the mass-continuity-based subdebris melt inversion method (Rounce et al., 2021). The spatial distribution of debris thickness from the current approach is very similar to that generated by Rounce et al. (2021). In both cases, the debris is thicker closer to the terminus and along the western margins of the glacier and thinner up-glacier. However, our thermal resistance-based debris thickness estimates indicate a mean debris thickness of 23.7 ± 7.8 cm from AST08 and 22.3 ± 4.8 cm from Landsat OLI, which is 39% (AST08) and 35% (Landsat OLI) less than the mean debris thickness modelled by Rounce et al. (2021). The difference in debris thickness estimates in the present study and Rounce et al. (2021) is expected due to (a) smaller debris-covered zone considered by Rounce et al. (2021) ~0.7 km² compared to this study (~1.2 km²) and (b) difference in the approaches and data inputs used for estimation of debris thickness. Similarly, supraglacial debris thickness was modelled for 4,689 glaciers in High Mountain Asia using downscaled ERA5-Land reanalysis data (McCarthy et al., 2022). The results from the study suggest a strong spatial variability in debris thickness both at the local and regional levels. Interestingly, the study indicated thinner debris concentrated at higher elevations up-glacier due to recent exhumation from the ice, while thicker debris was concentrated at lower elevations down-glacier where there tend to be large moraines and extensive debris, which also corroborates the current study.

5.8 Limitations and way forward

The empirical approach presented here relies on site-specific information (debris temperature and thickness measurements), which is expected to vary from glacier to glacier or within the same glacier. The large variation in debris thickness over small spatial scales prevents the universality of the empirical approach for wider application. The results of our study further indicate that the approach becomes insensitive to relatively thick (>50 cm) debris pixels. This provides further evidence that debris surface temperature becomes independent for thicker debris, as discussed in Ragettli et al. (2015) and Yong et al. (2016). However, the impact of this limitation will be insignificant for melt models for which the melt below a thick debris layer is generally low (Ranzi et al., 2004). It appears that a single value of debris thickness for a pixel (90 m × 90 m for AST08 and 60 × 60 for Landsat OLI) may not be representative when considering the heterogeneity of debris thickness and its variation on a scale smaller than 30 m × 30 m (Foster et al., 2012). Moreover, microclimatic conditions prevalent on the glacier surface, such as shading caused by surrounding mountains, ice cliffs, and supraglacial ponds, influence the spatial distribution of surface temperature (Mihalcea et al., 2008a; Ranzi et al., 2004). The impact of shadows in the current study was considered to be negligible, considering the acquisition time of remote sensing imageries (10:40 a.m.) and field observations (11:30 a.m.). Therefore, the small-scale variation in temperature from ice cliffs and crevasses was usually associated with inhomogeneous pixels with high variability of debris thickness (Transect T3; Figures 1E, 10). However, the coarse resolution of thermal imageries (both AST08 and Landsat OLI) could not account for such variation in temperature (usually more than a pixel of thermal imagery). Therefore, this should be acknowledged as an inherent limitation of the empirical approach. We further advocate for further high-precision studies of debris thickness that will ensure uncertainties associated with similar complex surfaces (supraglacial ponds, ice cliffs, aspects, and shadings, and also the meteorological variables, such as air temperature or wind) using a high-resolution airborne unmanned aerial vehicle (UAV). Better understanding of the debris thickness–temperature relationships for the derivation of the universal algorithm remains a challenge for future studies. The acquisition of more in-situ data could potentially solve this problem and could help in statistical modelling (such as semi-variograms) and interpolation (such as kriging) to capture debris thickness with finer details. The present study does not account for the variation of temperature with elevation, which we consider negligible in the context of the small-sized debris-covered zone of the glacier (~1.2 km²). However, the derivation of empirical relationships for separate elevation bands could potentially solve this issue (Reid et al., 2012; Mihalcea et al., 2008a; Yong et al., 2016; Reid and Brock, 2010). In conclusion, only a method capable of estimating and subtracting all the factors controlling surface temperature may reliably relate debris thickness to surface temperature for an accurate estimation of debris thickness through empirical approaches.

In the future, the thermal resistance approach would be highly beneficial for the derivation of debris thickness without the need for extensive field measurements in data-scarce Himalayan region. Though the spatial distribution of thermal resistance typically agreed well with observed debris thickness (r = 0.89; p < 0.001 for R_AST08 and r = 0.83; p < 0.002 for R_{Landsat OLI}) which motivated us to use thermal resistance as one variable for the estimation of debris thickness. However, earlier studies suggested actual values of thermal resistance to be significantly lower than field observations (Nakawo and Rana, 1999). This uncertainty in the estimated thermal resistance prevailed for the regions associated with supraglacial ponds, ice cliffs and bare ice areas (Nakawo and Rana, 1999). The thermal resistance of the regions corresponding to exposed ice cliffs was further reduced due to lower surface temperature (Nakawo and Young, 1982). On the contrary, small disagreement between modelled and observed melt rates due to unknown variations in meteorological conditions caused by microclimatic conditions were addressed in a different study instead of minimum values for thermal resistance (Suzuki et al., 2007). Adding to the discussion, the spatial variation in meteorological may reduce the thermal resistance, but it is unlikely to cause deviation in satellite-derived thermal resistances (Nicholson and Mertes, 2017). Although this limitation may exist at the same time, it allows the development of an understanding of the spatial pattern of debris thickness with limited meteorological and site-specific inputs. We believe that the approach is unable to capture exact local variations in temperature, which may influence the thermal resistance. One way to overcome this problem may be to apply the corrections to the incoming solar radiation and then resample these values of incoming solar radiation with the surface temperature pixels (30 m). Future studies should seek to quantify how much the debris thickness is underestimated by the spatially variable thermal resistance of mixed pixels and to develop a method that is able to accurately quantify the debris thickness for such pixels. Furthermore, to minimise the uncertainties associated with sensible heat fluxes and thermal conductivity (which were either neglected or considered constant in the current study) by gathering site-specific meteorological data and debris properties. While the glacier selected in the present study is small and a constant value for shortwave and longwave radiation across the glacier is acceptable, future efforts could be made by accounting for the effects of local topography (debris mounds and ice cliffs) on the distribution of these radiations. It is also possible to have an in-depth depth evaluation of reanalysis ERA-5 data based on field meteorological measurements that could be helpful to estimate biases there in and to estimate a general range of deviations between the two. Furthermore, it would be of great interest to compare reanalysis ERA-5 data to field meteorological data from other glaciers, especially for high-altitude glaciers in the Himalaya. The consistency and reliability of the approach can further be appraised by comparing the debris thickness maps obtained from spatially and temporally variable images in the future which can assist its wider application.

6 Summary and conclusion

The study presented here investigates the performance of empirical and thermal resistance debris thickness approaches against field measurements on the Hoksar Glacier, Kashmir Himalaya. The study used thermal imageries (Landsat OLI, 2017 and AST08, 2017) and reanalysis ERA-5 data for the assessment of debris thickness over the entire debris-covered zone of the glacier. Our major findings of the study are listed in the following:

• For homogenous debris thickness, we have noticed excellent coherence (r = 0.9; p < 0. 001 for T_AST08 and r = 0.88; p < 0.001 T_{Landsat OLI} for temperature) and (r = 0.9; p < 0.001 for T_AST08 and r = 0.87; p < 0.002 for T_{Landsat OLI} for debris thickness) between field temperature and thickness measurements with satellite temperature indicating that the accuracy of the estimated debris thicknesses to be maximum for such regions.

• From the empirical approach (both AST08 and Landsat OLI), a prominent deviation in debris thickness estimates for relatively thin debris-covered pixels was observed when compared to field data, which is possibly linked to higher spatial variability in surface temperature caused by patchy and moisture-laden debris layer.

• Over an entire debris-covered zone of the glacier, an average debris thickness of 18.9 ± 7.9 cm was observed from the field, which the empirical approach underestimated (12% for AST08 and 28% for Landsat OLI) and the thermal resistance approach overestimated by (6.2% for AST08 and 5.1% Landsat OLI), respectively.

• A close approximation of the thermal resistance approach (deviation ~11.2% for AST08 and 11.6% for Landsat OLI) with field measurements in contrast to the empirical approach (deviation ~26.9% for AST08 and 35% for Landsat OLI) makes it more reliable approach for derivation of debris thickness with reduced requirement of field data.

• The study further emphasises on evaluating the consistency and reliability of the thermal resistance approach by comparing the debris thickness maps obtained from spatially and temporally variable images and by in-depth examining of reanalysis data with field meteorological measurements for its universal application.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.

Author contributions

IA: Conceptualization, Data curation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing, Project administration. AS: Methodology, Supervision, Writing – review & editing. SR: Data collection, Supervision, Writing – review & editing. FL: Formal analysis, Resources, Writing – review & editing. PG: Writing – review & editing. BY: Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by Department of Science and Technology through Women Scientist Scheme (WOS-A) under DST/WOS-A/EA-52/2021.

Acknowledgments

Iram Ali gratefully acknowledges Department of Science and Technology for providing fellowship under WOS-A scheme and the project is entitled “A Synergistic Framework to Map Debris Thickness on Kashmir Himalayan Glaciers”.

Conflict of interest

The authors declare that there is no competing interest that would have influenced the results or discussions reported in the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^https://reverb.echo.nasa.gov

2. ^https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5

References

Ali, I. (2019). Remote sensing study for characterization of supraglacial debris in parts of Jhelum Basin. Jammu and Kashmir: Thesis, University of Kashmir Available at: http://hdl.handle.net/10603/443464.

Google Scholar

Ali, I., Shukla, A., and Romshoo, S. A. (2017). Assessing linkages between spatial facies changes and dimensional variations of glaciers in the upper Indus basin, western Himalaya. Geomorphology 284, 115–129. doi: 10.1016/j.geomorph.2017.01.005

Crossref Full Text | Google Scholar

Anderson, L. S., and Anderson, R. S. (2018). Debris thickness patterns on debris covered glaciers. Geomorphology 311, 1–12. doi: 10.1016/j.geomorph.2018.03.014

PubMed Abstract | Crossref Full Text | Google Scholar

Anderson, L. S., Armstrong, W. H., Anderson, R. S., and Buri, P. (2021). Debris cover and the thinning of Kennicott glacier, Alaska: in situ measurements automated ice cliff delineation and distributed melt estimates. Cryosphere 15, 265–282. doi: 10.5194/tc-15-265-2021

Crossref Full Text | Google Scholar

Aubry-Wake, C., Lamontagne Hallé, P., Baraër, M., McKenzie, J. M., and Pomeroy, J. W. (2023). Using ground-based thermal imagery to estimate debris thickness over glacial ice: fieldwork considerations to improve the effectiveness. J. Glaciol. 69, 353–369. doi: 10.1017/jog.2022.67

Crossref Full Text | Google Scholar

Benn, D. I., Bolch, T., Hands, K., Gulley, J., Luckman, A., Nicholson, L. I., et al. (2012). Response of debris-covered glaciers in the Mount Everest region to recent warming, and implications for outburst flood hazards. Earth-Sci. Rev. 114, 156–174. doi: 10.1016/j.earscirev.2012.03.008

Crossref Full Text | Google Scholar

Benn, D. I., and Owen, L. A. (1998). The role of the Indian summer monsoon and the mid-latitude westerlies in Himalayan glaciation: review and speculative discussion. J. Geol. Soc. 155, 353–363. doi: 10.1144/gsjgs.155.2.0353

Crossref Full Text | Google Scholar

Berthier, E., Schiefer, E., Clarke, G., Menounos, B., and Rémy, F. (2010). Contribution of Alaskan glaciers to sea-level rise derived from satellite imagery. Nat. Geosci. 3, 92–95. doi: 10.1038/ngeo737

Crossref Full Text | Google Scholar

Bhambri, R., Bolch, T., Chaujar, R. K., and Kulshreshtha, S. C. (2011). Glacier changes in the Garhwal Himalaya, India, from 1968 to 2006 based on remote sensing. J. Glaciol. 57, 543–556. doi: 10.3189/002214311796905604

Crossref Full Text | Google Scholar

Bisset, R. R., Nienow, P. W., Goldberg, D. N., Wigmore, O., Loayza-Muro, R. A., Wadham, J. L., et al. (2022). Using thermal UAV imagery to model distributed debris thicknesses and sub-debris melt rates on debris-covered glaciers. J. Glaciol., 1–16. doi: 10.1017/jog.2022.116

Crossref Full Text | Google Scholar

Bolch, T., Kulkarni, A., Kääb, A., Huggel, C., Paul, F., Cogley, J. G., et al. (2012). The state and fate of Himalayan glaciers. Science 336, 310–314. doi: 10.1126/science.1215828

PubMed Abstract | Crossref Full Text | Google Scholar

Boxall, K., Willis, I., Giese, A., and Liu, Q. (2021). Quantifying patterns of supraglacial debris thickness and their glaciological controls in High Mountain Asia. Front. Earth Sci. 9:657440. doi: 10.3389/feart.2021.657440

Crossref Full Text | Google Scholar

Brock, B. W., Mihalcea, C., Kirkbride, M. P., Diolaiuti, G., Cutler, M. E. J., and Smiraglia, C. (2010). Meteorology and surface energy fluxes in the 2005–2007 ablation seasons at the Miage debris-covered glacier, Mont Blanc massif, Italian Alps. J. Geophys. Res. 115:D09106.

Google Scholar

Brun, F., Wagnon, P., Berthier, E., Jomelli, V., Maharjan, S. B., Shrestha, F., et al. (2019). Heterogeneous influence of glacier morphology on the mass balance variability in High Mountain Asia. J. Geophys. Res. Earth 124, 1331–1345. doi: 10.1029/2018JF004838

Crossref Full Text | Google Scholar

Carenzo, M., Pellicciotti, F., Mabillard, J., Reid, T., and Brock, B. W. (2016). An enhanced temperature index model for debris covered glaciers accounting for thickness effect. Adv. Water Resour. 94, 457–469. doi: 10.1016/j.advwatres.2016.05.001

PubMed Abstract | Crossref Full Text | Google Scholar

Conway, H., and Rasmussen, L. A. (2000). Summer temperature profiles within supraglacial debris on Khumbu glacier, Nepal, IAHS Publication 264 (Symposium at Seattle 2000 – Debris-Covered Glaciers), 89–97.

Google Scholar

Dimri, A. P. (2006). Surface and upper air fields during extreme winter precipitation over the western Himalayas. Pure Appl. Geophys. 163, 1679–1698. doi: 10.1007/s00024-006-0092-4

Crossref Full Text | Google Scholar

Foster, L. A., Brock, B. W., Cutler, M. E. J., and Diotri, F. (2012). Instruments and methods: a physically based method for estimating supraglacial debris thickness from thermal band remote-sensing data. J. Glaciol. 58, 677–691. doi: 10.3189/2012JoG11J194

Crossref Full Text | Google Scholar

Fujita, K., and Sakai, A. (2014). Modelling runoff from a Himalayan debris-covered glacier. Hydrol. Earth Syst. Sci. 18, 2679–2694. doi: 10.5194/hess-18-2679-2014

Crossref Full Text | Google Scholar

Fyffe, C. L., Reid, T. D., Brock, B. W., Kirkbride, M. P., Diolaiuti, G., Smiraglia, C., et al. (2014). A distributed energy-balance melt model of an alpine debris-covered glacier. J. Glaciol. 60, 587–602. doi: 10.3189/2014JoG13J148

Crossref Full Text | Google Scholar

Gibson, M. J., Glasser, N. F., Quincey, J. D., Mayer, C., Rowan, A. V., and Irvine-Fynn, T. D. L. (2017). Geomorphology temporal variations in supraglacial debris distribution on Baltoro glacier, Karakoram between 2001 and 2012. Geomorphology 295, 572–585. doi: 10.1016/j.geomorph.2017.08.012

Crossref Full Text | Google Scholar

Gök, D. T., Scherler, D., and Anderson, L. S. (2023). High-resolution debris-cover mapping using UAV-derived thermal imagery: limits and opportunities. Cryosphere 17, 1165–1184. doi: 10.5194/tc-17-1165-2023

Crossref Full Text | Google Scholar

Harrison, S., Kargel, J. S., Huggel, C., Reynolds, J., Shugar, D. H., Betts, R. A., et al. (2018). Climate change and the global pattern of moraine-dammed glacial lake outburst floods. Cryosphere 12, 1195–1209. doi: 10.5194/tc-12-1195-2018

Crossref Full Text | Google Scholar

Herreid, S., and Pellicciotti, F. (2020). The state of rock debris covering Earth’s glaciers. Nat. Geosci. 13, 621–627. doi: 10.1038/s41561-020-0615-0

Crossref Full Text | Google Scholar

Hersbach, H. (2018). ERA5 hourly data on pressure levels from 1979 to present: Copernicus climate change service (C3S) climate data store (CDS). doi: 10.24381/cds.bd0915c6

Crossref Full Text | Google Scholar

Huss, M. (2011). Present and future contribution of glacier storage change to runoff from macroscale drainage basins in Europe. Water Resour. Res. 47, 1–14. doi: 10.1029/2010WR010299

Crossref Full Text | Google Scholar

Immerzeel, W. W., van Beek, L. P. H., Konz, M., Shrestha, A. B., and Biekens, M. F. P. (2012). Hydrological response to climate change in a glacierized catchment in the Himalayas. Climate Change 110, 721–736. doi: 10.1007/s10584-011-0143-4

Crossref Full Text | Google Scholar

Iwasaki, A., and Fujisada, H. (2005). “ASTER geometric performance,” in IEEE Transactions on Geoscience and Remote Sensing. 43, 2700–2706.

Google Scholar

Juen, M., Mayer, C., Lambrecht, A., Han, H., and Liu, S. (2014). Impact of varying debris cover thickness on ablation: a case study for Koxkar glacier in the Tien Shan. Cryosphere 8, 377–386. doi: 10.5194/tc-8-377-2014

Crossref Full Text | Google Scholar

Kanth, T. A., Shah, A. A., and Hassan, Z. U. (2011). Geomorphologic character and receding trend of Kolahoi glacier in Kashmir Himalaya. Recent Res. Sci. Technol. 3, 68–73.

Google Scholar

Kaul, M. N. (1990). Glacial and fluvial geomorphology of Western Himalayas. New Delhi: Concept Publishing Company.

Google Scholar

Kaul, V., Handoo, J. K., and Qadri, B. A. (1977). Seasons of Kashmir. Geograph. Rev. India 41, 123–130.

Google Scholar

Kayastha, R. B., Takeuchi, Y., Nakawo, M., and Ageta, Y. (2000). Practical prediction of ice melting beneath various thickness of debris cover on Khumbu glacier, Nepal, using a positive degree-day factor. Proceedings at Seattle, Washington, USA: IAHS Publications 264, 71–81.

Google Scholar

King, O., Bhattacharya, A., Bhambri, R., and Bolch, T. (2019). Glacial lakes exacerbate Himalayan glacier mass loss. Sci. Rep. 9:18145. doi: 10.1038/s41598-019-53733-x

Crossref Full Text | Google Scholar

Kirkbride, M. P., and Deline, P. (2013). The formation of supraglacial debris covers by primary dispersal from transverse englacial debris bands. Earth Surf. Process. Landf. 38, 1779–1792. doi: 10.1002/esp.3416

Crossref Full Text | Google Scholar

Kirkbride, M. P., and Warren, C. R. (1999). Tasman glacier, New Zealand: 20th-century thinning and predicted calving retreat. Glob. Planet. Chang. 22, 11–28. doi: 10.1016/S0921-8181(99)00021-1

Crossref Full Text | Google Scholar

Kraaijenbrink, P. D. A., Shea, J. M., Litt, M., Steiner, J. F., Treichler, D., Koch, I., et al. (2018). Mapping surface temperatures on a debris-covered glacier with an unmanned aerial vehicle. Front. Earth Sci. 6:64. doi: 10.3389/feart.2018.00064

Crossref Full Text | Google Scholar

Lejeune, Y., Bertrand, J. M., Wagnon, P., and Morin, S. (2013). A physically-based model of the year-round surface energy and mass balance of debris-covered glaciers. J. Glaciol. 59, 327–344. doi: 10.3189/2013JoG12J149

Crossref Full Text | Google Scholar

Marazi, A., and Romshoo, S. A. (2018). Streamflow response to shrinking glaciers under changing climate in the Lidder valley, Kashmir Himalayas. J. Mt. Sci. 15, 1241–1253. doi: 10.1007/s11629-017-4474-0

Crossref Full Text | Google Scholar

McCarthy, M., Miles, E., Kneib, M., Buri, P., Fugger, S., and Pellicciotti, F. (2022). Supraglacial debris thickness and supply rate in High-Mountain Asia. Commun. Earth Environ. 3:269.

Google Scholar

McCarthy, M., Pritchard, H., Willis, I. A. N., and King, E. (2017). Ground-penetrating radar measurements of debris thickness on Lirung glacier, Nepal. J. Glaciol. 63, 543–555. doi: 10.1017/jog.2017.18

PubMed Abstract | Crossref Full Text | Google Scholar

Mihalcea, C., Brock, B. W., Diolaiuti, G., D'Agata, C., Citterio, M., Kirkbride, M. P., et al. (2008a). Using ASTER satellite and ground-based surface temperature measurements to derive supraglacial debris cover and thickness patterns on Miage glacier (Mont Blanc massif, Italy). Cold Reg. Sci. Technol. 52, 341–354. doi: 10.1016/j.coldregions.2007.03.004

Crossref Full Text | Google Scholar

Mihalcea, C., Mayer, C., Diolaiuti, G., D’Agata, C., Smiraglia, C., Lambrecht, A., et al. (2008b). Spatial distribution of debris thickness and melting from remote sensing and meteorological data, at debris-covered Baltoro glacier, Karakoram, Pakistan. Ann. Glaciol. 48, 49–57. doi: 10.3189/172756408784700680

Crossref Full Text | Google Scholar

Mihalcea, C., Mayer, C., Diolaiuti, G., Lambrecht, A., Smiraglia, C., and Tartari, G. (2006). Ice ablation and meteorological conditions on the debris covered area of Baltoro glacier (Karakoram, Pakistan). Ann. Glaciol. 43, 292–300. doi: 10.3189/172756406781812104

Crossref Full Text | Google Scholar

Minora, U., Bocchiola, D., D’Agata, C., Maragno, D., Mayer, C., Lambrecht, A., et al. (2016). Glacier area stability in the Central Karakoram National Park (Pakistan) in 2001–2010: the “Karakoram anomaly” in the spotlight. Prog. Phys. Geogr. 40, 629–660. doi: 10.1177/0309133316643926

Crossref Full Text | Google Scholar

Murtaza, K. O., and Romshoo, S. A. (2017). Recent glacier changes in the Kashmir alpine Himalayas, India. Geocarto Int. 32, 188–205. doi: 10.1080/10106049.2015.1132482

Crossref Full Text | Google Scholar

Nakawo, M., and Rana, B. (1999). Estimate of ablation rate of glacier ice under a supraglacial debris layer. Geogr. Ann. 81, 695–701. doi: 10.1111/1468-0459.00097

Crossref Full Text | Google Scholar

Nakawo, M., and Young, G. J. (1981). Field experiments to determine the effect of a debris layer on ablation of glacier ice. Ann. Glaciol. 2, 85–91. doi: 10.3189/172756481794352432

Crossref Full Text | Google Scholar

Nakawo, M., and Young, G. J. (1982). Estimate of glacier ablation under a debris layer from surface temperature and meteorological variables. J. Glaciol. 28, 29–34. doi: 10.3189/S002214300001176X

Crossref Full Text | Google Scholar

Neve, E. F. (1910). Mt. Kolahoi and its northern glacier. Alp. J. 25, 39–42.

Google Scholar

Nicholson, L., and Benn, D. I. (2006). Calculating ice melt beneath a debris layer using meteorological data. J. Glaciol. 52, 463–470. doi: 10.3189/172756506781828584

Crossref Full Text | Google Scholar

Nicholson, L., and Benn, D. I. (2013). Properties of natural supraglacial debris in relation to modelling sub-debris ice ablation. Earth Surf. Process. Landf. 38, 490–501. doi: 10.1002/esp.3299

Crossref Full Text | Google Scholar

Nicholson, L. I., McCarthy, M., Pritchard, H. D., and Willis, I. (2018). Supraglacial debris thickness variability: impact on ablation and relation to terrain properties. Cryosphere 12, 3719–3734. doi: 10.5194/tc-12-3719-2018

Crossref Full Text | Google Scholar

Nicholson, L., and Mertes, J. (2017). Thickness estimation of supraglacial debris above ice cliff exposures using a high-resolution digital surface model derived from terrestrial photography. J. Glaciol. 63, 989–998. doi: 10.1017/jog.2017.68

Crossref Full Text | Google Scholar

Odell, N. E. (1963). The Kolahoi northern glacier, Kashmir. J. Glaciol. 4, 633–635. doi: 10.3189/S0022143000028148

Crossref Full Text | Google Scholar

Østrem, G. (1959). Ice melting under a thin layer of moraine, and the existence of ice cores in moraine ridges. Geogr. Ann. 41, 228–230. doi: 10.1080/20014422.1959.11907953

Crossref Full Text | Google Scholar

Patel, L. K., Sharma, P., Thamban, M., Singh, A., and Ravindra, R. (2016). Debris control on glacier thinning—a case study of the Batal glacier, Chandra basin, Western Himalaya. Arab. J. Geosci. 9, 1–8. doi: 10.1007/s12517-016-2362-5

Crossref Full Text | Google Scholar

Pellicciotti, F., Stephan, C., Miles, E., Herreid, S., Immerzeel, W. W., and Bolch, T. (2015). Mass-balance changes of the debris-covered glaciers in the Langtang Himal, Nepal, from 1974 to 1999. J. Glaciol. 61, 373–386. doi: 10.3189/2015JoG13J237

Crossref Full Text | Google Scholar

Ragettli, S., Pellicciotti, F., Immerzeel, W. W., Miles, E. S., Petersen, L., Heynen, M., et al. (2015). Unravelling the hydrology of a Himalayan catchment through integration of high resolution in situ data and remote sensing with an advanced simulation model. Adv. Water Resour. 78, 94–111. doi: 10.1016/j.advwatres.2015.01.013

Crossref Full Text | Google Scholar

Rana, B., Nakawo, M., Fukushima, Y., and Ageta, Y. (1997). Application of a conceptual precipitation-runoff model (HYCH-MODEL) in a debris-covered glacierized basin in the Langtang Valley, Nepal Himalaya, 1996. Ann. Glaciol. 15, 79–83. doi: 10.3189/S0260305500014087

Crossref Full Text | Google Scholar

Ranzi, R., Grossi, G., Iacovelli, L., and Taschner, S. (2004). Use of multispectral ASTER images for mapping debris-covered glaciers within the GLIMS project. In Proceedings of geoscience and remote sensing symposium, 2004 (IGARSS 2004) IEEE International, 2, 1144–1147.

Google Scholar

Rashid, I., Abdullah, T., and Romshoo, S. A. (2022). Explaining the natural and anthropogenic factors driving glacier recession in Kashmir Himalaya. India: Environmental Science and Pollution Research.

Google Scholar

Reid, T. D., and Brock, B. W. (2010). An energy-balance model for debris covered glaciers including heat conduction through the debris layer. J. Glaciol. 56, 903–916. doi: 10.3189/002214310794457218

Crossref Full Text | Google Scholar

Reid, T. D., Carenzo, M., Pellicciotti, F., and Brock, B. W. (2012). Including debris cover effects in a distributed model of glacier ablation. J. Geophys. Res. 117:D18105. doi: 10.1029/2012JD017795

Crossref Full Text | Google Scholar

Romshoo, S. A., Fayaz, M., Meraj, G., and Bahuguna, I. M. (2020). Satellite observed glacier recession in the Kashmir Himalaya, India, from 1980 to 2018. Environ. Monitor. Assess. 192:597. doi: 10.1007/s10661-020-08554-1

Crossref Full Text | Google Scholar

Romshoo, S. A., Murtaza, K. O., and Abdullah, T. (2022). Towards understanding various influences on mass balance of the Hoksar glacier in the upper Indus Basin using observations. Sci. Rep. 12:15669. doi: 10.1038/s41598-022-20033-w1-2

Crossref Full Text | Google Scholar

Rounce, D. R., Hock, R., McNabb, R. W., Millan, R., Sommer, C., Braun, M. H., et al. (2021). Distributed global debris thickness estimates reveal debris significantly impacts glacier mass balance. Geophys. Res. Lett. 48:e2020GL091311. doi: 10.1029/2020GL09131

Crossref Full Text | Google Scholar

Rounce, D. R., King, O., McCarthy, M., Shean, D. E., and Salerno, F. (2018). Quantifying debris thickness of debris-covered glaciers in the Everest region of Nepal through inversion of a subdebris melt model. J. Geophys. Res. 123, 1094–1115. doi: 10.1029/2017JF004395

Crossref Full Text | Google Scholar

Rounce, D. R., and McKinney, D. C. (2014). Debris thickness of glaciers in the Everest area (Nepal Himalaya) derived from satellite imagery using a nonlinear energy balance model. Cryosphere 8, 1317–1329. doi: 10.5194/tc-8-1317-2014

Crossref Full Text | Google Scholar

Rowan, A., Egholm, D., Quincey, D., Bryn, H., Evan, M., Katie, M., et al. (2020). Accelerating recent mass loss from debris-covered Khumbu glacier in Nepal, and projected response to climate change by 2200 CE. EGU general assembly 2020. Online, EGU2020-20189.

Google Scholar

Sattar, A., Haritashya, U. K., Kargel, J. S., and Karki, A. (2022). Transition of a small Himalayan glacier lake outburst food to a giant transborder food and debris flow. Sci. Rep. 12:12421. doi: 10.1038/s41598-022-16337-6

PubMed Abstract | Crossref Full Text | Google Scholar

Schauwecker, S. (2012). Mapping supraglacial debris thickness on mountain glaciers using satellite data: Validation of a new, physically-based method. Master thesis, Institute of Environmental Engineering Swiss Federal Institute of Technology, Zurich.

Google Scholar

Schauwecker, S., Rohrer, M., Huggel, C., Kulkarni, A., Ramanathan, A. L., Salzmann, N., et al. (2015). Remotely sensed debris thickness mapping of bara Shigri glacier, Indian Himalaya. J. Glaciol. 61, 675–688. doi: 10.3189/2015JoG14J102

Crossref Full Text | Google Scholar

Scherler, D., Wulf, H., and Gorelick, N. (2018). Global assessment of supraglacial debris-cover extents. Geophys. Res. Lett. 45, 11798–11805. doi: 10.1029/2018GL080158

Crossref Full Text | Google Scholar

Sharma, P., Patel, L. K., Ravindra, R., Singh, A. K. M., and Thamban, M. (2016). Role of debris cover to control specific ablation of adjoining Batal and Sutri Dhaka glaciers in Chandra Basin (Himachal Pradesh) during peak ablation season. J. Earth Syst. Sci. 125, 459–473.

Google Scholar

Shukla, A., and Ali, I. (2016). A hierarchical knowledge based classification for glacier terrain mapping –case study from Kolahoi glacier, Kashmir Himalayas. Ann. Glaciol. 57, 1–10. doi: 10.3189/2016AoG71A046

Crossref Full Text | Google Scholar

Shukla, A., Ali, I., Hassan, N., and Romshoo, S. A. (2016). Dimensional changes in the Kolahoi glacier from 1857 t0 2014. Environ. Monitor. Assess. 189, 1–18. doi: 10.1007/s10661-016-5703-7

Crossref Full Text | Google Scholar

Shukla, A., Arora, M. K., and Gupta, R. P. (2010). Synergistic approach for mapping debris-covered glaciers using optical–thermal remote sensing data with inputs from geomorphometric parameters. Remote Sens. Environ. 114, 1378–1387. doi: 10.1016/j.rse.2010.01.015

Crossref Full Text | Google Scholar

Shukla, A., and Yousuf, B. (2016). Evaluation of multisource data for glacier terrain mapping: a neural net approach. Geocarto. Int. 32, 569–587. doi: 10.1080/10106049.2016.1161078

Crossref Full Text | Google Scholar

Soncini, A., Bocchiola, D., Confortola, G., Minora, U., Vuillermoz, E., Salerno, F., et al. (2016). Future hydrological regimes and glacier cover in the Everest region: the case study of the upper Dudh Koshi basin. Sci. Total Environ. 565, 1084–1101. doi: 10.1016/j.scitotenv.2016.05.138

PubMed Abstract | Crossref Full Text | Google Scholar

Srigyan, M., Tripathi, N., Singh, S. K., Rathore, B. P., Oza, S. R., and Bahuguna, I. (2023). Understanding the spatial distribution and plausible genesis of supraglacial debris over the Himalaya-Karakoram region. Phys. Geogr. 44, 620–642. doi: 10.1080/02723646.2023.2202934

Crossref Full Text | Google Scholar

Stewart, R. L., Westoby, M., Pellicciotti, F., Rowan, A., Swift, D., Brock, B., et al. (2021). Using climate reanalysis data in conjunction with multi-temporal satellite thermal imagery to derive supraglacial debris thickness changes from energy-balance modelling. J. Glaciol. 67, 366–384. doi: 10.1017/jog.2020.111

Crossref Full Text | Google Scholar

Suzuki, R., Fujita, K., and Ageta, Y. (2007). Spatial distribution of thermal properties on debris-covered glaciers in the Himalayas derived from ASTER data. Bull. Glaciol. Res. 24:13.

Google Scholar

Takeuchi, Y., Kayastha, R. B., and Nakawo, M. (2000). Characteristics of ablation and heat balance in debris-free and debris-covered areas on Khumbu glacier, Nepal Himalayas, in the pre-monsoon season. IAHS Publications 264, 53–61.

Google Scholar

Taschner, S., and Ranzi, R. (2002). Comparing the opportunities of Landsat-TM and aster data for monitoring debris covered glacier in the Italian Alps within the GLIMS project. In Geoscience and remote sensing symposium, 2002. IGARSS ‘02. 2002 IEEE International, 2, 1044–1046.

Google Scholar

Tonooka, H. (2005). “Accurate atmospheric correction of ASTER thermal infrared imagery using the WVS method,” in IEEE Transactions on Geoscience and Remote Sensing. 43, 2778–2792.

Google Scholar

Yadav, R. K., Rupa Kumar, K., and Rajeevan, M. (2012). Characteristic features of winter precipitation and its variability over Northwest India. J. Earth Syst. Sci. 121, 611–623. doi: 10.1007/s12040-012-0184-8

Crossref Full Text | Google Scholar

Yin, D., Cao, X., Chen, X., Shao, Y., and Chen, J. (2013). Comparison of automatic thresholding methods for snow-cover mapping using Landsat TM imagery. Int. J. Remote Sens. 34, 6529–6538. doi: 10.1080/01431161.2013.803631

Crossref Full Text | Google Scholar

Yong, Z., Yukiko, H., Koji, F., ShiYin, L., and Qiao, L. (2016). Heterogeneity in supraglacial debris thickness and its role in glacier mass changes of the mount Gongga. Sci. China Earth Sci. 59, 170–184. doi: 10.1007/s11430-015-5118-2

Crossref Full Text | Google Scholar

Zhang, Y., Fujita, K., Liu, S., and Nuimura, T. (2011). Distribution of debris thickness and its effect on ice melt at Hailuogou glacier, south eastern Tibetan plateau, using in-situ surveys and aster imagery. J. Glaciol. 57, 1147–1157. doi: 10.3189/002214311798843331

Crossref Full Text | Google Scholar

Zhang, Y., Hirabayashi, Y., Fujita, K., Liu, S., and Liu, Q. (2013). Spatial debris-cover effect on the maritime glaciers of mount Gongga, south-eastern Tibetan plateau. Cryosphere Discuss. 7, 2413–2453. doi: 10.5194/tcd-7-2413-2013

Crossref Full Text | Google Scholar