Multifidelity Surrogate Models for Efficient Uncertainty Propagation Analysis in Salars Systems

Salars are complex hydrogeological systems where the high-density contrasts require advanced numerical models to simulate groundwater flow and brine transport. Applying those models over large spatial and temporal scales is important to understand the various subsurface processes in salars, but the associated computational cost hinders an analysis based on repetitive numerical simulations. Single fidelity surrogate modeling is a common approach to alleviate computational burden with computationally expensive physics-based models of high-fidelity. However, due to the complexity in salars modeling it might not be affordable to run high-fidelity simulations many times until we build a surrogate model of acceptable accuracy. Here, we investigate if multifidelity surrogate methods, that exploit information from inexpensive lower fidelity models, can show promise for computationally demanding tasks for salars systems. Additive, multiplicative and co-Kriging multifidelity surrogates are developed based on the combination of training data from low fidelity sharp interface models and a higher fidelity variable-density flow and solute transport model. Their performance is compared against a single fidelity Kriging surrogate model, and they are all employed to conduct a Monte-Carlo-based uncertainty propagation analysis where recharge, hydraulic conductivity and density differences between freshwater and brine are considered uncertain model inputs. Results showed that multifidelity methods are a promising alternative for time-intensive numerical models of salars under limited high-fidelity samples. In addition, sharp interface models, despite commonly used in coastal aquifer problems, can also be applied in salars modeling as cheap lower fidelity models for interface calculations via a multifidelity framework. The Monte-Carlo outputs based on the surrogate models, resulted in estimated probability density functions characterized by long tails, thus, highlighting the need to reduce parametric uncertainty in real world models of salars.

Introduction

Demand is increasing for supplies of lithium to enable the energy transition to be undertaken, particularly in the sphere of transport. Whilst lithium can be found from either hard rock or lithium brine sources, it is the latter that offers the most promise in terms of both deposit size and energy required for extraction. Lithium-rich brines are found in high Andean salars which are complex hydrogeological systems (Marazuela et al., 2019a; Boutt et al., 2021). Their complexity relates to the high variability of density and that the lithium is found in the salar nucleus associated with saturated brines. It is these saturated brines which require consideration of density contrasts in subsurface flow systems that renders their numerical modeling over large spatial and temporal scales a computationally challenging task (Simmons, 2005).

Earlier published works on these hydrologically closed groundwater basins, have demonstrated that numerical variable-density flow and solute transport (VDST) models are indispensable tools for investigating subsurface flow and brine patterns (Duffy and Al-Hassan, 1988; Rogers and Dreiss, 1995a,b; Fan et al., 1997; Holzbecher, 2005). A few studies have additionally used reactive transport modeling to investigate the brine plume evolution over time which adds significant complexity to the numerical solution (Bauer-Gottwein et al., 2007; Hamann et al., 2015). While the above past studies mostly developed small-scale numerical models focusing on the mixing area of salars, only recently large-scale VDST numerical models have been employed to study groundwater flow and brine transport (e.g., Marazuela et al., 2018). McKnight et al. (2021) studied the impact of hydraulic conductivity heterogeneity on the interface between freshwater and brine in salars while Marazuela et al. (2020) used a thermohaline flow model to describe the process of Lithium enrichment in the Salar de Atacama.

The increasing interest in simulating salar systems over large-spatial and temporal scales, enables a more realistic modeling approach for the understanding of the various subsurface processes involved, as well as for identifying hydrological and hydrogeological conditions that are important for brine development. Notwithstanding the evidence that numerical simulations based on VDST models can offer a reasonable representation of salar systems (Hamann et al., 2015), the associated computational burden might hinder their use in repetitive simulation tasks, such as uncertainty and sensitivity analysis. VDST models are based on the solution of a non-linear coupled system of partial differential equations for flow and transport by using advanced numerical codes (Younes et al., 1999). Despite the progress in computing power, there is continuous research to develop efficient numerical schemes for VDST simulations and improve their capabilities (e.g., Diersch and Kolditz, 2002; Ackerer and Younes, 2008; Konz et al., 2009; Younes et al., 2009; Hirthe and Graf, 2012).

To enable computationally demanding tasks with VDST models, many studies over the last 15 years have employed surrogate modeling techniques. Surrogate models or metamodels or emulators, are data-driven models which are trained on input-output data from physics-based numerical simulations and they are used to predict the original model's response to various inputs at a significantly reduced computational cost (Razavi et al., 2012a). Seawater intrusion management is a typical example where surrogate models are often employed to replace VDST models and search for optimal solutions (e.g., Sreekanth and Datta, 2010, 2011; Ataie-Ashtiani et al., 2014; Roy and Datta, 2017; Christelis et al., 2018, 2019; Lal and Datta, 2018; Ranjbar and Mahjouri, 2018; Song et al., 2018; Kopsiaftis et al., 2019; Yang et al., 2021). Also, there are fewer studies that utilized surrogate models for uncertainty/sensitivity analysis in density-dependent flow systems (e.g., Rajabi et al., 2015; Koohbor et al., 2019; Rajabi, 2019), but to the best of our knowledge none is associated yet with numerical modeling for salars.

Despite the general consensus about the benefits of using surrogate models for numerical simulations of excess computational cost, their effectiveness depends on the problem at hand (Razavi et al., 2012b). The general aim with surrogate modeling is to sample the time-intensive numerical model as parsimoniously as possible, without causing a significant loss in the predictive accuracy of the surrogate model. It is well-studied that the size and the quality of the available training dataset to build the surrogate models, plays a significant role for their successful application (Forrester and Keane, 2009). One challenging aspect for salars numerical simulations is the expected long runtimes particularly when large spatial and temporal scales are considered. In those cases, the construction of single fidelity surrogate models might struggle to provide a practical gain in the trade-off between accuracy and computational cost. This is mainly because only a few physics-based model runs (e.g. VDST model runs) are considered computationally affordable to provide a proper training dataset (Fernández-Godino et al., 2019a).

An alternative solution to this complication is to rely on multifidelity modeling. The scope of a multifidelity approach is to exploit the information derived from running multiple simulations of computationally efficient low/-er fidelity (LF) models and combine this approximate knowledge of the system with the limited data from the high/-er fidelity (HF) model runs. A process is then established which takes into account the discrepancies between the LF and the HF models to either tune the LF model response toward that of the HF model or construct a surrogate model which amalgamates both HF and LF data (Zhou et al., 2016). Simulation of physical systems can be conducted considering various levels of complexity and accuracy, either within the same model structure or by simplifying the mathematical description of the physical system. For example, LF versions of a HF VDST numerical model can be adopted by simply applying a much coarser grid resolution or by decreasing the dimensionality from 3D to 2D (e.g., Kerrou and Renard, 2010). For density-dependent flow systems in particular, there is a wide body of literature devoted to seawater intrusion modeling that develops LF models based on the sharp interface assumption to provide fast approximations of the time-intensive VDST simulations (e.g., Strack, 1976; Bakker, 2006; Pool and Carrera, 2011; Koussis et al., 2012, 2015; Lu et al., 2015). Recent studies have also presented LF models that are capable, under specific conditions, to successfully reproduce mixing in coastal aquifers and speed up multiple simulations while providing comparable results to the HF VDST models (Mazi and Koussis, 2021; Rozos et al., 2021).

To the best of our knowledge only a few studies in density-driven groundwater flow systems implement a fusion of HF and LF model data for computationally expensive simulation frameworks, and these are mostly found in seawater intrusion modeling (e.g. Kerrou and Renard, 2010; Christelis and Mantoglou, 2016, 2019; Dey and Prakash, 2020; Christelis, 2021). In general, multifidelity surrogate models have been less popular than surrogates of a single high-fidelity model in past groundwater and environmental modeling studies (Razavi et al., 2012a; Asher et al., 2015). One reason might be that multifidelity approaches often require bespoke handling for combining data of various fidelities in contrast to single fidelity approaches where robust techniques and software are readily available for use independently of the physical system under study. However, multifidelity methods have recently gained more attention in water resources modeling for computationally expensive problems of parameter estimation and uncertainty quantification (e.g., Mahmoodian et al., 2018; Moreno-Rodenas et al., 2018; Zhang et al., 2018; Zheng et al., 2019; Man et al., 2020; Menberg et al., 2020; Wu et al., 2020).

As the application of more realistic modeling approaches is expected to rise for the analysis of salar systems, it is of practical interest to explore efficient approaches for computationally demanding simulation tasks. To that end, the present study investigates the applicability of multifidelity surrogate modeling techniques for a large-scale VDST numerical model of a salars system. Various surrogate models have been proposed in the VDST modeling literature to replace the computationally expensive flow and transport codes. Here, we select standard Kriging and co-Kriging surrogate models for two reasons. First, co-Kriging is a unique type of multifidelity methods that has been successfully applied in other fields but has not received much attention yet in variable-density groundwater flow problems (Christelis, 2021). Furthermore, the interpolation/regression capabilities of Kriging-based surrogate models are considered beneficial for deterministic simulation problems (Razavi et al., 2012a; Luo et al., 2019; Mo et al., 2019). Obviously, other surrogate modeling techniques might perform better or worse than Kriging depending on the application (e.g., Babaei and Pan, 2016; Zhao et al., 2016; Fan et al., 2020). Second, as co-Kriging is an extension of standard Kriging, our selection justifies a fair comparison between those methods since some of the multifidelity approaches utilized here also apply standard Kriging models. The objectives of the present work are: (1) to study the impact of uncertainty in recharge, hydraulic conductivity and density contrasts on the freshwater-brine interface of a salars flow model, (2) to investigate if simplistic yet computationally efficient LF models can be successfully combined with HF models to analyze salar systems for specific settings and conceptualization, (3) to compare the performance of various multifidelity surrogate models for the emulation of a salars VDST model, and (4) to provide examples and findings on the use of multifidelity surrogate models for density-driven flow problems with large density contrasts, as they occur in salars systems.

Methodology

In the following sections, salars flow systems are briefly discussed and the conceptual model adopted for the present study is presented. Next, the LF and HF model structures as well as the surrogate models are described in more detail.

Salars as a Case Study

High Andean salars are found in the lithium triangle, situated in an area covered by northern Chile, south-west Bolivia and northern Argentina. The largest examples being Salar del Hombre Muerto, Argentina; Salar de Uyuni, Bolivia and Salar de Atacama, Chile. The latter is one of the largest source of lithium-rich brine in the world (Cabello, 2021) and has been exploited for over 20 years. Salars are typically sited in basin and range settings surrounded by volcanic deposits, usually andesite, tufa, and lavas. These are the source of mineralized lithium deposits which are leached into the salars (Risacher and Fritz, 2009). The salars themselves are sedimentary deposits ranging from clays, silts, and sands through to Halite, NaCl. Typically, salars are formed by catchment processes and are fed by surface water and groundwater inflows (Figure 1A). For mature salars with an exploitable brine, the outflow is via evaporation mainly from surface water ponds around the margin and from the center of the salar (nucleus) itself (Figure 1B). Evaporation has an exponential decreasing relationship with depth. This means that once the water table is below 0.5 m the salar surface then evaporation reduces markedly. Potential evaporation is also controlled by the salinity of the water being evaporated, with the magnitude decreasing with increasing brine concentration (Houston, 2006). Rainfall is very low, of the order of 10s mm/year, but rising to 150–200 mm/year as the elevation increases away from the salar itself (Marazuela et al., 2019b). Rainfall recharge is, therefore, very low if it occurs at all in the nucleus, but groundwater to the salar occurs from recharge in the wider catchment and higher ground. There is also periodic flooding of salars from surface water sources during the summer months and resulting in rapid recharge (Boutt et al., 2016). However, there is a growing realization of the importance of including the overall catchment of the salar (fresh water supplied) in any assessment of salar resources (Marazuela et al., 2019a).

FIGURE 1

Figure 1. Watershed, salar (A) and nucleus processes for a mature salar (B).

Circulation of brine in the nucleus (sinking on creation) is an important process controlling the ingress of fresh water and the position and nature of the brine-fresh interface (Rosen, 1994). Newly created brine is of a higher density than that below it and this can lead to instabilities (Wooding et al., 1997). Use of Rayleigh's number is helpful to determine when this may occur as it predicts the balance of convection with buoyancy forces (Fan et al., 1997). Given the geological complexity of the nucleus itself, sedimentary sequences, and deposition of Halites then vertical anisotropy is an important feature which may limit circulation patterns.

Model Geometry and Boundary Conditions

Given that the Salar de Atacama has been exploited for a number of decades, it has been widely studied and recently various aspects of flow and brine transport processes for this salar have been simulated using VDST models based on a vertical slice conceptualization (Marazuela et al., 2018, 2020; McKnight et al., 2021). Such an approach is a practical approximation of the inherent 3D dimensionality of the physical flow system, given the formidable computational cost of a large-scale 3D VDST model and the spatial and time resolution requirements to simulate high-density differences between freshwater and brine (Marazuela et al., 2018).

Therefore, the VDST numerical model of the present work is based on an idealized 2D vertical slice, conceptually similar to the numerical model instance presented in Marazuela et al. (2018) and McKnight et al. (2021). The horizontal extent of the model begins from the end of the salt flat nucleus, includes a mixing zone of 5 km and continues for another 10 km in the recharge area (Figure 2). This conceptualization ignores the simulation of the early forced convection and fingering phase (Hamann et al., 2015) as it is not the focus of the present study. Thus, the left constant concentration boundary represents the brine plume entering the mixing zone assuming it has been already fully developed into the salt flat nucleus, which is also the approach followed by McKnight et al. (2021). The system is simulated until head and brine distribution reach steady state conditions, after a long simulation period of 10,000 years. The constant head boundary condition of h = 0, which is applied at the top left of the model domain, is mimicking the evaporation boundary as in Marazuela et al. (2018). The bottom and the right boundaries represent no-flow boundaries. All aquifer units are simulated as confined aquifers.

FIGURE 2

Figure 2. Conceptual model of the 2D VDST numerical model.

As it is shown in Figure 2, direct recharge inputs are applied to the top of the model domain in the recharge area. It is assumed that recharge varies linearly from low values closer to the mixing zone up to higher values as moving further into the alluvial fans (recharge area). Several studies have investigated and discussed the challenges regarding the recharge mechanisms in salars (e.g., Risacher and Fritz, 2009; Uribe et al., 2015; Marazuela et al., 2019a; Boutt et al., 2021). For the purposes of this study, we consider recharge as a two-dimensional uncertain input where the first random variable is the recharge applied closest to the mixing zone (R_min in Figure 2) and the second random variable is the recharge applied at the last cell of the top model layer which is included in the designated recharge region (R_max in Figure 2). These two recharge values are considered as continuous random variables where R_min can take values in the closed domain (2, 15) as $\frac{mm}{year}$ while R_max can take values in the closed domain (100, 420) as $\frac{mm}{year}$. The assigned ranges were based on various recharge estimates found in the relevant salars literature as summarized in Boutt et al. (2021). Furthermore, it is assumed that hydraulic conductivity K1 of the upper layer (Aquifer 1 in Figure 2) is also a continuous random variable that takes values in (5, 100) as $\frac{m}{day}$. The range for hydraulic conductivity of the upper layer is based on the few single VDST runs performed in Marazuela et al. (2018). We also consider the maximum density of the brine D_max as a continuous random variable that takes values in (1, 150, 1, 230) as $\frac{kg}{m^3}$. This consideration allows us to simulate possible variations of density contrasts between brine and freshwater that might exist in different salars systems. Apart from those model properties the rest are considered constant for the numerical simulations. The values of aquifer properties are selected similarly to the baseline VDST model used in Marazuela et al. (2018) (Table 1).

TABLE 1

Table 1. Aquifer properties for the 2D vertical slice VDST model.

Fidelity of the Selected Simulation Models

We discuss below some specifications which defined the two levels of model fidelity for this study. First, as described in the section Model Geometry and Boundary Conditions, we employ a 2D vertical slice instead of a full 3D model to simplify the numerical simulations in terms of dimensionality and reduce the computational cost. As discussed in Marazuela et al. (2018), running a 3D VDST numerical model for the salar de Atacama at a large spatial scale is computationally unmanageable and certainly not a realistic option for multiple simulations based on personal desktop without any parallelization of the numerical code. The computational burden is further increased when VDST models are combined with geochemical reaction models to simulate brine evolution in salars including evapoconcentration (Hamann et al., 2015) as well as for thermohaline flow models where viscosity changes are taking into account (Marazuela et al., 2020). For example, Hamann et al. (2015) developed a multi-species reactive transport model to include the process of evapoconcentration. The associated computational burden with this approach is formidable even for small scale numerical models as Hamann et al. (2015) reported 30 days for a simulation domain based on a 2D vertical slice with horizontal length of 100 m and aquifer depth of 10 m. Also, according to Hamann et al. (2015), single-species VDST models were still able to replicate the major flow patterns obtained by the more complex reactive transport simulations. Therefore, and due to the exploratory nature of this work, our HF model is based on the solution of the standard coupled system of the non-linear partial differential equations for flow and non-reactive solute transport. The simulations were carried out using the finite-difference USGS numerical code SEAWAT-version 4 (Langevin and Guo, 2006). Despite the imposed simplifications, the average runtime with this HF model for a simulation period of 10,000 years until steady state, is ~1.5 h (using a 2.7 GHz Intel i5 processor and 8 GB of RAM in a 64-bit Windows 10 system). As an example, a small-scale Monte-Carlo (MC) simulation including 100 model runs would require approximately a week.

The LF model selected for this study, belongs to the category of one-fluid sharp interface models originally developed for coastal aquifer modeling and utilizes the flow potential formulation of Strack (1976). This model is based on Ghyben-Herzberg relation and Dupuit approximation while it neglects density variability in space and mixing between freshwater and saltwater. It also assumes horizontal and steady-state aquifer flow whereas saltwater is static (Strack, 1976). The depth to the interface is estimated using the Ghyben-Herzberg approximation and the computational effort to run this model is minimal. The single runtime of the LF model for the conceptualization shown previously in Figure 2 is ~0.004 s. This is a massive reduction in computational time compared to the VDST model to reach steady state flow and transport distribution in the model domain. Because we are simulating a vertical slice of the VDST model the corresponding LF model essentially becomes a 1D flow model which considers only the properties of the upper aquifer unit and the associated flow boundary conditions on the top of the VDST model domain. The discretization settings are at dx = 100m for both the HF and the LF model while the VDST model grid is refined vertically with dz = 10m.

Obviously, the computational gains from simulating the salar system using a sharp interface model is at the cost of reduced accuracy and significant limitations in capturing other more complex features of the VDST model output. Different LF models should be chosen if for example non-steady hydraulic stresses are applied to the HF model or specific information for brine distribution is required. For the purposes of this work, the sharp interface model can provide the required output information at a negligible computational cost. As discussed previously, we are interested here to investigate if a simplistic LF model can be corrected and provide a reasonable approximation of the HF model response under specific assumptions.

Marazuela et al. (2018) compared the output of their single baseline model run against sharp interface models also including the correction proposed by Pool and Carrera (2011). Interestingly, a visual inspection from that comparison showed that the empirical correction suggested by Pool and Carrera (2011) approximates better the average simulated mixing zone of brine, corresponding to a density value of about 1,100 $\frac{kg}{m^3}$. In essence, the correction of Pool and Carrera (2011) proposes a reduced relative density ratio as per $\epsilon *=\epsilon \left[1-{(\frac{{\alpha }_T}{b})}^{\frac{1}{6}}\right]$, where $\epsilon =\frac{({\rho }_s-{\rho }_f)}{{\rho }_f}$ with ρ_s being the seawater density and ρ_f the density of freshwater. The variable α_T is the transverse dispersivity of the corresponding VDST model and b is the thickness of the confined flow region. When these models are applied to salars systems the relative density ratio takes values beyond the typical contrast between seawater and freshwater and in the present study ρ_s now stands for densities which vary between 1,150 and 1,230 $\frac{kg}{m^3}$. That sets an interesting question on how well these models can approximate the brine mixing zone and what is the impact on the prediction skills of the multifidelity surrogate model. As both the VDST models and the model of Strack (1976) have been previously presented numerous times in the literature, their mathematical formulation is omitted here for brevity. Henceforth, the terms HF and VDST model will be used interchangeably and the same stands for the terms LF and the sharp interface model. For convenience, the LF model based on the original formulation of Strack (1976) will be denoted as LF1 and the version with the Pool and Carrera (2011) correction as LF2.

Single-Fidelity and Multifidelity Surrogate Models

Before presenting the surrogate models, we first describe the specifications for the model inputs and model outputs of this work. Let ${\text{X}}_H=\left\{{\text{x}}_H^{(1)},\dots ,{\text{x}}_H^{(n_H)}\right\}$ denote the n_H points where the HF VDST model is evaluated. Each x_H represents an 1 × p input vector, where here p = 4, of the uncertain input variables, R_min, R_max, K1 and D_max. The corresponding VDTS model evaluations on those n_H points are ${\text{Y}}_H=\left\{Y_H({\text{x}}_H^{(1)}),\dots ,Y_H({\text{x}}_H^{(n_H)})\right\}$ which represent the HF model output. The set Y_H is the quantity of interest (QoI) for the uncertainty analysis. Here, we define the QoI based on the contour line that corresponds to a density of 1,100 $\frac{kg}{m^3}$ from all VDST simulations. The QoI, denoted as y_ad, is the average depth from the top of the model domain to the 1,100 $\frac{kg}{m^3}$ density contour line. It captures the average fluctuation of a 1,100 $\frac{kg}{m^3}$ density contour line due to model input uncertainty. The selection of the 1,100 $\frac{kg}{m^3}$ density contour line, also used in Marazuela et al. (2018), is considered a reasonable approximation to the interface obtained by the LF models to separate the freshwater region from brine. Similarly, another set ${\text{X}}_L=\left\{{\text{x}}_L^{(1)},\dots ,{\text{x}}_L^{(n_L)}\right\}$ is defined for the n_L points where the LF models are evaluated. The corresponding LF model evaluations (sharp interface model with density correction LF2 or without LF1) on those n_L points are ${\text{Y}}_L=\left\{Y_L({\text{x}}_L^{(1)}),\dots ,Y_L({\text{x}}_L^{(n_L)})\right\}$. They represent the QoI discussed above, but the depth to the interface ξ is simplistically calculated based on the Ghyben-Herzberg approximation where $\xi =\frac{h_f}{\epsilon }$ for the original model of Strack (1976) while in the case of Pool and Carrera (2011) correction $=\frac{h_f}{{\epsilon }^{*}}$, with h_f being the freshwater head.

For the construction of a single fidelity Kriging model only the sets X_H and Y_H are required. In a KRG model, the scalar model response Y_H(x) is treated as generated by a stochastic process S (Liu et al., 2021):

$\begin{array}{ll}\begin{array}{c}S(x)=\underset{i=0}{\overset{k}{{{\displaystyle \sum }}^{\text{}}}}{a}_i{f}_i(x)+Z(x)\end{array}& (1)\end{array}$

where $\sum _{\text{i}=0}^{\text{k}}{a}_{\text{i}}{\text{f}}_{\text{i}}(\text{x})$ is a regression model which represents the global characteristics of the stochastic process S, with regression coefficients $\text{a}={\left[a_0,\dots ,a_{\text{k}}\right]}^T$ and f_i(x) are known regressions functions. The term Z(x) represents local spatial deviations and it is described by a zero mean Gaussian process with variance σ². Given the training data X_H and Y_H the covariance is expressed as $Cov\left[Z({\text{x}}_i),Z({\text{x}}_j)\right]={\sigma }^{2}R({\text{x}}_i,{\text{x}}_j)$ with i, j = 1, …, n_HF and R is the correlation function of any two training samples. Here, a Gaussian correlation model is selected and a zero-order polynomial for the regression model.

As mentioned previously, the use of LF models could be favorable in repetitive simulation tasks, particularly in cases where single runtimes of the HF model are computationally expensive. We consider here a set of common approaches presented in the literature of multifidelity surrogate modeling (Zaefferer et al., 2016; Fernández-Godino et al., 2019b). Additive and multiplicative corrections are implemented by constructing an approximation model of the difference (discrepancy) or the ratio between the HF and the LF model outputs. Here the discrepancy or ratio functions are approximated also by a KRG model as with the single fidelity approach presented above. In the case of the additive correction the following multifidelity surrogate model is developed:

$\begin{array}{ll}{\widehat{y}}_H=y_L(x)+\delta (x)& (2)\end{array}$

where ${\widehat{\text{y}}}_H$ represents the estimation of the HF model response, y_L(x) is the LF model output and δ(x) is the discrepancy function between HF and LF data. In the case of a multiplicative correction m(x) the estimation of the HF model response is:

$\begin{array}{ll}\begin{array}{c}{\widehat{y}}_H=m(x)•y_L(x)\end{array}& (3)\end{array}$

The hypothesis is that the LF model is capable to explain part of the high-fidelity model behavior and by applying those corrections the LF model response will better approximate that of the HF model. However, if the correlation between the LF and the HF model is not good the performance of a multifidelity surrogate declines. It is an active research topic to identify regions where there is less correlation between the HF and LF model via informative sampling strategies and improve the prediction skills of the multifidelity surrogate (Zhou et al., 2015, 2016). In the case where the LF model is considered computationally costly, albeit faster than the HF model, then an additional surrogate model can be constructed to approximate the LF model response (Zaefferer et al., 2016).

Finally, for the numerical experiments considered in this work we also focus on a special formulation of Kriging (KRG) to develop another multifidelity surrogate model. That is, the method of co-Kriging (coKRG) which typically amalgamates a larger amount of LF data with much fewer HF data to develop fast surrogate models (Forrester et al., 2007). As a result, the developed coKRG model is expected to predict the HF model response more accurately than using the LF model alone. Like all surrogate modeling methods, a successful coKRG model depends also on the available training samples and additionally on the relationship between the HF and the LF model. The coKRG models can be particularly useful when the HF model is expensive and one or more LF models are available to simulate the prominent features of the physical system at a much lower computational effort (Razavi et al., 2012b). The theory of coKRG has been introduced 40 years ago in geostatistics literature (e.g., Matheron, 1973). For a recent presentation of co-Kriging theory for surrogate modeling, readers are referred to Forrester et al. (2007) and Forrester et al. (2008).

For the coKRG models the X_H set is considered as a subset of X_L of the n_L training points. In the case of the coKRG surrogate model there is the combined set of all inputs as $\text{X}=\left(\begin{array}{c}{\text{X}}_L\\ {\text{X}}_H\\ \end{array}\right)$and of all outputs as $\text{Y}=\left(\begin{array}{c}{\text{Y}}_L\\ {\text{Y}}_H\\ \end{array}\right)$. Now, let the Gaussian process Z_L(•) and Z_H(•) to represent the local features of the LF and the HF models while the Gaussian process Z_d(•) to represent the difference between ρZ_L(•) and Z_H(•). Here m is a constant scaling factor which multiplies the LF model, and it is estimated through optimization (Forrester et al., 2008). The approximation of the HF model in the coKGR formulation is expressed as Kennedy and O'Hagan (2000) and Forrester et al. (2007):

$\begin{array}{ll}{Z}_H(x)={mZ}_L(x)+Z_d(x)& (4)\end{array}$

Here, we used the object-oriented ooDACE MATLAB toolbox (Couckuyt et al., 2014) to develop coKRG models and KRG models. A Latin Hypercube Sampling (LHS) method was used to generate the training dataset as well as the validation dataset for the surrogate models. Figure 3 presents a schematic workflow for the implementation of the single fidelity and the multifidelity surrogate models.

FIGURE 3

Figure 3. Workflow for the Monte-Carlo UP analysis based on the surrogate models.

Uncertainty Propagation Analysis

The single runtime of the 2D VDST model for this study is ~1.5 h. This poses computational difficulties for implementing a proper uncertainty propagation (UP) analysis given that a large number of simulations is required. For example, Rajabi et al. (2015) performed a convergence study on the mean and standard deviations of their QoI for the classic Henry problem in a Monte-Carlo-based UP analysis. They concluded that for the case of two uncertain parameters (permeability and freshwater inflow), the mean and standard deviation practically stabilize after 1,000 numerical simulations and at about 10,000 simulations the width of the confidence interval reached the lowest value. For the UP analysis here, even a Monte-Carlo (MC) simulation of 1,000 realizations based on the VDST model, for our four uncertain parameters, would require 62.5 days on a personal computer without any code parallelization.

We compare three different approaches for the UP analysis. The first approach is to employ the single fidelity KRG surrogate model based on a limited set of n_H sample points from the VDST model runs. The constrain on the available training sample size is based on the empirical rule for an offline training of a KRG model to be at least equal to n_H = 10 × p (Jones et al., 1998). In addition, this limitation emulates a situation closer to real-world conditions where the salars HF model might be extremely time-consuming and thus, a limited computational budget is affordable. The second approach is to employ the multifidelity methods where the HF points are combined with the LF data sample. The third and last approach is to directly resort to the LF sharp interface models and run an UP analysis. The comparison of the above frameworks serves the purpose of investigating differences from the UP analysis based on the surrogate model predictions and those provided by inaccurate but physics-based models for the salars system.

It is noted that uncertainty in model outputs is attributed only to the input parameters and any uncertainties due to the VDST model structure are neglected for the present work. Due to the exploratory nature of this work, we conduct a MC-based UP analysis assuming uniform distributions for all input parameters. A simple random sampling approach is utilized to generate a total of 20,000 values from the hypothetical uniform probability density functions (PDFs) of the uncertain model inputs. The corresponding MC outputs for the QoI are qualitatively analyzed based on non-parametric representations of their pdfs. This is performed by using the “ksdensity” algorithm (MATLAB R2021b) assuming a normal kernel type to estimate the shape of the pdfs from the MC runs.

Results

Comparisons Between LF and HF Model Outputs

Figure 4 shows a comparison between the LF and the HF calculated interfaces in the form of “envelope” plots (mean±stdev). These results are from the total available high fidelity training points X_H of size n_H = 40. The LF models cannot adequately capture the corresponding variability of the VDST model by showing a much lower sensitivity to the various inputs and thus a much narrower “envelope.” In other words, the LF models overestimate the brine plume development as compared to the VDST model. The mean sharp interface location is situated in smaller depths from the top of the model domain (1,200 m) which in turn implies that a smaller freshwater volume is estimated using the LF models. The LF2 model (cyan envelope) appears to share a small region of variability with the VDST model. Interestingly, for the conceptual salars model tested in this work, the response of the VDST model varies significantly, even for this small sample, which indicates a meaningful propagation of uncertainty to the QoI. What really matters though in constructing a multifidelity surrogate model is the correlation between LF and HF outputs (Fernández-Godino et al., 2019a). For the LF and the HF models, the correlation on the QoI is over 0.9 which is a promising condition for developing corrections and therefore multifidelity surrogate models.

FIGURE 4

Figure 4. Uncertainty “envelopes” of the simulated interface contours using the VDST model (gray color) the sharp interface model LF1 (orange color) and the sharp interface model LF2 (cyan color).

Validation and Comparison of the Surrogate Models

A separate validation set of size n_val = 10 was generated using a LHS design to calculate performance metrics on the prediction skills of the surrogate models. That is, the normalized root mean square error (NRMSE), mean absolute error (MAE) and correlation coefficient (R). NRMSE is normalized over the range of the HF validation output values for the QoI. As discussed in Fernández-Godino et al. (2019a), as more HF points are added to the training sample the use of multifidelity methods might progressively be either equally accurate or even less accurate than the single fidelity approach. To investigate this in the present study, we calculate performance metrics for all multifidelity approaches as well as for the corresponding single fidelity surrogate for different training sample sizes.

Four different sizes for the available HF training points are defined, that is 10, 20, 30, and 40. For the first four cases, different training points of corresponding size are randomly selected out of the total 40, to train the surrogates many times and evaluate the performance metrics based on how well they predict the validation points. This procedure allowed us to calculate the sample mean of the performance metrics based on each available training sample size and explore how sensitive is the surrogate model accuracy on the random selection of HF points. For the case where we use all 40 training points, the surrogates were fitted only once to the data as this is the maximum available number of HF points for training. The additive and multiplicative correction methods for the multifidelity surrogates utilize equal amount of data from the LF and the HF model. However, for the coKRG models two scenarios were tested, one where n_L = 100 and the other where n_L = 200. Since the co-Kriging concept is based on fusing a larger number of LF data with a much smaller set of HF data, by using a different size for the LF points we examine the impact of this selection on the multifidelity model accuracy. Figures 5–7 present the summary of this comparison based on the mean values of the performance metrics.

FIGURE 5

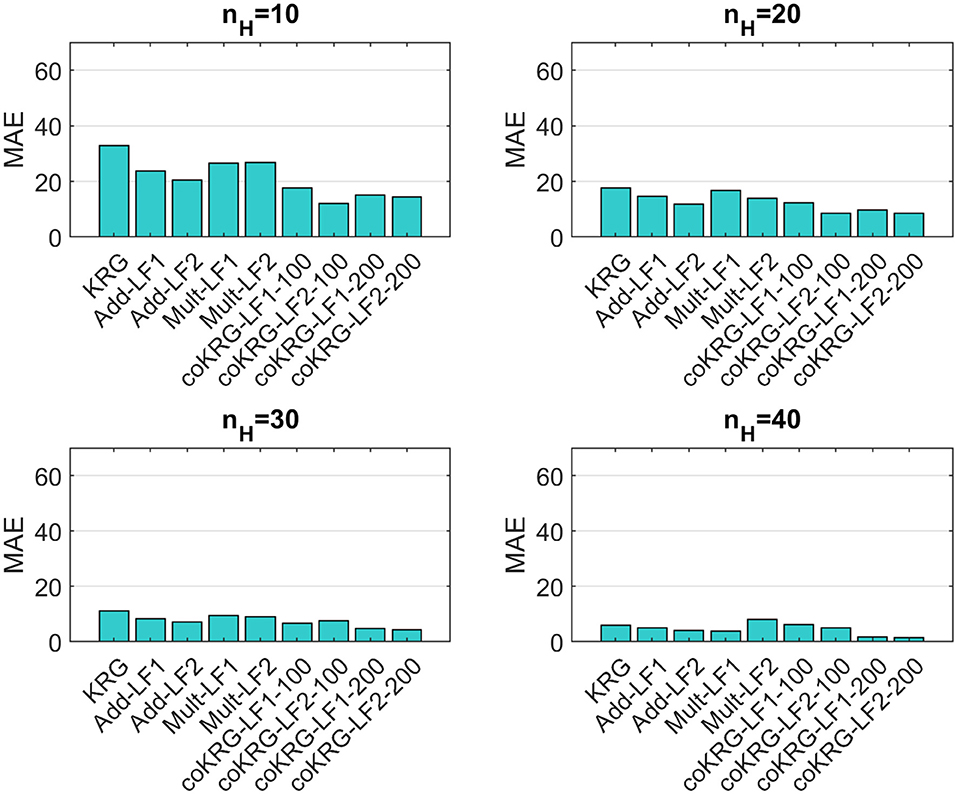
Figure 5. Comparisons of all methods on the average value of the MAE performance metric for various training sample sizes.

FIGURE 6

Figure 6. Comparisons of all methods on the average value of the NRMSE performance metric for various training sample sizes.

FIGURE 7

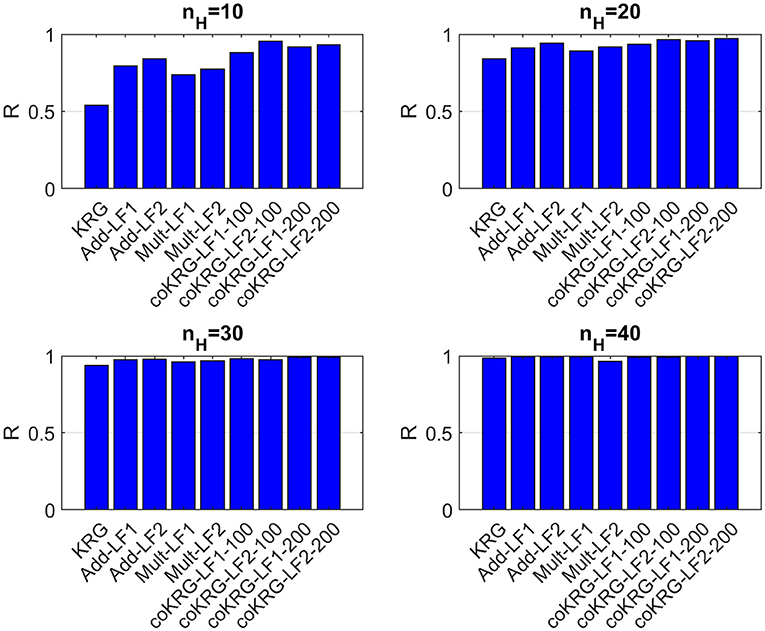
Figure 7. Comparisons of all methods on the average value of the R performance metric for various training sample sizes.

Various findings can be highlighted based on the above comparisons. First, the majority of multifidelity methods appear to outperform the single-fidelity approach for all training sizes although KRG compares well with the rest, when 30 and 40 HF points are used. This is a strong indication that, at least for the problem examined here, multifidelity methods can provide a good alternative for the case where the salars model are computationally expensive. The comparison among the multifidelity methods also shows interesting results. For example, regarding the simple correction approaches, the additive correction provided better scores than the multiplicative correction and compares well with coKRG models. While there is some variation regarding the type of the LF model being used to setup a multifidelity method (LF1 or LF2), most of the times by applying the Pool and Carrera (2011) correction better scores are obtained. This variation could be also attributed to the random generation of training samples for each run. However, it requires further examination to understand the implications for other VDST model settings. The coKRG models performed better than all other methods and in overall adding more LF points was beneficial for the accuracy of the coKRG model.

In terms of computational time, the KRG model was the faster approach to implement compared to the multifidelity methods since the latter include running the LF models as well. Even for coKRG models, which are the most expensive among the surrogates, the added computational time to train and predict the QoI is negligible compared to the VDST model run for the present study. This means that if we use the total 40 HF points the benefits from the multifidelity approach outweigh the minimal addition of computational time from running LF simulations, as compared to the single fidelity KRG model. However, training the surrogate models using a total of 40 VDST simulations represents the real computational cost which is equal to 2.5 days.

Surrogate-Based UP Analysis

As discussed in section Uncertainty Propagation Analysis, a MC-based UP analysis is performed assuming uniform distributions for the two recharge inputs, the hydraulic conductivity, and the maximum density. The computational cost of running a set of 20,000 simulations was trivial for the surrogate models requiring seconds. If an analyst has chosen to rely solely on the LF models, then 33 min were approximately required to run 20,000 model simulations.

The results from the UP analysis are presented on Figure 8 where KRG, LF1, LF2, and coKRG based on LF1 and LF2 models are compared in terms of the estimated PDFs for the QoI. As it is not computationally feasible to run the MC simulation on the 20,000 realizations of model inputs using the VDST model, for visual inspection we also provide the PDF estimation based on the limited VDST model runs obtained for this work (training plus validation data). In qualitative terms, the estimated PDFs based on the surrogates show a reasonable approximation of the estimated PDF obtained from the VDST model. The latter shows a slightly longer right tail which is not captured by the surrogates, and this might be attributed to the limited training sample. The coKRG models provided similar PDFs with slight mode differences (not visually distinct) and they are characterized by longer left tails toward larger depths from the top of the model domain than KRG and the LF models. This finding intuitively appears closer to the variability expected from the VDST model, with KRG also showing a similar trend, but requires further studies relying on larger VDST datasets to confirm if this statistical behavior is possible or it is artificially generated by the surrogates. On the contrary, the PDFs from the LF models show a smaller variance with values concentrated on depths closer to the top of the model domain (1,200 m). LF2 which applies the Pool and Carrera (2011) correction is shifted slightly toward lower depths but in overall the behavior is analogous to the LF1 model. The results demonstrate that the brine interface is most likely (median position) to be 150 m below the surface, but the distribution is skewed toward greater depths. Given the lack of confidence over the thickness of the salar deposits this shows the importance of taking steps to reduce uncertainty of the input parameters.

FIGURE 8

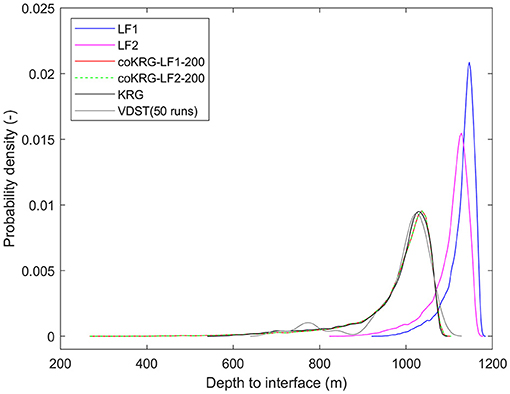
Figure 8. Estimated PDFs of the QoI (average depth to freshwater-brine interface) based on the surrogate models, the LF models and the HF model.

Discussion

The UP analysis based on the surrogate models developed in this work, shows that model input uncertainties originating from recharge, hydraulic conductivity and density contrasts might strongly affect the estimation of the interface between freshwater and brine in salars systems. As the general shape of the estimated PDFs for the QoI exhibit a left-skewed pattern, the risk of weak characterization of the interface in salars systems modeling appears strong in the absence of adequate hydrogeological/data for a real-world model. Given that we examined a large range of possible values for the hydraulic conductivity as well as for density and recharge, the MC simulation results imply that the various salar systems might have notable differences in terms of freshwater-brine interface dynamics. Whilst this work has shown its utility for the specific uncertainty analysis based on surrogate models, there are several other issues that could be used to address. For example, direct observations from boreholes do not go the full depth of the brine-bearing deposit. So aside from the usual problems of characterizing heterogeneity in complex geological environments there is considerable uncertainty over the depth of the deposit. Further the spatio-temporal variation of evaporation is not well-characterized in the present model. These features of the system are examples of what could be explored using the multifidelity approach. Given that these systems are increasingly exploited for their lithium-rich brines by pumping, then the method could be extended to include brine abstraction schemes. The LF model described here can include sinks which could be used to examine the impact of abstraction on the movement of the brine interface.

From a modeling perspective, real-world models of salars are characterized by extremely high computational burden and as a result 3D flow and brine transport simulations for large-scale salars are considered formidable. The application of multifidelity surrogate modeling appears promising in such cases where few numerical simulations are considered affordable, at least given the specifications of the problem examined in this study. The calculated performance metrics against validation data from the VDST model, showed that under a limited computational budget, multifidelity methods can potentially have a better performance than a single fidelity approach. However, our comparisons were limited here between KRG and coKRG models and further studies should investigate other surrogate models to generalize this finding. Particularly the coKRG models had a good prediction performance although simpler multifidelity methods such as the additive correction appear promising. The present computational gains obviously concern specific model settings and other LF models should be considered/developed for transient flow conditions or different mechanisms to approximate in salars systems. Despite that a more complex LF model will increase the overall computational time in a multifidelity approach, the anticipated gains should be still there for cases of extremely time-consuming HF models. It is noted also that the problem examined here involves some convenient features such as non-heterogeneous layered geological conceptualization while only parametric uncertainty was considered, neglecting model structural uncertainty.

Our approach was developed based on the concept of personal desktop analysis although it is possible for a water resources analyst to confront computationally intensive tasks through code parallelization or other promising computational methods (e.g., Esfahani and Datta, 2018; Xia and Shoemaker, 2021). Nevertheless, state-of-the-art computational resources might not be readily available to everyone while according to Razavi et al. (2012a) preprocessing effort on developing surrogate models should be added to the overall analyst time compared to direct use of the physics-based model, at least for certain cases. Given that each modeling application has unique features to be considered, demonstrating the potential of multifidelity approaches on a single desktop setting first, can then surely motivate further implementations using high-performance-computing technologies for such complex physical systems as is the case of salars.

Conclusions

Salars and other complex density-driven flow systems require the use of computationally demanding numerical models to simulate flow and solute transport. Thus, repetitive simulation tasks such as MC-based uncertainty analysis cannot be easily implemented due to the resulting computational burden which might be even up to several months using a personal computer with no code parallelization. Salars numerical modeling is an example where only a few high-fidelity model runs might be considered affordable to run and therefore, surrogate models of a single fidelity might struggle to alleviate the computational effort and acquire the desired prediction accuracy. To that end, efficient multifidelity modeling approaches for uncertainty analysis were developed here for a salars flow model.

A comprehensive Monte-Carlo simulation, including thousands of deterministic surrogate model runs was enabled by using only a few high fidelity VDST numerical simulations combined with runs from simplistic lower fidelity sharp interface models. Various simple multifidelity correction models as well as the method of co-Kriging were presented and compared. The general comparisons with the VDST model showed a good promise for multifidelity methods for exploring various aspects of uncertainties/sensitivities for numerical models of salars. The proposed multifidelity approaches are expected to be flexible for modification and inclusion of different model fidelities and conceptualizations of salars systems, as well as for other density-driven flow problems. Therefore, it is suggested that more studies should follow to develop multifidelity surrogate models or other promising surrogate modeling techniques to address the computational challenges associated with large-scale numerical models of salars that have just recently started to appear in the literature. Due to the increasing interest on salars systems, mainly for energy resources, efficient computational tools are considered a significant step to analyze flow and brine dynamics both for environmental and industry application purposes.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AH and VC: conceptualization and manuscript writing. VC: model development and model simulations. All authors contributed to the article and approved the submitted manuscript.

Funding

The work was supported by Innovate UK project no. 134012.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors publish with the permission of the Executive Director, British Geological Survey (UKRI).

References

Ackerer, P., and Younes, A. (2008). Efficient approximations for the simulation of density driven flow in porous media. Adv. Water Resour. 31, 15–27. doi: 10.1016/j.advwatres.2007.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Asher, M. J., Croke, B. F. W., Jakeman, A. J., and Peeters, L. J. M. (2015). A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 51, 5957–5973. doi: 10.1002/2015WR016967

CrossRef Full Text | Google Scholar

Ataie-Ashtiani, B., Hamed, K., and Mahdi, R. M. (2014). Optimal management of a freshwater lens in a small island using surrogate models and evolutionary algorithms. J. Hydrol. Eng. 19, 339–354. doi: 10.1061/(ASCE)HE.1943-5584.0000809

CrossRef Full Text | Google Scholar

Babaei, M., and Pan, I. (2016). Performance comparison of several response surface surrogate models and ensemble methods for water injection optimization under uncertainty. Comput. Geosci. 91, 19–32. doi: 10.1016/j.cageo.2016.02.022

CrossRef Full Text | Google Scholar

Bakker, M. (2006). Analytic solutions for interface flow in combined confined and semi-confined, coastal aquifers. Adv. Water Resour. 29, 417–425. doi: 10.1016/j.advwatres.2005.05.009

CrossRef Full Text | Google Scholar

Bauer-Gottwein, P., Langer, T., Prommer, H., Wolski, P., and Kinzelbach, W. (2007). Okavango Delta Islands: interaction between density-driven flow and geochemical reactions under evapo-concentration. J. Hydrol. 335, 389–405. doi: 10.1016/j.jhydrol.2006.12.010

CrossRef Full Text | Google Scholar

Boutt, D. F., Corenthal, L. G., Moran, B. J., Munk, L., and Hynek, S. A. (2021). Imbalance in the modern hydrologic budget of topographic catchments along the western slope of the Andes (21–25°S): implications for groundwater recharge assessment. Hydrogeol. J. 29, 985–1007. doi: 10.1007/s10040-021-02309-z

CrossRef Full Text | Google Scholar

Boutt, D. F., Hynek, S. A., Munk, L. A., and Corenthal, L. G. (2016). Rapid recharge of fresh water to the halite-hosted brine aquifer of Salar de Atacama, Chile. Hydrol. Process. 30, 4720–4740. doi: 10.1002/hyp.10994

CrossRef Full Text | Google Scholar

Cabello, J. (2021). Lithium brine production, reserves, resources and exploration in Chile: an updated review. Ore Geol. Rev. 128, 103883. doi: 10.1016/j.oregeorev.2020.103883

CrossRef Full Text | Google Scholar

Christelis, V. (2021). Surrogate-based optimization methods for coastal aquifer management (PhD Thesis). Available online at: https://dspace.lib.ntua.gr/xmlui/handle/123456789/53074

Google Scholar

Christelis, V., Kopsiaftis, G., and Mantoglou, A. (2019). Performance comparison of multiple and single surrogate models for pumping optimization of coastal aquifers. Hydrol. Sci. J. 64, 336–349. doi: 10.1080/02626667.2019.1584400

CrossRef Full Text | Google Scholar

Christelis, V., and Mantoglou, A. (2016). Coastal aquifer management based on the joint use of density-dependent and sharp interface models. Water Resour. Manag. 30, 861–876. doi: 10.1007/s11269-015-1195-4

CrossRef Full Text | Google Scholar

Christelis, V., and Mantoglou, A. (2019). Pumping optimization of coastal aquifers using seawater intrusion models of variable-fidelity and evolutionary algorithms. Water Resour. Manag. 33, 555–568. doi: 10.1007/s11269-018-2116-0

CrossRef Full Text | Google Scholar

Christelis, V., Regis, R. G., and Mantoglou, A. (2018). Surrogate-based pumping optimization of coastal aquifers under limited computational budgets. J. Hydroinformatics 20, 164–176. doi: 10.2166/hydro.2017.063

CrossRef Full Text | Google Scholar

Couckuyt, I., Dhaene, T., and Demeester, P. (2014). ooDACE toolbox: a flexible object-oriented Kriging implementation. J. Mach. Learn. Res. 15, 3183–3186. Available online at: https://jmlr.csail.mit.edu/papers/volume15/couckuyt14a/couckuyt14a.pdf

Google Scholar

Dey, S., and Prakash, O. (2020). Managing saltwater intrusion using conjugate sharp interface and density dependent models linked with pumping optimization. Groundw. Sustain. Dev. 11, 100446. doi: 10.1016/j.gsd.2020.100446

CrossRef Full Text | Google Scholar

Diersch, H.-J. G., and Kolditz, O. (2002). Variable-density flow and transport in porous media: approaches and challenges. Adv. Water Resour. 25, 899–944. doi: 10.1016/S0309-1708(02)00063-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Duffy, C. J., and Al-Hassan, S. (1988). Groundwater circulation in a closed desert basin: Topographic scaling and climatic forcing. Water Resour. Res. 24, 1675–1688. doi: 10.1029/WR024i010p01675

CrossRef Full Text | Google Scholar

Esfahani, H. K., and Datta, B. (2018). Fractal singularity–based multiobjective monitoring networks for reactive species contaminant source characterization. J. Water Resour. Plan. Manag. 144, 04018021. doi: 10.1061/(ASCE)WR.1943-5452.0000880

CrossRef Full Text | Google Scholar

Fan, Y., Duffy, C. J., and Oliver, D. S. (1997). Density-driven groundwater flow in closed desert basins: field investigations and numerical experiments. J. Hydrol. 196, 139–184. doi: 10.1016/S0022-1694(96)03292-1

CrossRef Full Text | Google Scholar

Fan, Y., Lu, W., Miao, T., Li, J., and Lin, J. (2020). Multiobjective optimization of the groundwater exploitation layout in coastal areas based on multiple surrogate models. Environ. Sci. Pollut. Res. 27, 19561–19576. doi: 10.1007/s11356-020-08367-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernández-Godino, M. G., Park, C., Kim, N.-H., and Haftka, R. T. (2019b). Review of multifidelity models. AIAA J. 57, 2039–2054.

PubMed Abstract | Google Scholar

Fernández-Godino, M. G., Park, C., Kim, N. H., and Haftka, R. T. (2019a). Issues in deciding whether to use multifidelity surrogates. AIAA J. 57, 2039–2054. doi: 10.2514/1.J057750

CrossRef Full Text | Google Scholar

Forrester, A., Sobester, A., and Keane, A. (2008). Engineering Design via Surrogate Modelling: A Practical Guide. New York, NY: John Wiley & Sons.

Google Scholar

Forrester, A. I. J., and Keane, A. J. (2009). Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 45, 50–79. doi: 10.1016/j.paerosci.2008.11.001

CrossRef Full Text | Google Scholar

Forrester, A. I. J., Sóbester, A., and Keane, A. J. (2007). Multifidelity optimization via surrogate modelling. Proc. R. Soc. Math. Phys. Eng. Sci. 463, 3251–3269. doi: 10.1098/rspa.2007.1900

CrossRef Full Text | Google Scholar

Hamann, E., Post, V., Kohfahl, C., Prommer, H., and Simmons, C. T. (2015). Numerical investigation of coupled density-driven flow and hydrogeochemical processes below playas. Water Resour. Res. 51, 9338–9352. doi: 10.1002/2015WR017833

CrossRef Full Text | Google Scholar

Hirthe, E. M., and Graf, T. (2012). Non-iterative adaptive time-stepping scheme with temporal truncation error control for simulating variable-density flow. Adv. Water Resour. 49, 46–55. doi: 10.1016/j.advwatres.2012.07.021

CrossRef Full Text | Google Scholar

Holzbecher, E. (2005). Groundwater flow pattern in the vicinity of a salt lake. Hydrobiologia 532, 233–242. doi: 10.1007/s10750-004-6421-7

CrossRef Full Text | Google Scholar

Houston, J. (2006). Evaporation in the Atacama Desert: an empirical study of spatio-temporal variations and their causes. J. Hydrol. 330, 402–412. doi: 10.1016/j.jhydrol.2006.03.036

CrossRef Full Text | Google Scholar

Jones, D. R., Schonlau, M., and Welch, W. J. (1998). Efficient global optimization of expensive black-box functions. J. Glob. Optim. 13, 455–492. doi: 10.1023/A:1008306431147

CrossRef Full Text | Google Scholar

Kennedy, M. C., and O'Hagan, A. (2000). Predicting the output from a complex computer code when fast approximations are available. Biometrika 87, 1–13. doi: 10.1093/biomet/87.1.1

CrossRef Full Text | Google Scholar

Kerrou, J., and Renard, P. (2010). A numerical analysis of dimensionality and heterogeneity effects on advective dispersive seawater intrusion processes. Hydrogeol. J. 18, 55–72. doi: 10.1007/s10040-009-0533-0

CrossRef Full Text | Google Scholar

Konz, M., Younes, A., Ackerer, P., Fahs, M., Huggenberger, P., and Zechner, E. (2009). Variable-density flow in heterogeneous porous media — laboratory experiments and numerical simulations. J. Contam. Hydrol. 108, 168–175. doi: 10.1016/j.jconhyd.2009.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Koohbor, B., Fahs, M., Ataie-Ashtiani, B., Belfort, B., Simmons, C. T., and Younes, A. (2019). Uncertainty analysis for seawater intrusion in fractured coastal aquifers: effects of fracture location, aperture, density and hydrodynamic parameters. J. Hydrol. 571, 159–177. doi: 10.1016/j.jhydrol.2019.01.052

CrossRef Full Text | Google Scholar

Kopsiaftis, G., Protopapadakis, E., Voulodimos, A., Doulamis, N., and Mantoglou, A. (2019). Gaussian process regression tuned by bayesian optimization for seawater intrusion prediction. Comput. Intell. Neurosci. 2019, 1–12. doi: 10.1155/2019/2859429

PubMed Abstract | CrossRef Full Text | Google Scholar

Koussis, A. D., Mazi, K., and Destouni, G. (2012). Analytical single-potential, sharp-interface solutions for regional seawater intrusion in sloping unconfined coastal aquifers, with pumping and recharge. J. Hydrol. 416–417, 1–11. doi: 10.1016/j.jhydrol.2011.11.012

CrossRef Full Text | Google Scholar

Koussis, A. D., Mazi, K., Riou, F., and Destouni, G. (2015). A correction for Dupuit–Forchheimer interface flow models of seawater intrusion in unconfined coastal aquifers. J. Hydrol. 525, 277–285. doi: 10.1016/j.jhydrol.2015.03.047

CrossRef Full Text | Google Scholar

Lal, A., and Datta, B. (2018). Development and implementation of support vector machine regression surrogate models for predicting groundwater pumping-induced saltwater intrusion into coastal aquifers. Water Resour. Manag. 32, 2405–2419. doi: 10.1007/s11269-018-1936-2

CrossRef Full Text | Google Scholar

Langevin, C. D., and Guo, W. (2006). MODFLOW/MT3DMS-based simulation of variable density ground water flow and transport. Ground Water 44, 339–351. doi: 10.1111/j.1745-6584.2005.00156.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Li, L., Zhao, S., and Song, S. (2021). A global surrogate model technique based on principal component analysis and Kriging for uncertainty propagation of dynamic systems. Reliab. Eng. Syst. Saf. 207, 107365. doi: 10.1016/j.ress.2020.107365

CrossRef Full Text | Google Scholar

Lu, C., Werner, A. D., Simmons, C. T., and Luo, J. (2015). A correction on coastal heads for groundwater flow models. Groundwater 53, 164–170. doi: 10.1111/gwat.12172

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, J., Ji, Y., and Lu, W. (2019). Comparison of Surrogate Models Based on Different Sampling Methods for Groundwater Remediation. J. Water Resour. Plan. Manag. 145, 04019015. doi: 10.1061/(ASCE)WR.1943-5452.0001062

CrossRef Full Text | Google Scholar

Mahmoodian, M., Carbajal, J. P., Bellos, V., Leopold, U., Schutz, G., and Clemens, F. (2018). A hybrid surrogate modelling strategy for simplification of detailed urban drainage simulators. Water Resour. Manag. 32, 5241–5256. doi: 10.1007/s11269-018-2157-4

CrossRef Full Text | Google Scholar

Man, J., Zheng, Q., Wu, L., and Zeng, L. (2020). Adaptive multifidelity probabilistic collocation-based Kalman filter for subsurface flow data assimilation: numerical modeling and real-world experiment. Stoch. Environ. Res. Risk Assess. 34, 1135–1146. doi: 10.1007/s00477-020-01815-y

CrossRef Full Text | Google Scholar

Marazuela, M. A., Ayora, C., Vázquez-Suñé, E., Olivella, S., and García-Gil, A. (2020). Hydrogeological constraints for the genesis of the extreme lithium enrichment in the Salar de Atacama (NE Chile): A thermohaline flow modelling approach. Sci. Total Environ. 739, 139959. doi: 10.1016/j.scitotenv.2020.139959

PubMed Abstract | CrossRef Full Text | Google Scholar

Marazuela, M. A., Vázquez-Suñé, E., Ayora, C., García-Gil, A., and Palma, T. (2019a). Hydrodynamics of salt flat basins: the Salar de Atacama example. Sci. Total Environ. 651, 668–683. doi: 10.1016/j.scitotenv.2018.09.190

PubMed Abstract | CrossRef Full Text | Google Scholar

Marazuela, M. A., Vázquez-Suñé, E., Ayora, C., García-Gil, A., and Palma, T. (2019b). The effect of brine pumping on the natural hydrodynamics of the Salar de Atacama: the damping capacity of salt flats. Sci. Total Environ. 654, 1118–1131. doi: 10.1016/j.scitotenv.2018.11.196

PubMed Abstract | CrossRef Full Text | Google Scholar

Marazuela, M. A., Vázquez-Suñé, E., Custodio, E., Palma, T., García-Gil, A., and Ayora, C. (2018). 3D mapping, hydrodynamics and modelling of the freshwater-brine mixing zone in salt flats similar to the Salar de Atacama (Chile). J. Hydrol. 561, 223–235. doi: 10.1016/j.jhydrol.2018.04.010

CrossRef Full Text | Google Scholar

Matheron, G. (1973). The intrinsic random functions and their applications. Adv. Appl. Probab. 5, 439–468. doi: 10.2307/1425829

CrossRef Full Text | Google Scholar

Mazi, K., and Koussis, A. D. (2021). Beyond pseudo-coupling: computing seawater intrusion in coastal aquifers with decoupled flow and transport equations. J. Hydrol. 593, 125794. doi: 10.1016/j.jhydrol.2020.125794

CrossRef Full Text | Google Scholar

McKnight, S. V., Boutt, D. F., and Munk, L. A. (2021). Impact of hydrostratigraphic continuity on brine-to-freshwater interface dynamics: implications from a two-dimensional parametric study in an arid and endorheic basin. Water Resour. Res. 57. doi: 10.1029/2020WR028302

CrossRef Full Text | Google Scholar

Menberg, K., Bidarmaghz, A., Gregory, A., Choudhary, R., and Girolami, M. (2020). Multifidelity approach to Bayesian parameter estimation in subsurface heat and fluid transport models. Sci. Total Environ. 745, 140846. doi: 10.1016/j.scitotenv.2020.140846

PubMed Abstract | CrossRef Full Text | Google Scholar

Mo, S., Shi, X., Lu, D., Ye, M., and Wu, J. (2019). An adaptive Kriging surrogate method for efficient uncertainty quantification with an application to geological carbon sequestration modeling. Comput. Geosci. 125, 69–77. doi: 10.1016/j.cageo.2019.01.012

CrossRef Full Text | Google Scholar

Moreno-Rodenas, A. M., Bellos, V., Langeveld, J. G., and Clemens, F. H. L. R. (2018). A dynamic emulator for physically based flow simulators under varying rainfall and parametric conditions. Water Res. 142, 512–527. doi: 10.1016/j.watres.2018.06.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Pool, M., and Carrera, J. (2011). A correction factor to account for mixing in Ghyben-Herzberg and critical pumping rate approximations of seawater intrusion in coastal aquifers: correction factor to control seawater. Water Resour. Res. 47. doi: 10.1029/2010WR010256

CrossRef Full Text | Google Scholar

Rajabi, M. M. (2019). Review and comparison of two meta-model-based uncertainty propagation analysis methods in groundwater applications: polynomial chaos expansion and Gaussian process emulation. Stoch. Environ. Res. Risk Assess. 33, 607–631. doi: 10.1007/s00477-018-1637-7

CrossRef Full Text | Google Scholar

Rajabi, M. M., Ataie-Ashtiani, B., and Simmons, C. T. (2015). Polynomial chaos expansions for uncertainty propagation and moment independent sensitivity analysis of seawater intrusion simulations. J. Hydrol. 520, 101–122. doi: 10.1016/j.jhydrol.2014.11.020

CrossRef Full Text | Google Scholar

Ranjbar, A., and Mahjouri, N. (2018). Development of an efficient surrogate model based on aquifer dimensions to prevent seawater intrusion in anisotropic coastal aquifers, case study: the Qom aquifer in Iran. Environ. Earth Sci. 77, 418. doi: 10.1007/s12665-018-7592-2

CrossRef Full Text | Google Scholar

Razavi, S., Tolson, B. A., and Burn, D. H. (2012a). Numerical assessment of metamodelling strategies in computationally intensive optimization. Environ. Model. Softw. 34, 67–86. doi: 10.1016/j.envsoft.2011.09.010

CrossRef Full Text | Google Scholar

Razavi, S., Tolson, B. A., and Burn, D. H. (2012b), Review of surrogate modeling in water resources. Water Resour. Res. 48, W07401. 10.1029/2011WR011527

Google Scholar

Risacher, F., and Fritz, B. (2009). Origin of salts and brine evolution of bolivian and chilean salars. Aquat. Geochem. 15, 123–157. doi: 10.1007/s10498-008-9056-x

CrossRef Full Text | Google Scholar

Rogers, D. B., and Dreiss, S. J. (1995a). Saline groundwater in Mono Basin, California: 1. Distribution. Water Resour. Res. 31, 3131–3150. doi: 10.1029/95WR02108

CrossRef Full Text | Google Scholar

Rogers, D. B., and Dreiss, S. J. (1995b). Saline groundwater in Mono Basin, California: 2. Long-term control of lake salinity by groundwater. Water Resour. Res. 31, 3151–3169. doi: 10.1029/95WR02109

CrossRef Full Text | Google Scholar

Rosen, M. R. (1994). The importance of groundwater in playas: A review of playa classifications and the sedimentology and hydrology of playas. Spec. Pap. Geol. Soc. Am. (1994) 289, 1– 18.

Google Scholar

Roy, D. K., and Datta, B. (2017). Fuzzy C-mean clustering based inference system for saltwater intrusion processes prediction in coastal aquifers. Water Resour. Manag. 31, 355–376. doi: 10.1007/s11269-016-1531-3

CrossRef Full Text | Google Scholar

Rozos, E., Mazi, K., and Koussis, A. D. (2021). Efficient stochastic simulation of seawater intrusion, with mixing, in confined coastal aquifers. Front. Water 3, 98. doi: 10.3389/frwa.2021.720557

CrossRef Full Text | Google Scholar

Simmons, C. T. (2005). Variable density groundwater flow: From current challenges to future possibilities. Hydrogeol J. 13, 116–119. doi: 10.1007/s10040-004-0408-3

CrossRef Full Text | Google Scholar

Song, J., Yang, Y., Wu, J., Wu, J., Sun, X., and Lin, J. (2018). Adaptive surrogate model based multiobjective optimization for coastal aquifer management. J. Hydrol. 561, 98–111. doi: 10.1016/j.jhydrol.2018.03.063

CrossRef Full Text | Google Scholar

Sreekanth, J., and Datta, B. (2010). Multi-objective management of saltwater intrusion in coastal aquifers using genetic programming and modular neural network based surrogate models. J. Hydrol. 393, 245–256. doi: 10.1016/j.jhydrol.2010.08.023

CrossRef Full Text | Google Scholar

Sreekanth, J., and Datta, B. (2011). Comparative evaluation of genetic programming and neural network as potential surrogate models for coastal aquifer management. Water Resour. Manag. 25, 3201–3218. doi: 10.1007/s11269-011-9852-8

CrossRef Full Text | Google Scholar

Strack, O. D. L. (1976). A single-potential solution for regional interface problems in coastal aquifers. Water Resour. Res. 12, 1165–1174. doi: 10.1029/WR012i006p01165

CrossRef Full Text | Google Scholar

Uribe, J., Muñoz, J. F., Gironás, J., Oyarzún, R., Aguirre, E., and Aravena, R. (2015). Assessing groundwater recharge in an Andean closed basin using isotopic characterization and a rainfall-runoff model: Salar del Huasco basin, Chile. Hydrogeol. J. 23, 1535–1551. doi: 10.1007/s10040-015-1300-z

CrossRef Full Text | Google Scholar

Wooding, R. A., Tyler, S. W., and White, I. (1997). Convection in groundwater below an evaporating Salt Lake: 1. Onset of instability. Water Resour. Res. 33, 1199–1217. doi: 10.1029/96WR03533

CrossRef Full Text | Google Scholar

Wu, W., Ren, J., Zhou, X., Wang, J., and Guo, M. (2020). Identification of source information for sudden water pollution incidents in rivers and lakes based on variable-fidelity surrogate-DREAM optimization. Environ. Model. Softw. 133, 104811. doi: 10.1016/j.envsoft.2020.104811

CrossRef Full Text | Google Scholar

Xia, W., and Shoemaker, C. (2021). GOPS: efficient RBF surrogate global optimization algorithm with high dimensions and many parallel processors including application to multimodal water quality PDE model calibration. Optim. Eng. 22, 2741–2777. doi: 10.1007/s11081-020-09556-1

CrossRef Full Text | Google Scholar

Yang, Y., Song, J., Simmons, C. T., Ataie-Ashtiani, B., Wu, J., Wang, J., et al. (2021). A conjunctive management framework for the optimal design of pumping and injection strategies to mitigate seawater intrusion. J. Environ. Manage. 282, 111964. doi: 10.1016/j.jenvman.2021.111964

PubMed Abstract | CrossRef Full Text | Google Scholar

Younes, A., Ackerer, P.h., and Mose, R. (1999). Modeling variable density flow and solute transport in porous medium: 2. Re-evaluation of the salt dome flow problem. Transp. Porous Media 35, 375–394. doi: 10.1023/A:1006504326005

CrossRef Full Text | Google Scholar

Younes, A., Fahs, M., and Ahmed, S. (2009). Solving density driven flow problems with efficient spatial discretizations and higher-order time integration methods. Adv. Water Resour. 32, 340–352. doi: 10.1016/j.advwatres.2008.11.003

CrossRef Full Text | Google Scholar

Zaefferer, M., Gaida, D., and Bartz-Beielstein, T. (2016). Multi-fidelity modeling and optimization of biogas plants. Appl. Soft Comput. 48, 13–28. doi: 10.1016/j.asoc.2016.05.047

CrossRef Full Text | Google Scholar

Zhang, J., Man, J., Lin, G., Wu, L., and Zeng, L. (2018). Inverse Modeling of Hydrologic Systems with Adaptive Multifidelity Markov Chain Monte Carlo Simulations. Water Resour. Res. 54, 4867–4886. doi: 10.1029/2018WR022658

CrossRef Full Text | Google Scholar

Zhao, Y., Lu, W., and Xiao, C. (2016). A Kriging surrogate model coupled in simulation–optimization approach for identifying release history of groundwater sources. J. Contam. Hydrol. 185–186, 51–60. doi: 10.1016/j.jconhyd.2016.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Q., Zhang, J., Xu, W., Wu, L., and Zeng, L. (2019). Adaptive multifidelity data assimilation for nonlinear subsurface flow problems. Water Resour. Res. 55, 203–217. doi: 10.1029/2018WR023615

CrossRef Full Text | Google Scholar

Zhou, Q., Shao, X., Jiang, P., Gao, Z., Zhou, H., and Shu, L. (2016). An active learning variable-fidelity metamodelling approach based on ensemble of metamodels and objective-oriented sequential sampling. J. Eng. Des. 27, 205–231. doi: 10.1080/09544828.2015.1135236

CrossRef Full Text | Google Scholar

Zhou, Q., Shao, X., Jiang, P., Zhou, H., and Shu, L. (2015). An adaptive global variable fidelity metamodeling strategy using a support vector regression based scaling function. Simul. Model. Pract. Theory 59, 18–35. doi: 10.1016/j.simpat.2015.08.002

CrossRef Full Text | Google Scholar