Raphael Payet-Burin1,2*
Mikkel Kromman2
Silvio J. Pereira-Cardenal2Kenneth M. Strzepek3
Peter Bauer-Gottwein1- 1Department of Environmental Engineering, Technical University of Denmark, Lyngby, Denmark
- 2Global Advisory - Policy, Planning and Infrastructure Development, COWI A/S, Lyngby, Denmark
- 3Joint Program on the Science and Policy of Global Change, MIT, Cambridge, MA, United States
Perfect foresight hydroeconomic optimization models are tools to evaluate impacts of water infrastructure investments and policies considering complex system interlinkages. However, when assuming perfect foresight, optimal management decisions are found assuming perfect knowledge of climate and runoff, which might bias the economic evaluation of investments and policies. We investigate the impacts of assuming perfect foresight by using Model Predictive Control (MPC) as an alternative. We apply MPC in WHAT-IF, a hydroeconomic optimization model, for two study cases: a synthetic setup inspired by the Nile River, and a large-scale investment problem on the Zambezi River Basin considering the water–energy–food nexus. We validate the MPC framework against Stochastic Dynamic Programming and observe more realistic modeled reservoir operation compared to perfect foresight, especially regarding anticipation of spills and droughts. We find that the impact of perfect foresight on total system benefits remains small (<2%). However, when evaluating investments and policies using with-without analysis, perfect foresight is found to overestimate or underestimate values of investments by more than 20% in some scenarios. As the importance of different effects varies between scenarios, it is difficult to find general, case-independent guidelines predicting whether perfect foresight is a reasonable assumption. However, we find that the uncertainty linked to climate change in our study cases has more significant impacts than the assumption of perfect foresight. Hence, we recommend MPC to perform the economic evaluation of investments and policies, however, under high uncertainty of future climate, increased computational costs of MPC must be traded off against computational costs of exhaustive scenario exploration.
Introduction
Developing hydropower and irrigation while preserving ecosystems will contribute to the Sustainable Development Goals (UN General Assembly, 2015), but might also increase competition for the scarce water resource. Therefore, decision-makers need tools that consider the interdependencies within the water–energy–food nexus (Bhave et al., 2016; Miralles-Wilhelm, 2016; Albrecht et al., 2018; Baldassarre et al., 2019; Rising, 2020). Hydroeconomic optimization models, which associate an economic impact to each management decision and thus transform a complex multi-objective management problem into a simpler single-objective problem (Harou et al., 2009; Bauer-Gottwein et al., 2017) are attractive candidates. In this category, models representing numerous nexus interactions and multiple reservoirs (Draper et al., 2003; Block and Strzepek, 2010; Kahil et al., 2018; Khan et al., 2018; Payet-Burin et al., 2019; Vinca et al., 2020) often assume perfect foresight. Perfect foresight is a common approach used in sectorial planning models (Keppo and Strubegger, 2010; Expósito et al., 2020), where the system is optimized over the whole planning period with assumed perfect knowledge of the future. This means that optimization models with perfect foresight anticipate future conditions, such as droughts, and adjust, for instance, by selecting crops with lower water requirements or storing additional water. In actual operation, water planners and managers do not have perfect foresight, and are limited by the availability and skill of existing forecasting systems. A more realistic way of modeling reservoir operation and agriculture decisions could improve the reliability of the results of investment evaluation and cost benefit analysis (Anghileri et al., 2016; Jahani et al., 2016; Sahu, 2016; Khadem et al., 2018).
Stochastic Dynamic Programming (SDP) (Soleimani et al., 2016; Scarcelli et al., 2017) and Stochastic Dual Dynamic Programming (SDDP) (Tilmant et al., 2012; Pereira-Cardenal et al., 2016) have been used to represent water management problems and infrastructure evaluation in a nexus context while considering the stochastic nature of the water inflow. However, SDP suffers the curse of dimensionality as problem complexity increases exponentially with problem size, hence it is restricted to applications with a limited number of reservoirs and interactions; while SDDP can be applied to larger systems, it is still limited to convex future benefits.
Simulation frameworks (Yates et al., 2005; Howells et al., 2013; Cervigni et al., 2015), do not assume perfect foresight, as the system management is determined for each time step using allocation rules. However, allocation rules are usually based on current or past socio-economic conditions and might not be economically optimal in another context (Pereira-Cardenal et al., 2016). This might lead to biased performances when exploring a range of possible scenarios, which is a key process when exploring robust decisions considering the large uncertainties of the future climate and socio-economic development (Herman et al., 2015, 2020; Bhave et al., 2016; Giuliani and Castelletti, 2016). In order to remediate this, the rules can be optimized by wrapping the simulation framework with an (multi-objective) optimization algorithm (e.g., Hadka and Reed, 2013; Kasprzyk et al., 2013; Maier et al., 2014; Bertoni et al., 2019; Gonzalez et al., 2020; Tomlinson et al., 2020). This does not only enable the evaluation of planning alternatives, but also gives insights on how specific infrastructure can be operated. The downside is that it can lead to computational barriers when analyzing a large range of scenarios for complex systems: Quinn et al. (2017) use a total of 1.7 million CPU hours with such a framework applied on the Red River basin. Therefore, it remains challenging to apply simulation-based optimization to large-scale problems considering multiple interactions between the water, agriculture, and energy sector.
Model Predictive Control (MPC) is an alternative that replicates potential operation, by iteratively solving the optimal management decisions using the available knowledge of the future at each time step (e.g., forecasts). Model Predictive Control was originally developed for power plants and refineries in 1970 and is now used in a large variety of fields from food processing to aerospace applications (Qin and Badgwell, 2003). MPC has many advantages: (1) it makes use of an existing optimization framework, (2) it does not suffer the curse of dimensionality, as computation costs do not increase exponentially with problem size (3) it can be applied to non-linear frameworks, (4) it is not limited to hydrologic uncertainty. The MPC framework has been applied in water resource studies: Khadem et al. (2018) apply a specific form of MPC, by solving the CALVIN perfect foresight model (Draper et al., 2003) year by year, still assuming perfect foresight of a year; Anghileri et al. (2016) apply MPC to a simple water resource system model to evaluate the value of forecasts; Ficchı̀ et al. (2016) use MPC to optimize the simultaneous operation of reservoirs, Beh et al. (2015) apply the MPC framework over a 10-year rolling planning horizon to select flexible water supply infrastructure with a simulation-based multi-objective optimization algorithm considering future uncertainties, and Martinsen et al. (2021) use MPC to evaluate the impact of assuming perfect foresight when evaluating the value of a water transfer project for irrigated agriculture. However, these studies all adopt a water-centered approach and have little or no consideration for the agriculture and energy sectors. The novelty of this study is to apply the MPC framework to an integrated model considering the water, energy, and agriculture sectors.
The purpose of this work is to investigate the impacts of assuming perfect foresight when evaluating the economic value of infrastructure and policies within the water–energy–food nexus. We use the open-source hydroeconomic optimization model WHAT-IF (Payet-Burin et al., 2019), which links representations of the water, energy, and agriculture systems in a holistic framework.
The study is organized as follow:
In Methods section we present the WHAT-IF model and the Model Predictive Control Framework. Overview of Two Study Cases section describes the study cases: a synthetic setup inspired by the Nile River and a large scale problem in the Zambezi River Basin from Payet-Burin et al. (2019), where water infrastructure and policies are planned to satisfy growing food and energy demands. In Discussion and Conclusion section we investigate the impacts of assuming perfect foresight when performing economic evaluation of investments through with-without analysis. In the Nile case, we validate the MPC framework against Stochastic Dynamic Programming and highlight some of effects of the perfect foresight assumption. We also compare it to a rule-based simulation framework. Using a large range of scenarios, we investigate in which cases the perfect foresight assumption affects the economic evaluation of two hypothetical projects. Finally, we perform the same analysis for the economic evaluation of hydropower expansion, irrigation development, and an environmental flow policy on the Zambezi River Basin.
Methods
The Hydroeconomic Optimization Model: What-If
WHAT-IF is a hydroeconomic optimization model, linking representations of the water, energy, and agriculture systems in a holistic framework (Payet-Burin et al., 2019). The model is open-source, and the latest code can be accessed at https://github.com/RaphaelPB/WHAT-IF. In WHAT-IF decision variables for water management (e.g., water storage and supply), energy management (e.g., power capacity construction, production, transmission, and supply) and agriculture management (e.g., crop choice, irrigation, transport, and supply) are solved to maximize the welfare economic objective function which is the sum of all consumer and producer surpluses (Figure 1). The model operates at a monthly time step for long hydrologic time series. It is a perfect foresight framework as optimal decisions are found with full knowledge of the future over the planning horizon.
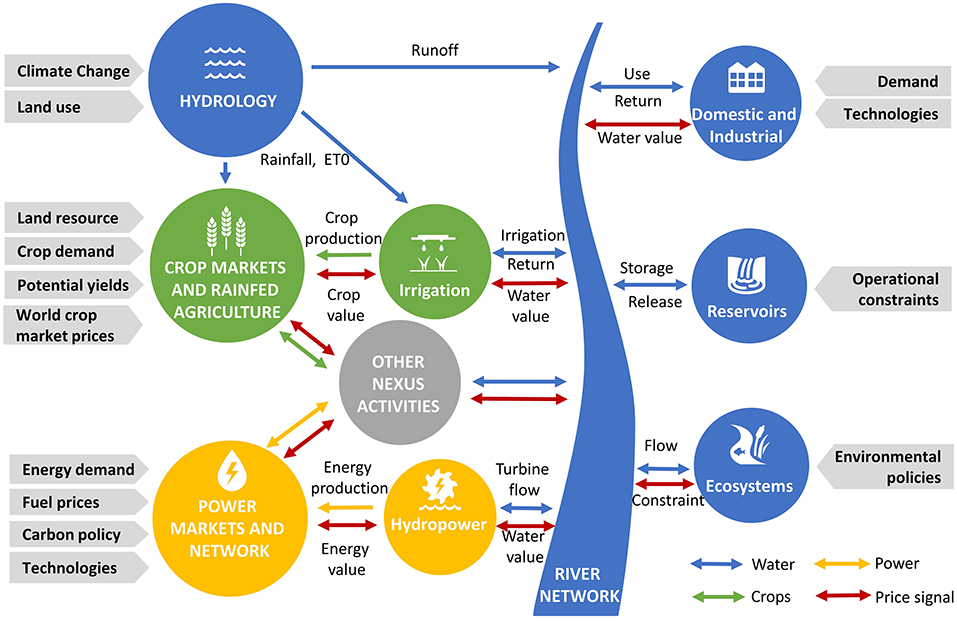
Figure 1. Representation of the main interrelations in the water–energy–food nexus in WHAT-IF. All flows are solved holistically by maximizing total consumer and producer surplus for the water, power, and crop commodities. This figure is reproduced from Payet-Burin et al. (2021).
The objective function of the model considers consumer and producer surplus for all commodities (φ0) and is formulated as:
where WSB represents the water supply benefits, WSC the water supply costs, CSB the crop supply benefits, CSC the crop supply costs, CPC the crop production costs, ESB the energy supply benefit, ETC the energy transmission costs, and EPC the energy production costs which are the sum of the energy operational costs, fuel consumption and CO2 emission costs.
In addition to the description of WHAT-IF in Payet-Burin et al. (2019), in the current version of the model, hydropower production is the product of releases and a volume-dependent head, which leads to a non-linear optimization model and more realistic reservoir release decisions.
The model is coded in the python programming language; the problem is formulated with Pyomo (Hart et al., 2017) and solved with the non-linear solver IPOPT (Wächter and Biegler, 2005) using the HSL mathematical software library (Research Councils UK, 2020).
Model Predictive Control Framework
The basic concept of Model Predictive Control (MPC) is to iteratively optimize decision variables (also called “control actions”) of a system over a forward moving time window at a given sampling interval. The MPC framework suits real-time water management, repetitively answering the question “given the current system state and the currently available information about the future what is the best decision now?” For example, every month, for the Colorado Reservoir System, the Bureau of Reclamation updates the “24-Month study” (Bureau of Reclamation, 2019) describing the expected behavior of the system for the next two years, based on which the operation rules for the current month are set. In this study, the MPC framework is implemented to simulate a more realistic operation of the water infrastructure than the one resulting from perfect foresight optimization runs, and thus, evaluate more accurately the potential economic impacts of nexus infrastructure investments and policies.
Figure 2 summarizes the framework: In every time step, a forecast of the hydrologic parameters is generated for the prediction horizon. The forecast might be an ensemble forecast, or a single forecast as in Figure 2. The prediction horizon is the time window for which the system is optimized (e.g., 2 years). The choice of the prediction horizon depends on the quality of the forecast, the time scales and memory effects inherent in the problem and the available computational resources. Over the prediction horizon all the decision variables are solved (e.g., water storage, and supply) using the perfect foresight model with the forecast information, but only the decision variables for the current time step are implemented. The process is repeated over the planning horizon (e.g., 30 years), at each time step the prediction horizon is moved forward, a new forecast is generated considering the new information available, and the optimal decision variables for the current time step are implemented. If the model contains a mix of monthly and yearly decision variables, the prediction horizon is adjusted to cover a complete year. Yearly decision variables of the model (e.g., crop choice and power capacity investments) are only determined for time steps that start a new year.
Figure 2. Model Predictive Control (MPC) framework. The methodology is illustrated with runoff as forecasted parameter with a single forecast, and reservoir storage as a decision variable; in the model all forecasted parameters and decision variables are solved simultaneously.
Regarding reservoir operation, the decisions taken in a given month might impact reservoir levels several years later. Because for large models it would be computationally too expensive to consider a very long prediction horizon (e.g., several decades), a storage target or hedging rule (You and Cai, 2008) at the end of the prediction horizon is implemented in order to account for the value of water in the reservoir beyond the prediction horizon. Khadem et al. (2018) suggest a complex but general method to evaluate the storage value; the MPC framework presented here is not as sensitive to the assumed end storage value, because only the first decisions are implemented, hence we choose a simple method based on the shadow value (or dual value) of water from a perfect foresight run.
To find the optimal decision variables from the forecast, different methods can be used. For a single forecast Fs the optimization model M is run once DVs = M(Fs) and resulting optimal decision variables for the current time step t0 are implemented . For an ensemble forecast of n members {Fk, k ϵ 1..n}, a simple approach is to run the model separately for each ensemble member {DVk = M(Fk), k ϵ 1..n} and assume that the optimal decision variables are the average of the ensemble of optimal decision variables . A third probabilistic method is to merge the individual problems from the different ensemble members into a single optimization problem DVe = M(Fk, k ϵ 1..n), in which the decision variables for the first time step are shared and the objective function obje is an average of the individual objective functions weighted by their respective likelihood K: obje = ∑objk·Kk, k ϵ 1..n.
Here we assume that only the hydrology is uncertain and that other parameters, such as energy demand and renewable energy production can be predicted. If intermittent renewable power sources play an important role, the same approach can be implemented with wind and sun forecasts in addition to hydrologic forecasts.
The parametrization of the MPC framework can be found in the Supplementary Materials where we evaluate: (1) the bootstrapping forecast performance and the impact of forecast quality, (2) the method to derive optimal decision variables based on the type of forecasts, and (3) the impact of the length of the prediction horizon. We use nearest neighbors bootstrapping (Lall and Sharma, 1996) to generate an ensemble forecast for the hydrologic parameters with 20 members. This ensemble forecast is converted to a 2-members forecast (high and low flow), for which the optimization model is solved over a 2-year prediction horizon, in a single probabilistic optimization problem merging the low and high-flow problems using equality constraints between decision variables in the current time step.
Overview of Two Study Cases
The Nile synthetic study case is used to demonstrate the MPC framework and evaluate the effects for a large range of scenarios. The Zambezi River Basin study case is used to demonstrate the applicability of the MPC framework to large-scale water–energy–food nexus models.
Nile Synthetic Study Case
To illustrate the methodology, we use a synthetic study case inspired by the High Aswan Dam (HAD) in Egypt (Figure 3). The dam receives inflow from Sudan and has an active capacity of 90 BCM (Billion Cubic Meters). We represent Egypt as a single water demand node of 53 BCM/year, with a seasonal profile and a demand curve. The demand curve is inspired from El-Gafy and El-Ganzori (2012), the average economic value of irrigation water is around 2 L.E/m3 (0.130$/m3), and there is about a factor 10 between high value crops such as vegetables and low value crops such as rice. The hydropower plant linked to the dam has a capacity of 2100 MW, producing around 10 000 GWh per year. The head in the reservoir varies from 36 to 64 m and the hydropower turbine capacity from 1,200 to 2,500 m3/s; for simplicity, we assume a linear head-volume dependence. Hydropower production is valued using a fixed output price of 50$/MWh. We use a monthly runoff time series at Dongola from 1970 to 2000. To simplify, the water share of Sudan (18.5 BCM/year) and the average evaporation from the dam (10 BCM/year) is subtracted from the inflow, leaving an average water availability of 58 BCM/year.
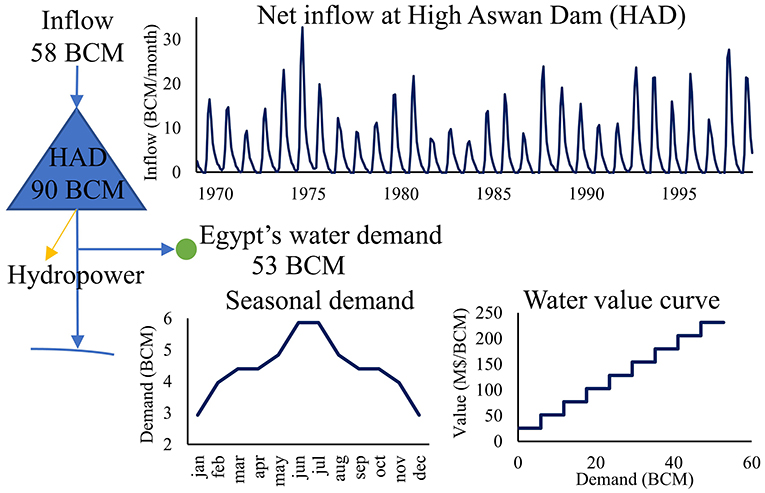
Figure 3. Conceptual scheme of the Nile synthetic study case. Water units are in Billion Cubic Meters (BCM).
The operation rule used in the simulation (SIM) framework is from Mobasher (2010), and works as follows: If the reservoir level in July is above 60 BCM, the water releases for the rest of the year are proportional to the July reservoir level (from 1,800 m3/s for 60 BCM to 2,850 m3/s for 90 BCM) or higher to fully satisfy the agricultural demand. If the reservoir level in July is lower than 60 BCM, the agriculture demand is curtailed by: 5% from 55 to 60 BCM, 10% from 50 to 55 BCM and 15% under 50 BCM. The releases are then proportional to the agricultural demand and no extra water for hydropower is released.
As a benchmark, we also implemented the stochastic dynamic programming (SDP) framework for this study case [see Loucks and Van Beek (2005) for a didactic presentation of the SDP method]. The main limitation of SDP is that it cannot be applied to larger systems, however, for this simple study case SDP is straightforward and can be used to validate the MPC method. We divide the inflow in three classes for each month: low, average, and high inflow, which correspond respectively to the 0 to 30th, 31 to 60th, and 61 to 100th percentiles of the inflows. We consider the 15th, 45th and 80th inflow percentiles to be representative inflows for the 3 classes. We find that the definition of classes has little impact on results. We then obtain storage water values in the High Aswan Dam for the different classes of inflow (see Supplementary Material) and use those to determine optimal release decisions.
Zambezi River Basin Study Case
We use the modeling framework and dataset of the Zambezi River Basin from Payet-Burin et al. (2019). The river basin is divided into 26 catchments with runoff and precipitation time series covering 40 years; the average yearly runoff is 114 109 m3. In each catchment, domestic, agricultural, and industrial water demands are represented, as well as environmental flow constraints at the level of the main wetlands (Kafue flats, Barotse plain, and Mana pools) and the Zambezi delta (Figure 4). The main reservoirs of the river basin (Itezhi-Tezhi, Kariba, and Cahora Bassa dams) have an active storage capacity of 127 109 m3 and are the main consumptive water user of the river basin through evaporation losses. The agricultural water demand is calculated based on FAO 56, crop yields are based on FAO 33, and the crop choice is part of the optimization framework. Unlike in Payet-Burin et al. (2019), rainfed production and crop markets are not represented, only irrigated agriculture is represented and valued at the farm level using FAO data (FAO, 2018). Thermal power is represented as aggregated production units per country. A power market per country is represented, including South Africa, with corresponding power demands. The power transmission network is represented with a transport model considering aggregated transmission lines between countries. A capacity expansion model represents additional investments in thermal and solar power.
Figure 4. Zambezi River Basin water–energy–food nexus framework.
We use the reference “2030” scenario from Payet-Burin et al. (2019), considering the forecasted water, crop and energy demands in the river basin in 2030 and the natural flooding environmental policy of 7,000 m3/s in February. The evaluated water infrastructure development plan (World Bank, 2010; Payet-Burin et al., 2019) considers 15 hydropower projects with 7.2 GW of new operating capacity and 336 000 ha of new areas equipped for irrigation, almost doubling the current irrigated area. To evaluate the MPC framework in different water scarcity levels, we consider three different climate change scenarios from Cervigni et al. (2015) as in Payet-Burin et al. (2019).
Results—Impact of Perfect Foresight on the Economic Evaluation of Investments and Policies
Nile Study Case
In this section we compare the Perfect Foresight (PF), Model Predictive Control (MPC), Stochastic Dynamic Programing (SDP), and Simulation (SIM) frameworks on the Nile synthetic case for a range of scenarios. The objective function of the PF, MPC, and SDP frameworks is to maximize total economic benefits from water demand satisfaction and hydropower production. The SIM framework follows the operation rule presented previously (Nile Synthetic Study Case section).
We observe that the global economic output in the four frameworks is very similar (Table 1); the main difference is that the PF framework leads to higher hydropower production and lower demand curtailments. The operation rule of the SIM framework might not be optimal for this synthetic case because it was designed for the real conditions, but we observe that it performs closely to the other frameworks in terms of total system benefits.
Table 1. Key indicators for the different frameworks on the Nile study case.
Regarding reservoir management, we observe two effects of perfect foresight: (1) high flows are anticipated by releasing additional water before, thus avoiding spills (release higher than turbine capacity), (2) low flows are anticipated by storing additional water before, achieving a better head management and leading to less water demand curtailment (Figure 5). Both effects together explain the higher hydropower production observed for the PF framework. We also observe that MPC and SDP lead to almost identical reservoir operations. MPC and SDP frameworks can be implemented in actual operation. Hence, we can assume that they represent a potential reality and that differences observed for PF and SIM are biases linked to the assumptions inherent in these frameworks.
Figure 5. Modeled reservoir management of the High Aswan Dam (HAD) for the different frameworks. MPC, PF, SIM, and SDP indicate Model Predictive Control, Perfect Foresight, Simulation, and Stochastic Dynamic Programming, respectively.
To investigate how these effects vary depending on the context, we compare results between the frameworks for different scenarios by varying runoff and water demand. Change in runoff and water demand is implemented by multiplying all values by a constant factor. Change in water demand is implemented as a scaling factor on the baseline demand curve. We see that the effects highlighted in Figure 5 vary in importance depending on the scenario (Figure 6).
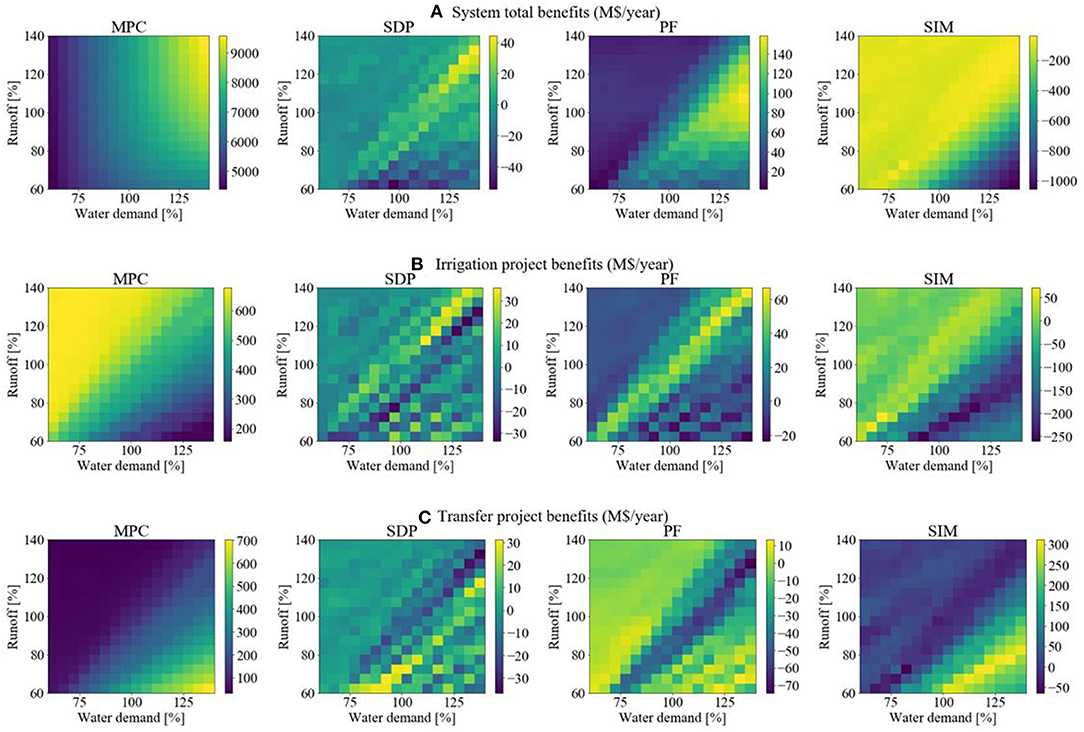
Figure 6. Economic evaluation of baseline (A) and project development (B, C) with the different frameworks. For Model Predictive Control (MPC) the absolute value is shown, for Stochastic Dynamic Programming (SDP), Perfect Foresight (PF), and Simulation (SIM) the incremental value compared to MPC is shown. Irrigation and Transfer benefits are calculated through with-without analysis.
The analysis of scenarios of total system benefits (Figure 6A) confirms that MPC and SDP behave similarly, even if trends of differences are visible, they are considerably smaller compared to other frameworks. That said, all frameworks are close in terms of total system benefits: PF overestimates benefits by +0.2% to +1.7%, while SIM underestimates benefits by −1 to −12%. The results by indicators are available in the Supplementary Material. The SIM framework assumes the same reservoir operation rule applies in all scenarios; as expected, it underperforms in scenarios different from the reference scenario, particularly when increasing water scarcity. However, for total system benefits, the uncertainty linked to the framework is small compared to other sources of uncertainties inherent in this type of analysis (e.g., data, temporal and spatial aggregation, other model assumptions).
In a second step, we investigate how the choice of framework affects the economic valuation of projects in a with-without analysis. We consider two (hypothetical) projects: (1) an irrigation extension project, corresponding to an increase in the water demand by 10% (implemented as a global scaling factor on current demand curves); and (2) a water transfer project adding 10% of water upstream of the dam, represented by a constant additional inflow of 0.45 109 m3 per month. We evaluate the economic impact of these projects (computed as total benefits with the projects minus total benefits without the project) for the different scenarios of runoff and initial water demand (Figures 6B,C). The impact of the irrigation project (Figure 6B) corresponds to two horizontal moves right in Figure 6A, and the impact of the water transfer project (Figure 6C) is similar to two vertical moves up.
We observe that:
(1) SDP and MPC behave similarly as for total system benefits, even if trends of differences are visible, they are smaller compared to other frameworks (Figures 6B,C).
(2) PF overestimates irrigation project benefits by 5–12% in the diagonal where water demand is close to water availability (Figure 6B). The reason is that the increase in water demand due to the irrigation project moves the system from a state where foresight has low value toward a state where foresight has high value (Figure 6A). PF underestimates transfer project benefits by −20 to −35% in the diagonal where water demand is slightly above water availability (Figure 6C). The value of additional water is underestimated with perfect foresight, because it moves the system from a state where foresight has high value toward a state where foresight has low value (Figure 6A). Outside the diagonal, PF is close to both MPC and SDP. With water abundance or stress, the value of foresight is respectively either low or stable, hence it does not affect the with-without analysis significantly.
(3) SIM underestimates irrigation project benefits by −40 to −80% (Figure 6B) in water-scarce scenarios (high demand and low availability). In water-abundant scenarios (high availability and low demand), SIM performs similarly to other frameworks, as the release rules are not stressed by water shortages. SIM overestimates transfer project benefits by +30 to +60% in water-scarce scenarios (Figure 6C), because the transfer project eases the water stress that SIM does not cope well with.
In contrast to global system benefits, the differences found in the with-without analysis can impact decision-making on project development. When performing the with-without analysis, the impact of assuming perfect foresight is more important in scenarios where the value of foresight varies between the with and the without run. This does not necessarily correspond to scenarios for which the impact of perfect foresight on total benefits is strongest. However, the value of investments varies significantly depending on the water demand and available runoff (with a factor 3–7), hence uncertainty in these parameters is likely to have more impact than the bias introduced by perfect foresight. In general, it is clearly inappropriate to use a non-adaptative simulation rule to explore scenarios with a different system state: as observed here, even small changes (e.g., +10% demand combined to −10% runoff) can lead to considerably different results (respectively −34% and +23% for the irrigation and water transfer project benefits).
Zambezi River Basin Study Case
We now apply the Model Predictive Control (MPC) framework to a large-scale nexus problem on the Zambezi River Basin considering multiple interactions between the water, energy and food systems. We evaluate the economic impact of different projects and policies from World Bank (2010) by performing with-without analyses for three different climate change scenarios from Cervigni et al. (2015). We compare the Perfect Foresight (PF) to the MPC framework in order to evaluate the bias introduced by the perfect foresight assumption (Table 2). The individual results of the largest hydropower and irrigation projects are highlighted, while “all projects” also include other investments.
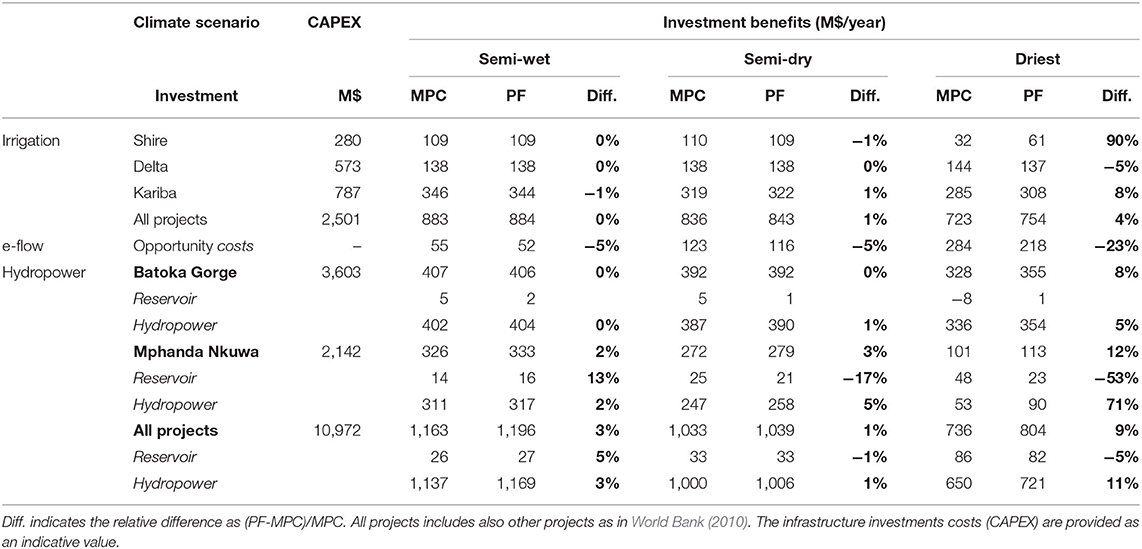
Table 2. Impact of the perfect foresight assumption on the economic evaluation of infrastructure development and policies.
The climate change scenarios from Cervigni et al. (2015), correspond to different water-scarcity levels; in the semi-wet, semi-dry and driest scenarios the water consumption represents respectively 17, 23, and 34% of the available runoff. We observe that for the semi-wet and semi-dry scenarios the differences between the PF and MPC frameworks are mostly under 5% (Table 2), which is small compared to other possible sources of uncertainty (e.g., climate, socio-economic development). However, for the driest scenario important differences appear for some investments (Figure 7).
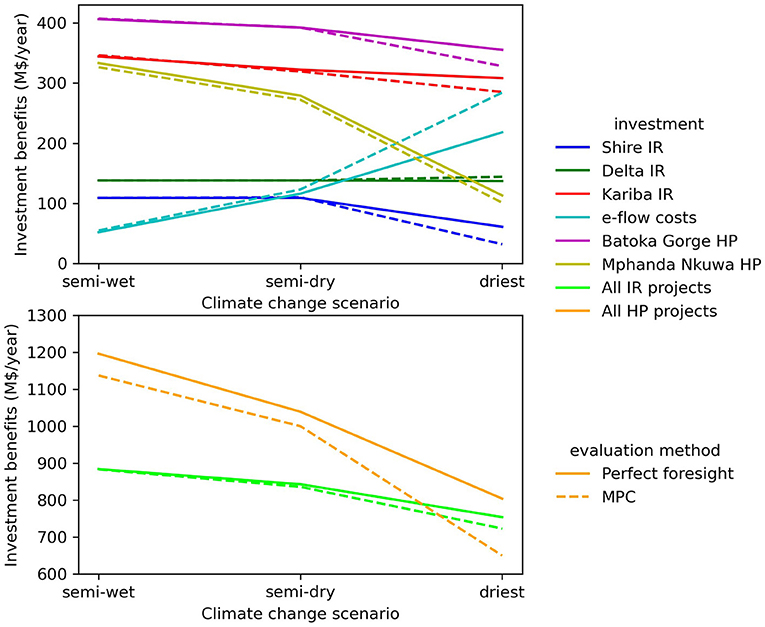
Figure 7. Impact of the perfect foresight assumption on the economic evaluation of infrastructure development and policies. “All projects” includes also other projects as in World Bank (2010). IR, irrigation; HP, hydropower, and e-flow costs represent opportunity costs of environmental flows, excluding direct and indirect benefits from enhanced ecosystems.
The aggregated economic value of all irrigation investments is only overestimated by 4% with perfect foresight (Table 2), but up to 90% for the Shire Irrigation investment, while the value is almost the same for the Delta irrigation investment. In Payet-Burin et al. (2019) the Shire River is found to be the most water-scarce zone with high inflow variability and low storage capacity, which explains why, with perfect foresight, the project is more profitable as water scarcity can be anticipated. The Delta irrigation project is in the Zambezi Delta, where there is the most flexibility due to all upstream reservoirs and where the water has the lowest value as there are no downstream uses, which might explain the small difference between the MPC and PF frameworks. When implementing all irrigation projects (Table 3), perfect foresight leads to higher agricultural production (+45 M$/year), which is partially due to higher irrigation water allocation (+241 Mm3/year) as less water is spilled downstream (−127 Mm3/year).
Table 3. Key indicators for the with-without analysis of selected investments and policies.
Environmental flow (e-flow) opportunity costs, which are the direct forgone benefits by ensuring a minimum flow to ecosystems (excluding the direct and indirect benefits of protecting ecosystems), are underestimated by 23% with the perfect foresight assumption. The difference is explained by lower trade-offs with agricultural production (−61 M$/year), energy production (−11 M$/year), and domestic and industrial water users (−6 M$/year) (Table 3). With perfect foresight low flows can be anticipated, hence extra water can be stored to accommodate ecosystems and other water users, while in actual operation, when low flows are not anticipated, high value water users might be curtailed in order to satisfy the environmental constraint (as we assume environmental flows have the highest priority).
The economic values of all hydropower projects are overestimated by 9% on average with perfect foresight (Table 2), and the variation between individual investments is small (+8% for Batoka Gorge, +12% for Mphanda Nkuwa). However, we see two opposite effects compensating each other: the value of the additional reservoir capacity in Mphanda Nkuwa is considerably underestimated with perfect foresight (−25 M$/year, −53%), while the value of the hydropower turbines is considerably overestimated (+47 M$/year, +71%). Hence, we find that the value of reservoirs tends to be underestimated with perfect foresight, while the value of hydropower plants is overestimated. When implementing all hydropower projects (Table 3), perfect foresight leads to an underestimation of trade-offs with the industrial and domestic water users (−8 M$/year) and agricultural production (−31 M$/year). While the additional hydropower production is almost the same for both frameworks, perfect foresight avoids more energy production costs by alternative sources (−31 M$/year). Similar effects are found for the impact of the e-flow policy and the irrigation development (Table 3): with perfect foresight the projects/policies lead to more hydropower curtailment, but to a lower economic impact on the energy system (lower energy production costs). The reason is that with perfect foresight hydropower curtailments are timed to minimize the need of extra power capacity development, while in actual operation, this is not feasible.
These numbers can be compared to the uncertainty linked to climate change (Figure 7); from the driest to the semi-wet scenario, the value of all irrigation projects varies from 723 to 883 M$/year (+22%), the value of all hydropower projects from 736 to 1,163 M$/year (+58%), and the opportunity costs of the environmental policy from 284 to 55 M$/year (−80%). Furthermore, in Payet-Burin et al. (2019), other factors such as yield growth, international crop prices, carbon taxes, and cost of renewable technologies are found to be as important regarding the uncertainty of the future value of investments.
In conclusion, when evaluating the economic impact of investments in the Zambezi River Basin, we find that the perfect foresight assumption has negligible impacts for the semiwet and semidry climate scenarios. In the driest climate scenario, some investment values are over or under-estimated by more than 20%, but overall, the uncertainty linked to the climate is more important than the bias linked to the perfect foresight framework. However, the perfect foresight assumption could impact the decision-making process when testing the robustness of investments regarding climate uncertainty.
Discussion and Conclusion
In this paper, we show how the Model Predictive Control framework can overcome the assumption of perfect knowledge of the future in hydroeconomic optimization models. The method is attractive as it does not necessarily require additional data and can be applied to complex large-scale models. We validate the method by comparing it to Stochastic Dynamic Programming for a simple study case. We highlight impacts of assuming perfect foresight: high flows are anticipated in the model by earlier water releases avoiding spills; low flows are anticipated by storing additional water avoiding curtailments. For a more complex system such as the Zambezi River Basin, we show that perfect foresight also results in better timing of hydropower production leading to less power capacity construction. By using a wide range of scenarios, we show that the importance of these effects is highly dependent on the system state. We find that perfect foresight overestimates total system benefits by <2% for all scenarios (compared to Model Predictive Control), while a pure simulation framework shows differences up to 12% for the water-scarcest scenarios. The specific focus of the paper is to analyze the impact of assuming perfect foresight in cost-benefit analysis of investments and policies through with-without analysis. On the Nile synthetic case, for some scenarios, the perfect foresight assumption is found to have no impact. But for other scenarios, the value of an irrigation project is overestimated by 5–12% while the value of a transfer project is underestimated by 20–35%. We also show that using a non-adaptative simulation rule is clearly inappropriate when exploring scenarios with a different system state as economic impacts are over and underestimated by more than 30% for a large range of scenarios. Hence, while perfect foresight can introduce bias in the economic analysis, the assumption seems more reasonable than using a simulation framework with static rules.
The impact of assuming perfect foresight is confirmed when applying the methodology to a large-scale problem on the Zambezi River Basin involving interactions between the water, energy and agriculture systems. Perfect foresight does not affect the economic evaluation of potential investments in two out of three climate change scenarios. However, in the driest climate change scenario, the value of one irrigation project is overestimated by 90% while other projects show little bias, the opportunity costs of an environmental flow policy are underestimated by 23%, the value of reservoir capacity development is underestimated by 5–53%, and the value of hydropower turbines are overestimated by 5–71%. In general, we find the impact to be less important for larger investments.
Contrary to total system benefits, the differences found in the with-without analysis can impact decision-making on project development. While perfect foresight provides an upper bound to total economic benefits of a system, this does not hold for economic evaluation of investments through with-without analysis. In with-without analysis, the impact of the perfect foresight assumption depends on the current system state, and the state toward which project moves the system. Because different effects have impacts on the results, it is difficult to predict in which cases the perfect foresight assumption will lead to biased cost-benefit results as it might vary from case to case. We can, however, formulate these general insights:
In water scarce situations (where demand is large relative to supply and/or variability is high relative to storage), perfect foresight will tend to overestimate benefits of infrastructure, because close to perfect water management generates large extra values. In abundant situations, perfect management is less valuable so perfect foresight will be closer to reality. With regards to infrastructure, perfect foresight will tend to overestimate the benefits of water use infrastructure (e.g., irrigation and turbines), while benefits of flow regulation infrastructure (e.g., reservoirs) tend to be underestimated.
Hence when using perfect foresight models, we recommend the use of a framework like Model Predictive Control to perform the economic evaluation of investments and policies, or to control the validity of the perfect foresight assumption. As a result of this work, investment analysis with the MPC framework can now be performed with little extra effort and data compared to the perfect foresight framework in the open-source WHAT-IF model. However, we find that the uncertainty linked to exogenous parameters like climate change (or socio-economic development not explored in this paper) might have more impact than the bias introduced by perfect foresight. While the framework is not limited by the curse of dimensionality, it does increase computation costs. If those become a burden when evaluating a large range of scenarios for robust decision-making, a trade-off must be found between uncertainty introduced by the perfect foresight assumption and uncertainty introduced by exploring fewer scenarios.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: the WHAT-IF model with the MPC framework is available on Github (https://github.com/RaphaelPB/WHAT-IF); different branches exist for the Nile and Zambezi study case. The dataset on the Zambezi study case is available in the Github repository as well as in https://zenodo.org/record/2646476#.X0UgejVS-uU.
Author Contributions
PB-G, SP-C, MK, and KS contributed to conception and design of the study. RP-B performed the model simulations and wrote the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
Innovation Fund Denmark (Grant No. 7038-00015B), COWIFonden (Grant No. C-137.02), and COWI A/S funded the industrial Ph.D. project in which this research was carried out.
Conflict of Interest
SP-C, RP-B, and MK were employed by COWI A/S, and KS was employed by Industrial Economics, Incorporated (IEc). The mentioned employments did not interfere with the present article.
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors also thank Alyssa McCluskey and Charles Fant for providing the runoff time-series for the Nile and Zambezi study case, respectively.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2021.778003/full#supplementary-material
References
Albrecht, T. R., Crootof, A., and Scott, C. A. (2018). The water–energy–food nexus : a systematic review of methods for nexus assessment. Environ. Res. Lett. 13, 1–26. doi: 10.1088/1748-9326/aaa9c6
Anghileri, D., Voisin, N., Castelletti, A., Pianosi, F., Nijssen, B., and Lettenmaier, D. P. (2016). Value of long-term streamflow forecasts to reservoir operations for water supply in snow-dominated river catchments. Water Resour. Res. 52, 4209–4225. doi: 10.1002/2015WR017864
Baldassarre, G., Di, S. M., Rusca, M., Cudennec, C., Garcia, M., Kreibich, H., et al. (2019). Sociohydrology: scientific challenges in addressing the sustainable development goals. Water Resour. Res. 2019, 6327–6355. doi: 10.1029/2018WR023901
Bauer-Gottwein, P., Riegels, N., Pulido-Velazquez, M., Harou, J. J., Cai, X., Davidsen, C., et al. (2017). “Hydroeconomic analysis,” in Handbook of Applied Hydrology, ed. V. Singh (New York, NY: McGraw-Hill), 36/1–36/7.
Beh, E. H., Maier, H. R., and Dandy, G. C. (2015). Adaptive, multiobjective optimal sequencing approach for urban water supply augmentation under deep uncertainty. Water Resourc. Res. 51, 1529–1551. doi: 10.1002/2014WR016254
Bertoni, F., Castelletti, A., Giuliani, M., and Reed, P. M. (2019). Discovering dependencies, trade-offs, and robustness in joint dam design and operation: an ex-post assessment of the Kariba Dam. Earth's Futur. 7, 1367–1390. doi: 10.1029/2019EF001235
Bhave, A. G., Conway, D., Dessai, S., and Stainforth, D. A. (2016). Barriers and opportunities for robust decision making approaches to support climate change adaptation in the developing world. Clim. Risk Manag. 14, 1–10. doi: 10.1016/j.crm.2016.09.004
Block, P., and Strzepek, K. (2010). Economic analysis of large-scale upstream river basin development on the Blue Nile in ethiopia considering transient conditions, climate variability, and climate change. J. Water Resourc. Plann. Manag. 136, 156–166. doi: 10.1061/(ASCE)WR.1943-5452.0000022
Bureau of Reclamation (2019). 24-Month Study. Available online at: https://www.usbr.gov/uc/water/crsp/studies/ (accessed November11, 2019).
Cervigni, R., Liden, R., Neumann, J. E., and Strzepek, K. M. (2015). Enhancing the Climate Resilience of Africa's Infrastructure: The Power and Water Sectors. Available online at: https://openknowledge.worldbank.org/handle/10986/21875. (accessed November 29, 2021).
Draper, A. J., Jenkins, M. W., Kirby, K. W., Lund, J. R., and Howitt, R. E. (2003). Economic-Engineering Optimization for California Water Management. J. Water Resour. Plan. Manag. 129, 155–164. doi: 10.1061/(ASCE)0733-9496(2003)129:3(155)
El-Gafy, I., and El-Ganzori, A. (2012). Decision support system for economic value of irrigation water. Appl. Water Sci. 2, 63–76. doi: 10.1007/s13201-012-0029-2
Expósito, A., Beier, F., and Berbel, J. (2020). Hydro-economic modelling for water-policy assessment under climate change at a river basin scale: a review. Water 12:1559. doi: 10.3390/w12061559
FAO (2018). FAOSTAT. Available online at: http://www.fao.org/faostat/en/#data/QC (accessed July 27, 2018).
Ficchì, A., Raso, L., Dorchies, D., Pianosi, F., Malaterre, P.-O., Van Overloop, P.-J., et al. (2016). Erratum for “Optimal Operation of the Multireservoir System in the Seine River Basin Using Deterministic and Ensemble Forecasts” by A. Ficchì, L. Raso, D. Dorchies, F. Pianosi, P.-O. Malaterre, P.-J. Van Overloop, and M. Jay-Allemand. J. Water Resour. Plan. Manag. 142:08215001. doi: 10.1061/(asce)wr.1943-5452.0000609
Giuliani, M., and Castelletti, A. (2016). Is robustness really robust? How different definitions of robustness impact decision-making under climate change. Clim. Change 135, 409–424. doi: 10.1007/s10584-015-1586-9
Gonzalez, J. M., Tomlinson, J. E., Harou, J. J., Martínez Ceseña, E. A., Panteli, M., Bottacin-Busolin, A., et al. (2020). Spatial and sectoral benefit distribution in water-energy system design. Appl. Energy 269:114794. doi: 10.1016/j.apenergy.2020.114794
Hadka, D., and Reed, P. (2013). Borg: an auto-adaptive many-objective evolutionary computing framework. Evol. Comput. 21, 231–259. doi: 10.1162/EVCO_a_00075
Harou, J. J., Pulido-Velazquez, M., Rosenberg, D. E., Medellín-Azuara, J., Lund, J. R., and Howitt, R. E. (2009). Hydro-economic models: concepts, design, applications, and future prospects. J. Hydrol. 375, 627–643. doi: 10.1016/j.jhydrol.2009.06.037
Hart, W. E., Laird, C. D., Watson, J.-P., Woodruff, D. L., Hackebeil, G. A., Nicholson, B. L., et al. (2017). Pyomo—Optimization Modeling in Python. New York: Springer International Publishing .
Herman, J. D., Quinn, J. D., Steinschneider, S., Giuliani, M., and Fletcher, S. (2020). Climate Adaptation as a control problem: review and perspectives on dynamic water resources planning under uncertainty. Water Resour. Res. 56:e24389. doi: 10.1029/2019WR025502
Herman, J. D., Reed, P. M., Zeff, H. B., and Characklis, G. W. (2015). How should robustness be defined for water systems planning under change? J. Water Resour. Plan. Manag. 141:509. doi: 10.1061/(ASCE)WR.1943-5452.0000509
Howells, M., Hermann, S., Welsch, M., Bazilian, M., Segerström, R., Alfstad, T., et al. (2013). Integrated analysis of climate change, land-use, energy and water strategies. Nat. Clim. Chang. 3, 621–626. doi: 10.1038/nclimate1789
Jahani, E., Mousavi, S. J., Afsharian, N., and Hoon, J. (2016). Assessing the role of foresight on future streamflows in storage-yield-reliability analysis of surface water reservoirs. Proc. Eng. 154, 1163–1168. doi: 10.1016/j.proeng.2016.07.530
Kahil, T., Parkinson, S., Satoh, Y., Greve, P., Burek, P., Veldkamp, T. I. E., et al. (2018). A continental-scale hydro-economic model for integrating water-energy-land nexus solutions. Water Resour. Res. doi: 10.1029/2017WR022478
Kasprzyk, J. R., Nataraj, S., Reed, P. M., and Lempert, R. J. (2013). Many objective robust decision making for complex environmental systems undergoing change. Environ. Model. Softw. 42, 55–71. doi: 10.1016/j.envsoft.2012.12.007
Keppo, I., and Strubegger, M. (2010). Short term decisions for long term problems—the effect of foresight on model based energy systems analysis. Energy 35, 2033–2042. doi: 10.1016/j.energy.2010.01.019
Khadem, M., Rougé, C., Harou, J. J., Hansen, K. M., Medellin-Azuara, J., and Lund, J. (2018). Estimating the economic value of interannual reservoir storage in water resource systems. Water Resour. Res. 54, 8890–8908. doi: 10.1029/2017WR022336
Khan, Z., Linares, P., Rutten, M., Parkinson, S., Johnson, N., and García-González, J. (2018). Spatial and temporal synchronization of water and energy systems: towards a single integrated optimization model for long-term resource planning. Appl. Energy 210, 499–517. doi: 10.1016/j.apenergy.2017.05.003
Lall, U., and Sharma, A. (1996). A nearest neighbor bootstrap for time series resampling. Water Resour. Res. 32, 679–693. doi: 10.1029/95WR02966
Loucks, D. P., and Van Beek, E. (2005). Water Resources Systems Planning and Management and Applications: An Introduction to Methods, Models and Applications. Paris, France: UNESCO and WL | Delft Hydraulics. Available online at: https://unesdoc.unesco.org/ark:/48223/pf0000143430.
Maier, H. R., Kapelan, Z., Kasprzyk, J., Kollat, J., Matott, L. S., Cunha, M. C., et al. (2014). Evolutionary algorithms and other metaheuristics in water resources: current status, research challenges and future directions. Environ. Modell. Softw. 62, 271–299, doi: 10.1016/j.envsoft.2014.09.013
Martinsen, G., Liu, S., Mo, X., Davidsen, C., Payet-Burin, R., and Bauer-Gottwein, P. (2021). The impact of assuming perfect foresight in hydroeconomic analysis of yellow river diversions to the Hai River Basin, China: a framework combining linear programming and model predictive control. Front. Water 3:648934. doi: 10.3389/frwa.2021.648934
Miralles-Wilhelm, F. (2016). Development and application of integrative modeling tools in support of food-energy-water nexus planning—a research agenda. J. Environ. Stud. Sci. 6, 3–10. doi: 10.1007/s13412-016-0361-1
Mobasher, A. M. A. (2010). Adaptive Reservoir Operation Strategies under Changing Boundary Conditions—The Case of Aswan High Dam Reservoir. PhD. Available online at: http://tuprints.ulb.tu-darmstadt.de/2342/. (accessed November 29, 2021).
Payet-Burin, R., Kromann, M., Pereira-Cardenal, S., Marc Strzepek, K., and Bauer-Gottwein, P. (2019). WHAT-IF: an open-source decision support tool for water infrastructure investment planning within the water–energy–food–climate nexus. Hydrol. Earth Syst. Sci. 23, 4129–4152. doi: 10.5194/hess-23-4129-2019
Payet-Burin, R., Kromann, M., Pereira-Cardenal, S., Strzepek, M. K., and Bauer-Gottwein, P. (2021). Nexus vs. silo investment planning under uncertainty. Front. Water 3:672382. doi: 10.3389/frwa.2021.672382
Pereira-Cardenal, S. J., Mo, B., Gjelsvik, A., Riegels, N. D., Arnbjerg-Nielsen, K., and Bauer-Gottwein, P. (2016). Joint optimization of regional water-power systems. Adv. Water Resour. 92, 200–207. doi: 10.1016/j.advwatres.2016.04.004
Qin, S. J., and Badgwell, T. A. (2003). A survey of industrial model predictive control technology. Control Eng. Pract. 11, 733–764. doi: 10.1016/S0967-0661(02)00186-7
Quinn, J. D., Reed, P. M., Giuliani, M., and Castelletti, A. (2017). Rival framings: a framework for discovering how problem formulation uncertainties shape risk management trade-offs in water resources systems. Water Resour. Res. 53, 7208–7233. doi: 10.1002/2017WR020524
Research Councils UK (2020). The HSL Mathematical Software Library. Available online at: http://www.hsl.rl.ac.uk/ (accessed July 17, 2020).
Rising, J. (2020). Decision-making and integrated assessment models of the water–energy–food nexus. Water Secur. 9:100056. doi: 10.1016/j.wasec.2019.100056
Sahu, R. K. (2016). Optimal Reservoir Operation using Stochastic Model Predictive Control. Doctoral dissertation, Massachusetts Institute of Technology.
Scarcelli, R. O. C., Zambelli, M. S., Soares, S., and Carneiro, A. A. F. M. (2017). Ensemble of Markovian stochastic dynamic programming models in different time scales for long term hydropower scheduling. Electr. Power Syst. Res. 150, 129–136. doi: 10.1016/j.epsr.2017.05.013
Soleimani, S., Bozorg-Haddad, O., and Loáiciga, H. A. (2016). Reservoir operation rules with uncertainties in reservoir inflow and agricultural demand derived with stochastic dynamic programming. J. Irrig. Drain. Eng. 142, 04016046. doi: 10.1061/(asce)ir.1943-4774.0001065
Tilmant, A., Kinzelbach, W., Juizo, D., Beevers, L., Senn, D., and Casarotto, C. (2012). Economic valuation of benefits and costs associated with the coordinated development and management of the Zambezi river basin. Water Policy 14, 490–508. doi: 10.2166/wp.2011.189
Tomlinson, J. E., Arnott, J. H., and Harou, J. J. (2020). A water resource simulator in Python. Environ. Model. Softw. 126:104635. doi: 10.1016/j.envsoft.2020.104635
UN General Assembly (2015). Transforming Our World: The 2030 Agenda for Sustainable Development. Available online at: https://sustainabledevelopment.un.org/post2015/transformingourworld/publication. (accessed November 29, 2021).
Vinca, A., Parkinson, S., Byers, E., Burek, P., Khan, Z., Krey, V., et al. (2020). The NExus Solutions Tool (NEST) v1.0 : an open platform for optimizing multi-scale energy–water–land system transformations. Geosci. Model Dev. 13, 1095–1121. doi: 10.5194/gmd-13-1095-2020
Wächter, A., and Biegler, L. T. (2005). On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Programm. 106, 25–57. doi: 10.1007/s10107-004-0559-y
Yates, D., Sieber, J., Purkey, D., and Huber-Lee, A. (2005). WEAP21—A demand-, priority-, and preference-driven water planning model. Part 1: Model characteristics. Water Int. 30, 487–500. doi: 10.1080/02508060508691893
Keywords: Model Predictive Control, perfect foresight, hydroeconomic models, water–energy–food nexus, climate change, water infrastructure planning, IWRM
Citation: Payet-Burin R, Kromman M, Pereira-Cardenal SJ, Strzepek KM and Bauer-Gottwein P (2021) The Impact of Assuming Perfect Foresight When Planning Infrastructure in the Water–Energy–Food Nexus. Front. Water 3:778003. doi: 10.3389/frwa.2021.778003
Received: 16 September 2021; Accepted: 23 November 2021;
Published: 14 December 2021.
Edited by:
Sreekanth J., Commonwealth Scientific and Industrial Research Organisation (CSIRO), AustraliaReviewed by:
Chrysi S. Laspidou, University of Thessaly, GreeceMohammad Reza Alizadeh, McGill University, Canada
Copyright © 2021 Payet-Burin, Kromman, Pereira-Cardenal, Strzepek and Bauer-Gottwein. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Raphael Payet-Burin, cmFweSYjeDAwMDQwO2Nvd2kuY29t