- Energy Geosciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA, United States
In various natural and engineered systems, mineral–fluid interactions take place in the presence of multiple fluid phases. While there is evidence that the interplay between multiphase flow processes and reactions controls the evolution of these systems, investigation of the dynamics that shape this interplay at the pore scale has received little attention. Specifically, continuum scale models rarely consider the effect of multiphase flow parameters on mineral reaction rates or apply simple corrections as a function of the reactive surface area or saturation of the aqueous phase, without developing a mechanistic understanding of the pore-scale dynamics. In this study, we developed a framework that couples the two-phase flow simulator of OpenFOAM (open field operation and manipulation) with the geochemical reaction capability of CrunchTope to examine pore-scale dynamics of two phase flow and their impacts on mineral reaction rates. For our investigations, flat 2D channels and single sine wave channels were used to represent smooth and rough geometries. Calcite dissolution in these channels was quantified with single phase flow and two phase flow at a range of velocities. We observed that the bulk calcite dissolution rates were not only affected by the loss of reactive surface area as it becomes occupied by the non-reactive non-aqueous phase, but also largely influenced by the changes in local velocity profiles, e.g., recirculation zones, due to the presence of the non-aqueous phase. The extent of the changes in reaction rates in the two-phase systems compared to the corresponding single phase system is dependent on the flow rate (i.e., capillary number) and channel geometry, and follows a non-monotonic relationship with respect to aqueous saturation. The pore-scale simulation results highlight the importance of interfacial dynamics in controlling mineral reactions and can be used to better constrain reaction rate descriptions in multiphase continuum scale models. These results also emphasize the need for experimental studies that underpin the development of mechanistic models for multiphase flow in reactive systems.
Introduction
Interactions between multiphase flow, geochemical reactions, and solute transport in fractured porous media are ubiquitous in Earth's critical zone and subsurface systems, and affect the dynamics of many environmental and energy engineering applications. Examples include supercritical CO2 (scCO2) injection, light non-aqueous phase fluid (LNAPL) contamination, and Enhanced Oil Recovery (EOR). In geologic carbon storage systems, the injected scCO2 displaces the native brine and can be trapped in small pores or can dissolve into the brine and react with the host rocks. The resulting mineral dissolution and precipitation can modify the porosity and permeability of the reservoirs and caprocks, affecting injectivity of the reservoirs and long-term storage security (Johnson et al., 2001, 2004; Xu et al., 2011b). In EOR, low-salinity water is injected to the oil reservoir to improve sweeping efficiency by modifying wettability via surface complexation reactions (Zhang et al., 2006; Kumar et al., 2011). In the shallow subsurface, LNAPL contamination of groundwater is a widespread environmental problem. Light non-aqueous phase fluid is insoluble in water and typically fluctuates with the water table. As a result, LNAPL is spread vertically following local drainage-imbibition cycles, which in turn affects the degradation and thus the fate of the contaminants (Ngien et al., 2012; Pan et al., 2016; Govindarajan et al., 2018). The interactions between two-phase flow and electrochemical reactions have also been identified as a research priority for the design of effective fuel cells, as gas bubbles (of e.g., H2 and O2) can be generated by side reactions during charging and affect power generation (Chen et al., 2017; Grunewald et al., 2021).
Continuum-scale numerical models are widely used to investigate and predict the evolution of fractured porous media caused by multiphase reactive transport processes. Models such as TOUGHREACT, OpenGeoSys, and PFLOTRAN are versatile tools that have been used to investigate scCO2 migration in fractured formations (Xu et al., 2011a, 2019; Xiao et al., 2020), dissolution, transport and biodegradation of non-aqueous phase fluid (NAPL) in shallow aquifers (Pruess, 2004; Popp et al., 2015; Sookhak Lari et al., 2019), and heat extraction using CO2 as a working fluid (Lichtner and Karra, 2014). These models however rely heavily on constitutive relations such as the Brooks and Corey equation and the van Genuchten equation that relates the water saturation with capillary pressure and relative permeability.
Pore-scale structural heterogeneity and processes that are not considered explicitly in the continuum description, however, could be important. For instance, microfluidic experiments from Karadimitriou et al. (2016, 2017) examined non-Fickian transport in a water-Fluorinert immiscible fluid system. The results demonstrated that the mass transfer rate between mobile–immobile zones under the two-phase flow condition is not constant, indicating that the conventional treatment of the mass transfer rate in the continuum scale Mobile–Immobile (MIM) model could introduce significant errors in the simulation. Pore-scale experiments from Jiménez-Martínez et al. (2015) using 2D microfluidic cells with homogeneous pore structures have also demonstrated that solute mixing can be significantly enhanced under multiphase flow conditions because of ramified finger flow structure, non-Fickian dispersion, and non-wetting phase clusters that limit the finger flow merging. Recent advancement in experimental techniques have also enabled direct observations of reactive transport in multiphase systems at the pore scale. Using biogenically calcite-functionalized micromodels, Song et al. (2018) observed a new microscale mechanism that affects reactive transport in the CO2-brine-calcite system. The CO2 gas phase can accumulate on the mineral surfaces following calcite dissolution, which protects calcite from further dissolution. Jiménez-Martínez et al. (2020) developed a high-pressure geomaterial microfluidic device and investigated mineral reactions in etched channels during co-injection of CO2-saturated brine and scCO2. They observed that the presence of scCO2 bubbles significantly changed both the flow dynamics and the reaction patterns, compared to the single phase flow experiments. In the competing channels with different widths, mineral dissolution was more homogenized and carbonate precipitation was enhanced in the low-velocity regions formed as a result of the presence of the bubbles, which was also confirmed by pore-scale Lattice Boltzmann Methods (LBM) simulations.
Pore-scale models provide an invaluable tool to further our understanding of pore-scale dynamics. Pore-network models (PNMs) are a computationally efficient option for simulating the reactive transport processes under two-phase flow conditions, but require simplifications of the geometric solid-fluid interface and assumptions about uniform aqueous concentrations within a pore (Xiong et al., 2016). Lattice Boltzmann Methods (Chen et al., 2013, 2015) and direct numerical simulations (DNS) (Haroun et al., 2010b; Marschall et al., 2012; Maes and Soulaine, 2018; Soulaine et al., 2018, 2021) provide alternatives that relax these restrictions. The LBM was able to reproduce experimental observations on wettability alteration during Low Salinity Water Flooding (Akai et al., 2020). It was also shown by Maes and Geiger (2018) using a DNS approach that the alternation is driven by the concentration of the potential determining ions (PDI) instead of pH. Moreover, a series of micro-continuum simulations showed that the production of CO2 bubbles resulting from carbonate dissolution may limit the subsequent dissolution and prevent the emergence of wormholes (Soulaine et al., 2018).
In spite of the growing use of fully-resolved pore-scale models (LBM or DNS) in multiphase reactive applications, they have not been used to understand how reaction rates are influenced by flow processes in the same way as it has been done in single-phase systems (e.g., Molins et al., 2012, 2014; Deng et al., 2018). In single phase systems, reactive surface area has been typically varied to account for flow dynamics and transport limitations. Pore-scale simulations have highlighted the complex dependence of the correction factor on pore-scale geometry and flow regimes (Deng et al., 2018). In multiphase systems, however, this information does not exist. As a result, multiphase continuum scale models rarely account for the effect of the flow dynamics on reaction rates. Further, reaction rates are commonly assumed to be independent of phase saturations (e.g., Xu et al., 2011a; Lichtner et al., 2015; Águila et al., 2020; Wu et al., 2021). Only in some rare instances, the reactive surface area is allowed to vary with liquid saturation. For example, in the active fracture module implemented in TOUGHREACT, the reactive surface area and thus reaction rate follows a power law relation with respect to the water saturation and the exponent is an empirical variable (Sonnenthal et al., 2005). However, there is still a lack of pore-scale studies and mechanistic understanding that support the development of this type of constitutive relationship for considering the impacts of multiphase flow on reaction rates.
Our study aims to bridge this gap, by performing a series of well-designed pore-scale multiphase reactive transport simulations. To this end, a pore-scale multiphase reactive transport modeling framework was developed by coupling OpenFOAM and CrunchTope. A set of simulations were performed with co-injection of air and CO2-acidified water into 2D calcite channels to examine calcite dissolution rate under a range of flow conditions. A sine wave geometry was used to introduce different levels of roughness in the channels. This simple geometry has been widely used to provide an idealized representation of surface roughness to investigate its impacts on fluid flow and chemical transport (Kitanidis and Dykaar, 1997; Bolster et al., 2009; Sund et al., 2015; Deng et al., 2018). Section Methodology details the modeling framework, the mathematical principles, and the simulation setups. The results of the numerical simulations, including analyses of the flow field and reaction rates, and observed relations between reaction rate and parameters such as saturation are presented in section Results. We discuss the broader implications of our study in section Discussion and conclude in section Summary and Conclusions.
Methodology
Our approach entails the simulation of two-phase flow and reactive transport in a series of synthetic geometries. For this purpose, we develop a modeling framework by coupling two widely used and thoroughly validated codes. In this section, we present this modeling framework and we describe the setup of the simulations.
Modeling Framework
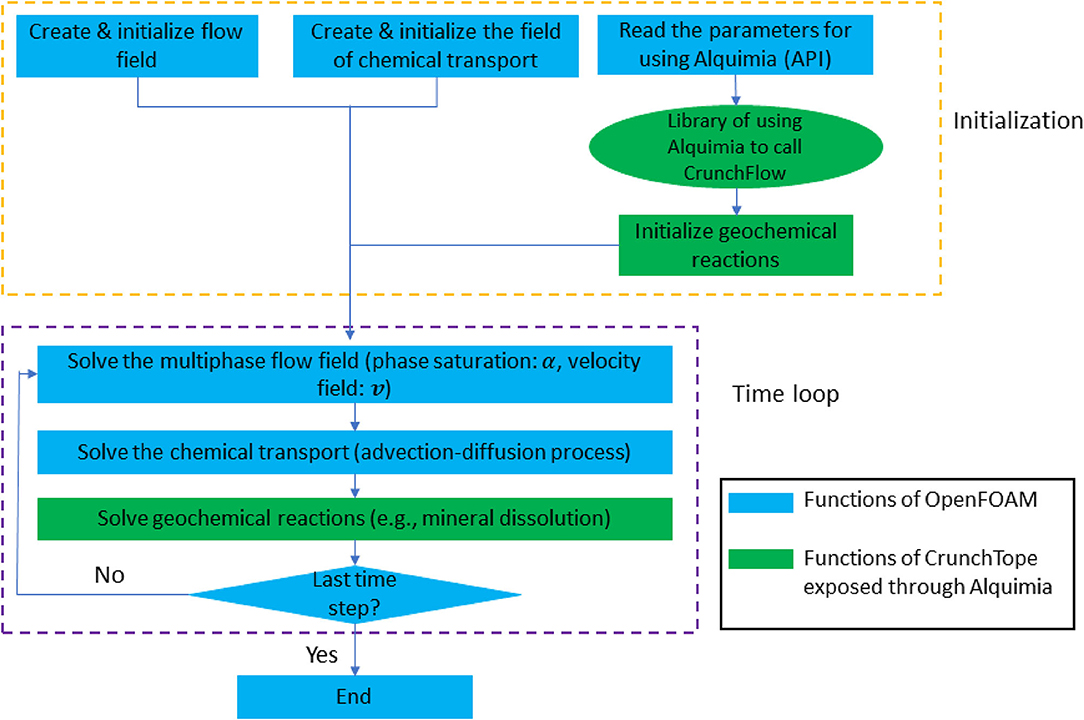
This pore-scale multiphase reactive transport modeling framework couples the geochemical reaction solver CrunchTope (Steefel et al., 2015) with the open source software package, OpenFOAM (open field operation and manipulation, OpenFOAM-v1812) and the related open source libraries, using Alquimia. Alquimia is a generic interface, which allows any flow and transport simulator to access geochemical reaction functionalities of existing, thoroughly validated codes such as CrunchTope (Andre et al., 2013). The modeling framework is referred to as CrunchFOAM for short.
Figure 1 illustrates the workflow of the modeling framework. The geochemical conditions and reaction kinetics are specified in the CrunchTope input files. The initial and boundary conditions for the flow and the transport of the primary chemical species are specified in OpenFOAM. Two-phase flow, transport, and geochemical reactions are solved sequentially following the operator splitting approach. The time stepping is controlled by the flow solver in OpenFOAM. Within each time step, the flow field from the two-phase flow solver is passed to the transport solver to calculate the concentrations of the primary species by solving the advection-diffusion equation. Afterwards, CrunchTope is called in each cell to calculate aqueous speciation and mineral reactions, and to update the concentration fields for transport in the next time step.
Flow
Two phase flow is solved using interFoam, the standard OpenFOAM solver for transient incompressible isothermal flow of two immiscible fluids. The solver implements a modified version of the Volume of Fluid (VoF) method, and its performance has been confirmed for capillary numbers larger than 10−5 (Deshpande et al., 2012; Shuard et al., 2016).
The VoF approach treats the two fluid phases as an effective single phase. The velocity and pressure fields are solved by the single-field incompressible Navier Stokes Equation and continuity equation (Hirt and Nichols, 1981).
where u is the velocity. Fluid density ρ, and viscosity μ are weighted averages of the two fluid phases based on the volume fraction (α) of a designated fluid, which is usually the wetting fluid
Fst is the surface tension force and defined as
where γ is the interfacial tension, κ = ∇·n is the interface curvature, n is the unit vector normal to the interface given by , is a Dirac function located on the interface.
The phase volume fraction α is solved by the following transport equation
where ur is the relative velocity between the two fluids/phases. It is typically defined as the compression velocity uc to ensure a sharp interface, and its amplitude is determined by the maximum of the single-field velocity
where Φ is the volumetric flux, Af is the cell surface area, 0 ≤ cα ≤ 1 limits the compression velocity below the maximum face flux velocity and is a user-specified coefficient (cα = 1 in our simulations). This formulation helps minimize numerical diffusion (Rusche, 2002).
The contact angle (θ) is defined at the solid boundary and the following equation needs to be satisfied (Aziz et al., 2018):
where ns is the normal vector to the solid wall.
Transport
For transport under multiphase flow conditions, the continuous species transfer (CST) method has been developed and implemented as a third-party solver in OpenFOAM (Haroun et al., 2010a; Marschall et al., 2012; Deising et al., 2016). The C-CST (compressive-CST) algorithm developed by (Maes and Soulaine, 2018) was implemented in this work as it minimizes numerical diffusion near the interface and ensures that the description of advection is fully consistent with the phase evolution equation (VoF equation). In this method, the transport of a species j dissolved in both phases is described by
where is the interpolation of the diffusion coefficient of the chemical species in the two phases
where Dj,w and Dj,nw is the diffusion coefficient of chemical j in the wetting and non-wetting fluid, respectively. Ψi describes the concentration jump at the interface
where Hj is Henry's law constant. In this study, mass transfer across the interface is not considered, and Hj is set to be a small value (1 × 10−12) to avoid zero denominators in Equation (9) when α = 0. Because only reactions in the aqueous phase are considered (see below), neglecting mass transfer across the interface implies that concentrations in the non-aqueous phase remain equal to the initial condition (which is zero).
Geochemical Reactions
Rj in Equation (9) accounts for the contribution of mineral reactions to the changes in the mass of chemical species j, and is described by the transition state theory rate law
where krxn is the kinetic coefficient (mol/m2·s), A is the surface area of the mineral phase (m2), and is determined directly from the geometry in OpenFOAM, and the chemical affinity term is calculated from the ion activity product (IAP) and the equilibrium constant of the mineral reaction (Keq). The aqueous reactions are assumed to reach equilibrium instantaneously and speciation is calculated based on the law of mass action and the concentrations of the primary species.
Simulation Setup
We investigate multiphase flow and reactive transport in a domain that seeks to represent a microcrack with an arbitrarily rough geometry, which can also be conceptualized as a sequence of pores. Figure 2 provides an illustration of the geometry used in our simulations. To save computational time, we assumed a symmetric geometry and simulated half of the domain. A T-junction structure is used at the inlet for the injection of the wetting and non-wetting phase. The width of the inlets is 25 μm. The reactive zone, where the reactive mineral is located and highlighted in the blue box in Figure 2, is 1mm long and has an average width (b) of 100 μm. The dimensions are comparable to previous modeling and micromodel studies of geomaterials (Deng et al., 2018; Song et al., 2018; Jiménez-Martínez et al., 2020) and to the fiber diameter in batteries (Chen et al., 2017). In addition to the reference flat channel, a single sine wave was used to represent pore scale roughness in the reactive zone, following (Deng et al., 2018).
where λ is the wavelength, and a is the amplitude. In order to explore different levels of roughness, a number of simulations were performed each with a different wavelength (Table 1). In all cases, an amplitude of 31.25 μm was used.
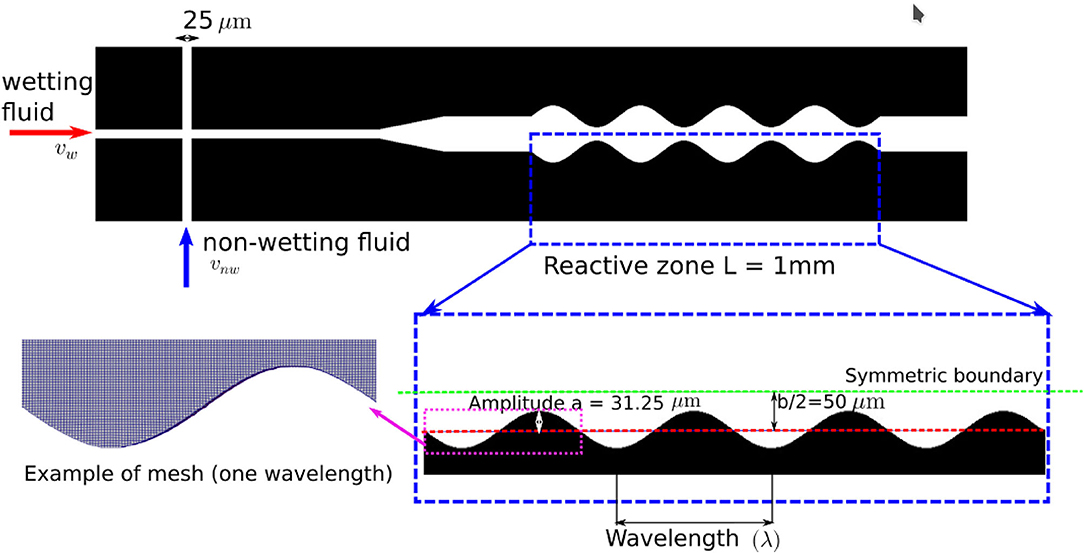
Figure 2. An illustration of the geometry and mesh used in our numerical simulations. Here, the reactive zone has 4 full sine waves and the mesh resolution is 2 μm.
The roughness in these sine wave geometries is measured by the surface roughness factor (SRF). It is defined as the ratio between the total surface area (Atotal), which is calculated by summing the patch area defined as the mineral wall in the mesh generated by OpenFOAM, and the nominal surface area, which is equivalent of the surface area of the flat geometry (Aflat).
The geometries were first generated by a Python script and Blender, and the STL files were then imported into OpenFOAM to generate the meshes using snappyHexMesh. The average mesh size was set to 2 μm. Although interFoam does not show convergence with decreasing mesh size (Pavuluri et al., 2018), this mesh size is comparable with the resolution used in previous studies that showed good results using interFoam in complicated pore structures (Yin et al., 2019; Carrillo et al., 2020). This mesh size also ensures that the single phase simulation results are not affected by further refinement.
Initially, the simulation domain is fully saturated with water except for the vertical branch of the T-junction, which is occupied by the non-wetting phase (i.e., air). The physical properties of the fluids are summarized in Table 2.

Table 2. Physical properties of fluids (ρw, water density; ρa, air density; μw, dynamic viscosity of water; μa, dynamic viscosity of air; γwa, interfacial tension between water and air; θ, contact angle).
A constant velocity boundary condition is applied at the inlets. For each geometry, three velocities for the wetting phase were simulated, which are 0.04, 0.1, and 0.4 m/s. The velocity of the non-wetting phase is a fraction of the wetting phase, and two ratios, 0.25 and 0.5, were used to control the frequency of the bubbles generated by the co-injection. This results in a Reynolds number (Re) of 1-10 and a capillary number (Ca) of ~10−4-10−3. The Ca-values are within the range that is relevant for typical reservoirs (Satter and Iqbal, 2016) and battery systems (Grunewald et al., 2021). At the outlet, the zero gradient boundary condition is applied for both flow and transport (Table 3).
Geochemical reactions are assumed to take place in the aqueous phase only. The solid phase in the reactive zone is composed of a single mineral, calcite. It dissolves in water, which has a NaCl concentration of 0.01 M/L and a pH of 5 due to dissolution of atmospheric CO2. The kinetic coefficients for the three elementary reaction pathways reported in Chou et al. (1989) for calcite dissolution are summarized in Table 4 and used in the simulations. The aqueous reactions and their equilibrium constants are summarized in Table 5. The activity coefficients used to convert concentrations to activities (aspecies) are calculated using the extended Debye-Hückle equation.
In this study, the geometry is not updated and we focus on steady state behavior. Given the time scale that is needed to reach steady state (within seconds as shown in section Results), the mineral reaction is not expected to cause any geometric change. The simulations were run until both the flow and reaction rate reached a steady state. For the analyses of calcite dissolution rate, the absolute average instantaneous reaction rate at a time point t () was calculated for both single-phase (m = s) and two-phase (m = t) flow systems as
is the instantaneous reaction rate in the wall grid cell n with a volume of Vn and wall surface area of An at time point t, is the volume fraction of the wetting phase, i.e., saturation, in the grid cell, and is the wetted surface area ratio within the local wall grid cell, which is approximated by .
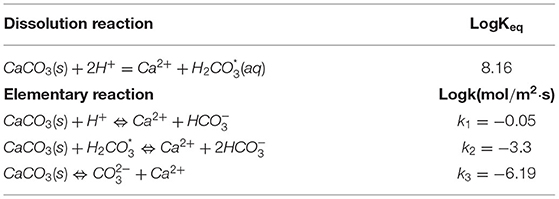
Table 4. Calcite dissolution reactions, the equilibrium constant, and the three reaction pathways with the kinetic coefficients.
In addition to the multiphase simulations described above, a single-phase simulation is performed for each roughness level (Table 1) and flow condition (Table 3), with the same total flux for comparison. These single-phase results are used to elucidate the multiphase effects on reaction rates. All the simulations were performed with the reactive transport solver described in Section Methodology and the saturation (α) is set to one for single-phase simulations.
Results
Reaction Rates
The co-injection of the wetting and non-wetting phases produces a series of gas bubbles that migrate through the reactive zone (Figure 3). The size and frequency of the gas bubbles are primarily controlled by the injection rate and the ratio between the wetting and non-wetting phase. Consistent with previous studies (van Steijn et al., 2010; Malekzadeh and Roohi, 2015; Mi et al., 2019), we observed that the bubble size is controlled by the ratio (vnw/vw) and the frequency is determined by magnitudes of vinw and vinnw. The diameter of the bubbles is 64 and 74 μm for vnw/vw of 0.25 and 0.5, respectively. In cases of large roughness, the shape of the gas bubbles changes temporarily at the narrow throats and can be recovered after entering the wide channel locations, i.e., sine wave troughs. Once the gas bubble flow is established, the hydrodynamics of the system reaches the steady state, as indicated by the average saturation, which is the mean of the phase field (α) in the reactive zone. The average saturation displays small oscillations around the steady state value when the bubbles enter or exit the reactive domain (Figures 4B,D). Figure 4A shows the temporal profiles of the average instantaneous reaction rates for the single-phase and two-phase cases for geometry c at vw = 0.1m/s with vw/vnw = 0.25. The reaction rate for the single phase flow simulation decreases initially as the calcite saturation state starts to increase following the dissolution reaction, and stabilizes at about 1.8 × 10−6 mol/m2s after ~0.04 s. This dissolution rate is comparable with the value reported in previous single phase reactive transport simulations in a similar system using the pore-scale code ChomboCrunch (Deng et al., 2018). Given the relatively high velocity and large Reynolds number, overall the system is far from equilibrium with respect to calcite and the reaction rate is relatively high. The concentration of the reactive solutes and thus calcite saturation index shows a thin boundary layer at the fluid-solid interface and the concentration gradient across the flow direction is large (Figures 4E,F). This is consistent with the observations in Deng et al. (2018) that the effect of transverse transport could be important in these cases.
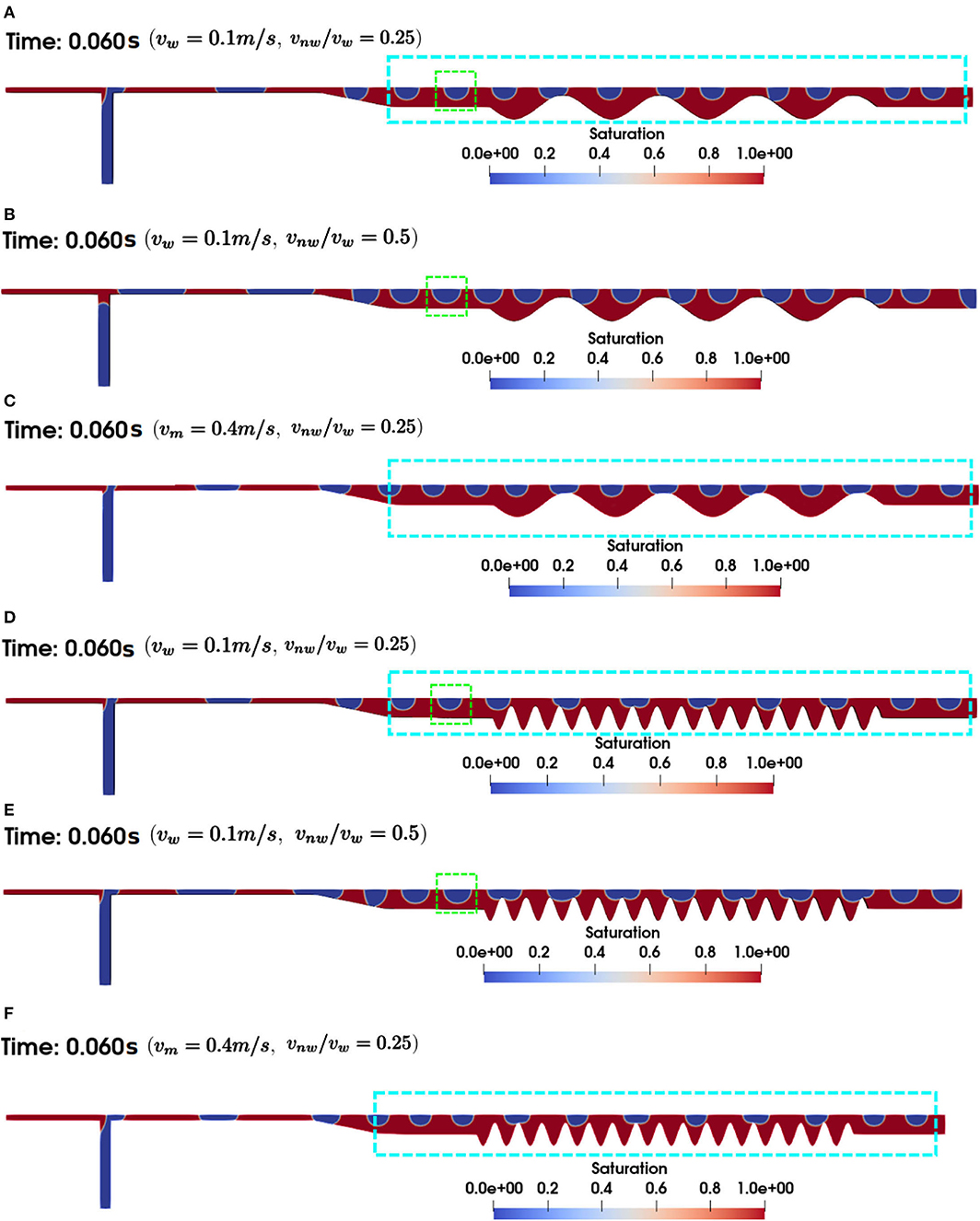
Figure 3. Established flow of gas bubbles for (A) geometry c, vinw = 0.1m/s, vinw/vinnw = 0.25; (B) geometry c, vinw = 0.1m/s, vinw/vinnw = 0.5; (C) geometry c, vinw = 0.4m/s, vinw/vinnw = 0.25; (D) geometry e, vinw = 0.1m/s, vinw/vinnw = 0.25; (E) geometry e, vinw = 0.1m/s, vinw/vinnw = 0.5; (F) geometry e, vinw = 0.4m/s, vinw/vinnw = 0.25. The blue box is used to guide the comparison of the number of bubbles, i.e., bubble frequency. The green box highlights a single bubble to illustrate the dependence of bubble size on the injection ratio.
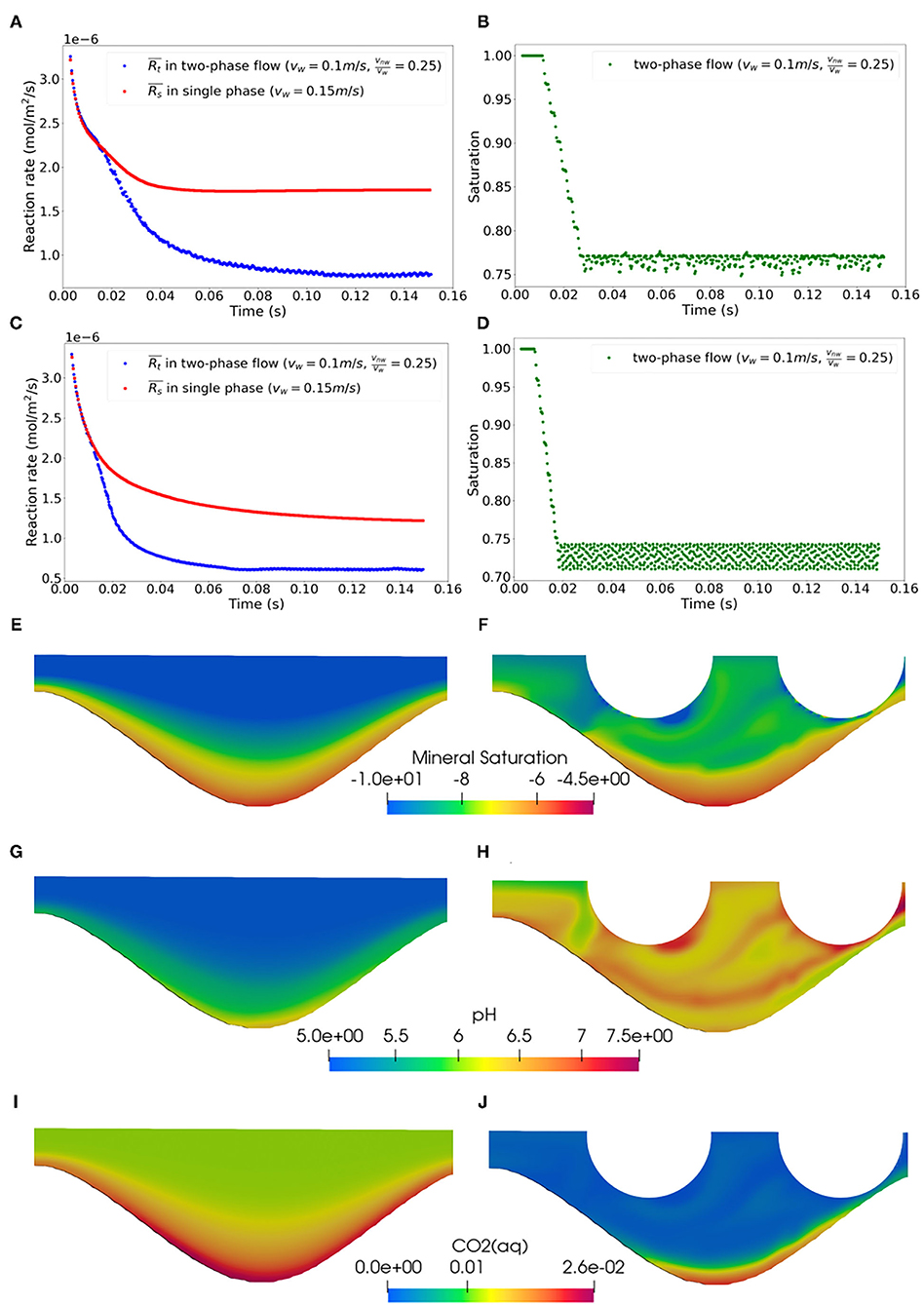
Figure 4. Temporal profiles of the average instantaneous reaction rates (A,C) and average saturation (B,D) in the reactive zone for geometry c (A,B) and e (C,D), vinw = 0.1m/s, vinw/vinnw = 0.25. Close-up spatial profiles of calcite saturation index (log(IAP/Keq)) (E,F), pH (G,H), and total CO2(aq) concentration (I,J) in geometry c for the (E,G,I) single and (F,H,J) two phase simulations at time 0.06s.
The reaction rate for the two phase flow simulation decreases over time as well. The initial decreasing trend overlaps with the single phase simulation as the gas bubbles have not entered the reactive zone. The decreasing trend diverges as the gas bubbles enter the reactive zone. reaches the steady state at ~0.8 × 10−6 mol/m2s after ~0.12 s. The steady state instantaneous reaction rate of the two phase flow case is significantly lower than that of the single phase flow case. This observation is also consistent across all geometries and flow conditions simulated. Figures 4C,D provide another example with similar results for geometry e under the same flow condition.
Mechanisms for Reaction Rate Modification in Two Phase Systems
Analysis of local reaction rate confirms that the lower reaction rate in the two phase flow case is partially attributed to the changes in accessibility of rock surface area. Figure 5A shows the phase field for geometry c at vw = 0.1m/s and vw/vnw = 0.25, and highlights that when the gas bubbles migrate through the narrow throats, the local reactive surface area becomes inaccessible to water-rock interactions (Figure 5B). In the experimental study of Song et al. (2018), CO2 gas bubbles generated by calcite dissolution were observed to block access of the reactive fluid phase to the mineral grain surfaces and thus local calcite dissolution is suppressed. Furthermore, in the corresponding single phase simulation (Figure 5C), the local reaction rates on the walls in the narrow throats (~2 × 10−6 mol/m2s) tend to be higher than those in the troughs. As such, even though the wetted surface area in the reactive zone—which provides a measure of accessible mineral surface area—is only reduced by <10% (Figure 5D), the reduction in the average reaction rate is much more significant (>50%).
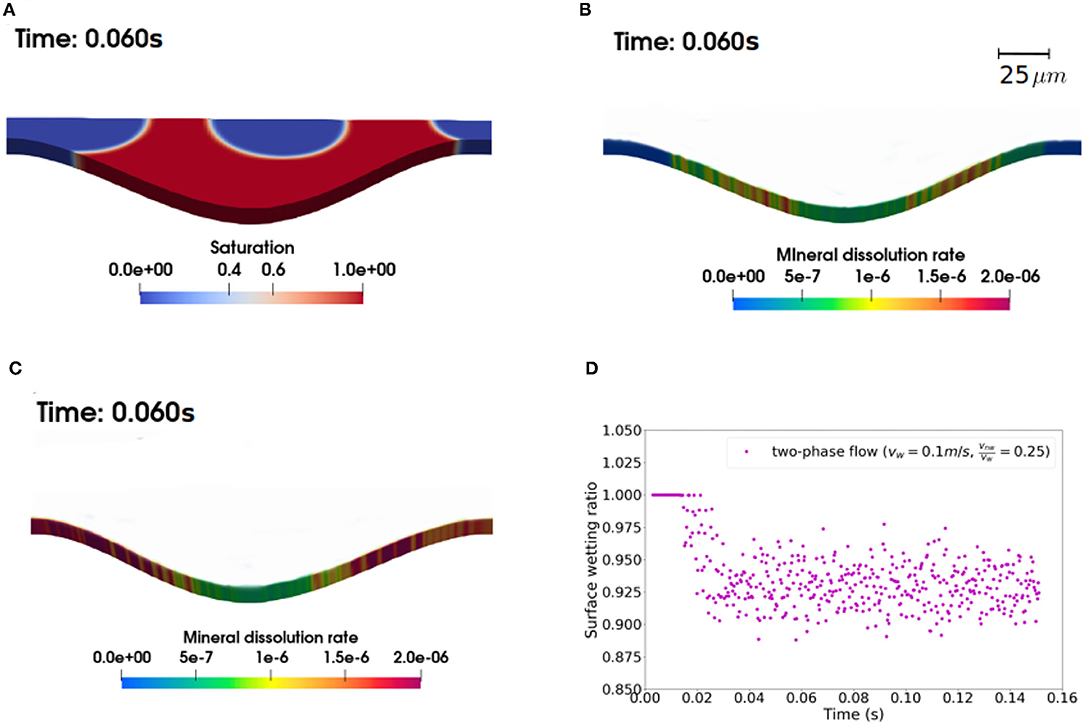
Figure 5. (A) A snapshot of saturation at time 0.06s; local mineral dissolution rates in (B) the two-phase and (C) single phase simulation at time 0.06s; (D) average ratio of wetted surface area within the reactive zone over time, for geometry c, vinw = 0.1m/s, vinw/vinnw = 0.25.
As shown in Figures 5B,C, the local reaction rate outside of the narrow throats that are occupied by the non-aqueous phase is also lower in the two-phase case than that in the single phase case. This indicates the presence of a stronger local transport limitation, which is also confirmed by the flow fields. Figures 6A,B compare the velocity vectors in the single and two-phase flow simulations for geometry c at vw = 0.1m/s and vw/vnw = 0.25. In the two phase case, as the gas bubbles migrate through the troughs, the width of the wetting phase is compressed and recirculation zones formed locally. In contrast, for the same geometry and flow rate, no recirculation zones were observed in the single phase simulation. The recirculating phenomenon has been observed experimentally and numerically in two-phase systems across a wide range of flow conditions with Ca between 1 × 10−7-1 × 10−2, as a result of the shear stress exerted by the fluid phase that migrates faster on the other fluid phase that is less mobile or immobile (Blois et al., 2015; Roman et al., 2016; Heshmati and Piri, 2018; Maes and Soulaine, 2018; Mohammadi Alamooti et al., 2020). Previous studies have highlighted that recirculation zones can be an important mechanism that traps the solutes (Bolster et al., 2014; Sund et al., 2015; Deng et al., 2018; Yoon and Kang, 2021), reducing local thermodynamic driving force (Figures 4E,F), i.e., the chemical affinity term in Equation (12). In addition, the pH is higher and total concentration of CO2(aq) is lower in the two phase case (Figures 4G–J), both would lead to a lower kinetic rate as given in Equation (15). Figures 5C,D show the flow fields for geometry e at the same flow conditions as Figures 5A,B. Similar patterns were observed. The recirculation zone is also more predominant in the troughs or the pore-body with the rougher geometry, accounting for a larger portion of the troughs. The dependence of the recirculation zone on pore morphology has also been observed in previous experimental studies (Heshmati and Piri, 2018).
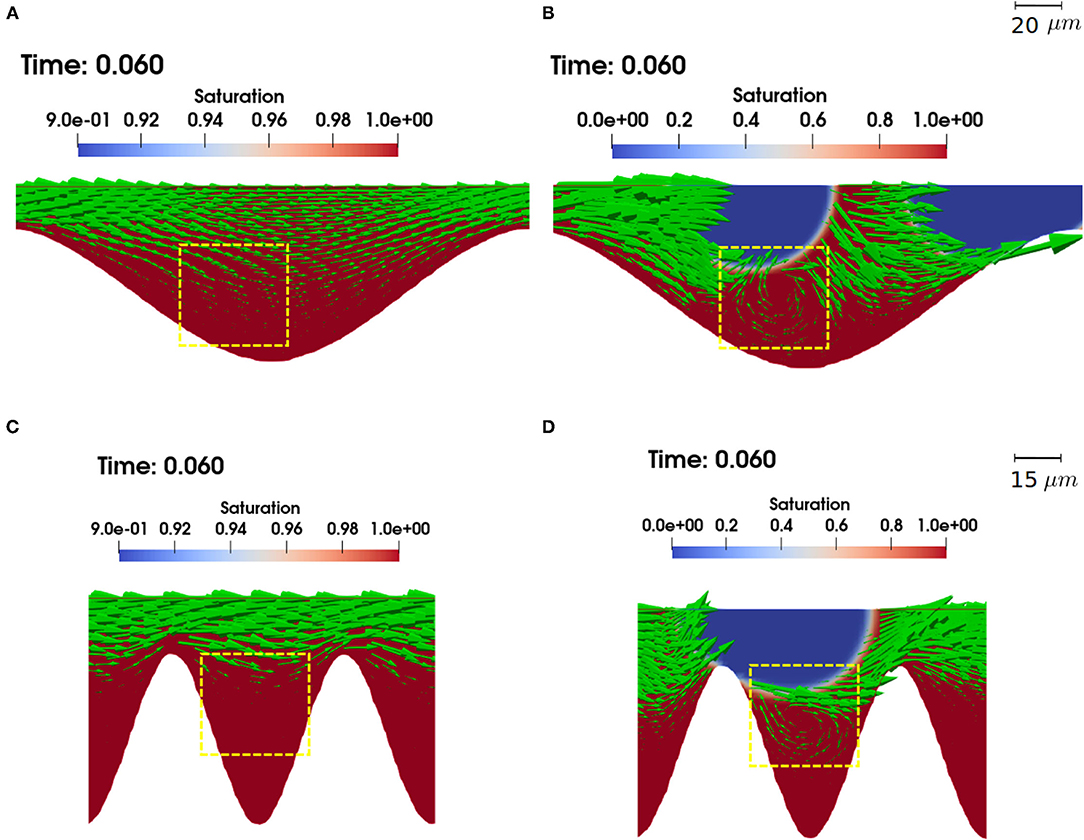
Figure 6. Vector plots showing the flow field in single phase (A,C) and two phase flow simulations (B,D) of geometry c (A,B) and geometry e (C,D) with vw = 0.1m/s, vw/ vnw = 0.25. The green/yellow boxes highlight the recirculation zones in the two flow simulations. The size of the arrows is scaled by velocity magnitude.
Correlation Between Reaction Rate Modification and Liquid Saturation
In order to gain some insights regarding constitutive relations that can be used to upscale the impacts of two-phase flow dynamics on reaction rate, Figure 7 summarizes the steady state reaction rates and saturations from the pore scale simulations. The ratio between the reaction rate of the two phase simulation and that of the corresponding single phase simulation is used to evaluate the effect of two-phase flow dynamics, specifically gas bubble migrations in 2D rough channels, on reaction rates. Liquid saturation is an indicator of the two-phase flow dynamics as is the case in many multiphase continuum models.
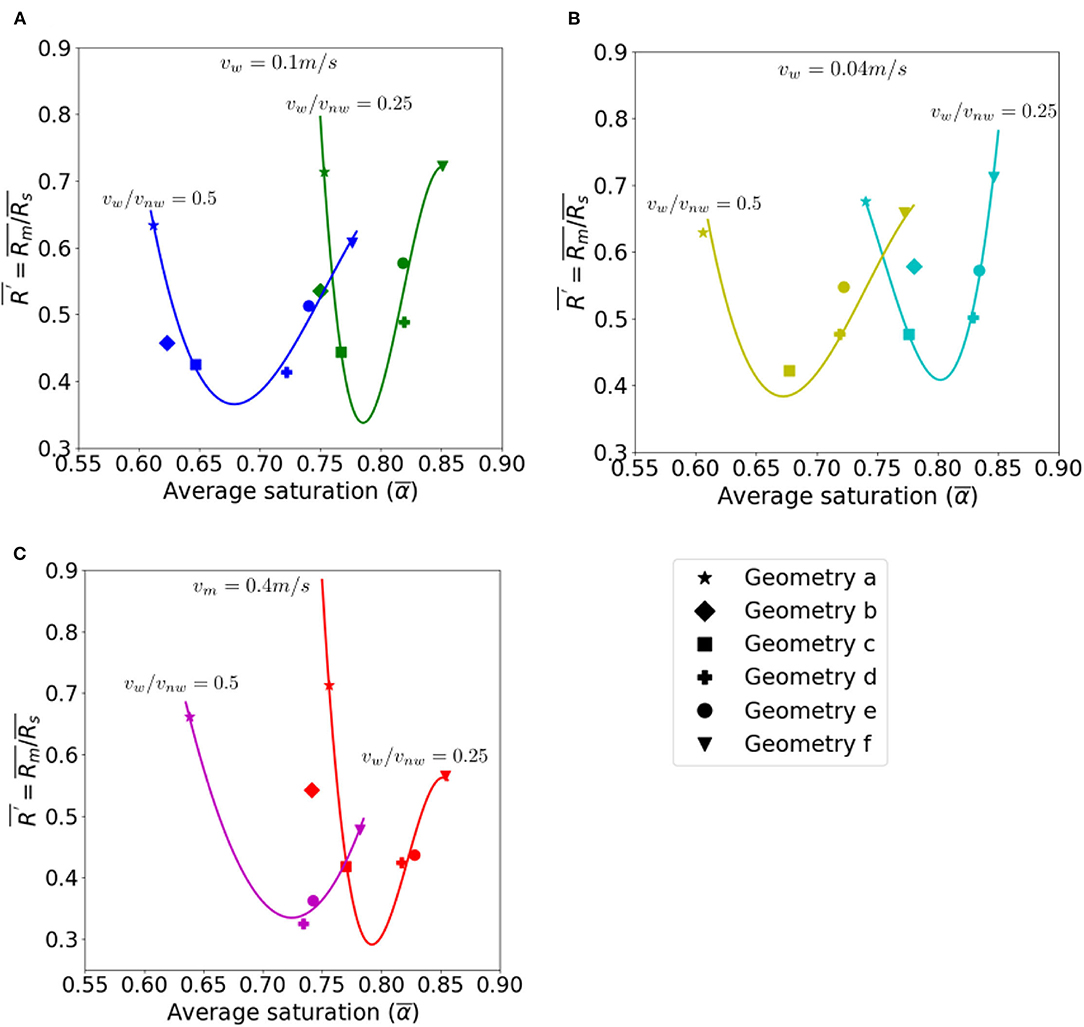
Figure 7. Ratio of the average instantaneous reaction rate between the two-phase and the corresponding single-phase flow simulation (R′) plotted against the average saturation (α). The data points are results from the pore-scale simulations and the solid lines are fitted curves using the third degree polynomials for (A) vw = 0.1m/s, vnw/vw = 0.25 (green) and vnw/vw = 0.5 (blue); (B) vw = 0.04m/s, vnw/vw = 0.25 (cyan) and vnw/vw = 0.5 (yellow); (C) vw = 0.4m/s, vnw/vw = 0.25 (red) and vnw/vw = 0.5 (purple). A few data points for geometry b and c at the high vnw/vw are excluded from the analyses because of bubble merging, which creates hydrodynamics that are not directly comparable to the rest of the simulations.
The impacts on reaction rate do not change monotonically with respect to the steady state saturation. For a given flow condition, the reaction rate ratio decreases as the steady state saturation increases for the less rough geometries (i.e., geometry a–c), whereas it increases with the saturation for the rougher geometries (i.e., geometry d–f). Figure 8 shows that the steady state saturation increases with roughness, and so does the wetted surface area ratio (except for the flat reference geometry). This indicates that if the surface area accessibility is the dominant mechanism of the reaction rate reduction in the two phase case, a higher saturation corresponding to a rougher geometry should result in a lower reduction in reaction rate in the two phase case. However, as shown in Figure 6, the other mechanism, i.e., the transport limitation of the recirculation zones, is stronger in the rougher geometry. This implies that reaction rate reduction due to transport limitation arising from the presence of the gas bubbles is more significant in the rougher geometries which also have higher saturations. The tradeoff between the two mechanisms can explain the inverted bell shape, which is observed for all flow conditions.
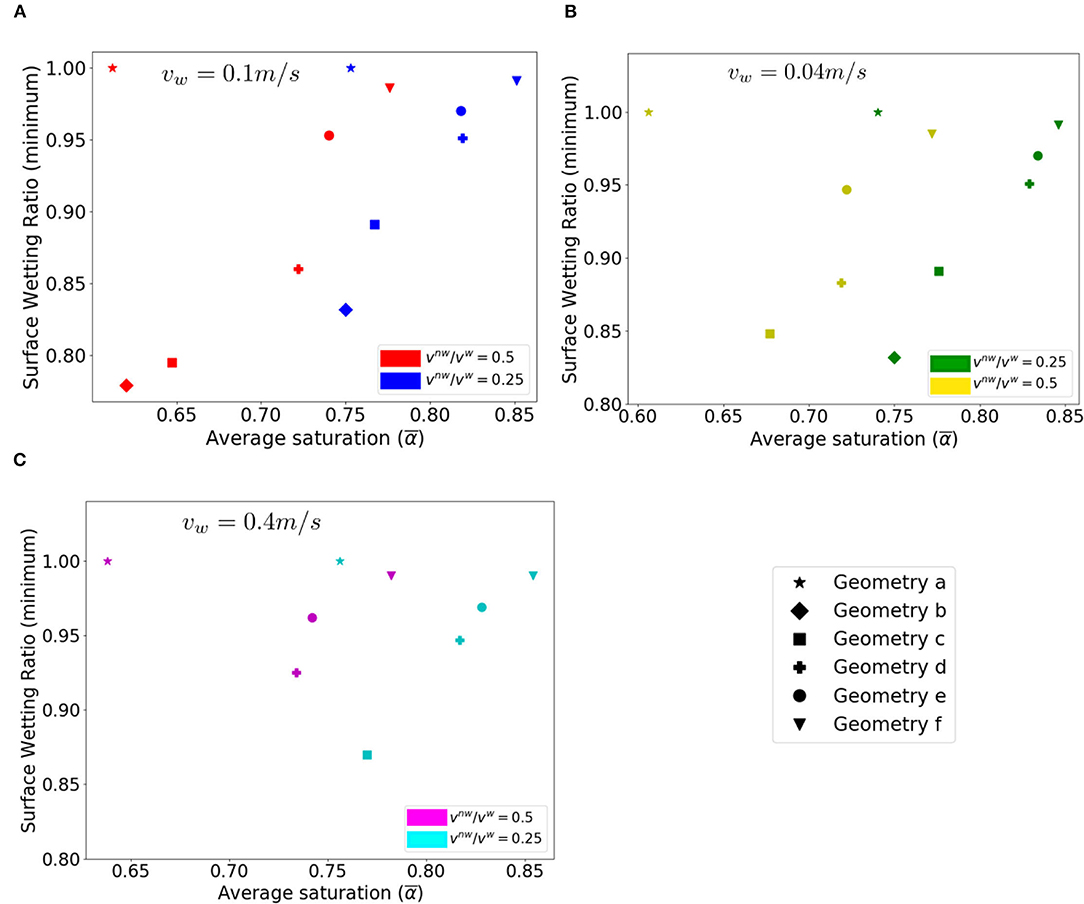
Figure 8. The fraction of the wetted surface area in the reactive zone in relation to the average saturation for different geometries with (A) vw = 0.1m/s, vnw/vw = 0.25 (blue) and vnw/vw = 0.5 (red); (B) vw = 0.04m/s, vnw/vw = 0.25 (green) and vnw/vw = 0.5 (yellow); (C) vw = 0.4m/s, vnw/vw = 0.25 (cyan) and vnw/vw = 0.5 (magenta).
This non-monotonic trend indicates that a power-law relationship will not apply. The guiding lines in Figure 7 were fitted using third degree polynomials, (Table 6). While the polynomial relationship provides a reasonable fit of the pore-scale modeling data statistically—the goodness of fitting as measured by R2 is larger than 0.95 in most cases (Table 6)—they are not meant to be directly implemented or at least caution should be exercised.
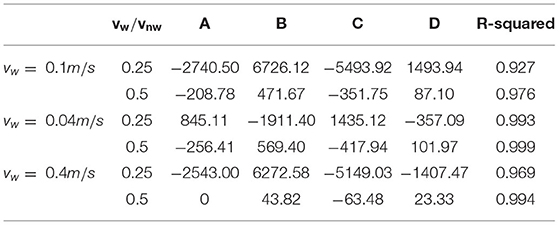
Table 6. Coefficients of polynomial equations and R-squared for the fitting curves in Figure 7.
Our observation is analogous to previously observed non-monotonic dependence on fluid saturation for other processes in the sense that competing mechanisms—because of their opposite “dependence” on saturation—are in play. For example, Jiménez-Martínez et al. (2017) reported that when saturation is above a threshold, mixing increases as saturation decreases because of stretching, whereas mixing decreases with saturation below the threshold as molecular diffusion becomes dominant. Our observations also reiterate the fact that saturation is a result of the multiphase dynamics and it alone does not provide a full description of the hydrodynamics in the system. For example, for a given flow condition in our simulations, saturation is determined by the roughness of the geometry, which can be expected for other more complex geometries. Given that both liquid saturation and reaction rate are dependent on the flow conditions and the geometries, future studies may focus on developing constitutive relations that are informed by the underlying physics or that explicitly integrate these controlling factors.
Discussion
In our simulations, the recirculation zone is the dominant hydrodynamic feature affecting the mineral dissolution rate. The development of recirculation zones have been observed in single phase systems at high velocity when the contribution of inertial effect becomes significant; and roughness allows recirculation zones to form under lower velocities (Deng et al., 2018). Our results illustrate that in two phase systems, momentum transfer across the fluid–fluid interface further extends the conditions under which recirculation zones form as also reported in previous studies (Heshmati and Piri, 2018). Other multiphase flow dynamics are also observed in our results albeit the simplified setup considered. For instance, in geometry b, a few simulations at the high and low flow velocities especially with large vw/vnw showed coalescence of the gas bubbles, which resulted in significantly lower saturation in the reactive zone. Bubble coalescence and breakup are widely observed phenomena that are dependent on fluid properties, velocities, and geometries (Jo and Revankar, 2009; Paulsen et al., 2014; Chen et al., 2017; Mahabadi et al., 2018; Ren et al., 2020; Grunewald et al., 2021). These processes are accompanied by the re-organization of the fluid–fluid interface and can introduce perturbations in the velocity field. The simulations with gas bubble coalescence were excluded from the analyses in section Correlation Between Reaction Rate Modification and Liquid Saturation as the new hydrodynamics is not directly comparable with the other simulations. Nonetheless, this observation highlights that compared to single phase systems in which a lower velocity typically transfers to a stronger transport limitation, the two phase systems require consideration of additional hydrodynamics that may arise at a different velocity (Blois et al., 2015).
A variety of complex hydrodynamics can arise from the migration of fluid–fluid interfaces depending on the velocity (e.g., capillary numbers) and pore morphology (e.g., Berg et al., 2013; Spurin et al., 2019; Li et al., 2021; Wang et al., 2021).
From a macroscopic perspective, as capillary number (Ca) increases, interface migration transitions from the capillary fingering regime with more random local movement to the viscous fingering with more stable displacement (Toussaint et al., 2012; Li et al., 2019; Grunewald et al., 2021). However, Ca alone does not provide a good description of the fluid–fluid interface dynamics (Armstrong et al., 2015), which is more sensitive to pore-scale roughness/morphology at low capillary numbers (Toussaint et al., 2012).
From a microscopic perspective, both the magnitude and direction of flow were observed to fluctuate before the arrival of the invading front (Roman et al., 2016; Li et al., 2017). Strong instabilities of the interface can also lead to pore-scale burst events such as Haines jumps and can increase local velocities by one–two orders of magnitude (Blois et al., 2015; Li et al., 2017, 2021). These hydrodynamics are reported to promote mixing and thus reactions in the liquid phases (Jiménez-Martínez et al., 2015, 2016, 2017), and may also increase local mineral reaction rates. In the study of Jiménez-Martínez et al. (2020), calcite dissolution rate in the two phase experiment with Ca = ~10−5 and vw/vnw = 1.0 is 68% of the dissolution rate in the single phase experiment. This is comparable to the simulation results in the smooth channel, e.g., the reaction rate ratio is ~64 and ~72% at vw = 0.1 m/s (i.e., Ca = ~3.5 × 10−4) for vw/vnw of 0.5 and 0.25, respectively (Figure 7). Their reaction rate ratio is slightly higher than what would be expected based on our simulations, which is likely because of the oscillation of gas bubbles in the presence of a system of channels and thus higher local velocity at the fluid–fluid interface, in addition to the continuous supply of CO2 from the co-injected scCO2 phase. The competition of different fluid pathways can result in more dynamic bubble migration and flow field rearrangement, which influences self-organization of the system, which is also illustrated in the column experiment of Ott and Oedai (2015) and the pore-scale numerical simulations of Soulaine et al. (2018). Geometry units such as pore-doublets can be used to capture such dynamics and thus offer additional insights (Mohammadi Alamooti et al., 2020; Alizadeh and Fatemi, 2021). More realistic geometries may be needed to fully examine the complexity of real systems, as flow instabilities are primarily driven by geometry when morphological heterogeneity is large (Li et al., 2017; Heshmati and Piri, 2018).
Water film is also an important contributor to the fluid–fluid interface (Li et al., 2019). While for the given Ca and channel width used in our study, water film is not expected to be well developed and thus contribute to transport significantly or affect our analyses (Roman et al., 2017), well-developed water film may become important in maintaining water-rock contact and transport pathways between isolated water parcels. For instance, water film has been observed during the drainage process in various experiments (Rücker et al., 2015; Schlüter et al., 2016; Roman et al., 2017; Moura et al., 2019). It enhances the connectivity between residual water and may cause the “snap-off” phenomenon, affecting the contact between water and the solid phase (e.g., rock) and the transport processes.
Overall, this study represents an early-stage effort in highlighting the importance of a dynamic coupling between reaction rates and multiphase flow dynamics. As such, it focuses on a specific geometric setup and a relatively limited number of flow scenarios. However, compared to the experimental studies that typically report temporally and/or spatially integrated reaction rates, our model provides information on local and instantaneous reaction rate along with detailed velocity field and solute transport, which helps to better explore microscopic mechanisms. The two mechanisms identified in our pore-scale two-phase reactive transport simulations—the surface area effect and local hydrodynamics—support recent observations from micromodel experiments (Song et al., 2018; Jiménez-Martínez et al., 2020). Moreover, the pore-scale perspective in the model enables insights into the impacts of multiphase flow dynamics on mineral reaction rate that have broader implications. Namely, results indicate that in addition to the fluid-solid interface, a direct measure of the reactive surface area, the fluid–fluid interface also plays an important role in controlling solid-phase reactions by modifying local hydrodynamics. As discussed above, local hydrodynamics that can affect mineral reaction rate is largely influenced by fluid–fluid interfaces, our study suggests that adding interfacial area in the formulation of reactive surface area in two-phase flow conditions in addition to saturation may be a logical step. In fact, it has been proposed to use the fluid–fluid interface as a measure of flow topology and thus an additional parameter in constitutive relations of relative permeability (Picchi and Battiato, 2018). Such consideration may be of particular interest in e.g., scCO2-brine systems where mass transfer across the fluid–fluid interface also affect fluid chemistry and thus mineral reaction rate.
In order to develop constitutive relations that faithfully reflect the coupling between mineral reaction rates and multiphase flow dynamics and are broadly applicable in natural and engineered fractured porous materials, systematic studies that explore a broader range of multiphase flow and geometric conditions are needed. While the modeling framework developed in this work can be adapted to consider these processes and thus provides a suitable modeling tool in a wide range of applications for pore-scale mechanistic investigations, it needs to be acknowledged that these investigations hinge upon further development of modeling capabilities for multiphase flow dynamics (Aboukhedr et al., 2018; Qin et al., 2020). For instance, there is still a lack of comprehensive comparison and benchmarking of pore-scale models for low Ca flow systems (Zhao et al., 2019). It has also been shown that because of the sensitivity of multiphase flow to local perturbations, a deterministic reproduction of the dynamics as observed in experiments with relatively large porous domains using numerical models is challenging, while statistical behaviors can still be captured (Ferrari et al., 2015). The consideration of reactions, however, may require higher spatial accuracy because the spatial variations (in mineral distribution and reaction rate) can be important. The impacts of multiphase hydrodynamics on aqueous reactions and mineral reactions may also need to be considered separately. Taking the recirculation zone as an example, it increases interfacial mass transfer (Maes and Soulaine, 2018), but reduces mineral reactions (Deng et al., 2018). These research needs further emphasize the need for experimental studies that underpin the development of mechanistic models for multiphase flow in reactive systems, and studies that expand our investigations from quasi-2D micromodels to 3D systems. The development of constitutive relations will also require the investigations be extended to larger scales, which calls for development of a complementary approach that leverages modeling and experiments at different scales (Blunt et al., 2013).
Summary and Conclusions
A pore-scale multiphase reactive transport model was established and used to investigate the dependence of mineral reaction rate on pore-scale two-phase flow dynamics. A series of numerical simulations were performed, in which CO2-acidified water and air were co-injected at a range of velocities into 2D calcite channels with different levels of roughness as defined by a single sine wave. The simulation results showed that gas bubbles migrating through the reactive zone as a result of the two-phase co-injection caused the reaction rate to be lower than that of the single phase flow simulation with the same total injection rate. Our analyses revealed that the decrease of the mineral reaction rate is caused by a combination of two mechanisms: the reduction in the wetted surface area and the transport limitations that arise from the two phase flow. In the rough geometries, the narrow throats are reaction hotspots in the single phase flow simulations, whereas these locations are occupied by gas bubbles periodically and thus not accessible for reactions. Meanwhile, the flow field showed clear “vortices,” i.e., recirculation zones, as the gas bubbles migrate through the trough of the sine wave. As a result, more reaction products are trapped in the trough and the local thermodynamic driving force and kinetic rates are reduced. Additionally, the correlations between fluid saturation and the extent of reaction rate reduction—which is measured by the ratio between the reaction rate from the two-phase flow simulation and that from the corresponding single phase simulation—were analyzed to provide insights for continuum-scale modeling. A non-monotonic relationship was observed, which is because the contribution from wetted surface area reduction and local transport limitation show opposite dependence on the roughness of the channel, which controls the saturation for a given flow condition. Through these numerical simulations, we highlighted the complexity of reactive transport in multiphase flow systems and identified two important mechanisms through which mineral reaction rates are affected. These results highlight the need for consideration of interfacial dynamics on mineral reaction rates in multiphase flow systems, and also emphasize the need for experimental studies that underpin the development of mechanistic models for multiphase flow in reactive systems.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon reasonable request, without undue reservation.
Author Contributions
PL contributed to developing the code, designing the study, performing the simulations and analyses, and writing the manuscript. HD designed the study, contributed to code development, simulation results analyses, and writing the manuscript. SM contributed to code development and writing the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by the Laboratory Directed Research and Development (LDRD) award from Berkeley Lab, provided by the Director, Office of Science of the U.S. Department of Energy (DOE), and by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, DOE, under contract No. DE-AC02-05CH11231. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank Julien Maes and Vitalii Starchenko for helpful discussions on OpenFOAM, and thank the reviewers for the constructive comments and suggestions.
References
Aboukhedr, M., Georgoulas, A., Marengo, M., Gavaises, M., and Vogiatzaki, K. (2018). Simulation of micro-flow dynamics at low capillary numbers using adaptive interface compression. Comput. Fluids 165, 13–32. doi: 10.1016/j.compfluid.2018.01.009
Águila, J. F., Samper, J., Mon, A., and Montenegro, L. (2020). Dynamic update of flow and transport parameters in reactive transport simulations of radioactive waste repositories. Appl. Geochem. 117, 104585. doi: 10.1016/j.apgeochem.2020.104585
Akai, T., Blunt, M. J., and Bijeljic, B. (2020). Pore-scale numerical simulation of low salinity water flooding using the Lattice Boltzmann Method. J. Colloid Interface Sci. 566, 444–453. doi: 10.1016/j.jcis.2020.01.065
Alizadeh, M., and Fatemi, M. (2021). Pore-doublet computational fluid dynamic simulation of the effects of dynamic contact angle and interfacial tension alterations on the displacement mechanisms of oil by low salinity water. Int. J. Multiphase Flow 143, 103771. doi: 10.1016/j.ijmultiphaseflow.2021.103771
Andre, B., Molins, S., Johnson, J., and Steefel, C. I. (2013). Alquimia Computer Software. Retreived from: https://github.com/LBL-EESA/alquimiadev (accessed August 01, 2013).
Armstrong, R. T., Evseev, N., Koroteev, D., and Berg, S. (2015). Modeling the velocity field during Haines jumps in porous media. Adv. Water Resour. 77, 57–68. doi: 10.1016/j.advwatres.2015.01.008
Aziz, R., Joekar-Niasar, V., and Martinez-Ferrer, P. (2018). Pore-scale insights into transport and mixing in steady-state two-phase flow in porous media. Int. J. Multiphase Flow 51–62. doi: 10.1016/j.ijmultiphaseflow.2018.07.006
Berg, S., Ott, H., Klapp, S. A., Schwing, A., Neiteler, R., Brussee, N., et al. (2013). Real-time 3D imaging of Haines jumps in porous media flow. Proc. Natl. Acad. Sci. U.S.A. 110, 3755–3759. doi: 10.1073/pnas.1221373110
Blois, G., Barros, J. M., and Christensen, K. T. (2015). A microscopic particle image velocimetry method for studying the dynamics of immiscible liquid–liquid interactions in a porous micromodel. Microfluid. Nanofluidics 18, 1391–1406. doi: 10.1007/s10404-014-1537-1
Blunt, M. J., Bijeljic, B., Dong, H., Gharbi, O., Iglauer, S., Mostaghimi, P., et al. (2013). Pore-scale imaging and modelling. Adv. Water Resour. 51, 197–216. doi: 10.1016/j.advwatres.2012.03.003
Bolster, D., Dentz, M., and Le Borgne, T. (2009). Solute dispersion in channels with periodically varying apertures. Phys. Fluids 21, 056601. doi: 10.1063/1.3131982
Bolster, D., Méheust, Y., Le Borgne, T., Bouquain, J., and Davy, P. (2014). Modeling preasymptotic transport in flows with significant inertial and trapping effects – the importance of velocity correlations and a spatial Markov model. Adv. Water Resour. 70, 89–103. doi: 10.1016/j.advwatres.2014.04.014
Carrillo, F. J., Bourg, I. C., and Soulaine, C. (2020). Multiphase flow modeling in multiscale porous media: an open-source micro-continuum approach. J. Comput. Phys. X 8, 100073. doi: 10.1016/j.jcpx.2020.100073
Chen, L., He, Y., Tao, W.-Q., Zelenay, P., Mukundan, R., and Kang, Q. (2017). Pore-scale study of multiphase reactive transport in fibrous electrodes of vanadium redox flow batteries. Electrochim. Acta 248, 425–439. doi: 10.1016/j.electacta.2017.07.086
Chen, L., Kang, Q., Robinson, B. A., He, Y.-L., and Tao, W.-Q. (2013). Pore-scale modeling of multiphase reactive transport with phase transitions and dissolution-precipitation processes in closed systems. Phys. Rev. E 87, 043306. doi: 10.1103/PhysRevE.87.043306
Chen, L., Kang, Q., Tang, Q., Robinson, B. A., He, Y.-L., and Tao, W.-Q. (2015). Pore-scale simulation of multicomponent multiphase reactive transport with dissolution and precipitation. Int. J. Heat Mass. Transf. 85, 935–949. doi: 10.1016/j.ijheatmasstransfer.2015.02.035
Chou, L., Garrels, R. M., and Wollast, R. (1989). Comparative study of the kinetics and mechanisms of dissolution of carbonate minerals. Chem. Geol. 78, 269–282. doi: 10.1016/0009-2541(89)90063-6
Deising, D., Marschall, H., and Bothe, D. (2016). A unified single-field model framework for Volume-Of-Fluid simulations of interfacial species transfer applied to bubbly flows. Chem. Eng. Sci. 139, 173–195. doi: 10.1016/j.ces.2015.06.021
Deng, H., Molins, S., Trebotich, D., Steefel, C., and DePaolo, D. (2018). Pore-scale numerical investigation of the impacts of surface roughness: upscaling of reaction rates in rough fractures. Geochim. Cosmochim. Acta 239, 374–389. doi: 10.1016/j.gca.2018.08.005
Deshpande, S. S., Anumolu, L., and Trujillo, M. F. (2012). Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 5, 014016. doi: 10.1088/1749-4699/5/1/014016
Ferrari, A., Jimenez-Martinez, J., Le Borgne, T., Méheust, Y., and Lunati, I. (2015). Challenges in modeling unstable two-phase flow experiments in porous micromodels. Water Resour. Res. 51, 1381–1400. doi: 10.1002/2014wr016384
Govindarajan, D., Deshpande, A. P., and Raghunathan, R. (2018). Enhanced mobility of non aqueous phase liquid (NAPL) during drying of wet sand. J. Contam. Hydrol. 209, 1–13. doi: 10.1016/j.jconhyd.2017.12.005
Grunewald, J. B., Goswami, N., Mukherjee, P. P., and Fuller, T. F. (2021). Two-phase dynamics and hysteresis in the PEM fuel cell catalyst layer with the lattice-boltzmann method. J. Electrochem. Soc. 168, 024521. doi: 10.1149/1945-7111/abe5e8
Haroun, Y., Legendre, D., and Raynal, L. (2010a). Direct numerical simulation of reactive absorption in gas–liquid flow on structured packing using interface capturing method. Chem. Eng. Sci. 65, 351–356. doi: 10.1016/j.ces.2009.07.018
Haroun, Y., Legendre, D., and Raynal, L. (2010b). Volume of fluid method for interfacial reactive mass transfer: application to stable liquid film. Chem. Eng. Sci. 65, 2896–2909. doi: 10.1016/j.ces.2010.01.012
Heshmati, M., and Piri, M. (2018). Interfacial boundary conditions and residual trapping: a pore-scale investigation of the effects of wetting phase flow rate and viscosity using micro-particle image velocimetry. Fuel 224, 560–578. doi: 10.1016/j.fuel.2018.03.010
Hirt, C. W., and Nichols, B. D. (1981). Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225. doi: 10.1016/0021-9991(81)90145-5
Jiménez-Martínez, J., Anna, P., de, Tabuteau, H., Turuban, R., Borgne, T. L., and Méheust, Y. (2015). Pore-scale mechanisms for the enhancement of mixing in unsaturated porous media and implications for chemical reactions. Geophys. Res. Lett. 42, 5316–5324. doi: 10.1002/2015GL064513
Jiménez-Martínez, J., Hyman, J. D., Chen, Y., William Carey, J., Porter, M. L., Kang, Q., et al. (2020). Homogenization of dissolution and enhanced precipitation induced by bubbles in multiphase flow systems. Geophys. Res. Lett. 47:e2020GL087163. doi: 10.1029/2020GL087163
Jiménez-Martínez, J., Le Borgne, T., Tabuteau, H., and Méheust, Y. (2017). Impact of saturation on dispersion and mixing in porous media: photobleaching pulse injection experiments and shear-enhanced mixing model. Water Resour. Res. 53, 1457–1472. doi: 10.1002/2016WR019849
Jiménez-Martínez, J., Porter, M. L., Hyman, J. D., William Carey, J., and Viswanathan, H. S. (2016). Mixing in a three-phase system: enhanced production of oil-wet reservoirs by CO2 injection. Geophys. Res. Lett. 43, 196–205. doi: 10.1002/2015GL066787
Jo, D., and Revankar, S. T. (2009). Bubble mechanisms and characteristics at pore scale in a packed-bed reactor. Chem. Eng. Sci. 64, 3179–3187. doi: 10.1016/j.ces.2009.04.006
Johnson, J. W., Nitao, J. J., and Knauss, K. G. (2004). Reactive transport modelling of CO2 storage in saline aquifers to elucidate fundamental processes, trapping mechanisms and sequestration partitioning. Geol. Soc. Lond. Spec. Publ. 233, 107–128. doi: 10.1144/GSL.SP.2004.233.01.08
Johnson, J. W., Nitao, J. J., Steefel, C. I., and Knauss, K. G. (2001). “Reactive transport modeling of geologic CO2 sequestration in saline aquifers: the influence of intra-aquifer shales and the relative effectiveness of structural, solubility, and mineral trapping during prograde and retrograde sequestration,” in First National Conference on Carbon Sequestration (Washington, DC: National Energy and Technology Laboratory USA), 14–17.
Karadimitriou, N. K., Joekar-Niasar, V., Babaei, M., and Shore, C. A. (2016). Critical role of the immobile zone in non-Fickian two-phase transport: a new paradigm. Environ. Sci. Technol. 50, 4384–4392. doi: 10.1021/acs.est.5b05947
Karadimitriou, N. K., Joekar-Niasar, V., and Brizuela, O. G. (2017). Hydro-dynamic solute transport under two-phase flow conditions. Sci. Rep. 7, 6624. doi: 10.1038/s41598-017-06748-1
Kitanidis, P. K., and Dykaar, B. B. (1997). Stokes flow in a slowly varying two-dimensional periodic pore. Transp. Porous Media 26, 89–98. doi: 10.1023/A:1006575028391
Kumar, R., and Mohanty, K. K., and Others (2011). “Sweep efficiency of heavy oil recovery by chemical methods,” in SPE Annual Technical Conference and Exhibition (Society of Petroleum Engineers). doi: 10.2118/146839-MS
Li, Y., Blois, G., Kazemifar, F., and Christensen, K. T. (2019). High-speed quantification of pore-scale multiphase flow of water and supercritical CO2 in 2-D heterogeneous porous micromodels: flow regimes and interface dynamics. Water Resour. Res. 55, 3758–3779. doi: 10.1029/2018WR024635
Li, Y., Blois, G., Kazemifar, F., Molla, R. S., and Christensen, K. T. (2021). Pore-scale dynamics of liquid CO2-water displacement in 2D axisymmetric porous micromodels under strong drainage and weak imbibition conditions: high-speed μPIV measurements. Front. Water 3:710370. doi: 10.3389/frwa.2021.710370
Li, Y., Kazemifar, F., Blois, G., and Christensen, K. T. (2017). Micro-PIV measurements of multiphase flow of water and liquid CO2 in 2-D heterogeneous porous micromodels. Water Resour. Res. 53, 6178–6196. doi: 10.1002/2017WR020850
Lichtner, P., and Karra, S. (2014). “Modeling multiscale-multiphase-multicomponent reactive flows in porous media: application to CO2 sequestration and enhanced geothermal energy using PFLOTRAN,” in Computational Models for CO2 Geo-sequestration and Compressed Air Energy Storage, eds R. Al-Khoury and J. Bundschuh (Boca Raton, FL: CRC Press), 81–136.
Lichtner, P. C., Hammond, G. E., Lu, C., Karra, S., Bisht, G., Andre, B., et al. (2015). PFLOTRAN User Manual: A Massively Parallel Reactive Flow and Transport Model for Describing Surface and Subsurface Processes. Technical Report, U.S. Department of Energy. doi: 10.2172/1168703
Maes, J., and Geiger, S. (2018). Direct pore-scale reactive transport modelling of dynamic wettability changes induced by surface complexation. Adv. Water Resour. 111, 6–19. doi: 10.1016/j.advwatres.2017.10.032
Maes, J., and Soulaine, C. (2018). A new compressive scheme to simulate species transfer across fluid interfaces using the volume-of-fluid method. Chem. Eng. Sci. 190, 405–418. doi: 10.1016/j.ces.2018.06.026
Mahabadi, N., Zheng, X., Yun, T. S., van Paassen, L., and Jang, J. (2018). Gas bubble migration and trapping in porous media: pore-scale simulation. J. Geophys. Res. Solid. Earth 123, 1060–1071. doi: 10.1002/2017JB015331
Malekzadeh, S., and Roohi, E. (2015). Investigation of different droplet formation regimes in a T-junction microchannel using the VOF technique in OpenFOAM. Microgravity Sci. Technol. 27, 231–243. doi: 10.1007/s12217-015-9440-2
Marschall, H., Hinterberger, K., Schüler, C., Habla, F., and Hinrichsen, O. (2012). Numerical simulation of species transfer across fluid interfaces in free-surface flows using OpenFOAM. Chem. Eng. Sci. 78, 111–127. doi: 10.1016/j.ces.2012.02.034
Mi, S., Weldetsadik, N. T., Hayat, Z., Fu, T., Zhu, C., Jiang, S., et al. (2019). Effects of the gas feed on bubble formation in a microfluidic T-junction: constant-pressure versus constant-flow-rate injection. Ind. Eng. Chem. Res. 58, 10092–10105. doi: 10.1021/acs.iecr.9b01262
Mohammadi Alamooti, A. H., Azizi, Q., and Davarzani, H. (2020). Direct numerical simulation of trapped-phase recirculation at low capillary number. Adv. Water Resour. 145, 103717. doi: 10.1016/j.advwatres.2020.103717
Molins, S., Trebotich, D., Steefel, C. I., and Shen, C. (2012). An investigation of the effect of pore scale flow on average geochemical reaction rates using direct numerical simulation. Water Resour. Res. 48, W03527. doi: 10.1029/2011WR011404
Molins, S., Trebotich, D., Yang, L., Ajo-Franklin, J. B., Ligocki, T. J., Shen, C., et al. (2014). Pore-scale controls on calcite dissolution rates from flow-through laboratory and numerical experiments. Environ. Sci. Technol. 48, 7453–7460. doi: 10.1021/es5013438
Moura, M., Flekkøy, E. G., Måløy, K. J., Schäfer, G., and Toussaint, R. (2019). Connectivity enhancement due to film flow in porous media. Phys. Rev. Fluids 4, 094102. doi: 10.1103/PhysRevFluids.4.094102
Ngien, S. K., Rahman, N. A., Bob, M. M., Ahmad, K., Sa'ari, R., and Lewis, R. W. (2012). Observation of light non-aqueous phase liquid migration in aggregated soil using image analysis. Transp. Porous Media 92, 83–100. doi: 10.1007/s11242-011-9892-9
Ott, H., and Oedai, S. (2015). Wormhole formation and compact dissolution in single- and two-phase CO2-brine injections. Geophys. Res. Lett. 42, 2270–2276. doi: 10.1002/2015GL063582
Pan, Y., Yang, J., Jia, Y., and Xu, Z. (2016). Experimental study on non-aqueous phase liquid multiphase flow characteristics and controlling factors in heterogeneous porous media. Environ. Earth Sci. 75, 75. doi: 10.1007/s12665-015-4888-3
Paulsen, J. D., Carmigniani, R., Kannan, A., Burton, J. C., and Nagel, S. R. (2014). Coalescence of bubbles and drops in an outer fluid. Nat. Commun. 5, 1–7. doi: 10.1038/ncomms4182
Pavuluri, S., Maes, J., and Doster, F. (2018). Spontaneous imbibition in a microchannel: analytical solution and assessment of volume of fluid formulations. Microfluid. Nanofluidics. 22:90. doi: 10.007/s10404-018-2106-9
Picchi, D., and Battiato, I. (2018). The impact of pore-scale flow regimes on upscaling of immiscible two-phase flow in porous media. Water Resour. Res. 54, 6683–6707. doi: 10.1029/2018WR023172
Popp, S., Beyer, C., Dahmke, A., and Bauer, S. (2015). Model development and numerical simulation of a seasonal heat storage in a contaminated shallow aquifer. Energy Proc. 76, 361–370. doi: 10.1016/j.egypro.2015.07.842
Pruess, K. (2004). The TOUGH codes—a family of simulation tools for multiphase flow and transport processes in permeable media. Vadose Zone J. 3, 738–746. doi: 10.2113/3.3.738
Qin, Z., Esmaeilzadeh, S., Riaz, A., and Tchelepi, H. A. (2020). Two-phase multiscale numerical framework for modeling thin films on curved solid surfaces in porous media. J. Comput. Phys. 413, 109464. doi: 10.1016/j.jcp.2020.109464
Ren, T., Zhu, Z., Zhang, R., Shi, J., and Yan, C. (2020). Visualization experiment of bubble coalescence in a narrow vertical rectangular channel. Front. Energy Res. 8, 96. doi: 10.3389/fenrg.2020.00096
Roman, S., Abu-Al-Saud, M. O., Tokunaga, T., Wan, J., Kovscek, A. R., and Tchelepi, H. A. (2017). Measurements and simulation of liquid films during drainage displacements and snap-off in constricted capillary tubes. J. Colloid Interface Sci. 507, 279–289. doi: 10.1016/j.jcis.2017.07.092
Roman, S., Soulaine, C., AlSaud, M. A., Kovscek, A., and Tchelepi, H. (2016). Particle velocimetry analysis of immiscible two-phase flow in micromodels. Adv. Water Resour. 95, 199–211. doi: 10.1016/j.advwatres.2015.08.015
Rücker, M., Berg, S., Armstrong, R. T., Georgiadis, A., Ott, H., Schwing, A., et al. (2015). From connected pathway flow to ganglion dynamics. Geophys. Res. Lett. 42, 3888–3894. doi: 10.1002/2015GL064007
Rusche, H. (2002). Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D., Imperial College London.
Satter, A., and Iqbal, G. M. (2016). “Reservoir rock properties,” Reservoir Engineering, ed A. Satter and G. M. Iqbal (Boston, MA: Gulf Professional Press), 29–79.
Schlüter, S., Berg, S., Rücker, M., Armstrong, R. T., Vogel, H.-J., Hilfer, R., et al. (2016). Pore-scale displacement mechanisms as a source of hysteresis for two-phase flow in porous media. Water Resour. Res. 52, 2194–2205. doi: 10.1002/2015WR018254
Shuard, A. M., Mahmud, H. B., and King, A. J. (2016). Comparison of two-phase pipe flow in openfoam with a mechanistic model. IOP Conf. Ser. Mater. Sci. Eng. 121, 012018. doi: 10.1088/1757-899X/121/1/012018
Song, W., Ogunbanwo, F., Steinsb,ø, M., Fern,ø, M. A., and Kovscek, A. R. (2018). Mechanisms of multiphase reactive flow using biogenically calcite-functionalized micromodels. Lab Chip 18, 3881–3891. doi: 10.1039/C8LC00793D
Sonnenthal, E., Ito, A., Spycher, N., Yui, M., Apps, J., Sugita, Y., et al. (2005). Approaches to modeling coupled thermal, hydrological, and chemical processes in the drift scale heater test at Yucca Mountain. Int. J. Rock Mech. Min. Sci. 42, 698–719. doi: 10.1016/j.ijrmms.2005.03.009
Sookhak Lari, K., Davis, G. B., Rayner, J. L., Bastow, T. P., and Puzon, G. J. (2019). Natural source zone depletion of LNAPL: a critical review supporting modelling approaches. Water Res. 157, 630–646. doi: 10.1016/j.watres.2019.04.001
Soulaine, C., Maes, J., and Roman, S. (2021). Computational microfluidics for geosciences. Front. Water 3:643714. doi: 10.3389/frwa.2021.643714
Soulaine, C., Roman, S., Kovscek, A., and Tchelepi, H. A. (2018). Pore-scale modelling of multiphase reactive flow: application to mineral dissolution with production of. J. Fluid Mech. 855, 616–645. doi: 10.1017/jfm.2018.655
Spurin, C., Bultreys, T., Bijeljic, B., Blunt, M. J., and Krevor, S. (2019). Intermittent fluid connectivity during two-phase flow in a heterogeneous carbonate rock. Phys. Rev. E 100, 043103. doi: 10.1103/PhysRevE.100.043103
Steefel, C. I., Appelo, C. A. J., Arora, B., Jacques, D., Kalbacher, T., Kolditz, O., et al. (2015). Reactive transport codes for subsurface environmental simulation. Comput. Geosci. 19, 445–478. doi: 10.1007/s10596-014-9443-x
Sund, N. L., Bolster, D., and Dawson, C. (2015). Upscaling transport of a reacting solute through a peridocially converging–diverging channel at pre-asymptotic times. J. Contam. Hydrol. 182, 1–15. doi: 10.1016/j.jconhyd.2015.08.003
Toussaint, R., Maloy, K. J., Meheust, Y., Lovoll, G., Jankov, M., Schaefer, G., et al. (2012). Two-phase flow: structure, upscaling, and consequences for macroscopic transport properties. Vadose Zone J. 11:vzj2011.0123. doi: 10.2136/vzj2011.0123
van Steijn, V., Kleijn, C. R., and Kreutzer, M. T. (2010). Predictive model for the size of bubbles and droplets created in microfluidic T-junctions. Lab Chip 10, 2513–2518. doi: 10.1039/c002625e
Wang, C., Mehmani, Y., and Xu, K. (2021). Capillary equilibrium of bubbles in porous media. Proc. Natl. Acad. Sci. U.S.A. 118, e2024069118. doi: 10.1073/pnas.2024069118
Wu, R., Chen, X., Hammond, G., Bisht, G., Song, X., Huang, M., et al. (2021). Coupling surface flow with high-performance subsurface reactive flow and transport code PFLOTRAN. Environ. Model. Softw. 137, 104959. doi: 10.1016/j.envsoft.2021.104959
Xiao, T., Xu, H., Moodie, N., Esser, R., Jia, W., Zheng, L., et al. (2020). Chemical-mechanical impacts of CO2 intrusion into heterogeneous caprock. Water Resour. Res. 56:e2020WR027193. doi: 10.1029/2020WR027193
Xiong, Q., Baychev, T. G., and Jivkov, A. P. (2016). Review of pore network modelling of porous media: experimental characterisations, network constructions and applications to reactive transport. J. Contam. Hydrol. 192, 101–117. doi: 10.1016/j.jconhyd.2016.07.002
Xu, T., Spycher, N., Sonnenthal, E., Zhang, G., Zheng, L., and Pruess, K. (2011a). TOUGHREACT Version 2.0: a simulator for subsurface reactive transport under non-isothermal multiphase flow conditions. Comput. Geosci. 37, 763–774. doi: 10.1016/j.cageo.2010.10.007
Xu, T., Zheng, L., and Tian, H. (2011b). Reactive transport modeling for CO2 geological sequestration. J. Pet. Sci. Eng. 78, 765–777. doi: 10.1016/j.petrol.2011.09.005
Xu, T., Zhu, H., Feng, G., Yang, Z., and Tian, H. (2019). Numerical simulation of calcite vein formation and its impact on caprock sealing efficiency – case study of a natural CO2 reservoir. Int. J. Greenhouse Gas Control 83, 29–42. doi: 10.1016/j.ijggc.2019.01.021
Yin, X., Zarikos, I., Karadimitriou, N. K., Raoof, A., and Hassanizadeh, S. M. (2019). Direct simulations of two-phase flow experiments of different geometry complexities using Volume-of-Fluid (VOF) method. Chem. Eng. Sci. 195, 820–827. doi: 10.1016/j.ces.2018.10.029
Yoon, S., and Kang, P. K. (2021). Roughness, inertia, and diffusion effects on anomalous transport in rough channel flows. Phys. Rev. Fluids 6, 014502. doi: 10.1103/PhysRevFluids.6.014502
Zhang, Y., and Morrow, N. R. Others (2006). “Comparison of secondary and tertiary recovery with change in injection brine composition for crude-oil/sandstone combinations,” in SPE/DOE Symposium on Improved Oil Recovery (Society of Petroleum Engineers). doi: 10.2118/99757-MS
Keywords: multiphase reactive transport, pore-scale, reaction rate, gas bubble, roughness
Citation: Li P, Deng H and Molins S (2022) The Effect of Pore-Scale Two-Phase Flow on Mineral Reaction Rates. Front. Water 3:734518. doi: 10.3389/frwa.2021.734518
Received: 01 July 2021; Accepted: 29 November 2021;
Published: 06 January 2022.
Edited by:
Harrie-Jan Hendricks Franssen, Helmholtz Association of German Research Centres (HZ), GermanyReviewed by:
Julien Maes, Heriot-Watt University, United KingdomJames E. McClure, Virginia Tech, United States
Copyright © 2022 Li, Deng and Molins. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hang Deng, aGFuZ2RlbmdAbGJsLmdvdg==; aGFuZ2RlbmczMTBAZ21haWwuY29t
 Pei Li
Pei Li Hang Deng
Hang Deng Sergi Molins
Sergi Molins