The Role of Basin Geometry in Mountain Snowpack Responses to Climate Change

Shea, Joseph M.; Whitfield, Paul H.; Fang, Xing; Pomeroy, John W.

doi:10.3389/frwa.2021.604275

ORIGINAL RESEARCH article

Front. Water, 11 February 2021

Sec. Water and Hydrocomplexity

Volume 3 - 2021 | https://doi.org/10.3389/frwa.2021.604275

This article is part of the Research Topic Water Resources of Mountainous Basins in a Changing Climate View all 4 articles

The Role of Basin Geometry in Mountain Snowpack Responses to Climate Change

$\nJoseph M. Shea,$ Joseph M. Shea^1,2^*

Paul H. Whitfield²

Xing Fang²

John W. Pomeroy²

¹Geography Program, University of Northern British Columbia, Prince George, BC, Canada
²Centre for Hydrology, University of Saskatchewan, Canmore, AB, Canada

Snowmelt contributions to streamflow in mid-latitude mountain basins typically dominate other runoff sources on annual and seasonal timescales. Future increases in temperature and changes in precipitation will affect both snow accumulation and seasonal runoff timing and magnitude, but the underlying and fundamental roles of mountain basin geometry and hypsometry on snowmelt sensitivity have received little attention. To investigate the role of basin geometry in snowmelt sensitivity, a linear snow accumulation model and the Cold Regions Hydrological Modeling (CRHM) platform driven are used to estimate how hypsometry affects basin-wide snow volumes and snowmelt runoff. Area-elevation distributions for fifty basins in western Canada were extracted, normalized according to their elevation statistics, and classified into three clusters that represent top-heavy, middle, and bottom-heavy basins. Prescribed changes in air temperature alter both the snow accumulation gradient and the total snowmelt energy, leading to snowpack volume reductions (10–40%), earlier melt onsets (1–4 weeks) and end of melt season (3 weeks), increases in early spring melt rates and reductions in seasonal areal melt rates (up to 50%). Basin hypsometry controls the magnitude of the basin response. The most sensitive basins are bottom-heavy, and have a greater proportion of their area at low elevations. The least sensitive basins are top-heavy, and have a greater proportion of their area at high elevations. Basins with similar proportional areas at high and low elevations fall in between the others in terms of sensitivity and other metrics. This work provides context for anticipating the impacts of ongoing hydrological change due to climate change, and provides guidance for both monitoring networks and distributed modeling efforts.

Introduction

In mountain basins, winter snowpacks typically represent the dominant component of warm-season streamflows (Cayan, 1996; Beniston, 1997; Barnett et al., 2005; Bales et al., 2006; Pomeroy et al., 2012). As a seasonal water reservoir, total snow volumes affect the timing and magnitude of the spring freshet, and can be contributing factors in large-scale flood events in western North America (Marks et al., 1998; Pomeroy et al., 2016). Li et al. (2017) demonstrate that 70% of stream flow in the western US originates as snow, despite snow being only 37% of the total annual precipitation. Changes in the timing of snowmelt are widely recognized as signs of a warming climate (Leith and Whitfield, 1998; Marks et al., 1998; Stone et al., 2002; Whitfield et al., 2002; Barnett et al., 2005; McCabe and Clark, 2005; Adam et al., 2009; López-Moreno et al., 2014; Rasouli et al., 2014), and how snow accumulation and snowmelt in mountain basins will respond to future climate change is a critical question.

Mountain Snow Accumulation and Melt

In mountains, the variation of snow depth with elevation can be complex (Pomeroy and Gray, 1995), though it typically increases with elevation (Langbein, 1947; Pomeroy and Brun, 2001; Barry, 2008; Grünewald and Lehning, 2011; Lehning et al., 2011). Vertical snow accumulation gradients in the mountains reflect orographic precipitation processes, time of year (Fitzharris, 1978) and redistribution by wind, vegetation and gravity (Ellis et al., 2010; MacDonald et al., 2010). Parsons and Castle (1959) suggested that the increasing snow water content with elevation could be represented as a “snow wedge” while Golding (1974) showed that snow depths in Marmot Creek were correlated with elevation but also affected by slope, aspect, and vegetation.

Zones of snow accumulation regimes have been defined based on hypsometry (Moore and Prowse, 1988), and accumulation totals will often decrease above a certain elevation threshold (Pomeroy and Gray, 1995; Grünewald et al., 2014; Zmax). In mountain environments, elevation is also a critical factor in determining snowpack sensitivity to climate change. Morán-Tejeda et al. (2013), for example, identified a threshold altitude of ~1,400 m in the Swiss Alps below which temperature is the main constraint. Sospedra-Alfonso et al. (2015) identified a similar threshold of ~1,560 m in the Rocky Mountains of Idaho and Montana. Warmer winters and shorter accumulation seasons will impact lower elevation snowpacks (Knowles and Cayan, 2004; Nolin and Daly, 2006; Bavay et al., 2013; Rasouli et al., 2015) to a greater degree than high-elevation snowpacks (Nayak et al., 2010; Klos et al., 2014; Harder et al., 2015; Pomeroy et al., 2015; Rasouli et al., 2019).

Mountain snowpack changes in recent decades have been widely examined, and declines in snowpack in the North American Cordillera are unprecedented and synchronous to springtime warming (Pederson et al., 2011). However, Mote et al. (2008, 2018) report large declines in snow water equivalent at low elevations and lesser declines at higher elevations in western United States. In colder climates, there are sometimes no declines observed at higher elevations (Harder et al., 2015) as warming rates have little effect on the phase of precipitation.

Mountain streamflow responses to climate change are also strongly elevation-dependent (Tennant et al., 2015). Schöner et al. (2009) showed that low elevation sites in the Austrian Alps have decreasing streamflow trends while high elevation sites were unchanged. Ongoing and projected climatic change in western North America will have profound impacts on the timing and magnitude of runoff derived from snow and ice in the near-term (Barnett et al., 2005; Adam et al., 2009), and the ratio of runoff from snow is predicted to decline by one third in a business as usual future scenario (Li et al., 2017). The specific role of basin hypsometry in the response of mountain basins to climate change has not been explored.

Basin Hypsometry

Topography plays an important role in the streamflow pattern of a basin (Horton, 1932). Basin geometry and area-altitude distributions (hypsometry) have been examined previously in the context of basin age and geomorphology (Strahler, 1952, 1957), erosional controls (Summerfield and Hulton, 1994), glaciation (Richmond, 1965; Brocklehurst and Whipple, 2004) and streamflow response (Langbein, 1947; Vivoni et al., 2008). Scaling relationships in many basins have led to methods to determine hydraulic and hydrological characteristics from basin geometry (Gray, 1961), and the hypsometric curve can indicate the relative importance of glaciation within a region (Brocklehurst and Whipple, 2004). How basin hypsometry affects hydrological responses to climate change remains an open question.

Basin hypsometries can be quickly extracted from digital elevation data, but have been underutilized for studies on regional hydrological change. Fassnacht et al. (2003) interpolated snow water equivalent across the Colorado River basin and found hypsometry information important in producing reliable estimates. Chevallier et al. (2014) compared interannual variation in seasonal snowcover, and the spatial distribution of glacierized area in Central Asia; they related the presence of snowcover and glaciers to hypsometry. Dey et al. (1989) used hypsometry to define where snow accumulates and thus affects the generation of water.

Luo and Harlin (2003) presented a theoretical travel time that is based upon basin hypsometry as a way of characterizing the effects of basin morphometry while Vivoni et al. (2008) demonstrated that runoff components are a function of the hypsometric form. Allamano et al. (2009) provided a minimalist model of flood generation using basin hypsometry and explained the attenuation of flood quantiles by the hypsometry of high-elevation basins. Comeau et al. (2009) compared hydrographs of glacierized and non-glacierized basins with similar hypsometry to isolate the glacial melt contribution to streamflow. Snehmani et al. (2015) established the relationship between meteorological parameters, temperature and snowfall, and seasonal snowcover in a glacierized catchment; incorporating hypsometry into the interpolation improved the accuracy of their model.

The role of hypsometry in snow accumulation and melt has been explored previously for individual basins or glaciers (Fitzharris and Garr, 1995; Evans et al., 2008; Shea and Immerzeel, 2016; McGrath et al., 2017). Snowmelt correlates with elevation through connections with temperature, snow cover, hypsometry and vegetation, and a critical elevation zone that varies through the melt season has been identified previously (Biggs and Whitaker, 2012). Jenicek et al. (2018) examined future changes in alpine snowpack and showed the largest relative decreases below 2,200 m.

A suite of models ranging from spatially lumped empirical approaches to spatially distributed physically-based models have been used to investigate individual basin or regional responses to climate change (Whitfield et al., 2002; Pomeroy et al., 2012; Rasouli et al., 2019). Yet structural, parametric, and input data uncertainty can limit the application of highly detailed models for resolving variations in responses between basins. As in other disciplines, simplified models that capture the key processes and critical hydrological functions allow specific components of a hydrological system to be examined, but sometimes can contain a difficult to quantify uncertainty (Koutsoyiannis, 2006; Fleming, 2009; Molini et al., 2011; Zeng et al., 2012; Whitfield, 2013). Recent modeling using physically based approaches and climate model outputs has shown a wide range of sensitivity to climate change and resulting coupling to streamflow regimes (Rasouli et al., 2019; López-Moreno et al., 2020).

Basin hypsometry, combined with local snow accumulation gradients, will ultimately determine the elevation range at which the majority of total snowpack volume occurs in any given basin. Many studies have reported increases in snow depth and snow water equivalent [SWE] with elevation; Supplementary Table 1 summarizes measured gradients and studies that considered the role of elevation in snow accumulation and subsequent redistribution. Rhea and Grant (1974) showed that 80% of the variance in snow depth could be explained by elevation and upwind barriers in the Colorado Rocky Mountains. In many studies and locations, elevation is a significant predictor of snow depth (Erickson et al., 2005; Deems et al., 2006, 2008; Casola et al., 2009; Dixon et al., 2014) but redistribution is important at local scales (Bernhardt and Schulz, 2010; Bernhardt et al., 2012; Ménard et al., 2014). Grünewald et al. (2013, 2014) showed that snow accumulations increase with elevation until wind and gravity redistribution reduce snow depths at higher elevations.

Objectives

The objectives of this study are to isolate the effects of basin geometry and hypsometry on the hydrological response of snow-dominated mountain basins to climate change. In particular, the role of hypsometry in regulating (a) total snowpack volumes and (b) the timing and magnitude of snowmelt runoff are examined using a model that prescribes vertical snow accumulation gradients and daily melt rates from surface energy balance calculations. The model is applied using synthetic forcing data and the real-world hypsometries of fifty mountain basins in western Canada. The methodology is designed to isolate the hypsometric influence on maximum snowpack volumes and snowmelt responses to climate warming, and so all basins have the same minimum and maximum elevation, but the distribution of area with elevation reflects individual basin geometries and the hypsometries were normalized to ensure comparability.

Data and Methods

To isolate the role of basin hypsometry, this modeling experiment applies regionally representative snow accumulation gradients and melt model forcing data to 50 mountain basins that have identical elevation ranges, but varying hypsometries. Model discretization was set up to consider only elevation, so differences in modeled snowpack volumes and snowmelt timing and rate arise solely from variations in hypsometry. Hypsometric data, regional climate assumptions, hydrological model setup, snowmelt metrics, and climate change experiments are discussed in this section.

Hypsometry

Fifty mountain basins adjacent to the Continental Divide in western Canada were selected for the analysis (Figure 1). These basins range in size from 670 to 23,817 km², and have an average size of 5,910 km². Average minimum, mean, and maximum elevations (and their standard deviations) of the 50 basins are 818 ± 306, 1,530 ± 322, and 2,897 ± 473 m, respectively.

FIGURE 1

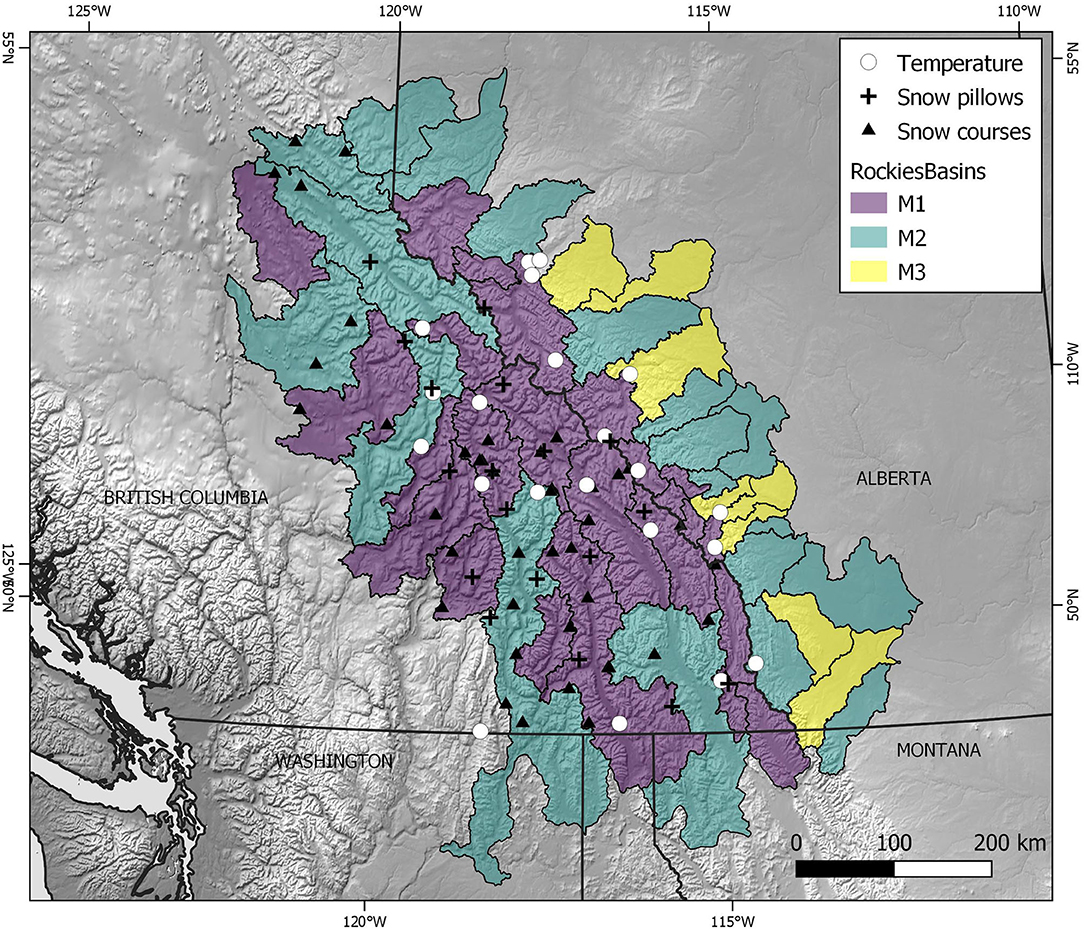
Figure 1. Location of 50 river basins, automated snow pillows, manual snow course sites, and temperature stations from the western Cordillera in southern Canada and northern USA used in this study. Basins are color coded by hypsometry class according to the cluster analysis.

Using basin outlines, digital elevation data were extracted at a 1 km resolution from the GLOBE elevation product (Hastings et al., 1999). For each basin, elevation profiles were produced and absolute and normalized hypsometries were generated using 49 elevation intervals (e.g., Figure 2). Basin hypsometries are generally insensitive to the resolution of the input elevation data used (Hurtrez et al., 1999), so the 1 km resolution data is assumed to be suitable.

FIGURE 2

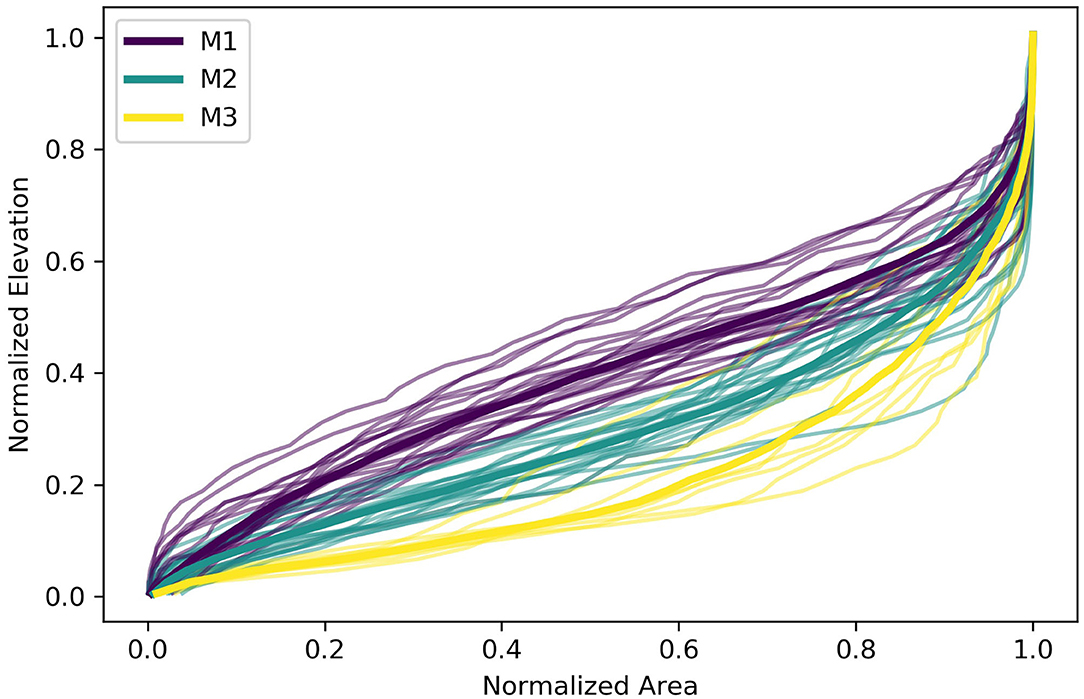
Figure 2. Normalized hypsometries for 50 mountain basins shown in Figure 1 (thin lines), color coded by cluster type. Mean cluster hypsometries are given by bold lines.

Normalized hypsometries (cumulative area vs. elevation) were clustered using a k-means cluster analysis implemented in Python. Three clusters were selected based on a scree plot of within-group sum of squares for different numbers of clusters. The resulting classifications (Figure 2) correspond to variations on the classic Strahler “Mature” hypsometry (Strahler, 1952, 1957) and are referred to here as “M1” (top heavy), “M2” (intermediate), and “M3” (bottom heavy).

Snow Accumulation

Snowfall in mountainous regions typically increases with elevation, though gradients can vary spatially and temporally (Table 1). In order to isolate the role of hypsometry on basin snow volume responses, a linear snowfall gradient of 0.50 mm w.e. m⁻¹ is assumed based on (1) winter (NDJF) climate normals from 61 stations in the region (Shea et al., 2004) and (2) gridded snowfall data from the ClimNA project (Wang et al., 2016). For simplicity, we assume that the elevation where snowfall is zero is at sea level (0 m), which is also consistent with the intercept obtained in seasonal snowfall-elevation regressions (Shea et al., 2004). To capture early season snowpack energetics, the snowpack is initialized for each basin on 1 January, and is assumed to represent the maximum snow accumulation in the basin. Transient snow accumulation and redistribution is not modeled in this study. Real-world accumulation gradients will show distinct regional and local differences based on climate, snow redistribution, orographic enhancement, vegetation, and slope and aspect, but these are neglected here in order to highlight the role of hypsometry.

TABLE 1

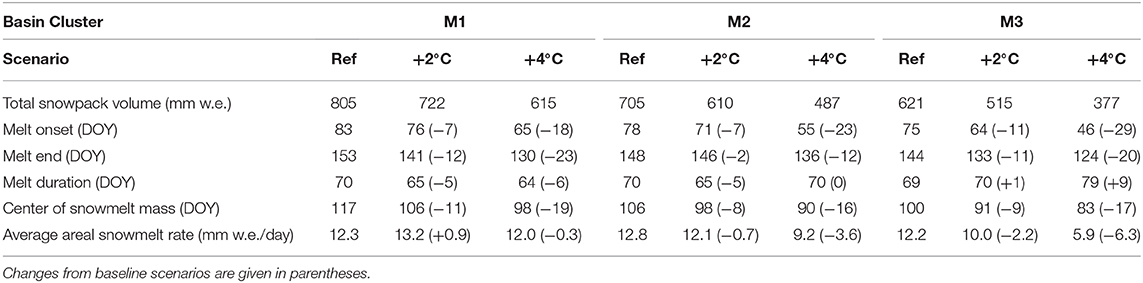
Table 1. Summary of snowpack volume and snowmelt metrics for three basin hypsometries and warming scenarios.

Compared with 18 long-term automatic snow pillows and 44 manual snow courses in British Columbia that range in elevation from 608 to 2,203 m (Supplementary Tables 2,3) the linear gradient provides a reasonable estimate of 1 April SWE (Figure 3). Observations of 1 April SWE are taken directly from the snow pillow data, and from snow course surveys taken within 1 week of 1 April. While the linear gradient does not take into account redistribution by wind and gravity, the role of slope and aspect in mid-winter ablation, or vegetation interception, the snowpack approximation is sufficient for the modeling purposes here. The calculated Root Mean Squared Error (RMSE) of 309 mm is lower than the interannual standard deviation of 1 Apr SWE at most sites, while the Mean Bias Error (MBE) of +130 mm reflects an overestimation of SWE. Overall, the linear accumulation model explains 52% of the variance in the observed 1 April SWE.

FIGURE 3

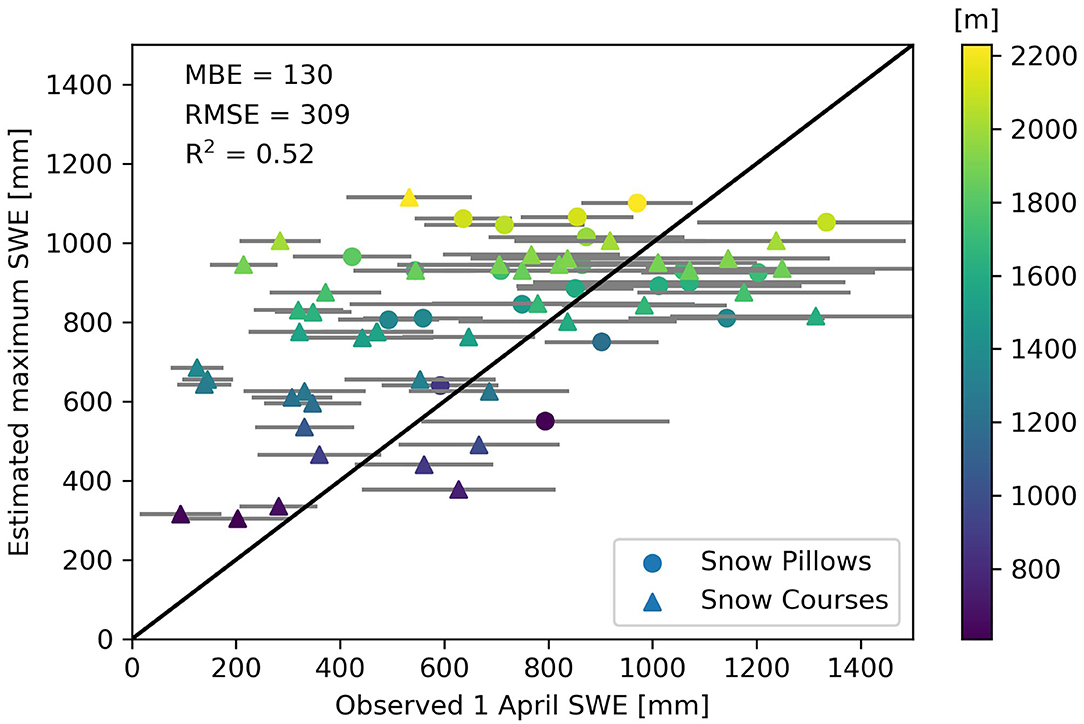
Figure 3. Mean observed 1 April SWE (± standard deviation) for 18 snow pillow sites (circles) and 44 manual snow course sites (triangles) within the study region (see Figure 1), versus maximum SWE estimated from a simple linear accumulation gradient of 0.50 mm w.e. m⁻¹. Points are color-coded by station elevation.

Snowmelt

Snowmelt was simulated using the Cold Regions Hydrological Modeling platform (CRHM) developed by Pomeroy et al. (2007). CRHM has been used extensively in mountain, prairie, and alpine regions to investigate snowpack energetics, melt, and hydrology (e.g., Ellis et al., 2010; Pomeroy et al., 2012; López-Moreno et al., 2013; Krogh et al., 2015; Rasouli et al., 2015).

CRHM is a modular modeling platform built on a library of processes that can be linked to simulate the hydrological response of hydrological response units (HRUs). As the current study is focused primarily on capturing the energetics of snowmelt across the elevation range of a synthetic basin, the routines for radiation, evaporation, snowmelt are the primary focus, and HRUs are represented by elevation band only. Slope and aspect are not factored into snowmelt calculations performed here, and landcover is assumed to be without vegetation.

To calculate snowmelt, CRHM applied here uses Energy-Budget Snowmelt Model (Gray and Landine, 1988) to account for fluxes of energy transferred to the surface through radiation, convection, conduction and advection, and calculates the change in internal energy of the snowpack (dU/dt):

\begin{array}{l} Q_{m} + Q_{N} + Q_{E} + Q_{H} + Q_{G} + Q_{D} = d U / d t & (1) \end{array}

where Q_m is the energy available for snowmelt, Q_N is net radiation, Q_E and Q_H are the latent and sensible heat fluxes, respectively, Q_G is the ground heat flux, and Q_D is the energy advected from external sources such as rain-on-snow. Fluxes directed into the snowpack are positive, and are calculated daily. This is one of the simplest and most robust energy budget snowmelt routines available and is suitable where there is uncertainty in meteorological inputs as it uses a daily timestep. Details on the energy budget calculations, model parameters, and routines can be found in Pomeroy et al. (2007) and Krogh et al. (2015). It should be noted that CRHM was configured here without infiltration, subsurface or surface storage or routing and was initialized with a simple elevational gradient snow accumulation and no snow redistribution.

For this experiment, CRHM was run in point mode using the midpoints of 49 elevation bands that span from 818 to 2,897 m. Model inputs include mean daily air temperature, and potential daily radiation calculated for 52.5N, −117.5W. For the purposes of this study, constant values were used for atmospheric transmissivity (0.7), cloudiness (50%), relative humidity (50%), and wind speed (2 m/s).

Mean daily air temperatures were simulated from a sinusoidal curve based on an average annual temperature of 10°C at sea-level, and an annual temperature range of 20°C. Natural air temperature variability and diurnal variations were simulated by adding a random diurnal variability with a range of ±5°C (Whitfield, 2014). This approach provides a reasonable approximation of monthly air temperatures (RMSE = 0.16°C, and MBE = −0.55°C) observed at stations that capture a range of elevations in the region (Figure 4).

FIGURE 4

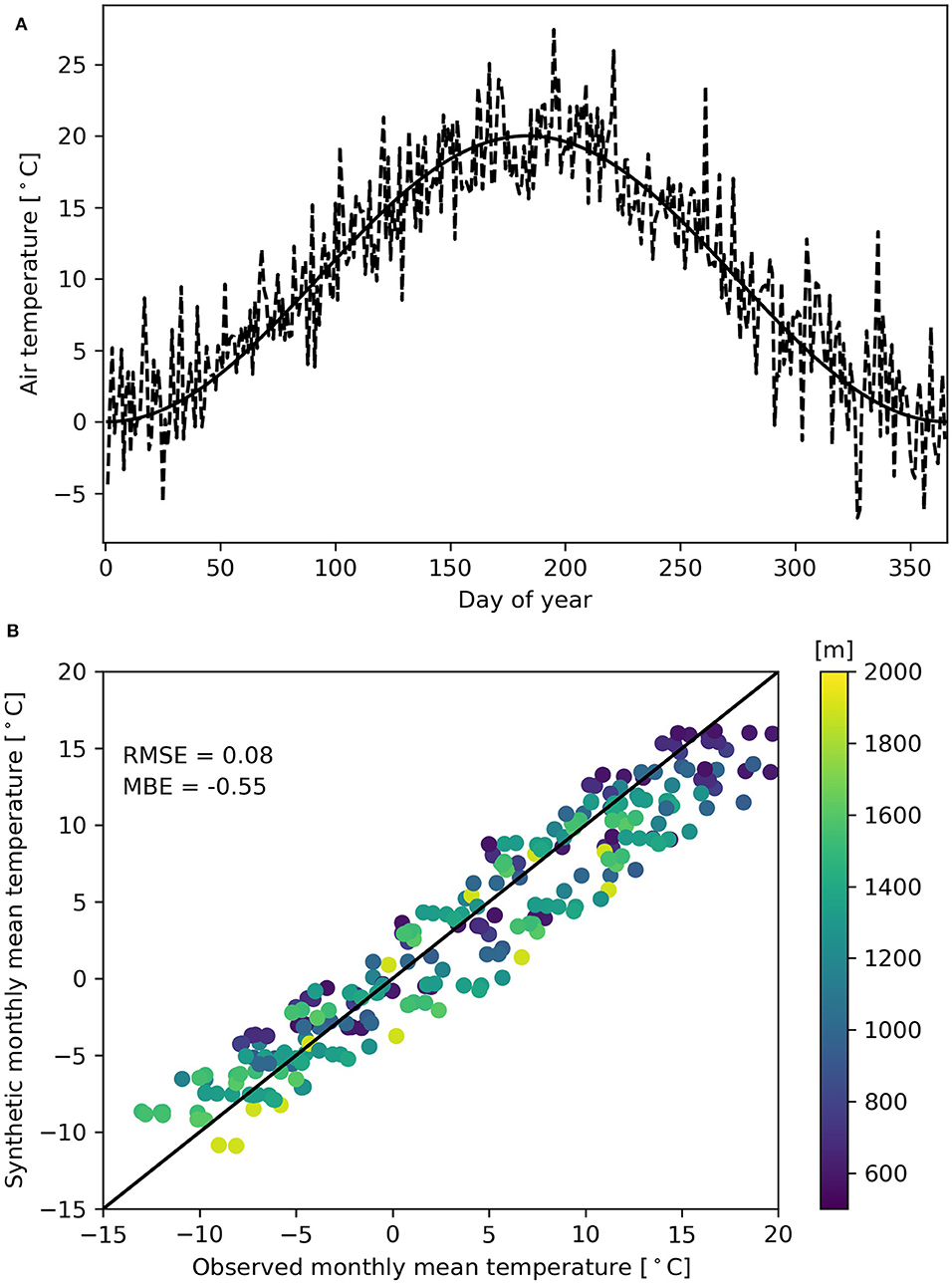
Figure 4. (A) Example synthetic annual temperature series for 2,000 m elevation. Mean daily temperatures (solid) are a function of day of year, and random noise (dashed) approximates diurnal variability. (B) Synthetic monthly temperatures vs. 1981–2010 monthly climate normals from 23 stations in the region (Figure 1). Points are color-coded by station elevation.

Climate Change, Snow Accumulation, and Snowmelt Timing

To examine the effects of hypsometry on basin-scale sensitivities to climate change, the model was first run for all 50 basins in a reference mode, using the synthetic accumulation and melt model inputs that reflect climate normals in the region. Scenarios of +2 and +4°C were then applied to the temperature series, and the linear snow accumulation gradient was changed to reflect the increase in minimum snowline elevation associated with each temperature scenario. CRHM was then re-run for each basin with the perturbed forcing data. Differences in basin snowpack and snowmelt responses to increased temperatures are thus a product of the hypsometry of the individual basins only. This approach does not consider differences in absolute elevations of each basin (which will affect both accumulation totals and melt energy) or regional/seasonal variations in either accumulation gradients (e.g., Figure 3) or air temperature gradients (Figure 4), or how these quantities might change with future climate change.

Snow Volume Changes

Observational and modeling evidence suggests that snowfall at higher elevations is less sensitive to warming than lower elevations (Mote et al., 2005; López-Moreno et al., 2009; Minder, 2010; Sproles et al., 2013). At Marmot Creek basin in the eastern Canadian Rockies, warming over the past half century had little effect on peak SWE at high elevations, and a large impact on peak SWE at low elevations and these differences are still evident in modeling the sensitivity to future climates (Harder et al., 2015; Fang and Pomeroy, 2020). To simulate a changing accumulation gradient that disproportionately affects lower elevations, the elevation where accumulation is assumed to equal zero (Z_min) is shifted upwards for different temperature scenarios. Accumulation is kept constant at the highest elevations, and the gradient is recalculated.

The change in Z_min is based on the prescribed temperature change (+2 or +4°C) and an assumed vertical temperature gradient of −0.0065°C/m. A +2°C temperature increase, for example, raises the minimum snowline elevation by 2/γ_S, or 333 m. To maintain the accumulation rate at the top of the basin the accumulation gradient changes from 0.50 to 0.56 mm w.e. m⁻¹. For a temperature increase of +4°C, the minimum snowline elevation increases by 666 m, and the accumulation gradient increases to 0.65 mm w.e. m⁻¹. The increase in snowline elevation and lack of change in snowfall volume are consistent with GCM simulations in the Swiss Alps (Gobiet et al., 2014).

Snowmelt Changes

Increases in air temperature will affect incoming longwave radiation, as well as the near-surface gradients of air temperature and vapor density that determine the turbulent heat fluxes. As a result, a warmer climate will affect the timing of melt onset, the center of snowmelt mass, and the duration of the snowmelt season. The effect of hypsometry on these metrics has not been previously isolated, as natural streamflows are inherently noisy and isolating the snowmelt component requires either streamflow separation techniques or detailed hydrological modeling (difficult in data-sparse regions). This approach thus provides a first-order estimate of the role of basin hypsometry in the timing and duration and hence rate of snowmelt.

For the baseline and temperature increase scenarios of +2 and +4°C, the following metrics for both (a) the mean hypsometries and for (b) each synthetic basin are calculated:

• total snowpack volume (ΣS_V)

• melt onset (SM₀₅): day of year where more than 5% of the snowpack volume has melted

• melt end (SM₉₅): day of year where 95% of the snowpack volume has been depleted

• center of snowmelt mass (SM₅₀): day of year where 50% of the snowpack has melted

• duration of the melt season (SM_D): number of days between 5 and 95% melt occurs

• areal snowmelt rate (mm w.e./day) between the 75th and the 25th percentile

Changes in snowpack volume and snowmelt metrics are grouped by the hypsometry clusters and temperature scenarios to identify how the hydrological response of snow-dominated basins are affected by basin shape.

Results

Three classes of basin hypsometry were identified in the cluster analysis (Figure 2). These include basins with a greater proportion of their area at low elevations “bottom-heavy” (M3, n = 8) basins with a greater proportion of their total area at higher elevations “top-heavy” (M1, n = 19), and basins with an equal mix of high and low elevations and cluster into the group referred to as (M2, n = 23). M1 basins were primarily found in the Monashee and Selkirk Mountains and western slopes of the Canadian Rockies in British Columbia and USA, M2 basins were found throughout the modeling domain and M3 basins were found exclusively on the eastern slopes of the Canadian Rockies in Alberta.

Snowpack Volumes

In mountain basins, a low percentage of the total area is found at high elevations (Figure 2). As a result, the total volume of snow stored at higher elevations is low (Figure 5) despite the higher rates of accumulation. Small changes in the accumulation gradient result in large reductions in total snowpack volume and significant differences in this response are observed for different basin hypsometries (Table 1). For the +2°C scenario, the increase in Z_min and the adjusted snow accumulation gradient result in total snowpack volume decreases between 10 and 17% from the baseline volume. For the +4°C scenario these losses increase to between 24 and 39%. Bottom-heavy basins, with a greater proportion of their area found at lower elevations, are particularly sensitive.

FIGURE 5

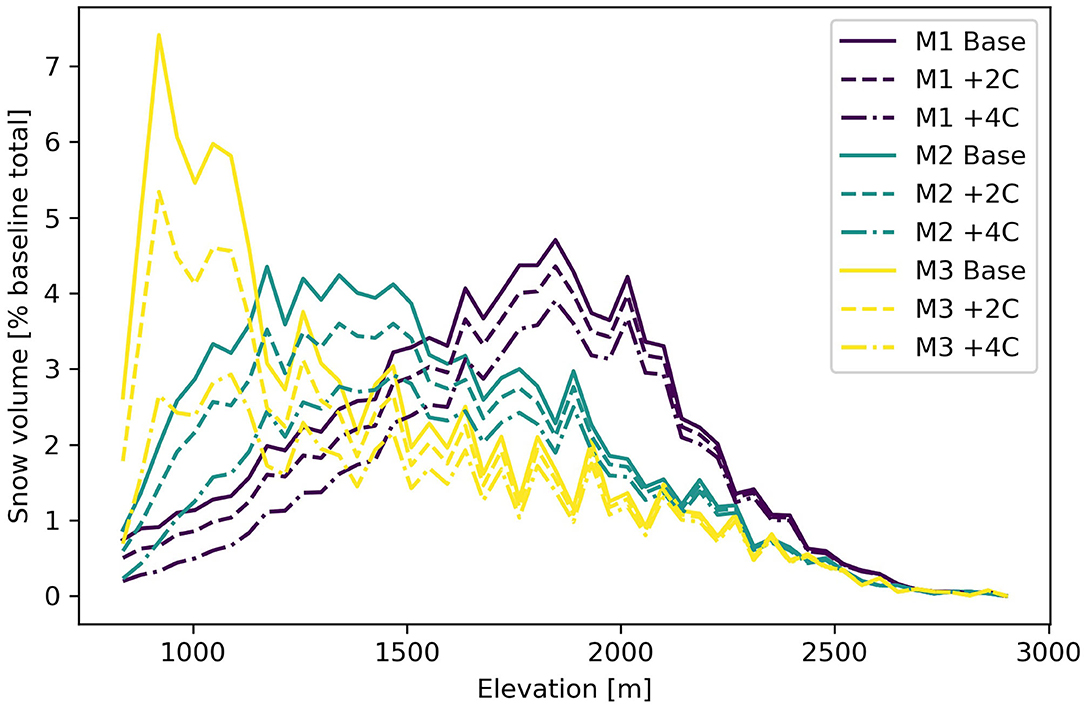
Figure 5. Basin snow volume in each elevation band as a percentage of total snow volume from the baseline scenario for three hypsometry profiles (Figure 2) and two temperature change scenarios.

The greatest reductions in snowpack volume are projected to occur at the lowest basin elevations (Figure 5). The effect of increased temperature on snow accumulation is greater at lower elevations than at higher elevation, and larger for +4°C than for +2°C. Bottom-heavy basins are again particularly sensitive, and show substantial decreases in snow volumes at their lowest elevations. At higher elevations the effect of warming on snowpack volumes cannot be distinguished, which is consistent with observational studies (Nolin and Daly, 2006; Harder et al., 2015; Rasouli et al., 2015).

The greatest absolute changes in snowpack volume will occur at lower elevations in bottom-heavy (M3) basins, but the modeling approach used here maintains a consistent proportional change in snowpack volume for any elevation regardless of the hypsometry. When applied to the individual basins, however, the spread of snowpack responses becomes apparent (Figure 6). Total snowpack losses of up to 45% are possible with M3 basins, which also tend to have a greater variability in their response. M1 top-heavy basins have the smallest within-cluster variability, and the lowest snow volume response.

FIGURE 6

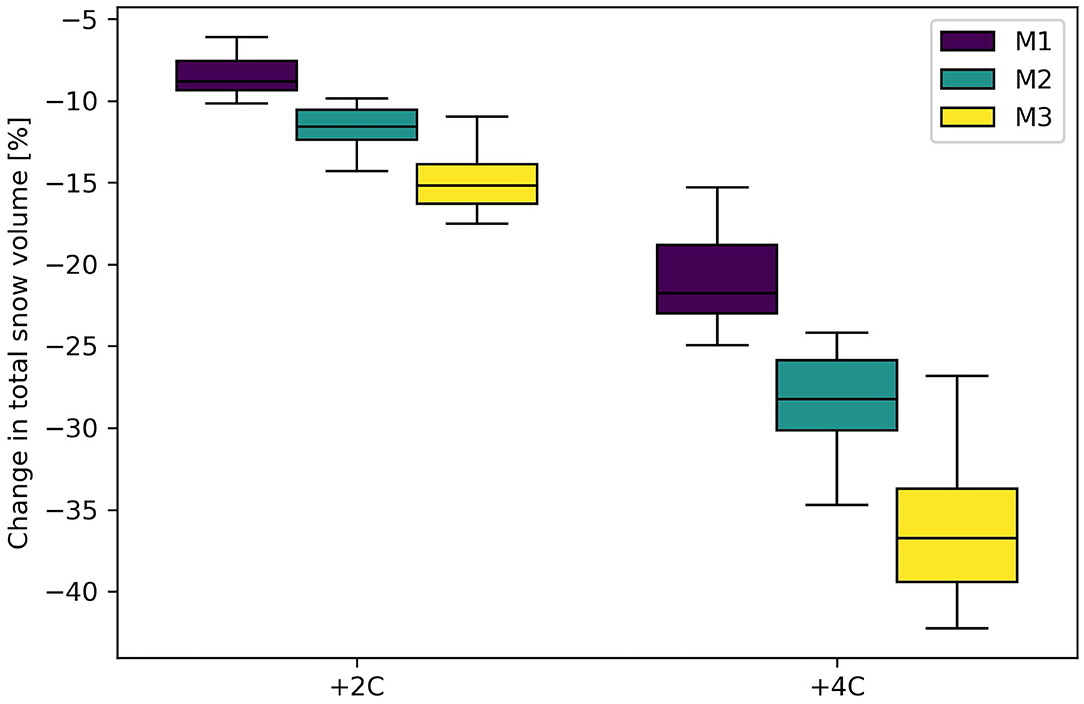
Figure 6. Changes in total snowpack volume for three different classes of basin hypsometry and two temperature scenarios, based on 50 normalized area-elevation profiles.

Bottom-heavy M3 basins show the largest decreases in total snowpack volumes relative to baseline conditions, with average losses of −16.5 ± 2.0% and −37.8 ± 4.7% for temperature increases of +2 and +4°C, respectively (Figure 6). Error bounds refer here to calculated standard deviations based on the basins in each cluster. Snowpacks in top-heavy M1 basins have a smaller response to temperature increases; changes of +2 and +4°C decrease total snowpack volumes by −9.9 ± 1.1% and −22.6 ± 2.6%, respectively. Intermediate M2 basins fall between these two extremes and the temperature changes result in total snow volume decreases of −13.0 ± 1.2% and −29.2 ± 2.8% for the two temperature increases (Figure 6).

With the approach used in this study, projected declines in snow volumes are greatest at the lowest elevations, which is consistent with observational data (Mote et al., 2005), climatological approaches (Nolin and Daly, 2006), and coupled atmospheric-hydrological modeling (Fang and Pomeroy, 2020). Using CGCM outputs and a snowpack model, Lapp et al. (2005) estimated that future snowpack volumes in the eastern Canadian Rockies could decrease by 38%. This closely matches the results for M3 basins, which are clustered on the eastern slopes of the Canadian Rockies.

Over the course of the melt season (Figure 7), changes in the timing of melt and the daily snowmelt rate (RSM) were observed. For top-heavy (M1) basins, RSM are similar for baseline, +2°C, and +4°C scenarios (12–13 mm w.e./day). For intermediate basins, melt rates of 12 mm w.e./day are also observed for baseline and +2°C scenarios, but at +4°C the rate of daily snowmelt decreases to 9 mm w.e./day. At the other end of the spectrum, bottom heavy basins (M3) show significant decreases in RSM, and move from 12 mm w.e./day (baseline) to 10 mm w.e./day (+2°C) to 6 mm w.e./day for +4°C scenarios.

FIGURE 7

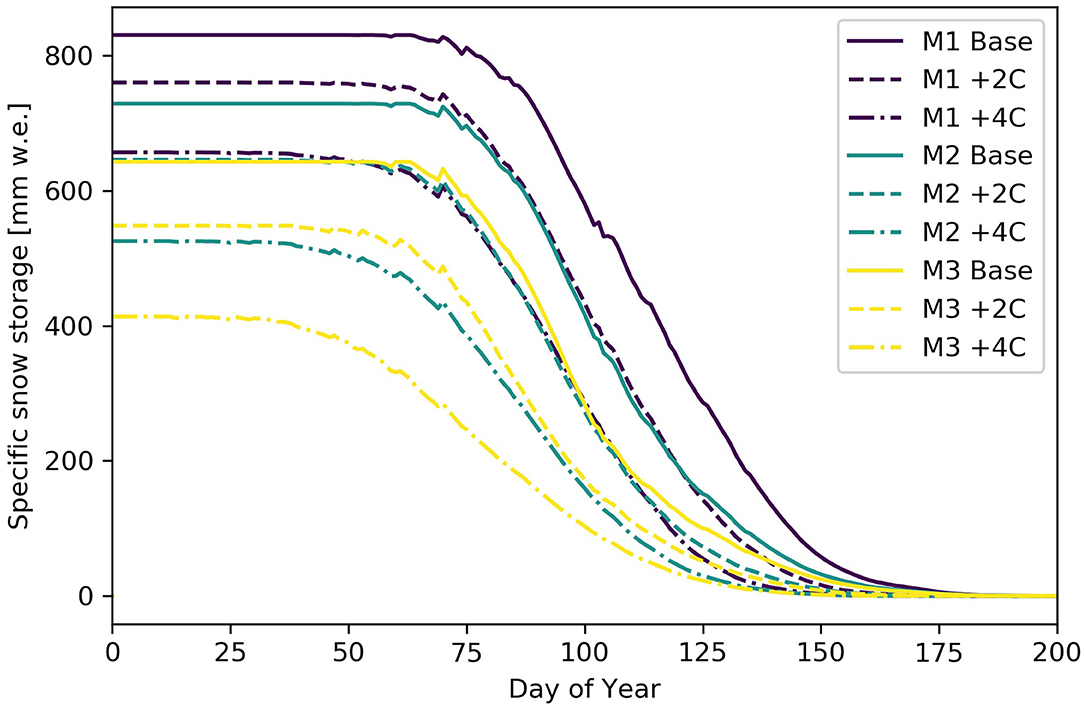
Figure 7. Specific snow storage for three idealized basin hypsometries and baseline (solid), +2°C (dashed), and +4°C (dot-dashed) scenarios.

Snowmelt Metrics

Prescribed temperature increases and the resulting changes to snow volumes and available melt energy produce substantial changes in snow storage and the timing of snowmelt (Figure 7, Table 1). Under warming scenarios, melt begins earlier in all basin types, and as a result, the center of snowmelt mass also advances (Figures 8, 9). For the different hypsometry classes, the shifts in center of snowmelt mass are approximately equal. Temperature increases of +2 and +4°C shift the center of snowmelt mass forward in the calendar year by 12–13 and 23–26 days, respectively (Table 1).

FIGURE 8

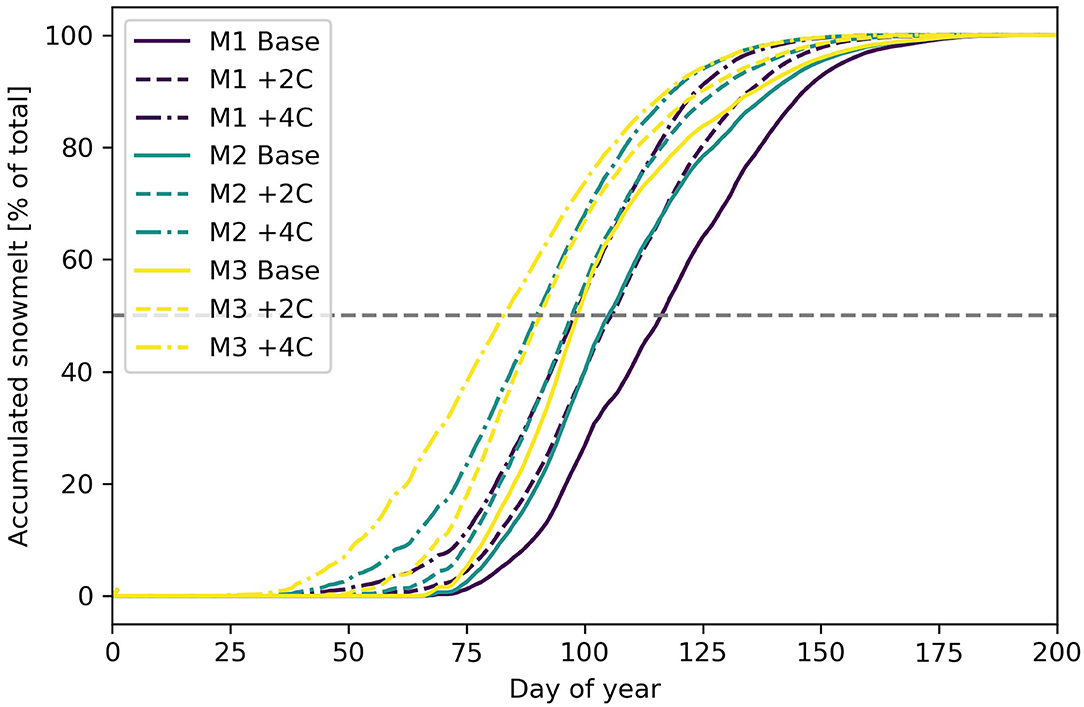
Figure 8. Accumulated snowmelt for temperature increases of +2° and +4°C, calculated for three hypsometry classes. The center of snowmelt mass corresponds to the intersection of the gray horizontal line and the accumulated snowmelt curves.

FIGURE 9

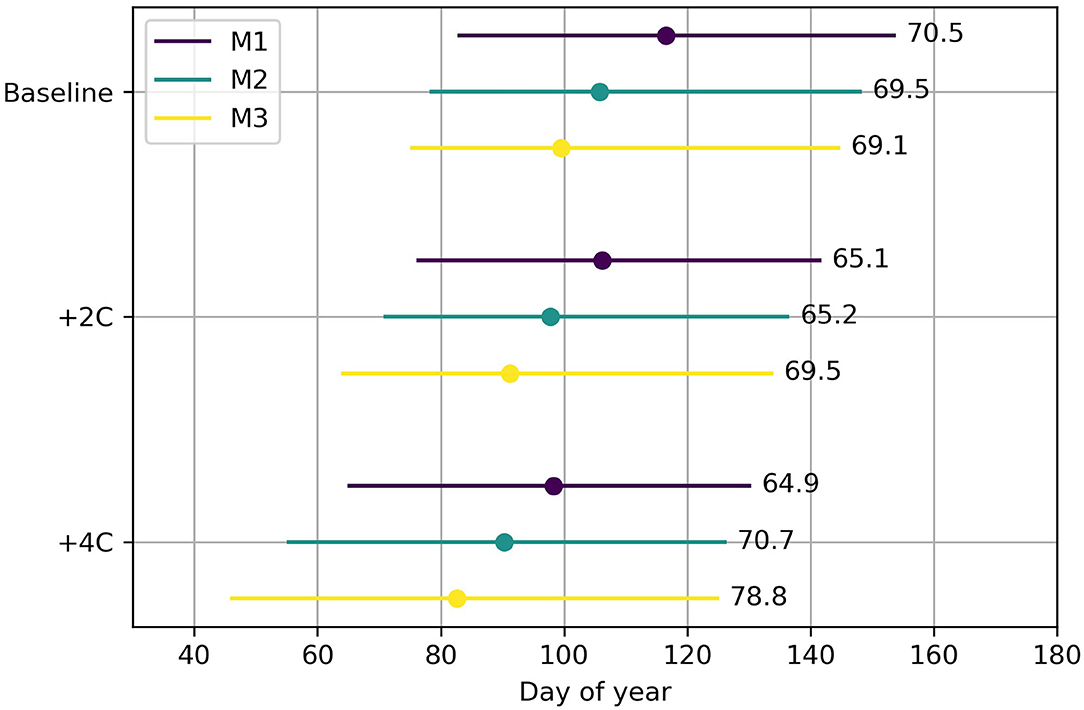
Figure 9. Summary of changes in melt season metrics. Horizontal lines indicate the melt season onset, center of snowmelt mass [large symbol] and end of melt season for the base case, +2 and +4°C temperature scenarios and 50 basin hypsometries. Numbers following the lines represent the mean duration of the snowmelt period.

Changes in melt onset are highly sensitive to basin hypsometry. Bottom-heavy “M3” basins show the greatest increases in melt onset (Figure 9) in response to warming. A temperature increase of +2°C results in a 5-day advance in melt onset, while a changes of +4°C results in snowmelt starting earlier by up to 18 days. Snowmelt seasons also end earlier under higher temperatures. At +2°C the snowmelt season ends 5–10 days earlier, but for +4°C the end of snowmelt is up to 17 days earlier (Figure 9) as accumulated snow is exhausted. Because of the different responses in melt onset and melt end, the duration of the melt season also changes (Figure 9). Basins with high proportional areas at higher elevations (M1) see the smallest changes for the duration of the melt season.

Bottom-heavy (M3) basins show the largest variability in changes to melt season duration (Figure 10), with a melt season that can be extended by up to almost 2 weeks. This is likely due to the large projected advances in the date of snowmelt onset, and only modest advances in the end of the snowmelt period. A related consequence is the decrease in average melt rates (Table 1, Figure 7). A greater degree of prescribed warming leads to greater variability in the calculated melt metrics for all basin types.

FIGURE 10

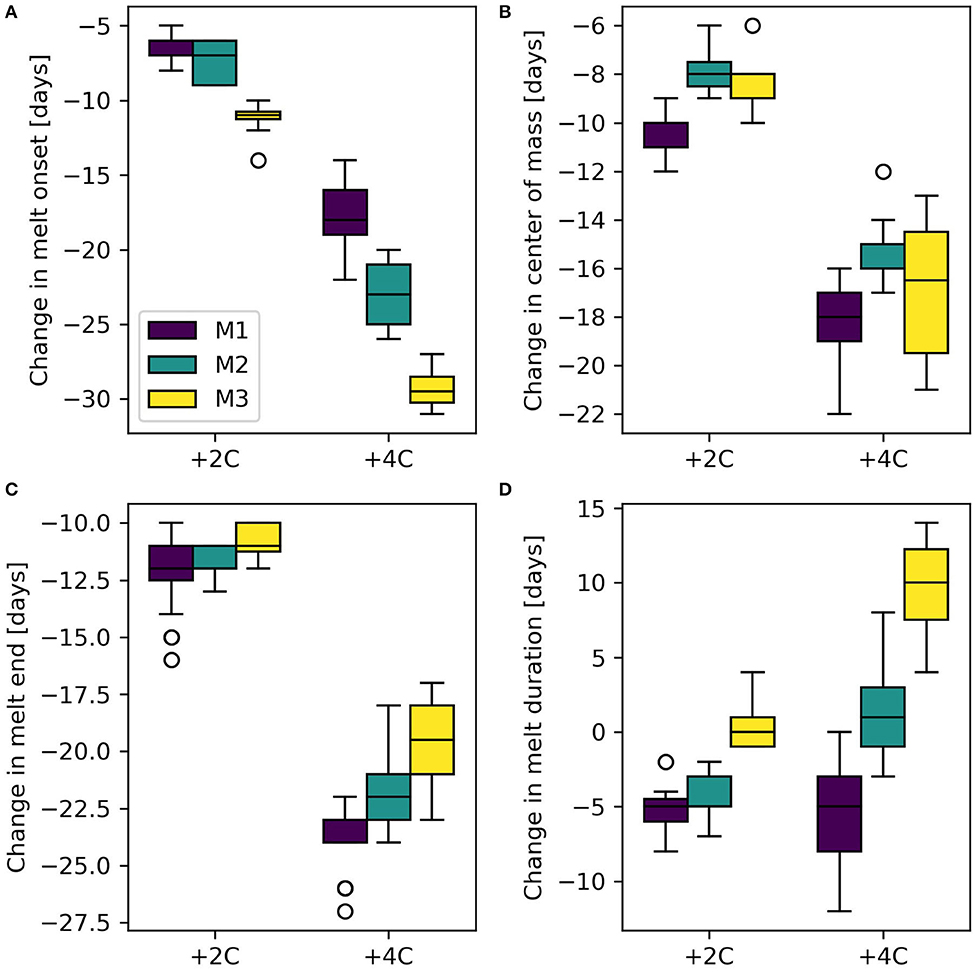
Figure 10. Boxplots of changes in melt season metrics for 50 basins sorted by hypsometry type: (A) melt onset, (B) center of melt, (C) melt end, and (D) melt season duration, for +2 and +4°C temperature scenarios.

Areal Snowmelt Rate

Basin hypsometry affects the timing of melt runoff, but also the areal average of the rate of daily snowmelt. Changes in basin-wide snowmelt rates can have potentially significant implications for spring flooding and rain-on-snow events (e.g., Pomeroy et al., 2016). Under the baseline scenario, bottom-heavy basins (M3) show the largest increases in early season melt rates, and also the largest declines in melt rates later in the summer as the snowpack and hence snow covered area (snow covered elevation bands) becomes depleted (Figure 11). Bottom-heavy M3 basins have the highest melt rates and melt occurs at higher rates earlier in the year than in other basins. With increased temperatures, early season melt rates increase compared to baseline conditions, particularly for M3 basins. Bottom-heavy M3 basins also see the largest absolute increase in daily snowmelt rates, and this occurs 2–4 weeks earlier than in either M2 or M1 basins. Increased average air temperatures will increase melt rates in earlier periods in all cases, but this impact is most pronounced in the M3 basins and least in the M1 basins, and is greater for higher rates of warming (Figure 11).

FIGURE 11

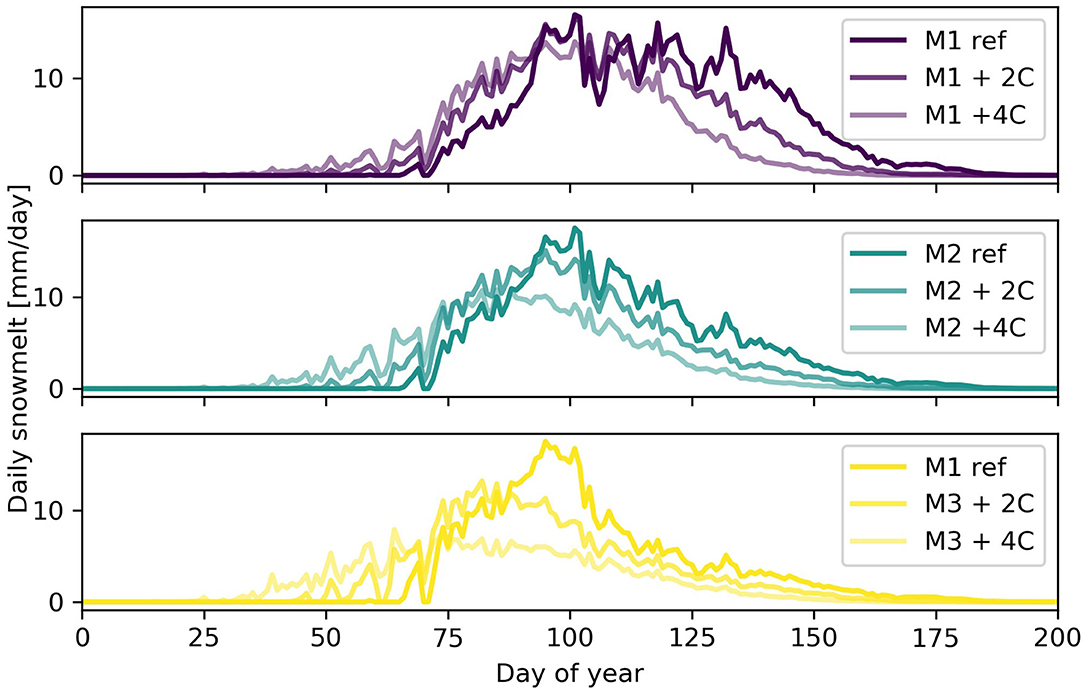
Figure 11. Daily snowmelt rates for three idealized hypsometries: M1 (top), M2, and M3 (bottom) and two temperature scenarios.

Discussion

Differences in basin hypsometry affect the accumulation and melting of snow, and could play a significant role in how basins will respond to future temperature increases. The hypsometric curves produced for 50 watersheds in western Canada can be broadly classified into three distinct hypsometric classes, which range from top-heavy (M1) to bottom-heavy (M3). While real-world spatial variations in climate and elevation will affect the response of a specific basin to climate change, hypsometry plays an important role in snowpack volumes and the rates and timing of snowmelt and this has not been addressed in recent global comparative studies using fixed basin shapes and elevation ranges (López-Moreno et al., 2020).

Warmer temperatures will advance the timing of melt, the end of the melt season, and the center of snowmelt mass earlier in the calendar year (e.g., Elias et al., 2015). Top-heavy basins with a greater proportion of area at higher elevations (M1) show little or no change in average melt rates, but the highest melt rates advance earlier in the season (Figure 11). Bottom-heavy basins are more sensitive to temperature increases, and exhibit the largest shifts to earlier snowmelt onset and center of snowmelt mass with warming (Figures 9, 10). Bottom-heavy basins (M3) also show significant reductions in mean and maximum seasonal daily melt rates that is not evident in top-heavy or intermediate basins (M1 and M2; Table 1). The discussion below connects this research to the role of hypsometry on basin hydrology, explores limitations and implications of the approach, and presents future directions for this research.

Additional Considerations

While elevation is the major influence on both snow accumulation and melt, other variables affect snow accumulation in mountain basins. Slope, aspect, wind redistribution, forest canopy, and crown density will all affect the snow accumulation gradient (Grünewald and Lehning, 2011; Lehning et al., 2011). Wind and gravity in particular play key roles in redistributing snow (Bernhardt et al., 2012; Kerr et al., 2013; Ayala et al., 2014; Musselman et al., 2015; Sommer et al., 2015; Freudiger et al., 2017; Bisht et al., 2018; Vionnet et al., 2020). Mott et al. (2014) demonstrate that orographic lifting of air masses affects snowfall deposition. Additional information on the vertical distribution of seasonal snowpacks, and their transient response to climate change, is required. Light Detection and Ranging (LiDAR) measurements of spatially distributed snow depths and SWE (Hopkinson et al., 2012; Grünewald et al., 2014; Painter et al., 2018; Harder et al., 2020) will complement ongoing snow pillow and snow course data, and significantly improve the modeling assumptions made here.

To isolate the role of hypsometry on hydrological response of snowmelt-dominated basins to climate change, this study uses synthetic temperature data based on climate normal and a fixed temperature gradient to extrapolate temperatures to higher elevations. While the approach generates reasonable estimates of monthly temperatures (Figure 4), temperature gradients can vary seasonally and spatially, and short duration inversion events are not captured. The spatial variability of precipitation across the region and as a result of redistribution (leeward vs. windward) is also neglected, and detailed meteorological forcing would be required to model the specific response of individual basins. HRUs were delineated based on elevation only, and the inclusion of vegetation will change the melt energetics and the results presented here. It remains an open question as to how much the sensitivity of a basin's snowpack to future climate change depends on hypsometry in comparison to other hydrologically relevant variables such as absolute elevation range, slope and aspect, precipitation gradients, snow redistribution, and vegetation.

Hantel et al. (2012) provide a snowline climatology for the Alps, and suggest that the sensitivity of the snowline is 166 ± 5 m°C⁻¹ in winter. The very simple accumulation model presented here prescribes a comparable snowline sensitivity of ~160 m°C⁻¹. In more humid climates with a less negative vertical temperature gradient, the shift in minimum snowline elevation would be more pronounced. Seasonal changes in snow accumulation gradients provide a proxy for how the snowpack volumes might change in response to climate warming. Low elevation snowmelt in spring acts to increase the snow accumulation gradient (Barry, 2008), which can be considered analogous to a precipitation phase change that is strongest at low elevations and acts to increase the snow accumulation gradient, as demonstrated in this study. The combined effects of increased precipitation, which was not addressed in this study, and increased warming will result in a narrower and steeper snow wedge in mountainous terrain (Brown et al., 2000). The loss of snow accumulation at lower elevations and in particular in “M3” basins (Table 1, Figures 5, 8) agrees with the steepening of the gradient in spring and its enhancement in warmer temperatures. Moore and Prowse (1988) suggest that spring snowmelt might be better estimated by using the altitudinal variation in snow accumulation.

While this study considered primarily the effect of basin hypsometry on snow accumulation and snowmelt, its results support previous work suggesting that certain basin types may be more sensitive to rain on snow events in the spring. Wayand et al. (2015) found that hypsometry and vegetation had similar impacts on rain-on-snow event magnitudes but that rainfall contribution was more important. Klos et al. (2014) investigated the rain/snow transition zone across complex terrain and mapped the likelihood of snow over rain in future climates to identify areas where shifts are likely to occur. Actively melting snowpacks have a high runoff efficiency and are very sensitive to rain-on-snow events (Fang and Pomeroy, 2016; Trubilowicz and Moore, 2017), small changes in temperature can directly affect the area/volume of snow that is actively melting (Figure 11).

Molini et al. (2011) captured the effect of temperature change on snowpack accumulation and melt with a minimalist model, and found that warmer temperatures reduce snowpack and accelerate melt. They noted that these effects, however, could be masked in measured streamflow series. While counterintuitive when only considering temperature impacts on snowmelt rate, decreased rates of snowmelt in response to climate warming were found by Pomeroy et al. (2015) and Musselman et al. (2017) and attributed to the advance of the timing of the snowmelt season into lower insolation periods of the year as temperatures rose. Decreasing early season snowmelt rates were not found here: instead, early season melt rates increased with climate warming for all basin hypsometries, and declines in early and mid-summer melt rates were observed (Figure 11).

The strong reduction in summer snowmelt rates appears to be confirmed by the observed increase in melt season duration for bottom-heavy (M3) basins (Figure 10), but this does not occur for all basins. Seasonally averaged melt rates decrease with warming for bottom-heavy and intermediate basins (Table 1), while top-heavy basins show no change in average melt rate with warming. The decrease in areal seasonal melt rates for M3 basins is likely due to depletion of snowcover at lower elevations later in the summer. The timing of peak melt rates has implications for spring flooding, and hypsometry could be used to identify sensitive catchments.

Modeling snowmelt in basins with complex hypsometry requires more vertical detail than is often used. Simple conceptual models will be unable to model adequately the effects of hypsometry with a few elevation bands. Results of this study suggest that increased vertical resolution is necessary to capture the effects of hypsometry when considering future temperature changes and hydrology in mountain basins.

The changes reported here have implications for snow monitoring strategies, regional hydrology, and water resources management. Snow pillows located exclusively at high or mid-elevations cannot capture the large changes in low-elevation snowpacks, and monitoring of snowlines and snow accumulation gradients requires greater granularity with respect to elevation. Warming temperatures will affect snow accumulation and snowmelt in mountain basins, and the potential for increased early season snowmelt in M1 and M2 type basins (Figure 11) suggests changes in the timing of the spring freshet, annual peak flows, and flood characteristics. Changes in the timing and duration of the snowmelt season are also highly relevant for water resource managers, and future research is required to evaluate the transferrability of our results. In order to adequately capture the effects of hypsometry on snow accumulation and melt, particularly with respect to a warming climate, increased vertical resolution may be required.

Conclusion

In many mountainous regions, the contributions of snowmelt dominate river runoff, and increased temperatures are widely recognized to result in changes in snow accumulation and seasonal runoff timing. However, the area-elevation distribution within a basin will affect its response to future climate change. In this study, a linear snow accumulation model and an energy budget snowmelt model (CRHM) were applied to the normalized hypsometries of 50 mountain basins in western Canada to examine the role of hypsometry in basin responses to climate change. Changes in total snow volumes, snow volumes by elevation band, and melt metrics (timing of melt onset, finish, duration, center of mass, and snowmelt rate) were examined with baseline, +2°C, and +4°C scenarios.

All basins responded strongly to changes in temperature, but the magnitude of the basin response also depended on hypsometry. With warming, snowmelt starts and ends earlier, the center of snowmelt mass shifts toward earlier in the season, the duration of the melt period increases in most cases, and basin snow volumes decrease as the minimum snow elevation increases and the snow accumulation gradient steepens. Areal snowmelt rates initially increase and then decline as the snowcovered fraction of the basin declines. There is no evidence that advancing the melt period earlier in the year to a lower insolation period reduces melt rates. With a prescribed temperature increase of +4°C, basin-wide snow accumulation decreases by up to 40%, melt onsets occur up to 25 days earlier, and the center of snowmelt mass is shifted by up to 20 days. Bottom-heavy basins are most sensitive, and top-heavy basins are least sensitive to prescribed temperature changes.

This study has shown the importance of hypsometry in estimating the sensitivity of mountain snowmelt hydrology to climate warming. Future research should also examine how hypsometry influences snow accumulation processes and how combinations of hypsometry and aspect work to influence the snow and hydrological regimes of mountain basins.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://doi.org/10.20383/102.0318.

Ethics Statement

Studies involving animal subjects: no animal studies are presented in this manuscript. Studies involving human subjects: no human studies are presented in this manuscript. Inclusion of identifiable human data: no potentially identifiable human images or data is presented in this study.

Author Contributions

JS, PW, and JP designed the study. JS and XF applied the CRHM model, and JS analyzed outputs and produced all figures. All authors contributed to the writing.

Funding

This research was supported by Canada First Research Excellence Fund's Global Water Futures program, the Canada Research Chairs and Canada Excellence Research Chairs programs, the Natural Sciences and Engineering Research Council of Canada (NSERC Discovery Grants to JS and JP) and the Alberta Innovates Water Innovation Program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2021.604275/full#supplementary-material

References

Adam, J. C., Hamlet, A. F., and Lettenmaier, D. P. (2009). Implications of global climate change for snowmelt hydrology in the twenty-first century. Hydrol. Process. 23, 962–972. doi: 10.1002/hyp.7201