- Department of Geology and Geophysics, University of Utah, Salt Lake City, UT, United States
Many particulate pollutants in the environment exist in non-spherical shape, but the influences of particle shape on pollutant migration and removal in groundwater systems are not well-understood. In this work, we simulated the three-dimensional translational and rotational motions of rod-shaped colloids in simple flow channels characterizing groundwater flow paths, with an aim to elucidate the underlying mechanisms for rod retention. Through an investigation of the interplay of multiple factors (e.g., aspect ratio, particle size/density, flow shear, channel dimension, and orientation relative to gravity), we determined under what conditions particle shape has the most pronounced impact on transport and retention under favorable deposition conditions (i.e., lacking repulsive energy barriers). Our results showed that in many cases, medium sized rods of ~0.4–2 μm in equivalent volume diameter exhibited much improved retention compared to equal-volume spheres, since for that size range, particle rotation from shape-induced fluid hydrodynamics and rotational diffusion were both important, which caused rods to drift considerably across flow streamlines to intercept collector surfaces. Particle rotation also allowed rods to travel farther downstream along flow channels for retention compared to spheres. The differences in retention between rods and spheres were more evident at relatively high fluid velocity, narrow flow channel, or when flow direction aligned with gravity. Our findings demonstrated that the effect of particle shape on pollutant transport and migration in groundwater systems was essential and provided important guidelines in optimizing parameter designs to utilize particle shape effect for better pollutant removal.
Introduction
Ellipsoidal particles have been shown to display distinct motion from their homogeneous spherical counterparts of equal volume in viscous fluid flows (Jeffrey, 1922; Kuzhir et al., 2011; Zhao and Van Wachem, 2013). However, the impacts of particle shape on colloidal pollutant migration in groundwater systems are not well-understood. In conjunction with particle shape, many other factors could influence particle transport and retention, such as colloid size, colloid surface property, fluid shear, direction of flow in relation to gravity, and the dimension, contour, and surface properties of flow channels (Yao et al., 1971; Johnson et al., 2007, 2010; Ma et al., 2011a,b; Nelson and Ginn, 2011; Trauscht et al., 2015; Fang et al., 2018). Understanding the influences of particle shape along with factors mentioned above on particle transport and deposition is important to a variety of processes, including contaminant removal from groundwater flow (Chen et al., 2017; Ta et al., 2018), tracking contaminant fate (Mendez et al., 2018), design of microfluidic devices (Gervais and Jensen, 2006; Unni and Chun, 2009; Sen Gupta, 2016), in view of the fact that the majority of natural or engineered particles encountered in these processes, such as clay particles, heavy metals, agglomerates, bacteria, or polymer molecules are often non-spherical in shape (Salerno et al., 2006; Wang and Keller, 2009; Doshi et al., 2010).
Due to the interplay of particle shape with other factors characterizing the physico-chemical properties of particle-fluid-channel systems, a consensus on the influences of particle shape on transport and retention cannot be reached from published experimental investigations (Gentile et al., 2008; Kolhar et al., 2013; Seymour et al., 2013; Thompson et al., 2013; Shave et al., 2019). Among these investigations, even with simple geometric channels involving only parallel planar surfaces (e.g., parallel plate flow chamber), experimental observations regarding whether particle shape had enhanced or decreased migration or retention were inconsistent (Gentile et al., 2008; Seymour et al., 2013; Shave et al., 2019). One main reason for the reported inconsistency may be a result of lacking systematic investigations of all the above-mentioned influential factors on particle transport over a wide parameter range, primarily due to experimental cost. For example, in many cases, each research group had their own customized experimental setup (e.g., specific channel dimension or orientation relative to the direction of gravity, tailored channel surface properties), which rendered difficult to compare findings among different research groups (Nelson and Ginn, 2005; Seymour et al., 2013; Thompson et al., 2013). Another reason might be due to the varying surface properties arising from the manufacturing processes (e.g., stretching, molding, synthesizing) of non-spherical shape particles (Caldorera-Moore et al., 2010; Seymour et al., 2013; Ma et al., 2020).
Numerical or theoretical studies on particle shape may be appealing because the complexities associated with the potential variations of particle or flow channel surface properties can be avoided. But numerical modeling has its own challenges in accurately accounting for the particle-flow-surface interactions, and in tracking the resultant three-dimensional translational and rotational motions of non-spherical particles. Because of these challenges and/or the computational intensities involved, existing numerical investigations focused on either the influences of fluid hydrodynamic interactions, which excluded Brownian motions (Geng et al., 2007; Gentile et al., 2008; Caldorera-Moore et al., 2010; Pillai et al., 2011; Ghanem et al., 2016), or the translational and rotational diffusion dynamics of non-spherical particles, which ignored fluid flow hydrodynamics (Mortensen et al., 2008; Drescher et al., 2011; Liu et al., 2012; Mahnama et al., 2014). We have established a three-dimensional transport model that overcame these challenges and can incorporate shape-included fluid hydrodynamics, Brownian translation and rotation, as well as distance- and orientation-dependent particle-surface interactions (Li and Ma, 2018, 2019). Simulations performed in the Happel sphere-in-cell model demonstrated that particle rotation due to non-spherical shape greatly affected colloidal transport and retention, and that the dependency of retention on particle shape varied greatly with parameters including particle size, surface properties of particle and channel walls, as well as flow velocity and channel dimension (Li and Ma, 2018, 2019). Just like the Happel model (which had curvilinear collector surfaces) has been widely used to represent curved channels in granular porous media, parallel plate models can represent straight channels in certain geological features (faults/fractures) in groundwater flow (Moreno and Tsang, 1994; Al-Hadhrami et al., 2003; Xizhe et al., 2019). As described above, while many experimental studies have been performed in parallel plate flow models to explore non-spherical colloidal transport (Bakker et al., 2003; Zvikelsky et al., 2008; Asadishad et al., 2011; Albarran et al., 2013; Stoll et al., 2017), a comprehensive numerical study of the effects of particle shape on transport and deposition in such flow geometries involving planar surfaces (e.g., parallel plate flow channels) is still lacking.
Using the Happel model framework, we have previously explored the influences of particle shape on colloidal transport and retention for a wide range of particle sizes (e.g., 0.1–10 μm, spanning from nanometer to micron range), aspect ratio (e.g., 1–6) and flow velocities (e.g., 0.1–200 m/day, representing groundwater flow velocities typically encountered in various aquafers) (Li and Ma, 2018). Under favorable deposition conditions (i.e., lacking particle-collector repulsion), simulations from the Happel model showed that medium size range rod-shaped colloids (e.g., 0.2–2 μm in diameter) displayed considerably higher retention (about a factor of 2–10) relative to their equal-volume spheres under relatively high flow velocities (e.g., 5–200 m/day) (Li and Ma, 2018). However, those simulations were conducted in the Happel model when flow direction was aligned with gravity and under a single porosity of 0.36, representing very narrow flow channels (~ 65 μm in width based on the grain diameter of 390 μm examined). Whether the retention trends between rods and spheres observed from the Happel model (with curved, narrow flow paths) can be transferred to flow geometries involving straight channels spanning a range of channel widths remain unknown.
For spherical particles, it is known that depending upon the direction of flow streamlines relative to gravity, gravitational settling could play an important role, especially for particles of large size or high density (Yao et al., 1971; Walt et al., 1985; Chen et al., 2010; Ma et al., 2011b; Chrysikopoulos and Syngouna, 2014). However, to the best of the authors' knowledge, the influences of gravity on the settling of non-spherical particles in shear flow have not been reported. But a better understanding on this is essential, because in most practical situations where the colloid filtration theories were applied, including groundwater aquifers, riverbank filtration or mineral separation systems, and blood vessels, fluid flow rarely aligns with the direction of gravity; rather, the flow paths could span a wide range of angles relative to the direction of gravity.
In this work, we will adapt our 3-D particle trajectory model (Li and Ma, 2018, 2019), which is capable of simulating particle orientation and position of rod-shaped particles (prolate ellipsoids), to study the transport and retention of rods in parallel plate flow geometry (which contains only planar surfaces). This simple geometry can represent faults and fractures in certain geological features in groundwater flow (Al-Hadhrami et al., 2003; Xizhe et al., 2019; Moreno and Tsang, 1994). It also provides easy demonstration of the orientation of moving rods relative to the collector planes; and enables us to explore the influences of flow channel orientation relative to the direction of gravity. We will investigate the interplay of many influential factors (i.e., aspect ratio, particle size, flow shear, flow channel dimension and orientation relative to gravity, particle density) on rod transport and retention for a wide parameter range, with a focus on the latter three (e.g., channel dimension, channel orientation in relation to gravity, particle density) that have not been previously investigated. The goal is to determine under what conditions particle shape has the most pronounced effects on the transport and retention of rod-shaped particles relative to their equal-volume spheres under favorable deposition conditions (lacking repulsive energy barriers) in various geometric models, which will provide guidance to better understand non-spherical particle transport in groundwater flow systems and to optimize design parameters for water filtration processes.
Simulation Methods
In this study, we developed a Lagrangian trajectory model to simulate the three-dimensional translation and rotation of ellipsoidal particles in representative parallel plate flow geometry (Figure 1). A well-controlled parabolic shear fluid flow can be established within the parallel plate channel and described analytically (Elimelech, 1994). To track particle position, an inertial frame (x = [x, y, z]) with its origin fixed on the stationary planar collector surface (see Figure 1) was utilized. To track particle orientation, the following two coordinate systems (whose origins were both attached to the center-of-mass of the particle) were employed: (1) one with axes parallel to three particle principal axes (particle frame, (); and (2) one with axes parallel to the corresponding axes of the inertial frame (co-moving frame, ). The angles between the corresponding axes of the particle frame and the co-moving frame define three Euler angles (φ, θ, and ψ) (Figure 1) and describe the orientation of the ellipsoidal particle during transport.
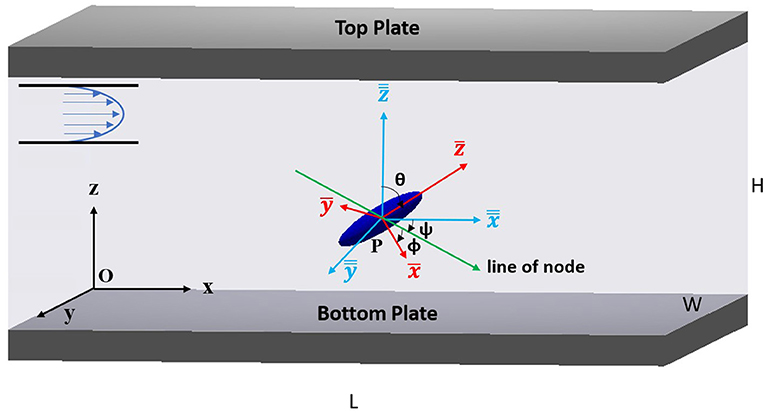
Figure 1. Representation of parallel plate simulation geometry including Euler angles and coordinate systems: inertial frame [x, y, z] with origin O on the bottom plate, particle frame and co-moving frame with origin P at the particle center. Fluid flow direction was along positive x. The insert showed the parabolic flow inside the channel.
For a rigid particle moving in viscous shear flow, its translational and rotational displacements during a short time step can each be obtained by adding the contributions from its deterministic motion and random motion as follows:
where Δt is the time step; Δx and ΔΩ are the translational and rotational displacement vectors, respectively; δx and δΩ are the respective displacements due to Brownian translation and rotation. The deterministic linear and angular velocity vectors (udet, ωdet) can be obtained following the equations of motion:
where m is the mass of the particle, I is the moment of inertia of the particle; and ∑ F and ∑ T represent the deterministic forces and torques acting on the particle, respectively. The deterministic forces considered in this work included virtual mass force, gravity, hydrodynamic fluid drag, shear lift, colloidal forces (e.g., van der Waals, electrostatic) and non-colloidal (steric) forces. The deterministic torques acting on the particle were derived from the forces that did not pass through the particle center of mass, e.g., colloidal forces and hydrodynamic fluid drag (Li and Ma, 2018). For an ellipsoid particle, the random displacements due to Brownian translation and rotation were modeled as stochastic processes for each degree of freedom (i.e., three translational and three rotational) using Einstein's equations in the particle frame (Perrin, 1934). The values for time step (Δt) were chosen to be greater than particle momentum relaxation time (see Table 1), so that Brownian motions can be described as random Markovian process; but at the same time, Δt must be sufficiently small so that the deterministic forces and torques during Δt could be assumed constant. Solving Equations (3) and (1) in the inertial frame yields the translational displacements of the particle (Li and Ma, 2018). Likewise, solving Equations (4) and (2) in the particle frame provides the rotational displacements of the particle, which we will describe briefly how to implement these equations in our model for ellipsoidal particles.
Specifically, for an ellipsoid moving in shear flow, Equation 4 can be decomposed as follows to obtain particle angular velocities in the particle frame (Zhang et al., 2001, 2007; Li and Ma, 2018):
where the components of the moment of inertia are (defining -axis as the major axis): , a is the ellipsoid semi-minor axis, β is ellipsoid aspect ratio (equal to major axis divided by minor axis); ,and , are the components of torques due to hydrodynamic fluid drag and colloidal forces in the particle frame, respectively.
Once the angular velocity vector of an ellipsoid was obtained from Equation (5), the time evolution of particle orientation in terms of quaternions (Euler parameters) can be computed as follows (Hughes, 1986):
where , , and were the components of particle angular velocity vector in the particle frame, q0, q1, q2, and q3 are the four Euler parameters. Euler parameters are interchangeable with Euler angles (Goldstein, 1980), but Euler parameters were frequently employed in the computational code, since the use of Euler angles are computationally expensive and would involve numerous trigonometric calculations and singularity problem (Li and Ma, 2018).
Detailed descriptions on how to solve the equations of motion, account for all the forces and torques, and incorporate Brownian translation and rotation can be found in our previous work (Li and Ma, 2018). The simple geometric feature in parallel plate channels greatly simplified some computational complexities involved, including computing particle-collector separation distance, or distance- and orientation-dependent colloidal interactions. A brief description of the computational algorithm was provided in the Supplementary Material along with other simulation details. Supplementary Table 1 provided information on the sizes/dimensions of rod-shaped particles and their equal-volume spheres simulated in this study. Throughout this work, unless specified otherwise, the sizes for rods referred to the diameters calculated based on their equal-volume spheres.
Parallel plate flow geometries with three different channel heights (spanning a range of 100 μm−2 mm) were simulated in this work to represent fracture aperture sizes encountered in groundwater systems (Table 1). The narrowest channel of 100 μm was comparable to the channel size previously explored in the Happel model (e.g., 65 μm) (Li and Ma, 2018). Our earlier work showed that for narrow channels, the impact of particle shape on retention was the most pronounced for rod particles from 0.2 to 2 μm with higher aspect ratio under relatively high velocity (Li and Ma, 2018). Hence, in this study we selected particle sizes from 0.2 to 6.6 μm, which bracketed the above-mentioned size range exhibiting evident effect of particle shape, to contrast retention behaviors between rods (with a higher aspect ratio of 6) and spheres of equal volume (aspect ratio of 1) under two representative velocities of 5 and 200 m/day (representing groundwater flow velocities typically encountered in aquafers). To investigate the influences of gravitational settling on non-spherical particle retention, two methods were used: (i) varying the orientation of parallel plate flow channels relative to the direction of gravity for particles of same density; (ii) varying particle density (e.g., 1.055, 2.0, and 4.0 g/cm3 representing polystyrene, silica and iron, respectively) for the same channel dimension and orientation. Other simulation parameters were provided in Table 1.
Results With Discussion
Influences of Particle Shape on Translational and Rotational Trajectories
Without diffusion or any external forces, a free rigid ellipsoidal particle would rotate indefinitely in a shear flow field, as predicted by Jeffrey (1922). Exemplary rotational trajectories for a sphere and a rod were provided in Figure 2, where Euler angle θ was the angle between the major axis of a rod particle and the direction perpendicular to the collector surface (Figure 1). Compared to the uniform rotation of a sphere, a rod particle rotated faster when its major axis was perpendicular to fluid flow (θ close to 0 or π), and slower when aligned with fluid flow (θ close to π/2) (Figure 2A), the well-known tumbling motion predicted by Jeffrey (1922). In addition, an inertial prolate ellipsoid particle oscillated periodically along the direction of the velocity gradient while rotating (Figure 2B). The speed of rotation and the magnitude of oscillation varied greatly with shear rate, particle aspect ratio, initial orientation, particle size, and distance to the collector surface (Li and Ma, 2018). The presence of external forces (e.g., gravity or colloidal interactions) would pull a rotating and oscillating rod toward the direction of such forces (Li and Ma, 2018). Diffusion (especially rotational diffusion) could perturb or completely alter both the translational and rotational trajectories of ellipsoids, depending upon the relative influences of fluid shear and rotational diffusion (Li and Ma, 2018).

Figure 2. Simulated particle trajectories for both 1μm spheres and their equivalent volume rod particles of aspect ratio 6 from parallel plate geometry Dimension I, under pore water velocity 5 m/day, with all external forces and Brownian motions ignored except for (C), in which all mechanisms were included. (A) Euler angle θ vs. distance for sphere and rod. (B) Particle center position in z-direction vs. distance for a single representative sphere and rod. (C) Particle center position in z-direction vs. distance for a single representative sphere and rod under normal simulation conditions (all mechanisms included).
As illustrated in Figure 2, compared to a homogeneous sphere, the non-spherical shape of an anisotropic particle affected greatly both its translation and rotation, which subsequently influence its transport and retention. The effect of particle shape on retention is often coupled with many other factors, such as flow hydrodynamics (Geng et al., 2007; Gentile et al., 2008), particle-collector interactions (Ghanem et al., 2016), and diffusion (Pillai et al., 2011; Li and Ma, 2018). In this study, we will consider only favorable conditions for attachment, where strong attractions exist when a particle approaches the collector surface such that retention will be rate-limited by particle transport process. Below, we will present simulation results from a parallel plate flow chamber demonstrating the coupled influences of particle shape with factors including shear flow velocity, flow channel dimension, orientation of flow channel relative to gravity, particle size and density on rod transport and attachment.
Influences of Flow Velocity on Particle Retention
Retention of colloids in model geometries is characterized by so-called collector efficiency, which represents the portion of particles retained in the model systems out of the total injected particles. Figure 3 showed the simulated collector efficiencies (η) for polystyrene rods and spheres of size 0.2–6.6 μm under pore water velocity of 5 and 200 m/day in Dimension I. Flow channel Dimension I had a length of 2 mm, width 1 mm, and height 2 mm, all of which were much greater than the particle sizes examined. Flow direction inside the channel was perpendicular to the direction of gravity. Spherical particles (aspect ratio of 1) basically followed a V-shaped retention trend vs. particle size for both fluid velocities, with a local minimum around particle size of 1 μm in diameter. This is in qualitative agreement with colloidal filtration theory predictions, despite the fact that those theories were formulated from idealized granular porous media representations such as Happel sphere-in-cell model, or hemispheres-in-cell model (Rajagopalan and Tien, 1976; Ma et al., 2009; Ma and Johnson, 2010; Nelson and Ginn, 2011; Fang et al., 2018). Also, from colloidal filtration theories, retention of small size spheres (e.g., <1 μm in diameter) were mostly due to Brownian motions (specifically, Brownian translation only, since Brownian rotation is irrelevant for homogeneous spheres), whereas retention of large size spheres (e.g., > 1 μm in diameter) were due to gravitational settling effect. Retention of spheres decreased when velocity was increased from 5 to 200 m/day (Figure 3A vs. Figure 3B), as expected from filtration theories (Yao et al., 1971; Rajagopalan and Tien, 1976; Ma et al., 2009; Ma and Johnson, 2010; Nelson and Ginn, 2011; Fang et al., 2018). As shown in Figure 2C, spherical colloids tend to follow flow streamlines, higher fluid velocity caused spheres to be transported downstream faster by convection, which led to decreased retention out of the fixed number of injected spheres compared to lower velocity.
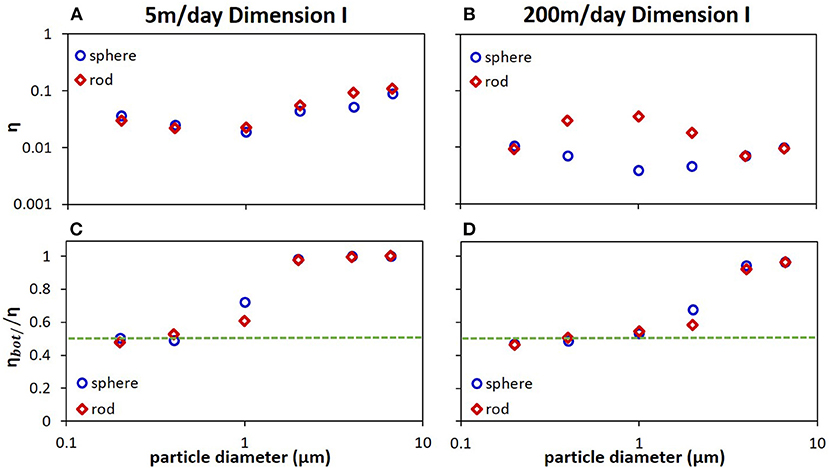
Figure 3. Simulated collector efficiencies (η) and the ratios of particles attached on the bottom plate to the total attachment (ηbot/η) as a function of particle size for polystyrene spheres (blue circles) and rods (dark red diamonds) from parallel plate model of Dimension I under favorable conditions at pore water velocity of 5 m/day (A,C) and 200 m/day (B,D). The green dotted line illustrated where attachment on the top plate equaled to that on the bottom plate (i.e., ηbot/η = 0.5). Flow direction was perpendicular to the direction of gravity. The statistical error was about 5–10%. Other simulation conditions were given in Table 1.
For rod-shaped particles, at 5 m/day flow velocity, their retention trend and magnitude were similar as those of spheres (Figure 3A); however, when velocity was increased to 200 m/day, their retention behavior was very different from that of spheres (Figure 3B). Instead of having a local retention minimum around 1 μm in equivalent diameter as spheres, rod particles exhibited a local retention maximum around this size. The retention of rods for ~ 400 nm to 2 μm size range was approximately a factor of 2–10 higher than that of spheres. Rods rotate in response to Brownian rotations, as well as shape-induced fluid hydrodynamics (e.g., tumbling motions), with rotation speed increasing as shear rate (or velocity) increases (Jeffrey, 1922; Perrin, 1934). Generally, Brownian rotations were significant for small size rods (e.g., <1 μm), whereas rotation due to fluid hydrodynamics were dominant for large size rods (e.g., > 1 μm). At 200 m/day velocity, rotation of rods around 400 nm to 2 μm size range due to fluid hydrodynamics and Brownian rotation became similarly important, the coupled influences of both caused rod particles within this size range to drift considerably across streamlines to intercept collector surfaces for greater attachment (e.g., see Figure 2C) (Li and Ma, 2018).
Simulations shown in Figure 3 were run in a parallel plate flow chamber where flow was directed perpendicular to gravity. Under this condition, gravity pulled both spheres and rods downward without altering their respective rotation/oscillation patterns, so that particles would attach more onto the bottom plate of flow channel. Figures 3C,D showed the portion of attachment onto the bottom plate out of the overall attachment for simulations corresponding to Figures 3A,B, respectively. As expected, gravitational settling was more evident for larger size spheres or rods (e.g., > 1 μm in diameter) at both 5 and 200 m/day but had relatively less influence at higher velocity (Figure 3C vs. Figure 3D). Also, from Figures 3C,D, the effect of gravitational settling on rod-shaped particles appeared weaker than that of spheres, which we will discuss more in the next section.
Influences of Flow Channel Dimension on Particle Retention
From our previous simulations within the Happel sphere-in-cell model, rods exhibited distinct retention behavior relative to spheres even under pore water velocity of 5 m/day (similar to Figure 3B at 200 m/day, where a local retention maximum was observed for rods around equivalent volume size 1 μm) (Li and Ma, 2018), but we did not see that distinction in parallel plate geometry at the same velocity (Figure 3A). One major difference in these geometrical models was the flow channel height, which was much narrower in the Happel model (e.g., <100 μm). Therefore, we have reduced the parallel plate geometry size from 2 mm by 2 mm by 1 mm (Dimension I) to two narrower geometries: 2 mm by 0.5 mm by 1 mm (Dimension II) and 1 mm by 0.1 mm by 1 mm (Dimension III), where the smallest channel dimension was only about 5 times of the largest particle size simulated. The simulated collector efficiencies for a range of particle sizes (200 nm-6.6 μm in diameter) for rods (aspect ratio 6) and spheres within the parallel plate geometry of Dimension II and Dimension III at pore water velocity of 5 and 200 m/day were plotted in Figures 4A–F, respectively. For both spheres and rods, retention was in general greater in narrower channels (Figure 3A vs. Figures 4A,E, 3B vs. Figures 4B,F). Moreover, the distinct retention between rods and spheres as demonstrated in the Happel model at 5 m/day was now evident in the parallel plate geometry with narrower flow channels (Dimensions II-III) (Figures 4A,E) at the same velocity, which indicated the importance of flow channel size on colloid transport and retention, especially for non-spherical particles. Also, one can see that within the narrow channels (Dimensions II-III), the local maximum retention for rods shifted to smaller particle size as velocity was increased from 5 to 200 m/day (Figure 4A vs. Figure 4B and Figure 4E vs. Figure 4F), reflecting the enhanced drifting phenomenon induced by flow hydrodynamics at higher fluid velocity for rod-shaped colloids as discussed above. Further, for a given velocity, the local maximum retention for rod-shaped colloids also shifted to smaller colloid sizes with decreasing channel height (Figures 3, 4, excepting Figure 3A).
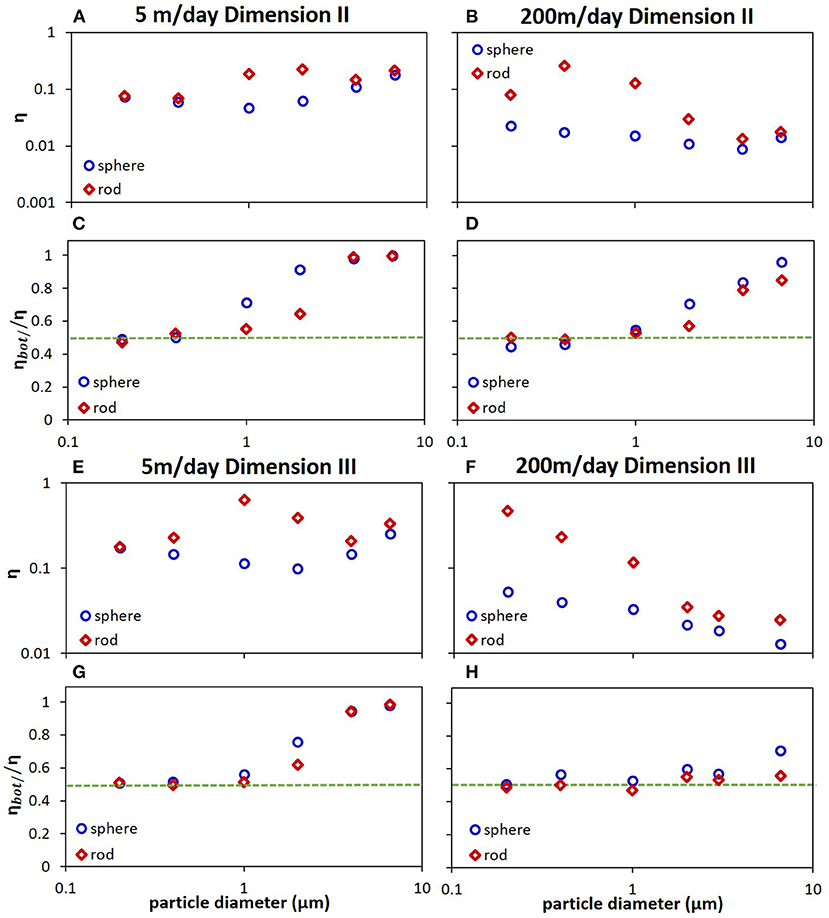
Figure 4. Simulated collector efficiencies (A,B,E,F) and the ratios of particles attached on the bottom plate to the total attachment (C,D,G,H) as a function of particle size for polystyrene spheres (blue circles) and rods (dark red diamonds) from parallel plate model of Dimension II (A–D) and Dimension III (E–H), under pore water velocity of 5 m/day (A,C,E,G) and 200 m/day (B,D,F,H). The green dotted line illustrated where attachment on the top plate equaled to that on the bottom plate (i.e., ηbot/η = 0.5). Flow direction was perpendicular to the direction of gravity. The statistical error was about 5–10%. Other simulation conditions were given in Table 1.
Parallel plate flow channel in Dimension III (100 μm in height) was almost as narrow as that in the Happel model (~ 65 μm) from our earlier work (Li and Ma, 2018), which allowed us to compare retention results from both geometries under the same pore water velocities. At lower velocity 5 m/day, retention trends from the parallel plates (Figure 4E) agreed qualitatively well with those from the Happel model (Figure 3 in Li and Ma, 2018) for both rods (aspect ratio 6) and spheres, in terms of local retention minimum around 2 μm for spheres, local retention maximum around 1 μm for rods, particle size range with the most pronounced retention differences between rods and spheres (~ 400 nm to 2 μm). But retention magnitudes in parallel plate geometry were much higher (about a factor of 5) than those in Happel model for both rods (aspect ratio 6) and spheres. The differences in retention magnitude between these two geometries could result from many factors associated with geometry differences, including fluid field distribution pattern, collector size, flow channel contour and dimension, particle injection plane, as well as flow channel orientation in relation to gravity. At higher velocity 200 m/day, similar retention behaviors were observed from both geometric models for rods (aspect ratio 6) and spheres (Figure 4F in this work vs. Figure 4C in Li and Ma, 2018) as those at 5 m/day, except for larger particle sizes > 2 μm, probably because in parallel plate geometry, flow direction was perpendicular to gravity, whereas in Happel model, flow direction was along with gravity. The observation that for narrow channels of similar width, retention in the parallel plate channel was ~5 times greater than that in the Happel model at both velocities may suggest that delivery of colloids to collectors for retention was more effective in straight channels than the curved ones formed by granular porous media (further investigation is needed along this line, but it is out of scope of this study).
Under favorable conditions, retention of colloids is governed by the transport process to the collector surfaces, close to which strong colloid-collector attractions can quickly immobilize nearby traveling particles. As shown in Figure 2, the non-spherical shape of particles alters their translation and rotational trajectories, causing rods to drift considerably across flow streamlines for greater probability of intercepting the collector surfaces. Nevertheless, the drift distances induced by particle shape were generally about tens of microns (e.g., see Figure 2C). In Supplementary Figure 1 in the Supporting Information, we plotted the limiting trajectory distances from the planar collectors (beyond which injected particles were not going to attach) for rods and spheres vs. particle diameter for simulations from the three different geometries (e.g., Figures 3A,B, 4A,B,E,F). One can see that the limiting trajectory distances correlated with overall retention trends remarkably well (comparing Supplementary Figure 1 with Figures 3A,B, 4A,B,E,F) for rods and spheres in all three channel dimensions, indicative of the significance of initial particle injection location on retention. Particles injected within the limiting trajectory distances (generally within a few hundreds of microns from the channel walls) had greater probability to be delivered near the collector walls for attachment. The differences in the limiting trajectory distances between rods and spheres within 400 nm to 2 μm size range demonstrated again that the non-spherical particle shape could alter particle trajectory for enhanced retention.
At a given velocity, the limiting trajectory distances obtained from Dimension I (2 mm by 2mm by 1 mm) and Dimension II (2 mm by 0.5 mm by 1 mm) were very similar for both rods and spheres (Supplementary Figure 1A vs. Supplementary Figures 1B,C vs. Supplementary Figure 1D), indicating that the limiting trajectory distances were not significantly affected by channel height. But the limiting trajectory distances from Dimension III (1 mm by 0.1 mm by 1 mm) were about 2–5 factors less than those from Dimensions I and II at the same velocity for both rods and spheres (Supplementary Figure 1). This could be primarily due to the shorter channel length of Dimension III, which was only half of that in Dimensions I and II. Since the three channel sizes explored in the current study were sufficiently wide with respect to all particle sizes examined, the relatively small differences in limiting trajectory distances indicated that all the transport and retention mechanisms operating in the wider channel (Dimension I) were also operating in the narrower channel (Dimensions II and III). To serve as a crude estimate of retention, one could use the area bounded within the limiting trajectory distances divided by the total cross area of injection plane (assuming uniform initial particle concentration as in our simulations) (see Supplementary Figure 2). Indeed, retention estimated from Supplementary Figure 2 matched remarkably well with the simulated collector efficiencies in Figures 3, 4. Channel Dimension III produced smaller limiting trajectory distances, but greater retention compared to channel Dimensions I and II, which primarily resulted from normalizing with respect to a smaller injection plane. In other words, in viscous shear flows, regardless of channel width, only those colloids that were initially injected close to the collector surfaces were likely to be delivered to the surfaces for attachment. The portion of total injected colloid population that could potentially hit the bounding walls was larger in narrow channels relative to wide ones. This also explains that the effect of particle shape on retention was more evident in narrower channels (e.g., Figures 4A,B vs. Figure 3), especially at relatively low fluid velocity (e.g., 5 m/day).
Influences of Flow Channel Orientation Relative to Gravity on Particle Retention
Simulation results shown in Figures 3, 4 were performed with the flow direction inside the parallel plate channels being perpendicular to gravity. Due to gravitational settling, more attachment was observed onto the bottom plate compared with the top one for larger size colloids (e.g., > 1 μm), as shown in Figures 3C,D, 4C,D,G,H) at both flow velocities. The effect of gravitational settling on retention became less important with increasing fluid velocity, which was true for both spheres and rods (Figure 3C vs. Figure 3D, Figure 4C vs. Figures 4D,G,H). This is expected because it is known that an object (regardless of shape) moving at higher velocity could better resist the gravitational pull if the velocity direction does not align with gravity. For both velocities, rods were observed to have less retention onto the bottom plate than spheres for certain sizes (e.g., 1–2 μm at 5 m/day, Figures 3C, 4C,E; 2–6.6 μm at 200 m/day, Figures 4D,H), which can be explained by the drifting phenomena of rods due to the combined influences of shape-induced fluid hydrodynamics and rotational diffusion as demonstrated in Figure 2C. Furthermore, the influence of gravitational settling seemed the least significant in the narrowest parallel plate channel at high velocity (see Figure 4H).
We then oriented the parallel plate channel (Dimension I) so that flow direction aligned with the direction of gravity and plotted simulated results in Figure 5 (other conditions were the same as those in Figure 3). Comparing Figure 5 with Figure 3, one can observe two big differences. First, since gravity was parallel to flow direction and also parallel to channel walls, it no longer caused colloids to drift across flow streamlines, so that retention of large size spheres decreased with increasing particle size at both 5 and 200 m/day (see Figures 5A,B). Second, the effect of particle shape on retention was more evident even at low velocity of 5 m/day for wider channels as in Dimension I; namely, retention of rods exhibited a local maximum around 2 μm in diameter (see Figure 5A vs. Figure 3A); and was greater than that of spheres for a wide size range (e.g., 1–6.6 μm). In addition, since flow aligned with the direction of gravity, the attachment of rods and spheres at both channel plates was similar (data not shown) for all particle sizes, as expected.
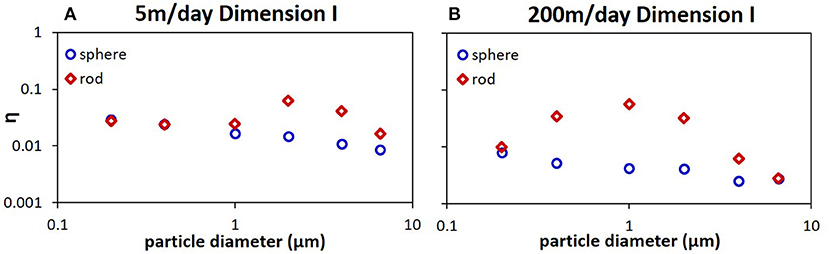
Figure 5. Simulated collector efficiencies as a function of particle size for polystyrene spheres (blue circles) and rods (dark red diamonds) from parallel plate model of Dimension I, under pore water velocity of 5 (A) and 200 m/day (B). Flow direction was aligned to the direction of gravity. The statistical error was about 5–10%. Other simulation conditions were given in Table 1.
Influences of Particle Density on Retention
Figure 6 plotted the simulated collector efficiencies of spherical and rod-shaped particles of varied densities (e.g., 1.055, 2.0, and 4.0 g/cm3 representing polystyrene, silica and iron, respectively) and sizes (400 nm-6.6 μm) from parallel plate geometry at velocity of 5 and 200 m/day. These simulations were run in Dimension I, where the flow direction inside the chamber was perpendicular to that of gravity. One can see that retention increased with increasing density for both spheres and rods and for both velocities (Figures 6A,B). At low velocity (e.g., 5 m/day), the impact of shape on retention was insignificant (Figure 6A); but heavier particles (e.g., silica, iron) predominantly deposited onto the bottom plate of flow chamber starting from sub-micron size range for both spheres and rods due to gravitational pull (Figure 6C). In fact, silica and iron particles over 1 μm almost all deposited to the bottom plate at 5 m/day (Figure 6C). At high velocity (e.g., 200 m/day), rod-shaped particles exhibited greater retention than spheres for medium particle sizes (e.g., ~ 400 nm−2 μm) for polystyrene, silica and iron particles (Figure 6B), due to drifting across flow streamlines from shape-induced rotation as described above. Again, for this size range particles, Figure 6 showed that rod-shaped colloids could travel farther downstream for retention at high velocity, despite the influence of gravitational pull, even for higher density particles such as silica or iron (see 1 μm size in Figure 6D).
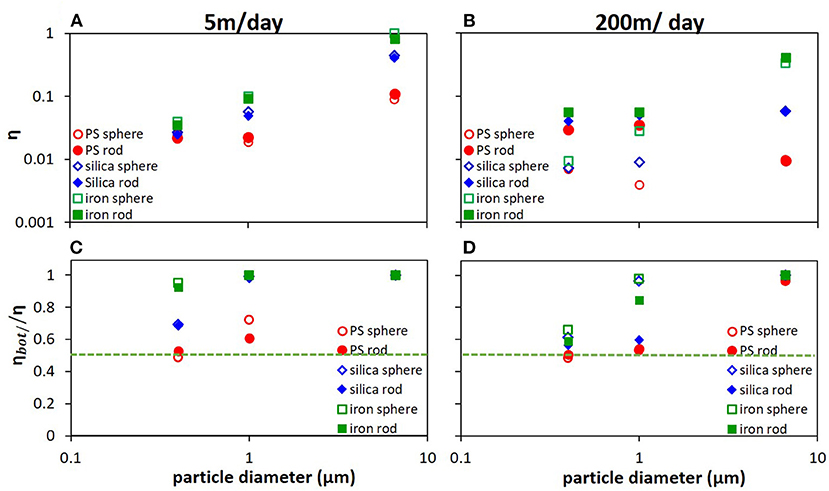
Figure 6. Simulated collector efficiencies (A,B) and the ratios of particles attached on the bottom plate to the total attachment (C,D) as a function of particle size for different particles: polystyrene spheres (open red circles), polystyrene rods (closed red circles), silica spheres (open blue diamonds), silica rods (closed blue diamonds), iron spheres (open green squares) and iron rods (closed green squares). The green dotted line illustrated where attachment on top plate equaled to that on bottom plate (i.e., ηbot/η = 0.5). Simulations were from parallel plate model of Dimension I, under pore water velocity of 5 (A,C) and 200 m/day (B,D) with flow perpendicular to gravity direction. The statistical error was about 5–10%. Other simulation conditions were identical as those for Figure 3.
Orientation and Distribution of Attached Particles
As illustrated in Figure 2A, both spheres and rod-shaped particles rotate in response to hydrodynamic fluid shear. Under favorable conditions, homogeneous spheres exhibited a nearly normal orientation distribution in terms of Euler angle θ as shown in Figure 7A, where the least retention around θ ≈ 0 or π was observed. Homogeneous rod particles also showed a wide range of attachment orientation, but the majority of the attached rods displayed an end-on orientation with one end tethered to the collector surface (Li and Ma, 2018) (Figure 7B), which also has been experimentally observed from other researchers (Constantino et al., 2016; Shave et al., 2019).
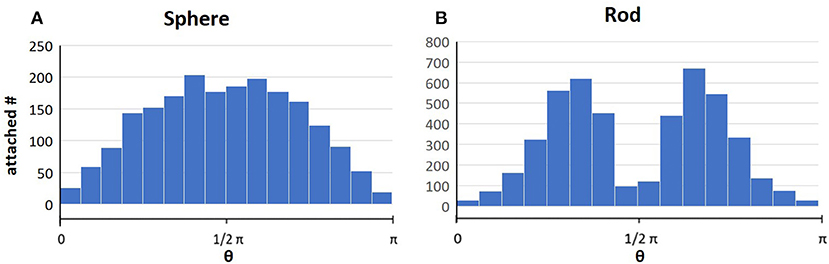
Figure 7. Simulated attachment orientations in terms of Euler angle θ for polystyrene spheres (A) and rods (B) (1 μm in equivalent volume diameter) in parallel plate geometry under pore water velocity of 5 m/day with flow direction perpendicular to gravity. Other simulation conditions were identical as those for Figure 3.
Under favorable conditions, colloid filtration theories predicted a log-linear retention profile (or exponential decay) with respect to transport distance (Tufenkji and Elimelech, 2004, 2005; Bouzarth and Minion, 2011). This was observed from our simulated attachment results in parallel plate chamber for spherical particles at both velocities (see Figures 8A,C). However, that was not the case for rod-shaped particles when the impact of particle shape on transport and retention was significant (Figures 8B,D). Because of their distinct rotational trajectories as demonstrated in Figure 2, rods could drift across flow streamlines for greater retention (especially for colloid size within ~ 400 nm ~ 2 μm at high velocities, see Figures 3B, 4A,B,E,F, 5A,B). Also due to this drifting phenomenon, rods could travel farther downstream for retention compared to their equal-volume spheres (Figures 8B,D). Hence, in order to effectively access the influences of particle shape on transport and retention, one should evaluate the attachment results over the entire collector surfaces, rather than randomly selected observation locations, which was especially crucial for experimental confirmation of shape effect (Shave et al., 2019).
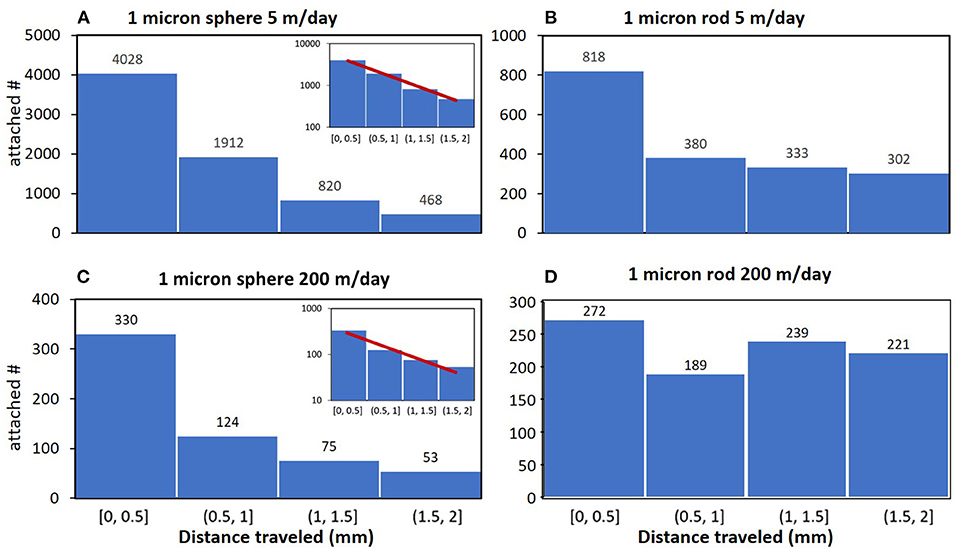
Figure 8. Simulated attachment distribution for polystyrene spheres and rods (1 μm in equivalent volume diameter) in parallel plate geometry (Dimension II with length increased to 2 mm) under pore water velocity of 5 m/day with flow direction perpendicular to gravity. Other simulation conditions were identical as those for Figure 3. The inserts in panels (A) and (C) illustrated the log-linear retention profile for spheres. The total numbers of particles injected into the systems were 27,000 for (A), and 12,000 for (B–D), respectively.
Summary and Conclusions
In this work, using a simple geometrical model (i.e., parallel plate flow chamber) where fluid flow pattern can be easily maintained as laminar flow, we systematically investigated the rotation and retention dynamics of rod-shaped colloids under the coupled influences of many factors including particle size and density, aspect ratio, fluid velocity, flow direction relative to gravity, channel dimension, and size. This study extended our investigation on non-spherical colloid transport and retention relative to our previous work in the Happel sphere-in-cell model (Li and Ma, 2018) in two main aspects. First, current work examined the factors that have not been previously studied, including flow channel dimension, flow orientation in relation to gravity, and particle density. Second, while the Happel geometry represents an idealized granular porous medium model, parallel plate channel represents another important feature in groundwater systems, namely, fracture aperture, or conduit. In this study, we have demonstrated that simulations in the parallel plate flow channels could qualitatively capture the retention trends for both rods and spheres for a wide particle size range under the same pore water velocity when the channel widths from both models were similar.
Our findings demonstrated that in many cases, particle shape had the most pronounced impact on rod-shaped colloids transport and retention for medium sized particles (equivalent volume size ~ 400 nm to 2 μm), because for this size range particles, the interplay of shape-induced fluid hydrodynamics and rotational diffusion caused rods to drift considerably across flow streamlines to intercept collector surfaces. Non-spherical particle shape also enabled rods to travel farther downstream along flow channel for retention relative to equal-volume spheres. In general, the impact of shape on colloidal transport and retention was more evident under relatively high fluid velocity, narrow flow channel, or when the flow direction was aligned with gravity. Therefore, it is crucial to take particle shape into account to fully understand colloid transport and migration behaviors for various environmental processes, because the majority of natural or engineered particles are non-spherical in shape. Moreover, our study has important implications on how to better utilize the impact of particle shape on retention for many practical applications, such as particle separation, water filtration and soil remediation. Our next step will be to investigate the impact of other non-spherical shapes (e.g., discoid, cylinder) on colloidal transport and retention in groundwater systems.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
HM developed the conceptual idea. KL established rod particle transport model in planar surface geometries and performed all simulations. Both authors contributed to the final manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This article was based upon work supported by the National Science Foundation Hydrologic Science Programs (EAR 1521421). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. We are grateful for the technical and facility support provided at the Center for High Performance Computing at the University of Utah. We thank Professors William P. Johnson, Yusong Li and Mathias Schubert and their research groups for their valuable inputs and discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frwa.2021.604204/full#supplementary-material
References
Albarran, N., Missana, T., Alonso, U., García-Gutiérrez, M., and López, T. (2013). Analysis of latex, gold and smectite colloid transport and retention in artificial fractures in crystalline rock. Colloid Surface A 435, 115–126. doi: 10.1016/j.colsurfa.2013.02.002
Al-Hadhrami, A., Elliott, L., Ingham, D., and Wen, X. (2003). Flows through horizontal channels of porous materials. Int. J. Energy Res. 27, 875–889. doi: 10.1002/er.923
Asadishad, B., Ghoshal, S., and Tufenkji, N. (2011). Method for the direct observation and quantification of survival of bacteria attached to negatively or positively charged surfaces in an aqueous medium. Environ. Sci. Technol. 45, 8345–8351. doi: 10.1021/es201496q
Bakker, D. P., Huijs, F. M., de Vries, J., Klijnstra, J. W., Busscher, H. J., and van der Mei, H. C. (2003). Bacterial deposition to fluoridated and non-fluoridated polyurethane coatings with different elastic modulus and surface tension in a parallel plate and a stagnation point flow chamber. Colloid Surface A 32, 179–190. doi: 10.1016/S0927-7765(03)00159-0
Bouzarth, E. L., and Minion, M. L. (2011). Modeling slender bodies with the method of regularized Stokeslets. J. Comput. Phys. 230, 3929–3947. doi: 10.1016/j.jcp.2011.02.017
Caldorera-Moore, M., Guimard, N., Shi, L., and Roy, K. (2010). Designer nanoparticles: incorporating size, shape and triggered release into nanoscale drug carriers. Exp. Opin. Drug Deliv. 7, 479–495. doi: 10.1517/17425240903579971
Chen, G., Hong, Y., and Walker, S. L. (2010). Colloidal and bacterial deposition: role of gravity. Langmuir 26, 314–319. doi: 10.1021/la903089x
Chen, K. C., Gu, Y., Sun, W., Dong, B., Wang, G. F., Fan, X. X., et al. (2017). Characteristic rotational behaviors of rod-shaped cargo revealed by automated five-dimensional single particle tracking. Nat. Commun. 8:1–10. doi: 10.1038/s41467-017-01001-9
Chrysikopoulos, C. V., and Syngouna, V. I. (2014). Effect of gravity on colloid transport through water-saturated columns packed with glass beads: modeling and experiments. Environ. Sci. Technol. 48, 6805–6813. doi: 10.1021/es501295n
Constantino, M. A., Jabbarzadeh, M. C., Fu, H. C., and Bansil, R. (2016). Helical and rod-shaped bacteria swim in helical trajectories with little additional propulsion from helical shape. Sci. Adv. 2:e1601661. doi: 10.1126/sciadv.1601661
Doshi, N., Prabhakarpandian, B., Rea-Ramsey, A., Pant, K., Sundaram, S., and Mitragotri, S. (2010). Flow and adhesion of drug carriers in blood vessels depend on their shape: a study using model synthetic microvascular networks. J. Controlled Release 146, 196–200. doi: 10.1016/j.jconrel.2010.04.007
Drescher, K., Dunkel, J., Cisneros, L. H., Ganguly, S., and Goldstein, R. E. (2011). Fluid dynamics and noise in bacterial cell-cell and cell-surface scattering. Proc. Natl. Acad. Sci. U.S.A. 108, 10940–10945. doi: 10.1073/pnas.1019079108
Elimelech, M. (1994). Particle deposition on ideal collectors from dilute flowing suspensions: mathematical formulation, numerical solution, and simulations. Sep. Sci. Technol. 4, 186–212. doi: 10.1016/0956-9618(94)80024-3
Fang, N., Chen, K. C., and Cheng, X. D. (2018). Characteristic rotational behaviors of rod-shaped cargo revealed by automated five-dimensional single particle tracking. Biophys. J. 114, 656A. doi: 10.1016/j.bpj.2017.11.3543
Geng, Y., Dalhaimer, P., Cai, S. S., Tsai, R., Tewari, M., Minko, T., et al. (2007). Shape effects of filaments versus spherical particles in flow and drug delivery. Nat. Nanotechnol. 2, 249–255. doi: 10.1038/nnano.2007.70
Gentile, F., Chiappini, C., Fine, D., Bhavane, R. C., Peluccio, M. S., Cheng, M. M. C., et al. (2008). The effect of shape on the margination dynamics of non-neutrally buoyant particles in two-dimensional shear flows. J. Biomech. 41, 2312–2318. doi: 10.1016/j.jbiomech.2008.03.021
Gervais, T., and Jensen, K. F. (2006). Mass transport and surface reactions in microfluidic systems. Chem. Eng. Sci. 61, 1102–1121. doi: 10.1016/j.ces.2005.06.024
Ghanem, N., Kiesel, B., Kallies, R., Harms, H., Chatzinotas, A., and Wick, L. Y. (2016). Marine phages as tracers: effects of size, morphology, and physico-chemical surface properties on transport in a porous medium. Environ. Sci. Technol. 50, 12816–12824. doi: 10.1021/acs.est.6b04236
Jeffrey, G. B. (1922). The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. London, Ser. A. 102, 161–179. doi: 10.1098/rspa.1922.0078
Johnson, W. P., Li, X., and Yal, G. (2007). Colloid retention in porous media: Mechanistic confirmation of wedging and retention in zones of flow stagnation. Environ. Sci. Technol. 41, 1279–1287. doi: 10.1021/es061301x
Johnson, W. P., Pazmino, E., and Ma, H. (2010). Direct observations of colloid retention in granular media in the presence of energy barriers, and implications for inferred mechanisms from indirect observations. Water Res. 44, 1158–1169. doi: 10.1016/j.watres.2009.12.014
Kolhar, P., Anselmo, A. C., Gupta, V., Pant, K., Prabhakarpandian, B., Ruoslahti, E., et al. (2013). Using shape effects to target antibody-coated nanoparticles to lung and brain endothelium. Proc. Natl. Acad. Sci. U.S.A. 110, 10753–10758. doi: 10.1073/pnas.1308345110
Kuzhir, P., Magnet, C., Bossis, G., Meunier, A., and Bashtovoi, V. (2011). Rotational diffusion may govern the rheology of magnetic suspensions. J. Rheol. 55, 1297–1318. doi: 10.1122/1.3626945
Li, K., and Ma, H. (2018). Deposition dynamics of rod-shaped colloids during transport in porous media under favorable conditions. Langmuir 34, 2967–2980. doi: 10.1021/acs.langmuir.7b03983
Li, K., and Ma, H. (2019). Rotation and retention dynamics of rod-shaped colloids with surface charge heterogeneity in sphere-in-cell porous media model. Langmuir 35, 5471–5483. doi: 10.1021/acs.langmuir.9b00748
Liu, Y., Tan, J. T., Thomas, A., Ou-Yang, D., and Muzykantov, V. R. (2012). The shape of things to come: importance of design in nanotechnology for drug delivery. Ther. Deliv. 3, 181–194. doi: 10.4155/tde.11.156
Ma, H., and Johnson, W. P. (2010). Colloid retention in porous media of various porosities: Predictions by the hemispheres-in-cell model. Langmuir 26, 1680–1687. doi: 10.1021/la902657v
Ma, H., Pazmino, E., and Johnson, W. P. (2011a). Surface heterogeneity on hemispheres-in-cell model yields all experimentally-observed non-straining colloid retention mechanisms in porous media in the presence of energy barriers. Langmuir 27, 14982–14994. doi: 10.1021/la203587j
Ma, H., Pazmino, E. F., and Johnson, W. P. (2011b). Gravitational settling effects on unit cell predictions of colloidal retention in porous media in the absence of energy barriers. Environ. Sci. Technol. 45, 8306–8312. doi: 10.1021/es200696x
Ma, H., Pedel, J., Fife, P., and Johnson, W. P. (2009). Hemispheres-in-cell geometry to predict colloid deposition in porous media. Environ. Sci. Technol. 43, 8573–8579. doi: 10.1021/es901242b
Ma, H. C., Bolster, W. P., Johnson, K., Li, E., Pazmino, K. M., Camacho, A. C., et al. (2020). Coupled influences of particle shape, surface property and flow hydrodynamics on rod-shaped colloid transport in porous media. J. Colloid Interface Sci. 577, 471–480. doi: 10.1016/j.jcis.2020.05.022
Mahnama, A., Ghorbaniasl, G., Allaei, S. M. V., and Nourbakhsh, A. (2014). Semi-analytical solution for the in-vitro sedimentation, diffusion and dosimetry model: Surveying the impact of the Peclet number. Colloids Surf. B 122, 324–331. doi: 10.1016/j.colsurfb.2014.06.063
Mendez, A., Castillo, L. E., Ruepert, C., Hungerbuehler, K., and Ng, C. A. (2018). Tracking pesticide fate in conventional banana cultivation in Costa Rica: a disconnect between protecting ecosystems and consumer health. Sci. Total Environ. 613, 1250–1262. doi: 10.1016/j.scitotenv.2017.09.172
Moreno, L., and Tsang, C. F. (1994). Flow channeling in strongly heterogeneous porous media: a numerical study. Water Resour. Res. 30, 1421–1430. doi: 10.1029/93WR02978
Mortensen, P. H., Andersson, H. I., Gillissen, J. J., and Boersma, B. J. (2008). On the orientation of ellipsoidal particles in a turbulent shear flow. Int. J. Multiphase Flow 34, 678–683. doi: 10.1016/j.ijmultiphaseflow.2007.12.007
Nelson, K. E., and Ginn, T. R. (2005). Colloid filtration theory and the happel sphere-in-cell model revisited with direct numerical simulation of colloids. Langmuir 21, 2173–2184. doi: 10.1021/la048404i
Nelson, K. E., and Ginn, T. R. (2011). New collector efficiency equation for colloid filtration in both natural and engineered flow conditions. Water Resour. Res. 47:W05543. doi: 10.1029/2010WR009587
Perrin, P. F. (1934). Mouvement Brownien d'un ellipsoide (I). Dispersion dielectrique pour des molecules ellipsoidales. Le J Phys Le Radium 10, 497–511. doi: 10.1051/jphysrad:01934005010049700
Pillai, J. D., Dunn, S. S., Napier, M. E., and DeSimone, J. M. (2011). Novel platforms for vascular carriers with controlled geometry. Iubmb Life 63, 596–606. doi: 10.1002/iub.497
Rajagopalan, R., and Tien, C. (1976). Trajectory analysis of deep-bed filtration with the sphere-in-cell porous media model. AlChE J. 22, 523–533. doi: 10.1002/aic.690220316
Salerno, M. B., Flamm, M., Logan, B. E., and Velegol, D. (2006). Transport of rodlike colloids through packed beds. Environ. Sci. Technol. 40, 6336–6340. doi: 10.1021/es0614565
Sen Gupta, A. (2016). Role of particle size, shape, and stiffness in design of intravascular drug delivery systems: insights from computations, experiments, and nature. Wiley Interdiscip. Rev. 8, 255–270. doi: 10.1002/wnan.1362
Seymour, M. B., Chen, G., Su, C., and Li, Y. (2013). Transport and retention of colloids in porous media: does shape really matter? Environ. Sci. Technol. 47, 8391–8398. doi: 10.1021/es4016124
Shave, M. K., Balciunaite, A., Xu, Z., and Santore, M. M. (2019). Rapid electrostatic capture of rod-shaped particles on planar surfaces: standing up to shear. Langmuir 35, 13070–13077. doi: 10.1021/acs.langmuir.9b01871
Stoll, M., Huber, F., Schill, E., and Schäfer, T. (2017). Parallel-plate fracture transport experiments of nanoparticulate illite in the ultra-trace concentration range investigated by Laser-Induced Breakdown Detection (LIBD). Colloid Surface A 529, 222–230. doi: 10.1016/j.colsurfa.2017.05.067
Ta, H. T., Truong, N. P., Whittaker, A. K., Davis, T. P., and Peter, K. (2018). The effects of particle size, shape, density and flow characteristics on particle margination to vascular walls in cardiovascular diseases. Expert Opin. Drug Deliv. 15, 33–45. doi: 10.1080/17425247.2017.1316262
Thompson, A. J., Mastria, E. M., and Eniola-Adefeso, O. (2013). The margination propensity of ellipsoidal micro/nanoparticles to the endothelium in human blood flow. Biomaterials 34, 5863–5871. doi: 10.1016/j.biomaterials.2013.04.011
Trauscht, J., Pazmino, E., and Johnson, W. P. (2015). Prediction of nanoparticle and colloid attachment on unfavorable mineral surfaces using representative discrete heterogeneity. Langmuir 31, 9366–9378. doi: 10.1021/acs.langmuir.5b02369
Tufenkji, N., and Elimelech, M. (2004). Deviation from the classical colloid filtration theory in the presence of repulsive DLVO interactions. Langmuir 20, 10818–10828. doi: 10.1021/la0486638
Tufenkji, N., and Elimelech, M. (2005). Spatial distributions of cryptosporidium oocysts in porous media: evidence for dual mode deposition. Environ. Sci. Technol. 39, 3620–3629. doi: 10.1021/es048289y
Unni, H. N., and Chun, Y. (2009). Colloidal particle deposition from electrokinetic flow in a microfluidic channel. Electrophoresis 30, 732–741. doi: 10.1002/elps.200800668
Walt, D. R., Smulow, J. B., Turesky, S. S., and Hill, R. G. (1985). The effect of gravity on initial microbial adhesion. J. Colloid Interface Sci. 107, 334–336. doi: 10.1016/0021-9797(85)90185-7
Wang, P., and Keller, A. A. (2009). Natural and engineered nano and colloidal transport: role of zeta potential in prediction of particle deposition. Langmuir 25, 6856–6862. doi: 10.1021/la900134f
Xizhe, L., Detang, L., Ruilan, L., Yuping, S., Weijun, S., Yong, H., et al. (2019). Quantitative criteria for identifying main flow channels in complex porous media. Pet. Explor. Dev. 46, 998–1005. doi: 10.1016/S1876-3804(19)60256-9
Yao, K.-M., Habibian, M. T., and O'Melia, C. R. (1971). Water and waste water filtration: concepts and applications. Environ. Sci. Technol. 5, 1105–1112. doi: 10.1021/es60058a005
Zhang, H., Ahmadi, G., and Asgharian, B. (2007). Transport and deposition of angular fibers in turbulent channel flows. Aerosol. Sci. Technol. 41, 529–548. doi: 10.1080/02786820701272004
Zhang, H., Ahmadi, G., Fan, F.-G., and McLaughlin, J. B. (2001). Ellipsoidal particles transport and deposition in turbulent channel flows. Int. J. Multiph. 27, 971–1009. doi: 10.1016/S0301-9322(00)00064-1
Zhao, F., and Van Wachem, B. G. M. (2013). Direct numerical simulation of ellipsoidal particles in turbulent channel flow. Acta Mech. 224, 2331–2358. doi: 10.1007/s00707-013-0921-3
Keywords: particle shape, colloid transport, ellipsoid, parallel plate flow channel, particle rotation
Citation: Li K and Ma H (2021) High Fluid Velocity and Narrow Channels Enhance the Influences of Particle Shape on Colloid Retention in Saturated Groundwater Systems Under Favorable Deposition Conditions. Front. Water 3:604204. doi: 10.3389/frwa.2021.604204
Received: 08 September 2020; Accepted: 21 January 2021;
Published: 16 February 2021.
Edited by:
Carl I. Steefel, Lawrence Berkeley National Laboratory, United StatesReviewed by:
Zhi Li, Lawrence Berkeley National Laboratory, United StatesMavrik Zavarin, United States Department of Energy (DOE), United States
Copyright © 2021 Li and Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huilian Ma, SHVpbGlhbi5tYUB1dGFoLmVkdQ==
 Ke Li
Ke Li Huilian Ma
Huilian Ma