Accounting for Temporal Variability of Streamflow in Estimates of Travel Time

Retention, processing, and transport of solutes and particulates in stream corridors are influenced by the travel time of streamflow through stream channels, which varies dynamically with discharge. The effects of streamflow variability across sites and over time cannot be addressed by time-averaged models if parameters are based solely on the characteristics of mean streamflow. We develop methods to account for the effects of streamflow variability on travel time and compare our estimates to flow-weighted (“effective”) travel time at 100 streams in the southeastern United States. Velocity time series were generated for each stream from multiple-year (median 15.5 years), high-frequency (15 min interval) records of instantaneous streamflow and field measurements of velocity and inverted to produce time series of specific travel time [T/L]. The effective travel times for streams are 60–90% of the specific travel time of mean streamflow because a large fraction of the total streamflow volume is discharged during higher flows with higher velocities. We find that adjusting the specific travel time of mean streamflow at a site by a factor of 0.81 generally accounts for the effect of a skewed streamflow distribution, but at-site estimates of the coefficient of variation of streamflow are necessary to resolve differences in streamflow variability between streams or changes in variability over time. For example, the effective travel time of urban streams is less than the effective travel of forested streams in the southeastern United States as a result of increased streamflow variability in urban streams. Effective travel time accounts for both the variation in velocity with streamflow and the large fraction of streamflow discharged during high flows in most streams and provides time-averaged models with limited capability to account for effects of streamflow variability that otherwise they lack. This capability is needed for continental-scale modeling where streamflow variability is not uniform because of heterogeneous surficial geology, hydro-climatology, and vegetation and for applications where streamflow variability is not stationary as a response to climate change or hydrologic alteration.

Introduction

The velocity of streamflow has two fundamental but distinct roles on the processing of solutes and particulates in river corridors: it determines the rate of downstream advective transport of materials in a channel and it affects the “turnover length” of streamflow, which is the distance that streamflow must travel for complete exchange with water in transient storage zones in river corridors (e.g., hyporheic sediments, in-channel alcoves, off-channel sloughs, and floodplains) (Newbold et al., 1983; Meyer and Edwards, 1990; Mulholland et al., 1990; Stream Solute Workshop, 1990; Czuba and Foufoula-Georgiou, 2014; Harvey, 2016). The ratio of downstream advective transport to in-channel processing (e.g., settling velocity of particulates or uptake velocity of nutrients) limits the efficiency of in-channel retention of fine sediment in river channels (Konrad, 2009), filtration of organic particulates by invertebrates (Wallace et al., 1977), and nutrient uptake by photosynthetic organisms (Hall et al., 2002). Turnover lengths indicate hydrologic connectivity of streamflow (fraction exchanged) with hyporheic and other storage zones and its contact time with reactive sediments (Hein et al., 2004; Schmadel et al., 2016; Harvey et al., 2019; Findlay, 1995). Given these roles, streamflow velocity or, inversely, travel time is a lynch pin for accurate accounting of material processing and loads through river networks.

Large-scale synoptic investigations (Konrad and Gellis, 2018), remotely-acquired data (Konrad et al., 2008) and spatially-distributed models (Czuba et al., 2018) can address spatial variability in streamflow velocity, but high-frequency measurements and dynamic models are needed to account explicitly for the temporal variability of travel time forced by streamflow and its resulting effects on biophysical processing (Konrad, 2009; Botter et al., 2010; Basu et al., 2011; Ye et al., 2012). It is more often the case that time-averaged models of material transport and reactivity are applied to river networks (Boyer et al., 2006; Mulholland et al., 2008; Alexander et al., 2009; Helton et al., 2011; Czuba and Foufoula-Georgiou, 2014; Gomez-Velez et al., 2015). The temporal distributions of streamflow velocity and travel time remain a critical gap for river basin and larger scale biogeochemical modeling over seasonal and longer timescales (Wollheim et al., 2006; Bergstrom et al., 2016; Raymond et al., 2016). Since streamflow cannot be presumed to be steady over these time scales, effective values of velocity, and travel time are used in time-averaged models (Wolman and Miller, 1960; Doyle, 2005; Basso et al., 2015; Harvey and Gooseff, 2015). Application of such models to assess impacts of climate, land use, or water management in river corridors, however, requires adjustments to the effective values of velocity or travel time to account for changes in temporal variability of streamflow.

Time-averaged biogeochemical models of river networks typically use the velocity, travel time, or hydraulic load (product of velocity and depth divided by reach length) for mean streamflow (Behrendt and Opitz, 1999; Wollheim et al., 2006; Alexander et al., 2009; Helton et al., 2011). Mean streamflow, however, does not represent the variability of streamflow, which ranges across streams because of spatial heterogeneity in geology, soils, climate, watershed size, drainage density, and land cover (Carlston, 1963; Thomas and Benson, 1970; Poff and Ward, 1989; Dettinger and Diaz, 2000; Konrad et al., 2005; Pagano and Garen, 2005; Poff et al., 2007; Jiménez Cisneros et al., 2014; Basso et al., 2015). Without a way to represent differences in streamflow variability in space or over time, time-averaged models have limited capability to account for the effects of basin scale, climate, and hydrologic alteration by land and water uses (Ensign and Doyle, 2006; Wollheim et al., 2006; Hall et al., 2009; Basu et al., 2011; Raymond et al., 2016).

Urban development in particular increases streamflow variability as a result of reduced storage of water in soil and land surface depressions and shorter, less resistant pathways for water to flow through drainage systems into channels. These changes result in more rapid runoff and greater flow peaks for a given storm (Leopold, 1968; Konrad and Booth, 2005). Despite efforts to manage urban stormwater, modification of streamflow regimes persists in urban areas (Paul and Meyer, 2001; Konrad et al., 2005; Chang, 2007; Smith et al., 2013). While structural changes in stream channels (e.g., lining the channel with concrete, removing emergent vegetation) reduces flow resistance and travel time, shorter travel times in urban streams can be expected simply as a result of the re-distribution of runoff from lower-flow to higher-flow periods.

Our objective is to develop a method for estimating the effective travel time in stream channels that accounts for streamflow variability at and across sites and can conveniently be applied in time-averaged modeling stream transport and reaction of processes with first-order kinetics. The method is generalized by using the variance and skew of a streamflow distribution for the estimate without prejudice to why streamflow has a particular skew and variance. Thus, it is transferrable to infer effects on processing and retention for any factor that is known to influence the moments of a streamflow distribution. Potential applications extend to the evaluation of retention and processing of sediment and nutrients (1) at regional-scales because of heterogeneity in geology and hydro-climatology, (2) across large river basins because of downstream reduction in streamflow variability, and (3) in the context of climate and land use changes that affect streamflow variability. We demonstrate how differences in travel time at decadal time scales can be inferred from differences in streamflow distributions as a result of urban development in the southeastern United States.

Methods and Materials

Effective Travel Time for First-Order Reaction Processes

For in-stream processes involving first-order kinetics of transformation or retention (e.g., nutrient uptake that is a constant fraction of nutrient concentration), the effective travel time of water through a reach, Tr_ef[T], can be derived by equating the mass flux calculated from a time-averaged model to the instantaneous mass flux integrated over time,

$\begin{array}{ll}kT{r}_{ef}\overline{C}\stackrel{\overline{Q}}{}={\displaystyle {\int }_{t=0}^T}kL{\frac{1}{u}}_t{C}_t{Q}_{t}dt& (1)\end{array}$

where k is the reaction rate constant, L is reach length, $\overline{C}$ is mean concentration of the constituent of interest, $\overline{Q}$ is mean discharge, T is the total time for the period for interest, C_t is concentration at time t, Q_t is discharge at time t, and u_t is velocity at time t. By simplifying Equation (1), the effective travel time reduces to the flow- and concentration-weighted, mean travel time,

$\begin{array}{ll}T{r}_{ef}=\frac{L}{T}{\displaystyle {\int }_{t=0}^T}\frac{C_t}{\overline{C}}\frac{Q_t}{\overline{Q}}\frac{1}{u_t}dt& (2)\end{array}$

We limit the analysis to cases where temporal variation in streamflow is much greater than the variation in first-order reaction rates, k is constant, and variation in concentration using the approximations $\frac{C_t}{\overline{C}}\approx 1$. These approximations allows Tr_ef to be calculated simply as the flow-weighted mean travel time:

$\begin{array}{ll}T{r}_{ef}=\frac{L}{T}{\displaystyle {\int }_{t=0}^T}\frac{Q_t}{\overline{Q}}\frac{1}{u_t}dt& (3)\end{array}$

Based on Equation (3), flow-weighted travel times will generally be shorter than time-averaged travel time because velocity increases with streamflow. For cases where concentration and first-order reaction rates vary over time, the effective travel depends on the joint probability of travel time, concentration, and first-order reaction rate [see Doyle (2005) for an example of temporally variable streamflow and concentration]. When concentration increases with streamflow and first-order reaction rates decrease with concentration (e.g., a saturation effect), Equation (3) would provide a better estimate than the time-averaged travel time, but travel time would still be under-estimated.

Specific Travel Time

Calculation of effective travel time with Equation (3) requires time series of discharge and travel time. While discharge time series are available from gages and can be extrapolated over a reach without significant inflows and outflows or simulated using spatially-distributed hydrologic models, time series of travel time are only available at locations with velocity meters, hydraulic models, or where travel time has been measured over a range of streamflow (Hubbard et al., 1982; Bergstrom et al., 2016). For gaged streams with velocity data, a stage or discharge time series can be transformed into velocity time series (Jobson, 2000) and inverted to produce a time series of specific travel time, τ_t = 1/u_t, [L/T] at the gage. The effective value (flow-weighted) of a distribution of specific travel times can be calculated from time series of discharge and velocity,

$\begin{array}{ll}{\tau }_{ef}=\frac{1}{TS}{\displaystyle \sum _{ts=1}^{TS}}\frac{Q_{ts}}{\overline{Q}}\frac{1}{u_{ts}}& (4)\end{array}$

where ts represents an individual time step in each time series, TS is the total number of values in each time series, and τ_ef is the effective value of specific travel time at the gage and time series used with units of [T/L].

Equation (4) is used to demonstrate the effects of streamflow variability on velocity and specific travel time. The velocity at a gage is not necessarily representative of velocity averaged over a reach but it is useful as an index of variation of the reach-averaged mean velocity over time (Hubbard et al., 1982). Specific travel time at a gage is likely to biased downward in comparison to the travel time for a longer reach because gage locations are typically selected in narrower sections that maintain measurable, downstream velocity even during low flows. The bias is likely to diminish as streamflow increases and flow becomes more uniform through the reach (Hubbard et al., 1982). As a result, the effect of streamflow variability on specific travel time at a gage indicated by this analysis is likely to be less than its effect on travel time at the reach-scale.

Overview of Analysis and Streams

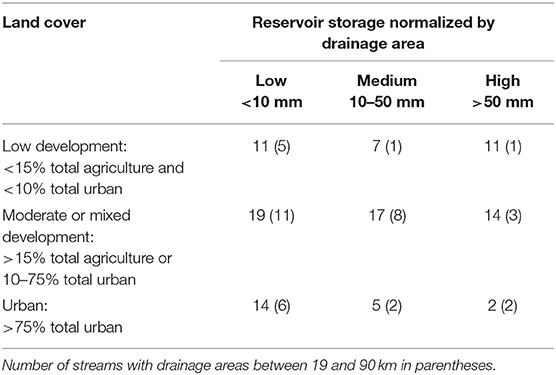
The analysis has three principal steps: (1) synthesize τ_ef distributions from multiple-year, instantaneous streamflow records and field-measured velocities for gaged streams spanning a range in streamflow variability; (2) apply and evaluate methods for estimating τ_ef; and (3) compare τ_t distributions characteristic of urban and undeveloped streams. We selected 100 gaged streams in the southeastern United States (Figure 1) from six Level III Ecoregions: Piedmont (76 streams), Blue Ridge (12 streams), Valley and Ridge (8 streams), Southeastern Plains (2 streams), North Piedmont (1 stream), and Southwestern Appalachians (1 stream) (Journey et al., 2015). The streams span a range of drainage areas (7–1000 km²) and were selected to represent streamflow modification by reservoirs and land uses. Normal reservoir storage volume (US Army Corps of Engineers, 2010) in each stream basin divided by basin area ranged from 0 to more than 3 m (median value of 12 mm). Agricultural land cover ranged from 0 to 33% (median 6.5%) of stream basin area. Urban land cover ranged from <1 to 100% (median 22%). The values for each stream are available in Konrad (2020).

FIGURE 1

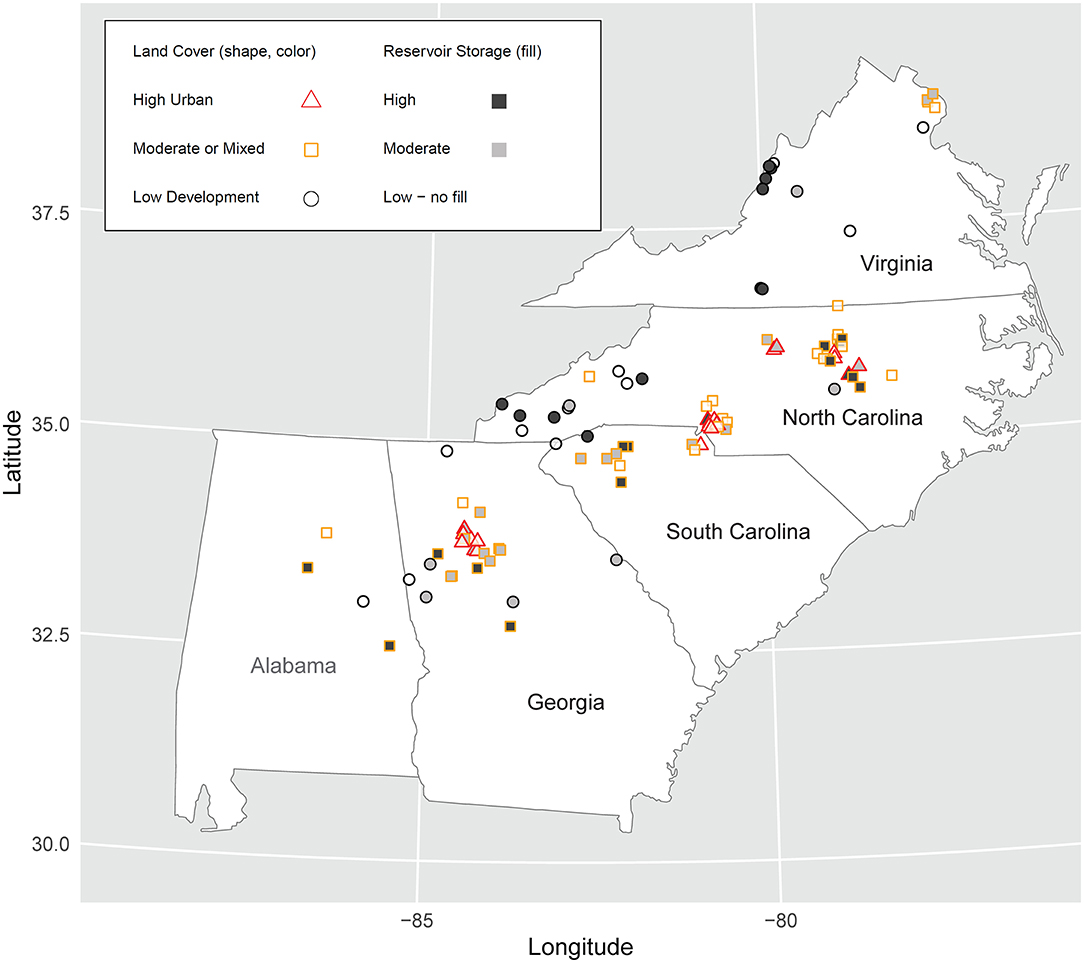
Figure 1. Location of streams in the southeastern US categorized by land cover and reservoir storage.

Stream size, land use, and streamflow regulation by reservoirs can all affect streamflow variability, so they are potential confounding factors when effects of urbanization on travel time. The coefficient of variation of streamflow distributions were examined in relation to drainage area, total agricultural and urban land cover in 2011 (Multi-Resolution Land Characteristics Consortium, 2019), and normal reservoir storage to identify domains where streamflow variability had little relation to each factor. These homoscedastic domains provided the basis for stratifying streams by size, land use, and regulation (Table 1).

TABLE 1

Table 1. Number of streams stratified by reservoir storage and land cover.

Although streams are distributed over the ranges of these factors, not all combinations are well-represented. Streams with drainage areas outside of the range from 19 to 90 km², moderate development, mixed land use, or reservoirs providing more than 10 mm of storage over the stream's drainage area are excluded from the analysis of urbanization (step 3). Travel time is examined in streams where streamflow is regulated by reservoirs, but we do not test for effects because of differences in how reservoirs are operated among streams (e.g., power production, water supply, or flood control).

Generating Specific Travel Time Distributions From Streamflow Time Series and Discrete Velocity Measurements

Available instantaneous streamflow records with a 15 min interval from 1 October 2000 to 30 September 2017 were retrieved from the National Water Information System (USGS, 2019). The length of the records ranged from 4 to 17 years among the streams with a median of 15.5 years. Field measurements of velocity and streamflow were retrieved for 1 October 2010 to 30 September 2017 at each site (Rantz, 1982; USGS, 2019). The period for field measurements relating measured velocity to discharge was limited to the most recent 7 years of the streamflow records to increase the likelihood that measurements were made at approximately the same section in each stream so that at-site variation in velocity is primarily due to variation in discharge rather than the location of the measurement section.

The measurement of stream velocity during unsteady flow may include a significant component of localized, flood-wave driven celerity that affects channel storage rather than contributing to the downstream advection of water. We eliminated measurements made during periods of unsteady flow by converting instantaneous stage measured at the gage during each measurement into values of hydraulic mean depth for the cross-section and eliminating those measurements when hydraulic mean depth changed by more than 10% during the measurement (USGS, 2019). After eliminating measurements made during unsteady flow, streams had between 26 and 96 remaining measurements (median of 52 measurements per site) to define the relation between instantaneous streamflow and velocity.

Specific travel times, τ_t, [s/m] are synthesized for each stream by transforming instantaneous streamflow, Q_t, into instantaneous velocity, u_t, and inverting the velocities, τ_t = 1/u_t. The transformation is based on linear regression of log of discrete streamflow measurements, Q_m, and log of mean cross-section velocity, u_m, for the measurements in a stream, s, using the function lm in R (R Core Team, 2019) to minimize the sum of the squared errors ε_m for each site,

$\begin{array}{ll}\text{ln }(u_m)={\beta }_{0,s}+{\beta }_{1,s}ln(Q_m)+{\epsilon }_m& (5)\end{array}$

where β_0,s is the intercept and β_1,s is the slope for stream s assuming that the functional form is a power law, u_m = β₀$Q_m^{\beta }$¹ (Rantz, 1982). The log of instantaneous travel time at time t, τ_t, is equal to the opposite of the velocity function applied to instantaneous streamflow,

$\begin{array}{ll}\text{ln }({\tau }_t)=\text{ln }\left(\frac{1}{u_t}\right)=-\left[{\beta }_{0,s}+{\beta }_{1,s}ln(Q_t)\right]& (6)\end{array}$

Methods for Estimating Effective Travel Time

Application of biogeochemical models across river networks requires spatially distributed estimates of effective travel time. While Equations (4)–(6) can be used at locations with measured velocities and streamflow time-series, we develop and evaluate three alternative methods for estimating τ_ef that could be applied more widely. Each method uses either a quantile or moment of a streamflow distribution, which could be calculated at gaged sites from streamflow records or, potentially, assigned to ungaged streams using a model. The overall purpose for the comparisons is to assess the viability of estimating τ_ef from an index streamflow rather than computing it directly from the τ_t distribution. The evaluation of the estimates with respect to streamflow variability is significant for both selecting the best method but also understanding the bias of using any of these method in comparisons across streams or scenarios where streamflow variability neither uniform in space or constant over time.

Direct calculation of τ_ef and all of the methods for estimating τ_ef depend on a known relation between discharge and travel time, which will be a primary source of uncertainty in any application. Estimation of τ_ef faces an additional issue of bias related to streamflow variability, which limits the utility of τ_ef estimates in comparative analyses across streams (e.g., in relation to basin size, climate, or land use) or over time (e.g., in relation to changes in climate, land use, or water management). Errors in estimates of τ_ef from each method are compared to the variance and higher moments of streamflow distributions to evaluate bias with streamflow variability.

The first method for estimating τ_ef uses the specific travel time for a fixed quantile of a streamflow distribution. This method accounts for the effect of streamflow variability on travel time generalized across sites but depends on a relatively consistent effect across sites for unbiased estimation. The effective discharge, Q_ef, that has a specific travel time equal to τ_ef is calculated by inverting Equation (6) and replacing τ_t with τ_ef for each stream,

$\begin{array}{ll}{Q}_{ef,s}=exp\left[{\beta }_{0,s}+\frac{ln\left({\tau }_{ef}\right)}{-{\beta }_{1,s}}\right]& (7)\end{array}$

The quantiles representing Q_ef are compared to each of the first three linear (L-) moment ratios (Hosking and Wallis, 1997) of the observed streamflow distributions for the 100 streams:

$\begin{array}{ll}\text{linear coefficient of variation},\text{ LCV}=\frac{{\lambda }_2}{{\lambda }_1};& (\mathrm{8a})\end{array}$

$\begin{array}{ll}\text{linear skew},\text{ LSK}=\frac{{\lambda }_3}{{\lambda }_2};\text{ and}& (\mathrm{8b})\end{array}$

$\begin{array}{ll}\text{linear kurtosis},\text{ LKU}=\frac{{\lambda }_4}{{\lambda }_2}& (\mathrm{8c})\end{array}$

where λ_i is the ith L-moment of the observed streamflow frequency distribution (Hosking, 2017). Systematic variation of the quantile for τ_ef with one or more of the L-moment ratios would indicate potential bias when using fixed quantile of streamflow distributions to estimate τ_ef among streams with differences in streamflow variability.

The second method for estimating τ_ef would adjust the travel time of mean streamflow for a stream, ${\tau }_{\overline{Q}}$, by a constant, τ^* = τ_ef:${\tau }_{\overline{Q}}$ representing the ratio of effective travel time to the travel time of mean streamflow. The effective travel time, $\widehat{{\tau }_{ef}}$, at a site is estimated as

$\begin{array}{ll}\widehat{{\tau }_{ef}}=exp\left[-{\beta }_{0,s}-{\beta }_{1,s}ln\left(\overline{Q}\right)\right]{\tau }^{*}& (9)\end{array}$

where ${\tau }_{\overline{Q}}$ is calculated by substituting $\overline{Q}$ for Q_t in Equation (6) using the regression coefficients β_0,s and β_1,s from Equation (5). The median cross-site ratio of τ_ef:${\tau }_{\overline{Q}}$ is used for τ^* in Equation (9).

We expect that τ^* will decrease with streamflow variability, so the third estimation method would adjust τ^* in Equation (9) based on a streamflow distribution's L-moment ratios. Our primary question is whether the LCV is adequate for adjusting τ^* to account for the effects of streamflow variability on τ_ef or higher-order moment ratios are necessary to prevent variability-biased estimation. The strength of the relation between the τ^* and each of the first three empirical L-moment ratios (Equations 8a,b,c) is tested using Kendall rank correlation coefficients. Finally, the L-moment ratio with the strongest correlation across sites is used to derive a power function for estimating τ^*:

$\begin{array}{ll}\widehat{{\tau }^{*}}=1-\left[{\beta }_2{\left(\frac{{\lambda }_j}{{\lambda }_i}\right)}^{{\beta }_3}\right]& (10)\end{array}$

fit for the selected L-moment ratio, $\frac{{\lambda }_j}{{\lambda }_i}$, using non-linear least squares regression (R Core Team, 2019).

Effects of Urban Runoff on Travel Time

The effects of streamflow variability on travel time are demonstrated for the case of urban land development, which increases streamflow variability as a result of the re-distribution of water from flow paths slowed by interactions with hillslope storage (depression and soil) to overland flow and low-resistance flow through engineered drainage systems. Streamflow and specific travel time distributions for streams draining urbanized watersheds are compared to those distributions for streams draining watersheds with low development (Table 1).

The Wilcoxon rank-sum test is applied to identify significant differences in travel time, velocity, and effective discharge between low-development and urban streams with low reservoir storage. L-moment ratios were not correlated with drainage area for low development streams with drainage areas between 19 and 90 km², so the analysis of urbanization is limited to streams in this range of drainage areas to control for effects from basin scale.

Generalized effects of urban hydrologic alteration are synthesized by comparing travel time distributions generated from two theoretical streamflow distributions: one characteristic of a low-development stream and the other characteristic of an urban stream. There is no standard theoretical distribution used to represent instantaneous streamflow (Schaefli et al., 2013; Blum et al., 2017) so Generalized Extreme Value (GEV), 4-parameter Kappa, and Generalized Logistic distributions are evaluated as potential functional forms for the theoretical distributions. Each of the three theoretical distribution is fit to each site using the method of L-moments (Hosking and Wallis, 1997), such that the L-moments for the theoretical distribution matches the empirical L-moments of the instantaneous streamflow distributions to the extent possible.

The fit of each theoretical distribution is evaluated at each site using the one-sample Kolmogorov-Smirnov test (R Core Team, 2019) and a two-sided probability, p < 0.05 that the sample was drawn from the distribution. The theoretical distribution that is acceptable at the largest number of sites is selected as the functional form for the probability distributions of instantaneous streamflow. To verify that the theoretical streamflow distribution reproduces τ_ef at a site, cumulative distributions of specific travel time and τ_ef are calculated from Equations (4) and (6) using the theoretical streamflow distributions.

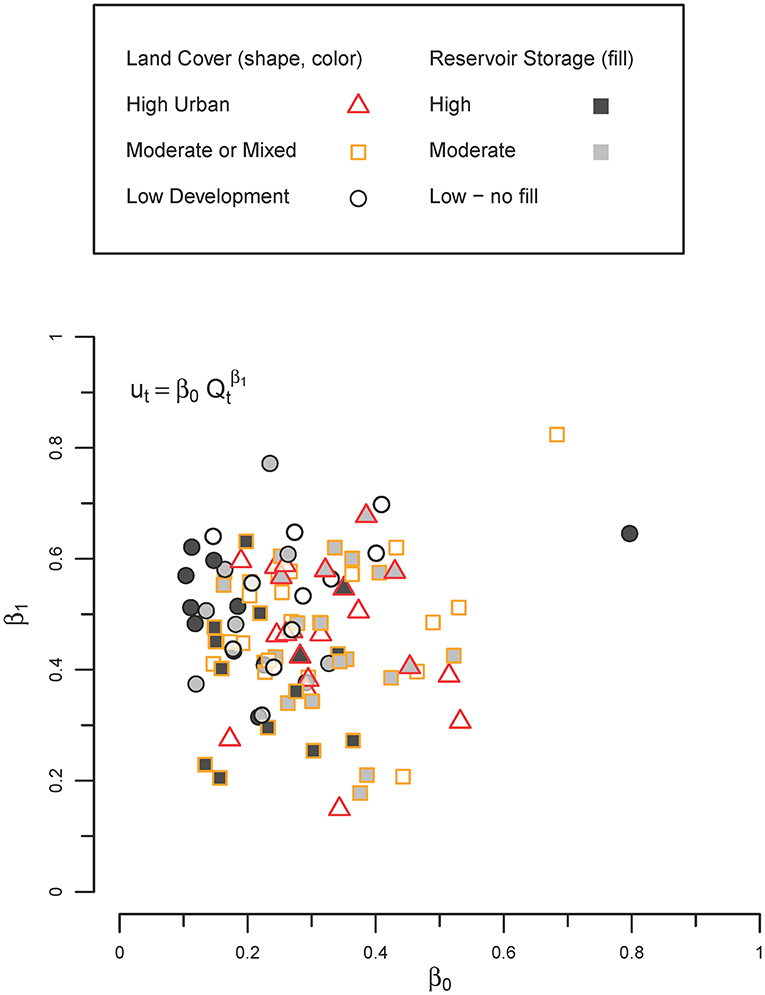
The characteristic parameters for a low-development stream and an urban stream are assigned using the median values of L-moment ratios for the five low-development streams and six urban streams with drainage areas between 19 and 90 km². The parameters of the velocity function are not correlated across sites (Figure 2), so the cross-site median values of all 11 streams (β₀ = 0.27, β₁ = 0.48) are used to calculate the specific travel times (Equation 6) characteristic of both the low-development stream and the urban stream. Using the same parameters in Equation (6) prevents differences related to channel hydraulics from affecting the travel time calculations.

FIGURE 2

Figure 2. Velocity function (Equation 5) parameters for 100 streams in the southeastern US.

Results

Effective Travel Times in Relation to Streamflow Distributions

The effective (flow-weighted mean) value of specific travel time varies among the 100 streams from τ_ef = 0.88–8.3 s/m (median of 3.1 s/m, Table 2). For streams with both low development and reservoir storage (n = 11, Table 1), τ_ef was negatively correlated with drainage area (Kendall rank correlation coefficient of −0.6, p < 0.01 that correlation coefficient is zero) indicating that smaller streams generally have longer travel times when compared to larger streams. The relation generally holds regardless of land use and regulation by reservoirs, but τ_ef still ranges widely among streams with approximately the same drainage area (Figure 3A).

TABLE 2

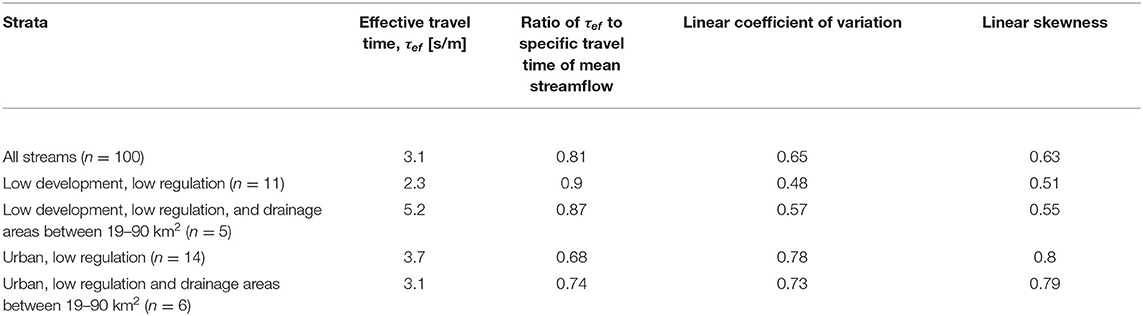
Table 2. Cross-site median values of travel time and instantaneous streamflow distribution statistics for five strata of streams.

FIGURE 3

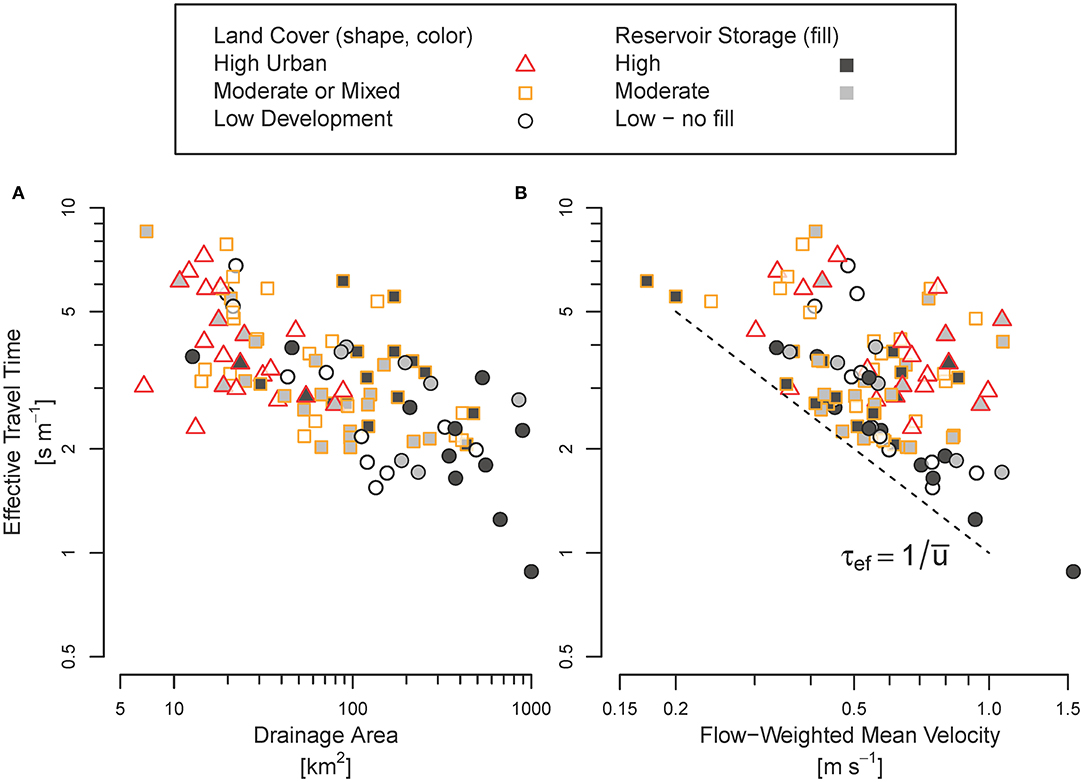
Figure 3. Effective (flow-weighted mean) value of specific travel time for 100 streams in the southeastern US in relation to: (A) the drainage area of their watersheds; and (B) flow-weighted mean velocity, with a dashed line indicating where travel time would be equal to the inverse of flow-weighted mean velocity.

Overall, τ_ef is poorly correlated with flow-weighted mean velocity (Kendall rank correlation of 0.1, p = 0.13 that correlation coefficient is zero) and, without exception, τ_ef is longer than the inverse of flow-weighted mean velocity in all streams (Figure 3B). The inverse relation between instantaneous velocity and specific travel time does not hold for their flow-weighted mean values because of the skew of the velocity distribution with respect to streamflow is inverted when its transformed into travel times using Equation (6): instantaneous velocities have larger deviations from their flow-weighted mean during high flows than low flows while, inversely, instantaneous travel times have larger absolute deviations from τ_ef during low flows than high flows. Flow-weighted mean velocity is influenced by both the velocity magnitude and volume of high flows. In contrast, τ_ef is sensitive to the long travel times during low flows despite their lower volumetric weighting. As a result, τ_ef cannot be estimated simply by inverting the flow-weighted mean velocity of a stream.

The quantile of a streamflow distribution that has a specific travel time equal to τ_ef is not consistent across sites: it ranges from the 0.52 (about median streamflow) to 0.97 (a relatively infrequent high flows) across streams (Figure 4). Across all sites, the quantile for τ_ef is <0.7 in only three streams–all with more than 50 mm of reservoir storage. The streamflow quantile corresponding to τ_ef is strongly correlated with both the linear skew (Figure 4A) and linear kurtosis of streamflow distributions (Kendall rank correlation coefficient >0.7, p < 0.001 that coefficient is zero for either). Variation in velocity with streamflow, which is indicated by the exponent, β₁, for the velocity function (Equation 6), does not account for much of the cross-site variation in the quantile of streamflow that has a specific travel time equal to τ_ef (Figure 4B).

FIGURE 4

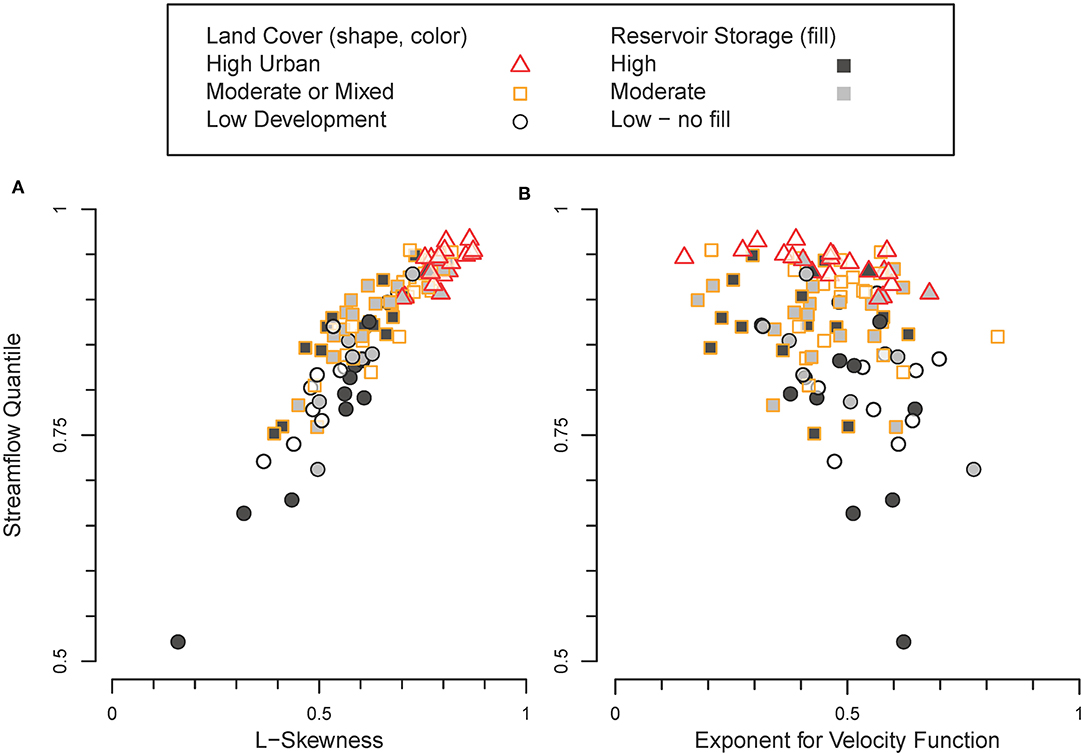
Figure 4. The streamflow quantile with a specific travel time equal to the effective travel time in relation to (A) linear (L-) skewness of the streamflow distribution and (B) the exponent for the velocity-discharge function (Equation 5).

Effects of Hydrologic Modification on Travel Time

The relation between streamflow variability and effective travel time leads to divergent responses of effective travel time to urbanization compared to reservoirs. Increased runoff from urbanized areas leads to higher variance and skew of instantaneous streamflow distributions (Table 2). As a result, a greater relative volume of streamflow has short travel times in urban streams compared to low-development streams (Wilcoxon rank sum test one-sided p < 0.001 that quantiles for τ_ef are equal for urban and low-development streams, Table 2). Channel modifications associated with urbanization (e.g., lining, straightening, removing obstruction, disconnection from overbank areas) typically increase the velocity of urban streams, but the re-distribution of runoff in response to urbanization (Figure 4A) rather than changes in channel hydraulics that affect either flow-weighted mean velocity (Figure 3B) or the variation of velocity with streamflow (Figure 4B) is likely the primary control on changes in the travel time for urban streams. In contrast, a reservoir that stores water during periods of high flow and releases it at lower flows reduces the skew of a streamflow distribution, resulting in τ_ef that represents the specific travel time of a lower quantile of streamflow (Figure 4A). Not all reservoirs are operated in ways that reduce the skew of a streamflow distribution, so their effect on travel time is less consistent that the effect of urbanization (Figure 4A).

Comparison of Methods for Estimating τ_ef

Positively skewed, at-site streamflow distributions generally result in effective travel times that are less than the specific travel times of either median or mean streamflow (Figures 4, 5). Using the specific travel time of the 0.89 quantile (the cross-site median value) of a streamflow distribution to estimate τ_ef at a site, the first estimation method had a RMSE of 1.2 s/m (Table 3). The second estimation method (Equation 9) adjusts the specific travel time of mean streamflow, ${\tau }_{\overline{Q}}$, (Figure 5) by the cross-site median ratio τ_ef:${\tau }_{\overline{Q}}$, τ^* = 0.81 and had a RMSE of 0.56 s/m.

FIGURE 5

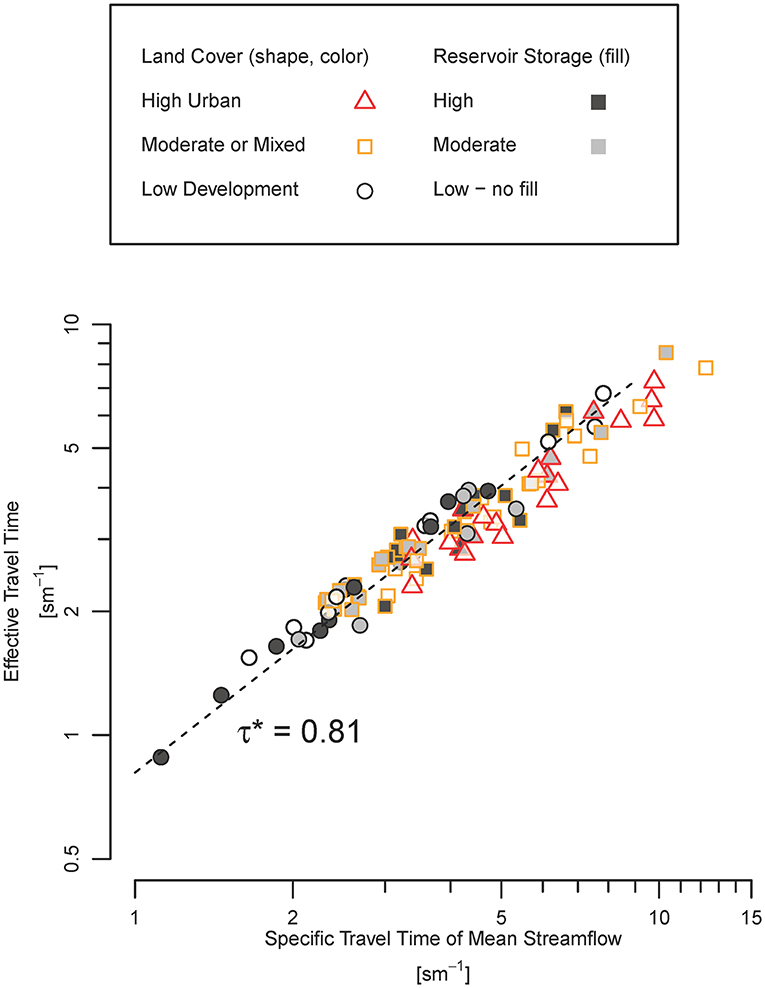
Figure 5. Specific travel time of mean streamflow and effective travel time for 100 streams in the southeastern United States. The cross-site median ratio is τ* = 0.81.

TABLE 3

Table 3. Summary of methods for estimating effective travel time.

The ratio indicates that τ_ef generally is about 20% shorter than ${\tau }_{\overline{Q}}$ and is needed to address this general bias from using mean streamflow to estimate τ_ef. Mean streamflow provides a better basis for estimating τ_ef (second method) than a fixed quantile (first method) because the mean value of a streamflow distribution is leveraged by the magnitude of high flows while a quantile reflects that time that streamflow is less than or equal a given magnitude without regard to how streamflow above or below the quantile is distributed.

The ratio of effective travel time in a stream to the specific travel time of its mean streamflow decreases as the variability of the stream's streamflow distribution increases (the inverse relation between τ^* and LCV in Figure 6). Thus, at-site estimation of τ_ef using the specific travel time of mean streamflow has increasing bias with streamflow variability. Urban streams, in particular, have highly variable and skewed streamflow distributions (Figures 4A, 6, respectively) and, as a consequence, effective travel times are much shorter that the travel time of mean streamflow (median τ^* = 0.69 for urban streams, Table 2) compared low-development streams (median τ^* = 0.9, p < 0.001 that τ^* of urban streams are equal to or greater than τ^* of low-development/low-regulation streams, one-sided Wilcoxon test).

FIGURE 6

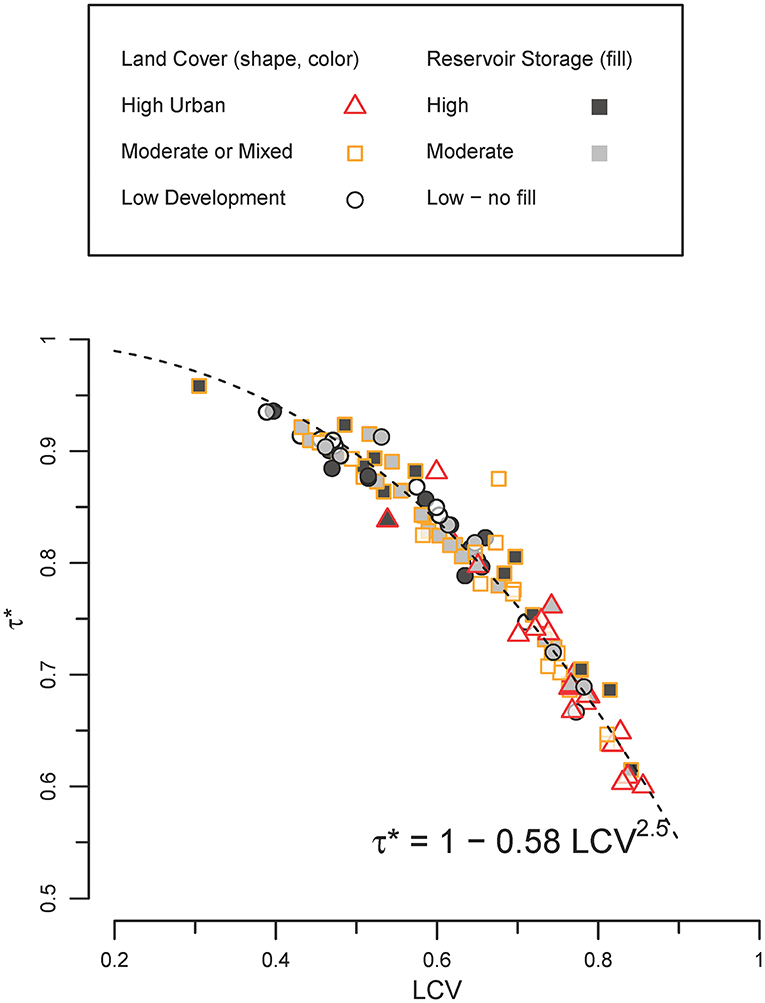
Figure 6. Ratio of flow-weighted travel time to travel time of mean streamflow, τ*, in relation to linear coefficient of variation, LCV. Dashed line is τ* = 1–0.58 LCV^2.5.

The third estimation method uses stream-specific values of τ^* based on the variability of the streamflow distribution for a stream to adjust the travel time of mean streamflow. Stream-specific values of τ^* vary inversely with the LCV of streamflow distributions (Figure 6) but can be estimated from LCV by the power function:

$\begin{array}{ll}\widehat{{\tau }^{*}}=1-0.58LC{V}^{2.5}& (11)\end{array}$

Estimates of τ_ef from Equation (9) with τ^* calculated for each site from Equation (11) had a RMSE 0.1 s/m (Table 3). The bias of estimates from the third method is substantially lower than from the other two methods (Table 2) indicating how the increasing variance of a streamflow distribution scaled by its mean value reduces effective travel time τ_ef.

Effect of Urbanization on Specific Travel Time

Streamflow distributions with variability characteristic of a low-development stream and an urban stream, respectively, were generated from a generalized extreme value (GEV). The GEV distribution provides a better approximation of instantaneous streamflow distributions than either the Kappa or Generalized Logistic distributions for all 100 streams but still could be rejected at 31 of them (two-sided p < 0.05 K-S test). Nonetheless, τ_ef calculated from Equation (6) using a GEV distribution fit to each stream to generate Q_t provides robust at-site estimates that closely matched τ_ef calculated from Equation (6) using observed streamflow values for Q_t (RMSE = 0.057 s/m; Figure 7).

FIGURE 7

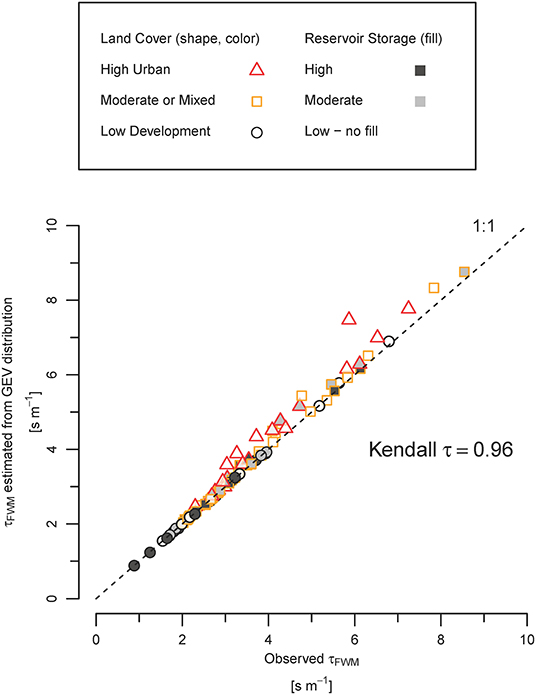
Figure 7. Flow-weighted mean travel time (τ_ef) calculated from the observed streamflow distribution and a GEV distribution fit to each stream using L-moments.

The median values of GEV-distribution parameters for small, urban streams (n = 6) are distinct from those for small low-development streams (n = 5) and generally indicate the urban streams have higher variance and skew (Figure 8, Table 4). As a result, the travel time distribution for the characteristic urban stream generally shifts toward larger volumes of water with shorter travel times (Figure 9). The characteristic urban stream has an 19% increase in the volume of streamflow with relative short travel times (<1 s/m) and a 21% decrease in streamflow with travel times between 2 and 4 s/m compared to the characteristic low-development stream (Figure 9A). The re-distribution of streamflow to higher flows in the urban stream generally increases the volume of urban streamflow with travel times < ~4 s/m (Figure 9B). The urban stream has slightly more streamflow with travel times >8 s/m (extremely low flow) than the low-development stream, but this represents a small portion (~2.5%) of total streamflow.

FIGURE 8

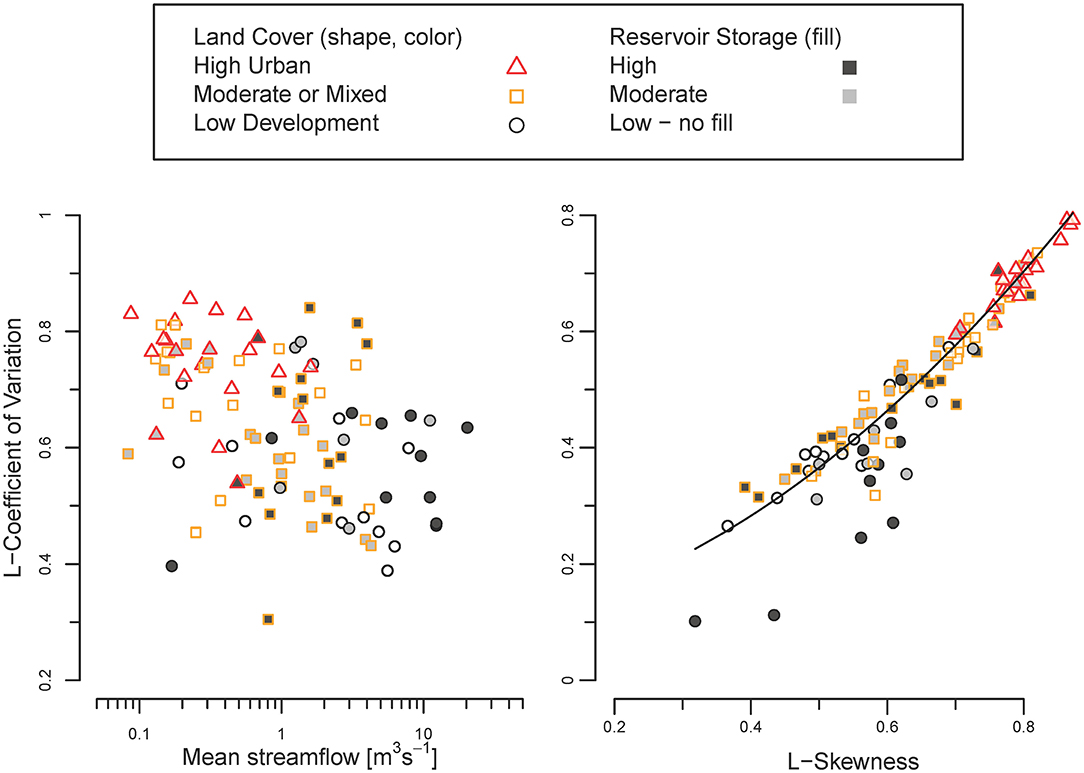
Figure 8. Linear moments for the instantaneous streamflow distributions of 100 streams in the southeastern United States. Line shows the relation between L-Skewness and L-Coefficient of Varation for generalized extreme value distributions.

TABLE 4

Table 4. Parameters used in the Generalized Extreme Value (GEV) distributions for characteristics streamflow distributions based on the median values for all streams, low-development streams with low reservoir storage and drainage areas between 19 and 90 km² (characteristic low-development stream), and urban streams with low reservoir storage and drainage areas between 19 and 90 km² (characteristic urban streams).

FIGURE 9

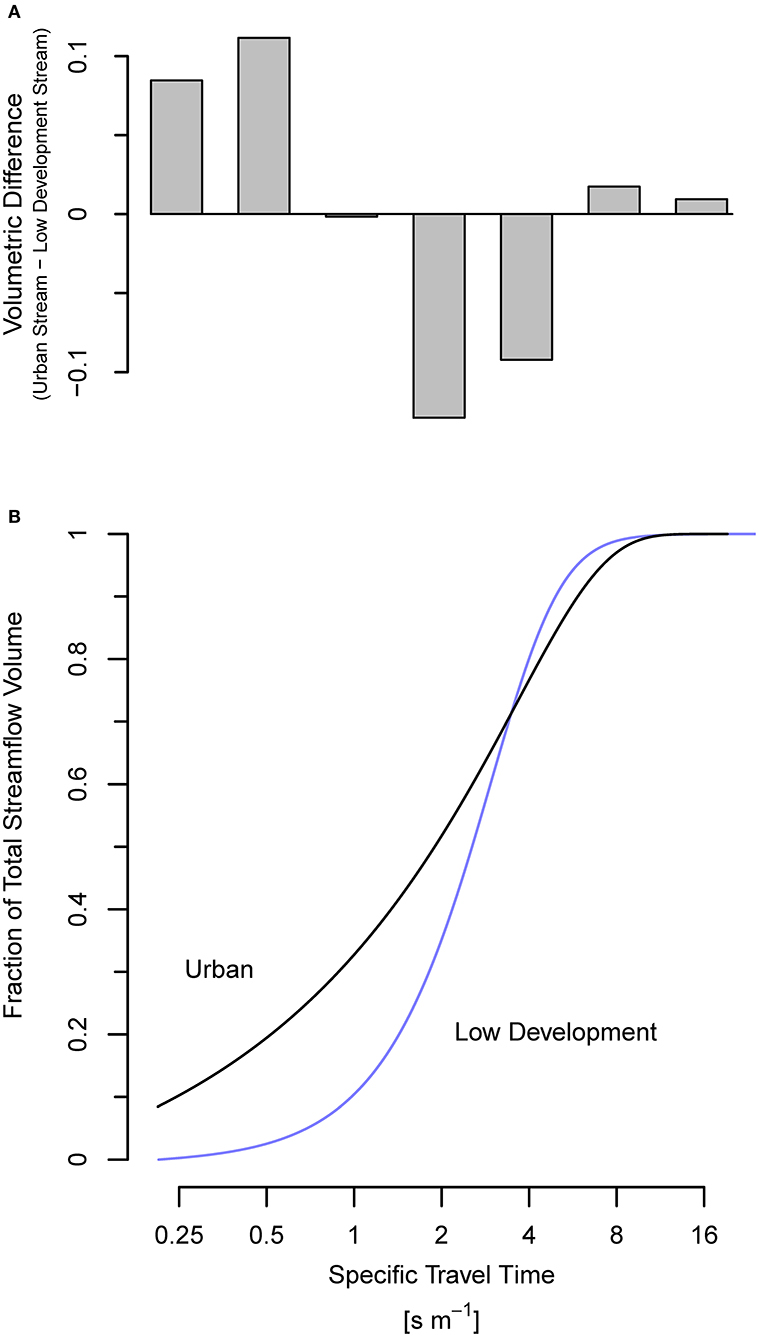
Figure 9. Travel-time distributions for characteristic a low-development and urban stream reach with (A) the marginal difference between the urban and low-development streams in standardized volume [fraction of total] for seven bins of travel time and (B) the cumulative distribution of streamflow by volume for the range of travel times from 0.2 to 20 s/m. Fraction of streamflow volume with travel times <0.2 s/m is 0% for the low-development stream and 8% for the urban stream.

Discussion

The specific travel time of mean streamflow is longer than the effective travel time of streamflow, τ_ef, over annual and longer time scales because streamflow distributions are positively skewed (Blum et al., 2017) with most of the total volume discharge during higher flows with shorter travel times (Figure 5B). The difference between τ_ef and the travel time of mean streamflow generally is about 20% (or equivalently τ^* ≈ 0.8). Streams with higher streamflow variability have a larger relative volume of high flows with short travel times and, thus, shorter effective travel times (Figure 6).

Flow-weighting of travel time in Equation (4) provides a physically based value of τ_ef, for modeling transport and processing at annual and longer time scales. Using τ_ef, rather than τ_Qmean in the empirical power-law expression for nitrogen removal proposed by Seitzinger et al. (2002), we would expect ~10% less nitrogen removal over a kilometer of channel. This is a significant difference in the mass of nitrogen retained, and it can have important cumulative effects for predictions at the river basin scale. While physically-based parameters have epistemic value for how processes scale over space and time and offer the promise of model parameterization from direct measurement, they do not necessarily improve model performance at calibration sites because of equifinality: parameters can compensate for each other's value resulting in comparable model performance for different parameter sets (Beven and Smith, 2015). Indeed, calibration of rate coefficients can offset the effect a particular travel time in a time-averaged biogeochemical model. Using the travel time of mean streamflow, however, will produce lower uptake velocities and deposition rates than models using τ_ef.

The primary reason for using effective travel times in time-average models is to increase the capability of such models to simulate the effects of streamflow variability. Simply using 80% of the travel time of mean streamflow (method 2), however, does not provide time-averaged models with capability to represent differences between streams as a result of streamflow variability. The third method we developed provides relatively accurate estimates of τ_ef (Table 3) but the at-site mean and variance of a streamflow distribution must be known to apply it. Low prediction skill of current models for the variance of streamflow (Farmer et al., 2014; Basso et al., 2015) is a crux for broader application of this estimation method to ungaged streams, but systematic variation in the LCV with land use (Figure 8) indicates the possibility for model-based estimation in some situations.

Effective travel time does not account for the dependencies of constituent concentrations on streamflow or first-order reaction rates on constituent concentrations. In cases where the temporal variability of concentrations and reaction rates are comparable to the variability of travel time, the joint distribution of streamflow, travel time, concentration, and first-order reaction rate is necessary to calculate an accurate, time-average mass flux for the process of interest (Doyle, 2005). If all such data were available, using a dynamic model would probably be preferable to a time-average model. Given that time series of velocity can be derived more widely (at streamflow gages with field measurements of velocity) than time series of concentration and reaction rate for any solute or particulate, adjustment of travel times is a pragmatic and broadly applicable approach to improve the capability of time-average river network models to represent effects of streamflow variability on biogeochemical processing in river networks.

For urban streams, a large fraction of the total runoff from the catchment is discharged during high-flow periods when streamflow has higher velocities in comparison to lower-flow periods. Even where stormwater detention controls peak flow rates, it has limited effectiveness reducing the volume of runoff during large storms (Booth et al., 2002; Hood et al., 2007; Smith et al., 2013). The volumetric differences between our characteristic undeveloped and urban streams are small for low flows longer travel time (e.g., >4 s/m), so substantial differences in processing would not be expected during low flow except for uptake or reactions with low mass-transfer coefficients. Difference only emerges for high flows when a large fraction of streamflow has short travel times (e.g., <1 s/m) in urban stream (Figure 7).

The effect of urbanization on nitrogen retention during base flow conditions is equivocal. In the desert Southwest, Grimm et al. (2005) documented less retention (longer uptake lengths) of experimental NO₃- additions in urban streams but a strong effect from discharge. Using an expanded set of 72 streams, Hall et al. (2009) found uptake lengths varied with specific discharge (streamflow divided by width) streamflow at the time of the experiment (“stream size”) but not land-use per se. Hall et al. (2009) recommended that hydrologic variability is critical for understanding differences in nitrogen retention at longer time scales. We propose streamflow variability is likely to reduce retention given the well-defined, inverse relation of effective travel time to streamflow variability (Figure 6), but verification would require high-flow experiments [e.g., Melis (2011)] and the integration of results for both low and high flows based on streamflow distributions.

Effects of streamflow variability on processing and retention in streams are important in the context of land use (Hall et al., 2009), variation between headwater streams and mainstem rivers (Gomez-Velez et al., 2015), and responses to climate change (Baron et al., 2013; Morse and Wollheim, 2014). Given the relation between effective travel time and variance of streamflow distributions (Figure 6), differences in travel time can be inferred broadly from the effects of drainage area (Figure 2) (Thomas and Benson, 1970; Dunne and Leopold, 1978), regional climate (Dettinger and Diaz, 2000), climate change (Pagano and Garen, 2005; Jiménez Cisneros et al., 2014), reservoirs (Figure 2) (Poff et al., 2007; Kroll et al., 2015), and engineered-drainage systems (King et al., 2015) on the variance of streamflow distributions. Globally, anthropogenic changes to streamflow continues to expand with more extensive drainage systems, river impoundments and diversions, and land cover conversion and changes in climate (Eng et al., 2013; Jiménez Cisneros et al., 2014; King et al., 2015; Kroll et al., 2015; Carlisle et al., 2019). As these factors affect streamflow variability, travel times in biogeochemical models need to be adjusted accordingly.

Conclusions

Streamflow variability forces dynamic processing and retention of materials in river networks. The effective (flow-weighted mean) travel time of streamflow generally is less than the travel time of mean streamflow over seasonal and longer time scales because a significant fraction of streamflow is discharged at high velocities during high flows in most streams. The effective travel time of streamflow is typically ~80% of the travel time of mean streamflow for 100 streams in the southeastern United States and increases with streamflow variability. Application of the travel time of mean streamflow introduces a systematic bias in modeling of processing and retention where streamflow variability is neither uniform across streams nor constant over time. This bias limits the capability of time-averaged river-networks models to resolve differences between streams or changes over time. Time-average models can gain the capability to represent effects of streamflow variability by adjusting the travel time of mean streamflow using the at-site coefficient of variation of streamflow. This approach provides a pragmatic way to connect our understanding of spatial patterns in streamflow variability and its response to climate and land use change to processing and retention of transported materials (e.g., sediment, nutrients, contaminants) in river networks.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: Instantaneous streamflow values and field measured velocity and streamflow are available from the US Geological Survey National Water Information System. Data derived in this investigation are available from US Geological Survey ScienceBase (https://doi.org/10.5066/P9665F6L).

Author Contributions

CK proposed the objective and approach for this research during a workshop lead by JH, JG-V, EB, and DS. NS, GS, JH, and CK designed the analysis for general validity and broad relevance. CK compiled data, implemented the analysis, and drafted the initial manuscript. All of the authors were involved in preparing the final manuscript.

Funding

This research was supported by the US Geological Survey as part of the Regional Stream Quality Assessment and the River Corridor Working Group at the John Wesley Power Center for Analysis and Synthesis.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

References

Alexander, R. B., Böhlke, J. K., Boyer, E. W., David, M. B., Harvey, J. W., Mulholland, P. J., et al. (2009). Dynamic modeling of nitrogen losses in river networks unravels the coupled effects of hydrological and biogeochemical processes. Biogeochemistry 93, 91–116. doi: 10.1007/s10533-008-9274-8

CrossRef Full Text | Google Scholar

Baron, J. S., Hall, E. K., Nolan, B. T., Finlay, J. C., Bernhardt, E. S., Harrison, J. A., et al. (2013). The interactive effects of excess reactive nitrogen and climate change on aquatic ecosystems and water resources of the United States. Biogeochemistry 114, 71–92. doi: 10.1007/s10533-012-9788-y

CrossRef Full Text | Google Scholar

Basso, S., Frascati, A., Marani, M., Schirmer, M., and Botter, G. (2015). Climatic and landscape controls on effective discharge. Geophys. Res. Lett. 42, 8441–8447. doi: 10.1002/2015GL066014

CrossRef Full Text | Google Scholar

Basu, N. B., Rao, P. S. C., Thompson, S. E., Loukinova, N. V., Donner, S. D., Ye, S., et al. (2011). Spatiotemporal averaging of in-stream solute removal dynamics. Water Resour. Res. 47:W00J06. doi: 10.1029/2010WR010196

CrossRef Full Text | Google Scholar

Behrendt, H., and Opitz, D. (1999). Retention of nutrients in river systems: dependence on specific runoff and hydraulic load. Hydrobiologia 410, 111–122. doi: 10.1023/A:1003735225869

CrossRef Full Text | Google Scholar

Bergstrom, A., McGlynn, B., Mallard, J., and Covino, T. (2016). Watershed structural influences on the distributions of stream network water and solute travel times under baseflow conditions. Hydrol. Process. 30, 2671–2685. doi: 10.1002/hyp.10792

CrossRef Full Text | Google Scholar

Beven, K., and Smith, P. (2015). Concepts of information content and likelihood in parameter calibration for hydrological simulation models. J. Hydrol. Eng. 20:A4014010. doi: 10.1061/(ASCE)HE.1943-5584.0000991

CrossRef Full Text | Google Scholar

Blum, A. G., Archfield, S. A., and Vogel, R. M. (2017). On the probability distribution of daily streamflow in the United States. Hydrol. Earth Syst. Sci. 21, 3093–3103. doi: 10.5194/hess-21-3093-2017

CrossRef Full Text | Google Scholar

Booth, D. B., Hartley, D., and Jackson, R. (2002). Forest cover, impervious-surface area, and the mitigation of stormwater impacts. J. Am. Water Resour. Assoc. 38, 835–845. doi: 10.1111/j.1752-1688.2002.tb01000.x

CrossRef Full Text | Google Scholar

Botter, G., Basu, N. B., Zanardo, S., Rao, P. S. C., and Rinaldo, A. (2010). Stochastic modeling of nutrient losses in streams: interactions of climatic, hydrologic, and biogeochemical controls. Water Resour. Res. 46:W08509. doi: 10.1029/2009WR008758

CrossRef Full Text | Google Scholar

Boyer, E. W., Alexander, R. B., Parton, W. J., Li, C. S., Butterbach-Bahl, K., Donner, S. D., et al. (2006). Modeling denitrification in terrestrial and aquatic ecosystems at regional scales. Ecol. Appl. 16, 2123–2142. doi: 10.1890/1051-0761(2006)016[2123:MDITAA]2.0.CO;2

PubMed Abstract | CrossRef Full Text | Google Scholar

Carlisle, D. M., Wolock, D. M., Konrad, C. P., McCabe, G. J., Eng, K., Grantham, T. E., et al. (2019). Flow Modification in the Nation's Streams and Rivers. Technical Report, U.S. Geological Survey Circular 1461, Reston, VA. doi: 10.3133/cir1461

CrossRef Full Text | Google Scholar

Carlston, C. W. (1963). Drainage Density and Streamflow. Technical Report, U.S. Geological Survey Prof. Paper 422–C, Washington, DC. doi: 10.3133/pp422C

CrossRef Full Text | Google Scholar

Chang, H. (2007). Comparative streamflow characteristics in urbanizing basins in the Portland Metropolitan Area, Oregon, USA. Hydrol. Process. 21, 211–222. doi: 10.1002/hyp.6233

CrossRef Full Text | Google Scholar

Czuba, C. R., Czuba, J. A., Magirl, C. S., Gendaszek, A. S., and Konrad, C. P. (2018). Effect of river confinement on depth and spatial extent of bed disturbance affecting salmon redds. J. Ecohydraul. 3, 4–17. doi: 10.1080/24705357.2018.1457986

CrossRef Full Text | Google Scholar

Czuba, J. A., and Foufoula-Georgiou, E. (2014). A network-based framework for identifying potential synchronizations and amplifications of sediment delivery in river basins. Water Resour. Res. 50, 3826–3851. doi: 10.1002/2013WR014227

CrossRef Full Text | Google Scholar

Dettinger, M. D., and Diaz, H. F. (2000). Global characteristics of stream flow seasonality and variability. J. Hydrometeorol. 1, 289–310. doi: 10.1175/1525-7541(2000)001<0289:GCOSFS>2.0.CO;2

CrossRef Full Text | Google Scholar

Doyle, M. W. (2005). Incorporating hydrologic variability into nutrient spiraling. J. Geophys. Res. 110:G01003. doi: 10.1029/2005JG000015

CrossRef Full Text | Google Scholar

Dunne, T., and Leopold, L. B. (1978). Water in Environmental Planning. New York, NY: W.H. Freeman and Company. 818.

Eng, K., Carlisle, D. M., Wolock, D. M., and Falcone, J. A. (2013). Predicting the likelihood of altered streamflows at ungauged rivers across the conterminous United States. River Res. Appl. 29, 781–791. doi: 10.1002/rra.2565

CrossRef Full Text | Google Scholar

Ensign, S. H., and Doyle, M. W. (2006). Nutrient spiraling in streams and river networks. J. Geophys. Res. 111:G04009. doi: 10.1029/2005JG000114

CrossRef Full Text | Google Scholar

Farmer, W. H., Archfield, S. A., Over, T. M., Hay, L. E., LaFontaine, J. H., and Kiang, J. E. (2014). A Comparison of Methods to Predict Historical Daily Streamflow Time Series in the Southeastern United States. Technical Report, U.S. Geological Survey Scientific Investigations Report 2014–5231, Reston, VA. doi: 10.3133/sir20145231

CrossRef Full Text | Google Scholar

Findlay, S. (1995). Importance of surface-subsurface exchange in stream ecosystems: The hyporheic zone. Limnol. Oceanogr. 40, 159—64. doi: 10.4319/lo.1995.40.1.0159

CrossRef Full Text | Google Scholar

Gomez-Velez, J., Harvey, J., Cardenas, M., and Kiel, B. (2015). Denitrification in the Mississippi River network controlled by flow through river bedforms. Nature Geosci. 8, 941–945. doi: 10.1038/ngeo2567

CrossRef Full Text | Google Scholar

Grimm, N. B., Sheibley, R. W., Crenshaw, C. L., Dahm, C. N., Roach, W. J., and Zeglin, L. H. (2005). N retention and transformation in urban streams. J. N. Am. Benthol. Soc. 24, 626–642. doi: 10.1899/04-027.1

CrossRef Full Text | Google Scholar

Hall, R. O. Jr., Bernhardt, E. S., and Likens, G.E. (2002). Relating nutrient uptake with transient storage in forested mountain streams. Limnol. Oceanogr. 47, 255–265. doi: 10.4319/lo.2002.47.1.0255

CrossRef Full Text | Google Scholar

Hall, R. O. Jr., Tank, J. L., Sobota, D. J., Mulholland, P. J., O'Brien, J. M., Dodds, W. K., et al. (2009). Nitrate removal in stream ecosystems measured by 15N addition experiments: total uptake. Limnol. Oceanogr. 54, 653–665. doi: 10.4319/lo.2009.54.3.0653

CrossRef Full Text | Google Scholar

Harvey, J., Gomez-Velez, J., Schmadel, N., Scott, D., Boyer, E., Alexander, R., et al. (2019). How hydrologic connectivity regulates water quality in river corridors. J. Am. Water Resour. Assoc. 55, 369–381. doi: 10.1111/1752-1688.12691

CrossRef Full Text | Google Scholar

Harvey, J., and Gooseff, M. (2015). River corridor science: hydrologic exchange and ecological consequences from bed forms to basins. Water Resour. Res. 51, 6893–6692. doi: 10.1002/2015WR017617

CrossRef Full Text | Google Scholar

Harvey, J. W. (2016). “Hydrologic exchange flows and their ecological consequences in river corridor in stream ecosystems in a changing environment,” in Stream Ecosystems in a Changing Environment, eds J. B. Jones and E. M. Stanley (Amsterdam: Elsevier), 1–83. doi: 10.1016/B978-0-12-405890-3.00001-4

CrossRef Full Text | Google Scholar

Hein, T., Baranyi, C., Reckendorfer, W., and Schiemer, F. (2004). The impact of surface water exchange on the nutrient and particle dynamics in side-arms along the River Danube, Austria. Sci. Total Environ. 328, 207–218. doi: 10.1016/j.scitotenv.2004.01.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Helton, A. M., Poole, G. C., Meyer, J. L., Wollheim, W. M., Peterson, B. J., Mulholland, P. J., et al. (2011). Thinking outside the channel: modeling nitrogen cycling in networked river ecosystems. Front. Ecol. Environ. 9, 229–238. doi: 10.1890/080211

CrossRef Full Text | Google Scholar

Hood, M. J., Clausen, J. C., and Warner, G. S. (2007). Comparison of stormwater lag times for low impact and traditional residential development. J. Am. Water Resour. Assoc. 43, 1036–1046. doi: 10.1111/j.1752-1688.2007.00085.x

CrossRef Full Text | Google Scholar

Hosking, J., and Wallis, J. (1997). Regional Frequency Analysis: An Approach Based on L-Moments. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511529443

CrossRef Full Text | Google Scholar

Hosking, J. R. M. (2017). L-Moments, R package lmom, Version 2.8, 2019-03-11. Available online at: https://cran.r-project.org (accessed May 20, 2020).

Hubbard, E. F., Kilpatrick, F. A., Martens, L. A., and Wilson, J. F. (1982). “Measurement of time of travel and dispersion in streams by dye tracing,” in Applications of Hydraulics, Book 3, Techniques of Water Resources Investigations of the United States Geological Survey, Chapter A9, version 1. Available online at: https://pubs.usgs.gov/twri/twri3-a9/pdf/twri_3-a9_ver1.pdf (accessed May 30, 2020).

Google Scholar

Jiménez Cisneros, B. E., Oki, T., Arnell, N. W., Benito, G., Cogley, J. G., Döll, P., et al. (2014). “Freshwater resources in climate change 2014: impacts, adaptation, and vulnerability. Part A: global and sectoral aspects,” in Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir, et al. (Cambridge: Cambridge University Press), 229–269.

Google Scholar

Jobson, H. E. (2000). Estimating the Variation of Travel Time in River by Use of Wave Speed and Hydraulic Characteristics. Technical Report, U.S. Geological Survey Water-Resources Investigations Report 00–4187, Reston, VA.

Google Scholar

Journey, C. A., Van Metre, P. C., Bell, A. H., Garrett, J. D., Button, D. T., Nakagaki, N., et al. (2015). Design and Methods of the Southeast Stream Quality Assessment (SESQA), 2014. Technical Report, U.S. Geological Survey Open-File Report 2015–1095, Columbia, SC. doi: 10.3133/ofr20151095

CrossRef Full Text | Google Scholar

King, K. W., Williams, M. R., and Fausey, N. R. (2015). Contributions of systematic tile drainage to watershed-scale phosphorus transport. J. Environ. Qual. 44, 486–494. doi: 10.2134/jeq2014.04.0149

PubMed Abstract | CrossRef Full Text | Google Scholar

Konrad, C., and Gellis, A. (2018). Factors influencing fine sediment on stream beds in the midwestern United States. J. Environ. Qual. 47, 1214–1222. doi: 10.2134/jeq2018.02.0060

PubMed Abstract | CrossRef Full Text | Google Scholar

Konrad, C. P. (2009). Simulating the recovery of suspended sediment transport and river bed stability in response to dam removal on the Elwha River, Washington. Ecol. Eng. 35, 1104–1115. doi: 10.1016/j.ecoleng.2009.03.018

CrossRef Full Text | Google Scholar

Konrad, C. P. (2020). Basin Characteristics and Travel Time Metrics for 100 Sites in the Southeastern United States. USGS Data Release, Reston, VA. doi: 10.5066/P9665F6L

CrossRef Full Text

Konrad, C. P., Black, R. W., Voss, F., and Neale, C. M. U. (2008). Integrating remote sensing and field methods to assess effects of levee setbacks on riparian and aquatic habitats in glacial-melt water rivers. River Res. Appl. 24, 355–372. doi: 10.1002/rra.1070

CrossRef Full Text

Konrad, C. P., and Booth, D. B. (2005). “Hydrologic changes in urban streams and their ecological significance,” in Effects of Urbanization on Stream Ecosystems, eds L. R. Brown, R. H. Gray, R. M. Hughes, and M. R. Meador (Bethesda, MD: American Fisheries Society), 157–177.

Google Scholar

Konrad, C. P., Booth, D. B., and Burges, S. J. (2005). Effects of urban development in the Puget Lowland, Washington, on interannual streamflow patterns: consequences for channel form and streambed disturbance. Water Resour. Res. 41:W07009. doi: 10.1029/2005WR004097

CrossRef Full Text | Google Scholar

Kroll, C. N., Croteau, K. E., and Vogel, R. M. (2015). Hypothesis tests for hydrologic alteration. J. Hydrol. 530, 117–126. doi: 10.1016/j.jhydrol.2015.09.057

CrossRef Full Text | Google Scholar

Leopold, L. B. (1968). Hydrology for Urban Land Planning: A Guidebook on the Hydrologic Effects of Urban Land Use. Technical Report, U.S. Geological Survey Circular 554, Washington, DC. doi: 10.3133/cir554

CrossRef Full Text | Google Scholar

Melis, T. S. (2011). Effects of Three High-Flow Experiments on the Colorado River Ecosystem Downstream From Glen Canyon Dam, Arizona. Technical Report, U.S. Geological Survey Circular 1366, Flagstaff, AZ. doi: 10.3133/cir1366

CrossRef Full Text | Google Scholar

Meyer, J. L., and Edwards, R. T. (1990). Ecosystem metabolism and turnover of organic carbon along a blackwater river continuum. Ecology 71, 668–677. doi: 10.2307/1940321

CrossRef Full Text | Google Scholar

Morse, N. B., and Wollheim, W. M. (2014). Climate variability masks the impacts of land use change on nutrient export in a suburbanizing watershed. Biogeochemistry 121, 45–59. doi: 10.1007/s10533-014-9998-6

CrossRef Full Text | Google Scholar

Mulholland, P., Helton, A., Poole, G., Hall, R., Hamilton, S., Peterson, B., et al. (2008). Stream denitrification across biomes and its response to anthropogenic nitrate loading. Nature 452, 202–205. doi: 10.1038/nature06686

PubMed Abstract | CrossRef Full Text | Google Scholar

Mulholland, P. J., Steinman, A. D., and Elwood, J. W. (1990). Measurement of phosphorus uptake length in streams: comparison of radiotracer and sTable P04 releases. Can. J. Fish. Aquat. Sci. 47, 2351–2357. doi: 10.1139/f90-261 (accessed May 30, 2020).

CrossRef Full Text | Google Scholar

Multi-Resolution Land Characteristics Consortium (2019). National Land Cover Database 2011. Available online at: https://www.mrlc.gov/data (accessed May 20, 2020).

Newbold, J. D., Elwood, J. W., O'Neill, R. V., and Sheldon, A. L. (1983). Phosphorus dynamics in a woodland stream ecosystem: a study of nutrient spiralling. Ecology 64, 1249–1265. doi: 10.2307/1937833

CrossRef Full Text | Google Scholar

Pagano, T., and Garen, D. (2005). A recent increase in western U.S. streamflow variability and persistence. J. Hydrometeor. 6, 173–179. doi: 10.1175/JHM410.1

CrossRef Full Text | Google Scholar

Paul, M. J., and Meyer, J. L. (2001). Streams in the urban landscape. Annu. Rev. Ecol. Syst. 32, 333–365. doi: 10.1146/annurev.ecolsys.32.081501.114040

CrossRef Full Text | Google Scholar

Poff, N. L., Olden, J. D., Merritt, D. M., and Pepin, D. M. (2007). Homogenization of regional river dynamics by dams and global biodiversity implications. Proc. Natl. Acad. Sci. U.S.A. 104, 5732–5737. doi: 10.1073/pnas.0609812104

PubMed Abstract | CrossRef Full Text | Google Scholar

Poff, N. L., and Ward, J. V. (1989). Implications of streamflow variability and predictability for lotic community structure: a regional analysis of streamflow patterns. Can. J. Fish. Aquat. Sci. 46, 1805–1818. doi: 10.1139/f89-228 (accessed December 20, 2019).

CrossRef Full Text | Google Scholar

R Core Team (2019). R Base Package, Version 3.6.2. The R Foundation for Statistical Computing. Available online at: https://cran.r-project.org/ (accessed December 20, 2019).

Rantz, S. E. (1982). Measurement and Computation of Streamflow. Technical Report, U.S. Geological Survey Water Supply Paper 2175, Washington, DC. doi: 10.3133/wsp2175

CrossRef Full Text | Google Scholar

Raymond, P. A., Saiers, J. E., and Sobczak, W. V. (2016). Hydrological and biogeochemical controls on watershed dissolved organic matter transport: pulse-shunt concept. Ecology 97, 5–16. doi: 10.1890/14-1684.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaefli, B., Rinaldo, A., and Botter, G. (2013). Analytic probability distributions for snow-dominated streamflow. Water Resour. Res. 49, 2701–2713. doi: 10.1002/wrcr.20234

CrossRef Full Text | Google Scholar

Schmadel, N. M., Ward, A. S., Lowry, C. S., and Malzone, J. M. (2016). Hyporheic exchange controlled by dynamic hydrologic boundary conditions. Geophys. Res. Lett. 43, 4408–4417. doi: 10.1002/2016GL068286

CrossRef Full Text | Google Scholar

Seitzinger, S. P., Styles, R. V., Boyer, E. W., Alexander, R. B., Billen, G., Howarth, R. W., et al. (2002). Nitrogen retention in rivers: model development and application to watersheds in the northeastern U.S.A. Biogeochem. 57, 199–237. doi: 10.1023/A:1015745629794

CrossRef Full Text | Google Scholar

Smith, B. K., Smith, J. A., Baeck, M. L., Villarini, G., and Wright, D. B. (2013). Spectrum of storm event hydrologic response in urban watersheds. Water Resour. Res. 49, 2649–2663. doi: 10.1002/wrcr.20223

CrossRef Full Text | Google Scholar

Stream Solute Workshop (1990). Concepts and methods for assessing solute dynamics in stream ecosystems. J. North Am. Benthol. Soc. 9, 95–119. doi: 10.2307/1467445

CrossRef Full Text | Google Scholar

Thomas, D. M., and Benson, M. A. (1970). Generalization of Streamflow Characteristics From Drainage-Basin Characteristics. Technical Report, U.S. Geological Survey Water Supply Paper 1975, Washington, DC. doi: 10.3133/wsp1975

CrossRef Full Text | Google Scholar

US Army Corps of Engineers (2010). 2009 National Inventory of Dams. Available online at: http://nid.usace.army.mil/ (accessed May 30, 2020).

USGS (2019). National Water Information System. U.S. Geological Survey, Reston, VA. doi: 10.5066/F7P55KJN

CrossRef Full Text | Google Scholar

Wallace, J. B., Webster, J. R., and Woodall, W. B. Jr. (1977). The role of filter feeders in stream ecosystems. Arch. Hydrobiol. 79, 506–532.

Wollheim, W. M., Vorosmarty, C. J., Peterson, B. J., Seitzinger, S. P., and Hopkinson, C. S. (2006). Relationship between river size and nutrient removal. Geophys. Res. Lett. 33:L06410. doi: 10.1029/2006GL025845

CrossRef Full Text | Google Scholar

Wolman, M. G., and Miller, J. P. (1960). Magnitude and frequency of forces in geomorphic processes. J. Geol. 68, 54–74. doi: 10.1086/626637

CrossRef Full Text | Google Scholar

Ye, S., Covino, T. P., Sivapalan, M., Basu, N. B., Li, H.-Y., and Wang, S.-W. (2012). Dissolved nutrient retention dynamics in river networks: a modeling investigation of transient flows and scale effects. Water Resour. Res. 48:W00J17. doi: 10.1029/2011WR010508

CrossRef Full Text | Google Scholar