Redirected walking method considering the interaction between users

Redirected walking (RDW), which enables users to walk in a larger virtual space than the physical space, is being applied to enable multiple people to perform activities in a vast VR space while avoiding collisions with each other in the same real space. A method called AFP-RDW, which uses scalar potentials, has been proposed as a control method for RDW. However, while the scalar potential can control the user’s position, it cannot control the user’s orientation. Therefore, APF-RDW cannot be directly used for interactions between users in situations where multiple people experience VR. In this study, we proposed a method to guide users to a position and posture where they can interact with each other by introducing artificial vector potentials (AVF) and walking path simulation. To verify the proposed method, we conducted simulation experiments assuming interaction with objects and other users, and the results suggest that users can interact with objects and other users in both physical and virtual spaces, even in VR experiences where multiple people share the physical and virtual spaces. The results suggest that users may be able to interact with objects, other users, and other users in VR experiences where multiple people share the physical and virtual spaces, respectively.

1 Introduction

Virtual reality (VR) emphasizes immersion and realism, and attempts have been made to incorporate actual walking into the movement to enhance these sensations. However, if real walking movements are directly incorporated into the VR space, the size of the movable VR space is limited by the size of the real space, and the advantages of VR, which can generate as large a space as computational resources allow, cannot be fully utilized.

Redirected Walking (RDW) has been proposed to solve this contradiction (Razzaque, 2005). RDW is a method that changes the user’s walking distance and direction in VR space by utilizing the superiority of vision in spatial perception and presenting images that differ from the user’s movements in real space in terms of the amount of change in the user’s position and posture in VR space. By using RDW to continue the VR experience while avoiding the boundaries and obstacles in the real space, it is possible to make the user perceive that they are walking in a virtual space that is wider than the physical space.

Initially, RDW was based on the assumption that a single user walks through a VR space. On the other hand, with the recent emergence of social VR such as VR Chat¹ and Horizon², there are more opportunities for multiple people to experience VR, and RDW methods that multiple people can use are required. In recent years, RDW methods that allow multiple people to coexist in a shared reality and VR space have been proposed (Bachmann et al., 2019; Lee et al., 2020; Dong et al., 2021; Min et al., 2020). However, most of them do not involve user-to-user contact. Since the coordinates in RDW do not match between real space and VR space, interactions involving user-to-user or user-to-object contact, such as contact between users, carrying objects, and delivering objects, are much more difficult tasks than user-user or user-object collision avoidance.

In this study, we propose a new RDW algorithm that enables user-to-user interaction under the RDW application by adding the following two elements to the existing method APF-RDW (Bachmann et al., 2019; Messinger et al., 2019).

• Redirection controller using gait simulation for effective gain and reset operations to guide to the target position and posture.

• Vector potentials guiding to target position and attitude

This method was validated in a simulation study and achieved the following two points.

• Improvement of object interaction accuracy

• Verification of interaction with others and objects under the application of RDW in VR experiences with three or more simulated users

2 Related works

2.1 Redirected walking

RDW is a method proposed by Razzaque (2005) for walking exploration in a vast VR space using limited real space. Suma et al. (2012a) classify RDW operations into subtle RDW and overt RDW. Subtle RDW includes gain manipulations that slightly shift the user’s direction of travel and rotation in real space to reflect them in VR space and methods that manipulate the spatial arrangement in VR space.

Steinicke et al. (2008a) proposed three basic gain manipulation methods: “translation gain,” “rotation gain,” and “curvature gain.” In contrast, (Langbehn et al., 2017) proposed “bending gain.” These four methods are currently the basic RDW operations. “Translation gain” is a manipulation to increase or decrease the amount of translation in the virtual space by multiplying the distance the user translates. “Rotation gain” is a manipulation to increase or decrease the amount of rotation in the virtual space by multiplying the angle at which the user rotates in place without translational movement. “Curvature gain” is a manipulation in which a user who tries to go straight in virtual space is given a small rotation so that they walk along a circular arc in real space while maintaining the sensation of going straight in virtual space. “Bending gain” is an extension of curvature operation and is a method to map the curvature of a path in real space and virtual space when walking on a circular path in both real and virtual space. Various threshold values for each gain have been reported (Li et al., 2022). Besides, (Grechkin et al., 2016) showed that the simultaneous application of translation and curvature gains does not affect the threshold value of each gain.

As a method for manipulating spatial arrangements, there are two fundamental techniques called “change blindness method” (Suma et al., 2011) and “impossible spaces” (Suma et al., 2012b), both proposed by Suma et al. Change blindness refers to the cognitive characteristic that humans have difficulty perceiving changes in discontinuous visual information due to factors such as looking away. This can manipulate the spatial configuration by relocating objects in the user’s blind spot. Impossible Space is a method that takes advantage of the preconception that space is static and compresses virtual space by dynamically changing the size and spatial arrangement of the virtual space itself.

Although it would be ideal in terms of immersiveness to move through the entire VR space using only subtle RDW, the limited manipulation of subtle RDW would make it difficult to avoid all collisions and represent the entire VR space. The RDW manipulation, called overt RDW, addresses this problem. One of the methods of overt RDW is “reset operation” proposed by Williams et al. (2007), which is a typical method that prevents users from deviating from the boundaries of their real environment or colliding with obstacles. Freeze Backup, Freeze Turn, and 2:1 Turn are representative methods of reset operations, and the most commonly used 2:1 Turn stops the user’s walking and then rotates the user with a 2:1 ratio between the physical and virtual spaces. Related to the reset operation, “distractor” (Peck et al., 2009; Suma et al., 2015) was proposed, which uses objects or content to reduce the sense of discomfort when the user performs the reset operation.

Other overt RDW methods include “seven-league-boots” (Interrante et al., 2007), which applies extremely large or small translation gains, and virtual stairs (Nagao et al., 2018), which presents the sensation of ascending and descending stairs.

2.2 Redirection controller

The above basic manipulations of RDW require a “redirection controller” that determines and operates the appropriate operation method and amount of operation according to the real-space environment, such as the positional relationship between the user and obstacles. Razzaque (2005) propose the following generalized redirection controller methods: “Steer-to-Center (S2C)” to guide the user to the center of the real space, “Steer-to-Orbit (S2O)” to guide the user along a predetermined trajectory, and “Steer-to-Multiple-Target (S2MT)” to guide the user to multiple predefined target positions. Later, (Hodgson and Bachmann, 2013) reported that S2C was the most effective method among these three methods in most cases. These controllers are versatile in that they do not require information about the virtual space, but they are limited in their ability to maintain immersion in the VR experience, as they require periodic reset operations. Furthermore, these controllers are designed for a single user and do not consider situations where multiple users perform redirected walking in the same real space.

In recent years, Lee et al. proposed “Steer-to-Optimal-Target (S2OT),” (Lee et al., 2019) an extension of generalized redirection using machine learning. This method successfully reduces the number of reset operations by using reinforcement learning to select targets in S2MT. Lee et al. also proposed “Multiuser-Steer-to-Optimal-Target (MS2OT)” (Lee et al., 2020), which extends S2OT to a multi-person and allows multiple users to avoid collisions.

Proposed at the same time as the general redirection controller is the script controller. Scripted controllers delineate both the real and virtual walking paths, managing the redirection of single or multiple users (Razzaque et al., 2001; Langbehn et al., 2020). The advantage of scripted controllers is that they can be optimized, and interruptions to the VR experience, such as reset operations that spoil the user’s immersion, can be minimized through proper design. On the other hand, the disadvantage of scripted controllers is the high cost of controller design and low versatility. A level and path design in VR spaces requires knowledge of redirected walking, a burden for ordinary VR developers. Besides, it is extremely difficult for developers and researchers with deep knowledge of redirected walking to envision all the situations in which multiple users interact. Reusing a script controller optimized for one environment for other VR or real environments is also usually difficult.

The predictive controller was proposed following the scripted and generalized controller. The predictive controller is a control method based on predicting the user’s walking path and applying an optimal redirection method. As methods for optimal redirection by path prediction, (Zmuda et al., 2013) proposed “Fully Optimized Redirected Walking for Constrained Environments (FORCE),” which optimize walking path in a constrained environment. Nescher et al. (2014) proposed “Model Predictive Control Redirection (MPCRed)” for dynamically choosing appropriate redirection controllers to optimize space and minimize costs. The advantage of these controllers is that they do not impose the same burden on the producer as the scripted controllers. The disadvantage is that these controllers require that the possible walking paths taken by the user be restricted, such as corridors or intersections. Therefore, it is difficult to use these methods in open spaces.

A reactive algorithm called “APF-RDW” that incorporates collision avoidance using Artificial Potential Fields (APF) was proposed by Bachmann et al. (2019). The details of this controller are described in Section 3.1. As a derivative of the reactive algorithm, “Pull/Push Reactive (P2R) Algorithm” proposed by Thomas and Rosenberg (2019), which has improved performance in physical spaces with obstacles and non-convex physical spaces. Research is also underway to extend APF-RDW to multiple users. Dong et al. (2021) proposed “Dynamic Density-based Redirected Walking (DDB-RDW),” an extension of ARF-RDW that uses the local density of the user, as a method using spatial location information. Since the main goal of these methods is collision avoidance, interaction with other people or objects is not considered.

2.3 RDW and interaction

It has been reported that when physical interaction is added to the VR experience, the user’s sense of presence is enhanced (Cheng et al., 2015; Hoffman, 1998). In general, it is said that the relative coordinates of the object in real space and VR space must match to perform the same interaction in real space and VR space, but in RDW, the coordinates do not match in real space and VR space. Kohli et al. (Kohli et al., 2005) guide the user to a point where the distance between the user and the prop in both real space and VR space is equal, and after the user reaches the point, the relative positions of the props are matched by rotation. Steinicke et al. (2008b) used a real space with a table to verify the effect of physical interaction with the table by applying translational, rotational, and curvature gains to the user. Matsumoto et al. (2017) proposed “Magic Table,” a tactile representation of an equilateral triangle or pentagonal table in VR space using only a square table in real space by applying rotation and curvature gains.

Thomas et al. (2020) extended the P2R algorithm and APF-RDW, and proposed a method to realize physical interaction at the target location by applying an attraction potential to the target location. Min et al. (2020) proposed a method to enable user interaction by matching the relative position-posture relationship of two users in VR and real space using quadratic programming.

In this study, as in Thomas et al. and Min et al.’s work, the aim is interaction in a VR space where the user’s path is not specified. It is considered that these methods can be further improved in the following points.

• Regarding the control of the user’s position in relation to the object to be interacted with, the method of attempting to interact with an object in an open walkable environment is the one by Thomas et al. In a simulation experiment, a real space of 10 m $\times$ 10 m was used to verify walking toward objects 5 m, 10 m, 20 m, and 30 m away in virtual space. However, in simulation experiments, a space of 10 m $\times$ 10 m is used and verified walking toward objects 5 m, 10 m, 20 m, and 30 m away in a virtual space.

• The control of the user’s posture concerning the object being interacted with is not considered.

• Regarding the number of people who experience VR with interaction, the Min et al. study focused on the interaction between two users, while the other studies focused on individual VR experiences, and the studies did not examine user-to-user or user-to-object interactions in VR experiences by three or more users.

This study proposes and verifies a method to solve the above problems.

3 Methods

Based on APF-RDW, we propose a novel RDW controller, AVF-RDW, that can guide the user to an interactable positional relationship by adding vector potentials that indicate attraction based on the target position and posture. In this section, we first explain the APF-RDW and then the AVF-RDW.

3.1 APF-RDW

Several redirection controllers using APF-RDW have been proposed, all using artificial scalar potentials. APF-RDW using scalar potentials could guide the user’s position in the virtual and real spaces but could not guide the user’s posture. We propose a novel RDW controller that combines artificial vector potential to guide the user’s position and posture. In this subsection, we first give an overview of the APF-RDW proposed by Messinger et al. (2019).

3.1.1 Artificial scalar potential field

The basic idea of APF-RDW is that each obstacle, physical boundary, or other user exerts a repulsive force on the user, and these forces are summed to determine the user’s safe direction. The vector of such individual repulsive forces is called the total force vector $\mathit{t}$. The $\mathit{t}$ is expressed as Equation 1: using the vector ${\mathit{w}}_{\mathit{i}}$ of the boundary segment $i$ of the real space used for the VR experience and the vector ${\mathit{u}}_{\mathit{j}}$ of the other user $j$. The boundary of the physical space is divided by segments of a defined length, as shown in Figure 1A.

$\mathit{t}={\displaystyle \sum _{i=0}^n}{\mathit{w}}_{\mathit{i}}+{\displaystyle \sum _{j=0}^{m-1}}{\mathit{u}}_{\mathit{j}}(1)$

where $n$ is the number of boundary segments in the real space and $m$ is the number of users in the real space.

Figure 1

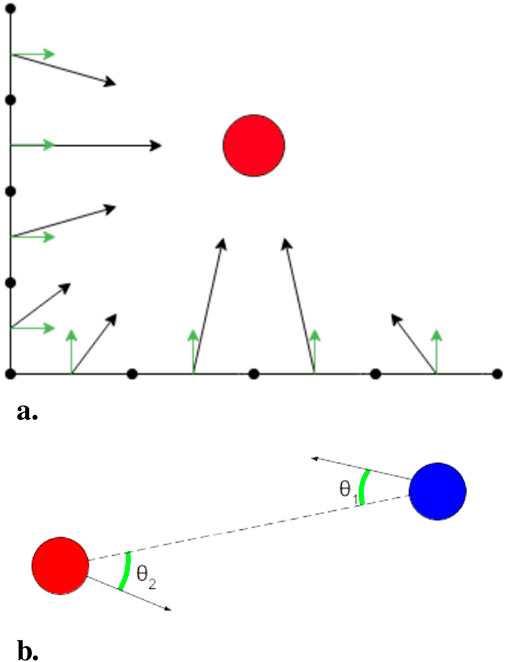
Figure 1. (A) Boundary segment. Red dots indicate users, black arrows indicate vector ${\mathit{w}}_{\mathit{i}}$, and green arrows indicate unit normal vector $\mathit{n}$. Reproduced from (Messinger et al., 2019) (B) The angles ${\theta }_1$ and ${\theta }_2$ formed by the direction vectors of the user and the other user and the lines passing through the user and the other user. Reproduced from (Bachmann et al., 2019).

Next, to explain ${\mathit{w}}_{\mathit{i}}$ and ${\mathit{u}}_{\mathit{j}}$, the vector ${\mathit{d}}_{\mathit{n}}$ is determined using the user’s position vector $\mathit{p}$ and the center of the segment or other user’s position vector ${\mathit{c}}_{\mathit{n}}$ as Equation 2.

${\mathit{d}}_{\mathit{n}}=\mathit{p}-{\mathit{c}}_{\mathit{n}}(2)$

Using ${\mathit{d}}_{\mathit{n}}$, ${\mathit{w}}_{\mathit{i}}$ is defined as Equation 3. Note that $\mathit{n}$ is a unit normal vector to the segment of the real space boundary (see Figure 1A.)

${\mathit{w}}_{\mathit{i}}=\left\{\begin{array}{cc}C{L}_i\frac{{\mathit{d}}_{\mathit{i}}}{\Vert {\mathit{d}}_{\mathit{i}}\Vert }\frac{1}{\Vert {\mathit{d}}_{\mathit{i}}{\Vert }^{\lambda }}\hfill & if\mathit{n}\cdot \frac{{\mathit{d}}_{\mathit{i}}}{\Vert {\mathit{d}}_{\mathit{i}}\Vert }>0\hfill \\ \mathbf{0}\hfill & Otherwise.\hfill \end{array}\right.(3)$

where $C$ is the scaling factor, $L_i$ is the segment length, and $\lambda$ is the decay ratios of the potentials.

Next, the previous study defines the variable $\kappa$ using the direction vectors of the user and the other user, and the angles ${\theta }_1$ and ${\theta }_2$ formed by the lines passing through the user and the other user, as Equation 4 (see Figure 1B).

$\kappa =clamp\left(\frac{\cos {\theta }_1+\cos {\theta }_2}{2},\mathrm{0,1}\right)(4)$

Using ${\mathit{d}}_{\mathit{n}}$ and $\kappa$, ${\mathit{u}}_{\mathit{j}}$ is defined as Equation 5.

${\mathit{u}}_{\mathit{j}}=\kappa \frac{{\mathit{d}}_{\mathit{j}}}{\Vert {\mathit{d}}_{\mathit{j}}\Vert }\frac{1}{\Vert {\mathit{d}}_{\mathit{j}}{\Vert }^{\gamma }}(5)$

where $\gamma$ is the decay ratios of the potentials.

If the direction of the vector $\mathit{t}$ calculated using the above equation is left relative to the user direction, the user will be guided to the left; if it is right, the user will be guided to the right.

Next, the amount of user rotation in the virtual space is explained when applying curvature or rotation gains. Let $v$ be the speed at which the user moves in translation, and let $V$ be the threshold speed at which the user is considered to be walking. If $v\ge V$, the redirection controller judges the user is walking; otherwise, the user is judged to stay in place. Here, we define the amount of rotation $movingRate$ in the virtual space when the user walks using the following Equation 6:

$movingRate=\left\{\begin{array}{cc}360\left(\frac{v}{2\pi r}\right)\hfill & ifv\ge V\hfill \\ 0\hfill & Otherwise.\hfill \end{array}\right.(6)$

where $r$ is a constant representing the curvature radius for curvature gains.

If it is determined that the user is not walking, the user is assumed to be rotating $\mathrm{\Psi }$ on the spot, and the amount of rotation $headRate$ in the virtual space is defined by the following Equation 7:

$headRate=\left\{\begin{array}{cc}\mathrm{\Psi }\ast aRS\hfill & ifv<V\hfill \\ 0\hfill & Otherwise.\hfill \end{array}\right.(7)$

where $aRS$ is an angular rate scaling factor based on the user’s direction of rotation. The $movingRate$ and $headRate$ are limited to the constants $maxMoveRate$ and $maxHeadRate$, respectively.

If there are other users or boundary segments closer than the radius of curvature, replace $movingRate$ with $movingRat{e}^{\prime }$ such as in Equations 8, 9. Where $d$ is the distance to the nearest other user or boundary segment, and $r$ is the radius of curvature as in Equation 6. Same as $movingRate$, $movingRat{e}^{\prime }$ is also capped at $maxMoveRate$.

$movingRat{e}^{\prime }=\left\{\begin{array}{cc}\left(1-t\right)\ast movingRate+t\ast maxMoveRate\hfill & ifd<r\hfill \\ movingRate\hfill & Otherwise.\hfill \end{array}\right.(8)$

$t=1-\frac{d}{r}(9)$

Using the above, the following Equation 10 determines the amount of user rotation in the virtual space at time $\mathrm{\Delta }t$ by applying curvature gain and rotation gain. If $baseRate$ is a constant and $baseRate>0$, the VR space rotates by $baseRate\mathrm{\Delta }t$ even if the user does not translate or rotate and remains stationary.

$\max \left(baseRate,movingRat{e}^{\prime },headRate\right)\mathrm{\Delta }t(10)$

3.1.2 Reset operation

In some cases, the user may be unable to avoid collisions with the boundary of the actual space or other users even if the user changes the direction of travel by RDW operation. Bachmann et al. (2019) use a reset method that rotates the user $360°$ in virtual space while the user rotates in physical space according to the following rotation gains in Equation 11:

$resetRotationGain=\left|\frac{360-\left|rotateAngle\right|}{rotateAngle}\right|(11)$

where $rotateAngle$ is the amount of rotation in physical space caused by the reset operation and is the angle between the direction the user faces and the vector $\mathit{t}$ (which is determined in Equation 1) in physical space. The vector $\mathit{t}$ is not updated during reset to prevent the rotation direction from changing during reset.

3.2 Proposed method

This study assumes that physical interaction is realized by matching the relative position and posture of the user and the interaction target in virtual and physical space. To achieve this objective, we performed reset simulations, AVF-RDW, a new Reset operation, and modified APF-RDW. Each of these items is described below.

3.2.1 Reset simulation

Reset operation, which is not included in the original APF-RDW, is needed to correct the walking path and improve the accuracy of physical interaction. Therefore, we decided to periodically perform simulations to determine when the reset operation should be performed to reduce the displacement of the user’s position and posture from the target (Figure 2A). This reset simulation is performed for each user. The simulation method applies to both stationary and moving target points. If other users are involved, the simulation is based on their current position and orientation.

Figure 2

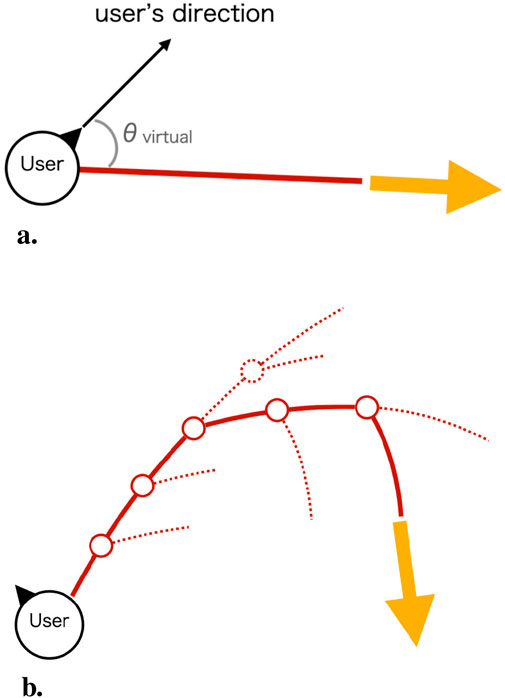
Figure 2. (A) Walking path in VR in simulation. (B) Walking path in real space in simulation. Solid lines indicate the optimal path, dotted lines indicate routes that diverged during the search process, and circles indicate intermediate points. In each figure, yellow arrows indicate the position and orientation of the target point in each space.

In the simulation, a physical space including a user, a boundary segment, and a target location is used with a walking speed $v_s$, a rotation angular velocity ${\varphi }_s$, and a translation gain $g_T=1$, and redirection controllers using the potential field of the 3.2.2 section and the 3.2.3 section are used to calculate the potential field of the redirection controller. With 3.2.3 section, we determine whether the target point in the real space can be reached by the maximum walking distance $\frac{d_v}{g_{\mathit{Tmin}}}$ in the real space, relative to the predicted walking distance $d_v$ to the target point in the virtual space.

First, the walking path and walking distance $d_v$ to the target point in virtual space are obtained by pathfinding. In this study, NavMesh Agent³ in Unity 2019.4 was used for pathfinding. Next, the user is made to walk along the path in the virtual space under the control of the redirection controller, and a midpoint is set for $t_r=1s$ of walking to search for the walking path, and the route branches at the midpoint with or without reset operation. Each route is branched until the upper limit of $n_s$ times of reset operations by route branching is reached, and a judgment is made as to whether the target point can be reached for all branched routes.

The following information is stored for routes determined to be reachable through search. After the simulation is completed for all routes, the information is sorted in ascending order according to the following priority order, and the information placed first is output as the simulation result.

1. For the distance $d_p$ walked to reach the target point and the minimum walking distance in physical space $\frac{d_v}{g_{\mathit{Tmax}}}$ when the walking distance in virtual space is $d_v$.

$\left\{\begin{array}{cc}0\hfill & if{d}_p\ge \frac{d_v}{g_{\mathit{Tmax}}}\hfill \\ 1\hfill & Otherwise\hfill \end{array}\right.(12)$

2. Number of reset operations $n_{\mathit{reset}}$

3. Difference in angle with the target attitude when reaching the target point in physical space ${\theta }_{\mathit{gap}}$

4. Distance walked before the first reset operation $d_{fr}$

5. Distance walked to reach the target point $d_r$

The simulations are performed in parallel at the following time intervals. To compress the computational complexity of the simulations, the time intervals are different for the stationary and moving conditions.

• If the target point is stationary: Every $t_r$ seconds, a walking simulation is performed from the user’s position after $t_{n}i$ seconds for each integer $i$ satisfying $0\le i<\frac{t_r}{t_n}$. During $t_{n}i$ seconds, the user’s motion is assumed to be straight ahead in both physical and virtual space with no gains applied as an approximation.

• If the target point moves: Simulation is performed every $t_n$ seconds.

where $t_r$ and $t_n$ are hyperparameters of the time dimension and assume $0<t_n\le t_r$.

3.2.2 AVF-RDW

APF-RDW proposed in the previous studies uses a potential field and can align the physical- and virtual-space positions but not the posture. To match the relative position and posture of the target point in physical- and virtual-space, we utilize an artificial vector field (AVF) instead of an artificial potential field.

In AVF-RDW, the force vector due to the vector potential of the target point is added to the total force vector $\mathit{t}$. Here, the total force vector, which also considers the vector potential, is denoted by ${\mathit{t}}^{\prime }$ as in Equation 13. In this study, interaction is prioritized for boundary segments and other users if they exist within a distance $d_{t^{\prime }}$ of the target point, and for the boundary segments $\mathit{i}$ and other users $\mathit{j}$.

In this study, interaction is prioritized for boundary segments and other users if they exist within a distance $d_{t^{\prime }}$ of the target point, and for the boundary segments $\mathit{i}$ and other users $\mathit{j}$.

${\mathit{t}}^{\prime }={\displaystyle \sum _{i=0}^n}{\mathit{w}}_{\mathit{i}}+{\displaystyle \sum _{j=0}^m}{\mathit{u}}_{\mathit{j}}+k_v\mathit{t}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t}(13)$

As shown in Equation 14, $k_v$ is defined by the angle between the path and the user ${\theta }_{\mathit{virtual}}$ (see Figure 2B) and prevents RDW manipulations unintentionally when the user is not facing the target point in the virtual space.

$k_v=clamp\left(\cos {\theta }_{\mathit{virtual}},\mathrm{0,1}\right)(14)$

The vector $\mathit{t}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t}$ is defined as follows.

In the case of $d_r\ge \frac{d_v}{g_{\mathit{Tmax}}}$ (including the case where the simulation results were not output), we define the centers of vector potentials $O_1$ and $O_2$ as shown in Figure 3. The line $O_1{O}_2$ and the vector indicating the target attitude are perpendicular, and $O_1$ and $O_2$ are assumed to be at a distance $d_p$ from the target point, respectively. The polar coordinate system $({\rho }_0,{\varphi }_0)$ centered at the target point and its basis vector $({\mathit{e}}_{\mathit{\rho }\mathit{0}},{\mathit{e}}_{\mathit{\varphi }\mathit{0}})$, the polar coordinate system $({\rho }_1,{\varphi }_1)$ centered at $O_1$ and its basis vector $({\mathit{e}}_{\mathit{\rho }\mathit{1}},{\mathit{e}}_{\mathit{\varphi }\mathit{1}})$, polar coordinate system $({\rho }_2,{\varphi }_2)$ centered at $O_2$ and its basis vectors $({\mathit{e}}_{\mathit{\rho }\mathit{2}},{\mathit{e}}_{\mathit{\varphi }\mathit{2}})$ to obtain vector fields ${\mathit{B}}_{\mathit{i}}^{\prime }(i=\mathrm{1,2})$ and the vector field $\mathit{S}$ is expressed as follows. The $s,p,Q,\zeta$ are constants.

$\mathit{S}=-s{\mathit{e}}_{\mathit{\rho }\mathit{0}}(15)$

However, the further away the target point is from the center of the coordinate system, the smaller the value of $|\mathit{B}|$ becomes, and the less effective the guidance to the target point becomes, so we add a vector field $\mathit{S}$ expressed by the following Equation 16, which gives a vector of size $s$ from the user’s position to the target point.

${\mathit{B}}_{\mathit{i}}^{\prime }={\left(-1\right)}^{i-1}\frac{Q}{{\left({\rho }_i+p\right)}^{\zeta }}{\mathit{e}}_{\mathit{\varphi }\mathit{i}}(16)$

Figure 3

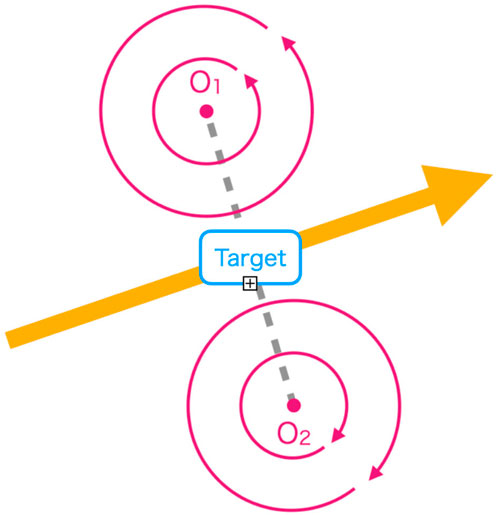
Figure 3. Vector field due to vector potentials. The pink arrow indicates the direction of the vector potential, and the yellow arrow indicates the target orientation. The distance from the target point to the center of the vector potentials is $d_p$.

Based on the above, the vector $\mathit{t}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t}$ is expressed as in Equation 17.

$\mathit{t}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t}=\mathit{S}+{\displaystyle \sum _{i=1}^2}{\mathit{B}}_{\mathit{i}}^{\prime }(17)$

If $d_p<\frac{d_v}{g_{\mathit{Tmax}}}$, it means the target point in physical space is too close to the virtual space, and it is impossible to match the relative coordinates between the virtual space and the target point in physical space by the translation gain. In this case, the system defines the potential of the target point to avoid the target point in physical space until the relative coordinates have an appropriate relationship. Then determine the vector $\mathit{t}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t}$ using the distance $d_{\mathit{target}}$ between the user and the target point in physical space and the potential decay ratio $\mu$ as in Equation 18

$\mathit{t}\mathit{a}\mathit{r}\mathit{g}\mathit{e}\mathit{t}=\frac{{\mathit{d}}_{\mathit{target}}}{\Vert {\mathit{d}}_{\mathit{target}}\Vert }\frac{1}{\Vert {\mathit{d}}_{\mathit{target}}{\Vert }^{\mu }}(18)$

The translation gain $g_T$ is determined using the walking distance in virtual space $d_v$ obtained in the 3.2.1 section, the walking distance in physical space $d_p$, and $g_{\mathit{Tmin}}$, $g_{\mathit{Tmax}}$ representing the minimum and maximum values of the translation gain, as shown in Equation 19. Note that $g_T=1$ is in the simulation, as mentioned in the Section 3.2.1.

$g_T=\left\{\begin{array}{cc}clamp\left(\frac{d_v}{d_p},g_{\mathit{Tmin}},g_{\mathit{Tmax}}\right)\hfill & if\frac{d_v}{g_{\mathit{Tmax}}}\le d_r\le \frac{d_v}{g_{\mathit{Tmin}}}\hfill \\ g_{\mathit{Tmax}}\hfill & Otherwise\hfill \end{array}\right.(19)$

3.2.3 Reset operation

From the simulation results shown in the Section 3.2.1, the distance $d_{fr}$ walked before the “first reset” operation in real space is obtained, and if the following conditions are met, the reset operation is determined to be necessary at distance $d_{fr}$.

• $n_{\mathit{reset}}\ne 0$:

• $d_r\ge \frac{d_v}{g_{\mathit{Tmax}}}$:

This means that the target point is not too close to the user and that translation gain can adequately compensate for the length of the walking path.

A reset operation is performed if the simulation does not update the decision when the user walks $d_{fr}$ in real space.

3.2.4 Modifications to APF-RDW

To enable interaction with objects and other users, the following modifications are added to APF-RDW as described in Section 3.1 in this study.

• In $movingRate$ of Equation 6, the radius of curvature is fixed at $r$. Still, (Sakono et al., 2021) reported that the discomfort of RDW is reduced when the radius of curvature varies continuously rather than being constant. Therefore, $movingRate$ in Equation 6 is replaced with the angle ${\theta }_t(0^{°}<{\theta }_{t^{\prime }}<{180}^{°})$ between the user direction and vector ${\mathit{t}}^{\prime }$, which determines the left and right guidance directions defined in Equation 13, as shown in Equation 20:

$movingRate=\left\{\begin{array}{cc}\min \left({\theta }_{t^{\prime }},360\left(\frac{v}{2\pi r}\right)\right)\hfill & ifv>V\hfill \\ 0\hfill & Otherwise.\hfill \end{array}\right.(20)$

• Messinger et al. (2019) method uses $movingRat{e}^{\prime }$ and $baseRate$ in Equation 8. When the author used these to experience RDW when the user is located near the boundary of the real space, it was found that $baseRate\mathrm{\Delta }t$ rotation occurs in the VR space even when the user does not translate or rotate and remains stationary. The VR space should not rotate when the user is stationary since the interaction is also intended to be performed while the user stands still. Therefore, this study does not use $baseRate$. It also occurs to us that with $movingRat{e}^{\prime }$ the maximum $maxMoveRate$ rotational gain per second is applied even when the user is moving slightly. $maxMoveRate$ is given as 15 deg/sec in the paper by Bachman et al. (Bachmann et al., 2019), which is a considerable amount of rotation. Therefore, we did not use $movingRat{e}^{\prime }$. Based on the above, Equation 10 is replaced with Equation 21:

$\max \left(movingRate,headRate\right)\mathrm{\Delta }t(21)$

4 Experiment 1

4.1 Purpose

The main purposes of experiment 1 are as follows.

• Comparison of the proposed method with the method by Thomas et al. (2020) for interaction with stationary objects, and verification of the effectiveness of guidance to the target position and orientation, and the effectiveness of the RDW method in avoiding collisions.

• Verification of the spatial dependence of the proposed method using several patterns for the location of target points and vector potentials.

4.2 Systems

An HP VR Backpack G2, a wearable VR PC with a 2.7-GHz Core i7 processor, 32 GB of main memory, and an NVIDIA GeForce RTX 2080 graphics card, was used to render the VR environment, system management, and record data. The simulation environment was implemented using Unity 2019.4.32 based on the OpenRDW Toolkit developed by Li et al. (2021), and experiments were conducted using the same version of Unity. OpenRDW Toolkit is a tool that allows RDW to be verified in a simulation environment and user studies and implements methods such as those by Thomas et al. (2020) as redirection controllers.

4.3 Experimental conditions

The experimental design has two factors: a four-level number of simulation users and a four-level potential field method. Regarding the number of simulated users, we used one to four simulated users. These simulated users walked toward targets displayed in the virtual environment under RDW while avoiding the others.

Regarding potential filed methods, three conditions $(1a),(1b),(1c)$ are proposed methods with varying parameters of vector potential defined in Equation 22, and $(1d)$ is the method proposed by Thomas et al. (2020). We chose the method of Thomas et al. as our comparison because similar to the APF-RDW proposed by Bachmann et al. (2019), the Thomas et al. algorithm employs an artificial potential function and could be extended to multi-user RDWs. It is also worth mentioning that the implementation of this method is included in OpenRDW (Li et al., 2021) to ensure reproducibility.

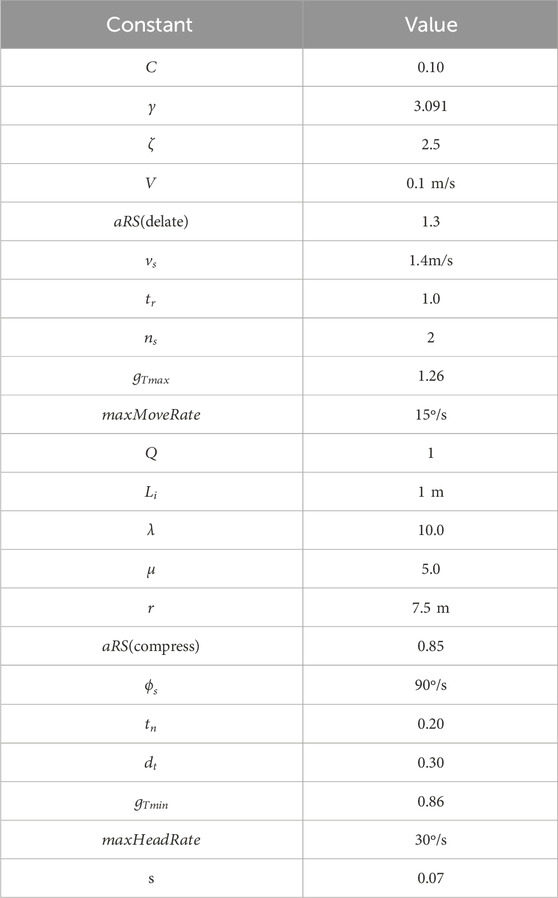
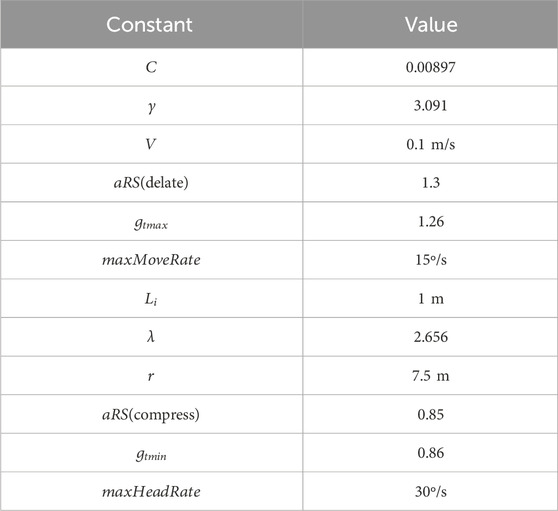
For the parameters of the vector potential, the distance $d_p$, which is the distance between the target point and the center of the vector potential that determines the magnitude of the vector potential at the target point, and the penalty $p$, which is a constant added to avoid the possibility of deadlock due to $\rho \to 0$ and $|\mathit{B}|\to \infty$ in Equation 15, were set so that the magnitude of the vector given by the vector potential at the location of the target point matches as follows:

$\left(d_p,p\right)=\left\{\begin{array}{cc}\left(0.3,0.7\right)\hfill & \left(1a\right)\hfill \\ \left(0.6,0.4\right)\hfill & \left(1b\right)\hfill \\ \left(0.9,0.1\right)\hfill & \left(1c\right)\hfill \end{array}\right.(22)$

These parameters were established based on preliminary validation. Except for $d_p$ and $p$, the parameters of the proposed method were set as shown in Table 1, which are the same parameters by Thomas et al. (2020).

Table 1

Table 1. Parameters used in the proposed method.

The above four conditions were verified for one to four simulated users, which are implemented in OpenRDW. The size of the physical space was 10 m × 10 m, and the size of the virtual space was set to infinity (Figure 4).

Figure 4

Figure 4. Task in Experiment 1. We measured position and posture deviations in physical and virtual space and the distance between resets using one to four simulated users. The green sphere represents the target point in the virtual environment, the blue line in the right figure represents the walking trajectory of the orange user in the virtual space, and the red line represents the walking trajectory in the real environment.

This part describes the simulation experiment trials in detail. First, a walking path with a total length of 1,000 m was determined by setting a target point at random distances between 10 and 40 m from an initial position as a walking path in the VR space and randomly selecting the direction in which the next target point would be located. Then, target points in real space corresponding to each target point of the walking path were randomly determined in an area at least 1 m away from the boundary segment of the physical space. These target points are assumed to be interaction points between the user and the objects present at the target points, as mentioned in Section 2.3 (in the simulation, the user only walks toward the target points and does not take any action related to interaction at the target points). The direction of the target point in both virtual and physical space was randomly determined. After starting the trial, each user started walking along the path at the same time, and the trial was terminated when all users completed the path or when one or more users remained in the same location for more than 50 s, and walking was judged to be impossible. The above trials were conducted three times for each condition.

4.4 Evaluation indices

In the experiments in this chapter, the following items are used as evaluation indices for comparison.

1. Positional alignment error between the target point and the user in physical space

2. Angular alignment error between the targets’ direction and the user’s direction in physical space (range: $0°-180°$)

3. Walking distance between reset operations in virtual space (Bachmann et al., 2019): walking distance between reset operations indicates RDW’s effectiveness in avoiding collisions.

The working hypothesis for this experiment is described below. It is conceivable that the larger the vector potential, the smaller the error in distance and posture from the target point. However, since the walking path detours along the potential of the target point, the number of resets required to reach the target point increases, and the walking distance between resets decreases. Compared to existing methods, the proposed method is considered to have an advantage in position error and angular error, but the distance between resets is expected to decrease because the number of resets increases to compensate for position error and angular error. Therefore, the working hypotheses for this experiment are as follows:

WH-1. Positional alignment error: $condition(1a)<condition(1b)<condition(1c)<condition(1d)$

WH-2. Angular alignment error: $condition(1a)<condition(1b)<condition(1c)<condition(1d)$

WH-3. Distance between resets: $condition(1d)>condition(1c)>condition(1b)>condition(1a)$

4.5 Result

Regarding the number of trials completed, one of the three trials in condition (1c) could not be completed for the case with one user. Among all the trials, the task went to the target point 115 times in condition (1c) and 119 times in the other conditions. One of the three trials in condition (1c) could not be completed for two participants. In all trials, the two participants faced the target point 195 times in condition (1c) and 258 times in the other conditions. In the case of three participants, one of the three trials in conditions (1b), (1c), and (1d), respectively, could not be completed. In all trials, the three participants performed the task toward the target point a total of 354 times in condition (1a), 308 times in condition (1b), 329 times in condition (1c), and 277 times in condition (1d). For the case of four users, two of the three trials in conditions (1c) and (1d), respectively, and one of the three trials in conditions (1a) and (1b), respectively, could not be completed. In all trials, the four participants performed the task toward the target point a total of 486 times in conditions (1a), 483 times in conditions (1d), and 482 times in conditions (1b) and (1c), respectively.

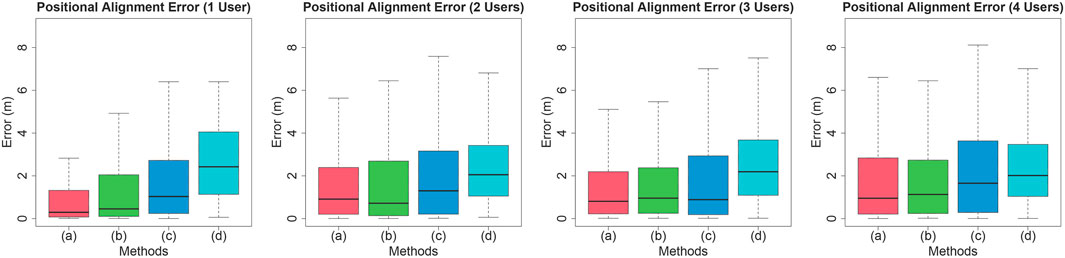
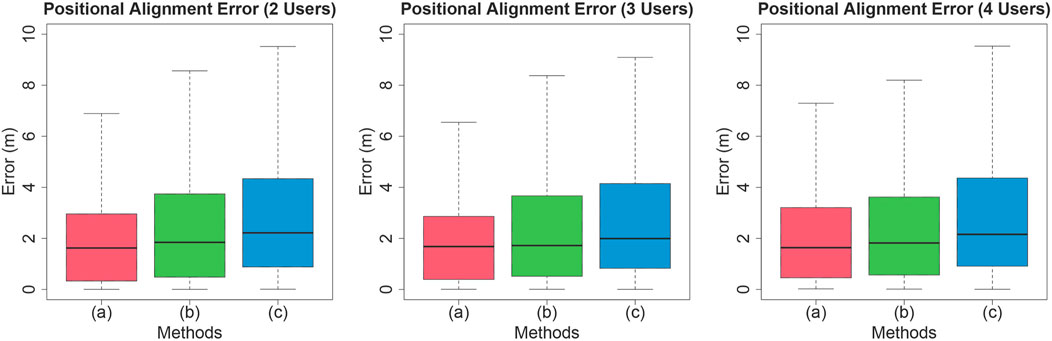
Figure 5 indicates the positional alignment error in combining the potential field conditions and the number of simulated user conditions. The Kolmogorov-Smirnov test was conducted as a normality test on positional alignment error when the target point is reached in virtual space, and the null hypothesis was rejected. A two-factor analysis of variance was conducted after applying the Aligned Rank Transform (ART), and significant differences were found for the main effect of the number of users$(F(\mathrm{3,4626})=5.25,p<0.01,partial{\eta }^2=0.0034)$, the main effect of the applied method$(F(\mathrm{3,4626})=68.87,p<0.001,partial{\eta }^2=0.043)$, and the interaction effect$(F(\mathrm{9,4626})=2.30,p<0.05,partial{\eta }^2=0.045)$, respectively. Multiple comparisons of the positional alignment error when there was only one user, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1c), (1a)-(1d), (1b)-(1d), and (1c)-(1d) ((1a)-(1b):$p=0.083,r=0.11$; (1a)-(1c):$p<0.01,r=0.21$; (1a)-(1d):$p<0.001,r=0.54$; (1b)-(1c):$p=0.18,r=0.088$; (1b)-(1d):$p<0.001,r=0.41$; (1c)-(1d):$p<0.001,r=0.32$) Multiple comparisons of the positional alignment error when there were two users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1d), (1b)-(1d), and (1c)-(1d). ((1a)-(1b):$p=0.053,r=0.028$; (1a)-(1c): $p=0.20,r=0.060$; (1a)-(1d):$p<0.001,r=0.31$; (1b)-(1c):$p=0.084,r=0.081$; (1b)-(1d):$p<0.001,r=0.31$; (1c)-(1d):$p<0.001,r=0.33$). Multiple comparisons of the positional alignment error when there were three users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1d), (1b)-(1d), and (1c)-(1d). ((1a)-(1b):$p=0.28,r=0.042$; (1a)-(1c):$p=0.41,r=0.0031$; (1a)-(1d):$p<0.001,r=0.36$; (1b)-(1c):$p=0.86,r=0.0069$; (1b)-(1d):$p<0.001,r=0.31$; (1c)-(1d):$p<0.001,r=0.29$). Multiple comparisons of the positional alignment error when there were four users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1c), (1a)-(1d), (1b)-(1c), (1b)-(1d), and (1c)-(1d). ((1a)-(1b):$p=0.41,r=0.026$; (1a)-(1c):$p<0.001,r=0.11$; (1a)-(1d):$p<0.001,r=0.27$; (1b)-(1c):$p<0.05,r=0.082$; (1b)-(1d):$p<0.001,r=0.23$; (1c)-(1d):$p<0.001,r=0.12$). The results show that there are significant differences between conditions (1a), (1b), and (1c), and condition (1d) regardless of the number of users. These results also mean that the position alignment error tends to be smaller when the distance $d_p$ is small, i.e., the vector potential near the target point is large.

Figure 5

Figure 5. Positional alignment error.

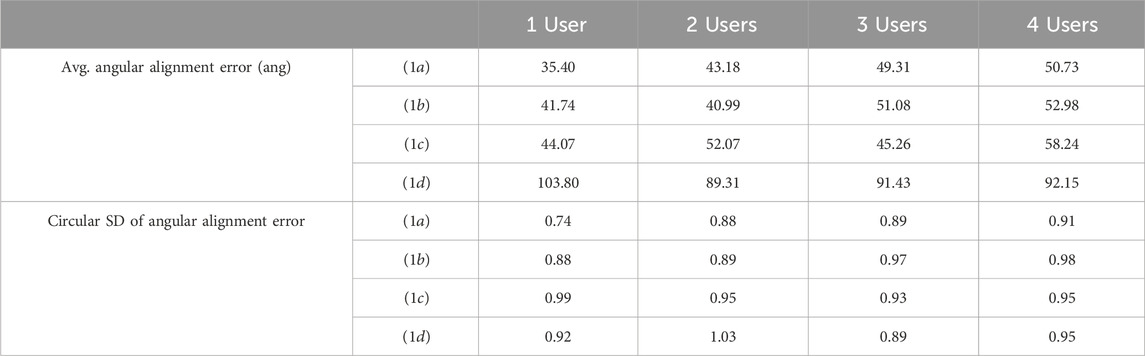
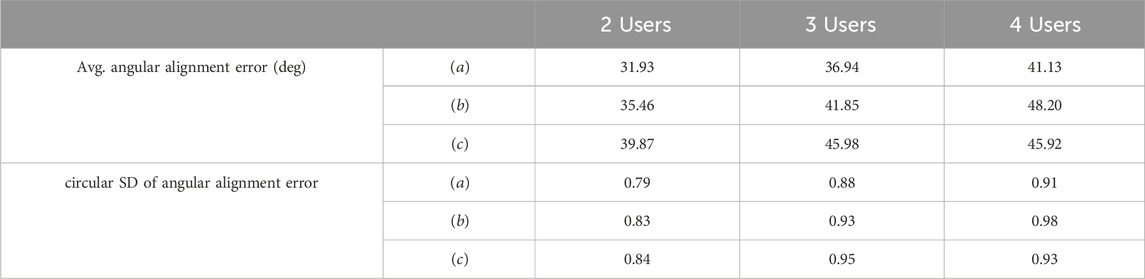
Table 2 shows the average angular alignment errors. The Harrison-Kanji test, which corresponds to a two-factor analysis of variance for angle data, was conducted on angular alignment error when the target point was reached in VR space. Significant differences were found for the main effect of the number of users$({\chi }^2(6)=22.68,p<0.001,\varphi =0.070)$, and the main effect of the applied method$({\chi }^2(6)=629.92,p<0.001,\varphi =0.37)$, respectively. No significant differences were found in the interaction effects$({\chi }^2(9)=35.73,p=1.00,\varphi =0.088)$. The null hypothesis was rejected when the Kuiper test was conducted to test the normality of the angular data for the angular alignment error when there was only one user. Therefore, multiple comparisons using Rao’s Equal Variance Test were conducted between the applied methods with the $p$ value corrected by the Holm method, and significant differences were found between (1a)-(1d), (1b)-(1d), and (1c)-(1d) ((1a)-(1b):$p=0.29,H_1=1.11$; (1a)-(1c):$p=0.23,H_1=1.43$; (1a)-(1d):$p<0.01,H_1=7.91$; (1b)-(1c):$p=0.76,H_1=0.10$; (1b)-(1d):$p<0.01,H_1=8.49$; (1c)-(1d):$p<0.01,H_1=8.70$). The null hypothesis was rejected when the Kuiper test was conducted to test the normality of the angular data for the angular alignment error when there were two users. Therefore, multiple comparisons using Rao’s Equal Variance Test were conducted between the applied methods with the $p$ value corrected by the Holm method, and no significant differences were found in any pairs ((1a)-(1b):$p=0.63,H_1=0.24$; (1a)-(1c):$p=0.12,H_1=2.38$; (1a)-(1d):$p=0.88,H_1=0.023$; (1b)-(1c):$p=0.059,H_1=3.56$; (1b)-(1d):$p=0.88,H_1=0.023$; (1c)-(1d):$p=0.88,H_1=0.023$). The null hypothesis was rejected when the Kuiper test was conducted to test the normality of the angular data for the angular alignment error when there were three users. Therefore, multiple comparisons using Rao’s Equal Variance Test were conducted between the applied methods with the $p$ value corrected by the Holm method, and no significant differences were found in any pairs ((1a)-(1b):$p=0.69,H_1=0.16$; (1a)-(1c):$p=0.34,H_1=0.92$; (1a)-(1d):$p=0.67,H_1=0.18$; (1b)-(1c):$p=0.22,H_1=1.49$; (1b)-(1d):$p=0.67,H_1=0.18$; (1c)-(1d):$p=0.67,H_1=0.18$). The null hypothesis was rejected when the Kuiper test was conducted to test the normality of the angular data for the angular alignment error when there were four users. Therefore, multiple comparisons using Rao’s Equal Variance Test were conducted between the applied methods with the $p$ value corrected by the Holm method, and no significant differences were found in any pairs ((1a)-(1b):$p=0.55,H_1=0.35$; (1a)-(1c):$p=0.058,H_1=3.58$; (a)-(d):$p=0.44,H_1=0.59$; (b)-(c):$p=0.19,H_1=1.71$; (1b)-(1d):$p=0.43,H_1=0.60$; (1c)-(1d):$p=0.43,H_1=0.61$). These results show that when there is only one user, the angle alignment error is significantly smaller for conditions (1a), (1b), and (1c) of the proposed method than for the control condition (1d).

Table 2

Table 2. Angular alignment error for each method and number of users.

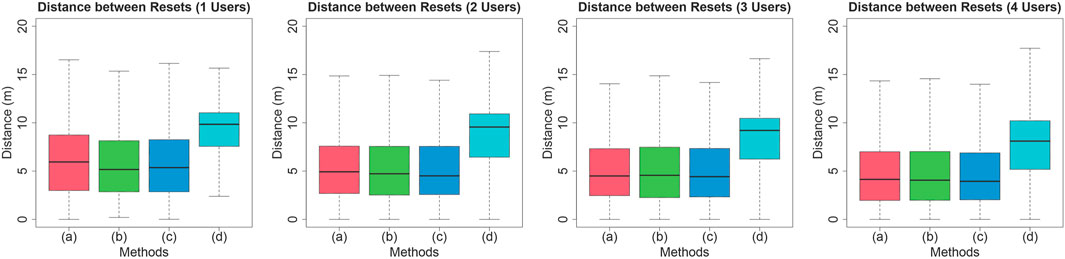
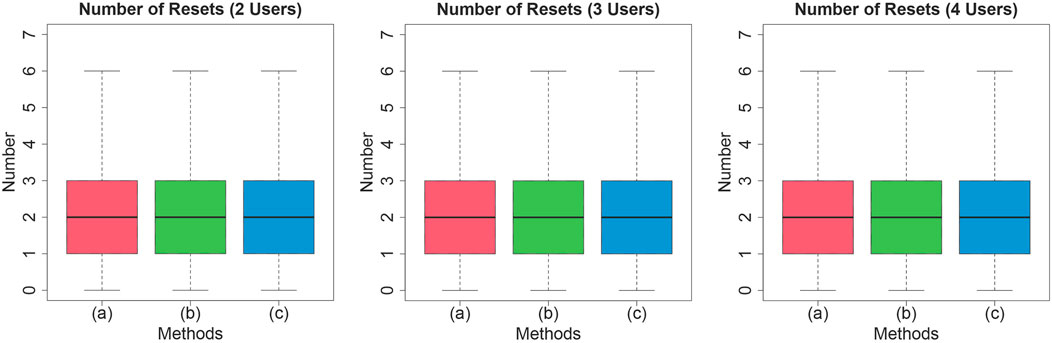
Figure 6 indicates the distance between resets in combining the four method conditions and the four user conditions. The Kolmogorov-Smirnov test was conducted as a normality test on distance between resets, and the null hypothesis was rejected. A two-factor analysis of variance was conducted after applying the ART, and significant differences were found for the main effect of the number of users $(F(\mathrm{3,20373})=111.46,p<0.001,partial{\eta }^2=0.016)$, the main effect of the applied method$(F(\mathrm{3,20373})=604.20,p<0.001,partial{\eta }^2=0.082)$, and the interaction effect$(F(\mathrm{9,20373})=2.12,p<0.05,partial{\eta }^2=9.3\times 10^{-4})$, respectively. Multiple comparisons of the distance between resets when there was only one user, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1d), (1b)-(1d), and (1c)-(1d). ((1a)-(1b):$p=0.066,r=0.057$; (1a)-(1c):$p=0.12,r=0.049$; (1a)-(1d):$p<0.001,r=0.45$; (1b)-(1c):$p=0.80,r=0.0078$; (1b)-(1d):$p<0.001,r=0.50$; (1c)-(1d):$p<0.001,r=0.49$) Multiple comparisons of the distance between resets when there were two users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1d), (1b)-(1d), and (1c)-(1d). ((1a)-(1b):$p=0.39,r=0.018$; (1a)-(1c):$p=0.27,r=0.024$; (1a)-(1d):$p<0.001,r=0.44$; (1b)-(1c):$p=0.79,r=0.0058$; (1b)-(1d):$p<0.001,r=0.45$; (1c)-(1d):$p<0.001,r=0.47$) Multiple comparisons of the distance between resets when there were three users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1d), (1b)-(1d), and (1c)-(1d). ((1a)-(1b):$p=0.39,r=0.018$; (1a)-(1c):$p=0.27,r=0.024$; (1a)-(1d):$p<0.001,r=0.44$; (1b)-(1c):$p=0.79,r=0.0058$; (1b)-(1d):$p<0.001,r=0.45$; (1c)-(1d):$p<0.001,r=0.47$) ((1a)-(1b):$p=0.46,r=0.013$; (1a)-(1c):$p=0.27,r=0.019$; (1a)-(1d):$p<0.001,r=0.44$; (1b)-(1c):$p=0.76,r=0.0052$; (1b)-(1d):$p<0.001,r=0.45$; (1c)-(1d):$p<0.001,r=0.45$) Multiple comparisons of the distance between resets when there were four users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (1a)-(1d), (1b)-(1d), and (1c)-(1d). ((1a)-(1b):$p=0.39,r=0.018$; (1a)-(1c):$p=0.27,r=0.024$; (1a)-(1d):$p<0.001,r=0.44$; (1b)-(1c):$p=0.79,r=0.0058$; (1b)-(1d):$p<0.001,r=0.45$; (1c)-(1d):$p<0.001,r=0.47$) ((1a)-(1b):$p=0.50,r=0.0095$; (1a)-(1c):$p=0.38,r=0.012$; (1a)-(1d):$p<0.001,r=0.36$; (1b)-(1c):$p=0.85,r=0.0026$; (1b)-(1d):$p<0.001,r=0.37$; (1c)-(1d):$p<0.001,r=0.37$) These results indicate that the proposed methods (1a), (1b), and (1c) have a significantly shorter distance between resets than the control condition (1d).

Figure 6

Figure 6. Distance between resets.

4.6 Discussion

First, let us examine the working hypotheses: For WH-1, the experimental results show a significant difference in distance alignment error between all the proposed method conditions and the control condition, indicating the superiority of the proposed method. Comparison between the proposed methods showed that the distance alignment error tended to be smaller when the distance between the vector potential and the target point was shortened. Therefore, the WH-1 was partially supported.

For WH-2, the experimental results show a significant difference in distance alignment error between all the proposed method conditions and the control condition, but no significant difference within the proposed method. Thus, WH-2 was partially supported.

For WH-3, there is a significant difference in the user’s walking distance between reset operations in the virtual space between method (1d) and the other methods, and no significant difference between (1a), (1b), and (1c). Therefore, as with WH-2, only the relationship between method (1d) and the other methods is supported. The shorter walking distance between resets in the proposed method means that resets are performed more frequently than in the existing method, which is likely to reduce immersion. However, in a study on user interaction under RDW by Min et al. (2020), the number of reset operations of the proposed method by Min et al. is about twice that of the existing method. This means that the number of resets for Min et al. and our proposed method is comparable.

Based on the above results, the proposed methods (1a), (1b), and (1c) are superior to the existing method (1d) in terms of distance and angle alignment errors. On the other hand, the distance between resets is shorter than that of the existing method. Therefore, it is desirable to use the proposed method when consistency between real and virtual positions and postures is required, such as physical interactions, and to use the existing scalar potential-based method in other situations. The comparison of vector potential parameters showed that the position error tended to be smaller in the order of (1a), (1b), and (1c), where the center of the vector potential was located closer to the target point, but there were no significant differences in angular error or distance between resets. From the above, it can be concluded that the user’s position and posture can be effectively guided by moving the center point of the vector potential closer to the target point and by limiting the range of influence of the vector potential to a certain range.

5 Experiment 2

5.1 Purpose

The main purposes of the experiment 2 are as follows.

• Verification of the effectiveness of guidance to the target position and orientation and the effectiveness of the RDW method in avoiding collisions for interaction with users who walk independently.

• Verification of the spatial dependence of the proposed method using several patterns for the location of target points and vector potentials.

5.2 Systems

As in the 4.2 section, HP VR Backpack G2 was used for rendering the VR environment, system management, and data recording. The simulation environment was implemented using Unity 2019.4.32 based on the OpenRDW Toolkit (Li et al., 2021). The following experiments were conducted using the same version of Unity.

5.3 Experimental conditions

In this simulation, the task design was similar to that of Min et al. (2020). The scenarios consisted of two users in random positions in virtual space approaching each other along a straight line (see Figure 7). In the previous study, the scenario ended when the two users were within an acceptable distance in virtual space, but in our simulation, not only the distance but also the posture of the two users was subject to evaluation.

Figure 7

Figure 7. Task in Experiment 2. Using one to four simulated users, we measured the displacement of position and posture in the physical and virtual space and the number of resets under conditions in which two of the simulated users physically interacted with each other. The figure shows two users approaching each other to interact physically. The green sphere represents the target point in the virtual environment for the orange user, and the blue line represents the walking trajectory of the orange user in the virtual space.

The experimental design has two factors: a three-level number of simulated users and a three-level vector potential parameter. Regarding the number of simulated users, we used between two and four simulated users. Of these, two simulated users interact with each other. In the case of a three-user simulation, two users interacted with each other, while the other user walked toward targets displayed in the virtual environment under RDW while avoiding the other users.

Regarding vector potential parameters, we set three different patterns of artificial vector potential parameters for simulated users interacting with each other. For the parameters of the vector potential, as in the 4.3 section, the distance $d_p$: between the target point and the center of the vector potential, and $p$ was set to $(d_p,p)=\{(2a):(0.3,0.7),(2b):(0.6,0.4),(2c):(0.9,0.1)\}$ as same as Equation 22. The parameters other than $d_p$ and $p$ in the proposed method were set as shown in Table 1 as in Section 4.3. The target here is the position of the other user who interacts with the system, as well as the posture of the other user, which is flipped 180° in the plane direction. For users who do not interact with others, the parameters of the APF-RDW were set as shown in Table 3, referring to the previous studies (Bachmann et al., 2019; Messinger et al., 2019).

Table 3

Table 3. Parameters used in APF-RDW for non-interacting users.

The above three conditions were verified with a real space size of $10\text{m}\times 10\text{m}$ and two, three, and four people, respectively. The size of the virtual space was set to $30\text{m}\times 30\text{m}$.

In this experiment, the task was performed 100 times per trial, changing the initial placement of the users. In physical space, the user’s initial placement was randomly generated at the beginning of each task from an area at least 1.0 m away from the boundary segment. If one or more users remained in the same location for more than 50 s during the trial and it was determined that walking was impossible, the trial was terminated at that point, and no further tasks were performed.

If $d_r>\frac{d_v}{g_{\mathit{Tmin}}}$ (, where the distance between user and target in real environment $d_r$, the distance between user and target in virtual environment $d_v$, and minimum translation gain $g_{\mathit{Tmin}}$) at the beginning of each task, it is impossible to reach the interaction target by applying any translation gain to the user in the simulation. For this reason, tasks in which the interacting users are in such a positional relationship with each other are excluded from the data.

5.4 Evaluation indices

In the experiments in this chapter, the following items are used as evaluation indices for comparison:

1. Positional alignment error between the target points and the users in physical space when each task ends

2. Angular alignment error between the targets’ direction and the user’s direction in real space when each task ends (range: $0°-180°$)

3. Number of resets by each user in each task (Min et al., 2020)

These data were obtained only from two interactive users.

As for the working hypotheses, as in Experiment 1, it is conceivable that the larger the vector potential, i.e., the shorter the distance between the vector potential and the target point, the smaller the error in distance and posture from the target point. However, since the walking path detours along the potential of the target point, the number of resets required to reach the target point increases, and the walking distance between resets decreases. The working hypotheses are as follows:

WH-4. Positional alignment error: $method(2a)<method(2b)<method(2c)$

WH-5. Angular alignment error: $method(2a)<method(2b)<method(2c)$

WH-6. Number of resets: $method(2a)>method(2b)>method(2c)$

5.5 Result

Regarding the number of trials completed, for the case of two users, out of ten trials, four trials could not be completed under condition (2a), five trials under condition (2b), and three trials under condition (2c). In all trials, the task was executed 816 times under condition (2a), 658 times under condition (2b), and 774 times under condition (2c). In addition, based on the 5.4 section, we excluded data for 143 cases in condition (2a), 125 cases in condition (2b), and 155 cases in condition (2c). For the case of three users, one trial could not be completed in condition (2a), four trials in condition (2b), and three trials in condition (2c) out of ten trials. In all trials, the task was executed 961 times under condition (2a), 760 times under condition (2b), and 826 times under condition (2c). In addition, based on the 5.4 section, we excluded data for 191 cases in condition (2a), 142 cases in condition (2b), and 169 cases in condition (2c). For the case of four users, out of ten trials, four trials could not be completed under condition (2a), one trial under condition (2b), and three trials under condition (2c). In all trials, the task was executed 848 times under condition (2a), 935 times under condition (2b), and 696 times under condition (2c). In addition, based on the 5.4 section, 140 data were excluded under condition (2a), 185 under condition (2b), and 162 under condition (2c).

Figure 8 indicates the positional alignment error in combining the potential field conditions and the number of simulated user conditions. The Kolmogorov-Smirnov test was conducted as a normality test on positional alignment error, and the null hypothesis was rejected. A two-factor analysis of variance was conducted after applying the ART, and significant differences were found for the main effect of the number of users$(F(\mathrm{2,13127})=5.25,p<0.01,partial{\eta }^2=8.0\times 10^{-4})$, and the main effect of the applied method ($F(\mathrm{2,13127})=104.67,p<0.001$, $partial{\eta }^2=0.016$), respectively. No significant differences were found in the interaction effects$(F(\mathrm{4,13127})=0.90,p=0.46,partial{\eta }^2=2.7\times 10^{-4})$. Multiple comparisons of the positional alignment error when there were two users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found in all pairs, (2a)-(2b), (2a)-(2c), and (2b)-(2c). ((2a)-(2b):$p<0.001,r=0.086$; (2a)-(2c):$p<0.001,r=0.17$; (2b)-(2c):$p<0.001,r=0.088$) Multiple comparisons of the positional alignment error when there were three users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found in all pairs, (2a)-(2b), (2a)-(2c), and (2b)-(2c). ((2a)-(2b):$p<0.01,r=0.051$; (2a)-(2c):$p<0.001,r=0.13$; (2b)-(2c):$p<0.001,r=0.080$) Multiple comparisons of the positional alignment error when there were four users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found in all pairs, (2a)-(2b), (2a)-(2c), and (2b)-(2c). ((2a)-(2b):$p<0.01,r=0.058$; (2a)-(2c):$p<0.001,r=0.15$; (b)-(c):$p<0.001,r=0.089$) These results indicate that the position alignment error is $(2a)<(2b)<(2c)$, thus supporting the working hypothesis WH-4.

Figure 8

Figure 8. Positional alignment error.

Table 4 indicates the angular alignment error in combining the potential field conditions and the number of simulated user conditions. The Harrison-Kanji test, which corresponds to a two-factor analysis of variance for angle data, was conducted on angular alignment error when the target point was reached in VR space. Significant differences were found for the main effect of the number of people who experienced the VR$({\chi }^2(4)=144.39,p<0.001,\varphi =0.10)$, and the main effect of the applied method$({\chi }^2(4)=84.00,p=0.26,\varphi =0.080)$, respectively. No significant differences were found in the interaction effects$({\chi }^2(4)=2.32,p=0.81,\varphi =0.013)$. The null hypothesis was rejected when the Kuiper test was conducted to test the normality of the angular data for the angular alignment error when there were two users. Therefore, multiple comparisons using Rao’s Equal Variance Test were conducted between the applied methods with the $p$ value corrected by the Holm method and significant differences were found in all pairs, (2a)-(2b), (2a)-(2c), and (2b)-(2c) ((2a)-(2b):$p<0.05,H_1=4.41$; (2a)-(2c):$p<0.001,H_1=21.75$; (2b)-(2c):$p<0.05,H_1=5.98$). The null hypothesis was rejected when the Kuiper test was conducted to test the normality of the angular data for the angular alignment error when there were three users. Therefore, multiple comparisons using Rao’s Equal Variance Test were conducted between the applied methods with the $p$ value corrected by the Holm method, and significant differences were found in all pairs, (2a)-(2b), (2a)-(2c), and (2b)-(2c) ((2a)-(2b):$p<0.01,H_1=6.92$; (2a)-(2c):$p<0.001,H_1=21.22$; (2b)-(2c):$p<0.05,H_1=4.025$). The null hypothesis was rejected when the Kuiper test was conducted to test the normality of the angular data for the angular alignment error when there were four users. Therefore, multiple comparisons using Rao’s Equal Variance Test were conducted between the applied methods with the $p$ value corrected by the Holm method and significant differences were found between (2a)-(2b) and (2a)-(2c) ((2a)-(2b):$p<0.001,H_1=11.30$; (2a)-(2c):$p<0.05,H_1=5.58$; (2b)-(2c):$p=0.26,H_1=1.27$). These results indicate that the angle error is $(2a)<(2b)<(2c)$ except for the 4-user condition, which partially supports the working hypothesis WH-5.

Table 4

Table 4. Angular alignment error.

Figure 9 indicates the number of reset operations in the combination of the potential field conditions and the number of simulated user conditions. The Lillefors test was conducted as a normality test on the number of resets, and the null hypothesis was rejected. A two-factor analysis of variance was conducted after applying the ART, and significant differences were found for the main effect of the number of users$(F(\mathrm{2,13127})=14.61,p<0.001,partial{\eta }^2=0.0022)$, and the main effect of the applied method$(F(\mathrm{2,13127})=4.09,p<0.001,partial{\eta }^2=6.2\times 10^{-4})$, and the interaction effects$(F(\mathrm{4,13127})=3.90,p<0.001,partial{\eta }^2=0.0012)$, respectively. Multiple comparisons of the number of resets when there were two users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (2a)-(2c). ((2a)-(2b):$p=0.25,r=0.022$; (2a)-(2c):$p<0.01,r=0.049$; (2b)-(2c):$p=0.17,r=0.026$) Multiple comparisons of the number of resets when there were three users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and significant differences were found between (2a)-(2c), and (2b)-(2c). ((2a)-(2b):$p=0.90,r=0.023$; (2a)-(2c):$p<0.01,r=0.046$; (2b)-(2c):$p<0.05,r=0.044$) Multiple comparisons of the number of resets when there were four users, using the Mann-Whitney U test, with the $p$ value corrected by the Holm method, were performed between the applied methods, and no significant differences were found in any pairs. ((2a)-(2b):$p=0.58,r=0.010$; (2a)-(2c):$p=0.11,r=0.030$; (2b)-(2c):$p=0.26,r=0.020$) These results indicate that the number of resets was significant $(2a)<(2c)$ except for the 4-user condition, but the working hypothesis WH-6 is not supported because $(2a)<(2b)<(2c)$ was not observed in any of the conditions.

Figure 9

Figure 9. Number of resets.

5.6 Discussion

In this experiment, as in Experiment 1, the superiority of condition (2a), where the distance between the center of the vector potential and the target is close, was observed.

Issues resulting from this experiment are as follows. The first issue is that this experiment was limited to a comparison between the proposed methods and did not directly compare them with the control condition. The reason for not adopting the control condition is that the RDW code that allows user interaction is not publicly available. In a previous study that is relatively close to the configuration of this experiment, (Min et al., 2020) reported that in a physical environment of 10 m square, the number of reset operations is 2.307 (SD = 1.365) for what they define as a recovery scenario and 1.481 (SD = 1.828) for a non-recovery scenario. Although the previous study used overt recovery in addition to subtle trajectory corrections and a different definition of the range of interactive areas, and therefore cannot be directly compared to the results of this study, the average number of resets 2.15 (SD = 0.986) times obtained from the simulations in this study and the number of resets in the previous study are not numerical significant different the number of resets in the previous study.

The second issue is that, as in Experiment 1, there are cases where trials cannot be completed. From this experiment, it is considered that the smaller the physical space, the greater the number of reset operations and the greater the possibility of deadlocks. Further improvement of this method is required to enable interaction without the risk of deadlock.

The third issue is an average error of about 2 m in the relative positions at the end of the task. The reasons for this error include the accuracy of the simulation and the execution time. As mentioned in the 3.2.1 section, the programs used in the simulation of the proposed method are processing at regular time intervals because they employ recursive processing, A* algorithm, and other processing-intensive programs. Therefore, handling users who move in real-time may have been difficult. Therefore, there is room for reconsideration of the simulation, such as using a different method.

In this study, we employed simulation experiments to explore the feasibility and stability of the proposed multi-user RDW method under constrained physical spaces. While simulations allowed us to systematically test parameter settings and interaction scenarios, we acknowledge that real-world factors—such as individual gait patterns, hardware-induced discomfort, and potential tracking errors—could influence the method’s effectiveness. Therefore, we plan to conduct controlled user studies in a 10 m $\times$ 10 m lab environment, enabling participants to walk, interact, and communicate in real time. These follow-up experiments will measure immersion levels, perceived naturalness of interaction, and physical safety to validate the practicality of AVF-RDW in real-world conditions.

Moreover, the proposed approach integrates walking-path search (e.g., A* algorithm) and repeated recalculation of artificial vector potentials, which can be computationally intensive for large user groups or high-frequency updates. To address real-time constraints, we are investigating two possible directions: 1) reducing the frequency of pathfinding by dynamically detecting when the user’s heading or target location remains consistent, and 2) using machine learning—particularly reinforcement learning—to optimize redirection parameters without exhaustive searches. Future work will also explore hardware-accelerated solutions (e.g., GPU-based parallelization) to further reduce latency.

6 Future work

Future issues to be addressed are as follows. The first step is to validate the proposed method through user studies. Since no user studies were conducted under the same conditions as the simulation experiments in this study, verifying the method’s usefulness in a real environment is necessary.

Although simulation experiments in this study partially confirmed the method’s usefulness, there are cases where the guidance does not reach a position and posture where interaction is possible, and further accuracy is needed. There are two main policies to improve this point: Method optimization. The method only introduces vector potentials on a trial basis and partially discusses optimizing their form or parameters. The method’s accuracy will be improved if the optimal form of vector potentials is formulated and the optimal arrangement of potentials and parameters is derived. Second, the simulation process used in this method employs recursive processing, which is very demanding for computational resources. Therefore, the frequency of simulation runs and the granularity of route branches in the walking search within the simulation are set to be highly constrained by computational resources. Developing an algorithm that more efficiently utilizes computational resources would improve accuracy by speeding up the response time of the simulation.

In addition, interaction in more complex real-world environments should also be discussed. In this study’s experimental environment, we did not test interaction in an environment with complex maps, such as obstacles and mazes in physical and virtual spaces. We also did not consider cases where the objects to interact with move independently or where more than three people interact.

7 Conclusion

In this study, we proposed a novel method for guiding the user in matching the relative position and posture of the target point in real and virtual spaces. We added a target point represented by artificial vector potentials to existing methods for realizing physical interaction. The proposed method is compared with existing methods in three different patterns with different parameters in two simulation experiments. The proposed method improved the accuracy of interaction in RDW compared to existing methods. It verified the interaction under the application of RDW when three or more people share a VR experience in a real or virtual space, which has not been done in previous studies. Although the proposed method needs further improvement, these results are expected to promote further research on interaction in RDW.

As this research suggests, the feasibility of interaction in RDW using artificial vector potentials has increased the possibility of easily available interactive VR experiences involving two or more users. Thus, this proposal will further enrich locomotion VR experiences in the future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SR: Software, Investigation, Methodology, Writing–original draft. KM: Conceptualization, Funding acquisition, Methodology, Writing–original draft, Writing–review and editing. TN: Supervision, Funding acquisition, Writing–review and editing. HK: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by JSPS KAKENHI Grant Number JP22K17929,JP22H03628, and JP23K24884.

Acknowledgments

In this paper, DeepL 24.11.21416769 was used for some parts of the English translation and proofreading.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://hello.vrchat.com

²https://www.oculus.com/horizon-worlds

³https://docs.unity3d.com/2019.4/Documentation/Manual/class-NavMeshAgent.html

References

Bachmann, E. R., Hodgson, E., Hoffbauer, C., and Messinger, J. (2019). Multi-user redirected walking and resetting using artificial potential fields. IEEE Trans. Vis. Comput. Graph. 25 (5), 2022–2031. doi:10.1109/tvcg.2019.2898764

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, L.-P., Roumen, T., Rantzsch, H., Köhler, S., Schmidt, P., Kovacs, R., et al. (2015). “Turkdeck: physical virtual reality based on people,” in Proceedings of the 28th annual ACM symposium on user interface software & Technology, 417–426.

Google Scholar

Dong, T., Shen, Y., Gao, T., and Fan, J. (2021). “Dynamic density-based redirected walking towards multi-user virtual environments,” in 2021 IEEE virtual reality and 3D user interfaces (VR) (IEEE), 626–634.

CrossRef Full Text | Google Scholar

Grechkin, T., Thomas, J., Azmandian, M., Bolas, M., and Suma, E. (2016). “Revisiting detection thresholds for redirected walking: combining translation and curvature gains,” in Proceedings of the ACM Symposium on applied perception, SAP ’16 (New York, NY, USA: Association for Computing Machinery), 113–120.

Google Scholar

Hodgson, E., and Bachmann, E. (2013). Comparing four approaches to generalized redirected walking: simulation and live user data. IEEE Trans. Vis. Comput. Graph. 19 (4), 634–643. doi:10.1109/tvcg.2013.28

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffman, H. G. (1998). “Physically touching virtual objects using tactile augmentation enhances the realism of virtual environments,” in Proceedings. IEEE 1998 virtual reality annual international symposium (cat. No. 98CB36180) (IEEE), 59–63.

Google Scholar

Interrante, V., Ries, B., and Anderson, L. (2007). “Seven league boots: a new metaphor for augmented locomotion through moderately large scale immersive virtual environments,” in 2007 IEEE symposium on 3D user interfaces (IEEE).

Google Scholar

Kohli, L., Burns, E., Miller, D., and Fuchs, H. (2005). “Combining passive haptics with redirected walking,” in Proceedings of the 2005 international conference on Augmented tele-existence, 253–254.

Google Scholar

Langbehn, E., Lubos, P., Bruder, G., and Steinicke, F. (2017). Bending the curve: sensitivity to bending of curved paths and application in room-scale vr. IEEE Trans. Vis. Comput. Graph. 23 (4), 1389–1398. doi:10.1109/tvcg.2017.2657220

PubMed Abstract | CrossRef Full Text | Google Scholar

Langbehn, E., Paulmann, H., Briddigkeit, D., Barnes, M., Husung, M., Kirsch, K., et al. (2020). “Frozen factory: a playful virtual experience for multiple co-located redirected walking users,” in SIGGRAPH asia 2020 XR, 1–2.

Google Scholar

Lee, D.-Y., Cho, Y.-H., and Lee, I.-K. (2019). “Real-time optimal planning for redirected walking using deep q-learning,” in 2019 IEEE conference on virtual reality and 3D user interfaces (VR) (IEEE), 63–71.

Google Scholar

Lee, D.-Y., Cho, Y.-H., Min, D.-H., and Lee, I.-K. (2020). “Optimal planning for redirected walking based on reinforcement learning in multi-user environment with irregularly shaped physical space,” in 2020 IEEE conference on virtual reality and 3D user interfaces (VR) (IEEE), 155–163.

Google Scholar

Li, Y.-J., Steinicke, F., and Wang, M. (2022). A comprehensive review of redirected walking techniques: taxonomy, methods, and future directions. J. Comput. Sci. Technol. 37 (3), 561–583. doi:10.1007/s11390-022-2266-7

CrossRef Full Text | Google Scholar

Li, Y.-J., Wang, M., Steinicke, F., and Zhao, Q. (2021). “Openrdw: a redirected walking library and benchmark with multi-user, learning-based functionalities and state-of-the-art algorithms,” in 2021 IEEE international symposium on mixed and augmented reality (ISMAR) (IEEE), 21–30.

Google Scholar

Matsumoto, K., Hashimoto, T., Mizutani, J., Yonahara, H., Nagao, R., Narumi, T., et al. (2017). “Magic table: deformable props using visuo haptic redirection,” in SIGGRAPH asia 2017 emerging technologies, 1–2.

Google Scholar

Messinger, J., Hodgson, E., and Bachmann, E. R. (2019). “Effects of tracking area shape and size on artificial potential field redirected walking,” in 2019 IEEE conference on virtual reality and 3D user interfaces (VR), 72–80.

Google Scholar

Min, D.-H., Lee, D.-Y., Cho, Y.-H., and Lee, I.-K. (2020). “Shaking hands in virtual space: recovery in redirected walking for direct interaction between two users,” in 2020 IEEE conference on virtual reality and 3D user interfaces (VR) (IEEE), 164–173.

Google Scholar

Nagao, R., Matsumoto, K., Narumi, T., Tanikawa, T., and Hirose, M. (2018). Ascending and descending in virtual reality: simple and safe system using passive haptics. IEEE Trans. Vis. Comput. Graph. 24, 1584–1593. doi:10.1109/tvcg.2018.2793038

PubMed Abstract | CrossRef Full Text | Google Scholar

Nescher, T., Huang, Y.-Y., and Kunz, A. (2014). “Planning redirection techniques for optimal free walking experience using model predictive control,” in 2014 IEEE symposium on 3D user interfaces (3DUI) (IEEE), 111–118.

Google Scholar

Peck, T. C., Fuchs, H., and Whitton, M. C. (2009). Evaluation of reorientation techniques and distractors for walking in large virtual environments. IEEE Trans. Vis. Comput. Graph. 15 (3), 383–394. doi:10.1109/tvcg.2008.191

PubMed Abstract | CrossRef Full Text | Google Scholar

Razzaque, S. (2005). “Redirected walking,” in PhD thesis. Chapel Hill, NC, USA: University of North Carolina at Chapel Hill.

Google Scholar

Razzaque, S., Kohn, Z., and Whitton, M. (2001). “Redirected walking,” in Eurographics 2001 - Short Presentations. Eurographics Association. doi:10.2312/egs.20011036

CrossRef Full Text | Google Scholar

Sakono, H., Matsumoto, K., Narumi, T., and Kuzuoka, H. (2021). Redirected walking using continuous curvature manipulation. IEEE Trans. Vis. & Comput. Graph. 27 (11), 4278–4288. doi:10.1109/tvcg.2021.3106501

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinicke, F., Bruder, G., Kohli, L., Jerald, J., and Hinrichs, K. (2008a). “Taxonomy and implementation of redirection techniques for ubiquitous passive haptic feedback,” in 2008 international conference on cyberworlds (IEEE), 217–223.

Google Scholar

Steinicke, F., Bruder, G., Ropinski, T., and Hinrichs, K. (2008b). “Moving towards generally applicable redirected walking,” in Proceedings of the virtual reality international conference (VRIC) (IEEE), 15–24.

Google Scholar

Suma, E. A., Azmandian, M., Grechkin, T., Phan, T., and Bolas, M. (2015). “Making small spaces feel large: infinite walking in virtual reality,” in ACM SIGGRAPH 2015 emerging technologies, 1.

Google Scholar

Suma, E. A., Bruder, G., Steinicke, F., Krum, D. M., and Bolas, M. (2012a). “A taxonomy for deploying redirection techniques in immersive virtual environments,” in 2012 IEEE virtual reality workshops (VRW) (IEEE), 43–46.

Google Scholar

Suma, E. A., Clark, S., Krum, D., Finkelstein, S., Bolas, M., and Warte, Z. (2011). “Leveraging change blindness for redirection in virtual environments,” in 2011 IEEE virtual reality conference (IEEE), 159–166.

Google Scholar

Suma, E. A., Lipps, Z., Finkelstein, S., Krum, D. M., and Bolas, M. (2012b). Impossible spaces: maximizing natural walking in virtual environments with self-overlapping architecture. IEEE Trans. Vis. Comput. Graph. 18 (4), 555–564. doi:10.1109/tvcg.2012.47

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, J., Hutton Pospick, C., and Suma Rosenberg, E. (2020). “Towards physically interactive virtual environments: reactive alignment with redirected walking,” in 26th ACM symposium on virtual reality software and Technology, 1–10.

Google Scholar

Thomas, J., and Rosenberg, E. S. (2019). “A general reactive algorithm for redirected walking using artificial potential functions,” in 2019 IEEE conference on virtual reality and 3D user interfaces (VR) (IEEE), 56–62.

Google Scholar

Williams, B., Narasimham, G., Rump, B., McNamara, T. P., Carr, T. H., Rieser, J., et al. (2007). “Exploring large virtual environments with an hmd when physical space is limited,” in Proceedings of the 4th symposium on Applied perception in graphics and visualization, 41–48.

Google Scholar

Zmuda, M. A., Wonser, J. L., Bachmann, E. R., and Hodgson, E. (2013). Optimizing constrained-environment redirected walking instructions using search techniques. IEEE Trans. Vis. Comput. Graph. 19 (11), 1872–1884. doi:10.1109/tvcg.2013.88

PubMed Abstract | CrossRef Full Text | Google Scholar