Commentary: MSH3 homology and potential recombination link to SARS-CoV-2 furin cleavage site

A commentary on
MSH3 Homology and potential recombination link to SARS-CoV-2 furin cleavage site.

By Ambati BK, Varshney A, Lundstrom K, Palú G, Uhal BD, Uversky VN and Brufsky AM (2022) Front. Virol. 2:834808. doi: 10.3389/fviro.2022.834808

Introduction

Coronaviruses are characterized by the spike glycoprotein, which consists of two domains: S1, which binds to angiotensin-converting enzyme 2 (ACE2) receptors on the host cell, and S2, which drives membrane fusion. A 12-nucleotide insertion (i.e., 5′-CCTCGGCGGCGA-3′) that codes a furin cleavage site (FCS) between S1 and S2 has been discovered in SARS-CoV-2 (1). FCS insertion at the S1–S2 junction is unique among known sarbecoviruses (SARS-CoV-2 subgenus) and offers a functional advantage (2). FCS presence is surprising, and its origin is debated. Ambati et al. (3) reported a sequence homology between SARS-CoV-2 FCS and the negative strand of a patented sequence, with a coincidence probability of 3.21 × 10⁻¹¹. Therefore, the authors suggested that the SARS-CoV-2 FCS could originate from a copy choice recombination in human cells in the context of viral research. This scenario is molecularly possible, but the computed coincidence probability may be erroneous.

Irrelevant probability and a posteriori information for a priori computation

The authors computed the probability of randomly finding the FCS pattern in a database of patented sequences and in a viral genome, such as SARS-CoV-2. This probability is irrelevant, as the authors decided to search for this pattern because it appeared in SARS-CoV-2. Hence, to assess if their finding could be due to chance, they should have computed the probability of finding the FCS pattern in only the database they queried, given that the appearance of the FCS in SARS-CoV-2 was the starting point.

In addition, instead of computing the probability of finding the 12-nucleotide pattern coding for the FCS identified a priori (before the BLAST research), the authors computed the probability of finding the 19-nucleotide 5′-CTCCTCGGCGGGCACGTAG-3′ pattern. This latter pattern is the original pattern extended by two nucleotides before and five nucleotides after the FCS. It corresponds to the extended homology that they found between SARS-CoV-2 and the patented sequence, which is, therefore, a posteriori information (after the BLAST research). To correctly consider the expandability of their homology, they should have computed the probability of finding one of the eight possible 19-nucleotide-long extensions without presuming its form: 5′-TAATTCTCCTCGGCGGGCA-3′, 5′-AATTCTCCTCGGCGGGCAC-3′, 5′-ATTCTCCTCGGCGGGCACG-3′, 5′-TTCTCCTCGGCGGGCACGT-3′, 5′-TCTCCTCGGCGGGCACGTA-3′, CTCCTCGGCGGGCACGTAG-3′, 5′-TCCTCGGCGGGCACGTAGT-3′, and 5′-CCTCGGCGGGCACGTAGTG-3′.

Finally, the reported match is on the negative strand of the patented sequence identified. This indicates that matches with the pattern’s reverse complement are also considered a discovery. Hence, they should have computed the probability of finding one of the eight possible extensions or one of their reverse complements (i.e., 16 patterns) in the queried database.

Probability to find patterns of length m in a sequence of length n

The authors computed the probability of finding a pattern (e.g., 5′-CTCCTCGGCGGGCACGTAG-3′) of length m in a sequence of length n as: $\left(n - m + 1\right){\left(\frac{1}{4}\right)}^m$.

This formula is inexact; as an illustration, let us compute the probability of finding the CG pattern (m = 2) among the 256 sequences of length n = 4 . Using the above-mentioned formula, 48 occurrences of the CG pattern are counted (16 occurrences for each sequence structure XXCG, XCGX, and CGXX). However, the number of sequences containing CG is not 48. Indeed, the sequence CGCG is counted twice: in both XXCG and CGXX structures. Therefore, the formula used by Ambati et al. leads to a probability of 48/256 = 18.75%, whereas the correct probability is 47/256 = 18.36%. If we assume, as the authors did, equal nucleotide frequencies and independence between nucleotides (memory-less sequence), the probability of finding a given pattern can be computed using a Markov chain model with one absorbing state (see Figure 1 illustrating the above-mentioned example).

FIGURE 1

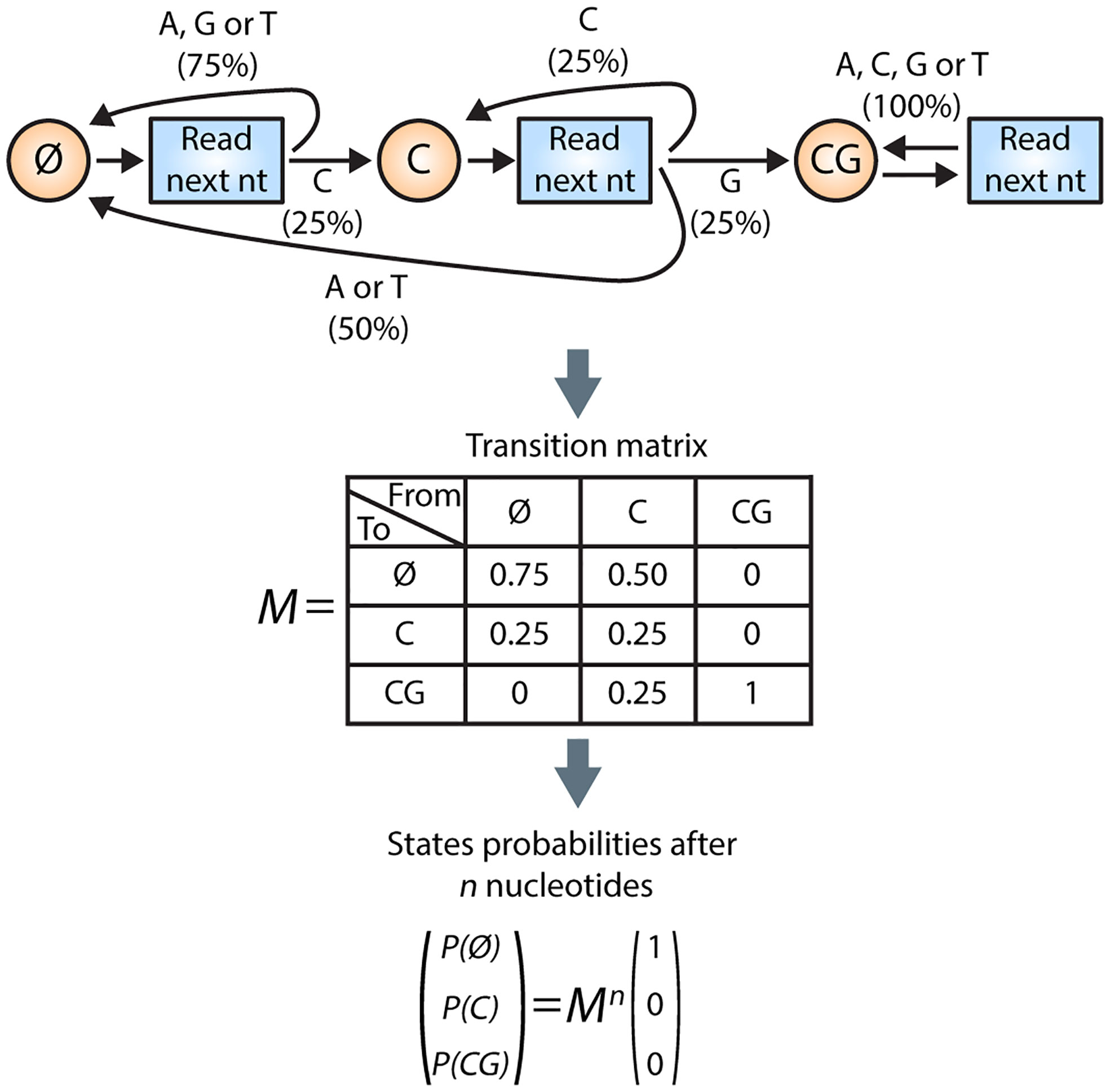
Figure 1 Illustration of a Markov chain to compute the probability to find the CG pattern in a sequence of length n . The Markov chain for this basic example contains three states: Ø, C, and CG. The chain starts in the Ø state and will read the nucleotides (nts) one by one. From state Ø, there is a 75% chance that the next nucleotide will not match the first nucleotide of the CG pattern. Therefore, from Ø state, the probability of reaching state C is only 25%, whereas the probability of remaining in state Ø is 75%. From state C, reading the next nucleotide gives three options (1): the next nucleotide is a G, leading to the CG state (with a probability of 25%) (2); the next nucleotide is again a C, i.e., we remain in the C state (with a probability of 25%); or (3) the next nucleotide is neither a C nor a G, resulting in a return to the Ø state (with a probability of 50%). When the CG state is reached, the pattern is found and, even if next nucleotides can be read, the chain is blocked in the CG state, a so-called absorbing state. This chain can be mathematically summarized by a transition matrix M. The probability of the three states after reading n nucleotides is given by the transition matrix at the power n multiplied by the initial conditions. Code to reproduce this basic example and the computation for the 19 nucleotides pattern is avalaible on OSF (https://osf.io/wsd5g/?view_only=0af888d0d29d452fa5dcb9cf769ae229).

This methodology can be extended to compute the probability of finding one of the 16 patterns using a Markov chain model with 16 absorbing states. Using the authors’ parameters (n = 3300), we found a probability of  1.49 × 10⁻⁷ , approximately 10 times higher than the probability obtained by Ambati et al. (1.19 × 10⁻⁸).

Search for a pattern in a large database

During their BLAST search, the authors queried a database of L = 24,712 sequences for the pattern that they had identified (5′-CTCCTCGGCGGGCACGTAG-3′). They approximated this experience as a binomial trial (statistically independent Bernoulli trials, with a success probability of p = 1.19 × 10⁻⁸ repeated 24,712 times) and computed the probability of finding exactly one sequence containing the pattern as L × p × (1 − p)^L − 1 . Several limitations can be reported:

1. This method assumes that all sequences in the database are independent.

2. It assumes that all sequences are 3330 nucleotides long.

3. It neglects the possibility of finding more than one sequence containing the pattern that they were looking for. The appropriate formula is 1 − (1 − p)^L .

4. They should have considered the other possible extensions of the pattern and their reverse complement, leading to a success probability of  p = 1.49 × 10⁻⁷ .

The actualized computation performed under assumptions 1 and 2 leads to a final coincidence probability of 0.0037 (rather than 3.21 × 10⁻¹¹).

Lacking information regarding the database

The authors did not provide information regarding the sequence length distribution in their database, except that the median length was 3,300. In addition, they did not indicate whether or not their computation is robust when assumption 2 is not met. To assess the robustness of the computations, we simulated several databases with a median length set at 3,300 nucleotides but with different distribution shapes for sequence lengths. The results indicated that the distribution did not substantially affect the final probability so long as the median length was kept constant.

Unfortunately, the authors did not provide details of their BLAST research. The patent database that they used contained 24,712 sequences. Yet, by querying BLAST, we obtained a database of 46,121,617 patent sequences with an average length of 560 nucleotides. The authors should give more details and justification for their query, especially if they queried the full database but a posteriori restricted their computation. Of note, with such a large database, and despite the fact that the average sequence length decreased, the probability of finding at least one sequence containing one of the 16 patterns previously mentioned may rise to 68% under assumption 2.

Conclusion

Epidemiological studies support the conclusion that the SARS-CoV-2 pandemic originated in Huanan market, and was not the product of a laboratory accident (4–6). Moreover, Sarbecovirus phylogeny is still sparsely known, and the sequencing of new SARS-CoV-2 relatives could help us to understand the emergence of the FCS (2, 4). According to the current phylogeny, FCS appeared independently six times in the Betacoronavirus lineages, demonstrating that FCS insertion is compatible with natural evolution (2, 7, 8). The probabilities provided by Ambati et al. seem inexact, and their BLAST search is not transparent enough. Based on our computations and BLAST research, the role of chance in this homology should not be dismissed.

Author contributions

HL and YD contributed equally in the methodological considerations, probabilities computation, and the writing of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

HL work was supported by an ARC (Association pour la Recherche sur le Cancer) PhD fellowship and a FRM (Fondation Recherche Médicale) PhD extension fellowship. YD received a national grant from the French Ministry of Higher Education, Research and Innovation.

Acknowledgments

We are grateful to Véronique Sébille for putting the authors in contact, setting up this collaboration.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Coutard B, Valle C, de Lamballerie X, Canard B, Seidah NG, Decroly E. The spike glycoprotein of the new coronavirus 2019-nCoV contains a furin-like cleavage site absent in CoV of the same clade. Antiviral Res (2020) 176:104742. doi: 10.1016/j.antiviral.2020.104742

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Chan YA, Zhan SH. The emergence of the spike furin cleavage site in SARS-CoV-2. Mol Biol Evol (2022) 39(1):msab327. doi: 10.1093/molbev/msab327

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ambati BK, Varshney A, Lundstrom K, Palú G, Uhal BD, Uversky VN, et al. MSH3 homology and potential recombination link to SARS-CoV-2 furin cleavage site. Front Virol (2022) 2. doi: 10.3389/fviro.2022.834808

CrossRef Full Text | Google Scholar

4. Holmes EC, Goldstein SA, Rasmussen AL, Robertson DL, Crits-Christoph A, Wertheim JO, et al. The origins of SARS-CoV-2: A critical review. Cell. (2021) 184(19):4848–56. doi: 10.1016/j.cell.2021.08.017

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Gao G, Liu W, Liu P, Lei W, Jia Z, He X, et al. Surveillance of SARS-CoV-2 in the environment and animal samples of the huanan seafood market. Res Square (2022). doi: 10.21203/rs.3.rs-1370392/v

CrossRef Full Text | Google Scholar

6. Worobey M, Levy JI, Malpica Serrano L, Crits-Christoph A, Pekar JE, Goldstein SA, et al. The Huanan seafood wholesale market in Wuhan was the early epicenter of the COVID-19 pandemic. Science (2022) 377(6609):951–9. doi: 10.1126/science.abp8715

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wu Y, Zhao S. Furin cleavage sites naturally occur in coronaviruses. Stem Cell Res (2021) 50:102115. doi: 10.1016/j.scr.2020.102115

CrossRef Full Text | Google Scholar

8. Sander A-L, Moreira-Soto A, Yordanov S, Toplak I, Balboni A, Ameneiros RS, et al. Genomic determinants of furin cleavage in diverse European SARS-related bat coronaviruses. BioRxiv (2021) 12:15 472779. doi: 10.1101/2021.12.15.472779

CrossRef Full Text | Google Scholar