A hierarchical model-based framework for evaluating probabilities of area-wide freedom from lymphatic filariasis infection based on sentinel site surveillance data

The design of population surveys to substantiate the elimination of disease transmission across large implementation units (IUs) has become important as many parasite control efforts approach their final stages. This is especially true for the global program to eliminate lymphatic filariasis (LF), which has successfully reduced infection prevalence in many endemic countries, such that the focus has shifted to how best to determine that the area-wide elimination of this macroparasitic disease has been achieved. The WHO has recommended a two-stage lot quality assurance sampling (LQAS) framework based on sampling children from selected clusters within an IU, called the Transmission Assessment Survey (TAS), for supporting such decision-making, but questions have emerged regarding the reliability of this strategy for assessing if LF transmission is broken effectively everywhere within an area. In this study, we develop and describe an alternative probabilistic framework that combines infection status information from longitudinal parasitological surveys of whole communities carried out in sentinel sites, imperfect diagnostic tests, and locally-applicable extinction thresholds predicted by transmission models, to overcome the problems associated with TAS. We applied the framework to LF infection and intervention data from the country of Malawi, and demonstrated how our hierarchical coupled model-sentinel site survey tool can be used to estimate the probability that LF transmission has occurred at the individual survey, village, and countrywide scales. We also further demonstrated how the framework can be used in conjunction with zonal or areal design prevalences to estimate the number of sentinel sites and durations of interventions required to acquire sufficiently high confidence that an area is free from infection. Our results indicate that the application of the spatially driven model-data freedom-from-infection tool developed here to follow up data from high-risk sentinel sites in a region may offer a highly cost-effective framework for guiding the making of high-fiducial and defensible area-wide LF intervention stopping decisions.

1 Introduction

A key development in reducing the burden of global diseases over the past two decades has been the construction and implementation of large-scale disease-specific interventions aimed at achieving the elimination of the major tropical parasitic diseases that have long afflicted populations in the Global South (1–5). The combining and indeed initiating of new financing models, strengthening of supply chains, and management of mass drug administration (MDA) with advances in biotechnological tools, including in the areas of drug development and diagnostic techniques (4, 6), by global programs designed and led by the WHO have led to significant reductions in the prevalence of many of these so-called “neglected tropical diseases” (7). Indeed, one outcome of this success has been the inclusion of ending the health impacts of these diseases as a critical component of the broader development agenda, including for meeting many of the proposed Sustainable Development Goals (SDGs) (4, 8). A particularly successful program in this regard is the Global Programme to Eliminate Lymphatic Filiariasis (GPELF), a debilitating mosquito-borne macroparasitic disease that, prior to the start of nationwide MDAs in 2000, was thought to have infected between 174 and 234 million individuals in 73 countries worldwide (9). By 2019, owing to more than 8.6 billion cumulative mass drug treatments delivered to the at-risk populations of these countries, the worldwide infection prevalence of this disease had declined by an impressive degree to 51 million, with 692 million people no longer thought to require further preventive treatments (10).

Although the progress made by the GPELF in reducing the worldwide prevalence and corresponding risk of infection in populations in which this disease is endemic is notable, questions have been raised regarding how best to determine disease elimination status and thus make reliable intervention termination decisions (11–15). The WHO currently recommends an epidemiological assessment strategy that involves conducting a series of infection surveys (based on either microfilaria (mf) or circulating antigen (CFA) indicators of infection) of entire communities in sentinel and randomly selected spot check sites initially, and subsequently of children aged 6–7 years surveyed from treated communities, to provide evidence for deciding if disease transmission has been interrupted in an implementation unit (IU), normally a district, so that IU-wide MDA stopping decisions can be made (16). The first survey in this strategy, termed the pre-Transmission Assessment Survey (pre-TAS), is to be conducted in all of the sentinel and spot check sites of IUs that have had at least five effective (> 65% coverage) rounds of annual MDA to evaluate if the community-level prevalence of mf and CFA are < 1% or 2%, respectively. If either of these targets is met in all the surveyed communities, then an IU can move into the surveillance phase, which involves carrying out a series of three subsequent longitudinal surveys of approximately 1,500 children belonging to the above ages sampled from across population clusters in an IU (17). At each of these follow-up surveys, the number of children who test positive for infection is evaluated against a predetermined cutoff value thought to represent the minimum average prevalence below which LF transmission is presumed to be unsustainable across the entire IU. If the infection prevalence falls below the set threshold in the first TAS (TAS 1), then annual MDA is stopped, and the IU is resurveyed two additional times (TAS2 and TAS3) over a 5-year period as part of post-MDA surveillance. An IU is deemed to have eliminated LF as a public health problem once all three TAS surveys are passed (16).

Although the above TAS strategy for guiding MDA stopping decisions has been followed by national LF programs since 2011, the methodology has increasingly come under scrutiny because of instances in which some IUs that initially were shown to pass TAS have reported recrudescence of infection following cessations of MDA (11, 18–23). Several factors leading to failures in using TAS for making reliable assessments of transmission breakage have recently been highlighted (20), raising questions regarding the possibility of reliably evaluating the achievement of LF elimination using the current TAS methods (13, 15, 24). First, the mounting empirical evidence from the field (11, 14, 18–25) and results from modeling studies (13, 26–29) have called into question whether meeting the TAS stopping criteria (crossing below the 1% mf or 2% CFA threshold) would indeed signify the breakage of LF transmission (indicated by CFA or mf prevalence remaining below 1% or 0.5%, respectively, in the sampled child subpopulation) in a community. Apart from the validity issue inherent to using the currently set threshold values for signifying the elimination of community transmission, a key topic also raised by these studies alludes to the likelihood of the occurrence of site-to-site variation in the elimination thresholds connected with LF transmission (26–28, 30–32). The variation in infection prevalence between survey sites is a major feature of LF transmission in a region, but this outcome is not accommodated for by the recommendation that a single area-wide target elimination threshold be used for classifying IUs equally everywhere in the current TAS-based MDA stopping methodology. Ignoring such heterogeneity in the present TAS methodology means that it is possible to classify an IU as having achieved LF elimination even when significant numbers of individual clusters within the IU from which children were sampled may still be transmitting infection (15). This is a critical flaw in the current TAS methodology that may result in false predictions of the achievement of LF transmission interruption throughout an IU or indeed across many different IUs. Furthermore, the strategy of sampling children to assess if transmission interruption has occurred in a community does not take account of prevalence levels in older age groups (13), with recent studies indicating that ignoring such residual infection in the latter groups can result in the maintenance of transmission in the post-MDA setting (23). LF has a long prepatent period (33–35), and therefore has a low prevalence in young children even when its prevalence is high in adults (36); this age-based discrepancy in prevalence will become even more pronounced as prevalence is reduced through MDA. These age-related patterns indicate that surveillance for making MDA stopping decisions may need to consider the use of community-based surveys that entail the sampling of both adults and children to obtain more reliable information regarding the cessation of community transmission (13, 23). Finally, assessments of when infection thresholds are met must also take into account the diagnostic performance (sensitivity and specificity) of the tests used to classify infection status (12, 32, 37). This is because since very few diagnostic tests are perfect, that is, with specificity and sensitivity values < 100%, their use in disease surveys would produce both false-positive and false-negative results, making it impossible to prove that a population is free from disease even with large sample sizes (12). However, as noted previously, if a sufficiently representative number of individuals are surveyed over an area, and the performance of the diagnostic test used and appropriate threshold values are taken into account, then it is possible to show how unlikely it is that a population has continuing infection (12, 38–40).

In an attempt to overcome the challenges with TAS as described above, we recently developed a new probabilistic tool that combines survey-based proof-of-freedom methods incorporating both the effects of sample sizes and imperfect diagnostics with parasite transmission model-estimated infection breakpoint values, and showed how such an integrated model-survey framework can be applied to longitudinal surveillance data on LF prevalence for predicting the probability of achieving infection freedom in a location (12). In this study, we extend the basic approach that focused on single community settings to take account of cluster-level variations in infection or transmission to support the effective making of area-wide freedom declarations. In addition, we focused the application of this method on the sentinel site community-level infection data that are normally collected in countries undergoing LF MDAs until pre-TAS assessments can be conducted to inspect the alternative value of using this type of data for overcoming the issue of the restricted use of child infection information alone in the current TAS protocol. Our focus on sentinel site data is also premised on the expectation that these surveillance sites (at least two per IU) are chosen from areas within an IU of high known transmission (high disease or infection prevalence or vector abundance), have larger sample sizes than the child–age clusters used in the TAS LQAS method, are expected not to be majorly affected by migration, and represent those sites in an IU that are likely to require the longest durations of interventions for interrupting LF transmission (16). Unlike the child-based cluster surveys used in the TAS methodology - in which because of random sampling of children between TAS iterations, persistent high prevalence clusters may not be revisited and thus may be missed during a TAS stage, - the LF sentinel sites are also followed throughout the course of the MDA program. This allows the stable tracking of changes in these high-risk worst-case transmission sites within an IU. While community-based surveys can be operationally more challenging, our results indicate that follow up of fewer sentinel sites coupled with the more reliable information this provides for determining transmission interruption within a region could in fact represent a more cost-effective approach than TAS for guiding the making of high fiducial LF MDA stopping decisions.

2 Methods

2.1 Data

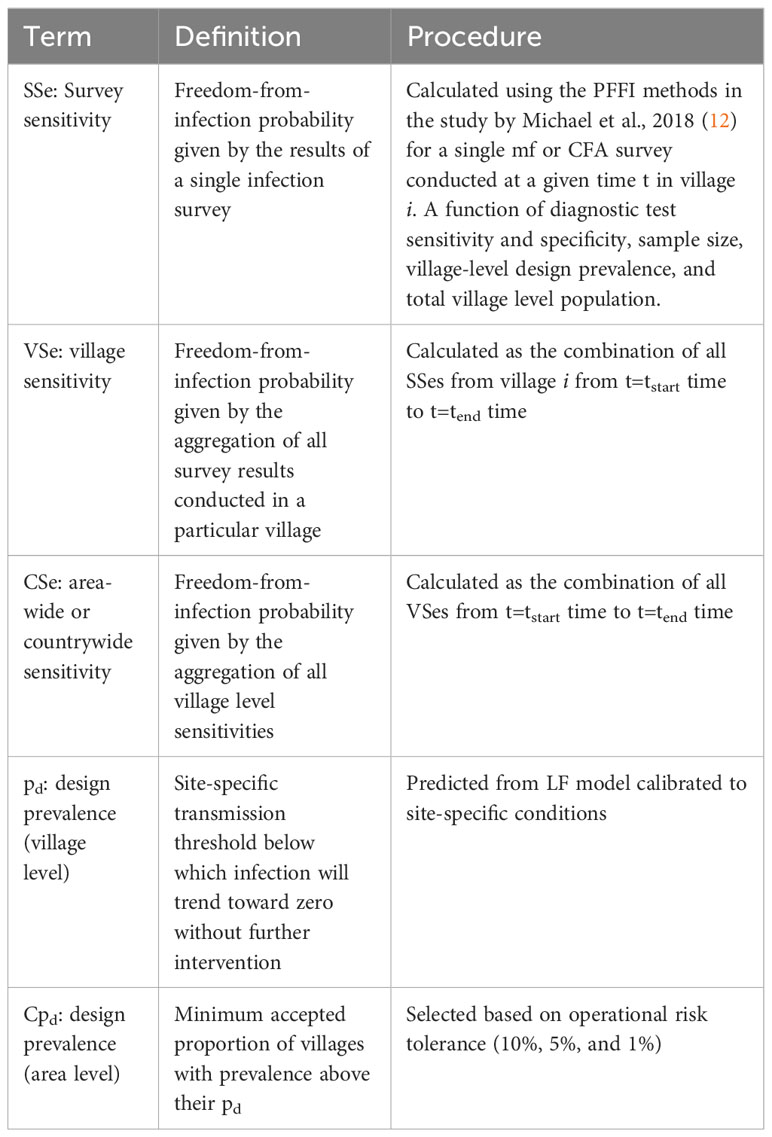
The data used in this research represent the typical sentinel site surveillance data collected by LF countries for the purpose of monitoring changes in infection prevalence due to MDA until the time when pre-TAS assessments are normally carried out (16). In this study, we selected 24 such sentinel sites that had undergone interventions against LF in Malawi for use in the proceeding analysis based on the quality and completeness of the provided data. The World Health Organization (WHO)’s Expanded Special Project for Elimination of Neglected Tropical Diseases (ESPEN) (41) data portal was used to extract microfilariae (mf) and circulating filarial antigen (CFA) survey information for the pre-MDA and MDA intervention periods in each of these 24 sites (Table 1). Mf presence was examined by blood smear (using sample volumes of between 60 µL and 100 µL) and CFA was assessed by the immunochromatographic card test (ICT). Baseline mapping surveys were conducted in Malawi between 2000 and 2003, which showed that baseline CFA prevalences ranged from 0% to 74.47% (Figure 1). Annual MDA with ivermectin and albendazole (IVM+ALB) started in 2008–2009 and continued into 2013, such that each study site received 5–6 rounds of MDA. The corresponding national-level annual MDA coverage information was available from the WHO Preventive Chemotherapy Transmission and Control (PCT) databank (42). In addition to MDA, vector control (VC) measures against the Anopheles mosquitoes responsible for LF transmission were also deployed in Malawi in the form of indoor residual spraying (IRS) and insecticide-treated bed nets (ITNs). We assembled national-level annual IRS and ITN coverage information from the Malaria Atlas Project (43). These MDA, ITN, and IRS coverage data are provided in Table S1 in the Supplementary Information (SI).

TABLE 1

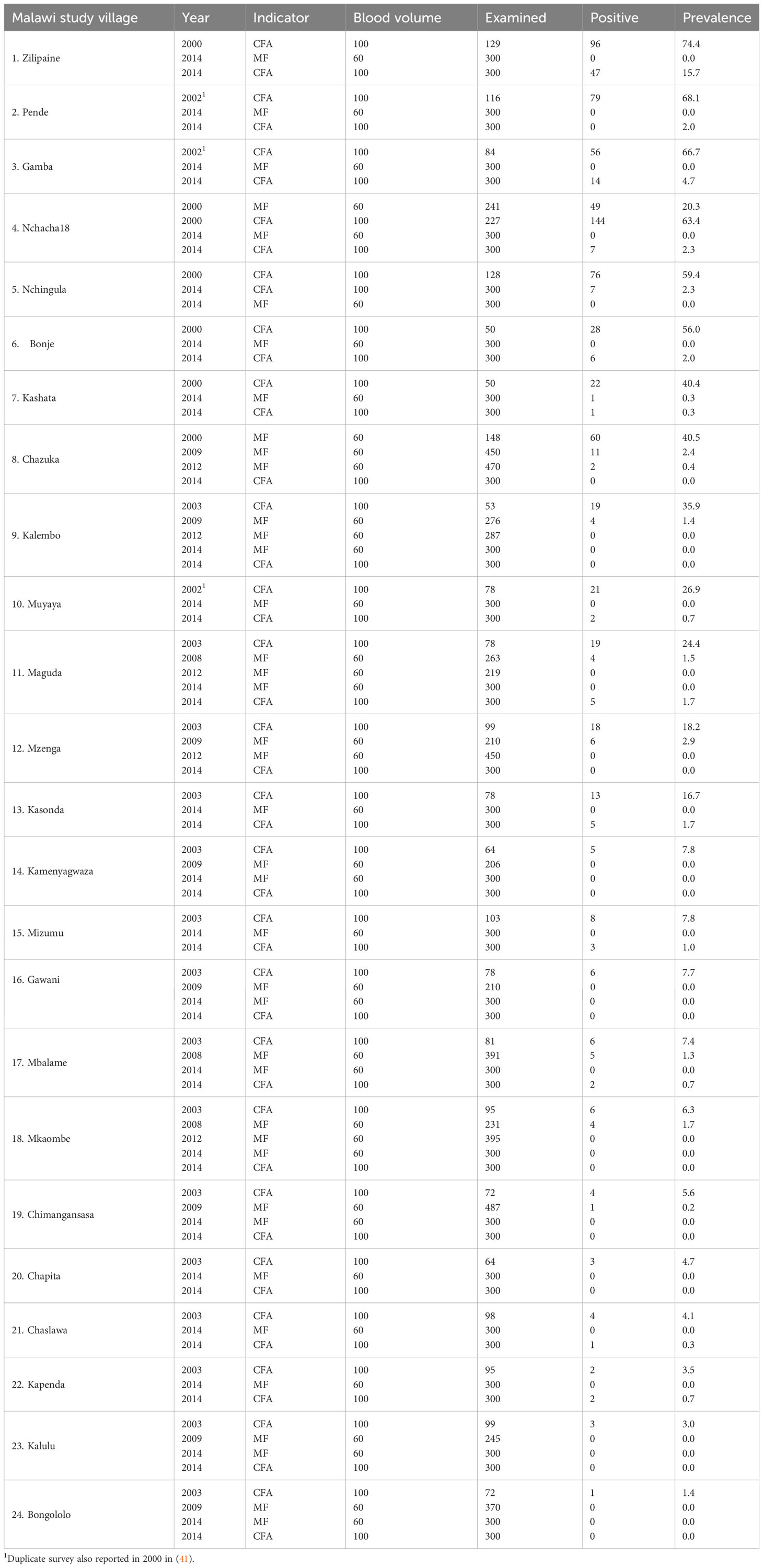
Table 1 Pre-intervention (2000–2003) and intervention (2008–2014) survey data for the selected 24 LF sentinel sites in Malawi (41).

FIGURE 1

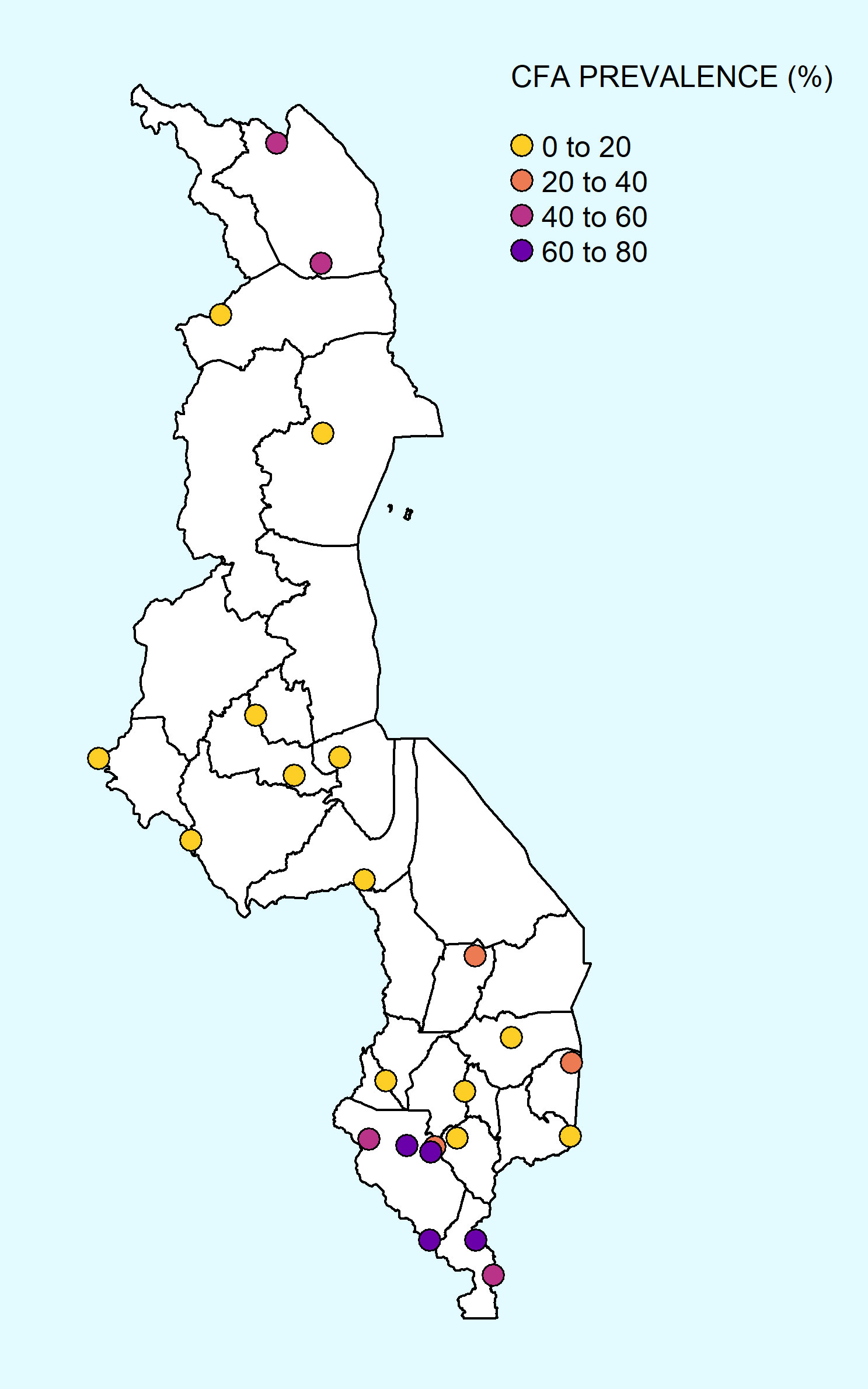
Figure 1 Map of the Malawi pre-intervention CFA prevalence data available from the ESPEN data portal for each of the 24 sentinel sites.

2.2 Lymphatic filariasis transmission model

The population-based LF transmission model employed in this study has been described in full in the literature, and is further elaborated in the SI (13, 26–28, 31, 44). In brief, the transmission dynamics of LF in this model were simulated by coupling age-structured non-linear partial differential equations describing changes in human infection, and an ordinary differential equation describing changes in infection intensity in mosquito vectors. The state equations comprising this model are:

$$\frac{\partial P(a,t)}{\partial t}+ \frac{\partial P(a,t)}{\partial a}=\lambda \frac{V}{H}h(a)\Omega (a,t)-\mu P(a,t)-\lambda \frac{V}{H}h(a)\Omega (a,t-\tau )\xi$$

$$\frac{\partial W(a,t)}{\partial t}+ \frac{\partial W(a,t)}{\partial a}=\lambda \frac{V}{H}h(a)\Omega (a,t-\tau )\xi - \mu W(a,t)$$

$$\frac{\partial M(a,t)}{\partial t}+ \frac{\partial M(a,t)}{\partial a}=as\varphi [W(a,t),k]W(a,t)-\gamma M(a,t)$$

$$\frac{\partial I(a,t)}{\partial t}+ \frac{\partial I(a,t)}{\partial a}=W_T(a,t)-\delta I(a,t)$$

$$\frac{\partial A(a,t)}{\partial t}+ \frac{\partial A(a,t)}{\partial a}={\alpha }_2 W_T(a,t)-{\gamma }_{2}A(a,t)$$

$$\frac{dL}{dt}=\lambda kg{\int }^{}\pi (a)(1-f(M))da - \sigma L-\lambda {\psi }_{1}L$$

As shown, the dynamics of filarial infection in human and vector populations are described through six population-averaged state variables that vary over age (a) and/or time (t), in which (P) captures the burden of pre-patent worms per human host; (W) represents the patent worm burden per human host; (M) describes the average microfilaria intensity; (I) measures the level of immunity against the microfilaria parasite that is generated by the total worm load; (A) measures the intensity of CFA; and (L) represents the average number of infective L₃ larval stages per mosquito as a consequence of ingesting mf from infected humans. The predicted changes in the mean densities of M and A were converted into prevalences using the negative binomial model relating mean intensity to prevalence (44, 45). These equations, functions, and the processes connecting each state variable and their parameters are described in the above articles, and are fully documented in Table S4 in the SI.

2.3 Predicting baseline Mf prevalence from observed CFA prevalence

Because there were both mf and CFA data available to describe LF prevalence following the initiation of MDA (and vector control interventions) in each site, we sought to model both indicators such that we could take advantage of all the infection information available. However, there was no mf data available at baseline for model calibration. The mechanistic relationship between mf and CFA is unclear, although the empirical relationship has been studied previously (46). To estimate the mf prevalence at baseline based on the observed CFA data, we put together a dataset from the published literature from a diverse group of sites (separate from the Malawi sites described above) that contained both baseline mf and CFA data records in parallel (Table S2 in the SI). We fitted a logistic regression model to this data in which CFA values were used as the predictor variable and mf values served as the response variable using the finalfit package in R (47). The best fit regression model was then used to estimate the baseline mf prevalence (with bootstrapped 95% confidence interval) from the observed CFA data for each Malawian site. Our LF transmission model (described below) was calibrated to both the observed baseline CFA and the estimated mf prevalence data following this procedure.

2.4 Bayesian melding site-specific model calibration

The Bayesian melding (BM) model calibration approach effectively integrates field data with the LF model to estimate models that can reliably capture the local transmission dynamics for a particular locality (26, 27, 30). In this study, we expanded on a previously developed variation of the BM procedure that relies on a pass/fail model selection criterion (31, 48). We began by assigning uniform prior distributions to each of the model parameters (Table S4 in the SI), including for the annual biting rate (ABR), which was unknown in our study sites. Based on published biting rate data from similar settings, the ABR prior was set to a range of between 500 and 15,000 (31). For each site, we randomly sampled 200,000 sets of parameters from these priors, which were then used as inputs to predict the baseline mf and CFA prevalences. These model outputs were evaluated against the observed community CFA prevalence and the estimated community mf prevalence for a particular site. Those parameter sets that produced CFA and mf prevalence predictions that were within the 95% confidence interval bounds of the data for both indicators were regarded as “passing,” and the others were regarded as “failing.” This pass/fail step generated the acceptable parameter vectors for describing the data behaviorally well in a particular site (49). The procedure was repeated for each study site, and the resulting site-specific models were then used to generate distributions of variables of interest (e.g., transmission breakpoints and infection trajectories following treatments) (26, 27, 30).

2.5 Breakpoint calculations

A previously developed numerical stability analysis approach was applied to each of the accepted parameter vectors to calculate the threshold biting rates (TBRs) and the distribution of mf and CFA prevalence breakpoints expected in a community (26, 27). First, to calculate the TBR associated with each parameter vector, we began by keeping all model parameters constant and progressively decreasing the average number of mosquitoes per human, V/H, from its baseline value to a threshold value below which the model always converges to 0% mf prevalence, regardless of the values of the endemic infective larval density, L*. The product of the number of bites per vector, γ, and this newly found V/H value is termed as the TBR (27).

Because vector control was used across all the LF sites in Malawi as a result of the country’s malaria program, in this study, we calculated infection breakpoints at the TBR condition. Given the site-specific TBR, the model will settle to either a zero or non-zero mf prevalence depending on the initial value of L*. Therefore, by starting with a very low value of L* and progressively increasing it in small step sizes, we estimate the minimum L* value, below which the model predicted zero mf prevalence, and above which the system progressed to a positive endemic infection state (27, 44). The corresponding mf and CFA prevalence at this threshold L* value was regarded as the human infection breakpoint for that indicator at TBR (27).

The distribution of breakpoints in a site can be described by an inverse empirical cumulative density function. We used this function, in conjunction with exceedance calculations (12, 50), to quantify the values of mf and CFA breakpoint prevalence thresholds reflecting a 95% elimination probability in a site, and use these values as the desired threshold values for serving as the site-specific design prevalences in the freedom-from-infection calculations reported below (12).

2.6 Freedom-from-infection calculations

Freedom-from-infection frameworks offer a method for calculating the probability that a population is free from infection based on the characteristics of the population infection surveys carried out in different settings (12, 38–40, 51). As discussed in the published literature, it is impossible to prove that a population is free from infection due to limitations of the surveillance sampling design and due to imperfect diagnostic tools (12, 38, 39). In our previous work (12), we presented a model-based framework for combining model-predicted site-specific transmission thresholds and infection survey results to estimate the probability that a particular site was free from infection (i.e., had reduced infection prevalence below the transmission threshold, which is termed the design prevalence, p_d). These calculations take into account the survey sample size, the number of positive tests, the village population size, the sensitivity and specificity of the diagnostic test, and the model-predicted design prevalence for the given site to estimate the probability that infection interruption has been attained. However, our previous method only allowed independent probability calculations to be made for a specific location at a particular point in time. In this study, we extend that method to allow probabilities to be calculated and aggregated over space and time.

2.6.1 Definitions

To calculate the aggregate probability of freedom from infection, we used the nested definitions of infection freedom probability proposed by Cannon 2002 (52). In this study, we define the probability of freedom at three hierarchical levels—the survey level, the village level, and the area-wide level (that is, any area larger than a village, such as a district, region, or country). For this study, the area of interest is the country of Malawi; therefore, the area-wide level refers to the country level. In this scheme, each level’s calculated probability of infection freedom comprises the lower-level surveillance components (e.g., the probability at the village level is made up of probabilities given by each survey conducted in the village and the probability at the area level is made up of probabilities given by each village in the region of interest). Following Cannon 2002 (52), the probability of freedom is designated as the “sensitivity” when referring to a component of a surveillance system deployed at a particular level and as “confidence” when referring to the probability of freedom given by the level’s overall surveillance system. Similar to Cannon 2002 (52), we will use the naming conventions given in Table 2.

TABLE 2

Table 2 Term definitions and symbols.

At a given level, sensitivity refers to the probability that infection would be detected by the surveillance component(s) if the prevalence was greater than or equal to the design prevalence of that level. Confidence has a similar definition but refers to the overall result as opposed to the component metric. The term probability of freedom will also be used interchangeably to describe the outcome at each level. The definition of design prevalence used in this study has been taken from our previous work and that of others (12, 38, 39) and specifies the maximum acceptable level of infection that can occur and yet signify that onward transmission may be broken (12). The design prevalence was defined differently at each level. At the village level, as in our previous work, we defined the design prevalence (p_d) using modeling results estimating the transmission breakpoint in a particular site. To be conservative, we used the 95% elimination probability threshold that was calculated as described above (see 2.5 Breakpoint calculations). At the area-wide level, we defined the design prevalence (Cp_d) to reflect the varying levels of risk tolerance (e.g., requiring 90%, 95%, or 99% of villages to meet their site-specific p_d).

In general, to calculate the confidence of freedom from infection at a given level, we used the corresponding component sensitivities. For example, at the lowest level we calculated the survey-level confidence based on the characteristics of the diagnostic tool and characteristics of the survey conducted. The survey-level confidence then became the sensitivity that was used to calculate the village-level confidence. In turn, the village-level confidence became the sensitivity that was used to calculate the area-level confidence. The details of the calculations carried out at each level are outlined below.

2.6.2 Calculations to aggregate spatiotemporal freedom-from-infection probabilities

The first probability of freedom calculations were made at the lowest level, that is, that of the survey. The survey sensitivity, SSe, was calculated using the freedom-from-infection framework described in Michael et al., 2018 (12). The sensitivity of a given survey testing for infection is a function of the sample size, diagnostic sensitivity and specificity, total village population, observed prevalence, and design prevalence. The survey sensitivity reflects the surveillance sensitivity for the given village at the given time only.

These results were then used to calculate the village level confidence. The village confidence, VSe, could be aggregated to reflect the sensitivity of a series of surveys over time. For each village, we calculated the overall confidence at time t using the equation below to combine survey sensitivities from one or more surveys from baseline to time t (i.e., for mf and/or CFA surveys).

$$VS{e}_t=1-\prod _{t=0}^{t=t}(1-SS{e}_t)$$

Similarly, we could combine the village-level sensitivities across an area of interest to estimate the area-level confidence of freedom (CSe). We used a similar equation to that given above but included the Cp_d to reflect the maximum number of acceptable infected villages in the area. In our analysis, we used a conservative value for Cp_d set to 1/N, in which N = the number of villages in the area.

$$CS{e}_t=1-\prod _{t=0}^{t=t}(1-C{p}_d*VS{e}_t)$$

2.7 Evaluating the effect of continued interventions and surveillance on freedom-from-infection probabilities

After carrying out calculations to assess the probability that Malawi was free from infection (given data to 2014) at the specified design prevalence estimated for each sentinel site, we sought to evaluate how the results would change over time with continued interventions and surveillance. To do this, we used our site-specific LF transmission models (calibrated as described above) to simulate the effects of continued MDA and VC from 2014 to 2020. We estimated the plausible MDA and VC coverage values from 2015 to 2020 using the missing data imputation methods included in the Amelia R package (53). Details of our intervention models are given in the SI. We simulated expected survey data from 2016 to 2018 based on the number of individuals predicted to be still positive for infection by the projections of our model, maintenance of the sample sizes used in the 2014 surveys, and inclusion of diagnostic performance values as used in Michael et al., 2018 (12) for mf and CFA detection with the use of blood smear examination and antigen tests respectively. We then included these additional surveys in the freedom-from-infection probability calculations to evaluate what impact they would have on village-level and country-level freedom-from-infection probability outcomes.

2.8 Assessing the relationship between the number of sentinel sites, country-level design prevalence, and country-level freedom-from-infection probability

In this study, we selected 24 Malawian LF sentinel villages based on data quality and availability. We hypothesized that the country-level probability of freedom would depend on the number of villages surveyed. To test this, we generated hypothetical survey results to reflect the data that would be available if up to 50 villages were surveyed in Malawi. These hypothetical surveys were simulated to represent 26 additional sites with CFA surveys conducted in 2003 and 2014 and an intermediate mf survey conducted in 2009, thus following the typical surveillance activities in Malawi. Survey sample sizes and the number of individuals testing positive were sampled randomly from the observed survey data in each year from the 24 base Malawi sentinel sites. Sampling was carried out using a uniform distribution with the minimum and maximum values calculated as the 5% and 95% quantiles to limit extreme outcomes. We then calculated the country-level freedom-from-infection probabilities given survey data from 1–50 sentinel sites at country-level design prevalences (Cp_d) of 10%, 5%, and 1% to assess the sensitivity of the results to these variables.

3 Results

3.1 Model calibration to baseline mf and CFA prevalence

In this study, we extended our Bayesian melding methodology to allow models to be calibrated using parallel prevalence data for two infection indicators, mf and CFA. Because baseline mf data were not available, we used a logistic regression model fitted to an external dataset of sites with parallel mf and CFA data to predict the likely mf prevalence at baseline in each of our study sites based on the observed CFA prevalence. The fitted logistic regression model and the predicted mf prevalence values, along with bootstrapped 95% confidence intervals, are presented in Figure S1 and Table S3 in the SI.

The predicted mf and observed CFA prevalence and their respective 95% binomial confidence intervals served as inputs for facilitating the calibration of our LF model based on the pass/fail method for each of the 24 Malawi sentinel villages (31, 48). The baseline CFA prevalence predicted by the locally calibrated models compared with the reported survey data for each of these villages is shown in Figure 2. The overlaps of the model predictions with the observed data points and their 95% confidence intervals indicate that the fitted models are able to capture the CFA data in each site well.

FIGURE 2

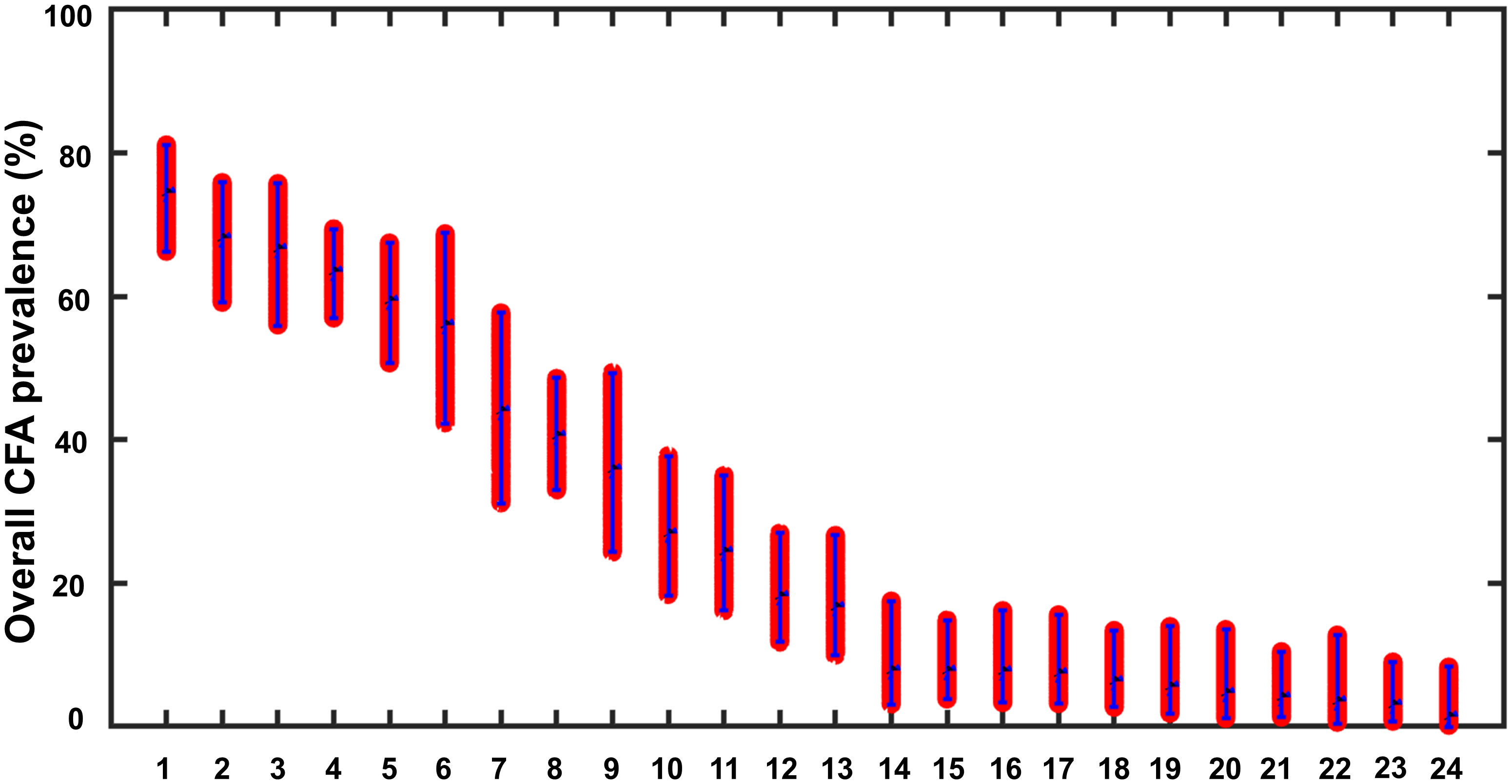
Figure 2 Model-predicted community CFA prevalence vs. observed survey prevalence based on immunochromatographic cart tests (ICT) (54). The model predictions for each site (numbered 1–24, see Table 1) are shown as red points and the surveyed overall CFA prevalences are shown in blue along with the corresponding 95% confidence intervals.

3.2 Calculation of site-specific transmission breakpoints

The numerical values of the CFA and mf 95% elimination probability thresholds for each of the LF sentinel sites are listed in Table 3. Because vector control was implemented in Malawi, the breakpoints were calculated under the TBR estimated for each of these sites (13, 27). These breakpoint values were used to set the site-specific design prevalences, p_d, in the subsequent freedom-from-infection calculations carried out in this study.

TABLE 3

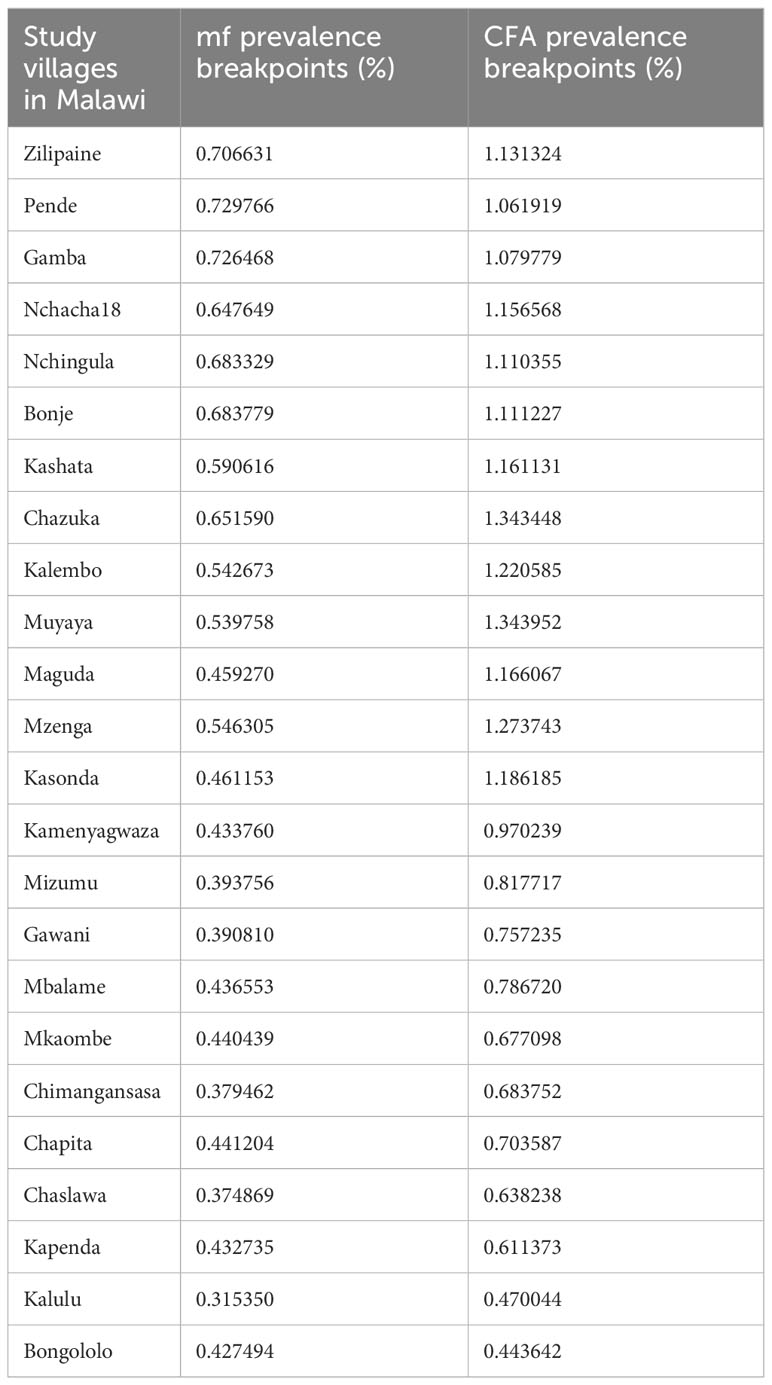
Table 3 Site-specific transmission breakpoint values (signifying a 95% probability of elimination) for mf and CFA prevalences (%), respectively, at the threshold biting rate (TBR) in each site.

3.3 Aggregated freedom-from-infection calculations

The application of the hierarchical freedom-from-infection calculator for aggregating the probabilities of infection freedom based on sensitivities estimated for each sentinel site (see the Methods section above) to quantify village-level and countrywide infection freedom status through time are shown in Figures 3, 4, respectively. The calculated cumulative village-level probabilities of freedom over time are shown in Figure 3 and suggest that each of the 24 study sites had a high probability (>95%) of achieving infection freedom by the year 2012 after 3–4 rounds of MDA, with the probability for some sites even reaching high levels by 2009.

FIGURE 3

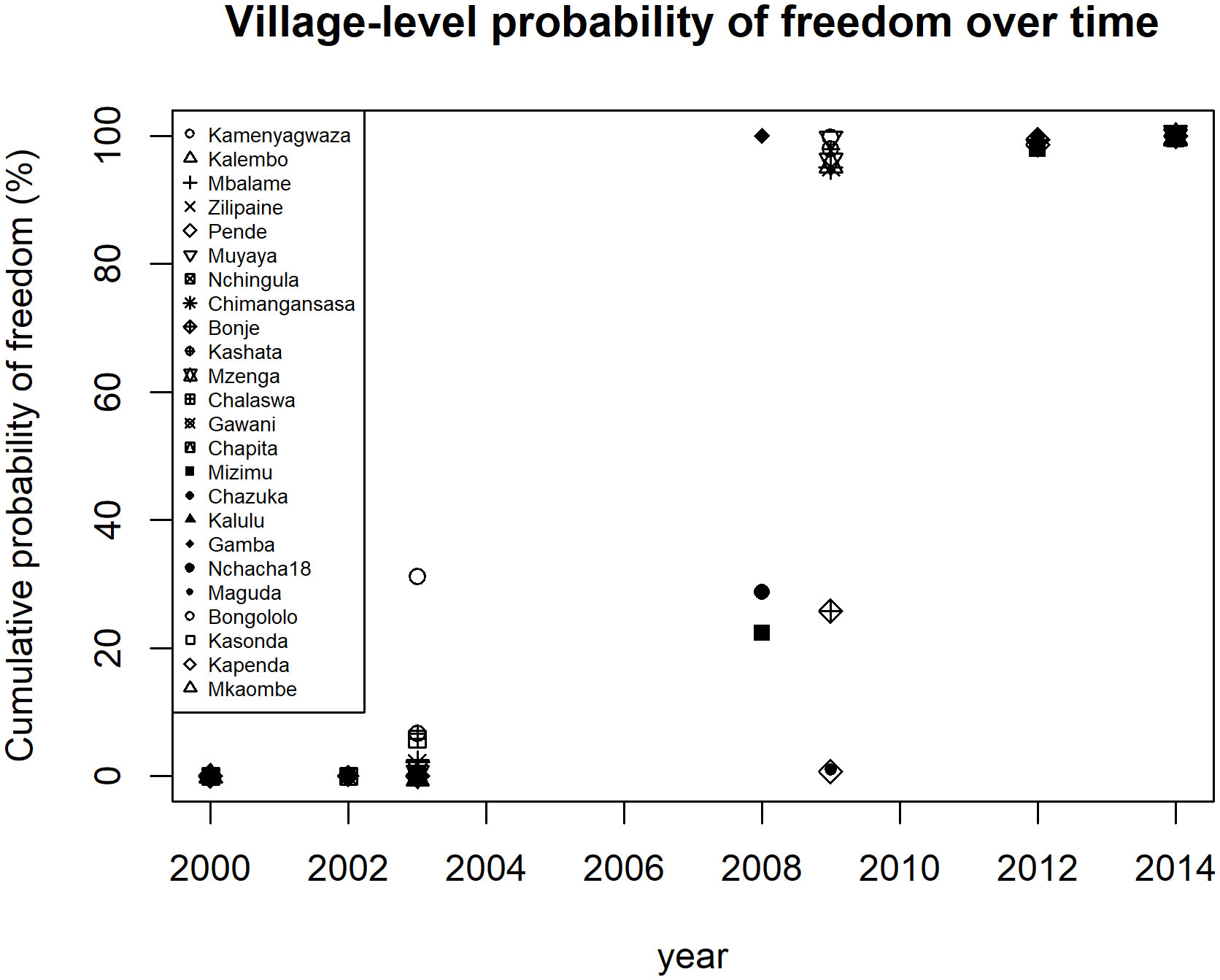
Figure 3 Cumulative probability of freedom from infection over time in each of the 24 Malawian study sites.

FIGURE 4

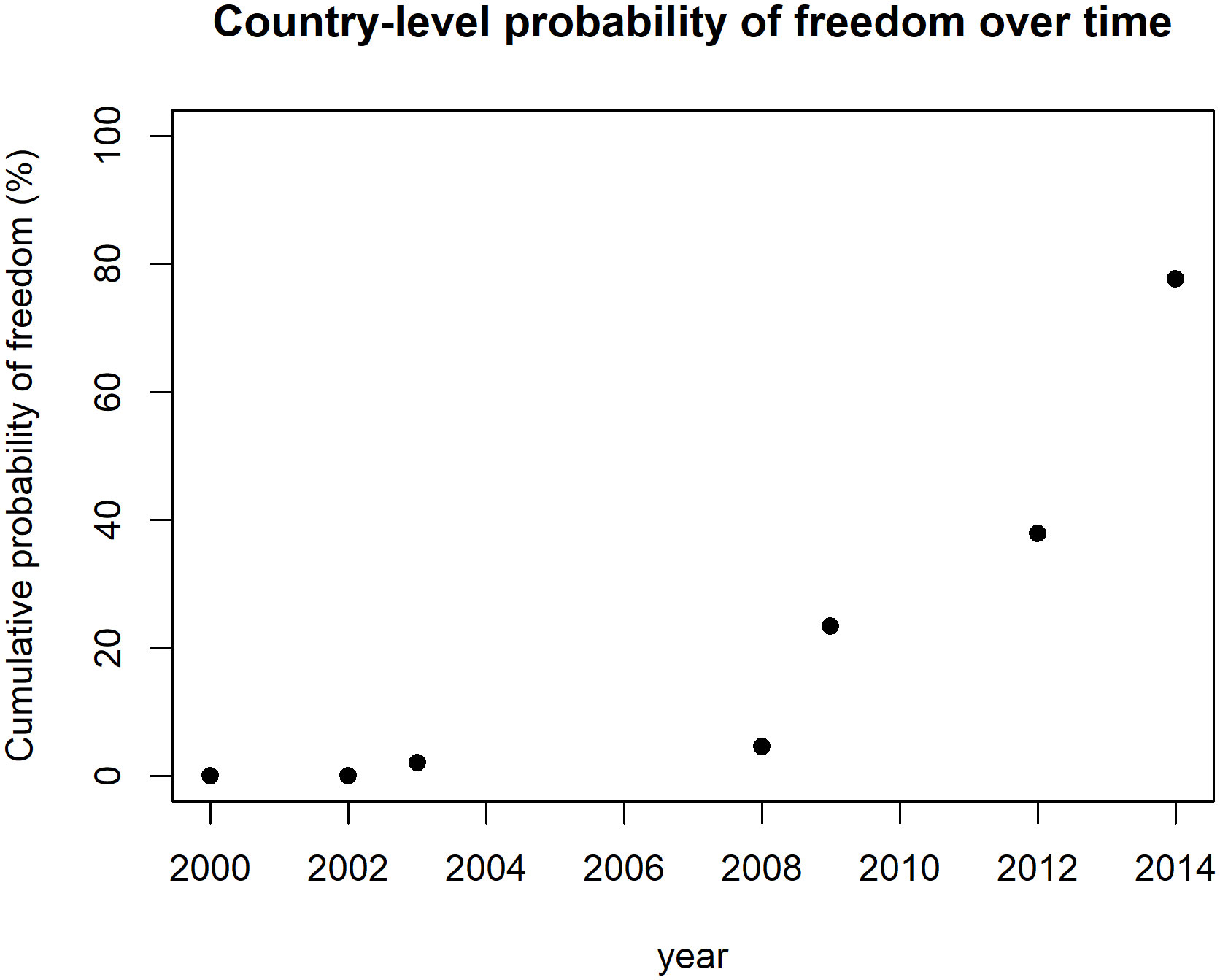
Figure 4 Cumulative probability of freedom from infection over time aggregated across sites to the year 2014.

When the village-level probabilities of freedom are aggregated to the country level, the cumulative probability increases over time, but does not reach levels as high as those of the individual villages (Figure 4). This shows that when village-specific sensitivities are combined, the corresponding confidence of achieving infection freedom at the higher zone or country level will be lower than that at the lower village (component) level (52). This is due to the impact of multiplying these sensitivities over all villages and the inclusion of the additional design prevalence, Cp_d, where we set this to 1/number of villages (N), or to reflect a risk tolerance of 95% given that we are sampling 24 sentinel sites. However, as we demonstrate below, this cumulative countrywide probability is also dependent on the length of surveys and number of villages surveyed.

3.4 Probability of freedom given model-based infection predictions with continued intervention and surveillance

To simulate the effect of continued interventions, we imputed MDA, IRS, and ITN coverage data beyond the observed data (i.e., 2014) to forecast the infection prevalences resulting from the extension of these drug and vector control interventions to the year 2020. The imputed coverage predictions are shown in Figures S2–S4 in the SI. We used the site-specific models to simulate the combined impacts of observed interventions (to 2014) followed by 6 additional years of interventions until 2020 on both the community level mf and CFA prevalence. We extracted the mf and CFA prevalence data predicted for 2016 and 2018 in each site (Table S6) and used these values to rerun the freedom-from-infection probability calculations. The results are shown in Figure 5, and indicate that the continuance of interventions and surveillance will result in a continuous increase in the cumulative country-level confidence for attaining infection freedom, which reached nearly 100% by 2018.

FIGURE 5

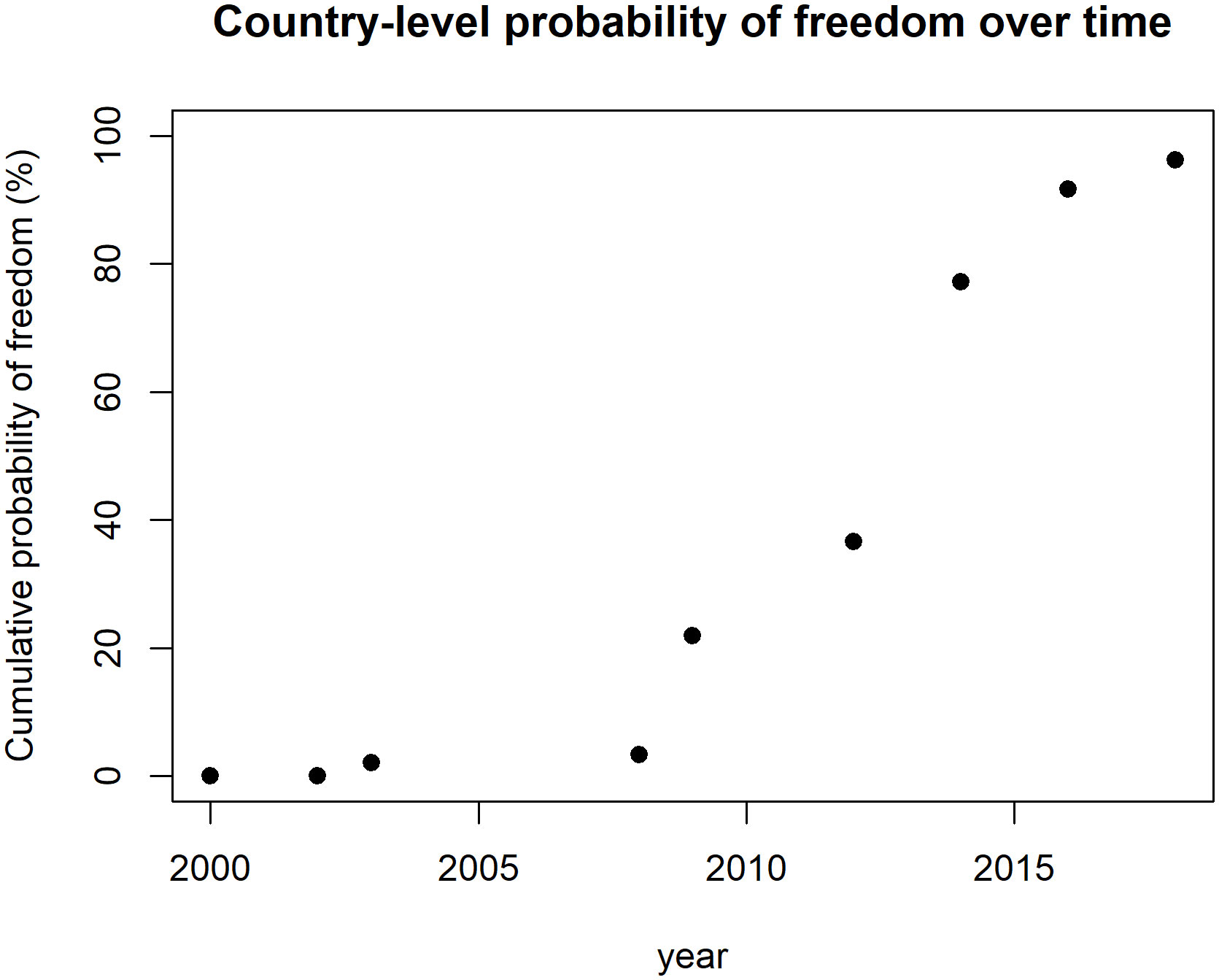
Figure 5 Country-level probability of freedom from LF infection in Malawi with longer interventions and surveillance.

3.5 Sensitivity of probabilities of freedom from infection to number of sentinel sites and area-wide design prevalence

We next conducted a sensitivity analysis to evaluate the impact of the number of sentinel sites surveyed and the country-level design prevalence, Cp_d on estimates of countrywide LF infection freedom probabilities. The results are shown in Figure 6. Increasing the Cp_d was found to have a potentially dramatic impact on the countrywide probability of freedom, with at least a 20% difference in the estimated probability of freedom when comparing Cp_d = 0.1 and Cp_d = 0.01 (i.e., 90% or 99% of villages must achieve their site-specific transmission thresholds, p_d, respectively). Interestingly, the effect of the number of survey sites on the overall probabilities of freedom from infection was somewhat variable depending on the choice of Cp_d. At smaller Cp_d values (e.g., = 0.01, at which 99% of villages must achieve their transmission thresholds), there was a relatively linear but smaller increase in the countrywide probability of freedom of sentinel sites 1–50. However, when larger values of Cp_d were chosen (e.g., 0.05 and 0.1, or at which 95% or 90% of surveyed sentinel villages, respectively, must attain their transmission thresholds), there was relatively little change in the countrywide probability of freedom beyond 25 sentinel sites. These results imply that if we required a very high level of zonal or countrywide sensitivity [e.g., increasing the proportion of survey villages that will meet their threshold thresholds in an area (e.g., to 99%)], then either a larger number of survey sites or longer durations of interventions would be required until we were sufficiently confident that an area was free from infection.

FIGURE 6

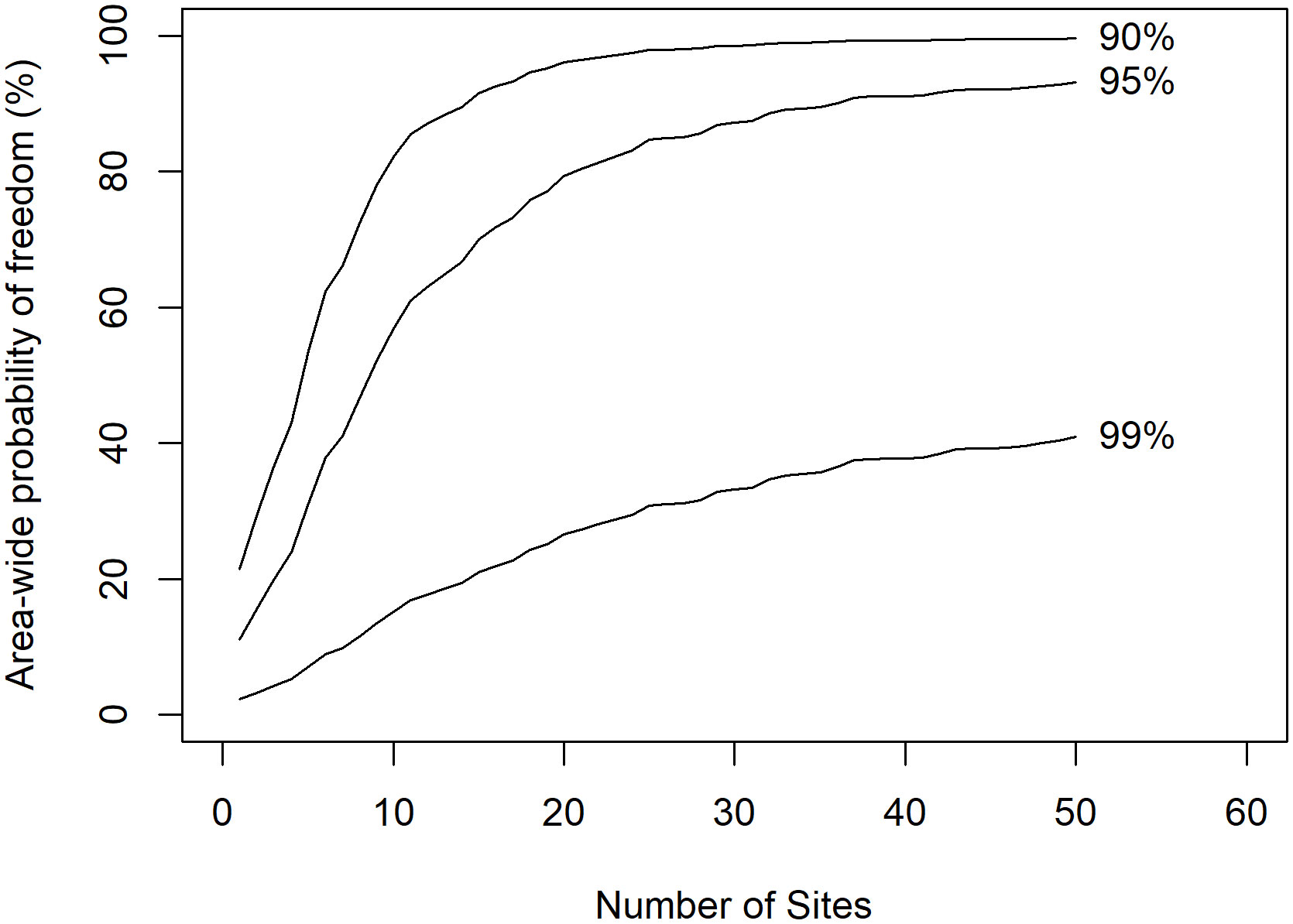
Figure 6 Area-wide probability of freedom from infection is dependent on the number of sites surveyed and the area-level design prevalence.

4 Discussion

In recent years, the two-stage lot quality assurance sampling (LQAS) survey has become a commonly used tool for undertaking global health surveillance and evaluation activities (15, 37, 55–57). It is recognized as an especially cost-effective tool for identifying acceptable vs. poorly performing units of a population spread across multiple distant locations/clusters, given that these LQAS surveys typically require sampling with fewer individuals than simple random sampling from a target population (55). In its simplest form—the basis for the WHO LF two-stage LQAS-based TAS framework—it is assumed that the spatial clustering of infection is low and that any clustering, if it occurs, can be countered by relying on setting small within-cluster samples, both of which in turn can act to reduce variance inflation in the calculations (55, 58). However, as has been highlighted by several studies, relying on low clustering may not be reliable and relying on small cluster sizes may not be cost-effective if more clusters need to be surveyed (55). These considerations raise questions about the non-critical use of this method for a given application.

This may be particularly true in the case of LF infections, which studies show can exhibit prominent spatial clustering across an IU even after the implementation of multiple rounds of MDAs (21–25, 36). Apart from disregarding this spatial heterogeneity, the LF TAS strategy also assumes perfect diagnostic performance, ignoring the fact that any imperfection in the performance of these tools can lead to complex interplays between sample sizes and decision rules (37). TAS also advocates the sampling of a segment (the 6- to 7-year-old age group) of the population for surveillance, which discounts the potential for prolonged transmission of the parasite in a community from continuing adult infection despite reduced infections in children (13, 23, 25). Finally, it is unclear if the globally set elimination threshold employed by TAS to guide the binary decision of either continuing with MDAs or stopping interventions is the right one applicable, not just for a single setting, but also for all settings and intervention conditions in a given spatial domain (26–28).

The above suggests that the current TAS strategy may not constitute a sufficiently robust surveillance tool to aid the consistent assessment of whether or not LF transmission has been broken in every IU (15). The misspecification of each component of TAS, viz., the value of the elimination threshold used in TAS (2% antigen prevalence), consideration of a single area (IU)-wide threshold to be used universally across all IUs, surveillance restricted to a possibly inappropriate section of the population, and non-consideration of diagnostic tool performance (16), can all combine to result in an IU passing TAS and yet still containing a significant number of individual villages or clusters exhibiting ongoing LF transmission. Both empirical and modeling studies attest to the real possibility of the likelihood of this negative outcome in the field (11, 13–15, 18, 20–25, 29, 36), a situation which will clearly obstruct the ongoing efforts to successfully achieve the global elimination of the disease.

In this study, we have evaluated an alternate hierarchical two-stage sampling framework, first developed and used for substantiating freedom from diseases in animal herd accreditation exercises (38–40, 52), which is based on combining longitudinal infection surveillance data from sentinel sites that are used by national LF programs to make decisions on whether or not to move to the TAS phase with transmission model-based estimates of elimination thresholds applicable to a site, to allow better predictions regarding if and when the transmission of LF has been interrupted in a spatial domain of interest to be made (12). We note that the developed integrated spatially hierarchical freedom-from-infection tool can overcome the key challenges posed by the current WHO TAS strategy for facilitating high-confidence area-wide decisions regarding whether or not parasite transmission interruption due to LF interventions may have occurred in a region thereby allowing the safe termination of control to be made. In particular, we note that although the inclusion of model-estimated cluster or site-specific infection breakpoints can overcome the problem of the arbitrarily and universally applied thresholds used by TAS, the use of survey-based proof-of-freedom methods that incorporate the impacts of sample size and diagnostic tool performance in the calculations can, on the other hand, also address the errors caused by their exclusion from TAS (12). Sentinel site surveillance additionally targets the whole community based on sampling up to 300 individuals who are over 6 years old; the larger sample size and coverage of the whole community means that data from such surveys may also be useful in countering the restricted sampling of young children using smaller sample sizes (approximately 50 per cluster) currently specified in the WHO TAS methodology (16).

Freedom-from-disease or freedom-from-infection calculations based on surveys use information on the size of the population to be screened, the sample size, the sensitivity and specificity of the diagnostic tests, and the maximum allowable prevalence (called the design prevalence), to quantify the probability of declaring a population disease-free or infection-free when the observed or measured prevalence lies below the design prevalence (12, 38–40, 51, 52). At the core of the method is the notion that it is impossible to prove that a population is free from a disease in an area even with large sample sizes, as there is always a chance that an infected individual may have been missed or that a test result is wrong (38, 39). However, even if it can never be entirely proved that a population is free from a disease, if enough individuals are surveyed over an area and the performance of the diagnostic test and the underlying population size are taken into account, then it is possible to calculate how unlikely it is that a population has continuing infection or disease given the allowable design prevalence (see the Methods section). A typical requirement using this methodology for substantiating that a population is free from infection or disease is to show with a probability exceeding 95% that a measured prevalence lies below the specified design prevalence, i.e., that we can expect parasite transmission to be broken when infection levels are detected to occur below this threshold. This 95% probability for detecting the disease below the design prevalence can be interpreted as the sensitivity of the freedom-from-disease survey ( (52); see the Methods section). As we have shown previously, to substantiate freedom of LF infection in a population with high confidence, the choice of the design prevalence should ideally reflect the prevalence threshold that indicates whether or not parasite extinction would occur if the detected prevalence of a disease in a population is found to be below this threshold (12, 26, 27, 30, 44). This means that rather than relative freedom from disease, which is the outcome to be expected when using an arbitrarily set threshold, the use of transmission breakpoint prevalences as design prevalences in these calculations would allow the demonstration of absolute freedom in the sense that any disease prevalence detected below such design prevalences would ultimately decline to the zero-extinction state (13, 27). We demonstrated in this regard how data-driven LF transmission models that allow the prediction of local infection breakpoint prevalences can be an important means of specifying these design prevalences when applying infection surveys for quantifying the likelihood of meeting the goal of parasite transmission elimination in a particular population (12).

Switching to two–stage cluster sampling for undertaking area-wide disease freedom calculations, as described and applied here, extends the single-stage village freedom assessments that we previously studied by taking account of the clustering of infection that occurs at and across local levels (32). A second design prevalence, e.g., Cpd, is, crucially, also included in these calculations to address the added uncertainties of sampling villages or communities from a population consisting of all such communities in a region. Again, given that this area-wide disease freedom or absence evaluation is based on samples of a fraction of communities within a region, we can never be 100% certain that all infected communities are included in the sample. We can, on the other hand, specify an areal design prevalence which lowers this risk, for example, by requiring that > 95% or 99% of communities meet their site-specific breakpoint thresholds, Pd, as sufficient for us to accept that we have achieved area-wide elimination of a disease (52). Note that the lowest Cpd value for a sample of communities is equal to one/number of villages; this immediately shows that the number of villages sampled sets a lower limit to the Cpd value, meaning that lowering the areal design prevalence in a region can only be achieved by increasing the sample size of the communities surveyed. Calculating the sensitivity of a two-stage sampling design for detecting infection is further carried out in a hierarchical series of steps. Thus, in our two-stage calculator, we first calculate the sensitivity of a single survey bout within a community, and then based on this sensitivity, the sensitivity for detecting infection at the village level. Based on the results at the individual village-level, we then assess the sensitivity at the zonal or regional level (52). Note that by treating each village separately in these calculations, such a scheme also enables us to take into account clustering and the lack of independence among individuals at the village level (52). However, given that sensitivity over time within a village is likely to come from the partial follow-up of the same individuals, higher levels of cumulative probabilities of freedom will arise more quickly if freedom calculations are conducted at the individual village level. In contrast, this will increase more slowly over time when village sensitivities are aggregated at the regional level, particularly at low areal design prevalences (compare Figures 3, 4).

The application of our two-stage hierarchical freedom-from-infection approach to the data tracking changes in LF infection prevalences based on repeat surveys carried out in sentinel sites for the country of Malawi has underscored not only many of the theoretical insights outlined above, but has also demonstrated the additional utility afforded by the tool in making effective area-wide transmission elimination assessments. The first significant result here is in relation to the values of the mf and CFA prevalence transmission breakpoints as estimated by our data-fitted models for each sentinel site population (see the Methods section for our Bayesian data-model calibration and breakpoint estimation using our model based on baseline data). The data in Table 3 shows, in line with our previous work on LF infection breakpoints (13, 26, 27, 30, 44), that the values of these thresholds below which transmission is most likely to be broken are at least one- to two-fold lower than the corresponding WHO threshold value used in TAS (i.e., 1% mf or 2% CFA prevalence). This instantly emphasizes the point that community LF transmission is not likely to be broken if the latter’s arbitrarily set thresholds, as employed by TAS, are used to assess transmission breakage (13, 27). Field data from a growing number of countries that have conducted post-intervention assessments are beginning to support these theoretical findings, indicating that persistent LF transmission may continue to occur in communities that have met the WHO endpoint criteria (11, 14, 18, 21–25, 36). The data in Table 3 also highlights another major feature of LF thresholds, viz., that values of infection thresholds will be one- to two-fold higher at the vector abundance-associated transmission biting rate (TBR) compared with when the vector population remains undisturbed [i.e., when the annual biting rate (ABR) is left unperturbed over the duration of MDA]. As we have demonstrated previously, this is a function whereby, as vector numbers or the biting rate is reduced to the TBR, the corresponding infection thresholds in the human population will increase until they reach their maximal value at TBR (26, 44). As noted previously, this relationship of LF thresholds with the prevailing vector population abundance means that combining MDA with vector control can significantly raise the probability of achieving parasite transmission interruption in a community owing simply to the fact that breakpoint values will be elevated and will reach values that can be breached earlier (44, 59, 60). Note that the mf and CFA breakpoints estimated and shown for TBR (Table 3) are also closer to the WHO-set thresholds, meaning, as we highlighted before, that the use of such thresholds to assess if LF transmission has been interrupted could be tenable in some settings (13, 27).

However, a clear finding illuminated by the results depicted in Table 3 is that LF infection thresholds can vary significantly between communities, with the prevalence variations (viz., the difference between the lowest and highest values) estimated for the present villages, for example, varying from 130% for mf breakpoints to 200% for the corresponding CFA breakpoints at TBR. These large percentage variations for both indicators illustrate the high levels of inter-community spatial heterogeneity that can underlie LF infection thresholds across a typical regional population, calling into question the use of the universal one-size-fits-all infection breakpoint values currently used in the WHO TAS strategy for assessing the stoppage of LF transmission across an IU.

The results on the cumulative probabilities of infection freedom achieved in the individual sentinel sites and across these sites over time as calculated by the hierarchical freedom-from-infection tool developed here are shown in Figures 3, 4. These show that, as predicted above, while the village-level disease freedom or absence probabilities had reached high levels even by 2012 (> 95%; Figure 3), the aggregated probability for Malawi as a whole, whilst also increasing with time, did not reach levels as high as those achieved in individual villages (Figure 4). Although this could partly be due to the correlation between successive rounds of tests when some individuals are re-tested (52), this outcome, as described above, is also an outcome of using the additional zonal level design prevalence, Cpd, to account for the extra level of uncertainty involved in sampling sentinel sites from all available endemic sites to make area-wide infection freedom decisions (52). As Figure 5 indicates, if the number of these sentinel sites is fixed, then the only way to increase the zonal (or country in the present case) probability of freedom is to increase the surveillance/intervention period. We thus show that if interventions in Malawi were to be extended from 2014 to 2018 at the levels of MDA, IRS, and ITN implemented to 2014, then given the Cpd value used (1/N), the number of sentinel sites surveyed (N = 24), and the predicted reduction in infection prevalence, then very high levels (close to 100%) of infection freedom would have been achieved in Malawi by 2018 compared with the lower probability estimated to 2014 (Figure 4). The probability of infection freedom that can be achieved over time is also highly sensitive to the Cpd value chosen; if this is decreased to low values to obtain a high level of confidence that area-wide infection has been achieved (e.g., 99%), then the time to achieve such very high zonal confidences will take significantly longer than that to achieve lower confidences (e.g., 95%) (Figure 6). The only way to decrease this time is by increasing the number of sentinel sites surveyed. This time-zonal design prevalence trade-off can be used to estimate the number of sites required to achieve an acceptable high level of zonal confidence that infection freedom has been achieved as early as possible. In this study, we showed that the follow-up of the prevalence declines observed and predicted in the 24 sentinel sites surveyed in Malawi was sufficient to allow at least 95% confidence that LF freedom would be achieved in Malawi by 2018 (for a Cpd value = 1/N) with continuation of MDA and vector control at the levels these were implemented in the country to 2014. If higher confidences (e.g., 99%) are required, then both the number of sentinel sites and the period of intervention/surveillance will need to be increased significantly (Figure 6).

The area-wide freedom probabilities predicted by our tool are sensitive both to the values of the locality-specific infection breakpoint values quantified by our LF model and their distribution between the present sentinel sites. In general, the lower the breakpoint prevalences and higher the degree of clustering in their between-survey site distribution, the lower the area-wide confidence that can be expected for a given sample size configuration (number of sentinel or survey sites and number of individuals surveyed per site) and performance of the diagnostic tools used to diagnose infection. Our results demonstrate that the use of sentinel sites and the application of vector control alongside MDA can ameliorate this challenge to a large degree. First, the use of sentinel sites by definition and in practical terms can reduce the spatial heterogeneity that may be observed for LF breakpoints by virtue of the fact that these sites represent the settings with the highest risk of transmission in a region. Note also here that since these high-risk sites are normally restricted to only two per IU as per WHO guidelines (16), programmatic decisions based on these sites can be made over areas much larger than IUs, which are normally districts. For example, for a small country like Malawi, we are able to make countrywide decisions based on data from just 24 sentinels. This will clearly lead to considerable cost savings associated with the need for surveying up to 30 clusters per IU (as recommended for carrying out TAS). Second, the use of vector control can raise the values of breakpoints for vector-borne diseases, such as LF (13, 59, 60). This can be seen clearly from the values of the breakpoints shown in Table 3 for mf and CFA in the current sentinel sites at ABR (applicable when MDA alone is used) vs. the corresponding values predicted at TBR (applicable when vector control is employed as a supplement to MDA). These results imply that national programs could use follow-up surveillance of infection data from sentinel sites not only to make pre-TAS decisions to stop MDA (16) but also to make post-intervention decisions (rather than switching to the more costly randomized 50 individuals × 30 cluster survey design currently used in the WHO TAS). This will also be true for the enhanced two-stage cluster survey approaches that have been developed recently to overcome the issues with imperfect diagnosis and spatial heterogeneity in infection to improve program decision-making using the globally set WHO-recommended thresholds (15, 37). The second implication, as noted previously (13, 26, 27, 59, 60), is that programs should now seriously consider including vector control with MDA if the prospects for successfully achieving the elimination of LF are to be accomplished in the reasonably near future.

Regardless, it is to be noted that surveys to assess the interruption of parasite transmission over large spatial domains can never allow intervention-stopping decisions to be made with 100% certainty. Spatial heterogeneity in thresholds, imperfect diagnostic tests, and sampling of a fraction of the endemic populations mean that one can only make probabilistic statements regarding the achievement of area-wide transmission elimination (12, 38, 39, 52). This in fact is also true of the WHO TAS approach, in which sample sizes and critical cut-off values are powered so that an IU has at least a 75% chance of passing if the true antigen prevalence is half the threshold level (2% for Culex, Anopheles, and Mansonia vector areas, and 1% for Aedes vector areas), and in addition, there is no more than a 5% chance of passing if the true prevalence is greater than or equal to the threshold level. This means that IUs passing the WHO TAS criteria may still contain sites that continue to transmit LF, as has been observed in several post-TAS field studies (11, 14, 18, 20–25, 36), even if perfect diagnostic tests are used and the spatial heterogeneity in cluster level infections is taken into account. Our tool, which combines model-estimated local thresholds with sentinel site surveillance and is designed to overcome the issues connected with the use of an inappropriate threshold, imperfect diagnostic tests, lower cluster sample sizes restricted to only the child subgroups, and spatial heterogeneity in extinction thresholds, is also, similar to the WHO TAS, probabilistic in nature, but, as discussed above, can be manipulated to make intervention stopping decisions that have significantly higher statistical support than those made using TAS. Applying the tool to sentinel-site data is also advantageous in that it can significantly bring down the cost of surveillance, although once we have attained a high confidence that area-wide LF elimination has been achieved by the use of this tool based on the follow-up of a relatively small set of high-risk sample sites, it would be advisable to include an additional stage based on surveys of randomly selected sites within a spatial domain of interest to certify that transmission has been broken effectively everywhere.

Our results suggest that the time has come to reappraise the use of the current TAS strategy for aiding decision-making regarding the sustained breakage of area-wide LF transmission. This study suggests that in this regard, the model-based area-wide freedom-from-infection tool described here could offer a better quantitative framework for determining the interruption of LF transmission in a spatial domain compared with the current TAS approach. Note also here that although the data used in the present analysis are based on mf and CFA, our framework can be easily adopted for any diagnostic tool, including for the current Filarial test strips. This is because if data from the application of the latter tool becomes available, our modeling framework would adjust the parameters specific to the tool in the model, just as the CFA/mf gain and decay terms were calibrated with data using the BM approach (as described in the Methods section). Given increasing evidence from the field that passing TAS is no guarantee that area-wide transmission has been achieved, we thus indicate that new strategies, such as the concept and tool developed here, need to be evaluated using appropriately designed field studies so that more reliable assessments regarding parasite elimination in a region may be made. Otherwise, we fear that there will be a real possibility that decisions to stop interventions will be supported even while transmission in communities continues, which will lead to the inevitable reemergence of infections over time, negating the considerable health gains that have been made thus far by national LF programs.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: EM and MS. Data management, extraction and analysis: MS, KN, YA, and EM. Original draft: MS and EM. Supervision and funding acquisition: EM. Revision of manuscript: MS, KN, YA, and EM. All authors contributed to the article and approved the submitted version.

Funding

This work was partially supported by the Bill and Melinda Gates Foundation through the NTD Modelling Consortium (grant number OPP1184344).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author EM declared that they were an editorial board member of Frontiers at the time of submission. This had no impact on the peer review process or the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fitd.2023.1233763/full#supplementary-material

References

1. Cochi SL, Hegg L, Kaur A, Pandak C, Jafari H. The global polio eradication initiative: progress, lessons learned, and polio legacy transition planning. Health Affairs. (2016) 35(2):277–83. doi: 10.1377/hlthaff.2015.1104

CrossRef Full Text | Google Scholar

2. Feachem RGA, Chen I, Akbari O, Bertozzi-Villa A, Bhatt S, Binka F, et al. Malaria eradication within a generation: ambitious, achievable, and necessary. Lancet (2019) 394(10203):1056–112. doi: 10.1016/S0140-6736(19)31139-0

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Strategic Advisory Group on Malaria Eradication. Malaria eradication: benefits, future scenarios and feasibility. A report of the Strategic Advisory Group on Malaria Eradication. Geneva: World Health Organization (2020).

Google Scholar

4. World Health Organization. Ending the neglect to attain the Sustainable Development Goals: a road map for neglected tropical diseases 2021–2030. Geneva: World Health Organization (2020).

Google Scholar

5. Raviglione M, Marais B, Floyd K, Lönnroth K, Getahun H, Migliori GB, et al. Scaling up interventions to achieve global tuberculosis control: progress and new developments. Lancet (2012) 379(9829):1902–13. doi: 10.1016/S0140-6736(12)60727-2

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hotez PJ, Pecoul B, Rijal S, Boehme C, Aksoy S, Malecela M, et al. Eliminating the neglected tropical diseases: translational science and new technologies. PloS Negl Trop Dis (2016) 10(3):e0003895. doi: 10.1371/journal.pntd.0003895

PubMed Abstract | CrossRef Full Text | Google Scholar

7. World Health Organization. Global report on neglected tropical diseases 2023. Geneva: World Health Organization (2023).

Google Scholar

8. Bangert M, Molyneux DH, Lindsay SW, Fitzpatrick C, Engels D. The cross-cutting contribution of the end of neglected tropical diseases to the sustainable development goals. Infect Dis Poverty. (2017) 6(1):73. doi: 10.1186/s40249-017-0288-0

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Local Burden of Disease 2019 Neglected Tropical Diseases Collaborators. The global distribution of lymphatic filariasis, 2000-18: a geospatial analysis. Lancet Glob Health (2020) 8(9):e1186–e94. doi: 10.1016/S2214-109X(20)30286-2

PubMed Abstract | CrossRef Full Text | Google Scholar

10. World Health Organization. Lymphatic filariasis Geneva 2022. Available at: https://www.who.int/news-room/fact-sheets/detail/lymphatic-filariasis.

Google Scholar

11. Garchitorena A, Raza-Fanomezanjanahary EM, Mioramalala SA, Chesnais CB, Ratsimbasoa CA, Ramarosata H, et al. Towards elimination of lymphatic filariasis in southeastern Madagascar: Successes and challenges for interrupting transmission. PloS Negl Trop Dis (2018) 12(9):e0006780. doi: 10.1371/journal.pntd.0006780

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Michael E, Smith ME, Katabarwa MN, Byamukama E, Griswold E, Habomugisha P, et al. Substantiating freedom from parasitic infection by combining transmission model predictions with disease surveys. Nat Commun (2018) 9(1):4324. doi: 10.1038/s41467-018-06657-5

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Sharma S, Smith ME, Bilal S, Michael E. Evaluating elimination thresholds and stopping criteria for interventions against the vector-borne macroparasitic disease, lymphatic filariasis, using mathematical modelling. Commun Biol (2023) 6(1):225. doi: 10.1038/s42003-022-04391-9

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Rebollo MP, Mohammed KA, Thomas B, Ame S, Ali SM, Cano J, et al. Cessation of mass drug administration for lymphatic filariasis in Zanzibar in 2006: was transmission interrupted? PloS Negl Trop Dis (2015) 9(3):e0003669. doi: 10.1371/journal.pntd.0003669

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Weiss PS, Michael E, Richards FO Jr. Simulating a Transmission Assessment Survey: An evaluation of current methods used in determining the elimination of the neglected tropical disease, Lymphatic Filariasis. Int J Infect Dis (2021) 102:422–8. doi: 10.1016/j.ijid.2020.10.077

PubMed Abstract | CrossRef Full Text | Google Scholar

16. World Health Organization. Monitoring and epidemiological assessment of mass drug administration in the global programme to eliminate lymphatic filariasis : a manual for national elimination programmes. Geneva: World Health Organization (2011).

Google Scholar

17. Chu BK, Deming M, Biritwum NK, Bougma WR, Dorkenoo AM, El-Setouhy M, et al. Transmission assessment surveys (TAS) to define endpoints for lymphatic filariasis mass drug administration: a multicenter evaluation. PloS Negl Trop Dis (2013) 7(12):e2584. doi: 10.1371/journal.pntd.0002584

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Boyd A, Won KY, McClintock SK, Donovan CV, Laney SJ, Williams SA, et al. A community-based study of factors associated with continuing transmission of lymphatic filariasis in Leogane, Haiti. PloS Negl Trop Dis (2010) 4(3):e640. doi: 10.1371/journal.pntd.0000640

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Lau CL, Sheridan S, Ryan S, Roineau M, Andreosso A, Fuimaono S, et al. Detecting and confirming residual hotspots of lymphatic filariasis transmission in American Samoa 8 years after stopping mass drug administration. PloS Negl Trop Dis (2017) 11(9):e0005914. doi: 10.1371/journal.pntd.0005914

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Strategic and technical advisory group for neglected tropical diseases subgroup on disease-specific indicators. Responding to failed transmission assessment surveys. Report of an ad hoc meeting. Geneva: World Health Organization. (2016).

Google Scholar

21. Rao RU, Nagodavithana KC, Samarasekera SD, Wijegunawardana AD, Premakumara WDY, Perera SN, et al. A comprehensive assessment of lymphatic filariasis in Sri Lanka six years after cessation of mass drug administration. PloS Negl Trop Dis (2014) 8(11):e3281. doi: 10.1371/journal.pntd.0003281

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Rao RU, Samarasekera SD, Nagodavithana KC, Goss CW, Punchihewa MW, Dassanayaka TDM, et al. Comprehensive assessment of a hotspot with persistent bancroftian filariasis in Coastal Sri Lanka. Am J Trop Med Hyg (2018) 99(3):735–42. doi: 10.4269/ajtmh.18-0169

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Sheel M, Sheridan S, Gass K, Won K, Fuimaono S, Kirk M, et al. Identifying residual transmission of lymphatic filariasis after mass drug administration: Comparing school-based versus community-based surveillance - American Samoa, 2016. PloS Negl Trop Dis (2018) 12(7):e0006583. doi: 10.1371/journal.pntd.0006583

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Goldberg EM, King JD, Mupfasoni D, Kwong K, Hay SI, Pigott DM, et al. Ecological and socioeconomic predictors of transmission assessment survey failure for lymphatic filariasis. Am J Trop Med Hyg (2019) 101(1):271–8. doi: 10.4269/ajtmh.18-0721

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lau CL, Sheel M, Gass K, Fuimaono S, David MC, Won KY, et al. Potential strategies for strengthening surveillance of lymphatic filariasis in American Samoa after mass drug administration: Reducing ‘number needed to test’ by targeting older age groups, hotspots, and household members of infected persons. PloS Negl Trop Dis (2021) 14(12):e0008916. doi: 10.1371/journal.pntd.0008916

CrossRef Full Text | Google Scholar

26. Michael E, Singh BK. Heterogeneous dynamics, robustness/fragility trade-offs, and the eradication of the macroparasitic disease, lymphatic filariasis. BMC Med (2016) 14:14. doi: 10.1186/s12916-016-0557-y

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Singh BK, Michael E. Bayesian calibration of simulation models for supporting management of the elimination of the macroparasitic disease, Lymphatic Filariasis. Parasit Vectors. (2015) 8:522. doi: 10.1186/s13071-015-1132-7

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Michael E, Singh BK, Mayala BK, Smith ME, Hampton S, Nabrzyski J. Continental-scale, data-driven predictive assessment of eliminating the vector-borne disease, lymphatic filariasis, in sub-Saharan Africa by 2020. BMC Med (2017) 15(1):176. doi: 10.1186/s12916-017-0933-2

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Prada JM, Davis EL, Touloupou P, Stolk WA, Kontoroupis P, Smith ME, et al. Elimination or resurgence: modelling lymphatic filariasis after reaching the 1% Microfilaremia prevalence threshold. J Infect Dis (2020) 221(Suppl 5):S503–S9. doi: 10.1093/infdis/jiz647

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Gambhir M, Bockarie M, Tisch D, Kazura J, Remais J, Spear R, et al. Geographic and ecologic heterogeneity in elimination thresholds for the major vector-borne helminthic disease, lymphatic filariasis. BMC Biol (2010) 8:22. doi: 10.1186/1741-7007-8-22

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Smith ME, Griswold E, Singh BK, Miri E, Eigege A, Adelamo S, et al. Predicting lymphatic filariasis elimination in data-limited settings: A reconstructive computational framework for combining data generation and model discovery. PloS Comput Biol (2020) 16(7):e1007506. doi: 10.1371/journal.pcbi.1007506

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Michael E, Malecela-Lazaro MN, Kazura JW. Epidemiological modelling for monitoring and evaluation of lymphatic filariasis control. Adv Parasit (2007) 65:191–237. doi: 10.1016/S0065-308X(07)65003-9

CrossRef Full Text | Google Scholar

33. Anderson DP, Ramsey DS, Nugent G, Bosson M, Livingstone P, Martin PA, et al. A novel approach to assess the probability of disease eradication from a wild-animal reservoir host. Epidemiol Infect (2013) 141(7):1509–21. doi: 10.1017/S095026881200310X

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Michael E. The population dynamics and epidemiology of lymphatic filariasis. Lymphatic Filariasis (2000) 1:41–81. doi: 10.1142/9781848160866_0003

CrossRef Full Text | Google Scholar

35. Witt C, Ottesen EA. Lymphatic filariasis: an infection of childhood. Trop Med Int Health (2001) 6(8):582–606. doi: 10.1046/j.1365-3156.2001.00765.x

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Coutts SP, King JD, Pa'au M, Fuimaono S, Roth J, King MR, et al. Prevalence and risk factors associated with lymphatic filariasis in American Samoa after mass drug administration. Trop Med Health (2017) 45:22. doi: 10.1186/s41182-017-0063-8

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Kazienga A, Coffeng LE, de Vlas SJ, Levecke B. Two-stage lot quality assurance sampling framework for monitoring and evaluation of neglected tropical diseases, allowing for imperfect diagnostics and spatial heterogeneity. PloS Negl Trop Dis (2022) 16(4):e0010353. doi: 10.1371/journal.pntd.0010353

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Cameron AR, Baldock FC. Two-stage sampling in surveys to substantiate freedom from disease. Prev Vet Med (1998) 34(1):19–30. doi: 10.1016/S0167-5877(97)00073-1

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Cameron AR, Baldock FC. A new probability formula for surveys to substantiate freedom from disease. Prev Vet Med (1998) 34(1):1–17. doi: 10.1016/S0167-5877(97)00081-0

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Martin P, Cameron A, Greiner M. Demonstrating freedom from disease using multiple complex data sources: 1: A new methodology based on scenario trees. Prev Vet Med (2007) 79(2-4):71–97. doi: 10.1016/j.prevetmed.2006.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

41. World Health Organization. Expanded special project for elimination of neglected tropical diseases. Available at: https://espen.afro.who.int/diseases/lymphatic-filariasis.

Google Scholar

42. World Health Organization. PCT Databank - Lymphatic filariasis (2020). Available at: https://www.who.int/teams/control-of-neglected-tropical-diseases/data-platforms/pct-databank/lymphatic-filariasis.

Google Scholar

43. Project MA. Malaria Atlas Project. Analytics for a malaria-free world 2020. Available at: https://data.malariaatlas.org/insecticide-treated-nets.

Google Scholar

44. Gambhir M, Michael E. Complex ecological dynamics and eradicability of the vector borne macroparasitic disease, lymphatic filariasis. PloS One (2008) 3(8):e2874. doi: 10.1371/journal.pone.0002874

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Anderson RM, Anderson B, May RM. Infectious diseases of humans: dynamics and control. Oxford: Oxford University Press (1992).

Google Scholar

46. Irvine M, Njenga S, Gunawardena S, Wamae CN, Cano J, Brooker S, et al. Understanding the relationship between prevalence of microfilariae and antigenaemia using a model of lymphatic filariasis infection. Trans R Soc Trop Med Hygiene. (2016) 110:118–24. doi: 10.1093/trstmh/trv096

CrossRef Full Text | Google Scholar

47. Harrison E, Drake T, Ots R. finalfit: quickly create elegant regression results tables and plots when modelling. R package (2020). Available at: https://github.com/ewenharrison/finalfit.

Google Scholar

48. Smith ME, Singh BK, Michael E. Assessing endgame strategies for the elimination of lymphatic filariasis: A model-based evaluation of the impact of DEC-medicated salt. Sci Rep (2017) 7(1):7386. doi: 10.1038/s41598-017-07782-9

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Spear RC, Hubbard A. Parameter estimation and site-specific calibration of disease transmission models. Adv Exp Med Biol (2010) 673:99–111. doi: 10.1007/978-1-4419-6064-1_7

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Reimer LJ, Thomsen EK, Tisch DJ, Henry-Halldin CN, Zimmerman PA, Baea ME, et al. Insecticidal bed nets and filariasis transmission in Papua New Guinea. N Engl J Med (2013) 369(8):745–53. doi: 10.1056/NEJMoa1207594

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Cameron A. Survey toolbox for aquatic animal diseases: a practical manual and software package. Canberra: Australian Centre for International Agricultural Research (2002).

Google Scholar

52. Cannon RM. Demonstrating disease freedom - combining confidence levels. Prev Vet Med (2002) 52(3-4):227–49. doi: 10.1016/S0167-5877(01)00262-8

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Honaker J, King G, Blackwell M. Amelia II: A program for missing data. J Stat Software (2011) 45(7):1–47. doi: 10.18637/jss.v045.i07

CrossRef Full Text | Google Scholar

54. Weil GJ, Lammie PJ, Weiss N. The ICT Filariasis Test: A rapid-format antigen test for diagnosis of bancroftian filariasis. Parasitol Today (1997) 13(10):401–4. doi: 10.1016/S0169-4758(97)01130-7

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Hund L, Bedrick EJ, Pagano M. Choosing a cluster sampling design for lot quality assurance sampling surveys. PloS One (2015) 10(6):e0129564. doi: 10.1371/journal.pone.0129564

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Lanata CF, Stroh G Jr., Black RE. Lot quality assurance sampling in health monitoring. Lancet (1988) 1(8577):122–3. doi: 10.1016/S0140-6736(88)90323-6

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Robertson SE, Valadez JJ. Global review of health care surveys using lot quality assurance sampling (LQAS), 1984-2004. Soc Sci Med (2006) 63(6):1648–60. doi: 10.1016/j.socscimed.2006.04.011

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Hund L, Pagano M. Extending cluster lot quality assurance sampling designs for surveillance programs. Stat Med (2014) 33(16):2746–57. doi: 10.1002/sim.6145

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Bockarie MJ, Pedersen EM, White GB, Michael E. Role of vector control in the global program to eliminate lymphatic filariasis. Annu Rev Entomol (2009) 54:469–87. doi: 10.1146/annurev.ento.54.110807.090626

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Michael E, Gambhir M. Vector transmission heterogeneity and the population dynamics and control of lymphatic filariasis. Adv Exp Med Biol (2010) 673:13–31. doi: 10.1007/978-1-4419-6064-1_2

PubMed Abstract | CrossRef Full Text | Google Scholar