The Antenna Base Plays a Crucial Role in Mosquito Courtship Behavior

Mosquitoes are vectors of pathogens that cause diseases like malaria, dengue fever, yellow fever, chikungunya and Zika. For mosquito control it is crucial to understand their hearing system, as mosquitoes’ courting behavior is mostly auditory. Many nonlinear characteristics of the mosquito hearing organ have been observed through behavioral studies and neural measurements. These enable mosquitoes to detect and synchronize to other mosquitoes. Many hypotheses concerning the role of the flagellum and the fibrillae of the antenna in mosquito hearing have been made, and neural processes have been considered as the origin of the nonlinearities. In this study we introduce a geometric model based on the morphology of the mosquito antenna base. The model produces many of the observed nonlinear characteristics, providing evidence that the base of the antenna plays a crucial role in mosquito hearing. Even without neural processing, the antenna response to sound produces behaviorally relevant cues that can inform about the presence, location, and sex of other mosquitoes.

1 Introduction

Mosquitoes are amongst the deadliest animals on earth, as they are vectors of pathogens that cause diseases like malaria, dengue fever, yellow fever, chikungunya and Zika, that cause over 700,000 deaths per year and inflict suffering on more than 50 million people (1, 2). However, out of over 3,500 extant species only around 100 are invasive (3). Still, 40 to 80% of the global population are at risk of one or more major vector-borne diseases (VBD) (2, 4).

When regional proliferation of a dangerous mosquito species has been identified, interventions by means of insecticide spraying, Sterile Insect Technique (SIT) or Incompatible Insect Technique (IIT) can be carried out (5, Chap 20) to protect the population. In the SIT (5), male mosquitoes are sterilized, e.g., by means of x-ray radiation, and then released into the wild. Mating with sterile mosquitoes decrease the females’ reproductive potential, which can ultimately reduce the population. In the IIT male mosquitoes are infected with Wolbachia bacteria that causes cytoplasmic incompatibility, i.e., uninfected females mated to infected males fail to produce viable progeny, leading to an effect similar to SIT. A third option is the release of insects with a dominant lethal (RIDL) gene. This lethal gene is female-specific, so all progenies are male.

In vector surveillance programs the adult occurrence is an important indicator for classifying risk of arbovirus outbreak (6). Here, mosquitoes are trapped and then morphologically identified and counted by trained staff, which is time consuming and labor intensive (2). Acoustical sensors (7–9) offer an efficient alternative. Through acoustic analysis and machine learning they automatically classify, i.e., identify, and count mosquito species and sex. Unfortunately, the transfer from the lab to real world conditions is not robust so far, i.e., environmental sounds impede identification and counting.

As sound is a crucial sexual stimulant in many mosquito species (10, 11), and mosquitoes identify, recognize, localize and approach other mosquitoes “seemingly unerringly” (12) by means of sound (11, 13–19), understanding their auditory system may help us automatically identifying and counting mosquito species and sex in the future and, eventually, understand and control mosquitoes’ acoustic courtship behavior that has been observed, e.g., in Aedes aegypti (10, 14, 16), Anopheles albimanus (12), Anopheles subpictus (13), Culex quinquefasciatus (18, 20) and Toxorhynchites brevipalpis (17), and generalized to “the most intensely studied vector species” (18). Note, however, that some mosquito species, like Sabethes cyaneus (21), do not rely on acoustic communication for mating. Consequently, our model does not generalize to all mosquitoes but rather to those listed above, which exhibit an acoustical mating behavior.

It has been pointed out that there is a need for more detailed biomechanical analyses of mosquito antennae, but that there are technical limitations in deducting knowledge from measurements due to the small size of mosquito antennae (22). In this paper we introduce and evaluate a biologically-inspired model of the mosquito antenna base. The model is an analysis-by-synthesis approach that enables us to find out more about the nonlinear transduction mechanisms inside the mosquito antenna that enables them to detect, identify and localize other mosquitoes of the same and other species. Through this inductive reasoning approach, we induce how mosquito hearing may work, which may be confirmed, complemented, or rejected by deductive measurements in the future.

2 Mosquito Hearing

Mosquitoes are amongst the best-hearing insects (22). The periphery of the mosquito hearing organ is the antenna pair. The morphology of the antenna is described, e.g., in (13, 23–25) and depicted in (19, 23, 26, 27). An antenna consists of a flagellum, the pedicel, and the scape. As can be seen in Figure 1 (left), the flagellum has a shaft (bold black line) to which fibrillae of multiple lengths are attached. The flagellum is deflected by sound waves through viscose drag. The flagellum is suspended by its base in the pedicel (19). In the pedicel, the base of the flagellum shaft is surrounded by a bulb. The bulb is not deflected through sound waves in air. We therefore consider the flagellum and its shaft as motile and the bulb of the pedicel as immotile. The immotile bulb of the pedicel contains the Johnston’s Organ (JO). The lowest segment of the antenna base is the scape. It contains muscles and the nerves that connect the sensory organ with the mosquito brain. The scape is out of scope of the present antenna model and not included in our figures.

FIGURE 1

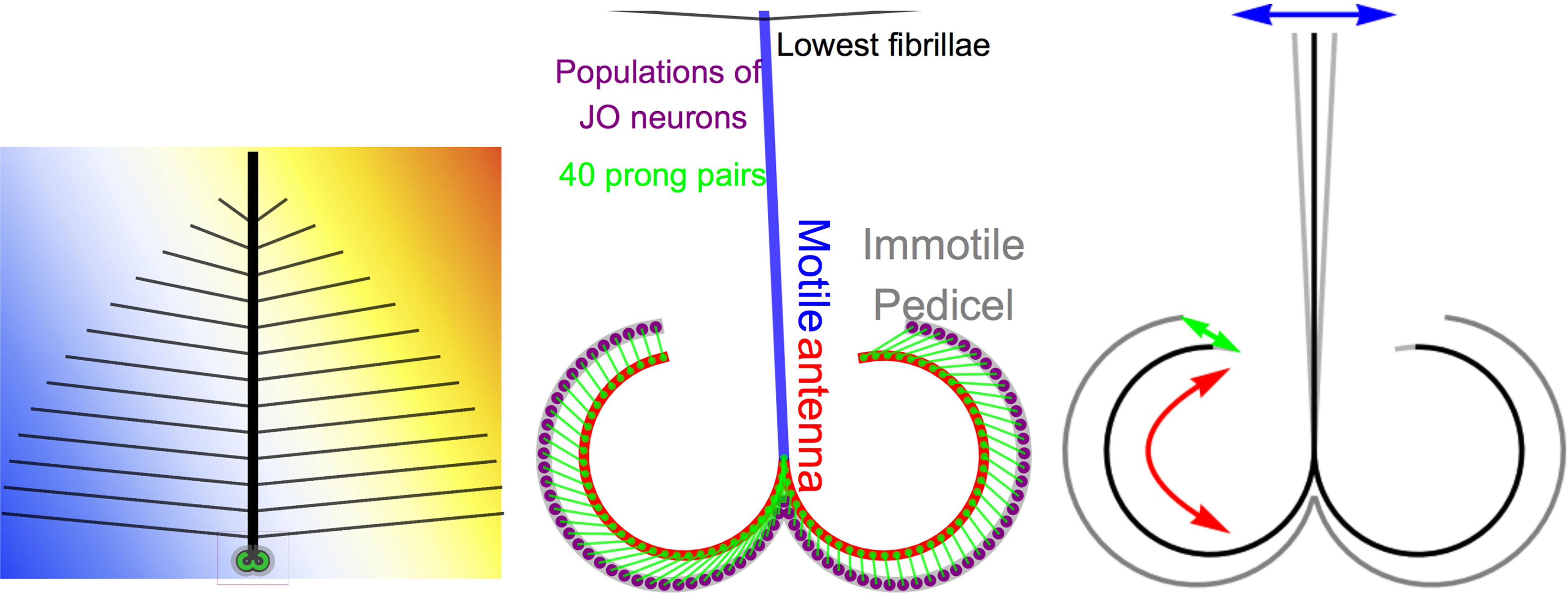
Figure 1 Mosquito antenna in a sound field (left). The antenna base (center) contains the linear (blue) and curved (red) part of the motile antenna. The curved part contains prongs (green dots) which are connected (green lines) to populations of neurons (purple dots) on the Johnstons’s organ (JO), which is embedded in the immotile pedicel (gray). The model in motion can be seen on https://youtu.be/D4yNbGvX4lU. Most importantly, the model produces a transfer from deflection (blue arrows) over rotation (red arrows) to stretch/compression (green arrows), which produces new frequencies.

In the JO mechanoreceptors sense particle velocities (28). This helps for hearing sound sources. But the JO is also a somatosensory system, as the mosquito may detect wind as well as its own flight tone, which are necessary for navigation. Furthermore, the JO contains thermoreceptors and different types of chemoreceptors. Consequently, the 15,000 neurons in the JO are not exclusively auditory (29).

Auditory neurons in the JO are tuned to frequencies between 85 to 470 Hz (30) and mechano-electrical transduction is limited to frequencies below 400 Hz. This is true for both female and male mosquitoes (18). When flying, the mosquito’s wing beats produce a flight tone, i.e., a harmonic spectrum with a fundamental frequency that roughly lies between 200 Hz and 1200 Hz (9, 31). The fundamental frequency mainly depends on species and sex but can be influenced by flight maneuvers, age, humidity, or temperature (see e.g. [32, p. 299]).

Throughout most species, the male mosquito is considerably smaller, creating a much higher fundamental frequency. Note that mosquitoes are very small compared to the wavelengths that their wing beats produce, so they can be considered as point sources whose sound energy largely remains within their near field rather than propagating to the far field [33, Chap. 5]. Consequently, mosquitoes seem to hear each other only over a range of up to about 10 centimeters (16, 17, 29, 34, 35), even though it has been shown that they can also hear loud sounds from much larger distances (29). The mosquitoes’ frequency tuning implies that many mosquitoes cannot even directly hear male mosquitoes, as males exclusively create inaudibly high frequencies (13). However, during mate attraction, mosquitoes of the same species but opposite sex synchronize (16). Synchronization is also referred to as tune-in (18), harmonic convergence (16) and frequency locking (36) in the mosquito literature, and as lock-in or entrainment in other domains [e.g., (33, 37, 38)]. Every second wing beat of the female mosquito is synchronous to every third wing beat of the male mosquito, so what matches are the second partial of the male mosquito and the third partial of the female mosquito. In musical terms, they produce a fifth, not a unison. Mate attraction is bi-directional, i.e., both male and female mosquitoes modulate their flight tones to create the fifth (16), which tends to lie above 1 kHz. It is assumed that sound is the major sexual stimulant in many mosquito species (10), as courtship and copulation only takes place between flying mosquitoes and not, if either of the mosquitoes is at rest [(5, p. 20, 10, 39, 40, p. 324)]. At the same time, even in absence of female mosquitoes, male mosquitoes have been found to copulate with loudspeakers if they play the right sound (40, p.57). Note that the synchronization alters between perfect and imperfect match, creating beats every now and then.

As mosquitoes tend to synchronize at a frequency that they cannot even hear directly (18), hypothesize a “nonlinear interaction between her own flight tones and those of a nearby male”. This hypothesis is supported by the finding that most auditory neurons in the JO are tuned to 190 to 270 Hz (30) and mosquitoes are most sensitive to frequencies below 200 Hz (18). This frequency region lies below most emitted mosquito sounds but rather covers the difference frequency between the harmonics of two wing beat sounds. We also refer to the difference frequency as the beat frequency. This frequency difference can refer to the fundamental frequency of a male and a female mosquito of the same species. Mosquitoes could hear the fundamental frequency difference of their own and a nearby wing beat. However, it has been found that mosquitoes also synchronize to the recording of an opposite sex mosquito when the fundamental frequency has been removed, and even when only a pure tone near their synchronization frequency is being played (16). So, another reason for the frequency tuning seems to be that it corresponds to the frequency difference of their overtones in the initial state of their synchronization progress during mating, i.e., to the beat frequency (20). During synchronizing, the beat frequency may fluctuate between zero and some hundred Hertz. In both cases nonlinearities in the auditory system are necessary to produce a difference frequency, i.e., to represent the beat frequency.

The fact that mosquitoes approach not only other mosquitoes, but even sound sources that produce an inaudible high pure tone near their preferred synchronization frequency (16) is evidence that the difference frequencies enable mosquitoes to localize sound sources.

Another nonlinearity that has been observed is that periodic oscillations in the JO as well as acoustically evoked field potentials often exhibit a frequency doubling compared with the stimulation frequency (11, 13, 30, 39, 41). The doubled frequency can even be stronger than the original stimulation frequency. The intensity and the number of harmonic frequencies depends on the intensity of the input signal (39). However, the strength of the doubling is different between different prongs (40). So, in addition to difference frequencies, harmonic distortion seems to take place, in which the doubled frequency may dominate the biomechanical and neural response at least at some locations along the JO.

It has been observed that some axons of the JO sensory unit respond in anti-phase to each other (30). This is likely to happen because mechanical motion of the antenna creates anti-phase excitation at the JO, so the axons respond in anti-phase in order to amplify the excitation.

The origin of such nonlinearities that enable mosquitoes to synchronize is still an open question, but understanding the mechanisms underlying the selection of conspecific mates “(…) could open the door to novel ways of attracting or trapping and killing males or females” (42). Our model sheds light on the nature of the nonlinear interaction in mosquito hearing, beginning in the mosquito antenna base, as “[f]uture research is needed to resolve these questions, but in either case, it seems, the sensory periphery will take a centre-stage role.” (34).

In summary, a number of nonlinearities has been observed in the mosquito antenna:

1. harmonic distortions

(a) that can even be stronger than the input frequency

(b) whose number and intensity depend on the prong location

(c) whose number and intensity depend on the intensity of the input signal

2. anti-phase responses

3. difference frequency between female and male f₀

4. difference frequency near the synchronization frequency

5. difference frequencies provide localization information

We use these 5 observations as criteria to evaluate to what degree the antenna base contributes to the nonlinearities that enable mosquitoes to detect, localize and synchronize to other mosquitoes.

3 Related Work

Avitabile et al. (26) model the antenna mechanics as a forced-damped oscillator. However, the model simplifies the curved septa as a straight line instead of sticking to the actual geometry of the mosquito antenna morphology, and it has physically implausible properties (43), so the model needs some further explorations to be explanatory for the nonlinear processing in the mosquito antenna.

Saltin et al. (27) model an antenna flagellum using a finite element method and conclude that the main function of the varying stiffness along the length of the flagellum could serve for mechanical frequency selectivity, i.e., bandpass filtering and amplification of some specific frequencies and attenuation of others. This is in agreement with the observations of (44) who model the flagellum as a damped harmonic oscillator with a series of filters.

Mhatre (45) reviews a number of additional insect ear models that mostly aim at exploring active amplification through biophysical and neurobiological considerations.

All of these models concentrate on physical properties of the flagellum and partly assume additional nonlinearities in the neural mechanisms of mosquito hearing. The model in (39) goes one step back and considers mostly the rotation of the basilar plate relative to the pedicel. With only little additional filtering, their model produces the difference frequency of a two-tone input, as well as harmonic distortions. These are two of the above-listed criteria. Our model does the same but sticks much closer to the morphological geometry of the mosquito antenna to be able to meet all of the above-listed criteria.

4 Mosquito Antenna Model

Our antenna model is a geometric model based on (46). As a simplification we neglect physical properties, like mass, material stiffness, sound impedance, restoring forces, etc. Instead, we consider all parts of the antenna as perfectly rigid and the connection between the motile and immotile part of the antenna as perfectly flexible. This is a reasonable simplification, as the antenna is a structure that is very small compared to the wavelengths that is receives and stiff compared to the surrounding air, so the “flagellum moves like a stiff rod rocking about its socket when stimulated at frequencies below or around the best frequency” (22). The model approximates the morphological relations of the antenna base as described for Culex quinquefasciatus (15, 23), Culex pipiens pipiens (30), Toxorhynchites brevipalpis (17, 19, 26, 27), Aedes aegypti (24), Anopheles subpictus (13), Anopheles arabiensis (27) and Anopheles gambiae (47) (19). examined the auditory system of Toxorhynchites brevipalpis but generalize their findings to mosquito hearing, so this morphology is certainly representative for many mosquito species.

The model is illustrated in Figure 1 (center). It assumes a motile flagellum (blue) whose deflection equals the particle deflection of the incoming sound waves. At the distal end of the scape, the antenna flagellum is extended by the curved septa (s, red)

$\begin{array}{ll}s(\varphi )=\left|\cos (\varphi +d(t))\right|,\frac{3\pi }{4}\le \varphi \le \frac{9\pi }{4}& (1)\end{array}$

Here, d(t) is the deflection of the antenna, which is proportional to the particle deflection caused by sound waves. Together, the flagellum and the septa comprise the motile antenna part. The flagellum and the septa meet at the socket, the basilar plate at ϕ = π. The motile septa contains 40 prong pairs (green dots) at

$\begin{array}{ll}{\varphi }_{s,i}(t)=d(t)+\frac{3\pi }{4}+i\frac{6\pi }{4\times 79},i=0,\dots ,79.& (2)\end{array}$

These are connected to auditory nerve cells of the Johnston’s organ (JO, purple) via the attachment cells of the scolopidia (green lines), which are located at the discrete positions

$\begin{array}{ll}{\varphi }_{p,i}=\frac{3\pi }{4}+i\frac{6\pi }{4\times 79},i=0,\dots ,79& (3)\end{array}$

along the immotile pedicel

$\begin{array}{ll}p(\varphi )=0.2+\left|\cos (\varphi )\right|,\frac{3\pi }{4}\le \varphi \le \frac{9\pi }{4}.& (4)\end{array}$

We consider the pedicel immotile and perfectly rigid, so the rotation of the septa is restricted to $\frac{\pi }{4}<d(t)<\frac{3\pi }{4}$. From a macroscopic viewpoint, our antenna model describes a transform from deflection (blue arrow) to rotation (red arrow) as depicted in Figure 1 (right). However, as illustrated in Figure 1 (center), the model imposes a one-to-many transform: the deflection d(t) of the flagellum creates 80 rotations, one at each prong. These rotations stretch and compress the attachment cells of the scolopidia at 80 locations like

$\begin{array}{ll}{r}_i(t)={\left|\left|p({\varphi }_{p,i})-s({\varphi }_{s,i}(t))\right|\right|}_2& (5)\end{array}$

which is the Euclidean distance between the septa and the pedicel at the locations of the 80 prongs. These are functions of time because the septa moves as a function of time.

So, the input of the model is a continuous function d(t) or a discrete time series d[τ] that represents the flagellum deflection caused by an incoming sound wave. Likewise, the output can be the continuous functions r_i(t) or discrete time series r_i[τ]. We use capital letters to indicate that we are dealing with the frequency spectrum after a Discrete Fourier Transform (DFT), i.e.,

$\begin{array}{ll}D(\omega )=\text{DFT}[d(t)]& (6)\end{array}$

and

$\begin{array}{ll}{R}_i(\omega )=\text{DFT}[r_i(t)].& (7)\end{array}$

In nature, the antenna is deflected by sound waves. The wing beats of the mosquito itself creates a flight tone that propagates to its antenna pair. Furthermore, the flight tones of other mosquitoes travel to the antenna. Consequently, the antenna is deflected by superposition of the mosquito’s own wing beat sound, the wing beat sound of other mosquitoes and additional ambient sounds.

In the mosquito the stretch and compression of the attachment cells open channels that cause neural activity in the auditory part of the antennal nerve (30). However, the neural encoding and further processing is out of scope of this paper.

5 Evaluation

The evaluation of our mosquito antenna model is explorative and qualitative. We examine which of the 5 nonlinear characteristics of mosquito hearing is reproduced by the model.

As the deflection of the antenna D(ω) and the stretch and compression of attachment cells take place at different orders of magnitude, we normalize amplitudes as

$\begin{array}{ll}D(\omega )[\text{dB}]=20\left(\underset{10}{\log }\frac{D(\omega )}{\max |D(\omega )|}\right)& (8)\end{array}$

and

$\begin{array}{ll}{R}_i(\omega )[\text{dB}]=20\left(\underset{10}{\log }\frac{R_i(\omega )}{\max |R_i(\omega )|}\right),& (9)\end{array}$

respectively. Due to this normalization, all amplitudes take values ≤ 0 dB, where D(ω) = 0 dB refers to the loudest input frequency and R_i(ω) = 0 dB to the strongest response frequency at the ith prong.

5.1 Harmonic Distortion

First, we input a pure tone with a frequency of 1200 Hz to the model. Figure 2 illustrates the frequency spectrum of the input signal D(ω) (orange) and the antenna response R_i(ω) (blue) of prongs number 0 (left) and 11 (center). In both cases the antenna responds with the input frequency and additional harmonic overtones, as suggested by criteria 1. Harmonic distortion can be observed at all prongs and always contains even and odd integer multiples of the incoming frequency. However, the amplitude distribution is different for different prongs, as suggested by criteria 1b. At prong 11 the first overtone has an even larger amplitude than the fundamental frequency. This is in agreement with the frequently observed frequency doubling (13, 30, 39) evident at different prongs, and with criteria 1a. As illustrated in Figure 3, the frequency doubling is even clearer visible in the time domain than in frequency domain. Every input cycle the prong output exhibits two cycles.

FIGURE 2

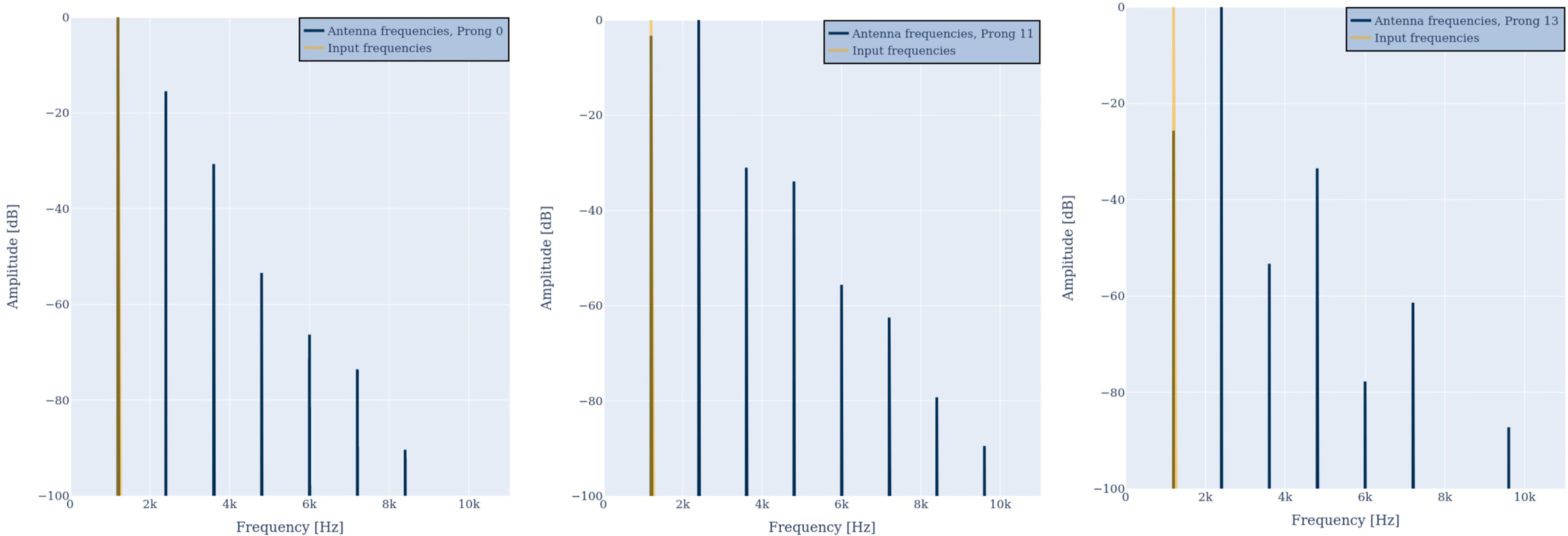
Figure 2 Antenna response R₀(ω) (blue, left) and R₁₁(ω) (blue, center) to a single frequency of 1200 Hz (orange). The output spectrum either peaks at the input frequency or the double frequency. Additional harmonic overtones are visible. When reducing the amplitude of the input by a factor of 2 (right) the distribution of distortion frequencies in R₁₁(ω) changes and the distortion factor reduces.

FIGURE 3

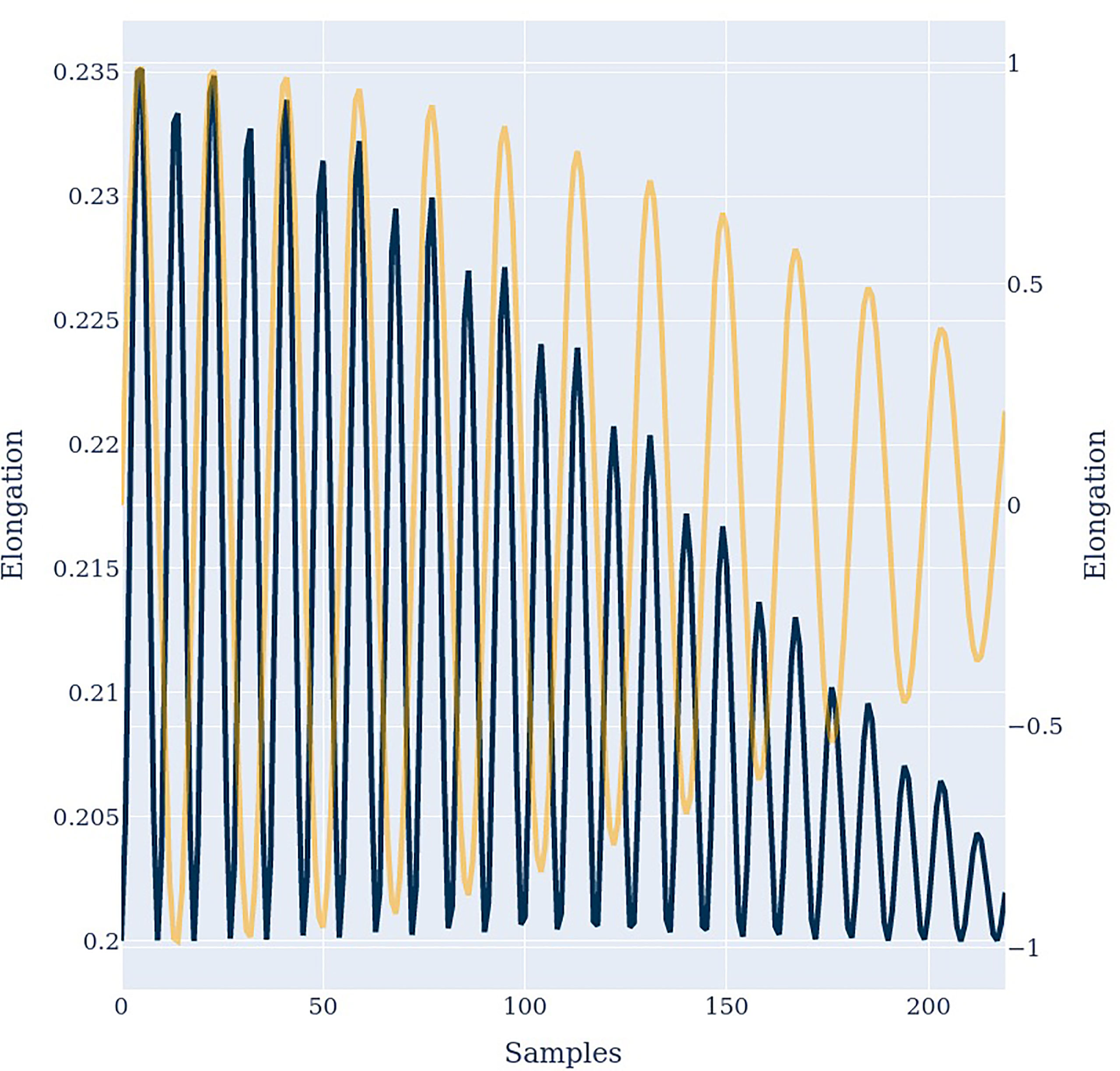
Figure 3 The input signal (orange) and the antenna output signal in the time domain. A frequency doubling similar to Figure 5 can be observed.

When reducing the amplitude of the input spectrum D(ω) by a factor of 2 (center vs. right in Figure 2) the distribution of harmonic distortion frequencies in R₁₁(ω) changes and the overall distortion factor reduces. This is in agreement with criteria 1c.

5.2 Anti-Phase Response

Figure 4 shows the antenna response in time domain at two different prongs. It can be observed that the two prongs respond in anti-phase to each other, as suggested by criteria 2.

FIGURE 4

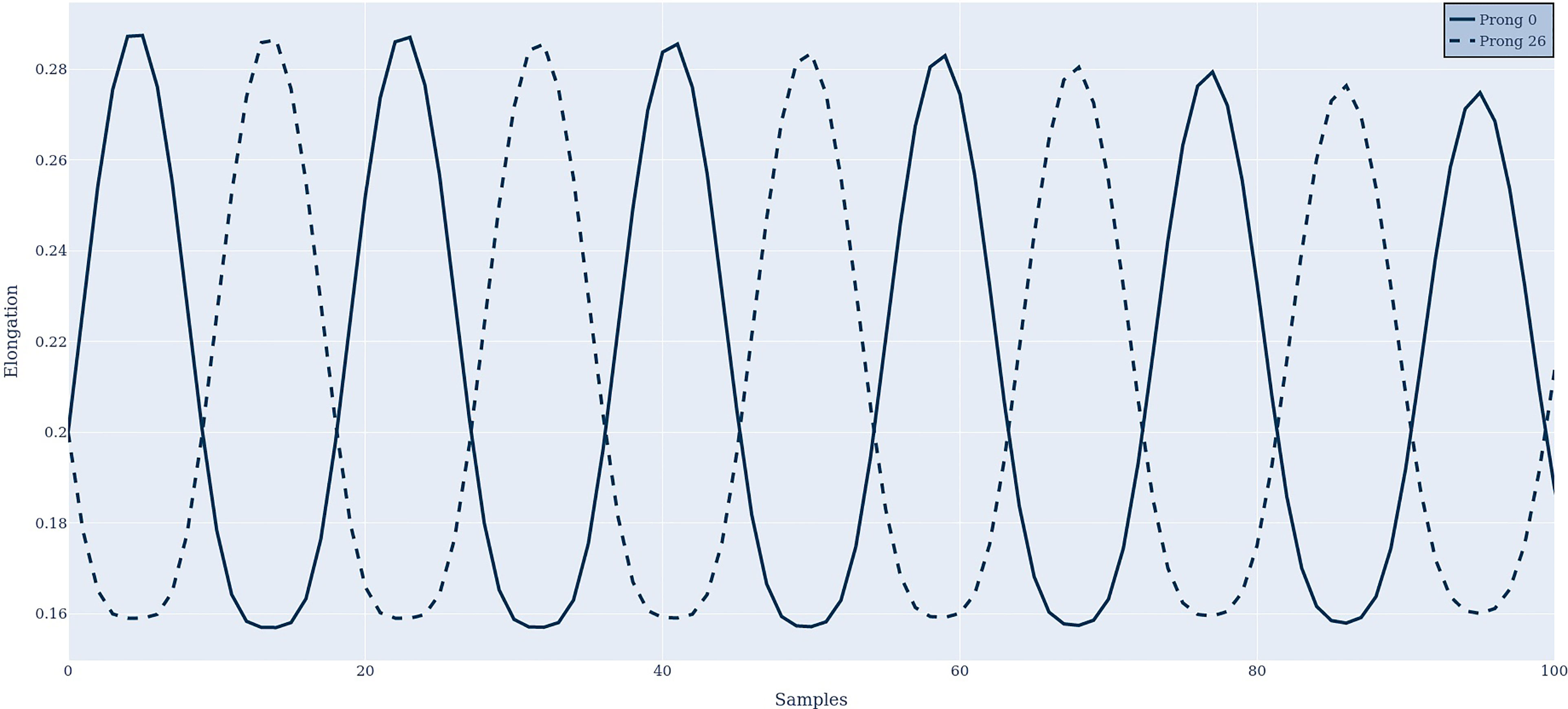
Figure 4 The antenna response in the time domain at prongs 0 and 26, when stimulated with two frequencies of 1200 Hz and 1240 Hz.

5.3 Difference Tones

Note that exciting the antenna with a single frequency simulates a very simple scenario in which a passive mosquito is exposed to a sine wave. To simulate flight, we input a superposition of two proximate pure tones of f_int=1200 and f_ext=1240 Hz to the model. One of these frequencies simulates a frequency from the wing beat of the modeled mosquito (internal) the other, of another mosquito nearby (external). The exemplary result of two different prongs is illustrated in Figure 5. The same behavior concerning the strong representation of the input frequencies in the output time series can be observed. Again, the number and amplitude of distortion products depends on the prong number (cf. R₀(ω), left and R₁₃(ω), center). The amplitude of the double frequencies can even be stronger than the amplitude of the two input frequencies.

FIGURE 5

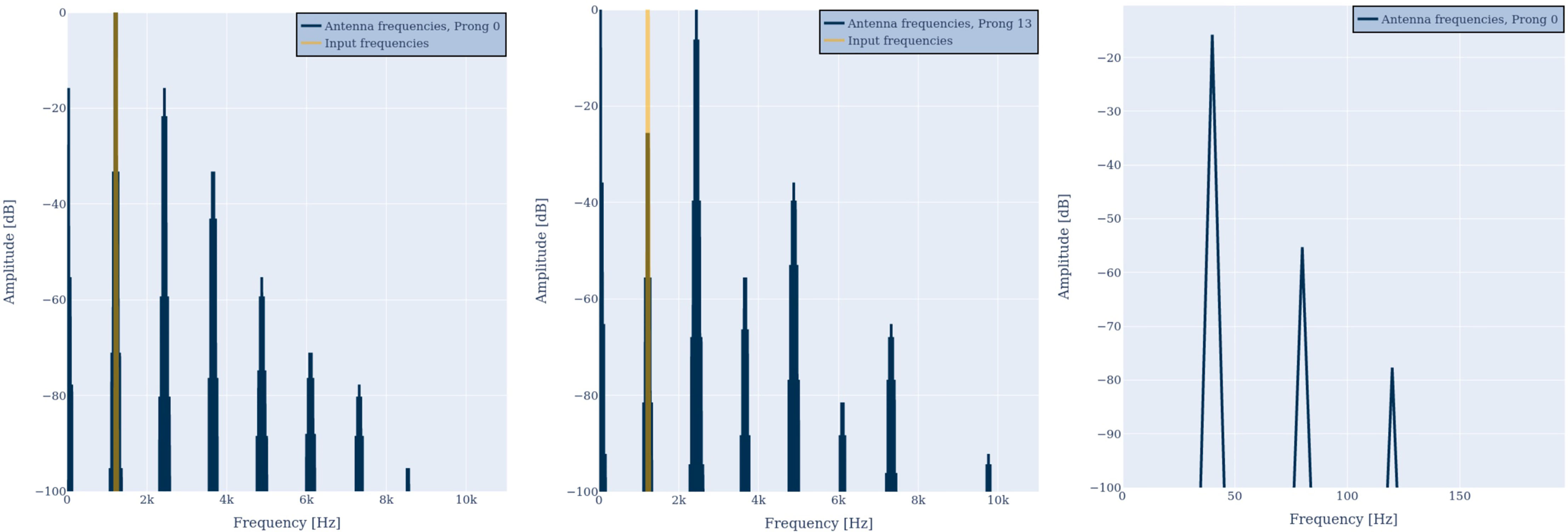
Figure 5 Antenna outputs R₀(ω) (left) and R₁₃(ω) (center), when evoked by two proximate frequencies of 1200 and 1240 Hz. The highest amplitude can be found at the input frequencies, their octaves, or their difference frequency. Zooming into the low-frequency region (right) shows the beat frequency plus harmonic distortion.

In addition, a low-frequency component is visible at most prongs. In the prong output, these low-frequency components can even be stronger than the amplitudes of the original input frequencies, as illustrated in Figure 5 for R₁₃(ω) (center). As can be seen in Figure 5 (right), the low frequency components are the difference frequency of the two input frequencies, i.e., f_beat = f_ext−f_int=40 Hz, which is in accordance with criteria 4. In addition, harmonic distortion can be observed, i.e., 80 Hz and 120 Hz.

5.4 Real Mosquitoes

As it has been shown that mosquito hearing is limited to frequencies below 470 Hz it has been deduced that mosquitoes respond to the frequency difference of overtones when performing the synchronization. To verify this, we simulated the synchronization experiment of (16) who observed the synchronization behavior of a male Aedes aegypti when exposed to a simulated female Aedes aegypti’s flight tones. We insert the flight tone of a modeled male Aedes aegypti m_int superimposed with the flight tone of a female Aedes aegypti m_ext (internal vs. external) to deflect the flagellum. The model output is 40 different time series that represent the stretch and compression of attachment cells at the individual prongs.

At first, we approximate the natural male mosquito (m_int) wing beat sound with a fundamental frequency of 636 Hz and its J = 2 multiples 1272 Hz and 1908 Hz. We observed that the amplitudes of overtones of natural mosquitoes decrease. We simulated this property by reducing the amplitude g₀ = 1 of the first overtone to g₁ = 0.95 and the second overtone to g₂ = 0.8

$\begin{array}{ll}{m}_{\mathrm{int}(t)={\Sigma }_{j=1}^J{g}_j\sin (2\pi j636\text{ Hz }t).}& (10)\end{array}$

This equation represents the sound input to the antenna in time domain, i.e., d(t), when a mosquito flies. Figure 6 illustrates the sound input in frequency domain, i.e., D(ω), together with the response R₀(ω). With only the input of the flying mosquito itself, the response only contains the input frequencies plus harmonic distortion. No excitation inside the audible frequency region < 470 Hz can be observed.

FIGURE 6

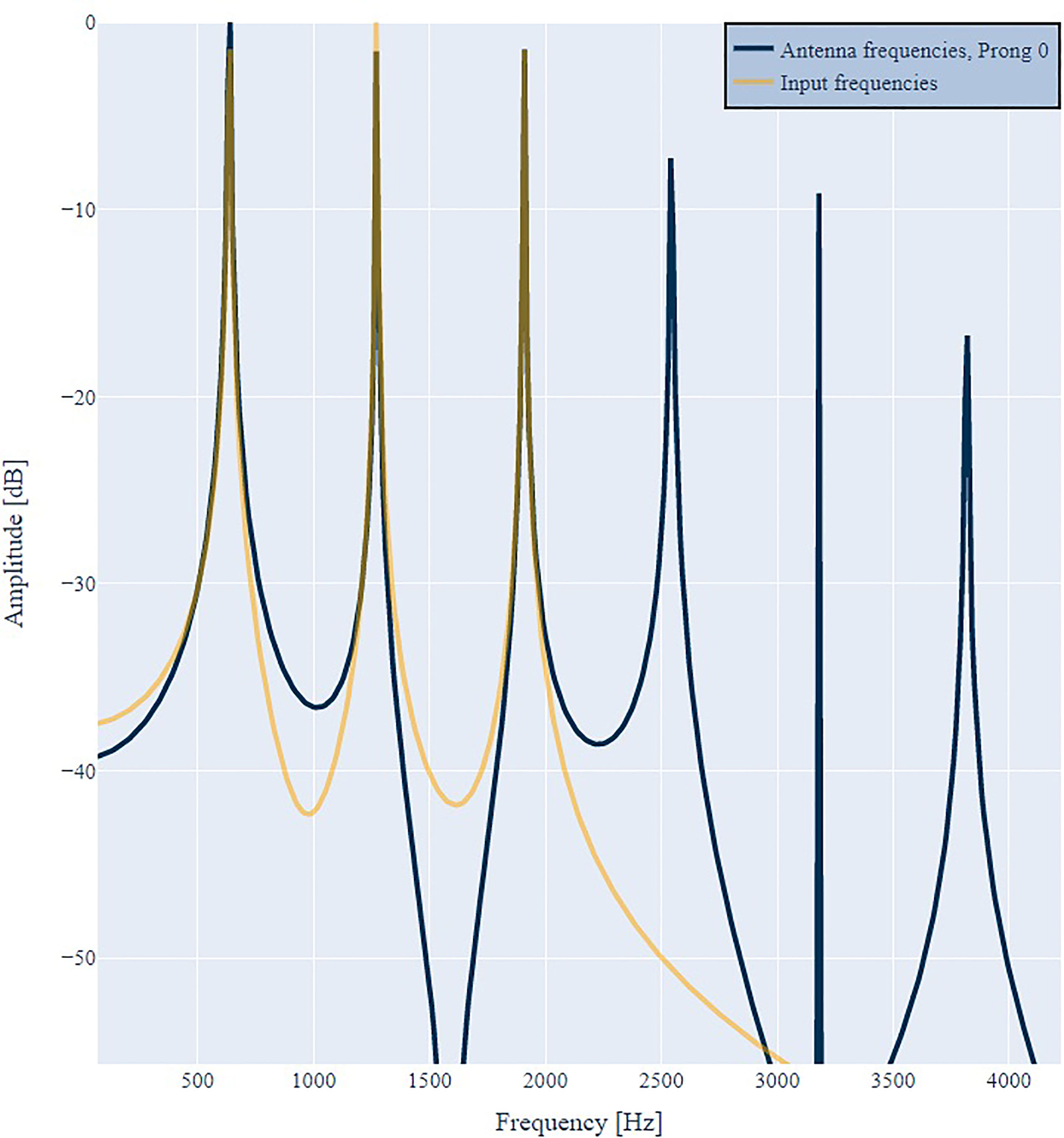
Figure 6 Spectrum of an artificially created mosquito signal with frequencies of 636 Hz, 1272 Hz, 1908 Hz and the reaction of its antenna. The orange signal describes the input signal, while the blue signal describes the reaction of the antenna.

In the next step we simulate two Aedes Aegypti mosquitoes trying to synchronize with each other. This is illustrated in Figure 7. The harmonic spectrum of the male mosquito (green) is represented by the harmonic series of 636 Hz, 1272 and 1908 Hz. The harmonic spectrum of the female mosquito is represented by frequencies of 400 Hz, 800 Hz and 1200 Hz. The male’s first harmonic overtone at 1272 Hz is close to the female’s second harmonic overtone at 1200 Hz, similar to the pure tone example in Figure 5. The purple signal represents the antenna output R₁(ω). Again, the antenna output contains all input frequencies. In addition, all difference frequencies can be found, most importantly 1272 Hz – 1200 Hz = 72 Hz, 800 Hz – 636 Hz = 164 Hz and 636 Hz – 400 Hz = 236 Hz, which lie well inside the audible frequency region of mosquitoes. This is in agreement with criteria 3 and 4.

FIGURE 7

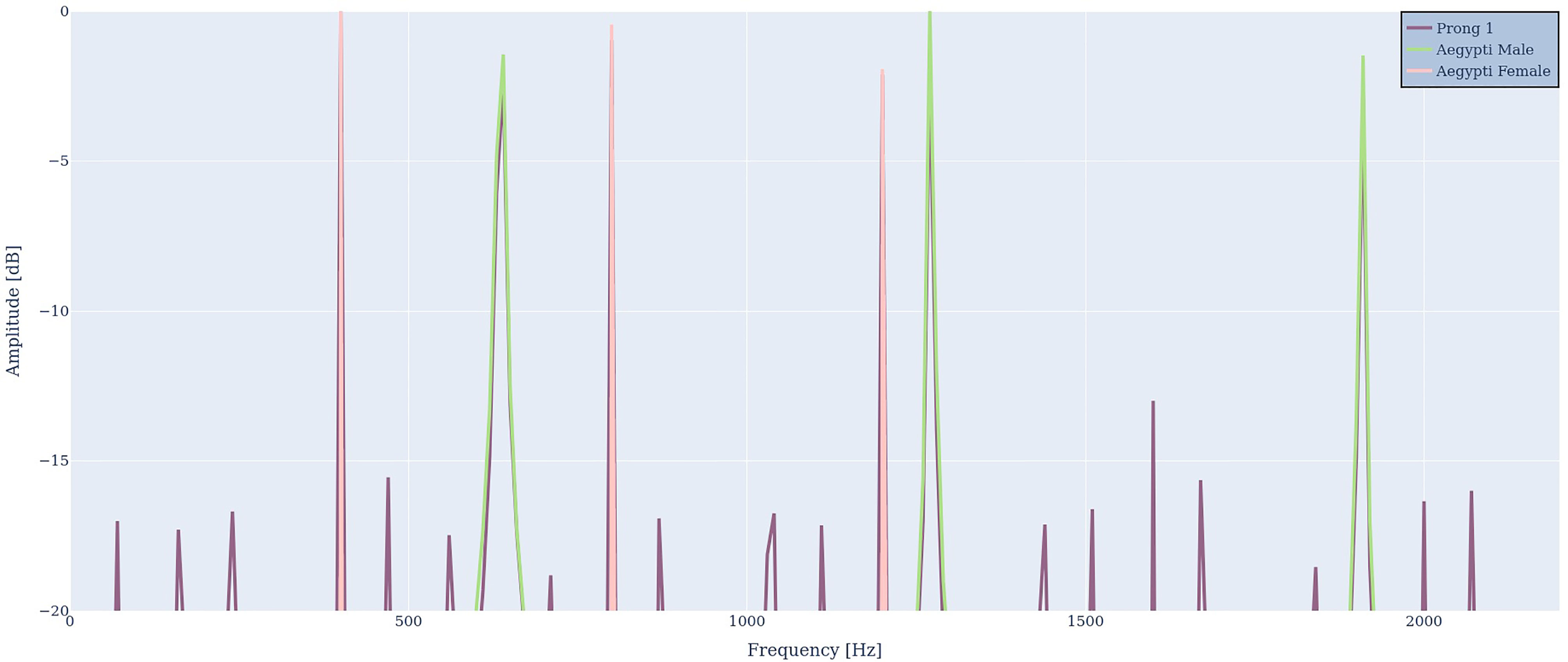
Figure 7 Two virtual mosquitoes with fundamental frequencies of 400 Hz (red) and 636 Hz (green) serve as an input spectrum D(ω), which creates the output spectrum R₁(ω) (purple) that contains the input frequencies plus difference frequencies and harmonic distortion.

We reduced the fundamental frequency of the simulated male in steps of 6 Hz down to the perfect synchronization ratio of 600 Hz. As expected, the output continues to show the input frequencies, harmonic distortion, and all frequency differences. The perfectly synchronized mosquito spectra are illustrated in Figure 8. As can be seen, all low-frequency components vanished, except for the difference between the fundamental frequencies, i.e., 600 Hz – 400 Hz = 200 Hz.

FIGURE 8

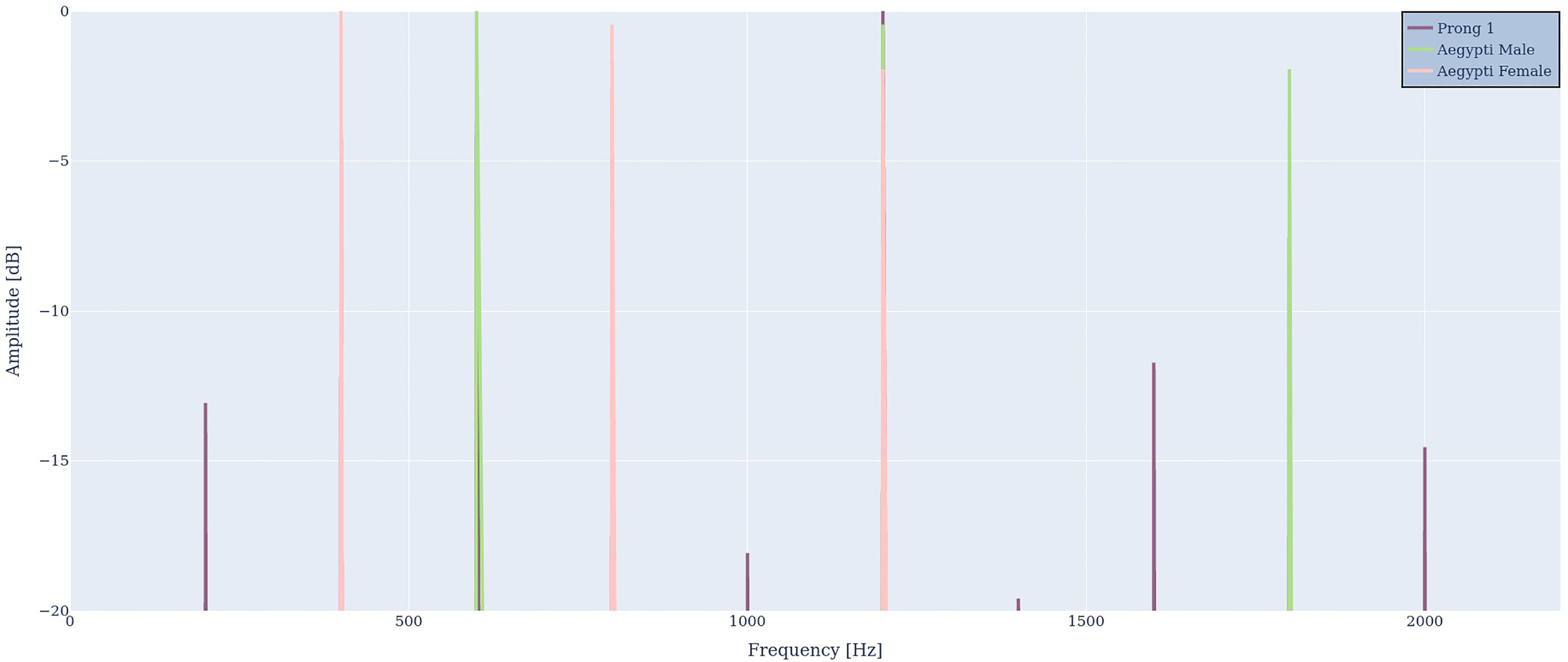
Figure 8 Perfectly synchronized male (green) and female mosquito (red) frequencies. Again, the input frequencies, harmonic distortion and the difference frequency are visible in the output R₁(ω) (purple).

As a next step, we analyzed a recording of real mosquitoes during their synchronization process. The recorded spectrum and the response at prong 0 are illustrated in Figure 9. We used a bandpass filter between 550 and 1700 Hz to eliminate the noise outside the relevant frequency region of mosquito mating. As can be seen, the signal-to-noise ratio lies in the order of 25 dB. The model output exhibits the same characteristics as observed with artificial mosquito spectra: Over a wide frequency range, the model output resembles the model input. In addition, the output contains harmonic distortion, i.e., high-frequency peaks on the right of the original input spectrum. Most importantly, the antenna response contains the difference frequencies. The broad low-frequency peaks I, II and III correspond to the difference frequencies I=f2-f1, the proximate frequencies II=f4-f3 and f5-f4, and III=f2-f2.

FIGURE 9

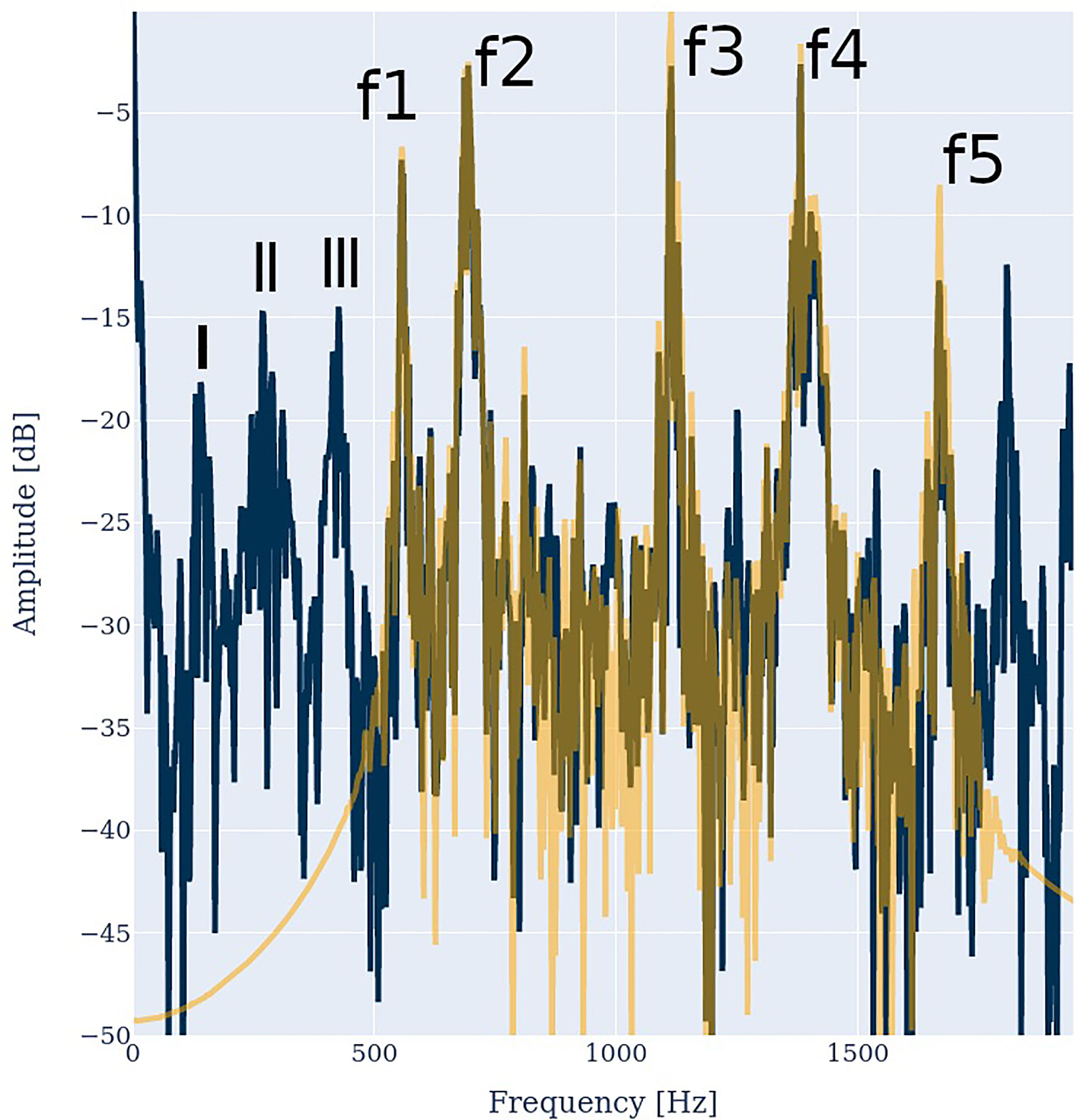
Figure 9 Spectrum of two synchronizing mosquitoes (orange) and response at prong 0 (blue). The female frequencies are f1=555 Hz, f3=1112 Hz and f5=1665 Hz, the male frequencies are f2=688 Hz and f4=1383 Hz. Their difference frequencies I=f2-f1=133 Hz, the broad peak II=f4-f3 = 271.

Note that the peaks at f1 to f5 are no distinct peaks, but rather double or even quadruple peaks, as both mosquitoes altered their wing beat rate during the recording. The difference frequencies of such double peaks are also represented near the lower end of the output spectrum, like the peaks near 0 Hz and 25 Hz. These may provide valuable synchronization information for the mosquito.

Hz and f5-f4 =282 Hz and III=f3-f2 =424 Hz are clearly visible.

5.5 Localization Cues

As mosquitoes are very small compared to the wavelengths that their wing beats produce, we model them as point source (48). Here, the inverse distance law is valid for sound pressure, i.e., the amplitude is proportional to the inverse of the distance r, like

$\begin{array}{ll}\widehat{A}\propto \frac{1}{r}& (11)\end{array}$

We simulated a male mosquito (m_ext) with three partials as before, and a female mosquito (m_int) with the different partials. This yields six input frequencies, three of which are produced by the modeled mosquito, three, by the other mosquito. Following (48) the input spectra at one antenna are calculated by superposition of the propagated spectrum of the female mosquito with the spectrum of the male mosquito like

$\begin{array}{ll}D(\omega )=m_{ext}(\omega )\frac{e^{ikr}}{r}+m_{\mathrm{int}}(\omega ),& (12)\end{array}$

where e ≈ 2.718 is Euler’s number, i is the imaginary unit defined as i² = -1 and r is the Euclidean distance between sound source and each antenna.

We modeled two antennae 0.125 mm apart from each other, which is a typical antenna distance (19). Then, we put the external mosquito at three different angles of 30°, 60° and 90° at two different distances, namely 1.5 cm and 3 cm away from the center of the antennae. The results of this simulation are summarized in Table 1.

TABLE 1

Table 1 Strongest inter antennal amplitude difference per angle calculated for the three difference tones between two flying mosquitoes. Especially near the most sensitive frequency region the difference offers a robust localization cue.

The amplitudes of the input spectra ${\widehat{A}}_{f_{\text{in}}}$ as well as the Inter antennal Amplitude Differences (IAD) of the input spectra IAD_fin, are determined by Eq. 12. When doubling the distance of the sound source, the amplitude reduces by approximately 6 dB. In motion, this is a distance cue that is also utilized by humans and other animals (49, chap. 4). The IAD of the input frequencies depends on distance and angle. As can be seen in the Table 1, it may lie in a range below 0.072 dB. In humans and other animals, Inter aural Level Differences (ILD) inform about the direction of a sound source (49, chap. 4).

So, the relationship between $\widehat{A}$ and distance as well as the relationship between IAD and angle should provide mosquitoes with localization cues. However, in order to be utilizable by a mosquito, these relationships need to take place at frequencies below 470 Hz. Our virtual male mosquito does not produce a single frequency inside the audible hearing range of the modeled female mosquito. But as could be seen already in Figure 7, the superposition of the female and male flight tones produces three difference frequencies f_out, namely 72 Hz, 164 Hz and 236 Hz, in addition to the three frequencies f_in from the male mosquito m_ext. In Table 1 we provide the $\widehat{A}$ and IAD of f_tout together with those of f_in. It can be seen that the localization cues are almost equal, i.e., they are perfectly transferred to the difference frequencies that lie below 470 Hz. This fulfills criteria 5, i.e., the antenna produces audible sound source localization cues due to the nonlinearities that produce difference frequencies.

6 Discussion

Our model is based on the geometry of the mosquito antenna morphology. The fact that this model is able to produce all 5 observations that have been made in real mosquitoes provides evidence that many of the complicated nonlinearities can be attributed already to the periphery of mosquito hearing, i.e., the antenna base, rather than to purely neural processing. This has many implications. Most importantly, the model allows us to reflect findings from a new perspective and to approach answers to open questions on the basis of antenna base morphology, rather than on the basis of flagellum mechanics or neural efferents.

For example (16) carried out synchronization experiments between real mosquito pairs and the synchronization of a mosquito to artificial sounds played through an ear bud speaker and measured neural responses in the JO of a male mosquito. They conclude that the upper limit of hearing in mosquitoes is 2000 Hz and not the widely accepted 470 Hz, because responses were even measurable when the artificial sound contained only frequencies above 800 Hz. Naturally, the flight tone of the male mosquito, whose neural response to stimuli has been measured, contains no frequencies below the 470 Hz either. However, they mention that they were able to detect neural response to high-frequency inputs, when setting their high-pass filter down to 1 or less Hz, but not when choosing 100 Hz, i.e., they detected low-frequency neural activity as a response to a superposition of high-frequency sounds. Our model suggests that the auditory neurons in mosquitoes do not directly respond to such high frequencies, but rather to the frequency differences produced by the antenna as shown in our model. Only through the interplay of the male mosquito flight tone and the artificial signal, the antenna produces motions with frequency components below 100 Hz that excite the neurons. Consequently, the neural activity is not a response to high-frequency input, but to the frequency difference between multiple high-frequency inputs that create a low-frequency response (<100 Hz) already in the antenna. The neuronal low-frequency response simply represents the low-frequency motion that is mechanically induced by the nonlinear transform from deflection to rotation inside the antenna base. Mosquitoes detect the frequency difference and either try to minimize it, to ensure that the external harmonic series contains integer multiples of their self-produced frequencies, or they try to adjust their wing-beat rate in such manner that a species-specific low-frequency peak emerges. This low-frequency peak would be the difference in fundamental frequency during perfect synchronization. This frequency could correspond with a resonance frequency of the flagellum and the best frequency of a number of auditory neurons, so that the mosquito is extraordinary sensitive to it.

Lapshin and Vorontsov (30) found anti-phase responses in electrical measurements inside the JO and already speculated that the mechanical motion of the antenna may cause them. Our model supports this speculation and provides evidence that these anti-phase responses result from the geometry of the antenna base morphology, namely the curved septa.

Windmill et al. (41) wrote that “The presence of a strong frequency doubled component in an otherwise undistorted signal reinforces the hypothesis that, rather than a by-product of some unknown mechanical property, this effect is strongly correlated with the active neuromechanical amplification produced by the Johnston’s organ’s neurons.” Even though active neuromechanical amplification is likely to happen, our model sheds light on the “unknown mechanical property”, indicating that the transfer from deflection to rotation in the antenna base may cause the frequency doubling at some prong locations.

The antenna model from (39) is illustrated in Figure 10. The model simplifies the basilar plate and septa as a line rather than a curve. Here, the authors connect the septa to the JO in the pedicel by pairs of attachment cells above and below the septa. This symmetry creates anti-phase responses, as the attachment cells above the basilar plate are compressed when the attachment cells below the basilar plate are stretched and vice versa. However, the actual mosquito antenna does not exhibit this symmetry of attachment cells, as can be seen in illustrations in (13, 15, 17, 23, 24, 26, 27). In contrast, the geometry in our model is in accordance with these illustrations and descriptions of the mosquito antenna but still produces anti-phase responses.

FIGURE 10

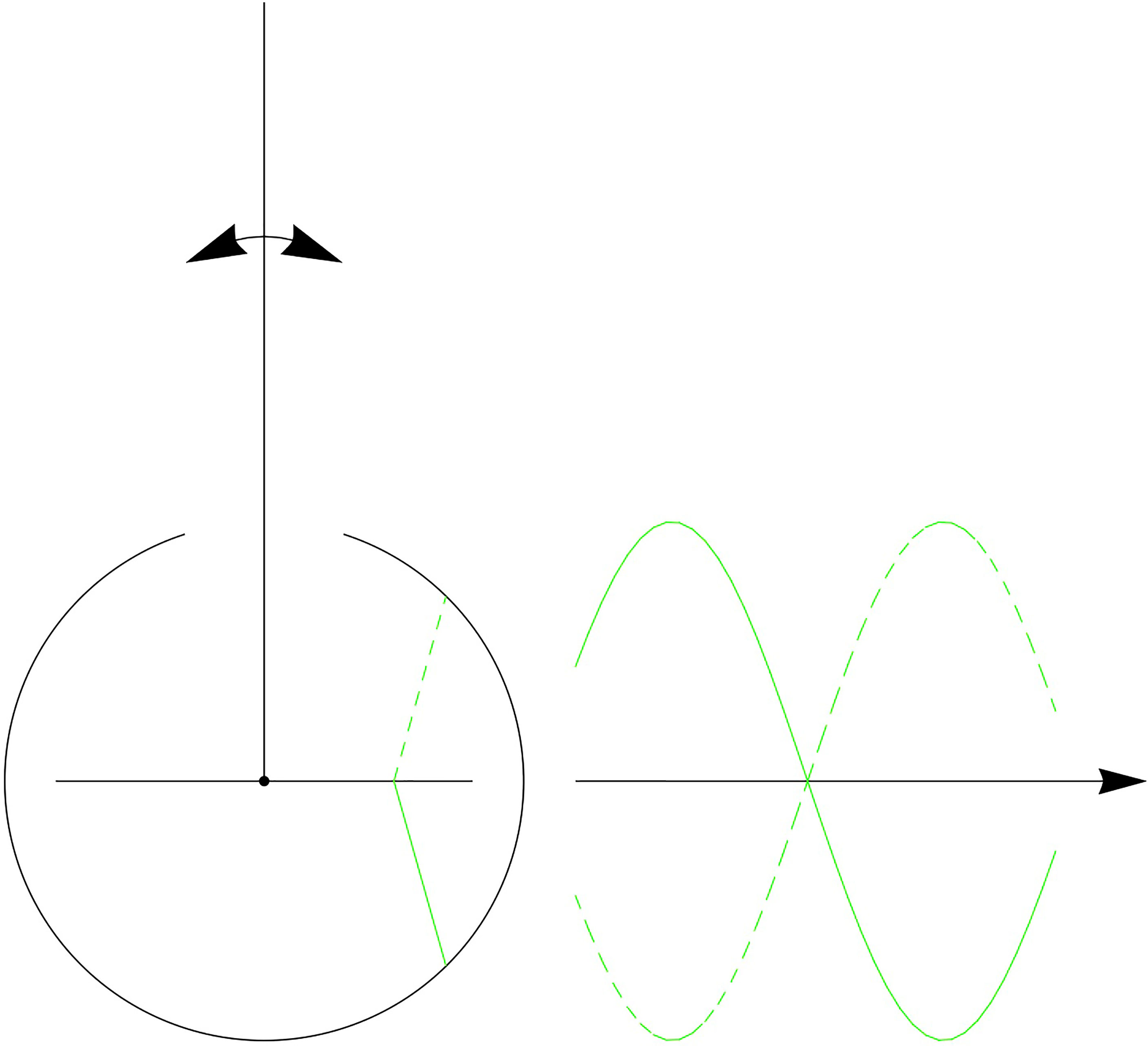
Figure 10 Antenna model by (39): symmetric attachment cells create anti-phase responses.

The model in (26) looks very similar but lacks the pairwise attachment cells. The authors had to add a neural model to produce nonlinearities. Our model produces such nonlinearities already without including neural afferents or efferents. It could therefore be a more realistic pre-processor for neural mosquito hearing models.

Roth (50) assumed that the long fibrillae in male mosquito antennas resonate with female wing beat frequencies, enabling them to detect females. This assumption seems plausible, as male mosquitoes have a much bushier antenna than female mosquitoes. However, this assumption does not sufficiently explain how female mosquitoes are able to synchronize to male mosquitoes at inaudibly high frequencies. Our model does not support or contradict the assumption of resonating fibrillae, but it provides evidence that even in the absence of fibrillae, the antenna clearly indicates the presence and even the location of a mosquito through nonlinear interplay of two flight sounds. This means the model explains – in a reasonable, morphologically plausible way – how both male and female mosquitoes are able to detect the presence and location of one another.

From acoustical and mechanical considerations (13) derived that a direction-dependent distortion factor enables mosquitoes to localize sound sources. This hypothesis was supported by electrode measurements inside the pedicel during magnetic antenna stimulation (51). Our model exhibits harmonic distortions whose intensity depends on distance rather than on direction. However, as harmonic distortion only produces frequencies outside the hearing range of mosquitoes, it is unlikely that mosquitoes can actually make use of such cues. Instead, our model indicates that the nonlinear transform from deflection to rotation inside the antenna base produces difference frequencies in the most-sensitive frequency region of mosquitoes. Furthermore, inter antennal amplitude differences have been observed. These are angle dependent and provide the mosquito with a localization cue for source direction, just as inter aural level differences in human hearing. The existence of inter antennal cues in our antenna base model may explain why mosquitoes have an antenna pair and not just one single antenna. Consequently, our model suggests that localization may be realized through a combination of mono antennal and biantennal cues, just as the monaural and binaural cues in human sound source localization.

Lapshin (11) measured neural responses to single frequencies using glass electrodes in the JO. They compared the threshold for passive mosquitoes with the threshold during simulated mosquito flight. They observed that the threshold of neural response typically dropped by 8 dB within the frequency region from 80 to 120 Hz for flying mosquitoes compared to resting mosquitoes. One exception was a frequency around 40 Hz. Here, the threshold dropped on average by 26 dB (maximum by 56 dB ()!). Our model provides evidence that this low-frequency component is prominently created through the nonlinear combination of internal and external mosquito wingbeat sounds inside the antenna base during courtship. This explains how this amazing amplification can be achieved through mechanical pre-processing. Furthermore, our model yields a possible explanation why this frequency is amplified so much: It appears that mosquitoes synchronize by minimizing the low-frequency component. Consequently, the beat frequency that results from proximate frequencies near the synchronization frequency (roughly in the order ≤72 Hz) has to be amplified much stronger than the other beat frequencies, like the difference between the fundamental frequencies, e.g., 636 Hz–400 Hz = 236 Hz.

Furthermore (11), could show that the acoustic sensitivity of both female and male mosquitoes increased considerably during simulated flight, even though females exhibit much fewer fibrillae and auditory neurons. Our model provides evidence that a lot of the nonlinear processing during flight results from the transformation of deflection to rotation inside the antenna base, rather than at the level of the fibrillar or neural processing: In contrast to the sexually dimorphic flagellum, the antenna base is morphological similar in female and male mosquitoes.

Koch (52) modeled the mechanics of two mosquito flagellum shafts as rigid beams with one free and one clamped end. She could show that magnitude and phase relationship between both antenna deflections provides a strong and unique directional cue. She derived this from simulations with an inaudibly high frequency of an external male, in absence of an internal female sound. However, our model provides evidence that the deflections stay represented in the low-frequency domain when adding an internal female sound. The combination of her physical flagellum shaft model and our antenna base model could provide stronger and more plausible sound source localization cues than each of the individual models.

Lapshin and Vorontsov (30) observed that many auditory neurons in the JO are tuned to frequencies between 190 to 270 Hz, which corresponds to the f₀ difference of male and female mosquitoes (20). already stated that “(t)his difference is generated in the JO responses as a result of intermodulation distortion products (DPs) caused by non-linear interaction between male–female flight tones in the vibrations of the antenna”. Our model provides evidence where and how the antenna produces these distortion products, namely inside the antenna base through the transfer from deflection of the flagellum over rotation of the curved septa to stretch/compression of the attachment cells. Moreover, other difference frequencies fall into this region, too, especially during the act of synchronization. Our localization experiment adds another possible explanation for the high number of neurons that are tuned to this frequency region: inter antennal amplitude differences are most prominent in this frequency region, so it is likely that not only neurons responsible for frequency detection but also for source localization are tuned to these frequencies.

Lapshin (11) found the frequency deviation and twice the frequency deviation neurally represented during simulated flight experiments. Our model suggests that these deviations are already produced mechanically in the antenna base and only passively represented or actively amplified through auditory neurons.

In contrast to many mosquito species — like Aedes aegpti and Aedes albopictus, Anopheles dirus and Anopheles minimus and Culex quinquefasciatus (9) — the fundamental frequency of male and female Tachina brevipalpis is similar. Still (17), observed that mosquitoes of both sexes would alter their wing beat frequency to synchronize with a pure tone as long as its frequency deviated less that 60 Hz from their own fundamental frequency. They conclude that mosquitoes can detect many frequency deviations, i.e., beat frequencies between many frequency pairs, to synchronize. Our model supports this assumption, as not only the beat frequency of overtones near the typical synchronization frequency of 1200 Hz is represented by the antenna response, but also the deviation between fundamental frequencies and between proximate partials. It appears that mosquitoes’ strategy during synchronization is either to minimize the lowest frequency component, which appears to be difference between the frequencies that lie closest to the favored synchronization frequency, or to produce a certain low-frequency distortion product that is typical for the conspecific mating procedure. However, as communication may be much more complex than that, it is even possible that mosquitoes do not aim at producing a single low-frequency distortion product, but a certain pattern or sequence of patterns. This would explain why in synchronization experiments only 22 to 39% of all males and 30 to 35% of all females approached and synchronized to static, generated sound (16). Maybe static sounds produce the right low-frequency distortion products, but not the right progression over time.

Given these results, we suggest using an antenna model with a curved septa as a biologically-inspired pre-processor rather than using the raw audio as an input to neural models of mosquito hearing. Furthermore, we suggest not to underestimate the importance of the antenna base in addition to investigations that concentrate on flagellum mechanics and auditory efferents. Our model provides evidence that the mosquito antenna base delivers reliable cues that enable mosquitoes to detect the presence of other mosquitoes, to localize them, and to synchronize by means of minimizing the lowest frequency represented in the antenna response.

As acoustics seem to be an important sexual stimulant in many mosquito species, understanding their hearing system may be helpful in the future to support the fight against vector-borne diseases, like malaria, dengue fever and yellow fever by means of:

• automatic acoustic identification of mating swarm sites

• acoustically dispelling mosquitoes

• species- and sex-specific luring into traps for

 - manual or

 - automatic mosquito monitoring (recognition and counting of vector species)

 - SIT and IIT preparation

7 Conclusion

In this paper we introduced a biologically inspired mosquito antenna model. The model exhibits many of the characteristics that have been observed through neural and behavioral studies of real mosquitoes: The model produces harmonic distortions whose number and intensity depend on the intensity of the input signal and the location of the prong. Some prongs exhibit an anti-phase response, which has been observed in neural measurements of real mosquitoes. The model produces the difference frequencies between the fundamental frequency of the male and female mosquito as well as the frequency difference between overtones. These frequency differences lie well inside the hearing range of a mosquito, even if the input signal lies outside their hearing range. The intensity of the difference frequencies is distance-dependent, providing a source distance cue. When modeling two antennae, the model produces inter-antennal level differences at the beat frequency, providing localization cues comparable to the inter-aural level differences of humans and other animals with paired ears.

The fact that our geometric model meets all of the 5 above-mentioned criteria that have been observed in real mosquitoes is evidence that the geometry of the antenna morphology plays a crucial role in mosquito hearing. Already the periphery produces many of the observations that had been attributed to neural activity and efferents [see e.g., (14), (15) and (19)]. These nonlinearities enable mosquitoes to detect, localize, and synchronize to one another, i.e., to carry out their courtship behavior which is mandatory for mating. The model made the important role of the antenna base evident, which is underestimated, or at least underrepresented in the study of mosquito hearing and courtship behavior.

The current state of the model neglects physical properties which may be included as filters in the future. Adding physical properties will certainly make the model even more explanatory. Neurally, the stretch and compression of the attachment cells, as calculated in our model, is neurally encoded and processed further inside the mosquito’s auditory system. This processing has to be implemented in the future to gain an even deeper understanding of mosquito hearing and courtship behavior.

Data Availability Statement

Publicly available datasets were utilized in this study. This data can be found here: MOSQUITO ANTENNA REPOSITORY - https://github.com/HughIdiyit/mosquito_antenna.

Author Contributions

TZ conceptualized and implemented the original mosquito antenna model and started to evaluate it with artificial sounds. FW and AH reimplemented the model, evaluated it further, with artificial mosquitoes and with real mosquito recordings. All authors contributed equally to the literature research, manuscript preparation and audio analysis.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Thomas Barkowsky and the Mobile4D-team for fruitful discussions and continuous feedback. We also thank Myat Su Yin, Peter Haddawy and their team at MIRU for continuous exchange of ideas and a huge number of mosquito recordings and the establishing of the mosquito song network. We thank Michael Weber from Biogents for fruitful discussions and the many mosquito recordings they provided. Lastly, we thank Paul Barmsen from tiny drops, who introduced us to his mosquito control network and provided us with additional mosquito recordings.

References

1. World Health Organization. Evaluation of Genetically Modified Mosquitoes for the Control of Vector-Borne Diseases. (2020). Available at: https://www.who.int/publications/i/item/9789240013155 (Accessed accessed: 2020-12-14).

Google Scholar

2. World Health Organization. Guidelines for Dengue Surveillance and Mosquito Control. Manila: WHO Library Cataloguing in Publication Data (2003).

Google Scholar

3. Tandina F, Doumbo O, Yaro AS, Traoré SF, Parola P, Robert V. Mosquitoes (Diptera: Culicidae) and Mosquito-Borne Diseases in Mali, West Africa. Parasites Vectors (2018) 11:467. doi: 10.1186/s13071-018-3045-8

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Senevirathna U, Udayanga L, Ganehiarachchi GASM, Hapugoda M, Ranathunge T, Gunawardene NS. Development of an Alternative Low-Cost Larval Diet for Mass Rearing of Aedes Aegypti Mosquitoes. BioMed Res Int (2020) 2020:1053818. doi: 10.1155/2020/1053818. Paper number.

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Alphey L, Benedict M, Bellini R, Clark GG, Dame DA, Service MW, et al. Sterile-Insect Methods for Control of Mosquito-Borne Diseases: An Analysis. Vector-Borne Zoonotic Dis (2010) 10:295–311. doi: 10.1089/vbz.2009.0014

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Pacific Community and the World Health Organization Division of Pacific Technical Support. In: Manual for Surveillance and Control of Aedes Vectors in the Pacific. Suva, Fiji: The Pacific Community (SPC) and World Health Organization (WHO) (2020) (Accessed 18/01/2022).

Google Scholar

7. Vasconcelos D, Nunes N, Ribeiro M, Prandi C, Rogers A. Locomobis: A Low-Cost Acoustic-Based Sensing System to Monitor and Classify Mosquitoes. In: 16th IEEE Annual Consumer Communications & Networking Conference (CCNC). Las Vegas, NV, USA: IEEE (2019). p. 1–6. doi: 10.1109/CCNC.2019.8651767

CrossRef Full Text | Google Scholar

8. Vasconcelos D, Yin MS, Wetjen F, Herbst A, Ziemer T, Förster A, et al. Counting Mosquitoes in the Wild: An Internet of Things Approach. In: Proceedings of the Conference on Information Technology for Social Good, vol. GoodIT ‘21. New York, NY, USA: Association for Computing Machinery (2021). p. 43–8. doi: 10.1145/3462203.3475914

CrossRef Full Text | Google Scholar

9. Yin MS, Haddawy P, Nirandmongkol B, Kongthaworn T, Chaisumritchoke C, Supratak A, et al. A Lightweight Deep Learning Approach to Mosquito Classification From Wingbeat Sounds. In: Proceedings of the Conference on Information Technology for Social Good, vol. GoodIT ‘21. . New York, NY, USA: Association for Computing Machinery (2021). p. 37–42. doi: 10.1145/3462203.3475908

CrossRef Full Text | Google Scholar

10. Nijhout HF. Control of Antennal Hair Erection in Male Mosquitoes. Biol Bull (1977) 153:591–603. doi: 10.2307/1540608

CrossRef Full Text | Google Scholar

11. Lapshin DN. The Auditory System of Blood-Sucking Mosquito Females (Diptera, Culicidae): Acoustic Perception During Flight Simulation. Entomological Rev (2012) 93:135–49. doi: 10.1134/S0013873813020012

CrossRef Full Text | Google Scholar

12. Offenhauser WH, Kahn MC. The Sounds of Disease-Carrying Mosquitoes. J Acoustical Soc America (1949) 21:462–3. doi: 10.1121/1.1917085

CrossRef Full Text | Google Scholar

13. Tischner H. Über Den Gehörsinn Von Stechmücken. Acustica (1953) 3:335–43.

Google Scholar

14. Jackson JC, Robert D. Nonlinear Auditory Mechanism Enhances Female Sounds for Male Mosquitoes. Proc Natl Acad Sci (2006) 103:16734–9. doi: 10.1073/pnas.0606319103

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Andrés M, Seifert M, Spalthoff C, Warren B, Weiss L, Giraldo D, et al. Auditory Efferent System Modulates Mosquito Hearing. Curr Biol (2016) 26:2028–36. doi: 10.1016/j.cub.2016.05.077

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Cator LJ, Arthur BJ, Harrington LC, Hoy RR. Harmonic Convergence in the Love Songs of the Dengue Vector Mosquito. Science (2009) 323:1077–9. doi: 10.1126/science.1166541

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Gibson G, Warren B, Russell IJ. Humming in Tune: Sex and Species Recognition by Mosquitoes on the Wing. J Assoc Res Otolaryngol (2010) 11:527–40. doi: 10.1007/s10162-010-0243-2

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Warren B, Russell I. Mosquitoes on the Wing “Tune in” to Acoustic Distortion. AIP Conf Proc (2011) 1403:479–80. doi: 10.1063/1.3658134

CrossRef Full Text | Google Scholar

19. Göpfert MC, Robert D. Active Auditory Mechanics in Mosquitoes. Proc R Soc Lond B (2001) 268:333–9. doi: 10.1098/rspb.2000.1376

CrossRef Full Text | Google Scholar

20. Simoes PM, Ingham RA, Gibson G, Russell IJ. A Role for Acoustic Distortion in Novel Rapid Frequency Modulation Behaviour in Free-Flying Male Mosquitoes. J Exp Biol (2016) 219:2039–47. doi: 10.1242/jeb.135293

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hancock R, Foster W, Yee W. Courtship Behavior of the Mosquito Sabethes Cyaneus (Diptera: Culicidae). J Insect Behav (1990) 3:401–16. doi: 10.1007/BF01052117

CrossRef Full Text | Google Scholar

22. Göpfert MC, Briegel H, Robert D. Mosquito Hearing: Sound-Induced Antennal Vibrations in Male and Female Aedes Aegypti. J Exp Biol (1999) 202:2727–38. doi: 10.1242/jeb.202.20.2727

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Warren B, Lukashkin AN, Russell IJ. The Dynein–Tubulin Motor Powers Active Oscillations and Amplification in the Hearing Organ of the Mosquito. Proc Biol Sci (2010) 277:1761–9. doi: 10.1098/rspb.2009.2355

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Boo KS, Richards A. Fine Structure of the Scolopidia in the Johnston’s Organ of Male Aedes Aegypti (L.) (Diptera: Culicidae). Int J Insect Morphol Embryol (1975) 4:549–66. doi: 10.1016/0020-7322(75)90031-8

CrossRef Full Text | Google Scholar

25. Schwartzkopff J. Die Akustische Lokalisation Bei Tieren. In: Autrum H, Bünning E, Frisch Kv, Hadorn E, Kühn A, Mayr E, et al, editors. Ergebnisse Der Biologie. Berlin, Heidelberg: Springer Berlin Heidelberg (1962). p. 136–76.

Google Scholar

26. Avitabile D, Homer M, Champneys AR, Jackson JC, Robert D. Mathematical Modelling of the Active Hearing Process in Mosquitoes. J R Soc Interface (2010) 7:105–22. doi: 10.1098/rsif.2009.0091

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Saltin BD, Matsumura Y, Reid A, Windmill JF, Gorb SN, Jackson JC. Material Stiffness Variation in Mosquito Antennae. J R Soc Interface (2019) 16:20190049. doi: 10.1098/rsif.2019.0049

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Davis EE, Sokolove PG. Lactic Acid-Sensitive Receptors on the Antennae of the Mosquito, Aedes Aegypti. J Comp Physiol (1976) 105:43–54. doi: 10.1007/BF01380052

CrossRef Full Text | Google Scholar

29. Menda G, Nitzany EI, Shamble PS, Wells A, Harrington LC, Miles RN, et al. The Long and Short of Hearing in the Mosquito Aedes Aegypti. Curr Biol (2019) 29:709 – 714.e4. doi: 10.1016/j.cub.2019.01.026

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Lapshin DN, Vorontsov DD. Frequency Organization of the Johnston’s Organ in Male Mosquitoes (Diptera, Culicidae). J Exp Biol (2017) 220:3927–38. doi: 10.1242/jeb.152017

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Chen Y, Why A, Batista G, Mafra-Neto A, Keogh E. Flying Insect Classification With Inexpensive Sensors. J Insect Behav (2014) 27:657–77. doi: 10.1007/s10905-014-9454-4

CrossRef Full Text | Google Scholar

32. Matthews RW, Matthews JR. Insect Behavior. 2nd edn. Dordrecht: Springer (2010). doi: 10.1007/978-90-481-2389-6

CrossRef Full Text | Google Scholar

33. Ziemer T. Psychoacoustic Music Sound Field Synthesis. In: No. 7 in Current Research in Systematic Musicology. Cham: Springer (2020). doi: 10.1007/978-3-030-23033-3

CrossRef Full Text | Google Scholar

34. Albert JT, Kozlov AS. Comparative Aspects of Hearing in Vertebrates and Insects With Antennal Ears. Curr Biol (2016) 26:R1050–61. doi: 10.1016/j.cub.2016.09.017

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Göpfert MC, Robert D. Nanometre-Range Acoustic Sensitivity in Male and Female Mosquitoes. Proc R Soc Lond (2000) 267:453–7. doi: 10.1098/rspb.2000.1021

CrossRef Full Text | Google Scholar

36. Yang N, Long Z, Wang F. Harmonic Synchronization Model of the Mating Dengue Vector Mosquitoes. Chin Sci Bull (2012) 57:4043–8. doi: 10.1007/s11434-012-5445-z

CrossRef Full Text | Google Scholar

37. Ziemer G, Hinse P. Relation of Maximum Structural Velocity and Ice Drift Speed During Frequency Lock-In. In: 24th International Conference on Port and Ocean Engineering Under Arctic Conditions (POAC). Busan, Korea: Port and Ocean Engineering under Arctic Conditions (POAC) (2017). p. POAC17–071. Available at: http://worldcat.org/issn/03766756.

Google Scholar

38. van Noorden L. Auto-Correlation and Entrainment in the Synchronous Reproduction of Musical Pulse: Developments in Childhood. Proc – Soc Behav Sci (2014) 126:117–8. doi: 10.1016/j.sbspro.2014.02.336

CrossRef Full Text | Google Scholar

39. Arthur BJ, Wyttenbach RA, Harrington LC, Hoy RR. Neural Responses to One- and Two-Tone Stimuli in the Hearing Organ of the Dengue Vector Mosquito. J Exp Biol (2010) 213:1376–85. doi: 10.1242/jeb.033357

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wishart G, van Sickle GR, Riordan DF. Orientation of the Males of Aedes Aegypti (L.) (Diptera: Culicidae) to Sound. Can Entom. (1962) 94:613–26. doi: 10.4039/Ent94613-6

CrossRef Full Text | Google Scholar

41. Windmill JFC, Jackson JC, Pook VG, Robert D. Frequency Doubling by Active In Vivo Motility of Mechanosensory Neurons in the Mosquito Ear. R Soc Open Sci (2017) 5:171082. doi: 10.1098/rsos.171082

CrossRef Full Text | Google Scholar

42. Diabate A, Tripet F. Targeting Male Mosquito Mating Behaviour for Malaria Control. Parasites Vectors (2015) 8:347. doi: 10.1186/s13071-015-0961-8

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Berkhausen B. Modeling of a Mosquito Antenna in a Soundfield in Python. Bremen: Bachelor’s thesis, University of Bremen (2021).

Google Scholar

44. Su MP, Andres M, Boyd-Gibbins N, Somers J, Albert JT. Sex and Species Specific Hearing Mechanisms in Mosquito Flagellar Ears. Nat Commun (2018) 9:3911. doi: 10.1038/s41467-018-06388-7

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Mhatre N. Active Amplification in Insect Ears: Mechanics, Models and Molecules. J Comp Physiol A (2015) 201:19–37. doi: 10.1007/s00359-014-0969-0

CrossRef Full Text | Google Scholar

46. Ziemer T, Koch J, Sa-Ngamuang C, Yin MS, Siai M, Berkhausen B, et al. A Bio-Inspired Acoustic Detector of Mosquito Sex and Species. J Acoustical Soc America (2020) 148:2480–0. doi: 10.1121/1.5146873

CrossRef Full Text | Google Scholar

47. Boppana S, Hillyer JF. Hemolymph Circulation in Insect Sensory Appendages: Functional Mechanics of Antennal Accessory Pulsatile Organs (Auxiliary Hearts) in the Mosquito Anopheles Gambiae. J Exp Biol (2014) 217:3006–14. doi: 10.1242/jeb.106708

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Ziemer T, Bader R. Complex Point Source Model to Calculate the Sound Field Radiated From Musical Instruments. Proc Meetings Acoustics (2016) 25:035001. doi: 10.1121/2.0000122

CrossRef Full Text | Google Scholar

49. Becker N, Petric D, Zgomba M, Boase C, Dahl C, Madon M, et al. Mosquitoes and Their Control. 2nd ed. Berlin Heidelberg: Springer (2010). doi: 10.1007/978-3-540-92874-4

CrossRef Full Text | Google Scholar

50. Roth LM. A Study of Mosquito Behavior. An Experimental Laboratory Study of the Sexual Behavior of Aedes Aegypti (Linnaeus). Am Midland Nat (1948) 40:265–352. doi: 10.2307/2421604

CrossRef Full Text | Google Scholar

51. Keppler E. Ãœber Das Richtungshören Von Stechmücken. Z Naturforsch (1958) 13:280–4. doi: 10.1515/znb-1958-0503

CrossRef Full Text | Google Scholar

52. Koch J. A Bio-Inspired Approach to Explore the Workings of the Mosquito’s Hearing Organ [Bachelor’s Thesis]. University of Bremen (2021). doi: 10.13140/RG.2.2.20854.47682

CrossRef Full Text | Google Scholar