- 1 Department of Clinical and Experimental Epilepsy, University College London Institute of Neurology, London, UK
- 2 Magnetic Resonance Imaging Unit, National Society for Epilepsy, Buckinghamshire, UK
- 3 Wellcome Trust Centre for Neuroimaging, University College London Institute of Neurology, London, UK
This review attempts to place the concept of connectivity from increasingly sophisticated neuroimaging data analysis methodologies within the field of epilepsy research. We introduce the more principled connectivity terminology developed recently in neuroimaging and review some of the key concepts related to the characterization of propagation of epileptic activity using what may be called traditional correlation-based studies based on EEG. We then show how essentially similar methodologies, and more recently models addressing causality, have been used to characterize whole-brain and regional networks using functional MRI data. Following a discussion of our current understanding of the neuronal system aspects of the onset and propagation of epileptic discharges and seizures, we discuss the most advanced and ambitious framework to attempt to fully characterize epileptic networks based on neuroimaging data.
Introduction
The brain is essentially an electro-chemical network. Connectivity is at the center of the problem of Epilepsy since its defining element is the occurrence of seizures, which essentially are periods of abnormal inter-neuronal synchrony. Unanswered questions that are central to an improved understanding of the mechanisms of epilepsy include some which implicate connectivity directly, such as: Why does ictal activity spread? Why do seizures persist in some patients, following surgical resection? Why do focal insults often give rise to recurrent seizures, i.e., epilepsy? And some which do so less directly: Why do spike and wave discharges and seizures occur when they do? Why does the spatial relationship between the generators of interictal discharges and seizures vary between patients? Answers to these questions would fundamentally improve our ability to eliminate seizures.
The difficulty of pinning down the concept of brain connectivity has already been noted (Horwitz, 2003). Nonetheless at the macroscopic scale (brain) connectivity can be partitioned into three main concepts: (i) anatomical (or structural) connectivity measured in terms of physical (and chemical) connections between neuronal populations or individual neurons, (ii) “functional” connectivity by which we mean the statistical similarity between activities in distributed neuronal populations, and (iii) “effective” connectivity, which speaks to the directed influence the activity of one region exerts onto another region’s activity in a given context (Sporns, 2010). This distinction is useful for our discussion in that the measurement instruments and data analytical tools at our disposal have mainly focused on each aspect separately (but see Guye et al., 2008).
Here we focus on connectivity of neuronal activity, reflected in electrophysiological (LFP, EEG, MEG) and hemodynamic (functional MRI, fMRI) signals measured in humans and animals, but with reference to structural connectivity when possible. In the following, we will focus on connectivity assessed in relation to events or to (transient) brain states.
We are motivated by the following two perceived needs: firstly, to relate the various measures of connectivity found in the field of epilepsy research to the more general language of functional and effective connectivity as used in neuroscience (neuroimaging) and secondly, to gage the potential benefits of applying state-of-the-art connectivity methods to answer scientific questions raised within the field of human epilepsy research.
We begin by reviewing basic principles of connectivity, followed by a description of connectivity measurement and quantification methodologies. We then review some of the main findings of basic studies of connectivity in epilepsy, focusing on human data but making essential links to animal studies. The last part of this review describes the latest developments in models of coupled (distributed) generators of EEG/MEG and fMRI signals, with the view of scrutinizing their possible role as a bridge between scales of understanding in epilepsy.
Definitions, Principles, and the Characterization of Connectivity in Epilepsy
Because of the history of brain connectivity analysis, the functional/effective dichotomy is a convenient starting point for our discussion. As we shall see, a priori, both forms of connectivity are aimed at identifying the presence and strength of connections between network nodes and, when possible, their directionality. However, a further ambition of effective connectivity is to allow the inference of (biophysical) mechanisms by which causal links are expressed in measured neuroimaging signals. The study of effective connectivity is, therefore, usually a more model-based (or hypothesis-driven) approach than that of functional connectivity. It is worth noting that the term functional connectivity is not commonly encountered in the field of epilepsy, particularly in relation to EEG data although its use has increased recently in view of growing interest in resting-state fMRI data.
EEG: Propagation, Spread, Source Mapping, and Connectivity
A key concept in epilepsy is propagation, which is usually understood to mean the observation of similar patterns or of signals with different patterns but all suspected of reflecting a common underlying phenomenon, on an increasing number of EEG recording channels. This is particularly relevant for seizure activity, where it can be commonly observed on intracranial EEG recordings (Brazier, 1972; Tao et al., 2007b). There does not seem to be a formal distinction between “spread” and “propagation” in the field of epilepsy, although the term spread can be seen as implying spatial contiguity and possibly a more passive process than propagation, which therefore may be more general. Propagation, and synchronization to take one of the commonly used measures of propagation, implies connectivity and therefore the various ways of characterizing propagation discussed below are connectivity measures. In the following, measures of functional connectivity dominate as there have been very few studies attempting to characterize effective connectivity in epilepsy.
Signal space connectivity
Continuing with the example of EEG recorded within the brain the problem of characterizing propagation is confounded by the fact that the most prominent feature may not necessarily reflect the driving source (“pacemaker”; Brazier, 1972; Pijn et al., 1990). Therefore, early efforts to address the specific problem of identifying the driving component focused on correlation and phase lag analysis in the temporal domain or coherence in the frequency domain (Walter, 1963). In general, the propagation velocity is expected to be large and therefore quantitative methods to detect and measure small inter-channel time differences were developed. In principle, methods based on spectral estimates such as coherence analysis may be best suited to study phenomena of sufficient duration, such as seizures, while correlation linear or non-linear may be applied to shorter epochs (Allen et al., 1992). Event coincidence analysis of icEEG data recorded in TLE has been used to identify sets of networks involved in interictal epileptiform discharge (IED) generation with good reproducibility (Bourien et al., 2005; Wendling et al., 2009b). For extended discharges (e.g., focal or generalized seizures) inter-channel phase difference analyses, evaluated for a specific frequency (Brazier, 1972) or over a range of frequencies showing a sufficiently high degree of coherence and linear relationship between phase difference and frequency (Gotman, 1983) have been used to characterize propagation. Relaxation of the assumption of linearity, which can be violated in epilepsy, has lead to the use of more general measures of association (e.g., mutual information and non-linear correlation ratio: h2) to study seizure propagation (Pijn et al., 1990, 1992; Bartolomei et al., 2001; Wendling et al., 2001, 2009a; Guye et al., 2006). The ability to identify reliable pre- or early ictal connectivity patterns has obvious implications for our ability to predict seizures (Litt and Lehnertz, 2002; Mormann et al., 2007; see Hughes, 2008 for an interesting historical account).
Another application of the concept of connectivity in epilepsy has been the more recent attempts to identify syndrome-specific patterns in resting-state EEG data. For example, the concept of generalized synchronization has been used to identify functional connectivity differences in resting-state scalp EEG at the global level or regionally based on icEEG between patient groups with potential diagnostic value (Monto et al., 2007; Bettus et al., 2008; Douw et al., 2010). Below, we will discuss how the same approach has been used on fMRI data.
Scalp EEG and MEG source space connectivity
Changes in scalp EEG/MEG field topography reflect a combination of changes in source morphology and strength, and noise (Ebersole and Hawes-Ebersole, 2007). Although subjective, the interpretation of changes in scalp EEG patterns in terms of lobar localization, lateralization, and generalization forms an integral part of clinical practice. However, characterization of neural connectivity based on quantitative analyses of scalp EEG in signal space is particularly problematic because the signals result from propagation through the head and subject to fundamental ambiguities of source identification (Schoffelen and Gross, 2009). Furthermore, even for such simple events as focal spikes, propagation, or spread can result in severe violations of the modeling assumptions, such as synchronized activity over a relatively limited cortical area for the case of the single moving dipole. The demonstration that 10 cm2 of synchronously active cortex is necessary to produce a visually recognizable spike on scalp EEG (Tao et al., 2005, 2007a) suggests that point dipole mapping may often break down. Nonetheless, source tracking has been used to characterize spike propagation within the brain, possibly down to the sub-lobar level although careful interpretation of any localizing information is required in view of the above caveats (Ebersole and Hawes-Ebersole, 2007). Ictal activity represents a much greater challenge due to the length and complexity of the events, with rare studies attempting to link the intracranial and scalp EEG representations of ictal spread (Tao et al., 2007b). The observed complex dynamic patterns of synchrony mean that we are even further from useful source-based analyses than for interictal discharges.
It is beyond the scope of this review to discuss the entire range of generator models available to the investigator and clinician, from the single moving equivalent current dipole (ECD) to distributed source models of cortical patches. However, these can be characterized as essentially static, and address the problem of estimating spatial activity profile under various spatial constraints at each time point. This can be taken to reflect a lag between our understanding of the biophysics of generator geometry (point dipole as a representation of EPSP and IPSP in the pyramidal neuron) versus that of generator dynamics. Although there have been recent efforts to incorporate the temporal dimension to source estimation, the use of such techniques to assess spread remains to be assessed (Daunizeau et al., 2006).
The spread of epileptiform activity, measured as the ratio of the regional MEG dipole source strength in a distributed model over the local noise level, has been mapped (statistically) at 2.5 ms intervals showing realistic patterns in a few children with focal epilepsy, comparing advantageously to the results of serial ECD fitting for interictal activity (Shiraishi et al., 2005a,b) and for discharges in the early ictal period (Tanaka et al., 2009).
In generalized epilepsy, EEG/MEG source phase synchrony analysis based on its surrogate measure, instantaneous narrow-band frequency locking, has been used to study long-range cortical synchronization during 3-Hz generalized spike-wave discharges, allowing the identification of a consistent fronto-central network, in agreement with other localization studies (Amor et al., 2009).
Causality and effective connectivity
A number of generalized measures of signal synchrony possess asymmetry which has been used to infer “driver-response” relationships (Le Van Quyen et al., 1998; Quiroga et al., 2002). However, the causality inferred from these has been shown to be dubious in the presence of noise (Quiroga et al., 2000) although there are examples of agreement with clinical data (Le Van Quyen et al., 1998). Of note is the use of generalized synchrony on icEEG (inter-channel spike peak time delay measurements) to validate a model of effective connectivity during seizures based on fMRI data in a rat model of epilepsy [David et al., 2008a; see Section “Signal Generation and Effective Connectivity Modeling in Epilepsy” on dynamic causal modeling (DCM)].
Granger causality (GC, sometimes referred to as Granger–Geweke causality; see Kaminski et al., 2001) is based on the notion that one signal can be called causal with respect to another if the latter can be better predicted by using information from the former. The directed transfer function (DTF; Kaminski and Blinowska, 1991), which was subsequently shown to be a generalization of GC, has been used to study information flow on icEEG data recorded during epileptic seizures (Franaszczuk and Bergey, 1998). More recently, a dynamic form of GC has been proposed for the study of epileptic spike propagation measured with MEG (Lin et al., 2009). The method can be used to track changes in effective connectivity based in the temporal and frequency domains over sub-spike time scales.
Dynamic causal modeling is a model of effective connectivity based on a biophysically realistic generative model of the signals and there are versions of DCM for EEG, MEG, and fMRI (see Section “Signal Generation and Effective Connectivity Modeling in Epilepsy” for a more detailed discussion of DCM). DCM is a relatively novel approach that was introduced as a generic formalism for studying effective connectivity in a seminal paper by Friston et al. (2003). In brief, at the heart of DCM is a set of bilinear differential equations (of the same form as Newtonian motion equations) that relate the rate of change in regional neuronal activity in terms of linearly separable components that reflect the influence of other regional state variables (Friston et al., 2003). One of DCM’s main claims is that it attempts to model neuronal states through generative models in contrast to other approaches to effective connectivity such as Granger causal modeling, which model the signals (Friston, 2009). DCM has been used to study plasticity in the human epileptic focus using evoked responses measured intracranially (David et al., 2008b).
Functional MRI: Functional and Effective Connectivity
Compared to EEG or even MEG, fMRI is a newcomer in the toolkit available to investigators interested in studying epileptic activity. Among the attractive aspects of the technique in comparison with EEG and MEG are: its capacity to image the entire brain more or less uniformly without the need to solve the inverse problem, its spatial resolution and the potentially complimentary nature of the information it provides (hemodynamic). The addition of simultaneous EEG recording means that one is able to correlate the fMRI time series data with subclinical (unpredictable and brief) events, such as IED, with the aim of mapping the associated hemodynamic changes.
Ictal events can also be studied, either fortuitously or intentionally, although the occurrence of seizures in the scanner poses a specific health hazard which requires special attention. Although a priori simultaneous EEG is not always necessary to study ictal events using fMRI in a given patient depending on clinical features it can be an important source of information. Without EEG and in absence of clinical manifestations or ictal trigger, fMRI can be used to study the resting-state brain hemodynamics without reference to any specific event, allowing comparing features of the fMRI signal such as inter-regional temporal correlation patterns (i.e., functional connectivity) across patient groups, for example (Guye et al., 2008, 2010).
There have now been more than 100 publications describing fMRI studies of epileptic activity in humans, mostly with simultaneous EEG recording and using a general linear modeling approach, which have revealed sometimes complex patterns of IED or seizure-related BOLD changes in a large proportion of the cases studied. Using this approach maps containing multiple significant BOLD clusters can be said to represent networks to the extent that the signals in those regions show a sufficient high degree of correlation with the modeled waveform. However, in the context of functional connectivity, it is worth remembering that the fact that two signals significantly correlated with a third (e.g., a modeled signal) does not imply that the former are significantly correlated with each other. Therefore, fMRI functional connectivity analyses are typically based on calculating inter-regional correlations directly from the data. For example, Waites et al. (2006) showed differences in resting-state functional connectivity patterns in the language network in patients with TLE compared to a group of healthy controls. Also in TLE, studies of resting-state fMRI connectivity have focused on identifying asymmetries with possible clinical implications (Bettus et al., 2009, 2010).
In the above studies, the characterization of networks is performed based on correlation analyses of time series data acquired over extended periods of rest, without reference to specific events, and do not address causality. There have been a few applications of DCM to fMRI data in epilepsy to study effective connectivity in networks associated with generalized spike-wave discharges (David et al., 2008a; Vaudano et al., 2009). The final section of this article focuses on DCM, in particular its possible role in elucidating the pathological mechanisms responsible for epileptic activity based on electrophysiological and hemodynamic data.
Electrophysiological Markers of Epilepsy: Ictal and Interictal Epileptiform EEG Patterns
The epileptiform patterns commonly observed on scalp EEG recordings from patients with epilepsy can be categorized as arising focally or appearing simultaneously over a large region or propagating to many remote locations. The identification and characterization of these patterns form an important element of the patient’s assessment and subsequent management. As for all types of brain activity neural interactions form a central element in the onset, continuation and cessation of epileptic activity. In this section we review the phenomenology of epileptic activity and the underlying neural interactions but with special emphasis on the aspects of connectivity that can be measured using human brain imaging and electrophysiology.
The Generators of Epileptiform Activity
While our understanding of the basic neurophysiology of the generators of epileptic activity has been derived from studies at the microscopic level, we envisage increasingly direct links with phenomenology at higher scales and that these will be made through biophysically realistic models of whole-brain signals, such as DCM (to be discussed in Section “Signal Generation and Effective Connectivity Modeling in Epilepsy”). The possibility of identifying and characterizing the pathological substrate of whole-brain data within such a framework would rest on models capable of representing the neurophysiological excesses and deficiencies described below, be they node-specific or network-wide, at the appropriate scale.
Interictal discharges
Interictal epileptiform discharges include spikes, which are fast electrographic transients lasting less than 70 ms and sharp waves, which last 70–120 ms (de Curtis and Avanzini, 2001); these occur rarely (<1%) in healthy individuals (Gregory et al., 1993), and are strongly associated with epilepsy (Marsan and Zivin, 1970). IEDs are generated by the synchronous “activation” of a large numbers of neurons – in order to be detectable by scalp EEG, the synchronous activation of 10–20 cm2 of gyral cortex is necessary (Tao et al., 2007a). Excitatory postsynaptic potentials following activation of glutamate receptors cause an influx of sodium into dendrites (current sink), and the consequent flow of sodium from the soma (current source). The intracellular correlate of the interictal spike is the paroxysmal depolarizing shift (Matsumoto and Marsan, 1964), a slow depolarizing potential with a high frequency (>200 Hz) burst of action potentials. A number of pathological mechanisms have been proposed to underlie the interictal spike, including changes in the intrinsic burst properties of neurons (increased neuronal excitability) and increased network excitability (secondary to changes in neurotransmission and/or neuronal connectivity).
Interictal epileptiform discharges are usually followed by a slow wave lasting hundreds of milliseconds. This depends upon the activation of hyperpolarizing GABA(A) and GABA(B) receptor-mediated currents and calcium-dependent potassium currents (de Curtis and Avanzini, 2001; McCormick and Contreras, 2001). Therefore, IEDs activate hyperpolarizing currents, resulting in a post-spike refractory period during which neuronal activity is inhibited (de Curtis and Avanzini, 2001). Increased interictal spiking occurs after seizures, raising the possibility that this is a compensatory antiepileptic response (de Curtis and Avanzini, 2001). Indeed, experiments in entorhinal cortex–hippocampal slice preparations have confirmed the antiepileptic potential of spikes. Spike discharges generated in the CA3 region inhibited epileptic activity in the entorhinal cortex, so that sectioning of part of the hippocampal circuitry, preventing invasion of the entorhinal cortex by these spikes, led to potentiation of entorhinal cortex seizure activity (Barbarosie and Avoli, 1997). This leads to two important conclusions: first, interictal spikes can have a lasting inhibitory effect; second, they can have this effect remote from where the spikes arise. This is critical for understanding cortico-cortical signal propagation as single spikes may disrupt propagation by, in effect, silencing cortical areas.
Fast oscillations
Ripple oscillations (100–200 Hz) are physiological phenomena that occur in relationship with hippocampal sharp waves. An observation in epileptic tissue is the presence of even higher frequency (250–500 Hz) oscillations, also termed fast ripples, which seem to be a marker of epileptogenicity (Bragin et al., 1999; Jacobs et al., 2009). These can occur in association with IEDs but also may precede seizures. It is likely that most high frequency oscillations are generated in and remain restricted to small areas of neocortex, but more rarely can occur over larger areas which may be more indicative of epileptogenic cortex (Schevon et al., 2009). There remains controversy about the mechanisms generating such high frequency oscillations. These have been proposed to be due either to a barrage of high frequency inhibitory postsynaptic potentials from fast spiking interneurons impinging on relatively depolarized principal cells (Trevelyan, 2009) or to the synchronous firing of principal neurons coupled through non-synaptic mechanisms such as gap junction (providing direct electrical coupling of neurons; Roopun et al., 2010).
Partial seizures
Spike discharges can precede a seizure with progressively less effective after-hyperpolarizations in mesial temporal lobe epilepsy (King and Spencer, 1995); however, the hallmark of seizure activity is the build up of fast activity that is usually initially spatially confined, and is distinct from IEDs. The mechanisms underlying this activity are unclear but it has been proposed to represent the excessive firing of a group of principal neurons, perhaps coupled through gap junctions (Traub et al., 2001). This pattern evolves to high amplitude spikes that occur at a lower frequency. Two questions concerning seizures arise: first, what is it that triggers a seizure? And second, what is it about an area of cortex that makes it epileptogenic? The first question is far from clear; there are conflicting data from analysis of preictal data (see Mormann et al., 2007) that suggest that there may be changes occurring minutes before the seizure (i.e., the seizure results as a critical point of network activity is reached). The transition from normal to epileptiform behavior is probably caused by greater spread and neuronal recruitment secondary to a combination of enhanced connectivity, enhanced excitatory transmission, a failure of inhibitory mechanisms, and changes in intrinsic neuronal properties. The second question is therefore easier to address as many of these changes have been described, but it is unclear which are most important (Walker et al., 2007). Indeed, it is likely that there is no unique process and that cortex can become epileptogenic via a variety of mechanisms, examples of which are given below.
During the development of epilepsy (epileptogenesis) changes have been documented in neuronal properties (Su et al., 2002), ion channel expression (Bernard et al., 2004; Shah et al., 2004), and GABAergic inhibition (Obenaus et al., 1993; Cossart et al., 2001). Moreover GABA(A) receptor potentials can and shift from hyperpolarizing to depolarizing (potentially excitatory; Cohen et al., 2002; and the effect of this on, for example, the BOLD response to GABAergic inhibition is not clear). Excitatory transmission is potentiated not only through changes in receptors (Lieberman and Mody, 1999; Porter et al., 2006), but also through sprouting of excitatory fibers (Tauck and Nadler, 1985). Sprouting has been most clearly demonstrated in the dentate gyrus in which recurrent collaterals form between dentate granule cells, and this hyper-connectivity promotes the formation of local excitatory circuits and hyper-excitability. Importantly, however, the probability of a connection between any two granule cells is low and the observed hyper-excitability may be explained by non-random connectivity and the formation of a few, highly connected “hub” cells (Morgan and Soltesz, 2008), a feature of small-world networks. Epileptogenic insults are also associated with gliosis, altering the regulation of external potassium (Lux et al., 1986) and contributing to the release of neurotransmitters into the extracellular space (Tian et al., 2005). There are also changes in non-synaptic mechanisms involving increases in ephaptic transmission and the expression of gap junctions which may promote neuronal synchronization (Jefferys, 1995). Suggesting that the local spread of seizure activity can occur independent of axonal connections.
Some of these changes (e.g., excitatory fiber sprouting, gliosis, neuronal death) have an obvious anatomical correlate and can be easily quantified by microscopic and, on occasion, macroscopic tools. Moreover, pathologies leading to these changes such as stroke, tumors, cortical dysgenesis, traumatic brain injury are often clearly evident, and although the hallmark of these pathologies (e.g., brain damage) may not be the substrate for the epileptogenic process, they are an indicator of an epileptogenic process. However, these clear anatomical changes are not necessary for a network to become epileptogenic and certain changes (e.g., in ion channels and receptors) may only be apparent with functional investigation. Therefore, epileptogenic cortex may not always be discernible using anatomic techniques.
Absence seizures and 3 Hz spike-wave discharges
Absence seizures are generalized seizures which are generated within the thalamocortical loop. This depends upon the recruitment of reticular thalamic neurons by the neocortex. These in turn hyperpolarize (inhibit) thalamocortical neurons. This activates various ionic currents, resulting in the rebound burst firing of thalamocortical neurons which project onto and excite neocortical neurons and so the cycle repeats (McCormick and Contreras, 2001). Absences were originally believed to be generated subcortically, by thalamic neurons initially driving the recruitment of neocortical neurons. However, paroxysmal oscillations within thalamocortical loops in absence seizures in rats seem to originate in the somatosensory cortex rather than the thalamus, with synchronization mediated by rapid intracortical propagation of seizure activity (Meeren et al., 2002). This is supported by anatomical evidence in humans of subtle cortical structural abnormalities in some patients with absence seizures (Woermann et al., 1999). Indeed, this and the potential of focal pathological change in the medial frontal lobe to generate absence-like seizures have blurred the distinction between focal and generalized epilepsies.
Propagation of Epileptic Activity: Observations and Mechanisms
Both IEDs and seizures propagate, by which we mean that the pathological EEG pattern spreads to distant brain areas, reflecting recruitment of neuronal activity in those areas. This occurs locally due to local connections and networks and at more distant sites through longer range connections. However, recruitment depends on not only connections between different brain regions but also the ease with which a brain region can be recruited (see below). In some situations the observed propagation pattern can be rationalized based on general anatomical knowledge and can be correlated with the evolution of clinical signs (in the case of seizures), however these can significantly vary from event to event and our general understanding of these patterns remains poor; studies comparing patient-specific structural connectivity (MRI tractography) with interictal and ictal propagation patterns are just beginning to emerge (Hamandi et al., 2007; Diehl et al., 2010).
Nonetheless, the mechanisms underlying propagation and recruitment at these different scales are probably quite similar, though may differ for interictal and ictal activity. An IED can be considered in three distinct mechanistic stages: initiation, propagation, and termination (Pinto et al., 2005). The threshold for initiation depends upon the balance of excitation and inhibition. However, propagation velocity depends solely upon excitation, probably because the delay between excitatory activity and the recruitment of inhibitory activity provides a window during which an IED can propagate unimpeded by inhibition. The termination of an IED is a complex process including depolarizing block and synaptic inhibition.
The propagation of seizures is more complex because, by necessity, these are longer lasting and so cannot depend on the short-lived delay between excitatory and inhibitory activity. Focal seizure activity recruits local inhibitory neurons which importantly provide a strong “surround” inhibition limiting the spread and time course of the abnormal activity (Prince and Wilder, 1967). This inhibitory constraint provides a mechanism that limits seizure activity in both temporal and spatial domains. Repeated seizure activity can however result in the breakdown of this constraint and seizure propagation. Moreover, the speed of propagation is dependent upon the strength of inhibition with faster propagation occurring with less powerful inhibitory constraint (Trevelyan et al., 2006, 2007a). Furthermore, the arrangement of synaptic inhibition (divergent) in which feed-forward inhibition will constrain a number of pyramidal cells results in a stepwise recruitment of groups of principal neurons as inhibition fails. The mechanisms underlying the breakdown of the inhibitory constraint are unclear and may not be unique.
Although propagation of seizure activity may be well-defined, the propagation of discharges that occur during seizure activity is less certain. Ictal activity is prolonged and so having propagated to a region, later repetitive discharges during the ictus will spread according to the pattern of the connections of that area and the strength of surrounding inhibition. It is therefore possible that later discharges during the ictus may back propagate to areas from which the seizure has spread (Trevelyan et al., 2007b). This is also observed with human recordings.
Signal Generation and Effective Connectivity Modeling in Epilepsy
In this section we consider the scope for uni- and multi-modal data to be brought together in a biophysically realistic modeling and data statistical analysis framework, namely DCM.
Why should We Attempt Model-Based Effective Connectivity Analyses to Study Epilepsy?
As can be abstracted from the previous sections, initiation, propagation, and termination of epileptiform activity are thought to result from the complex interplay between the natural balance of excitation and inhibition within the system and some pathological perturbations of various physiological processes, e.g., neuromodulatory activity (impacting upon neuronal excitability). This is most probably the reason why epilepsy expresses itself at so many different spatial and temporal scales of observation, from e.g., genetic disruptions of biomolecular neuronal properties (e.g., conformational change of ion channels, see Steinlein, 2004) to macroscopic structural abnormalities (e.g., cortical thickness in temporal lobe epilepsy, see Bernhardt et al., 2010), through impaired resting-state activity (e.g., phasic suspension of the attentional network; see Gotman et al., 2005; Hamandi et al., 2006; Laufs et al., 2007).
At first glance, it does not seem possible to embrace the diversity of these traits within a common comprehensive theoretical framework. However, it must be the case that adequately realistic models of brain dynamics, in conjunction with appropriate brain activity measurements, can reveal the link between these phenomena (Wendling, 2008). This is because whether or not a given trait is related to epilepsy has to do with the observed correlation between its occurrence and the presence of epileptiform brain activity, such as focal seizures or generalized spike-wave discharges. For example, if a model is able to account for basic cellular mechanisms such as the impact of neurotransmitter levels onto average ion channel dynamics, it might be able to link genetic observations to neuroimaging. If such a model was also able to account for the relative proportion of cell types in different cortical layers (e.g., pyramidal cells in layer IV and excitatory/inhibitory interneurons in layer VI), it might be able to predict dynamical changes resulting from sufficiently specified loss of gray matter. Finally, if it was based on the notion of a distributed brain network to capture observed transient and steady-state macroscopic dynamics, it might well be an appropriate tool to understand the large-scale structure of epileptogenic brain networks.
Having said this, the model alone, even if exquisitely realistic, cannot disambiguate between different candidate scenarios about, e.g., what is it that triggers, propagates and/or terminates an observed seizure. This is because the seizure etiology is expected to vary greatly across patients, or even within patients. In other words, the mechanisms that lead to the seizures are context-dependent. Hence, one cannot predict those a priori, on a patient-by-patient basis.
Taken together, this means that one wants to embed sophisticated biophysical models into the statistical data analysis, with the aim of exploiting the specificities of the observed (neuroimaging) data to identify the subject-specific relevant mechanisms underlying epileptiform activity. This is the basic idea behind DCM (Friston et al., 2003). The DCM framework has two main components: biophysical modeling and probabilistic statistical data analysis. Realistic neurobiological modeling is required to simulate observed brain network dynamics. However, context-dependent variables of these models cannot be known a priori, e.g., whether or not activity-dependent plasticity did occur. Therefore, statistical techniques (embedding the above biophysical models) are necessary for statistical inference on these context-dependent effects, which are the experimental questions of interest.
DCM: State-of-the-Art
Nevertheless, existing implementations of DCM restrict the application of this generic perspective to more specific questions that are limited either by the unavoidable simplifying assumptions of the underlying biophysical models and/or by the bounded efficiency of the associated statistical inference techniques. In brief, the validity of DCM relies upon a careful balance between the realism of the underlying biophysical models and the feasibility of the statistical treatment. This has motivated the development of many variants of DCM, focusing on either of the two DCM components. To date, about 30 DCM methodological articles have been published in the peer-reviewed literature (see Daunizeau et al., 2010 for a recent review).
The (Bayesian) statistical treatment of DCM eventually provides model parameter estimates (synaptic time constants, action potential thresholds, adaptation effects, etc…) and the model marginal likelihood. The latter quantity measures how likely is a model given the measured (neuroimaging) dataset, and is used to perform statistical model comparison. This statistical component of DCM is further described below (see DCM: Statistical Data Analysis). This can be useful to identify epileptogenic mechanisms that are a priori likely to underlie ictal or interictal epileptiform activity.
In brief, DCM for fMRI data includes a simple dynamical model of coupled brain regions as well as a model of neurovascular coupling, relating neural activity to BOLD time series. In addition, it comes in three flavors:
- whether or not distinct excitatory and inhibitory populations are considered within each region of the brain network
- whether or not one includes spontaneous (stochastic) fluctuations in the brain network dynamics
- whether or not (non-linear) gating effects, whereby activity in one area enables or disables a connection between two other areas, are assumed to underlie observed brain dynamics.
In its simplest form, Bayesian model comparison was used in Vaudano et al. (2009) to assess the structure of the epileptogenic network in terms of the role of three brain structures, namely thalamus, prefrontal cortex, and precuneus in seizure generation or facilitation using EEG–fMRI data in seven patients with idiopathic generalized epilepsy (IGE). The findings lead the authors to hypothesize a role for the precuneus as a form of modulator of generalized spike-wave activity, and by extension, of the occurrence of absence seizures, linking spontaneous fluctuations in brain state as reflected by the so-called Default-Mode Network of brain activity (Raichle et al., 2001) to the occurrence of epileptic discharges (Vaudano et al., 2009; Carney et al., 2010).
David et al. (2008a) performed concurrent fMRI and icEEG measurements to measure the spread of excitation in a genetically defined type of epilepsy in rodents. It is important to note that in these studies, the onset of EEG epileptic activity (back-shifted in time in the case of David et al., 2008a) was treated as the input (knowledge of which is required, except – exceptionally – for stochastic DCMs) in families of models, where each model was distinguished by the choice of input node, for comparison to identify the best model. One may question the meaning of intrinsic activity being treated as an input in this context, given that DCM was conceived based on extrinsic inputs under experimental control. In fact, this can be interpreted as embodying the empirical assumption that the initial cause of the modeled effects corresponds to the time of GSW onset. It is worth remembering that the families of models considered and the DCM results are as good as the assumptions, which they are based on (Penny et al., 2004). Daunizeau et al. (2010) has used model comparison on stochastic DCMs for fMRI to provide evidence in favor of the existence of (non-linear) thalamic gating effects onto the cortico-thalamic loop during interictal activity1.
“Neural mass” models in DCMs for EEG/MEG/LFP data are typically considerably more complex than in DCMs for fMRI. This is because the temporal information on neural activity, which can be extracted from electrophysiological measurements, can only be captured by models that represent neurobiologically detailed mechanisms. Here, each region is assumed to be composed of three interacting subpopulations (pyramidal cells, spiny-stellate excitatory and inhibitory interneurons) whose (fixed) intrinsic connectivity was derived from an invariant meso-scale cortical structure (Jansen and Rit, 1995). The temporal dynamics of each subpopulation relies on two operators: a temporal convolution of the average presynaptic firing rate yielding the average postsynaptic membrane potential and an instantaneous sigmoidal mapping from membrane depolarization to firing rate (see Figure 1). This forms the basic building block of DCMs for EEG/MEG/LFP data, in the sense that it summarizes the activity within one brain region that composes the large-scale network. Such basic building block has already been extensively used in the context of epilepsy (see, e.g., Wendling, 2008).
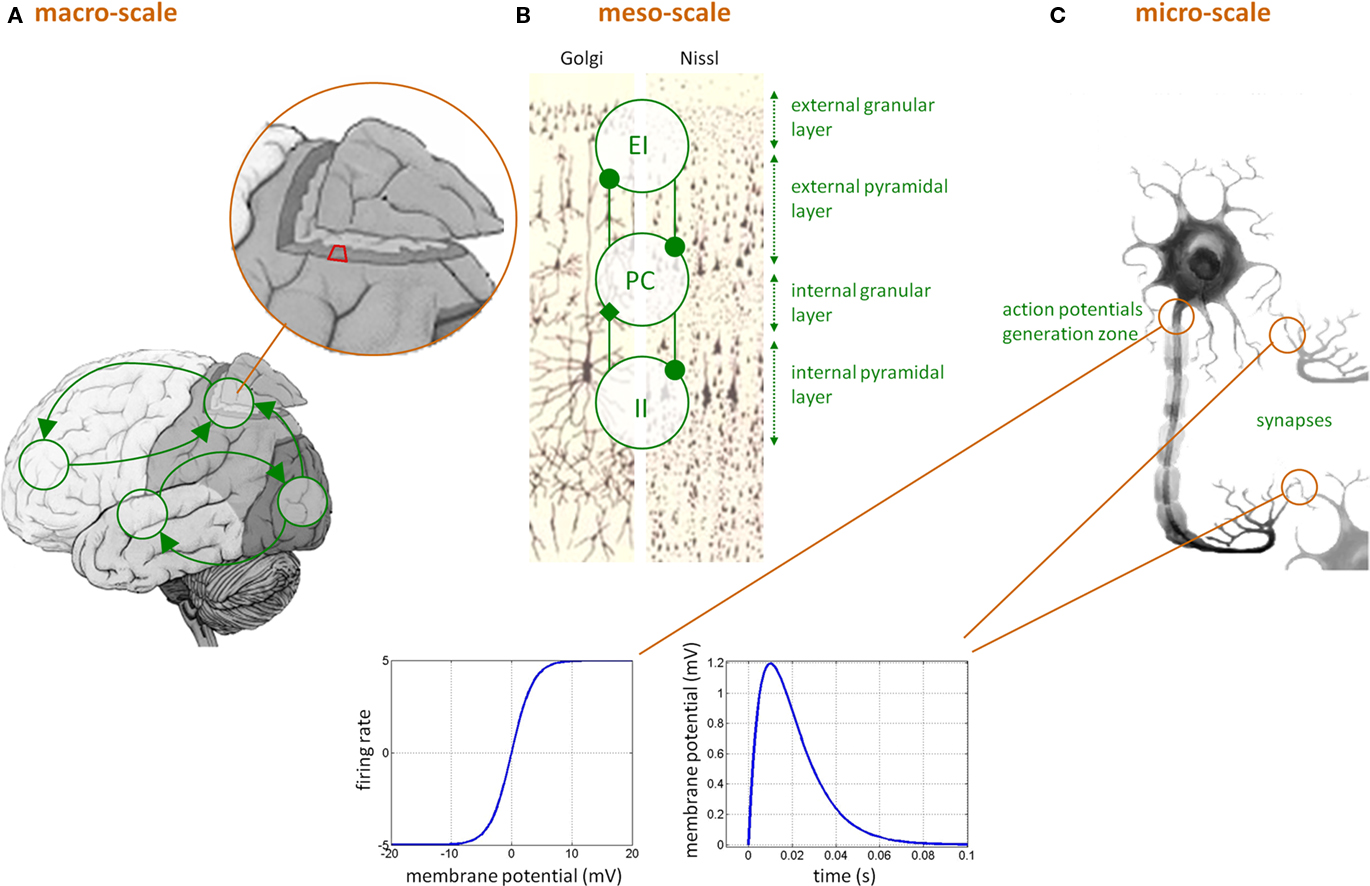
Figure 1. Dynamic causal modeling for EEG/MEG data. (C) Neuronal features at the micro-scale that affect the level of the neural ensemble, i.e., at the meso-scale (B): (i) sigmoidal transformation, describing how mean postsynaptic membrane potential is linked to mean presynaptic firing rate, and (ii) temporal convolution (kernel shown) of mean presynaptic firing rate yielding mean postsynaptic membrane depolarization. (B) The meso-scale properties that affect the macro-scale (A), i.e., within-region invariant connectivity structure between pyramidal cells (PC), excitatory interneurons (EI), and inhibitory interneurons (II) subpopulations across cortical layers. (A) The macro-scale effective connectivity structure.
Critically though, the qualitative nature of the network dynamics relates to the between-areas connectivity structure. In DCM for EEG/MEG/LFP data, three qualitatively different extrinsic (excitatory) connections types are considered (cf. Felleman and Van Essen, 1991): (i) bottom-up or forward connections that originate in agranular layers and terminate in layer IV, (ii) top-down or backward connections that connect agranular layers, and (iii) lateral connections that originate in agranular layers and target all layers. Lastly, the model can include the propagation of electromagnetic fields through head tissues to address the problem of spatial mixing of the respective contributions of cortically segregated sources in the measured scalp EEG/MEG data (see e.g., Mosher et al., 1999). Existing variants of DCM for EEG/MEG and LFP (local field potential data) are related to:
- which data features one wants to model, i.e., evoked responses in the time domain, steady-state responses in the frequency domain, induced responses in the time-frequency domain, oscillations in the (within-frequency band) phase domain, etc;
- whether or not voltage-dependent effects on membrane ion conductances are included in the model;
- whether local spatial propagation effects are considered, in relation to the size of the brain regions participating in the network.
The previously mentioned work by David (2007) is a first step toward understanding the gradual recruitment of the epileptogenic network that gives rise to epileptic discharges within the framework of DCM. Some of the critical pathological mechanisms discussed in the previous section can already be assessed through DCM analyses. This is because one can include these in terms of a priori beliefs onto model parameters (e.g., altered voltage-dependent sodium channel kinetic time constants) or even on model structure (e.g., anatomically localized cell type-specific neuronal death), and quantify how likely they are, given observed brain dynamics.
DCM: Statistical Data Analysis
The need for neurobiological plausibility can make DCMs fairly complex, compared to conventional regression-based models of effective connectivity, such as structural equation modeling (SEM; McIntosh and Gonzalez-Lima, 1994; Büchel and Friston, 1997) or autoregressive models (Harrison et al., 2003; Roebroeck et al., 2005). This complexity induces potential non-identifiability problems, requiring novel sophisticated model inversion techniques that are typically cast within a Bayesian framework. For example, the non-linearities of the models, as well as the dimension of the dynamical systems involved, have necessitated the development of dedicated approximate inference schemes, namely variational Bayes (VB; see e.g., Beal, 2003). In brief, VB is an iterative algorithm that indirectly optimizes an approximation to both the model evidence (used for model comparison) and the posterior density (for parameter estimation), under simplifying assumptions about the form of the latter distribution (see, e.g., Friston et al., 2007). Furthermore, developments have been required to address Bayesian model comparison for group studies. Stephan et al. (2009) address random effects on models at the between-subjects level, i.e., accounting for group heterogeneity or outliers. This second-level analysis provides the so-called “exceedance probability,” of one model being more likely than any other model, given the group data. It also introduced model space partitioning, which allows one to compare subsets of all models considered, integrating out uncertainty about any aspect of model structure other than the one of interest. This work was recently extended to allow for comparisons between model families of arbitrary size and for Bayesian model averaging within model families Penny et al. (2010). Allowing statistical inference at the level of families of model is important whenever the question of interest may correspond to more than one model within the comparison set (e.g., serial versus parallel connectivity structure).
Note that using the model evidence to compare models against each other means that the most likely model may not be the model “fitting best” the data. One should remember that measuring the fit (e.g., percentage of variance explained) is not a very good measure for the quality of a model. This has to do with the fact that minimizing residuals can lead to severe lack of generalizability. Correcting the fit with complexity penalty terms is the hallmark of Bayesian inference schemes, which, as a consequence, do not try to minimize the residuals. Within a Bayesian framework, it is thus perfectly acceptable to reasonably compromise data fit, if this guaranties improved generalizability. Guessing whether or not this trade-off is optimal by looking at the fit itself is impossible without factoring in the complexity of the model. In other words, any optimal Bayesian inversion only explains in the data what is estimated to be generalizable, i.e., reproducible across repetitions of the same experiment, given the explanatory factors at hand.
Besides, we would like to further comment on the causal aspect of DCM. It is not because DCM relies upon a dynamical formulation that it assesses causal influences from evidence of temporal precedence (as, e.g., GC techniques do; see Valdes-Sosa et al., 2011 for a comprehensive discussion). Time is certainly an important dimension of causal influences, but definitely not the main component of DCM for fMRI, which, compared to the underlying neural events, is poorly temporally resolved. Causality can be inferred from non-symmetrical shared variance2 (e.g., see Pearl, 2000). DCM was designed to capture these effects. The motivation for including the temporal dimension in DCM is actually to allow for feedback influences (loopy causal systems), rather than to detect temporal precedence. This is why DCM is more (though not entirely) immune to heterogeneous hemodynamic delays than, e.g., GC analyses (David et al., 2008a).
Finally, we would like to stress that DCM is ultimately not an exploratory analysis: it is meant to test/compare precise hypotheses about brain function. Furthermore, its mathematical form is explicitly based on generic assumptions about brain organization, e.g., that the brain enjoys a hierarchical structure. This means that DCM is optimally used to answer a specific class of questions, typically: whether or not feedback/feed-forward influences within the network vary as a function of experimental manipulations or perturbations (such as diseases). In the context of epilepsy, examples of DCM-relevant questions are: (i) whether ictal activity propagates from a region that triggers epileptiform activity, or rather that epileptiform activity emerges from self-excitatory influences throughout the network; or (ii) how does the system reconfigures itself (short-term plasticity) during the interictal to ictal transition. DCM is probably not the right data analysis tool to address more loosely defined questions about brain organization, e.g., can we get a global picture of the networks active during the fMRI data acquisition session?…
DCM: Limitations
Neuroanatomical and neurophysiological studies have been crucial in motivating the basic modeling assumptions that underlie DCMs for fMRI and electrophysiological data. However, one may question whether all neurobiological facts relevant for explaining neuronal population dynamics are represented in existing DCMs. This question is of particular importance for DCMs of electrophysiological data, from the healthy or diseased brain, which have much more fine-grained representations of neuronal mechanisms than DCM for fMRI.
For example, macro-scale propagation effects, mediated by distance-dependent lateral connections, have not yet been properly accounted for3. These effects can be thought of as wave propagation in a complex medium, leading to spatiotemporal pattern formation or self-organization. Since the early work by Amari (1977), much effort has been invested in developing a neural field theory (e.g., see Deco et al., 2008 and references therein); incorporating these ideas into the DCM framework may prove fruitful.
Also, it is well known that neurons are subject to internal (e.g., thermal) noise, which may still have an impact at the population scale (see e.g., Soula and Chow, 2007 for “finite size” effects). If this is the case, the neural ensemble dynamics would deviate from the mean-field theoretical treatment that underlies most current modeling efforts in macro-scale neural dynamics (including DCMs).
Perhaps most importantly, there are several neurophysiological processes at the micro-scale that have been neglected in existing DCMs, notably activity-dependent plasticity, i.e., continuously modified activity-dependent efficacy of synaptic transmission. This includes different forms of short-term plasticity, such as synaptic depression/facilitation or spike-timing dependent plasticity, and long-term plasticity, such as long-term potentiation (LTP) and depression (LTD). An important task for the future will be to evaluate whether the above processes are necessary for explaining, e.g., the transition from interictal to ictal activity, as observed with presently available recording techniques.
Concerning DCM for fMRI, the above phenomena are not explicitly modeled4. This may (or may not) be a lesser concern than for electrophysiological DCMs, since it is unlikely that these fine-grained mechanisms are accurately reflected in and can be inferred from BOLD data. Instead, physiological details of the neurovascular coupling are perhaps more important (see Stephan et al., 2004 for review). So far, it neglects the potential influence of inhibitory activity on the hemodynamic response, which is a likely explanation for deactivations (Shmuel et al., 2006; Sotero and Trujillo-Barreto, 2007). Furthermore, there is no realistic account of the metabolic cascade that relates synaptic activity and neuronal metabolism to the vasodilatation kinetics (Riera et al., 2006). This is mainly due to the simplistic account of neuronal activity in DCMs for fMRI, which does not disambiguate between, e.g., postsynaptic membrane depolarization and presynaptic firing rate. Also, DCM for fMRI has ignored the important role of glial cells (Takano et al., 2006; Iadecola and Nedergaard, 2007). We refer the interested reader to Rosa et al. (2010) for further reading on the current debate regarding the neurovascular coupling.
Many DCM validation studies have been conducted (see Daunizeau et al., 2010 for a review). Among these, the most far-reaching experimental assessment of the validity of DCM analyses so far was done by David et al. (2008a), who performed concurrent fMRI and intracerebral EEG measurements to measure the spread of excitation in a genetically rat model of absence epilepsy. In brief, this study (i) provides supportive evidence for the validity of DCM for inferring network structure from fMRI data and (ii) stresses the importance of having a realistic model of neurovascular coupling. Clearly, further validation studies will be needed. Further invasive in vivo measurements of electrical (e.g., implantable miniaturized probes or clinical electrodes (combined with fMRI: Vulliemoz et al., 2010) and optical (e.g., two-photon laser scanning microscopy) signals are likely to be very useful for such an experimental validation (Riera et al., 2008).
Criticisms have also been raised against the statistical component of DCM. Most of these are related to the generic properties of the VB algorithm, which is essentially an approximation scheme. We refer the reader to Daunizeau et al. (2010) for a comprehensive critical review of the biophysical, statistical and practical aspects of DCM. In addition, it has often been advocated that the computational complexity of DCM prevents any analysis of a large-scale brain network containing more than a handful of nodes/regions. This is supposed to be due to the fact that one may have to compare a number of models that is an exponentially increasing function of the number of nodes (curse of dimensionality). Also, it has been argued that the proportion of explained variance in the measured signals was “low,” even for the “best” models within the comparison set (this has sometimes been referred to as a form of “underfitting”). However, recent developments in the statistical treatment of DCM render these claims irrelevant:
- The use of Savage–Dickey ratios within a Bayesian framework allows one to derive the model evidence of any model that can be derived as a reduction of a full “reference” model (i.e., the DCM corresponding to an entirely connected network)5. This means that one has to perform only one numerical inversion (that of the full model) in order to compare all other possible reduced models (i.e., networks lacking connections). This makes it possible to compare thousands of models in a few seconds (Friston et al., 2011).
- Following recent developments in probabilistic identification of stochastic systems (Friston et al., 2008; Daunizeau et al., 2009b), the first steps toward stochastic DCMs are now being taken (Daunizeau et al., 2011, submitted;Li et al., 2011). These models extend the current deterministic DCM framework by accounting for unspecific perturbations to the network dynamics. As a result, the proportion of explained variance drastically increases. Note that being a Bayesian scheme, stochastic DCM does not suffer from overfitting, which is the hallmark of frequentist statistical techniques.
Having said this, no increase in the sophistication of the statistical treatment of DCM can legitimately be said to guarantying the validity of the overall data analysis. This is already evident when considering the bounded realism of the underlying biophysical models (c.f. above comments). But more generally, the validity of DCM may well be context-dependent. Thus, the relevance of DCM within the context of epileptogenic networks has to be quantitatively assessed, by cross-validating the analyses with established results in the field. In addition, it may be necessary to extend the current DCM approach, in order to account for effects that may a priori be playing a key role when investigating the genesis, spread and termination of epileptic events using neuroimaging techniques. We will come to this in the next section.
DCM: Relevant Potential Extensions
Despite being so far the most far-reaching experimental assessment of the validity of fMRI DCM analyses so far, the study in David et al. (2008a) stressed the importance of having a model of neurovascular coupling. The concurrent use of two important neuroimaging modalities (i.e., EEG and fMRI data) raises the need for an integrated framework, whereby the same model is complementarily informed by the characteristic spatial and temporal resolutions of both datasets, beyond the use of EEG purely as a temporal event marker for fMRI modeling or DCM for example (Vaudano et al., 2009). This appears to be, despite a number of acknowledged theoretical and experimental concerns (see Daunizeau et al., 2009c for a review about EEG–fMRI information fusion), a promising future avenue for studying whole-brain, millisecond range, spontaneous or evoked paroxysmal activity and to characterize the underlying networks.
But more importantly, other potential extensions of the existing DCM framework can be considered to be relevant for studying epilepsy:
• Field DCMs: By incorporating elements of neural field theory (see Amari, 1977), field DCMs could account for local macro-scale propagation effects. The basic idea here is to account for the distributed nature of brain activity (see Daunizeau et al., 2009a for a first step toward field DCMs). Among other phenomena, this could be helpful to assess within-region spread and boundaries of paroxysmal activity (e.g., inhibitory surrounding effects).
• Stochastic DCMs: Accounting for stochastic inputs to the network may be of particular importance for studying pathological resting-state data, whereby coherent activity within the network is not driven by experimentally controlled inputs to the system (which is usually the case in fMRI studies of epilepsy). In addition, provided that the probabilistic inversion schemes are properly extended (cf. Friston et al., 2008; Daunizeau et al., 2009b), this could also increase the stability of the statistical treatment of DCM (e.g., robustness to “missing regions”).
• Plastic DCMs: Aberrant long- and short-term synaptic plasticity may play a key role in the gradual recruitment of regions within the epileptogenic network. An attractive goal is to extend the current DCM framework and, under due consideration of the limits of statistical inversion, represent different neurobiological mechanisms of synaptic plasticity more explicitly, such that their relative importance for explaining a patient-specific measurement of ictal and interictal activity can be disambiguated by model selection. Autonomous (activity-dependent) plastic effects may turn out to be particularly important to explain phase transition phenomena, e.g., transition from interictal to ictal activity (and back).
These modeling extensions could also benefit from the development of explicitly controlled experimental paradigms, provided that they can be undertaken ethically. For example, the use of seizure-inducing repetitive sensory or electrical stimulation might provide a statistically very powerful way of disclosing the properties of the epileptogenic network. Also, its interaction with non-pathological functional networks might be studied in the context of standard neuropsychological tasks. Lastly, trans-cranial magnetic stimulation (TMS) and/or deep-brain stimulation (DBS) could be used to causally interfere with parts of the network, providing exquisite information about the specific role of brain regions within a reciprocally connected network. Such experimental paradigms can easily be modeled with DCM, as is routinely done nowadays within the context of non-clinical neuropsychological research studies.
Discussion and Conclusion
The problem of characterizing the causal chains that give rise to and take place during epileptic events is central to our understanding of epilepsy, with vital consequences for the development of improved seizure management strategies. Following a period dedicated to the identification of regional abnormalities, we envisage that studies of epileptic activity and its substrate will focus increasingly on network aspects. We also believe that the long-term aim of developing non-invasive (whole-brain) neuroimaging techniques capable of solving the presurgical localization problem, by the very nature of the data they provide, goes hand in hand with this vision.
We have seen the progressively more sophisticated use of the various forms of data available to the investigator interested in studying epileptic networks, from scalp EEG to fMRI and alluded to increasingly sophisticated models. We have seen how the characterization of connectivity based on signal propagation relies on empirical rules mainly based on measures of association. This approach has been most rigorous and informative in relation to EEG signals measured intracranially. Access to hemodynamic brain signals measured non-invasively during spontaneous epileptic activity in humans is a novel and potentially important avenue for the study of the temporal relationship between activities in different brain regions in a complementary way to electrophysiological study. For example, such studies may be able to reveal changes taking place over long time scales more easily than using electrophysiological techniques.
In the context of attempts to characterize the networks involved in seizure onset, propagation and cessation based on macroscopic measurements such as EEG/MEG and fMRI, the lack of a complete understanding, particularly in humans, of the underlying network dynamics poses a challenge and therefore an opportunity. This is because we do not really know what we are looking for with neuroimaging; the limitations of our gold standard (currently icEEG and post-surgical outcome) are clear to see. Therefore, we are still essentially at the stage of mapping hemodynamic changes based on temporal coincidence with scalp EEG and/or clinical manifestations. Even if we had a more complete electrophysiological description of such networks which for example could be used to devise more sophisticated GLMs, we do not yet fully understand the relationship between neuronal activity as measured using the most advanced electrophysiological techniques, such as depth EEG, and the BOLD signal (see Buzsaki et al., 2007; Logothetis, 2008). This makes the comparison of measures of connectivity based on the two types of data even more complex.
Nonetheless, the advent of models of effective connectivity such as DCM, incorporating increasingly sophisticated models of neuronal activity at various scales, combined with our improved understanding of the interictal and ictal states and the transition between them offers the opportunity for the first time to explore epileptic networks over the entire brain in a mechanistic, causal framework through model comparison. Efforts to tackle this challenge have already been made in relation to generalized spike-wave activity and absence seizures, due to the presence of a good rationale for a limited number of alternative models. The challenge is much greater in focal epilepsy where the phenomenology is much more varied. In addition, through our increasing understanding of the integrative aspects of brain activity derived from whole-brain cognitive neuroimaging studies this may help us answer questions such as: What is the interaction between fluctuations in connectivity associated with normal brain activity and the networks associated with paroxysmal events? Why do spikes and seizures occur when they do?
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
- ^Stochastic DCM refers to an extension of the DCM framework, whereby one assumes that activity within network nodes may by driven by unknown (random or stochastic) inputs, in addition to experimentally controlled inputs and influences from other areas. In other words, in addition to the usual DCM parameters, one has to estimate the trajectory of neural noise that may have distorted the response of the system to known inputs. The key idea here is that neural noise can extend the dynamical repertoire of the system in a non-trivial way. Besides, stochastic DCM reduces to deterministic DCM by a priori constraining the neural noise variance to 0.
- ^Pearl takes the following example: one actually infers that rains causes the grass to be wet (and not the reverse), because it does not rain each time the grass is wet (due to other – independent – influences, e.g., the gardener), but the grass is wet each time it is raining.
- ^But see Daunizeau et al. (2009a) for a “standing wave” approximation to local propagation effects.
- ^But see David (2007), David et al. (2008b), and Stephan et al. (2008) for phenomenological accounts of activity-dependent plasticity effects.
- ^Savage–Dickey ratios rely upon simple conditional probability calculus to numerically derive the relative evidence of nested models from the divergence between prior and posterior distributions of the full model. Loosely speaking: if any hypothesis (e.g., θ = 0) is more probable under the posterior than under the prior, then it means that the data affords evidence in favor of the hypothesis. It turns out that adding such hypotheses to the full model defines nested models, i.e., models with fixed (zero) connections in the network. We refer the interested reader to Friston et al. (2011) and references therein.
References
Allen, P. J., Smith, S. J. M., and Scott, C. A. (1992). Measurement of interhemispheric time differences in generalised spike-and-wave. Electroencephalogr. Clin. Neurophysiol. 82, 81–84.
Amari, S. (1977). Dynamics of pattern formation in lateral inhibition type neural fields. Biol. Cybern. 27, 77–87.
Amor, F., Baillet, S., Navarro, V., Adam, C., Martinerie, J., and Le Van Quyen, M. (2009). Cortical local and long-range synchronization interplay in human absence seizure initiation. Neuroimage 45, 950–962.
Barbarosie, M., and Avoli, M. (1997). CA3-driven hippocampal-entorhinal loop controls rather than sustains in vitro limbic seizures. J. Neurosci. 17, 9308–9314.
Bartolomei, F., Wendling, F., Bellanger, J. J., Regis, J., and Chauvel, P. (2001). Neural networks involving the medial temporal structures in temporal lobe epilepsy. Clin. Neurophysiol. 112, 1746–1760.
Beal, M. (2003). Variational Algorithms for Approximate Bayesian Inference. Ph.D. thesis, Gatsby Computational Unit, University College London, London.
Bernard, C., Anderson, A., Becker, A., Poolos, N. P., Beck, H., and Johnston, D. (2004). Acquired dendritic channelopathy in temporal lobe epilepsy. Science 305, 532–535.
Bernhardt, B. C., Bernasconi, N., Concha, L., and Bernasconi, A. (2010). Cortical thickness in temporal lobe epilepsy. Neurology 74, 1776–1784.
Bettus, G., Bartolomei, F., Confort-Gouny, S., Guedj, E., Chauvel, P., Cozzone, P. J., Ranjeva, J. P., and Guye, M. (2010). Role of resting state functional connectivity MRI in presurgical investigation of mesial temporal lobe epilepsy. J. Neurol. Neurosurg. Psychiatry. 81, 1147–1154.
Bettus, G., Guedj, E., Joyeux, F., Confort-Gouny, S., Soulier, E., Laguitton, V., Cozzone, P. J., Chauvel, P., Ranjeva, J. P., Bartolomei, F., and Guye, M. (2009). Decreased basal fMRI functional connectivity in epileptogenic networks and contralateral compensatory mechanisms. Hum. Brain Mapp. 30, 1580–1591.
Bettus, G., Wendling, F., Guye, M., Valton, L., Regis, J., Chauvel, P., and Bartolomei, F. (2008). Enhanced EEG functional connectivity in mesial temporal lobe epilepsy. Epilepsy Res. 81, 58–68.
Bourien, J., Bartolomei, F., Bellanger, J. J., Gavaret, M., Chauvel, P., and Wendling, F. (2005). A method to identify reproducible subsets of co-activated structures during interictal spikes. Application to intracerebral EEG in temporal lobe epilepsy. Clin. Neurophysiol. 116, 443–455.
Bragin, A., Engel, J. Jr., Wilson, C. L., Fried, I., and Mathern, G. W. (1999). Hippocampal and entorhinal cortex high-frequency oscillations (100–500 Hz) in human epileptic brain and in kainic acid – treated rats with chronic seizures. Epilepsia 40, 127–137.
Brazier, M. A. (1972). Spread of seizure discharges in epilepsy: anatomical and electrophysiological considerations. Exp. Neurol. 36, 263–272.
Büchel, C., and Friston, K. J. (1997). Modulation of connectivity in visual pathways by attention: cortical interactions evaluated with structural equation modelling and fMRI. Cereb Cortex 7, 768–778.
Carney, P. W., Masterton, R. A. J., Harvey, A. S., Scheffer, I. E., Berkovic, S. F., and Jackson, G. D. (2010). The core network in absence epilepsy – differences in cortical and thalamic BOLD response. Neurology 75, 904–911.
Cohen, I., Navarro, V., Clemenceau, S., Baulac, M., and Miles, R. (2002). On the origin of interictal activity in human temporal lobe epilepsy in vitro. Science 298, 1418–1421.
Cossart, R., Dinocourt, C., Hirsch, J. C., Merchan-Perez, A., De Felipe, J., Ben-Ari, Y., Esclapez, M., and Bernard, C. (2001). Dendritic but not somatic GABAergic inhibition is decreased in experimental epilepsy. Nat. Neurosci. 4, 52–62.
Daunizeau, J., David, O., and Stephan, K. E. (2010). Dynamic causal modelling: a critical review of the biophysical and statistical foundations. Neuroimage (in press).
Daunizeau, J., Kiebel, S. J., and Friston, K. J. (2009a). Dynamic causal modeling of distributed electromagnetic responses. Neuroimage 47, 590–601.
Daunizeau, J., Friston, K. J., and Kiebel, S. J. (2009b). Variational Bayesian identification and prediction of stochastic nonlinear dynamic causal models. Physica D 238, 2089–2118.
Daunizeau, J., Laufs, H., and Friston, K. J. (2009c). “EEG-fMRI information fusion: biophysics and data analysis,” in EEG-fMRI-Physiology, Technique and Applications, eds C. Mulert and L. Lemieux (Heidelberg: Springer), 511–522.
Daunizeau, J., Mattout, J., Clonda, D., Goulard, B., Benali, H., and Lina, J. M. (2006). Bayesian spatio-temporal approach for EEG source reconstruction: conciliating ECD and distributed models. IEEE Trans. Biomed. Eng. 53, 503–516.
David, O., Guillemain, I., Saillet, S., Reyt, S., Deransart, C., Segebarth, C., and Depaulis, A. (2008a). Identifying neural drivers with functional MRI: an electrophysiological validation. PLoS Biol. 6, 2683–2697. doi: 10.1371/journal.pbio.0060315
David, O., Wozniak, A., Minotti, L., and Kahane, P. (2008b). Precital short-term plasticity induced by 1 Hz stimulation. Neuroimage 39, 1633–1646.
de Curtis, M., and Avanzini, G. (2001). Interictal spikes in focal epileptogenesis. Prog. Neurobiol. 63, 541–567.
Deco, G., Jirsa, V. K., Robinson, P., Breakspear, M., and Friston K. J. (2008). The dynamic brain: from spiking neurons to neural masses and cortical fields. Plos. Comput. Biol. 4, e1000092. doi: 10.1371/journal.pcbi.1000092
Diehl, B., Tkach, J., Piao, Z., Ruggieri, P., LaPresto, E., Liu, P., Fisher, E., Bingaman, W., and Najm, I. (2010). Diffusion tensor imaging in patients with focal epilepsy due to cortical dysplasia in the temporo-occipital region: electro-clinico-pathological correlations. Epilepsy Res. 90, 178–187.
Douw, L., de Groot, M., van Dellen, E., Heimans, J. J., Ronner, H. E., Stam, C. J., and Reijneveld, J. C. (2010). ‘Functional connectivity’ is a sensitive predictor of epilepsy diagnosis after the first seizure. PLoS ONE 5, e10839. doi: 10.1371/journal.pone.0010839
Ebersole, J. S., and Hawes-Ebersole, S. (2007). Clinical application of dipole models in the localization of epileptiform activity. J. Clin. Neurophysiol. 24, 120–129.
Felleman, D. J., and Van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47.
Franaszczuk, P. J., and Bergey, G. K. (1998). Application of the directed transfer function method to mesial and lateral onset temporal lobe seizures. Brain Topogr. 11, 13–21.
Friston, K. (2009). Causal modelling and brain connectivity in functional magnetic resonance imaging. PLoS Biol. 7, e33. doi: 10.1371/journal.pbio.1000033
Friston, K. J., Harrison, L., and Penny, W. D. (2003). Dynamic causal modelling. Neuroimage 19, 1273–1302.
Friston, K. J., Li, B., Daunizeau, J., and Stephan K. E. (2011). Network discovery with DCM. Neuroimage (in press).
Friston, K. J., Mattout, J., Trujillo-Barreto, N. J., Ashburner, J., and Peeny, W. (2007). Variational free energy and the Laplace approximation. Neuroimage 34, 220–234.
Friston, K. J., Trujillo-Barreto, N. J., and Daunizeau, J. (2008). DEM: a variational treatment of dynamical systems. Neuroimage 42, 849–885.
Gotman, J. (1983). Measurement of small time differences between EEG channels: method and application to epileptic seizure propagation. Electroencephalogr. Clin. Neurophysiol. 56, 501–514.
Gotman, J., Grova, C., Bagshaw, A., Kobayashi, E., Aghakhani, Y., and Dubeau, F. (2005). Generalized epileptic discharges show thalamocortical activation and suspension of the default state of the brain. Proc. Natl. Acad. Sci. U.S.A. 102, 15236–15240.
Gregory, R. P., Oates, T., and Merry, R. T. (1993). Electroencephalogram epileptiform abnormalities in candidates for aircrew training. Electroencephalogr. Clin. Neurophysiol. 86, 75–77.
Guye, M., Bartolomei, F., and Ranjeva, J. P. (2008). Imaging structural and functional connectivity: towards a unified definition of human brain organization? Curr. Opin. Neurol. 21, 393–403.
Guye, M., Bettus, G., Bartolomei, F., and Cozzone, P. J. (2010). Graph theoretical analysis of structural and functional connectivity MRI in normal and pathological brain networks. MAGMA 23, 409–421.
Guye, M., Regis, J., Tamura, M., Wendling, F., McGonigal, A., Chauvel, P., and Bartolomei, F. (2006). The role of corticothalamic coupling in human temporal lobe epilepsy. Brain 129, 1917–1928.
Hamandi, K., Powell, H. W., Laufs, H., Symms, M. R., Barker, G. J., Parker, G. J., Lemieux, L., and Duncan, J. S. (2007). Combined EEG-fMRI and tractography to visualise propagation of epileptic activity. J. Neurol. Neurosurg. Psychiatry 79, 594–597.
Hamandi, K., Salek-Haddadi, A., Laufs, H., Liston, A., Friston, K., Fish, D. R., Duncan, J. S., and Lemieux, L. (2006). EEG-fMRI of idiopathic and secondarily generalized epilepsies. Neuroimage 31, 1700–1710.
Harrison, L., Penny, W. D., and Friston, K. (2003). Multivariate autoregressive modeling of fMRI time series. Neuroimage 19, 1477–1491.
Hughes, J. R. (2008). Progress in predicting seizure episodes with nonlinear methods. Epilepsy Behav. 12, 128–135.
Iadecola, C., and Nedergaard, M. (2007). Glial regulation of the cerebral microvasculature. Nat. Neurosci. 10, 1369–1376.
Jacobs, J., Levan, P., Châtillon, C. E., Olivier, A., Dubeau, F., and Gotman, J. (2009). High frequency oscillations in intracranial EEGs mark epileptogenicity rather than lesion type. Brain 132(Pt 4), 1022–1037.
Jansen, B. H., and Rit, V. G. (1995). Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biol. Cybern. 73, 357–366.
Jefferys, J. G. (1995). Nonsynaptic modulation of neuronal activity in the brain: electric currents and extracellular ions. Physiol. Rev. 75, 689–723.
Kaminski, M., Ding, M., Truccolo, W. A., and Bressler, S. L. (2001). Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol. Cybern. 85, 145–157.
Kaminski, M. J., and Blinowska, K. J. (1991). A new method of the description of the information flow in the brain structures. Biol. Cybern. 65, 203–210.
King, D., and Spencer, S. (1995). Invasive electroencephalography in mesial temporal lobe epilepsy. J. Clin. Neurophysiol. 12, 32–45.
Laufs, H., Hamandi, K., Salek-Haddadi, A., Kleinschmidt, A. K., Duncan, J. S., and Lemieux, L. (2007). Temporal Lobe Interictal Epileptic Discharges Affect Cerebral Activity in ‘‘Default Mode’’. Brain Regions. Human Brain Mapping 28, 1023–1032.
Le Van Quyen, M., Adam, C., Baulac, M., Martinerie, J., and Varela, F. J. (1998). Nonlinear interdependencies of EEG signals in human intracranially recorded temporal lobe seizures. Brain Res. 792, 24–40.
Li, B., Daunizeau, J., Stephan, K. E., Penny, W., and Friston K. J. (2011). Stochastic DCM and generalized filtering. Neuroimage (in press).
Lieberman, D. N., and Mody, I. (1999). Properties of single NMDA receptor channels in human dentate gyrus granule cells. J. Physiol. 518(Pt 1), 55–70.
Lin, F. H., Hara, K., Solo, V., Vangel, M., Belliveau, J. W., Stufflebeam, S. M., and Hamalainen, M. S. (2009). Dynamic Granger–Geweke causality modeling with application to interictal spike propagation. Hum. Brain Mapp. 30, 1877–1886.
Litt, B., and Lehnertz, K. (2002). Seizure prediction and the preseizure period. Curr. Opin. Neurol. 15, 173–177.
Lux, H. D., Heinemann, U., and Dietzel, I. (1986). Ionic changes and alterations in the size of the extracellular space during epileptic activity. Adv. Neurol. 44, 619–639.
Marsan, C. A., and Zivin, L. S. (1970). Factors related to the occurrence of typical paroxysmal abnormalities in the EEG records of epileptic patients. Epilepsia 11, 361–381.
Matsumoto, H., and Marsan, C. A. (1964). Cortical cellular phenomena in experimental epilepsy: interictal manifestations. Exp. Neurol. 9, 286–304.
McCormick, D. A., and Contreras, D. (2001). On the cellular and network bases of epileptic seizures. Annu. Rev. Physiol. 63, 815–846.
McIntosh, A. R., and Gonzalez-Lima, F. (1994). Structural equation modelling and its application to network analysis in functional brain imaging. Hum. Brain Mapp. 2, 2–22.
Meeren, H. K., Pijn, J. P., Van Luijtelaar, E. L., Coenen, A. M., and Lopes da Silva, F. H. (2002). Cortical focus drives widespread corticothalamic networks during spontaneous absence seizures in rats. J. Neurosci. 22, 1480–1495.
Monto, S., Vanhatalo, S., Holmes, M. D., and Palva, J. M. (2007). Epileptogenic neocortical networks are revealed by abnormal temporal dynamics in seizure-free subdural EEG. Cereb. Cortex 17, 1386–1393.
Morgan, R. J., and Soltesz, I. (2008). Nonrandom connectivity of the epileptic dentate gyrus predicts a major role for neuronal hubs in seizures. Proc. Natl. Acad. Sci. U.S.A. 105, 6179–6184.
Mormann, F., Andrzejak, R. G., Elger, C. E., and Lehnertz, K. (2007). Seizure prediction: the long and winding road. Brain 130(Pt 2), 314–333.
Mosher, J. C., Leahy, R. M., and Lewis, P. S. (1999). EEG and MEG: forward solutions for inverse methods. IEEE Trans Biomed Eng. 46, 245–259.
Obenaus, A., Esclapez, M., and Houser, C. R. (1993). Loss of glutamate decarboxylase mRNA-containing neurons in the rat dentate gyrus following pilocarpine-induced seizures. J. Neurosci. 13, 4470–4485.
Pearl, J. (2000). Causality: Models, Reasoning, and Inference. New York: Cambridge University Press.
Penny, W., Joao, M., Flandin, G., Daunizeau, J., Stephan, K. E., Friston, K. J., Schofield, T., and Leff, A. P. (2010). Comparing families of dynamic causal models. Plos Comput. Biol. 6, e1000709. doi: 10.1371/journal.pcbi.1000709
Penny, W. D., Stephan, K. E., Mechelli, A., and Friston, K. J. (2004). Comparing dynamic causal models. Neuroimage 22, 1157–1172.
Pijn, J. P., Velis, D. N., and Lopes da Silva, F. H. (1992). Measurement of interhemispheric time differences in generalised spike-and-wave. Electroencephalogr. Clin. Neurophysiol. 83, 169–171.
Pijn, J. P., Vijn, P. C., Lopes da Silva, F. H., Van Ende, B. W., and Blanes, W. (1990). Localization of epileptogenic foci using a new signal analytical approach. Neurophysiol. Clin. 20, 1–11.
Pinto, D. J., Patrick, S. L., Huang, W. C., and Connors, B. W. (2005). Initiation, propagation, and termination of epileptiform activity in rodent neocortex in vitro involve distinct mechanisms. 25, 8131–8140.
Porter, B. E., Cui, X. N., and Brooks-Kayal, A. R. (2006). Status epilepticus differentially alters AMPA and kainate receptor subunit expression in mature and immature dentate granule neurons. Eur. J. Neurosci. 23, 2857–2863.
Prince, D. A., and Wilder, B. J. (1967). Control mechanisms in cortical epileptogenic foci. “Surround” inhibition. Arch Neurol. 16, 194–202.
Quiroga, R. Q., Arnhold, J., and Grassberger, P. (2000). Learning driver-response relationships from synchronization patterns. Phys. Rev. E 61, 5142–5148.
Quiroga, R. Q., Kraskov, A., Kreuz, T., and Grassberge, P. (2002). Performance of different synchronization measures in real data: a case study on electroencephalographic signals. Phys. Rev. E 65, 041903.
Raichle, M. E., MacLeod, A. M., Snyder, A. Z., Powers, W. J., Gusnard, D. A., and Shulman, G. L. (2001). A default mode of brain function. Proc. Natl. Acad. Sci. U.S.A. 98, 676–682.
Riera, J. J., Schousboe, A., Waagepetersen, H. S., Howarth, C., and Hyder, F. (2008). The micro-architecture of the cerebral cortex: functional neuroimaging models and metabolism. Neuroimage 40, 1436–1459.
Riera, J. J., Wan, X., Jimenez, J. C., and Kawashima, R. (2006). Nonlinear local electrovascular coupling. I: a theoretical model. Hum. Brain Mapp. 27, 896–914.
Roebroeck, A., Formisano, E., Goebel, R. (2005). Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage 25, 230–242.
Roopun, A. K., Simonotto, J. D., Pierce, M. L., Jenkins, A., Nicholson, C., Schofield, I. S., Whittaker, R. G., Kaiser, M., Whittington, M. A., Traub, R. D., and Cunningham, M. O. (2010). A nonsynaptic mechanism underlying interictal discharges in human epileptic neocortex. Proc. Natl. Acad. Sci. U.S.A. 107, 338–343.
Rosa, M. J., Daunizeau, J., Friston, K. J. (2010). EEG-fMRI integration: a critical review of biophysical modelling and data analysis approaches. J. Integr. Neurosci. 9, 453–476.
Schevon, C. A., Trevelyan, A. J., Schroeder, C. E., Goodman, R. R., McKhann, G. Jr., and Emerson, R. G. (2009). Spatial characterization of interictal high frequency oscillations in epileptic neocortex. Brain 132(Pt 11), 3047–3059.
Schoffelen, J. M., and Gross, J. (2009). Source connectivity analysis with MEG and EEG. Hum. Brain Mapp. 30, 1857–1865.
Shah, M. M., Anderson, A. E., Leung, V., Lin, X., and Johnston, D. (2004). Seizure-induced plasticity of h channels in entorhinal cortical layer III pyramidal neurons. Neuron 44, 495–508.
Shiraishi, H., Ahlfors, S. P., Stufflebeam, S. M., Takano, K., Okajima, M., Knake, S., Hatanaka, K., Kohsaka, S., Saitoh, S., Dale, A. M., and Halgren, E. (2005a). Application of magnetoencephalography in epilepsy patients with widespread spike or slow-wave activity. Epilepsia 46, 1264–1272.
Shiraishi, H., Stufflebeam, S. M., Knake, S., Ahlfors, S. P., Sudo, A., Asahina, N., Egawa, K., Hatanaka, K., Kohsaka, S., Saitoh, S., Grant, P. E., Dale, A. M., and Halgren, E. (2005b). Dynamic statistical parametric mapping for analyzing the magnetoencephalographic epileptiform activity in patients with epilepsy. J. Child Neurol. 20, 363–369.
Shmuel, A., Augath, M., Oeltermann, A., and Logothetis, N. K. (2006). Negative functional MRI response correlates with decreases in neuronal activity in monkey visual area V1. Nat Neurosci. 9, 569–577.
Sotero, R. C., and Trujillo-Barreto, N. J. (2007). Biophysical model for integrating neuronal activity, EEG, fMRI and metabolism. Neuroimage 39, 290–309.
Soula, H., and Chow, C. C. (2007). Stochastic dynamics of a finite size spiking neural network. Neural Comput. 19, 3262–3292.
Stephan, K. E., Harrison, L. M., Penny, W. D., and Friston, K. J. (2004). Biophysical models of fMRI responses. Curr. Opin. Neurobiol. 14, 629–635.
Stephan, K. E., Kasper, L., Harrison, L., Daunizeau, J., Den Ouden, H., Breakspear, M., and Friston K. J. (2008). Nonlinear dynamic causal models for fMRI. Neuroimage 42, 649–662.
Stephan, K. E., Penny, W. D., Daunizeau, J., Moran, R., and Friston K. J. (2009). Bayesian model comparison for group studies. Neuroimage 46, 1004–1017.
Su, H., Sochivko, D., Becker, A., Chen, J., Jiang, Y., Yaari, Y., and Beck, H. (2002). Upregulation of a T-type Ca2+ channel causes a long-lasting modification of neuronal firing mode after status epilepticus. J. Neurosci. 22, 3645–3655.
Takano, T., Tian, G. F., Peng, W., Lou, N., Libionka, W., Han, X., and Nedergaard, M. (2006). Astrocyte-mediated control of cerebral blood flow. Nat. Neurosci. 9, 260–267.
Tanaka, N., Cole, A. J., von Pechmann, D., Wakeman, D. G., Hamalainen, M. S., Liu, H., Madsen, J. R., Bourgeois, B. F., and Stufflebeam, S. M. (2009). Dynamic statistical parametric mapping for analyzing ictal magnetoencephalographic spikes in patients with intractable frontal lobe epilepsy. Epilepsy Res. 85, 279–286.
Tao, J. X., Baldwin, M., Hawes-Ebersole, S., and Ebersole, J. S. (2007a). Cortical substrates of scalp EEG epileptiform discharges. J. Clin. Neurophysiol. 24, 96–100.
Tao, J. X., Baldwin, M., Ray, A., Hawes-Ebersole, S., and Ebersole, J. S. (2007b). The impact of cerebral source area and synchrony on recording scalp electroencephalography ictal patterns. Epilepsia 48, 2167–2176.
Tao, J. X., Ray, A., Hawes-Ebersole, S., and Ebersole, J. S. (2005). Intracranial EEG substrates of scalp EEG interictal spikes. Epilepsia 46, 669–676.
Tauck, D. L., and Nadler, J. V. (1985). Evidence of functional mossy fiber sprouting in hippocampal formation of kainic acid-treated rats. J. Neurosci. 5, 1016–1022.
Tian, G. F., Azmi, H., Takano, T., Xu, Q., Peng, W., Lin, J., Oberheim, N., Lou, N., Wang, X., Zielke, H. R., Kang, J., and Nedergaard, M. (2005). An astrocytic basis of epilepsy. Nat Med. 11, 973–981.
Traub, R. D., Whittington, M. A., Buhl, E. H., LeBeau, F. E., Bibbig, A., Boyd, S., Cross, H., and Baldeweg, T. (2001). A possible role for gap junctions in generation of very fast EEG oscillations preceding the onset of, and perhaps initiating, seizures. Epilepsia 42, 153–170.
Trevelyan, A. J. (2009). The direct relationship between inhibitory currents and local field potentials. J. Neurosci. 29, 15299–15307.
Trevelyan, A. J., Sussillo, D., and Yuste, R. (2007a). Feedforward inhibition contributes to the control of epileptiform propagation speed. J. Neurosci. 27, 3383–3387.
Trevelyan, A. J., Baldeweg, T., van Drongelen, W., Yuste, R., and Whittington, M. (2007b). The source of after discharge activity in neocortical tonic-clonic epilepsy. J. Neurosci. 27, 13513–13519.
Trevelyan, A. J., Sussillo, D., Watson, B. O., and Yuste, R. (2006). Modular propagation of epileptiform activity: evidence for an inhibitory veto in neocortex. J. Neurosci. 26, 12447–12455.
Vaudano, A. E., Laufs, H., Kiebel, S. J., Carmichael, D. W., Hamandi, K., Guye, M., Thornton, R., Rodionov, R., Friston, K. J., Duncan, J. S., and Lemieux, L. (2009). Causal hierarchy within the thalamo-cortical network in spike and wave discharges. PLoS ONE 4, e6475. doi: 10.1371/journal.pone.0006475
Vulliemoz, S., Carmichael, D. W., Rosenkranz, K., Diehl, B., Rodionov, R., Walker, M. C., McEvoy, A. W., and Lemieux, L. (2010). Simultaneous intracranial EEG and fMRI of interictal epileptic discharges in humans. Neuroimage 54, 182–190.
Waites, A. B., Briellmann, R. S., Saling, M. M., Abbott, D. F., and Jackson, G. D. (2006). Functional connectivity networks are disrupted in left temporal lobe epilepsy. Ann. Neurol. 59, 335–343.
Walker, M., Chan, D., and Thom, M. (2007). “Hippocampus and human disease,” in The Hippocampus Book, eds P. Andersen, R. Morris, D. G. Amaral, T. Bliss, and J. O’Keefe (Oxford: Oxford University Press), 769–812.
Walter, D. O. (1963). Spectral analysis for electroencephalograms: mathematical determination of neurophysiological relationships from records of limited duration. Exp. Neurol. 8, 155–181.
Wendling, F. (2008). Computational models of epileptic activity: a bridge between observation and pathophysiological interpretation. Expert Rev. Neurother. 8, 889–896.
Wendling, F., Ansari-Asl, K., Bartolomei, F., and Senhadji, L. (2009a). From EEG signals to brain connectivity: a model-based evaluation of interdependence measures. J. Neurosci. Methods 183, 9–18.
Wendling, F., Bartolomei, F., and Senhadji, L. (2009b). Spatial analysis of intracerebral electroencephalographic signals in the time and frequency domain: identification of epileptogenic networks in partial epilepsy. Philos. Trans. Math. Phys. Eng. Sci. 367, 297–316.
Wendling, F., Bartolomei, F., Bellanger, J. J., and Chauvel, P. (2001). Interpretation of interdependencies in epileptic signals using a macroscopic physiological model of the EEG. Clin. Neurophysiol. 112, 1201–1218.
Keywords: epilepsy, connectivity, neuroimaging, EEG, modeling
Citation: Lemieux L, Daunizeau J and Walker MC (2011) Concepts of connectivity and human epileptic activity. Front. Syst. Neurosci. 5:12. doi: 10.3389/fnsys.2011.00012
Received: 05 August 2010;
Accepted: 24 February 2011;
Published online: 22 March 2011.
Edited by:
Silvina G. Horovitz, National Institutes of Health, USAReviewed by:
Robert Turner, Max Planck Institute for Human Cognitive and Brain Sciences, GermanyHeiko J. Luhmann, Institute of Physiology and Pathophysiology, Germany
Copyright: © 2011 Lemieux, Daunizeau and Walker. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Louis Lemieux, Department of Clinical and Experimental Epilepsy, University College London Institute of Neurology, Queen Square, London WC1N 3BG, UK.e-mail:bC5sZW1pZXV4QGlvbi51Y2wuYWMudWs=


